А. В. Соловьев управленческие решения учебное пособие

Вид материала

Учебное пособие

Содержание 10.Модели и методы принятия решений. Методы моделирования . Модели теории игр. Подробнее Теория игр Стохастические игры Игры с полной информацией Важное замечание. Модели теории очередей или оптимального обслуживания. Разработка сценариев Некоторые закономерности образования очередей Что же такое задержка обработки вызова Модели управления запасами. Пример компании Тойота Статистический контроль процессов (SPC) Комплексное управление качеством (TQM) Реинжиниринг бизнес процессов (RBP) Тотальное управление деньгами (TCM) Модели линейного программирования. Подробнее. Для более глубокого изучения

Подобный материал:

• Учебно-методическое пособие по дисциплине Управленческие решения Ярославль, 2011, 991.2kb.
• Г. В. Плеханова (технический университет) А. С. Соловьев, А. Е. Козярук история развития, 1301.37kb.
• Учебное пособие для студентов специальности 061100 «Менеджмент организации», 1784.91kb.
• Тематика курсовых работ по дисциплине «Управленческие решения», 14.8kb.
• Учебно-методический комплекс по дисциплине управленческие решения Специальность, 320.93kb.
• А. В. Соловьев теория организаций учебное пособие, 2585.23kb.
• Соловьев А. В. Исследование систем управления учебное пособие Москва 2010 содержание, 3153.37kb.
• Учебное пособие 2006 удк 65. 01 (075. 8) Разработка управленческого решения, 1134.62kb.
• Учебное пособие Житомир 2001 удк 33: 007. Основы экономической кибернетики. Учебное, 3745.06kb.
• Учебное пособие, 2003 г. Учебное пособие разработано ведущим специалистом учебно-методического, 783.58kb.

10.Модели и методы принятия решений.

В процессе разрешения сложных проблем с целью усиления способности менеджеров к принятию обоснованных и объективных решений могут применяться различные научные методы их разработки и оптимизации, которые принято делить на два основных класса: методы моделирования и методы экспертных оценок.

Методы моделирования .

Методы моделирования (называемые также методами исследования операций) базируются на использовании математических моделей для решения наиболее часто встречающихся управленческих задач.

Разработка и оптимизация решения конкретной проблемы методами моделирования – довольно сложная процедура, которая может быть представлена последовательностью основных этапов:

1. Постановка задачи;
   
2. Определение критерия эффективности анализируемой операции;
   
3. Количественное измерение факторов, влияющих на исследуемую операцию;
   
4. Построение математической модели изучаемого объекта (операции);
   
5. Количественное решение модели и нахождение оптимального решения;
   
6. Проверка адекватности модели и найденного решения анализируемой ситуации;
   
7. Корректировка и обновление модели.
   

Количество всевозможных конкретных моделей почти так же велико, как и число проблем, для решения которых они разработаны.

Наиболее распространённые типы моделей: модели теории игр; модели теории очередей или оптимального обслуживания; модели управления запасами; модели линейного программирования.

Модели теории игр.

Большинство хозяйственных операций можно рассматривать как действия, совершаемые в условиях противодействия.

К противодействиям следует относить такие факторы, как авария, пожар, кража, забастовка, нарушение договорных обязательств и т.п. Однако наиболее массовый случай противодействия – конкуренция. Поэтому одним из важнейших условий, от которого зависит успех организации, является конкурентоспособность. Очевидно, что возможность прогнозировать действия конкурентов – существенное преимущество для любой коммерческой организации. Принимая решение, следует выбирать альтернативу, позволяющую уменьшить степень противодействия, что в свою очередь снизит степень риска. Такую возможность предоставляет менеджеру теория игр, математические модели которой побуждают анализировать возможные альтернативы своих действий с учётом возможных ответных действий конкурентов.

Первоначально разработанные для военно-стратегических целей модели теории игр применяются в бизнесе для прогнозирования реакции конкурентов на принимаемые решения, например, на изменение цен, выпуск новых видов товаров и услуг, выход на новые сегменты рынка и т.п.

Так, принимая решение об изменении уровня цен на свои товары, руководство фирмы должно прогнозировать реакцию и возможные ответные действия основных конкурентов. И если с помощью модели теории игр будет установлено, что, например, при повышении цены конкуренты не сделают того же, организация, чтобы не попасть в невыгодное положение, должна отказаться от этой альтернативы и поискать другое решение проблемы.

Следует, однако, отметить, что используются эти модели довольно редко, так как слишком упрощены по сравнению с реальными экономическими ситуациями, настолько изменчивыми, что полученные прогнозы бывают не слишком достоверны.

Подробнее

Теория игр

Теория игр это один из разделов современной математики, в котором изучаются проблемы, связанные с принятием решений в условиях нехватки информации.

Свое название этот раздел получил потому что именно в большинстве игр с несколькими участниками, нам приходится принимать решение (делать ход), не зная точно, как поступит противник.

В этой статье мы рассмотрим следующую проблему: как принимать решение, если кто-то или что-то вам противодействует. Вот несколько примеров подобной ситуации:


Игра в шахматы или шашки. Участвуют два игрока, каждый из которых стремится нанести урон своему противнику.


Принятие производственного плана предприятия. Здесь также есть выбор и также есть противодействие, со стороны конкурентов и со стороны потребителей продукции, которые могут купить продукцию, а могут и не купить.


Принятие решения о дате и способе восхождения на горную вершину. Здесь противодействующая сторона погода, которая может помочь, а может и помешать.


В приведённых выше примерах есть общее и есть различия. Общего здесь то, что приняв то или иное решение, мы ожидаем определённый выигрыш и какой-то ущерб. Выигрыш нам нужен максимально большой, а ущерб минимально возможный. И всегда остается риск ошибки.

Различие в этих примерах заключается в разной степени осведомленности. В шахматах каждый игрок обладает всей полнотой информации. Вся информация о позиции доступна каждому из них, и ни один из игроков не знает о расположении фигур больше другого. И если кто-то выиграет, а кто-то проиграет, то только потому, что умение играть у них различное. Но, повторимся, информацией они обладают одинаковой. Такие игры называются играми с полной информацией.

Таких игр достаточно много. Но есть и другие игры в которых часть информации скрыта, как например в карточных играх, в которых противники не видят карт друг друга. Или, есть игры в которых какие-то параметры хода определяются бросанием кубика (например нарды), то есть появляется элемент случайности. Элемент случайности есть и в карточных играх. Здесь он определяется случайной раздачей карт. Такие игры называются по разному. Например, есть красивый термин «стохастические игры». Мы в дальнейшем также будем пользоваться этим термином.

Стохастические игры характеризуются наличием случайности и необходимостью принятия решения в отсутствие информации о игровой ситуации и возможных действиях противника.

Необходимо заметить, что игры с полной информацией можно рассматривать, как стохастические если учесть, что принимающий решение, реально редко в состоянии действительно полно проанализировать ситуацию. А проанализировать игровую ситуацию от начала игры до самого конца, в принципе возможно только в самых примитивных играх, например крестики – нолики на доске 3х3.

Но это если анализ ведёт человек. Если же анализ игры ведёт компьютер, чьи счетные возможности существенно выше, то для него игры с полной информацией и стохастические отличаются очень существенно.


В чем состоит задача игрока


Просто говоря, задача игрока выиграть. Но не всегда это можно сформулировать так однозначно. Например, нельзя стремится покорить горную вершину ценой гибели альпинистов, например нельзя стремится выиграть сражение ценой гибели значительной части армии и т.д.

То есть очень и очень часто понятие победы в игре звучит существенно сложнее. Приведем несколько возможных целей:

1. Добиться ситуации которая означает выигрыш. В шахматах это мат королю противника.
   
2. Получить максимально возможную выгоду, например максимальную прибыль в торговой операции.
   
3. Обеспечить себе минимально возможный ущерб, минимальные затраты физической энергии при переноске грузов.
   

Для реализации поставленной окончательной цели игрок ставит себе цели промежуточные, которые позволят ему достигнуть целей окончательных. Это, например, провести шашку в дамки, Срубить ферзя противника и т.д. В целом цели игрока можно разделить на две большие группы: стратегические цели, ставящиеся на длительное время (большое количество ходов или других игровых действий), тактические цели которые игрок стремится реализовать за небольшое количество ходов.

Отсюда ясно, что теория игр должна дать нам методы помогающие разрабатывать стратегии поведения игрока и тактические приёмы помогающие в реализации данных стратегий. Игры с полной информацией и стохастические игры отличаются очень сильно поэтому в дальнейшем мы будем рассматривать их по отдельности.


Игры с полной информацией


Оценочная функция

Прежде всего нам необходимо дать точные определения что такое хорошая позиция игрока и что такое плохая позиция. Ясно, что выбор стратегии должен производится таким образом, чтобы реализация этой стратегии приводила к хорошей позиции.

Любой игрок, владея даже только основами игры, принимает решение о своем ходе не случайным образом. Он знает некоторые правила позволяющие ему оценивать качество позиции. Например, русские шашки, если в результате хода отдав одну шашку можно взять две шашки противника, то это хорошо, а если будут потери и ничего взамен то это плохо. Таким образом количество шашек на доске это фактор качества позиции. Чем своих шашек больше, тем лучше, а чем больше шашек у противника тем хуже.

Конечно, это не единственный фактор. Например, важное значение имеет количество дамок. Можно разработать и другие факторы качества игры. Чем игрок опытнее, тем большее количество факторов качества ему известно.

Из этого же примера видно, что факторы по своей значимости неодинаковы. Одна единственная дамка может полностью компенсировать недостаток в обычных шашках. Поэтому для каждого фактора необходимо ещё установить его важность в виде числа которое называют весом. Вес не единственная характеристика фактора качества. Существует ещё величина фактора. Например, пусть мы выделили в качестве фактора наличие дамки. Дамок может быть несколько а следовательно вес фактора необходимо умножить на их количество, чтобы оценить влияние данного фактора на игру.


Важное замечание. Необходимо очень хорошо понять, что не существует общего способа выявить все факторы влияющие на игру и определить их веса. Это определяется только опытом игрока и его личными знаниями о данной игре.

Более того, любая система факторов будет только приблизительно правильной, так как она не учитывает взаимного влияния факторов и их зависимости от хода игры. Например, пешка в шахматах имеет различный вес в зависимости от того, стоит она на второй горизонтали (то есть на своём месте) или на предпоследней (то есть может следующим ходом превратиться в ферзя) и т.д.

Но все эти вопросы мы сейчас рассматривать не будем. Мы займемся ими позже.


Пусть у нас есть система факторов, определены их веса и количества, как вычислить качество позиции? Таким образом мы приходим к понятию оценочной функции. Введём обозначения. Пусть a_i - это фактор с номером i p_i – вес данного фактора. Тогда величина P называется оценочной функцией и она равна следующему выражению

P = p₁a₁ + p₂a₂ +…..+p_na_n


Чем значение этой функции больше, тем позиция соответствующая данной функции лучше. Все что теперь должен сделать игрок – это просчитать оценочную функцию для всех возможных ходов и выяснить который из них даёт наилучший результат.

Дерево перебора.


Правда необходимо заметить, что перебор всех возможных вариантов только на один ход вперёд даёт не слишком много информации. Ход выгодный сейчас, может привести к невыгодной позиции в некотором будущем. Любой игрок знает, что считать варианты игры надо на несколько ходов вперёд, чем глубже тем лучше, конечно с учетом личных способностей к таким расчётам. Для просчёта различных вариантов игры строится специальная структура называемая деревом вариантов или деревом перебора. Построим пример и рассмотрим как связываются понятия дерева перебора и оценочная функция.

Пусть дана двоичная игра. Неважно в чём заключаются её правила, важно только то, что в каждой ситуации любой игрок, чья очередь хода имеет только два варианта ответа. Тогда, любую часть игры начиная с некоторой позиции можно представить в виде дерева, вершины которого это игровые ситуации, а дуги соединяющие вершины это варианты хода. Вот как это выглядит:

Решение принимает первый

игрок



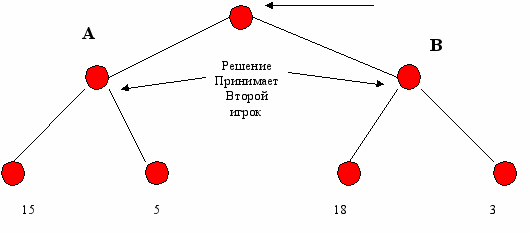
Это дерево перебора вариантов на два хода вперёд, один свой и один ход противника. Числа подписанные под кружками на самом нижнем уровне это значения оценочной функции в этих позициях. Заметим, что значения оценочной функции в промежуточной позиции нас не интересуют. Это от того, что цель анализа - поиск хорошей конечной позиции.

Первый игрок может принять решение выбрать ход А и он может принять решение выбрать ход В. Если он выберет ход А, то он может надеется получить в качестве выигрыша 15 очков. Если же он выберет ход В, то его надежда составит 18 очков. Это предварительное рассуждение говорит о том, что первый игрок, тот который ведёт анализ должен выбрать ход В. Однако необходимо посмотреть насколько оправданы его надежды.


Метод минимакса


Проблема первого игрока в том, что он не один, ему противостоит второй игрок и не учитывать его возможные действия нельзя. Надо что-то предположить о действиях второго игрока и мы предположим, что он будет играть наиболее сильным образом. Другими словами можно сказать, что второй игрок будет стремится не дать первому игроку максимального выигрыша.

Вернемся к дереву нашей двоичной игры. Предположим, первый игрок выбрал вариант А. Теперь очередь выбора за вторым. Так как он не должен давать первому сильнейшей позиции, то его ход будет в позицию с оценочной функцией = 5. В случае же выбора первым игроком хода В, второй игрок должен выбрать ход ведущий в позицию с оценочной функцией 3.

Из этих рассуждений ясно, что на самом деле второй игрок может рассчитывать только на два варианта 3 или 5. Это худшие из возможных и из них он может выбрать лучший. Поэтому метод такого выбора и называется минимаксом (из минимальных максимальные). Наилучший вариант 5 поэтому первый игрок должен выбрать ход А, что противоречит предыдущему простейшему рассуждению.


Заключение. Таким образом, построение алгоритма игры заключается в решении двух проблем: как построить оценочную функцию правильно описывающую игру и как построить и просмотреть дерево вариантов.

Модели теории очередей или оптимального обслуживания.

Они используются для нахождения оптимального числа каналов обслуживания при определённом уровне потребности в них. К ситуациям, в которых такие модели могут быть полезны относятся, например, определение количества телефонных линий, необходимых для ответов на звонки клиентов; троллейбусов на маршруте, необходимых, чтобы на остановках не скапливались большие очереди; операционистов в банке, чтобы клиенты не ждали, пока ими смогут заняться и т.п. Проблема здесь заключается в том, что дополнительные каналы обслуживания (больше телефонных линий, троллейбусов или банковских служащих) требуют дополнительных ресурсов, а их загрузка неравномерна (избыточная пропускная способность в одни периоды времени и появление очередей – в другие). Следовательно, нужно найти такое решение, которое позволяет сбалансировать дополнительные расходы на расширение каналов обслуживания и потери от их недостатка. Модели теории очередей как раз и служат инструментом нахождения такого оптимального решения.


Подробнее

Теория и практика математического описания очередей вызовов

При определении оптимального уровня обслуживания и формировании штата call-центров очень важно четко представлять себе основные законы “поведения” очередей вызовов. Их знание позволит вам определять реалисти-чные целевые технологические параметры обработки вызовов, планировать работу call-центра и оперативно изменять алгоритмы его работы в соответствии с изменяющимися условиями.

Математические модели “поведения” очередей вызовов позволяют выявить динамику взаимодействия ключевых технологических параметров работы call-центра, таких, как число операторов, загрузка каналов связи, значение задержки ответа на вызов. Все эти знания являются необходимым условием для формирования стратегии развития call-центра и выработки системы операционных решений.

Разработка сценариев

В call-центрах для определения необходимого числа операторов и оценки основных параметров очередей на обслуживание пользуются специальными калькуляторами очередей, которые рассчитывают нагрузку call-центра с помощью широко известной

C-формулы Эрланга, учитывающей случайный характер поступления вызовов, или же посредством программы, моделирующей процесс образования очередей. Прогонка различных сценариев работы call-центра с применением такой программы — хороший способ изучения поведения очередей для выработки компромиссного решения по использованию ресурсов call-центра.

Наиболее адекватный уровень точности расчета основных параметров call-центра в большинстве случаев достигается при использовании получасовых временных интервалов. При этом все сценарии работы персонала call-центра оцениваются с помощью следующих четырех исходных параметров:

Среднее время разговора (в секундах). В программу вводится предполагаемое среднее время разговора для анализируемых получасовых интервалов.

Среднее время обработки вызова (в секундах). Вводится предполагаемое среднее время обработки вызова для анализируемых получасовых интервалов.

Число вызовов. Вводится предполагаемое число вызовов для анализируемых получасовых интервалов.

Время ожидания в очереди, определяющее уровень обслуживания (в секундах). Например, если ставится задача по обеспечению такого уровня обслуживания, при котором операторы осуществляют обработку 90% вызовов в интервале не более 20 с, в программу вводится параметр “20 с”.

На основе этого набора исходных данных осуществляется расчет всех контрольных производственных параметров call-центра при варьировании числа задействованных операторов (табл. 1). Ниже дано подробное объяснение каждого из этих параметров:

Число операторов, требующихся для обработки очередей и доступных для обработки вызовов. В данном случае 34 оператора будут обеспечивать уровень обслуживания, формулируемый как “82% вызовов должны быть обработаны в течение 20 с”.

P(O): вероятность задержки обработки вызова (для строгой формальной формулировки — вероятность задержки большей, чем 0 с). Другими словами, вероятность того, что вызов попадет в очередь ожидания. В данном примере примерно 29% вызовов будут обрабатываться с задержкой. Это означает, что 71% клиентов будут обслуживаться без задержки, т. е. немедленно соединяться с оператором.

ASA (Average Speed of Answer): среднее время ожидания ответа, или условное среднее время ожидания в очереди. В приведенном в табл. 1 примере call-центр с 34 операторами имеет параметр ASA, составляющий 13 с. ASA представляет собой среднюю задержку всех вызовов, включая и те, которые были обработаны без задержки. Обратите внимание, что интервал времени в 13 с, рассчитанный математически в качестве некоей средней величины, не является типовым, поскольку большинство вызовов обрабатываются быстрее, а некоторые ждут значительно дольше. Поэтому параметром ASA часто пользуются не совсем корректно, без четкого понимания механизма усреднения.

DLYDLY (Average Delay of Delayed Calls): среднее значение задержки всех задержанных вызовов, или реальное среднее время ожидания в очереди, т. е. среднее значение задержки только тех вызовов, которые действительно были задержаны. В приведенном примере — это 43 с.

Q1: среднее число вызовов в очереди в любое время суток, включая то время, когда очереди в действительности нет. Q1 включает в себя все вызовы, в том числе и те, что не попадают в очереди (значения Q1 очень полезны при сравнении их с параметрами Q2 в следующей колонке таблицы).

Q2: среднее число вызовов в очереди на обслуживание, когда все операторы заняты, или реальная средняя длина очереди. В нашем примере с 34 операторами мы предполагаем, что при образовании очереди в ней будут находиться в среднем 6 вызовов. Этот параметр очень полезен при мониторинге работы call-центра в реальном времени, а также при определении параметров, описывающих условия перегрузки.

SL (Service Level): уровень обслуживания. Это процент вызовов, которые должны быть обработаны в заданное время.

OCC (Percent Agent Occupancy): занятость оператора — процент рабочего времени, которое он затрачивает на обработку вызовов, включая время разговора и время обработки вызова после звонка. Остальное рабочее время — это время когда оператор доступен, т. е. находится в состоянии ожидания вызовов.

TKLD. Данный параметр характеризует нагрузку на каналы связи call-центра в Эрлангах и вычисляется как время разговора + условное среднее время ожидания в очереди, умноженные на число вызовов в течение часа. (Реальный трафик, приходящийся на каналы связи в получасовые интервалы времени, составляет половину от тех значений, которые приведены в табл. 1)

Некоторые закономерности образования очередей

При повышении уровня обслуживания занятость уменьшается. Действительно, при улучшении обслуживания занятость должна уменьшиться, поскольку время ожидания между обрабатываемыми вызовами увеличивается. При высокой занятости операторы будут обрабатывать один вызов за другим с маленьким промежутком между вызовами или вообще без него. Вызовы начинают накапливаться в очереди, и уровень обслуживания падает. В самом худшем случае при 100%-ной занятости уровень обслуживания очень низок, так как все абоненты вынуждены тратить некоторое время на ожидание в очереди на обслуживание.

Закон уменьшения полезного эффекта. При низком уровне обслуживания добавление одного или двух операторов значительно улучшает ситуацию. Однако при дальнейшем увеличении штата операторов вы обнаружите, что полезный эффект от этого начинает снижаться. Руководители call-центров, которые стремятся поднять уровень обслуживания, могут обнаружить, что для существенного улучшения дел им потребуется не так уж много ресурсов. С другой стороны, если вы хотите стать лучшими из лучших, вам придется пойти на значительные расходы, связанные с наймом операторов.

При увеличении числа операторов параметр ASA уменьшается. Те, кто хоть раз ожидал обслуживания в очереди, прекрасно понимают эту закономерность: очередь тем меньше, чем больше прилавков или продавцов.

По мере увеличения числа операторов загрузка каналов связи уменьшается. Если для обработки некоторого объема вызовов привлекать меньше операторов, это повлечет за собой увеличение нагрузки на каналы связи, пропорциональное уменьшению времени задержки обработки вызовов. Прямые расходы на поддержку процесса ожидания в очереди называются стоимостью задержки обслуживания. Она складывается из ежедневных расходов на оплату каналов связи, которые задействуются при поддержке вызова на линии в процессе его нахождения в очереди.

Что же такое задержка обработки вызова

Хороший вопрос для любого менеджера, занимающегося качеством обслуживания: “А что происходит с вызовом, на который операторы не отвечают в течение Y с?” Ответить на этот вопрос очень помогают программы, вычисляющие возможные задержки с обработкой вызовов.

В приведенном выше примере 34 оператора обеспечивают уровень обслуживания, гарантирующий прием 82% вызовов в течение 20 с. 65 абонентов будут ожидать обслуживания 5 с и более. Через 5 с семеро из этой очереди дождутся ответа оператора, в следующие 5 с — еще шесть и т. д. (табл. 2). При таком уровне обслуживания один звонящий может ожидать ответа в течение 3 мин.

Обратите внимание на важный момент: из-за случайного характера поступления вызовов у разных абонентов будет разная история дозвона, даже если они звонят в один и тот же 30-минутный интервал времени и даже если call-центр обеспечивает заданный уровень обслуживания. Некоторые сall-центры экспериментируют, пытаясь установить два уровня обслуживания, когда, например, 80% вызовов обрабатываются в течение 20 с, а остальные — в течение 60 с, но это невозможно, поскольку “80% за 20 с” и “100% за 60 с” принципиально разные уровни обслуживания. При нахождении компромиссного решения вам все равно придется ответить на один ключевой вопрос: какой самый плохой сценарий обработки вызовов согласна допустить ваша организация?

***

Демонстрация приведенных выше основных компромиссных решений является очень полезной при общении с менеджерами, утверждающими бюджеты call-центров. Каким будет ваш уровень обслуживания, если уменьшить штат операторов на пять человек? что нужно сделать, чтобы достичь уровня обслуживания 90% вызовов за 20 с? почему вы не можете обеспечить уровень обслуживания в “80% за 20 с” при занятости операторов, равной 95%? Эти вопросы обязательно коснутся и вас, и, чтобы получить ответы на них, нужно иметь специальные знания..

Модели управления запасами.

Любая организация должна поддерживать некоторый уровень запасов своих ресурсов, чтобы избежать простоев или перерывов в технологических процессах и сбыте товаров или услуг. Для производственной фирмы необходимы определённые запасы материалов, комплектующих изделий, готовой продукции, для банка – денежной наличности, для больницы – лекарств, инструментов и т.д. Поддержание высокого уровня запасов повышает надёжность функционирования организации и избавляет от потерь, связанных с их нехваткой. С другой стороны, создание запасов требует дополнительных издержек на хранение, складирование, транспортировку, страхование и т.п. Кроме того, избыточные запасы связывают оборотные средства и препятствуют прибыльному инвестированию капитала, например, в ценные бумаги или банковские депозиты.

Модели управления запасами позволяют найти оптимальное решение, т.е. такое решение, при котором уровень запаса, который минимизирует издержки на его создание и поддержание при заданном уровне непрерывности производственных процессов.


Подробнее


Одним из наиболее существенных факторов, определяющих эффективность операционных расходов, а также уровень организации финансового менеджмента для многих промышленных и торговых компаний, является размер товарных запасов. С позиции финансиста идеальным состоянием для ведения бизнеса должно быть отсутствие каких-либо товарных запасов при полном обеспечении производственного процесса всеми необходимыми компонентами. Сегодня, в силу ряда объективных причин, для большинства предприятий добиться полного отсутствия товарных "излишеств" не представляется возможным. И если от запасов нельзя избавиться, то ими необходимо управлять.

Запасы и конкуренция. Соперничество двух крупнейших мировых экономических систем - США и Японии в середине 80-х годов характеризовалось явным превосходством последней в области промышленного производства. Основой конкурентного преимущества японцев явилось резкое снижение издержек производства и, как следствие, рыночных цен на продукцию машиностроительной, электронной и других капиталоемких отраслей. Принятая американцами политика протекционизма в отношении собственных товаропроизводителей, как ответная реакция на дешевый импорт японских товаров, не давала желаемых результатов: азиатские конкуренты продолжали теснить североамериканских производителей на обоих полушариях планеты. Исследования, проведенные ведущими аналитиками и экономистами США и Европы в 1985-1987 гг., показали, что одним из основных условий превосходства японцев являются незначительные (минимальные) товарные запасы. Данный подход к организации производства позволил, в первую очередь, снизить инвестиционную базу, что в свою очередь значительно увеличивает доходность инвестиций (ROI) при прочих равных условиях. Позже система, используемая японскими менеджерами, получила название "точно в срок" (аббревиатура JIT), которая и была в дальнейшем положена наиболее успешными компаниями Америки в основу комплексного планирования потребностей в материалах (MRP). Сегодня данная система трансформировалась в особую экономическую дисциплину - логистику. JIT означает, что процесс производства должен быть организован таким образом, чтобы сырье и материалы были доставлены к месту производства в тот момент времени, когда в них возникает необходимость, а готовые изделия тут же отправлены заказчику или потребителю.

Пример компании Тойота

Одним из классических примеров претворения в жизнь метода "точно в срок" является фирма Тойота, которая построила свой бизнес таким образом, что около 90% всех поставщиков этого автомобильного монстра сосредоточены в предместье Тойото. При этом подавляющее большинство комплектующих доставляются к месту сборки в течение нескольких часов или минут до того как они будут использованы. Данное обстоятельство позволяет компании значительно сократить операционные расходы и избавиться от непроизводительного труда. Однако подобная организация конвейера требует повышенных требований к качеству всех элементов производственного процесса: наличие даже незначительного брака в комплектующих способно парализовать целую производственную линию. Это еще раз доказывает, что управление товарно-материальными запасами по системе JIT тесно взаимосвязано с менеджментом качества TQM.

Статистический отчет, подготовленный Национальной ассоциацией производителей США в 1997 г., свидетельствует, что наибольшего успеха среди исследованных 385-ти предприятий добились 16%, внедривших у себя систему JIT, а проведенный опрос подтвердил готовность еще 53% компаний перейти к данной системе снабжения. Не случайно среди первопроходцев JIT в США стали Ford, General Motors, Hewlett-Packard, Intel, Motorola, Campbell Soup, GE и многие другие крупные производители. Именно внедрение JIT во многом позволило данным промышленным гигантам отстоять свои рыночные позиции.

Новая философия снабжения. Передовая практика внедрения системы JIT показала, что понятие "точно в срок" гораздо шире, чем обыкновенное сокращение товарных запасов. Современный наиболее прогрессивный опыт менеджмента в области организации снабжения и сбыта был основан на диалектическом развитии четырех принципиальных элементов:

Статистический контроль процессов (SPC). Этот подход, по сути, и явился первоначальным прообразом JIT и был принят на вооружение компаниями уже сразу после Второй Мировой войны. Данная концепция была основана на организации такой системы контроля на предприятии, которая исключает наличие "входящего" брака на всех этапах производства и, как результат, отсутствие дефектов на "выходе". Современные компании не могут полностью соответствовать принципам системы "точно в срок", если поставщики (как внешние, так и внутренние) допускают даже незначительный процент бракованных изделий.

Метод статистического контроля процессов был основан на так называемой "идее отсутствия дефектов", сформулированной Филиппом Кросби (Philip Crosby), который утверждал, что "качество свободно".

Комплексное управление качеством (TQM). Концепция комплексного или тотального управления качеством появилась примерно в конце 70-х - начале 80-х годов как логическое продолжение SPC и была основана на необходимости повышения качества всех компонентов (факторов) производства. Применение методов TQM требовало повышения всех качественных показателей производства и сервиса, а не только устранения дефектов сырья и выпускаемой продукции.

Научное обоснование метода комплексного (тотального) управления качеством связывают с именем того же Кросби и его единомышленников Деминга и Джурана, которые считали, что контролировать необходимо не качество продукта, а качество организации производства. При таком подходе каждый сотрудник должен отвечать за повышение качества на собственном технологическом участке. Они также считали, что внедрение принципов TQM должно избавить компании от необходимости содержать огромные отделы технического контроля (ОТК).

Реинжиниринг бизнес процессов (RBP). На рубеже 80-90-х гг. философия TQM была дополнена новым комплексным понятием в менеджменте корпораций, который получил название RBP. Концепция реинжиниринга была основана на допущении о возможности и необходимости перманентного совершенствования всех бизнес-процессов, включая и управление запасами. Основным методом RBP стал процесс постоянной оптимизации, а главными целями - обеспечение максимальной экономии расходов и полное уничтожение непроизводительного труда (NVA). Несмотря на относительную молодость метода RBP, большинство идей, положенных в его основу, известны экономистам уже не первое десятилетие.

Само понятие реинжиниринга бизнес-процессов и его принципы были впервые сформулированы в статьях, опубликованных в 1990 г. Хаммером (Hammer) и его коллегами Давенпортом и Шортом (Davenport and Short).

Тотальное управление деньгами (TCM). С середины 90-х и до сегодняшних дней самой передовой концепцией в области менеджмента является концепция ТСМ, которая основана на приоритете денежных потоков над всеми остальными объектами управления. Но это не означает, что SPC, TQM и RBP "больше ни на что не годны": данные элементы не утратили своей актуальности, а стали всего лишь средствами в обеспечении процесса тотального управления деньгами. Система "точно в срок" также стала одной из составляющих ТСМ. Отныне философия управления запасами должна быть подчинена не качеству или оптимальности, или "удовлетворению запросов клиентов" и т. д., а только увеличению реального дохода. Другими словами компании, принявшие на вооружение ТСМ-подход, должны выпускать не качественный продукт, а тот, который обеспечивает максимальную прибыль во времени. Еще одним важнейшим достижением ТСМ стала окончательная "победа прибыли над маркетингом". Сегодня наиболее прогрессивные компании наконец-то поняли, что маркетинг должен быть подчинен финансовым целям увеличения дохода, а не наоборот.

Отцом концепции тотального управления деньгами по праву считается Альфред М. Кинг (Alfred M. King), который впервые дал научное обоснование метода ТСМ в своей книге Total Cash Management. Основная идея работы Кинга заключается в том, что в целях управления компанией предпочтение должно отдаваться денежным потокам.

Методы управления. Как мы уже сказали, одним из обязательных условий эффективного управления товарными запасами является учет влияния их размеров на денежные потоки компании. Условно все материальные расходы по обслуживанию запасов можно разделить на три большие группы:

• затраты, связанные с организацией закупок;
  
• затраты, связанные с хранением;
  
• убытки, связанные с неадекватностью наличия запасов.
  

Проблемы, связанные с управлением перечисленными расходами, могут быть решены на основе построения модели оптимального размера заказа (EOQ). Основным условием построения данной модели выступает разделение затрат на те, которые прямо пропорциональны размеру запасов, и те, которые находятся в обратной зависимости от количества накопленных ресурсов.

Решение задачи оптимизации размеров тех или иных наименований товаров на складе для торгового предприятия может быть проведено по следующей формуле:



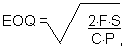
где F - фиксированные затраты на формирование одного заказа; S - объем продаж данного товара за период; С - переменные затраты, которые зависят от размера запасов на складе; Р - закупочная цена товарной единицы.

После того как будет установлен оптимальный уровень запасов, достаточно не сложно установить момент, в который необходимо сделать заказ. Этот момент будет определен при умножении дней изготовления и доставки товаров поставщиком на количество реализованных товаров за день. Полученное количество товаров представляет собой тот уровень запасов данной номенклатуры, при котором следует направить следующий заказ поставщику.

Решение данных простых задач в компаниях со значительной номенклатурой товаров (крупное производство, супермаркет и т. д.) невозможно без использования адаптированных ERP-систем управления товарными запасами.

Метод планирования ресурсов предприятия (Enterprise Resource Planning или сокращенно ERP) позволяет при помощи внедрения специализированного программного обеспечения управлять товарными запасами с учетом динамики изменения всех факторов производства и с соблюдением общей стратегии и тактики развития компании. Пионерами в применении метода ERP стали такие всемирно известные компании-гиганты розничной торговли как Wаl-Mart, Dayton Hadson, Kmart. Это связано, в первую очередь, с тем, что данные компании имели наибольший удельный вес товарных запасов в общей структуре всех активов.

Вейн Худ (Wayn Hud), признанный авторитет в области идеологии организации розничной торговли еще в конце 80-х годов писал: "В конце 90-х компьютерные технологии подобные ERP разделят всех розничных торговцев на победителей и побежденных. Компании, которые не намереваются инвестировать средства в современные компьютерные технологии, даже если они переживают не лучшие времена, никогда не смогут стать победителями".

Модели линейного программирования.

Их применяют для нахождения оптимального решения в ситуации распределения дефицитных ресурсов при наличии конкурирующих потребностей. Например, с помощью модели линейного программирования управляющий производством может определить оптимальную производственную программу, т.е. рассчитать, какое количество изделий каждого наименования следует производить для получения наибольшей прибыли при известных объемах материалов и деталей, фонде времени работы оборудования и рентабельности каждого типа изделия. Большая часть разработанных для практического применения оптимизационных моделей сводится к задачам линейного программирования. Однако с учётом характера анализируемых операций и сложившихся форм зависимости факторов могут применяться и модели других типов: при нелинейных формах зависимости результата операции от основных факторов – модели нелинейного программирования; при необходимости включения в анализ фактора времени – модели динамического программирования; при вероятностном влиянии факторов на результат операции – модели математической статистики (корреляционно-регрессионный анализ).


Подробнее. Для более глубокого изучения