Сравнить составленный конспект с текстом лекции, внести коррективы. Восстановить доказательства теорем. Изложить содержание одного из разделов 4 14 структурно по аналогии с содержанием лекции. Отношение делимости на множестве целых чисел

Вид материала

Конспект

Содержание 6.1. Отношение делимости на множестве целых чисел 6.2. Деление с остатком 6.3. НОД нескольких целых чисел Пример. Найдём НОД(2585, 7975). 7975 2585

Подобный материал:

• 1 Пространства комплекснозначных функций, определенных на множестве целых чисел, 127.47kb.
• Применение Признака Паскаля. 9 Выводы. 10 Заключение. 10 Список используемой литературы., 93.57kb.
• Лекция Понятия множества и элементы множества. Способы задания множеств, 353.91kb.
• Структурно курс состоит из 3 разделов и 8 тем. Раздел I. Предмет природопользования, 124.15kb.
• Критерии оценки качества лекции, 33.79kb.
• Ю. Б. Гиппенрейтер Введение в общую психологию. Лекции 1,2, 45.86kb.
• Такие разные лекции, 101.86kb.
• Пояснительная записка Курс по выбору "Делимость целых чисел", 33.55kb.
• Задача 1 (Районная олимпиада 2010, 7 класс). Возможно ли подобрать 2010 целых чисел,, 111.85kb.
• Лекции по учебной дисциплине «судебная медицина и судебная психиатрия» Тема, 4326.19kb.

Лекция 6. Основы теории делимости целых чисел

Задания.

1. Сравнить составленный конспект с текстом лекции, внести коррективы.

2. Восстановить доказательства теорем.

2. Изложить содержание одного из разделов 6.4-6.14 структурно по аналогии с содержанием лекции.

6.1. Отношение делимости на множестве целых чисел

Обозначения. N = {1, 2, 3,…} – множество натуральных чисел.

Z  = {…, –3, –2, –1, 0, 1, 2, 3, …} – множество целых чисел.

Определение. О двух целых числах а и b говорят, что а делится на b (обозначают а  b), если  с , такое, что a = b  c.

Свойства делимости (теоремы о делимости).

1. Отношение делимости рефлексивно, то есть ( а  ) (а  а).
   

Доказательство очевидно, в силу свойства единицы: a = а  1.

2. Отношение делимости транзитивно, то есть ( а, b, c  ) (а  b, b  c  а  c).
   

Доказательство.

Шаг	Утверждение	Аргументация
1	а  b	дано
2	 q , a = b  q	из (1) по определению делимости
3	b  c	дано
4	 p , b = c  p	из (3) по определению делимости
5	a = (c  p)  q	из (2) и (4) по свойству равенства
6	a = c  (p  q), p  q, p  q = r	из (5) согласно ассоциативности умножения целых чисел, по определению целых чисел, обозначение
7	a = c  r, r	из (6) с учётом введённого обозначения
8	а  с	из (7) по определению делимости

3. Отношение делимости сохраняется при изменении знака делимого или/и делителя, то есть (а  b)  [(–а)  b]; [а  (–b)]; [(–a)  (–b)].
   

Доказательство.

Шаг	Утверждение	Аргументация
1	а  b	дано
2

4. Если а  b и с  b, то (а  с)  b.
   

Доказательство.

Шаг	Утверждение	Аргументация
1	а  b	дано
2

5. Если а  b и с , то ас  b.
   

Доказательство.

Шаг	Утверждение	Аргументация
1	а  b	дано
2

6. Если а  b и с не делится на b, то (а  с) не делится на b.
   

Доказательство.

Шаг	Утверждение	Аргументация
1	(а  с)  b	допущение
2	 q , a  с = b  q	из (1) по определению делимости
3	 q , с = b  q  а	из (2) по определению разности целых чисел
4	b  q  b	свойство 5
5	а  b	дано
6	с  b	из (2)-(4) по свойству 4
7	с не делится на b	дано
8	не верно, что (а  с)  b	(6) и (7) – противоречивые утверждения
9	Если а  b и с не делится на b, то (а  с) не делится на b	из (7)

7. Любое целое число делится на 1.
   
8. Для любого целого числа а справедливо утверждение: 0  а.
   

Доказательство (для случая а = 0).

?...

9. Если а  b и а  0, то  а    b .
   

Доказательство.

Шаг	Утверждение	Аргументация
1	а  b	дано
2	а  0	дано
3	 q , a = b  q	из (1) по определению делимости
4	 q   1	из (2) и (3) по свойству абсолютной величины целого числа
5	a = (c  p)  q	из (2) и (4) по свойству равенства
6	 а  = b  q 	из (3) по свойству равенства
7	 b  q  =  b    q 	свойство модуля
8	 а  = b    q 	из (6) и (7) – транзитивность равенства
9	 а ,  b ,  q   N	свойство абсолютной величины целого числа отличного от нуля
10	 а    b 	из (8)и (9) по свойству произведения натуральных чисел

(9.1) Если 1  а, то а =  1.

(9.2) Если а  b и b  a, то а =  b.

6.2. Деление с остатком

Определение 1. О двух целых числах а и b (b  0) говорят, что а делится на b с остатком, если  q, r  , такие, что a = bq + r, причём 0  r <  b .

Свойство делимости с остатком (теорема о делимости с остатком).

( а, b  , b  0) (! q, r  ,) (a = bq + r, 0  r <  b  )

Доказательство.

1. Докажем факт существования, то есть,

( а, b  , b  0) ( q, r  ,) (a = bq + r, 0  r <  b  )

1. а, b  , b  0.
   

Выпишем в виде последовательности множество чисел, кратных b:

…, (–2) b, (–1) b, 0b, 1b, 2b,…

и рассмотрим часть последовательности: 0b, 1b, 2b,…

Пусть qb – наибольшее из кратных b, не превосходящих а, тогда

qb  а  (q +1)b.

Выполним ряд преобразований в стремлении получить требуемое равенство: 0  а – qb  (q +1)b – qb;

0  а – qb  b.

Обозначив разность через r, получим, 0   r  b, r = а – qb, или

a = bq + r, 0   r  b

2. а, b  , b  0.
   

(–b)  0, а для всякого положительного числа, согласно 1.1, имеем:  a = (–b)q + r, 0   r  (–b), что равносильно

a = b(–q) + r, 0   r  (–b)

Из подчеркнутого (1.1 и 1.2) и определения модуля, следует

( q, r  ,) (a = bq + r, 0  r <  b  ).

2. Докажем факт единственности (от противного).

Предположим, что для некоторой пары чисел a и b существует два разложения: q₁  q₂  и  r₁ r₂

a = bq₁ + r₁, 0  r₁   b ,

a = bq₂ + r₂, 0  r₂   b .

Тогда bq₁ + r₁ = bq₂ + r₂,  r₁ – r₂    b .

Продолжим преобразовывать первое равенство

bq₁ – bq₂ = r₂  – r₁, 

b(q₁ – q₂) = r₂  – r₁, 

По определению делимости, (r₂  – r₁) делится на b.

По свойству 9 делимости целых чисел, если (r₂  – r₁) делится на b, то модуль (r₂  – r₁) больше или равен модуля b, то есть  r₁ – r₂    b .

Получили противоречие: одновременно выполняются два неравенства:

 r₁ – r₂    b  и  r₁ – r₂    b . Противоречие возникло из-за неверности допущения о существовании двух различных пар: q₁  q₂  и  r₁ r₂. Следовательно, q₁ = q₂ = q и  r₁= r₂ = r, что означает «единственность деления с остатком».

6.3. НОД нескольких целых чисел

Определение 1. Целое число  (  0) называется общим делителем целых чисел а₁, а₂,…, а_п, если каждое из этих чисел делится на .

Определение 2. Целое число d (d  0) называют наибольшим общим делителем (НОД) целых чисел а₁, а₂,…, а_п, если

2.1. d – общий делитель этих чисел,

2.2. d  , где  – любой другой общий делитель этих чисел.

Теорема 1. НОД целых чисел определяется с точностью до знака.

Доказательство (метод …).

Пусть d₁ и d₂ – два различных наибольших общих делителя чисел а₁, а₂,…, а_п,

то есть . Надо доказать, что

По определению 2, признак 2.1, d₁ и d₂ – общие делители чисел а₁, а₂,…, а_п.

По определению 2, признак 2.2,

если d₁ – наибольший общий делитель чисел а₁, а₂,…, а_п, то d₁  d₂,

если d₂ – наибольший общий делитель чисел а₁, а₂,…, а_п, то d₂  d₁.

Согласно свойству делимости (9.2), если d₁  d₂ и d₂  d₁, то d₂ =  d₁, то есть НОД определяется с точностью до знака.

Пример. Найдём НОД(135, –180).

₁₃₅ = {1, 3, 5, 9, 15, 27, 45, 135},

₁₈₀ = {1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 45, 60, 90, 180},

₁₃₅  ₁₈₀ = {1, 3, 5, 9, 15, 45},

НОД(135, –180) = 45

Определение 3. Алгоритм Евклида – способ нахождения НОД целых чисел.

Лемма 1. а  b  НОД (а, b) = b.

Доказательство.

Шаг	Утверждение	Аргументация
1	а  b	дано
2	b  b	свойство делимости (1)
3	b – общий делитель а и b	из (1) и (2) по определению общего делителя
4	c – другой общий делитель а и b	допущение
5	b  с	из (4) по определению общего делителя
6	b – наибольший общий делитель а и b, т.е. НОД (а, b) = b	из (3) и (5) по определению НОД целых чисел, обозначение

Лемма 2. Пусть а = bq + r, abr 0, тогда НОД (а, b) = НОД (b, r).

Доказательство (подведение под понятие).

Другими словами, нужно доказать: если


1. Докажем для а = bq + r: если  – общий делитель а и b, то  – общий делитель b и r.  

а = bq + r, abr 0. Обозначим  – общий делитель а и b. Тогда, по определению общего делителя, а  , b  . Если сумма делится на , и одно из слагаемых делится на , то другое слагаемое тоже делится на  (следствие из свойства делимости (4)), то есть r  . Если же b   и r  , то, по определению общего делителя,  – общий делитель b и r.  

Докажем, по аналогии, для а = bq + r: если  – общий делитель b и r, то  – общий делитель а и b. 

 

2. Обозначим d = НОД (а, b). Докажем, что d = НОД (b, r).


Итак, а = bq + r, abr 0  НОД (а, b) = НОД (b, r).

Теорема 2 (алгоритм Евклида). НОД двух целых чисел равен последнему ненулевому остатку в алгоритме Евклида: (a, b Z, ab  0) (НОД (а, b) = r_п)

а = bq₀ + r₁, 0  r₁   b,

b = r₁q₁ + r₂, 0  r₂   r₁,

r₁ = r₂q₂ + r₃, 0  r₃   r₂,…

………… r_п–2 = r_п–1q_п–1 + r_п, 0  r_п   r_п–1

r_п–1 = r_пq_п .

Доказательство (используя Лемму 2).


Замечание. Так как остатки в алгоритме Евклида – натуральные числа, образующие убывающую последовательность, то процесс алгоритма конечен.

Пример. Найдём НОД(2585, 7975).

7975 2585

7755 3

2585 220 – первый остаток

220 11

385

220

220 165 – второй остаток

165 1

165 55 – третий остаток, последний в алгоритме Евклида

165 3

0 – деление без остатка

Итак, НОД(2585, 7975) = 55.

Теорема 3 (алгоритм Евклида). Если НОД п целых чисел – а₁, а₂,…, а_п – равен , и НОД (, а_п+1) = d, то НОД (а₁, а₂,…, а_п, а_п+1) = d.

Доказательство (подведение под понятие).

3.1. Докажем, что d – общий делитель а₁, а₂,…, а_п, а_п+1.

Шаг	Утверждение	Аргументация
1	НОД (, ап+1) = d	дано
2	  d, ап+1  d	из (1) по определению НОД (признак 2.1)
3	НОД (а1, а2,…, ап) = 	дано
4	а1  , а2  , … , ап  	из (1) по определению НОД (признак 2.1)
5	а1  d, а2  d, … , ап  d	из (2) и (4) по свойству транзитивности отношения делимости
6	d – общий делитель а1, а2,…, ап, ап+1	из (2) и (5) по определению общего делителя целых чисел

3.2. Докажем, что, если d₁ – другой общий делитель а₁, а₂,…, а_п, а_п+1, то d  d₁.

Если d₁ – другой общий делитель а₁, а₂,…, а_п, а_п+1, то d₁ – общий делитель для а₁, а₂,…, а_п; по условию, НОД (а₁, а₂,…, а_п) = , следовательно (по определению НОД),   d₁. Это значит, что d₁ – один из делителей . (*)

По другому условию, НОД (, а_п+1) = d, то есть   d и d – наибольший делитель . (**)

Из утверждений (*) и (**) следует, что d  d₁.

Оформим доказательство 3.2 в таблицу.

Шаг	Утверждение	Аргументация
1	d1 – общий делитель а1, а2,…, ап, ап+1	дано
2
3
4
5
6

По определению НОД целых чисел, из 3.1 и 3.2 следует, что НОД (а₁, а₂,…, а_п, а_п+1) = d.

Замечание. Из теоремы 3 вытекает способ последовательного определения НОД нескольких целых чисел а₁, а₂,…, а_п:

1. НОД (а₁, а₂) = d₁.
   
2. НОД (d₁, а₃) = d₂.
   
3. НОД (d₂, а₄) = d₃.
   
4. …
   
5. НОД (d_п–1, а_п) = d = НОД (а₁, а₂,…, а_п).
   

Свойства НОД (теоремы о НОД).

(1) Наибольшим общим делителем целых чисел является наибольший положительный делитель изо всех общих делителей этих чисел.

Доказательство (подведение под понятие).

Обозначим d = НОД (а₁, а₂,…, а_п),  – наибольший из положительных делителей чисел а₁, а₂,…, а_п, следовательно, а₁  , а₂  , … , а_п  .

(а)  Рассмотрим случай, когда НОД (а₁, а₂,…, а_п) = d, а  – другой общий делитель. В этом случае или d > , или d = .

(б)  Рассмотрим случай, когда  – наибольший (по условию) общий делитель, а d – другой общий делитель. В этом случае или  > d , или  = d .

Из (а) и (б) следует, что  = d, то есть  = НОД (а₁, а₂,…, а_п).

(2) НОД (kа, kb) = k НОД (a, b).

Другими словами,


Доказательство.

Рассмотрим и преобразуем правую часть равенства (к виду левой части).

Будем находить НОД (a, b) по алгоритму Евклида: .

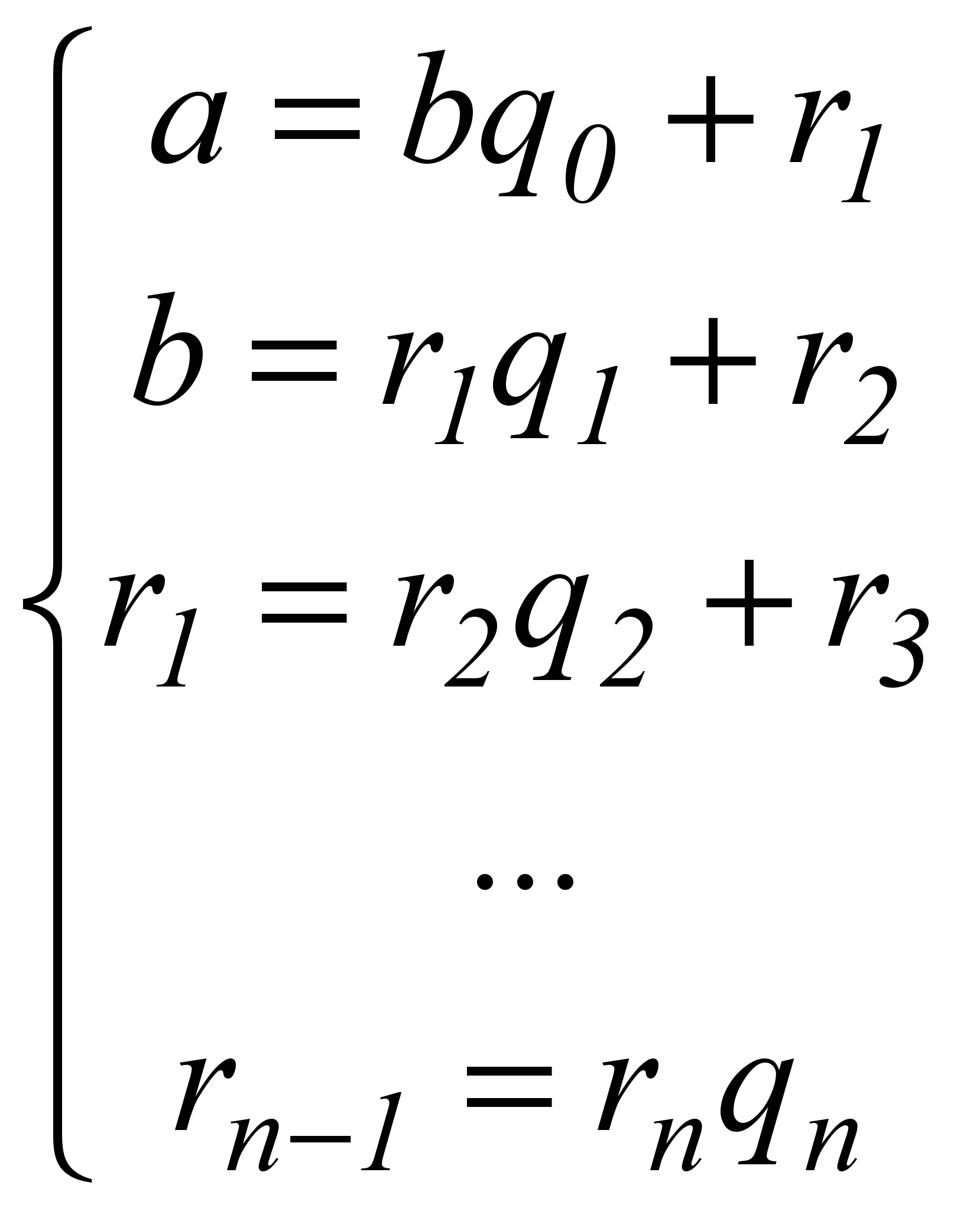Умножим систему на k, получим: .

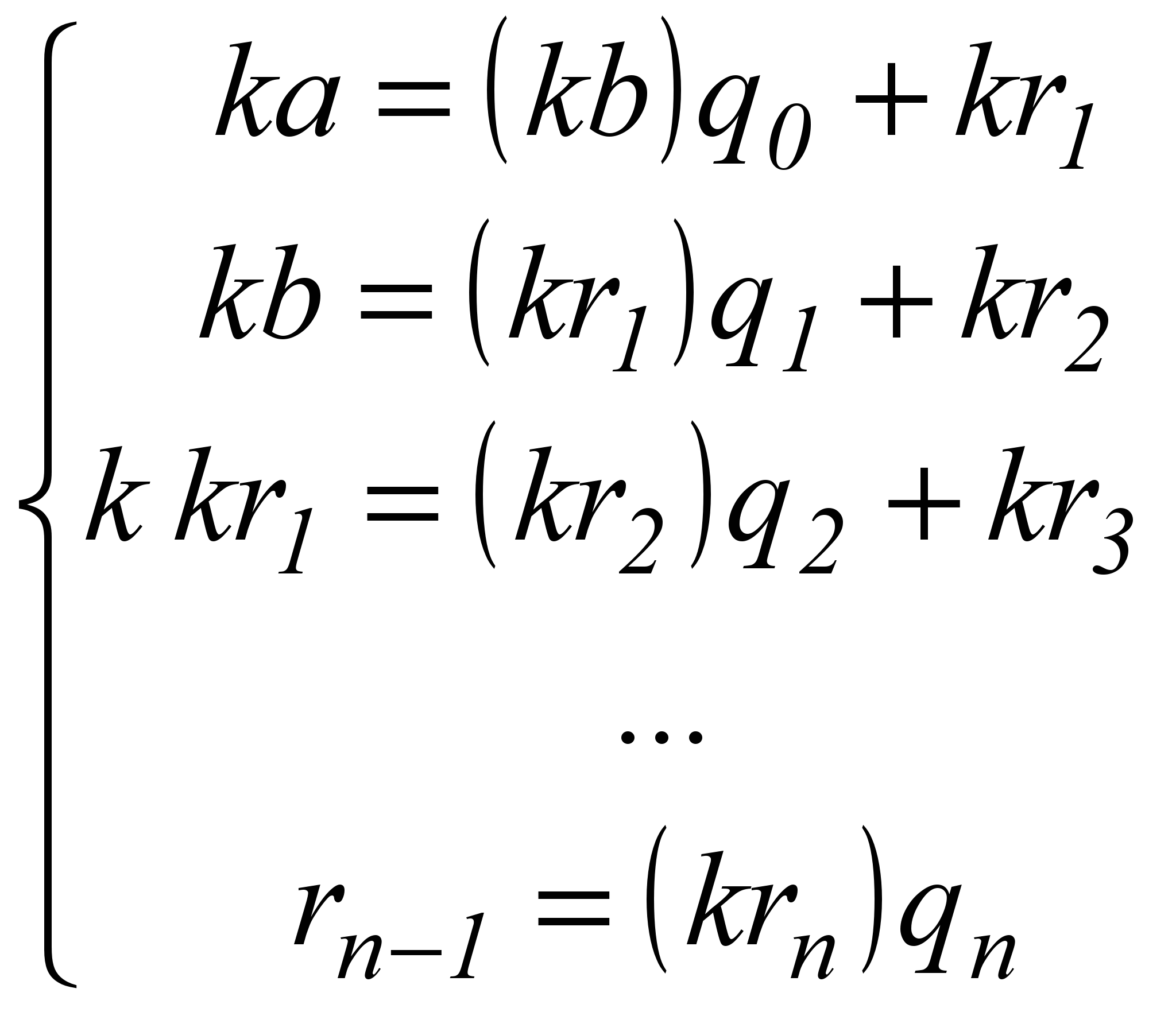По теореме 2 (алгоритму Евклида),

для первой системы, НОД (a, b) = r_n,

для второй системы, НОД (kа, kb) = kr_n . Из этого следует, что

НОД (a, b) = k НОД (a, b).

(3) Если d  = НОД (а, b), то существуют такие целые числа х и у, что  aх + bу = d.

Доказательство.

Рассмотрим алгоритм Евклида: .

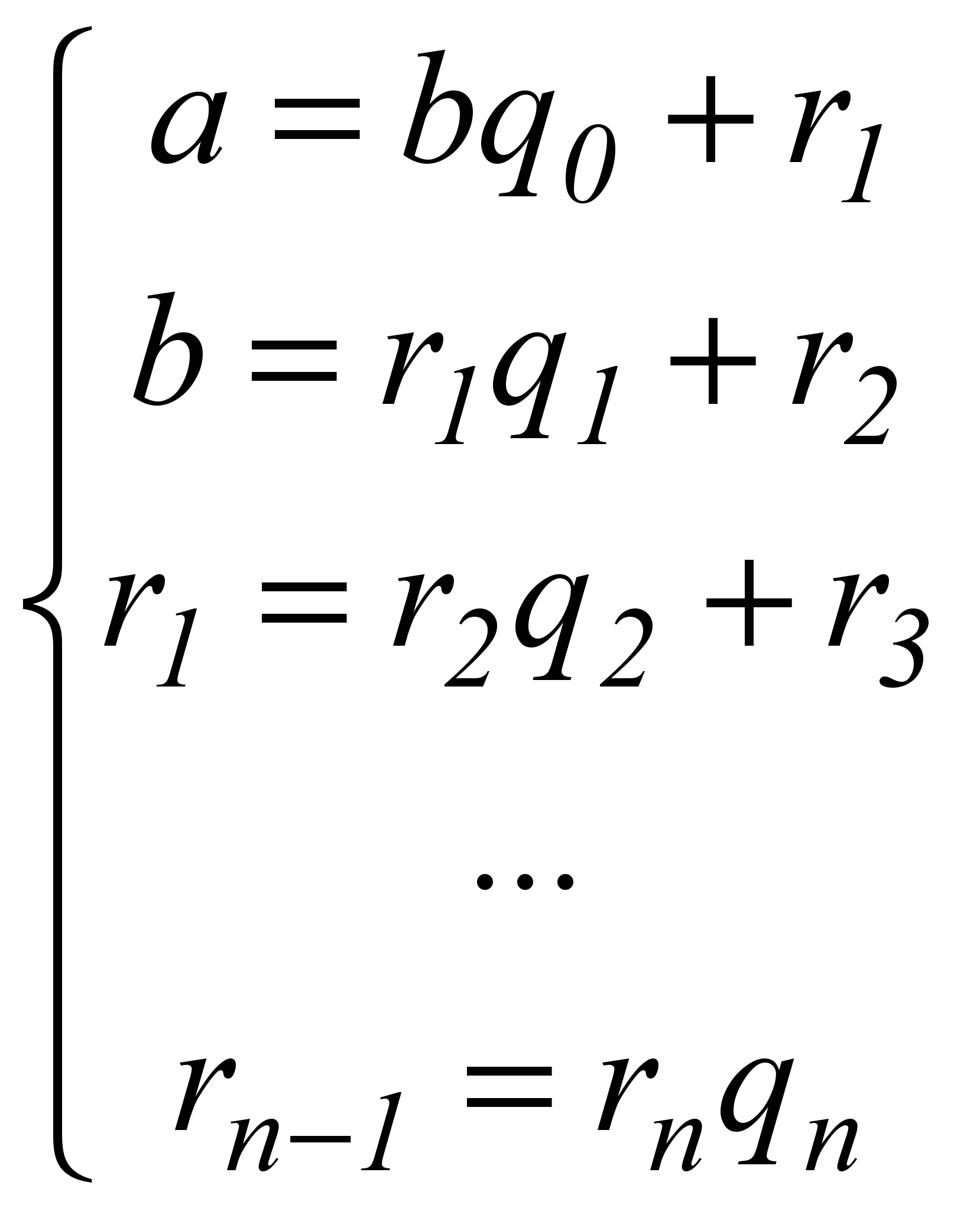Из каждого равенства выразим остатки. Получим

r₁ = a  1 + b  (– q), где х = 1, у = – q;

r₂ = b + r₁  (– q) = b + (a  1 + b  (– q))  (– q) = a  (– q₁) + b  (1 + q₁q₂),

где х = – q₁, у = 1 + q₁q₂;

и т.д.

r_n = a  x* + b y*,

но  r_n = НОД (a, b), а НОД (а, b) = d (дано). Значит, d = aх + bу.

6.4. Взаимно-простые числа и их свойства

6.5. НОК, свойства НОК

6.6. Простые числа и их свойства

6.7. Основная теорема арифметики

6.8. Мультипликативные числовые функции

6.9. Функция Е(х) и её применение

6.10. Конечные цепные дроби

6.11. Подходящие дроби и их свойства

6.12. Распределение простых чисел

6.13. Асимптотический закон распределения простых чисел

6.14. Систематические числа