Студент группы ас-1-05
| Вид материала | Документы |
- Выполнил студент группы, 39.74kb.
- Грибановский, С. П. Студент пятого курса, факультета экономики и права, отделения «социология»,, 55.7kb.
- Иващенко е лена д митриевна, 157kb.
- Выполнил студент 1 группы, 286.61kb.
- Отчет о преддипломной практике студент группы, 9.91kb.
- Е дать все ответы на вопросы, возникающие у предприятия, 305.65kb.
- Методические указания по выполнению и оформлению контрольной работы. Варианты контрольных, 141.29kb.
- Реферат Тема: Международный терроризм, 389.51kb.
- Вариант 1 Ответьте на нижеприведенные вопросы и обоснуйте свой ответ (не более 3 стр, 89.56kb.
- Вариант 1 Ответьте на нижеприведенные вопросы и обоснуйте свой ответ (не более 3 стр, 117.15kb.
Барзиков Константин Васильевич
студент группы АС-1-05
Научный руководитель: Фомичева Ольга Евгеньевна
доц., к.т.н.
Московский государственный горный университет
АЛГОРИТМ НАХОЖДЕНИЯ ПУТИ НА ПЛОСКОСТИ С ОБХОДОМ ПРЕПЯТСТВИЙ НА ОСНОВЕ КЛЕТОЧНЫХ АВТОМАТОВ ТИПА «МУРАВЕЙ»
ALGORITHM FOR FINDING AN TRAECTORY IN THE PLANE WITH AVOIDING OBSTACLES BASED ON CELL AUTOMATICS TYPE “ANT”
Алгоритм нахождения оптимального пути на основе клеточных автоматов был разработан в рамках исследований в области искусственного интеллекта, производимых в ООО «Интеллект» руководителем отдела ИИ Игиным Г. А. совместно с автором. Реализации данного алгоритма могут применяться как наглядное пособие для демонстрации работы адаптивных систем, а также и в практических реализациях, например, в беспилотных летательных аппаратах. Игиным, а также другими исследователями были показаны разнообразные преимущества и перспективы применения вероятностных алгоритмов и клеточных автоматов, как более гибких и быстродействующих [6, 7, 8].
Алгоритм использует клеточное поле с евклидовой метрикой, на котором заранее нанесены точка начальной позиции, точка цели и препятствия в виде массива точек (см. рис. 1).
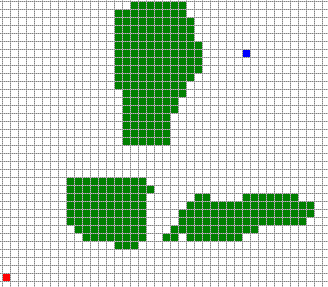
Рис. 1. Клеточное поле.
Координаты муравья первоначально совпадают с координатами точки старта. Муравей может двигаться по всему клеточному полю, за исключением клеток, занимаемых препятствиями и координат своих предыдущих положений. Все клетки, на которых побывал муравей, помечаются, как часть его траектории. Когда координаты муравья совпадут с координатами цели, алгоритм завершается.
В начале каждой итерации для каждой клетки из окрестности муравья проверяется, не является ли она препятствием или предыдущим положением муравья. В окрестности может быть не более восьми и не менее одной свободной клетки (для рассматриваемой реализации). На первом шаге рассматривается восемь клеток (если рядом нет препятствий), на последующих – не более семи (одну клетку занимает предыдущее положение муравья). Рассмотрим первую итерацию при отсутствии в окрестности муравья препятствий (см. рис. 2).
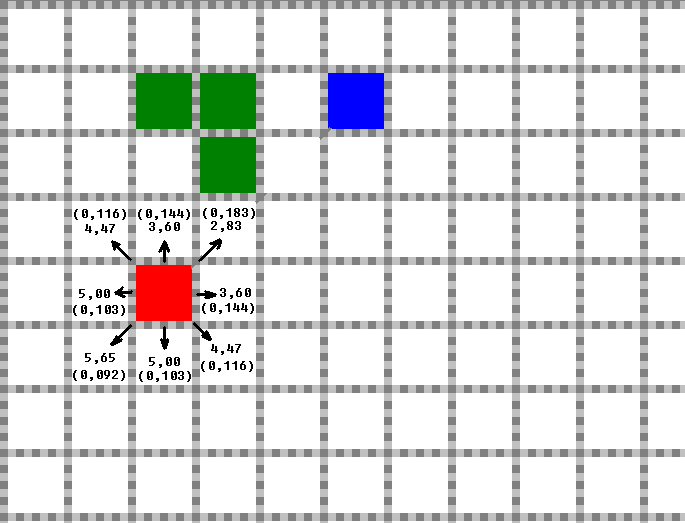
Рис. 2. Первая итерация алгоритма. В клетках указаны евклидовы расстояния от них до цели. В скобках указаны вероятности перехода.
Все восемь клеток вокруг муравья свободны и для них получены евклидовы расстояния до цели. После этого по полученным значениям расстояний вычисляются вероятности перехода в соответствующие клетки. Вычисления осуществляются по стандартной формуле:
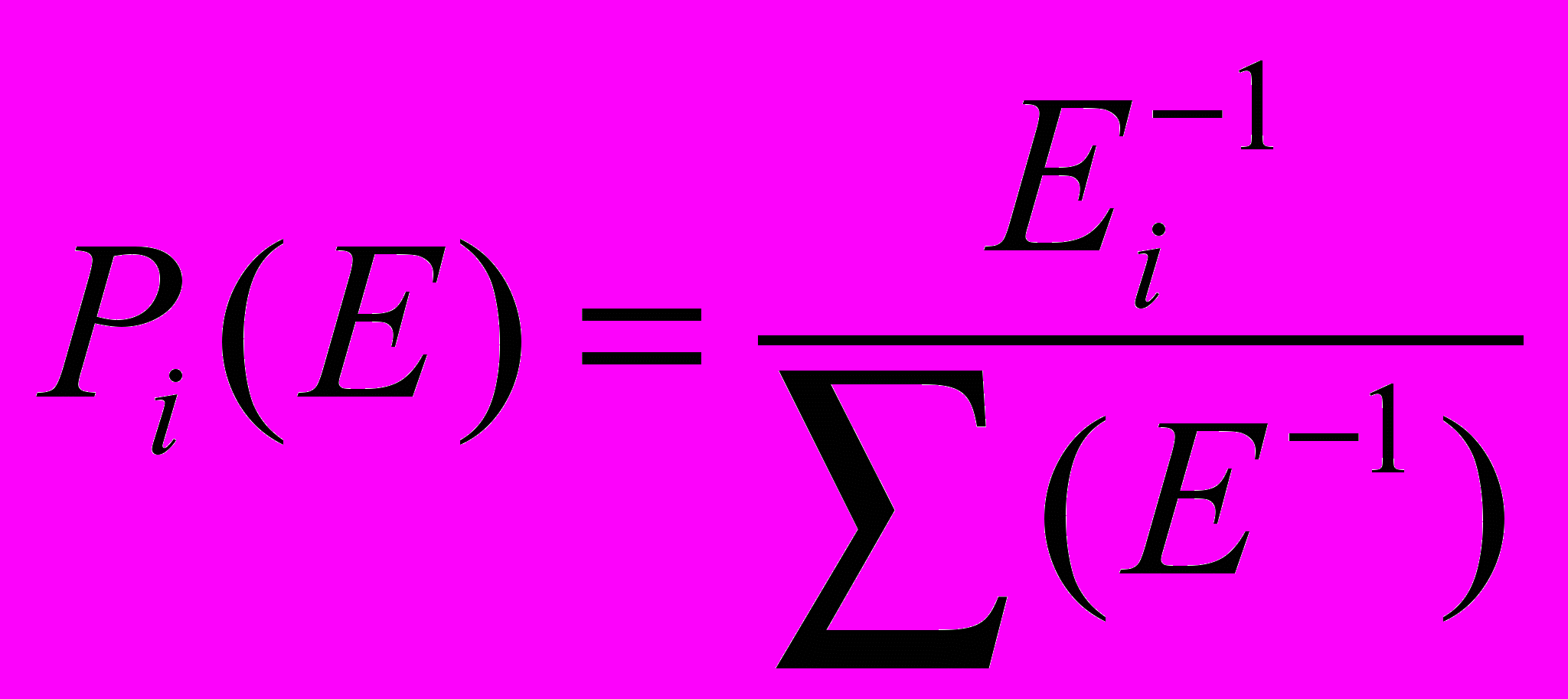
где
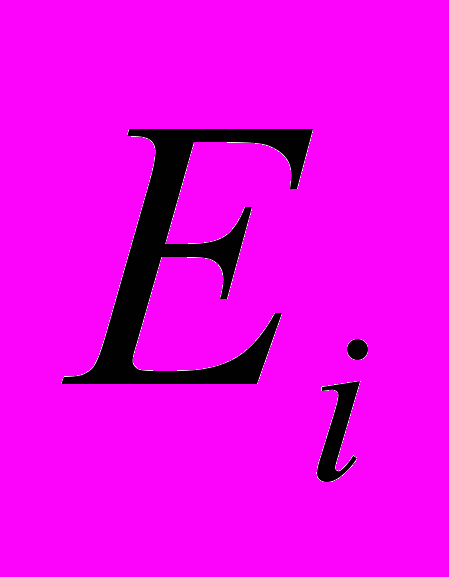 -- евклидово расстояние для i-той точки, а
-- евклидово расстояние для i-той точки, а 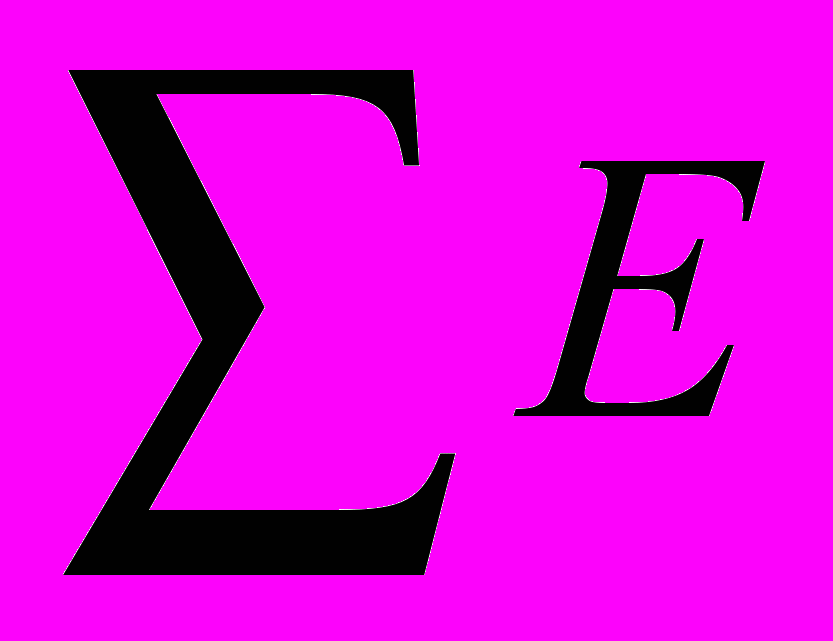 – сумма всех найденных во время итерации расстояний. Полученные вероятности характеризуют полную группу событий. Хотя вероятность того, что муравей сделает шаг не в сторону цели, отлична от нуля, это необходимо для обеспечения гибкости алгоритма, т.к. движение не в сторону цели может быть правильным в случае обхода препятствия, которое присутствует на поле, но пока не зафиксировано алгоритмом. Допустим, что муравей переместился в левую верхнюю клетку, как в наиболее вероятную. Тогда рассматриваемые клетки будут выглядеть следующим образом (см. рис. 3).
– сумма всех найденных во время итерации расстояний. Полученные вероятности характеризуют полную группу событий. Хотя вероятность того, что муравей сделает шаг не в сторону цели, отлична от нуля, это необходимо для обеспечения гибкости алгоритма, т.к. движение не в сторону цели может быть правильным в случае обхода препятствия, которое присутствует на поле, но пока не зафиксировано алгоритмом. Допустим, что муравей переместился в левую верхнюю клетку, как в наиболее вероятную. Тогда рассматриваемые клетки будут выглядеть следующим образом (см. рис. 3).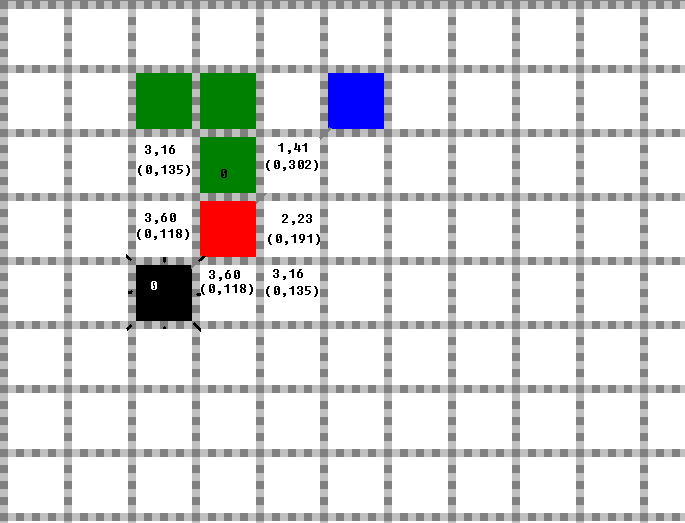
Рис. 3. Вторая итерация алгоритма.
На рисунке 6 видно, что чем меньше свободных клеток для перехода и чем ближе цель, тем больше вероятность, что муравей переместится в нужном направлении.
Оптимальный путь находится через несколько прогонов алгоритма, путем выбора траектории, состоящей из наименьшего количества клеток. Возможно также осуществление параллельных прогонов независимых друг от друга нескольких муравьев на одном клеточном поле.
Блок-схема алгоритма в его программной реализации на компьютере представлена на рис. 4.
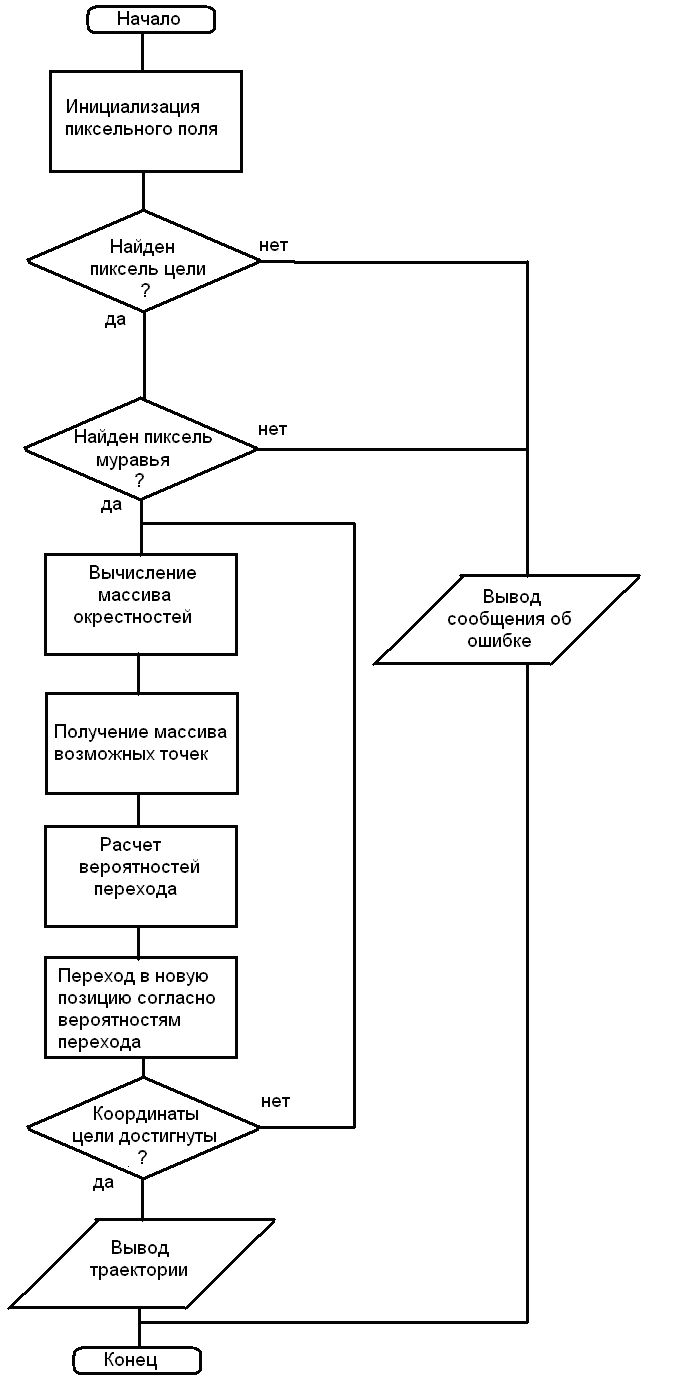
Рис. 4. Блок-схема алгоритма.
Представленный в статье алгоритм может быть доработан, что предоставляет большую свободу действий для будущих исследований. Алгоритм может быть значительно усовершенствован, если использовать неевклидову метрику, дополнить алгоритм возможностью параллельных муравьев, расширить окрестность рассматриваемых точек и т.д. Возможности клеточных автоматов вообще и, в частности, вероятностных алгоритмов малоисследованны и обладают большим внедренческим потенциалом [9].
Литература
- Интернет-ресурс: ссылка скрыта
- Интернет-ресурс: ссылка скрыта
- Князев Б. А., Корепанов А. А., Кудрявцев А. С., Морозов И. И. Электрический ток в газах и жидкостях. Учебно-методическое пособие. – Новосибирск, 2008.
- Анненков Ю. М. Основы электротехнологий. Учебно-методическое пособие. – Томск: Изд. ТПУ, 2005.
- Интернет-ресурс: ссылка скрыта
- Расстригин Л. А. Адаптация сложных систем. – Рига: Изд. «Зинатне», 1981.
- Терехов С. А. Введение в сети Байеса. Сессия МИФИ. – М., 2003.
- Игин Г. А. Динамические нейронные матрицы и система пяти процессов «У-Син». Доклад. – М.: НПО «Интеллект», 2007.
- Плотникевич М. Н. Процессы дифракции, интерференции и других преобразований электромагнитных волн, как вероятностные вычислители. Доклад. – М.: НПО «Интеллект», 2008.
Аннотация
Представленный в статье алгоритм позволяет решить задачу нахождения оптимального пути с обходом препятствий, т.е. частный случай задачи о коммивояжере. В качестве платформы решения задачи используется вероятностный клеточный автомат типа «муравей».
Ключевые слова
искусственный интеллект, задача о коммивояжере, клеточный автомат, вероятностный алгоритм
