Ун-т «Дубна». Курс «Компьютерные сети»
| Вид материала | Лекция |
- Ун-т «Дубна». Курс «Компьютерные сети», 488.73kb.
- Ун-т «Дубна». Курс «Компьютерные сети», 371.9kb.
- Ун-т «Дубна». Курс «Компьютерные сети», 560.01kb.
- Ун-т «Дубна». Курс «Компьютерные сети», 276.95kb.
- Ун-т «Дубна». Курс «Компьютерные сети», 547.71kb.
- Ун-т «Дубна». Курс «Компьютерные сети», 546.8kb.
- Ун-т «Дубна». Курс «Компьютерные сети», 676.23kb.
- Урок по теме «Компьютерные сети. Интернет», 157.31kb.
- Ун-т «Дубна». Курс «Компьютерные сети», 611.15kb.
- Лекция Глобальные сети. Интернет. Корпоративные компьютерные сети, 89.75kb.
Ун-т «Дубна». Курс «Компьютерные сети».
Лекция 5.
- Графовые модели сетей.
- Алгоритмы поиска путей с минимальной стоимостью.
- Объединение сетей. Автономные области.
- Маршрутизация. Требования, классификация.
Компьютерные сети часто представляют в виде графов, где вершинами (узлами) являются коммутаторы и маршрутизаторы сетей, а линии связи представляют собой ребра графа.
Граф G(E,V) состоит из объектов двух типов – вершин и ребер, причем каждое ребро определяется как неупорядоченная пара вершин. V – можество вершин, Е – множество ребер.
Вершины называются смежными, если ребро, определяемое парой этих вершин, принадлежит множество Е ребер данного графа.
Величина графа характеризуется количеством вершин |V| - порядком, а число ребер называется размером графа.
Граф часто представляют в виде матрицы смежности А=(a_i,j), где
A_i,j=1, если (i,j) принадлежит E, и 0 иначе.
Два ребра, инцидентные одной и той же паре, называются параллельными, если ребро инцидентно одной вершине – оно называется петлей. Граф, в котором отсутствуют петли и параллельные ребра, называется простым.
Путь от вершины i до вершины j – такая последовательность вершин и ребер, которая начинается с вершины i, заканчивается вершиной j, причем каждое ребро инцидентно двум вершинам, соседним с ним в этой последовательности. Путь называется простым, если каждое ребро и каждая вершина присутствуют только однажды. В простом графе путь может быть определен как последовательность вершин, в которой каждая вершина является смежной с предыдущей и следующей вершиной в последовательности и ни одна из вершин не повторяется.
Цикл - путь, начинающийся и заканчивающийся в одной и той же вершине.
Граф называют связным, когда существует путь между любыми двумя его вершинами.
В ориентированном графе каждое ребро – упорядоченная пара вершин.
Взвешенный граф – каждому ребру поставлено в соответствие некоторе число.
Во взвешенном графе длиной пути называется сумма весов всех ребер пути.
Компьютерные сети можно представить в виде ориентированного графа. Решение о выборе маршрута в сети эквивалентоно поиску пути в графе.
Практически во всех сетях с коммутацией пакетов и в объединенных сетях решение о выборе маршрута принимается на основе одного из критериев.
- Выбирается маршрут с минимальным количеством ретрансляционных участков (хопов), которым соответствуют ребра, им присвавается единичный вес, невзвешенный граф.
- Каждому участку ставится в соответствие величина, называемая стоимостью передачи. Обратно пропорциональна пропускной способности, прямо пропорциональна текущей нагрузке на линию, либо комбинация этих двух параметров. Плюс финансовая стоимость передачи. В этом случае имеем задачу найти путь с наименьшей стоимостью для каждой пары узлов. Соответствует задача поиска пути с наименьшей длиной во взвешенном ориентированном графе.
Дерево – простой связный граф из N вершин и N-1ребер.
Большинство применяемых в сетях алгоритмов поиска маршрута с наименьшей стоимостью представляют собой вариации одного из двух алгоритмов – алгоритм Дейкстры (Dijkstra) и алгоритм Беллмана-Форда (Bellman – Ford).
Алгоритм Дейкстры.
Алгоритм находит кратчайшие пути от данной вершины-источника до всех остальных вершин, перебираю пути в порядке увеличения их длин.
Работа алгоритма проходит поэтапно.
На К-м шаге алгоритм «знает» К кратчайших путей к К вершинам, ближайшим к вершине-источнику. Эти вершины образуют множество Т.
На К+1 шаге к множеству Т добавляется вершина, ближайшая к вершине-источнику среди вершин, не входящих в Т.
При добавлении каждой новой вершины определяется путь к ней от источника.
N – множество вершин сети
S – вершина источник
T- множество уже обработанных алгоритмом вершин.
W(i,j) – стоимость линии от вершины i до j. Равнее 0 либо бесконечности, если вершины не соединены напрямую.
L(n) – минимальная стоимость пути от s (вершины-источника) до вершины n, из известных на данный момент алгоритму.
Дерево – связующее дерево для вершин множества Т, включая ребра, входящие в пути с наименьшей стоимостью от источника до каждой вершины множества Т.
Алгоритм состоит из трех шагов. 1й – инициализация, 2й и 3й повторяются до тех пор, пока количество вершин в Т не совпадет с общим числом вершин N.
Шаг 1.
Т={s} – множество исследованных вершин состоит только из вершины-источника.
L(n) = w(s,n) – стоимости начальных путей к соседним вершинам представляют собой просто стоимости линий связи.
Шаг 2.
Среди вершин j, не принадлежащих Т, ищем вершину Х, такую, что
L(x)= min L(j).
Добавляем Х к Т и к дереву. Добавляем к дереву ребро, инцидентное Х, составляющее компонент пути L(x) с минимальной стоимостью.
Шаг 3.
L(n) = mni[L(n),L(x)+w(x,n)] для всех n, не принадлежащих Т.
Т.е. обновление пути с минимальной стоимостью.
Алгоритм завершает работу, когда все вершины добавлены к Т, т.е. всего |V|=N итераций.
К моменту окончания работы алгоритма значение L(x), поставленное в соответствие каждой вершине, представляет минимальную длину пути от вершины-источника s до вершины Х. Дерево представляет собой связующее дерево исходного ориентированного графа, определяющего пути с минимальной стоимостью (длиной) от вершины-источника до всех остальных вершин. Т.е. каждый узел знает свой узел-предшественник, тот в свою очередь знает свой узел-предшественник и т.д.
Время работы алгоритма Дейкстры растет пропорционально N2. Алгоритм выполняет N-1 итерацию, а количество операций, выполняемых на каждой итерации i , пропорционально (N-i), т.е. всего надо проделать N(N+1)/2 операций.
Шаг T L(B) L(C) L(D) L(E) L(F)
----------------------------------------------------------------------------------------------------
0 A 2,A 5,A 1,A
1 AD 2,A 4,D 2,D
2 ADE 2,A 3,E 4,E
3 ADEB 3,E 4,E
4 ADEBC 4,E
5 ADEBCF
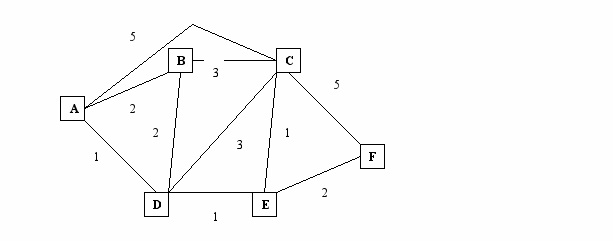
Алгоритм Беллмана – Форда.
Требуется найти кратчайшие пути от заданной вершины при условии, что эти пути состоят максимум из одного ребра, затем из двух ребер и т.д.
S – вершина-источник
W(i,j) – стоимость линии от вершины i до j. Равно бесконечности, если вершины не соединены напрямую.
H – максимальное количество ребер в пути на текущем шаге алгоритма.
L(h,n) – минимальная стоимость пути от s (вершины-источника) до вершины n, при условии что путь состоит не более чес из h ребер.
Алгоритм состоит из двух шагов – (1) инициализации и (2) обновления.
Шаг 2 повторяется до тех пор, пока стоимости путей не перестанут меняться.
Шаг 1.
L(0,n)= infinity для всех n кроме s.
L(h,s)=0
Шаг 2.
Для всех n, не равных s, вычисляем
L(H+1,n)= min [ L(h,j)+w(j,n)]
Соединяем вершину N с предыдущей j, для которой находится минимальное значение, удаляем любое соединение n с предыдущей вершиной, образованное на более ранней итерации.
ТО, при Н=К, для каждой вершины получателя n, алгоритм сравнивает потенциалтьный путь от s до n длиной К+1 с путем длиной К, существовавшим на предыдущей итерации. Если предыдущий путь имеет меньшую стоимость – он сохраняется. Если же стоимость более длинного пути меньше – то сохраняется новый путь длиной К+1. Он состоит из пути длиной К, найденном на предыдущей итерации до некоей вершины j и прямого пути от j до n. По завершении работы алгоритма имеем связующее дерево графа.
h L_h(B) L_h(C) L_h(D) L_h(E) L_h(F)
0
1 2,A-B 5,A-C 1,A-D
2 2,A-B 4,A-D-C 1,A-D 2,A-D-E 10,A-C-F
3 2,A-B 3,A-D-E-C 1,A-D 2,A-D-E 4,A-D-E-F
4 2,A-B 3,A-D-E-C 1,A-D 2,A-D-E 4,A-D-E-F
Время работы алгоритма Б–Ф пропорционально N*|E| (алгоритм выполняет N-1 итерацию, а каждая итерация включает определение веса каждого ребра.
Результаты работы алгоритмов Беллмана – Форда и Дейкстры совпадают при условии неизменности топологии и стоимости линий.
Если стоимость линий меняется со временем – нужны «динамические обобщения» алгоритмов, учитывающие изменения. Для сравнения алгоритмов в этой ситуации нужно учитывать как время работы каждого алгоритма, так и объем информации, которую требуется хранить в узлах и объем информации, которой необходимо обмениваться. Имеет значение также выбранный вариант реализации алгоритма.
Так, для алгоритма Б-Ф при рассмотрении каждой вершины требуется знание стоимости линии, связывающей данную вершину с соседними, а также суммарную стоимость пути к каждой из этих соседних вершин от источника. Каждая вершина может хранить эту информацию о путях к соседним вершинам и их стоимости и время от времени обмениваться ею со своими непосредственными соседями. ТО, для обновления данных о путях каждая вершина может применять формулу Б-Ф из шага 2, используя информацию от своих соседей
Что касается алгоритма Дейкстры – на шаге 3 каждая вершина должна обладать полной информацией о топологии сети, т.е. каждая вершина должна знать стоимость всех линий связи в сети.
Основные принципы маршрутизации
Маршрутизация включает в себя два основных компонента:
(1) определение оптимальных маршрутов,
(2) транспортировка пакетов через объединенную сеть.
Internet изначально строился как сеть, объединяющая большое количество независимых систем. С самого начала в его структуре выделяли магистральную сеть (core backbone network), а подключенные к магистрали сети рассматривались как автономные системы (autonomous system, AS).
Магистраль и каждая из автономных систем имели свои собственные административное управление и протоколы маршрутизации. Необходимо подчеркнуть, что деление на автономные системы не связано прямо с делением Internet на сети и домены имен.
Когда количество маршрутизаторов становится слишком большим – накладные расходы на вычисление, хранение и обмен данными о маршрутах становятся неприемлемыми. Для упрощения задачи и используется административная автономия.
Автономная система (AS) объединяет сети, где маршрутизация осуществляется под общим административным руководством (по общим алгоритмам выбора маршрутов и протоколам). Все автономные системы имеют уникальный 16-разрядный номер, который присваивается централизованно соответствующим административным органом Internet.
Автономная система
- представляет множество маршрутизаторов и сетей, управляемых единственной организацией,
- состоит из группы маршрутизаторов, обменивающихся информацией на основе единого протокола,
- обладает связностью (в смысле теории графов), за исключением случаев неисправностей.
Маршрутизаторы, применяемые для формирования сетей и подсетей внутри автономной системы, называются внутренними шлюзами (interior gateway), а те, с помощью которых автономные системы подключаются к магистрали сети, — внешними шлюзами (exterior gateway). Магистраль сети также является автономной системой.
Используемые внутри автономных систем протоколы маршрутизации называются протоколами внутренних шлюзов (Interior Gateway Protocol, IGP), а протоколы обмена маршрутной информацией между внешними шлюзами и шлюзами магистральной сети — протоколами внешних шлюзов (Exterior Gateway Protocol, EGP).
Изменение протоколов маршрутизации внутри какой-либо автономной системы не влияет на работу остальных автономных систем. Поэтому детальная топологическая информация остается внутри автономной системы, которую внешние шлюзы представляют для остальной части Internet как единое целое.
Алгоритмы маршрутизации
Требования к алгоритмам маршрутизации:
- Оптимальность
- Простота и низкие непроизводительные затраты
- Живучесть и стабильность
- Быстрая сходимость
- Гибкость
- Масштабируемость
Классификация алгоритмов
Алгоритмы маршрутизации могут быть классифицированы по типам:
- Простые, cтатические или динамические
- Одномаршрутные или многомаршрутные
- Одноуровневые или иерархические
- Одношаговые или многошаговые
- Внутридоменные и междоменные
- Алгоритмы состояния канала или вектора расстояний
Простые, статические или динамические алгоритмы
Простая маршрутизация:
- случайная маршрутизация, когда прибывший пакет посылается в первом попавшемся (неперегруженном) направлении, кроме исходного;
- лавинная маршрутизация, когда пакет широковещательно посылается по всем возможным направлениям, кроме исходного;
Статическая маршрутизация: таблицы маршрутизации изменяются администратором сети.
Динамические (адаптивные) алгоритмы маршрутизации подстраиваются к изменяющимся обстоятельствам сети в масштабе реального времени. Они выполняют это путем анализа поступающих сообщений об обновлении маршрутизации. Обеспечивают реакцию на неисправности и перегрузки.
Плюсы
- Можно ожидать повышения производительности для пользователей сети
- Возможность борьбы с перегрузкой сети
Минусы
– усложнение алгоритмов выбора маршрута, так что больше времени уходит на обработку.
- стратегия зависит от информации о состоянии сети. Передача такой информации, в свою очередь, сама создает нагрузку на сеть.
- Применение адаптивных стратегий в определенных ситуациях может приводить к зацикливаниям и другим патологиям.
Одномаршрутные или многомаршрутные алгоритмы. Некоторые сложные протоколы маршрутизации обеспечивают множество маршрутов к одному и тому же пункту назначения.
Одноуровневые или иерархические алгоритмы
Некоторые алгоритмы маршрутизации оперируют в плоском пространстве, в то время как другие используют иерархии маршрутизации.
В иерархических системах маршрутизаторы домена могут сообщаться с маршрутизаторами других доменов. В одноуровневых системах - только в пределах своего домена
Одношаговые или многошаговые алгоритмы
В таблицах маршрутизации для каждого адреса назначения указывается только следующий маршрутизатор, а не вся их цепочка от начального до конечного узла. В соответствии с этим подходом маршрутизация выполняется по распределенной схеме — каждый маршрутизатор отвечает за выбор только одного этапа пути, а окончательный маршрут складывается в результате работы всех маршрутизаторов, через которые проходит данный пакет. Такие алгоритмы маршрутизации называются одношаговыми.
Одношаговая маршрутизация с помощью IP-адресов
В стеке TCP/IP маршрутизаторы и конечные узлы принимают решения о том, кому передавать пакет для его успешной доставки узлу назначения, на основании так называемых таблиц маршрутизации (routing tables). Вид зависит от конкретной реализации маршрутизатора.
Следующая таблица представляет собой типичный пример таблицы маршрутов, использующей IP-адреса сетей. В этой таблице в столбце "Адрес сети назначения" указываются адреса всех сетей, которым данный маршрутизатор может передавать пакеты. В стеке TCP/IP принят так называемый одношаговый подход к оптимизации маршрута продвижения пакета (next-hop routing) - каждый маршрутизатор и конечный узел принимает участие в выборе только одного шага передачи пакета.
| Адрес сети назначения | Адрес следующего маршрутизатора | Номер выходного порта | Расстояние до сети назначения |
| 56.0.0.0 | 198.21.17.7 | 1 | 20 |
| 56.0.0.0 | 213.34.12.4. | 2 | 130 |
| 116.0.0.0 | 213.34.12.4 | 2 | 1450 |
| 129.13.0.0 | 198.21.17.6 | 1 | 50 |
| 198.21.17.0 | - | 2 | 0 |
| 213. 34.12.0 | - | 1 | 0 |
| default | 198.21.17.7 | 1 | - |
Если в таблице маршрутов имеется более одной строки, соответствующей одному и тому же адресу сети назначения, то при принятии решения о передаче пакета используется та строка, в которой указано наименьшее значение в поле "Расстояние до сети назначения".
Существует и прямо противоположный, многошаговый подход — маршрутизация от источника (Source Routing). В соответствии с ним узел-источник указывает в отправляемом в сеть пакете полный маршрут его следования через все промежуточные маршрутизаторы. Такой способ не требует построения и анализа таблиц маршрутизации. Это ускоряет прохождение пакета по сети и разгружает маршрутизаторы, но при этом большая нагрузка ложится на конечные узлы.
Внутридоменные или междоменные алгоритмы
Некоторые алгоритмы маршрутизации действуют только в пределах доменов; другие - как в пределах доменов, так и между ними.
Дистанционно-векторные алгоритмы (Distance Vector Algorithm, DVA);
В алгоритмах дистанционно-векторного типа (которые представляют собой распределенное приложение алгоритма Бэлмана-Форда) каждый маршрутизатор периодически и широковещательно рассылает по сети вектор, компонентами которого являются расстояния от данного маршрутизатора до всех известных ему сетей. Под расстоянием обычно понимается число транзитных узлов. Получив вектор от соседа, маршрутизатор пересчитывает таблицу и рассылает новое значение вектора по сети. В конце концов, каждый маршрутизатор узнает информацию обо всех сетях и о расстоянии до них через соседние маршрутизаторы.
Основная структура ВДА – таблица расстояний, где указаны расстояния до каждого из узлов сети через каждого ближайшего соседа.
Строки: все узлы сети – адресаты,
Столбцы: узлы - ближайшие соседи.
Т.О., каждый узел знает наименьшую стоимость пути от каждого из своих соседей до каждого адресата. Когда он вычисляет новую минимальную стоимость – он сообщает об этом всем своим соседям. Те обновляют свои таблицы, делают свои вычисления в рамках алгоритма Б-Ф и сообщают результат (новую минимальную стоимость), в свою очередь, своим соседям и т.д., пока ситуация не устаканится, т.е. пока стоимости не перестанут изменяться. С этого момента алгоритм становится статическим и не меняется до тех пор, пока стоимость какой-либо линии не изменится.
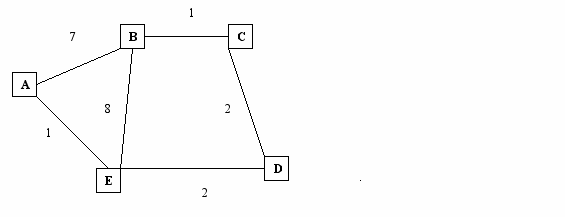
Пример. Таблица стоимости пути от Е до адресата через соседние узлы.
Адресат A B D
A 1 14(EBCDEA) 5(EDEA)
B 7(EAEDCB) 8 5(EDCB)
C 6(EAEDC) 9(EBC) 4(EDC)
D 4(EAED) 11(EBCD) 2
Алгоритмы состояния каналов (Link State Algorithm, LSA).
Алгоритмы состояния каналов (основаны на алгоритме Дейкстры) позволяют каждому маршрутизатору получить достаточную информацию для построения точного графа связей сети. Все маршрутизаторы работают на основании одинаковых графов, в результате процесс маршрутизации оказывается более устойчивым к изменениям конфигурации. «Широковещательная» рассылка производится только при изменениях состояния связей, что в надежных сетях происходит не так часто.
Во время инициализации маршрутизатор определяет стоимость линий для каждого из своих интерфейсов. Далее он передает эту информацию всем узлам объединенной сети. Далее маршрутизатор следит за состоянием своих линий, при значительном изменении он вновь объявляет о стоимости своих линий все остальным маршрутизаторам конфигурации.
Каждый маршрутизатор имеет информацию от всех маршрутизаторов конфигурации и может рассчитать кратчайший путь к каждой сети и сформировать таблицу маршрутизации с данными о первом ретрансляционном участке в направлении потенциального получателя.
Алгоритмы LS фактически направляют небольшие корректировки по всем направлениям, в то время как ВД алгоритмы отсылают более крупные корректировки только в соседние маршрутизаторы.
Сравнение двух алгоритмов.
- Объем обмена данными. VDA – каждый маршрутизатор посылает сведения о маршрутах своим соседям. LSA – каждый маршрутизатор посылает сведения о маршрутах всем остальным маршрутизаторам.
- Тип посылаемой информации. VDA – оценка стоимости путей ко все сетям. LSA – точная стоимость линий к смежным сетям.
- Частота обмена. VDA – информация посылается регулярно, через определенные промежутки времени (30 сек.) LSA – информациа посылается в случае значительных изменений.
- Алгоритм. VDA – На основе полученных оценок стоимости путей маршрутизатор выбирает следующий ретрансляционный участок в рамках распределенного алгоритма Б-Ф. LSA – Маршрутизатор сначала строит описание топологии сети, а потом может пользоваться любым алгоритмом для выбора маршрута. На практике используетсмя алгоритм Дейкстры.
Борьба с патологиями и перегрузкой.
Расщепление горизонта (split horizon) - нет смысла посылать информацию в том направлении, откуда она пришла, т.к. маршрутизатор, посылающий информацию – ближе к источнику изменений, чем вы. Ускорение процесса обнаружения разрыва сети.
Правило негодного встречного маршрута (poisoned reverse) – устанавливается счетчик обновлений (16). Если у двух маршрутов маршрутизаторы указывают друг на друга – объявление о встречных маршрутах с расстоянием 16 немедленно прерывает цикл.
Устанавливается конечное время жизни каждой записи в таблице маршрутизации. (180 сек=30 сек*5). Если запись не обновилась – она считается недействительной.
Показатели алгоритмов (метрики маршрутизации)
Метрики -– значения стоимости, поставленные в соответствие каждому ретрансляционному участку) – могут назначаться разными способами. Выбор метрики отражается в заголовке IP-протокола.
- Длина маршрута определяется числом промежуточных узлов, точнее – числом ретрансляционных участков (хопов). Каждому участку назначается стоимость 1. Минимизируется объем вычислений.
- Максимальная Надежность. Метрика настраивается заранее либо основывается на недавней истории неисправностей.
- Минимальная Задержка. Зависит от времени пересылки по конкретному участку, определяется задержкой распространения сигнала в соответствии физическими параметрами канала и средней задержкой стояния в очереди, которая динамически измеряется каждым маршрутизатором.
- Ширина полосы пропускания. Максимальная пропускная способность. Метрика заранее настраивается на основе скорости передачи данных. Длительность бита в наносекундных интервалах. 10-мегабитный канал – 10. 56-килобитная линия 1785.
- Минимальная Стоимость Связи. Может использоваться если для линий связи может быть назначена реальная денежная сумма.
Пример колебательного процесса для алгоритма состояния связей.
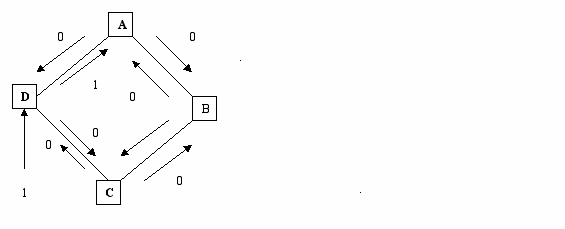
Пусть стоимость линий определяется трафиком.
Узел С видит путь с наименьшей стоимостью до А – СВА.
Узел В видит путь до А – ВА.
Поэтому оба узла направляют свой трафик против часовой стрелки.
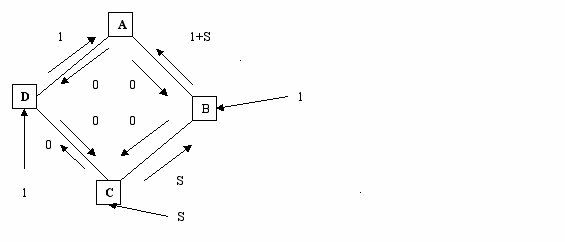
При следующем запуске алгоритма узлы С и В «видят», что трафик по часовой стрелке «дешевле», так что определяют пути наименьшей стоимости по часовой стрелке. С: СDА, В: ВСDА
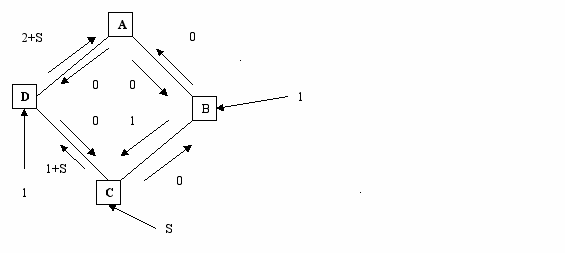
При следующем запуске алгоритма узлы В,С,D обнаруживают, что путь по часовой стрелке более дорогой и снова одновременно меняют направление трафика.
