Ун-т «Дубна». Курс «Компьютерные сети»

Вид материала

Лекция

Содержание Мерой информации Групповое кодирование Код Хаффмана По поводу последнего требования Факсимильное сжатие Код Хаффмана Модифицированный код Хаффмана. Арифметическое кодирование. Алгоритм LZ77 4 режима работы DCT Квантование Сжатие без потерь. Формат с переменным разрешением Произвольный доступ Произволный доступ Быстрая перемотка взад\вперед

Подобный материал:

• Ун-т «Дубна». Курс «Компьютерные сети», 408.34kb.
• Ун-т «Дубна». Курс «Компьютерные сети», 488.73kb.
• Ун-т «Дубна». Курс «Компьютерные сети», 371.9kb.
• Ун-т «Дубна». Курс «Компьютерные сети», 560.01kb.
• Ун-т «Дубна». Курс «Компьютерные сети», 276.95kb.
• Ун-т «Дубна». Курс «Компьютерные сети», 546.8kb.
• Ун-т «Дубна». Курс «Компьютерные сети», 676.23kb.
• Урок по теме «Компьютерные сети. Интернет», 157.31kb.
• Ун-т «Дубна». Курс «Компьютерные сети», 611.15kb.
• Лекция Глобальные сети. Интернет. Корпоративные компьютерные сети, 89.75kb.

Ун-т «Дубна». Курс «Компьютерные сети».

Лекция 8.

- Методы сжатия данных

- Алгоритмы сжатия без потерь

- Алгоритмы сжатия с потерями

- Стандарты JPEG, MPEG

Принципы сжатия данных

Несмотря на постоянно увеличивающуюся пропускную способность сетей, пользовательские приложения сталкиваются с задержками передачи данных из-за постоянного растущего объема трафика.

Сжатие данных предоставляет возможность при сохранении пропускной способности сети снизить задержки, с которыми сталкиваются приложения. Поэтому методы сжатия данных являются важным аспектом передачи данных по компьютерным сетям.

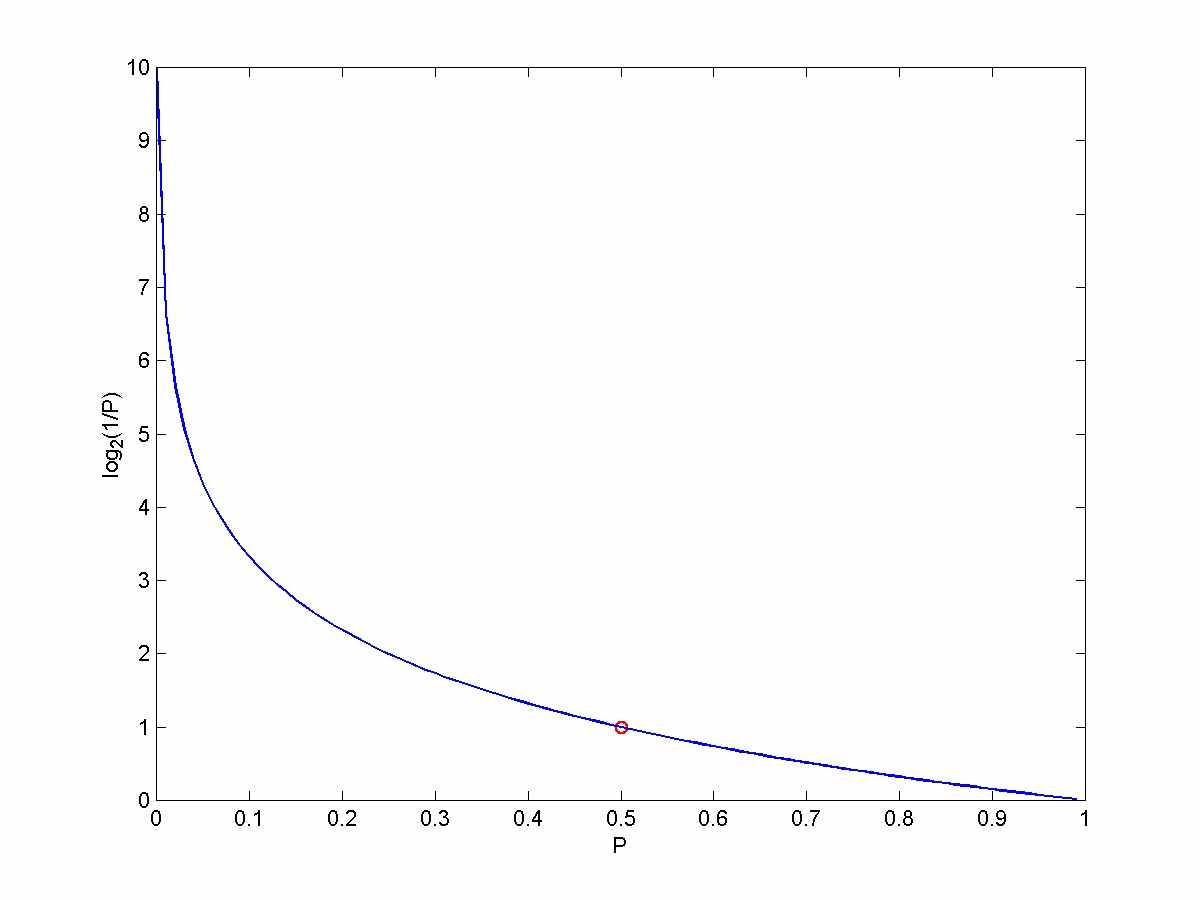
Мерой информации может служить величина, обратная вероятности некоторого события. Эту количественную единицу информации предложил в 1928 году Хартли, изучая телеграфную связь.

I(x) = log₂(1/P(x)) = -log(P(x)).

Единица информации называется битом.

Один бит, с равной вероятностью принимающий значения 0 и 1, несет в себе один бит информации: Log₂(1/0.5)=1. Строка из двух битов может принимать 4 равновероятных значения, так что Log₂(1/0.25)=2. Таким образом, второй бит добавляет один бит информации.

Когда вероятность события приближается к 1, количество информации приближается к 0. Наоборот, когда вероятность события приближается к 0, количество информации растет в бесконечность.



Концепция энтропии была предложена в 1948г Шенноном.

Энтропия – это среднее количество информации, получаемое от значения случайной переменной.

Пусть имеется случайная переменная Х, способная принимать значения х1, х2, х3, … соответственно с вероятностями Р(х1), Р(х2), … В последовательности из К переменных результат х с номером М будет выбран в среднем К*Р(х_М) раз. Тогда среднее количество информации, получаемое от К событий, составит

S = К*Р₁*log(1/P₁) + … + K*P_N*log(1/P_N), где P_N = P(x_N).

H(X) = S/K = ₁^N P_j*log(1/P_j) = -₁^N P_j*log(P_j).

Величина H называется энтропией Х.

Пример. Пусть Х принимает два значения Р и (1-Р).

Н(Р,1-Р) = -Р*log(P)-(1-P)*log(1-P).



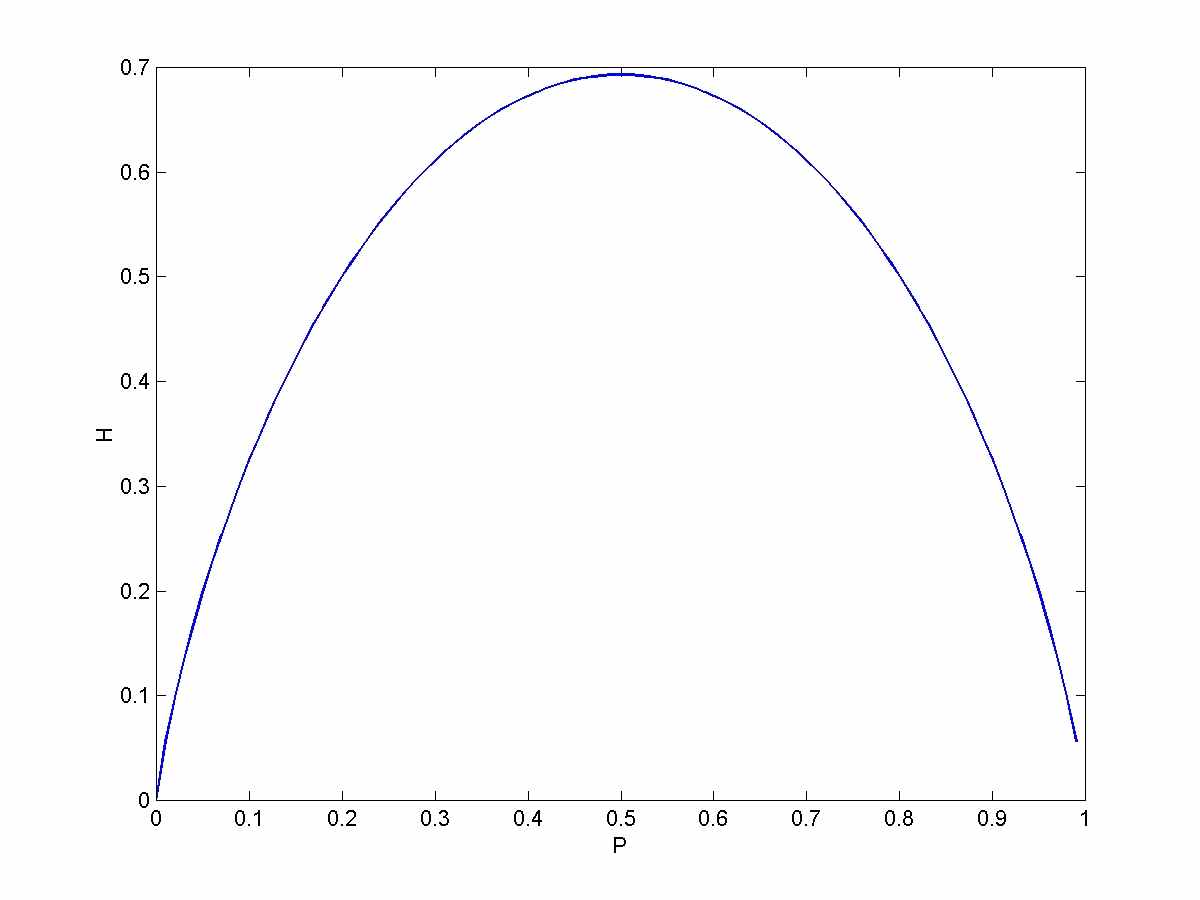
Если одно из событий Р или (1-Р) является достоверным, т.е. если Р принимает значения 0 либо 1, то Н = 0. Максимальное значение Н достигается при Р=0.5, т.е. когда события равновероятны.

Можно показать, что для случайной переменной с К результатами ее энтропия также будет максимальной, когда результаты равновероятны.

Одно из важных приложений концепции энтропии – алгоритмы сжатия данных. Энтропия определяет количество битов, требуемых для представления данных без потери информации – т.е. в рамках алгоритмов сжатия данных энтропия представляет собой меру максимально возможного сжатия без потерь. Можно показать, что оптимальный код позволяет получить среднюю длину кодового слова, не более чем на 1 бит, превышающую энтропию исходного набора символов.

Принцип сжатия состоит в следующем. Практически все формы представления данных (текст, числа, видео и т.д.) содержат избыточные элементы. Данные могут быть сжаты с целью экономичного хранения и снижения потребностей в пропускной способности. Когда данные прибывают по сети либо извлекаются из места хранения, должна быть возможность их распаковать, восстановив исходную форму. Для этого при сжатии удаляемые элементы должны замещаться другими (кодироваться) таким образом, чтобы пользователь мог восстановить исходную информацию.

Существуют две основные разновидности сжатия данных – сжатие без потерь (lossless compression) и сжатие с потерями (loss compression).

При сжатии без потерь информация не теряется, восстановленные данные идентичны исходным. Эффективность сжатия без потерь ограничена энтропией источника данных.

В случае сжатия с потерями распакованные данные могут быть приемлемым (в соответствии с некоторым критерием) приближением к исходным данным. Например, при сжатии изображений критерием является неотличимость с точки зрения человеческого глаза восстановленных изображений от исходных.

Сжатие без потерь.

Методы группового кодирования.

Один из старейших и простейших методов сжатия известен как метод подавления нулей или подавления пробелов (null suppression, blank suppression). До сих пор применяется в IBM-ском протоколе BISYNC (Binary Synchronous Communication Protocol – двоичный синхронный протокол связи).

Данные сканируются в поисках строк нулей (пробелов), каждая последовательность нулей заменяется двух-символьным кодом, состоящим из специального символа и числа пробелов в строке. Такая схема позволяет сделать короче все строки из трех и более пробелов (нулей). Оценки показывают, что экономия может даже от такого простого метода составить от 30 до 50 %.

Групповое кодирование – обобщение метода подавления нулей. Применяется для подавления повторяющихся данных любого типа. Счетчик ищет последовательности повторяющихся символов и заменяет их трехсимвольным кодом, состоящим из специального символа – индикатора сжатия, за которым следует повторяющийся символ и число повторений. Таким образом, данный подход позволяет сократить любые последовательности повторяющихся символов длиной 4 и больше. Коэффициент сжатия (отношение длины несжатого текста к длине сжатого) зависит от текста, но в среднем составляет 1.5.

Код Хаффмана

Пусть есть случайная переменная Х, принимающая 8 значений хj с определенными вероятностями Pj. Мы хотим закодировать сообщение, состоящее из последовательности случайных выпадений xj в двоичном виде. Один из вариантов состоит в кодировании сообщения трех-битовыми комбинациями (их как раз 8 вариантов).

Более экономичная стратегия состоит в использовании кода переменной длины, причем более длинные двоичные слова назначаются наименее вероятным значениям переменной Х, а более вероятные слова кодируются более короткими словами. Такой технический прием реализован в азбуке Морзе и лежит в основе алгоритма Хаффмана. Можно показать, что оптимальный код должен удовлетворять требованиям

(1) никакие два разных сообщения не должны состоять из одинаковых последовательностей битов. Гарантируется уникальность кодирования любого сообщения.

(2) никакое кодовое слово не должно совпадать в префиксом другого кодового слова. Гарантируется, что сообщение может быть декодировано шаг за шагом: при продвижении слева направо – как только последовательность совпадет с кодовым словом, декодирующий алгоритм производит соответствующее назначение.

(3) Символы с большей вероятностью должны кодироваться более короткими кодовыми словами. Если P1
(4) Два кодовых символа с наименьшей вероятностью должны иметь одинаковую длину и отличаться только последней цифрой.

Пример кода, нарушающего два первых требования.

Х1 – 0; х2 – 010; х3 – 01; х4 – 10.

Двоичная последовательность 010 может соответствовать одному из трех сообщений: х2; х3 х1; х1 х4.

По поводу последнего требования. Действительно, пусть LN>L(N-1). Кодовое слово N-1 не может быть префиксом кодового слова N. Поэтому первые N-1 цифры кодового слова N составляют уникальную комбинацию, следовательно, последнюю цифру можно отбросить, поскольку различие все равно есть в каком-нибудь другом разряде, кроме последнего.

Итак, собственно алгоритм Хаффмана. Сначала упорядочиваем символы по убыванию вероятностей. Объединяем последние два символа в один с вероятностью, равной сумме их вероятностей. Их коды будут одинаковыми, кроме последнего разряда, назначаем 0 и 1. Теперь имеем новый набор из N-1символов. Располагаем их снова по убыванию вероятностей, присваиваем 0 и 1 последним двум символам (это будет предпоследний разряд) и повторяем всю процедуру заново до тех пор, пока символы не кончатся.

Пример.

X1 – 0.55 x1 0.55 x1 0.55 (0) 0

X2 – 0.20 x3+x4 0.25 (0) x3+x4+x2 0.45 (1) 11

X3 – 0.15 (0) x2 0.20 (1) 100

X4 – 0.10 (1) 101

Метод Хаффмана является простым и относительно эффективным в реализации. Данный подход лежит в основе многих алгоритмов сжатия.

Можно показать, что он позволяет достичь максимального сжатия, если все вероятности представляют собой отрицательные степени 2. Можно также показать, что эффективность кода Хаффмана повышается, если кодировать не отдельные символы, а блоки символов.

Факсимильное сжатие (сжатие изображений).

Черные и белые точки кодируются нулями и единицами, далее производится групповое сжатие. Сейчас используются другие методы.

Код Хаффмана. Последовательности черных и белых точек разной длины можно рассматривать как элементы алфавита источника, которые кодируются по алгоритму Хаффмана. Однако получается слишком длинный алфавит, соответственно длина кода тоже очень большая.

Модифицированный код Хаффмана. Длина каждой серии черных и белых точек представляется как величина, кратная 64 плюс остаток. Тогда каждая серия точек может быть представлена парой чисел (кратность и остаток). Эти значения кодируются методом Хаффмана (отдельно для кратностей и для остатков).

Код READ

Дополнительного увеличения производительности можно добиться, если учитывать корреляцию между последовательностями черных и белых серий точек на соседних линиях. Как правило, в типичных документах около 50% черно-белых переходов находятся точно под соответствующими переходами в предыдущей строке, а еще 25% отличаются всего на одну точку. Поэтому с большой эффективностью можно определить порядка 75% переходов цвета.

Длины серий кодируются в соответствии с расположением так называемых переключающих элементов – это точка цвета, отличного от цвета предыдущей точки на той же самой линии.

Переключающий элемент кодируется расстоянием до одной из двух опорных точек – либо предыдущего переключающего элемента на той же линии, либо переключающего элемента предыдущей линии (в зависимости от конфигурации, срабатывает вертикальный или горизонтальный режим).

Как правило, переключающие элементы находятся в пределах трех позиций от предыдущего по вертикали или горизонтали. Так что требуется не слишком много элементов для кодирования на основе метода Хаффмана.

В тех редких случаях, когда переключающий элемент находится вдали от переходов на предыдущей линии – следующие две серии кодируются на основе модифицированного алгоритма Хаффмана.

Кроме того, «для верности», на каждой К-й линии осуществляется кодирование по Хаффману. Число К зависит от разрешения.

Арифметическое кодирование.

Арифметическое кодирование предназначено для более высоких коэффициентов сжатия за счет усложнения вычислений. Изображение обрабатывается таким образом, чтобы вероятности приближались к степеням 2. Используется в стандартах jpeg и mpeg.

Как уже сказано – средняя длина кода для символьного набора Х не может быть меньше энтропии Н(Х), т.е. энтропия – нижняя граница объема сжатых данных.

При объединении символов и кодировании блоков по К символов получим

H(X) < E(L)/K < H(X)+1.

Т.О. существует способ повышения эффективности алгоритма сжатия за счет кодирования блоков.

Если нужно отправить сообщение длиной N символов, мы можем использовать блок длиной N, т.е. обращаемся с каждым сообщением как с одним из MN возможных результатов, где М – количество атомарных символов, N – длина сообщения.

Вероятность появления каждого символа и каждой последовательности символов длины < N откладывается как соответствующий интервал на единичном отрезке. Далее, каждый интервал кодируется – код соответствует двоичному представлению дробной части интервала.

Алгоритмы совпадения строк.

Метод Хаффмана и арифметическое кодирование основаны на знании статистики сжимаемых данных. При этом последовательности символов фиксированной длины кодируются кодами переменной длины. Другой подход – алгоритмы совпадения строк. Входные последовательности переменной длины кодируются в коды фиксированной длины. Не требуется априорная оценка статистики.

В 1977 Зива (Zib) и Лемпель (Lempel) предложили алгоритм LZ77, который положил начало серии алгоритмов, используемых в pkzip, gzip, gif и др.

Используется факт, что слова и фразы в потоке текста (элементы изображений) повторяются с большой вероятностью. Когда встречается повторяющаяся последовательность, она может быть заменена коротким кодом (фиксированной длины). Программа сжатия ищет подобные участки и формирует коды, которыми заменяет эти участки на выходе. Те же коды, в принципе, в дальнейшем могут использоваться для обозначения новых последовательностей. Надо только, чтобы алгоритм был определен таким образом, чтобы знать текущее соответствие между кодами и последовательностями исходных данных.

Алгоритм LZ77

Исходный текст преобразуется в двоичный код – каждый символ кодируется 1+8-разрядный двоичный АSCII-код. Далее ищем совпадения.

Используются два буфера. В скользящем буфере предыстории хранятся N только что обработанных символов источника, а в упреждающем буфере – следующие L символов. Алгоритм пытается найти соответствие между двумя и более символами из начала упреждающего буфера и строкой в скользящем буфере предыстории.

Если соответствие не обнаружено, первый символ сдвигается из упреждающего буфера в буфер предыстории, а самый старый символ из буфера предыстории отбрасывается. При этом проверенный символ выводится в окончательный текст в исходном виде (1+8-разрядный двоичный АSCII-код).

Если соответствие найдено – ищем самое длинное совпадение. Оно кодируется тремя символами (индикатор, указатель, длина), затем скользящее окно сдвигается на столько символов, сколько было закодировано.

Недостатком является конечный размер окна. Если окно маленькое – многие совпадения не будут обнаружены. Если окно большое – существенно увеличивается объем работы.

LZ78, LZW

Проблема с размером окна обходится путем создания словаря вместо окна. В словарь помещаются все одно-символьные строки и соответствующие коды. Далее, добавляются по мере работы алгоритма много-символьные строки, а также соответствующие коды.

Просматривая текст, алгоритм ищет в словаре строку максимальной длины, совпадающую с входной строкой. Если совпадение обнаружено, она кодируется в выходном тексте кодом из словаря, а в словарь включается строка, представляющая найденное совпадение плюс следующий символ, если только длина строки не достигла заранее заданной максимальной длины. Этой новой строке присваивается код. В следующий раз будет возможность закодировать в выходном тексте более длинную последовательность символов.

Таким образом, входные символы обрабатываются, чтобы получить совпадающие строки все большей и большей длины, пока длина строк не достигнет заранее заданной длины.

Пример. A B A B C B A B A B A A A A A A

Сначала в словаре имеем все односимвольные строки:

A – 1; B – 2; C – 3.

Смотрим первый символ А. Найдено совпадение с одно-символьной строкой из словаря. Кодируем слово А кодом 1. Включаем в словарь двух-символьную строку АВ – 4.

Смотрим второй символ В. Найдено совпадение с одно-символьной строкой из словаря. Кодируем слово В кодом 2. Включаем в словарь двух-символьную строку ВА – 5.

Смотрим третий символ. Найдено совпадения 3го и 4го символов с двухсимвольной строкой АВ. Кодируем 3й и 4й символы кодом 4. Включаем в словарь трех-символьную строку АВС – 6.

Смотрим 5й символ. Найдено совпадение с одно-символьной строкой С. Кодируем слово С кодом 3. Включаем в словарь двух-символьную строку СВ – 6.

Смотрим 6й символ. Найдено совпадение с двух-символьной строкой ВА. Кодируем слово ВА кодом 5. Включаем в словарь трех-символьную строку ВАВ – 7. И так далее.

Словарь не передается явно алгоритму распаковки. Вместо этого алгоритм распаковки создает идентичный словарь в процессе распаковки. Это возможно благодаря тому, что строка, соответствующая коду, всегда встречается раньше самого кода.

Сжатие с потерями

Сжатие без потерь накладывает жесткую нижнюю границу на размер любого файла или сообщения. Этой границей является энтропия этого файла. Сжатие без потерь позволяет восстановить исходные данные с точностью до бита. Эта характеристика необходима для текстовых файлов, баз данных, объектных модулей и т.д. Однако существует много типов файлов, для которых не требуется абсолютно точного восстановления исходных данных. К ним относятся, например, аудио- и видео-клипы и неподвижные изображения. В этих случаях допускается некоторое количество ошибок при восстановлении исходных данных, так что может применяться сжатие с потерями. Ключевым вопросом сжатия с потерями является компромисс между коэффициентом сжатия и точностью восстановления данных. Понятно, что чем выше степень сжатия, тем ниже качество восстановленных данных. Цель любого алгоритма сжатия с потерями состоит в достижении высоких коэффициентов сжатия за счет потери некоторых битов таким образом, чтобы восстановленные данные были достаточно близки к оригиналу.

Дискретное косинусное преобразование (Discrete Cosine Transform)

Этот метод представляет собой преобразование массива пикселов в массив коэффициентов DCT (значений пространственной частоты). Метод обратим с точностью до ошибок округления. DCT сам по себе не производит сжатия, но преобразует данные в форму, удобную для сжатия.

Для обозначения яркости пикселов черно-белого изображения используются, как правило, 8-битовые значения, так что 0 означает белый цвет, а 255 – черный. Обычно производится смещение уровня отсчета: от -128 до 127. Обработка цветного изображения производится аналогично, отдельно по каждой из трех цветовых компонент (красный, желтый, синий).

Таким образом, после оцифровки имеем массив (матрицу) данных, к которым применяем дискретное косинусное преобразование.

В результате применения DCT мы получаем вместо исходного массива данных массив той же размерности для коэффициентов DCT. На их основе путем обратного дискретного преобразования можно восстановить исходные данные с точностью до ошибок округления.

Фишка в том, что исходные данные представляются как сумма косинусных функций разной частоты с разными коэффициентами. Поскольку обычно в изображениях нет резких переходов яркости, т.е. данные в этом смысле «гладкие», можно ожидать, что коэффициенты при косинусах с высокими частотами (большие N) окажутся малыми, и этими коэффициентами можно будет пренебречь. За счет отбрасывания малых коэффициентов как раз и достигается экономия. Восстановленное с уменьшенным числом коэффициентов изображение (по формулам обратного DCT-преобразования) будет мало отличаться от исходного.

Недостаток состоит в «размытых» переходах при передаче изображения c резкими переходами яркости.

Волновое сжатие (DWT)

Метод дискретного вейвлет-преобразования (Discrete Wavelet Transform) основан на тех же принципах. Исходные данные представляются в виде суммы элементарных вейвлет-функций с соответствующими коэффициентами. Отличие в том, что вейвлет-функции определены на конечном участке значений аргумента, а для остальных значений аргумента равны 0. Каждая вейвлет-функция представляет собой растянутую или суженную единичную элементарную волну, называемую материнской. Путем вейвлет-преобразования можно получить для сигнала, протяженного по времени, или изображения соответствующие DWT-коэффициенты, которые, как и в случае DCT, позволяют упростить обработку сигнала или изображения. В том числе, можно отбросить члены с незначительным вкладом. С другой стороны, добавляя все более сжатые компоненты, можно представлять сигнал или изображение, вообще говоря, с произвольной степенью разрешения.

Простейшей элементарной волной, применяемой в вейвлет-анализе, является волна Хаара – Haar wavelet. Из базовой волны получается набор функций.

_________________________________________________________



Стандарт JPEG

Группой JPEG (Joint Photography Experts Group) разработан набор стандартов сжатия неподвижных изображений с непрерывно изменяющимся тоном – как монохромных, так и цветных. Стандарт JPEG создавался для удовлетворения широких потребностей – от издательских систем и передачи фотографий по сетям до использования изображений в медицинских целях.

Типичное оцифрованное изображение (фотография) занимает порядка 700 000 кбайт. Передача его по каналу с пропускной способностью 64 Кбит\сек займет около полутора минут. Стандарт JPEG позволяет уменьшить объем в 24 раза, до 30 000 кбайт, так что для передачи по той же 64-килобитной линии потребуется менее 4 секунд.

Стандартом JPEG определено 4 режима работы.

Последовательный режим, основанный на DCT. Фазы сжатия и распаковки состоят из трех основных этапов. Алгоритм последовательно обрабатывает 8\8-пиксельные блоки потока монохромного изображения. Сжатие цветного изображения включает сжатие каждого из трех цветовых компонентов по очереди.

1. DCT
   
2. Квантование. На вход поступает матрица S. Для заданной таблицы квантования Q для каждого элемента матрицы S вычисляется Q/S и округляется до целого. На выходе получаем матрицу квантованных DCT-коэффициентов в виде 8-битовых значений (на самом деле коэффициенты были более длинные, так что происходит экономия за счет округления), содержащую много нулей в ячейках со старшими номерами столбцов\строк (правая нижняя часть матрицы). При удачном подборе таблицы квантования (при малых индексах столбцов\строк значения меньше, при больших большие) можно добиться высокого коэффициента сжатия при еле заметных для человеческого глаза искажениях.
   
3. Сжатие без потерь. Сначала из квантованной DCT-матрицы вычитаются элементы предыдущего блока. Поскольку элементы соседних блоков не слишком сильно отличаются – получаем более маленькие числа и много нулей. Затем элементы разностной матрицы упорядочиваются зигзагообразно. В результате получается строка с длинной последовательностью нулей в конце, которая заменяется символом конца строки. Эта строка кодируется уже энтропийным методом (Хаффмана или АК).
   

При распаковке применяется обратная последовательность шагов. Полученный результат будет отличаться от исходной матрицы (главным образом, в области высоких частот).

Прогрессивный режим DCT.

Используется для быстрого получения приблизительного декодируемого изображения. Полезен, если декодер отделен от кодера каналом с низкой пропускной способностью. Наблюдатель быстро получает грубое приближение к изображению, после чего постепенно видит все более четкие версии. В этом методе изображение отображается за несколько проходов.

В методе спектральной селекции на первом проходе передается только элемент (0,0) DCT-матрицы, На следующем проходе – другие элементы в зигзагообразном порядке.

В методе последовательного приближения элементы (0,0) также посылаются отдельно, затем на каждом проходе посылается все большее число разрядов DCT-коэффициентов. Таким образом их точность возрастает с каждым проходом.

Режим без потерь.

Позволяет достичь сжатия только в два раза. Обрабатывается сразу все матрица пикселов изображения, а не отдельные блоки. Используется прогнозирующая модель. Из каждого элемента матрицы изображения вычитается предсказательное значение, основанное на значениях уже обработанных соседних пикселов. В результирующейматрице многие значения равны 0, а другие невелики, что позволяет ее упаковать более компактно по сравнению с исходной.

Далее производится энтропийное кодирование по Хаффману или АК.

Иерархический режим.

Кодирующий модуль на основе любого из предыдущих режимов формирует последовательность изображений с убывающим в два раза разрешением до заданного минимального значения разрешения. Фактически, производится фильтрация низких частот. Далее изображение с минимальным разрешением сжимается в одном из режимов. Изображение с более высоким разрешением получается из негу путем распаковки, интерполяции запаковки результата.Эти шаги повторяются до получения изображения с нужным разрешением. Данный режим дает возможность увидеть изображение на устройствах с разной разрешающей способностью.

Стандарт JPEG 2000

- Вместо DCT используется DWT, что обеспечивает лучшее воспроизведение резких переходов.

- Формат с переменным разрешением. Изображение хранится с несколькими разрешениями без избыточности.

- Область интереса. Возможность кодирования части изображения с более высоким качеством. Прогрессивная передача данной области прежде всего остального изображения.

- Произвольный доступ. Возможность доступа к части изображения без распаковки всего изображения.

Стандарт MPEG

Стандарт MPEG (работы начаты в 1988) разработан для хранения и передачи сжатых видеоизображений и ассоциированного с ними звука. Видеосигнал может быть сжат до скорости передачи 1.5 Мбит\сек, что обеспечивает приемлемое качество воспроизведения.

Движущееся изображение представляет собой последовательность неподвижных картинок. Соответственно, можно добиться сжатия, независимо сжимая каждый кадр. Но можно добиться и большего, учитывая, что разница между соседними кадрами невелика. Исследования показывают, что использование «избыточности» кадров позволяет дополнительно сжать данные в три раза.

Видеоизображение рассматривается как последовательность кадров. Кадр обрабатывается по типу неподвижного изображения (DCT, квантование, Хаффман). Это внутрикадровый режим.

В межкадровом режиме сходные блоки пикселей заменяются указателем на один из блоков. Главное – в процессе распаковки расположить кадры в правильном порядке.

При этом необходимо обеспечить

1. Произволный доступ. Доступ к любой точке последовательности видеокадров. Любой кадр должен быть декодирован за ограниченное время. Значит должны быть кадры доступа, закодированные только во внутрикадровом режиме.
   
2. Быстрая перемотка взад\вперед. Этот эффект по сути представляет более сложную форму произвольного доступа.
   

В основе алгоритма межкадрового сжатия MPEG лежит идея компенсации движения. Этот подход основан на том, что часть изображения в кадре остается неизменной и мало отличается от соседнего кадра. Поэтому промежуточные кадры можно восстанавливать на основе опорных кадров. Для компенсации движения (motion compensation) используются два подхода – предсказание и интерполяция.

При интерполяции кодирование промежуточных кадров производится на основе двух соседних опорных (следующего и предыдущего).

При предсказательном кодировании используется предыдущая информация – опорный кадр (якорный кадр, anchor frame) и «вектор движения», отражающий динамику изменения «подвижной» части текущего кадра относительно якорного.

Таким образом, у нас три типа кодирования кадров

1. Intraframe (I). Внутренний кадр, независимое неподвижное изображение. Кодируется по стандарту JPEG.
   
2. Predicted frame (P). Кадр, закодированный с учетом предыдущего, якорного, кадра.
   
3. Bidirectional interpolated frame (B). Кадр, закодированный с помощью предыдущего и последующего якорных кадров.
   

Внутренние кадры используются как кадры доступа при перемотке. Интерполяционные кадры могут кодироваться только на основе внутренних и предсказанных. Сам интерполяционный кадр не может быть опорным для другого интерполяционного кадра. Каждый предсказанный кадр кодируется на основе предыдущего внутреннего либо предсказанного кадра. Кадры объединяются в группы, состоящие из одного опорного кадра, нескольких предсказанных и нескольких интерполированных кадров. Сначала распаковываются опорные кадры, затем на их основе декодируются предсказанные, а далее – интерполированные кадры.

Пример: I В B P B P B I В B P B P B I В B P B P B