Автор Ридель Валерий Вольдемарович учебно-методический комплекс
| Вид материала | Учебно-методический комплекс |
- Самме Георгий Вольдемарович (ф и. о.) учебно-методический комплекс, 259.31kb.
- Самме Георгий Вольдемарович (ф и. о.) учебно-методический комплекс, 294.35kb.
- Баженов Валерий Клавдиевич, к т. н., доцент, учебно-методический комплекс, 1242.91kb.
- Баженов Валерий Клавдиевич, к т. н., доцент, учебно-методический комплекс, 1602.69kb.
- Баженов Валерий Клавдиевич, к т. н., доцент, учебно-методический комплекс, 1625.53kb.
- Баженов Валерий Клавдиевич, к т. н., доцент учебно-методический комплекс, 659.55kb.
- Учебно-методический комплекс удк ббк п рекомендовано к изданию Учебно-методическим, 1762.72kb.
- Коноваленко Валерий Адольфович, кандидат психологических наук, ст преподаватель кафедры, 511.49kb.
- Автор Космодамианский Андрей Сергеевич (Ф. И. О) учебно-методический комплекс, 414.17kb.
- Автор Космодамианский Андрей Сергеевич (Ф. И. О) учебно-методический комплекс, 320.73kb.
Задачи 21-30
Решить систему уравнений методом простой итерации и методом Зейделя с точностью
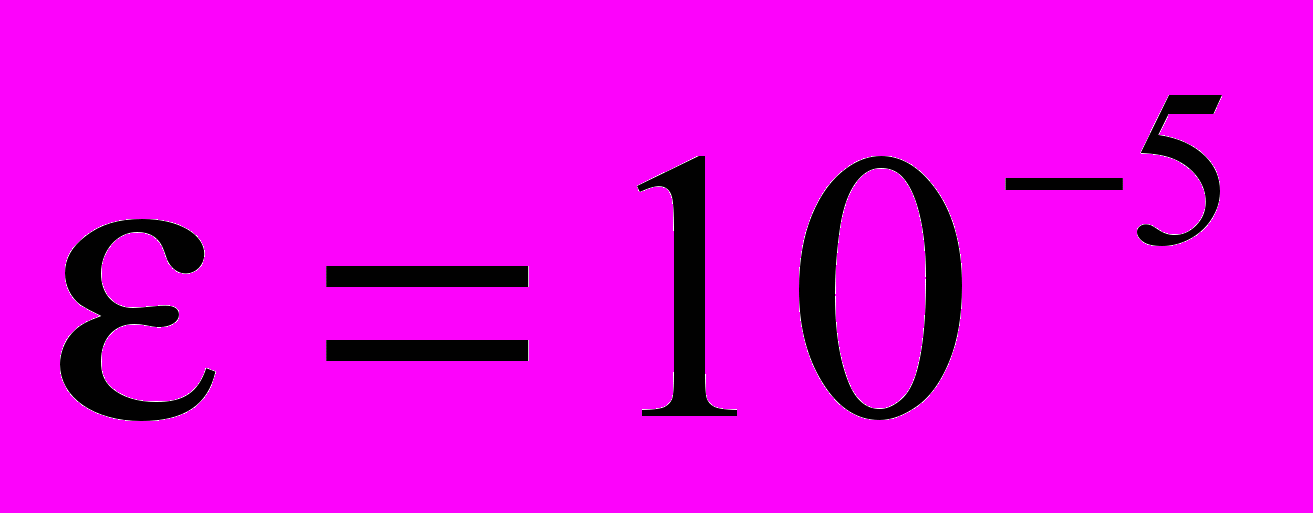, сравнить эти итерационные методы по числу итераций; по эффективности (трудность реализации метода, объем памяти, общие затраты времени выполнения на ЭВМ)| Вариант | Исходные данные |
| |  |
| |  |
| |  |
| |  |
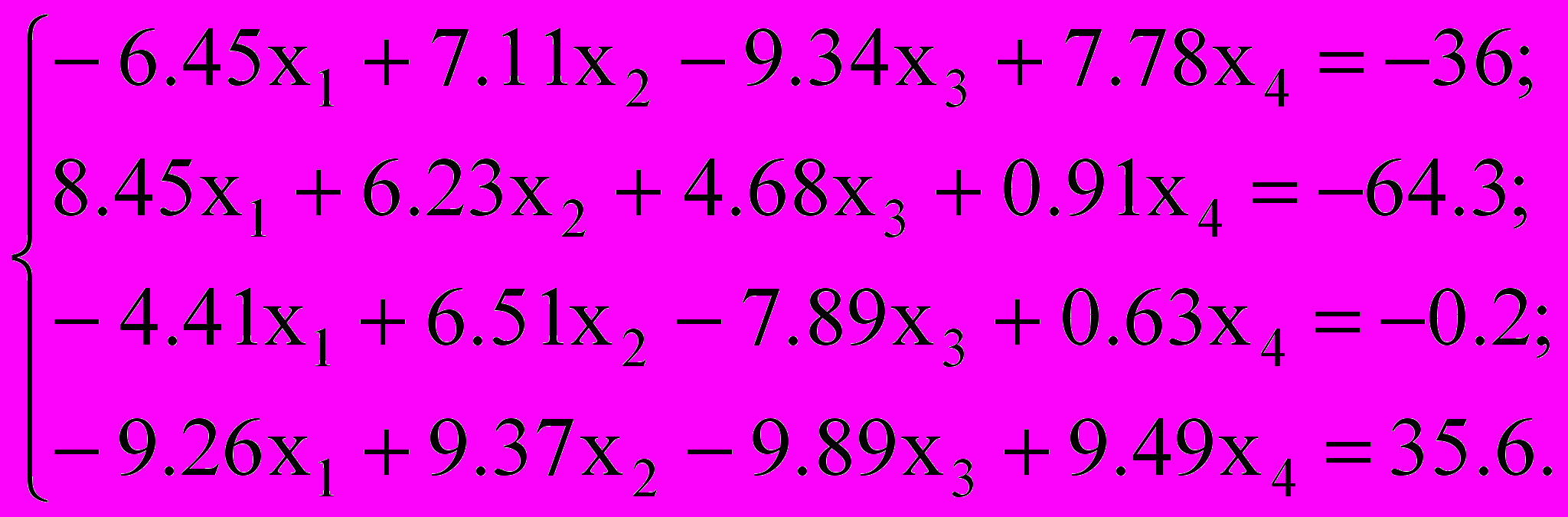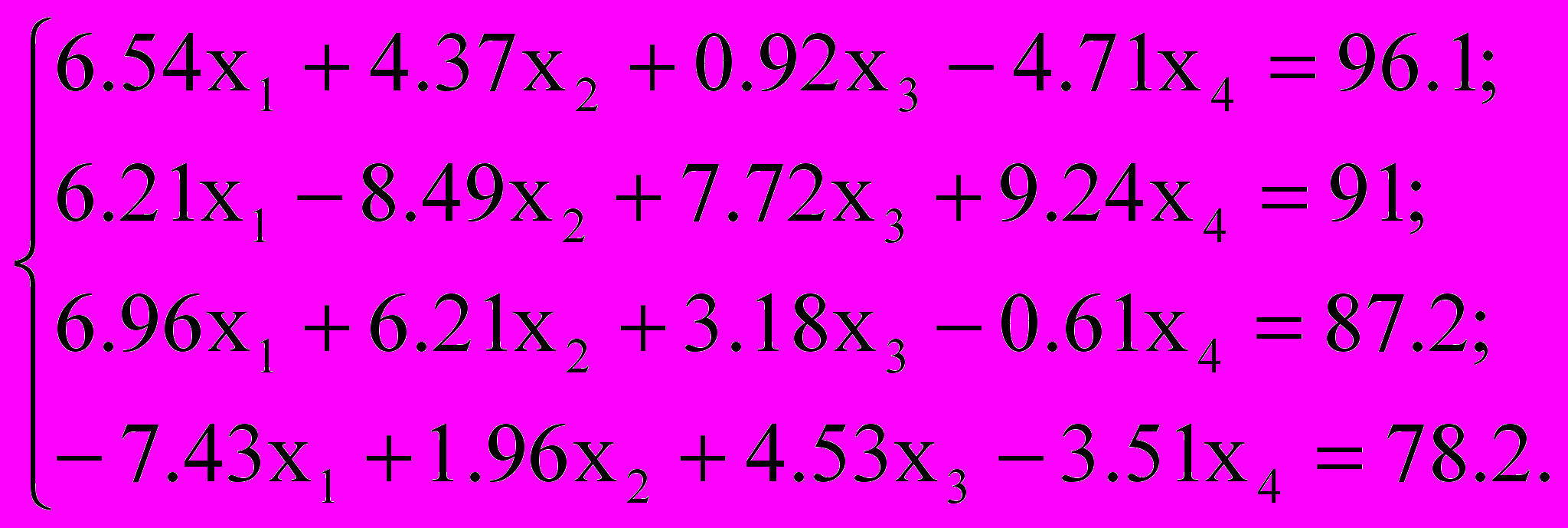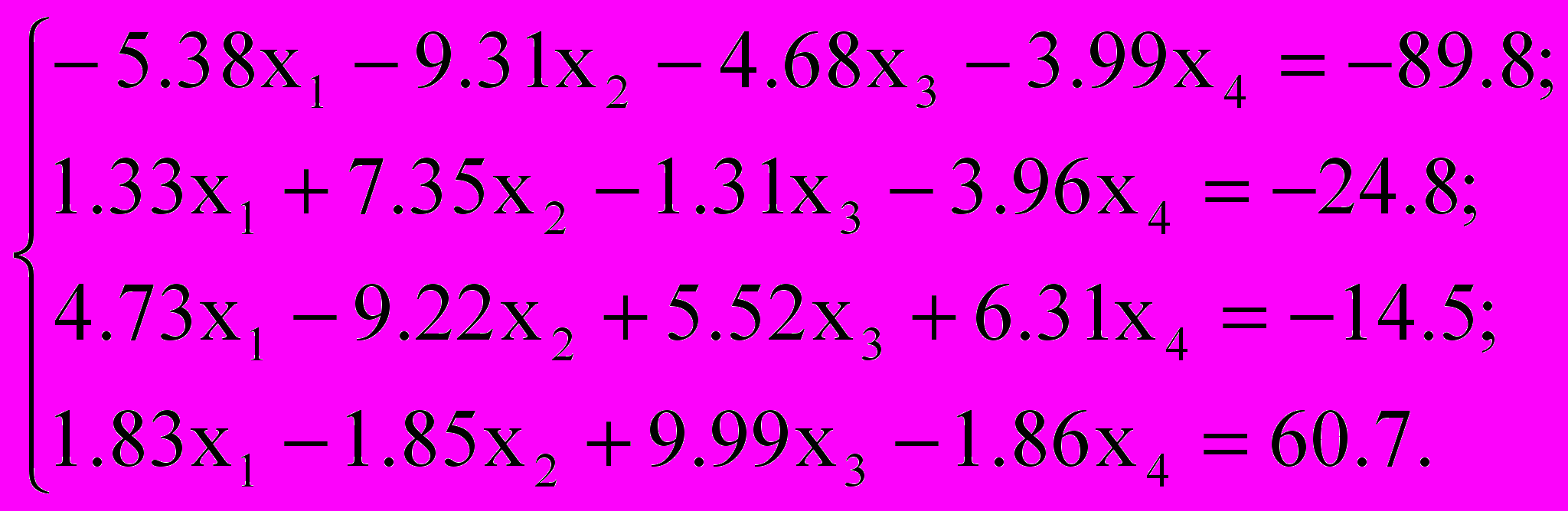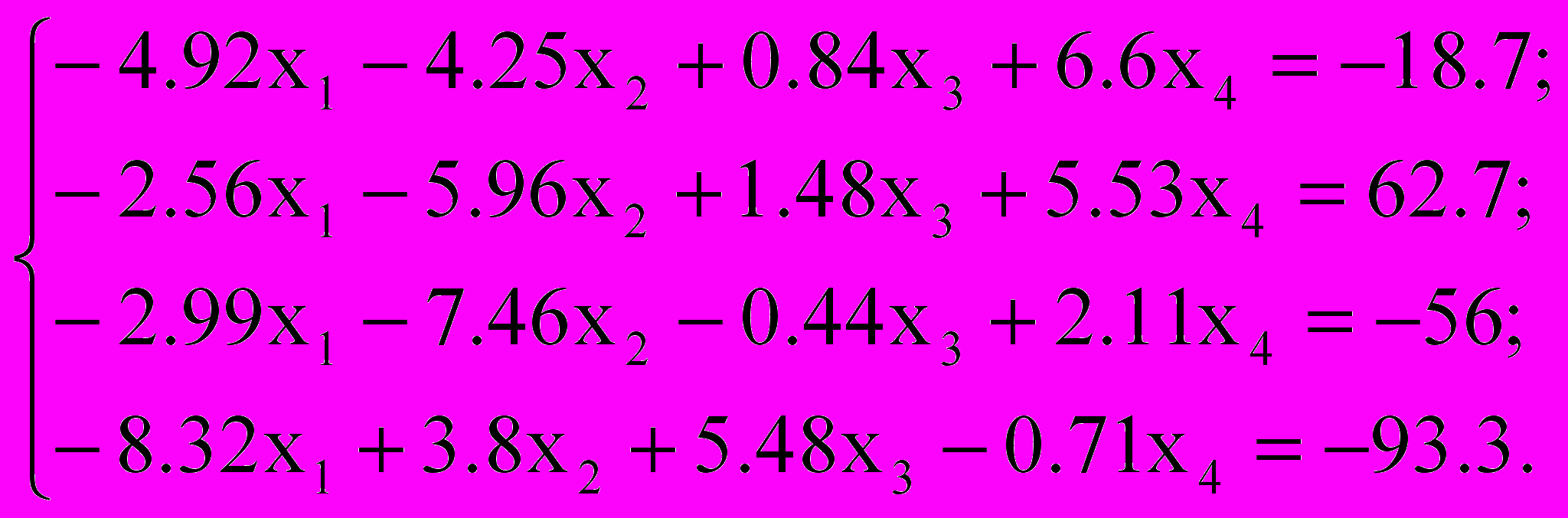| Вариант | Исходные данные |
| |  |
| |  |
| |  |
| |  |
| |  |
| |  |
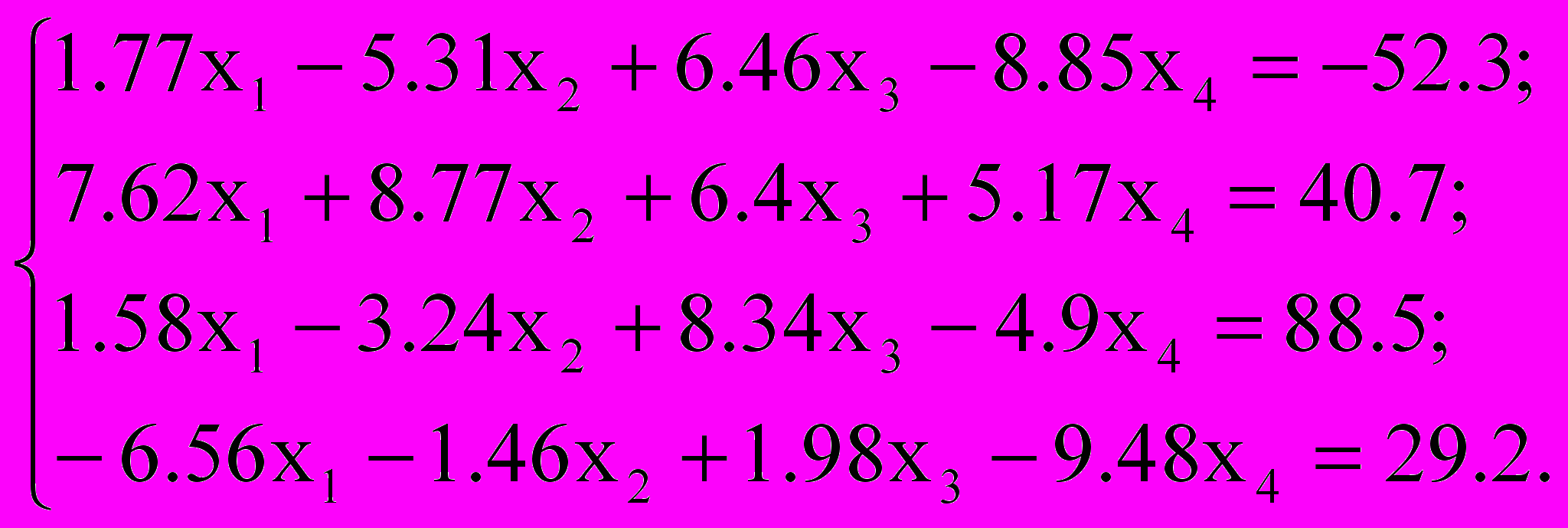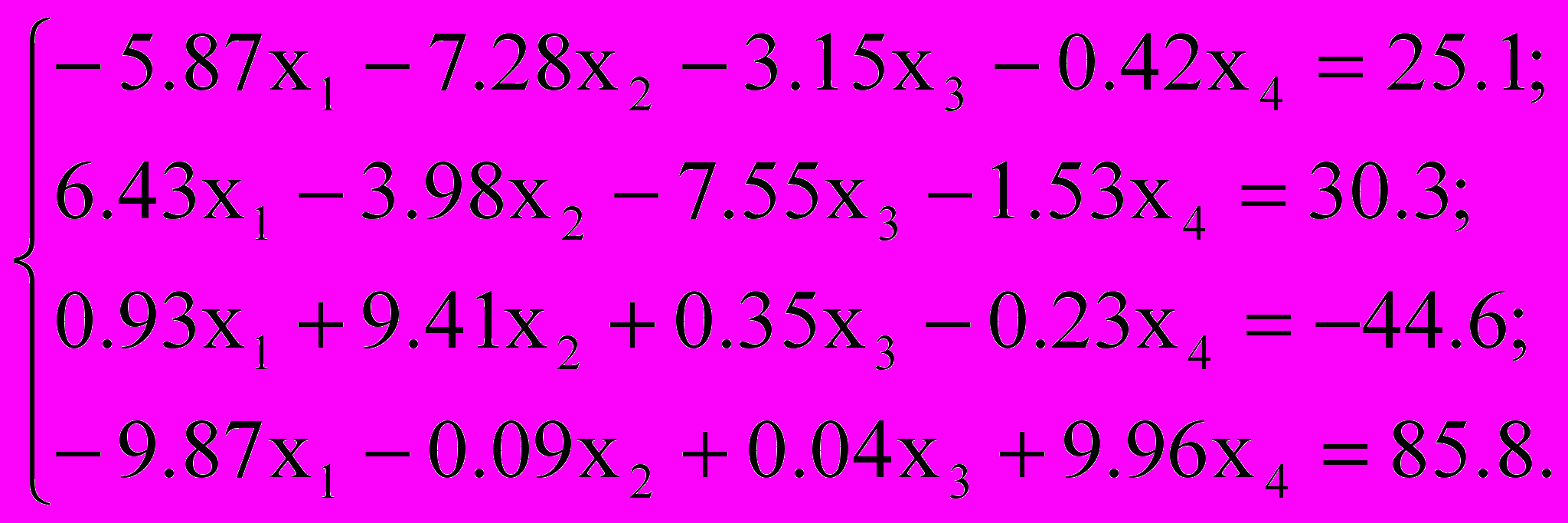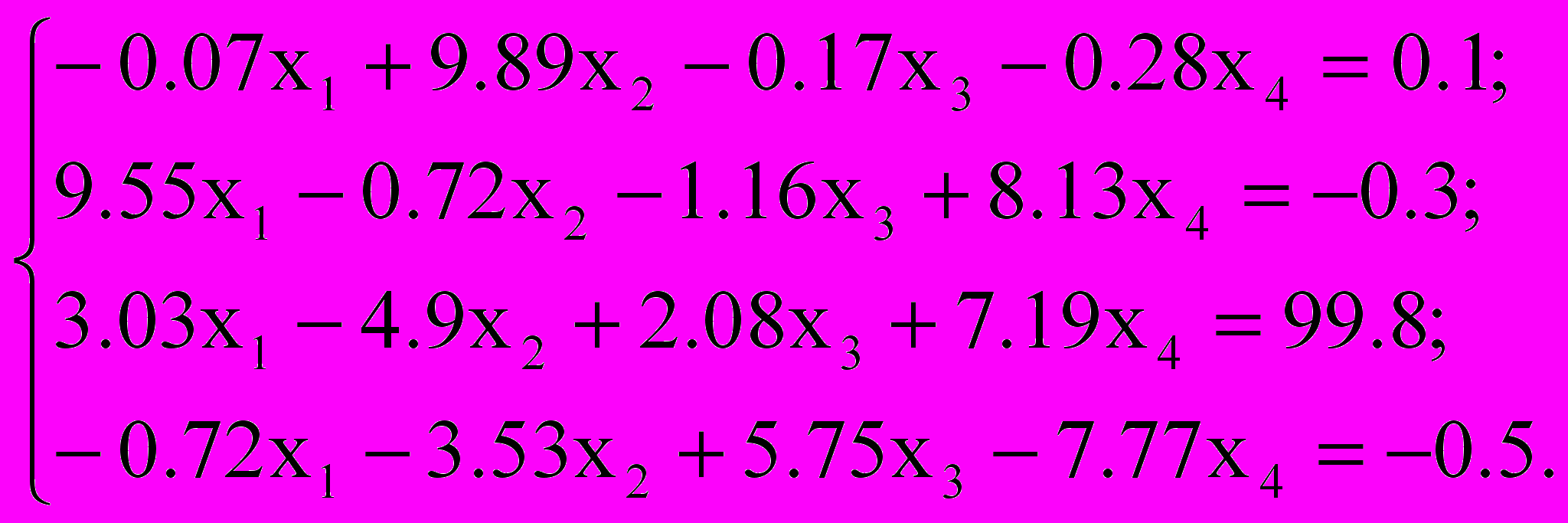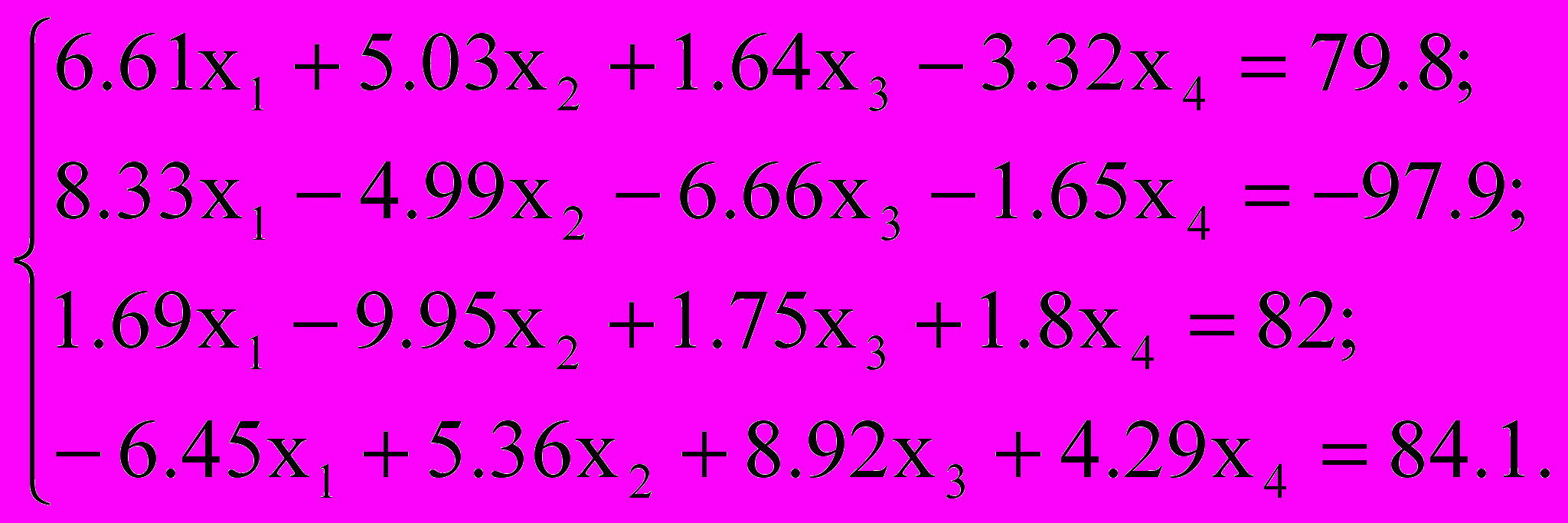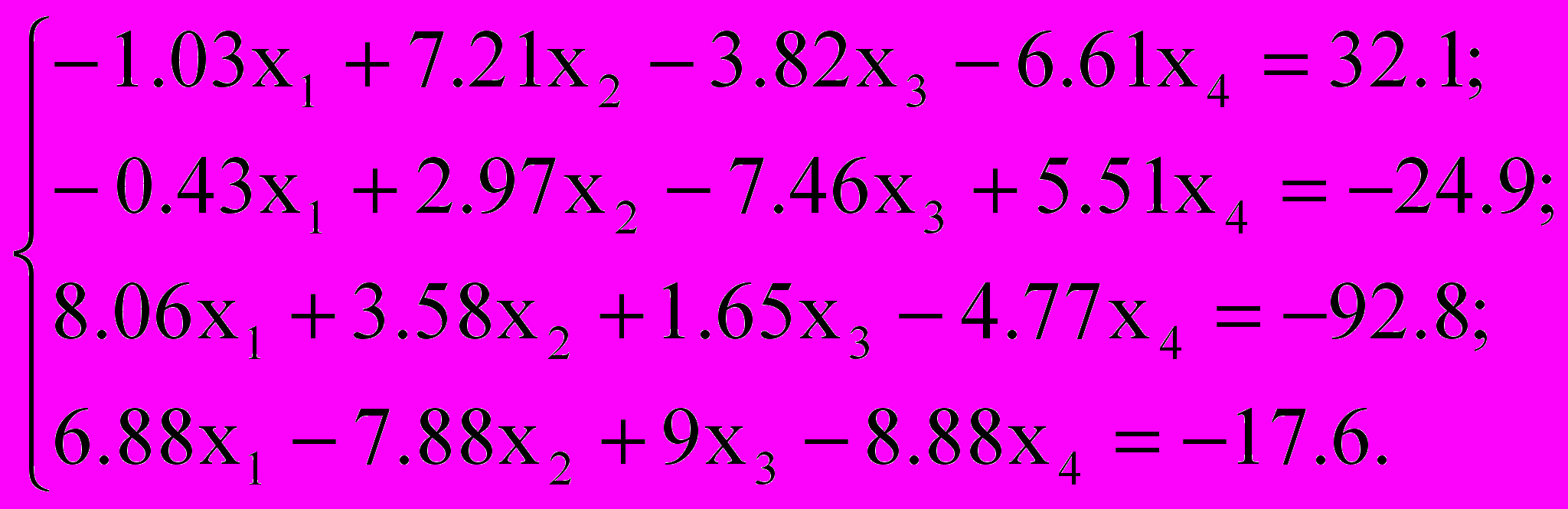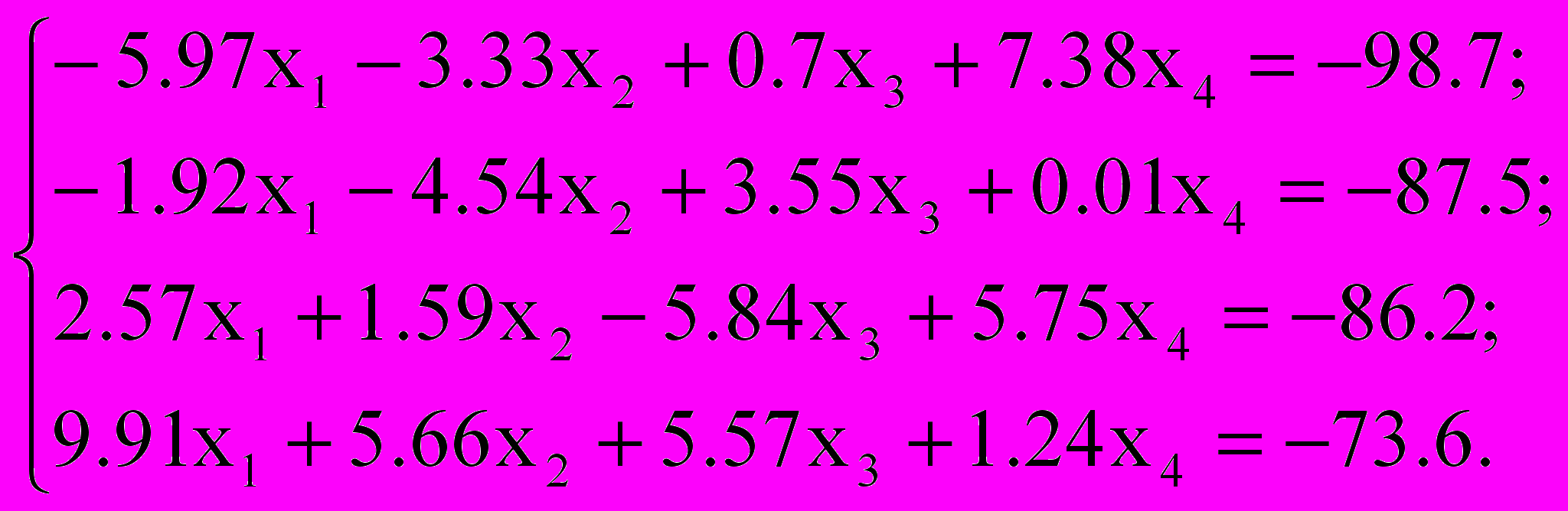Задачи 31-40
По таблице исходных данных рассчитать параметры следующих функций:
а) линейной y=ax+b;
б) степенной y=axb;
в) показательной y=abx;
г) равносторонней гиперболы y=a+b/x.
| Вариант | Исходные данные | Вариант | Исходные данные | ||
| 1 | х | y | 6 | х | y |
| 61,10 60,80 60,18 59,20 58,10 55,20 49,10 | 49,10 48,60 50,10 52,20 53,60 58,10 69,10 | 60,80 60,00 58,60 57,30 56,10 50,40 46,80 | 49,40 49,80 53,40 55,20 56,20 59,9 67,4 | ||
| 2 | х | у | 7 | х | у |
| 61,8 60,0 58,7 56,1 54,2 50,6 47,1 | 49,0 49,3 52,8 55,2 57,5 63,1 68,2 | 60,8 59,1 57,9 55,7 54,3 52,6 49,1 | 50,8 53,3 54,3 57,6 60,7 64,1 67,7 | ||
| 3 | х | у | 8 | х | у |
| 60,1 59,2 58,6 55,4 53,1 52,0 49,9 | 49,0 52,1 53,2 56,6 59,5 66,6 67,8 | 63,1 61,9 59,6 57,2 57,1 50,9 47,1 | 49,8 49,3 53,3 56,1 57,3 64,1 66,6 | ||
| 4 | х | у | 9 | х | у |
| 60,3 59,1 58,7 58,1 54,5 50,3 47,1 | 49,9 54,8 56,9 57,1 62,3 66,1 67,3 | 61,7 60,4 58,1 57,2 53,4 49,4 45,9 | 49,8 51,1 53,2 57,3 61,5 66,4 68,8 | ||
| 5 | х | у | 10 | х | у |
| 59,2 59,0 54,2 55,6 53,1 57,8 60,9 | 49,7 50,5 51,9 54,4 57,3 64,8 49,0 | 58,1 57,5 56,4 55,1 53,4 50,2 46,1 | 49,1 51,2 53,0 54,6 57,6 60,1 61,8 |
Задачи 41-50
I. Методом Данилевского найти собственные значения и собственные векторы матрицы
| Вариант | Исходная матрица | Вариант | Исходная матрица |
| 1 | 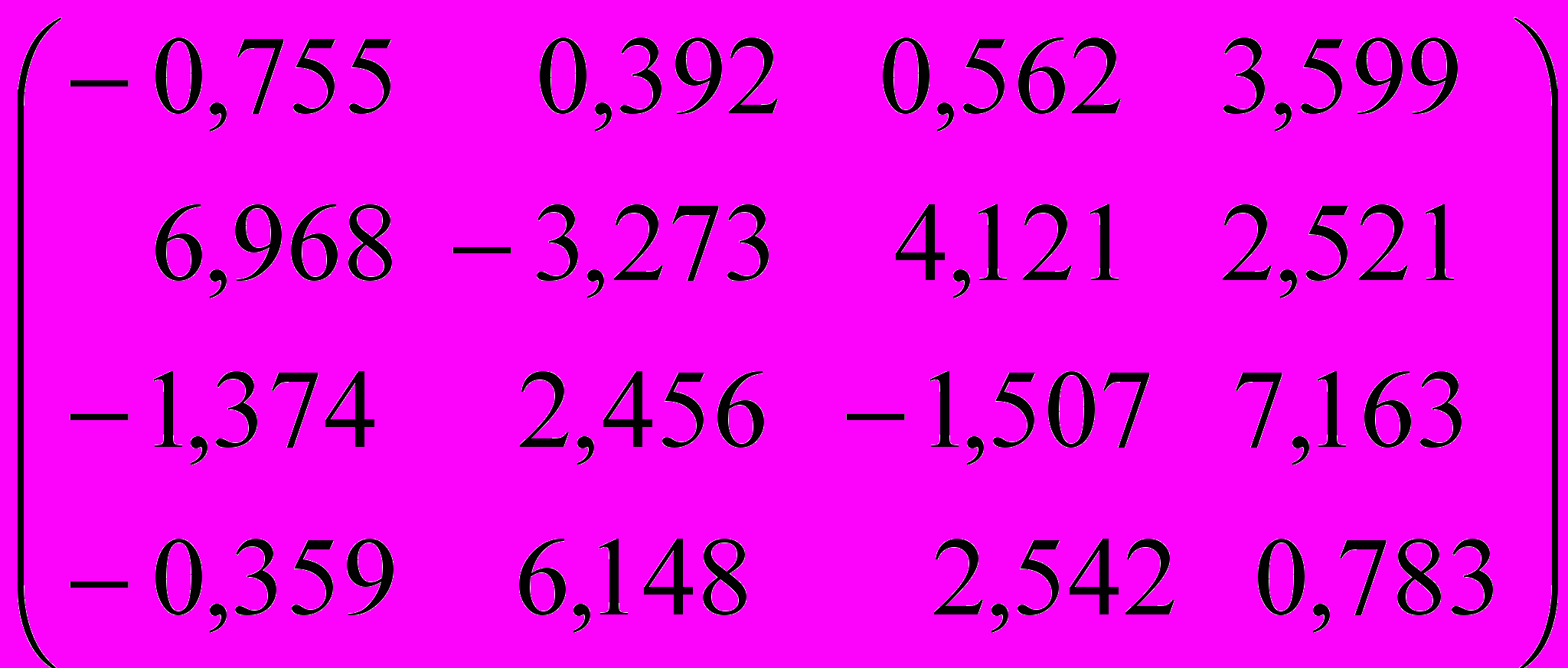 | 2 |  |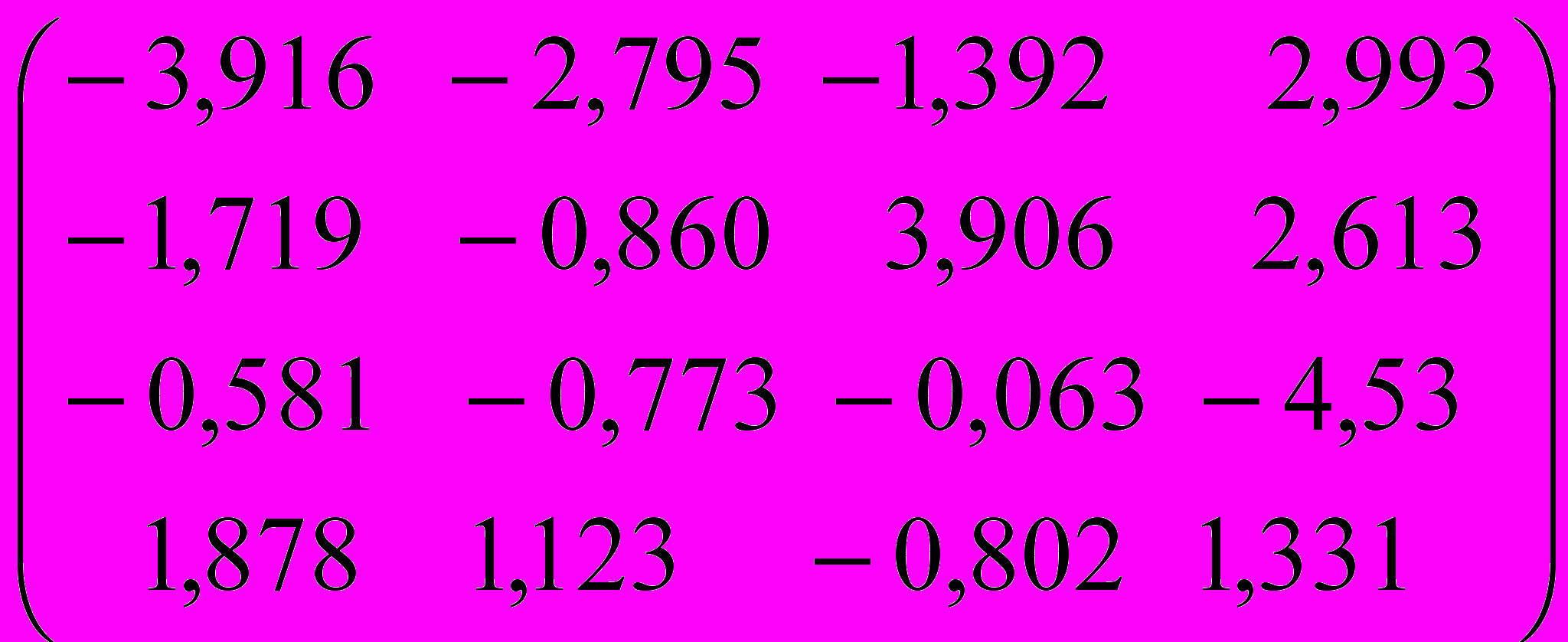
| 3 |  | 4 |  |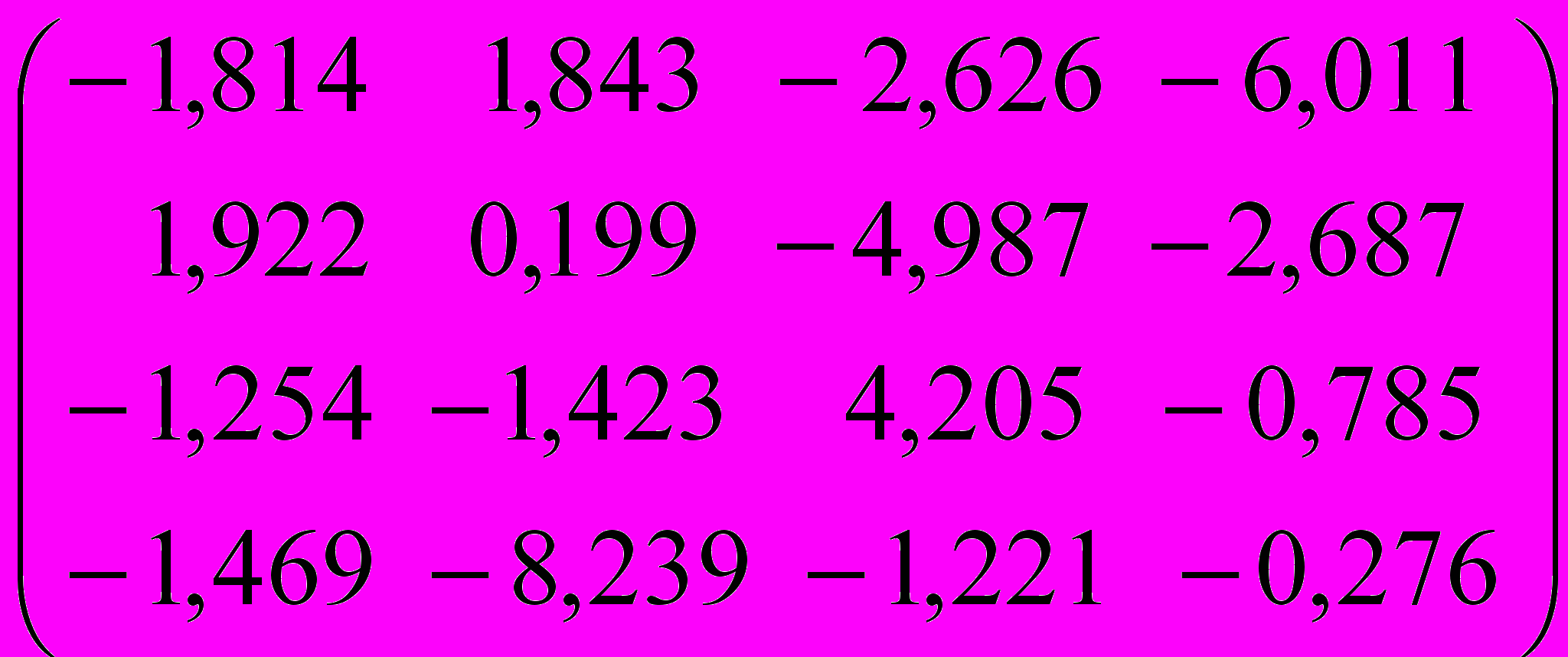
| 5 |  | 6 |  |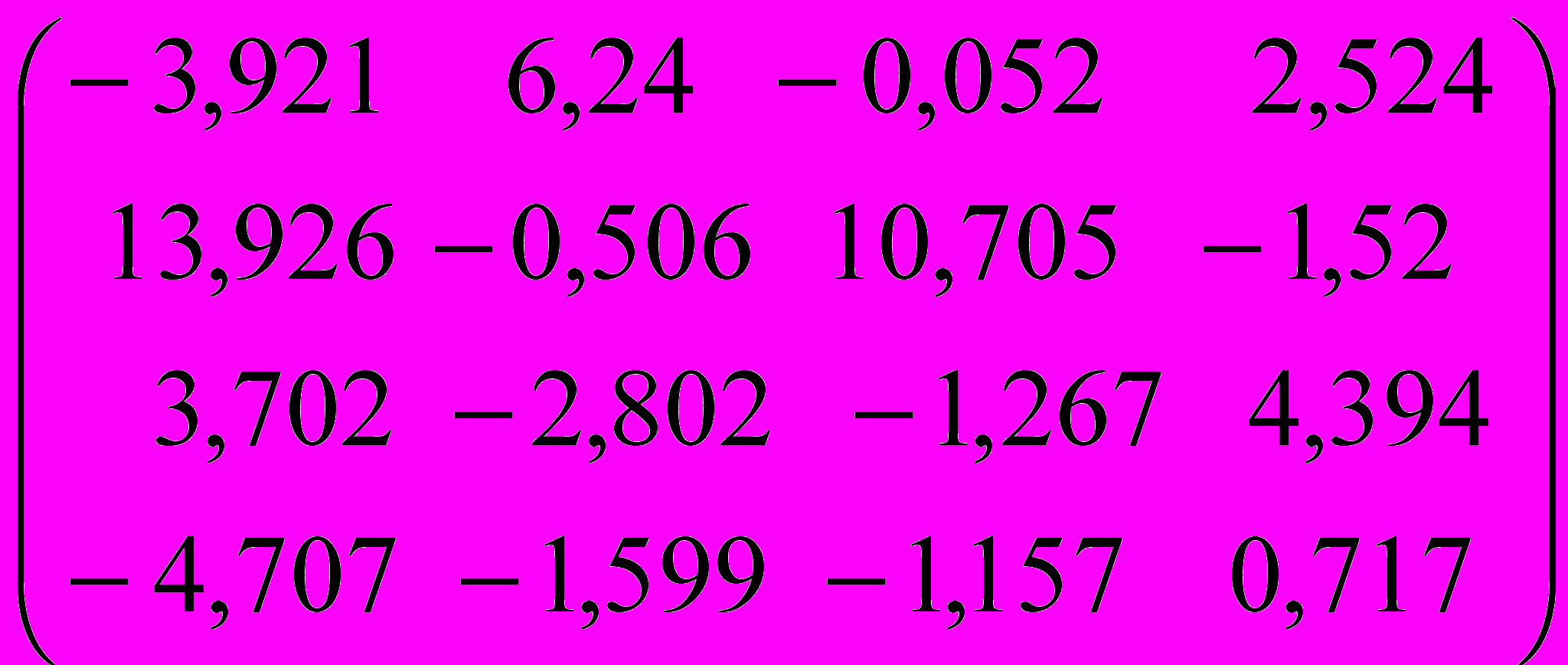
| 7 | 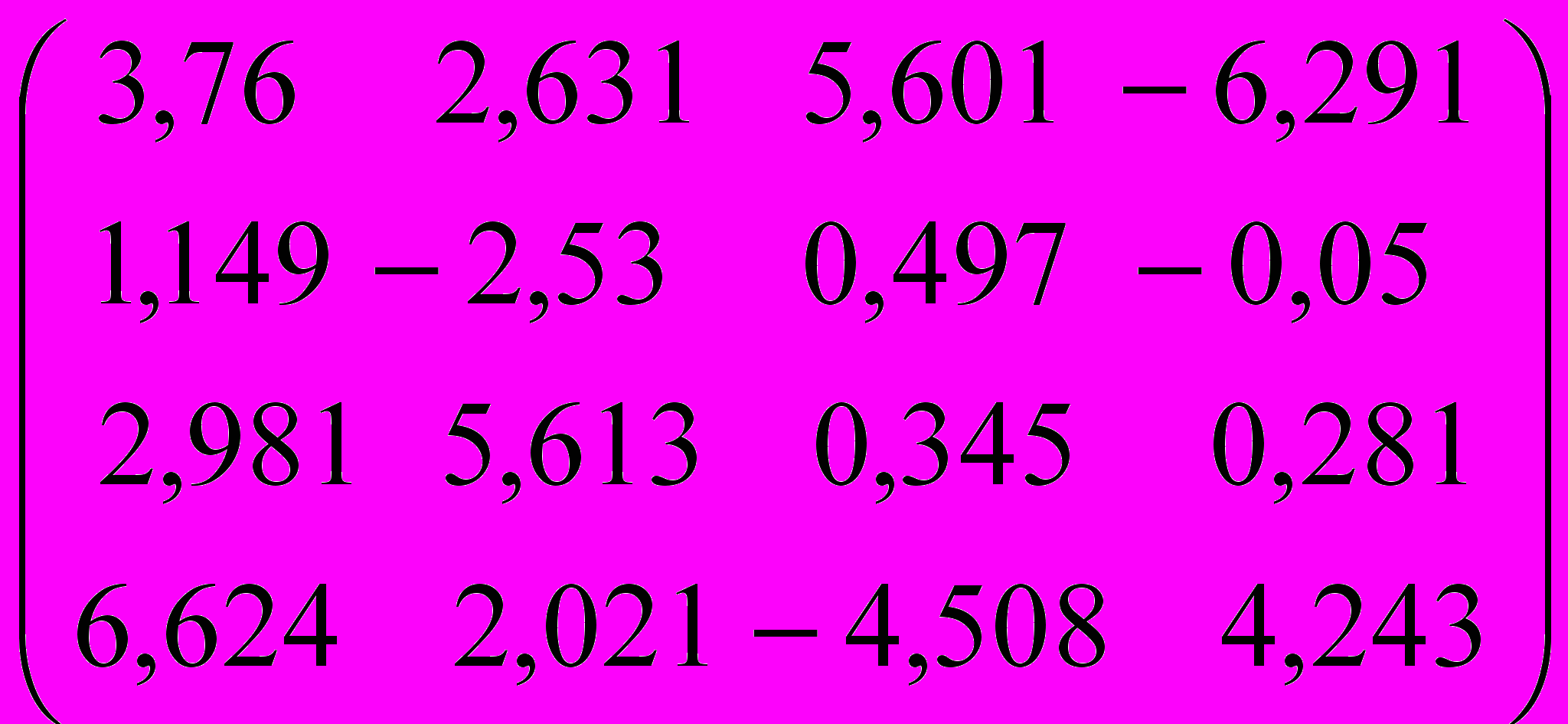 | 8 |  |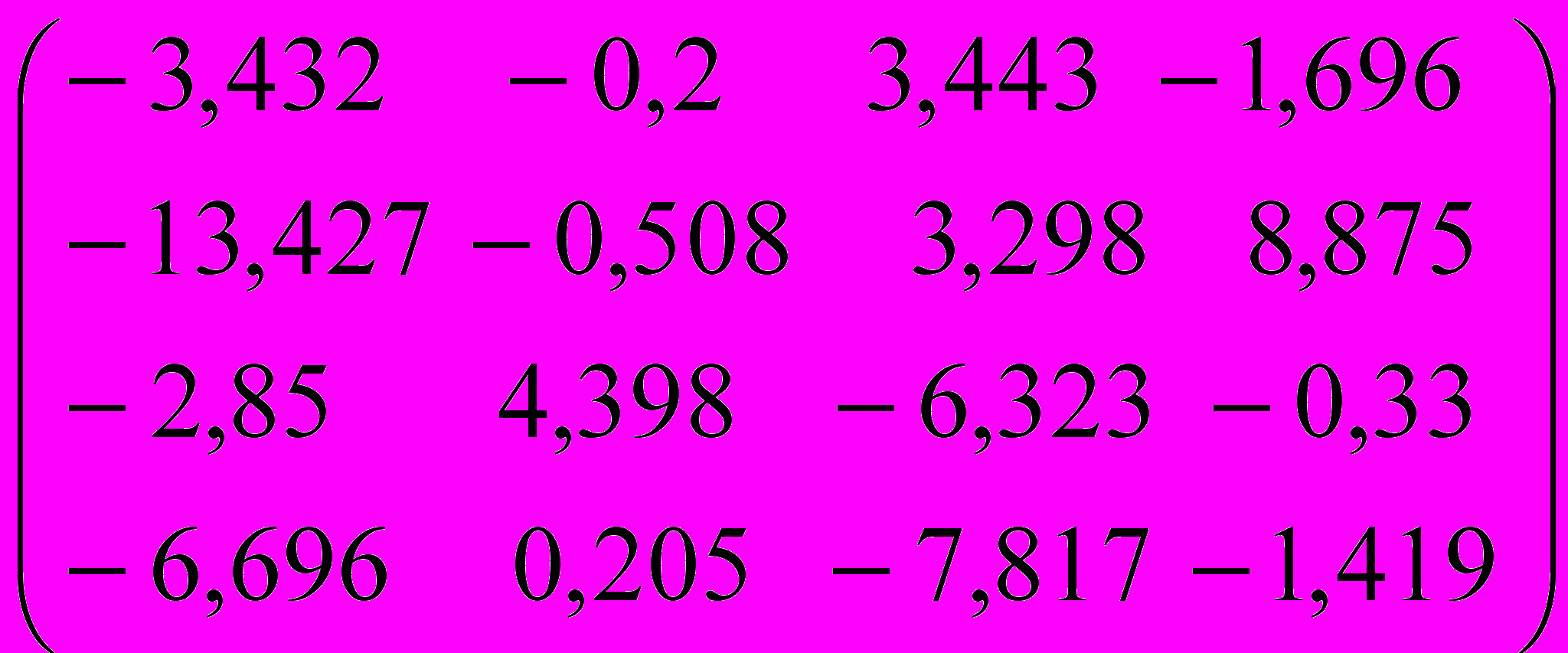
| 9 |  | 10 |  |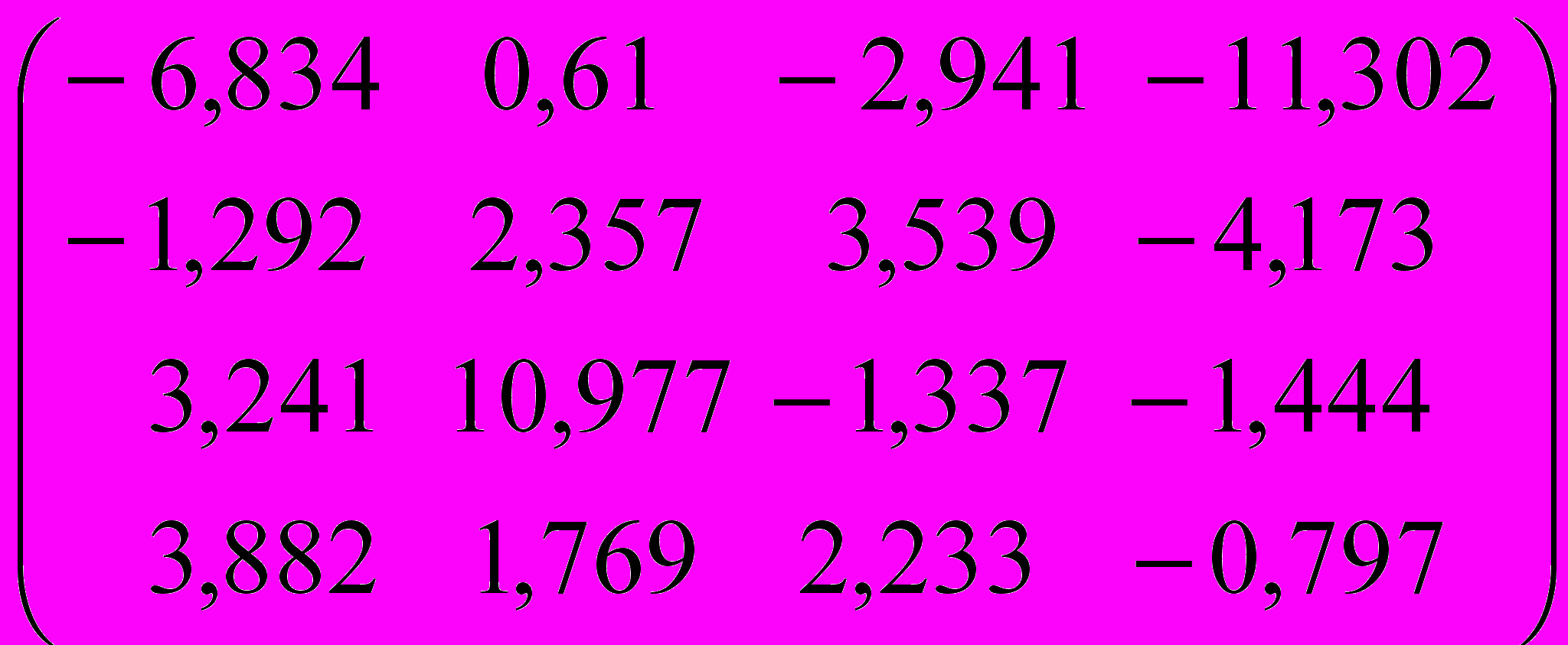
II. Найти собственные значения и соответствующие им собственные векторы матрицы методом Крылова и методом, вычисляющим все собственные значения и векторы симметрической положительно определенной матрицы.
| 1. 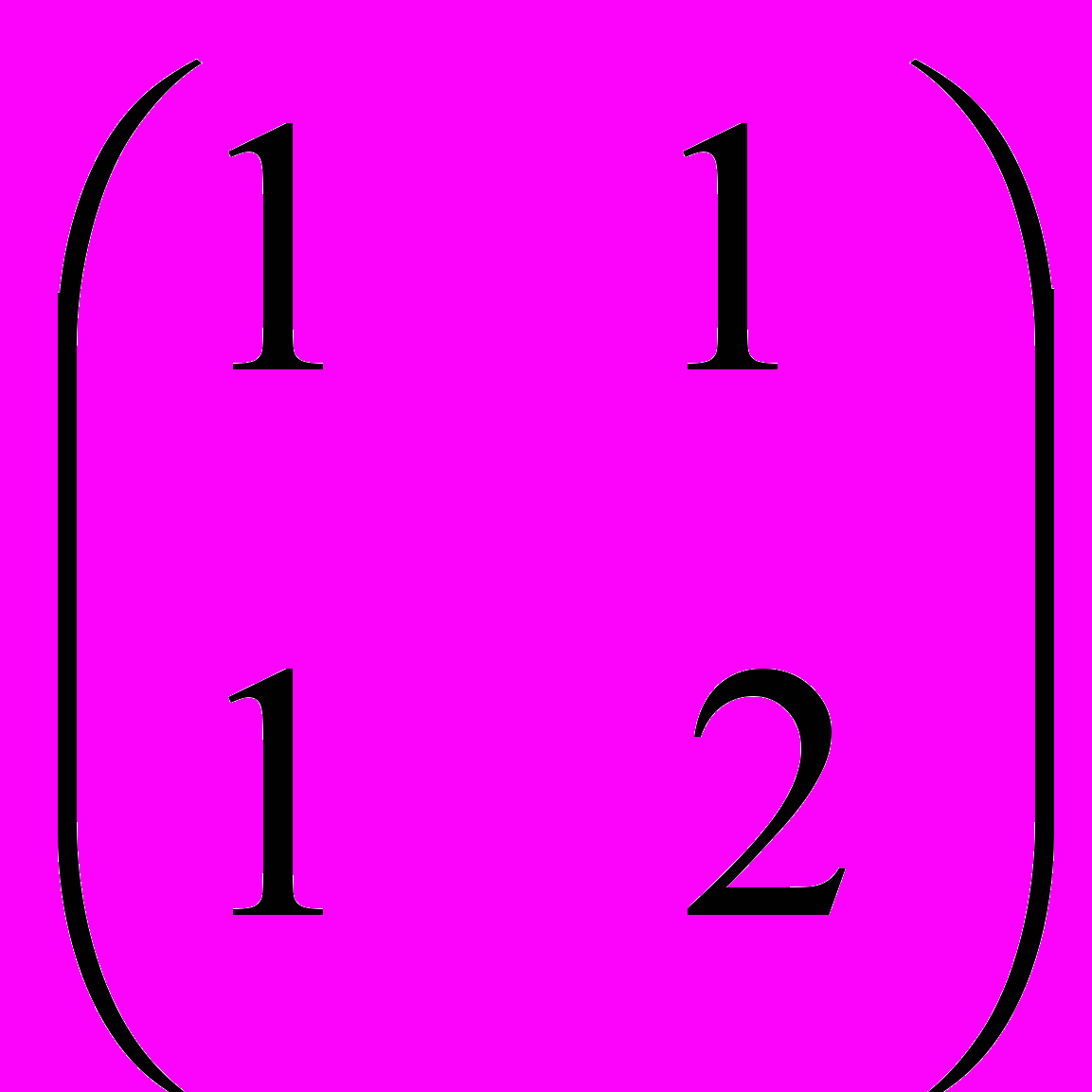 | 2. 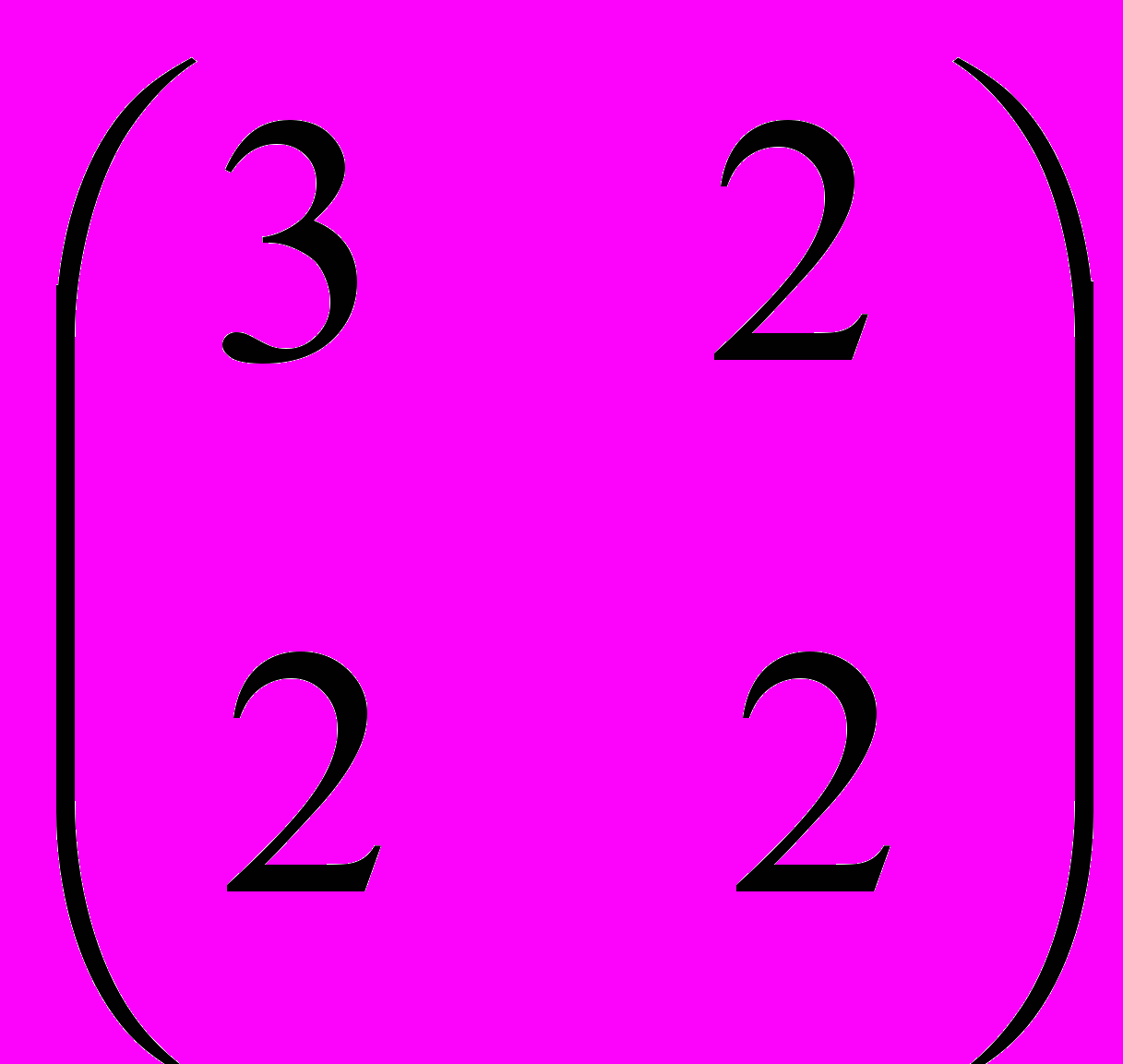 | 3. 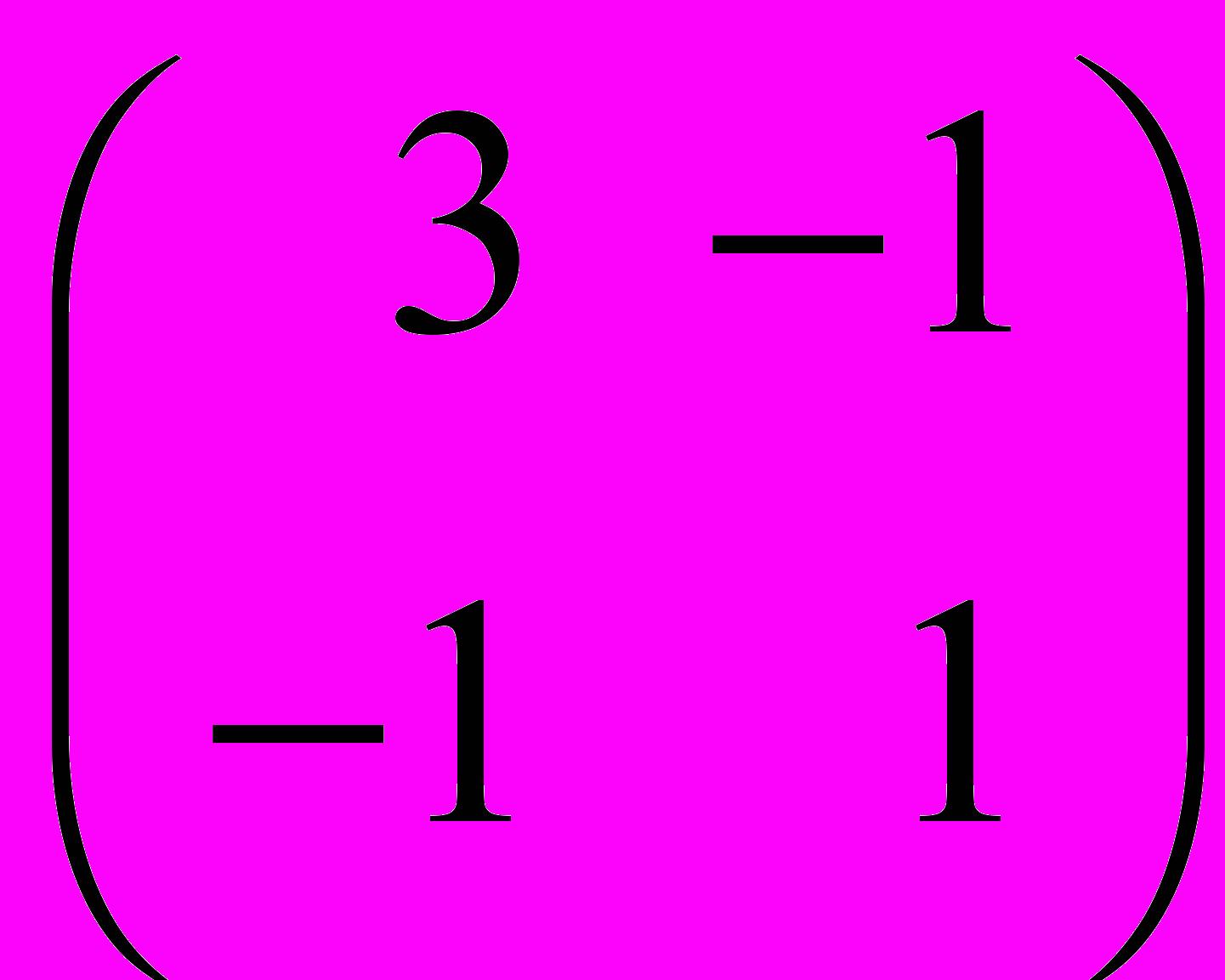 | 4. 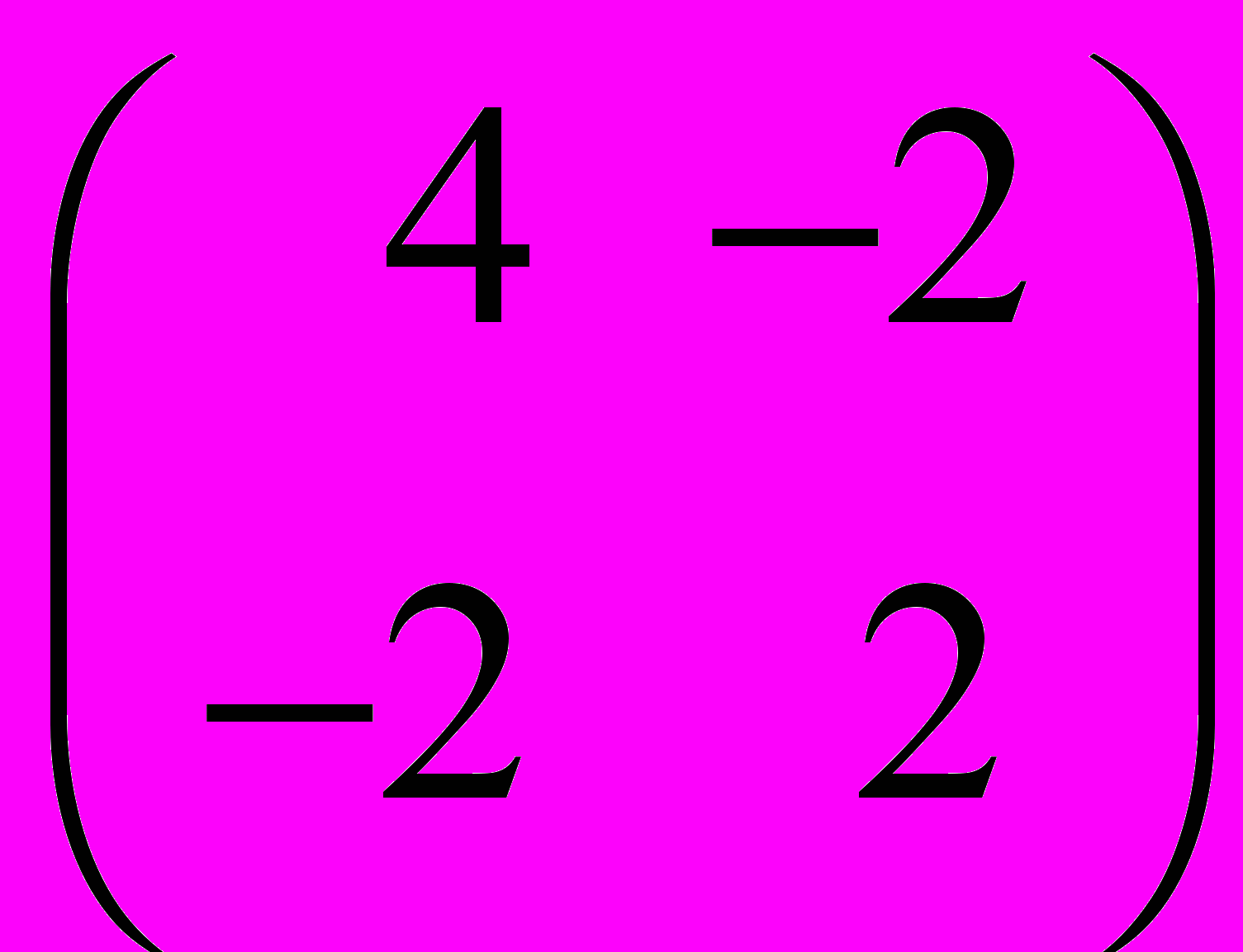 | 5.  |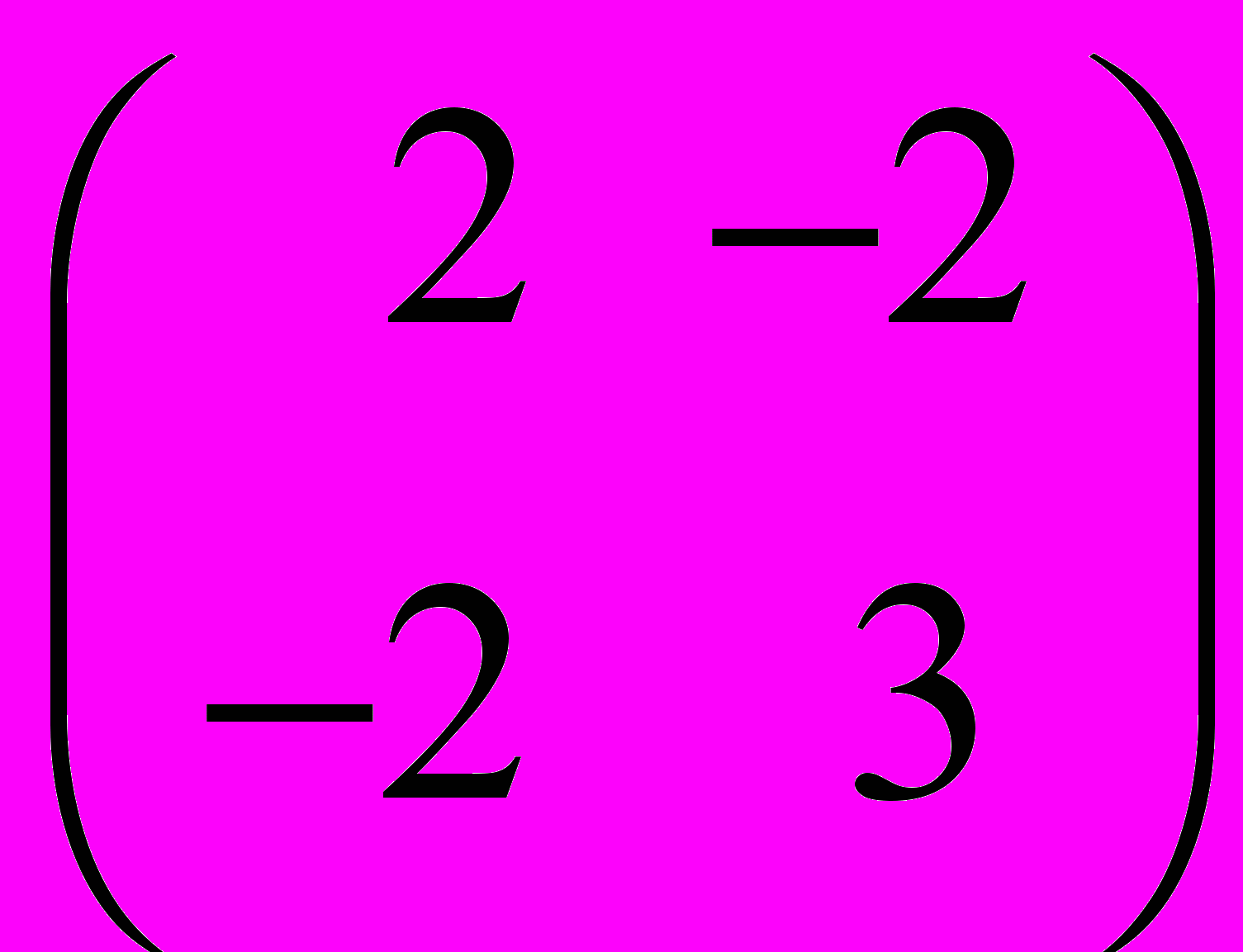
| 6.  | 7. 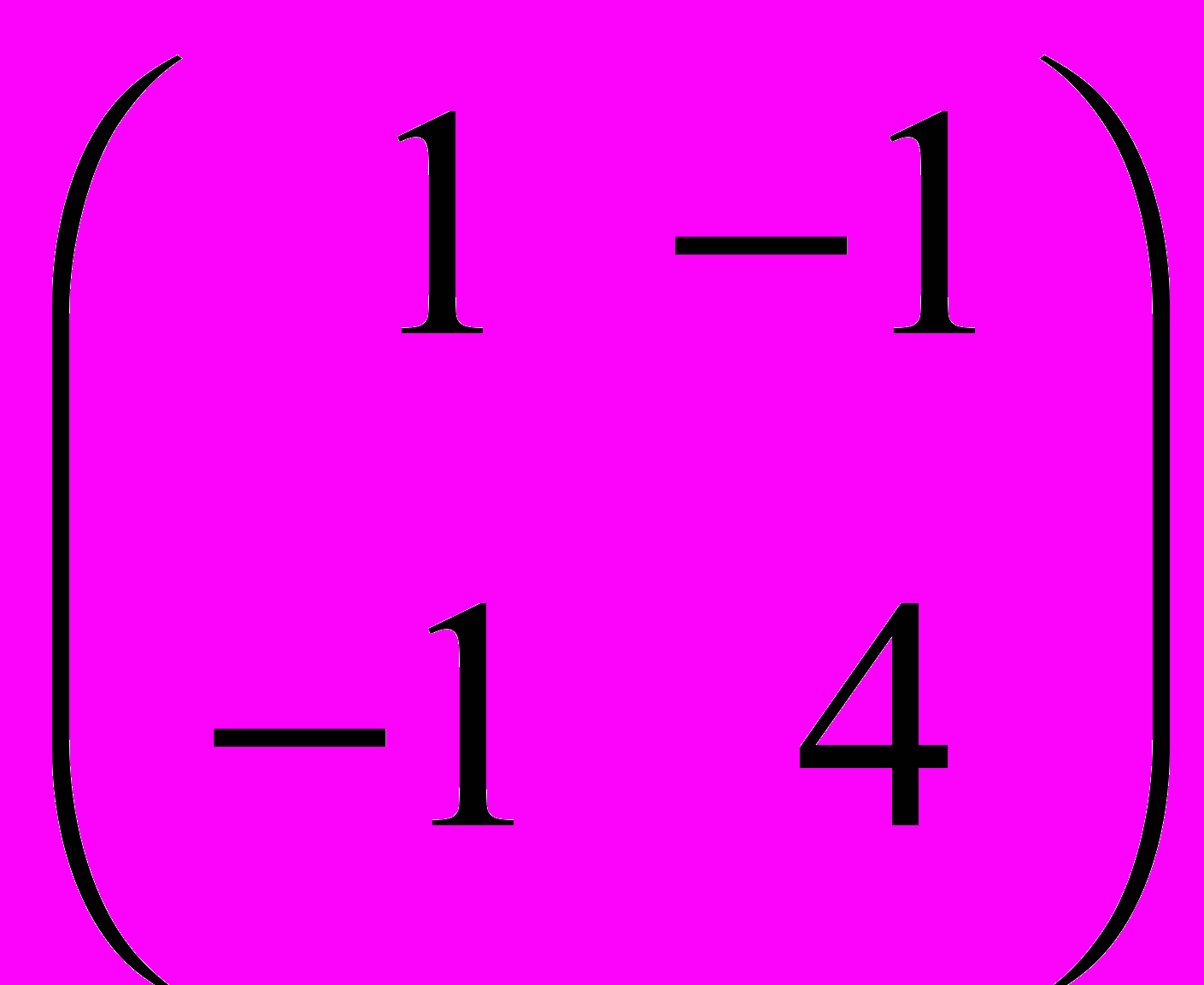 | 8. 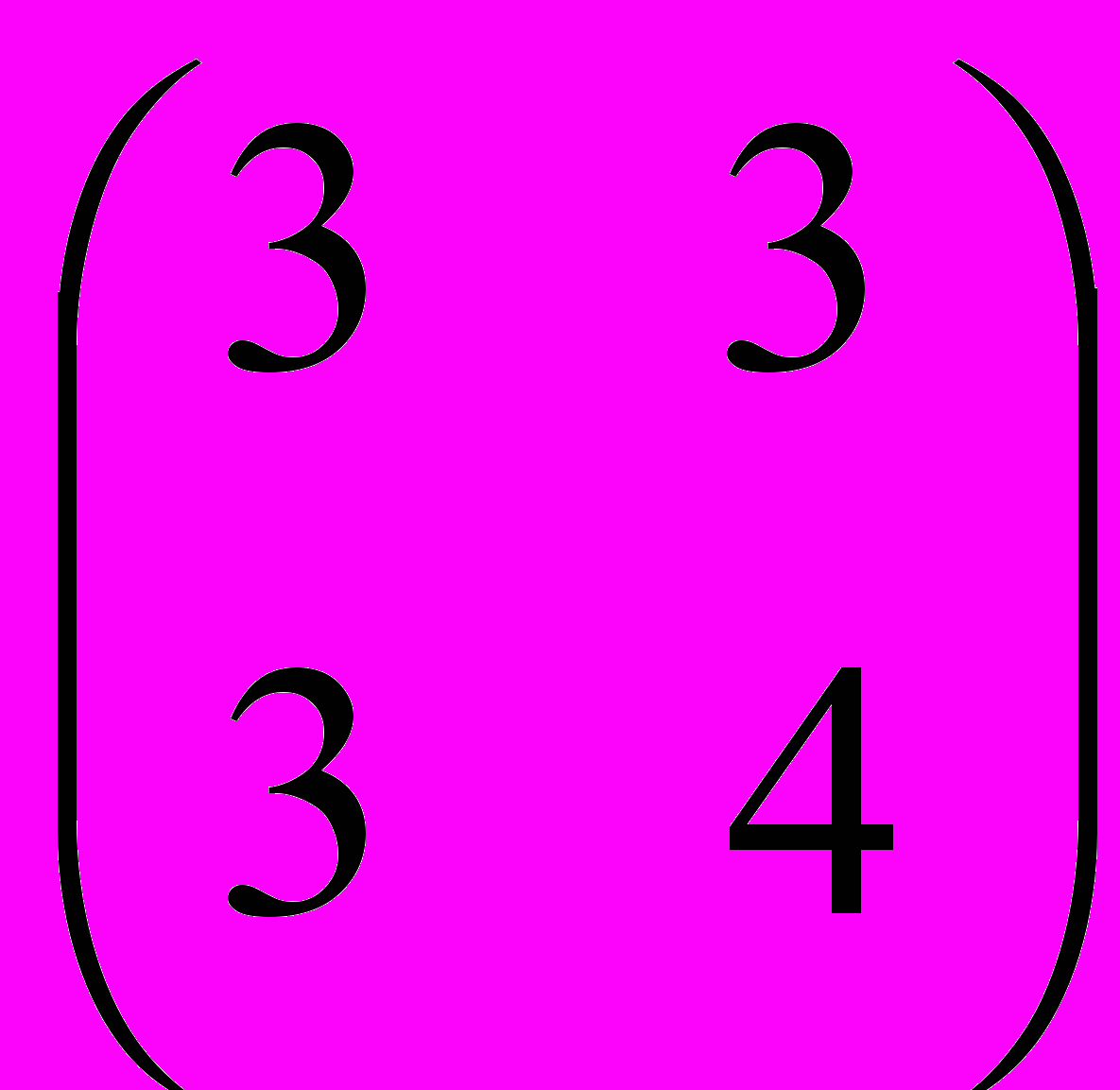 | 9. 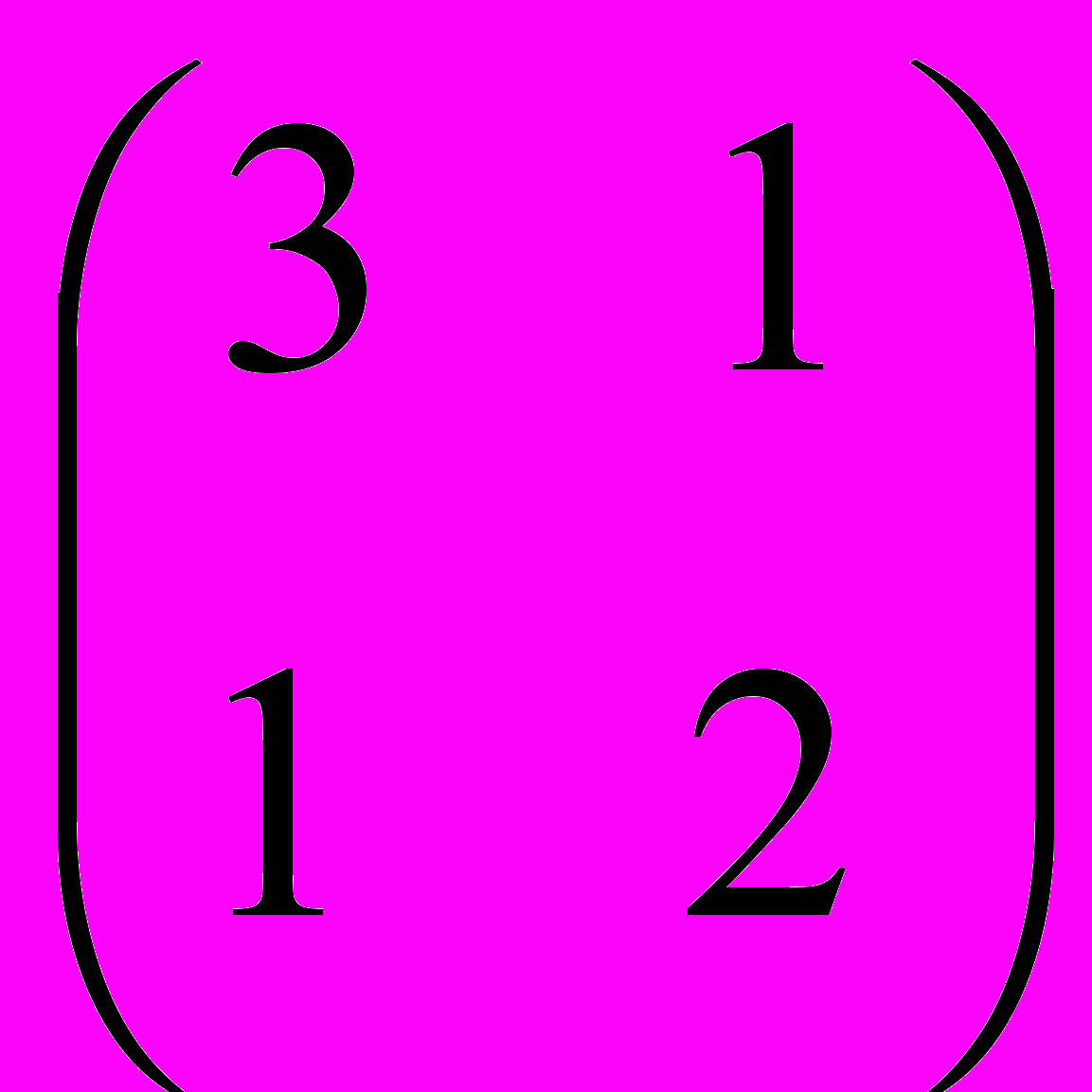 | 10.  |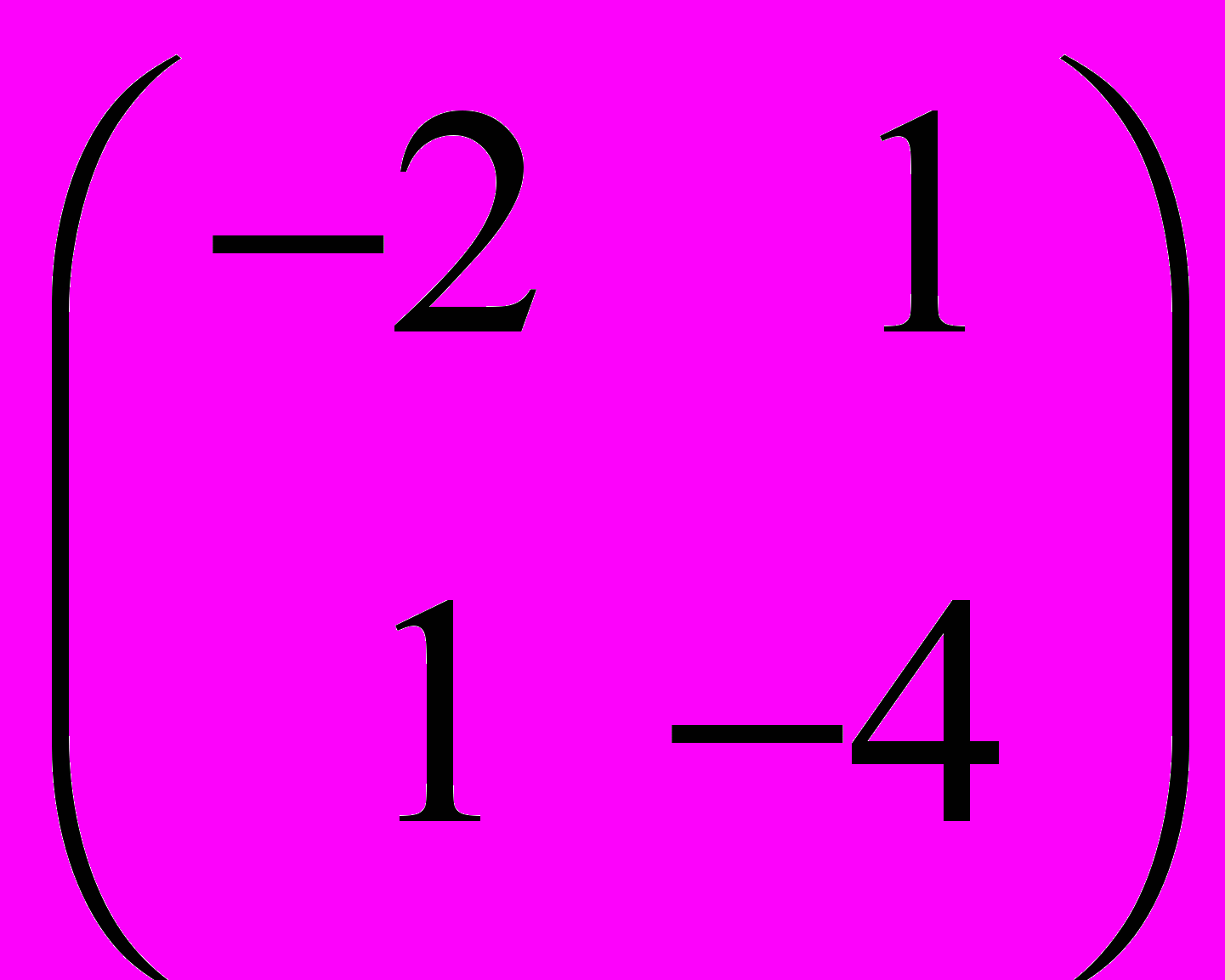
Задачи 51-60.
I. Реализовать прямой Фурье-анализ для заданного числа гармоник N=10 и затем синтез заданной функции. Кусочно-линейная функция задана в виде таблицы дискретных данных, через равные интервалы времени с.
II. Реализовать улучшенное моделирование сигналов на основе спектрального подхода для сведения эффекта Гиббса к минимуму.
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y1 | 0 | 0 | 0.5 | -0.5 | 0.5 | 0 | 0 | 0.5 | -0.5 | 0.5 |
| y2 | 0 | 0 | 0.5 | 0 | 0.5 | 0.5 | -0.5 | 0 | 0.5 | 0 |
| y3 | 0.5 | -0.5 | 0 | 0.5 | 0 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| y4 | 0.5 | -0.5 | 0 | 0.5 | 0 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| y5 | 1 | -1 | 1 | 0 | -1 | 1 | ! | 1 | 1 | 1 |
| y6 | 1 | -1 | 1 | 0 | -1 | 0.5 | -0.5 | 0.5 | -0.5 | 1 |
| y7 | 0.5 | -0.5 | 0.5 | -0.5 | -0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| y8 | 0.5 | -0.5 | 0.5 | -0.5 | -0.5 | -0.5 | 0.5 | -0.5 | -0.5 | 0.5 |
| y9 | 0 | 0 | 0 | -1 | 0.5 | 0 | 0 | 0 | 0 | 0 |
| y10 | 0 | 0 | 0 | -1 | 0.5 | -0.5 | 0.5 | -0.5 | -0.5 | 0.5 |
| y11 | -0.5 | 0.5 | -0.5 | -0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| y12 | -0.5 | 0.5 | -0.5 | -0.5 | 0.5 | 0 | 0. | 0.5 | 0 | -0.5 |
| y13 | 0 | 0 | 0 | 0 | 1 | -0.5 | 0.5 | -0.5 | -0.5 | 0.5 |
| y14 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| y15 | 0.5 | 0.5 | -0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| y16 | 0.5 | 0.5 | -0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| y17 | 1 | ! | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| y18 | 1 | 1 | 0 | 1 | 0 | -0.5 | 0.5 | -0.5 | -0.5 | 0.5 |
| y19 | 0 | 0 | 0.5 | 0 | 0.5 | 0 | 0 | 0 | 0 | 0 |
| y20 | 0 | 0 | 0.5 | 0 | 0.5 | 0 | 0 | 0 | 0 | 0 |
6. ИНФОРМАЦИОННО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Рекомендуемая литература
Основная
- Бахвалов Н.С, Жидков Н.П., Кобельков Г.М. Численные методы. — М.: Наука, 2003.
Дополнительная
- Дьяконов В.П. Вейвлеты. От теории к практике. – М.: СОЛОН-Р, 2002.
- Бахвалов Н.С., Лапин А.В., Чижонков Е.В. Численные методы в задачах и упражнениях. — М.: Высшая школа, 2003.
- Катаева Л.Ю. Лабораторный практикум по численным методам (I, II части). Н.Новгород: Изд-во НГТУ, 2003.
- Катаева Л.Ю. Основы использования SciLab и реализация основных численных методов. (электронный учебник).
- Катаева Л.Ю. Численные методы. Алгоритмы и программная реализация на Си.(электронный учебник), 2004.
- Голубев А.И. Численные методы. Курс лекций в двух частях. — Саров: РФЯЦ-ВНИИЭФ, 2000.
- Вержбицкий В.М, Численные методы. (Математический анализ и обыкновенные дифференциальные уравнения). — М.: Высшая школа, 2001.
- Дьяконов В.П. Компьютерная математика. Теория и практика. М.: Нолидж, 2001.
- Блистанова Л.Д., Голечков Ю.И. Математика. Методические указания по выполнению контрольных заданий для студентов-заочников I курса всех специальностей.Часть 2. — М.: РГОТУПС, 2000. (3/1/4).
- Амосов А.А., Дубинский Ю.А., Конченое Н.А. Вычислительные методы для инженеров. — М.: Высшая школа, 1994,
- Годунов С.К., Рябенький В.С. Разностные схемы. — М.: Наука, 1977.
- Воеводин В.В. Вычислительные основы линейной алгебры. — М.: Наука, 1977.
- Волков Е.В. Численные методы. — М.: Наука, 1982.
- Икрамов Х.Д. Численные методы линейной алгебры, — М.: Знание (сер. «Математика и кибернетика»), 1987.№ 4.
- Калиткин Н.Н. Численные методы. — М.: Наука, 1978,
- Марчук Г.И. Методы вычислительной математики. — М.: Наука, 1977.
- Самарский А.А., Гулин А.В. Численные методы. — М.: Наука, 1989.
- Рябенький В.С. Введение в вычислительную математику. — М: Наука, 1993.
- Шестаков А.А., Голечков Ю.И, Математическое моделирование. Ч. 1 и 2. — М.: ВЗИИТ, 1993.
- Гельфонд А.О. Исчисление конечных разностей. — М: Наука, 1967.
- Манзон Б.М. Мар1е V Роwer Еdition. — М.: Инф. – изд. дом «Филинъ», 1998.
- Голечков Ю.И., Блистанова Л.Д. Математика. Методические указания по выполнению контрольных заданий для студентов-заочников I курса всех специальностей. Часть 1. — М.; РГОТУПС, 1999. (3/1/3).
- Голечков Ю.И. Математика. Методические указания по выполнению контрольных заданий № 6-8 для студентов-заочников II курса инженерно-технических специальностей. Ч. 3. — М.: РГОТУПС, 1999. (3/1/5).
- Сборник задач по методам вычислений: Уч. пос./Под ред. П.И. Монастырного. — 2-е изд. — М.: Физматлит, 1994.
- Жуков АИ. Метод Фурье в вычислительной математике. — М.: Наука, Физматлит, 1992.
ИНТЕРНЕТ РЕСУРСЫ
- Пакет разработан Scilab Group INRIA-Rocquencourt Metalau Project. Свободно распространяемую версию пакета вместе с полной документацией на английском языке в формате PDF можно получить по адресу ссылка скрыта.
- ссылка скрыта
- ссылка скрыта
Материально-техническое и/или информационное обеспечение дисциплины
1. Персональный компьютер. Расчетные компьютерные программы: Maxima, SciLab, MathLab, MathCAD, Simulink, Excel (на выбор).
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ СТУДЕНТОВ
1. ОБЩИЕ УКАЗАНИЯ
Успешное освоение дисциплины предполагает активное, творческое участие студента путем планомерной, повседневной работы.
Изучение дисциплины следует начинать с проработки рабочей программы, особое внимание, уделяя целям и задачам, структуре и содержанию курса.
2. САМОСТОЯТЕЛЬНАЯ РАБОТА
Самостоятельная работа студентов по изучению программных материалов является основным видом учебных занятий по дисциплине “Вычислительная математика”.
Умение самостоятельно работать необходимо не только для успешного овладения курсом обучения, но и для творческой деятельности в учреждениях, учебных заведениях. Следовательно, самостоятельная работа является одновременно и средством, и целью обучения.
Основными видами самостоятельной работы студентов по курсу дисциплины являются:
работа на лекциях;
выполнение практических заданий;
выполнение курсовой работы;
самостоятельная работа над учебными материалами с использованием конспектов и рекомендуемой литературы;
групповые и индивидуальные консультации;
подготовка к экзамену.
На лекциях излагаются лишь основные, имеющие принципиальное значение и наиболее трудные для понимания и усвоения теоретические и практические вопросы.
Теоретические знания, полученные студентами на лекциях и при самостоятельном изучении курса по литературным источникам, закрепляются при выполнении лабораторных и контрольных работ.
Целями проведения практических занятий являются:
обучение студентов умению использовать имеющиеся шаблоны оформления;
контроль самостоятельной работы студентов по освоению курса;
обучение навыкам профессиональной деятельности.
При выполнении курсовой работы обращается особое внимание на выработку у студентов умения пользоваться научно-технической литературой, грамотно выполнять и оформлять документацию.
Текущая работа над учебными материалами представляет собой главный вид самостоятельной работы студентов. Она включает обработку конспектов лекций путем систематизации материала, заполнения пропущенных мест, уточнения схем и выделения главных мыслей основного содержания лекции. Для этого используются имеющиеся учебно-методические материалы и другая рекомендованная литература.
Просмотрите конспект сразу после занятий, отметьте материал конспекта лекций, который вызывает затруднения для понимания. Попытайтесь найти ответы на затруднительные вопросы, используя рекомендуемую литературу.
Работу с литературой рекомендуется делать в следующей последовательности: беглый просмотр (для выбора глав, статей, которые необходимы по изучаемой теме); беглый просмотр содержания и выбор конкретных страниц, отрезков текста с пометкой их расположения по перечню литературы, номеру страницы и номеру абзаца; конспектирование прочитанного.
Регулярно отводите время для повторения пройденного материала, проверяя свои знания, умения и навыки по контрольным вопросам.
Если самостоятельно не удалось разобраться в материале, сформулируйте вопросы и обратитесь за помощью к преподавателю на консультации.
На групповых и индивидуальных консультациях студенты завершают уточнение учебных материалов применительно к подготавливаемым мероприятиям (зачет, выполнение курсовой работы и др.).
Подготовка к экзамену осуществляется студентами самостоятельно.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ ПРЕПОДАВАТЕЛЕЙ
Методический комментарий по данному блоку
Методика преподавания учебной дисциплины решает следующие основные задачи:
определяет задачи обучения студентов по дисциплине;
научно обосновывает содержание учебной программы, намечает последовательность ее изучения в комплексе с другими дисциплинами;
определяет пути реализации принципов обучения при изучении дисциплины, формы и методы обучения;
вырабатывает требования к методической подготовке преподавателей;
изучает историю методики преподавания дисциплины;
внедряет передовой опыт обучения;
вырабатывает рекомендации по воспитанию обучаемых в процессе изучения дисциплины.
В соответствии с этими задачами осуществляется отбор научного материала, его систематизация и переработка в интересах развития и совершенствования содержания учебной дисциплины.
Методика разработана применительно к утвержденной рабочей программе для студентов-заочников со сроком обучения 6 лет с учетом требований Государственного образовательного стандарта высшего профессионального образования по специальности 230101.65, вычислительные машины, комплексы, системы и сети (ВМ), и вооружает преподавателей необходимыми знаниями, способствует их внедрению в практику обучения и воспитания студентов.
Выбор методов проведения занятий обусловлен учебными целями, содержанием учебного материала, временем, отводимым на занятия.
На занятиях в тесном сочетании применяется несколько методов, один из которых выступает ведущим. Он определяет построение и вид занятий.
На лекциях излагаются лишь основные, имеющие принципиальное значение и наиболее трудные для понимания и усвоения теоретические и практические вопросы.
Теоретические знания, полученные студентами на лекциях и при самостоятельном изучении курса по литературным источникам, закрепляются при выполнении практических работ и курсовой работы.
Целями проведения практических занятий являются:
приобретение практических навыков работы с прикладными программами;
контроль самостоятельной работы студентов по освоению курса;
обучение навыкам профессиональной деятельности.
Цели практических занятий достигаются наилучшим образом в том случае, если им предшествует определенная подготовительная внеаудиторная работа. Поэтому преподаватель обязан довести до всех студентов график выполнения практических занятий с тем, чтобы они могли заниматься целенаправленной самостоятельной работой.
Перед началом практического занятия преподаватель должен удостовериться в готовности студентов к выполнению практических заданий путем короткого собеседования.
Работы рекомендуется выполнять в той последовательности, в которой они написаны, потому что в некоторых работах используются элементы, полученные в предыдущей работе.
При выполнении курсовой работы обращается особое внимание на выработку у студентов умения пользоваться научно-технической литературой, оптимальными приемами работы с программными продуктами.
На занятиях со студентами должны широко использоваться разнообразные средства обучения, способствующие более полному и правильному пониманию темы лекции или лабораторного занятия, а также выработке практических навыков по работе с ППО.
К средствам обучения студентов относятся:
речь преподавателя;
технические средства обучения: - персональные компьютеры с установленным прикладным программным обеспечением;
- учебники, учебные пособия, лекции в электронном виде.
МАТЕРИАЛЫ ТЕКУЩЕГО, ПРОМЕЖУТОЧНОГО И ИТОГОВОГО КОНТРОЛЯ
Для проведения зачетов (экзаменов) в письменной или тестовой форме разрабатывается перечень вопросов, утверждаемый заведующим кафедрой. В перечень включаются вопросы из различных разделов курса, позволяющие проверить и оценить теоретические знания студентов и умение применять их для решения практических задач.
Зачет (экзамен) в письменной форме проводится одновременно для всех студентов академической группы. Время выполнения задания составляет не более одного академического часа. При проведении зачета (экзамена) в письменной форме оценка выставляется на основе правил, принятых кафедрой, которые должны быть сообщены студентам до начала зачетной (экзаменационной) сессии.
Аналогичные правила могут быть заложены в программы компьютерного тестирования.
При контроле знаний в устной форме преподаватель использует метод индивидуального собеседования, в ходе которого обсуждает со студентом один или несколько вопросов из учебной программы. При необходимости могут быть предложены дополнительные вопросы, задачи и примеры. По окончании ответа на вопросы преподаватель объявляет студенту результаты сдачи зачета (экзамена).
Контрольные вопросы по курсу «Вычислительная математика»
Формула Лагранжа
- Полином какой степени является интерполяционным полиномом Лагранжа при (n+1) узлах?
- Может ли формула Лагранжа применяться для экстраполяции?
- Что влияет на точность интерполяции при использовании полинома Лагранжа?
- Можно ли применять полином Лагранжа для не равноотстоящих узлов?
- К какому классу функций относится функция, задаваемая интерполяционной формулой Лагранжа?
- Как можно повысить точность интерполяции при использовании формулы Лагранжа?
Формула Ньютона
- Может ли формула Ньютона применяться для экстраполяции?
- Как можно повысить точность интерполяции при использовании формулы Ньютона?
- В чем разница между первой и второй интерполяционными формулами Ньютона?
- Какой степени можно получить интерполяционный полином при трех заданных точках?
Сплайновая интерполяция
- Что называется кубическим сплайном?
- Сколько коэффициентов необходимо определить для построения кубического сплайна?
- Зачем требуются дополнительные граничные условия?
Аппроксимация
- Дайте определение аппроксимации.
- Чем отличается аппроксимация от интерполяции?
- Можно ли удовлетворить условию прохождения через все точки при аппроксимации таблично заданной функции?
- Можно ли повысить точность при одновременном увеличении в несколько раз всех весовых коэффициентов?
- Можно ли с помощью метода наименьших квадратов найти параметры неполиномиальной аппроксимирующей функции?
- Какая система уравнений называется нормальной системой?
- На каких условиях построено получение нормальной системы уравнений?
Отделение корней нелинейных уравнений
- Зачем необходимо отделять корни?
- Можно ли аналитически отделить корни для функции имеющей разрывы?
- Какие точки при отделении корней называются критическими?
Методы уточнения корней
- Геометрический смысл метода половинного деления (проиллюстрировать)?
- Всегда ли можно вычислить корень, с заданной точностью используя метод половинного деления?
- Какими свойствами должна обладать функция, чтобы можно было найти корень методом половинного деления?
Метод хорд
- Для нахождения, каких корней применяется метод хорд?
- В чем заключается геометрический смысл метода хорд?
- Всегда ли можно вычислить корень, с заданной точностью используя метод хорд?
- Какими свойствами должна обладать функция, чтобы можно было найти корень методом хорд?
- Какой конец хорды неподвижен при реализации метода хорд?
Метод Ньютона
- В чем заключается геометрический смысл метода Ньютона?
- Из каких соображений выбирается в методе Ньютона первое приближение?
- Какие условия должны выполняться, чтобы можно было решать уравнение методом Ньютона?
Метод простой итерации
- Какой функцией заменяется левая часть решаемого уравнения в методе простой итерации?
- Что называется сходимостью метода простой итерации?
- В каком случае итерационный процесс сходится при методе простой итерации?
- Какой условие должно выполняться, чтобы метод простой итерации сходился?
Алгебраические уравнения
- Зачем нужны приближенные методы для решения алгебраических уравнений?
- В каком случае можно точно определить количество корней, используя правило Декарта?
- Как найти общее число корней алгебраического уравнения?
Системы нелинейных уравнений
- Как проводится отделение корней при решении систем нелинейных уравнений?
- От чего зависит сходимость метода Ньютона-Рафсона?
- Можно ли обеспечить сходимость метода итераций при решении систем нелинейных уравнений?
- Как влияет на решение выбор начального приближения?
Системы линейных уравнений
- Какие методы называются точными при решении системы линейных уравнений?
- Какие методы называются приближенными при решении системы линейных уравнений?
- От чего зависит сходимость методы итераций?
- Как в методе Гаусса можно контролировать накопление вычислительных ошибок?
- При каких условиях метод итераций сходится?
- В чем отличие метода Зейделя от метода итераций?