Интегральные логические элементы
| Вид материала | Лабораторная работа |
- Время, требуемое для выполнения проекта 7 недель, 14 часов, 8.75kb.
- Тема урока : «Базовые логические элементы», 87.8kb.
- Классификация элементов вычислительных средств, 641.33kb.
- Тема Уроки 1 Логические основы компьютера Урок Логические элементы и переключательные, 96.75kb.
- Сумцова Ольга Владимировна Логические основы построения компьютера Темы игры: Основные, 54.64kb.
- Контрольная работа по теме «Элементы математической логики», 36.88kb.
- Пояснительная записка к извещению №3 об изменении ост в 11 0998-99 «Микросхемы интегральные., 297.02kb.
- Темы Лекции Практика, 13.65kb.
- Урок №17 тема урока логические основы построения ЭВМ, 117.09kb.
- Курс, специальность: «Прикладная информатика (в экономике)» 1 семестр (лекции 36 часов;, 84.15kb.
Лабораторная работа
ИНТЕГРАЛЬНЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
Цель: ознакомление студентов с принципами построения и функционирования простейших элементов и узлов цифровой техники.
Для цифровой электроники характерно то, что функционирование ее происходит в двоичной системе счисления, оперирующей только двумя цифрами: нуль (0) и единица (1), а математическим аппаратом, на основе которого проектируются и реализуются цифровые устройства, является алгебра логики (булева алгебра).
Как известно, предметом рассмотрения алгебры логики являются высказывания (утверждения), которые могут оказаться либо истинными, либо ложными. Следовательно, истинность высказывания может принимать, подобно цифрам в двоичной системе счисления, только два значения: "истинно" соответствует цифре 1 и «ложно» - цифре 0.
Простые высказывания, объединенные логическими операциями (связями), образуют сложное высказывание или, другими словами, логическую функцию логических переменных. Если простые высказывания обозначить буквами А, В, С,..., а сложное- буквой F, то логические операции можно записать математически. Напомним три основных типа логических операций.
Логическое умножение (операция И), или конъюнкция (обозначается
 или
или 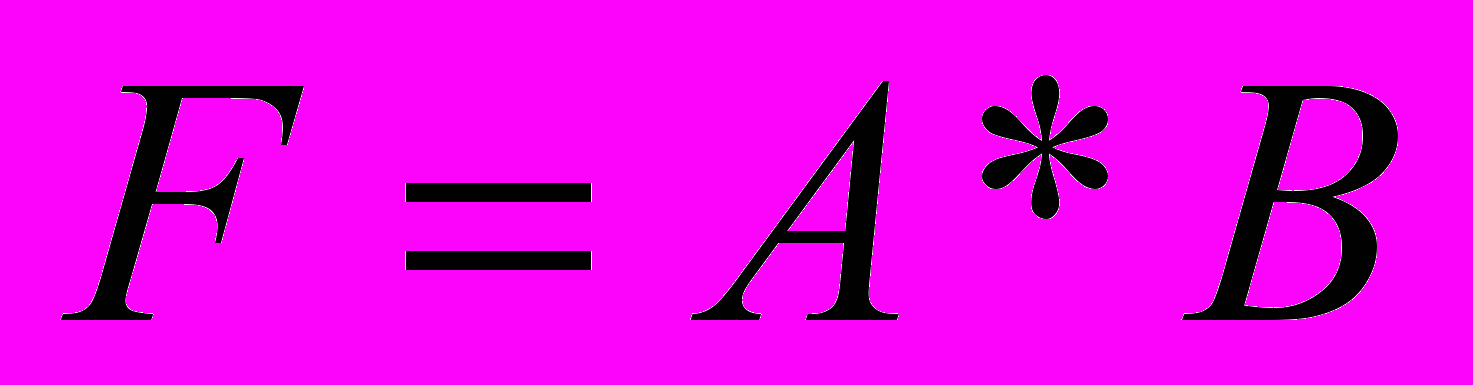 , или еще проще
, или еще проще 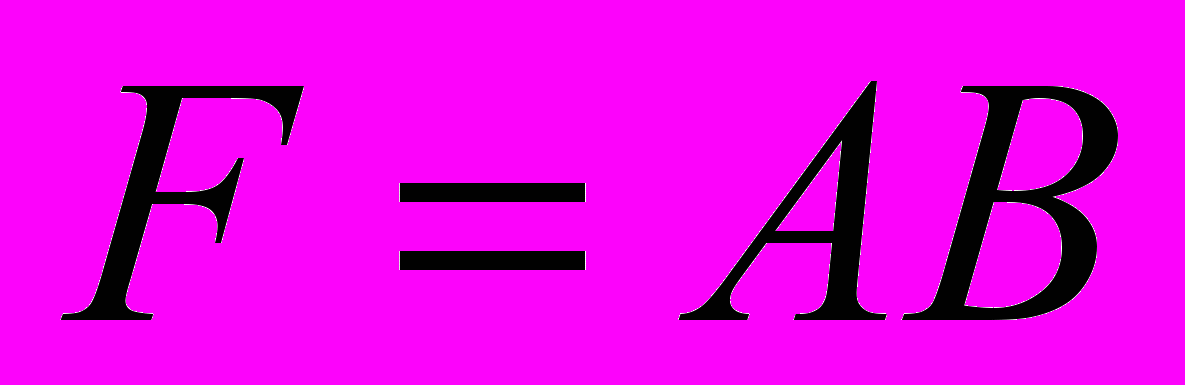 , читается «А и В»). Эта операция означает, что сложное высказывание истинно лишь тогда, когда истинны все (в данном случае два) простые высказывания. Записанная в виде таблицы истинности, где показаны значения F в зависимости от значений А и В, операция конъюнкции имеет вид:
, читается «А и В»). Эта операция означает, что сложное высказывание истинно лишь тогда, когда истинны все (в данном случае два) простые высказывания. Записанная в виде таблицы истинности, где показаны значения F в зависимости от значений А и В, операция конъюнкции имеет вид: | А | B | F |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логическое сложение (операция ИЛИ), или дизъюнкция (обозначается
 , читается «А или В»). Эта операция означает, что сложное высказывание истинно, если истинно хотя бы одно из простых высказываний, и тем более, если истинны оба высказывания:
, читается «А или В»). Эта операция означает, что сложное высказывание истинно, если истинно хотя бы одно из простых высказываний, и тем более, если истинны оба высказывания:| А | B | F |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Логическое отрицание (операция НЕ), или инверсия (обозначается
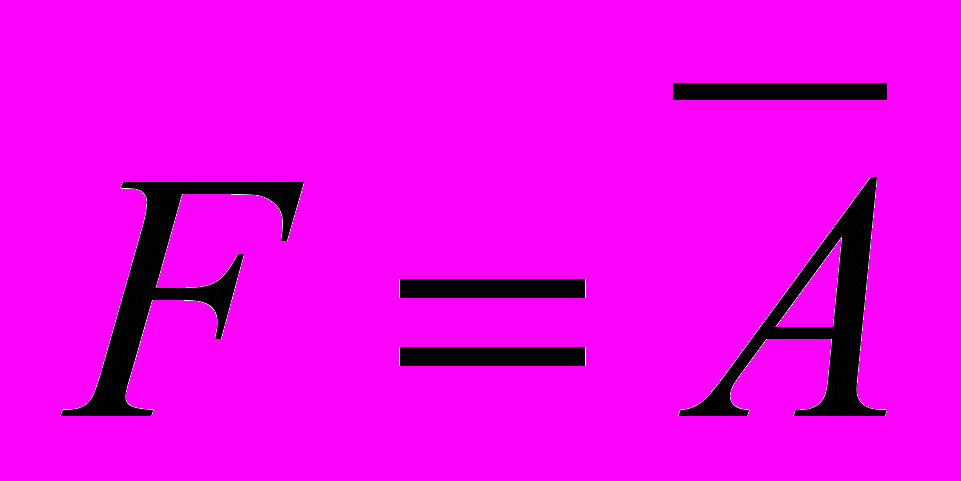 , читается «не А»). Эта операция означает, что сложное высказывание истинно, если простое ложно, и наоборот.
, читается «не А»). Эта операция означает, что сложное высказывание истинно, если простое ложно, и наоборот.| А | F |
| 0 | 1 |
| 1 | 0 |
В соответствии с тремя основными операциями алгебры логики в схемах цифровых устройств используются следующие логические элементы:
- элемент И (называемый также схемой логического умножения, конъюктором, схемой совпадения);
- элемент ИЛИ (схема логического сложения, дизъюнктор, сборка);
- элемент НЕ (схема логического отрицания, инвертор).
Этот набор элементов называют основным базисом или основной функциональной полной системой элементов. Последнее означает, что с помощью этих элементов можно создать схему, осуществляющую любую сколь угодно сложную логическую операцию.
В интегральной схемотехнике широко используют элементы других базисов, выполняющие одновременно две логические операции: ИЛИ-НЕ (стрелка Пирса, обозначаемая
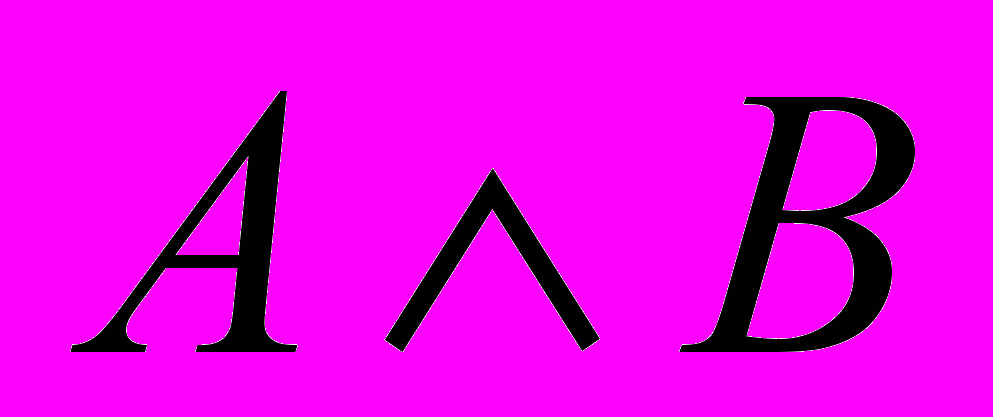 ) или И-НЕ (штрих Шеффера, обозначаемый
) или И-НЕ (штрих Шеффера, обозначаемый  ). Заметим, что каждый из этих двух элементов также представляет собой функционально полную систему элементов.
). Заметим, что каждый из этих двух элементов также представляет собой функционально полную систему элементов.По виду кодирования двоичных цифр электрическими сигналами на входе и выходе элементы дискретной техники делятся на потенциальные и импульсные.
В потенциальных элементах нулю и единице соответствуют два резко отличающихся уровня напряжения, называемые высоким и низким уровнями (табл 1.). При этом напряжения могут быть как положительными, так и отрицательными относительно точки, электрический потенциал которой принимается равным нулю вольт.
Таблица 1
| Полярность уровней напряжения | Вид логики | |
| положительная | отрицательная | |
| Положительная | 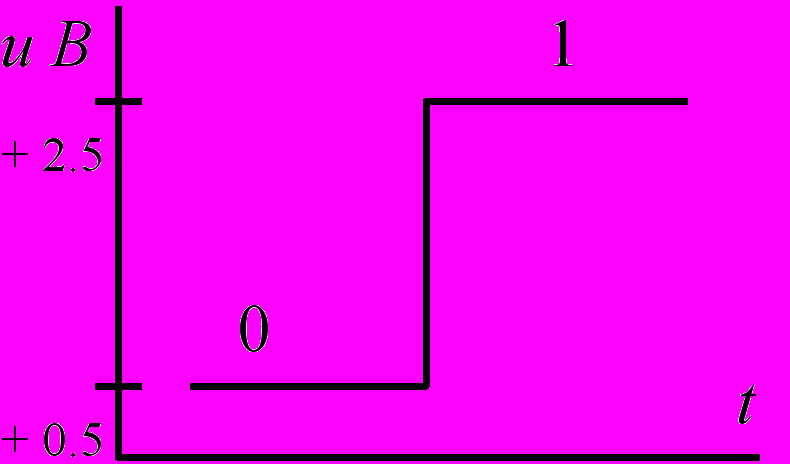 | 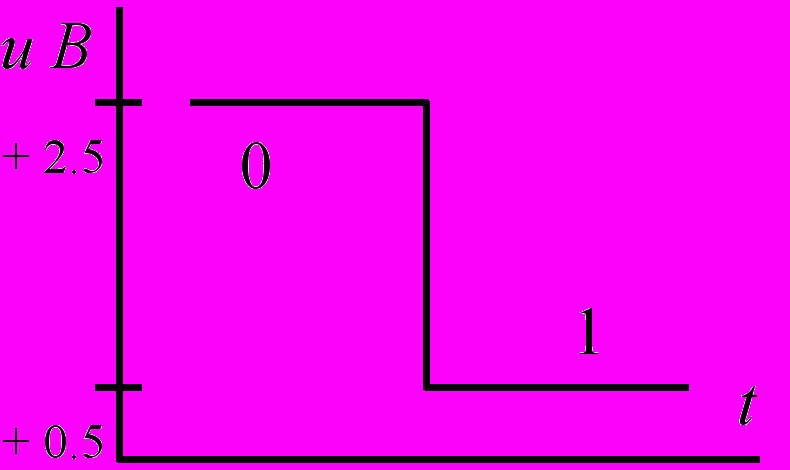 |
| Отрицательная | 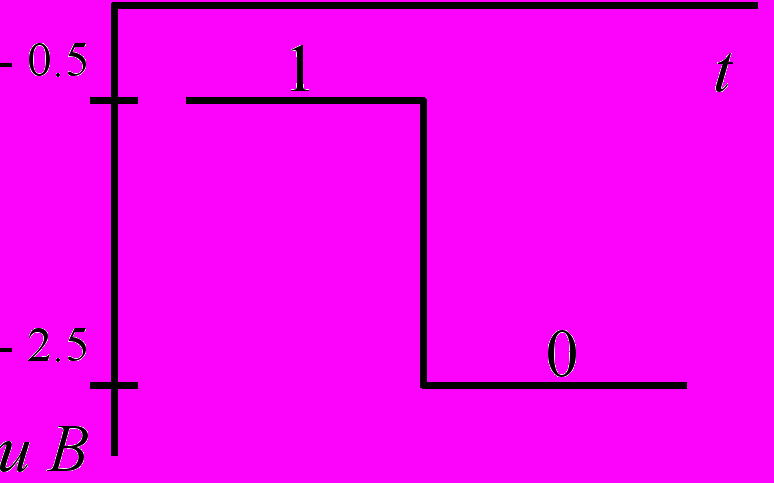 | 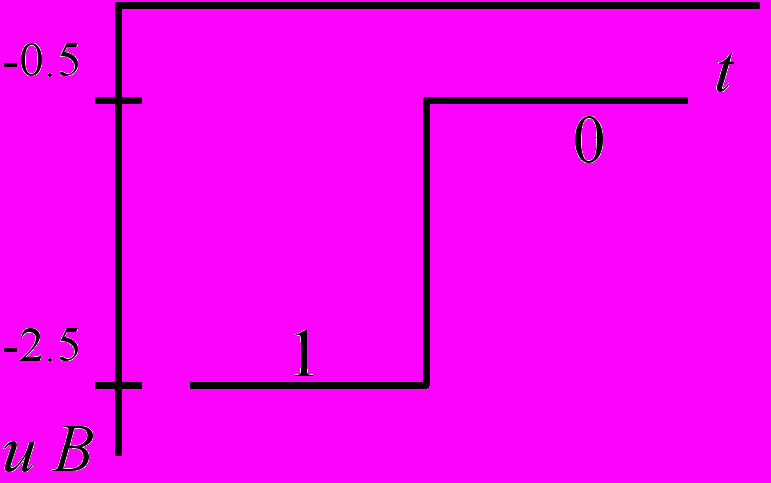 |
Различают элементы, работающие в положительной (позитивной) и отрицательной (негативной) логике.
В положительной логике за логическую единицу принят высокий уровень напряжения (например, +2,5 В при положительной полярности уровней напряжений или -0,5 В при отрицательной полярности уровней напряжений, как показано в левой части табл. 1), а за логический нуль - низкий уровень (т.е. +0,5 В при положительной или -2,5 В при отрицательной полярности уровней напряжения).
В отрицательной логике кодирование логических 1 и 0 противоположное (оно обозначено в правой части табл. 1).
Комбинационными, или логическими, называются функциональные узлы, содержащие только логические элементы и не содержащие элементов памяти (триггеров). Состояние логического функционального узла однозначно определяется комбинацией входных сигналов и не зависит от предыдущего состояния. К логическим относятся такие цифровые узлы, как шифраторы, дешифраторы, сумматоры, устройства сравнения, мультиплексоры, преобразователи кодов и др.
На практике часто приходится синтезировать даже простейшие комбинационные схемы, реализующие элементарные логические операции, используя заданный элементный базис. Например, может возникнуть задача реализации логических функций И, ИЛИ, НЕ на базисе И-НЕ или ИЛИ-НЕ. Для такого синтеза можно использовать основные тождества алгебры логики:
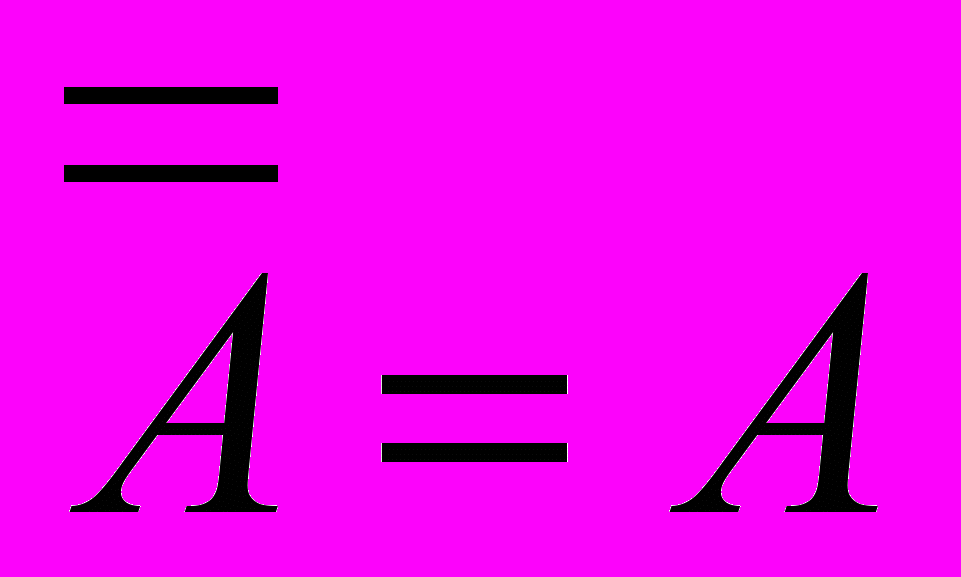
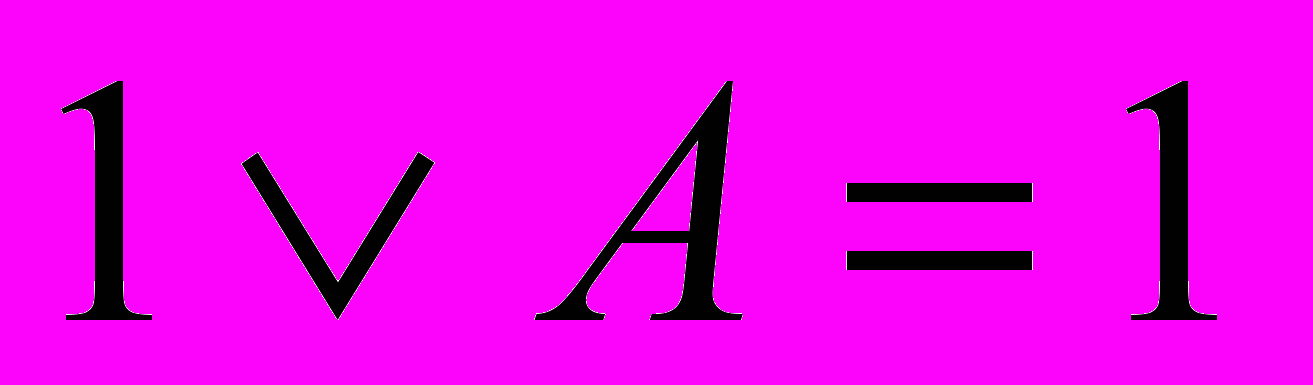 ;
;  ;
; ;
; 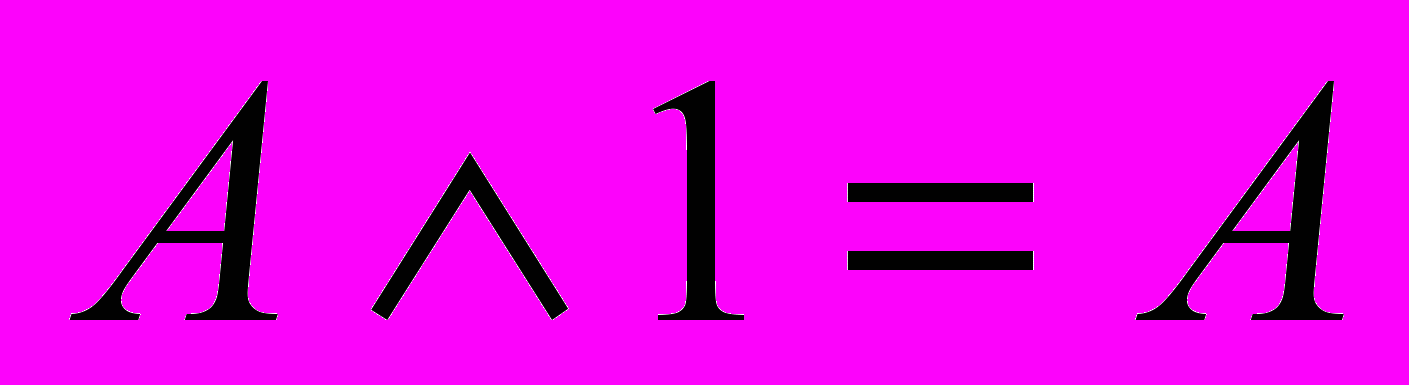 ;
;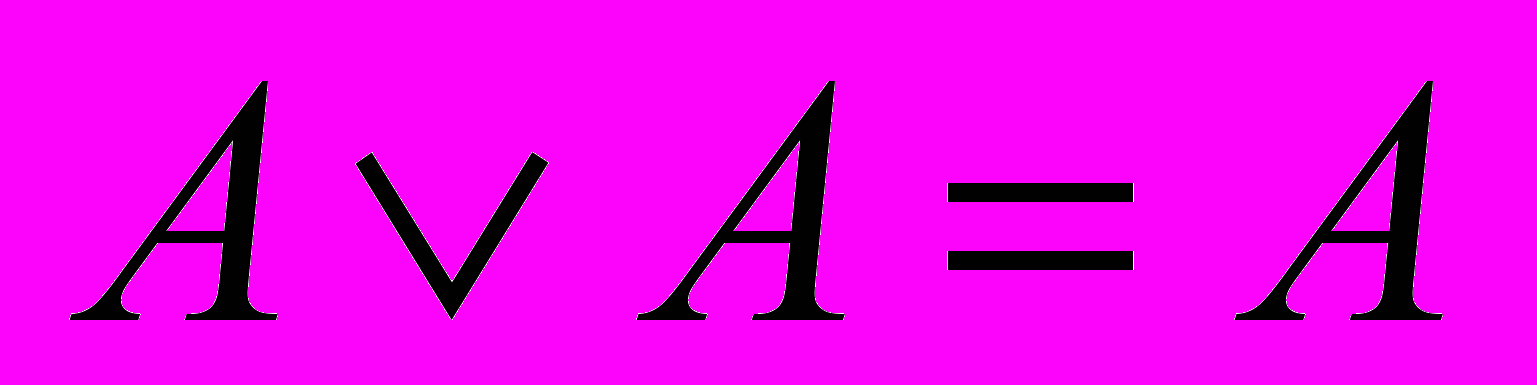 ;
; 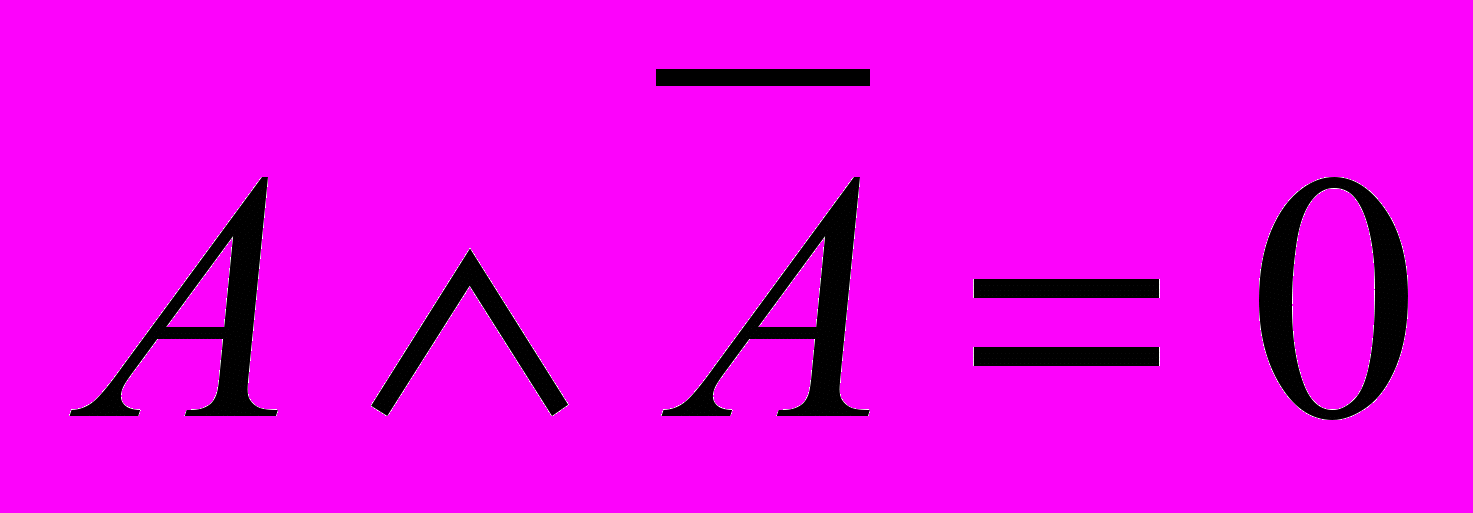 ;
;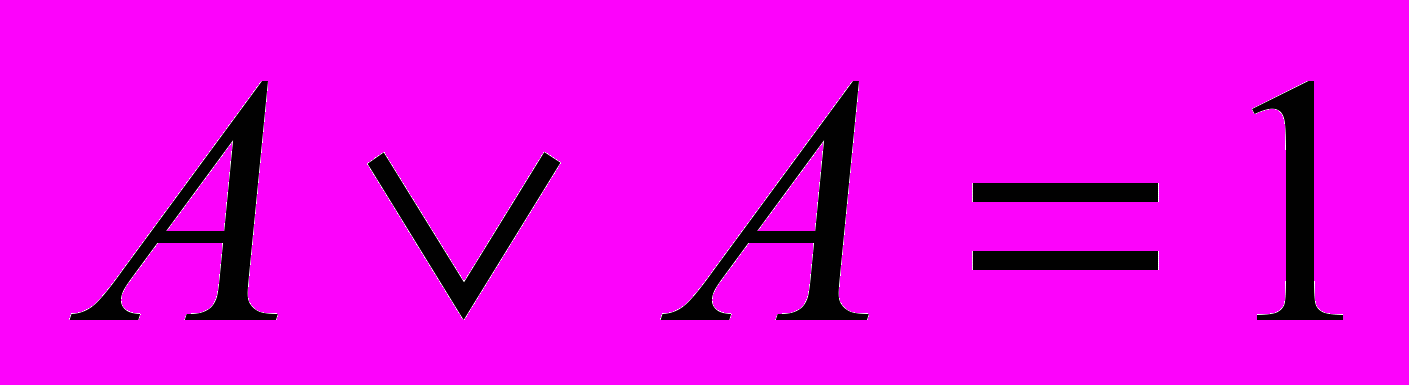 ;
;Для преобразования логического умножения в логическое сложение или наоборот используют правило Де-Моргана:

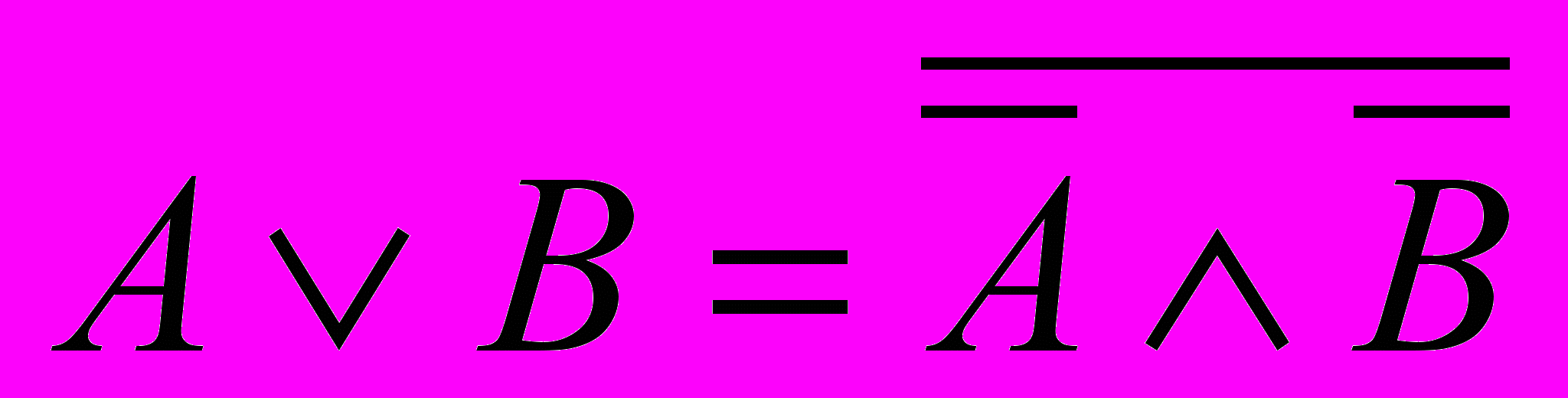
В алгебре логики, как и в обычной алгебре, действуют переместительный, сочетательный и распределительный законы:


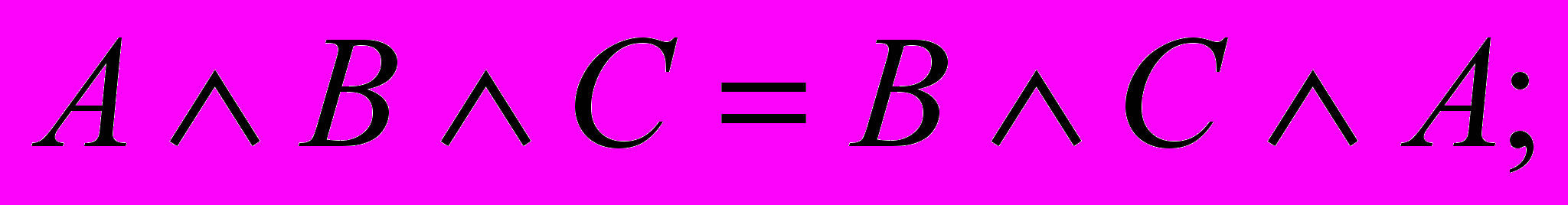

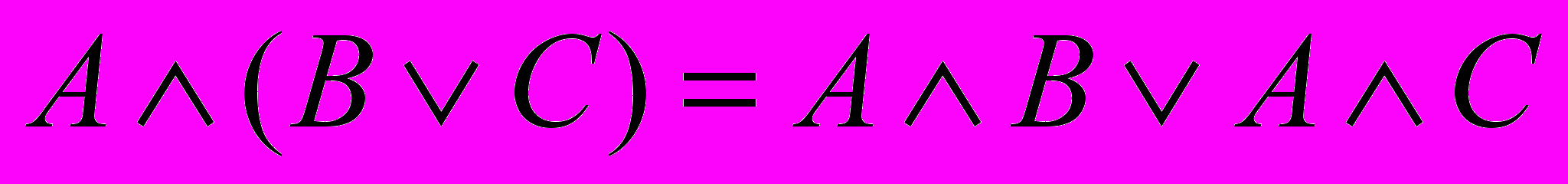 .
.В таблице 2 приведены полезные свойства булевых функций И, ИЛИ, НЕ.
Рабочее задание
1. Исследование логических элементов И-НЕ, ИЛИ-НЕ
Подключите интегральные схемы серии ТТЛ, реализующие функции И-НЕ (К155 ЛА3) и ИЛИ-НЕ (К155 ЛЕ1) к источнику питания и исследуйте их работу. Проверьте выполнение таблицы истинности. Справочная информация по микросхемам приведена в приложении 1. Подайте на вход одного ЛЭ И-НЕ прямоугольные импульсы и исследуйте выходные сигналы элемента. Измерьте время нарастания и время спада выходного напряжения.
2. Реализация функции не (инверсии)
Условное графическое обозначение элемента показано на рис. 1.2. Синтезируйте и соберите на наборном поле стенда элемент И, используя элемент 2И-НЕ (возможны 2 варианта). Выход Y соедините с осциллографом. На вход «а» подайте сигнал логической единицы, а затем - логического нуля. Зафиксируйте значения выходного сигнала исследуемого элемента. Все значения входного и соответствующего выходного сигналов занесите в таблицу истинности. Напишите аналитическое выражение функции и начертите временную диаграмму для входной и выходной переменных.
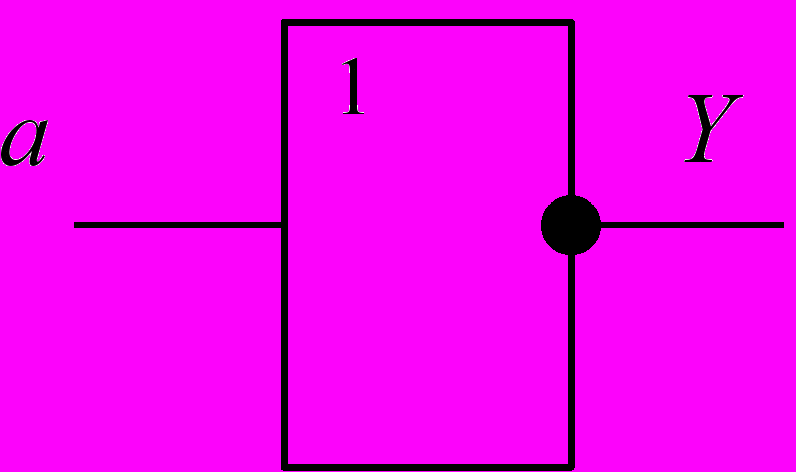
Рис. 1.2
3. Реализация функции и (конъюнкции)
Условное графическое обозначение элемента показано на рис. 1.3. Используя в качестве базиса элемент 2И-НЕ синтезируйте и соберите на наборном поле схему, реализующую функцию И. Выход Y соедините с осциллографом. Подключая входы «a» и «b» к гнездам «0» и «1» на вспомогательном устройстве, подайте на входы следующие комбинации сигналов:
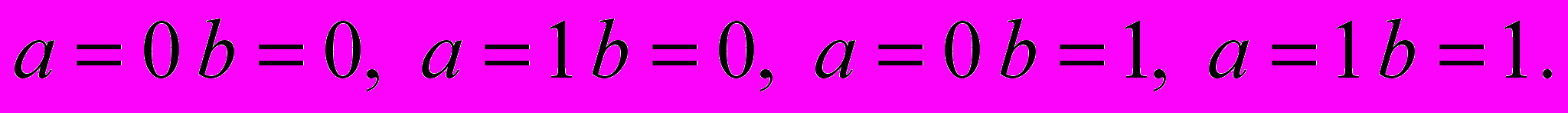 Все значения входных и выходных сигналов занесите в таблицу истинности. Напишите аналитическое выражение функции и начертите временную диаграмму для входных и выходной переменных.
Все значения входных и выходных сигналов занесите в таблицу истинности. Напишите аналитическое выражение функции и начертите временную диаграмму для входных и выходной переменных.
Рис. 1.3
4. Реализация 3-х входовой схемы И
Используя в качестве базиса элемент 2И-НЕ синтезируйте и соберите на наборном поле схему, реализующую функцию 3И и исследуйте ее, как это описано в предыдущем пункте задания. Все значения входных и выходных сигналов занесите в таблицу истинности. Напишите аналитическое выражение и составьте временную диаграмму.
5. реализация функции или (дизъюнкции)
Условное графическое обозначение элемента показано на рис.1.4. Синтезируйте, используя правило Де-Моргана, элемент ИЛИ на базисе И-НЕ. Соберите синтезированную схему на наборном поле лабораторной установки и исследуйте ее, как это описано в предыдущем пункте задания. Все значения входных и выходных сигналов занесите в таблицу истинности. Напишите аналитическое выражение и составьте временную диаграмму.
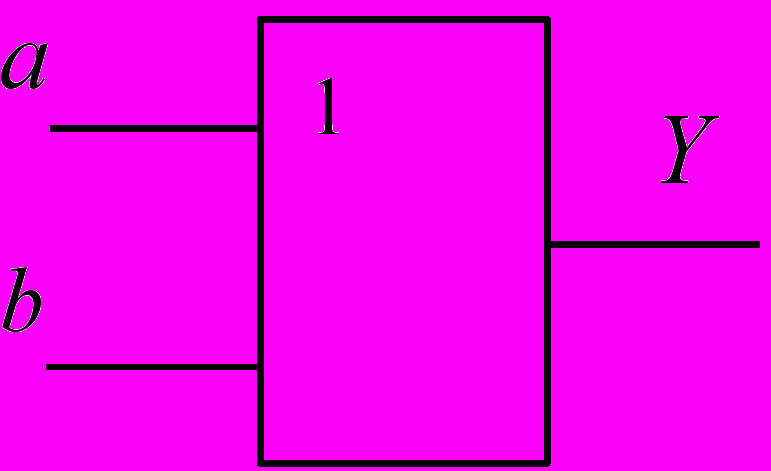
Рис. 1.4
6. реализация функции или-не
Условное графическое обозначение элемента показано на рис.1.5. Для синтеза функции воспользуйтесь результатами предыдущих пунктов задания. Заполните таблицу истинности полученной комбинационной схемы. Запишите аналитическое выражение заданной функции и постройте временную диаграмму.

Рис. 1.5
7. реализация функции суммирование по модулю 2
Сумматор по модулю 2 - цифровой узел с m входами и одним выходом. В частном случае при числе входов, равном 2, сумматор по модулю 2 выполняет функцию логического элемента «ИСКЛЮЧАЮЩЕЕ ИЛИ».
Условное графическое обозначение элемента «ИСКЛЮЧАЮЩЕЕ ИЛИ» показано на рис.1.6. На наборном поле собрать схему согласно рис.1.7. Заполните таблицу истинности полученной комбинационной схемы и постройте временную диаграмму. Запишите аналитическое выражение для функции «ИСКЛЮЧАЮЩЕЕ ИЛИ».

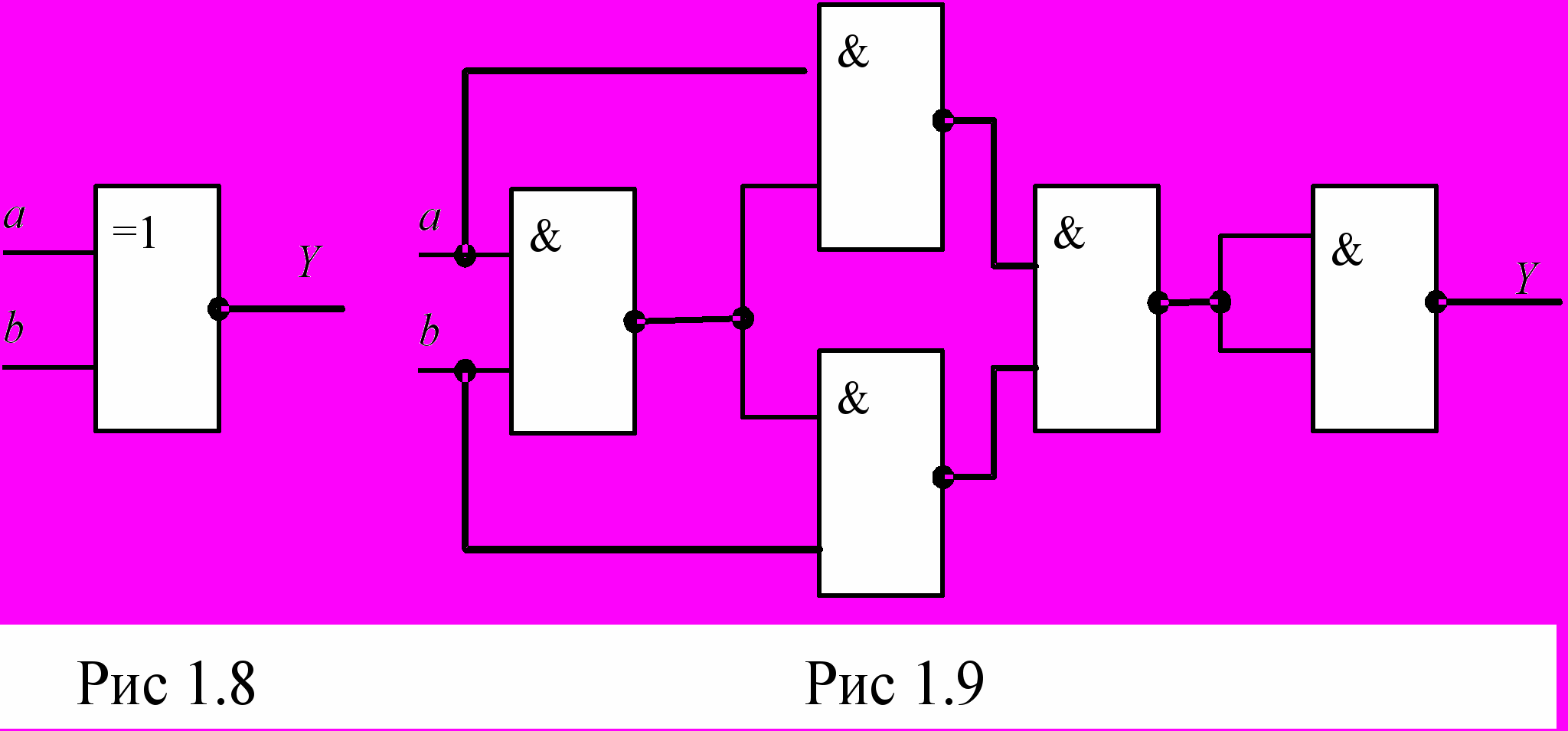
8. Реализация функции эквивалентности
Условное графическое обозначение элемента показано на рис.1.8. На наборном поле соберите схему согласно рис.1.9. Заполните таблицу истинности полученной комбинационной схемы и постройте временную диаграмму. Запишите аналитическое выражение для функции «ЭКВИВАЛЕНТНОСТЬ».
9. Построение передаточной характеристики ЛЭ ТТЛ.
В качестве исследуемого ЛЭ серии ТТЛ используйте ЛЭ И-НЕ. Схема подключения приборов для снятия передаточной характеристики
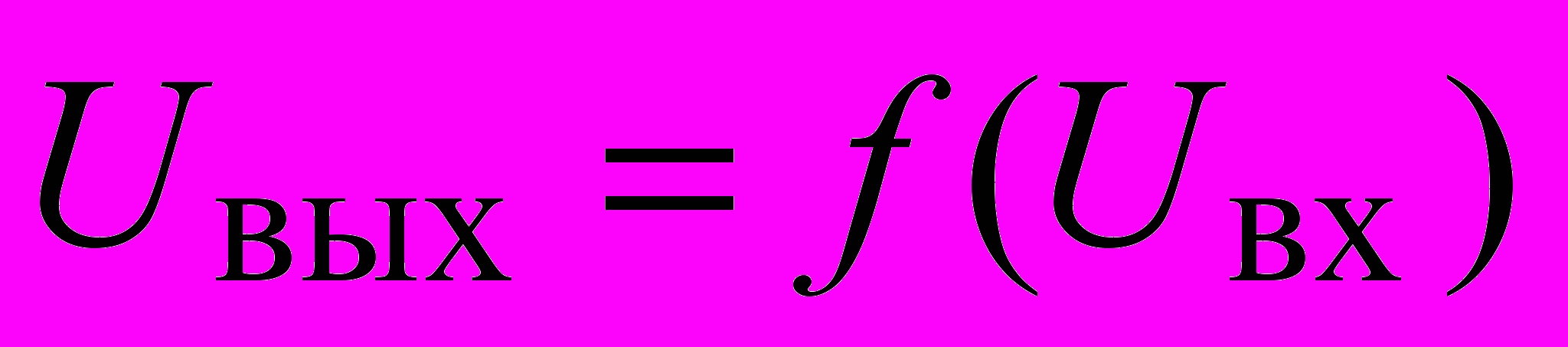 разрабатывается студентами самостоятельно. Необходимы приборы: регулируемый источник питания, вольтметр, осциллограф.
разрабатывается студентами самостоятельно. Необходимы приборы: регулируемый источник питания, вольтметр, осциллограф. Приложение 1
| Параметр | Значение |
 , мА , мА | 16 |
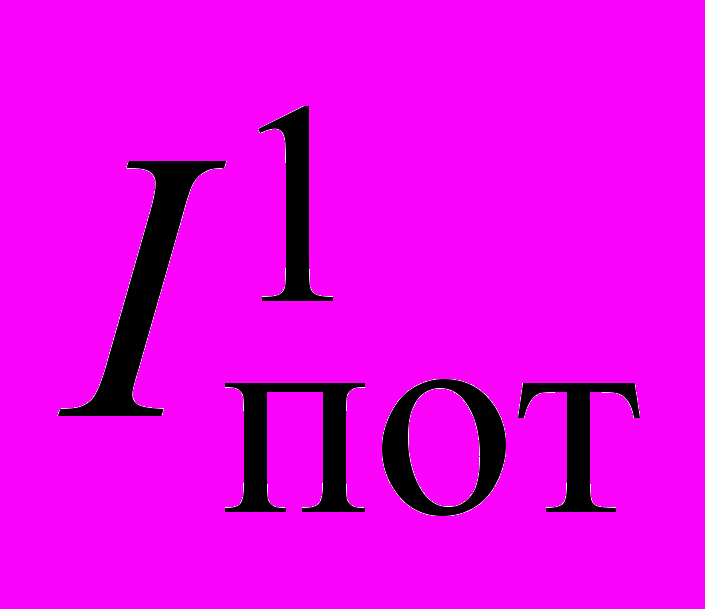 , мА , мА | 8 |
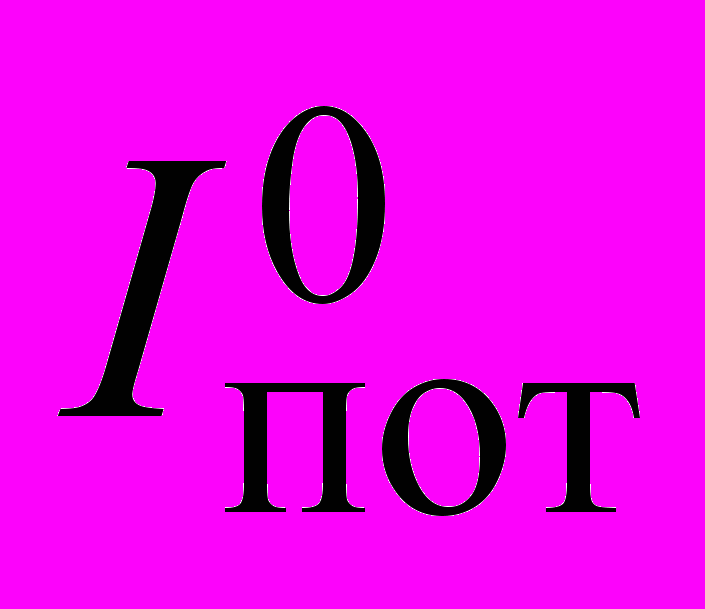 , мА , мА | 12 |
 , нс , нс | 22 |
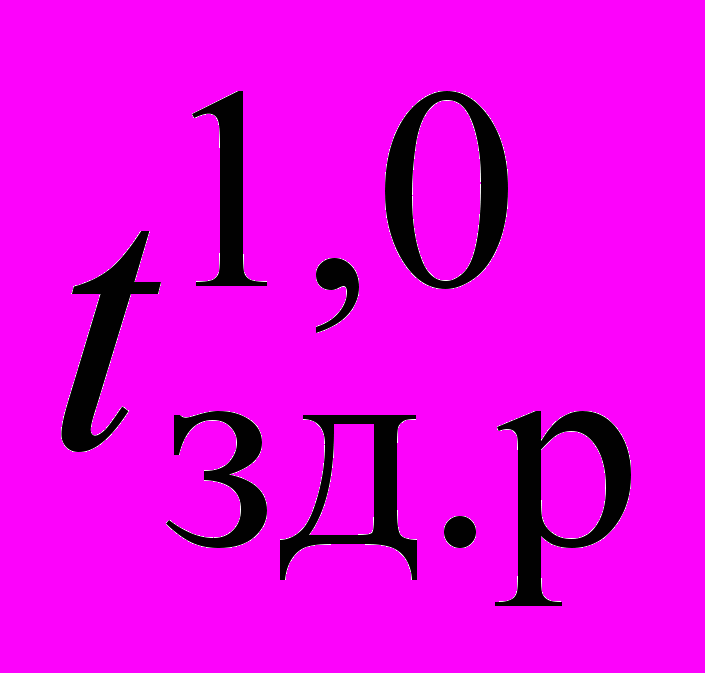 , нс , нс | 15 |
 Микросхема К155ЛА3
Микросхема К155ЛА3 | Параметр | Значение |
 , мА , мА | 16 |
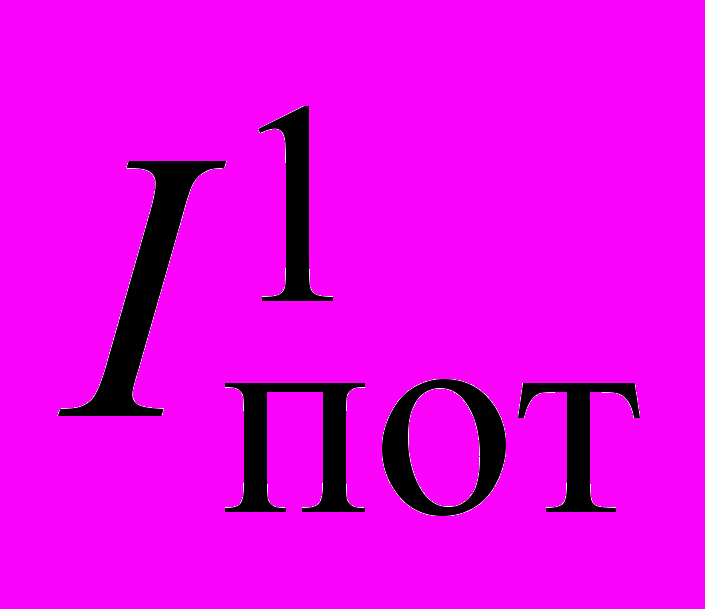 , мА , мА | 16 |
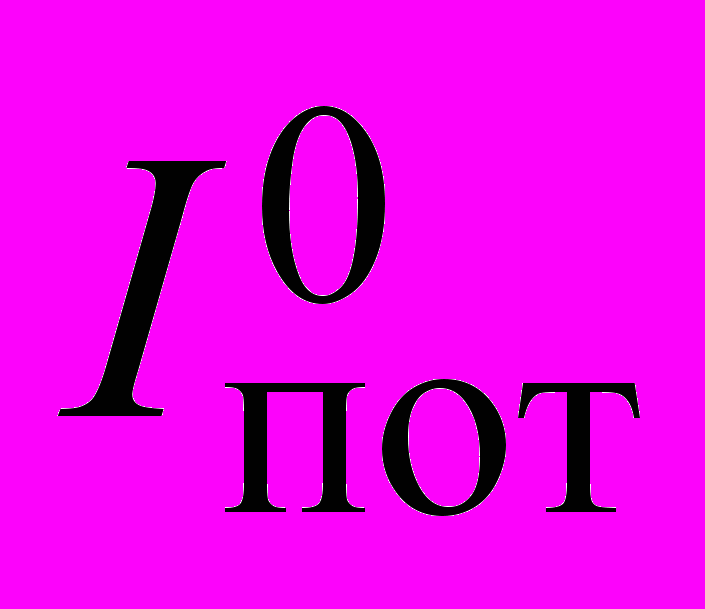 , мА , мА | 27 |
 , нс , нс | 15 |
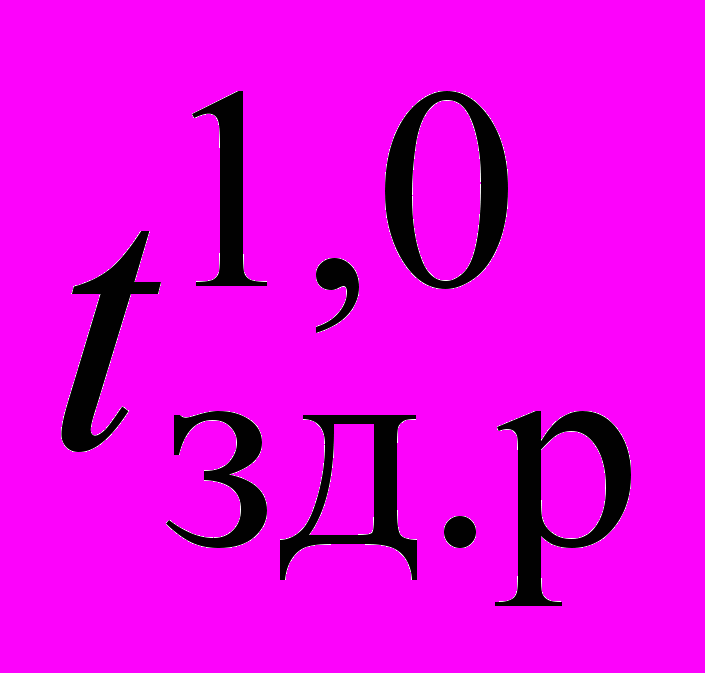 , нс , нс | 15 |
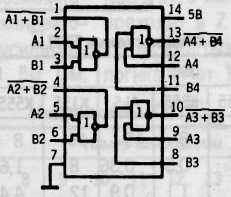 Микросхема К155ЛЕ1
Микросхема К155ЛЕ1
