Geum.ru

Тема Уроки 1 Логические основы компьютера Урок Логические элементы и переключательные схемы Цель урока

Вид материалаУрок

Содержание


Общие замечания к уроку. М
Примерный ход урока.
S= (avbvp
Урок 4. Логические схемы элементов компьютера. Многоразрядный сумматор. Триггер.
Подобный материал:
Тема 1. Уроки 1-4. Логические основы компьютера

Урок 1. Логические элементы и переключательные схемы

Цель урока: Расширить знания учащихся по теме «Логические основы работы компьютера», научить строить простейшие переключательные схемы, познакомиться с эволюцией технологии создания переключателей.

Примерный ход урока.

Урок можно начать с обсуждения следующего вопроса: «Мы определяем компьютер как автоматическое устройство обработки информации, представленной в виде цифрового двоичного кода. В то же время, компьютер – это устройство, состоящее из различных электронных элементов, представляющих собой простейшие электрические схемы. Каким образом происходит обработка аналогового (электрического) сигнала, как он преобразуется в цифровой код?» Из курса 8-9 класса учащиеся помнят, что наличие электрического сигнала в цепи соответствует логической единице (истине), отсутствие тока – логическому нолю (ложь). А логические операции осуществляют логические элементы, которые технически реализуются с помощью переключательных схем.

Поскольку ученикам знакомо понятие логических схем и логических элементов(§1.6.3), то знакомство с переключательными цепями можно организовать, выводя по-очереди на экран изображения элементарных электрических схем (представленных на рис. 2.1 и 2.2). Предложите ученикам предположить, какой логической операции соответствует каждая из схем. Обязательно сделайте выводы: конъюнкцию реализуют последовательно соединённые переключатели, дизъюнкцию – параллельно соединённые переключатели, последовательно подключенные к участку цепи.

Предложите ученикам построить электрическую цепь, работающую по принципу инвертора. Где необходимо разместить переключатель, чтобы логика работы схемы соответствовала инвертору? (Лампочка должна светиться, если тока нет, и наоборот). Отметьте важный вывод: для реализации операции отрицания переключатель, значение сигнала которого инвертируется, необходимо разместить параллельно участку цепи, через которую протекает ток.

Затем дайте задание ученика изобразить схему для логической формулы, представленной в примере параграфа 2.1.1.

Логические схемы можно рассматривать как модель реализации логических операций, на самом деле в современных компьютерах используются более сложные микросхемы, работающие с высокой скоростью.

Познакомиться с историей развития физической реализации переключателей учащиеся могут по учебнику (например, одна группа учеников – разбираются с работой электромагнитного реле, а другая – с электронным реле на базе триода). Затем представители групп по заранее подготовленным педагогом слайдам с рисунками рассказывают об изученных процессах и раскрывают особенности обработки электрических сигналов.

В заключение, повторите основные моменты урока по таблице основных понятий.

Домашнее задание. §2.1.1, вопросы и задания после параграфа. Можно дать задание упр.№4 оформить в текстовом редакторе.

Урок 2. Логические схемы элементов компьютера. Полусумматор. Одноразрядный сумматор.

Цель урока: Выяснить, как связаны алгебра логики и двоичная арифметика, изучить реализацию операции сложения двух, трёх двоичных цифр в устройстве компьютера, познакомиться с принципами работы полусумматора и одноразрядного сумматора.

Общие замечания к уроку. Материал данного урока сложен теоретически, поэтому важно, чтобы ученики как можно больше этапов урока выполнили самостоятельно, а учителю отводится роль ведущего, направляющего деятельность обучающихся. Когда ученики не только слушают учителя, а сами приходят к основным выводам, участвуют в получении новой информации, результаты освоения намного выше.

Примерный ход урока. Проверьте, есть ли вопросы по домашнему заданию (3-5 минут).

Полусумматор (10 минут) На прошлом уроке учащиеся познакомились с простыми электрическими цепями, выполняющими функции элементарных логических элементов.

Можно задать вопрос ученикам: Как связана алгебра логики и тот факт, что компьютер работает с информацией, представленной в двоичном коде, а вычислительный процесс производится в двоичной системе счисления? Наверняка Вы получите правильный ответ. Если нет – воспользуйтесь объяснением, приведённым в учебнике.

В учебнике представлена таблица сложения одноразрядных двоичных чисел, можно вывести её на экран и предложить учащимся разобраться, что означают столбцы S и Р, если складывать значения одноразрядных двоичных чисел А и В.

Предложите ученикам составить формулы для вычисления значений Р и S, они следуют из таблиц истинности. Затем пусть ученики построят логическую схему, на вход которой подаются сигналы А и В, а на выходе получаются P и S. Для проверки выведите на экран схему, представленную на рис. 2.6.

Сообщите, что полученная схема моделирует работу полусумматора двоичных чисел, покажите его схематичное обозначение. Обсудите, почему устройство так называется?

Сумматор (25 минут). Предложите подумать над следующим вопросом: можно ли воспользоваться полусумматором для выполнения суммы двоичных чисел, состоящих из нескольких цифр, т.е. многоразрядных двоичных кодов? Очевидно, что нет, так как устройство полусумматора не учитывает переносимой единицы.

Вспомните механизм выполнения сложения многоразрядных двоичных чисел, разберите пример, подобный тому, что приведён в учебнике, обратите внимание учащихся на случай переноса 1 в следующий разряд.

Сообщите, что для реализации суммы одноразрядных чисел с учётом переносимой единицы используется устройство одноразрядный сумматор, и предложите подумать, как должна выглядеть схема одноразрядного сумматора, сколько у него должно быть входов и выходов? Пусть ученики сами построят схематичное изображение одноразрядного сумматора.

Для более детального изучения сумматора предложите ученикам заполнить таблицу сложения 3-х одноразрядных двоичных чисел, где 3-е число (Р0) обозначает переносимую цифру (из предыдущего результата сложения). Получите таблицу, аналогичную табл. 2.2 параграфа.




A
B
P0
P
S


0
0
0
0
0


0
1
0
0
1


1
0
0
0
1


1
1
0
1
0


0
0
1
0
1


0
1
1
1
0


1
0
1
1
0


1
1
1
1
1

Из данной таблицы можно получить логические формулы для P(A,B,P0) и S(A,B,P0). Для вывода формул используют метод синтеза логических формул по таблице истинности: составляют логические выражения для всех строк таблицы, где функция имеет значение 1, и объединяют их операцией дизъюнкция. Затем упрощается выражение. Для Р получаем:

P(A,B,P0) = A&B V B&P0 V A&P0 V A&B&P0 = B&P0 V A&P0 V A&B&(1V P0)=
A&B V B&P0 V A&P0

Для S выражение можно быстро получить, если проанализировать строки с номерами 1,2,3,5. Нетрудно заметить, что эти строки соответствуют операции AVBV P0, за исключением строк 4,6,7, где S=0, а P0=1, что выражается формулой: (AVBVP0)&¬ P0. Строке 8 соответствует выражение: A&B&P0. Общее выражение для S:

S= (AVBVP0)&¬ P0V (A&B&P0)

Предложите ученикам построить логическую схему, реализующую сложение 3-х двоичных цифр с использованием полусумматоров.

На вход первого ПС подаются значения А и В, в результате получаются промежуточные значения S’ и P’. Значение S’ суммируется с P0 (третьей двоичной цифрой), в результате получается значение S, а полученное значение переносимого разряда, обозначенное как P”, логически складывается с P’. В результате получаем схему, представленную в учебнике на рис. 2.7. Отмечаем, что данная схема - модель реализации сложения 3-х двоичных цифр с использованием полусумматоров.

Домашнее задание. Изучить §2.1.2 (стр. 168-170), уметь объяснять принципы работы полусумматора и одноразрядного сумматора. Построить логическую схему реализации сложения 3-х двоичных цифр с использованием функций P и S (по формулам 3,4 учебника).

Практическое задание:

1. В среде электронной таблицы воспроизвести таблицу 2.1 для полусумматора, используя логические формулы (1), (2).

2. В среде электронной таблицы воспроизвести таблицу 2.2 для одноразрядного сумматора, используя логические формулы (3), (4).


Урок 3. Логические схемы элементов компьютера. Урок-практикум по моделированию работы полусумматора и одноразрядного сумматора.

Цель урока: Закрепить на практике полученные знания о принципах работы полусумматора и одноразрядного сумматора, используя электронные таблицы.

Примерный ход урока:
  1. Проверить домашнее задание. Построение таблиц по логическим формулам не должно было вызвать затруднение, а вот логическую схему обязательно надо обсудить. Выведите на экран схему работы одноразрядного сумматора, обратите внимание учащихся, что фактически в схеме представлены два полусумматора. Процесс моделирования с использованием средств информационных технологий позволяет визуально убедиться в теоретически обоснованных принципах, в частности работы полусумматора и сумматора, закрепить полученные знания.
  2. Практическое задание:
    1. Смоделируйте на электронной таблице логическую схему полусумматора, как показано на рисунке:



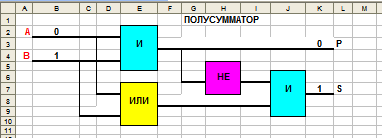
Протестируйте работу схемы, перебрав все варианты значений входных параметров А и В. Сопоставьте полученные результаты с результатами домашнего задания.
    1. Смоделируйте на электронной таблице логическую схему одноразрядного сумматора, как показано на рисунке:



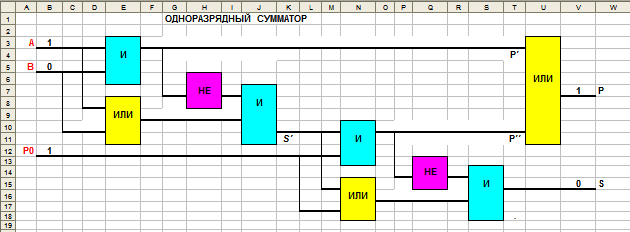
Протестируйте работу схемы, перебрав все варианты значений входных параметров А, В, Р0. Сопоставьте полученные результаты с результатами домашнего задания 2.

Домашнее задание. Изучить §2.1.2 (с.168-171), самостоятельно разобраться с устройством и принципами работы многоразрядного сумматора. Построить модель двухразрядного сумматора на электронной таблице. Протестировать ее работу. Принести или прислать файл с выполненной работой.

Урок 4. Логические схемы элементов компьютера. Многоразрядный сумматор. Триггер.

Цель урока: Изучить конструкцию и принципы работы многоразрядного сумматора и триггера. Познакомиться с понятием «регистровая память компьютера».

Примерный ход урока:
  1. (10-15 минут) Проверьте, как ученики самостоятельно освоили конструкцию многоразрядного сумматора. Можно предложить следующее задание: Представьте, что процессор компьютера производит вычисления с четырёхразрядными двоичными числами. Ответьте на вопросы:
  1. Сколько сумматоров необходимо для выполнения суммы двух целых чисел? (3 и 1 полусумматор)
  2. Изобразите схему работы 4-разрядного сумматора,
  3. Определите, какие значения получат S0, S1, S2, S3, S4 , Р0, Р1, Р2, Р3, если А=0110, В=0111
  4. Где хранятся двоичные коды слагаемых?
  5. Что означает ситуация «целочисленное переполнение»? Возникла ли она в данном примере?
  6. В каком устройстве компьютера используется многоразрядный сумматор?
  7. Как выполняются другие арифметические операции – умножение, вычитание, деление?
  8. В состав какого устройства компьютера входит многоразрядный регистр?
  9. Где хранятся данные, обрабатываемые сумматором? Сумматор – это устройство в составе компьютера, которое выполняет вычисления над данными, хранящимися во внутренней памяти компьютера, вместе с исполняемой программой. Для хранения аргументов выполняемой в данный момент команды (например, слагаемых), используются специальные ячейки процессора – регистры.
  1. (20-25 минут). Основным элементом регистровой и внутренней памяти является 1 бит, который несёт 1 бит информации, принимая одно из двух устойчивых состояний (0 или 1). Память должная быть технически реализована так, чтобы 1 бит памяти мог устойчиво сохранять значение и быстро переходить из одного состояния в другое. Таким элементом электронной схемы компьютера, реализующий 1 бит регистров процессора и статической памяти, называется триггером.

Кратко расскажите историю изобретения триггера, выведите на экран схему RS-триггера.

Важными в объяснении должны стать следующие моменты:
  • разное назначение входов S,R. Вход S предназначен для установки нового устойчивого состояния устройства -1(включение), а вход R – сброс 1(выключение).
  • поочередная подача импульсных электрических сигналов;

Выведите на экран логическую схему RS-триггера, объясните назначение обратной связи, дополнительного выхода.

Пусть учащиеся построят логическую схему триггера и отметят на ней, какие значения установятся на входах и выходах после подачи сигнала на S и его снятия, а затем - подачи сигнала на вход R.

В заключение, по структурограмме, представленной в конце параграфа, повторите основные понятия, изученные в рамках темы «Логические схемы элементов компьютера».

Домашнее задание. Повторить материал §2.1.2, подготовить доклады по материалам §2.2, 2.3.




ooter.php"; ?>