Geum.ru

Использование структурно-феноменологической модели для описания вязкоупругих свойств тренированной резины с разными типами наполнителей

Вид материалаДокументы

Содержание


Исследуемые материалы
Алгоритм получения констант модели
Подобный материал:
УДК 539.3

Использование структурно-феноменологической модели для описания вязкоупругих свойств тренированной резины с разными типами наполнителей

А. Г. Пелевин, А. Л. Свистков, В. В. Шадрин

Институт механики сплошных сред УрО РАН, 614013 Пермь, ул. Акад. Королёва, 1, pelevin@icmm.ru


Аннотация

В работе проведены исследования с резинами на основе одного эластомера и различных типов наполнителя. Проведены разрывные и циклические эксперименты на стенде Testometric FS-100ST. Полученные из экспериментов данные о равновесных и вязкоупругих свойствах материала были описаны с помощью структурно-феноменологической модели. Получена оценка влияния наполнителей на механические свойства материалов.


Исследуемые материалы


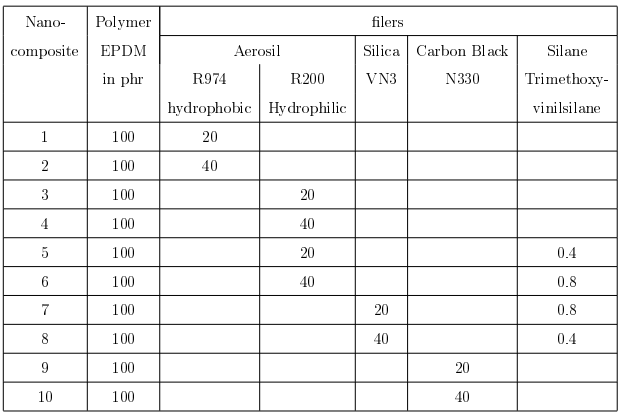
Одним из направлений научных исследований в области резин является создание моделей эластомерных нанокомпозитов, позволяющих в перспективе осуществить разработку основ виртуального проектирования новых материалов. В Институте механики сплошных сред УрО РАН получены результаты моделирования механических свойств резин на основе этилен-пропилен-диеновый стирольного каучука. Из Германии (Leibniz Institute of Polymer Research Dresden) получены 10 пластинок (85 х 50 х 2.5 мм) с оригинальными составами резины EPDM, отличающихся типом и содержанием наполнителей (см. таб.). Образцы вырублены штанцевым ножом с ориентацией оси образца вдоль узкой стороны пластинки, остальные образцы вырубались в направлении длинной стороны пластинки. Из каждой пластинки вырублено по 7 образцов. Для обеспечения чистоты реза штанцевым ножом из 7 опробованных составов смазки наилучшим оказалась мыльная эмульсия.

EPDM – это обозначение этилен-пропилен-диеновый каучука, входящего в состав резиновой смеси (EPDM – ethylene propylene diene monomer rubber). Этилен-пропиленовые каучуки имеют превосходную атмосферо- и озоностойкость, высокую термо-, маслостойкость и износостойкость, но также и высокую воздухопроницаемость, устойчивы в агрессивных средах, обладают хорошими диэлектрическими свойствами; предел прочности при растяжении 20-28 МПа, относительное удлинение 400-600%, эластичность по отскоку 40-52 % (наполнитель - активная сажа). В качестве наполнителей применялись Aerosil R974, Aerosil 200 без специальной обработки и модифицированный Si69, Ultrasil VN3 без специальной обработки и модифицированный Si69, Carbon Black N330. Массовое содержание наполнителя равнялось 20 phr и 40 phr.

Таблица. Исследуемые материалы резины EPDM





а б

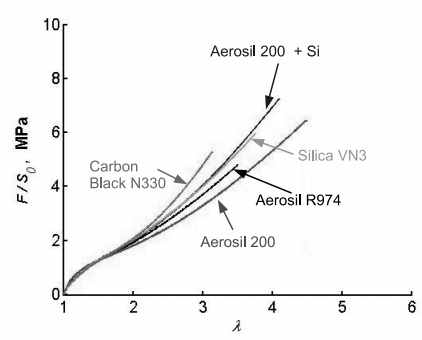
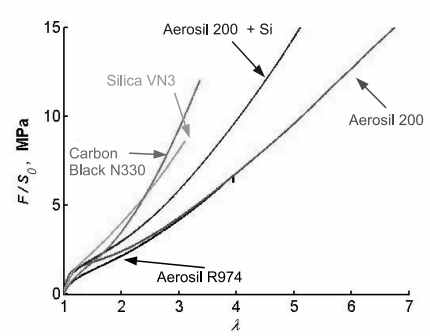
Рис. 1 Эксперименты на разрыв с постоянной скоростью до разрыва материалов с содержанием наполнителя а—20 phr и b—40 phr


Для исследуемых образцов были проведены эксперименты на разрыв с целью анализа механического поведения. На рисунке 1-а изображены графики растяжения с постоянной скоростью до разрыва материалов с содержанием наполнителя 20 phr, на рисунке 2-б — графики для материалов с содержание наполнителя в 40 phr. Материалы с содержанием наполнителя 20 phr показывают практически одинаковое механическое поведение на начальном участке деформирования для кратности удлинений меньше λ<2, а наибольшее упрочнение показываю материялы с наполнителем Carbon Black и наполнителями Aerosil 200 и Silica VN3, с модификацией поверхности наполнителя. Материалы с содержанием наполнителя 40 phr уже показывают достаточное различное механическое поведение, особенно на начальном участке деформирования. Наибольшее упрочнение показываю материялы с наполнителем Carbon Black и наполнителями Aerosil 200+Si и Silica VN3+Si, с модификацией поверхности наполнителя. Материал с наполнителем Aerosil 200+Si с модификацией поверхности, показывает наибольший модуль упругости на начальном участке деформирования, а при увеличении кратности растяжений происходит падения напряжений.

После экспериментов на разрыв с другой партией тех же по составу материалов были проведены циклические эксперименты для теоретического описания с помощью структурно-феноменологической модели, которую можно представить с помощью схемы, показанной на рис. 3. Особенности использования тензорных определяющих уравнений опубликованы в статьях [1–4].



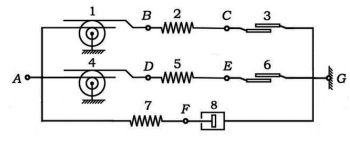
Рис. 2 Схематическое изображение используемой математической модели. Каждый элемент на схеме является иллюстрацией тензорных уравнений, сформулированных для конечных деформаций; где 1,2 — трансмиссионные, 2,5,7 — упругие, 3,6 — пластические, 8 — вязкий элементы


Эксперимент состоял из двух одинаковых циклов. Цикл деформирования включал в себя нагружение с постоянной скоростью до кратности удлинений λ=2, релаксации напряжений в течении 30 минут, разгрузки с постоянной скоростью до нулевых напряжений, отдых материала в течении 30 минут. Таким образом после первого нагружения в первом цикле мы наблюдали процесс размягчения Малинса, во втором цикле мы наблюдали вязкоупругое поведение тренированного материала (рис. 3). Данные для равновесной кривой материала на участке деформирования от λ=1 до λ=1.8, определялись как среднее между кривой нагрузки и разгрузки второго цикла деформирования на этом участке, далее к полученным данным прибавлялась точка определяющая конец релаксации и начала разгрузки. Для получения недостающих точек производили интерполяцию массива.

Используя структурно-феноменологическую модель [1] (рис. 2) и учитывая опыт получения констант модели [5], было получено теоретическое описание равновесных кривых и вязкоупругого поведения тренированного материала.

В работе мы будем описывать вязкоупругое поведение уже тренированного материала, в котором все пластические процессы уже завершились (мы не будем описывать первое нагружение, а лишь учтем его последствия).


Алгоритм получения констант модели

Шаг 1.

Для начала опишем упругое поведение полимерной матрицы, с помощью первого трансмиссионного и второго упругого элементов. Объемная плотность свободной энергии материала на этом шаге 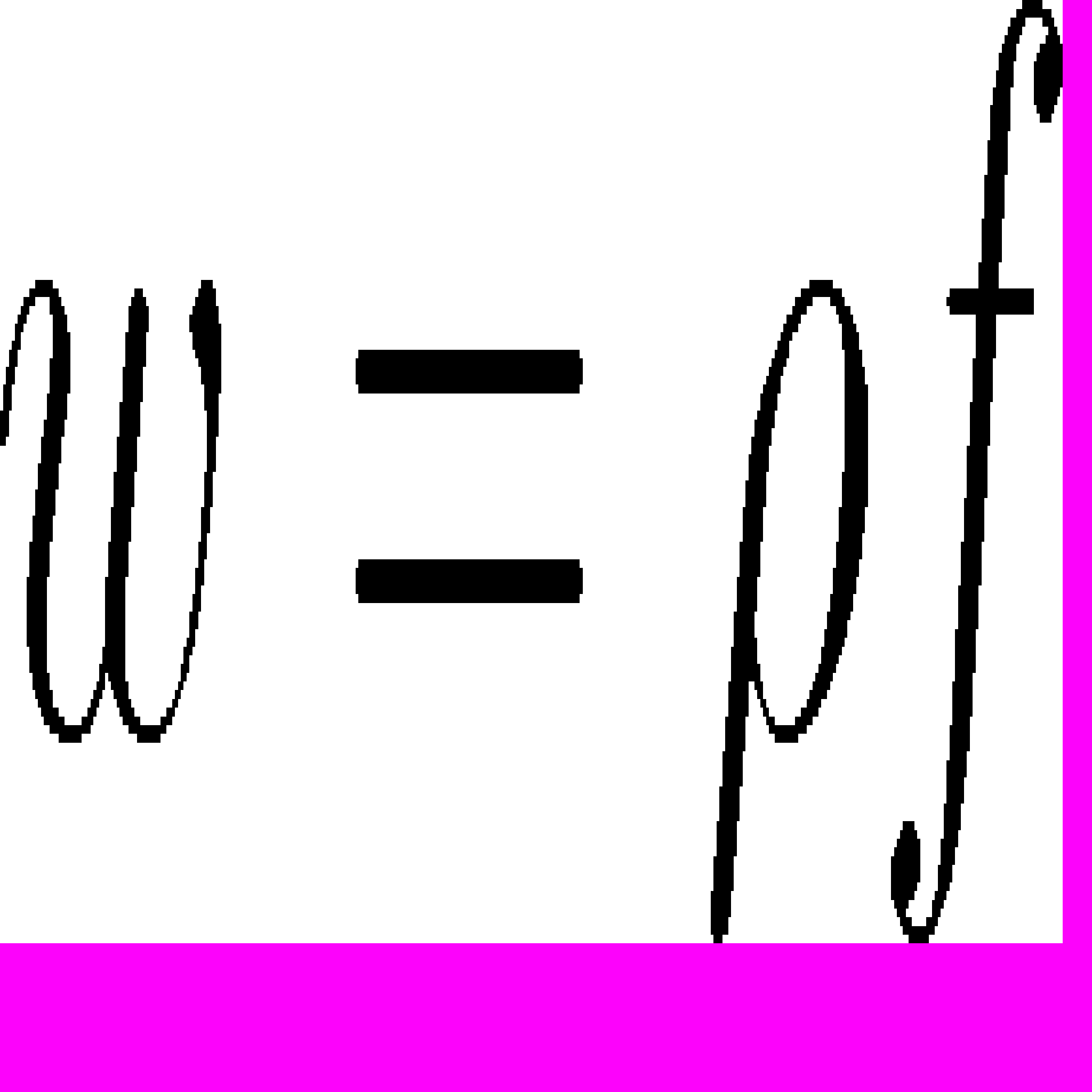является функцией только кратностей удлинений второго элемента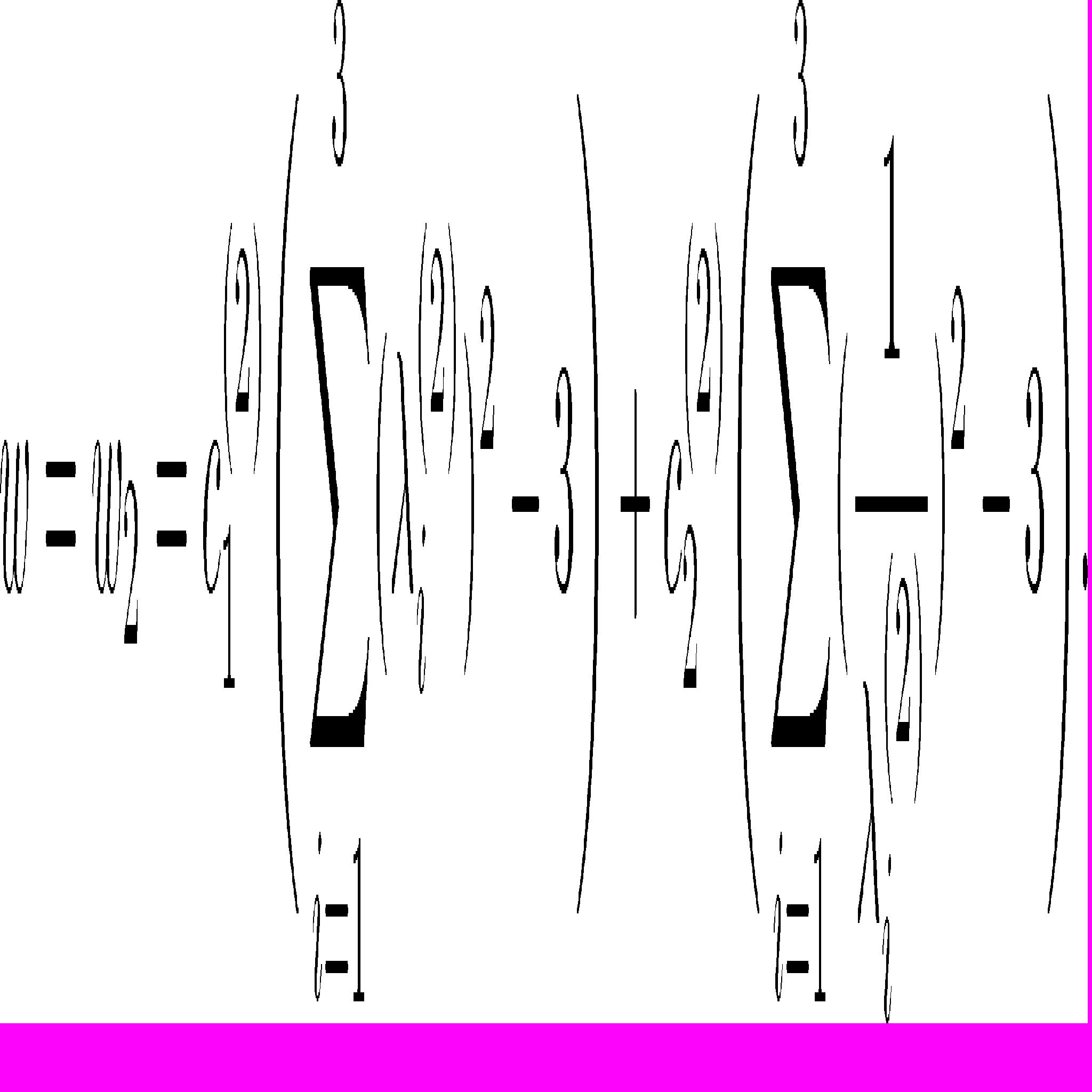



Накопление пластических деформаций происходит только на первом цикле деформирования. На следующем цикле материал ведет себя как упругий. В экспериментальных данных учтем остаточную деформацию после первого нагружения, которая будет производиться в результате первого нагружения и учитываться в модели третьим пластическим элементом. Так как мы будем описывать поведение тренированного материала, то теоретическая кривая будет выходит как раз из величины остаточной деформации.

Найдем константы 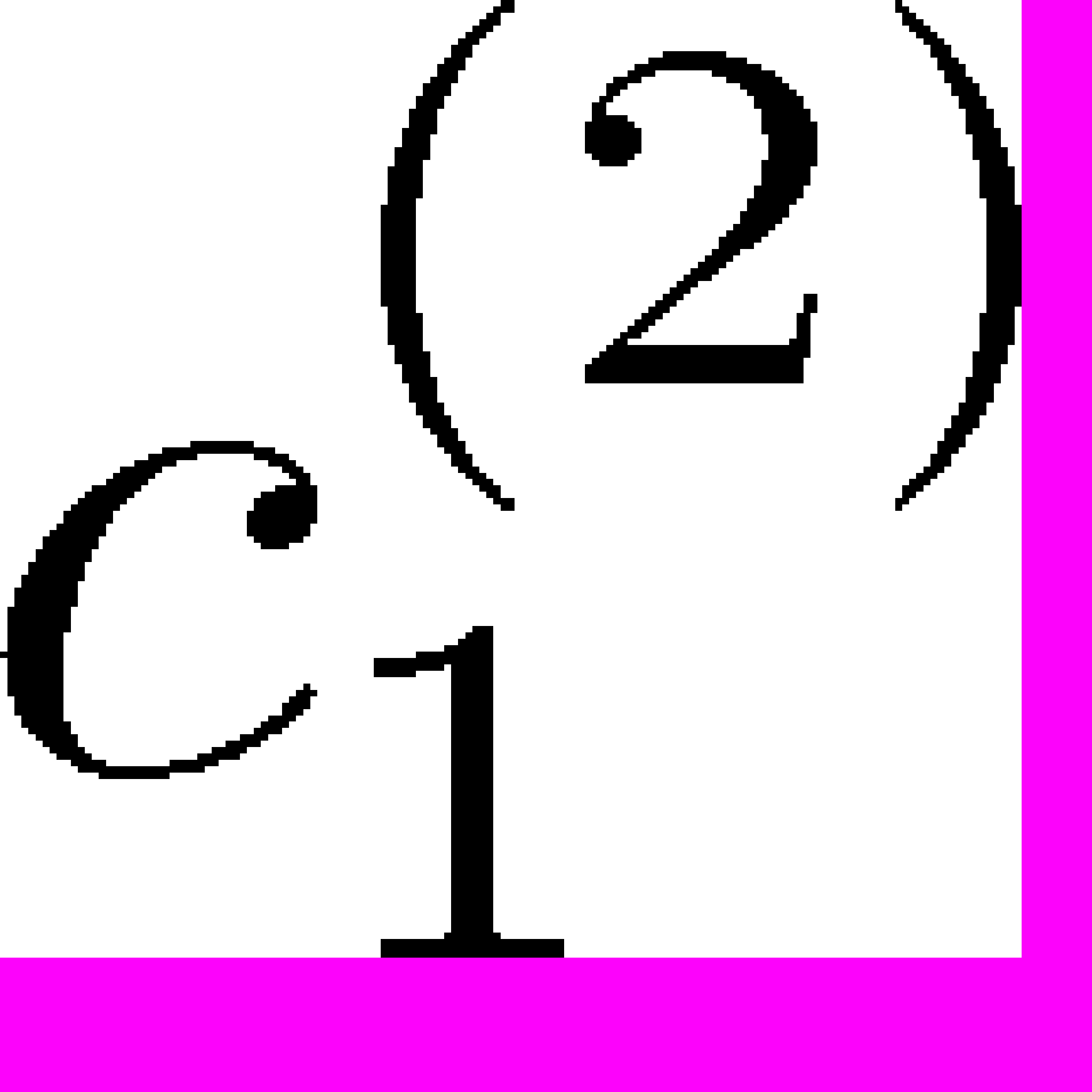, 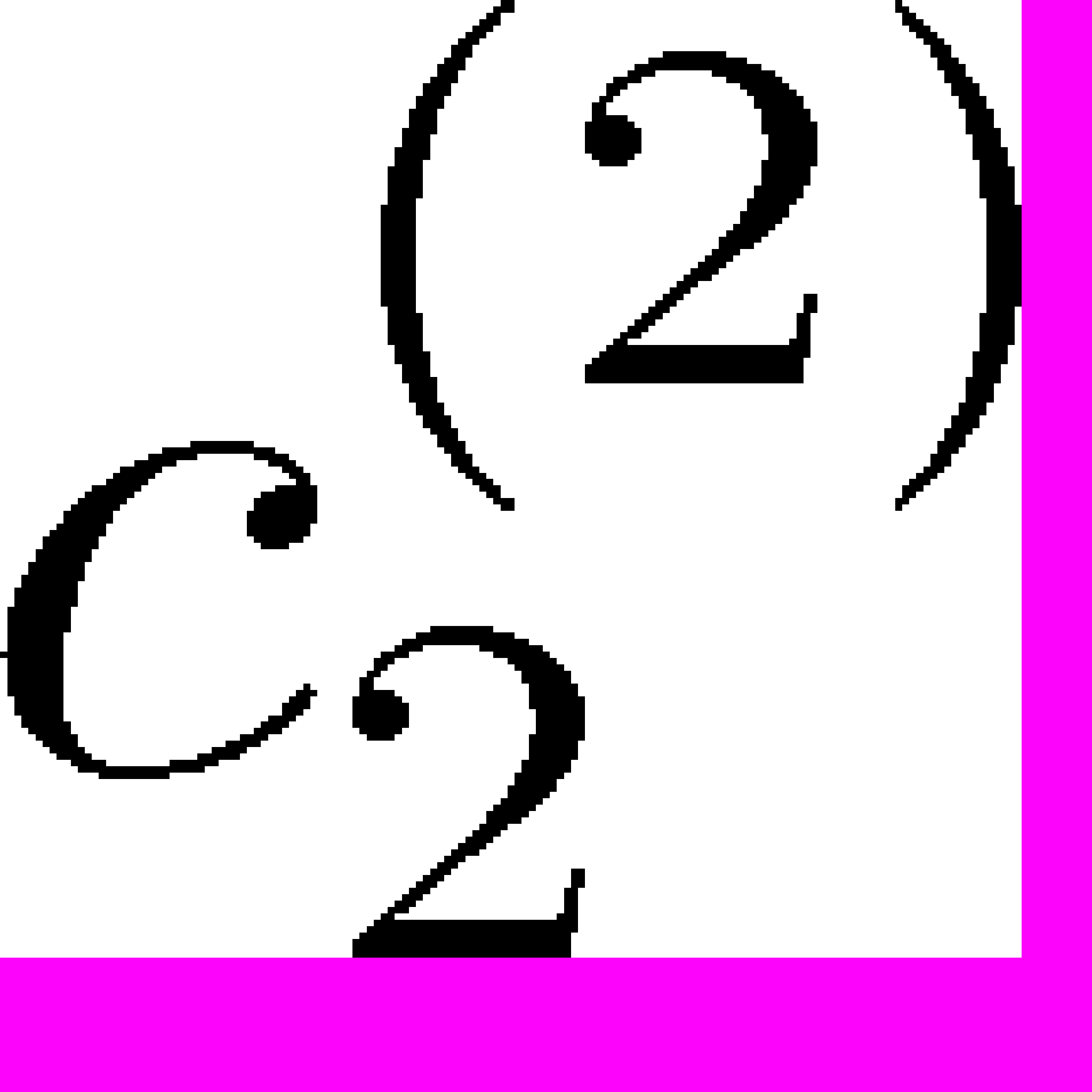упругого элемента и значения передаточного числа 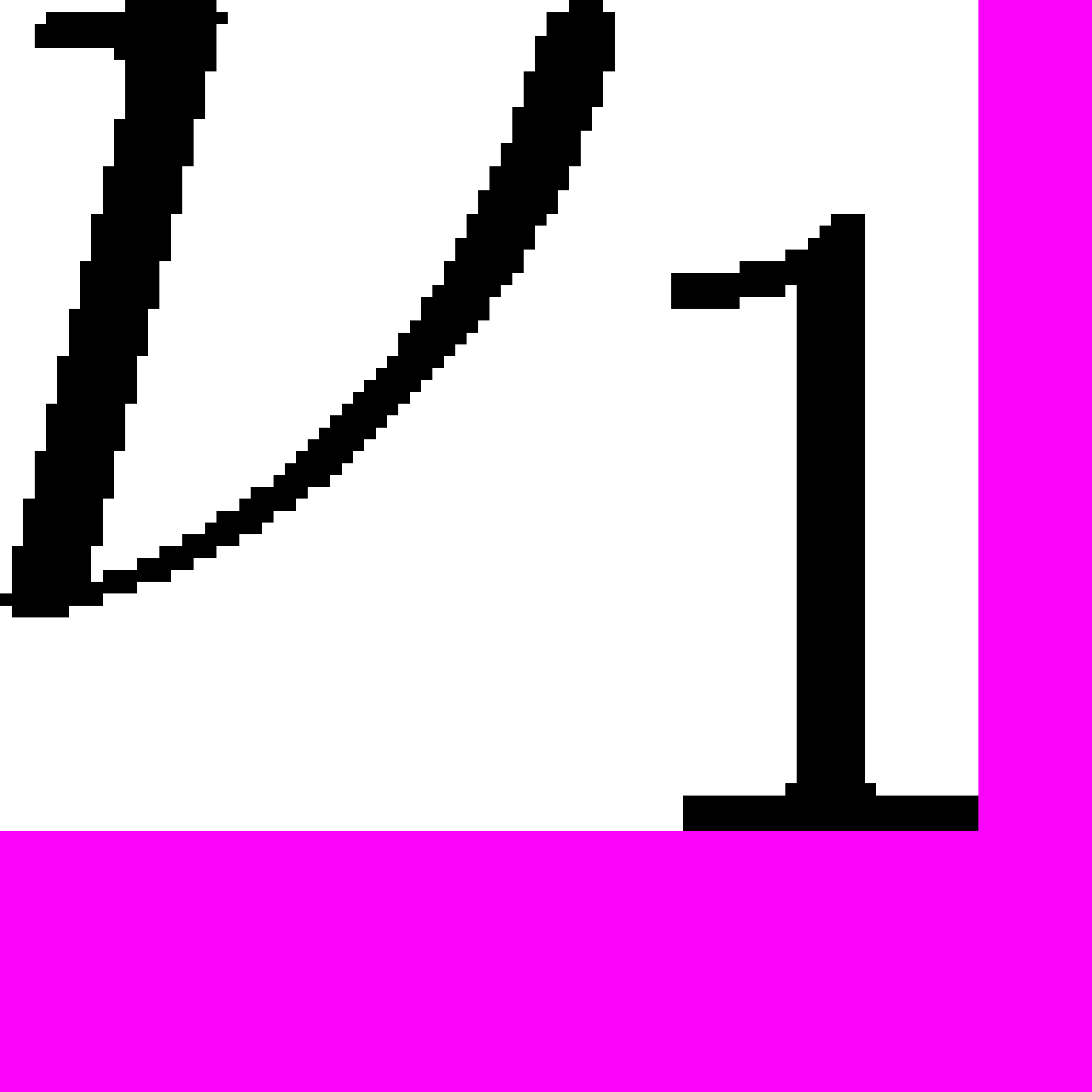первого трансмиссионного элемента для всех образцов. Будем считать, что для каждого образца передаточное число 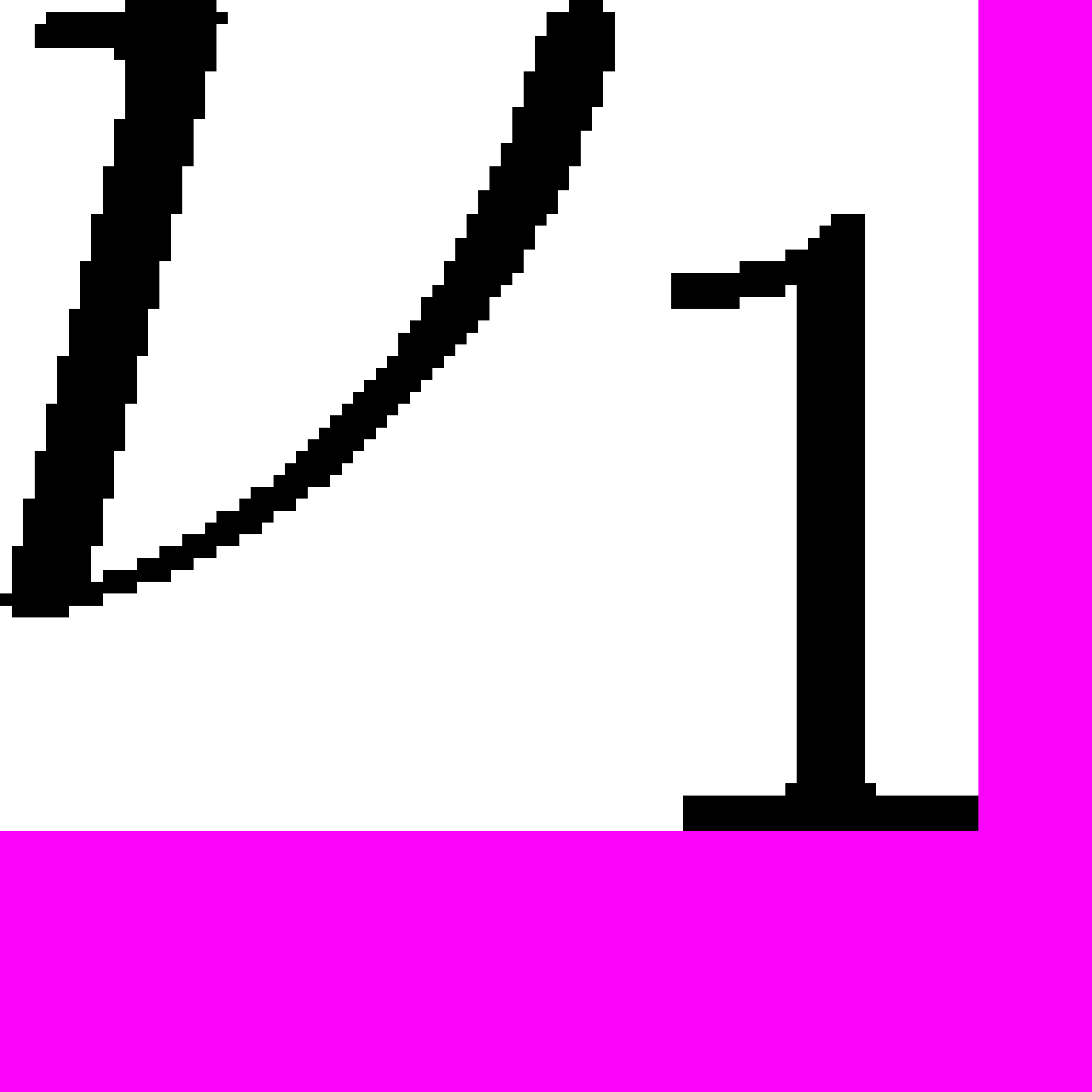имеет свое значение, в то время как константы 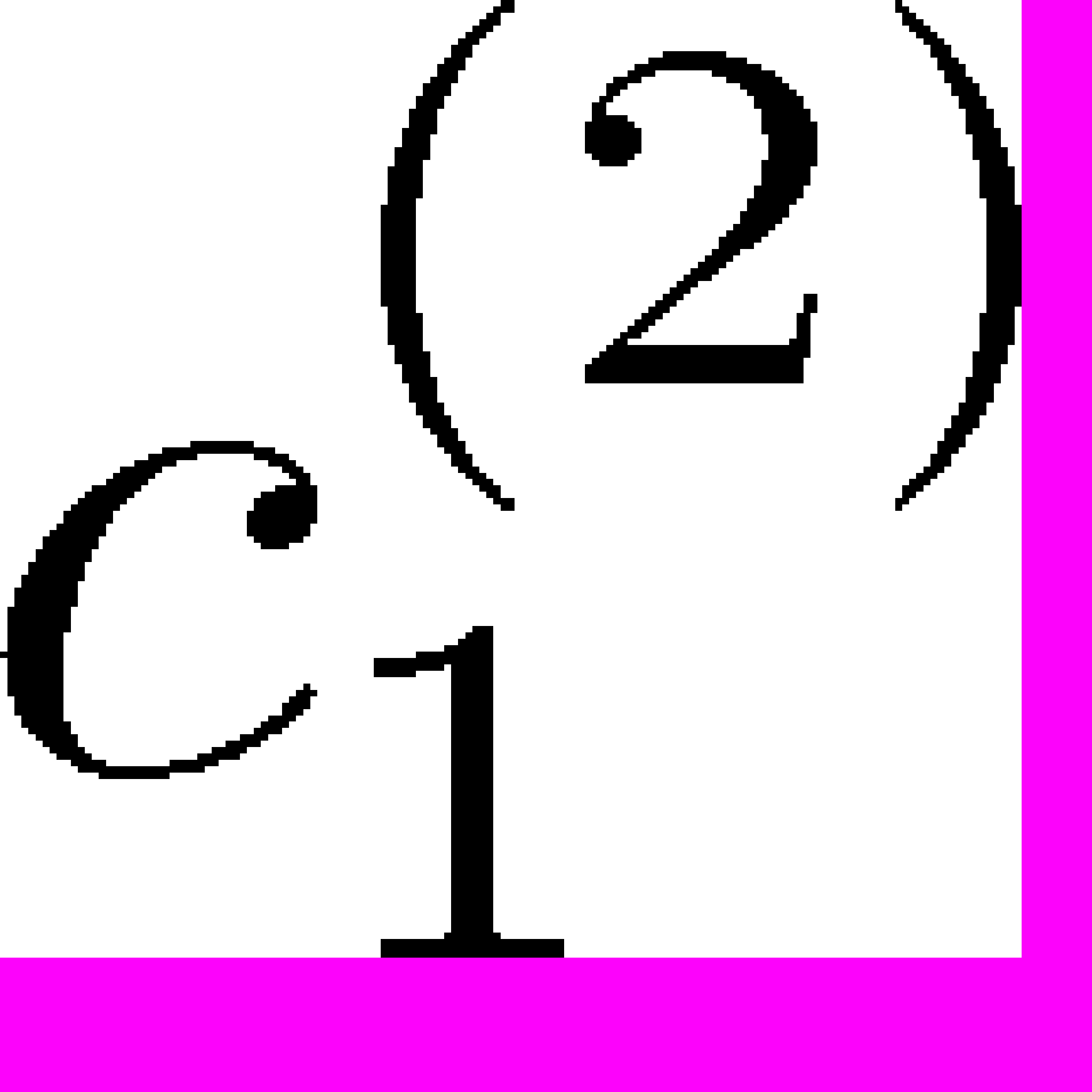, 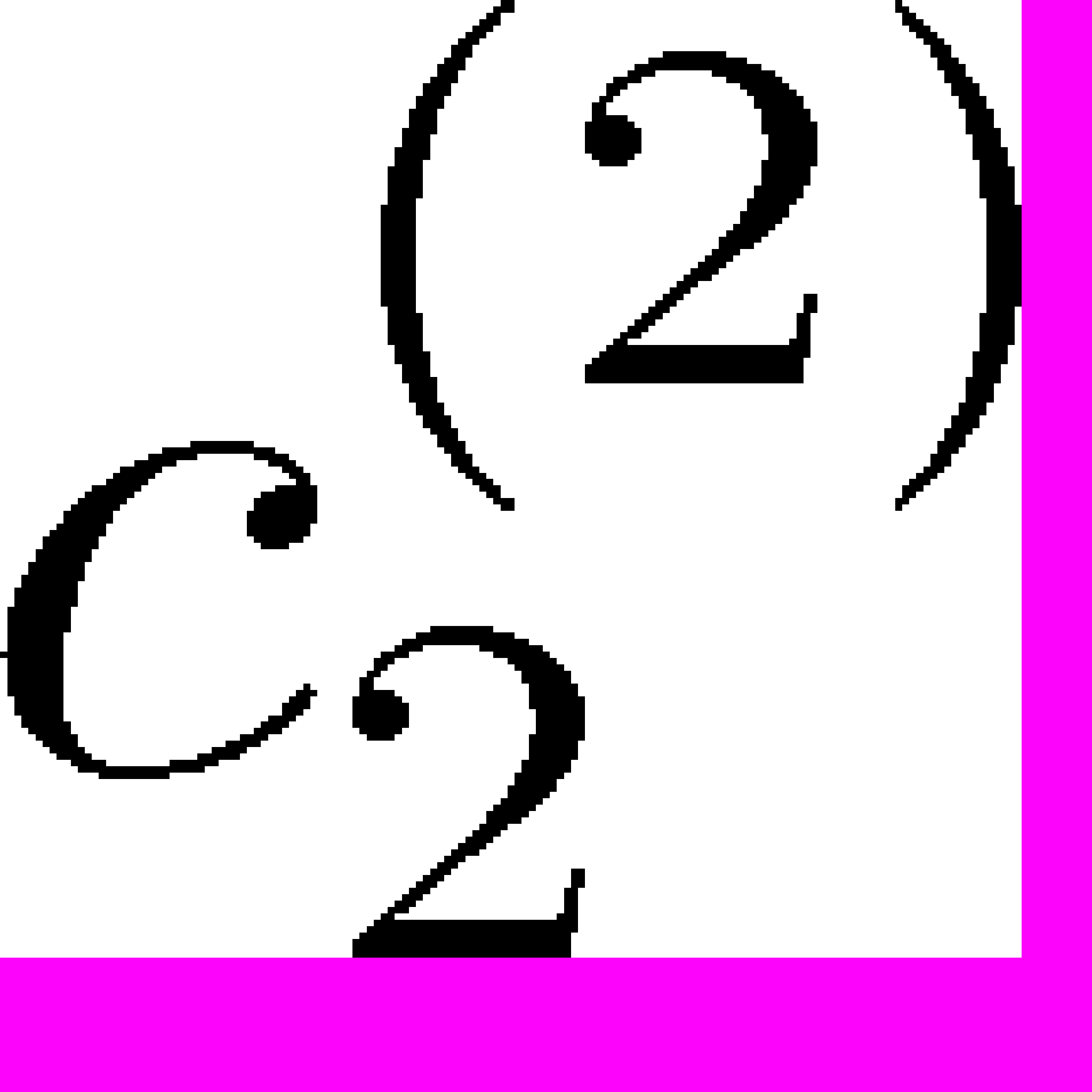являются общими для всех образцов. Хоть образцы у нас различные, однако полимер один и тот же. Поэтому мы сделаем предположение, что упругие константы 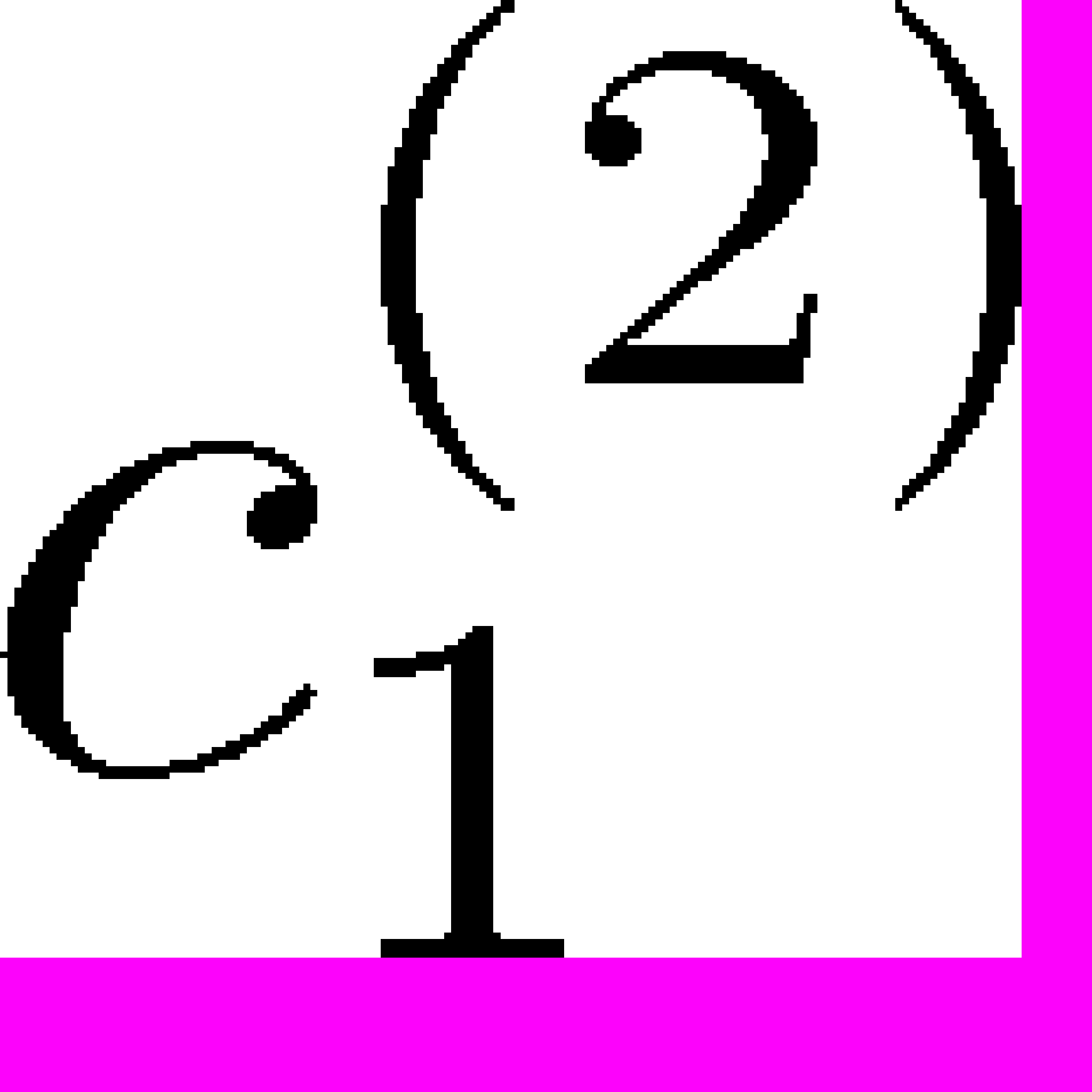, 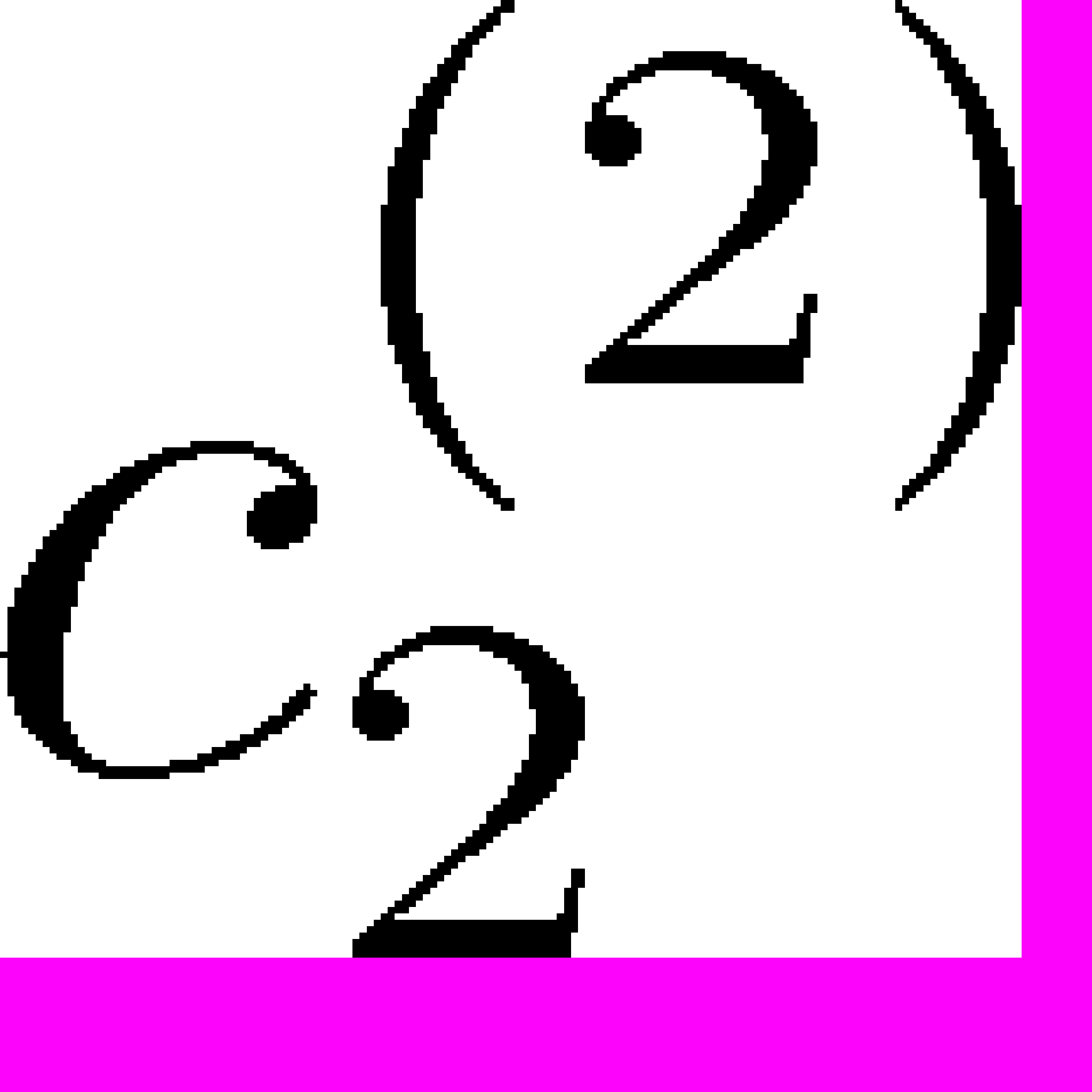будут характеризовать полимерное связующие, а трансмиссионное число — влияние наполнителя. Для нахождения констант, будем использовать равновесную кривую. Теоретическая кривая должна совпасть с равновесной кривой по крайней мере до крастности удлинений λ=1.7. полученная с теоретическая кривая для 4,6,8 и 10-го образцов показана на рис.3 штрих-пунктирной линией. Речь о прохождении теоретической кривой через остальные равновесные точки пойдет позже.

Шаг 2.

При построении математической модели механического поведения резины мы будем использовать гипотезу о том, что в материале при деформировании происходит образование высокопрочных волокон. Полимерные волокна образуются из ориентированной эластомерной матрицы в слоях вокруг включений [6]. Слой эластомера вокруг включения имеет существенно большую прочность по сравнению с неориентированной полимерной матрицей. При деформировании полимерного композита образуются волокна из высокоориентированного полимера, которые определяют прочность материала. Эти волокна образуются во время растяжения между двумя близко расположенными включениями, высокопрочные слои которых пересекаются [1,7,8].

Напомним, что при первом нагружении происходит размягчение материала и все пластические процессы, образование волокон, как раз происходит в результате пластического течения. Добавим к модели еще один упругий, трансмиссионный и пластический элементы для описания механического поведения сформированных при первом нагружении волокон.

Учитывая гипотезу о поведении волокон, потенциал свободной энергии среды 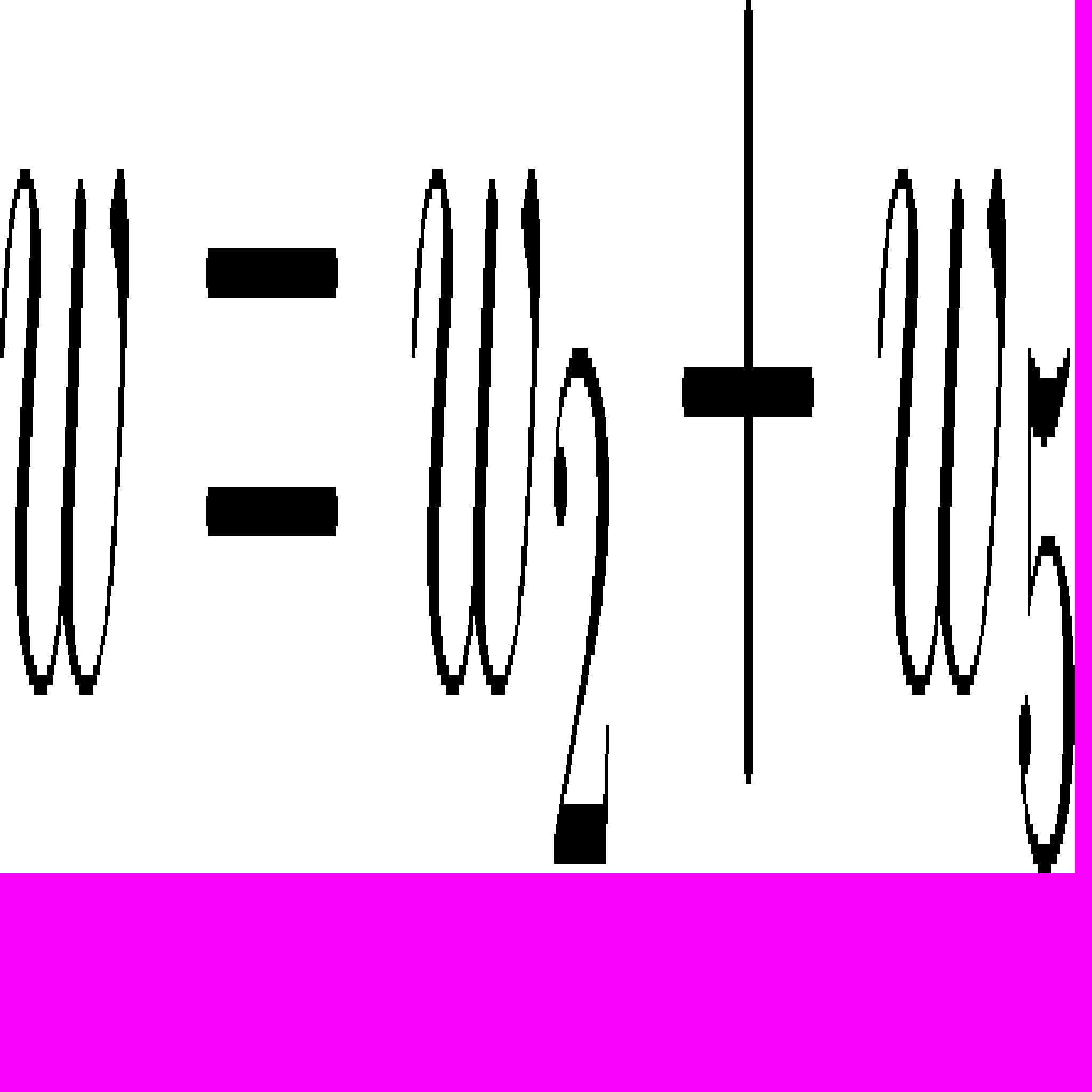, в которой потенциал 5-го упругого элемента, который описывает поведение волокон, запишем ввиде:

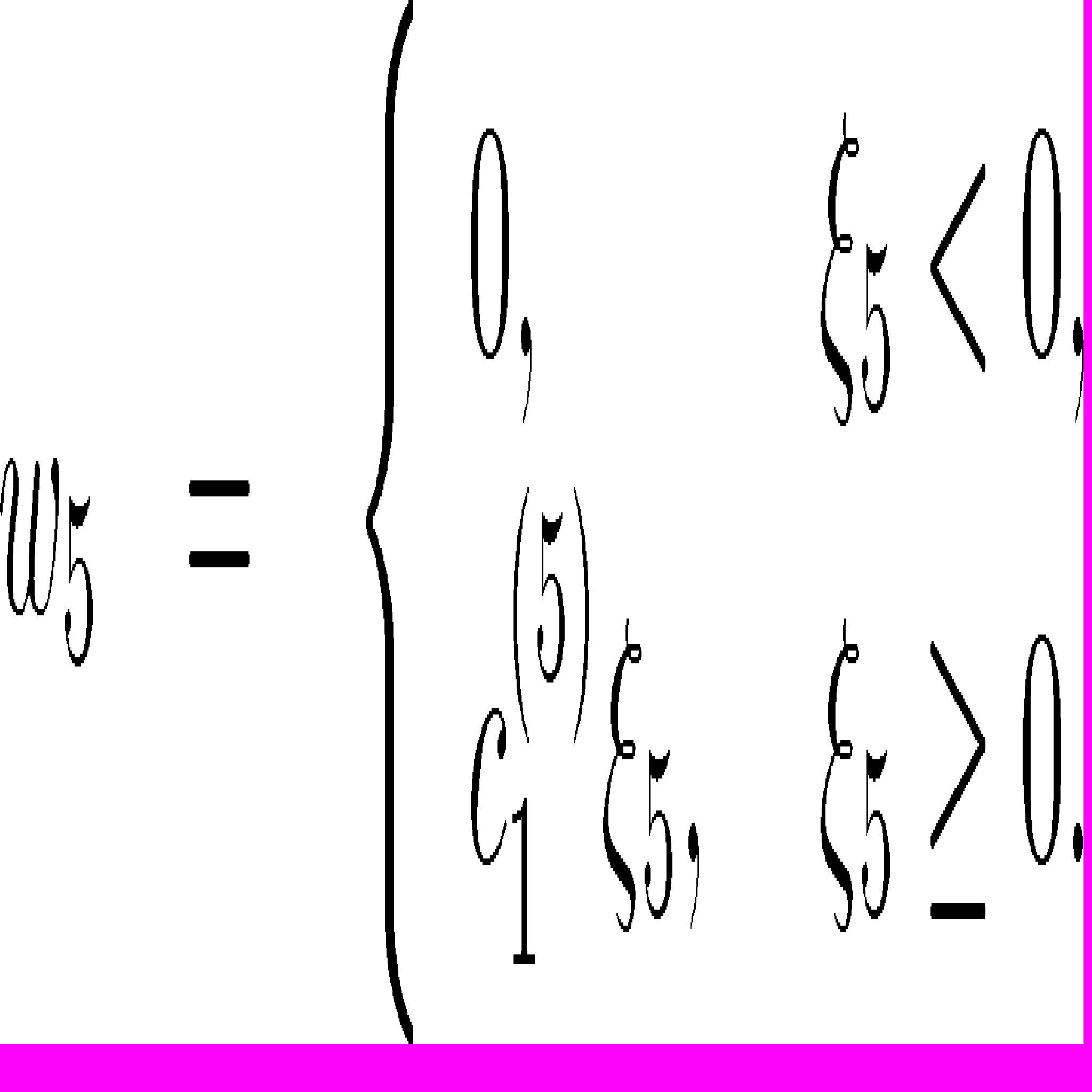, и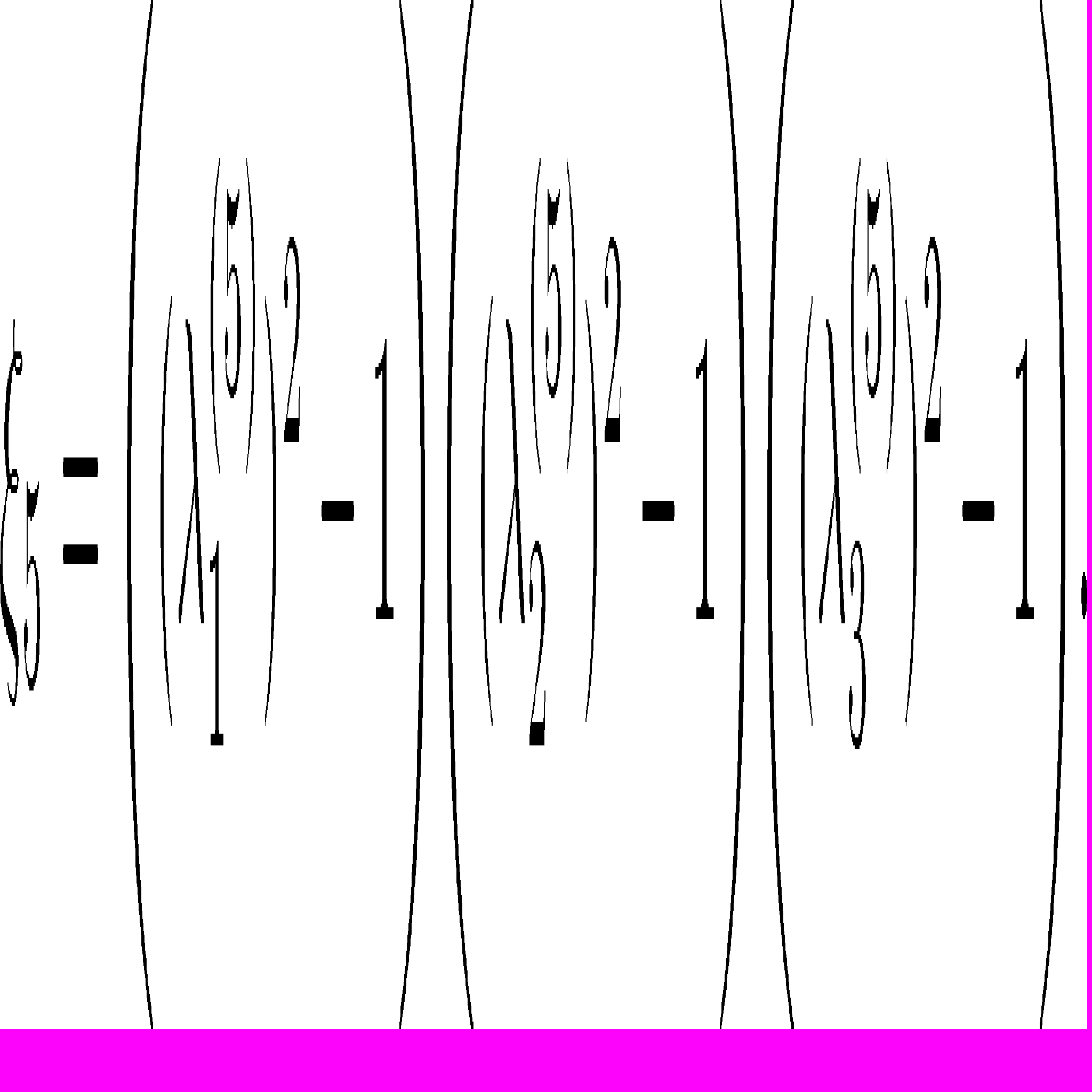

Считаем, что упругие элементы характеризуют связующее, поэтому константу 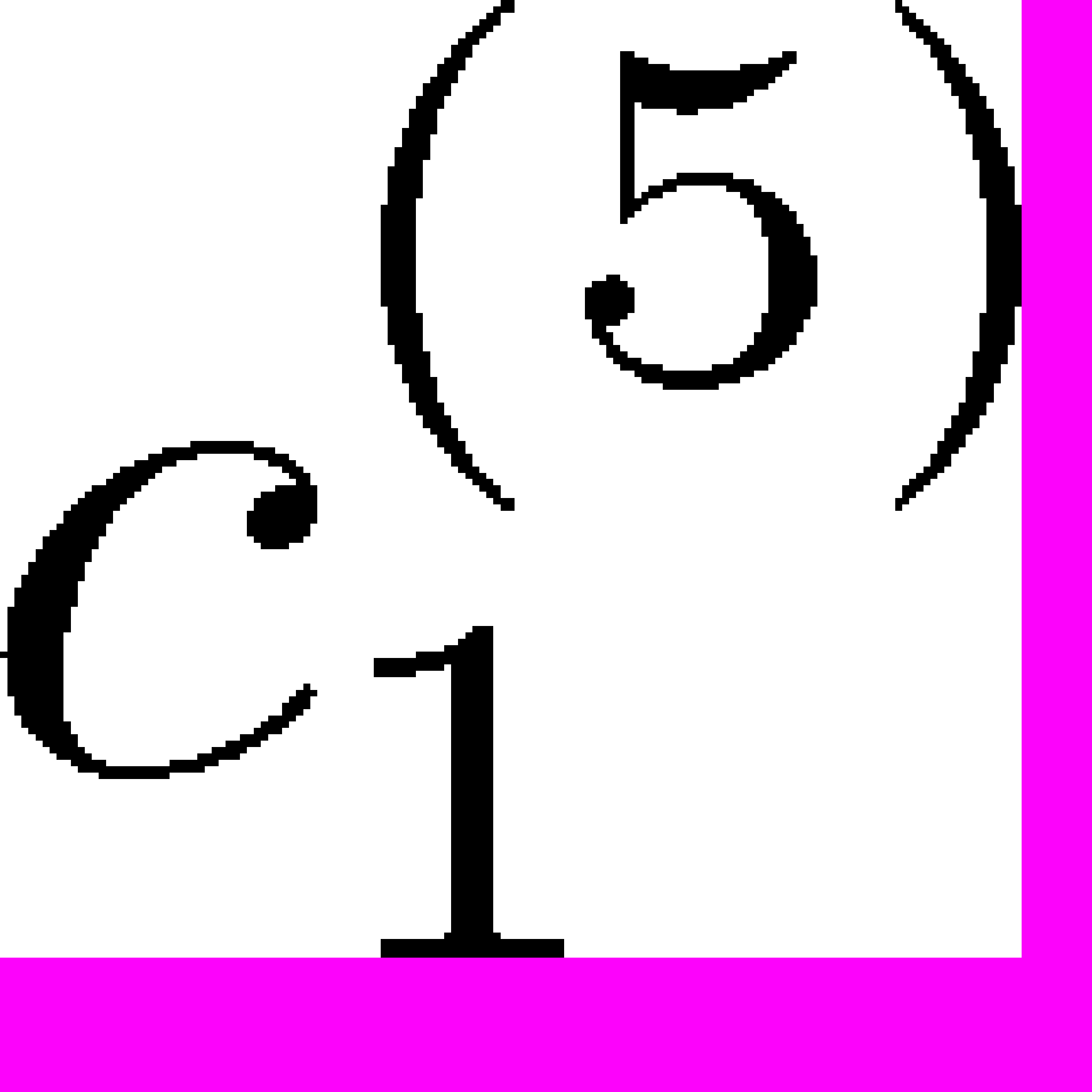возьмем для всех образцов одну и туже. Константу 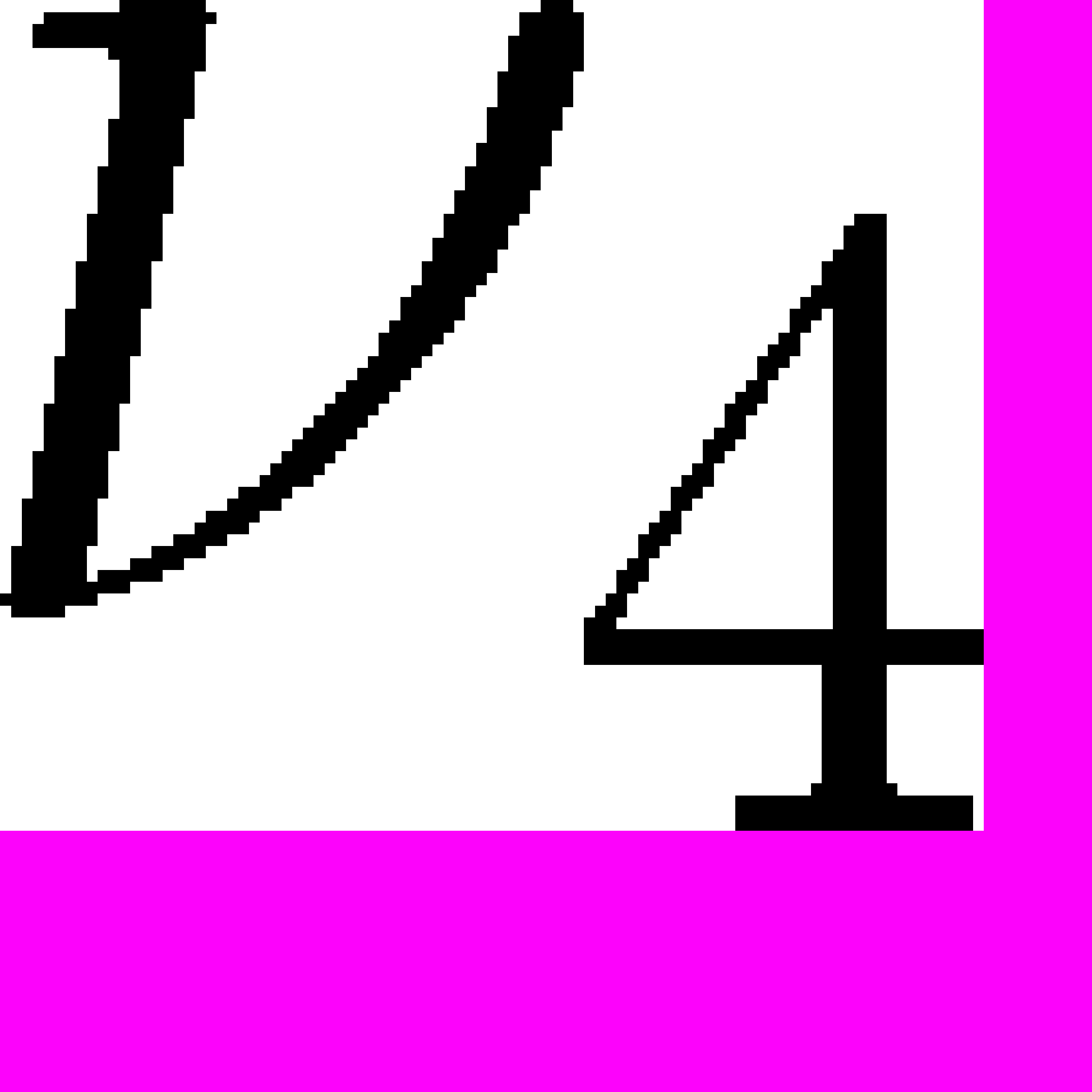четвертого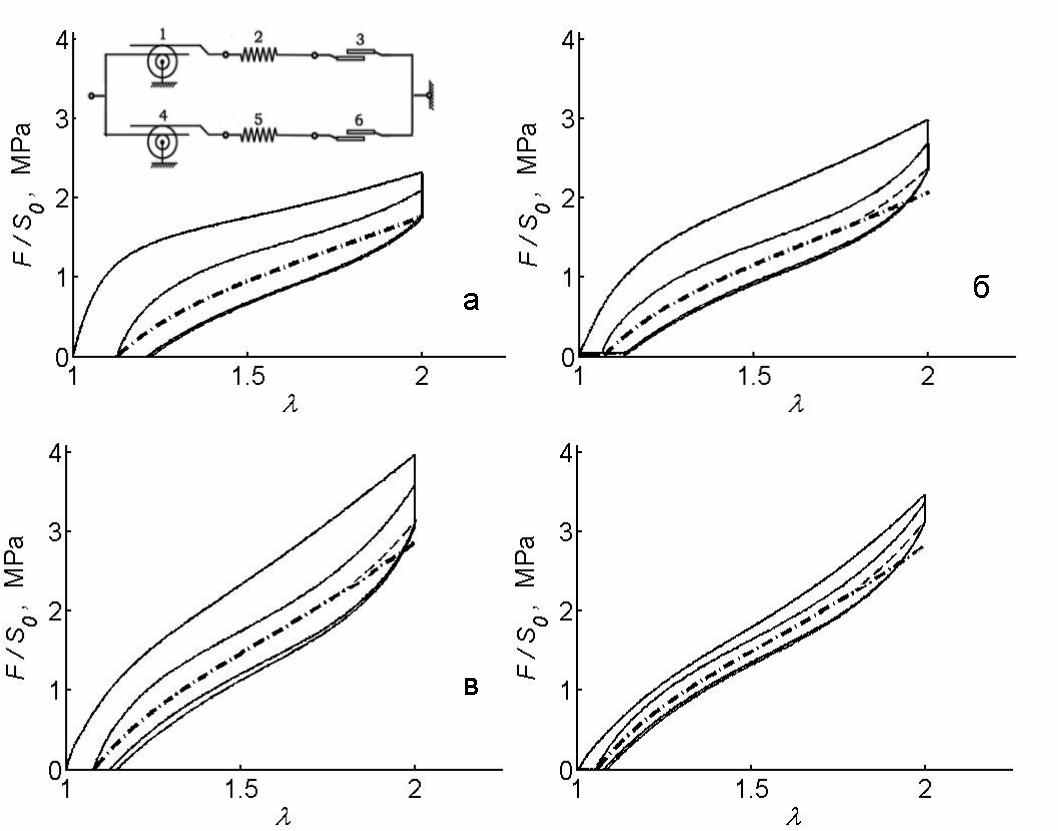



Рис. 3 Модель материала на втором шаге; экспериментальные данные для образцов с номерами 4,6,8,10 — сплошная линия; теоретические данные модели на данном шаге для образцов с номерами 4,6,8,10 — штрих пунктирной линия; теоретические данные модели на первом шаге (без учета волокон) для образцов с номерами 4,6,8,10 — пунктирной линия; a — для материала под номером 4; б — 6; в — 8; г — 10


трансмиссионного элемента определим для каждого образца. Действие шестого пластического элемента мы определим по остаточной деформации волокон λ5pl, после первого нагружения. Модель, используемая на этом шаге и полученная с ее помощью теоретическая кривые для 4,6,8 и 10-го образцов показана на рис. 3 пунктирной линией. Напомним, что на рис.3 пунктирной линией обозначены данные моделирования шага 1 (для 1-го, 2-го и 3-го элементов схемы). Штрих пунктирная и пунктирные линии совпадают до определенной кратности удлинения, а после начинают расходиться. Эта точка и есть остаточная деформация волокон λ5pl. Также заметим, что на рис.3-a пунктирная линия слилась со штрих пунктирной, это происходит из-за того, что действие волокон для 4-го исследуемого образца получается незначительным. Таким образом, по результатам моделирования, рис.3 можно сделать вывод, что действие волокон будет незначительным для 4 образца. И наоборот наиболее значительное действие волокон будет о образцов под номерами 6, 8 и 10.

Шаг 3.

Далее мы добавим к нашей модели седьмой упругий и восьмой вязкий элементы, для описания вязкоупругого поведения. Потенциал свободной энергии среды представим в виде суммы 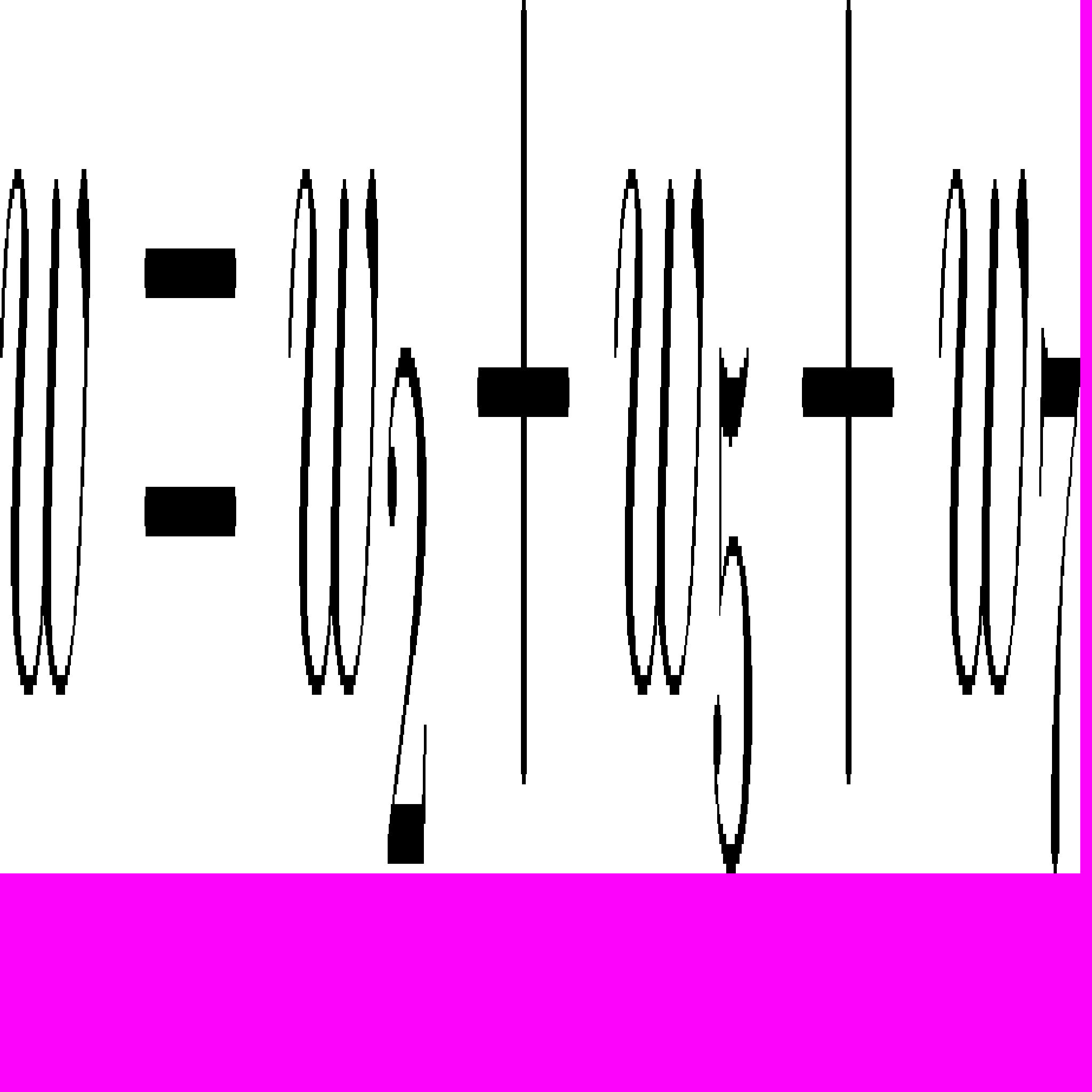, в которой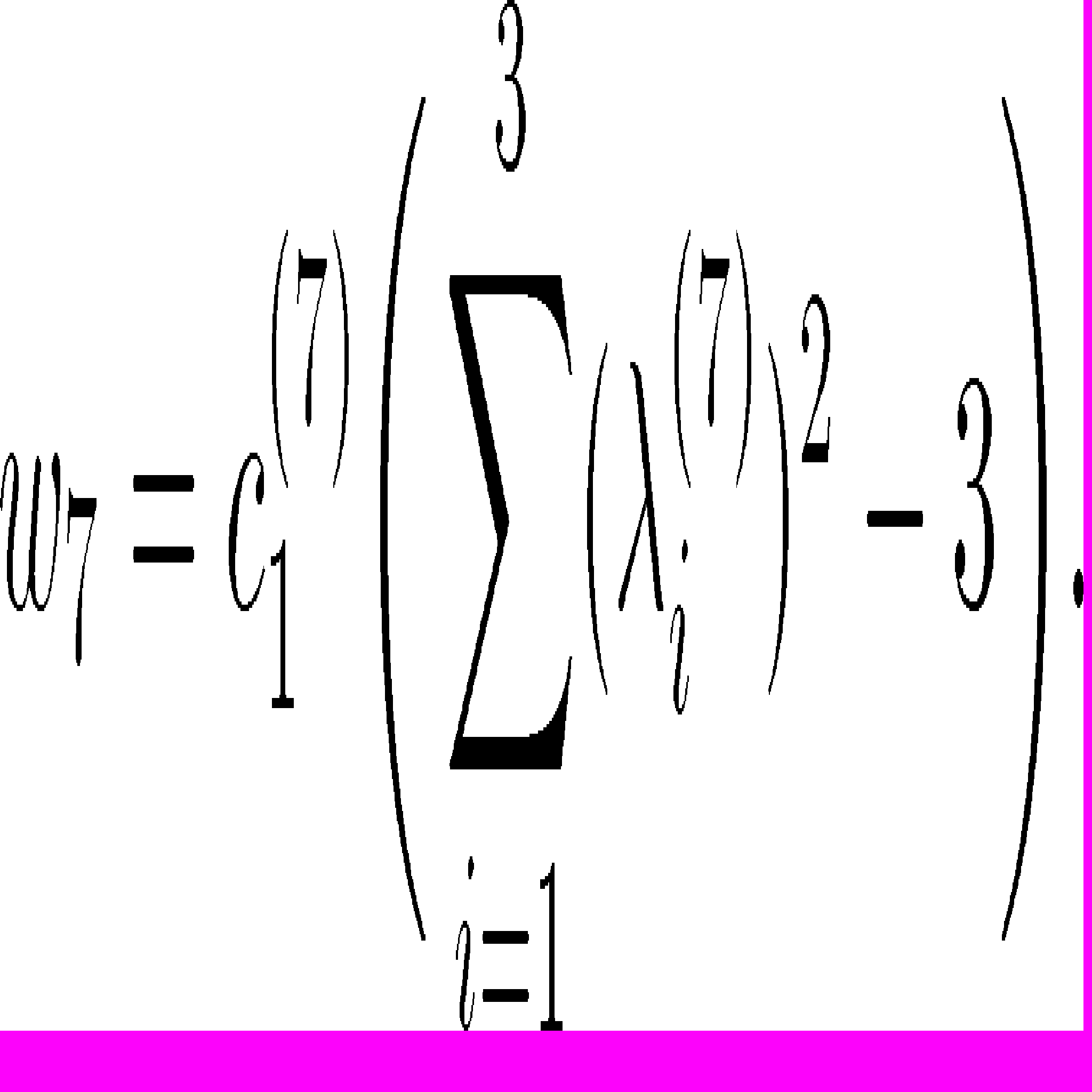



Свойства вязкого элемента определим с помощью следующего коэффициента вязкости 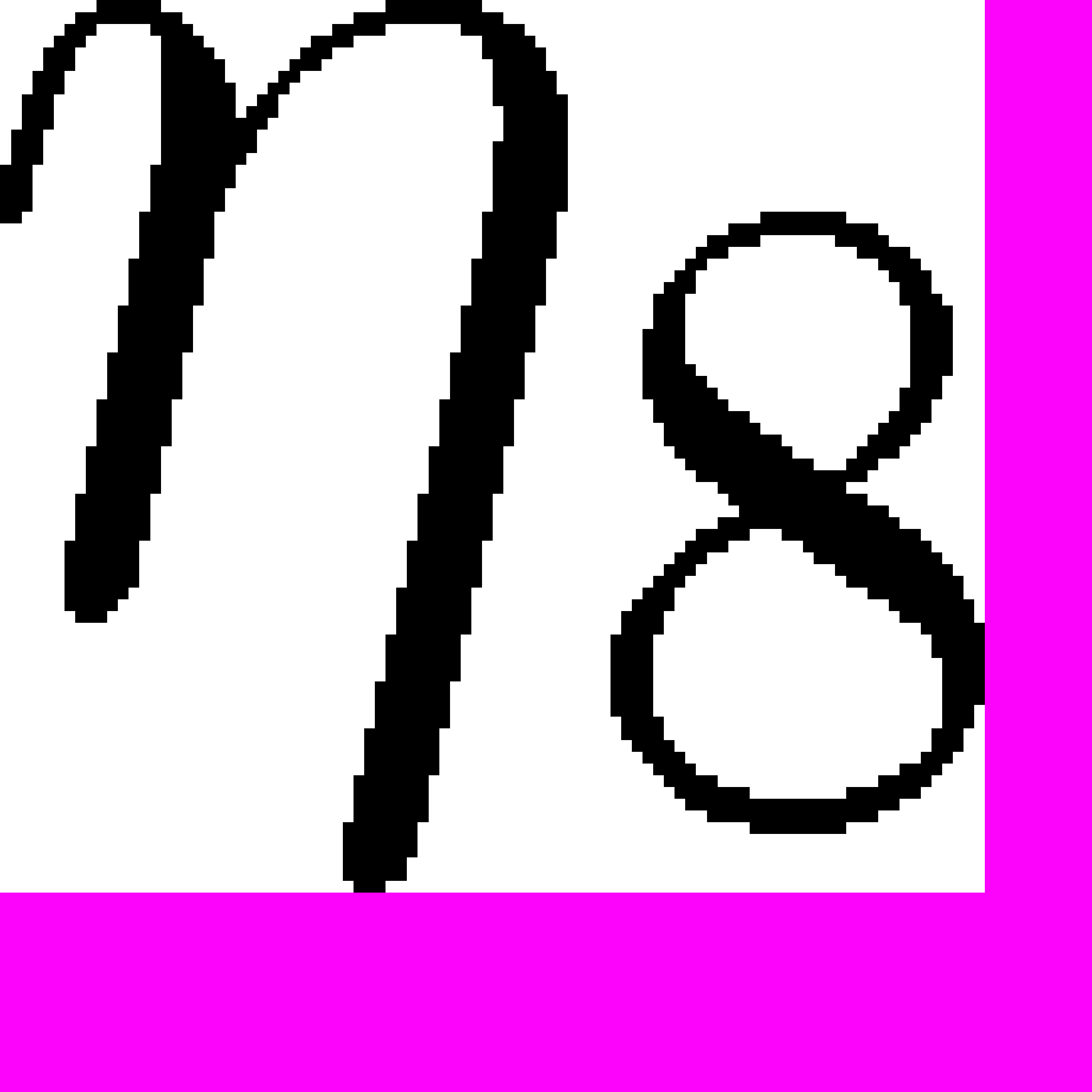для 8-го упругого элемента.

Значения для 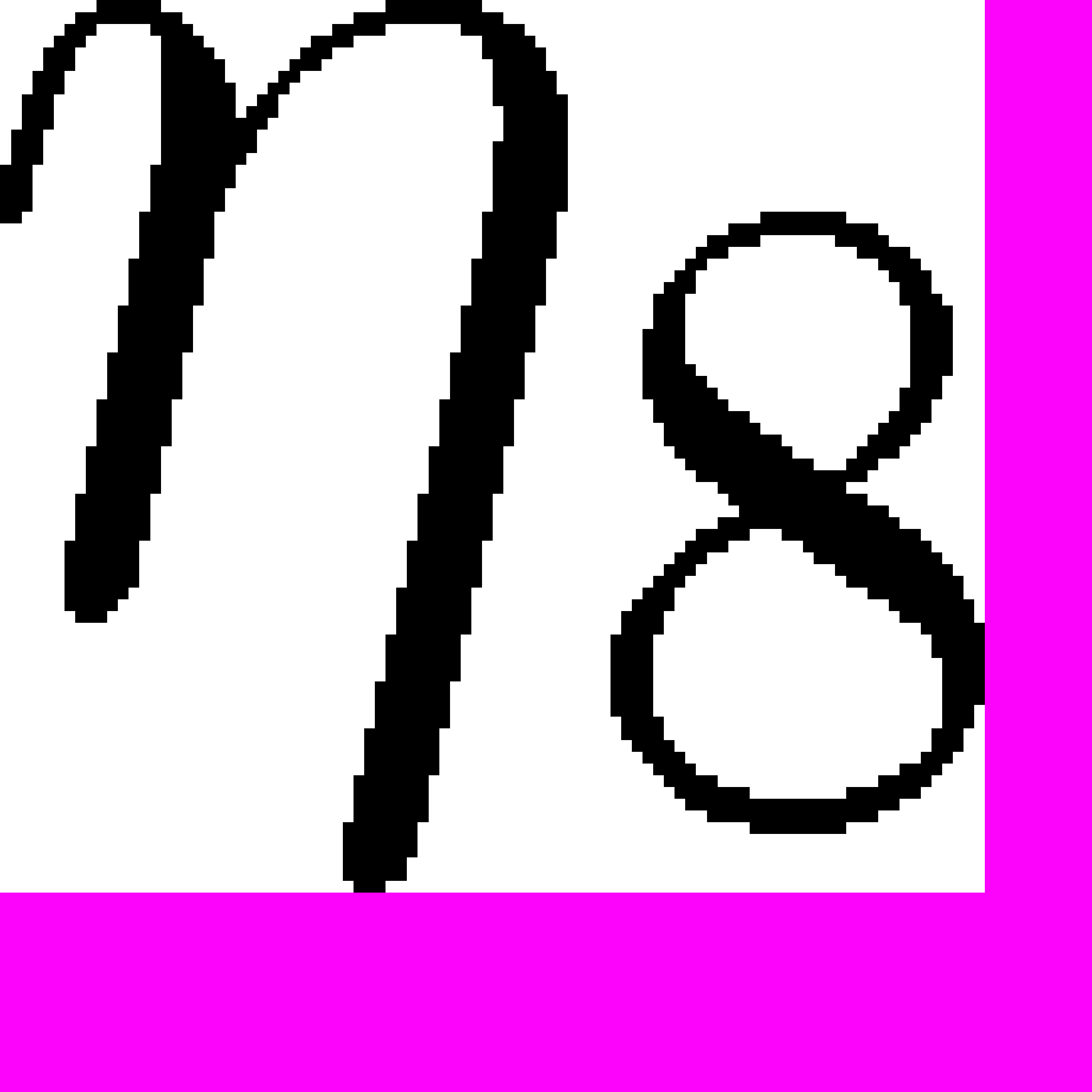, аппроксимируем ее следующей зависимостью:

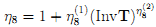, где 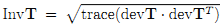, а константы 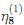и 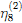подбираются так, чтобы описать нагрузку и разгрузку для кратности удлинений λ<1.8.

Шаг 4.

На четвертом шаге мы добавим к найденной зависимости 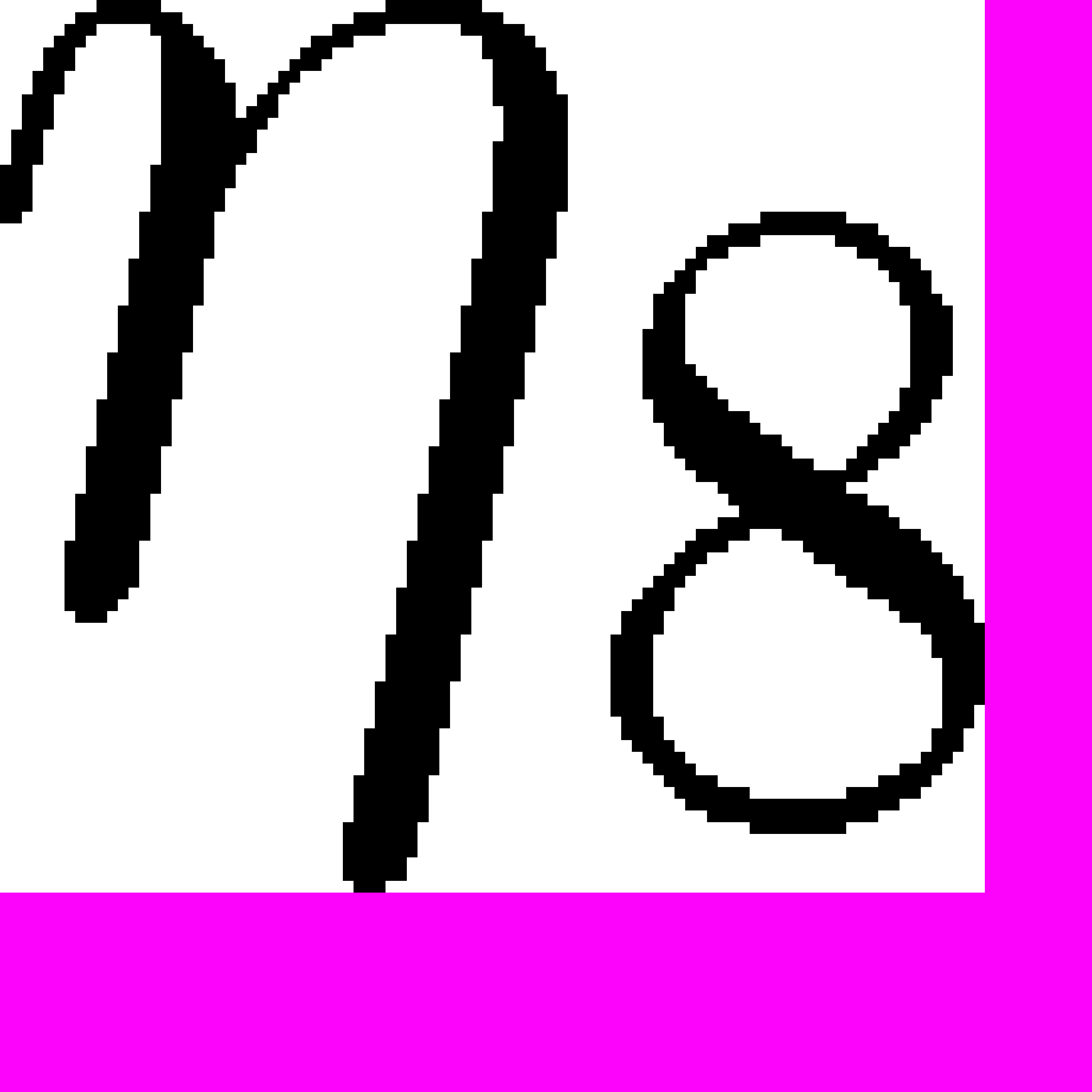слагаемое для теоретического описания нагрузки и разгрузки для кратности удлинений λ>1.8. Из работы [5] мы знаем, что в выражении вязкости существует слагаемое, которое зависит от максимальной кратности удлинений. Это слагаемое оказывает тем меньше влияния на механическое поведение, чем меньше текущая кратность удлинений относительно максимальной. Чтобы описать этот процесс мы представим 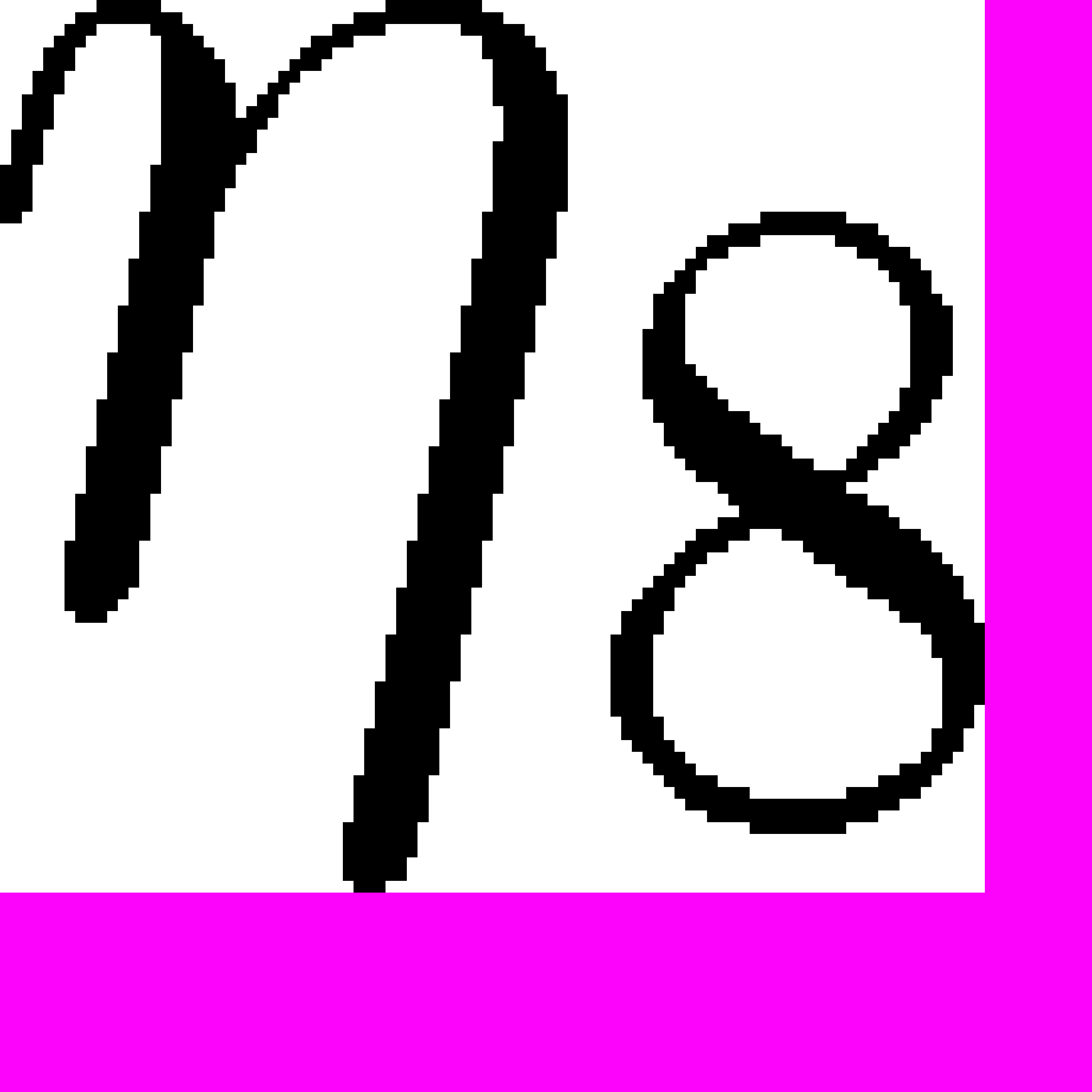следующим образом

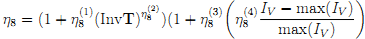, где инвариант 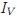вычисляется по формуле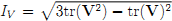

Результаты моделирования и модель приведены на рис.4 пунктирной линией.

Выводы

— предлагается методика испытания эластомерных композитов с цикличной траекторией нагружения. Это позволяет получить из одного эксперимента информацию о размягчении материала и вязкоупругих свойствах материала;

— предлагаемая методика эксперимента позволяет построить равновесную кривую материала, где исключаются вязкоупругие свойства эластомера;



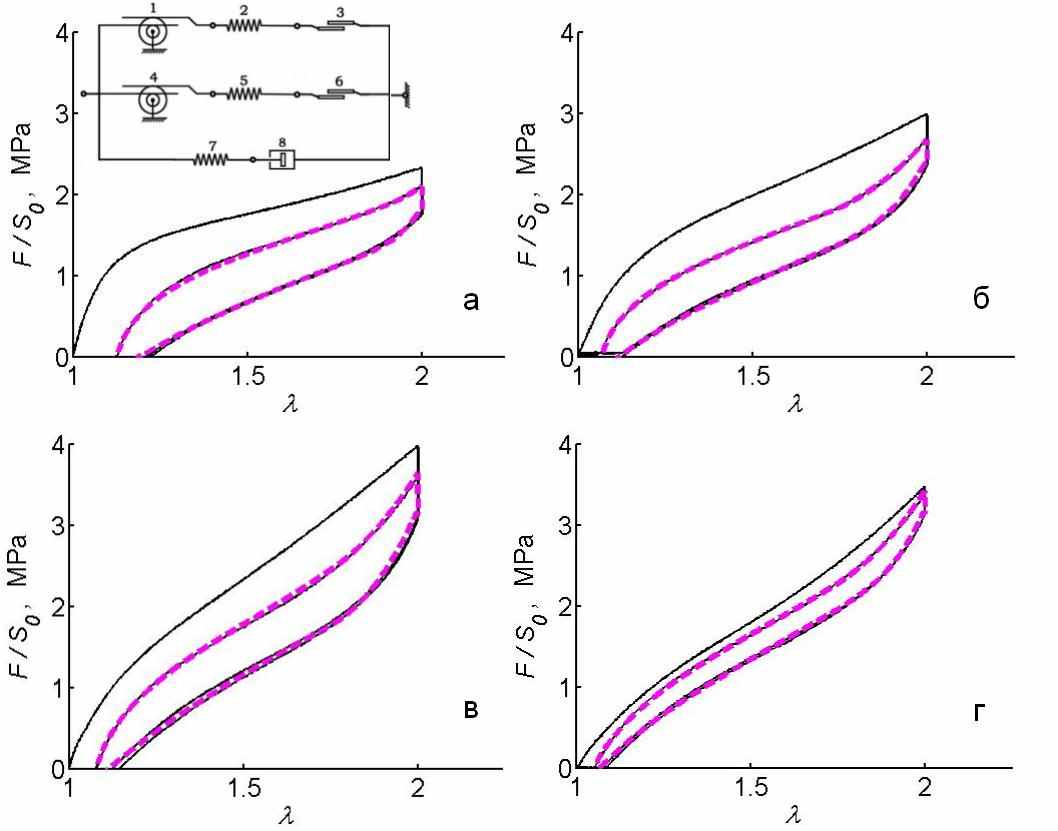
Рис. 4 Модель материала; экспериментальные данные для образцов с номерами 4,6,8,10 — сплошная линия; теоретические данные модели на данном шаге для образцов с номерами 4,6,8,10 — штрих пунктирной линия; теоретические данные модели на первом шаге (без учета волокон) для образцов с номерами 4,6,8,10 — пунктирной линия; a — для материала под номером 4; б — 6; в — 8; г — 10


— на основании структурно-феноменологической модели эластомерного композита построены теоретические описания тренированных материалов, которые хорошо согласуются с экспериментальными данными.

— анализ экспериментов на разрыв (рис.1) и результатов моделирования (данные о волокнах рис.3) показывает, что эластомер, наполненный неактивным, инертным наполнителем Aerosil R200 имеет наименьшую прочность по сравнению с активным и модифицированным наполнителем.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (грант 09–08–00530-а) и программы фундаментальных исследований РАН 09-Т-1-1006


Библиографический список


  1. Свистков А.Л.,Lauke B. Структурно-феноменологическое моделирование механического поведения резин // Высокомолекулярные соединения. Сер. А. 2008. Т. 50, № 5. C. 892–902.
  2. Морозов И.А., Свистков А.Л. Структурно-феноменологическая модель механического поведения резины // Механика композиционных материалов и конструкций, 2008. Т. 14. № 4. С. 583-596.
  3. Свистков А.Л., Лауке Б. Дифференциальные определяющие уравнения несжимаемых сред при конечных деформациях // Прикладная механика и техническая физика. 2009. Т. 50, № 3. С. 158–170.
  4. Stckelhuber K. W., Svistkov A.L., Pelevin A.G., Heinrich G. Impact of filler surface modification on large scale mechanics of styrene butadiene/silica rubber composites // Macromolecules. 2011. V. 44. No. 11— P. 4366-4381.
  5. Пелевин А.Г., Свистков А.Л., Адамов А.А., Lauke B., Heinrich G. Алгоритм поиска констант в модели механического поведения резины // Механика композиционных материалов и конструкций. 2010. Т. 16, № 3. С. 312–328.
  6. Fukahori Y. The mechanics and mechanism of the black reinforcement of elastomers // Rub. Chem. Tech. 2003. Vol. 76. № 2. P. 548–565.
  7. Свистков А.Л., Комар Л.А., Heinrich , Lauke . Моделирование процесса формирования слоев ориентированного полимера около частиц наполнителя в полимерных нанокомпозитах // Высокомолек. соед. А. 2008. Т. 50. № 5. С. 903–910.
  8. Шадрин В.В., Корнев Ю.В., Гамлицкий Ю.А. Изменение свойств резины в результате модификации поверхности частиц углеродного наполнителя // Механика композиционных материалов и конструкций. 2009. Т.17. № 3.С. 401–410.



Use of structurally-phenomenological model for the description of viscoelastic properties of the first-loaded rubber with different types of fillers

A. G. Pelevin, A. L. Svistkov, V. V. Shadrin



Institute of continuous media mechanics UB RAS , street Academ. Koroleva, 1, 614013 Perm

Researches are conducted in work with rubbers on the basis of one elastomer and various types of a filler. rupture and cyclic experiments at stand Testometric FS-100ST are made. The data obtained from experiments about equilibrium and viscoelastic properties of a material has been described by means of structurally-phenomenological model. The estimation of influence of fillers on mechanical properties of materials is received.