Лекция n13 Лекция 1 3
| Вид материала | Лекция |
СодержаниеЭффект Допплера Ударные волны Маха U движущегося автомобиля. В этом случае U |
- «Социальная стратификация и социальная мобильность», 46.19kb.
- Первая лекция. Введение 6 Вторая лекция, 30.95kb.
- Лекция Сионизм в оценке Торы Лекция Государство Израиль испытание на прочность, 2876.59kb.
- Текст лекций н. О. Воскресенская Оглавление Лекция 1: Введение в дисциплину. Предмет, 1185.25kb.
- Собрание 8-511 13. 20 Лекция 2ч режимы работы эл оборудования Пушков ап 8-511 (ррэо), 73.36kb.
- Концепция тренажера уровня установки. Требования к тренажеру (лекция 3, стр. 2-5), 34.9kb.
- Лекция по физической культуре (15. 02.; 22. 02; 01. 03), Лекция по современным технологиям, 31.38kb.
- Лекция посвящена определению термина «транскриптом», 219.05kb.
- Тема Лекция, 34.13kb.
- Энергоснабжениеапк лекция, доц. Уринцова Л. В. 2/309, 28.44kb.
ЛЕКЦИЯ N13
Лекция 13.
Лекция 13.
стоячие волны. эффект допплера. ударные волны маха
Стоячие волны тоже часто рассматривают как интерференционное явление, имеющее, однако, свои особенности.
Представим себе, что имеются две плоские волны,
распространяющиеся вдоль оси Х навстречу друг другу:
 . Такую ситуацию можно получить, если к крюку, вбитому в стену, привязать веревку, свободный конец которой совершает гармонические колебания
. Такую ситуацию можно получить, если к крюку, вбитому в стену, привязать веревку, свободный конец которой совершает гармонические колебания 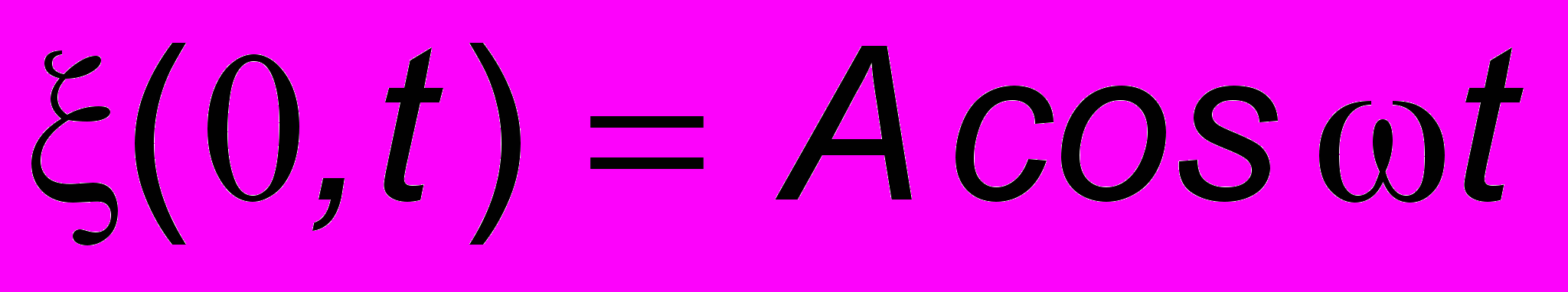 , возбуждаемые, например, электромотором. Возникающий при отражении волны от стенки фазовый сдвиг, равный /2, в данном случае принципиальной роли не играет, и, простоты ради, мы его учитывать не будем. Применяя формулу (4.6а) получим уравнение результирующего колебательного процесса:
, возбуждаемые, например, электромотором. Возникающий при отражении волны от стенки фазовый сдвиг, равный /2, в данном случае принципиальной роли не играет, и, простоты ради, мы его учитывать не будем. Применяя формулу (4.6а) получим уравнение результирующего колебательного процесса: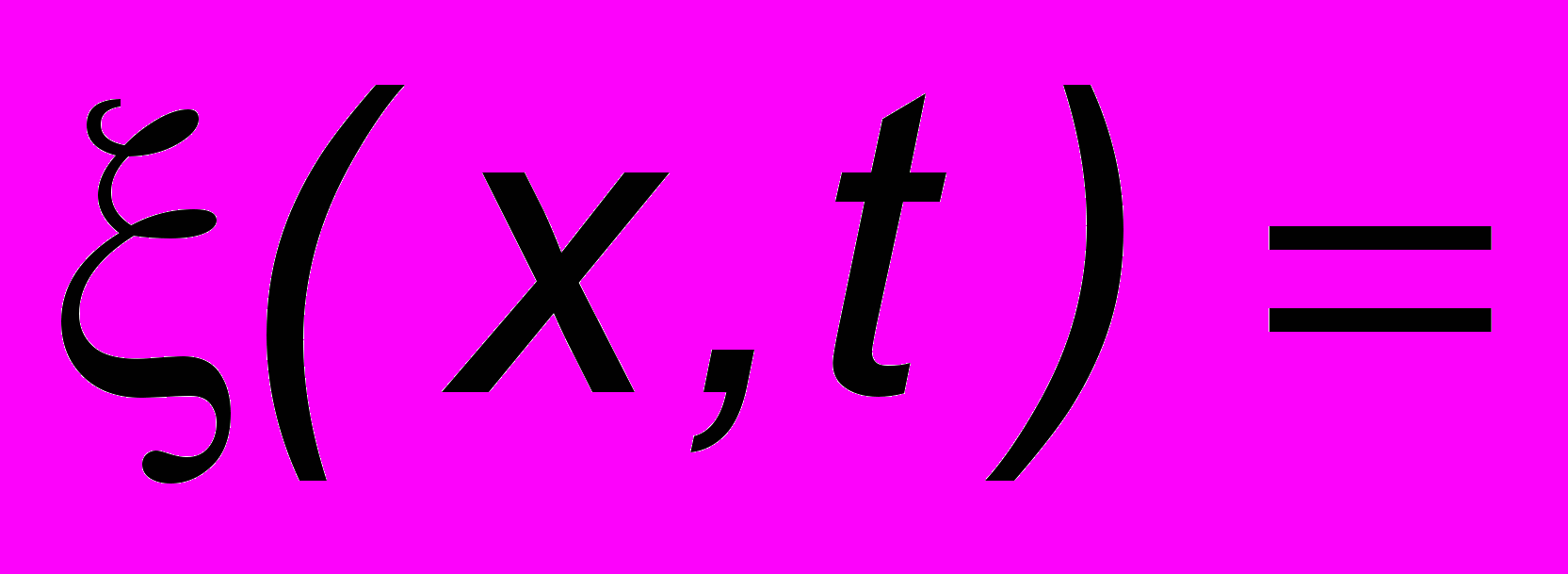
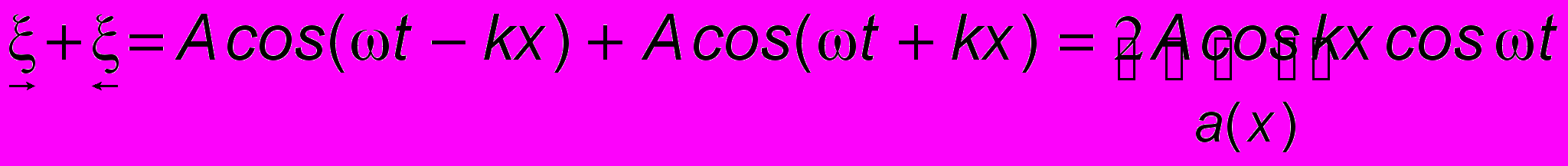 . (13.1)
. (13.1)Э
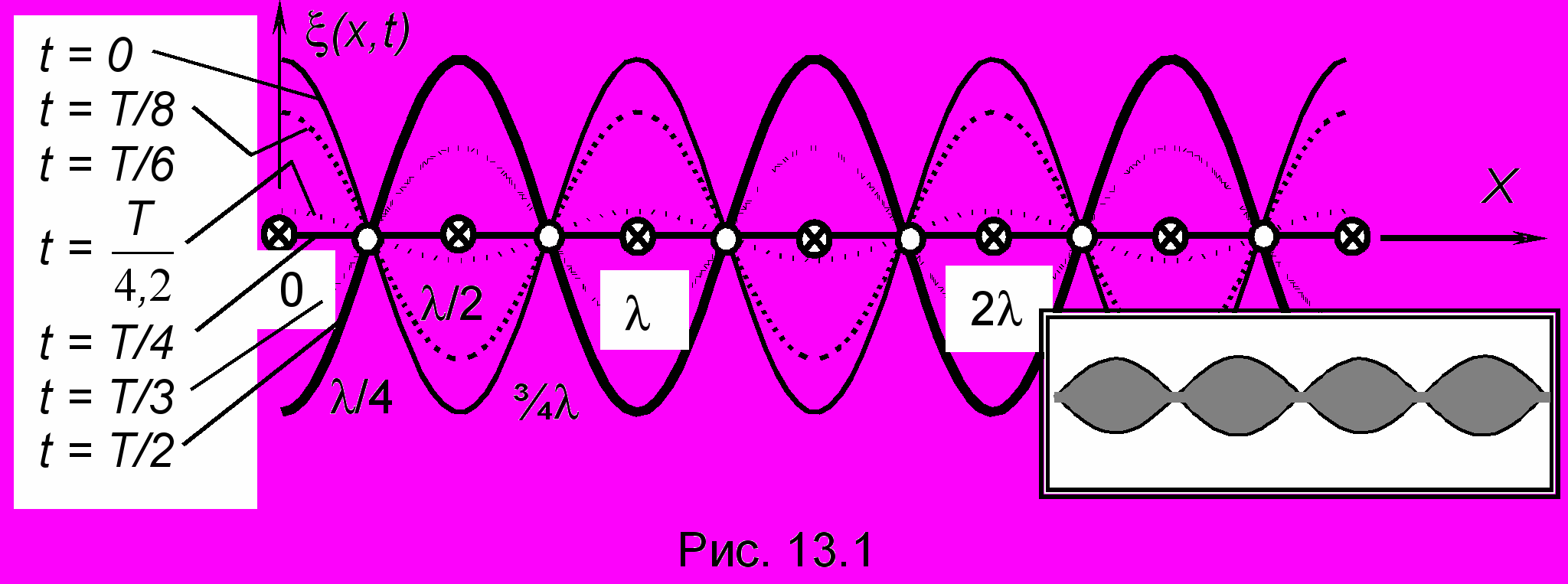
то уравнение совсем не похоже на уравнение бегущей волны: аргумент у cos не t kx), а просто t. Получается, что разные точки веревки будут совершать гармонические колебания с разными амплитудами, зависящими от участка веревки (т.е. от координаты х), однако распространяющейся волны не будет. Такие колебания называются стоячей волной. Из (13.1) видно, что амплитуда стоячей волны
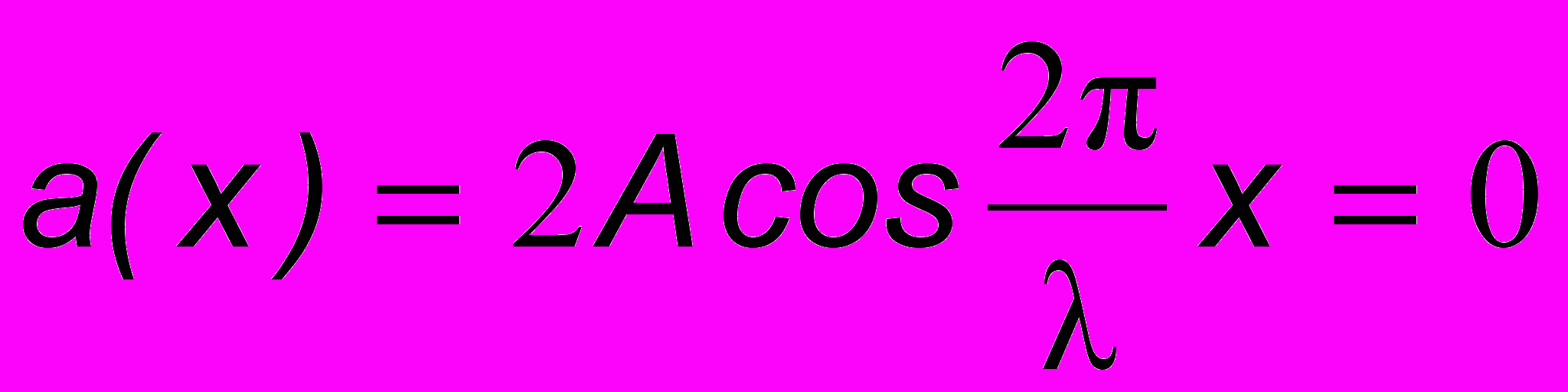 всегда в точках
всегда в точках 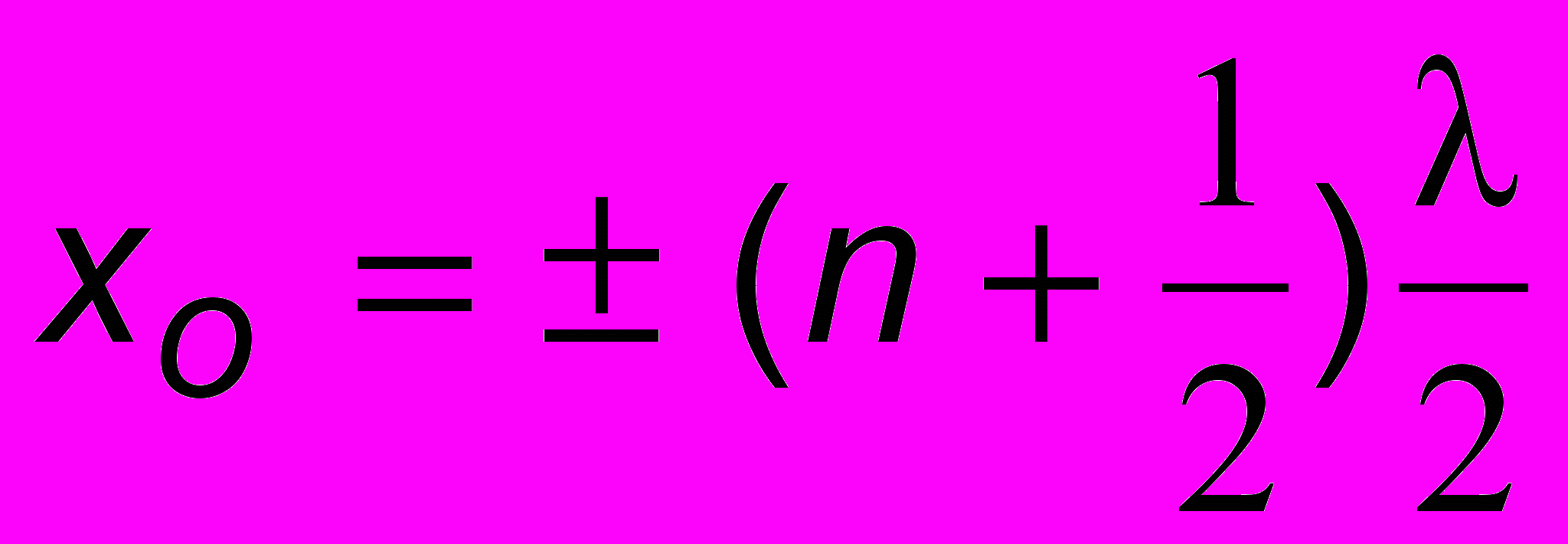 , где n = 0, 1, 2,... Такие точки называются узлами стоячей волны. Между ними, т.е. в точках
, где n = 0, 1, 2,... Такие точки называются узлами стоячей волны. Между ними, т.е. в точках 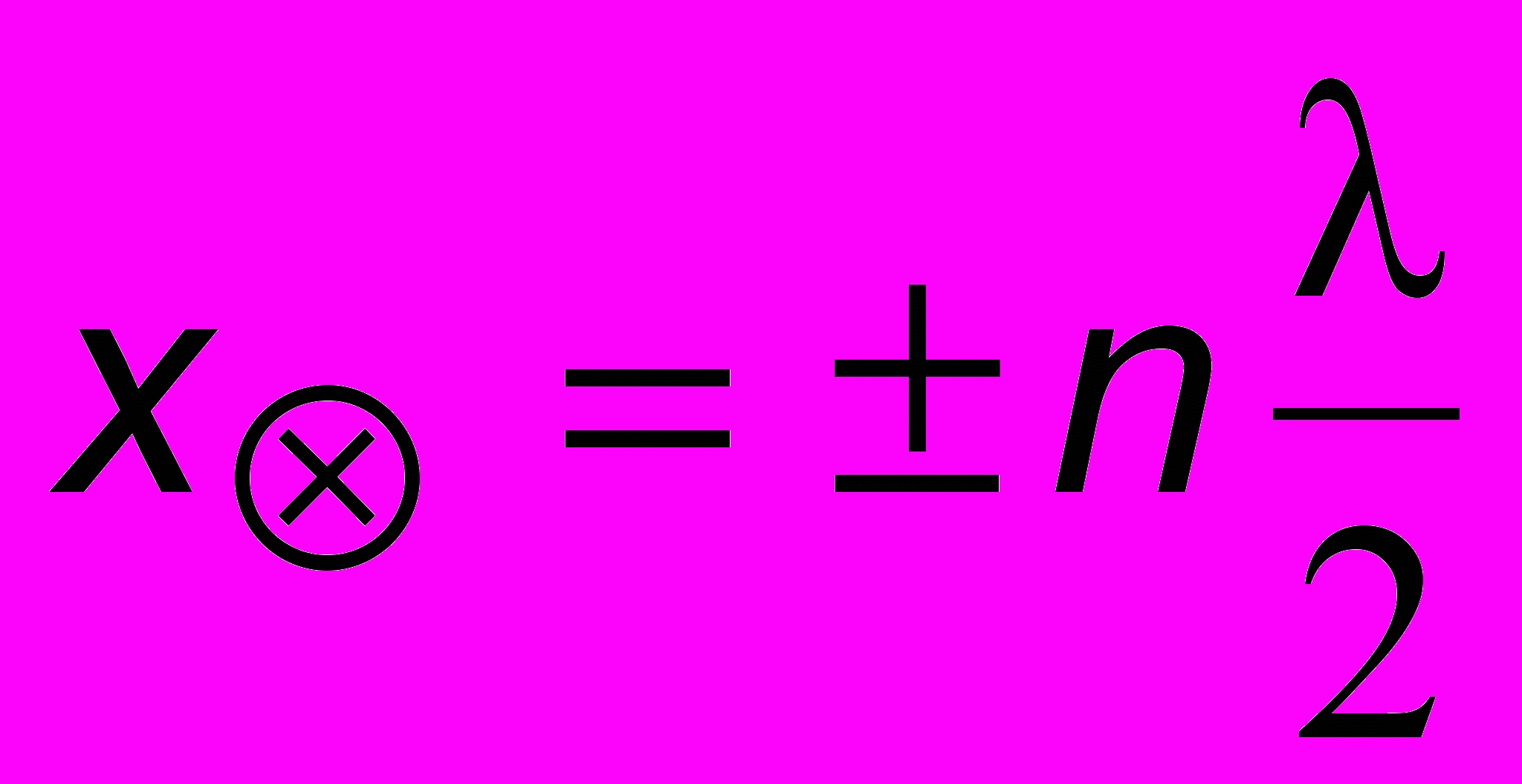 , где n = 0, 1, 2,... амплитуда a(x) может принимать свое максимально возможное значение a(x) = 2А. Такие точки называются пучностями. Изобразим профиль веревки для некоторых характерных моментов времени (рис. 13.1). Видно, что максимальные амплитуды достигаются в пучностях в моменты времени, кратные Т/2, а в момент времени Т/4 и далее через каждые полпериода смещение всех частиц равно нулю. Внизу на врезке показана картина, которую видит наблюдатель.
, где n = 0, 1, 2,... амплитуда a(x) может принимать свое максимально возможное значение a(x) = 2А. Такие точки называются пучностями. Изобразим профиль веревки для некоторых характерных моментов времени (рис. 13.1). Видно, что максимальные амплитуды достигаются в пучностях в моменты времени, кратные Т/2, а в момент времени Т/4 и далее через каждые полпериода смещение всех частиц равно нулю. Внизу на врезке показана картина, которую видит наблюдатель.Р
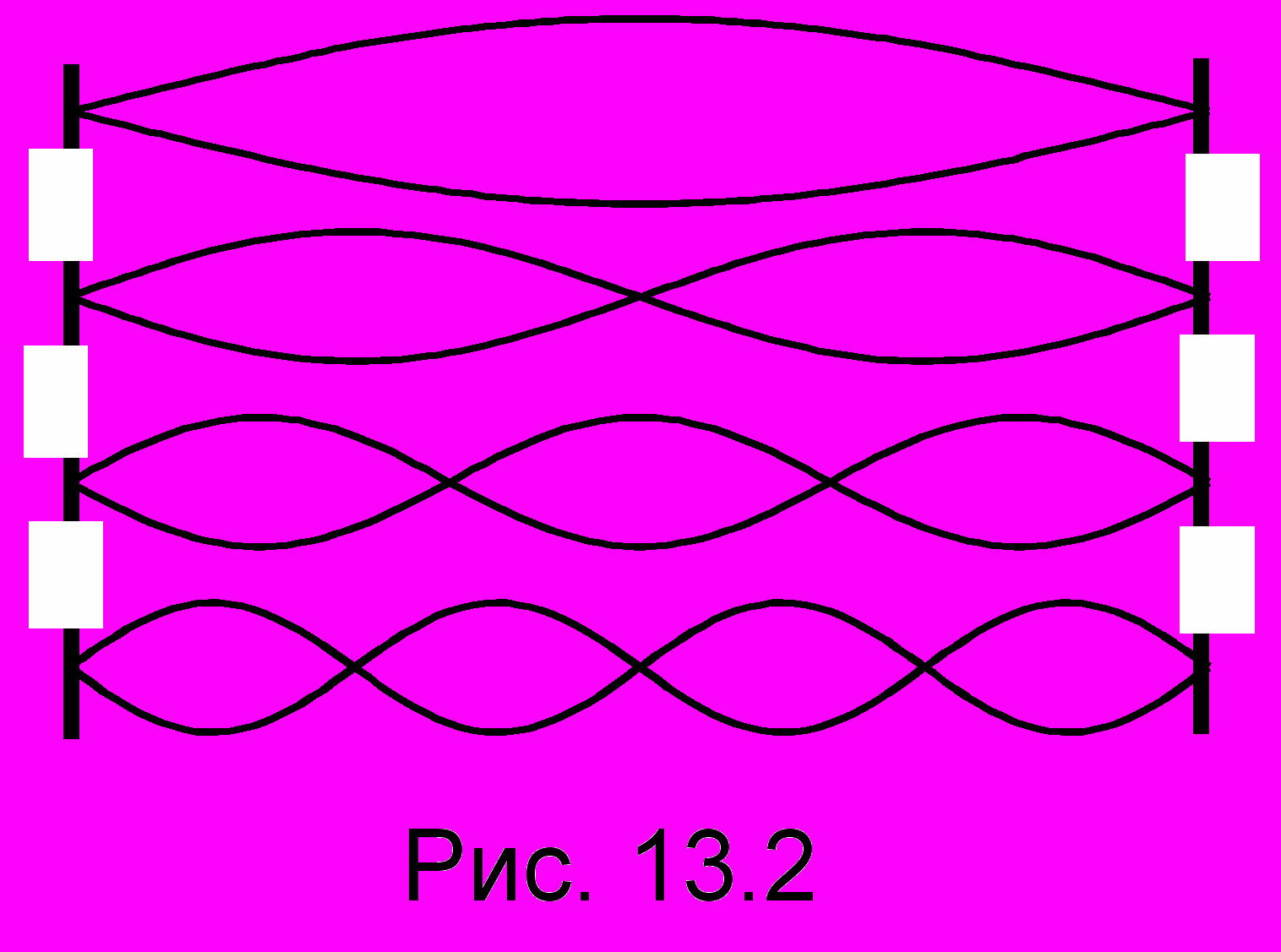
еальная картина стоячих волн зависит от граничных условий среды. Рассмотрим струну длиной L, закрепленную у обоих концов, в которой взаимодействуют встречные бегущие поперечные волны (как это имеет место при возбуждении струны любого музыкального инструмента). Так как струна у концов закреплена, то там колебаний нет, и потому на концах всегда будут узлы. Возможные картины стоячих волн в такой струне показаны на рис. 13.2. Установим важную закономерность: всякий раз на полной длине струны укладывается целое число полуволн, соответствующих распространяющейся бегущей волне. Верхняя картинка:
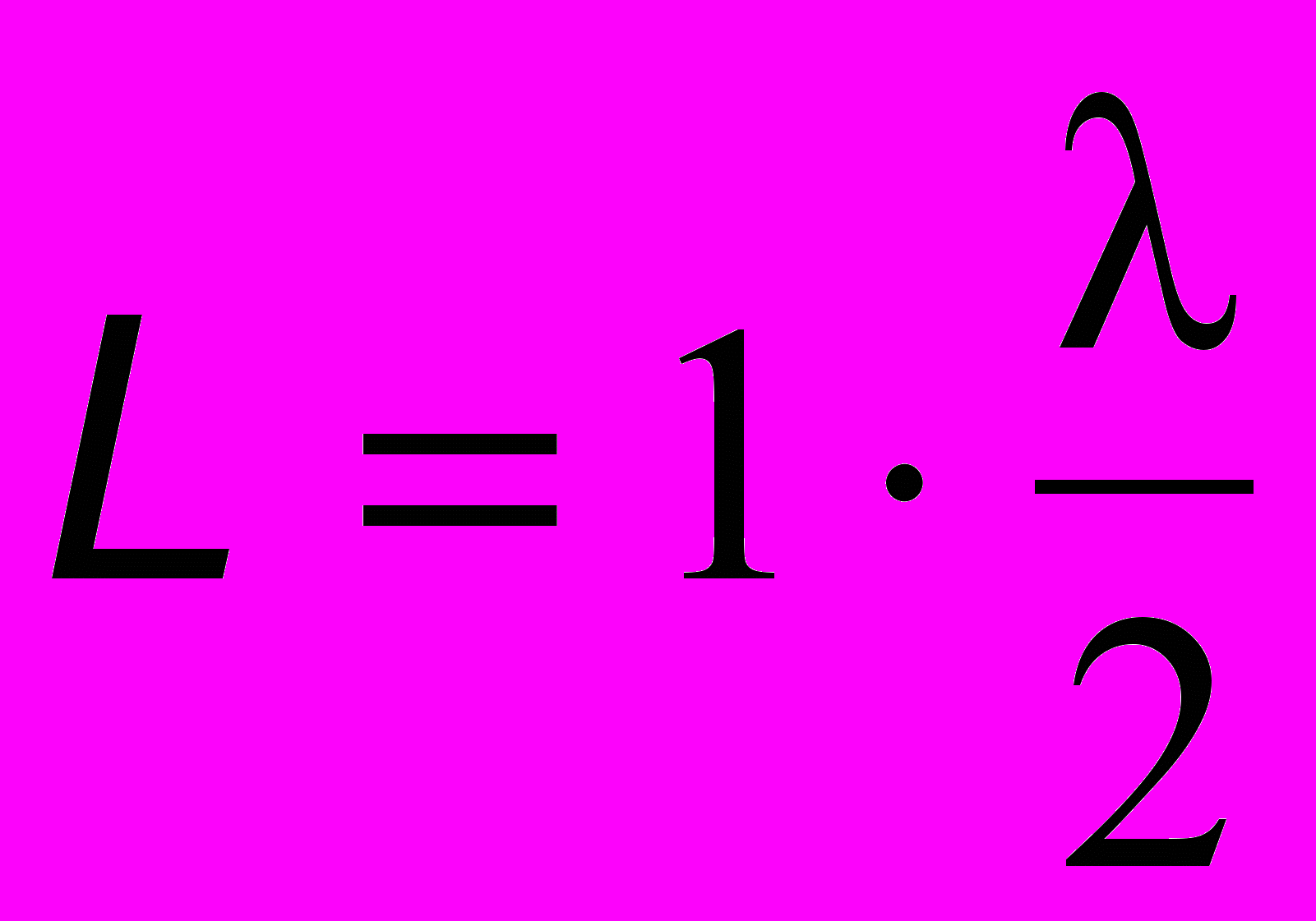 , далее
, далее  и т.д. Вспомним, что = V/ (где - частота, а V - фазовая скорость бегущей волны, связанная с плотностью материала струны , массой m, диаметром d и силой натяжения F соотношением
и т.д. Вспомним, что = V/ (где - частота, а V - фазовая скорость бегущей волны, связанная с плотностью материала струны , массой m, диаметром d и силой натяжения F соотношением  ). Тогда для общего случая получим:
). Тогда для общего случая получим: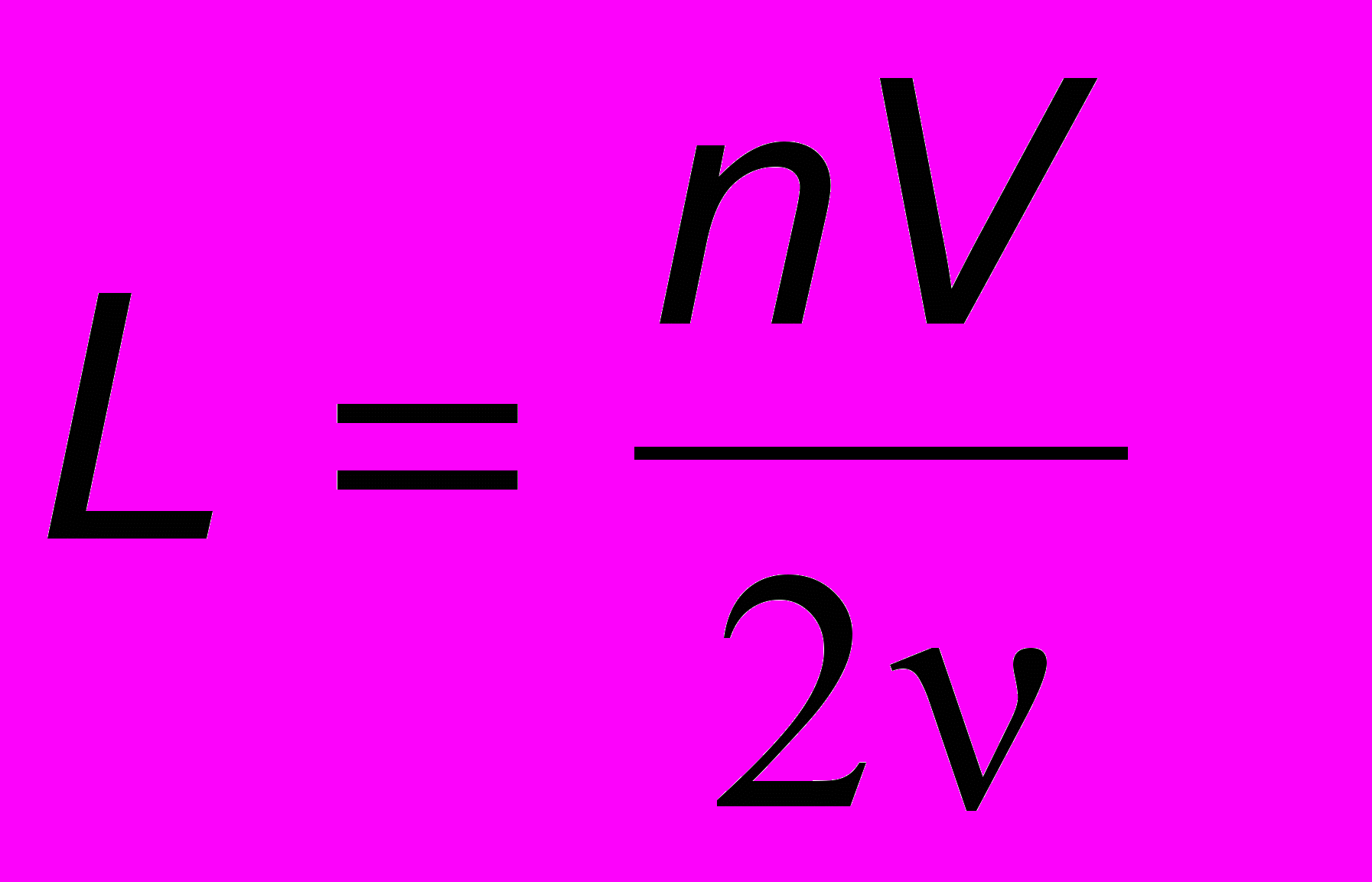 , откуда
, откуда 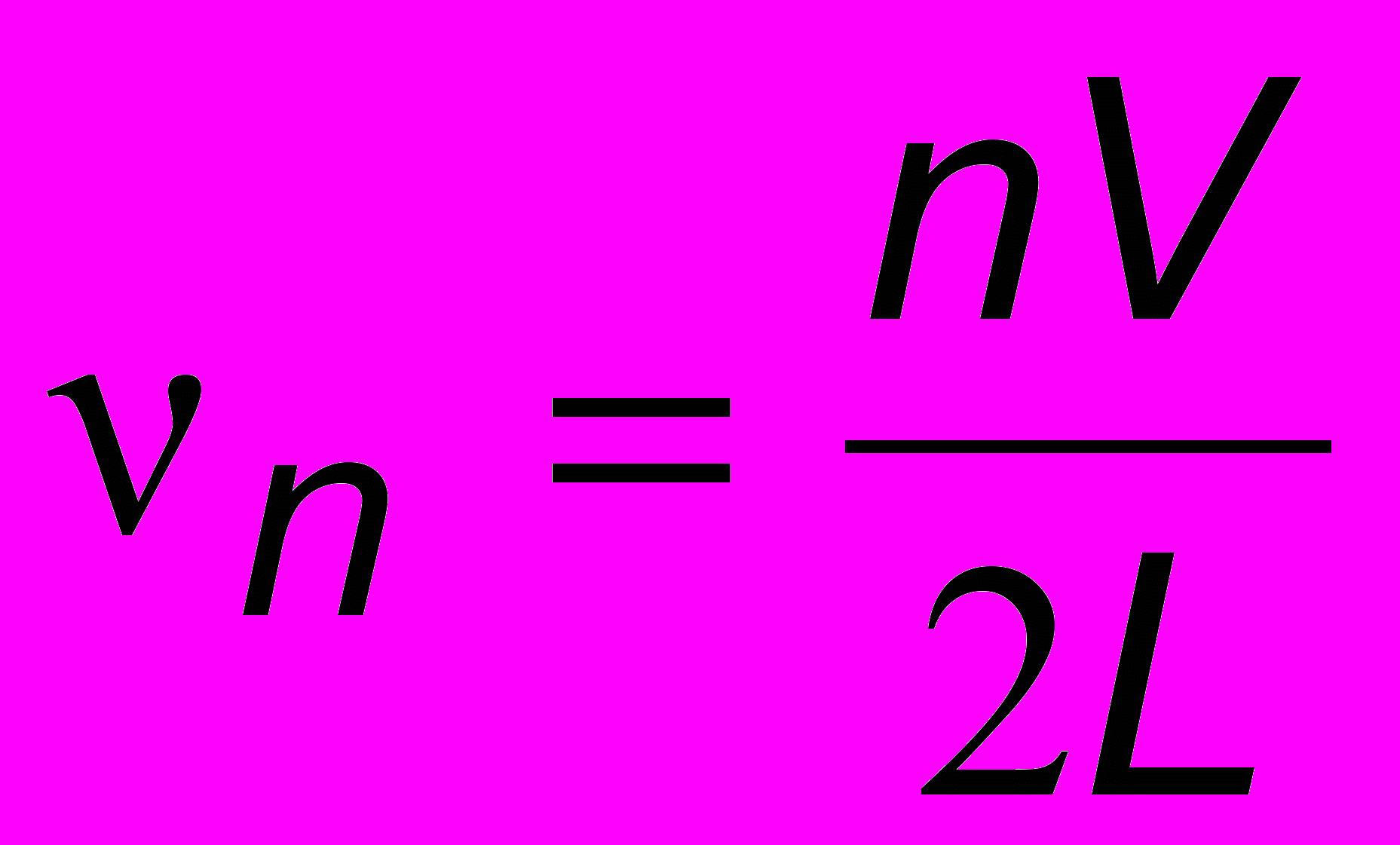 , где n = 1, 2, 3, ... . Последнюю формулу называют спектром собственных частот колебаний струны. Индекс
, где n = 1, 2, 3, ... . Последнюю формулу называют спектром собственных частот колебаний струны. Индекс n, присвоенный частоте, отражает тот факт, что набор частот дискретен, т.е. меняется скачкообразно от одного значения к другому. Если просто ущипнуть гитарную струну или провести смычком по скрипичной струне, то в сложном звуке (см. рис. 1.1 или 5.4) будет преобладать основная частота (n = 1). Музыканты знают прием - флажолет - когда струна гитары или скрипки звучит на октаву выше1. Это первая гармоника (n = 1) основного тона2. Более высокие гармоники заметной амплитуды на музыкальных инструментах возбудить невозможно, однако если струну из немагнитного материала расположить между полюсами магнита, а через струну пропускать переменный ток регулируемой частоты от генератора, то возникающая сила Ампера заставит струну колебаться с частотой генератора, и если эта частота близка к одной из частот спектра
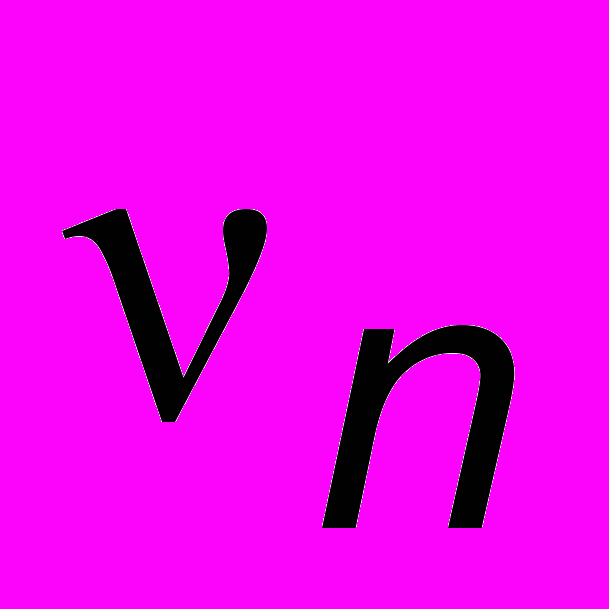 , то в струне возникает резонанс, в результате чего на струне отчетливо наблюдается одна из картинок рис. 13.2, соответствующая данной собственной частоте. Для стержня, закрепл
, то в струне возникает резонанс, в результате чего на струне отчетливо наблюдается одна из картинок рис. 13.2, соответствующая данной собственной частоте. Для стержня, закрепл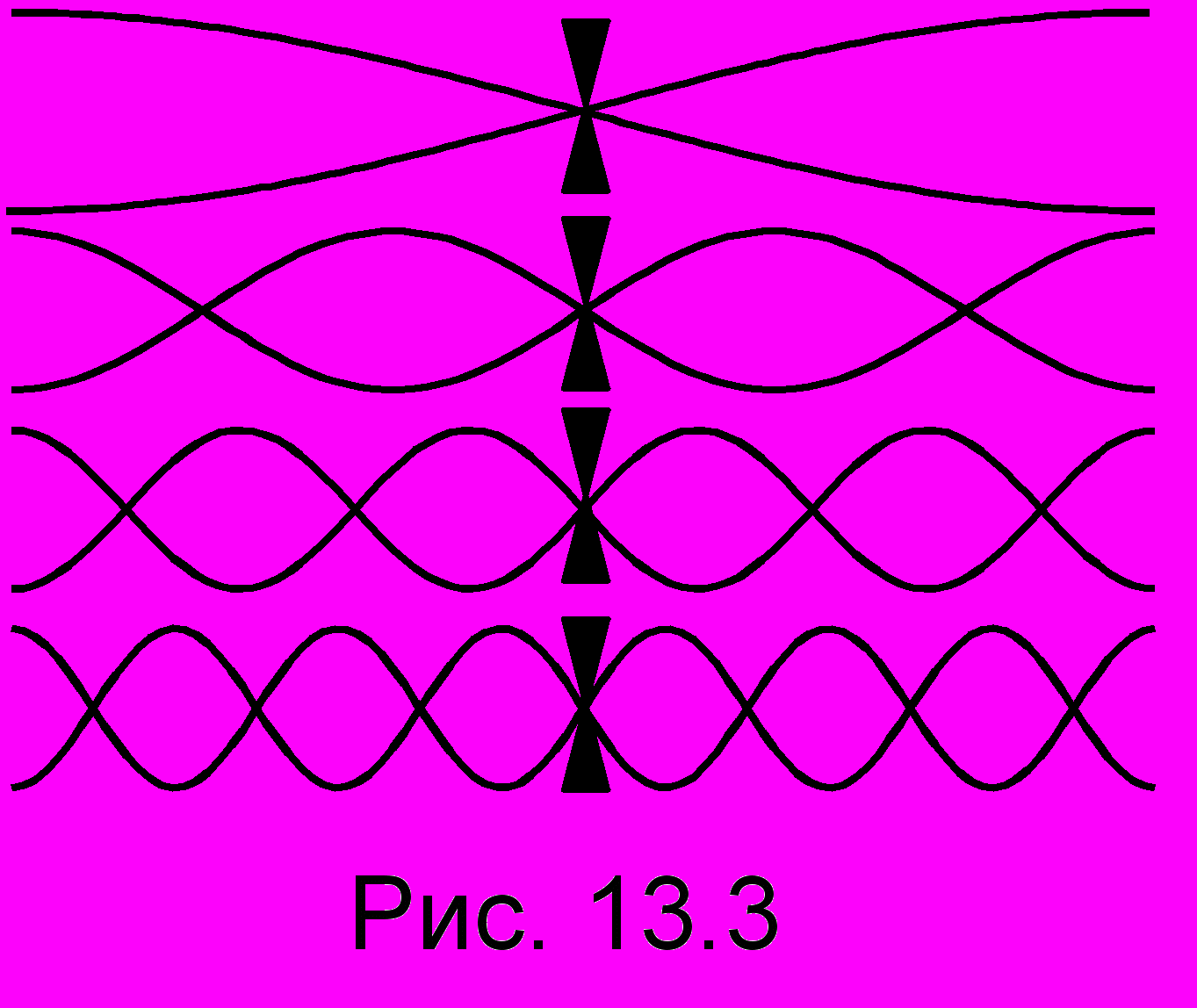 енного посредине, получим картинки, изображенные на рис. 13.3. Посредине, где стержень закреплен, смещения нет, и там, естественно, всегда будет узел. На свободных же концах будут пучности. Поступая, как и в предыдущем случае, получим, что на стержне всякий раз укладывается нечетное число полуволн. Получим
енного посредине, получим картинки, изображенные на рис. 13.3. Посредине, где стержень закреплен, смещения нет, и там, естественно, всегда будет узел. На свободных же концах будут пучности. Поступая, как и в предыдущем случае, получим, что на стержне всякий раз укладывается нечетное число полуволн. Получим  . Заметим, что в стержне могут возбуждаться не только поперечные (как в струне), но и продольные волны. Тогда картинки рисунка 13.3 следует воспринимать не как наблюдаемые профили, а как графики отклонений в продольном направлении в данном сечении. Ведь в этом случае колебания будут происходить вдоль стержня, который сам изгибаться не будет.
. Заметим, что в стержне могут возбуждаться не только поперечные (как в струне), но и продольные волны. Тогда картинки рисунка 13.3 следует воспринимать не как наблюдаемые профили, а как графики отклонений в продольном направлении в данном сечении. Ведь в этом случае колебания будут происходить вдоль стержня, который сам изгибаться не будет.С

тоячие волны можно возбудить в органной трубе, закрытой у одного конца (рис. 13.4), где всегда будет узел. У открытого конца будет пучность. В отличие от стержня, здесь могут иметь место только продольные волны. Видно из рисунка, что на длине трубы L укладывается нечетное число четвертей длин волн, откуда
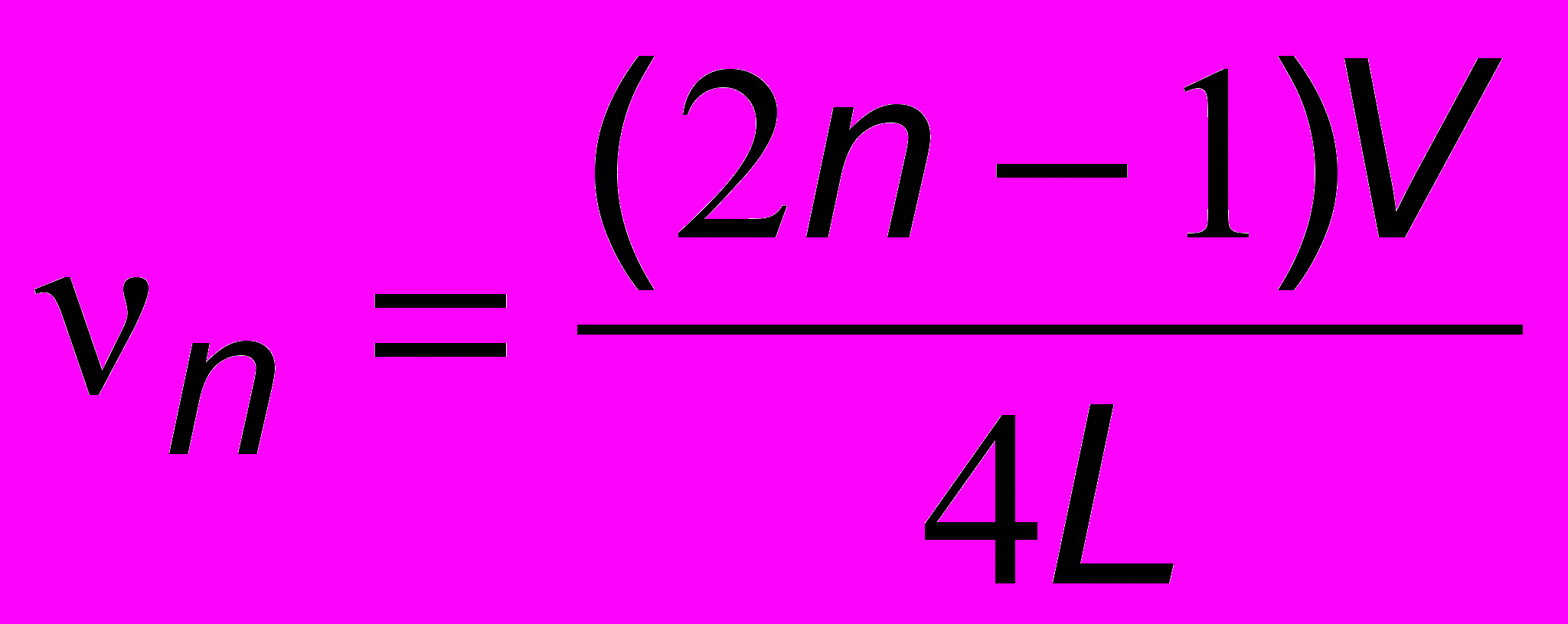 . Посчитаем теперь, какую частоту может генерировать самая длинная в России органная труба длиной L 9,5 м, находящаяся в Московском концертном зале им. П.И. Чайковского. При скорости звука V = 340 м/с для основной частоты n = 1 получим
. Посчитаем теперь, какую частоту может генерировать самая длинная в России органная труба длиной L 9,5 м, находящаяся в Московском концертном зале им. П.И. Чайковского. При скорости звука V = 340 м/с для основной частоты n = 1 получим 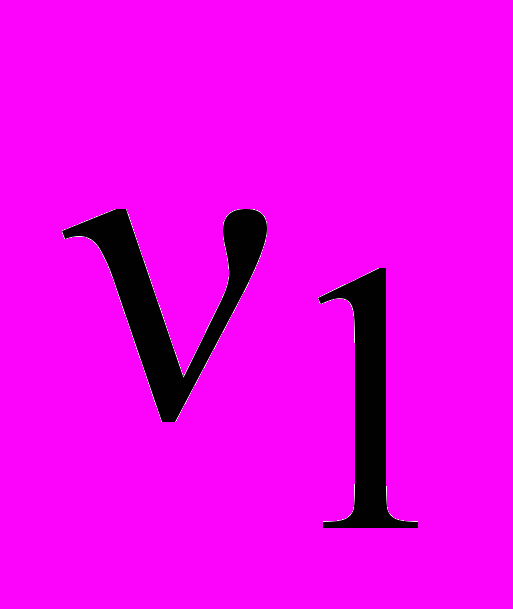 = 9 Гц. Эта частота приходится на неслышимый нами инфразвук (0 < < 20 Гц), оказывающий малоизученное психологическое воздействие на организм человека (см. лекцию 9): на нас сильно воздействует звук, который мы даже не слышим!
= 9 Гц. Эта частота приходится на неслышимый нами инфразвук (0 < < 20 Гц), оказывающий малоизученное психологическое воздействие на организм человека (см. лекцию 9): на нас сильно воздействует звук, который мы даже не слышим!Рис. 13.4 также описывает стоячую волну (поперечную или продольную) в стержне, закрепленном у одного конца. Такие картинки можно визуально наблюдать на длинной телескопической автомобильной антенне при движении автомобиля.
Э
ффект Допплера - очень интересное волновое явление, которое в последнее время стало играть важную роль и в инженерном деле. Он был открыт в 1825 г.3 и заключается в том, что частота сигнала, который посылается некоторым источником отличается от частоты, которая принимается некоторым приемником, если источник или приемник (или оба вместе) движутся. В оригинальном эксперименте Допплера к наблюдателю с абсолютным слухом, находившемуся на перроне вокзала, приближалась, а затем удалялась от него открытая железнодорожная платформа с духовым оркестром. Музыканты выдували одну и ту же ноту, которую неподвижный наблюдатель определял на слух. При приближении платформы обнаруживалось повышение частоты тона, а при удалении - понижение. Это явление наблюдается и для упругих, и для электромагнитных волн, однако описывается по-разному, поскольку упругие волны распространяются всегда в среде, а ЭМ волны могут распространяться и в вакууме. Начнем с упругих волн. В этом случае говорят об эффекте Допплера в акустике.
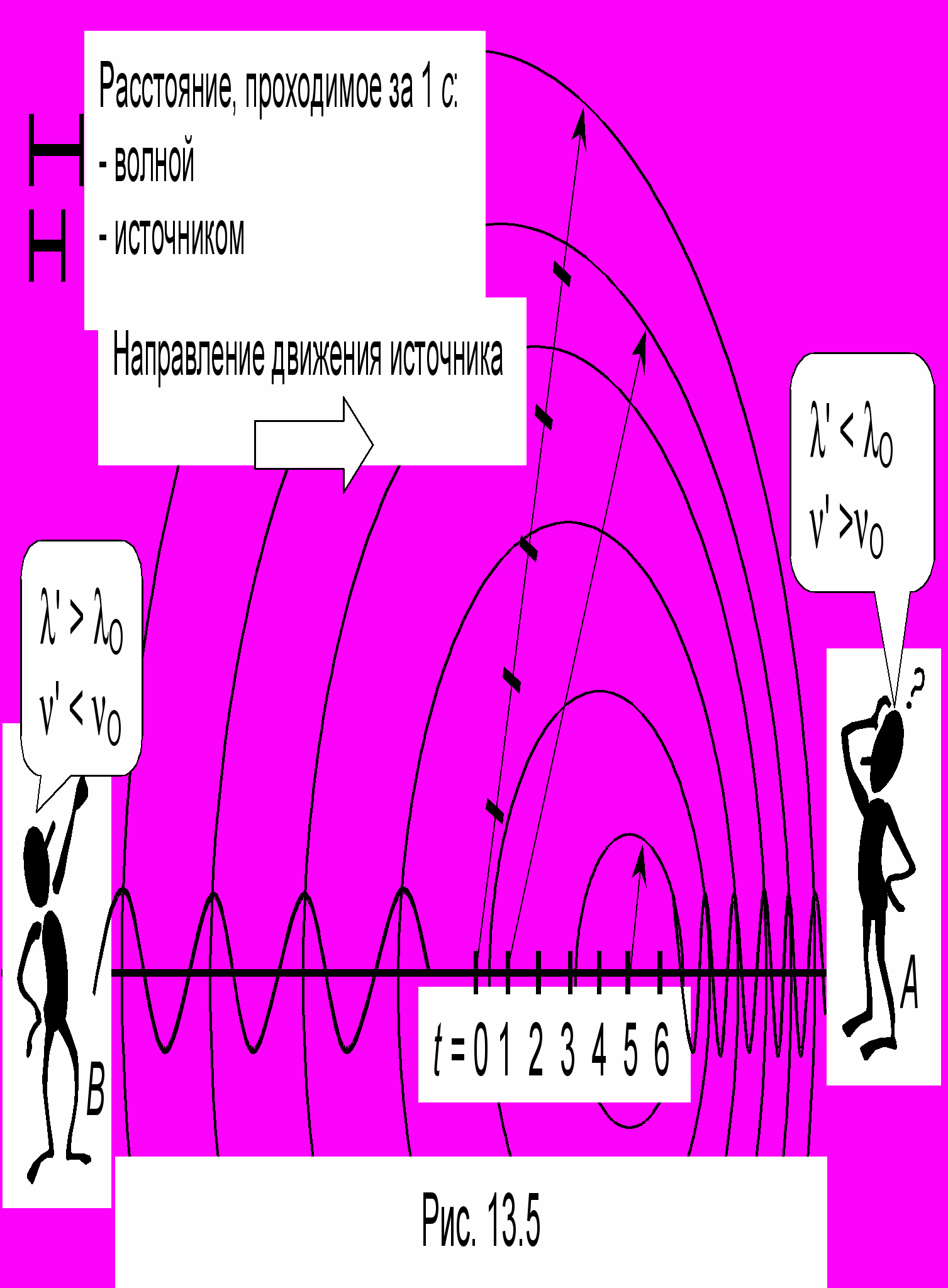
Будем считать, что точечный источник движется относительно неподвижной среды со скоростью u по направлению к неподвижному наблюдателю А и от неподвижного наблюдателя В (рис. 13.5), а волна движется относительно среды со скоростью V, распространяясь в виде сферы во все стороны. Пусть для простоты рассуждений частота источника 0 = 1 Гц (одно колебание в секунду), т.е. каждую секунду, начиная от t = 0, источник посылает в окружающее пространство "горб" синусоиды4. Рассмотрим волновую картину, которая сформируется за 6 секунд. Считая, что V > u, выберем произвольный масштаб для расстояния, проходимого волной и источником за 1с (в левом углу рисунка). Горб, испущенный источником в момент t = 0, распространится за 6 секунд на расстояние, соответствующее самой большой сфере, показанной на рисунке. Следующий горб будет испущен через 1 с, когда источник будет находиться в положении t = 1. За оставшиеся 5 с горб распространится в пределах сферы меньшего радиуса, центр которой, естественно, находится не в точке t = 0, а в точке t = 1. Таким образом, к моменту t = 5 очередному горбу останется только одна секунда5. Для наблюдателя А, к которому движется источник, волна как бы «сжимается», и вместо волны 0 = V /0 он воспримет волну длиной ' = V /' < 0 с частотой ' > 0 . Напротив, для наблюдателя В волна «растянется»: ' > 0 ; ' < 0.
Пусть - время, за которое волна, испущенная в момент t = 0, дойдет до приемника (наблюдателя). Так как частота 0 есть число колебаний за 1 с, то число испущенных за время колебаний равно 0, а расстояние, на которое они распространятся в сторону наблюдателя А, равно (V - u). Таким образом воспринимаемая наблюдателем А длина волны будет
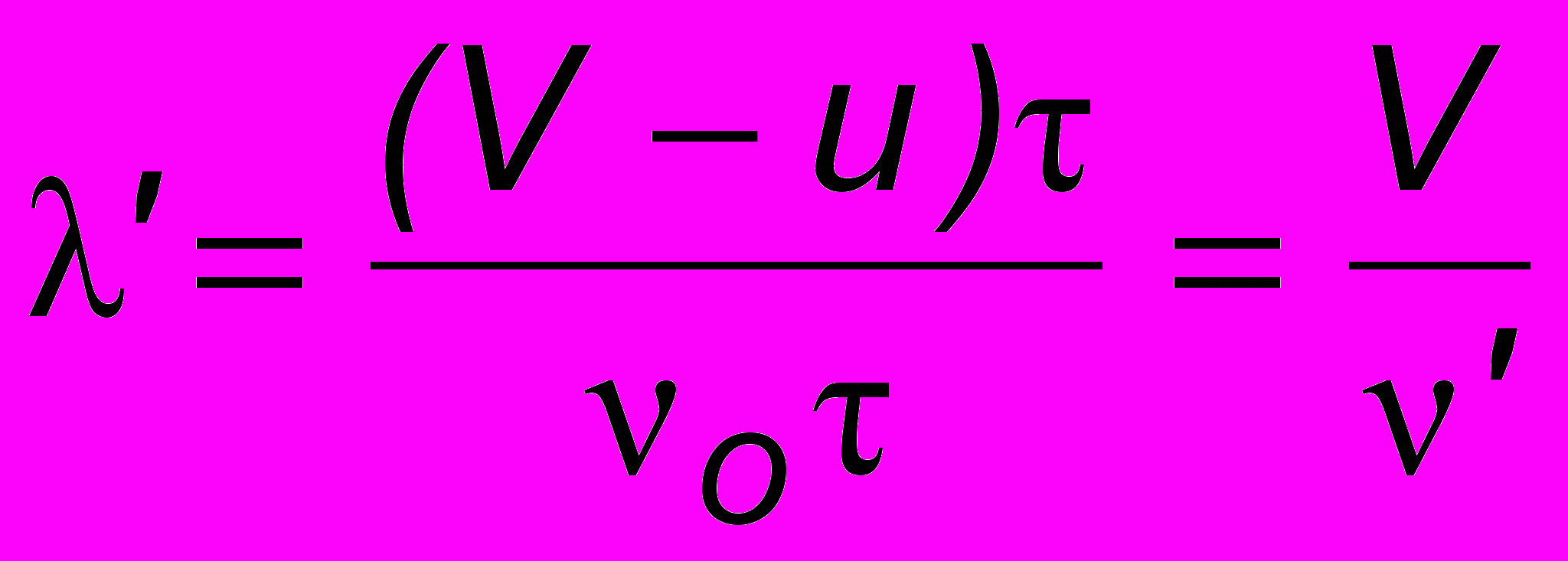 , а воспринимаемая частота
, а воспринимаемая частота 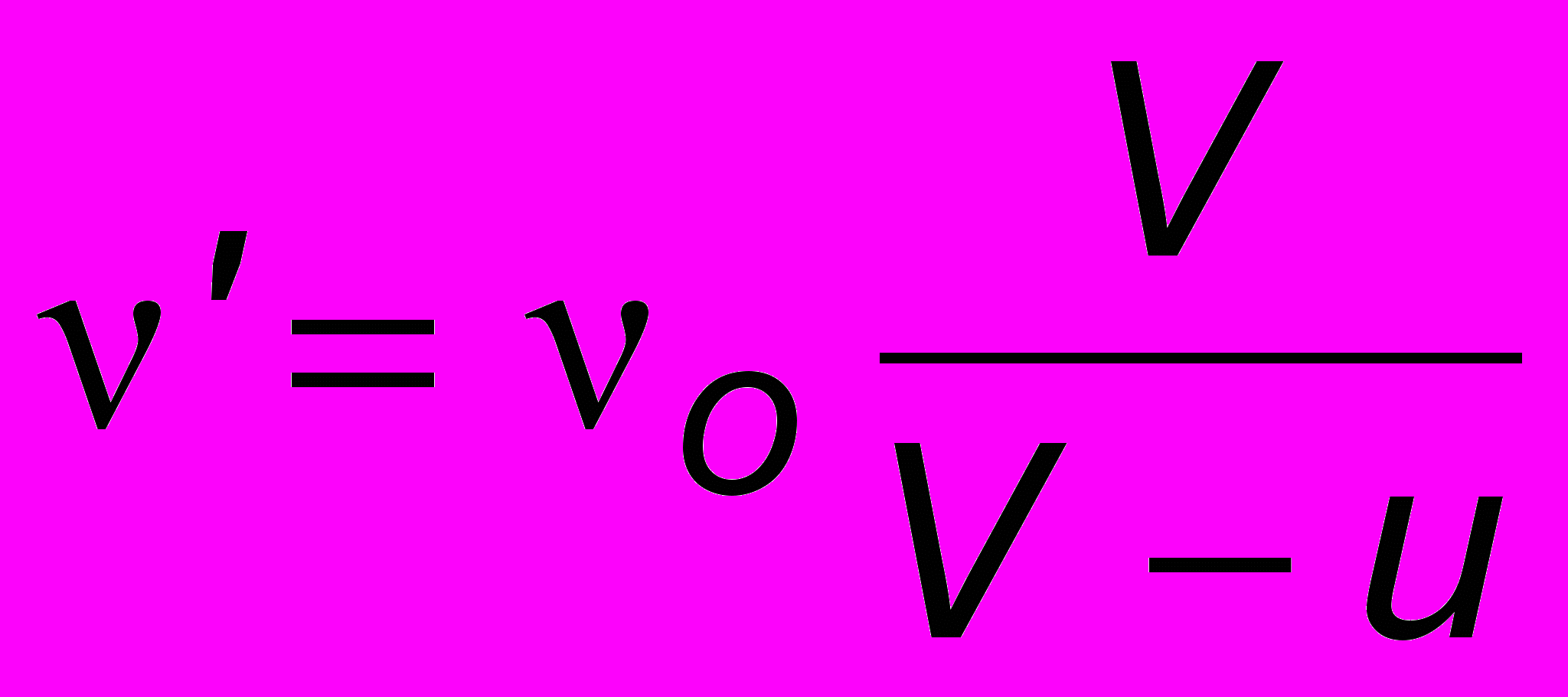 . Если же приемник еще и движется навстречу волне со скоростью
. Если же приемник еще и движется навстречу волне со скоростью 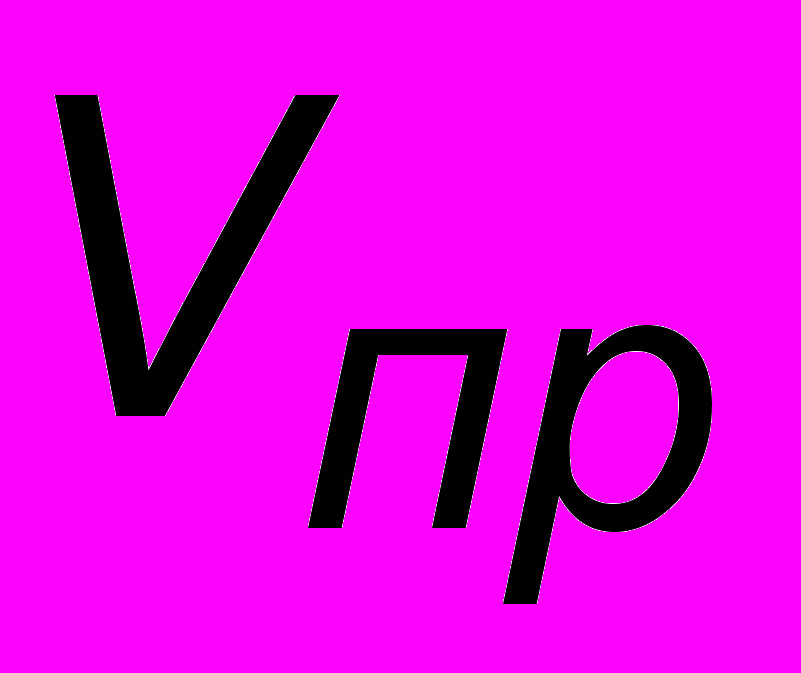 , то
, то 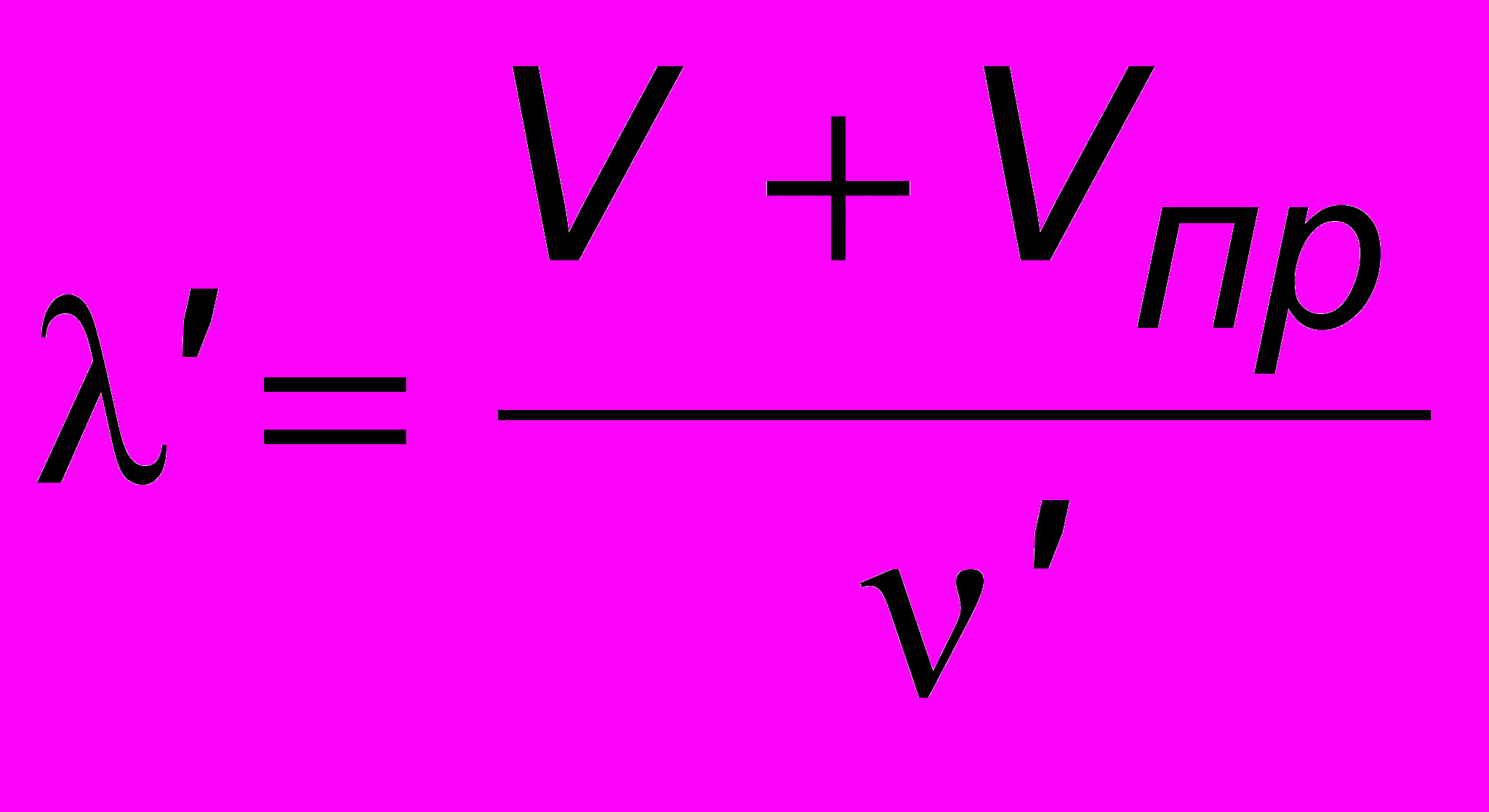 и окончательно
и окончательно . (13.2)
. (13.2)Нетрудно видеть, что эта формула исчерпывает все возможные случаи взаимного движения источника и приемника, если принять к сведению следующее правило знаков:
V > 0 - всегда;
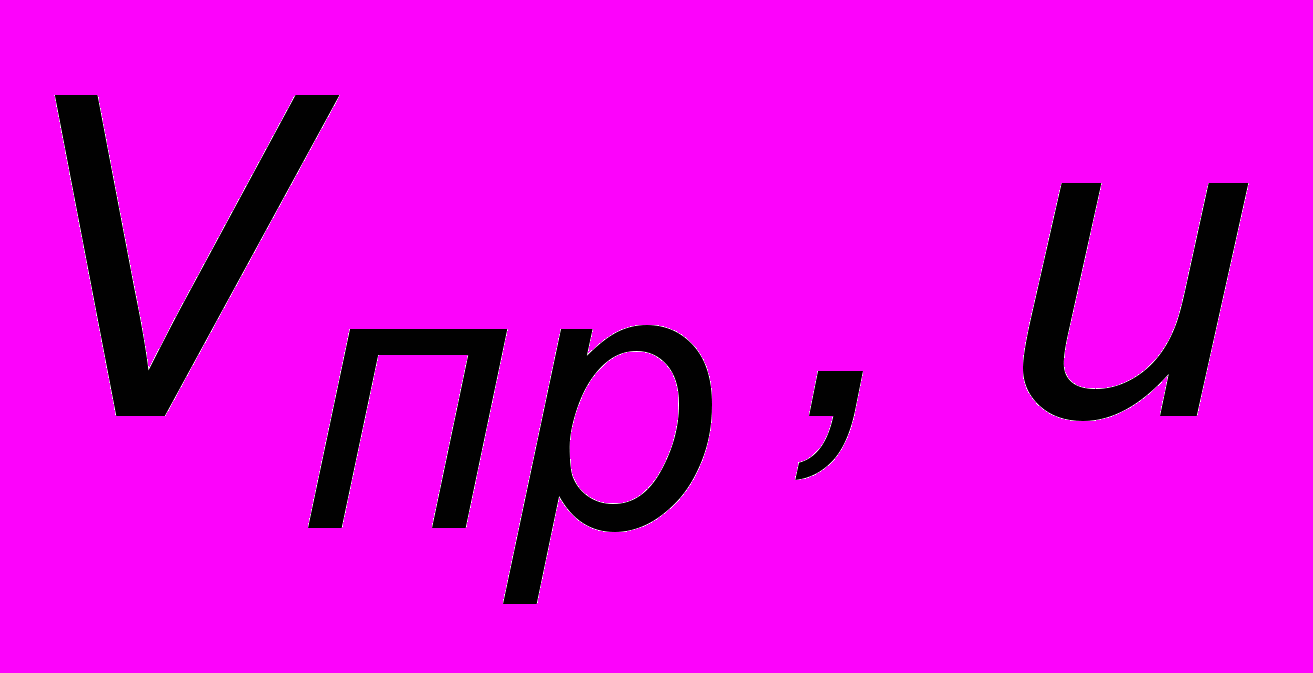 > 0 - для сближения;
> 0 - для сближения; 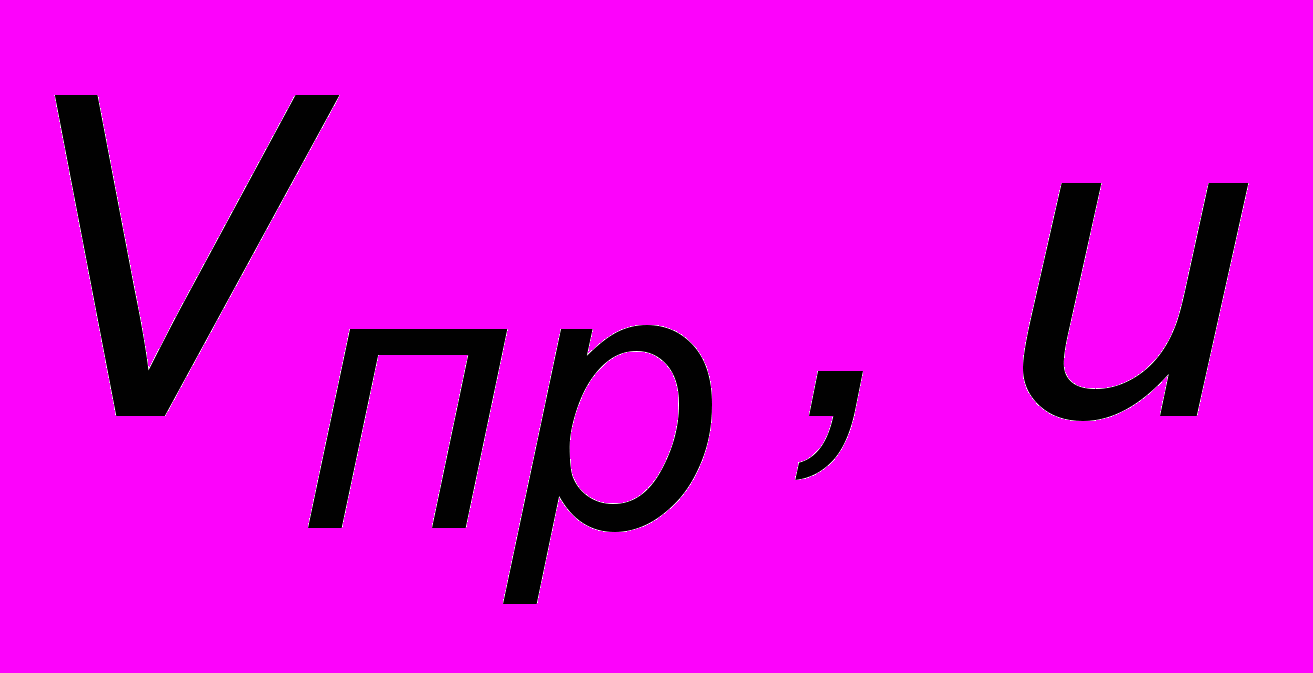 < 0 - для удаления.
< 0 - для удаления.Ударные волны Маха образуются, когда скорость источника превышает скорость звука (u > V). Как и прежде рассмотрим волновую картину через 6 с после начала колебаний. Выполняя аналогичные построения, получим картину, изображенную на рис. 13.6. Как видно из построения, получается волна, фронт которой образует увеличивающийся в размерах конус с углом раствора = arcsin (V/u). Это так называемая ударная волна Маха6. Такую волну порождает взмах хлыстом или движение самолета со сверхзвуковой скоростью. Наблюдатель при этом слышит громкий хлопок. Часто говорят, что самолет "преодолевает звуковой барьер", хотя на самом деле он мог его преодолеть вскоре после взлета и далее двигаться с постоянной скоростью u > V.
Д
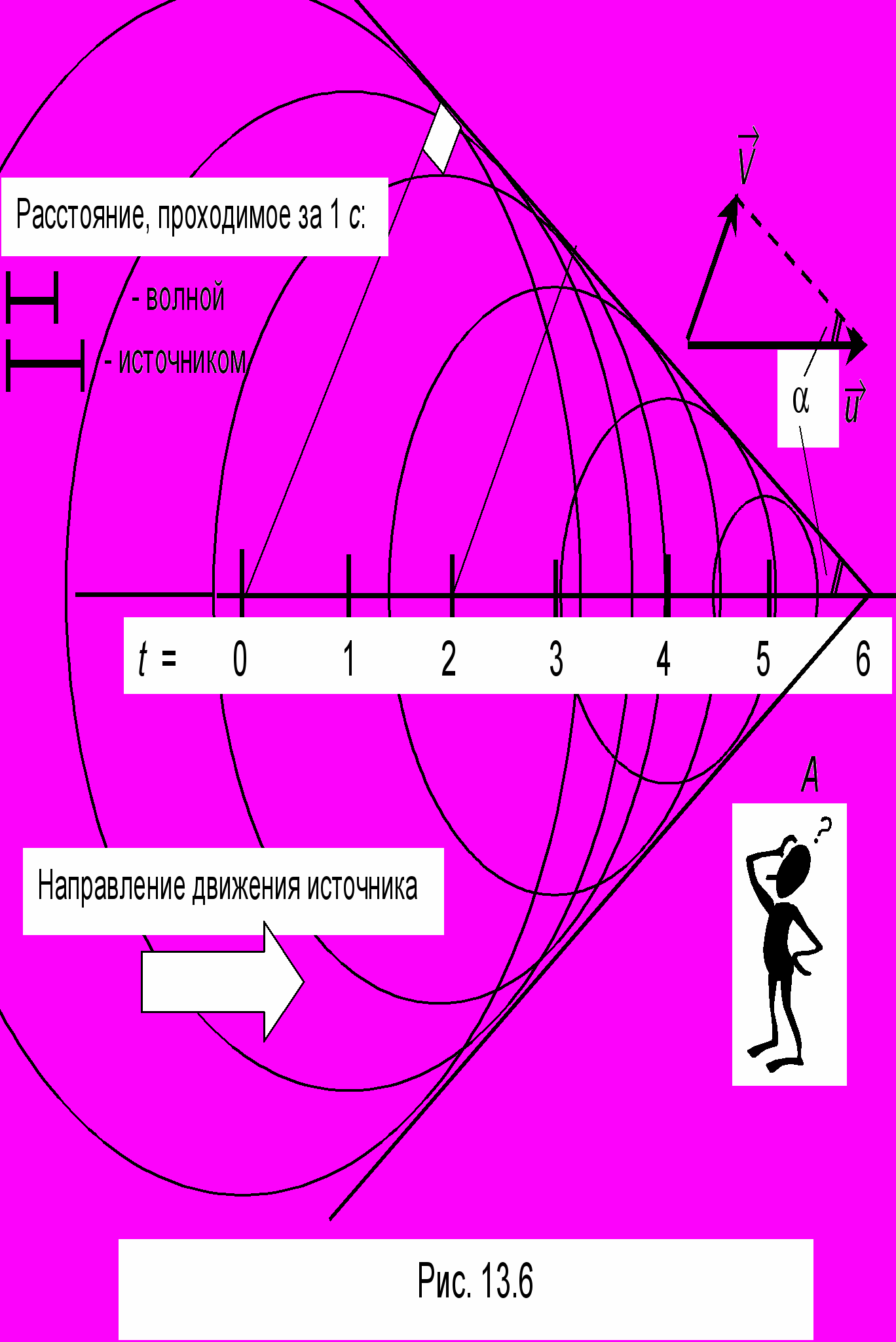
ва наблюдателя, находящиеся поодаль друг от друга услышат хлопок, естественно, в разное время - по мере достижения образующей конуса барабанных перепонок. Аналогом этой волны является поверхностная волна на воде с "треугольным" фронтом, возбуждаемая катером.
Рассмотрим теперь эффект Допплера для ЭМ волн. Так как ЭМ волны могут распространяться в пустом пространстве и, в отличие от упругих волн, не нуждаются в наличии некоей среды - эфира - то имеет смысл говорить лишь об относительной скорости U приемника по отношению к источнику (или наоборот, что одно и то же). Пусть, как и в лекции 3, часть 1, имеется условно неподвижная система К и движущаяся относительно нее равномерно со скоростью U система К', у которой ось х' скользит вдоль оси x системы K, а у = у' и х = х'
(см. рис. 1.4, часть 1). Пусть далее с системой К связан источник, посылающий плоскую волну
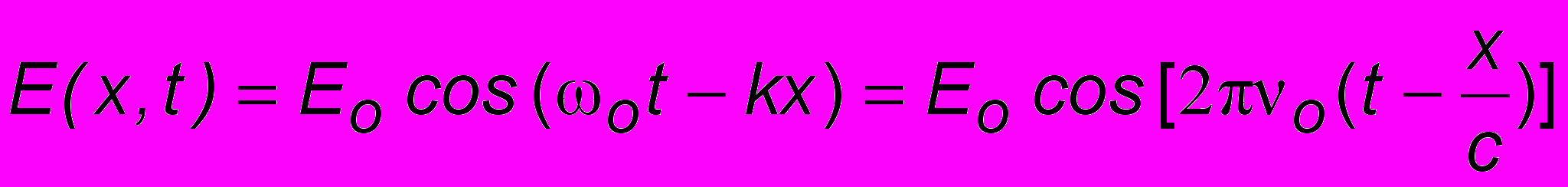 , (13.3)
, (13.3)а с К' связан приемник, воспринимающий волну
 . (13.4)
. (13.4)Подставляя в (13.3) преобразования Лоренца (3.3, часть1), имеющие вид
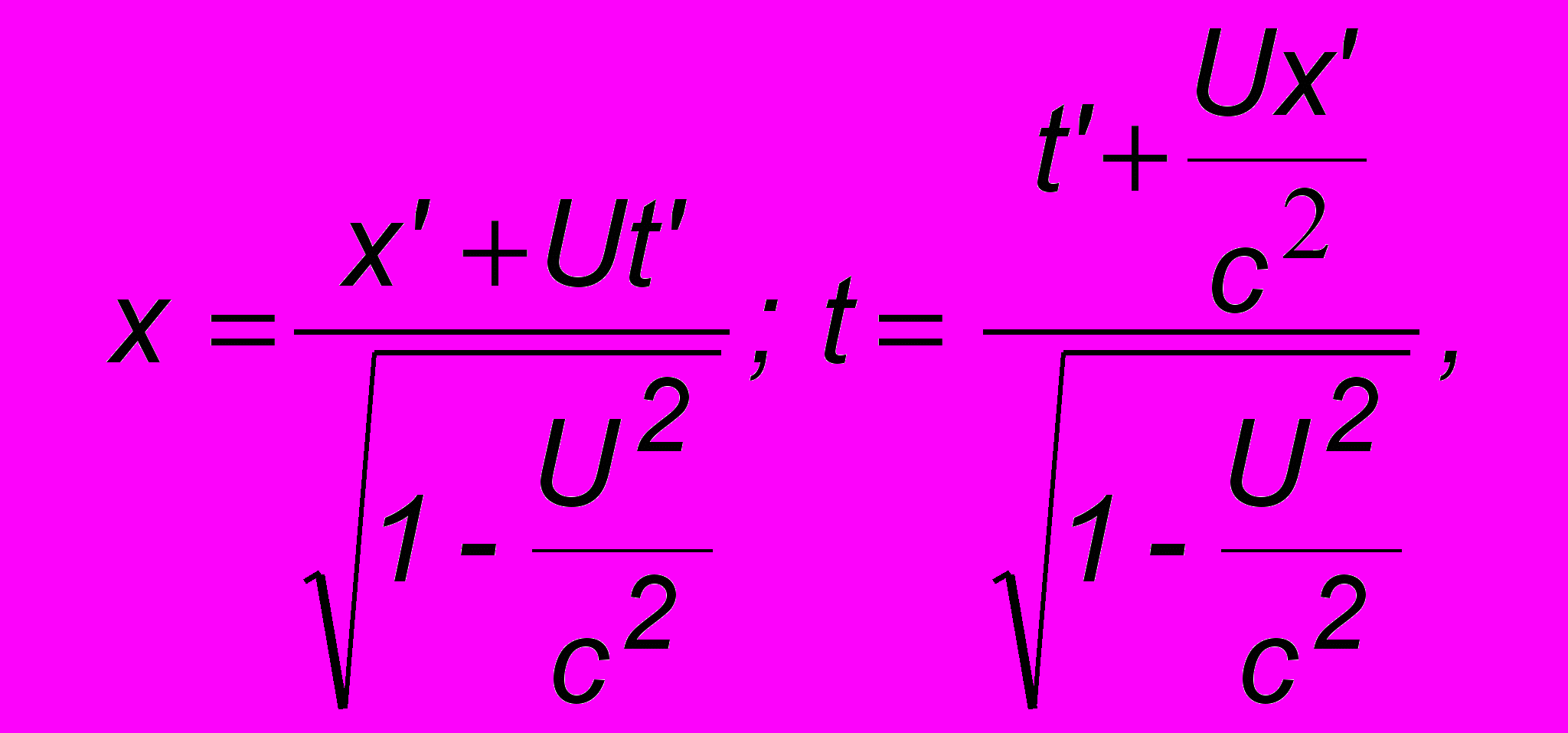 получим
получим E(x,t)
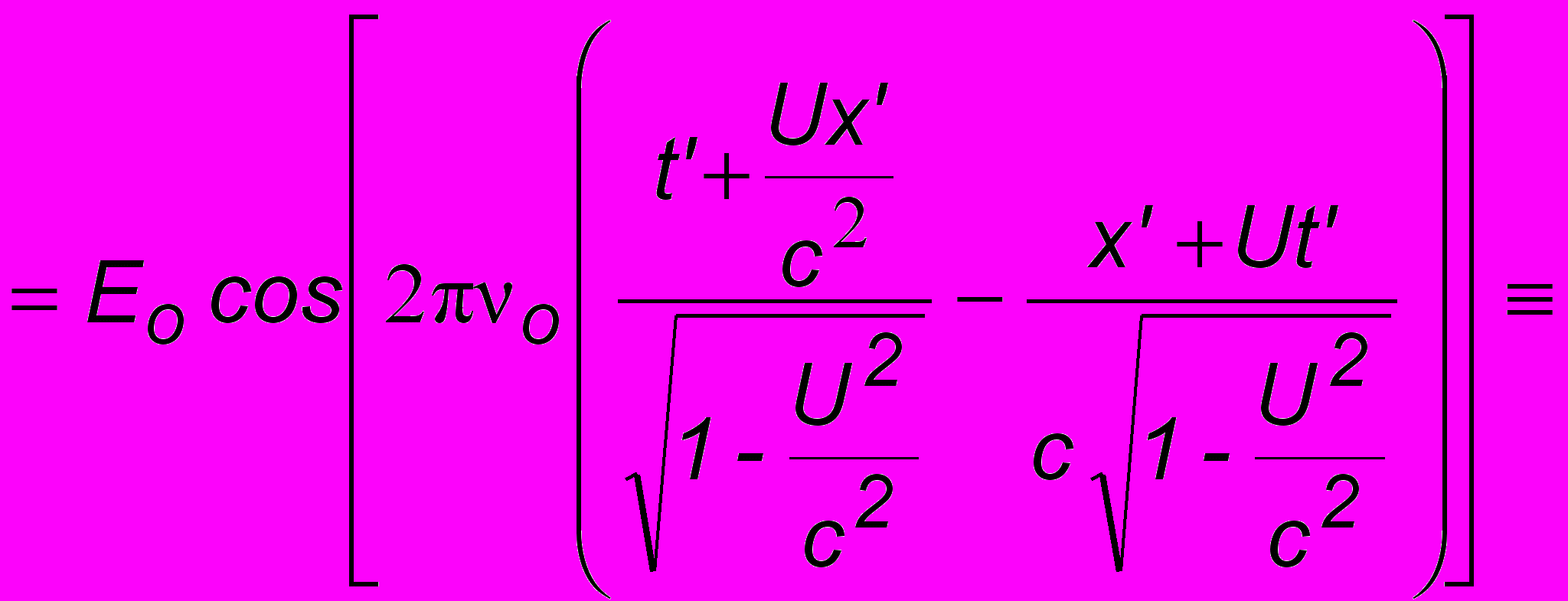
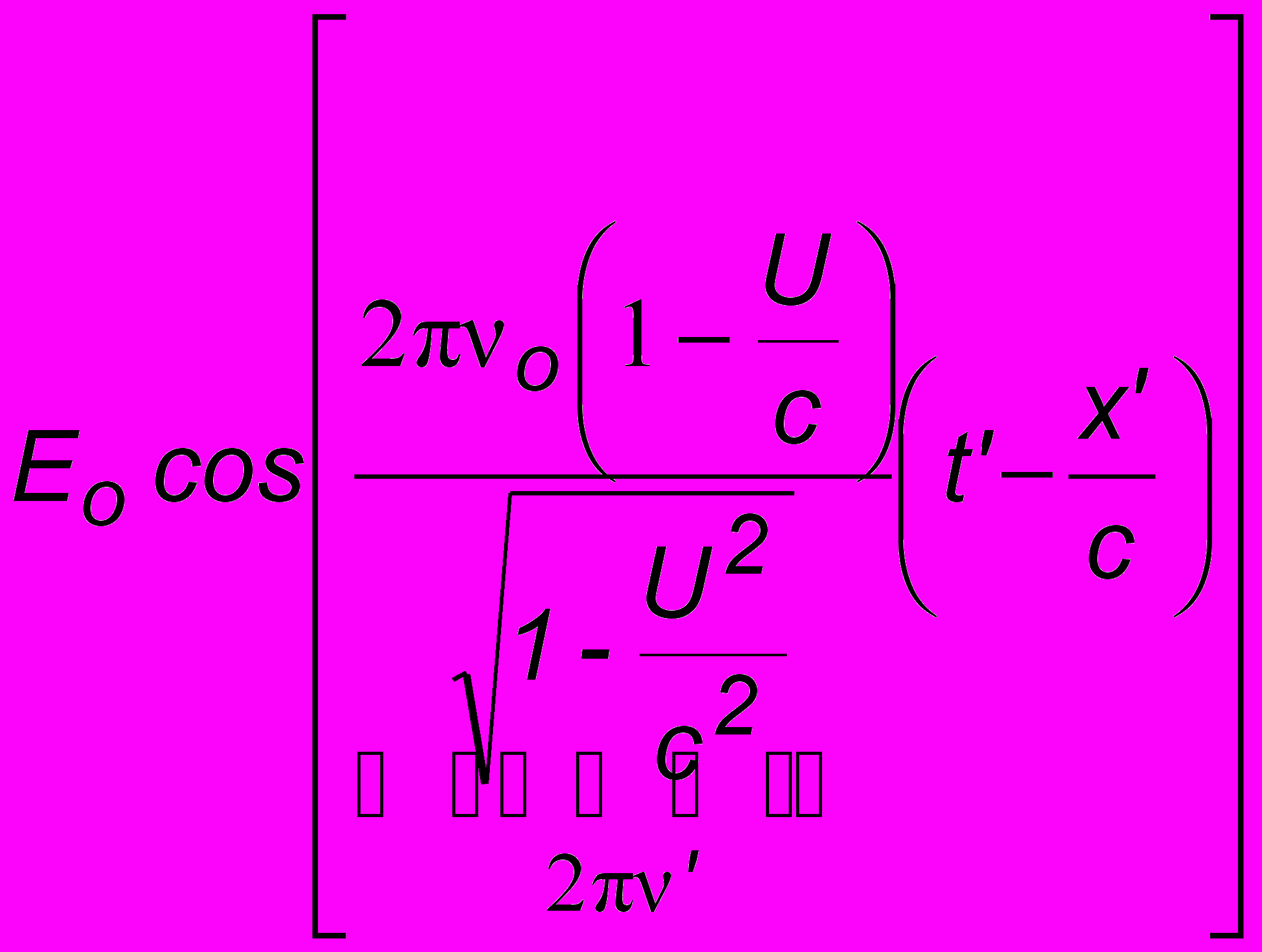 и поэтому коэффициент перед
и поэтому коэффициент перед 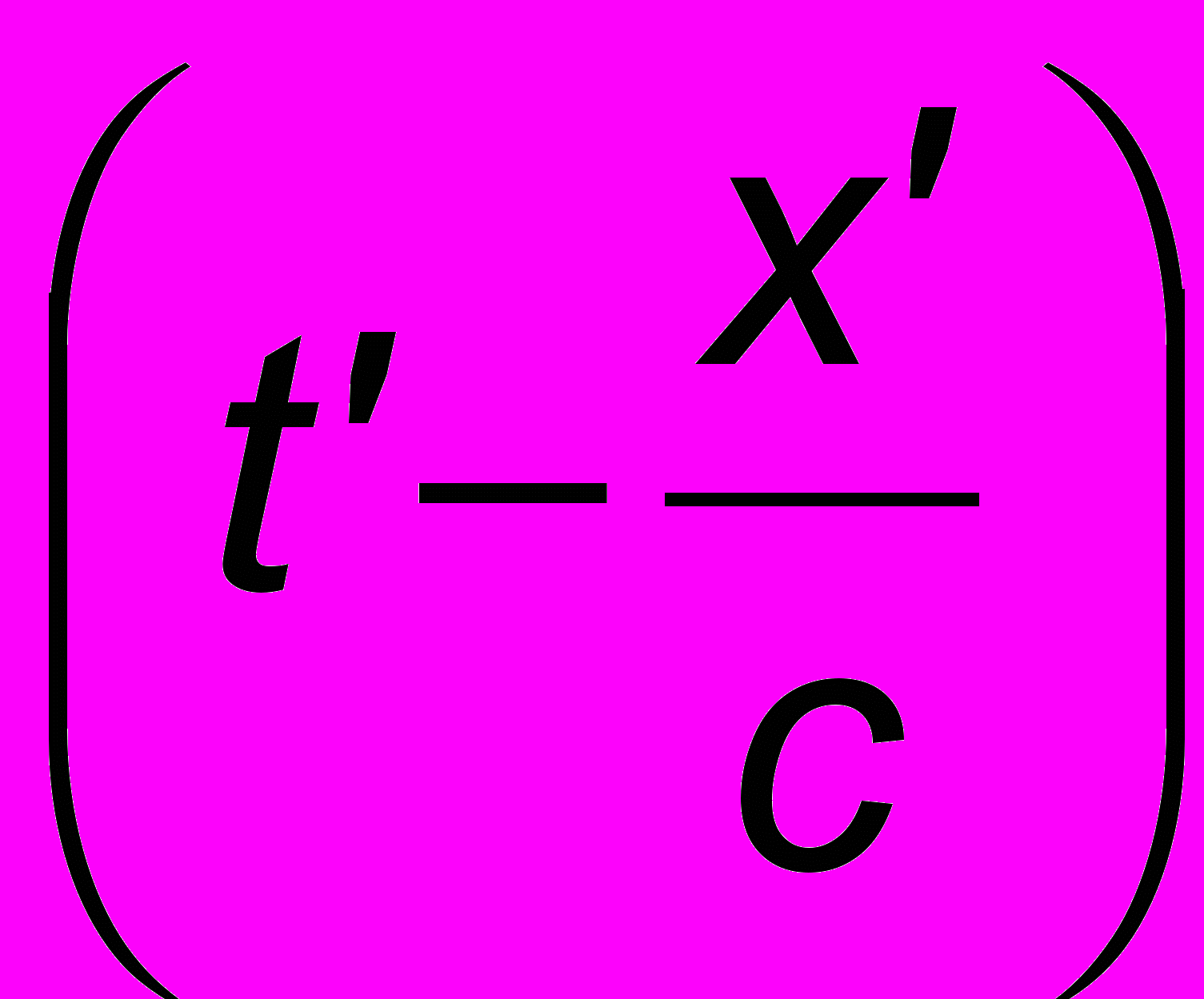 есть не что иное как круговая частота
есть не что иное как круговая частота 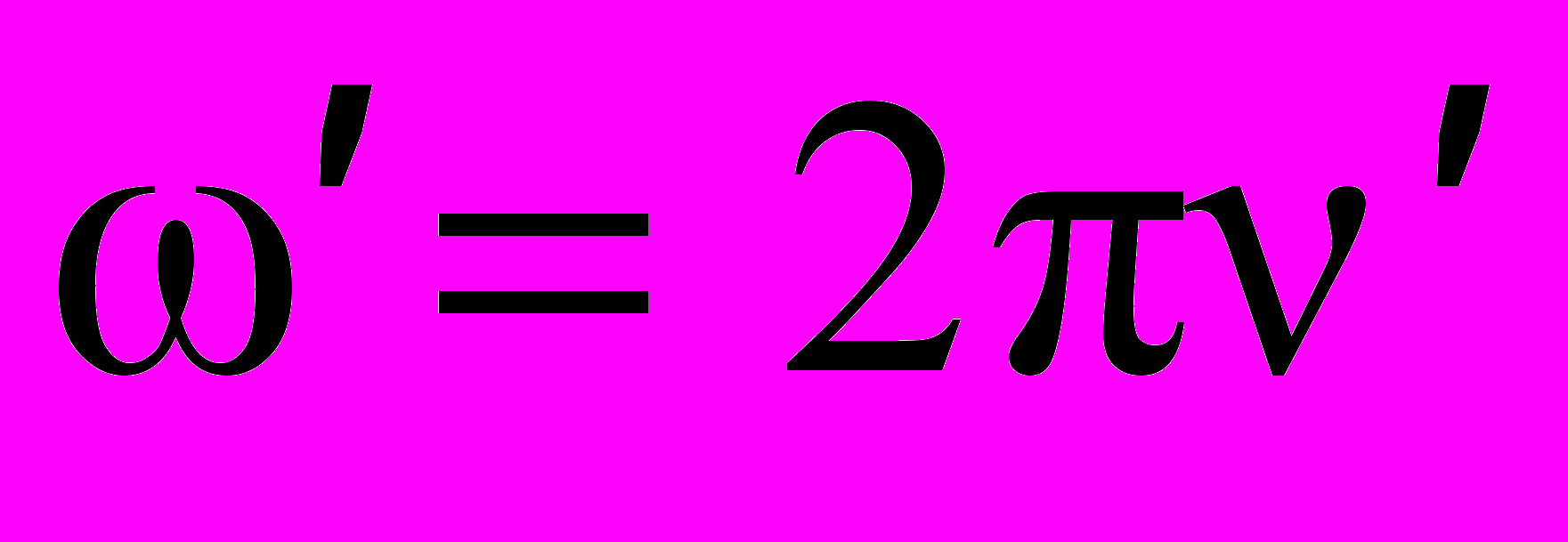 . Таким образом
. Таким образом 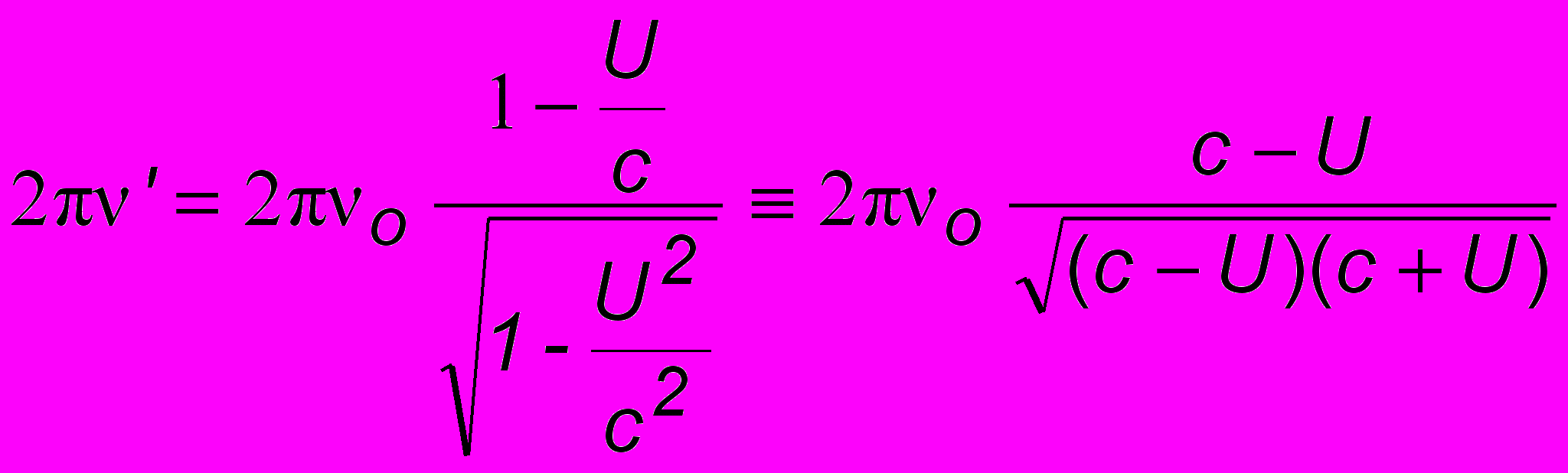
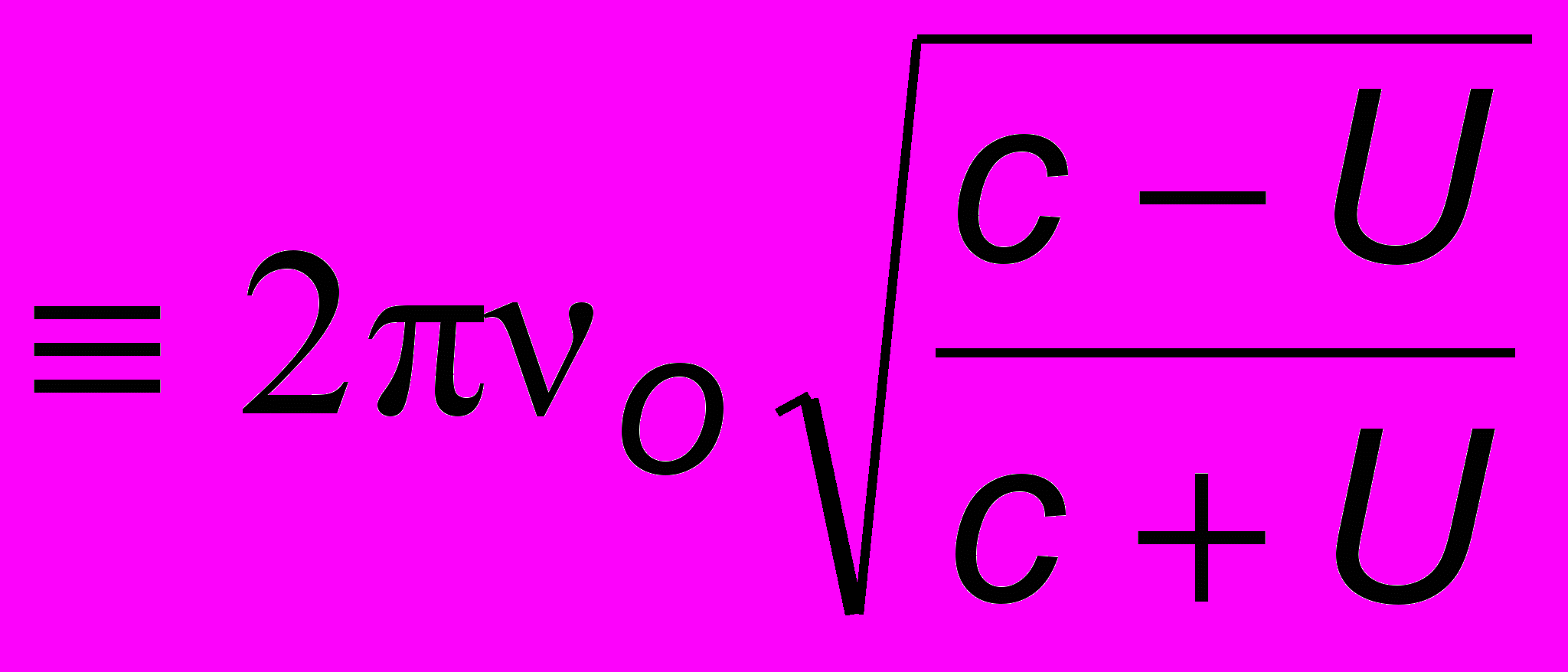 .
.При этом система K' (с неподвижным в ней приемником) удалялась от системы К (с неподвижным источником). Если считать, как ранее в акустическом случае, что U > 0 для сближения и U < 0 для удаления, то в последней формуле следует поменять U на (-U). Окончательно
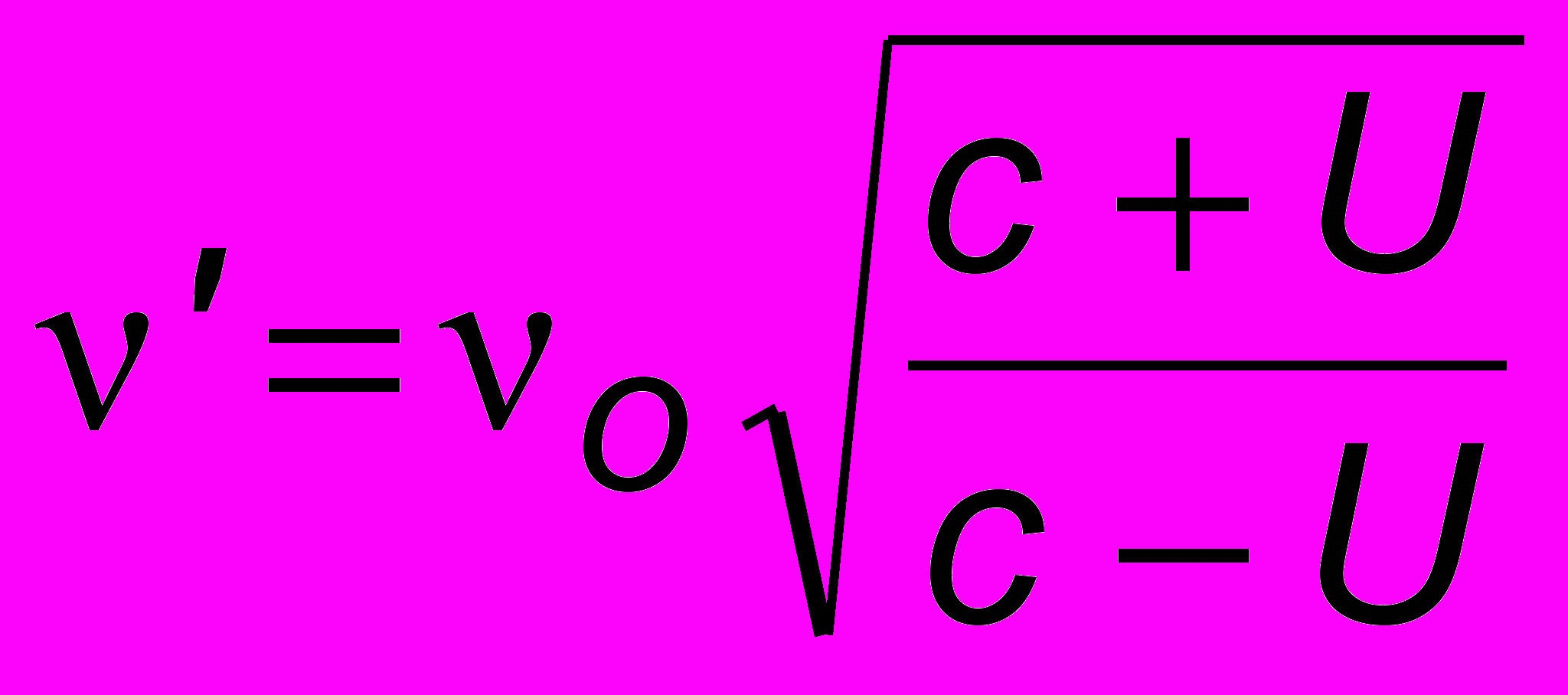 . (13.5)
. (13.5)Анализ линий спектра излучения удаленных космических объектов показывает, что положение этих линий сдвинуто в сторону бóльших длин волн. Явление это называют красным смещением. По-видимому, оно подтверждает гипотезу Фридмана7 о расширяющейся Вселенной. Согласно этой гипотезе, Вселенная образовалась в результате большого взрыва, и находится в состоянии расширения, которое затем должно смениться сжатием. Если такое расширение имеет в настоящий момент место, то удаление излучающего объекта (например, звезды Альфа Центавра) от наблюдателя будет сопровождаться уменьшением частоты (увеличением длины волны) в соответствии с (13.5).
Эффект Допплера обусловливает естественную ширину спектральных линий. В самом деле, неподвижная молекула должна была бы излучать узкую спектральную линию частоты О. Однако молекулы совершают хаотическое тепловое движение с некоторой средней тепловой скоростью U относительно спектрографа, который здесь играет роль приемника. Поскольку при хаотическом движении молекулы все направления равновероятны, то с одинаковой вероятностью она может двигаться как от спектрографа, так и по направлению к нему. Поэтому в (13.5) перед U возможны оба знака. Таким образом, ширина спектральной линии, зарегистрированной спектрографом, определится интервалом
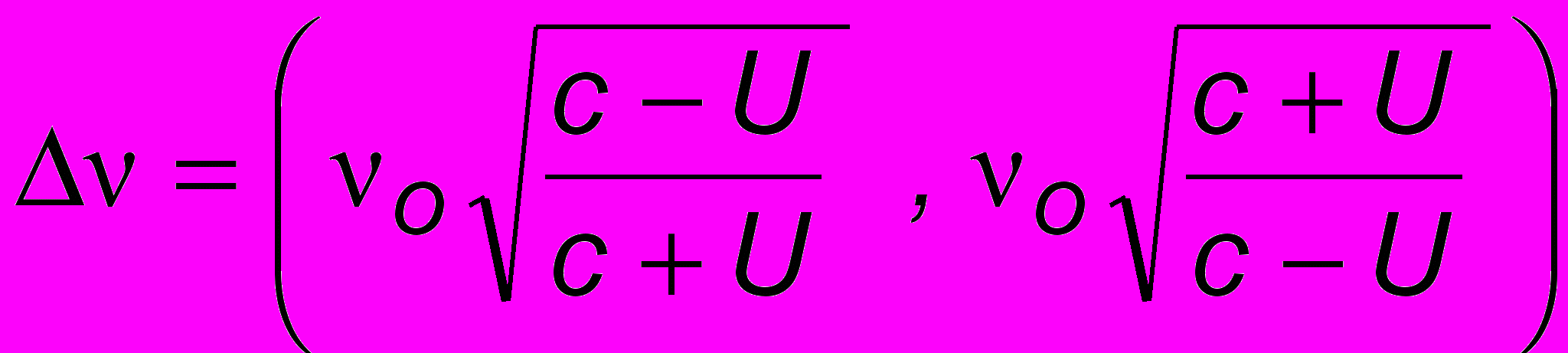 , обусловливающим допплеровское уширение спектральной линии О. Таким образом, наличие допплеровского уширения обусловливает принципиальный естественный предел совершенствованию спектрометрической техники, преодолеть который невозможно никаким повышением качества проектируемых инженерных приборов.
, обусловливающим допплеровское уширение спектральной линии О. Таким образом, наличие допплеровского уширения обусловливает принципиальный естественный предел совершенствованию спектрометрической техники, преодолеть который невозможно никаким повышением качества проектируемых инженерных приборов.Эффект Допплера используется в арсенале ГИБДД в приборе для определения скорости U движущегося автомобиля. В этом случае U/c << 1. Представим корень в (13.5) как
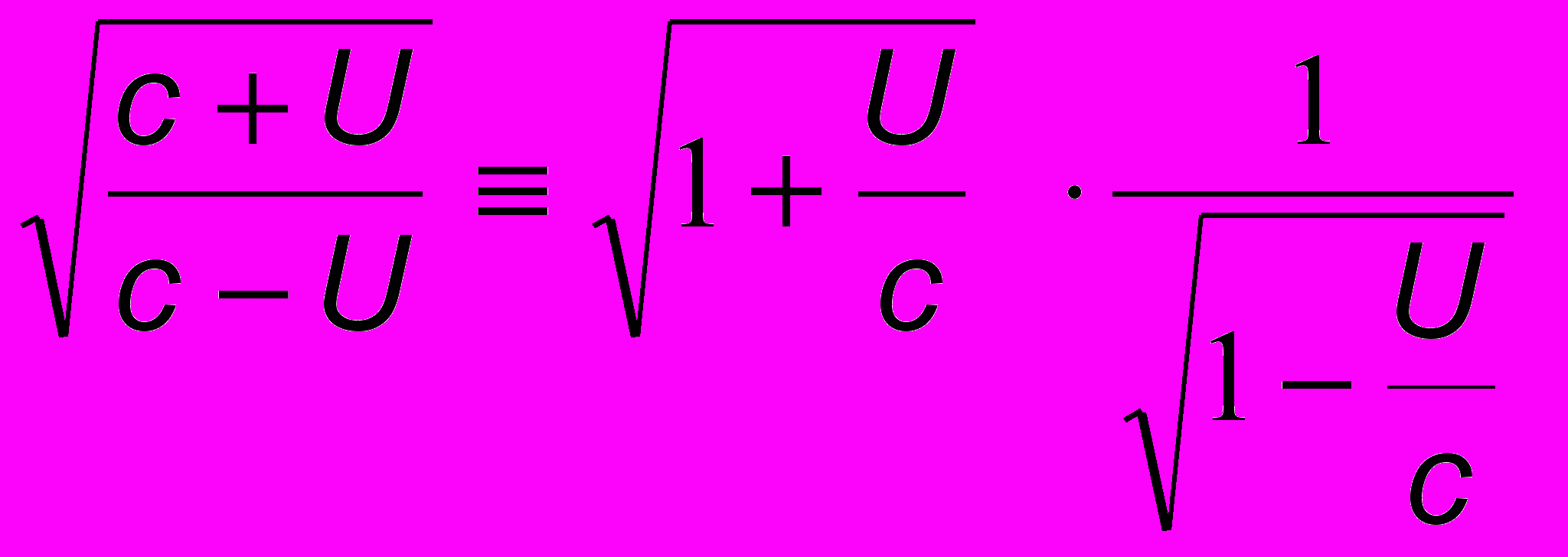
и воспользуемся разложениями в ряд по
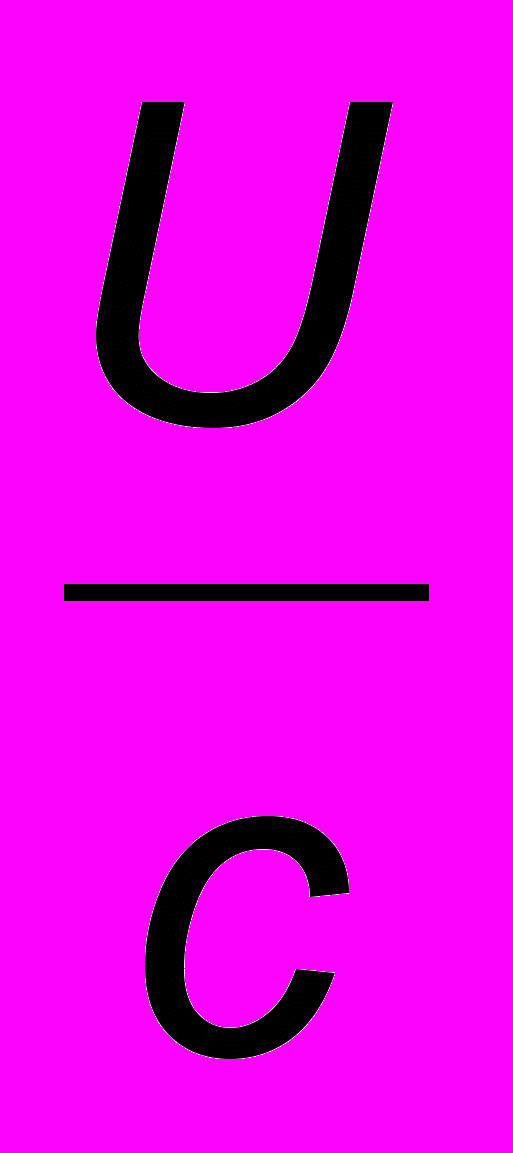 :
: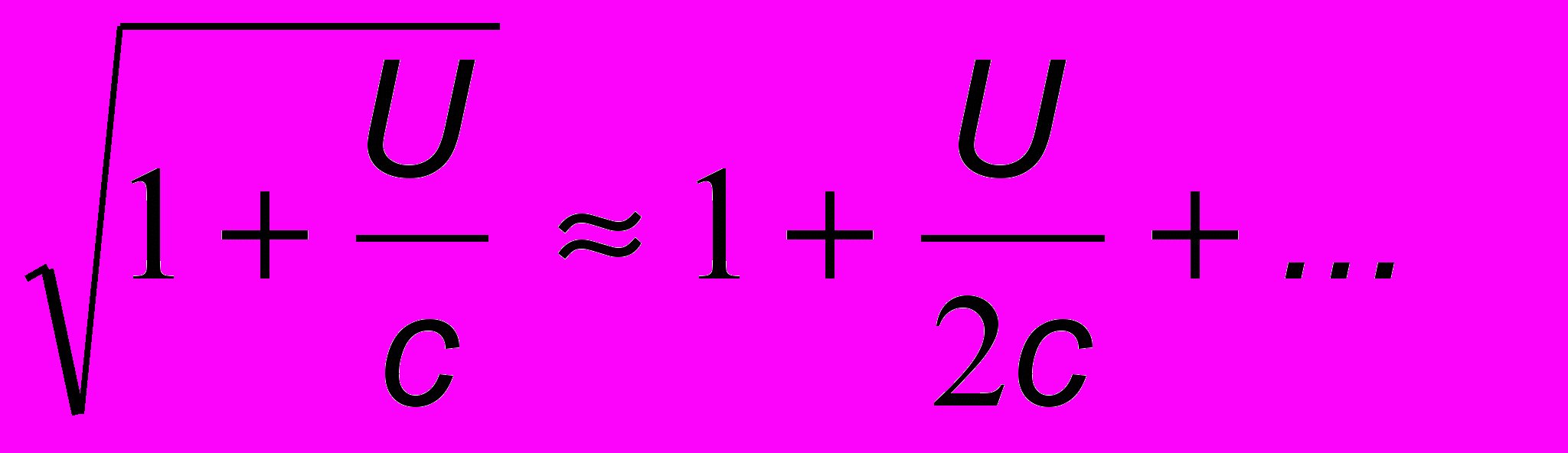 и
и 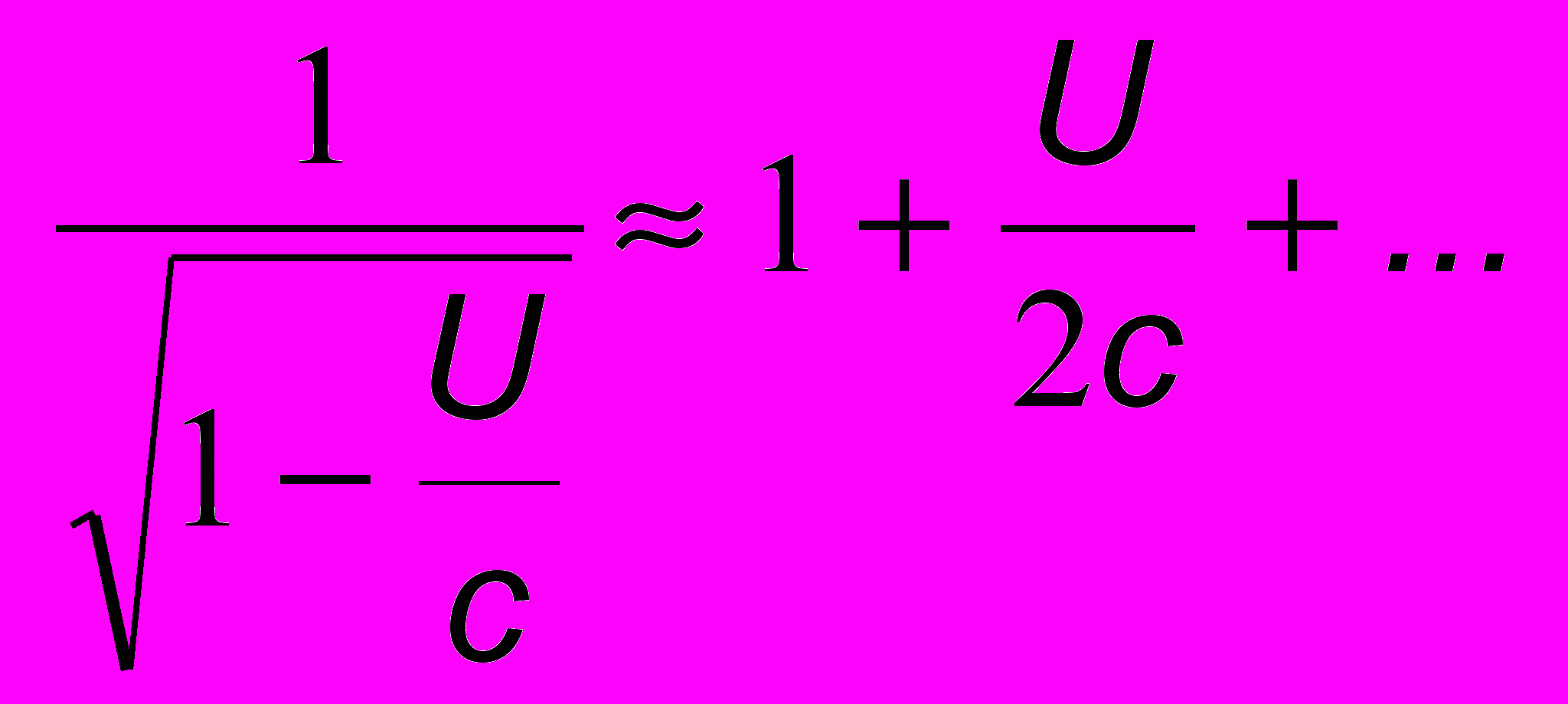 . Только первые два слагаемых в этих разложениях одинаковы. Остальные, которые отличаются друг от друга, - меньшего порядка, и мы их отбрасываем. Поэтому для малых U получим для частоты ’ , воспринимаемой водителем, значение
. Только первые два слагаемых в этих разложениях одинаковы. Остальные, которые отличаются друг от друга, - меньшего порядка, и мы их отбрасываем. Поэтому для малых U получим для частоты ’ , воспринимаемой водителем, значение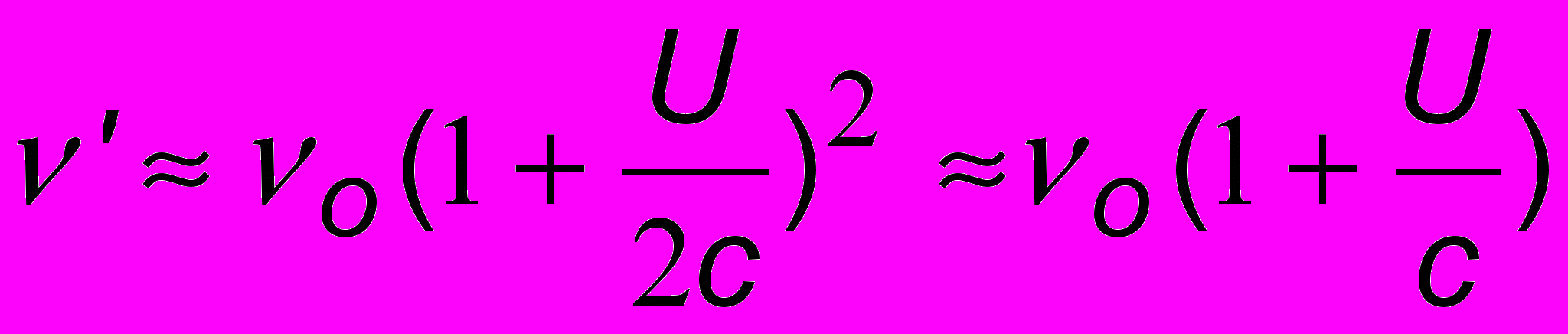 . (13.6)
. (13.6)Сигнал этой частоты отражается назад к сотруднику ГИБДД и воспринимается его радаром как сигнал, идущий от движущегося источника – автомобиля. Воспринимаемая гаишником частота ” опять-таки определится формулой (13.6), где вместо о надо теперь подставить ’. Поэтому
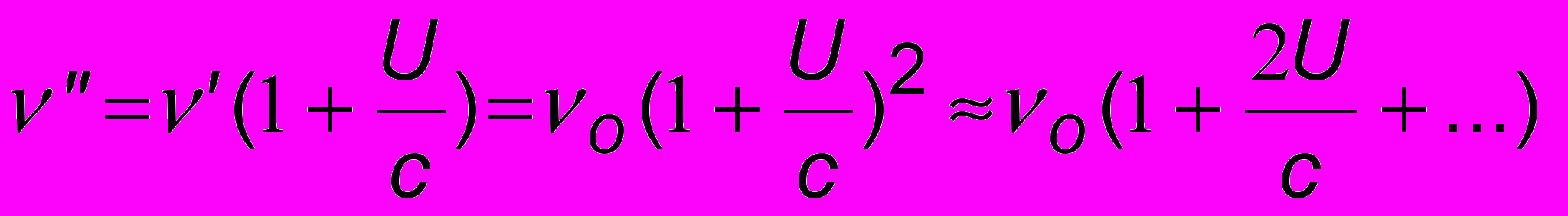 .
.Для нахождения скорости автомобиля (рис. 13.7) используется радар, излучающий электромагнитные волны длины О = 3 см (О = с/ = 1010 Гц). Радар одновременно является и источником, посылающим излучение частоты О, и приемником, регистрирующим отраженное излучение частоты ”. К
 ак следует из последнего соотношения, разность частот посланного и принятого сигнала = ”-O = 2OU/c, отсюда U = c /(2O). В результате взаимодействия коллинеарных колебаний с близкими частотами ” и O возникнут биения с частотой (см. ЛЕКЦИЮ 4). Современные, не слишком дорогие приборы, которыми оснащены службы ГИБДД, способны обнаружить биения с частотой не менее 100 Гц. Таким образом, минимально возможная обнаружимая скорость равна
ак следует из последнего соотношения, разность частот посланного и принятого сигнала = ”-O = 2OU/c, отсюда U = c /(2O). В результате взаимодействия коллинеарных колебаний с близкими частотами ” и O возникнут биения с частотой (см. ЛЕКЦИЮ 4). Современные, не слишком дорогие приборы, которыми оснащены службы ГИБДД, способны обнаружить биения с частотой не менее 100 Гц. Таким образом, минимально возможная обнаружимая скорость равна 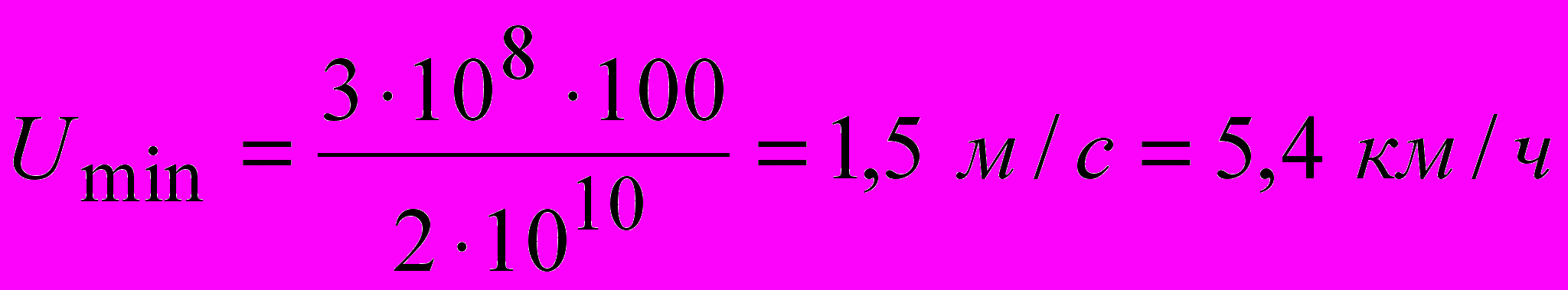 .
.1 Флажолет на гитаре удается лишь хорошим музыкантам. На скрипке - совсем наоборот.
2 К сожалению, в нумерации гармоник существует путаница. Иногда основную частоту называют первой гармоникой, первую гармонику - второй и т.д.
3 Родным городом Х. Допплера, как и В. Моцарта, является австрийский Зальцбург.
4 Будем помнить, что звук в воздухе - продольные волны, и аналогию с профилем поперечной волны ("горб") мы здесь используем ради наглядности.
5 Радиусы трех только что рассмотренных сфер показаны на рис. 13.5 стрелками.
6 Э. Мах (1838-1916) - выдающийся австрийский физик, подвергшийся за субъективный идеализм беспощадному разгрому в главном философском произведении В.И. Ленина "Материализм и эмпириокритицизм" (см. любое издание). Его теория ударных волн не входила в советские учебные программы и рассматривалась лишь в спецкурсах без ссылки на первоисточник.
7 А.А.Фридман (1888-1925) - советский физик, впервые выдвинувший гипотезу о расширяющейся вселенной. Американский астроном Хаббл дополнил гипотезу идеей о начальном большом взрыве (Big Bang).
