Учебное пособие для учащихся «Русский язык 10-11 классы» Д. Э. Розенталь, М., «Дрофа», 2000 г. Тип программы

Вид материала

Учебное пособие

Содержание Контрольная работа N1. Геометрия” учебник для 10 – 11 кл. общеобразовательных учреждении, авторы: Атанасян Л.С. и др., М., “Просвещение” 2000г. Глава I. Параллельность прямых и плоскостей. Глава II. Глава III. Глава IV. 2 . Учебное пособие для учащихся: Учебник: Химия 10 кл, О.С. Габриелян. Изд. «Дрофа». Тип программы: базовый

Подобный материал:

• Мустаева Составитель Мустаева Е. С., учитель русского языка и литературы мноу «Гимназия, 218.38kb.
• Рабочая учебная программа учебного предмета русский язык, 855.15kb.
• Программа по русскому языку. 5-9 классы*, 534.27kb.
• Черниковой Маргариты Владимировны по учебному курсу «Русский язык» 8 класс Базовый, 149.53kb.
• И. В. Абрамова Учебная рабочая программа, 715.44kb.
• Соловьева Ирина Алексеевна 2010- 2011 уч год пояснительная записка, 1237.62kb.
• Пояснительная записка, 1088.13kb.
• Синтаксис словосочетания и простого предложения, 821.61kb.
• Примерные программы отдельных учебных предметов Часть 1: 5-6 классы Русский язык, 3749.51kb.
• Название ресурса, 21.54kb.

Контрольная работа N1.


1. Вычислите без таблиц и калькулятора:

а) cos 390°; б) tg; в) sin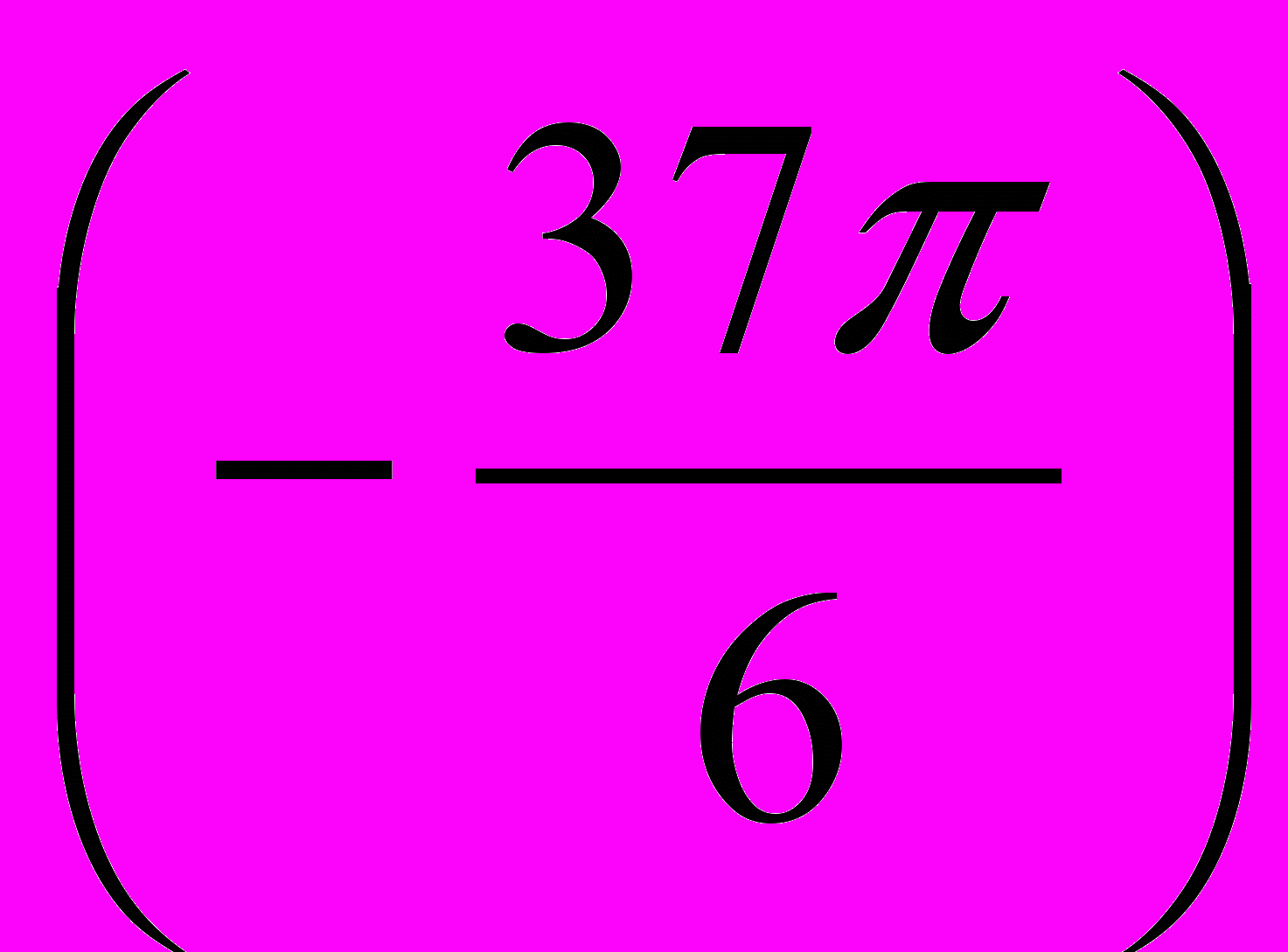

2. Дано: cos=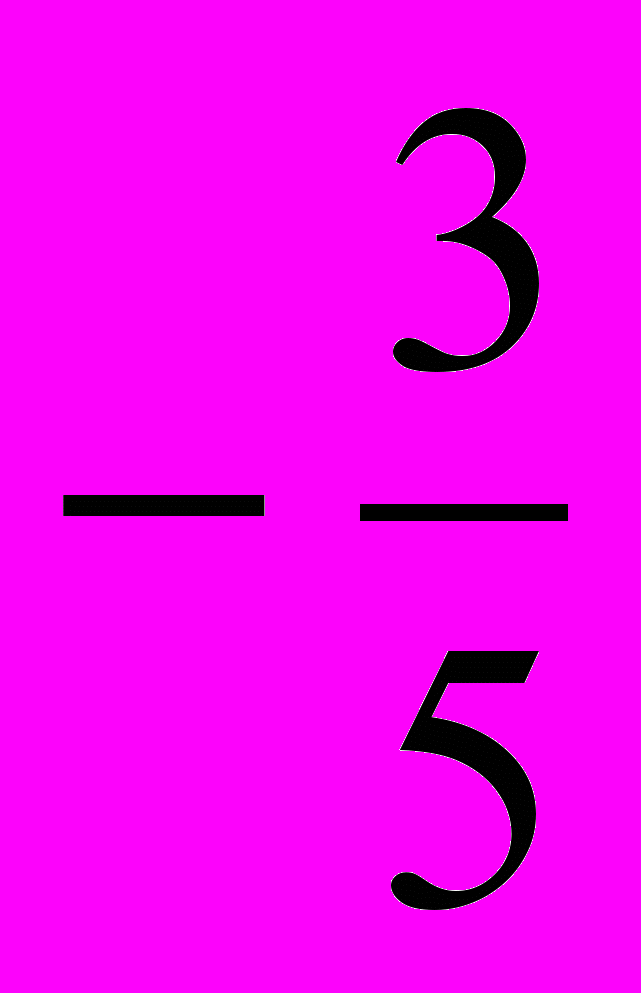, 90º<<180º. Найдите

а) sin; б) sin 2; в) cos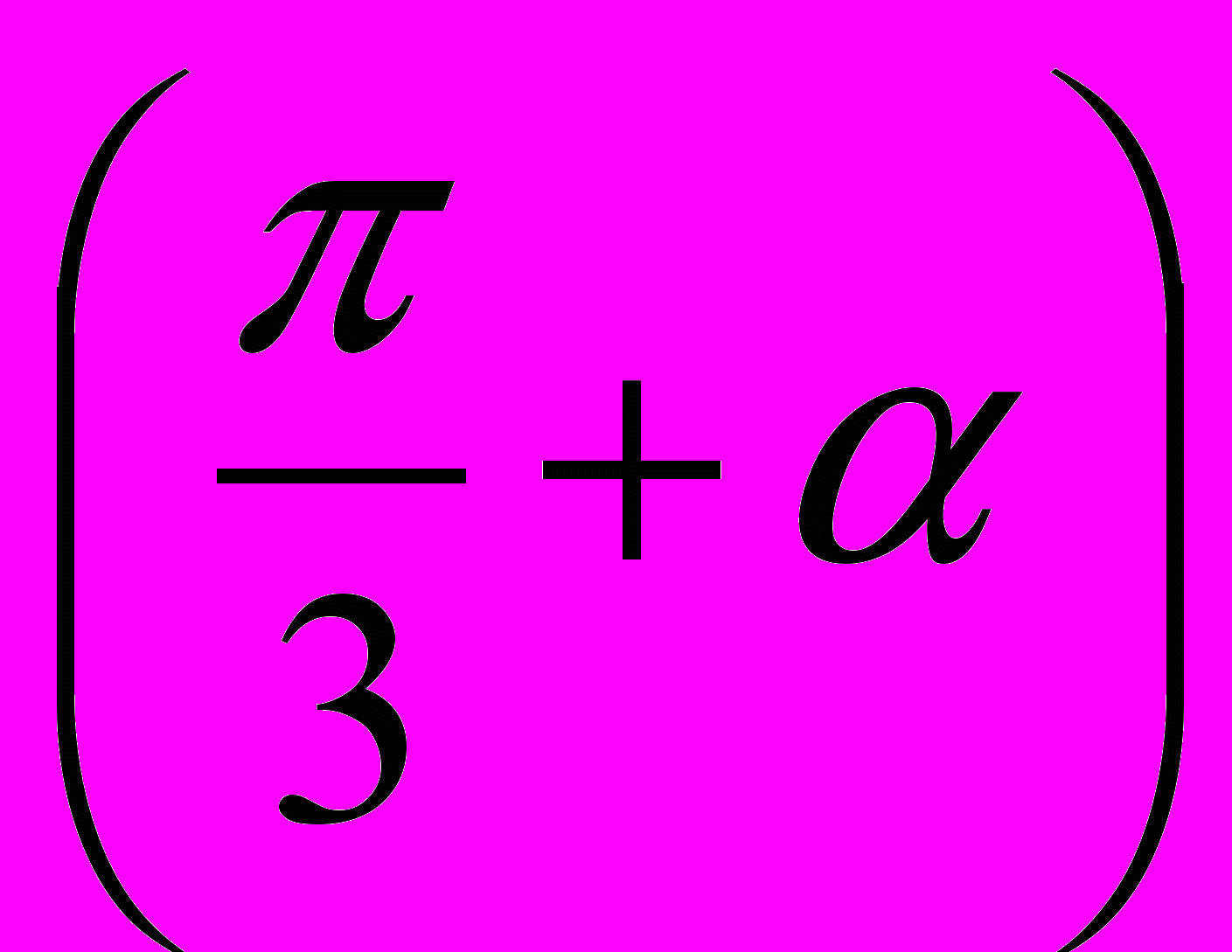

3. Докажите тождество

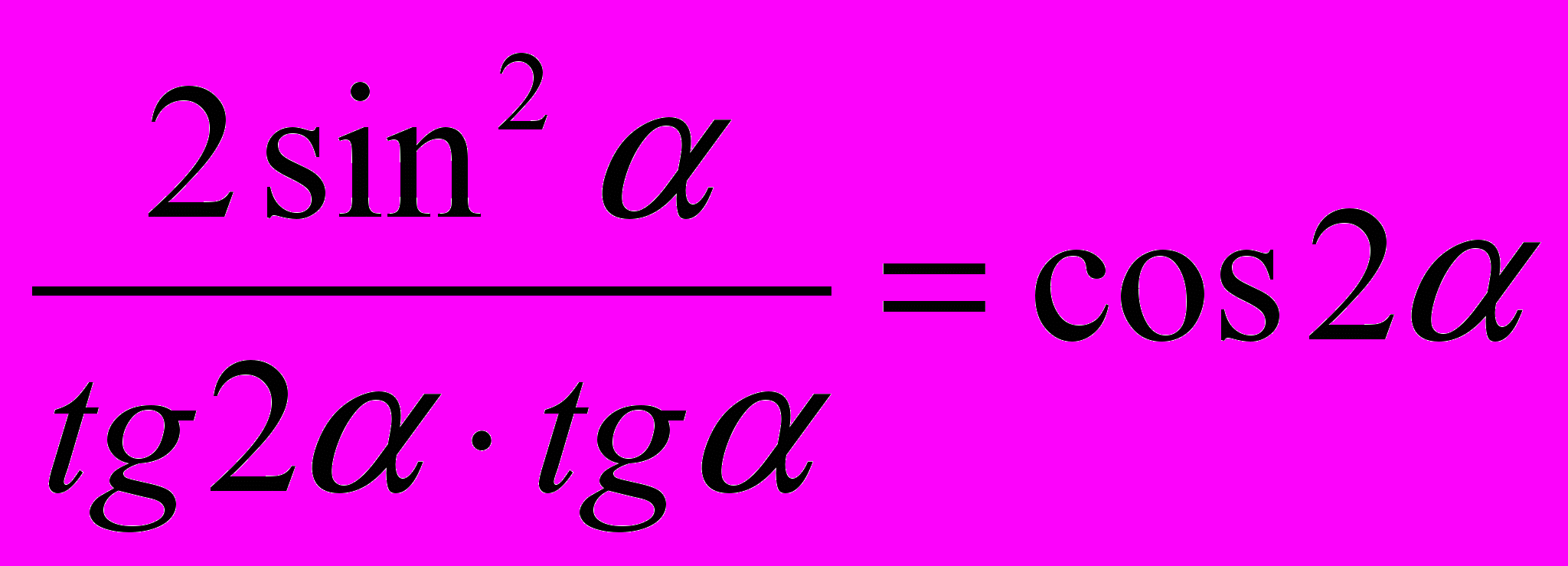
4. Вычислите


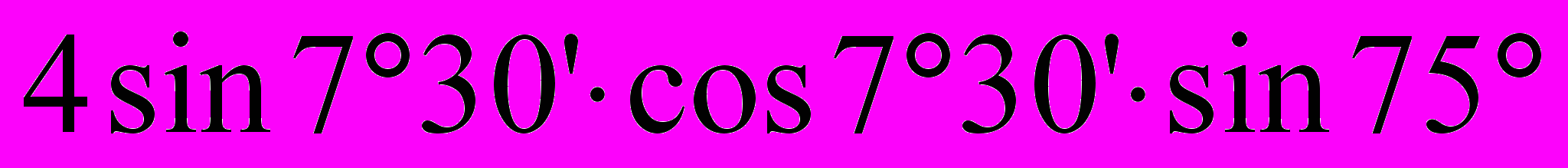
Контрольная работа N2.

1. По графику функции:
   

а) найдите область определения и область значений функции;

б) укажите точки пересечения графика с осью Ох и осью Оу;

в) укажите промежутки знакопостоянства функции;

г) укажите промежутки возрастания и убывания функции;

д) найдите точки максимума и минимума;

е) укажите максимум и минимум функции;

ж) выясните, четная или нечетная функция.








1

О

- 6 - 4 - 1 1 4 6


2. Докажите, что функция f(x) = 2x⁴ + 3cosx является четной

3. Укажите область определения функции
   
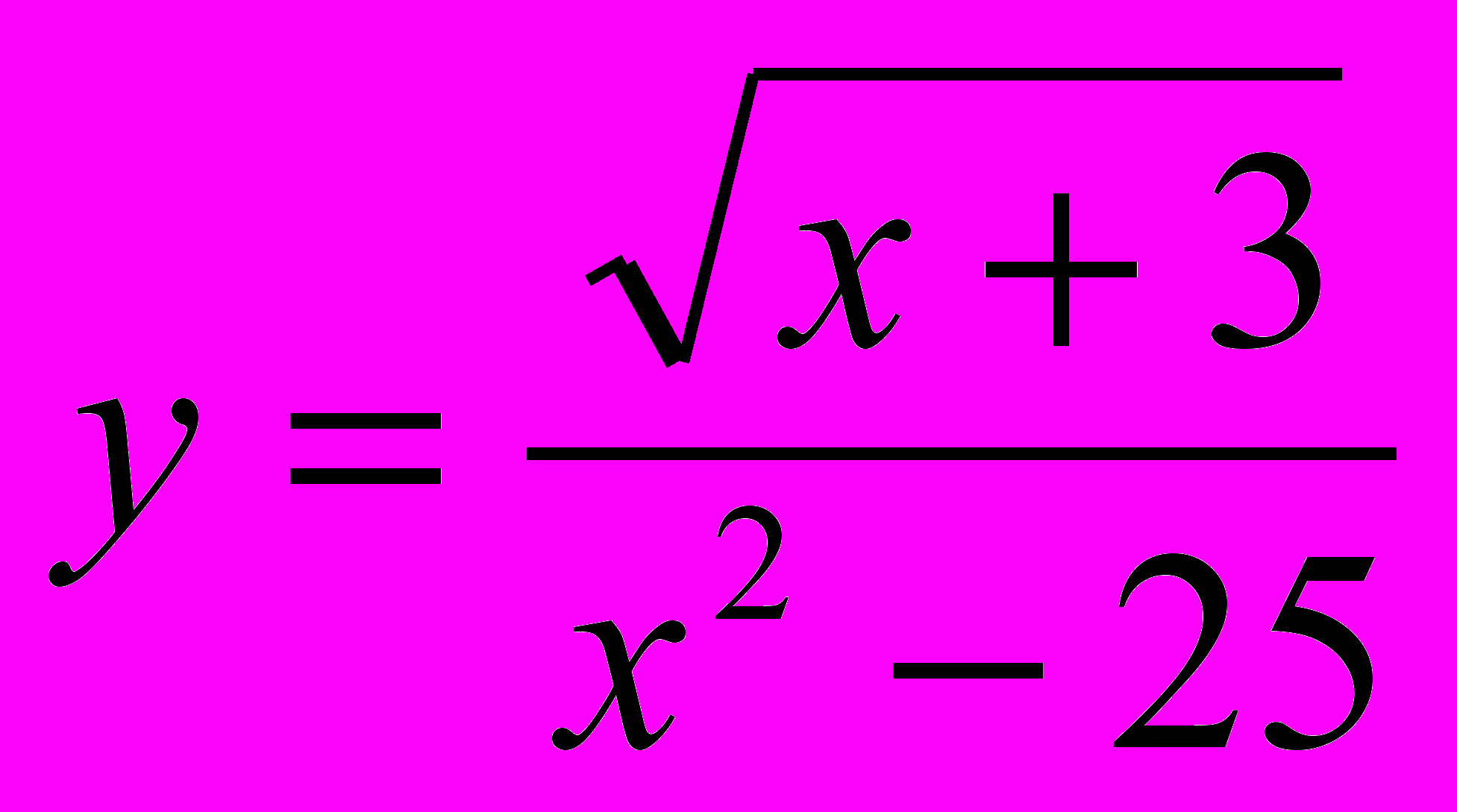
4. Укажите область определения и область значений функции 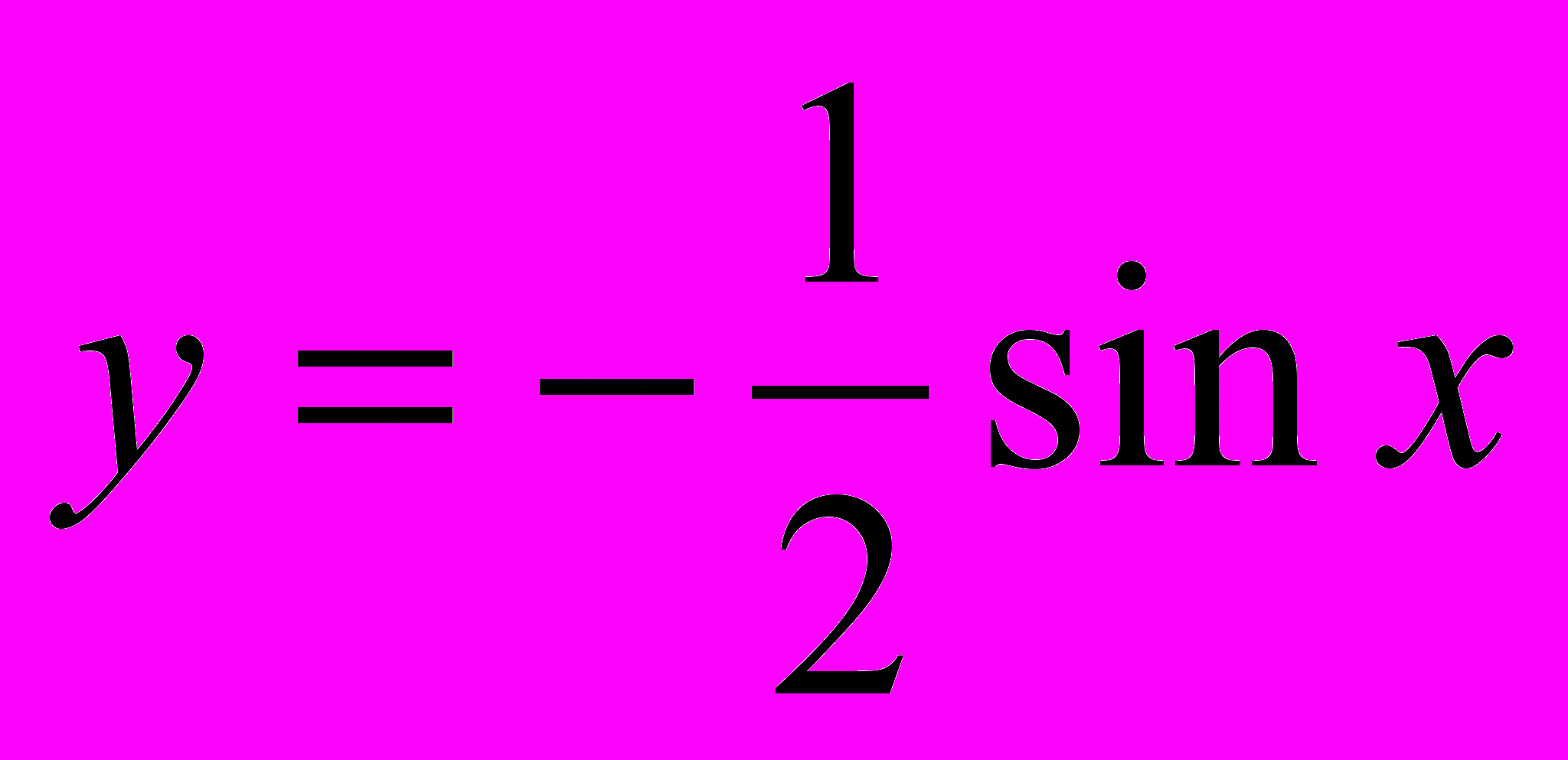и постройте ее график
   
5. Вычислите
   

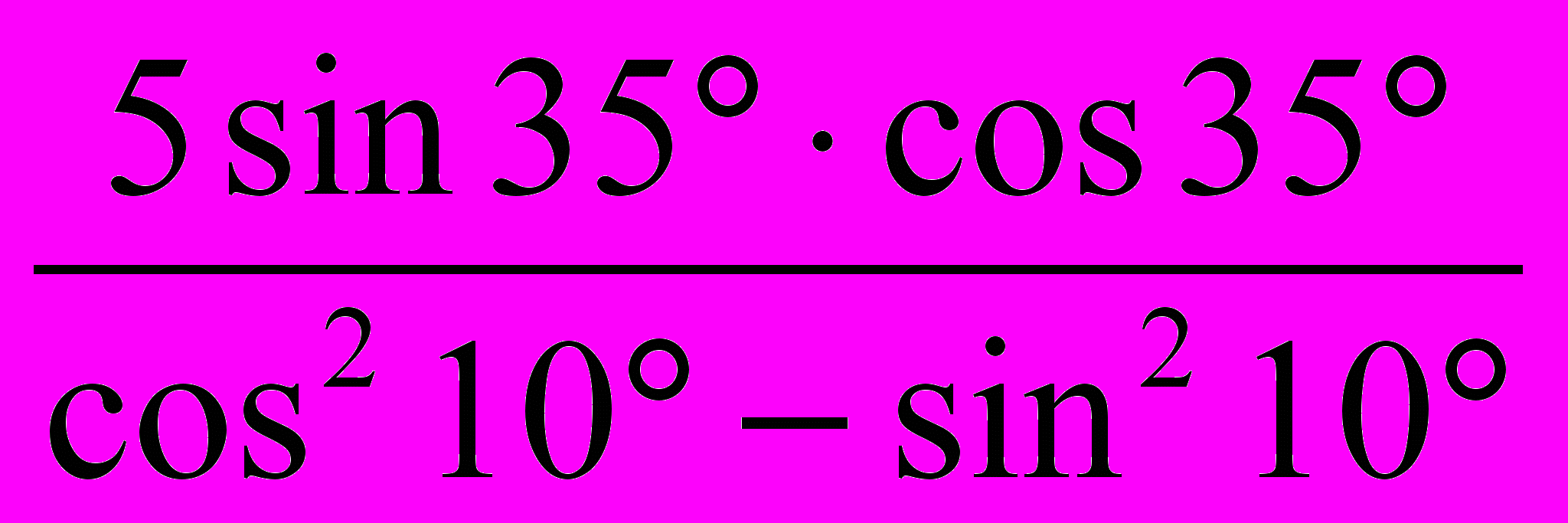
Контрольная работа N3.

1. Решите уравнение:

а) ;

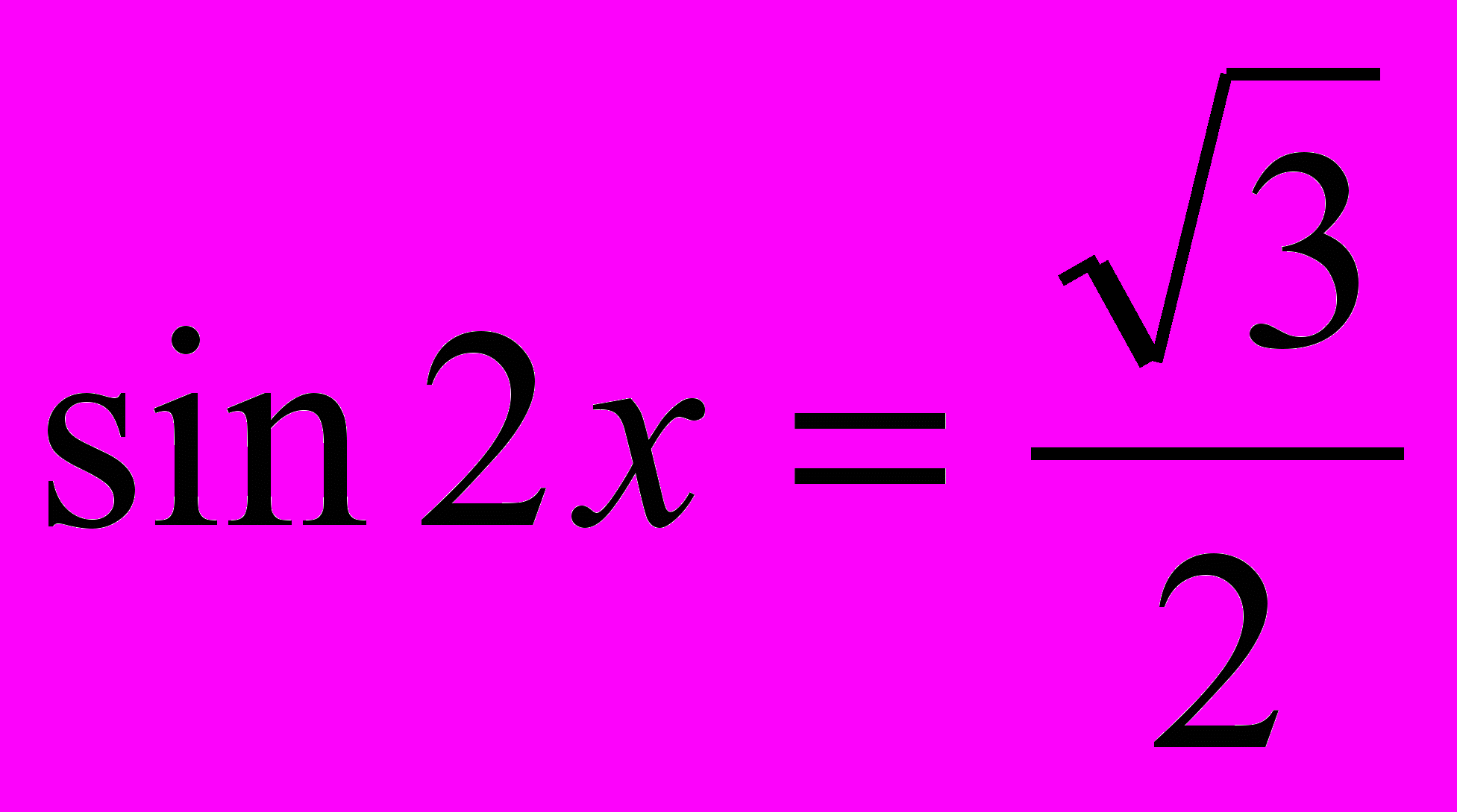б) ;

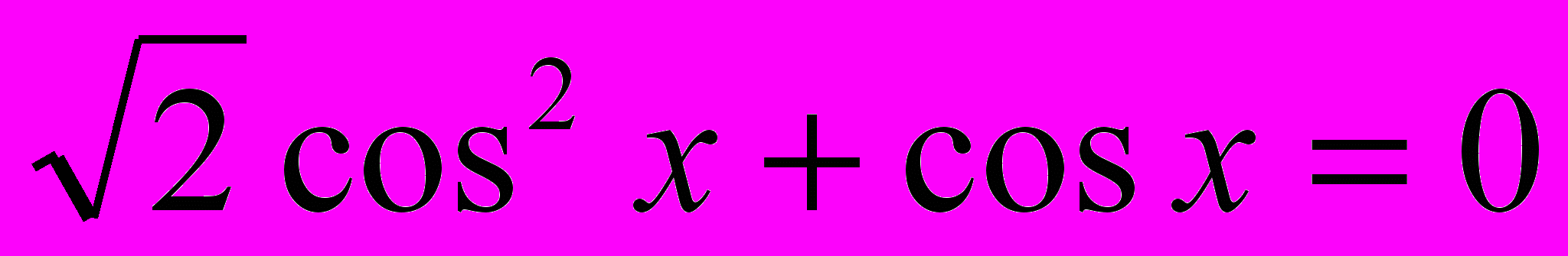в) ;

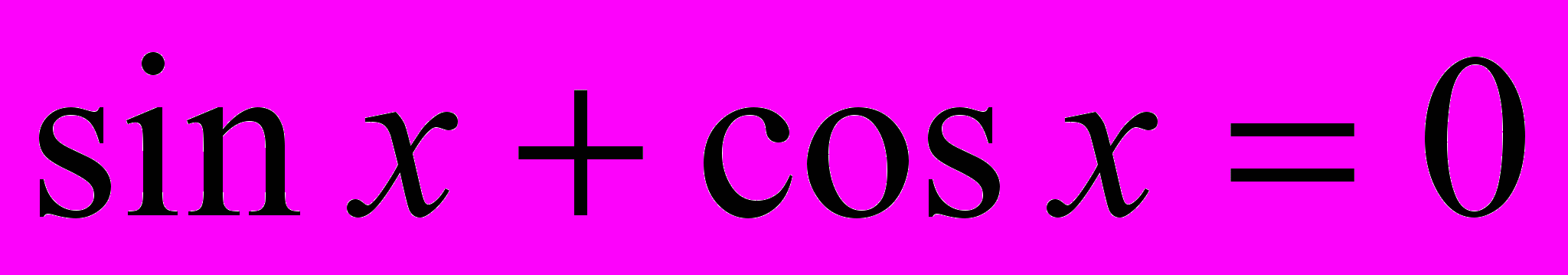г) .


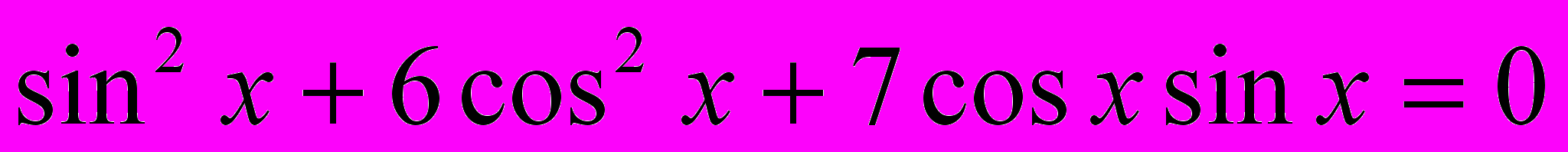2. Решите неравенство:

а) 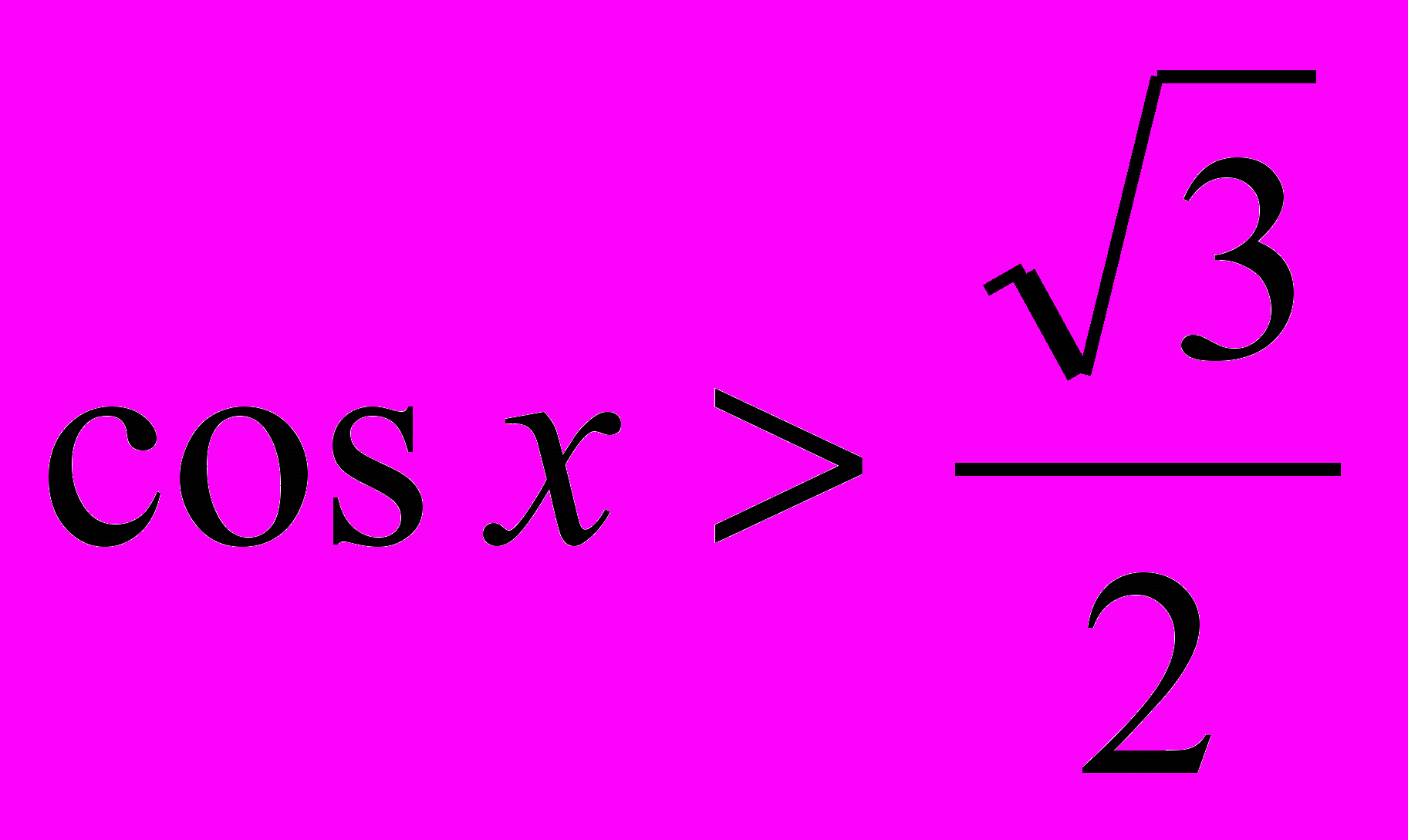; б)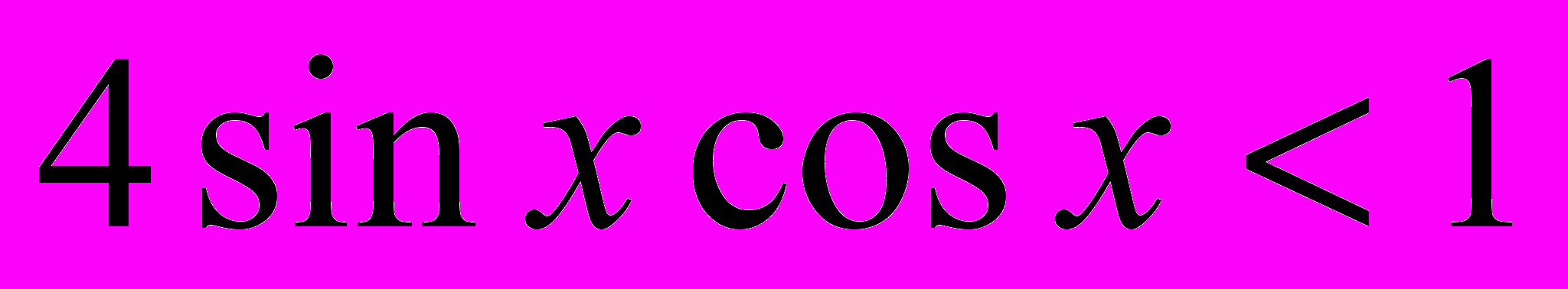

3. Решите систему уравнений


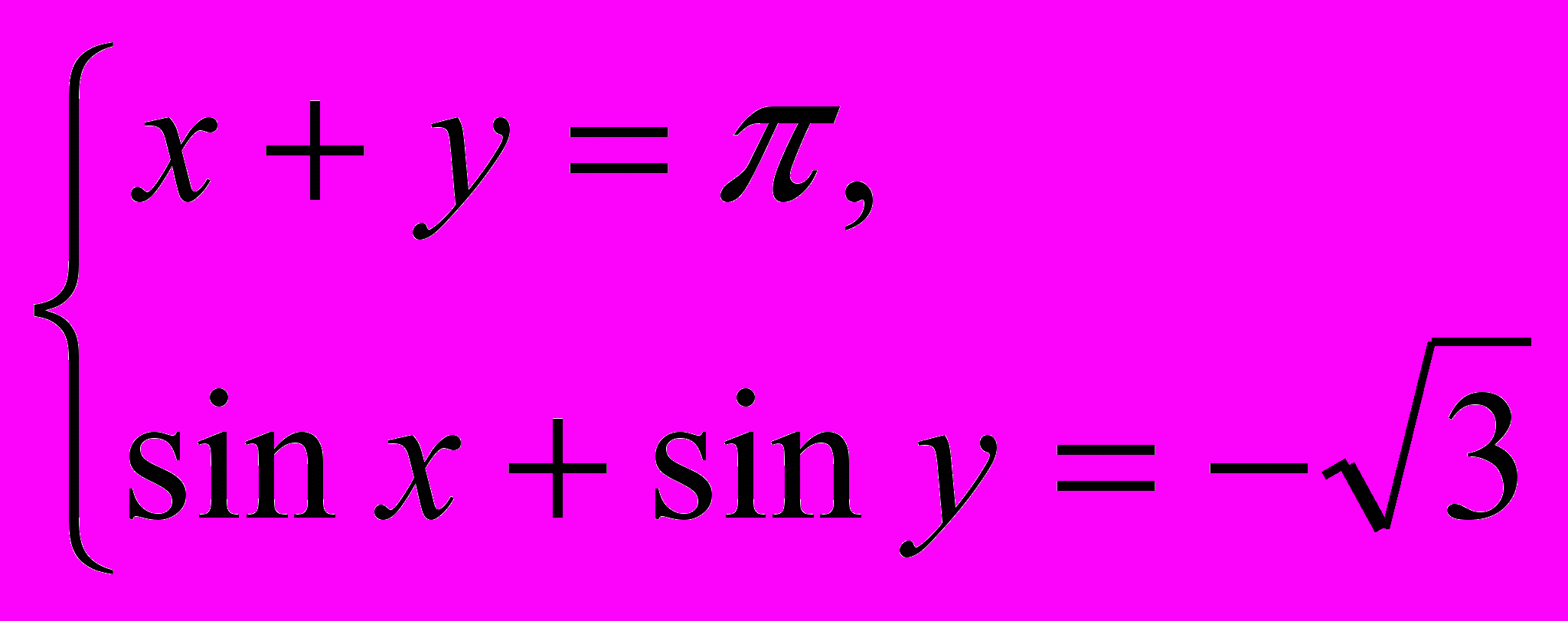
Контрольная работа N4.

1. Для функции у = 3х – 2 найдите приращение функции Δу, если заданы х₀ и Δх.
   
2. Найдите производную функции:
   

а) f(x) = 4x³ – 3x²; в) φ(х) = (2х – 1)³

б) g(x) = ;

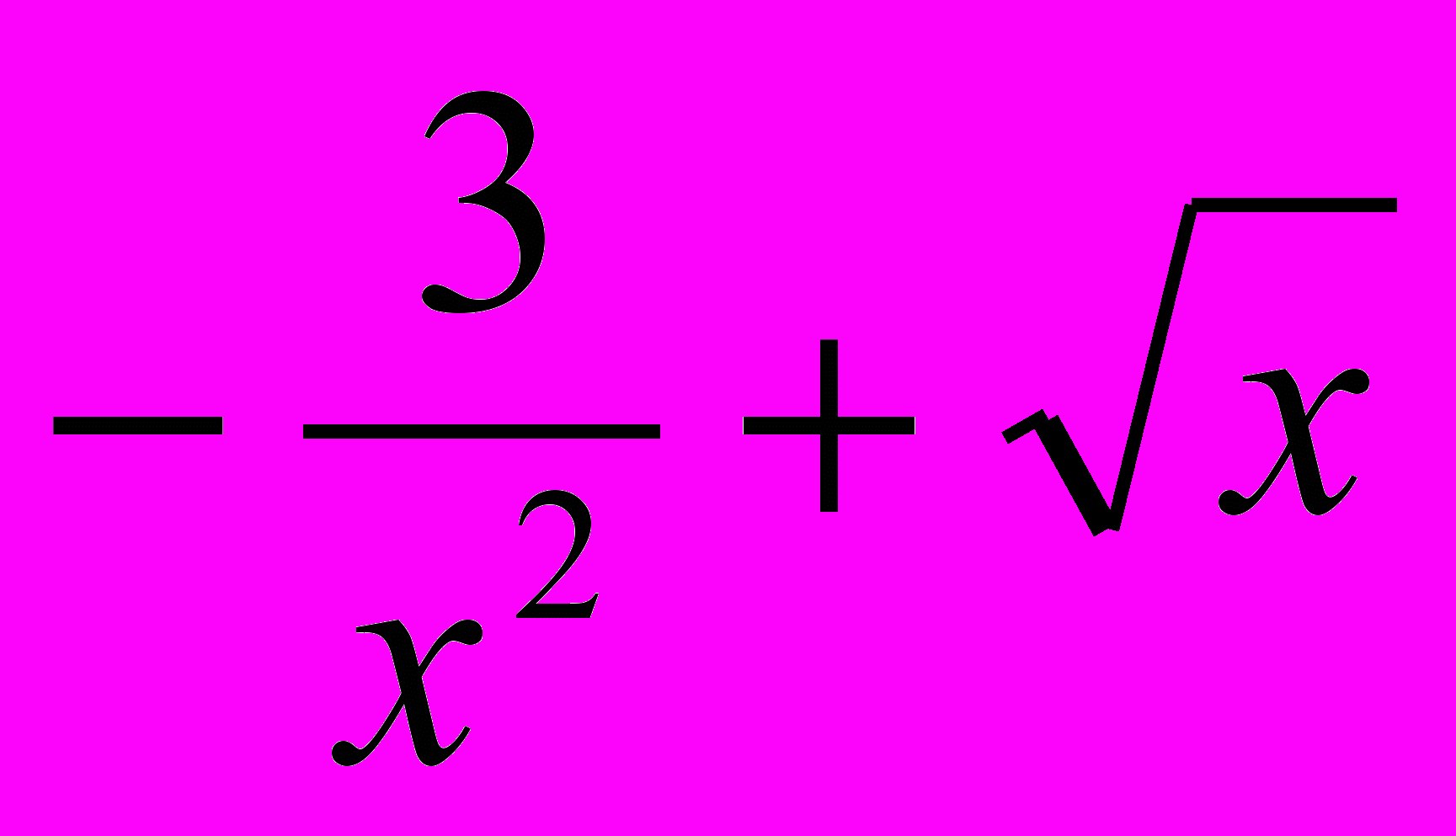3. Найдите производную функции:
   

а) ;

б) ;

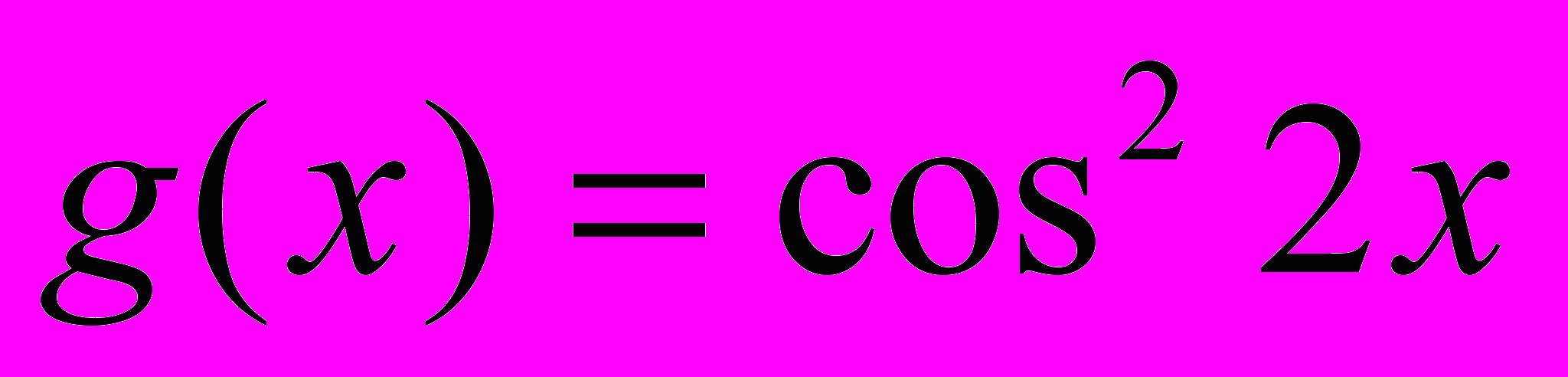в) 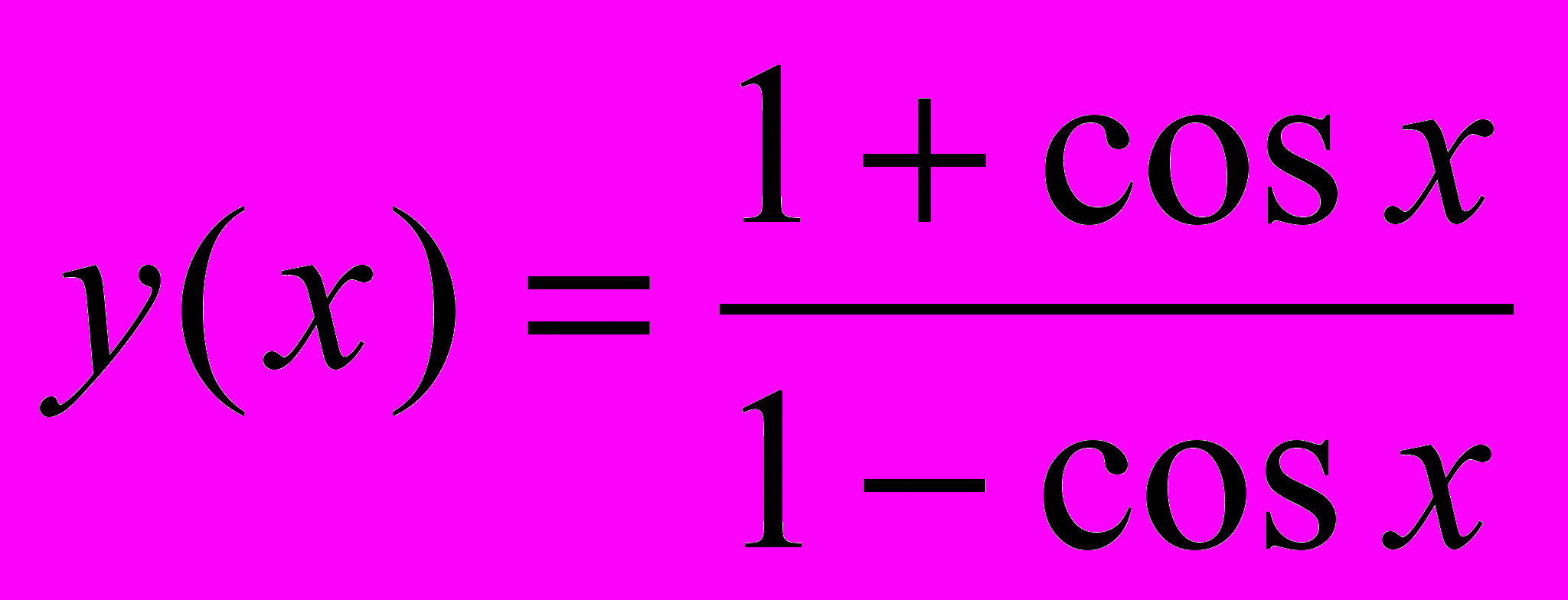и вычислите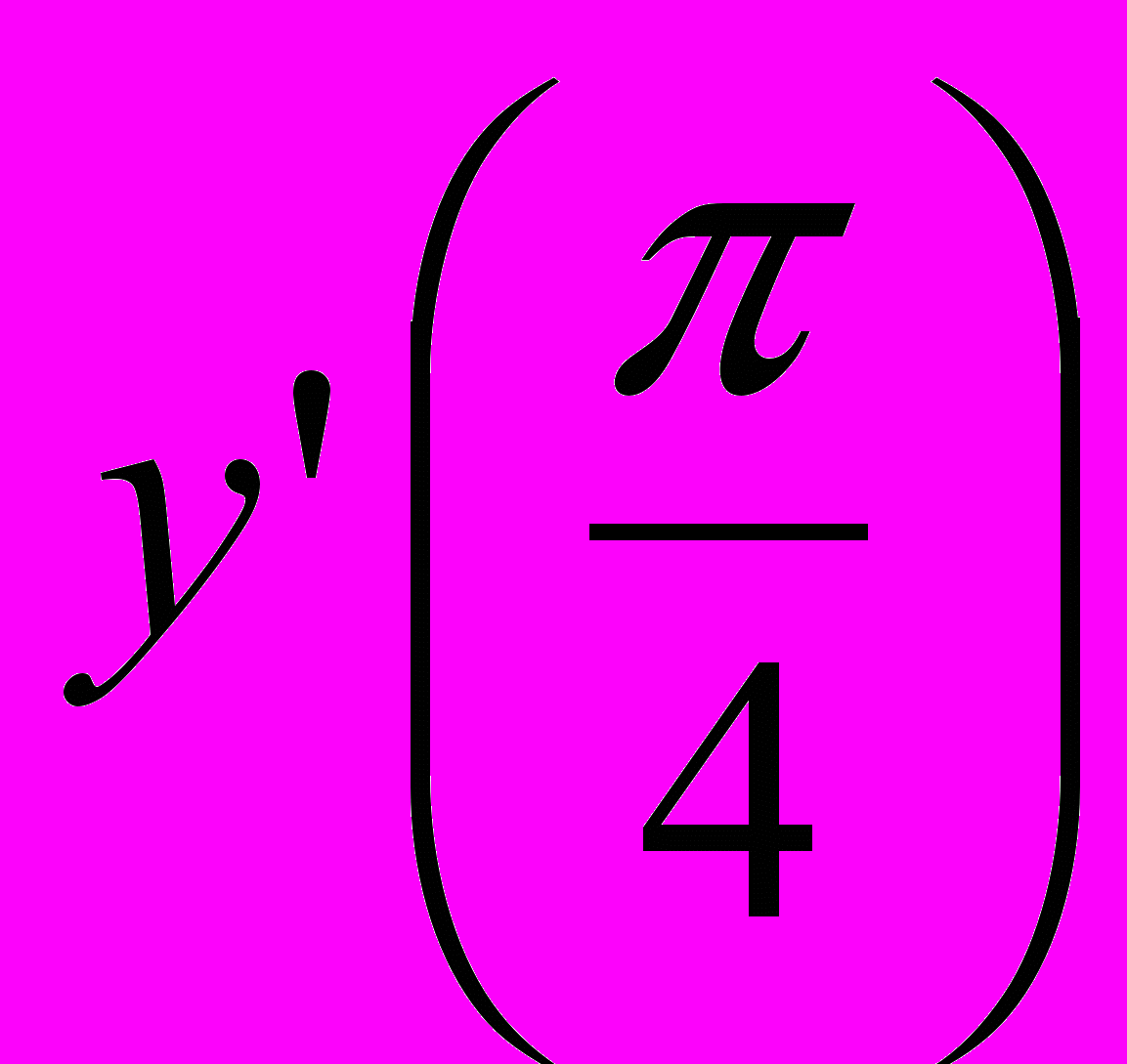


Контрольная работа N5.


1. Решите неравенство 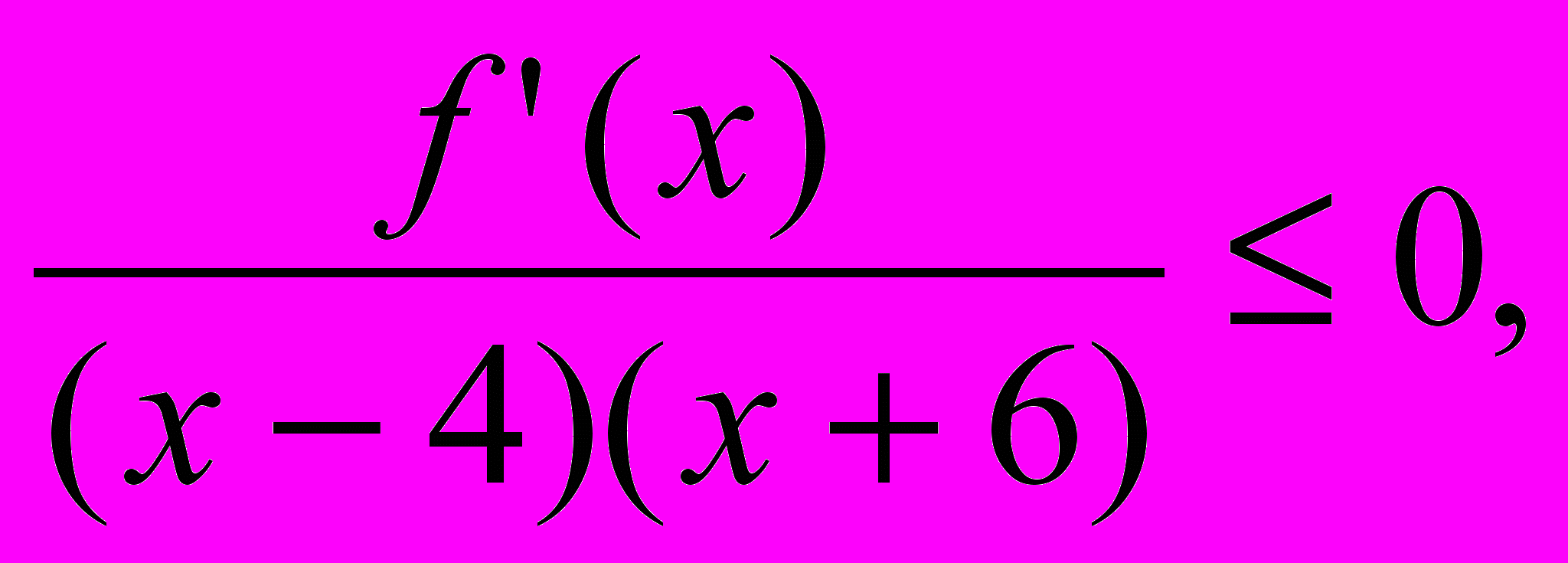где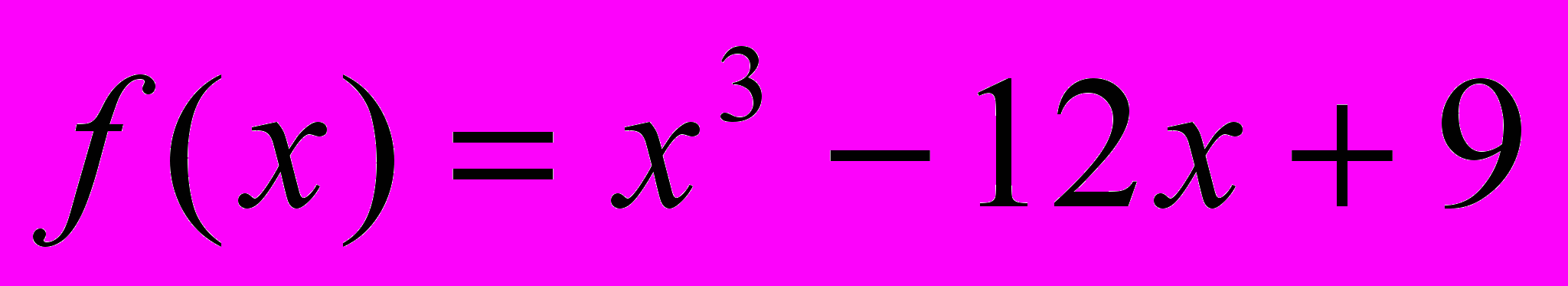

2. Найдите тангенс угла наклона касательной к графику функции f(x) = х³ + 27 в точке пересечения этого графика с осью абсцисс.

3. Найдите скорость точки в момент времени t = 1 с, если она движется прямолинейно по закону x(t) =5t – t² – 1 (координата x(t) измеряется в сантиметрах)

4. Составьте уравнение касательной к кривой f(x) = 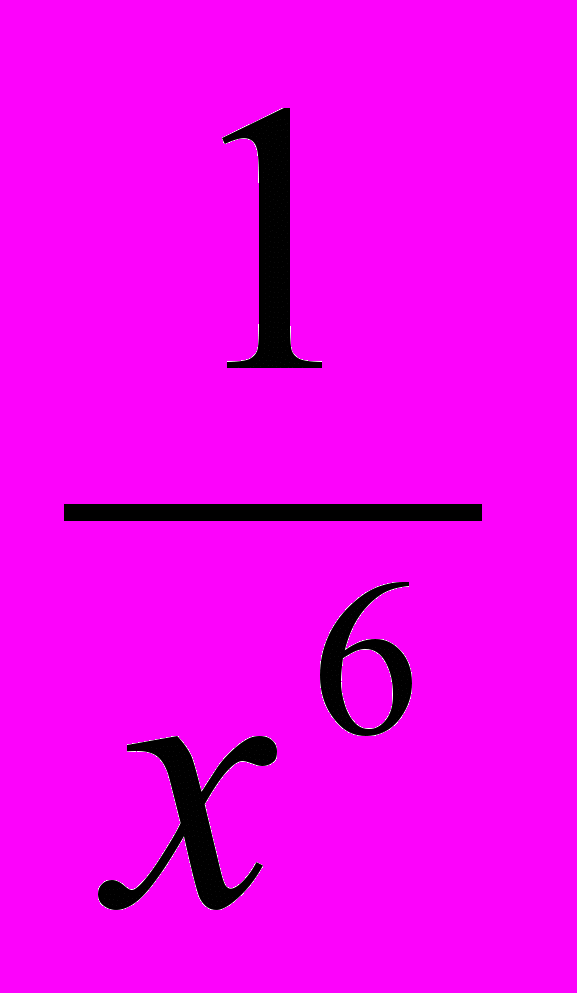в ее точке с абсциссой х₀ = 1.

5. При каком значении m прямая y = x – 1 является касательной к графику функции f(x)=x²-3x +m?


Контрольная работа N6.


1. Исследуйте функцию f(x) = – x³ + 3x² и постройте ее график.

2. Объясните, почему функция не имеет точек экстремума:

а) 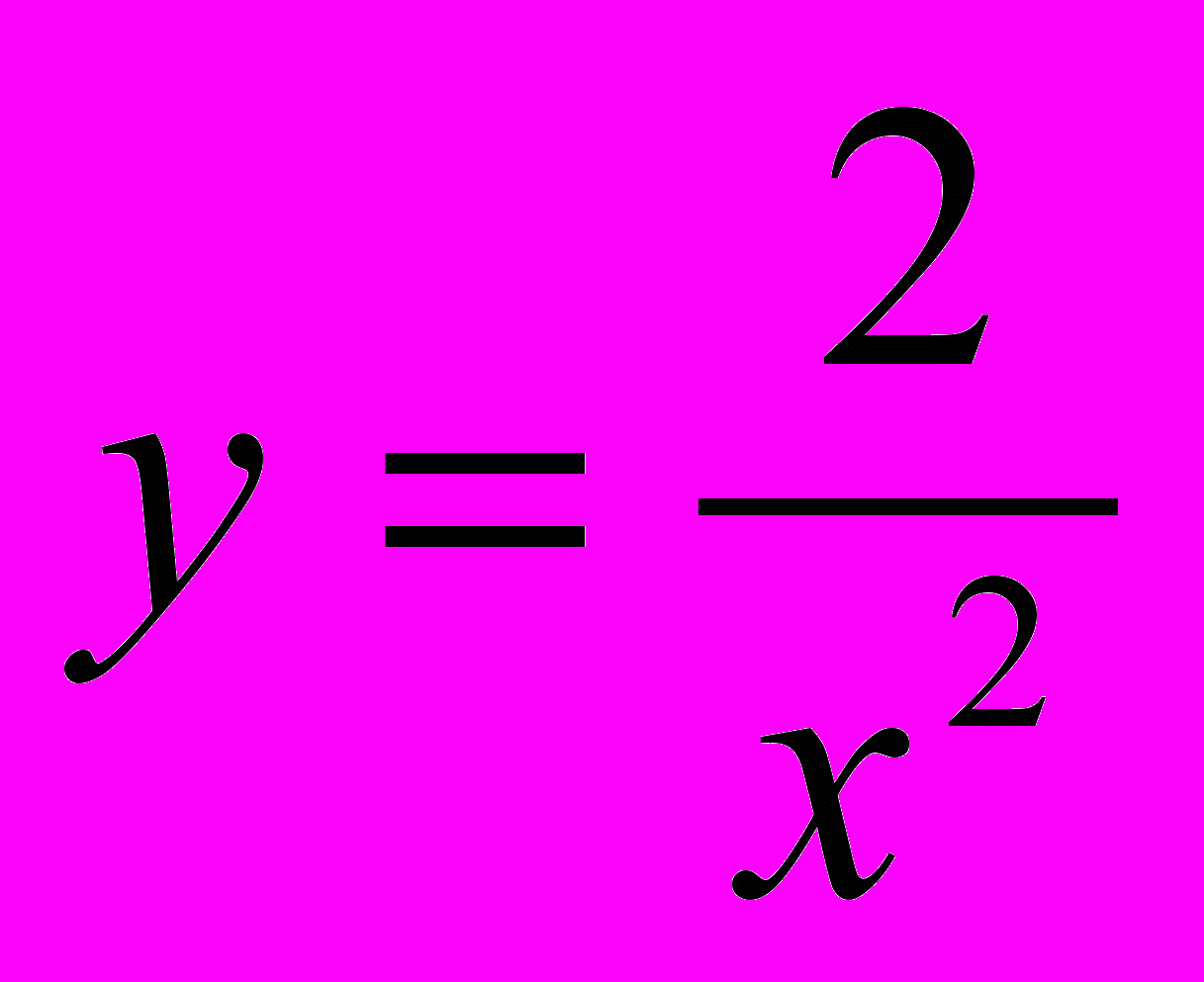; б) y = tg 2x

3. Найдите наибольшее и наименьшее значение функции:

а) 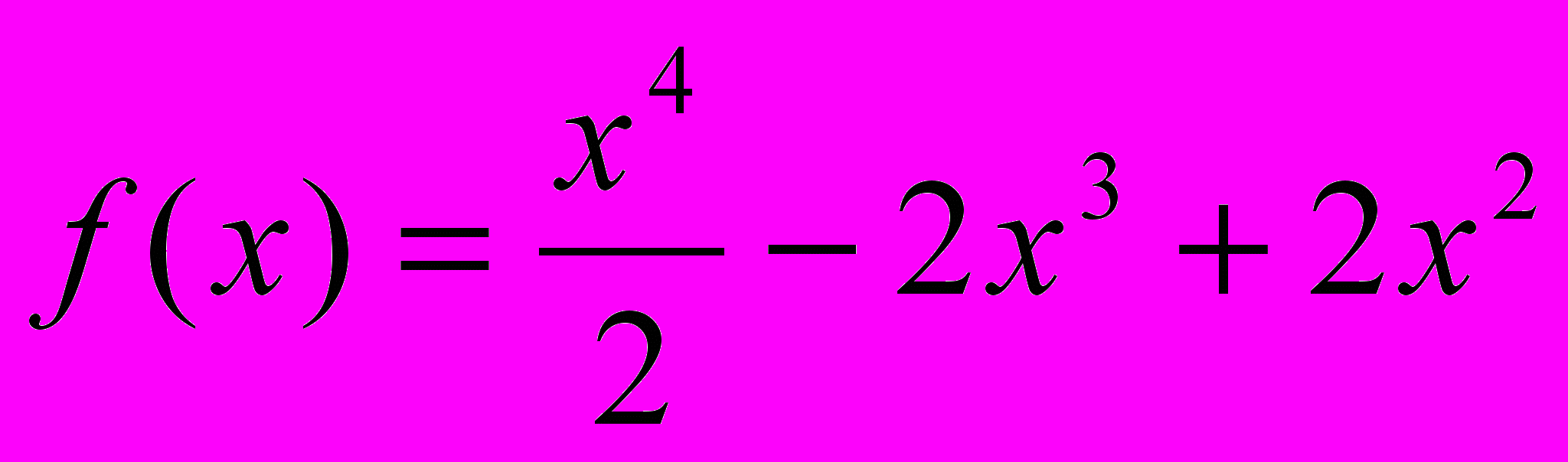на отрезке [- 1; 2]

б) 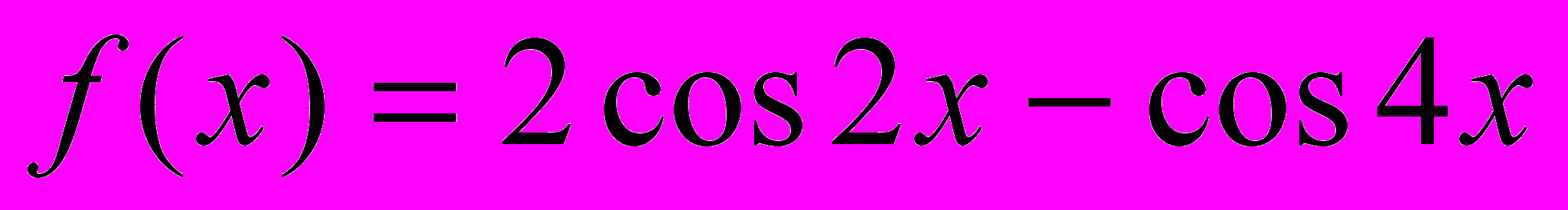на отрезке

4. При каких значениях b функция у = х⁵ + 5bx возрастает на всей числовой прямой?


Контрольная работа №7 (2 часа)


1. Решите уравнение:

а) sinx – cos2x + 1 = 0; б) 3 + sin2x = 4sin²x

2. Решите неравенство:

а) 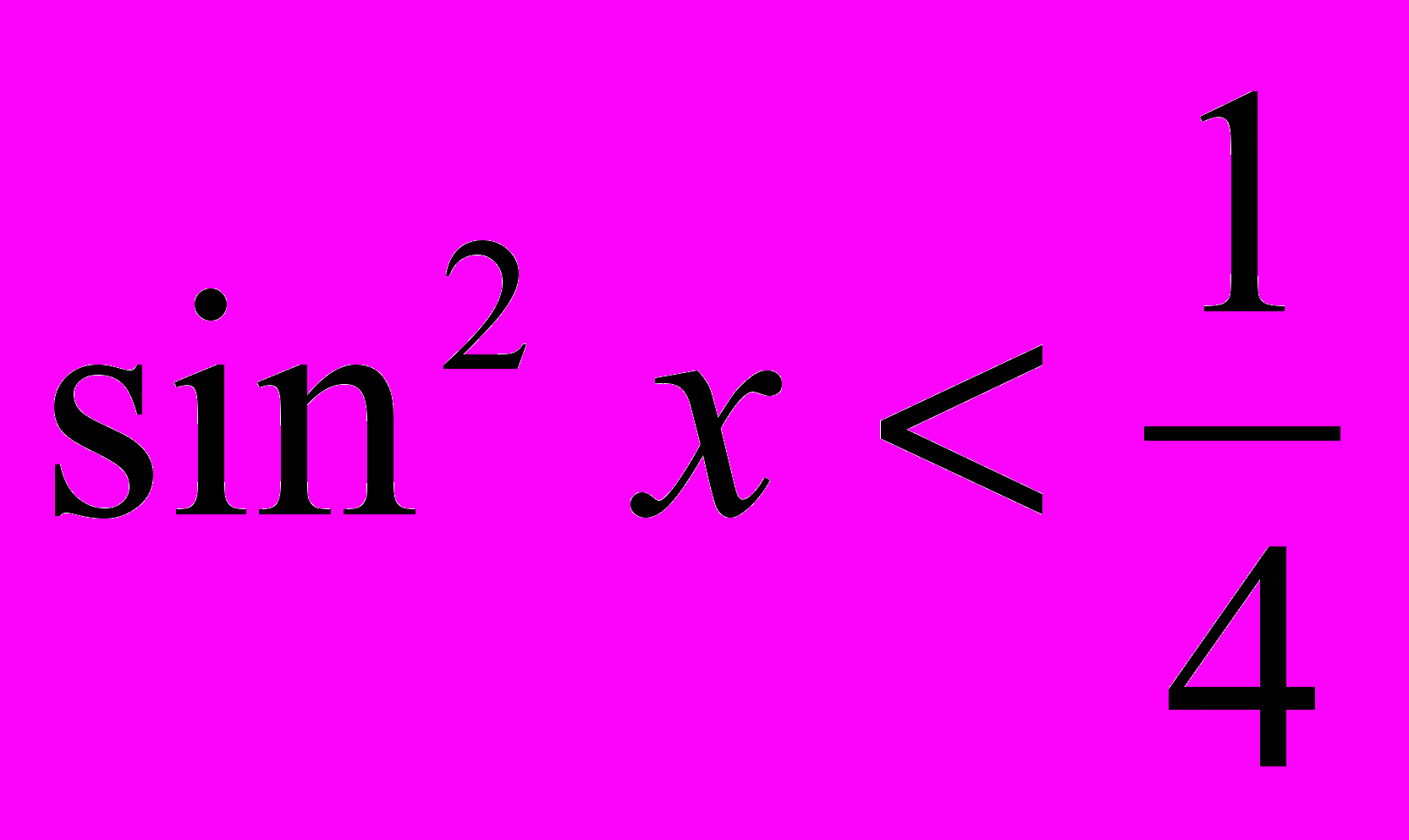; б) tgx – 1 > 0

3. Найдите градусную меру угла наклона касательной в точке 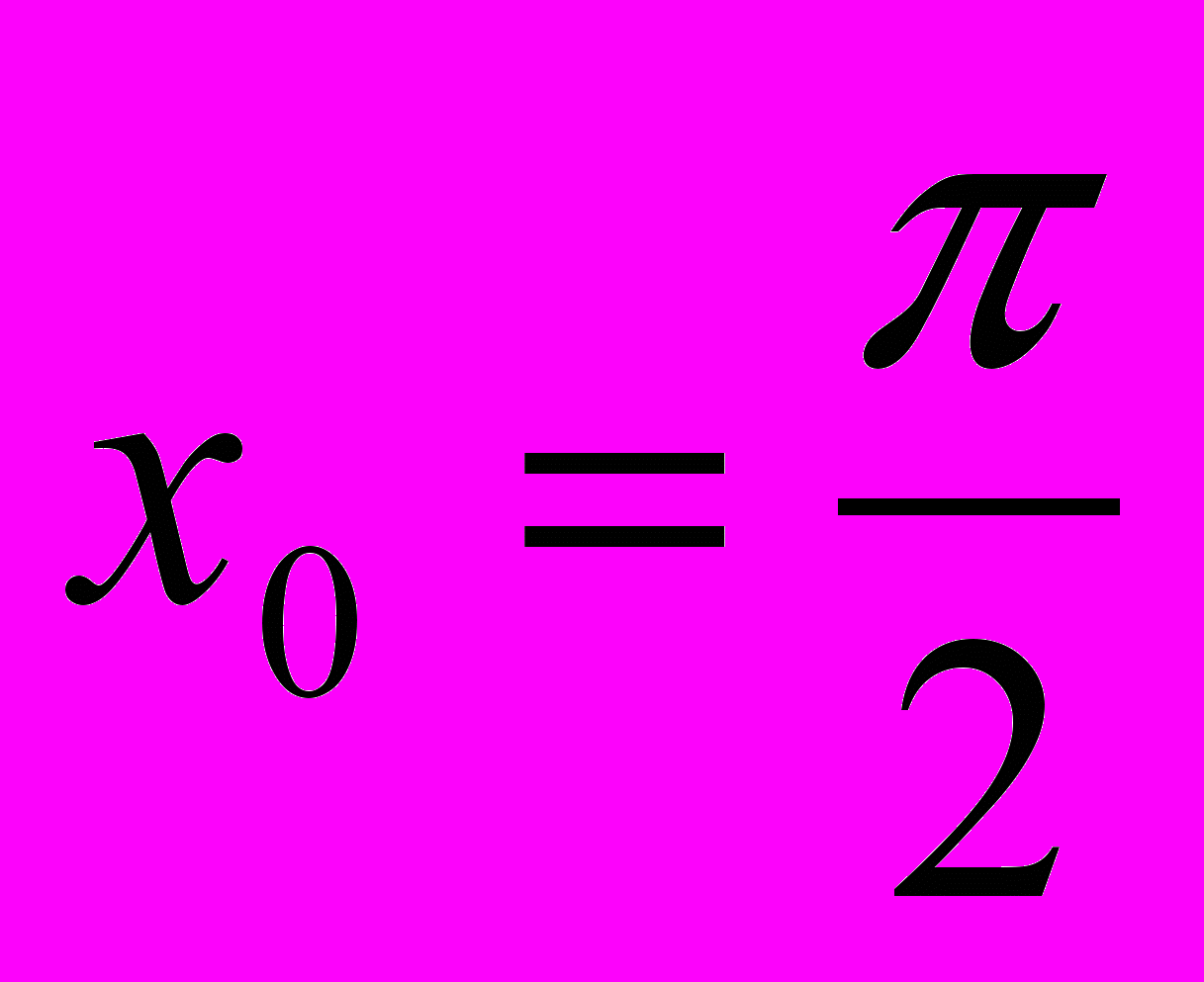к графику функции у = sin²3x.

4. Найдите наименьший положительный корень уравнения 3y – y’= 0, где у = sin3x.

5. Постройте график функции у = - 2х³ + 3х² – 5.


ГЕОМЕТРИЯ


Календарно-тематическое планирование уроков геометрии

Количество часов в неделю: 2 .

Учебное пособие для учащихся: “ Геометрия” учебник для 10 – 11 кл. общеобразовательных учреждении, авторы: Атанасян Л.С. и др., М., “Просвещение” 2000г.

Тип программы: базовый.

№ п/п	Тема	Количество часов		Контрольные, практические работы	Сроки
		по программе	по плану	по плану	по плану
1.	Введение. Аксиомы стереометрии и их следствия (пп. 1-3) Самостоятельная работа №1	5	5		Сентябрь.
2.	Глава I. Параллельность прямых и плоскостей. пп. 4-6:Самостоятельная работа №2 пп. 7-9 Контрольная работа №1 (п.1-п.9) пп.10-14 Контрольная работа №2	19	19	2	Октябрь-декабрь
3.	Глава II. Перпендикулярность прямых и плоскостей. пп. 15-18: Самостоятельная работа №3 пп. 19-21: Самостоятельная работа №4 пп. 22-24 Контрольная работа №3 (пп.15-24)	20	20	1	Декабрь-февраль.
4.	Глава III. Многогранники. пп.25-27: Самостоятельная работа №5 пп.28-30: Самостоятельная работа №6 пп.31-33 Контрольная работа №4 (пп.25-33)	12	12	1	Март.
5.	Глава IV. Векторы в пространстве. пп.34-41 Зачет	6	6		Апрель.
6.	Итоговое повторение.	6	6		Май.

1 полугодие.

Контрольная работа N1.


1.Дано ABCDA₁B₁C₁D₁- куб.

1.Докажите, что AB и CD являются скрещивающимися прямыми.

2.Найдите угол между прямыми.

А) AB и CC₁

Б) AB и CD₁

С) BD и CD₁

2.Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены отрезками последовательно.

А) Выполните рисунок к задаче.

Б) Докажите, что полученный четырехугольник есть ромб.


Контрольная работа N2.


1. Прямые a и b лежат в параллельных плоскостях. Могут ли эти прямые быть а) параллельными б) скрещивающимися. Выполните рисунок.

2.Через точку О, лежащую между параллельными плоскостями и 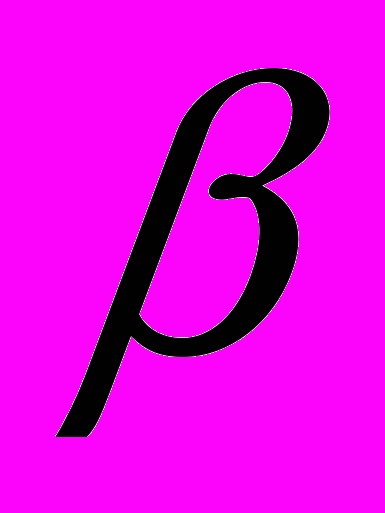, проведены прямые l и m. Прямая l пересекает плоскости и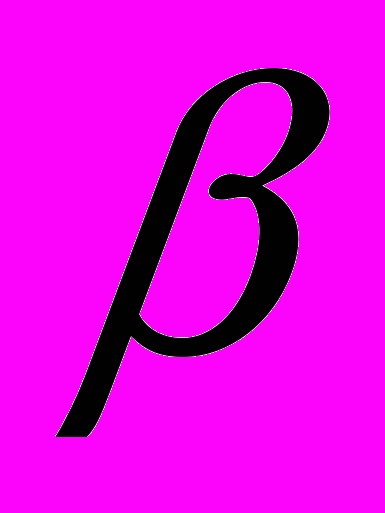 в точках А₁ и А₂ соответственно, прямая m – в точках В₁ и В_2. Найдите длину отрезка А₂В₂, если А₁В₁ = 12см., В₁О : ОВ₂ = 3 : 4 .

3. Изобразите параллелепипед ABCDA₁B₁C₁D₁ и постройте его сечение плоскостью, проходящей через точки M, N, K, если M, N, K – середины ребер AB, BC, DD₁ соответственно.


2 полугодие.

Контрольная работа N3.

1. Диагональ куба равна 6 см. Найдите:
   

а) ребро куба;

б) косинус угла между диагональю куба и плоскостью одной из его граней.

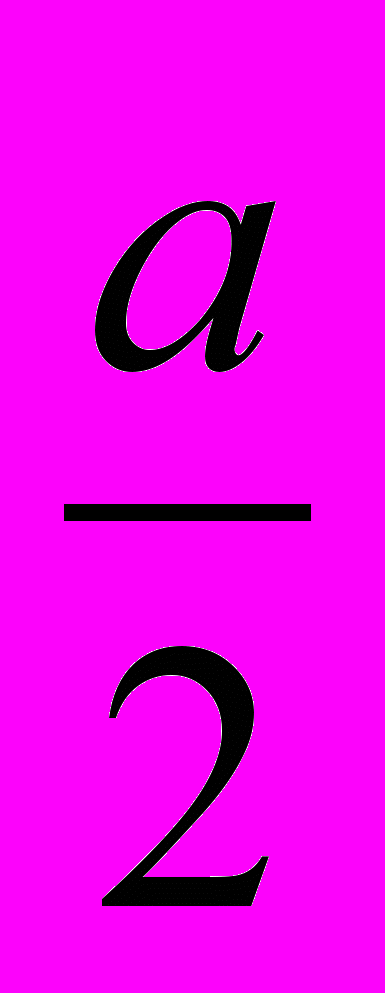2. Сторона AB ромба ABCD равна а, один из углов ромба равен 60º. Через сторону AB проведена плоскость на расстоянии от точки D.

а) Найдите расстояние от точки С до плоскости .

б) Покажите на рисунке линейный угол двугранного угла DABМ, М.

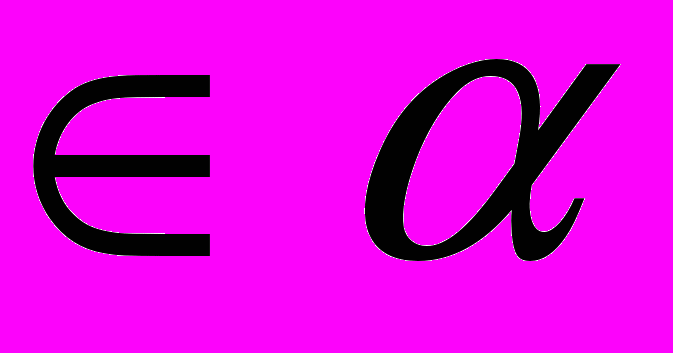в) Найдите синус угла между плоскостью ромба и плоскостью .


Контрольная работа N4.

1. Основанием пирамиды DABC является правильный треугольник ABC, сторона которого а. Ребро DА перпендикулярно к плоскости ABC, а плоскость DBC составляет с плоскостью ABC угол 30º. Найдите площадь боковой поверхности пирамиды.

2. Основанием прямого параллелепипеда ABCDA₁B₁C₁D₁ является ромб ABCD, сторона которого а и угол равен 60º. Плоскость AD₁C₁ составляет с плоскостью основания угол 60º. Найдите:

а) высоту ромба;

б) высоту параллелепипеда;

в) площадь боковой поверхности параллелепипеда;

г) площадь поверхности параллелепипеда.


Контрольная работа N5.


1.Дан параллелепипед ABCDA₁B₁C₁D₁ . Укажите вектор с началом и концом в вершинах параллелепипеда, равный

а) + +

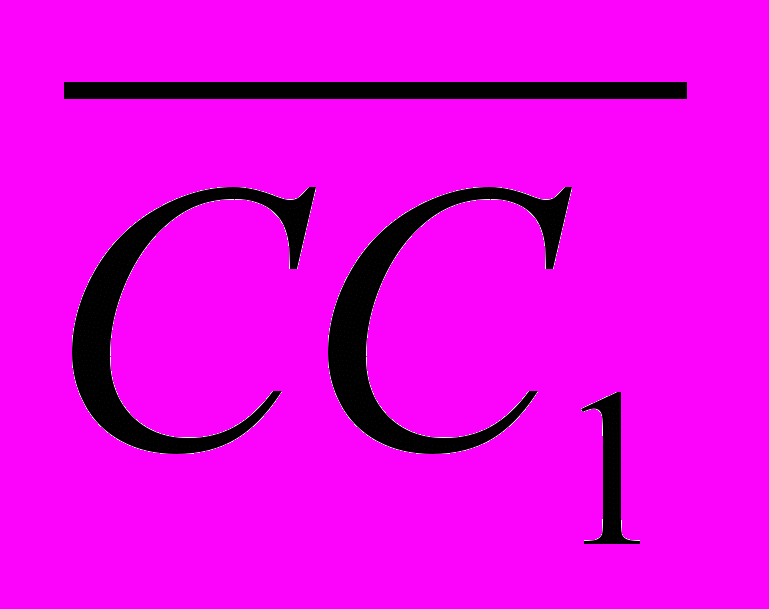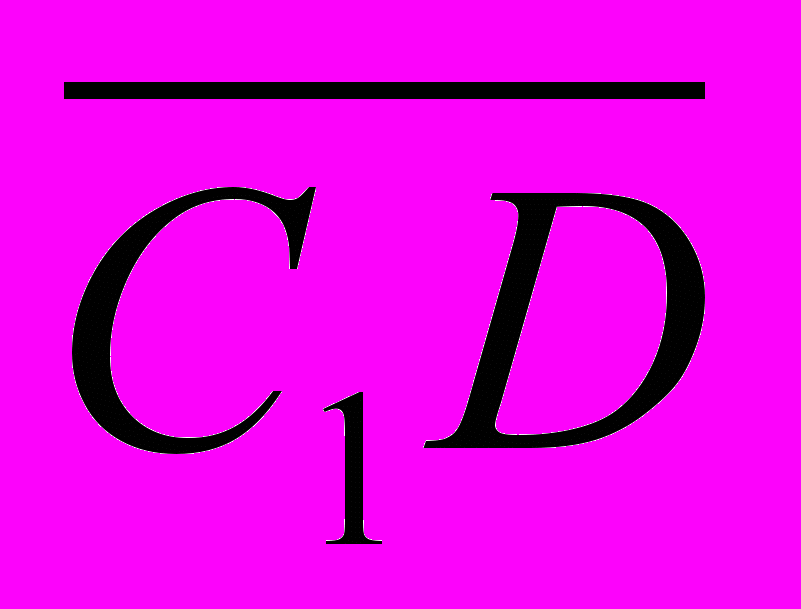
б) + - +

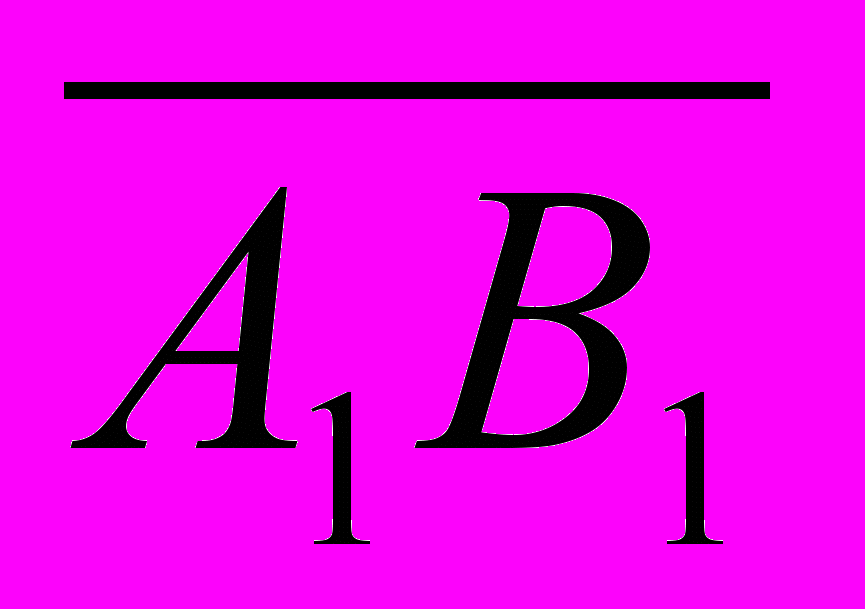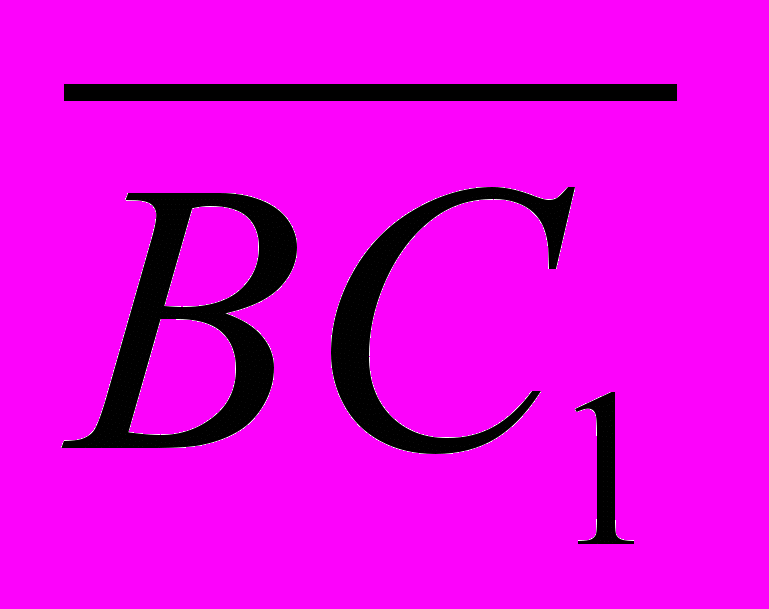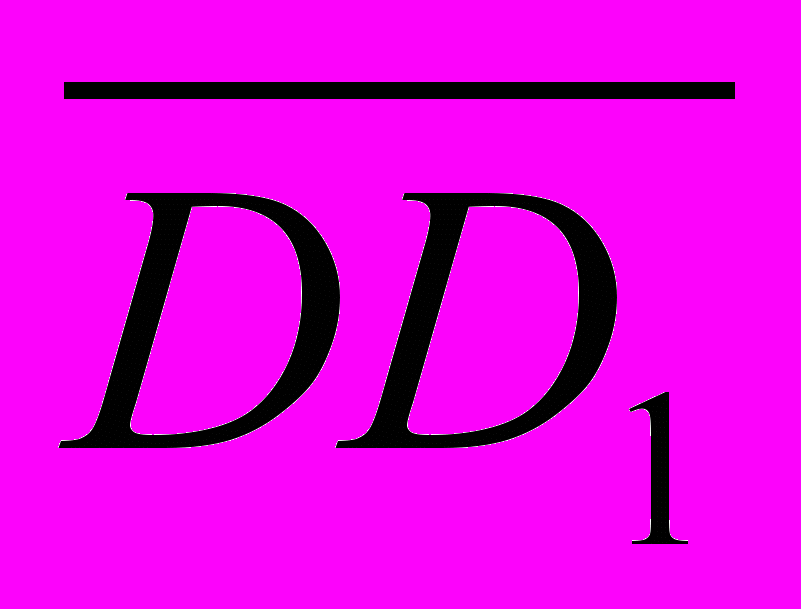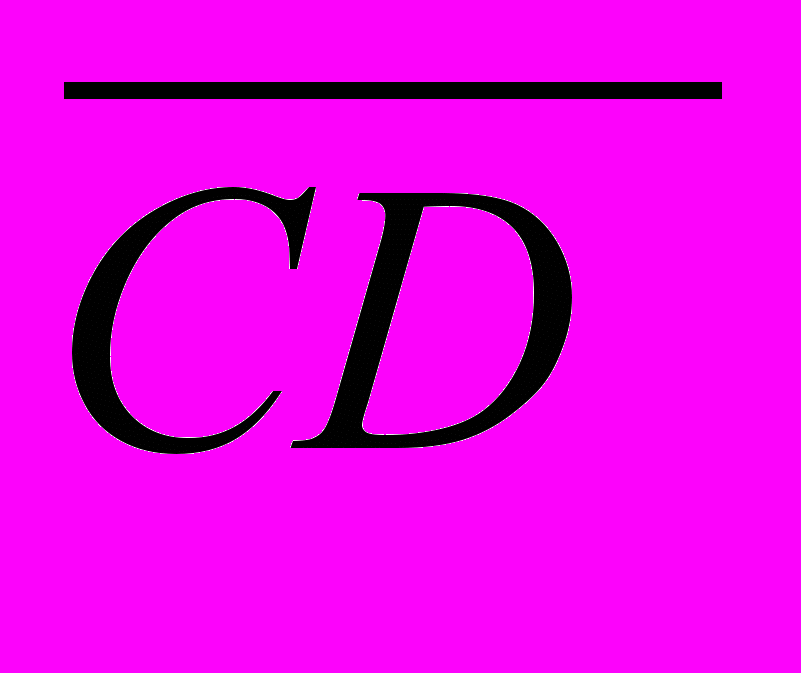
в) -

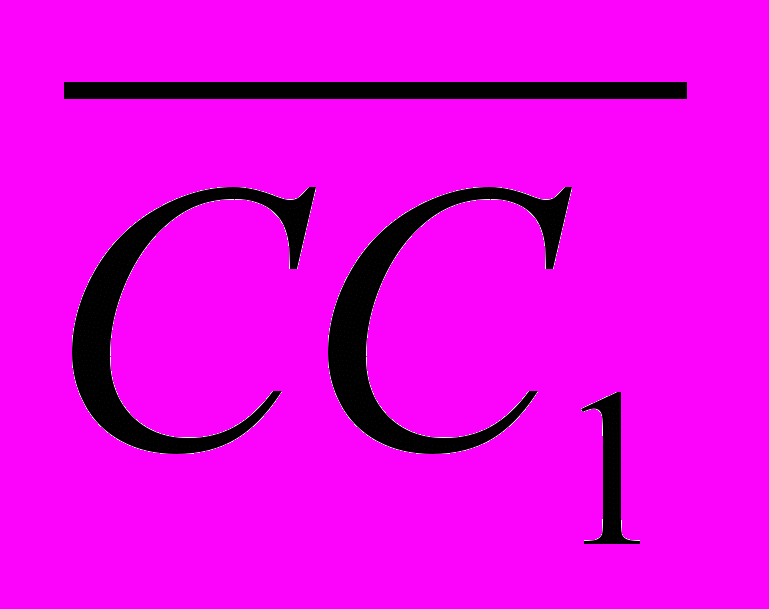
2.В пирамиде MABC основанием является прямоугольник ABCD, AB = 8cм., BC = 15см..

Найдите

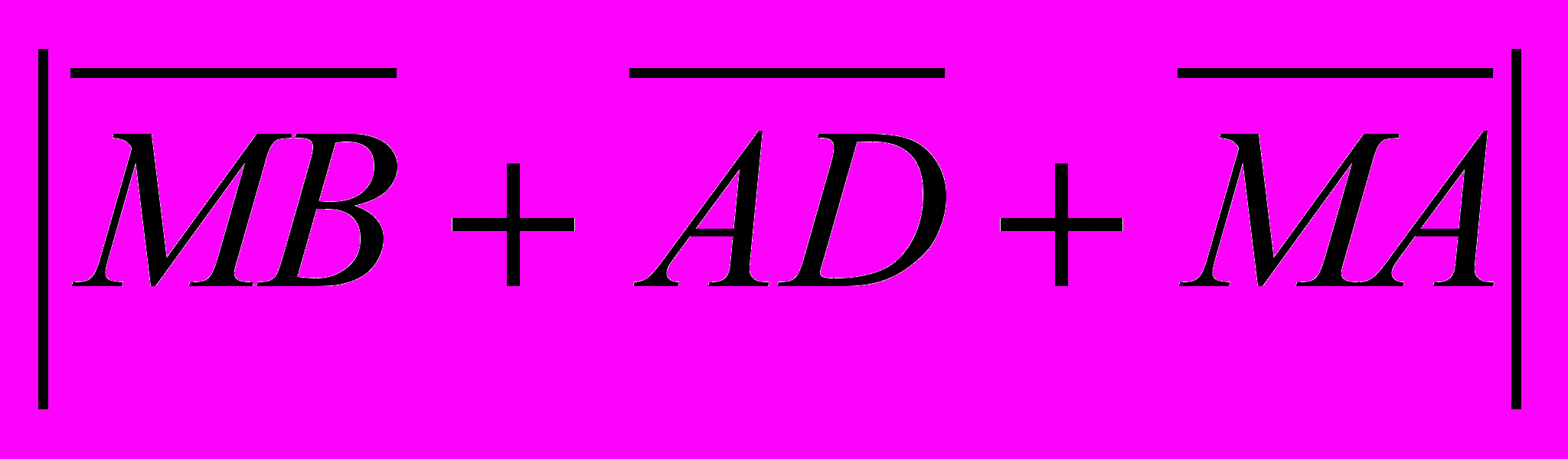
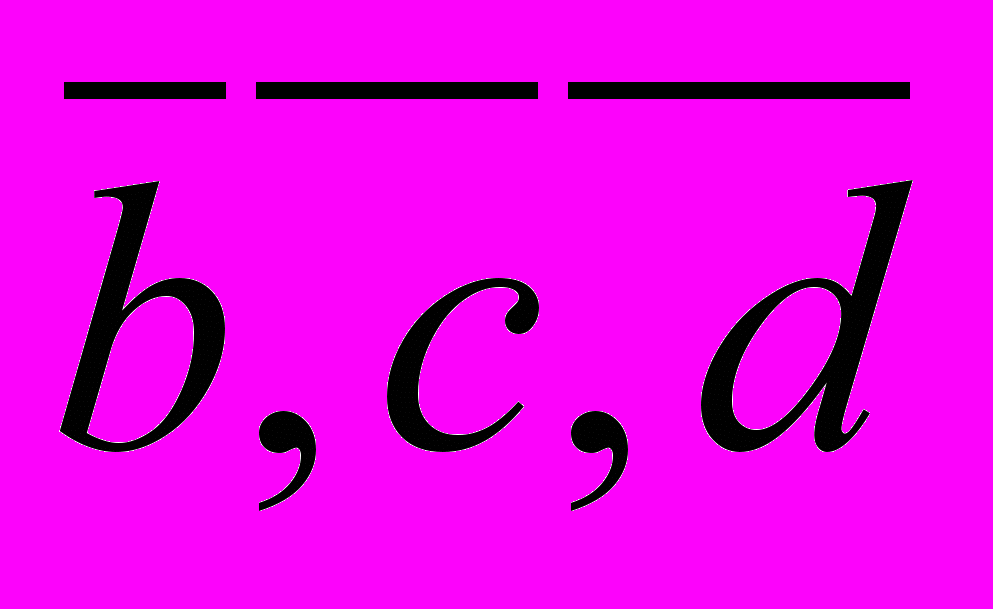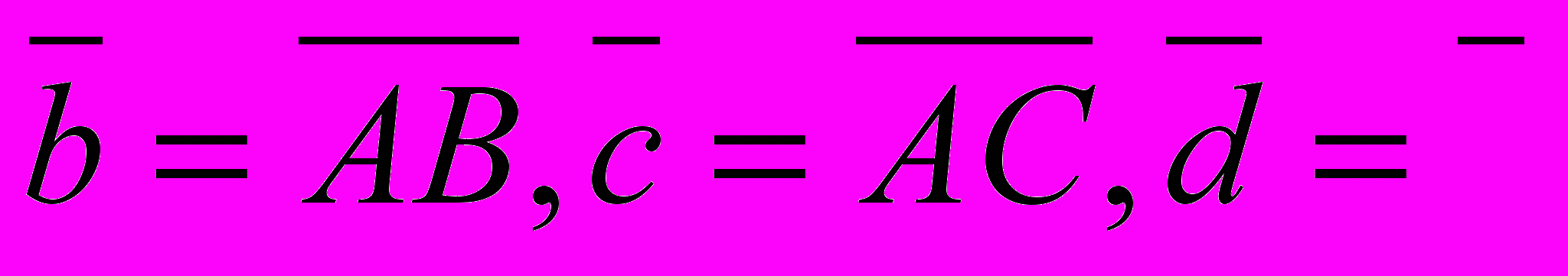3.В тетраэдре DABC точка E - середина ребра AD а точка M - пересечение медиан грани BDC . Разложите вектор EM по векторам если AD


ХИМИЯ

Учитель: Кузнецов Ю. М. Количество часов в неделю: 2 .

Учебное пособие для учащихся: Учебник: Химия 10 кл, О.С. Габриелян. Изд. «Дрофа».

Тип программы: базовый.

Дата	Тема занятия	На что обратить внимание	Задание
с е н т я б р ь	Введение		§ 1. упр 1-7.
	1) Предмет органической химии
	2) Теория строения вещества А.М. Бутлерова	Пояснение теории; химическое строение и св-ва вещества; изомерия	§ 2. упр 1-7.
	3) Строение атома углерода	Орбитали; электронные и графические формулы атома углерода	§ 3. упр 1-5.
	4) Валентное состояние атома	Химические связи; образование молекул	§ 4. упр 1-4.
	Строение и классификация органических соединений		§ 5. упр 1-5.
	1) Классификация органических соединений
	2) Номенклатура органических соединений	Уметь записывать название соединений по названию формул	§ 6. упр 1,2.
	3) Изомерия	Знать примеры изомеров	§ 7. упр 1-7.
	Химические реакции в органической химии		§ 8. упр 1-4.
	1) Типы химических реакций	Уметь показать на примерах

о к т я б р ь	Углеводороды		§ 10. упр 1-10.
	1) Нефть, природный газ	Знать состав и продукты, которые можно получить из нефти и газа
	2) Алканы	Гомологический ряд; общая формула; строение молекулы; изомерия; Реакции характерные для алканов	§ 11. упр 1-4, 6,7,8. §11. упр 5,9-12.
	3) Алкены	Гомологический ряд; общая формула; строение молекулы; изомеры; номенклатура; Реакции характерные для алкенов	§12. упр 1,2,4. §12. упр 3,5-9.
	4) Алкины	Гомологический ряд; общая формула; строение молекулы; изомеры; номенклатура; Реакции характерные для алкинов	§13. упр 1-3,5. §14. упр 4,6-8.
	5) Каучук, реакция полимеризации		§14. упр 4-6.
	6) Арены	Бензол, строение, химические св-ва	§16. упр 1-2, 3-9.
	7) Генетическая связь классами углеводородов		повторение