Курс IV семестры 7, 8 лекции 49 часов Экзамен нет семинары 16 часов Зачет с оценкой 7, 8 семестры

Вид материала

Лекции

Содержание Программу составил д.ф.-м.н., проф. Белолипецкий А.А.

Подобный материал:

• Курс IV семестры 8 (весенний) лекции 16 часов Экзамен 8 семестр (весенний), 30.19kb.
• Курс, 1-й семестр лекции (51 час), экзамен практикум на ЭВМ (68 часов), зачет (с оценкой), 24.4kb.
• Аннотация примерной программы дисциплины «Бухгалтерский учет и анализ», 52.81kb.
• И. Г. Петровского утверждаю заведующий кафедрой С. Ф. Блуменау 200 Рабочая программа, 116.12kb.
• Курс, 3-й семестр лекции (48 часов), экзамен практикум на ЭВМ (64 часа), зачет с оценкой, 60.04kb.
• Аннотация примерной программы дисциплины «Налоговое администрирование», 99.39kb.
• Обязательный курс Объем учебной нагрузки: Курс читается в течение трех семестров: 3,4,5, 581.17kb.
• Бакалаврская программа Обязательный курс Курс: гфб-1 Семестр: 2 Количество кредитов:, 356.08kb.
• Аннотация программы дисциплины " Теоретические основы электротехники" Направление подготовки, 21.86kb.
• Программа дисциплины Нейропсихология Направление подготовки специалистов, 29.9kb.

министерство образования и науки российской федерации

Московский физико-технический институт

(государственный университет)


УТВЕРЖДАЮ

Проректор по учебной работе

Ю.А. Самарский

« 25 » февраля 2011 г.

П Р О Г Р А М М А

по курсу АКТУАРНАЯ МАТЕМАТИКА

по направлению 010900

факультет ФУПМ

кафедра математических основ управления

курс IV

семестры 7, 8

лекции – 49 часов Экзамен – нет

семинары – 16 часов Зачет с оценкой – 7, 8 семестры

лабораторные занятия – нет

самостоятельная работа – 2 часа в неделю

ВСЕГО ЧАСОВ – 65

Программу составил

д.ф.-м.н., проф. Белолипецкий А.А.

Программа обсуждена на заседании

кафедры математических основ управления

11 февраля 2011 года.

Заведующий кафедрой Гуз С.А.

Актуарную математику можно рассматривать как прикладную часть теории случайных процессов, изучающую риски, возникающие при финансовых расчетах между страхователями и страховщиками. Настоящий курс посвящен изложению основ актуарной математики.

Часть I

1. Теория полезности и страхование.
   
2. Теорема об оптимальном страховании.
   
3. Модели краткосрочного страхования жизни.
   
4. Аппроксимация суммы случайных исков с помощью нормального распределения и распределения Пуассона.
   
5. Формулы для распределения вероятностей суммы целочисленных случайных исков.
   
6. Функции выживания. Остаточное и округленное остаточное время жизни. Их математические ожидания и дисперсии.
   
7. Интенсивность смертности. Таблицы продолжительности жизни.
   
8. Связь табличных величин с функцией выживания.
   
9. Интерполяция непрерывных актуарных функций дискретными табличными величинами.
   
10. Аналитические законы смертности.
    

Простейшая модель долгосрочного страхования. Смешанное страхование жизни. Разовые нетто-премии.

11. Отсроченное страхование.
    
12. Виды страхования с переменной страховой выплатой.
    
13. Страхование с выплатой в конце года смерти.
    
14. Перестрахование.
    
15. Рекуррентные уравнения и коммутационные функции.
    

Часть II

16. Введение в финансовую математику. Потоки платежей. Понятие аннуитета.
    
17. Актуарная приведённая стоимость аннуитета.
    
18. Непрерывные аннуитеты.
    
19. Дискретные аннуитеты.
    
20. Аннуитеты с m-кратными годовыми выплатами.
    
21. Аннуитеты с переменными выплатами.
    

23. Нетто-премии с выплатами, распределенными по годам. Модели с непрерывными выплатами премий.

24. Нетто-премии в моделях с ежегодными выплатами.

25. Нетто-премии при m-кратных ежегодных выплатах.

26. Резервы нетто-премий в непрерывных моделях.

27. Четыре вида формул для резервов нетто-премий в непрерывных моделях.

28. Резервы нетто-премий в дискретных и полунепрерывных моделях.

29. Рекуррентные формулы для резервов нетто-премий в дискретных моделях.

30. Распределение потерь по годам действия полиса. Теорема Хэттендорфа.

31. Дифференциальное уравнение Тиле для резервов нетто-премий в непрерывных моделях.

32. Страхование жизни нескольких лиц. Состояние совместной жизни, состояние выживания последнего.

33. Общее симметрическое состояние. Теорема Шуэтта– Несбитта.

34. Примеры асимметричных аннуитетов и видов страхования.

35. Специальные типы годовых выплат:

а) пожизненный аннуитет с n-летними гарантированными выплатами;

б) аннуитет с компенсирующей доплатой;

в) страхование семейного дохода.

36. Страхование пенсионных выплат.

37. Модели коллективных рисков. Роль производящих функций моментов в анализе коллективных рисков.

38. Теория разорения. Модель Крамера–Лундберга. Коэффициент Лундберга и его связь с вероятностью разорения.


Литература


1. Bower N.L. s et. al. Actuarial mathematics. Published by the Society of Actuaries of USA. 1997/пер. Н. Бауэрс, Х. Гербер, Д. Джонс и др. Актуарная математика. – М.: Янус-К, 2001. – 655 с.

2. Гербер Х. Математика страхования жизни. – М.: Мир, 1995. – 154 с.

3. Фалин Г.И., Фалин А.И. Введение в актуарную математику. – М.: Изд-во Моск. Ун-та, 1994. – 85 с.

4. Фалин Г.И. Математические основы страхования жизни и пенсионных схем. – М.: Изд-во мех.-мат.ф-та МГУ, 1996.

5. Четыркин Е.М. Финансовая математика. – М.: Дело, 2005. – 395 с.

6. Белолипецкий А.А., Горелик В.А. Экономико-математические методы. – М.: Академия, 2010. – 368 с.


Подписано в печать 25.02.11. Формат 60 ´ 84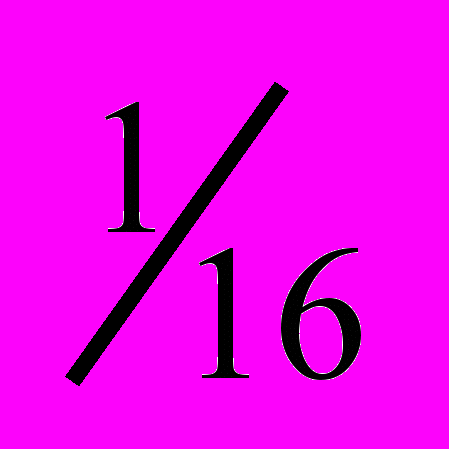. Бумага офсетная.

Печать офсетная. Усл. печ. л. 0,25. Уч.-изд. л. 0,2.

Тираж 100 экз. Заказ №


Государственное образовательное учреждение

высшего профессионального образования

Московский физико-технический институт (государственный университет)

Отдел автоматизированных издательских систем «ФИЗТЕХ-ПОЛИГРАФ»

141700, Моск. обл., г. Долгопрудный, Институтский пер., 9.