Преподавание в школе не может сводиться только к тому, чтобы вооружить учащихся определённым запасом знаний

Вид материала

Урок

Содержание Слайд 8 прочитай Слайд 9 заполни таблицу Слайд 10 запиши вывод Слайд 11, слайд 12 Медианы треугольника делят, его на шесть равнове­ликих треугольников. Способ III

Подобный материал:

• И. С. Тургенев: «Россия без каждого из нас обойтись может, но никто из нас без нее, 67.01kb.
• Анализ урока и профессиональной деятельности учителя, 168.27kb.
• Г. Х. Андресена (110 слов) Статья, 242.34kb.
• План мероприятий Примерный срок (год) реализации, 53.46kb.
• О преподавании химии в общеобразовательных учреждениях калининградской области в 2009-2010, 268.66kb.
• Безотметочное оценивание знаний учащихся в начальной школе, 322.55kb.
• Безотметочное оценивание знаний учащихся в начальной школе, 606.07kb.
• Сучетом этого строится преподавание физики в Нижнепоповской 8-летней школе, 40.09kb.
• Защита программ от нелегального копирования и использования, 117.03kb.
• Программа дисциплины Преподавание психологии в высшей школе для направления 030300, 122kb.

Муниципальное общеобразовательное учреждение Матреногезовская средняя общеобразовательная школа Алексеевского района Белгородской области


Активные формы работы на уроках математики

как фактор развития

ведущих умений и навыков учащихся


Подготовила:

учитель математики

Бутенко О.В.


2010 г.

Преподавание в школе не может сводиться только к тому, чтобы вооружить учащихся определённым запасом знаний. Необходимо добиться высокого уровня мышления, с тем, чтобы учащиеся могли в дальнейшем самостоятельно расширять и углублять свои знания, применять их в смежных областях, находить решения в новых ситуациях. Поэтому важно обучать школьников основным приёмам умственной деятельности, сформировать у них умение анализировать и сопоставлять факты, делать обобщения.

И математика , на мой взгляд, как ни какой другой предмет способна выполнить эту задачу. Вот почему основной задачей в своей педагогической деятельности считаю учить школьников думать, рассуждать, делать выводы. Для осуществления этого требуется умело организовывать мыслительную деятельность учащихся , улучшающую усвоение материала и развивающую в них внимательность, гибкость ума. Следствие чего является высокая активность учащихся при обучении.

На уроках я стараюсь давать возможность ученику экспериментировать и не бояться ошибок, воспитывать в учащихся смелость быть не согласным с учителем. Но учить школьника высказывать свои мысли можно, когда на уроке царит атмосфера дружелюбия, увлечённости, понимания. Поэтому, перед тем как приступить к изучению какой- либо темы, я много времени уделяю поискам активных форм и методов обучения, продумывая каждый урок, ибо урок, по словам В. А. Сухомлинского, первая искра, зажигающая факел любознательности.

Все рассматриваемые ниже приёмы активизации познавательной деятельности систематизировались в течение многих лет, все они используются в моей работе и приводят меня желаемому результату при обучении математике .

Так, для закрепления навыков счета и усвоения основных алгебраичес­ких формул использую «Математический тренажер».СЛАЙД 2

Задания распределены по разделам. Раздел со­стоит из нескольких вариантов, в каждом из кото­рых 20 задач, записанных в столбец.

При тренировке учащийся берет полоску (или лист) бумаги и кладет ее справа от столбца, по ко­торому собирается работать. Вычисляя, ученик за­писывает только ответы, не переписывая самого условия. Если встретилось задание, которое ученик пока не в состоянии выполнить, он пропускает его и решает следующее. За определенное время уче­ник должен записать как можно больше правиль­ных ответов. По истечении заданного времени он может сверить свои решения с ответами СЛАЙД 3 - ответы желательно поместить на оборотной стороне листа и разрешить ребятам переворачивать эти листы лишь после того, как прошло контрольное время.

Предлагаемые таблицы можно использовать для самостоятельных, проверочных и зачетных работ. Но самое выгодное — это работа с тренажером в начале урока, когда по сигналу учителя («Внима­ние, приготовились, начали!») класс работает стро­го определенное время (1—5 мин). По команде «Стоп» каждый прерывает свою работу и подсчи­тывает количество правильных ответов п, полу­ченных за время t, и скорость счета V (V = 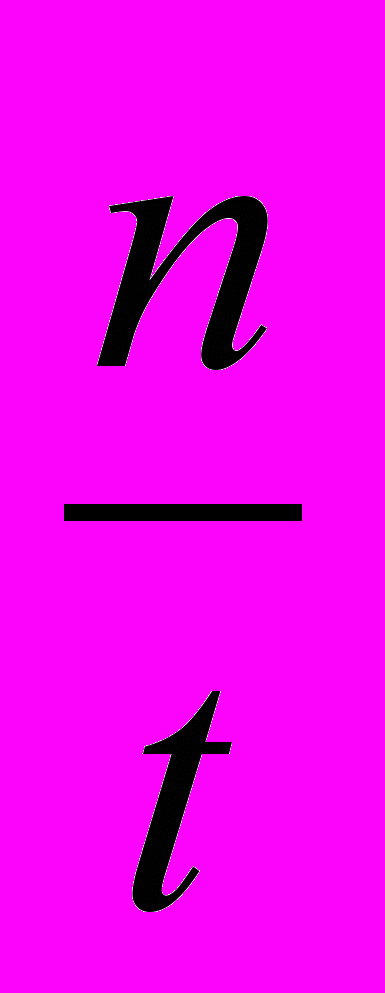). СЛАЙД 4

Время от времени для объективности есть смысл проводить контрольный счет, где проверку ответов осуществляет либо сосед по парте, либо учитель.

Время работы определяется в зависимости от уровня подготовки класса, но в любом случае, вначале стоит давать больше, затем меньше времени на одну и ту же таблицу. Например, на таблицу № 1 можно сначала уделять 3 мин и дове­сти это время до 1 мин.

Практически во всех таблицах задания послож­нее расположены в конце. Каждый ученик может работать с тренажером самостоятельно. Рост ско­рости счета — это показатель работы ученика. Таб­лицы для подсчета скорости счета даются к каждо­му заданию.

Использую очень многие игры. Игры помогают учащимся быть внимательными и незаметно для себя добиваться хороших результатов. Игровые и занимательные задачи способствуют воспитанию интереса к математике, развитию внимания, мышления. Для развития активности и внимания учащихся про вожу устный счёт элементами игры.

Авторы книги «Учимся рассуждать и доказывать» И.Л. Никольская и Е.Е. Семенов предлагают метод проведения игры «Да - Нет»: ученики могут отве­чать вслух на поставленные вопросы, но тогда игра слишком шумна. Или такой метод: поднимать фона­рики, изготовленные из цветной бумаги: красный фо­нарик означает «Нет», зеленый - «Да». Можно так­же поднимать руку при верном ответе и не подни­мать при неверном.

Я использую несколько иной вариант - графичес­кий диктант, где «Да» изображается отрезком __, а нет – уголком Λ . В результате ответов на вопросы полагается «график», по которому очень легко опре­делить, верно ответил ученик или нет.

Например, после изучения темы «Натуральные числа» составляю вопросы и объясняю, что ребята, отвечая на вопросы, должны установить, истинны или ложны следующие утверждения. СЛАЙД 5

1. Каждое натуральное число всегда записывается с помощью трех различных цифр.
   
2. Трехзначное число всегда записывается с помо­щью трех различных цифр.
   
3. Число 10000000 - наибольшее натуральное чис­ло.
   
4. Вычитание является действием, обратным сло­жению.
   
5. Вычитание подчиняется переместительному за­кону.
   
6. Число 1 - наименьшее натуральное число.
   
7. Не каждое натуральное число имеет предыду­щее.
   
8. Разность всегда меньше уменьшаемого.
   

У ребят в тетради появляется график:

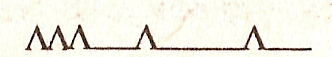
Вопросы можно составить на два варианта , и подобрать их так, что «гра­фик» может получиться одинаковым, или на один вариант.

Проверку можно осуществить различными спосо­бами:

учитель собирает ответы и проверяет;

с помощью проектора (са­мопроверка или взаимопроверка);

писать ответы под копировку (верхний лист сда­ется, а второй проверяется учеником).

После сдачи работ ответы желательно обсудить вместе.

Для правильной организации работы по формированию у учащихся познавательного интереса с помощью прогностических методов стараюсь оптимально сочетать методы как субъективного характера, так и объективного. Субъективный путь организации учебной деятельности — это методы убеждения, объяснения, информирования. Объективный — создание условий, в которых у учащегося возникли бы мотивы к учебной деятельности, чтобы он начал действовать. И тогда, если сама эта деятельность вызовет у него интерес, удовольствие, радость, азарт, то можно надеяться, что у ребенка постепенно возникнет потребность в такой деятельности, а, значит формируется устойчивый познавательный интерес к ней.

Например, чтобы вызвать у учащихся интерес к изучению формул сокращенного умножения и к их применению, организую соревнования "Учитель-класс" СЛАЙД 6 на вычисление значений числовых выражений вида 199 * 201, 25² +2 * 25 * 5 +5², (17 +3) ( 17²-17 * 3 +3²). Я выполняю вычисления быстро и устно, дети — долго и письменно. Их привлекает эта разница. У них возникает желание и самим научиться так считать, как я.

Красота всегда притягательна, в об­разовательном процессе она не оставля­ет равнодушным никого: ни учителя, ни учащихся, ни их родителей. Потому она так важна в учебном познании, с ее по­мощью можно усилить интерес детей к ма­тематической деятельности, стимулиро­вать их поиск, создать условия для еди­нения эмоционального и рационального и тем самым усилить развивающий эф­фект обучения.

В приложении «Математика» неодно­кратно приводились задания при изучении координат на плоскости. Эти задания, безусловно, по­лезны для учащихся, поскольку вызывают у них удивление, пробуждают фантазию, раз­вивают эстетические наклонности. Однако дидактическая ценность большинства таких заданий невелика, бедно и их математичес­кое содержание. Между тем, имеется нема­ло возможностей для включения красивых фигурок в содержательную математическую деятельность поискового или даже исследо­вательского характера. Красота будет при­тягивать учеников к выполнению заданий, а исследовательская направленность деятель­ности - увлекать их познавательным поис­ком, значительно возрастает интерес к учеб­ной работе.

Приведу примеры заданий исследова­тельского характера на координатной плос­кости с использованием красивых фигурок. СЛАЙД 7


СЛАЙД 8 ПРОЧИТАЙ

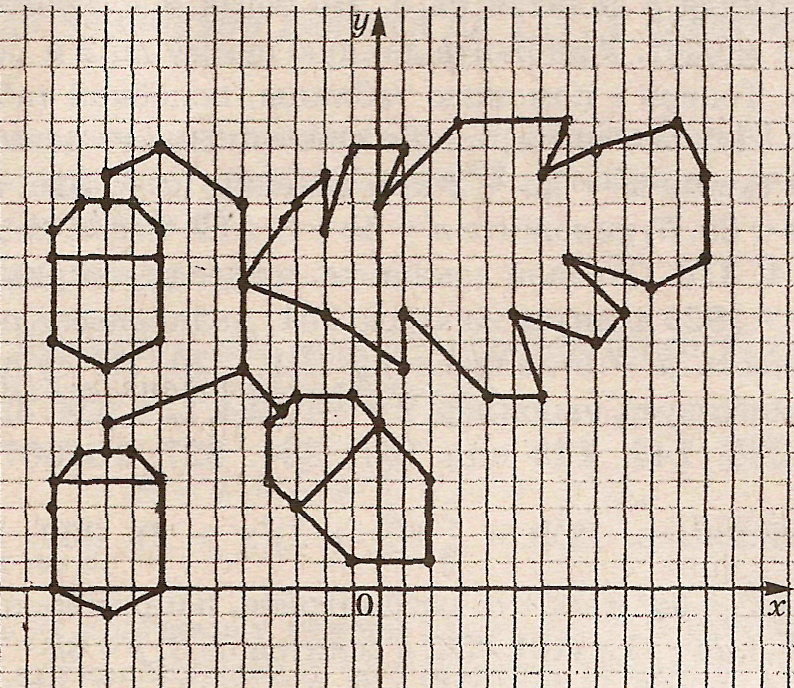На рисунке изображена веточка дуба с тремя желудями. Причем два желудя совершенно одинаковы.

ПОДУМАЙ

• Как взаимосвязаны координаты точек изображений верхнего и нижнего желудей?

• Вообще, как изменятся координаты точек фигуры, если переместить эту фигуру на некоторое число единиц вверх (вниз) по вертикали?

ВЫПОЛНИ

• Пронумеруй узловые точки изображений обоих желудей одина­ковыми числами от 1 до 9.

• Опре­дели координаты всех точек верхнего желудя и запиши их в первой строке таблицы, приведенной ниже.

• Найди координаты точек нижнего желудя и запиши их во вто­рой строке таблицы.

• Сравни координаты соответствую­щих точек изображений и сделай вывод.

СЛАЙД 9 ЗАПОЛНИ ТАБЛИЦУ

Номера узловых точек	1	2	3	4	5	6	7	8	9
Координаты узловых точек верхней фигуры
Координаты узловых точек нижней фигуры

СЛАЙД 10 ЗАПИШИ ВЫВОД

Если переместить изображение фигуры вертикально вниз (вверх) по координатной

плоскости, то абсциссы его точек _____________________________, а орди­наты ________________________________________на одно и то же число, равное_____________ ,

Iна которое выполнено перемещение.


Активизацию познавательной деятельности учащихся не представляю без активизации их внимания. Недостаточное внимание мешает ученикам принимать полноценное участие в коллективной работе на уроке, приводит к непониманию учебного материала, плохого запоминания, ошибок при выполнении заданий.

Коллективную и индивидуальную внимание учащихся активизирует такими приемами, как метод эвристической беседы, , самостоятельные задания, которые предусматривают активизацию внимания учащихся (например, самостоятельно закончить некоторое тождественное преобразование , решить уравнение, воспроизвести только что изложенное доказательства математического утверждения (или его фрагмент), выполнить задачу, аналогичное рассматриваемом учителем и т.д.), сравнение результата своих действий с образцом (контроль), прием самоконтроля на разных этапах урока, различного рода дидактической опоры (наглядно-образные или логические схемы, планы-конспекты и т.д.).

В условиях модернизации образования происходит стремительное внедрение информационных технологий в деятельность всех участников образовательного процесса. Благодаря информатизации образования совершенствуются содержание и методы обучения, педагог из источника знаний превращается в организатора деятельности обучающихся по самостоятельному приобретению новых знаний, умений и навыков.

Традиционная форма проведения урока математики не позволяет в полной мере осуществлять индивидуальный подход к каждому ученику, что актуально в современном образовании.

Одним из решений указанной проблемы на уроках математики может стать использование компьютерных технологий. Для учителя это даёт, прежде всего, экономию учебного времени. Происходит уровневая дифференциация –ученик выбирает содержание своего образования, степень усвоения. Учитель в данном случае обеспечивает возможность каждому школьнику овладеть знаниями на обязательном или более высоком уровне, исходя из личной заинтересованности самого школьника. Применение таблиц, алгоритмов, схем по предмету позволит ученику упорядочить систему своих знаний, закрепить навыки путём выполнения заданий.

Использование информационно-коммуникационных технологий возможно на различных этапах урока математики: актуализация опорных знаний, изучение и закрепление новой темы, проверочная работа.

Я заведую кабинетом информатики, поэтому и уроки математики проходят в кабинете , который оснащён всеми необходимыми техническими средствами. С помощью компьютера возможно выполнение учениками тестовых работ, в том числе и сети Интернет, что особенно актуально при подготовке к ЕГЭ. Школьники сами могут выступать в роли авторов электронных тестов. Интернет может использоваться и в других видах деятельности на занятии. Таким образом, повышается мотивация к изучению не только математики, но и информатики.

На своих уроках я использую компьютерные презентации . Активизируют внимание и интерес детей анимированные слайды. Так , например, можно «оживить» с помощью анимации текстовые задачи на движение .Освоив основные возможности компьютерной презентации, ученики самостоятельно готовят чертежи к задачам, предпочитают чаще работать у доски, чем в тетрадях. СЛАЙД 11, СЛАЙД 12

Большие возможности открываются у учителя при использовании электронных учебных пособий (электронных учебников). Совместное применение текстовой и звуковой информации, графики, видеофрагментов, анимации, принципа интерактивности нереально на бумаге. Это содействует усилению эмоционально-личностного восприятия учениками нового материала; применение электронного учебника позволяет повысить интерес к предмету математики. Таким образом, ученик становится активным соавтором урока, организует собственную работу,  одновременно контролируя себя. СЛАЙД 13 Я использую в своей работе учебное пособие «Готовимся к ЕГЭ». Оно содержит все справочные материалы в объёме, необходимом для подготовки к ЕГЭ. Специальные интерактивные тренажеры позволяют развить навыки подготовки к экзамену в тестовой форме. Программа комментирует действия ученика, выдает подсказки и ссылки на справочник в случае неверного ответа. В режиме зачета учащиеся выполняют экзаменационные задания на время.

Познавательный интерес – это один из важнейших мотивов учения. Под влиянием познавательного учебная работа даже у слабых учеников протекает более продуктивно. Но далеко не всё в учебном материале может быть для учащихся интересно. И тогда выступает источник познавательного интереса – процесс деятельности. Чтобы возбудить желание учиться нужно развивать потребность ученика заниматься познавательной деятельностью, то есть в самом процессе её учащийся должен находить привлекательные стороны.

Путь к этому лежит через разнообразную самостоятельную работу учащихся, организованную в соответствии с особенностью интереса, занимательность, а также через творческие работы учащихся.

Самостоятельное выполнение заданий – самый надёжный показатель качества знаний, умений и навыков учащихся. Ученик, получая теоретически обоснованные способы действий, знания, может самостоятельно вырабатывать подобные способы при решении поставленных проблем.

Так, при изучении темы «Наибольшее, наименьшее зна­чения функции» я использую практическую самостоятельную работу. На первом уроке идет объяснение темы, закрепление на упражнениях типа: «Найти наибольшее, наименьшее значения функции... на отрезке... или на интервале...» Подборку упраж­нений (в учебнике их очень мало) нетрудно осуществить материалам открытого банка заданий , размещенного в сети Internet. . Среди заданий на дом даю одно неожиданное: «Из квадрата со стороной 12 см изготовить открытую сверху коробку, вырезав по углам квадратики. Вычислить объем коробки».

На втором уроке предлагаю вначале самостоятельно выполнить за­дание: СЛАЙД 14 «Найти наибольшее, наименьшее значения функции V(x)=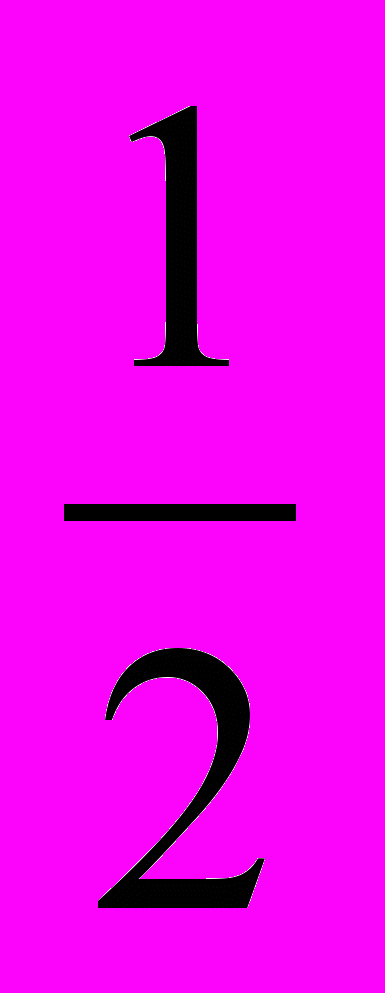x²(12—х) на отрезке [0; 12]». Это и проверка усвоения темы предыдущего урока, и возможность просмотреть домашнее задание (со­брать коробочки), и, главное, переходное задание к задачам на оптимиза­цию. Работу обязательно проверяю, например с помощью проектора. К объяснению темы приступаю с демонстрации исходного квадрата и тех коробочек, которые изготовили учащиеся, с указанием их объемов, бумажный квадрат у всех был одинакового размера, а объемы коробо­чек получились разные. Выясняем, в каком случае коробочка имеет наибольший объем. Пусть MN =x см , тогда AM = 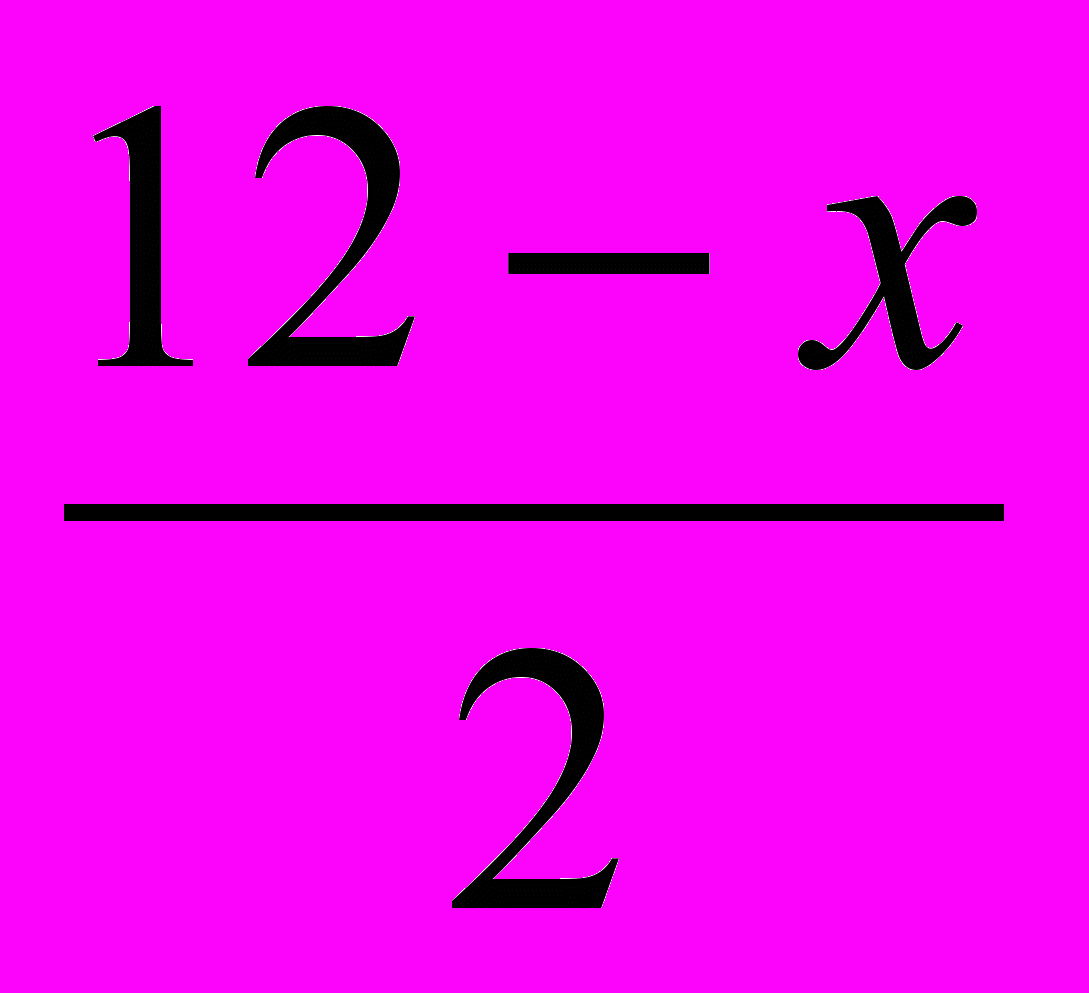см,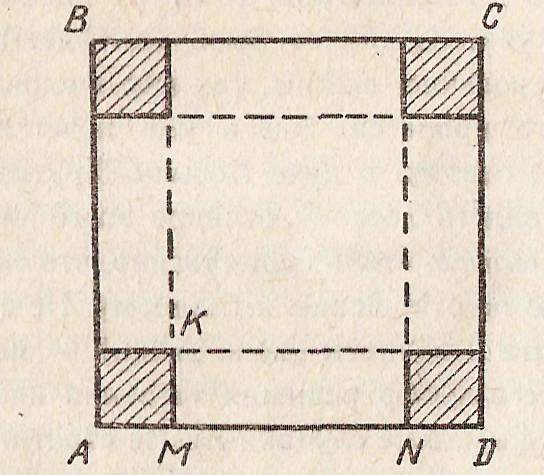



Объем коробочки: V = x². 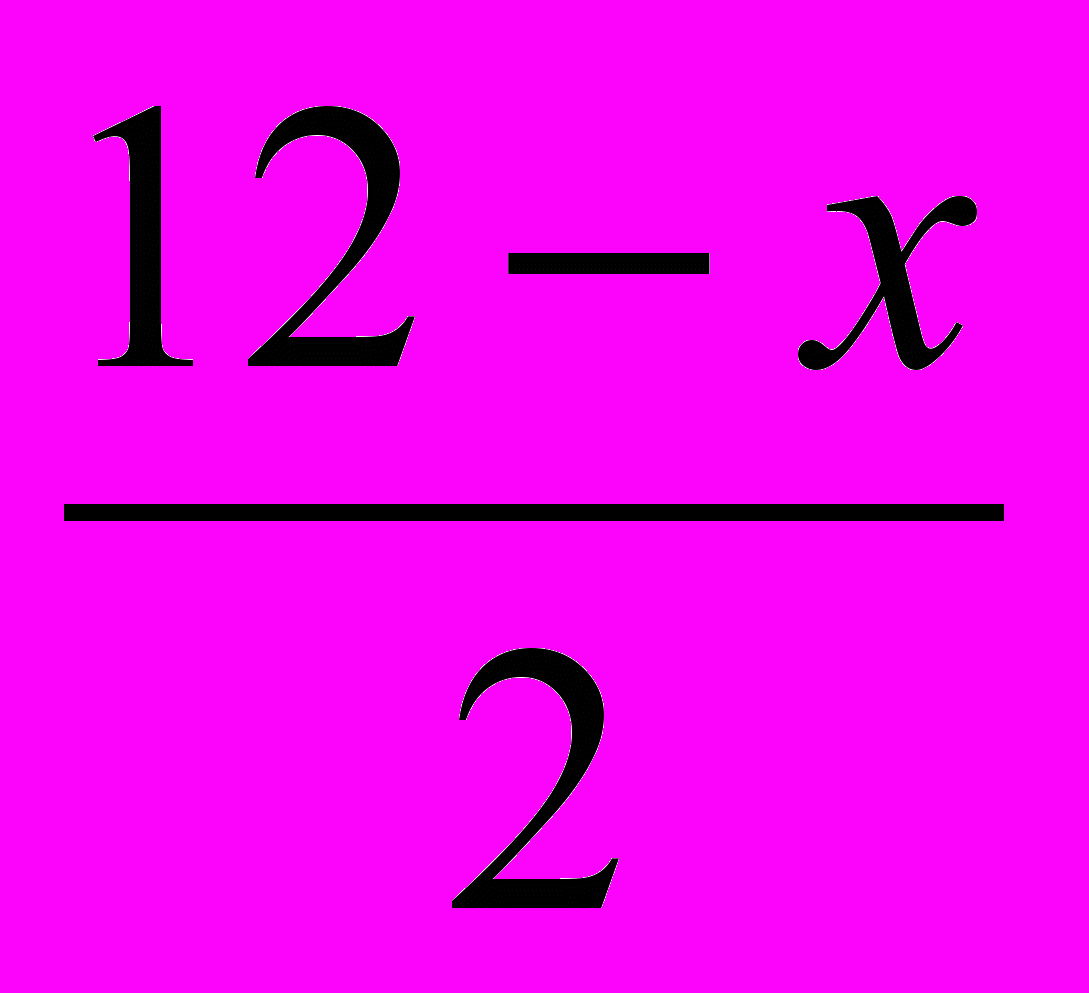= 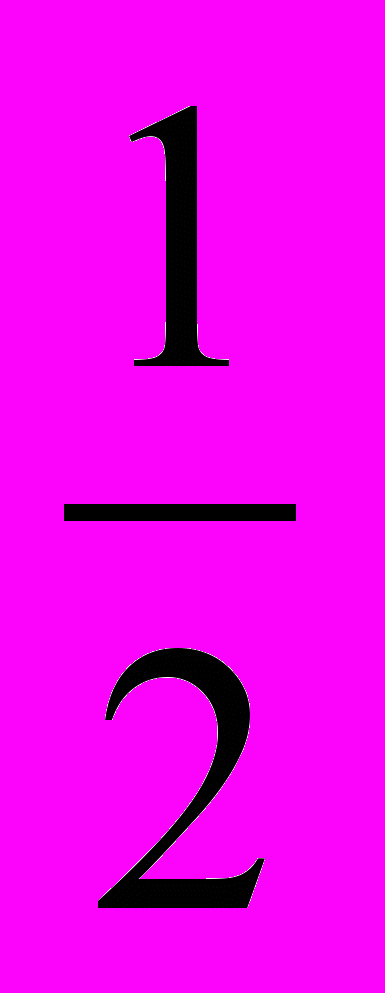x²(12—х) . Находим наибольшее значение функции V(x)=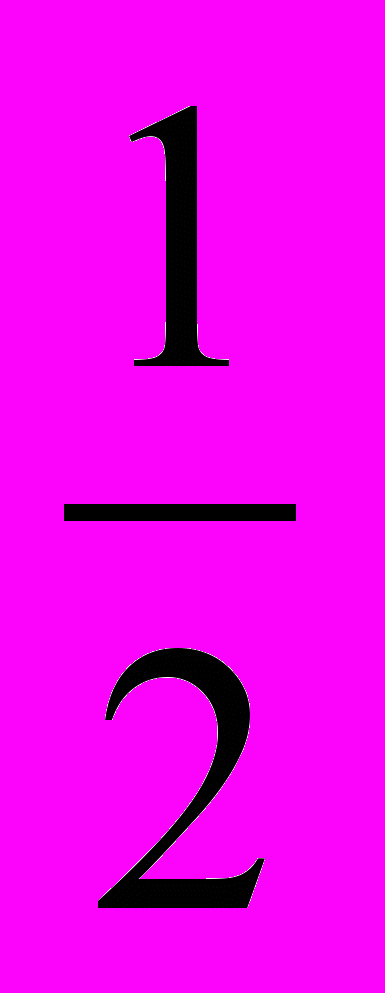x²(12—х) на отрезке [0; 12] . Эта задача была решена в начале урока.

Таким образом, в этой части урока все внимание учащихся сосре­доточивается на составлении математической модели задачи. Немаловажен и эмоциональный фактор: чья же коробочка имеет наибольший объем? Решение подобной задачи в общем виде (оно дано в учебнике) усваивается большинством учащихся легко, и чаще всего они выполняют его самостоятельно. Далее на уроке решается одна-две задачи и пред­лагается новая практическая работа: «Изготовить коробку наибольшего объема из .листа прямоугольной формы. Размер листа каждый берет свой». Обычно эта работа вызывает вопросы у слабых учеников — они получают дополнительную консультацию.

На третьем уроке комментируется выполненная практическая ра­бота, решаются задачи. Третий урок — урок самостоятельной работы.

Конечно, за три урока охватить всю тему невозможно, но предло­женный подход вызывает к ней интерес, вырабатывает определен­ный практический навык.

Одно из эффективных средств развития интереса к учебному предмету дидактическая игра. Она вызывает у детей живой интерес к процессу познания, активизирует их деятельность и помогает легче усвоить учебный материал.

В геометрии известны задачи и теоремы, которые до­пускают несколько способов решения, что, безусловно, ак­тивизирует познавательную деятельность учащихся, спо­собствует их творческому развитию. Решая задачу несколь­кими непохожими друг на друга способами, учащиеся при­влекают разнообразный теоретический материал из всего курса. Одной из таких наиболее известных теорем являет­ся теорема Пифагора, доказываемая большим количеством способов, а также задачи о свойствах биссектрисы угла делить противоположную сторону на части, пропорциональ­ные прилежащим, и задача о свойствах медиан треуголь­ника, делящих его на шесть равновеликих треугольников.

В планиметрии есть замечательная теорема, которая незаслуженно обделена вниманием авторов традиционных школьных учебников по геометрии, так как допускает несколько различных вариантов решения с привлечени­ем большого количества теоретических вопросов. Это тео­рема о свойствах медиан треугольника: СЛАЙД 15

Медианы треугольника делят, его на шесть равнове­ликих треугольников.

Чтобы доказать эту теорему, предварительно доказываем утверждение задачи: «Медиана треугольника делит его на два равновеликих треугольника». Затем класс делиться на группы, каждая из которых должна доказать теорему, одним из четырех способов. СЛАЙД 16

Способ I. Воспользоваться только что доказанным утверж­дением и свойством площадей фигур, которая формули­руется так: если фигура состоит из нескольких фигур, то ее площадь равна сумме площадей этих фигур.

Способ II Воспользоваться следующими свойствами:

1) свойством площадей треугольников, имеющих равные углы: площади треугольников, имеющих равные углы, относятся как произведение сторон, заключающих рав­ные углы;

2) свойством медиан: медианы в точке пересечения де­лятся в отношении 2:1, считая от вершины.

Способ III. Воспользоваться для вычисления площади тре­угольников формулой S= 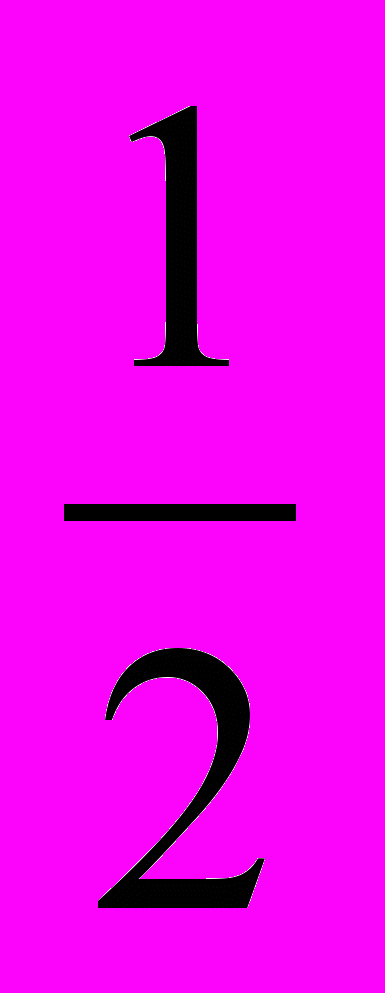absin А.

Способ IV. Воспользоваться свойством средней линии треугольника и теорему Фалеса.

Представитель каждой группы выносит решение своей задачи на доску для обсуждения.

Регулярное использование на уроках математики системы специальных задач и заданий, направленных на развитие познавательных возможностей и способностей, расширяет математический кругозор, способствует математическому развитию, повышает качество математической подготовленности, позволяет детям более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.

Из урока в урок стараюсь возбуждать, укреплять и развивать познавательные интересы учащихся, делать содержание своего предмета богатым, глубоким, привлекательным, а способы познавательной деятельности учащихся разнообразными, творческими, продуктивными.

Эффективность процесса обучения математике в наше время определяется многими факторами, но главная роль принадлежит учителю.

Наша задача, как преподавателей, прежде всего, воспитать активно мыслящую личность. От нашего умения управлять процессом формирования знаний учащихся, развитием их мышления во многом зависит, сможет ли ученик творчески подойти к изучаемому материалу.