3. Принципы классификации и классификация термодинамических процессов. Ответ

Вид материала

Документы

Содержание Диаграмма растворимости двойной системы, компоненты которой А и В ограниченно растворимы друг в друге 41. Теория возникновения скачка потенциалов на границе раздела фаз металл-раствор. Теория двойного электрического слоя. Ответ. Образование двойного электрического слоя  (металл активный) Образование двойного электрического слоя (металл малоактивный) Физическую адсорбцию Химическую адсорбцию Теория мономолекулярной адсорбции Ленгмюра Уравнение  Фрейндлиха 70. Основные свойства ВМС. Структура, форма и гибкость макромолекул. Особенности поведения их в растворе.Ответ. В зависимости от расположения звеньев в ВМС различают три вида структур. Сетчатая (пространственная или трехмерная) структура. Сетчатые полимеры представляют собой трехмерные структуры, образованные св Неограниченное набухание Ограниченное набухание

Подобный материал:

• Классификации, 174.29kb.
• Классификация камней, 798.47kb.
• I. Принципы классификации информации стр, 372.02kb.
• Вопросы к экзамену по курсу лекций «Ферменты», 26.87kb.
• Методика и порядок работ по определению, классификации и идентификации процессов. Описание, 707.68kb.
• Согласно со ст. 5 Федерального закона от 24. 11. 1996 №132-фэ «Об основах туристской, 125.21kb.
• Экзамен по патологической анатомии на всех факультетах состоит, 142.04kb.
• 1. Расчет процессов рабочего цикла дизеля, 607.38kb.
• Вопросы к экзамену по дисциплине «Финансовое право», 24.76kb.
• Программа курса тема классификация стран. Типы стран мира количественные и качественные, 105.41kb.

3. Принципы классификации и классификация термодинамических процессов.

Ответ.

Процесс изменения характеристических функций под воздействием термодинамических параметров называют термодинамическим процессом.

         Используется несколько типов классификации термодинамических процессов:

• по мониторингу за изменением параметров термодинамические процессы подразделяются на:
  

         1) изотермический (Т = const.);

         2) изобарический    (Р = const.);

         3) изохорический    (V = const.);

         4) адиабатный         (А = const.);

         5) неравновесный    (ΔР ≠ ΔТ ≠ ΔV ≠ 0);

         6) равновесный        (ΔР = ΔТ = ΔV = 0).

• по направлению термодинамического процесса
  

1) обратимый процесс (допускающий возможность возвращения системы в исходное состояние без того, чтобы в окружающей среде остались какие-либо изменения.);

                   2) необратимый процесс (идет только в одном направлении).

• по характеру взаимодействия с окружающей средой:
  

                   1) самопроизвольный процесс (совершается под воздействием внутренней энергии системы);

                   2) вынужденный процесс (совершается под воздействием энергии окружающей среды).


12. Вычислить тепловой эффект реакции: СО + NH_3(г) = HCN_(г) + H₂O_(г) при 25⁰С, если энтропия образования аммиака, цианистого водорода, водяного пара и оксида углерода (II) соответственно равны: -45,19; -31,2; -241,8; -110,5 кДж/моль.

Решение.

Тепловой эффект химической реакции равен разности сумм теплот образования продуктов реакции и исходных веществ, умноженных на стехиометрические коэффициенты.

           

Для реакции: СО + NH_3(г) = HCN_(г) + H₂O_(г)

∆H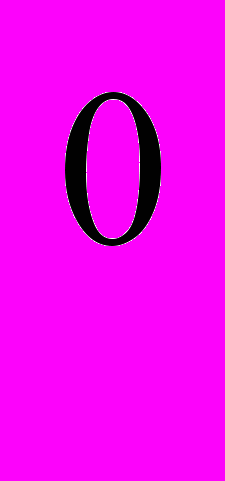_{298 х.р.} = ∆H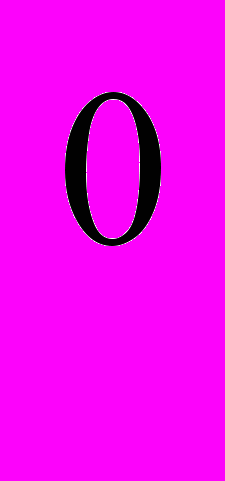₂₉₈ (Н₂О_(г.)) + ∆H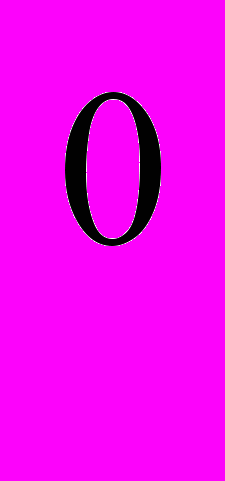₂₉₈ (HCN_(г.)) - ∆H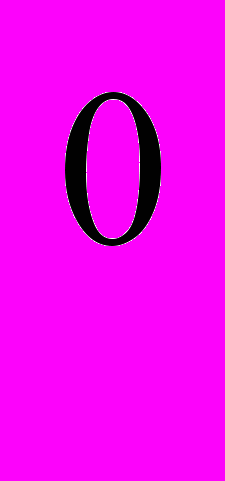₂₉₈ (NH_{3 (г)}) - ∆H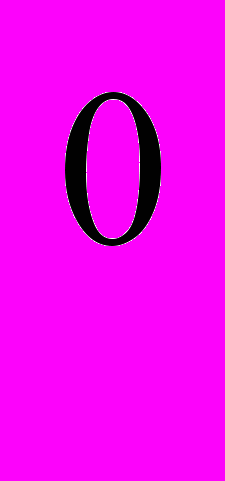₂₉₈ (СО _(г)) =

= (-241.8) + (-31,2) - (-45,19) – (-110,5) = -117,31 кДж

В данной реакции выделяется 117,31 кДж


29. Диаграммы состояния ограниченно растворимых друг в друге жидкостей. Правило рычага.

Ответ.

П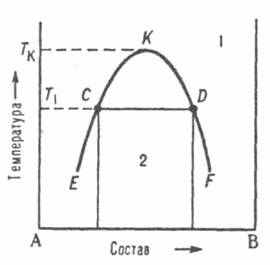ри отсутствии в системе твердых фаз диаграмма состояния состоит из области существования одной жидкой фазы (области гомогенности) и области сосуществования двух насыщенных жидких растворов разного состава, образующих несмешивающиеся друг с другом слои. Кривая, разделяющая эти области, называется бинодалью. Так, при температуре Т₁ в равновесии находятся раствор компонента В в А (его состав отвечает точке С) и раствор А в В (его состав отвечает точке D). Если однородный раствор 1 охладить до температуры Т₁, он распадется на две жидкие фазы.


Диаграмма растворимости двойной системы, компоненты которой А и В ограниченно растворимы друг в друге;

1 - область существования однородного раствора,

2 - область сосуществования двух насыщенных растворов;

ECKDF - бинодаль,

CD - нода,

К - верхняя критическая точка растворимости.


Обычно при повышении температуры взаимная растворимость жидкостей увеличивается, поэтому по своим свойствам оба насыщенных раствора, составы которых изменяются по отрезкам бинодали ЕК и KF, сближаются. Наконец, при температуре T_к различие между ними исчезает; эта температура называется критической температурой растворимости (смешения), выше нее может существовать лишь одна жидкая фаза. Большинство систем с расслоением растворов характеризуются только одной критической температурой растворимости, чаще всего верхней, т. е. на диаграмме состояния имеют незамкнутую снизу бинодаль. В некоторых системах бинодаль имеет форму замкнутой кривой (овал), т. е. система имеет две температуры смешения верхнюю и нижнюю.

В точках, расположенных в гетерогенных областях диаграммы можно определить состав равновесных фаз, а также число молей или массу этих фаз. Это возможно осуществить с помощью правила рычага: соотношение фаз в любой точке отрезка (при любой тем­пературе) опре­деляется плечами горизонтального ры­чага, проведенного через данную точку.


41. Теория возникновения скачка потенциалов на границе раздела фаз металл-раствор. Теория двойного электрического слоя.

Ответ.

Существует несколько теорий, объясняющих механизм возникновения скачка потенциала на границе раствор - металл. Наиболее современной является сольватационная теория электродного потенциала. Согласно этой теории скачок потенциала обусловлен двумя процессами:

1. Диссоциацией атомов металла на ионы и электроны внутри металла.

2. Сольватацией ионов металла, находящихся на поверхности металла, при соприкосновении их с раствором, содержащим молекулы растворителя. Обе стадии и общая реакция на границе раствор - металл могу быть записаны в следующем виде:



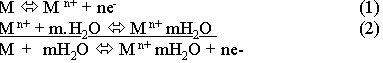
Каждая стадия имеет отдельную энергетическую характеристику: для первой - это работа выхода катиона Е_m , для второй - энергия сольватации Е_s. Соотношение: Е_m /Е_s определяет начальное направление процесса при контакте металла с раствором, заряд и потенциал, возникающие на границе раздела фаз.

Работа выхода катиона и энергия сольватации зависят от природы металла, иона и растворителя. Следовательно соотношение между Е_m и Е_s для различных металлов и растворителей неодинаково.

При Е s>Е m начальный процесс будет заключаться в переходе металла в раствор:



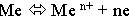
с последующей гидратацией ионов



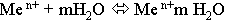
В этом случае металл получает отрицательный, а раствор положительный заряды.

Если Е s<Е m,то начальный процесс будет представлять собой выделение металла из раствора:



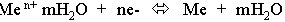
и металл получит положительный заряд, а раствор отрицательный. Процесс разделения зарядов на границе будет происходить до тех пор, пока энергия катионов металла на поверхности не станет равной энергии катионов в растворе. При их равенстве на границе раствор - металл устанавливается равновесие

Me + mH₂O <= >M n+mH₂O + ne

Таким образом, на границе металл - раствор возникает двойной электрический слой. Создается пограничная разность потенциалов, называемая электронным потенциалом.

Е_m и Е_s зависят от природы растворителя. Если жидкая вода - чистая вода, то качественно картина для всех металлов однозначна металл заряжается отрицательно, а прилежащий слой жидкости - положительно. Количественно же концентрация Meⁿ⁺ может очень сильно отличаться для различных металлов.

Если погрузить металлический электрод в раствор его соли, то могут реализоваться два механизма образования двойного электрического слоя. Химически активные металлы, такие как Na, Al, Zn и т.п., характеризуются большой разностью Е_s > Е_m и металл заряжается отрицательно.



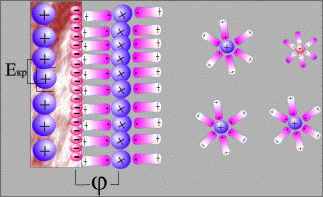
Образование двойного электрического слоя  (металл активный)

При погружении благородных (малоактивных) металлов Cu, Ag, Au и т.д. в раствор своей соли Е_s < Е_m. В этом случае происходит осаждение ионов металла на электроде, который при этом заряжается положительно, а в при электродном пространстве накапливается избыточный отрицательный заряд за счет анионов соли или ионов OH-



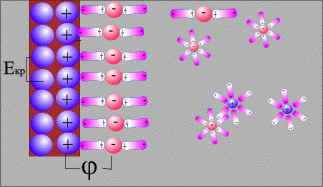
Образование двойного электрического слоя (металл малоактивный)

Абсолютное значение электродного потенциала измерить невозможно, поскольку введение любых измерительных зондов неизбежно приводит к новой контактной разности потенциалов. В связи с этим измеряют разность потенциалов между данным электродом и электродом сравнения, потенциал которого условно принимают равным нулю.

.


54. Адсорбция на твердых адсорбентах. Уравнение Фрейндлиха. Теория адсорбции Ленгмюра и его уравнения. Определение констант уравнения Фрейндлиха и Ленгмюра.

Ответ.

Адсорбция на твердых адсорбентах вызывается физическими или химическими силами, соответственно различают:

Физическую адсорбцию – возникает за счет Ван-дер-ваальсовых взаимодействий. Она характеризуется обратимостью и уменьшением адсорбции при повышении температуры. Например, адсорбция инертных газов на угле.

Химическую адсорбцию – осуществляется путем химического взаимодействия молекул адсорбента и адсорбата. Обычно необратима и локализована, повышение температуры способствует ее протеканию. Например, адсорбция кислорода на вольфраме при высоких температурах.

Обычно протекает физико-химическая адсорбция, когда основная масса адсорбированного вещества связывается сравнительно слабо и лишь небольшая часть – прочно.

Теория мономолекулярной адсорбции Ленгмюра основывается на следующих положениях.

1)  Адсорбция является локализованной и вызывается силами, близкими к химическим.

2)  Адсорбция происходит не на всей поверхности адсорбента, а на активных центрах, которыми являются выступы либо впадины на поверхности адсорбента, характеризующиеся наличием т.н. свободных валентностей. Активные центры считаются независимыми (т.е. один активный центр не влияет на адсорбционную способность других), и тождественными.

3)  Каждый активный центр способен взаимодействовать только с одной молекулой адсорбата; в результате на поверхности может образоваться только один слой адсорбированных молекул.

4)  Процесс адсорбции является обратимым и равновесным – адсорбированная молекула удерживается активным центром некоторое время, после чего десорбируется; т.о., через некоторое время между процессами адсорбции и десорбции устанавливается динамическое равновесие.
 

В состоянии равновесия скорость адсорбции равна скорости десорбции. Скорость десорбции прямо пропорциональна доле занятых активных центров (х), а скорость адсорбции прямо пропорциональна произведению концентрации адсорбата на долю свободных активных центров (1 – х): 

и

Максимально возможная величина адсорбции Г_о достигается при условии, что все активные центры заняты молекулами адсорбата, т.е. х = 1. Отсюда следует, что х = Г / Г_о. тогда:

(1) или (2)

Уравнение (2) есть изотерма мономолекулярной адсорбции, связывающая величину адсорбции Г с концентрацией адсорбата С.

Здесь b – некоторая постоянная для данной пары адсорбент-адсорбат величина (отношение констант скоростей десорбции и адсорбции), численно равная концентрации адсорбата, при которой занята половина активных центров. При описании процесса адсорбции газов в уравнении концентрация может быть заменена пропорциональной величиной парциального давления газа:



Теория мономолекулярной адсорбции Ленгмюра применима для описания некоторых процессов адсорбции газов и растворенных веществ при небольших давлениях (концентрациях) адсорбата.


Уравнение  Фрейндлиха

Теоретические представления, развитые Ленгмюром и Поляни, в значительной степени идеализируют и упрощают истинную картину адсорбции. На самом деле поверхность адсорбента неоднородна, между адсорбированными частицами имеет место взаимодействие, активные центры не являются полностью независимыми друг от друга и т.д. Все это усложняет вид уравнения изотермы. Г. Фрейндлих показал, что при постоянной температуре число молей адсорбированного газа или растворенного вещества, приходящееся на единицу массы адсорбента (т.н. удельная адсорбция x/m), пропорционально равновесному давлению (для газа) или равновесной концентрации (для веществ, адсорбируемых из раствора) адсорбента, возведенным в некоторую степень, которая всегда меньше единицы:

или                           

Показатель степени n и коэффициент пропорциональности а в уравнении Фрейндлиха определяются экспериментально. Логарифмируя уравнения , получаем:

         или          ,

Где х – количество адсорбированного вещества; m – масса адсорбента; a и n – константы.       

Т.о., зависимость логарифма удельной адсорбции от логарифма концентрации (давления) графически выражается прямой линией, отсекающей на оси ординат отрезок, равный lg a, тангенс угла наклона которой к оси абсцисс равен по величине показателю степени при давлении или концентрации:

                        

70. Основные свойства ВМС. Структура, форма и гибкость макромолекул. Особенности поведения их в растворе.


Ответ.


Макромолекулы состоят из большого числа (сотен и тысяч) атомов, связанных между собой основными химическими связями (обычно – ковалентными, для которых характерна определенная пространственная направленность).

Макромолекула – это молекула высокомолекулярного вещества, состоящая из многократно повторяющихся атомных групп (одного или нескольких видов), обычно называемых структурными звеньями. Число, которым выражается количество повторяющихся звеньев, называется коэффициентом или степенью полимеризации. В различных ВМС степень полимеризации в среднем имеет величину от нескольких сотен до нескольких десятков тысяч. Число звеньев у отдельных макромолекул того же химического состава может существенно колебаться. Таким образом, высокомолекулярные вещества являются смесями молекул с различными коэффициентами полимеризации (смеси полимергомологов). Эта их особенность называется полидисперсностью. Вследствие этого по отношению к ВМС можно говорить лишь о средних значениях молекулярных масс.

В зависимости от расположения звеньев в ВМС различают три вида структур.

Линейная (цепная) структура. В макромолекулах этой структуры каждое звено связано только с соседними звеньями, образуя неразветвленную цепь главных валентностей.

Разветвленная структура образуется при ответвлении от главной цепи боковых цепей, вследствие связи некоторых звеньев более чем с двумя соседними. Если боковые цепи располагаются по одну сторону основной цепи, то такое размещение атомов называется цис-положением, а расположение по разные стороны – транс-положением. Получены также, изотактические полимеры, отличающиеся особо регулярным строением макромолекул. В них при правильном чередовании звеньев боковые группы располагаются симметрично по спирали.

Сетчатая (пространственная или трехмерная) структура. Сетчатые полимеры представляют собой трехмерные структуры, образованные связанными между собой цепями.

Если звенья полимера состоят из одинаковых групп, их называют гомополимерами, а если из повторяющихся нескольких различных групп атомов, - сополимерами. Если в цепи подряд расположено по несколько одинаковых групп, а затем несколько других их называют блок-сополимерами.

Физико-химические и механические свойства ВМС обусловлены химическим строением, степенью полимеризации, расположением структурных звеньев в пространстве. Линейные макромолекулы обладают значительной гибкостью, которая является следствием возможности поворота звеньев вокруг соседних. Повороты звеньев являются следствием тепловых колебаний, которые с ростом температуры облегчаются. За счет поворотов звеньев макромолекулы сравнительно легко скручиваются, переходя из распрямленного состояния.

Особенности поведения ВМС в растворе.

Растворению высокополимера предшествует его набухание – полимер поглощает значительное количество растворителя, увеличиваясь в объеме и весе. Набухание не всегда заканчивается растворением.

Неограниченное набухание – заканчивается растворением, в этом случае связь между макромолекулами полимера слабая, межмолекулярная. Энергии теплового движения молекул растворителя достаточно для разделения молекул полимера.

Ограниченное набухание – не переходит в растворение, такие полимеры называют «сшитыми» (резина – в ней макромолекулы каучука соединены через молекулы серы), а так же макромолекулы, имеющие большое количество полярных группировок (белки).

Если обозначить массу полимера до набухания m₀, а массу полимера после набухания m, то отношение 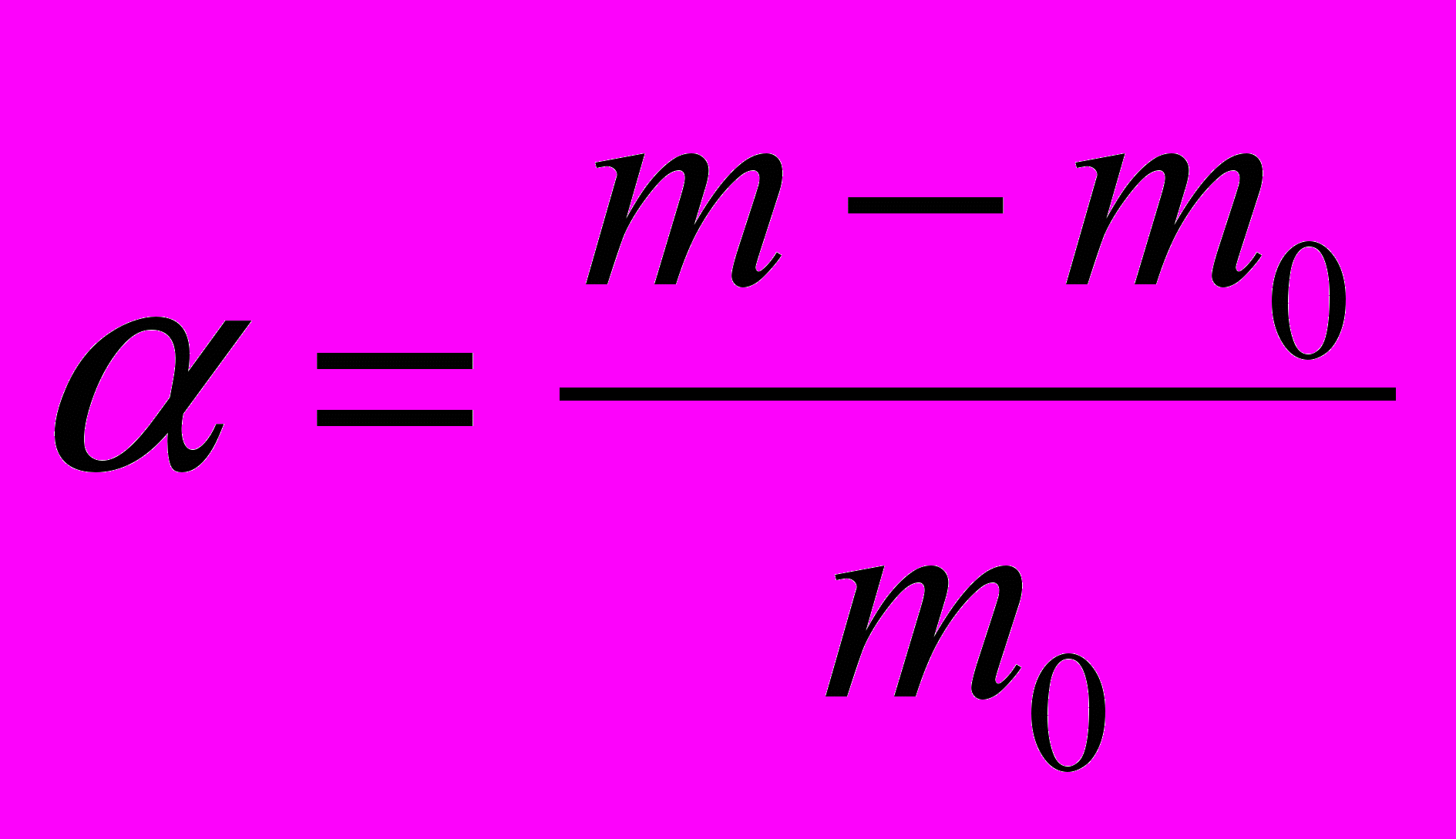можно назвать степенью набухания. Выраженная таким образом степень набухания численно равна количеству жидкости поглощенной одним килограммом полимера.


81. Вычислить ра_H+ и степень диссоциации в 0, 1 м растворе двухлоруксусной кислоты (К_а = 5 _*10^-2), содержащем, кроме того, 0,1 м хлорида натрия.

Решение.

Ионная сила раствора определяется ионами сильного электролита:

NaCl = Na⁺ + Cl^-

концентрации ионов натрия и хлора можно принять равными 0,1 моль/л, тогда ионная сила раствора:

.

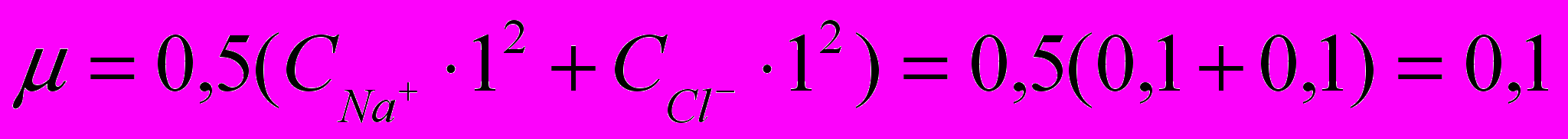Для данной ионной силы по справочнику найдем значение коэффициента активности для ионов Н⁺ и CHCl₂COO^-: fH⁺=0,87, fCHCl2COO^-=0,76

CHCl₂COOH CHCl₂COO^- + H⁺

Пусть диссоциирует х моль кислоты, тогда равновесные активности ионов CHCl₂COO^- и H⁺ соответственно равны 0,76х и 0,87х, а кислоты (0,1 – х) моль/л.





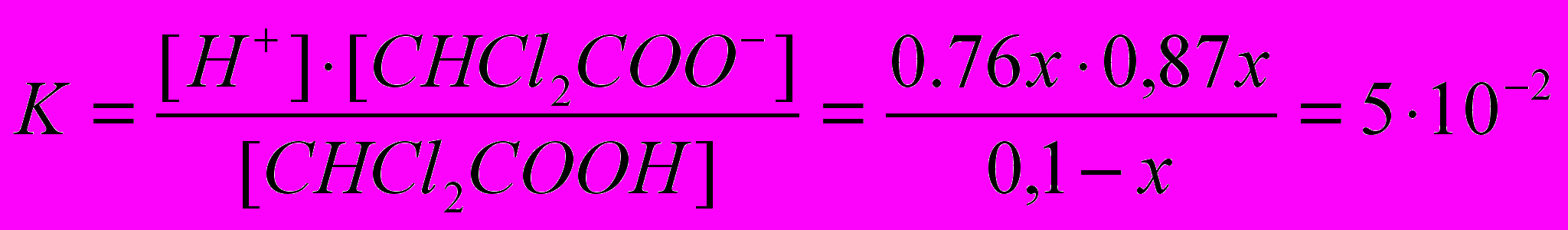
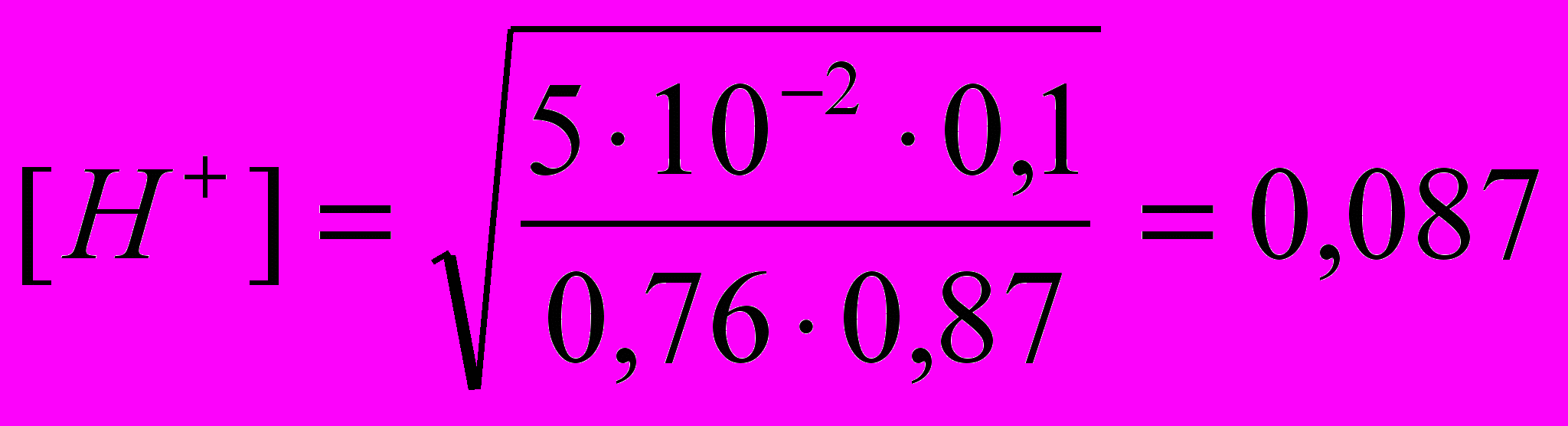
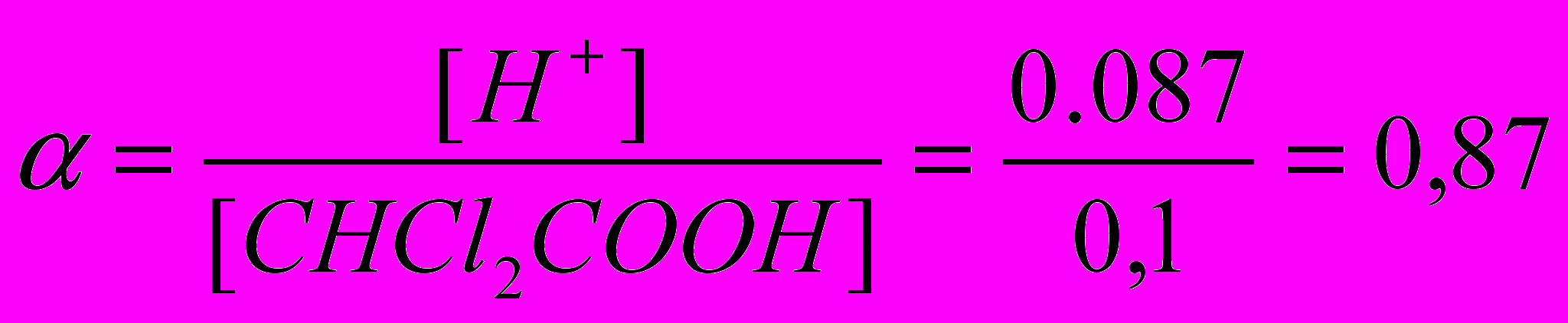или 87%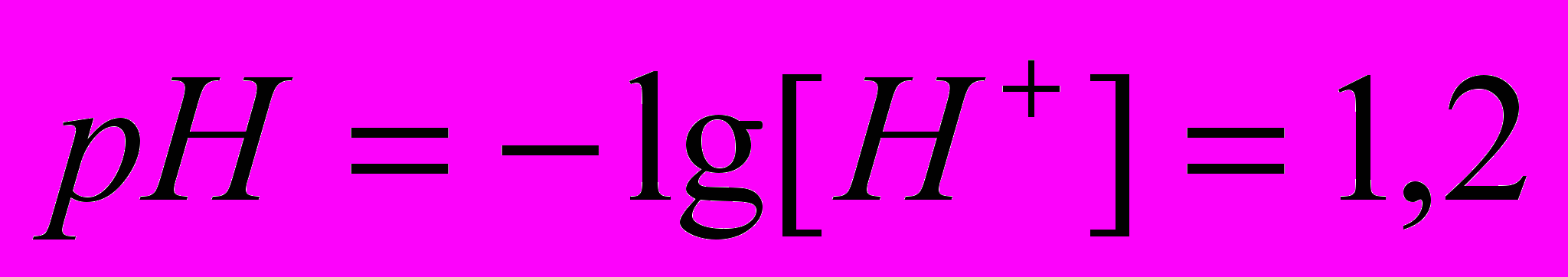



100. Определить рН исследуемого раствора с помощью гальванического элемента, составленного из каломельного и стеклянного электродов. ЭДС элемента при 298 К равна 0,52 В, 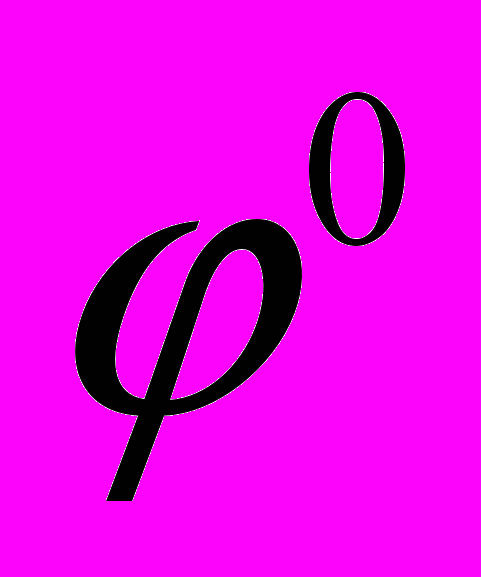_калом =0,285 В, а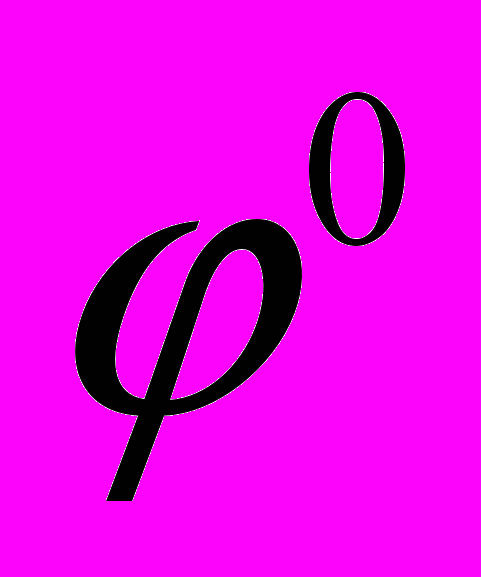_стекл = 0,35 В. Запишите гальванический элемент, реакции протекающие на электродах.

Решение.

Hg,Hd₂Cl₂Ag, |Cl^-| исследуемый раствор |стекл. мембрана| |H⁺ | AgCl

Каломельный электрод обратим относительно анионов хлора, ему отвечает реакция:

2Hg + 2Cl^- - 2е = Hd₂Cl₂

Уравнение Нернста для него имеет вид:

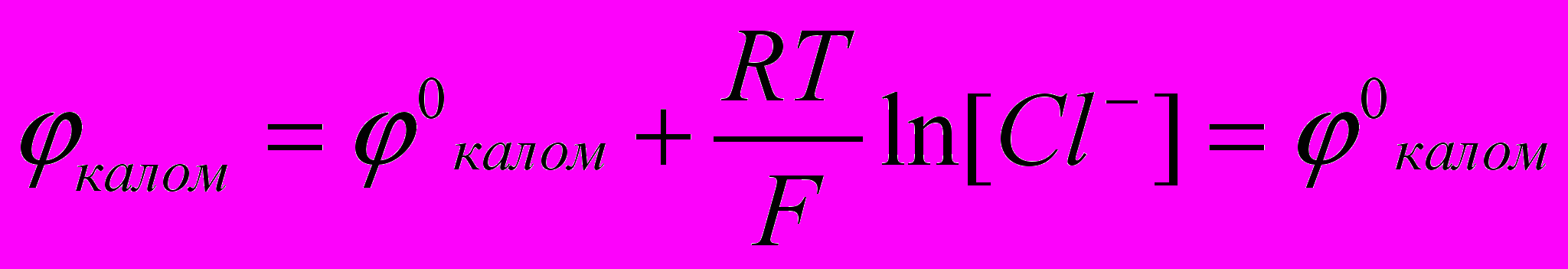
Потенциал стеклянного электрода с водородной функцией, т.е. обратимого по отношению к иону Н⁺ выражается уравнением:



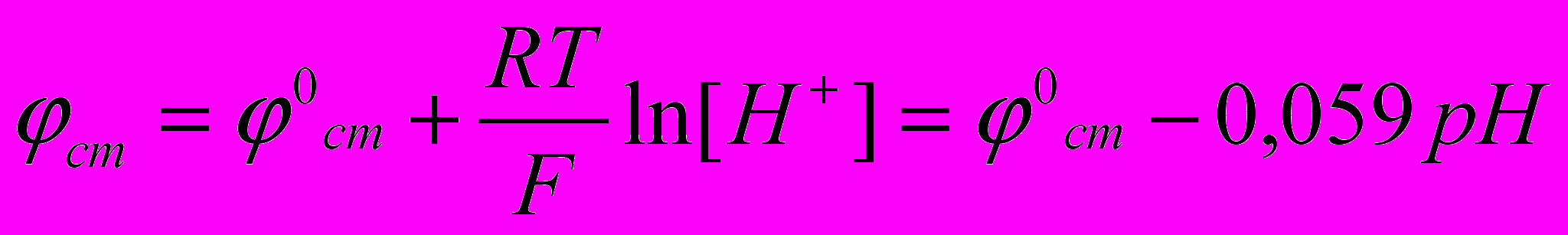
ЭДС элемента равна:

Е = _стекл - _калом , отсюда _стекл = Е - _калом = 0,52 – 0,285 = 0,235В

тогда

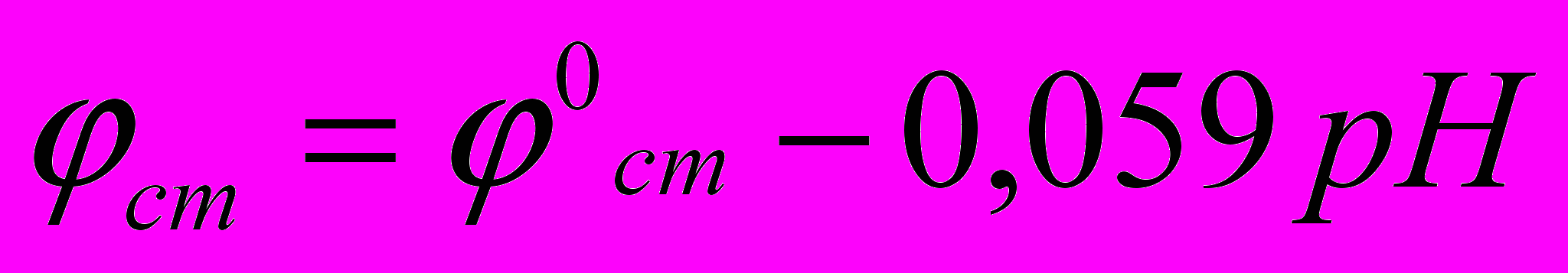, или 0,235 = 0,35 – 0,059рН

Отсюда рН = 1,1


     


106. Рассчитать поверхностный избыток для 0,1 М раствора органических кислот при 298 К, если поверхностная активность пропановой кислоты 0,89, бутановой 0,29, пентановой 0,085. Соблюдается ли для приведенного ряда правило Траубе?

Решение.

По уравнению изотермы адсорбции Гиббса находим поверхностный избыток: 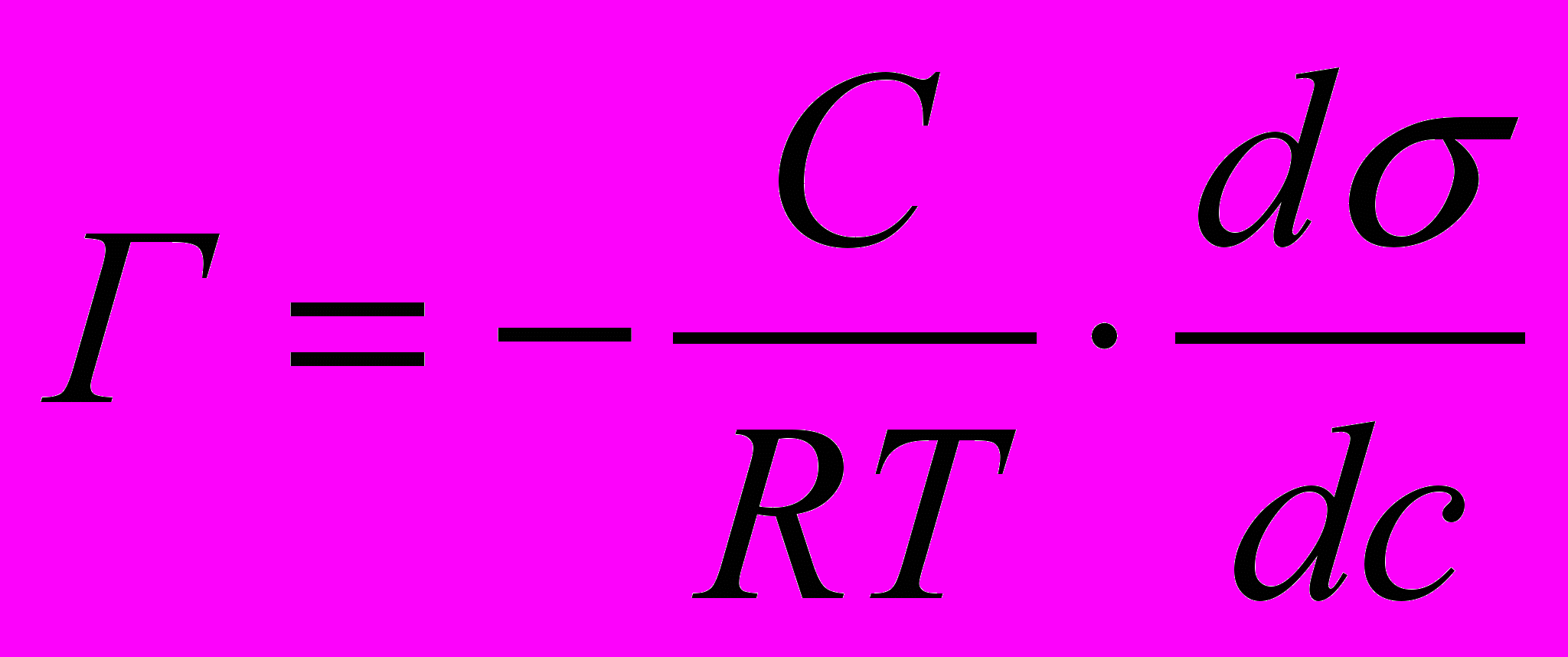, величина q = 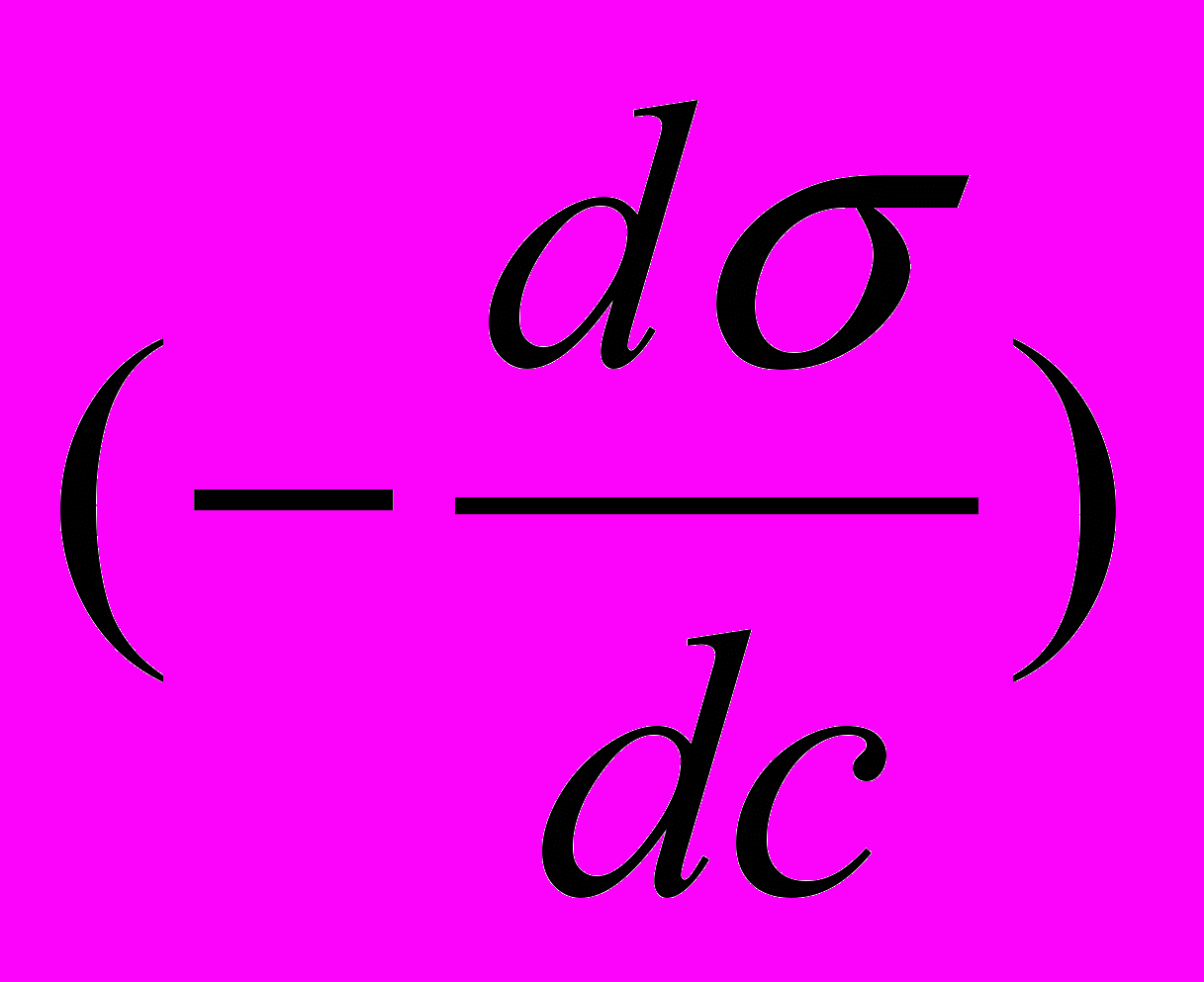- поверхностная активность, тогда:

Для раствора пропановой кислоты:

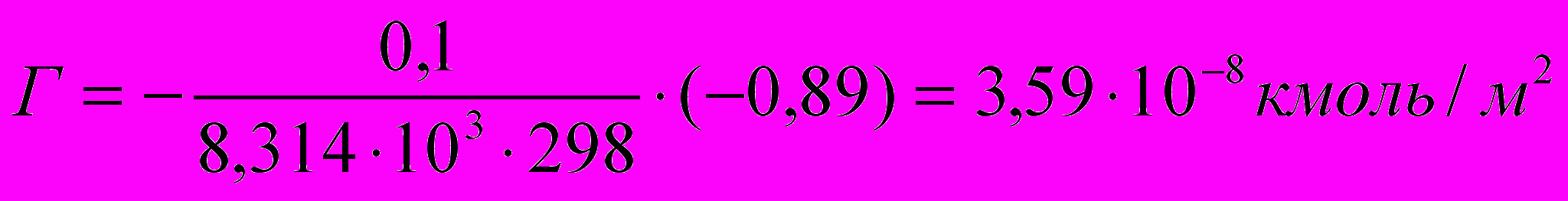
Для раствора бутановой кислоты:

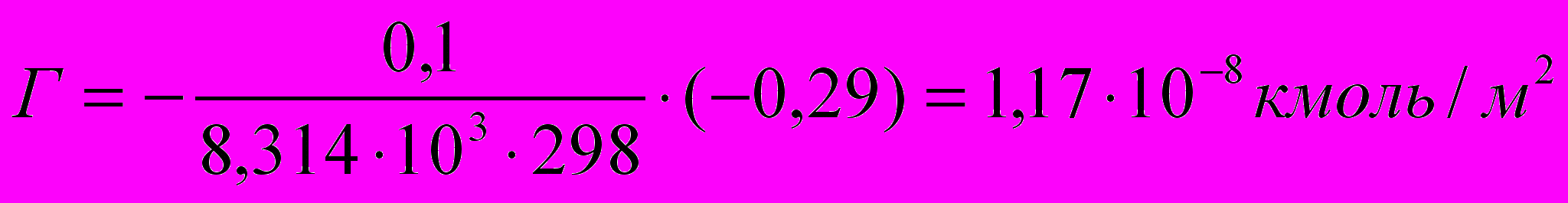
Для раствора пентановой кислоты:

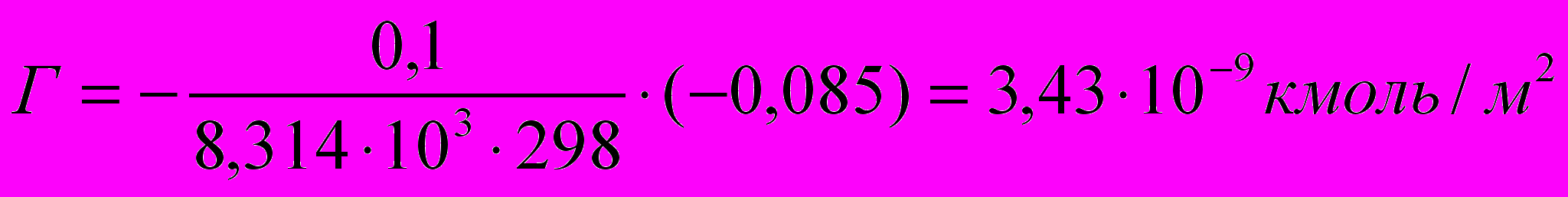
Согласно правилу Траубе для водных растворов ПАВ поверхностная активность жирных кислот, спиртов, аминов и других веществ в гомологических рядах на границе раствор-воздух возрастает в 3,2 раза при увеличении углеводородной цепи на каждую СН₂- группу:

q _n+1 / q _n =const ≈ 3,2,

где n - число метиленовых групп, тогда:





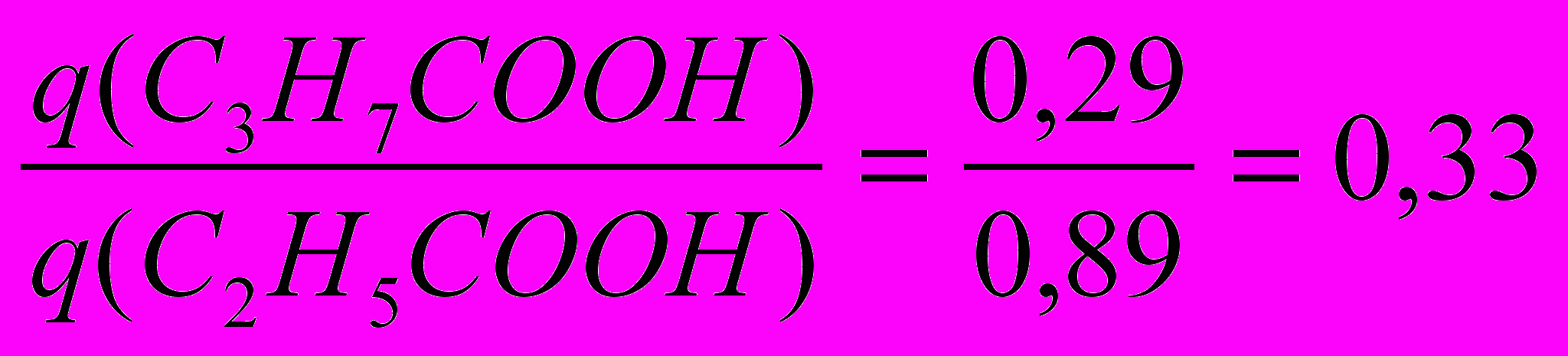
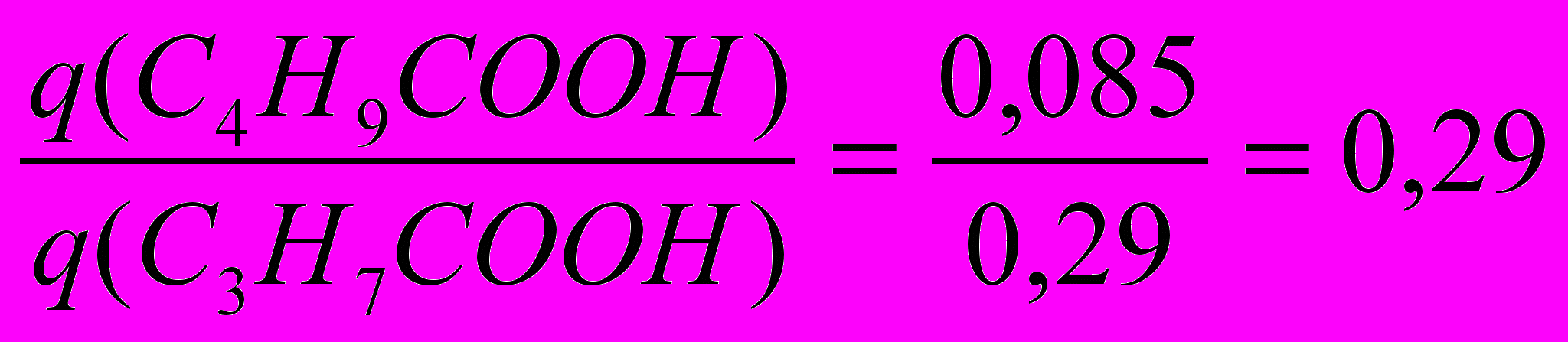
Для приведенного ряда растворов правило Траубе не соблюдается.

159. Коллоидный раствор получен в результате реакции обмена при смешивании равных объемов 0,002 н раствора FeCl₃ и 0,01 н раствора K₄[Fe(CN)₆]. Напишите и объясните формулу мицеллы золя и схему ее строения. Покажите расчетами, какой из электролитов: K₂SO₄; Mg(NO₃)₂; NH₄Cl, будет иметь меньший порог коагуляции для получения золя.

Решение.

4FeCl₃ + 3K₄[Fe(CN)₆] = Fe₄[Fe(CN)₆]₃ + 12KCl

При заданных концентрациях будет избыток K₄[Fe(CN)₆]. В результате реакции в растворе останутся ионы К⁺, Cl^-, [Fe(CN)₆]^4-.

Твердые частицы Fe₄[Fe(CN)₆]₃ будут составлять ядро мицеллы золя,

т.о. ядро – m Fe₄[Fe(CN)₆]₃.

В соответствии с правилом избирательной адсорбции ионов Пескова-Фаянса на поверхности ядра будут адсорбироваться ионы [Fe(CN)₆]^4-, поэтому адсорбционный слой состоит из n[Fe(CN)₆]^4-. В результате адсорбции ядро приобретает отрицательный заряд (равный +4n). За счет электрического взаимодействия к отрицательно заряженному ядру будут притягиваться положительно заряженные ионы К⁺, образуется слой противоионов – 4(n-x) К⁺.

Сумма зарядов адсорбционного слоя и слоя противоионов будет составлять заряд гранулы:

(-4)_*n + (+1)_*4_*(n-x) = -4n + 4n – 4x = -4x

Поскольку заряд гранулы -4х, то для нейтрализации понадобится 4х ионов K⁺,

т.о. диффузный слой – 4х K⁺.

Формула мицеллы золя:

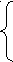
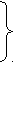_-4х

m Fe₄[Fe(CN)₆]_{3 *} n[Fe(CN)₆]^4- _* 4(n-x) К⁺ _* 4x К⁺


В соответствии с правилом Шульце-Гарди:

• коагулирующий ион должен иметь заряд, противоположный заряду гранулы;
  
• чем выше заряд иона, тем выше его коагулирующая способность.
  

Коагулировать этот золь будут положительно заряженные ионы. Из имеющихся положительных ионов: K⁺; Mg²⁺; NH₄⁺, наибольший заряд имеет ион Mg²⁺. Поэтому наименьший порог коагуляции будет иметь Mg(NO₃)_2.


168. Вычислить относительную, удельную и приведенную вязкость 0,1М раствора спирта при комнатной температуре (22⁰С), если он вытекает из вискозиметра в течение 6 мин 45 сек, а для такого же объема воды при тех же условиях требуется 1 мин 45 сек. При расчете учесть, что р=0,809 г/см³, р_о = 0,996 г/см³. Вязкость воды при 22⁰С равна 1 сантипуаз.

Решение.

Относительная вязкость определяется как отношение вязкости раствора 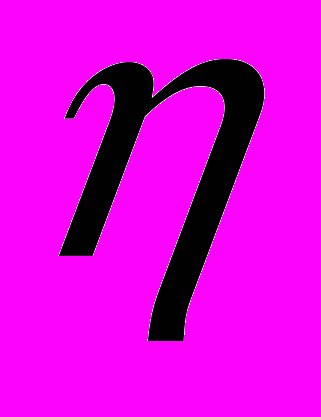к вязкости чистого растворителя :



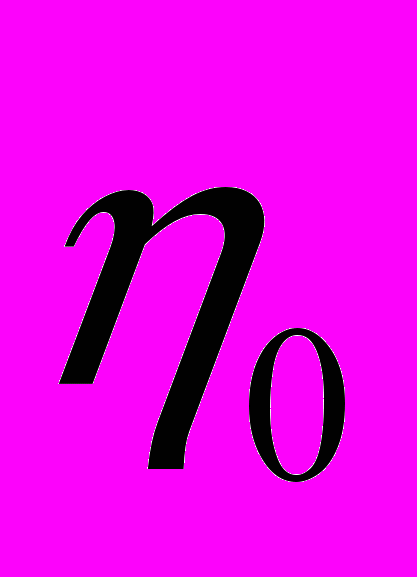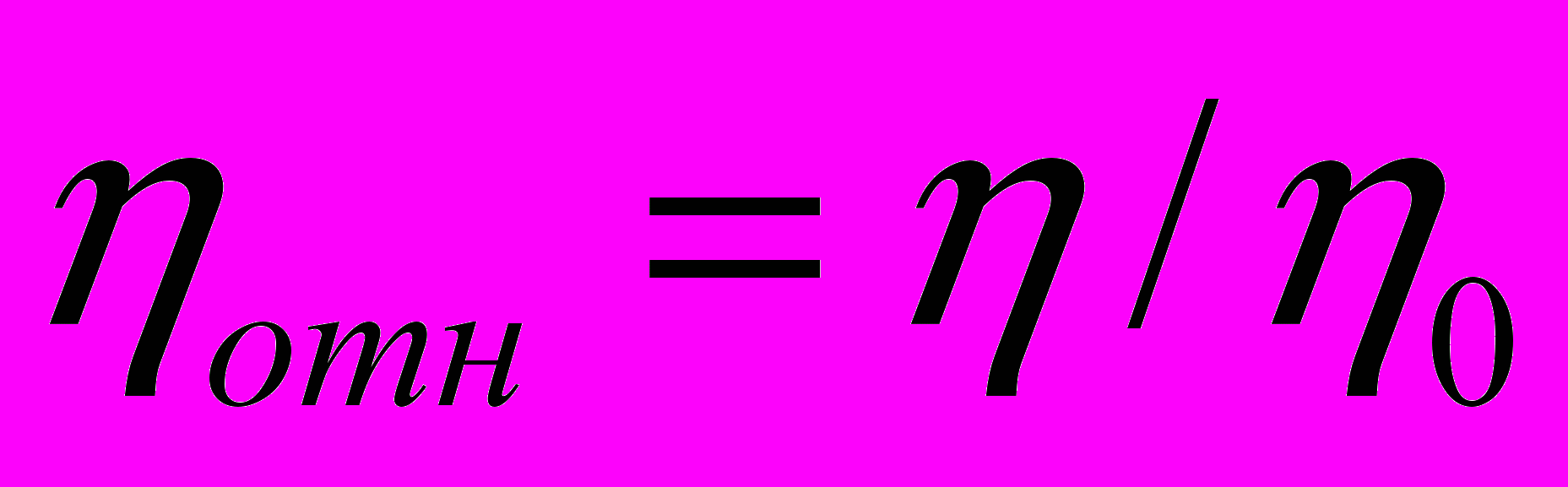
Удельная вязкость раствора представляет собой приращение вязкости за счет растворенного вещества, отнесенное к вязкости растворителя:



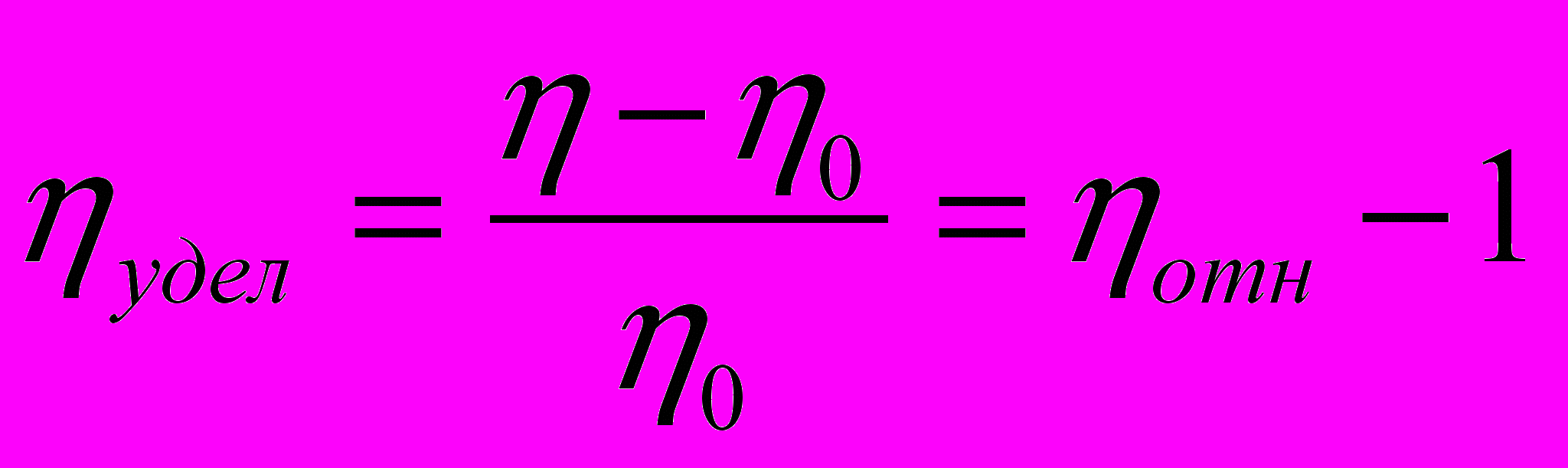
Согласно уравнению Пуазейля можем записать: ,

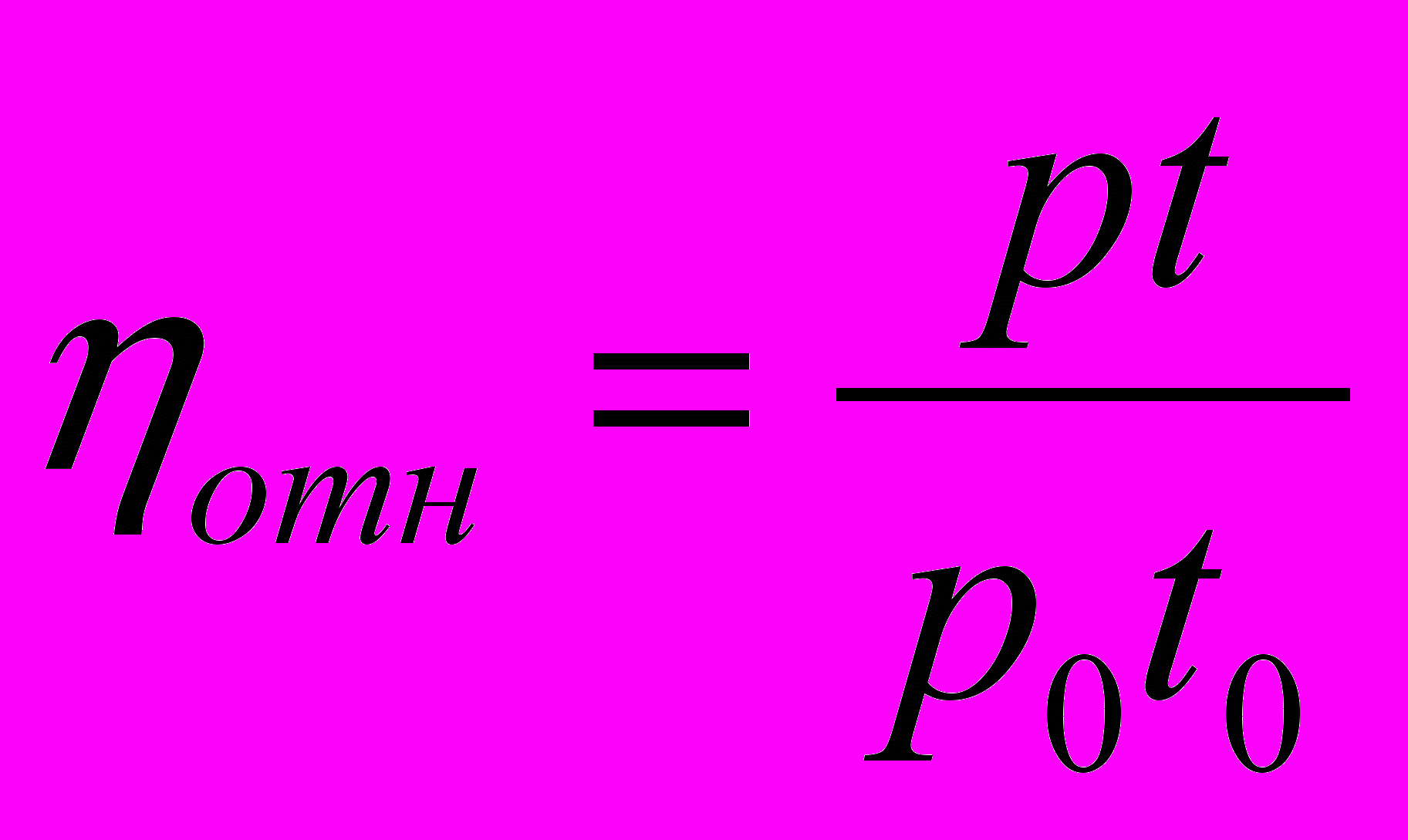где р и р₀ – соответственно плотность раствора и растворителя;

t и t₀ – время истечения раствора и растворителя.

Тогд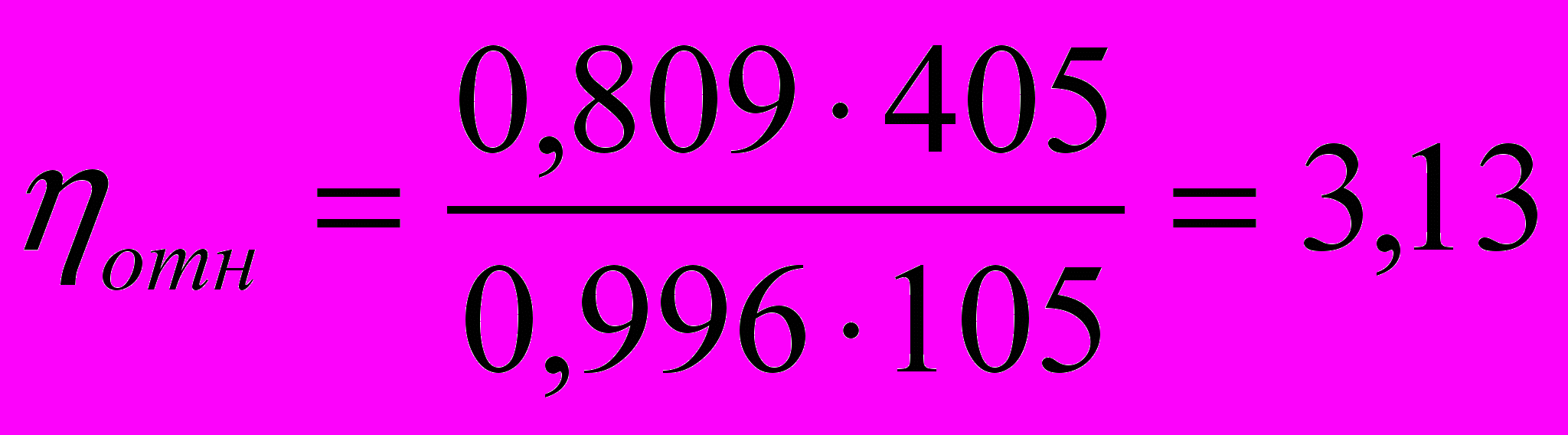а а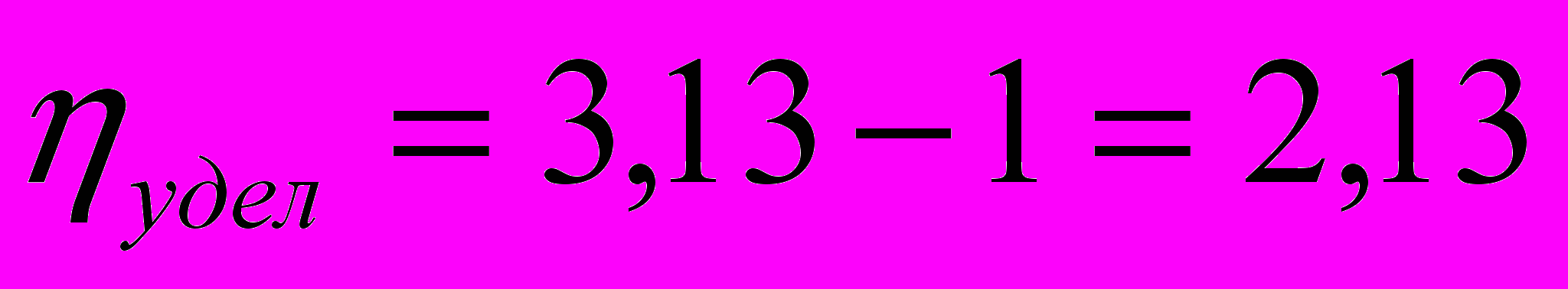

Приведенная вязкость 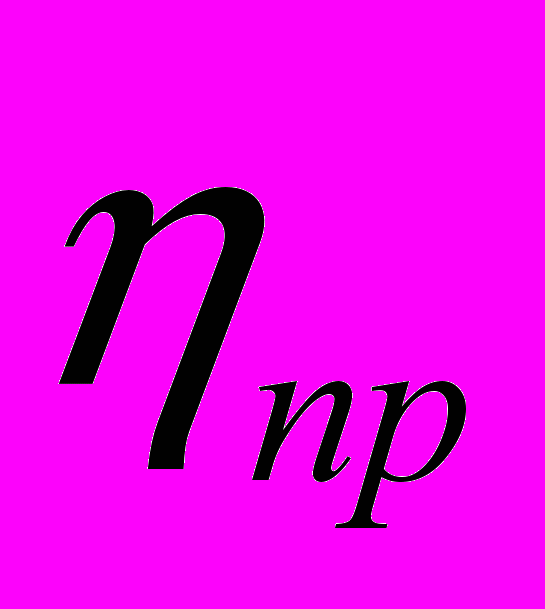есть отношение удельной вязкости к концентрации раствора с: