Взаимосвязь задач динамики и статики сплошных и составных деревянных конструкций

Вид материала

Автореферат диссертации

Содержание Структура и объем диссертации.

Подобный материал:

• Указания по монтажу металлических и деревянных конструкций монтаж металлических конструкций, 297.4kb.
• Отчет об участии в выставке «Научно-технические и инновационные достижения России», 90.34kb.
• Перспективные направления расчетных исследований динамики и прочности многокомпонентных, 237.01kb.
• Инженерного анализа «Синтез, анализ и оптимальное проектирование составных оболочечных, 121.6kb.
• Лекция №3 Применение эксперимента для построения математических моделей статики объектов, 134.24kb.
• 1. Общие положения, 1633.21kb.
• Конференция молодых ученых, 77.83kb.
• Лесопромышленный комплекс «Создание лесоперерабатывающего производства по инновационной, 4542.07kb.
• Курсовая работа по дисциплине «Статистика» на тему "Аналитические показатели рядов, 396.09kb.
• Шаблон оформления статьи по материалам доклада на XVI зимней школе по механике сплошных, 35.63kb.

Публикации. По теме диссертации опубликовано 42 печатные работы, в том числе 24 статьи в центральной печати, 3 патента на изобретения.

Структура и объем диссертации. Диссертация состоит из введения, семи глав, общих выводов, рекомендаций по проектированию, библиографии и двух приложений. Список использованной литературы содержит 215 наименований, в том числе 41 зарубежных. Работа изложена на 386 страницах, включая 200 рисунков, 53 таблицы.


Содержание работы


Во введении обсуждается актуальность темы, формулируется цель и задачи исследования, положения, выносимые на защиту, научная новизна работы, достоверность экспериментальных и теоретических (численных) исследований, практическая ценность и апробация работы, показаны структура и объем диссертации, количество публикаций по работе, изложено краткое ее содержание.

В первой главе рассматриваются виды конструкций с упруго-податливыми связями. Дается краткая характеристика составных балок из различных строительных материалов, анализируется область их применения при реконструкции и усилении существующих конструкций.

Наиболее часто составные стержни встречаются в деревянных конструкциях. Они могут выполняться на врубках, на механических связях (болты, гвозди, нагели, шпонки и т.д.), а также на клею. В 30-х годах ХХ века при отсутствии производств для изготовления клееных деревянных конструкций (КДК) широкое применение нашли деревянные составные балки на врубках, на цилиндрических и пластинчатых нагелях, на мягких и жестких шпонках и колодках. Шагом вперед было создание дощатогвоздевых и комбинированных (с соединениями на гвоздях и болтах) балок, позволяющих перекрывать пролеты до 12 м. Как развитие дощато-гвоздевых появились клееные балки с фанерной стенкой (плоской и волнистой), в которых сами стенки за счет низкого модуля сдвига фанеры обладают значительной податливостью. По аналогии с балками выполнялись составные стержни, эффективно работающие на продольный изгиб и внецентренное сжатие (стержни-пакеты, стержни с короткими прокладками и стержни с длинными накладками).

Большой вклад в развитие методов расчета составных стержней с упруго-податливыми связями внесли зарубежные ученые Ф. Энгессер, Д. Носсбаум, Р. Мизес, И. Ратцердорфер. Первые работы отечественных ученых по расчету составных стержней принадлежат С.П. Тимошенко. В дальнейшем большой вклад в решение задач поперечного и продольного изгиба составных стержней внесли А.В. Дятлов, П.Ф. Плешков, А.Р. Ржаницын, В.З. Власов, В.Ф. Иванов, Г.В. Свенцицкий, Б.А. Освенский, В.С. Деревягин, М.Е. Каган и др. Теоретические основы расчета составных стержней, разработанные Ржанициным А.Р., широко используются в расчетной практике и в настоящее время, однако слабым местом в его теории является неопределенность коэффициента жесткости соединительного шва составных конструкций.

Пространственные конструкции с упруго-податливыми соединениями отдельных элементов представлены деревянными ребристо-кольцевыми куполами. Дается краткая характеристика деревянных купольных покрытий, анализируются области рационального применения деревянных куполов в строительстве и существующие методы расчета ребристо-кольцевых куполов, излагаются основные задачи исследования.

В отечественном строительстве стержневые купола проектировались и строились под руководством крупных архитекторов М.Ф. Казакова, В.П. Стасова и др. Позднее, в 30-х годах в СССР было построено несколько ребристых куполов, куполов-оболочек и кружально-сетчатых куполов, разработкой и проектированием которых занимались советские ученые Г.Г. Карлсен, В.Ф. Иванов, Г.В. Свенцицкий, Б.А. Освенский, М.Е. Каган и др. В послевоенное время получили развитие клееные конструкции, разработкой и исследованием которых занимаются ряд отраслевых и проектных институтов (ЦНИИСК им.В.А. Кучеренко, ЦНИИЭП им. Б.С. Мезенцева, ЦНИИПромзданий, ЛенЗНИИЭП, ПИ-1, Гомельгражданпроект и др.), кафедры в политехнических и строительных вузах (МГСУ, СПбГАСУ, Ростовский ИСУ, МАрхи, АЛТА и др.). Вопросам конструирования и расчета куполов из клееной древесины посвящены работы М.С. Туполева, Е.И. Светозаровой, В.И. Травуша, Я.Ф. Хлебнова, К.П. Пятикрестовского, Ю.А. Барашкова, А.А. Журавлева и др. Отмечается, что в ближайшее время эти конструкции могут найти более широкое применение в отечественном строительстве в качестве большепролетных покрытий для зданий различного функционального назначения.

Особую значимость приобретает применение легких купольных покрытий для строительства в сейсмически активных районах. Рассматриваются особенности круглых в плане зданий и сооружений, а также реологические свойства древесины, определяющие повышенную сейсмостойкость деревянных куполов.

Приводится краткий анализ существующих методов расчета ребристо-кольцевых куполов. Методы, где купола рассчитываются как плоские конструкции, основаны на рассмотрении трехшарнирной арки или арки с условными затяжками (Н.С. Стрелецкий). Использование свойств циклической симметрии таких конструкций позволило Шенг Ши разработать метод, при котором решение системы разлагается на несколько задач с меньшим числом неизвестных. Дальнейшее развитие этот метод получил в работах Д.В. Вайнберга и В.Г. Чудновского, М.Е. Липницкого. Инженерный метод расчета ребристо-кольцевых куполов предложен В.А. Лебедевым.

Рассмотрены методы определения сейсмической нагрузки. Их анализ позволил выбрать для дальнейших исследований спектральный метод.

Актуальное значение имеют проблемы динамического контроля качества строительных конструкций, в том числе собственно контроль качества конструкций на этапе изготовления, уточнение их расчетных схем и определение фактической несущей способности конструкций при реконструкции и усилении.

Рассматривается задача уточнения расчетных схем по результатам динамических испытаний конструкций и их элементов. Учитывая относительно низкий модуль упругости древесины и податливость соединений, в конструкциях из древесины понятие «жесткое сопряжение» неприемлемо. Податливость жестких узлов приводит в статически определимых системах к увеличению перемещений, а в статически неопределимых – к перераспределению усилий между элементами конструкций. Используя вибрационные методы, по динамическим характеристикам конструкций можно оценить не только качественно степень податливости заделки элементов, но и уточнить характеристики податливости жесткого узла, а также учесть эффект защемления в шарнирном узле и характер перераспределения усилий. Работы по данному направлению в нашей стране отсутствуют.

Проведен анализ способов возбуждения колебаний, среди которых рассматриваются вынужденные и свободные колебания конструкций.

Состояние вопроса определило направление и задачи исследования.

Вторая глава посвящена разработке и развитию теоретических основ вибрационного метода моделирования составных балок и пластинок, базирующегося на исследовании во взаимосвязи двух видов их деформирования – поперечного изгиба и свободных колебаний, которые описываются дифференциальными уравнениями эллиптического типа четвертого порядков:

(1)

где использованы общепринятые в строительной механике обозначения. Если функцию прогибов представить в виде произведения максимального прогиба на единичную функцию W = W₀f(x,y) и подставить ее в дифференциальные уравнения (1), то после их интегрирования по площади получим:

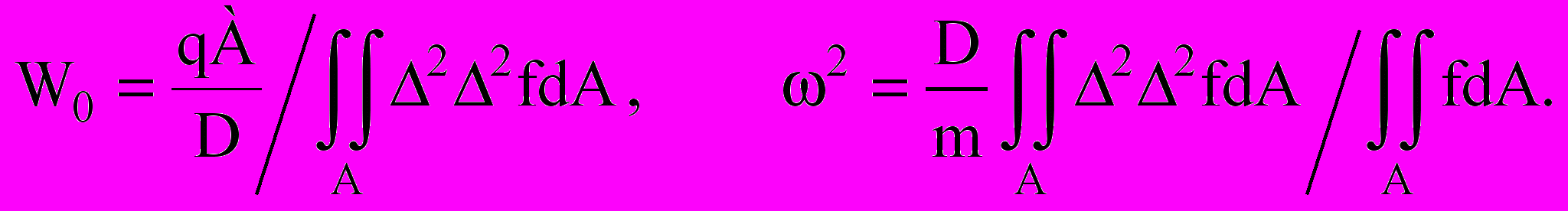(2)

Функцию прогибов можно также приближенно представить в виде однопараметрической функции 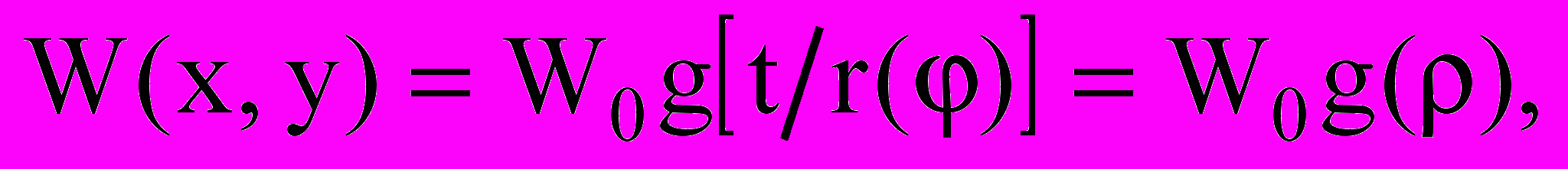где r = r(φ) – полярное уравнение контура пластинки, t и φ – полярные координаты, ρ – безразмерная полярная координата. Эта функция описывает некоторую поверхность, линии уровня которой подобны контуру и подобно расположены. Такое представление функции прогибов оправдано тем, что для некоторых задач, связанных с расчетом круглых и эллиптических пластинок, она точно удовлетворяет и дифференциальному уравнению, и граничным условиям. Подстановка этой функции в выражения (2) после проведения довольно сложных интегро-дифференциальных преобразований приводит к приближенным зависимостям:

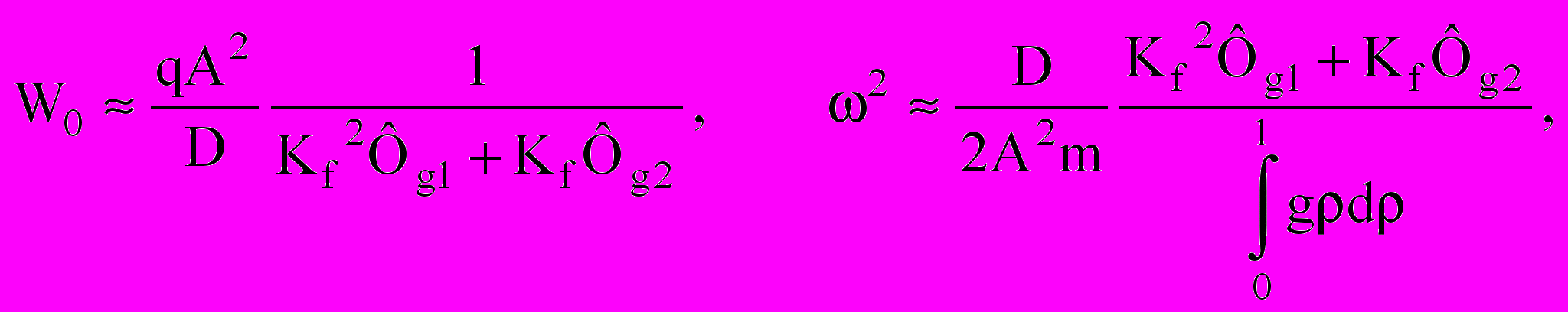(3)

где





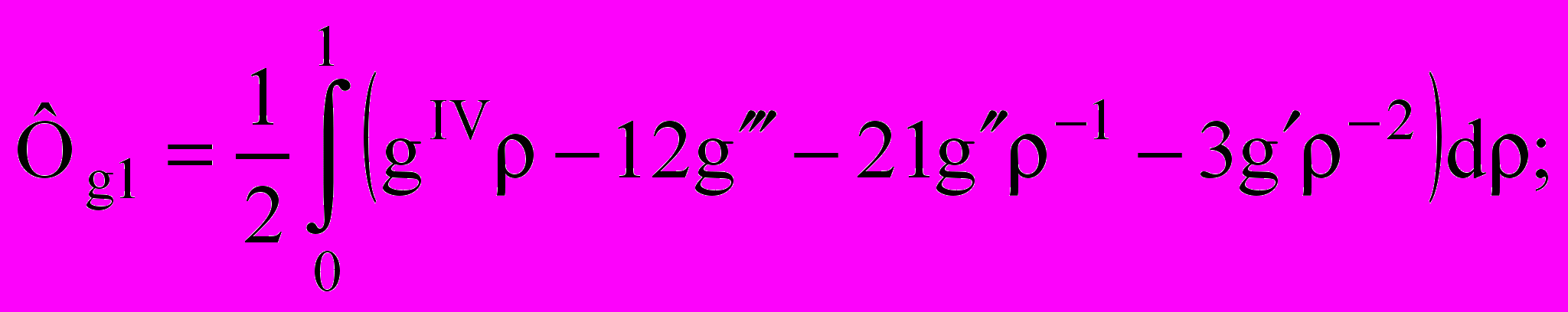
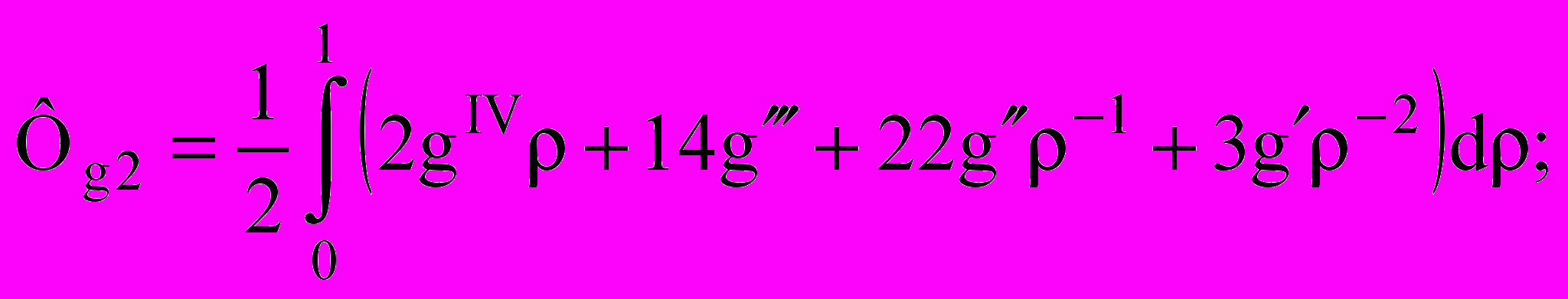
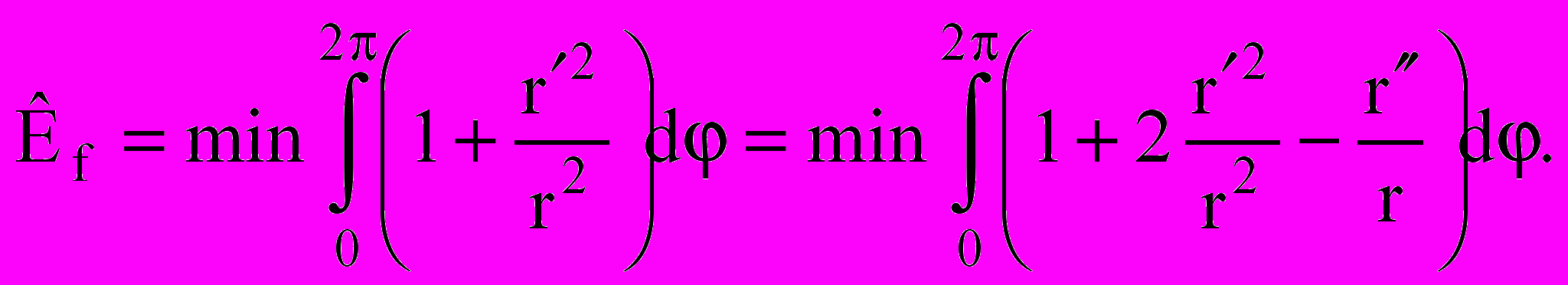
Последний интеграл имеет отношение к пластинкам с однородными граничными условиями и носит название коэффициента формы области (пластинки). Он широко используется при решении двумерных задач теории упругости с помощью изопериметрического метода и метода интерполяции по коэффициенту формы. Знак приближенного равенства в выражениях (3) поставлен в связи с приближенностью задания функции прогибов, однако это позволило в явном виде выделить коэффициент формы из получаемых интегро-дифференциальных соотношений и эффективно использовать его свойства и закономерности.

Поскольку значения определенных интегралов, входящих в выражения (3), являются постоянными числами, зависящими от точности выбора функции g(), то их можно объединить с коэффициентами пропорциональности:

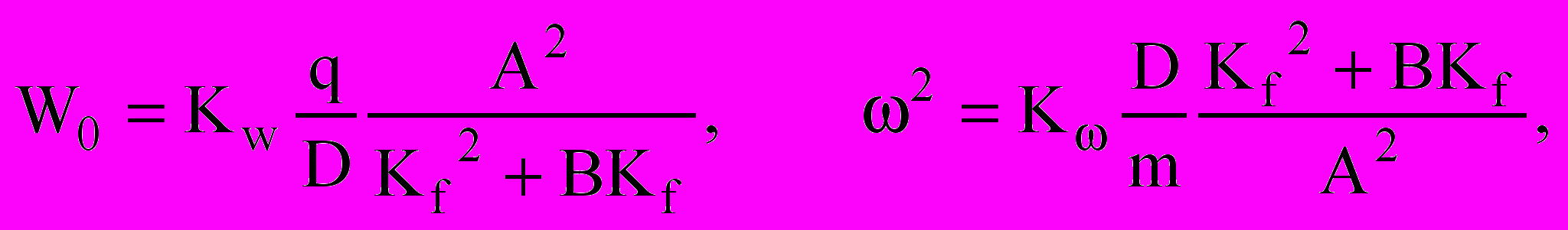(4)

где

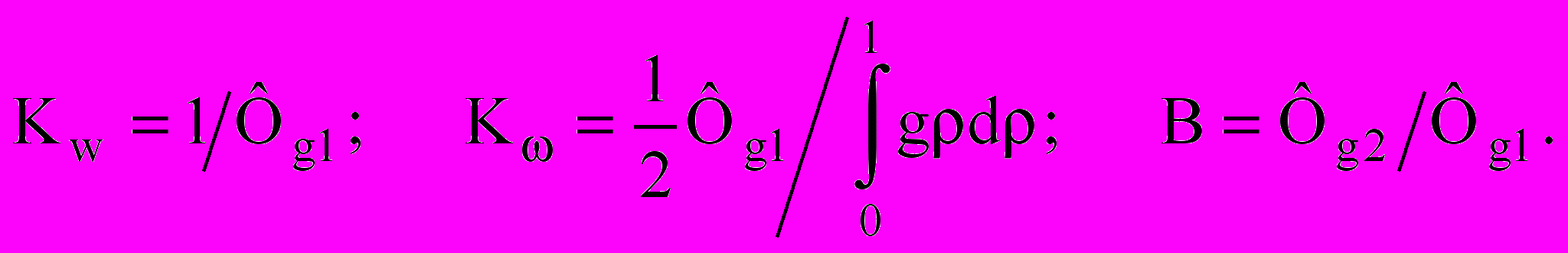
Умножив выражения (4) друг на друга, получим:

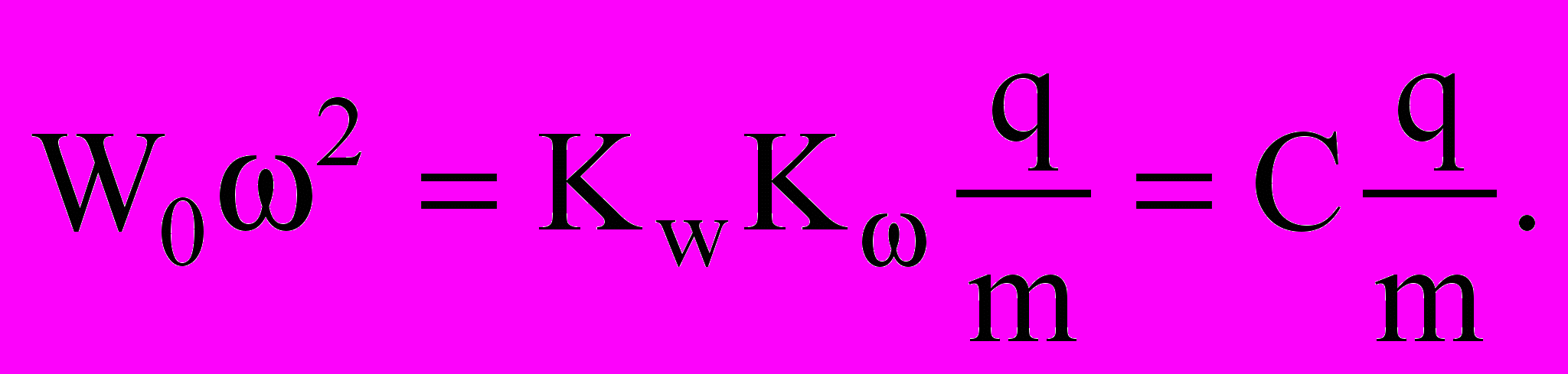(5)

Как показали результаты численного эксперимента, для всего множества пластинок с любыми граничными условиями значения коэффициента пропорциональности К изменяются в ограниченных пределах от 4/π для бесконечно вытянутых пластинок (балок с жесткостью D) до (4/π)² – для круглых пластинок, то есть

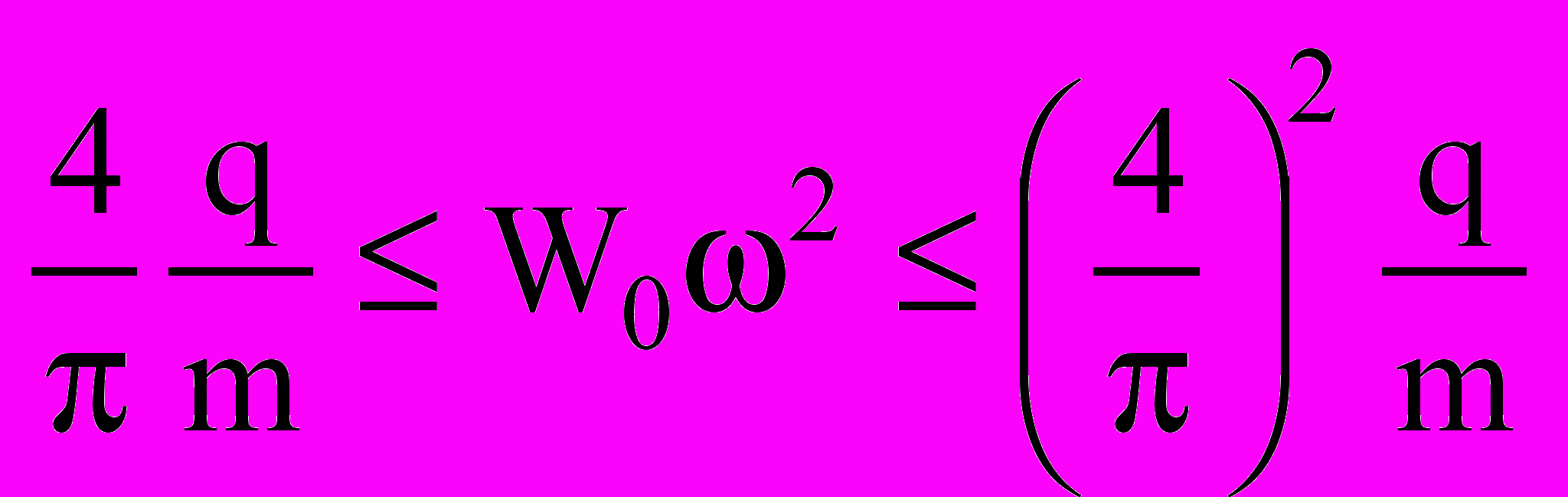. (6)

Закономерность (6) носит фундаментальный характер, связывая строгой функциональной зависимостью две интегральные физические характеристики W₀ и ω в разных видах деформации пластинок. В математической записи этой закономерности отсутствует изгибная жесткость, а это значит, что открываются перспективы ее использования для контроля и оценки жесткости составных конструкций по их основной частоте колебаний вне зависимости от степени совместности работы отдельных слоев таких конструкций. Это свойство позволяет использовать указанную закономерность для определения жесткости конструкций балочного типа по основной частоте колебаний, что играет важную роль для составных балок, поскольку они имеют неопределенную жесткость шва и изгибную жесткость сечения за счет податливости связей, соединяющих отдельные слои.

При реконструкции зданий и сооружений одним из наиболее распространенных методов усиления конструкций балочного типа является наращивание (или подращивание) второго несущего слоя с обеспечением мер их совместной работы. Весьма перспективным является способ, когда наращиваемый слой имеет более жесткие граничные условия, чем усиливаемая конструкция. Например, усиление сверху многопролетной статически определимой балки, разрезной на опорах, монолитным неразрезным слоем; усиление шарнирно опертой однопролетной балки сверху (или снизу) дополнительным слоем, имеющим жесткое защемление на опорах (рисунок 1).

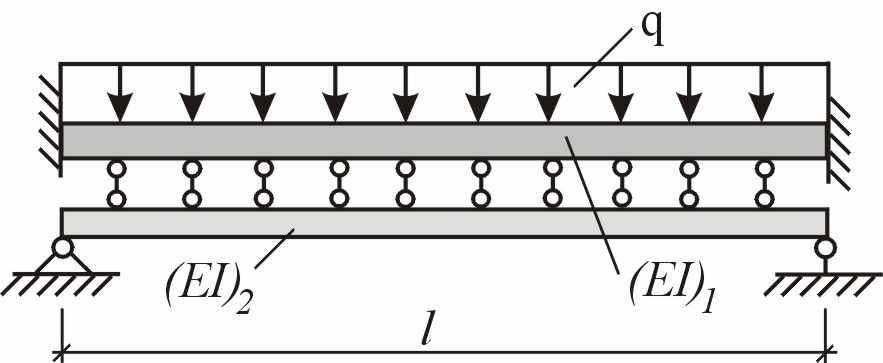Рисунок 1 – Составная балка с поперечными связями

Одной из важных задач является определение коэффициента жесткости составных балок, имеющих возможность свободного сдвига по контактной поверхности. Эта задача легко решается обычными методами строительной механики. Используя закономерность (5) можно связать частоту колебаний основного тона с коэффициентом жесткости балки:

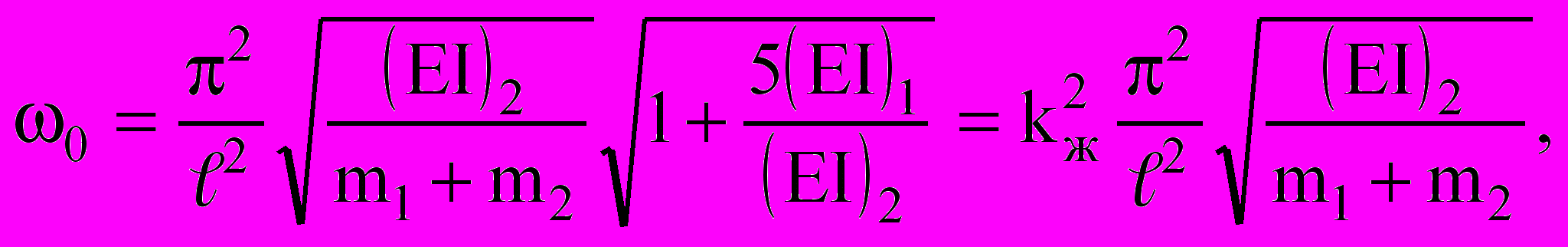(7)

где 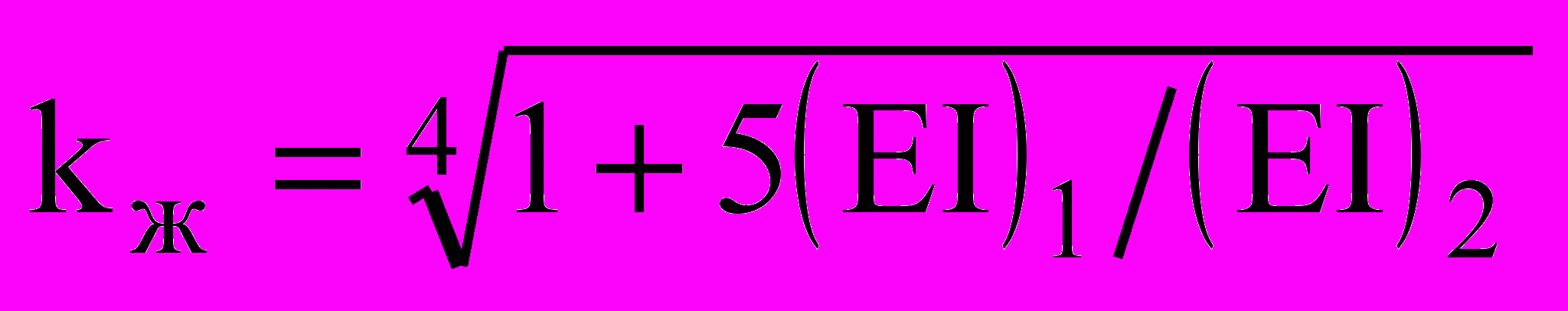; (ЕI)₁ и (ЕI)₂ – соответственно изгибные жесткости усиливающего и усиливаемого слоев балки.

Рассматривая различные условия закрепления усиливаемого и усиливающего слоёв и сопоставляя полученные частоты колебаний, можно сделать заключение, что все промежуточные значения коэффициента жесткости находятся между двух границ:

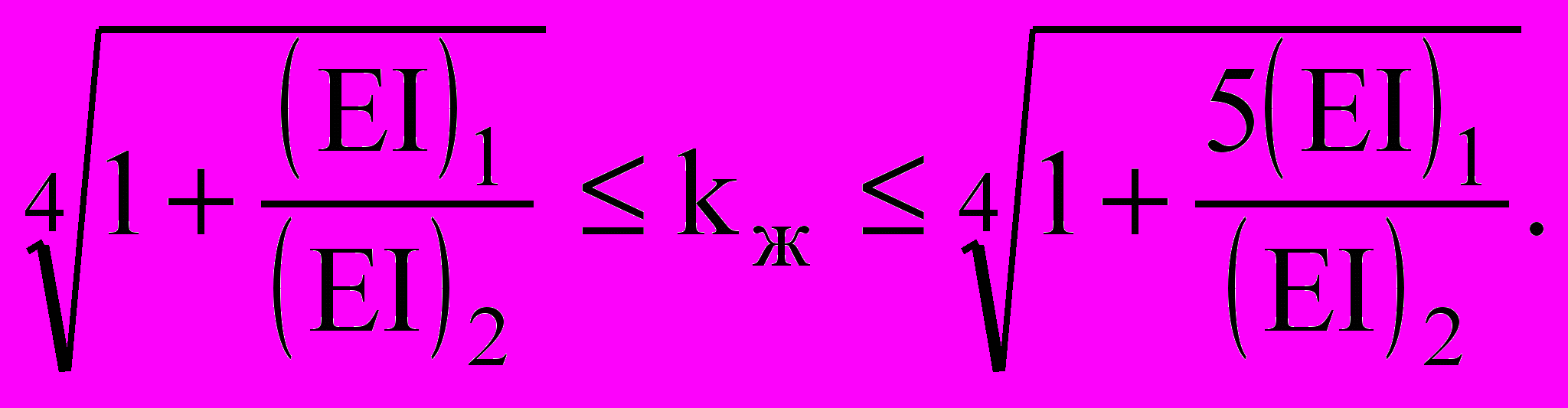(8)

В общем виде для неопределенных условий подкрепляющего слоя основную частоту колебаний двухслойной балки можно представить зависимостью (7). При этом при неизвестной основной частоте колебаний двухслойной балки можно найти k_ж:

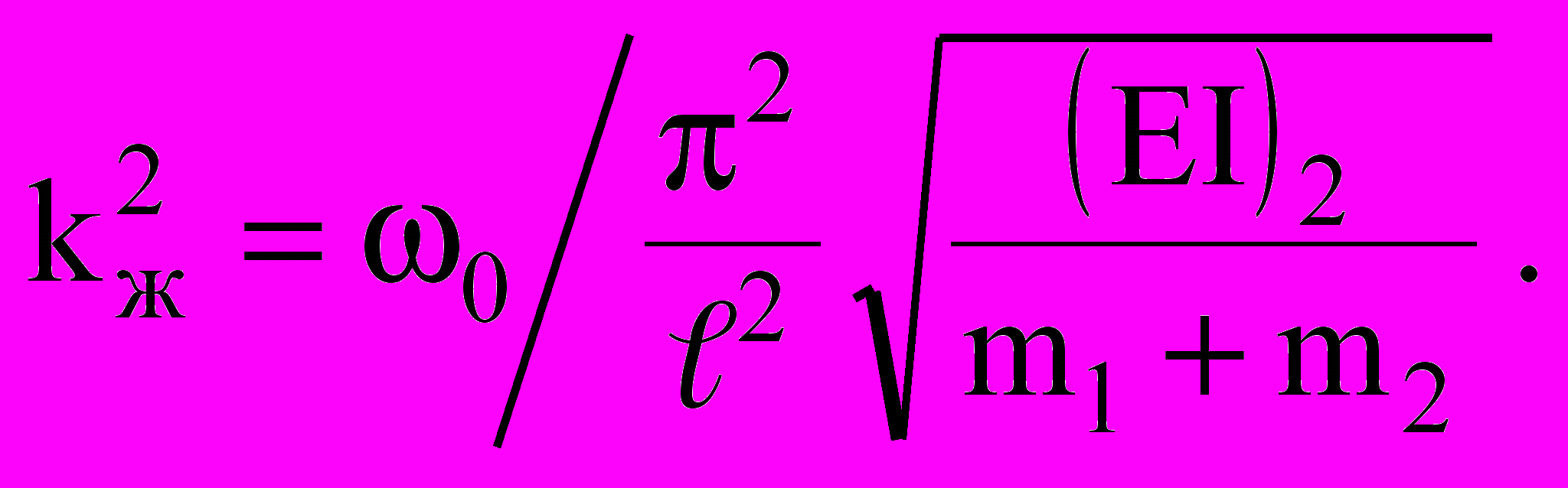(9)

Если сдвиг слоев по контактной поверхности стеснен, то возникает проблема определения коэффициента жесткости составной балки, и одна из решенных задач посвящена определению совместности работы многослойных балок вибрационным методом, который позволяет по частотам собственных колебаний конструкций оценить степень их совместной работы. Рассматриваются 5 типов балок: слой 1; слой 2; балка, состоящая из двух слоев, не связанных между собой; двухслойная балка, слои которой связаны при помощи упруго-податливых связей; балка цельного сечения, равного сечению двухслойной балки. Очевидно, что балка с большей изгибной жесткостью будет иметь наибольшую частоту колебаний. Поэтому в качестве критерия, характеризующего степень совместности работы двухслойной конструкции, можно использовать параметр К в виде корня квадратного из отношения изгибных жесткостей или соотношение частот колебаний:

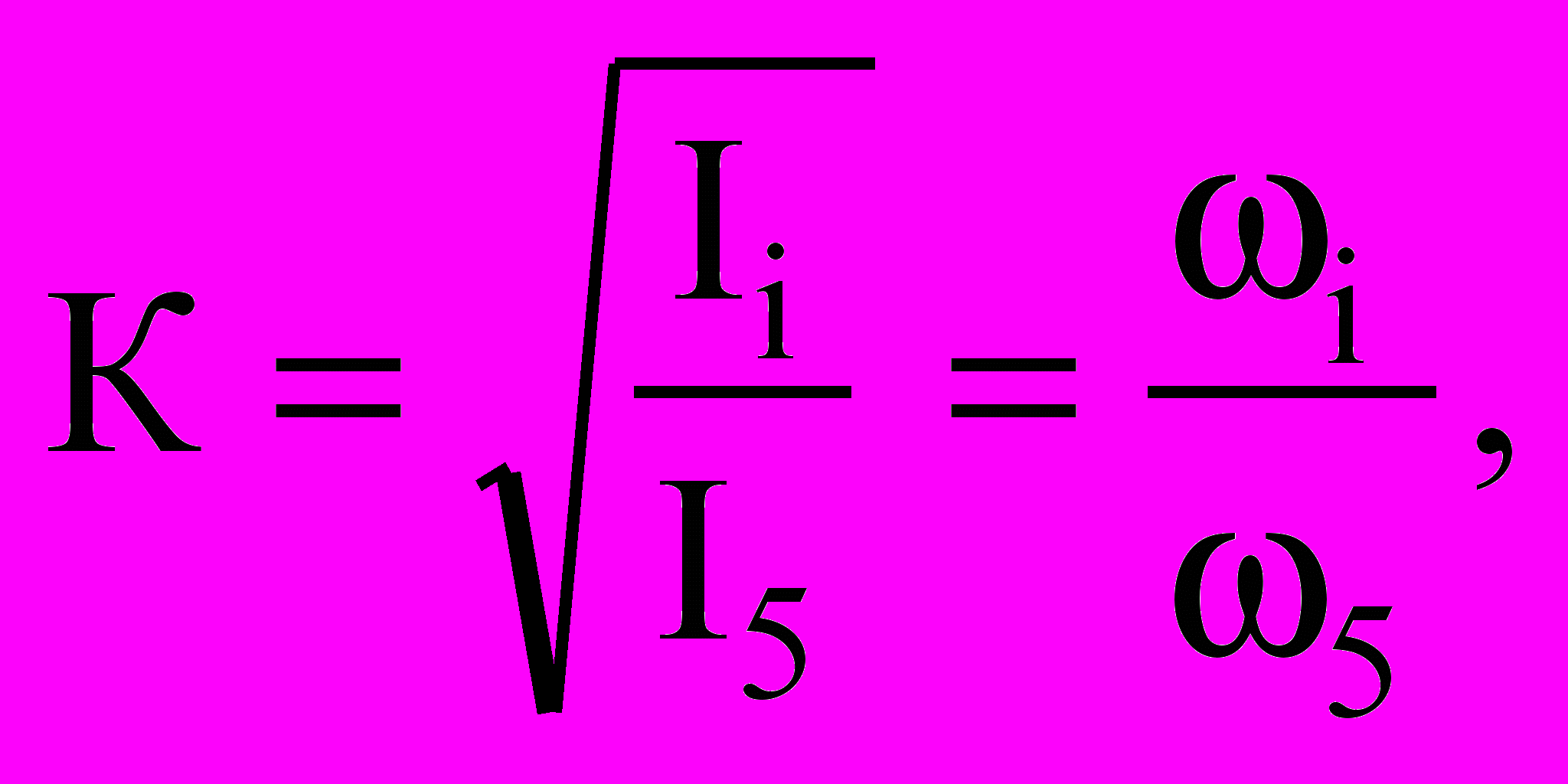(10)

где I₅ и ω₅ – момент инерции и частота колебаний балки цельного сечения;

I_i и ω_i – момент инерции и частота колебаний двухслойной балки.

Из этого выражения видно, что для сплошной балки К = 1, а для балок, соединенных совместно, всегда К < 1. Для балок с различным материалом и жесткостью слоев получим следующую общую зависимость:

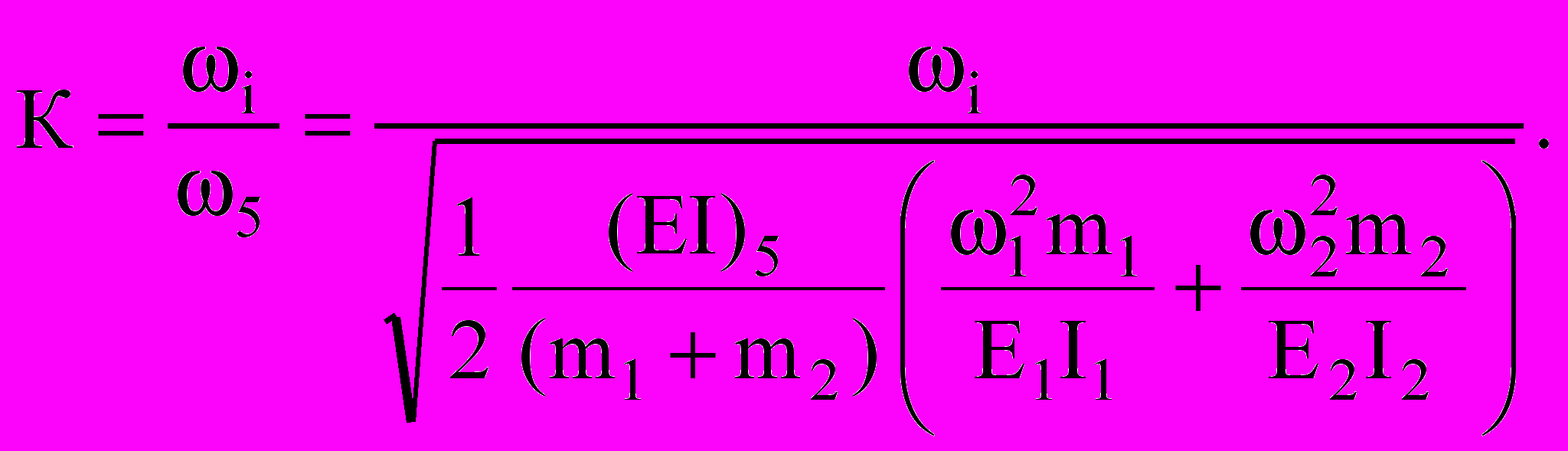(11)

При расчете деревянных конструкций с вертикальными стыками необходимо знать величину изгибной жесткости стыка. Для этого разработан способ, суть которого состоит в построении эмпирической зависимости «прогиб – основная частота колебаний балки»:

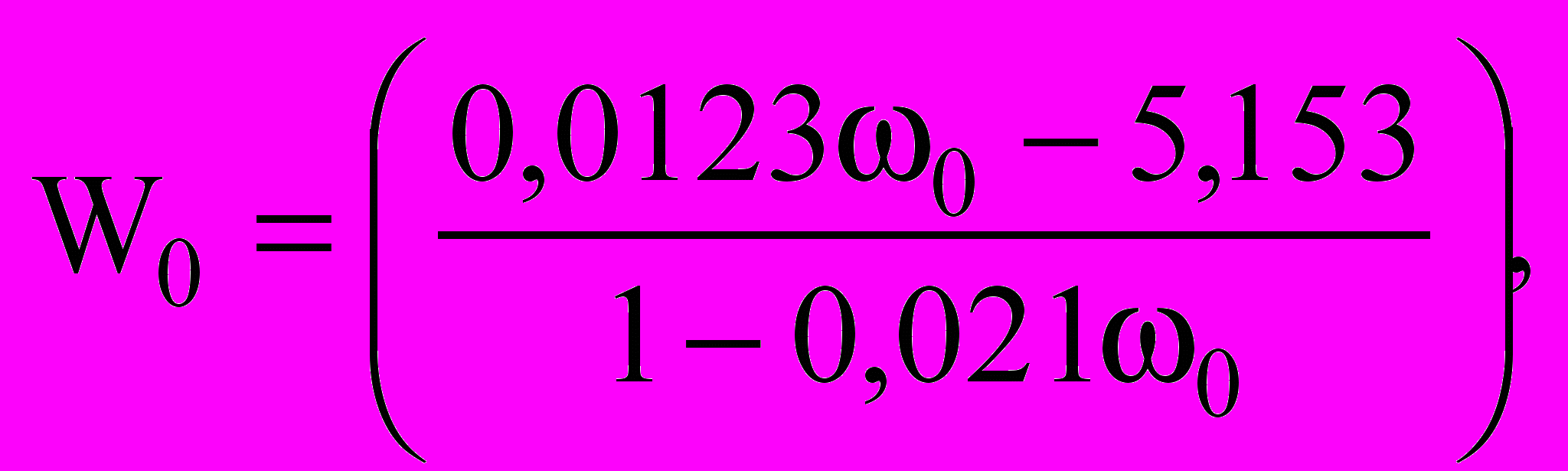(мм), (12)

по результатам теоретических исследований таких балок в широком диапазоне изменения отношения изгибных жесткостей стыка и основного сечении балки (EI)_с/(EI)_б – от 0,007 до 1 (рисунок 2).

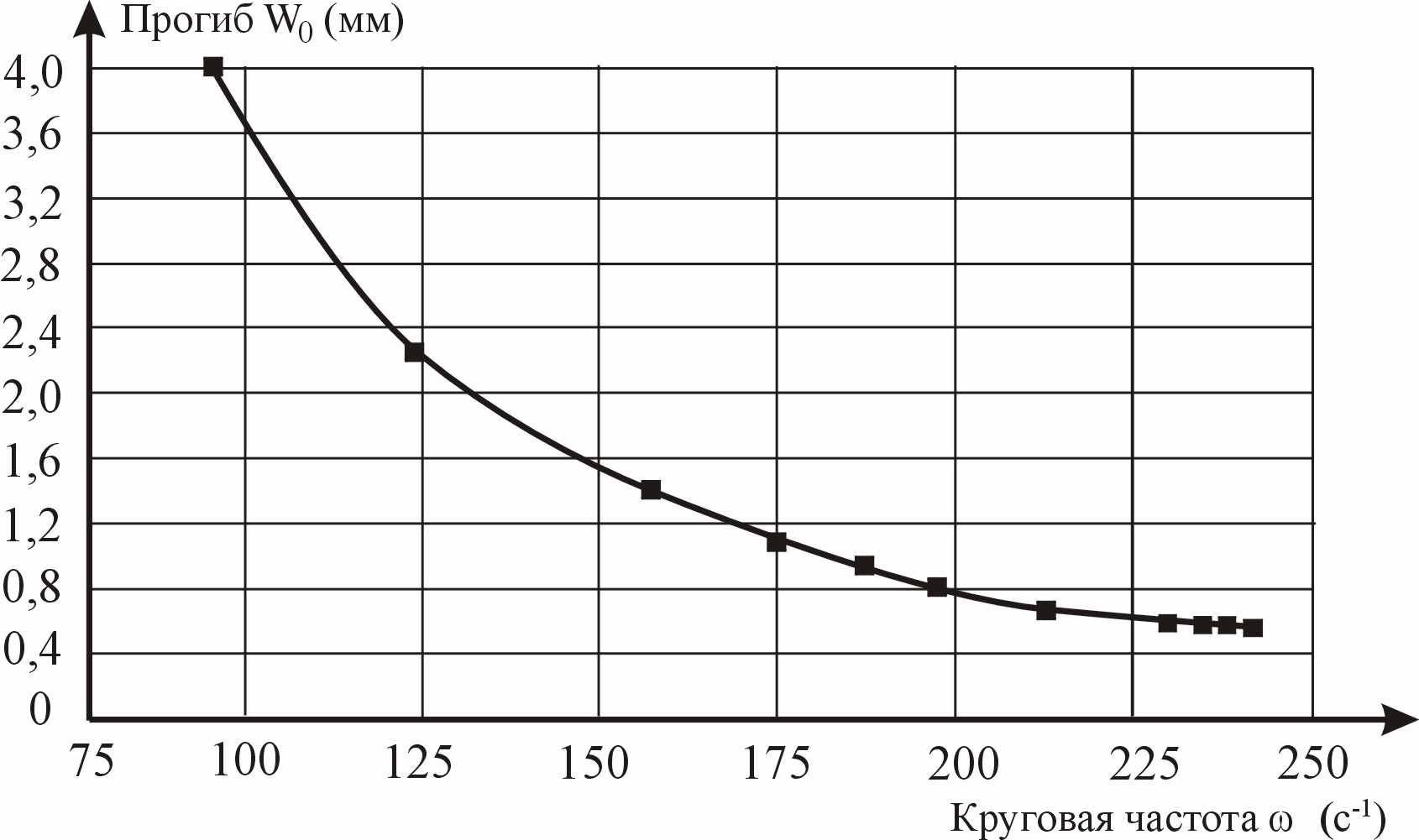Рисунок 2 – Зависимость W0 – ω0 для деревянной балки с вертикальным укрупнительным стыком

Зависимость (12) подтверждается экспериментально с точностью 4,22%. Таким образом, рассмотренный способ позволяет оценивать интегрально жесткость составной деревянной балки с различными изгибными жесткостями укрупнительных стыков.

В развитие предыдущей задачи изгибная жесткость стыкового соединения определяется экспериментально-теоретическим путем для балок с неопределенными граничными условиями.

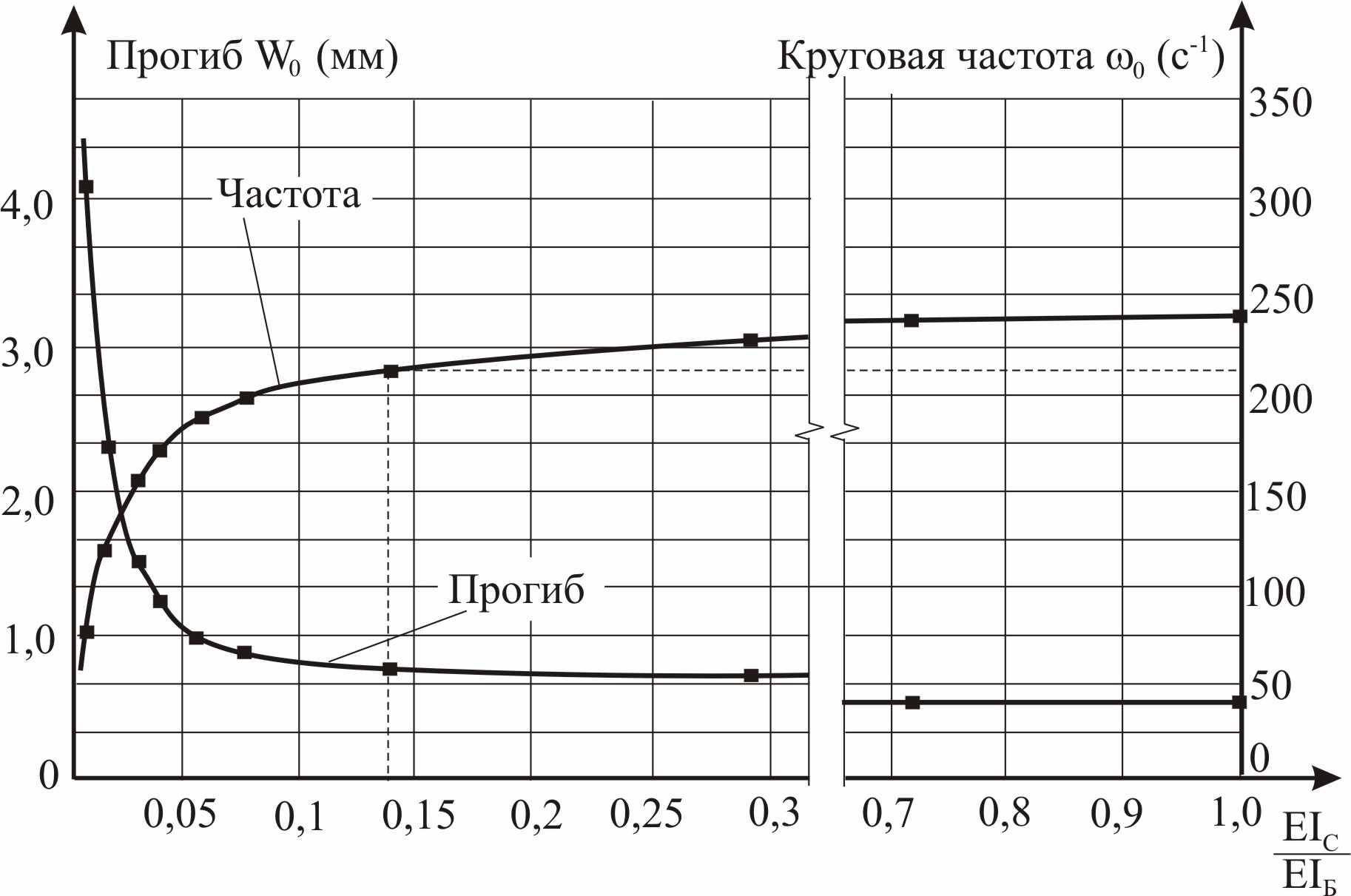Рисунок 3 – Зависимости 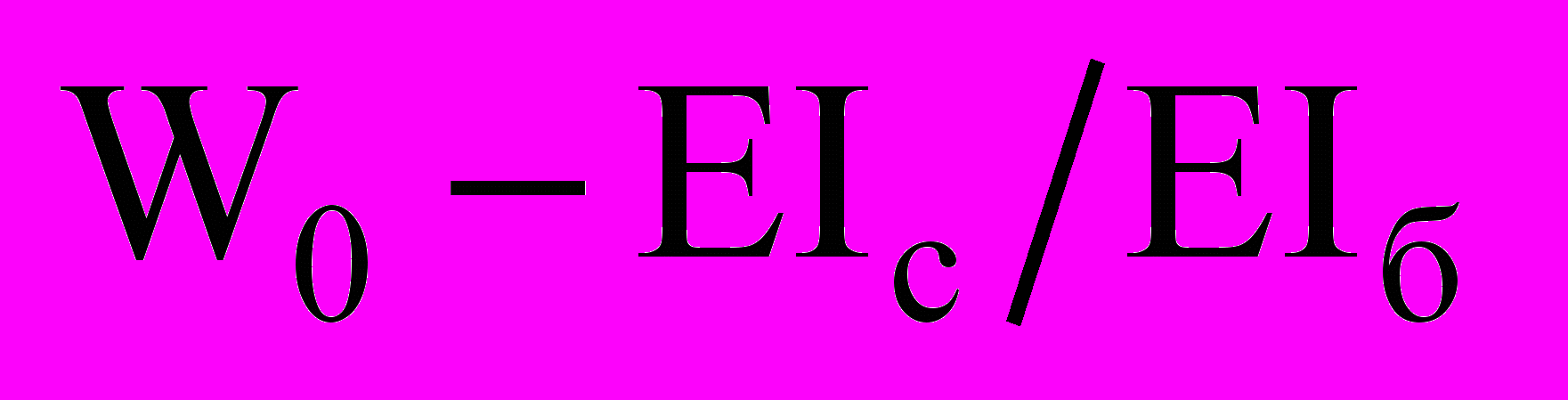и 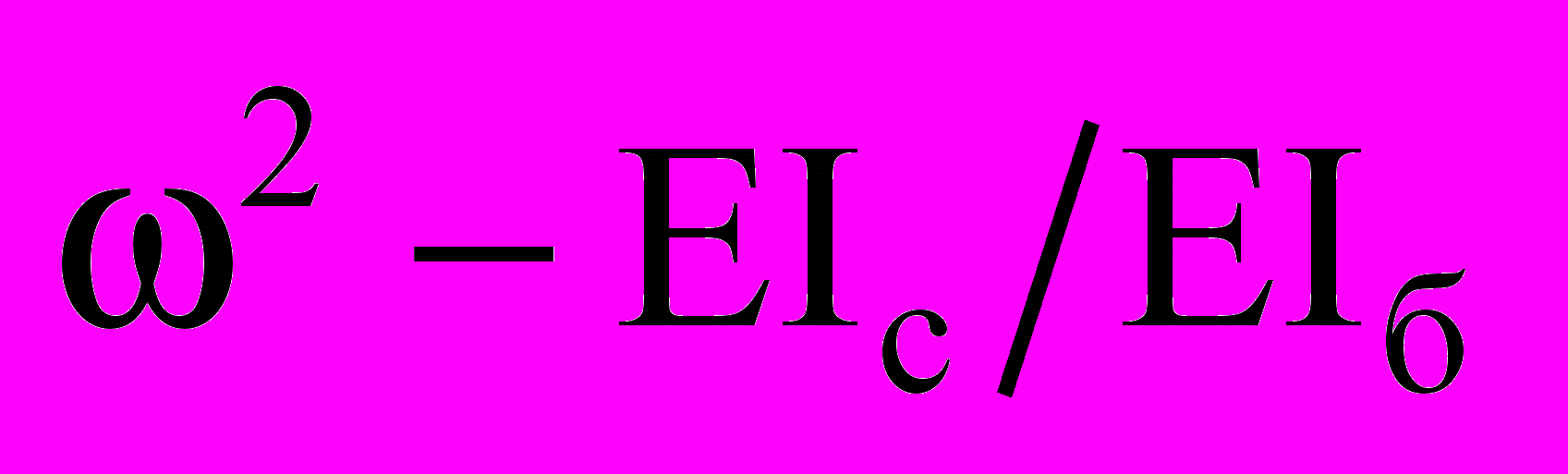для составной балки с вертикальным стыком

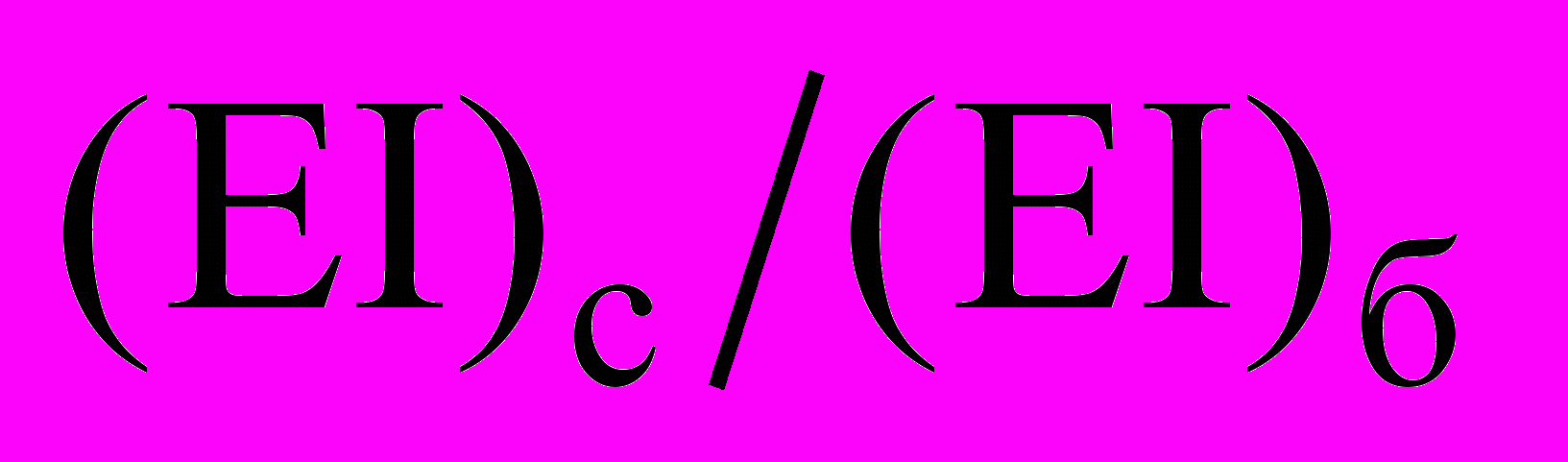По величине максимального прогиба или по основной частоте колебаний определяется изгибная жесткость укрупнительного стыка. Для реализации предлагаемого способа по данным предыдущей задачи, полученным на основе численного эксперимента, построена зависимость W₀ – k и ω₀ – k, здесь k = (рисунок 3). По этим данным построены аппроксимирующие зависимости

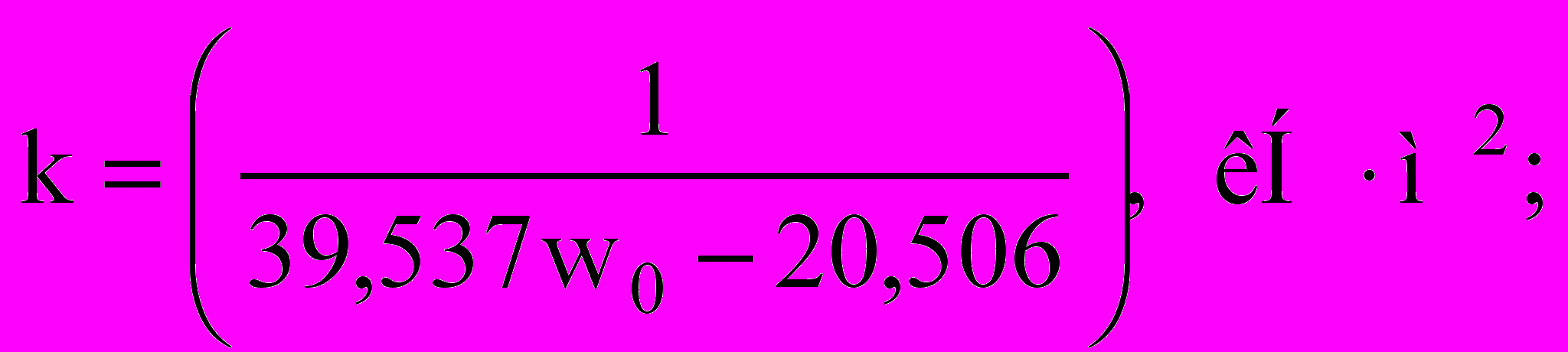(13)

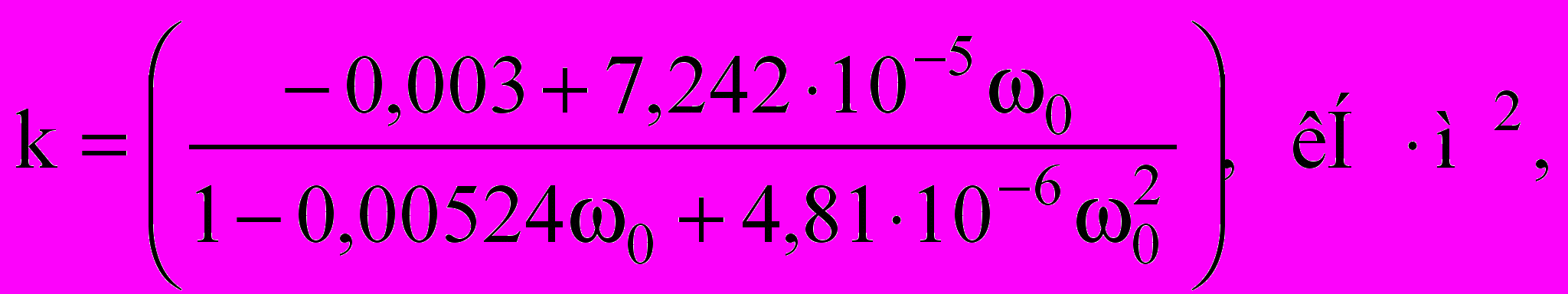(14)

с помощью которых можно по величине максимального прогиба или по основной (или первой резонансной) частоте колебаний определять изгибную жесткость укрупнительного стыка с точностью в пределах 2%. Если балка изготовлена с несколькими вертикальными укрупнительными стыками по одному и тому же проекту, то изгибную жесткость каждого стыка можно брать по результатам экспериментального исследования балки с одним стыком. Изложенная методика определения жесткости вертикального стыка составной балки применима и для определения жесткости горизонтального стыка в многослойных балках, если их слои изготовлены из одного и того же материала.

Проведены численные исследования составных двух- и многослойных составных балок с регулярным расположением поперечных связей и связей сдвига. Расчетная схема таких балок приведена на рисунках 4 и 5. Всего рассматривались 3 типа двухслойных балок с разными сечениями слоев, а также трехслойная и пятислойная балки.



Рисунок 4 – Расчетная схема двухслойной балки с равномерным

распределением поперечных связей и связей сдвига

а)

б)

Рисунок 5 – Расчетная схема двухслойной балки с локально

установленными связями сдвига (а) и с локально установленными

поперечными связями и связями сдвига (б)

При проведении исследований определялись частоты основного тона поперечных собственных колебаний балок и их максимальные прогибы от равномерно распределенной статической нагрузки в зависимости от жесткости связей сдвига (ЕА)_СС. Жесткость связей сдвига изменялась от 0 до 10⁸ кН. Очевидно, что при (ЕА)_СС = 0 слои работают без сопротивления сдвигу по контактной поверхности, а при (ЕА)_СС = 10⁸ кН составная балка будет работать как балка сплошного сечения. Кроме того, по результатам расчета подсчитывался коэффициент

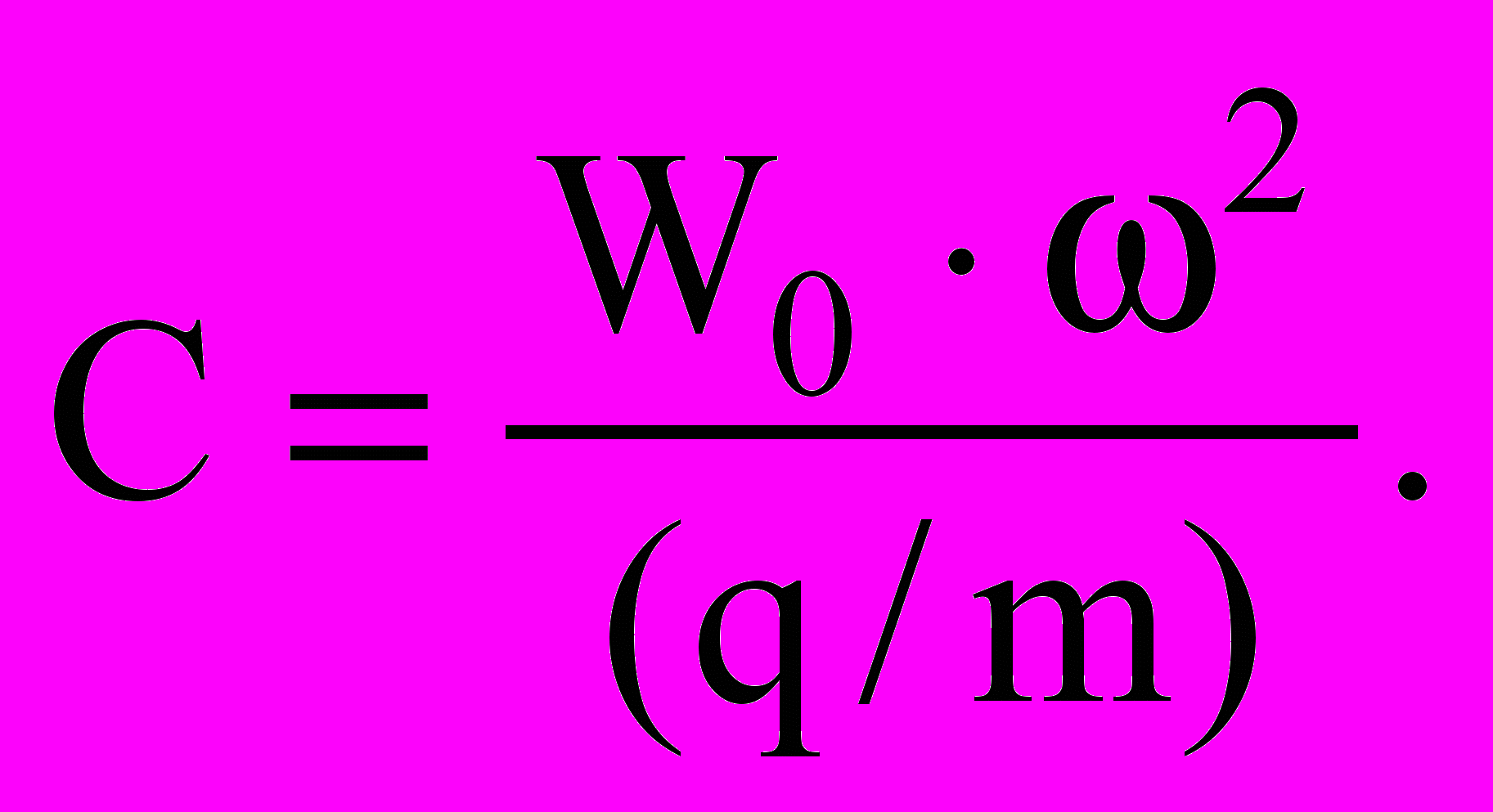(15)

По результатам исследований построены графики изменения частот колебаний основного тона и прогибов, а также коэффициента С в зависимости от жесткости связей сдвига и жесткости слоев. Характерные кривые для двухслойной балки сечением b × h₁ + b × h₂ = 50×100 + 50×100 мм приведены на рисунках 6 и 7.

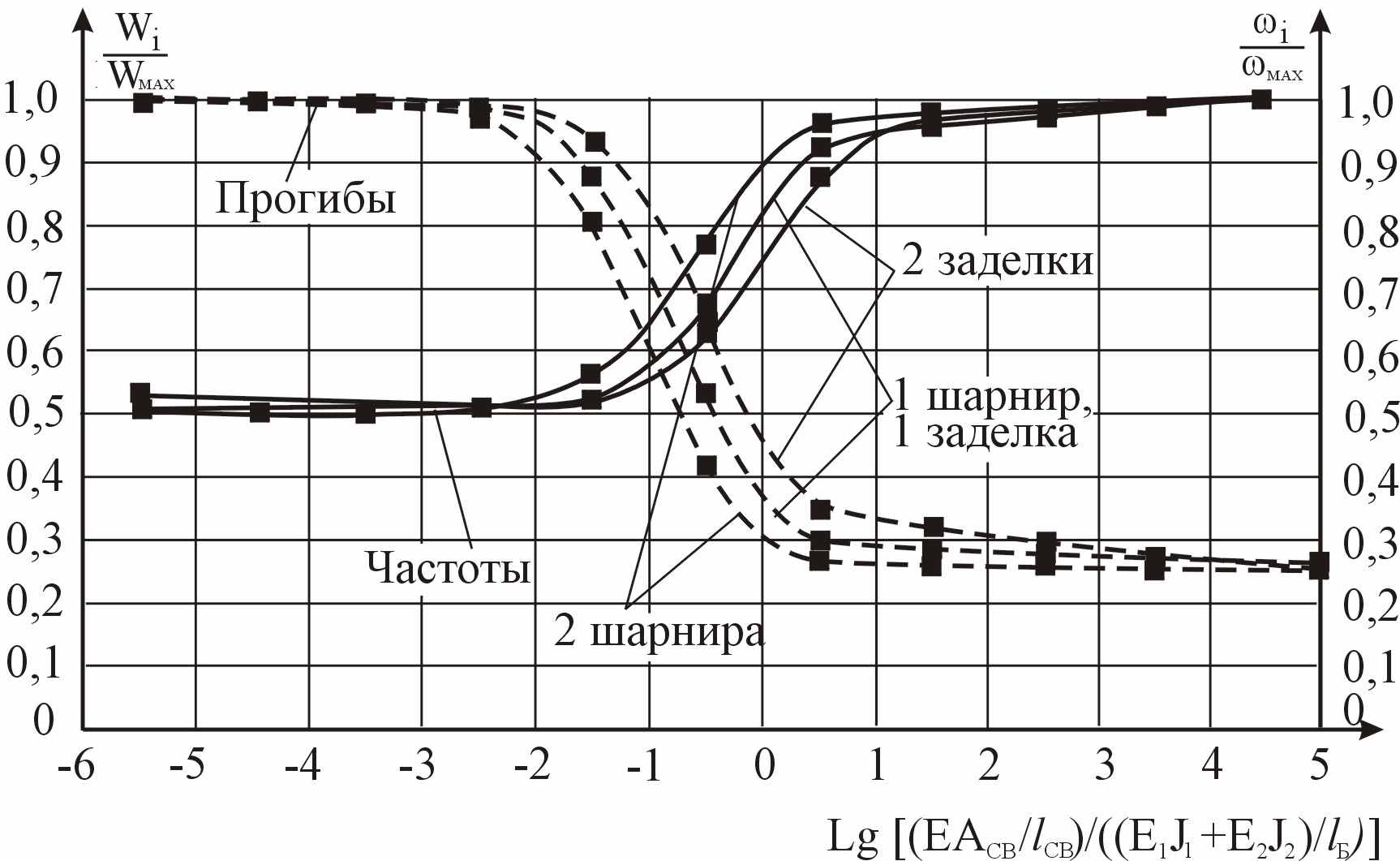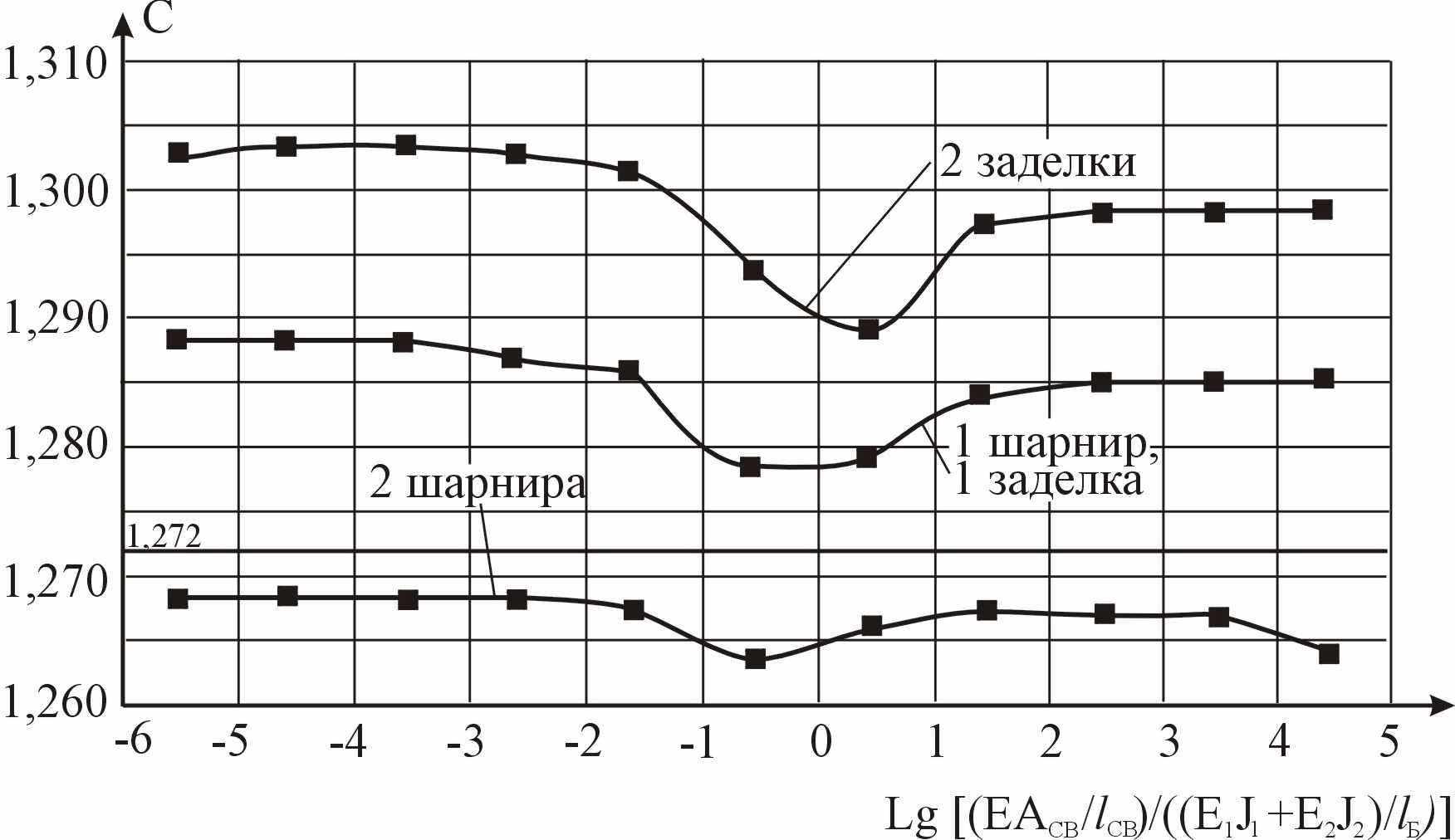Рисунок 6 – Изменение собственных частот колебаний и максимальных прогибов от статической нагрузки в зависимости от жесткости связей сдвига балки сечением b × h1 + b × h2 = 50×100 + 50×100 мм	Рисунок 7 – Изменение коэффициента С в зависимости от жесткости связей сдвига балки сечением b × h1 + b × h2 = = 50×100 + 50×100 мм

Для трех- и пятислойных балок характер изменения частот собственных колебаний и прогибов, а также коэффициента С аналогичен графикам, приведенным на рисунках 6 и 7.

Результаты, полученные численным методом и аналитически, отличаются незначительно – до 4% для частот колебаний и прогибов, а коэффициент С – в пределах от -6,5% до +2,5%, что свидетельствует о работоспособности предложенной расчетной схемы для численного расчета составных балок.

Была исследована также зависимость (5) для однопролетных балок, подкрепленных в пролете упругими опорами (рисунок 8). Жесткость упругих опор Е_оп∙А_оп изменялась от 0 кН до 10⁷ кН.

В процессе исследования изменялась жесткость упругих опор Е_оп∙А_оп от 0 кН до 10⁷ кН. По результатам исследований построены графики изменения круговой частоты основного тона собственных поперечных колебаний ω и прогибов от статической нагрузки W₀ (рисунок 9), а также график изменения коэффициента С для двутавровой балки (рисунок 10).



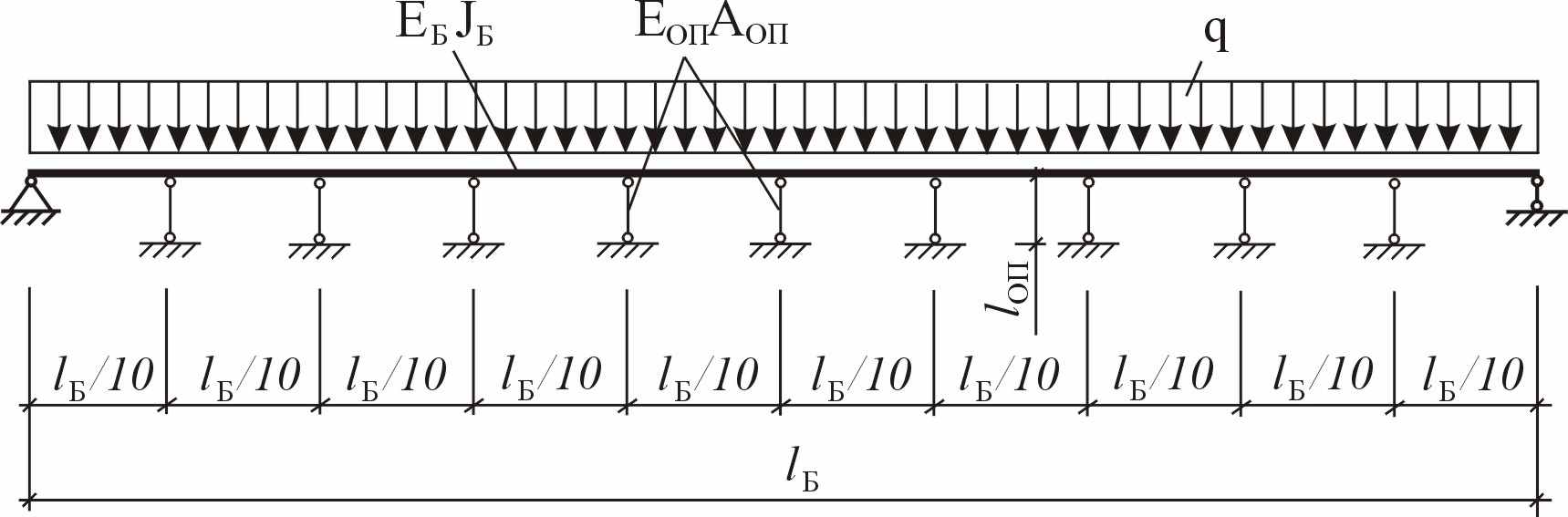
Рисунок 8 – Расчетная схема однопролетной балки,

подкрепленной в пролете упругими опорами

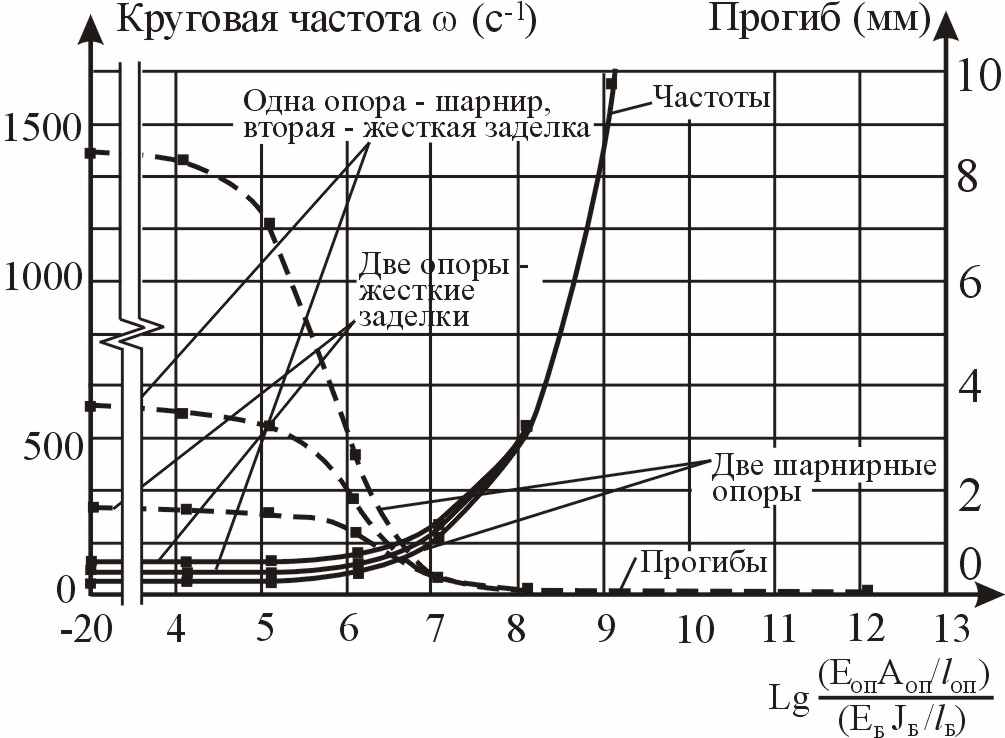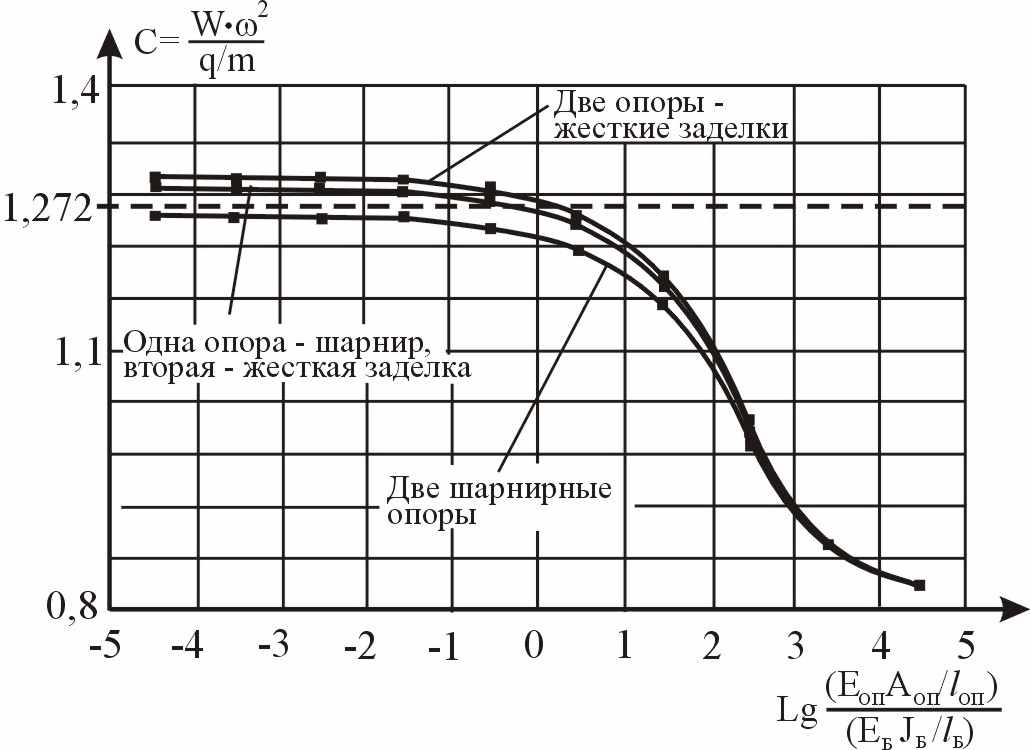Рисунок 9 – Изменение частот собственных колебаний и прогибов в зависимости от жесткости упругих опор Еоп∙Аоп	Рисунок 10 – Изменение коэффициента С в зависимости от жесткости упругих опор Еоп∙Аоп

Основные частоты поперечных колебаний и максимальные прогибы, вычисленные аналитически при жесткости опорных стержней Е_оп∙А_оп = 0 (что означает свободно лежащую однопролетную балку, работающую без сопротивления колебаниям и перемещениям со стороны упругих опор), с точностью до 4,0% повторяют результаты численных исследований. Можно считать, что при значениях Е_оп∙А_оп ≤ 10³ кН балку можно рассматривать как однопролетную. При больших значениях Е_оп∙А_оп данную конструкцию следует рассматривать как многопролетную балку на упругих промежуточных опорах. Оценив частоты собственных колебаний балки, возможно определение степени податливости промежуточных опор, а по частоте собственных колебаний можно прогнозировать прогибы балок от статических нагрузок.

При исследовании взаимосвязи параметров поперечного изгиба и свободных колебаний двухпролетной балки с упруго-податливым стыком над средней опорой укрупнительный стык имитировался конечным элементом-вставкой жесткостью EJ_В, длина которого составила 1/300 пролета L. Схемы балок приведены на рисунке 11.

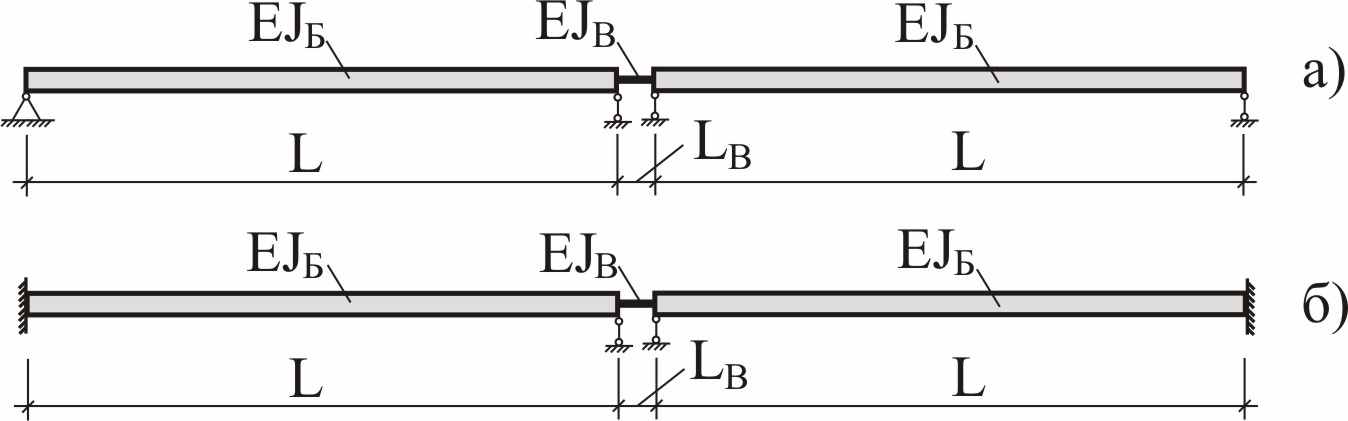Рисунок 11 – Схемы балок с упруго-податливым укрупнительным стыком над средней опорой

Варьировалась изгибная жесткость конечного элемента-вставки и схемы закрепления балки на крайних опорах. При соотношении EJ_В/ EJ_Б = 1 получается двухпролетная неразрезная балка постоянного сечения, а при соотношении EJ_В/ EJ_Б = 0 в сечении над средней опорой получается шарнир и двухпролетная балка распадается на две взаимно независимые однопролетные балки.

По результатам численных исследований построены графики изменения частот колебаний основного тона и максимальных прогибов балки в зависимости от соотношения изгибных жесткостей вставки и балки, которые приведены на рисунке 12, а графики изменения абсолютных значений изгибающих моментов приведены на рисунке 13.

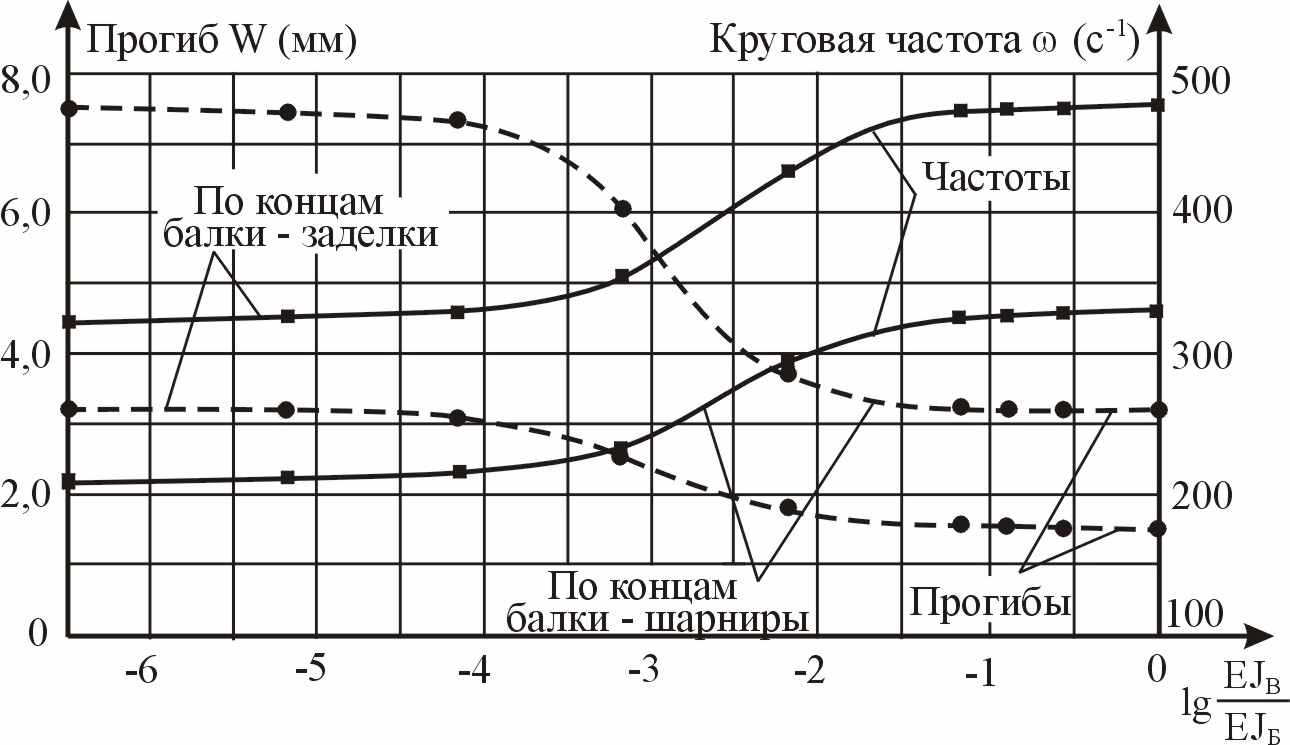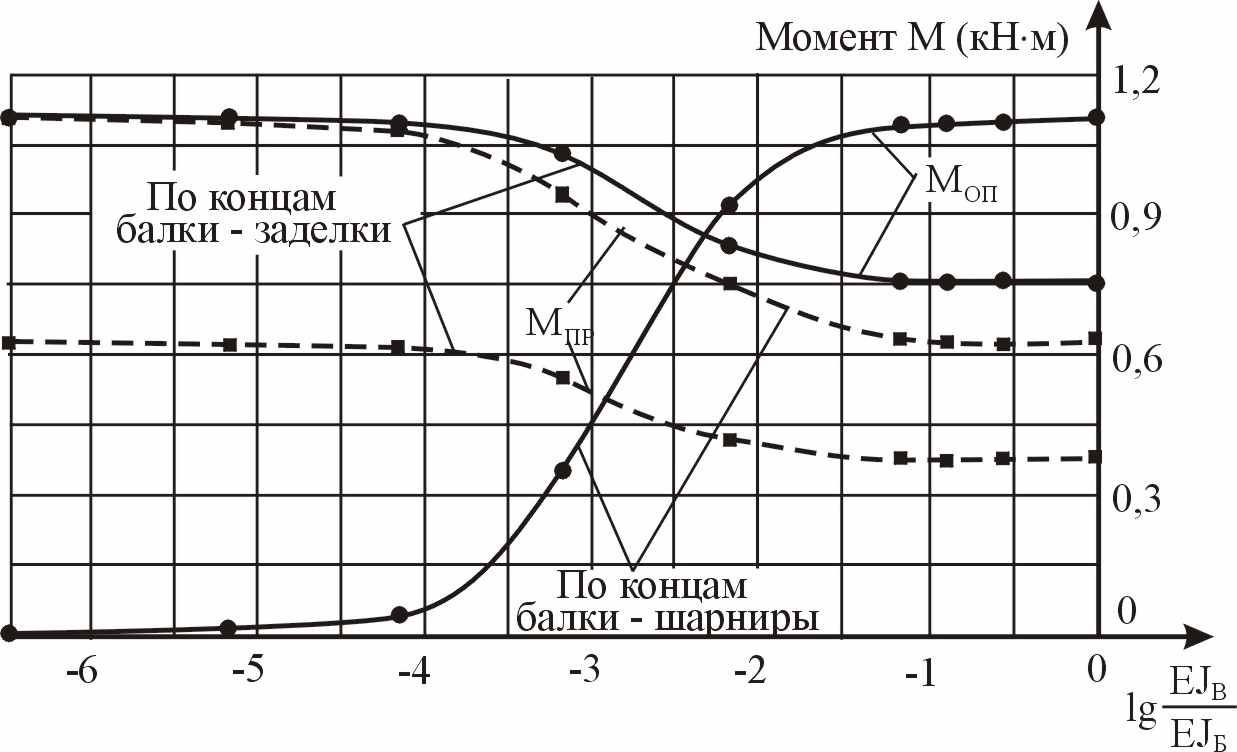Рисунок 12 – Зависимость прогибов и частот собственных колебаний балок от жесткости вставки	Рисунок 13 – Изменение максимальных пролетных и опорных моментов в двухпролетной балке в зависимости от жесткости вставки

Анализ графиков показывает, что характер изменения контролируемых параметров для балок с различными условиями закрепления по концам практически одинаков. Наиболее интенсивно эти параметры изменяются при соотношении изгибных жесткостей вставки и балки при значениях lg(EJ_В/ EJ_Б) = -4…-1. Значения коэффициента С для двухпролетных балок отличаются от теоретических значений в пределах от -0,5% до +2,5%.

Наиболее интенсивно изменяются опорные и пролетные моменты в балках с крайними шарнирными опорами. При значениях параметра lg(EJ_В/ EJ_Б) ≈ -2,45 графики опорных и пролетных моментов пересекаются, что означает их равенство по абсолютной величине, при этом изгибающие моменты меньше максимальных значений примерно на 30%.

Поскольку закономерность (5) имеет отношение и к пластинкам, было исследовано поведение коэффициента С для оболочки вращения в виде конуса в зависимости от отношения высоты оболочки к диаметру. Предельной формой такой конической оболочки будет круглая пластинка. В качестве расчетной конструкции была принята оболочка вращения в виде конуса диаметром 36 м, а толщина ее принималась 50, 100, 200, 300 и 500 мм. По результатам исследований построены графики w₀ – H/D, ω – H/D и С – H/D (рис. 14…16).

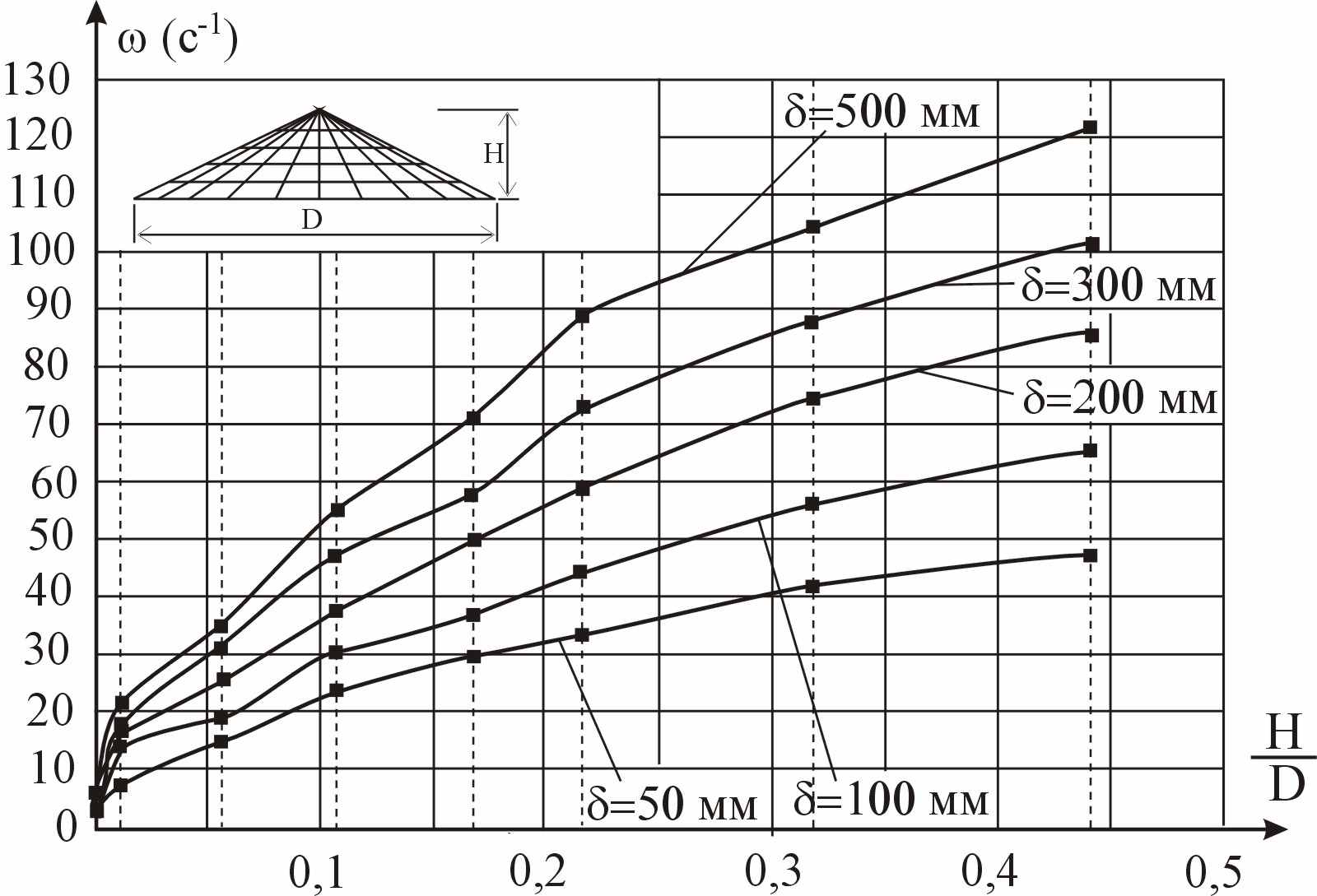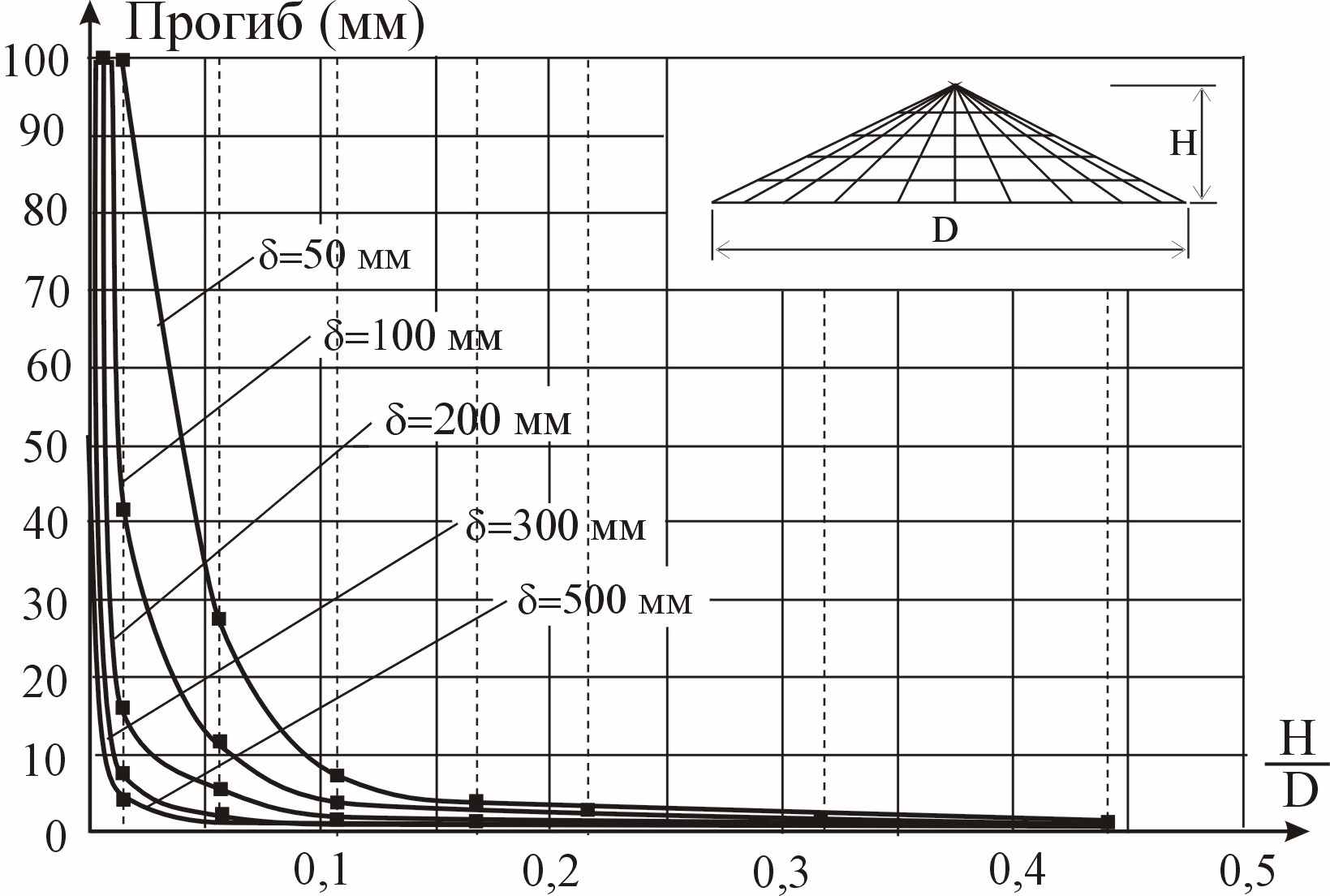Рисунок 14 – Частоты колебаний оболочки в зависимости от высоты конструкции	Рисунок 15 – Прогибы оболочки в зависимости от высоты конструкции

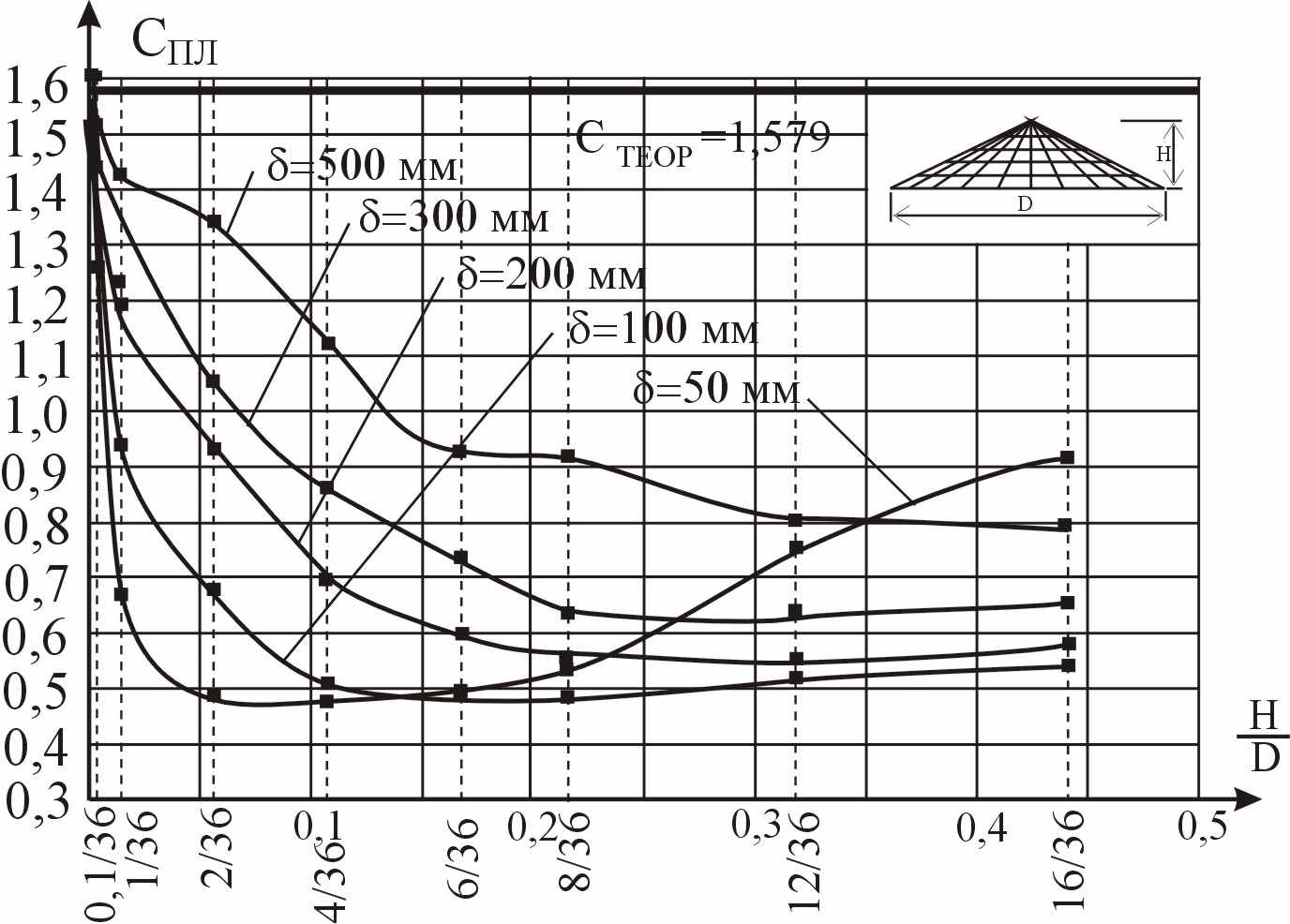
Рисунок 16 – Зависимости параметра С_пл от высоты оболочки

Следует отметить, что для пластинок коэффициент С_пл остается практически постоянным при различной толщине и изменяется в пределах от +2,47% до -1,71% от теоретического значения С_пл = 1,579. При построении графиков учитывались максимальные прогибы оболочек, положение которых с увеличением высоты конструкции H перемещается из середины примерно в четверть пролета. Найденные зависимости изменения параметра С_пл при изменении высоты оболочки вращения позволяют связать решение задачи об её свободных колебаниях с задачами деформирования конструкции при статических нагрузках и наоборот.