Geum.ru

Шаблон оформления статьи по материалам доклада на XVI зимней школе по механике сплошных сред

Вид материалаДоклад

Содержание


Оформление формул.
Оформление иллюстраций
Цитируемая литература
Лурье С.А., Белов П.А.
Подобный материал:
ШАБЛОН ОФОРМЛЕНИЯ СТАТЬИ ПО МАТЕРИАЛАМ ДОКЛАДА

НА XVI ЗИМНЕЙ ШКОЛЕ ПО МЕХАНИКЕ СПЛОШНЫХ СРЕД


А.А. Автор1, Б.Б. Соавтор2, С.С. Другой-Соавтор3


1Институт механики сплошных сред УрО РАН, 614013 г. Пермь, ул. Академика Королева, д.1

2Пермский государственный ун-т, 614000 г. Пермь, ул.Букирева, д.15

3Пермский государственный технический ун-т,614000 г. Пермь, Комсомольский просп., д. 29а


Далее следует основной текст статьи. Требования к оформлению статьи приближены к требованиям представления статей в журнал «Вычислительная механика сплошных сред». Общий объем статьи не должен превышать 5 страниц и размер 3 Мб.

Статья присылается в виде файла с расширением *.pdf.

Оформление формул. Все формулы следует вставлять с помощью редакторов формул Microsoft Equation 3.0 или Math Type. Формулы, выключенные из текста, вставляются после абзацного отступа и отделяются сверху и снизу пустыми строками. Нумерация должна быть сквозной по всему тексту. Для написания номера следует использовать арабские цифры, заключенные в круглые скобки. Номер формулы прижимается к правому краю страницы. Нумерация и текст комментариев к формулам набирается в основном тексте, а не в редакторе формул. Ссылка на формулу в тексте – цифра в круглых скобках.

Для набора формул использовать математический стиль и следующие шрифты и начертания:


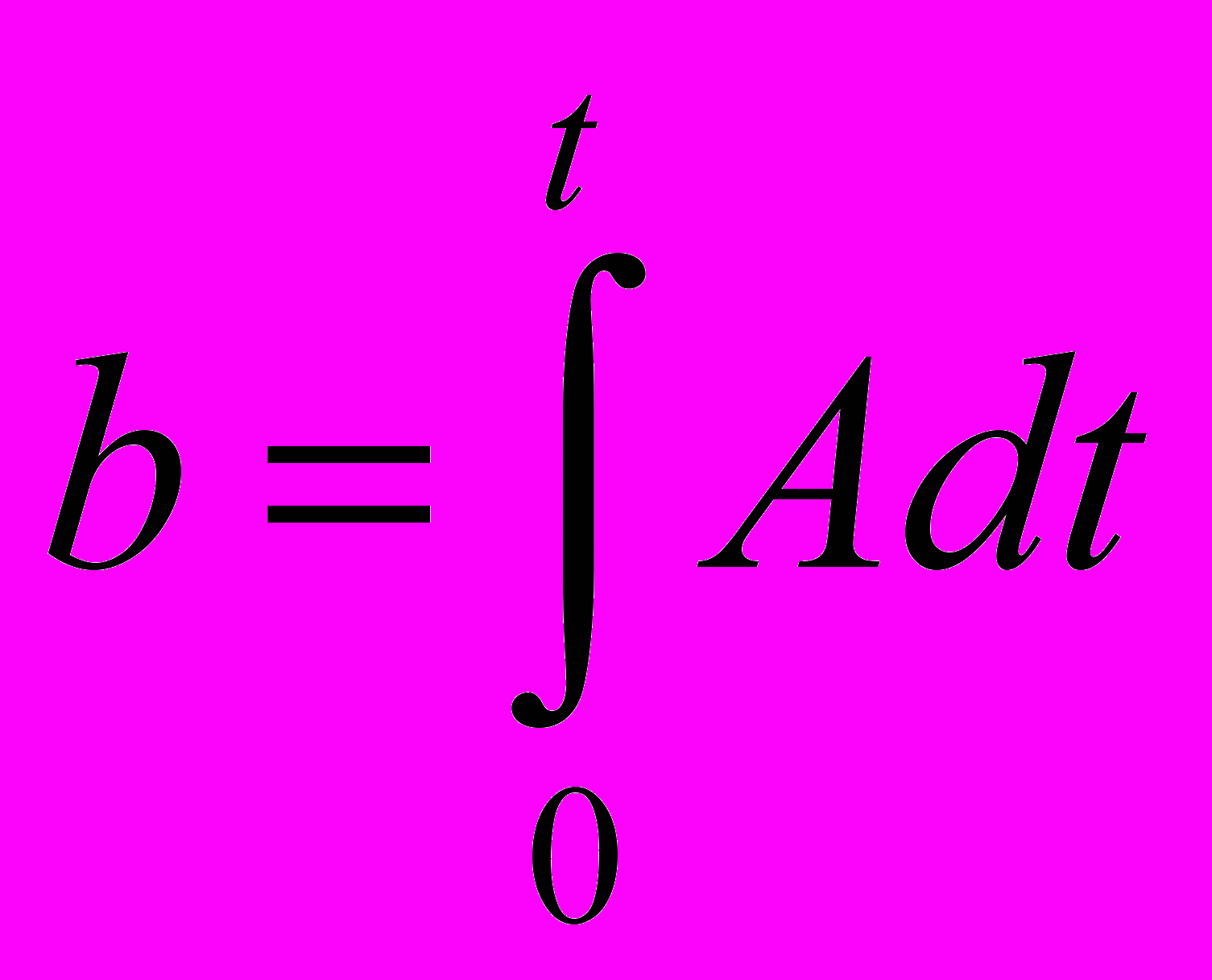(1)


Таблицы. Заголовок следует располагать сверху и придерживаться следующей структуры (после абзацного отступа):

Таблица 1. Название таблицы (Шрифт Times New Roman, начертание обычное, размер 10 пунктов)

Все графы в таблицах должны иметь заголовки и быть разделены вертикальными линиями. Сокращения слов в таблицах не допускаются. Для набора текста, цифр внутри таблицы использовать шрифт Times New Roman, начертание обычное, размер 10 пунктов, отступы слева и справа – 0, межстрочный интервал одинарный, без абзацного отступа. Текст в таблице выравнивается по центру. Если в тексте одна таблица, она не нумеруется.

Оформление иллюстраций. Иллюстрации должны быть черно-белыми. Рекомендуемое разрешение растровых изображений не более 300 dpi, штриховых – не более 600 dpi.

На подписях к осям обозначения переменных отделять от единиц измерения запятой (V, м/с) и располагать слева и снизу от осей. Минимальная толщина линий – 0,1 pt.

Подписи к рисункам оформлены по правилам основного текста (шрифт Times New Roman, начертание обычное, размер 10 пунктов, отступы слева и справа – 0, межстрочный интервал одинарный, без абзацного отступа). Текст выравнивается по центру. Рисунки, состоящие из нескольких фрагментов, помечать строчными буквами русского алфавита ниже фрагмента и за его пределами.

Для ссылки на рисунок в тексте использовать сокращение (Рис. 1) или (Рис. 1, а). В контексте слово «рисунок» писать полностью.

Текст может обтекать рисунок по большей стороне, либо сверху и снизу.

Цитируемая литература приводится в порядке упоминания работ в виде нумерованного списка с заголовком «Литература». В основном тексте номер ссылки на источник цитирования заключается в прямые скобки. Если ссылка включает несколько следующих подряд источников, она должна иметь вид [1–5], т.е. номера разделяются неразрывным дефисом без пробелов.

Для оформления списка использовать шрифт Times New Roman, начертание обычное, размер 10 пунктов, межстрочный интервал одинарный, выравнивание – по ширине. Положение номера по левому краю, отступ 0 см, положение текста после табуляции 1 см, отступ 1см.

Ссылка на гранты.


Литература
  1. Матвеенко В.П., Шардаков И.Н., Труфанов Н.А. Метод геометрического погружения в теории упругости. – Екатеринбург: Изд - во УрО РАН, 1999. – 298с.
  2. Юрлова Н.А. Об одном варианте обратной задачи поиска механических характеристик оболочек вращения // Вестник ПГТУ. Математика и прикладная математика. – Пермь: Изд-во ПГТУ, 1996. – № 1. – С. 80–86.
  3. Бабкин Д.В., Клигман Е.П., Матвеенко В.П., Юрлова Н.А. Оптимизация динамических характеристик вязкоупругих и электровязкоупругих элементов летательных аппаратов // V международная конференция «Авиация и космонавтика – 2006»: Тезисы докладов, 23-26 октября 2006 г., Москва. – С. 106–107.
  4. Лурье С.А., Белов П.А. Теория сред с сохраняющимися дислокациями. Частные случаи: среды Коссера и Аэро-Кувшинского, пористые среды, среды с «двойникованием» // Сб. трудов конференции «Современные проблемы механики гетерогенных сред», 2005. – М.: Институт прикладной механики РАН, 2005. – С. 235 268.
  5. В.В. Корепанов, М.А. Кулеш, В.П. Матвеенко, И.Н. Шардаков, Аналитические и численные решения статических и динамических задач несимметричной теории упругости // Физ. мезомех. – 2007. – Т. 10, № 5. – С. 77–90.
  6. Физическая мезомеханика и компьютерное конструирование материалов // Под ред. В.Е.Панина. – Новосибирск: Наука, 1995.– Т. 1. – 298 с.
  7. Писаренко В.Ф., Примаков И.М., Шнирман М.Г. Поведение деформируемого массива подвижных элементов // Дискретные свойства геофизической среды / Под ред. М.А.Садовского. – М.: Наука, 1989. – С. 76–84
  8. Свойства элементов: Справочник / Под ред. Г.В. Самсонова. – М.: Металлургия, 1976. – Ч. 1. Физические свойства. – 599 с.
  9. Попов С. В. Численная реализация метода геометрического погружения для пространственных задач теории упругости и ее численные аспекты / Автореферат диссертации к.ф. - м.н. – Пермь, 1996. – 16 с.




© Автор А.А., Соавтор Б.Б., Другой-Соавтор С.С., 2009