Geum.ru

Перспективные направления расчетных исследований динамики и прочности многокомпонентных фрагментов конструкций водо-водяных ру н. А. Махутов, С. М. Каплунов, Н. Г. Вальес, Т. Н. Фесенко, В. А. Панов

Вид материалаИсследование

Содержание


L, можно представить в виде: V
Список литературы
Подобный материал:
ПЕРСПЕКТИВНЫЕ НАПРАВЛЕНИЯ РАСЧЕТНЫХ ИССЛЕДОВАНИЙ ДИНАМИКИ И ПРОЧНОСТИ МНОГОКОМПОНЕНТНЫХ ФРАГМЕНТОВ КОНСТРУКЦИЙ ВОДО-ВОДЯНЫХ РУ


Н.А.Махутов, С.М.Каплунов, Н.Г.Вальес, Т.Н.Фесенко, В.А.Панов

ИМАШ РАН, Москва, Россия


Анализ аварийных ситуаций, вызванных чрезмерной вибрацией труб теплообменных аппаратов, показал, что именно отсутствие вибрационных исследований на стадии проектирования и предопределило неизбежность происшедших повреждений, а также необходимость ремонта и существенной модернизации конструкций в самом начале их эксплуатации. В процессе вибраций труб внутри отверстий в направляющих пластинах может происходить истирание и унос материала с поверхностей как трубы, так и дистанционирующей решетки в отверстии. В случае достаточно интенсивного развития фреттинг-износа происходит образование в трубе сквозных свищей и возникновение нежелательных и опасных протечек между контурами энергоустановки. Фреттинг-износ, вызванный вибрацией, представляет собой, таким образом, основной по важности источник разрушений и аварий теплообменников, не уступая в этом отношении даже коррозии.

Исследование процессов износа, проводимые в нашей стране и за рубежом показали, какую важную роль играет вид движения трубы в зазоре [1-3] среди факторов, определяющих интенсивность износа,. Оно может сопровождаться ударами по нормали к поверхности перегородки и косыми ударами с проскальзыванием. Эти режимы могут быть проанализированы только с учетом зазоров между трубой и перегородкой.

В докладе последовательно рассмотрены следующие основные вопросы:

- исследование природы и механизмов гидродинамического возбуждения

вибрации трубных пучков;

- анализ устойчивости колебаний пучков труб различных типов;

- расчет динамического отклика элементов трубных пучков;

- формирование критериев оптимизации для данного класса динамических систем;

- решение задачи оптимизации для конкретного теплообменного трубного пучка.

Гидродинамическое возбуждение вибраций теплообменных пучков труб связано с коллективными процессами в пучке, состоящем из большого числа труб, когда возбуждающие силы порождаются нестационарным отрывным течение в межтрубном пространстве. Математическое описание явления требует разработки и использования достаточно сложных моделей, в первую очередь, наиболее опасных механизмов возбуждения колебаний пучков труб и плохообтекаемых конструкций цилиндрической формы, а также создания надежных расчетных методов для описания этих моделей. Для решения таких задач необходим комплексный подход, основанный на сочетании численных экспериментов на ВМ и экспериментальных исследований на натурных и модельных объектах.

На основании экспериментальных наблюдений 4-9 по специфике проявления различают несколько характерных механизмов возбуждения, а именно: турбулентный бафтинг, периодический вихревой отрыв и гидроупругое возбуждение. Предложенная модель численного эксперимента 10,11 применима для полного воспроизведения всех основных механизмов возбуждения колебаний трубных пучков, а именно: периодического вихревого отрыва и гидроупругого возбуждения (рис.1).

Возможность проявления именно гидроупругого возбуждения является недопустимым для спроектированного теплообменного аппарата, в первую очередь, в связи с аварийным выходом из строя трубного пучка.



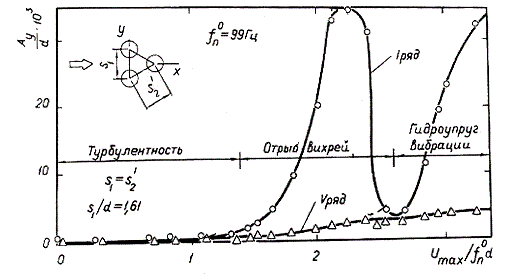
Рис.1. Механизмы возбуждения колебаний для трубных пучков.


При проектировании, в первую очередь, необходимо проводить оценку возможности гидроупругого возбуждения трубного пучка, и только после этого имеет смысл расчет амплитуд колебаний, вызванных упругими гидродинамическими механизмами возбуждения.

Поэтому для решения многочисленных задач обтекания необходим комплексный подход, основанный на сочетании численных экспериментов на ВМ и экспериментальных исследований на натурных и модельных объектах [1,4,5].

На основе известного опыта в области численного моделирования рассматриваемых процессов [10] предложен и развит модернизированный метод дискретных вихрей (в дальнейшем именуемый как ММДВ). В рамках предложенной математической модели ограничиваемся исследованием течения в рамках плоской модели и рассматриваем задачу об отрывном обтекании одиночного либо двух круговых профилей. При этом жидкость полагается несжимаемой. Рассматриваются течения в диапазоне чисел Рейнольдса Re » 2×103¸105, характерном для реальных теплообменных пучков (Re=U∞d/ν, где U∞ – скорость обтекания цилиндра, d – диаметр цилиндра, ν – кинематическая вязкость жидкости).

При решении задачи течение разбивается на две области: область течения вязкой жидкости в тонких пограничных слоях и область внешнего течения, где жидкость полагается невязкой, а само течение – потенциальным. Вихревой след, образующийся за профилями в результате явления отрыва, моделируется набором дискретных вихрей, которые вносятся во внешнее течение из точек отрыва пограничного слоя в расчетные моменты времени. Положения точек отрыва на профилях могут определяться из уравнений пограничного слоя или с помощью известных экспериментальных данных. Положения точек отрыва на профиле в данной модели будем считать определенными, например, с помощью известного эксперимента [4].



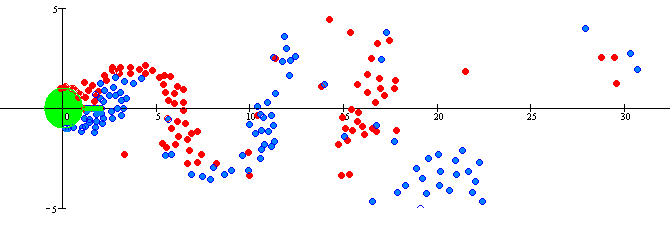
Рис.2.Дорожка Кармана для цилиндра с ребром,

подсчитанная методом дискретных вихрей.


Предложенная в работе [10] модель для расчета отрывного обтекания трубы позволяет учитывать влияние числа Re путем выбора точки отрыва пограничного слоя с поверхности трубы на основе известной экспериментальной зависимости для вязкой жидкости. Многочисленными расчетами показано, что полученные при таком подходе расчетные количественные характеристики течения для одиночной неподвижной и колеблющейся трубы (частота изменения подъемной силы, значения коэффициентов силы лобового сопротивления и подъемной силы (рис.3.), а также параметры дорожки Кармана (рис.2.) хорошо согласуются с известными экспериментальными данными в практически важном диапазоне чисел .

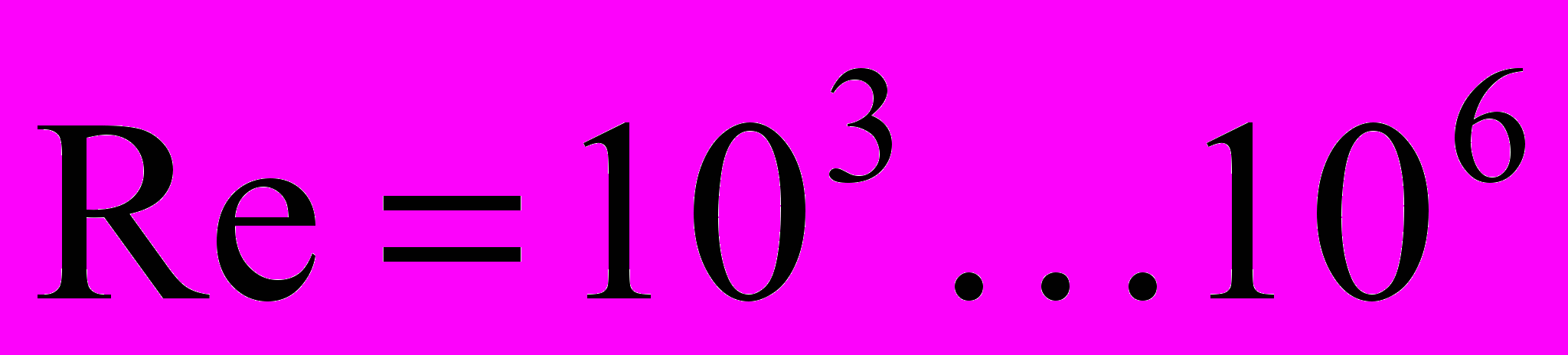Использование предложенной модели позволило получить зависимость переменных гидродинамических сил, возбуждающих колебания труб, от числа Re, что весьма важно, так как для плохообтекаемых тел, подобных цилиндру, подъемная сила и сила сопротивления могут меняться на порядок в небольшом диапазоне чисел Re.

Данная модель применена также для расчета отрывного обтекания одиночных труб, колеблющихся как вдоль, так и поперек потока, а также для трубы в режиме автоколебаний. Модель позволяет установить ширину зоны затягивания и амплитудно-частотные характеристики режима. В работах [10,11] дается подробная методика расчета и приводятся особенности метода численного эксперимента применительно к решению этих задач. С помощью этой модели рассматривается также задача об отрывном обтекании ряда труб, которая имеет принципиальные отличия по сравнению с задачей об одиночной трубе (рис.4).




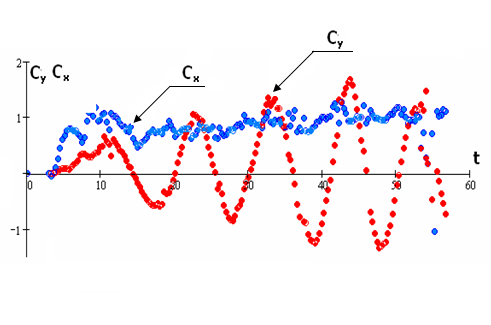
Рис.3. Расчет гидродинамических сил для цилиндра,

колеблющегося в потоке жидкости.


Форму рассматриваемого тела можно представить либо с помощью соответствующего конформного отображения (искомой трубы на круг), либо с помощью дискретных поверхностных особенностей [12]. Первый подход обеспечивает точное описание формы тела, однако оказывается довольно трудоемким [12], а второй подход намного проще, но предусматривает выполнение граничного условия нулевой нормальной скорости лишь для заданного числа контрольных точек. В данной работе используется как метод поверхностных особенностей (или метод вихревой решетки) несмотря на его недостатки, так и метод конформных отображений.

На основе имеющихся экспериментальных данных была разработана математическая модель гидроупругого возбуждения колебаний пучка труб внешним поперечным потоком. В этой математической модели гидродинамической взаимодействие между колеблющимися трубами учтено в наиболее общем виде (в рамках гипотезы линейности дестабилизирующих сил).




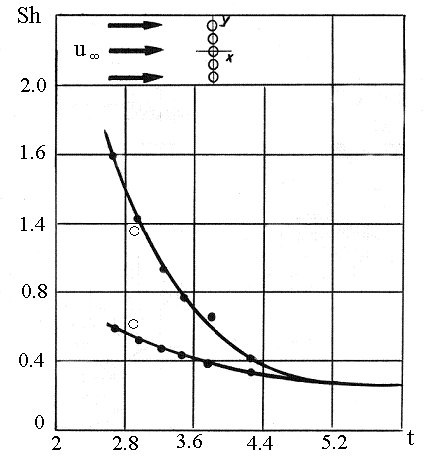
Рис.4.Число Струхаля для одиночного ряда труб.

.-эксперимент, о- расчет.

Задача изучения гидроупругого возбуждения сведена к анализу устойчивости невозмущенного состояния упругих труб. На основании теоретического исследования математической модели получены необходимое и достаточное условие устойчивости, выраженное в наглядной форме через безразмерные параметры системы. Введена матрица линейной гидродинамической связи как характеристика гидродинамических сил. Для ее определения предлагается проводить серии вычислений нестационарных гидродинамических сил, где в каждом варианте только один из профилей системы совершает гармонические колебания с небольшой амплитудой 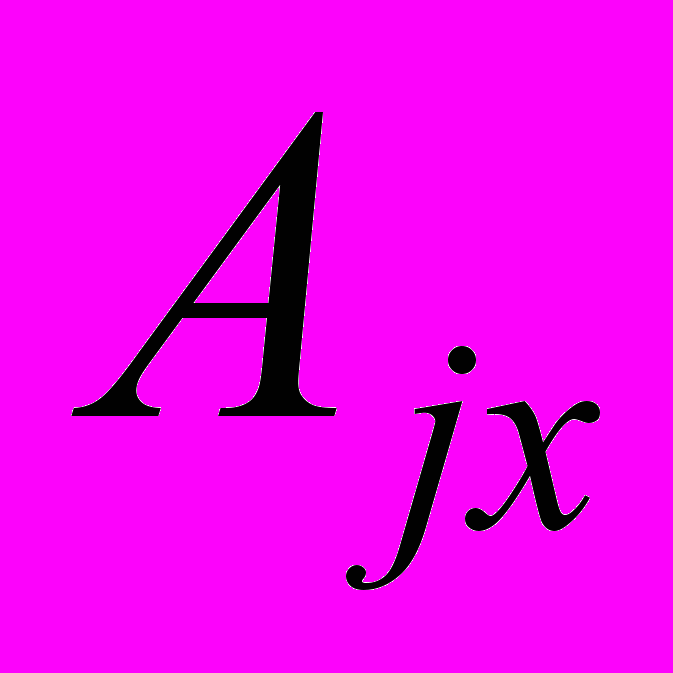() на частоте , направленные вдоль оси x или y. Варьируя безразмерную частоту колебаний профилей, можно получить зависимость элементов матрицы линейной гидродинамической связи от .

Для корректного определения матрицы линейной гидродинамической связи требуется вычисление и обработка продолжительных реализаций гидродинамических сил. В связи с этим, основное требование к полученному алгоритму – минимизация времени вычислений. Требуемое повышение его быстродействия достигается за счет использования специализированной методики решения граничной задачи в области, ограниченной системой круговых контуров. Применение такой методики дает значительный выигрыш в быстродействии по сравнению с методом коллокаций.

.

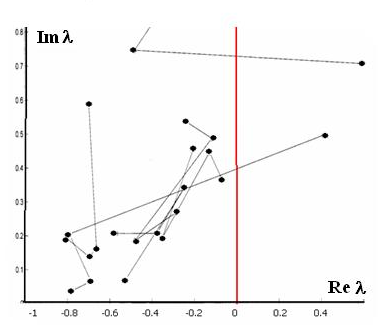
Рис.5.Переход корней характеристического уравнения

в положительную область. Потеря устойчивости системы.


В соответствии с полученным алгоритмом создана оригинальная программа, позволяющая проводить расчет продолжительных реализаций нестационарных гидродинамических сил при отрывном обтекании системы круговых профилей, колеблющихся по заданному закону. С помощью этой программы проводились численные эксперименты, в которых определялись матрицы линейной гидродинамической связи для конкретных пучков труб. После вычислений соответствующих матриц проводится анализ устойчивости системы и определяются критические значения таких параметров системы, как скорость и другие (рис.5,6).

Разработанный алгоритм для численного определения матрицы гидродинамических сил основан на усовершенствованной модели дискретных вихрей. Достоверность его использования проверена путем сравнения результатов расчетов с известными экспериментальными данными по величине и частоте изменения гидродинамических сил, а также по параметрам дорожек Кармана.

Данный подход при исследовании явления гидроупругого возбуждения колебаний трубных пучков и полученные результаты могут успешно использоваться на стадии проектирования теплообменных аппаратов для определения области параметров, в которой невозможна нормальная безопасная эксплуатация агрегата.



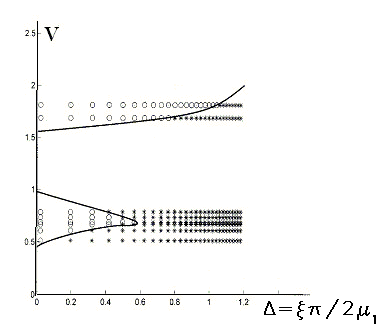
Рис.6. Численное определение областей устойчивости для трубного ряда

или однорядного пучка.


Полученное путем анализа математической модели необходимое и достаточное условие устойчивости реализовано в наглядной форме через безразмерные параметры системы. Это условие позволяет обоснованно проводить обобщение имеющихся экспериментальных данных о критических значениях параметров системы. Входящие в условие устойчивости безразмерные параметры определяют критерии подобия для гидроупругого возбуждения, что необходимо при экспериментальном (и расчетном) моделировании исследуемого пучка и процессов, что находится в полном согласии с выводами и критериями, получаемыми с использованием теории подобия и размерности.

Определение величины критической скорости теплоносителя в зависимости от безразмерного параметра, включающего в себя величину декремента колебаний и безразмерный массовый параметр пучка, позволяет оперативно диагностировать уже введенный в эксплуатацию теплообменный аппарат на наличие в конструкции недопустимого гидроупругого возбуждения.

В реальных теплообменных аппаратах трубы в пучках опираются на дистанционирующие решетки, установленные с зазорами относительно них. Учет данных зазоров необходим при рассмотрении вопросов надежности функционирования данного вида систем. Предлагаемая авторами математическая модель позволяет рассчитывать динамический отклик элемента пучка многоопорных труб с зазорами, причем гидродинамическое возбуждение в зависимости от скорости поперечного потока включает срыв вихрей с труб и их гидроупругую связь между собой. Коэффициенты гидроупругой связи между трубами определялись методами численного эксперимента из решения задачи об обтекании группы профилей цилиндров как описано выше.

Данный алгоритм позволяет определять характерные перемещения, виброскорости, контактные нагрузки, пути скольжении и время контакта для труб теплообменника с учетом их реального дистанционирования. Эти величины являются определяющими для нахождения виброизноса труб в местах их контакта с промежуточными опорами.

Расчетная схема представлена на рис. 7. Для описания вибраций труб в пучке используются уравнения изгибных колебаний стержней. Реакции промежуточных опор вводятся в правые части уравнений как импульсные силы [1].





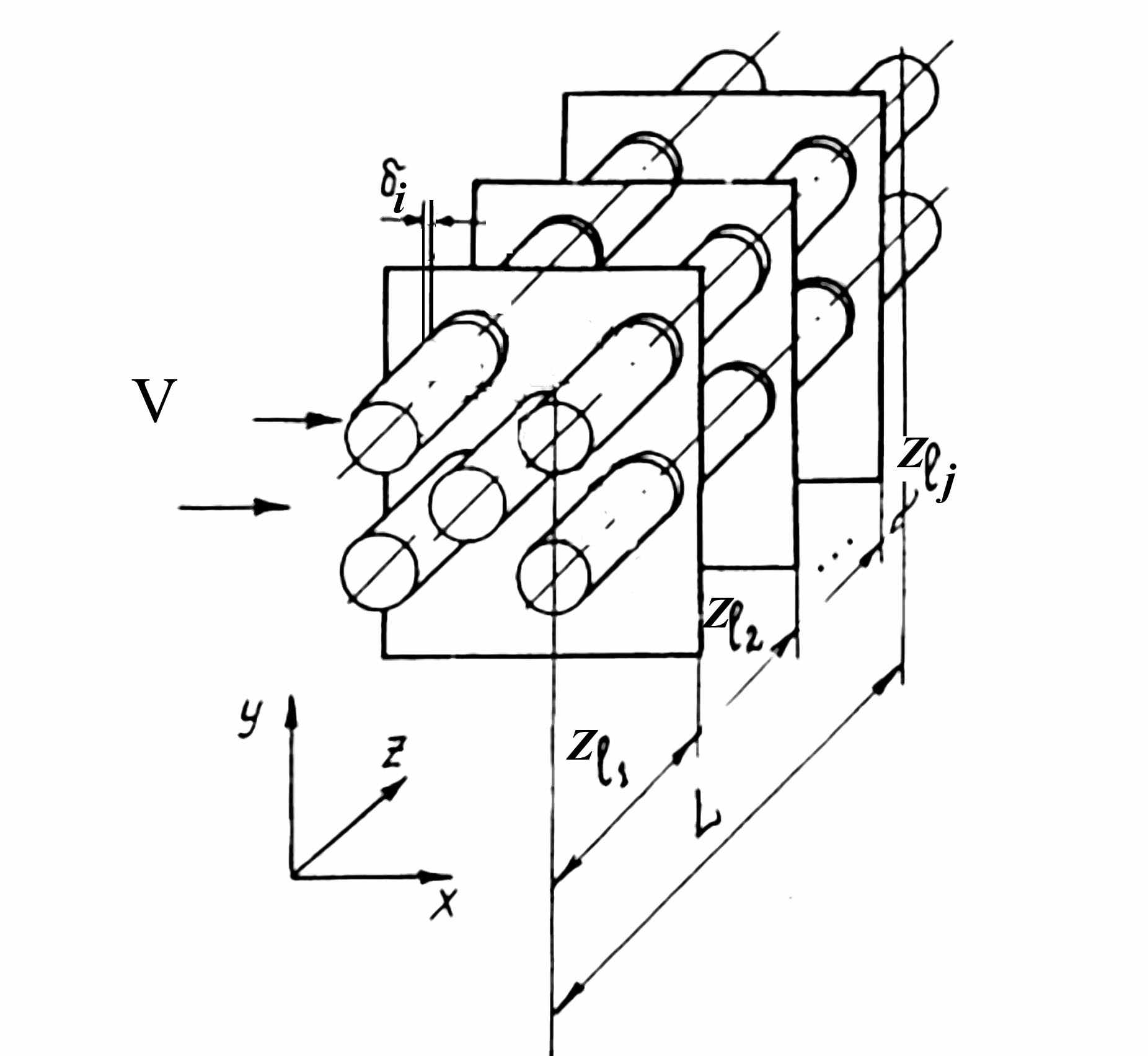
Рис.7. Расчетная схема с учетом промежуточных опор.




Рис.8. Расчетная схема с учетом промежуточных опор для j-й трубы.


Для определения динамического отклика трубного пучка необходимо численно решить 2k систем дифференциальных уравнений

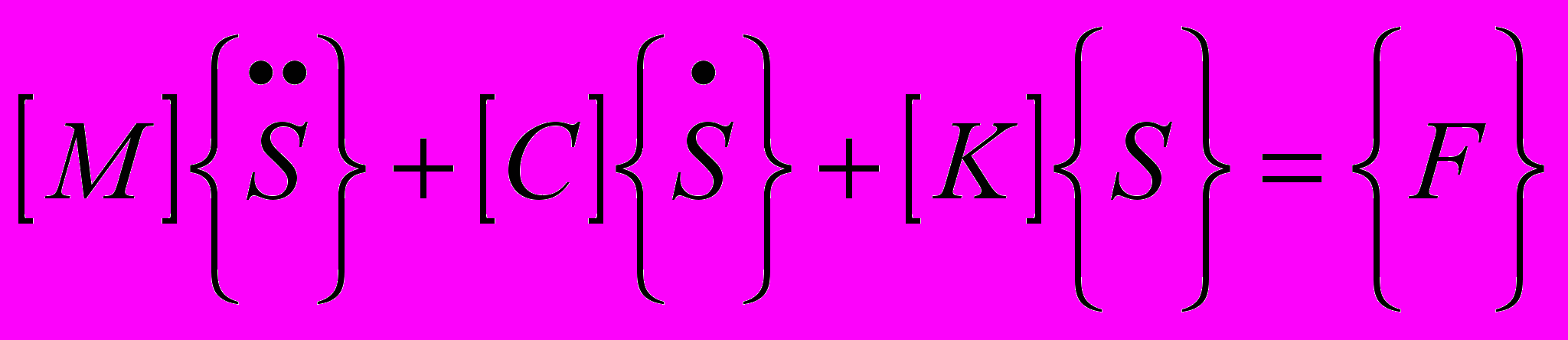, (1)

где [M], [C], [K] – есть матрицы масс, демпфирования и жесткости соответственно, а {S},{F} – обобщенные векторы смещения и внешней нагрузки. Матрицы [M], [C], [K] имеют размерность 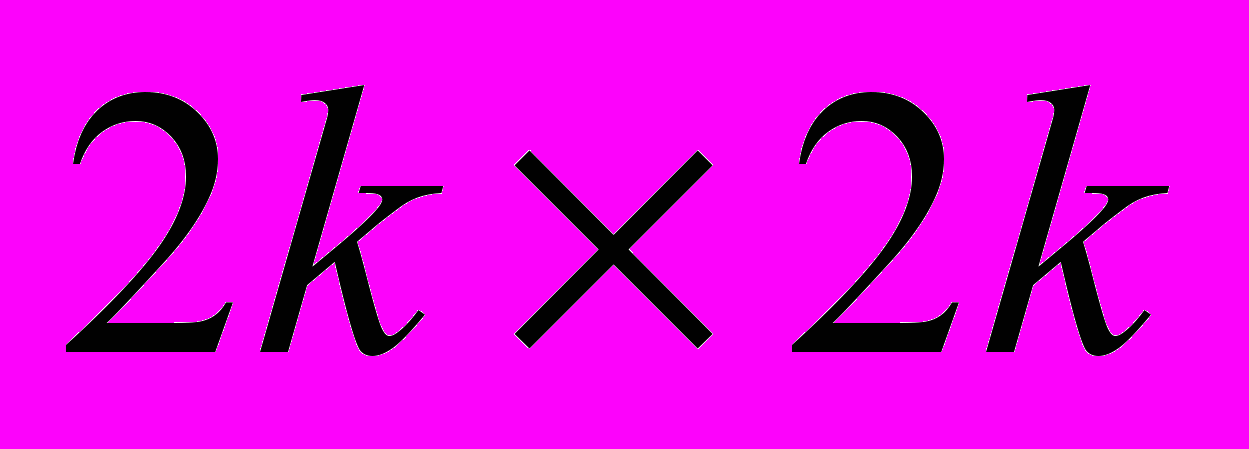, k – количество труб.

Элементы трубного ряда совершают орбитальные движения, и модель прямого удара при контакте с дистанционирующими решетками для них не приемлема. В работе принята модель косого удара с нормальной и тангенциальной составляющими силы реакции опор [2,3].

При описании контактного взаимодействия в нормальном направлении диссипация энергии при ударе не учитывается и выражение для нормальных сил принимается в следующем виде:

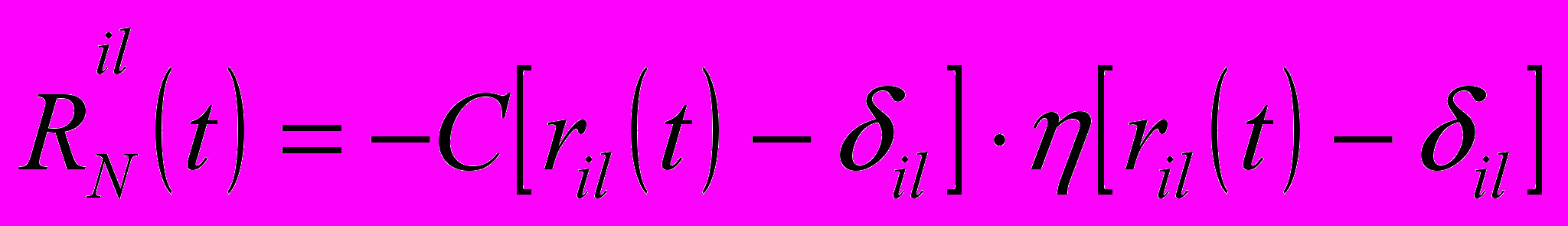, (2)

где 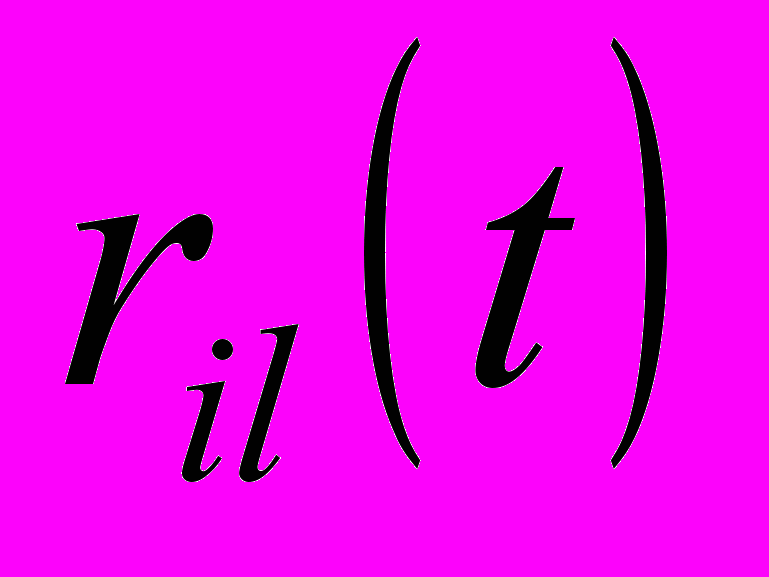– радиальное перемещение трубы в l-й опоре, 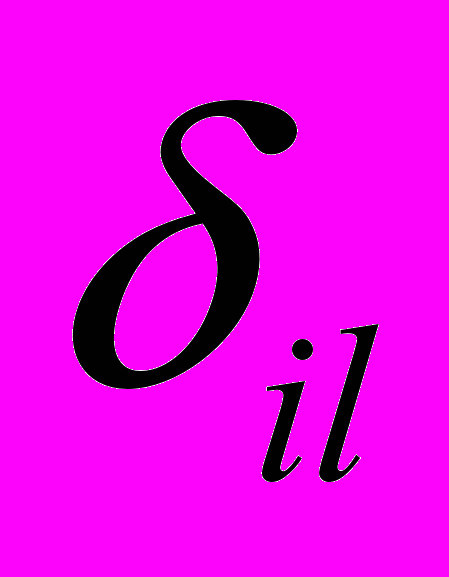– зазор в l-й опоре, 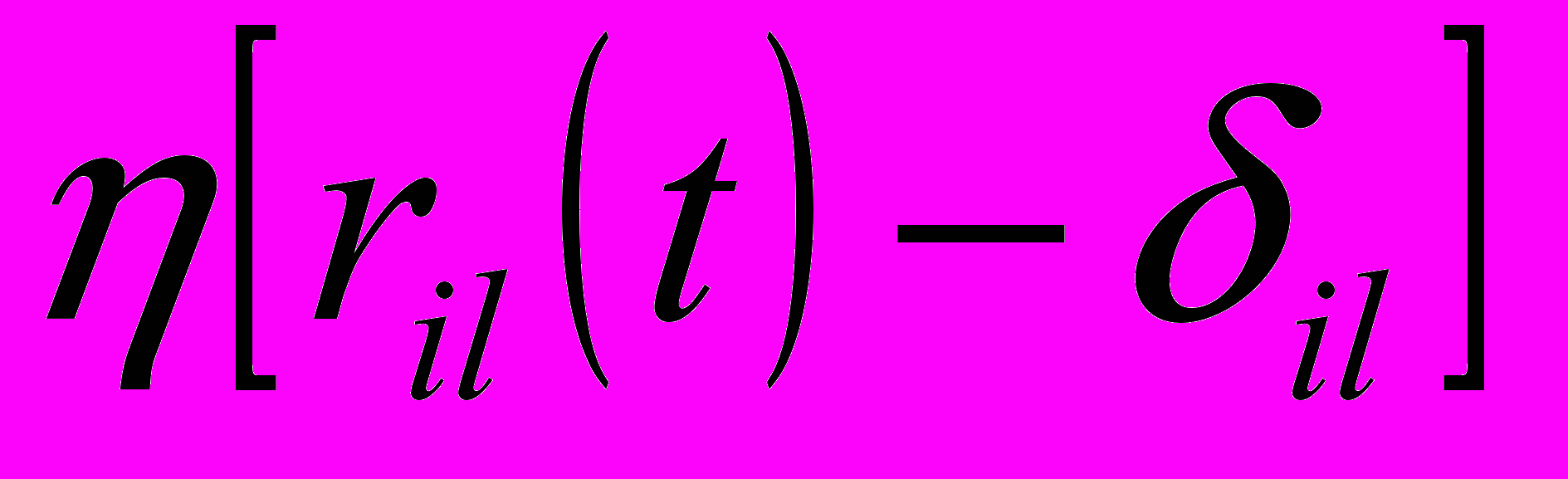– функция Хевисайда (в программе реализовано посредством условных операторов).

Для расчета тангенциальных сил косого удара использована гипотеза сухого трения, т.е. тангенциальная сила связана с нормальной силой и направлена против движения.

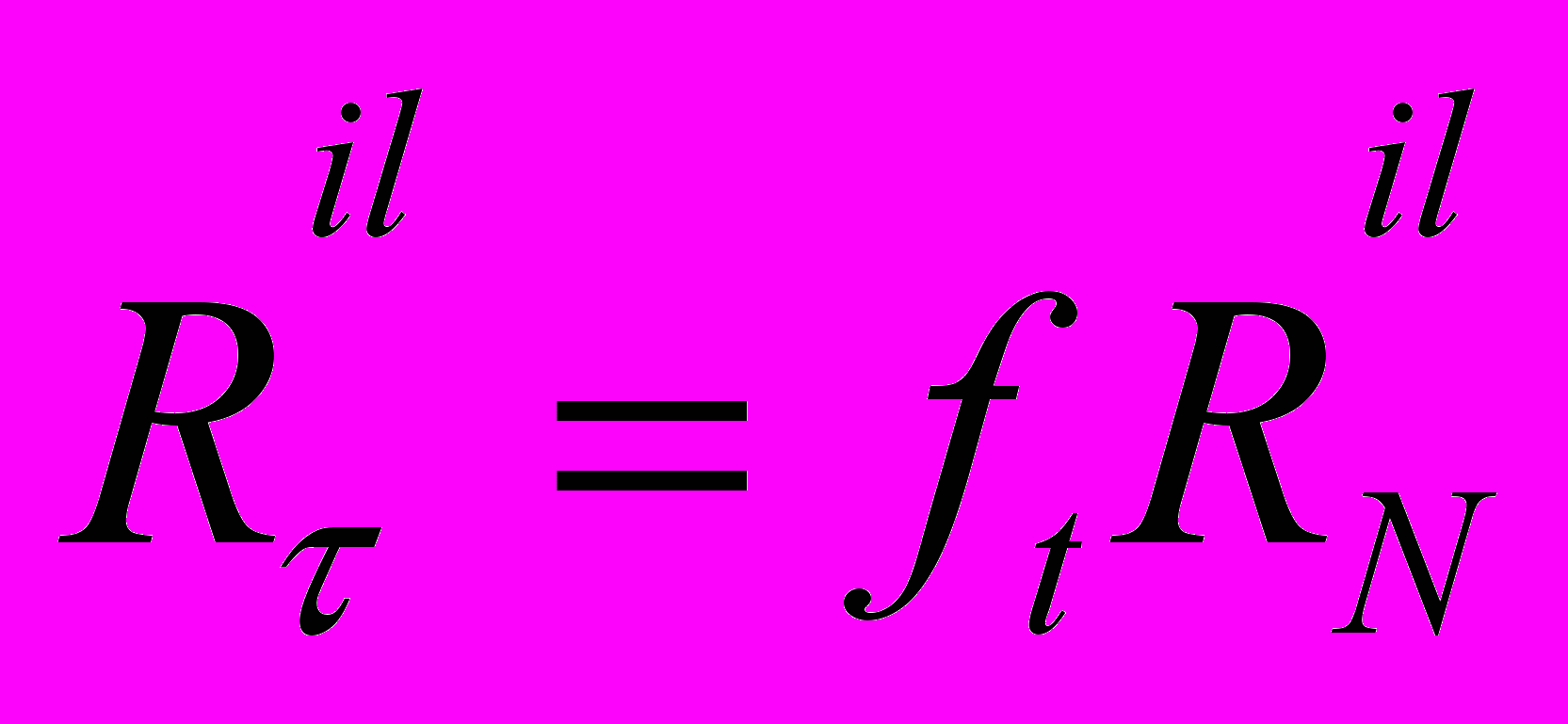, (3)

где 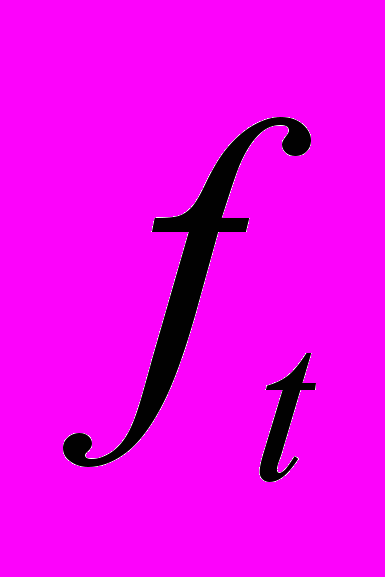– коэффициент сухого трения, принимается 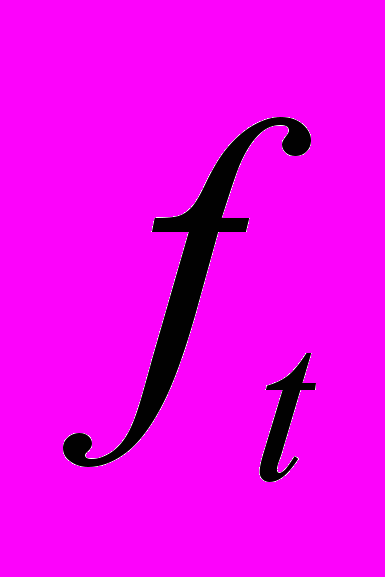= 0,2 [3].

Полная реакция для i-й трубы в первой промежуточной опоре определяется геометрическим суммированием сил:

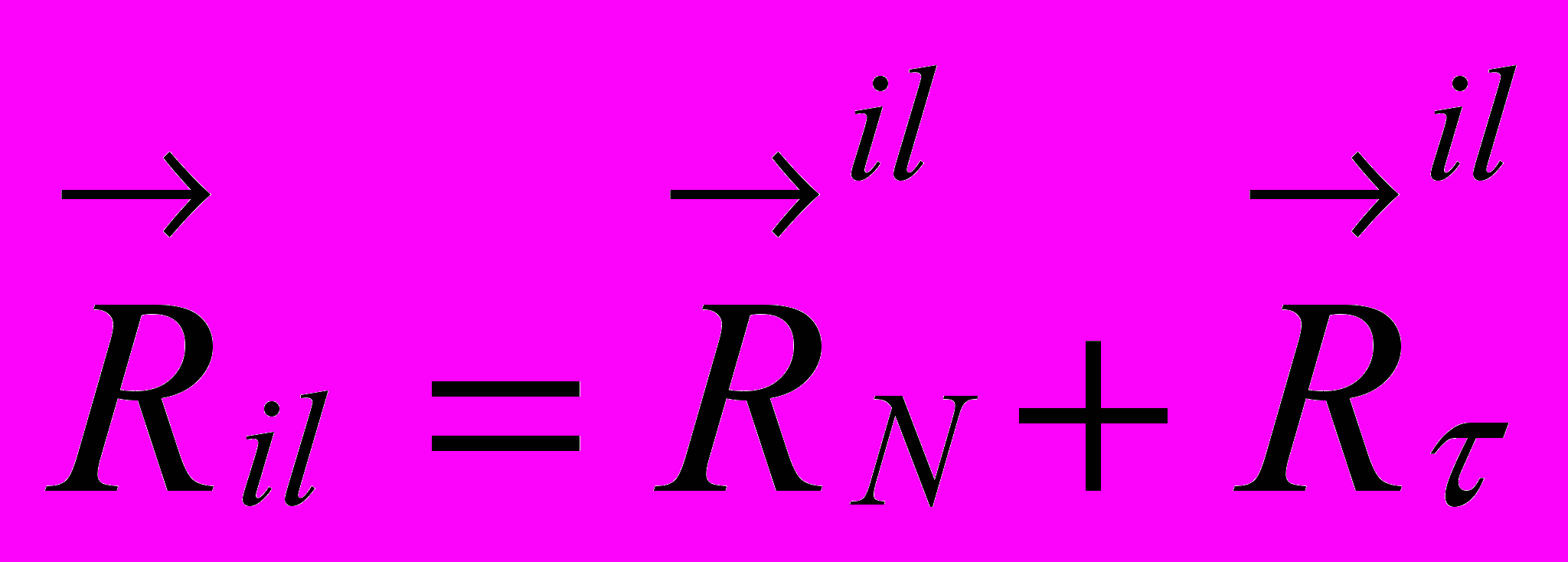, (4)

Для решения динамической задачи (1) авторами использован метод пошагового интегрирования Вильсона [14]. Этот метод может быть использован для произвольной структуры элементов с физическими и геометрическими нелинейностями. Метод Вильсона является неявным разностным методом, а поэтому его реализация допускает большую по сравнению с явными методами величину шага, с которым можно двигаться по времени.

К основным параметрам оценки ресурса конструкции в первую очередь относятся такие факторы как виброизнос труб в промежуточных опорах, напряжения изгиба и характерная частота их знакоизменения в процессе колебаний. В стратегии исследований динамики трубных систем исходили из того, что среди факторов, влияющих на износ, выделяются в первую очередь конструктивные: диаметральный зазор между трубой и промежуточной перегородкой, количество и расположение опор. Во вторую очередь, как следствие наличия первой группы, рассматривается группа динамических факторов: тип движения трубы, отклонение трубы под влиянием потока, частота и амплитуда сил соударения в контакте.

Для подавления негативных последствий, вызванных колебаниями труб в пучке, необходимо было бы увеличить количество дистанционирующих элементов, однако это привело бы к ряду других негативных явлений, например, увеличению гидравлического сопротивления и снижению интенсивности тепломассообмена. Таким образом, задача оптимизации расположения промежуточных опор является весьма сложной и важной. Время до разрушения труб определяется виброизносом и циклической прочностью, зависящими от амплитуды напряжений и количества циклов нагружения. На данный момент отсутствуют достоверные зависимости между износом и усталостью для данного узла в данной среде, в связи с чем многомерная оптимизация конструктивных параметров трубного пучка проводится путем минимизации двух критериальных параметров: по износу и по усталости. Учитывая вышеизложенное, для выбора оптимальной конструкции использован метод теории планируемого эксперимента (ПЛП-поиска).


Согласно зависимости И.В. Крагельского [15], объем материала, удаленного на пути трения L, можно представить в виде:

VL=KBFNL, (5)

где KB – коэффициент виброизноса, FN – нормальная сила контакта между трубой и опорой, L – путь трения.

В данной работе значения контактной силы FN, как и путь, пройденный трубой при касании опоры в единицу времени L, определяются из численного эксперимента.

В соответствии с работой [15] для одних и тех же пар трения, при одних и тех же условиях (среда, температура и т.д.) – критерий оптимизации по виброизносу будет представлять собой

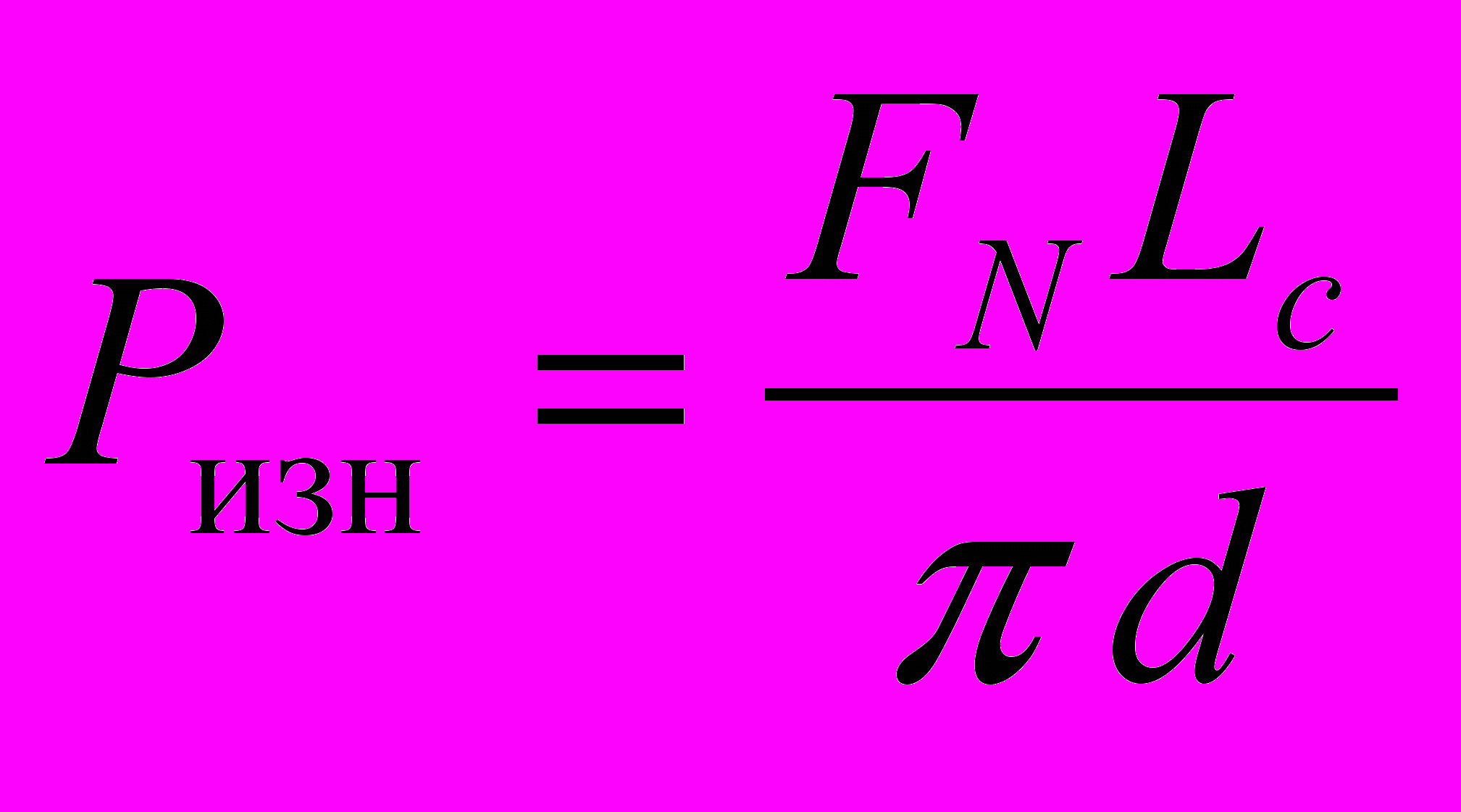, (6)

где Lc – путь трения за 1 секунду.

Минимизация этого параметра позволит повысить ресурс конструкции, однако, в этом критерии есть еще и практическая польза. Ведь зная значения коэффициента виброизноса и среднюю ширину опоры, можно найти эквивалентную глубину виброизноса за заданное время t, с:

.

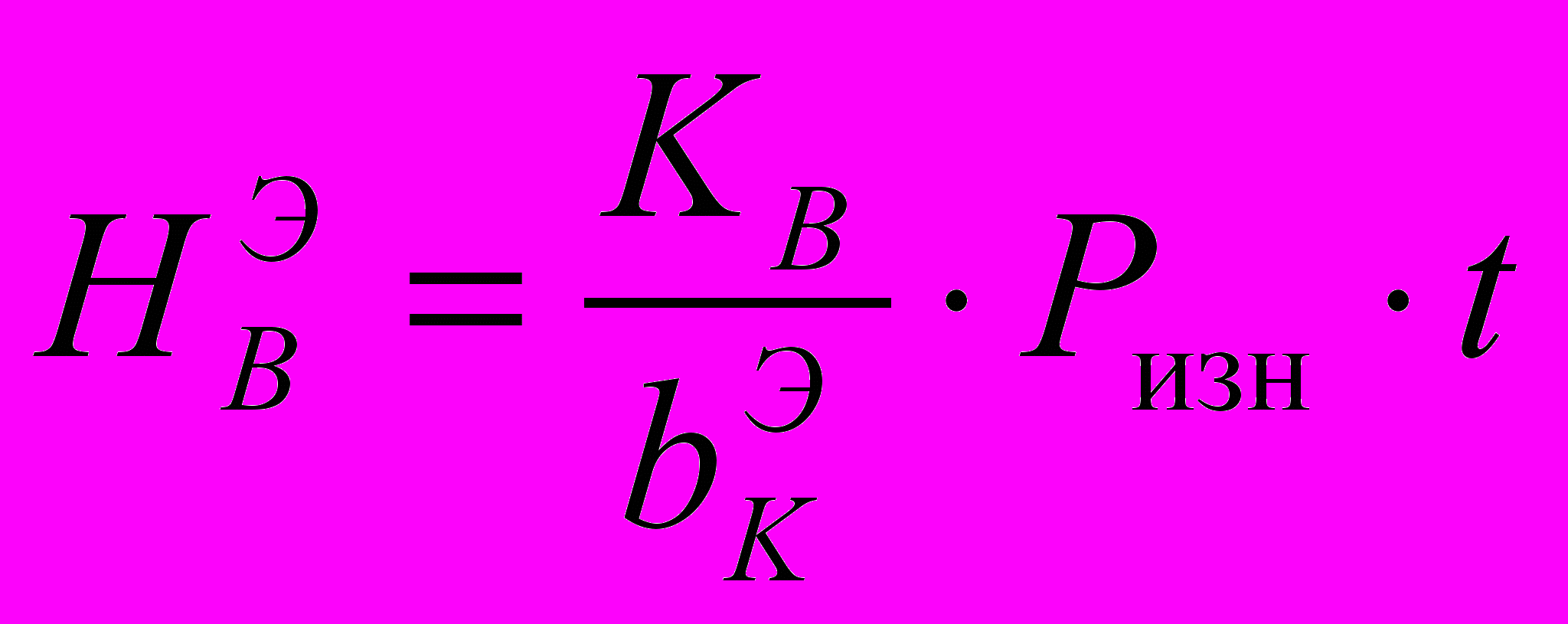Условие прочности при наличии различных циклических нагрузок определяется известным выражением 1:

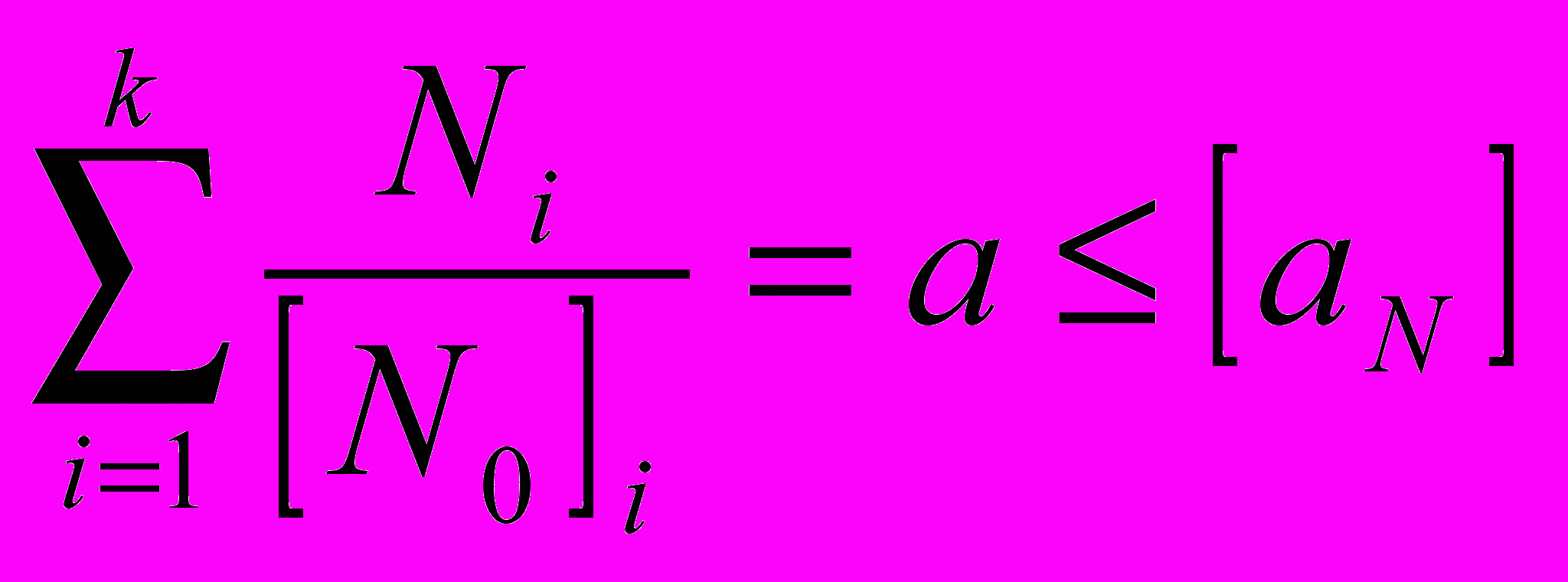, (7)

где: Ni – число циклов i-го типа за время эксплуатации; k – общее число типов циклов; [N0]i – допускаемое число циклов i-го типа; a – накопленное усталостное повреждение, предельное значение которого [aN] = 1.

Количество допускаемых циклов в нашем случае напрямую зависит от амплитуды изгибных колебаний. Количество циклов есть произведение основной частоты функции напряжений на время эксплуатации в данном режиме. Колебательный процесс для данных нелинейных систем является сложным. Происходит наложение собственных частот колебаний и частот вынуждающих сил, при этом частотный состав в отклике зависит от величин зазоров в промежуточных опорах и их расстановки. Для нахождения частот колебаний в работе применен метод дискретного преобразования Фурье.

Исходя из вышесказанного, критерием, характеризующим усталостную прочность, является минимальная амплитуда изменений напряжений изгиба в соответствующих направлениях

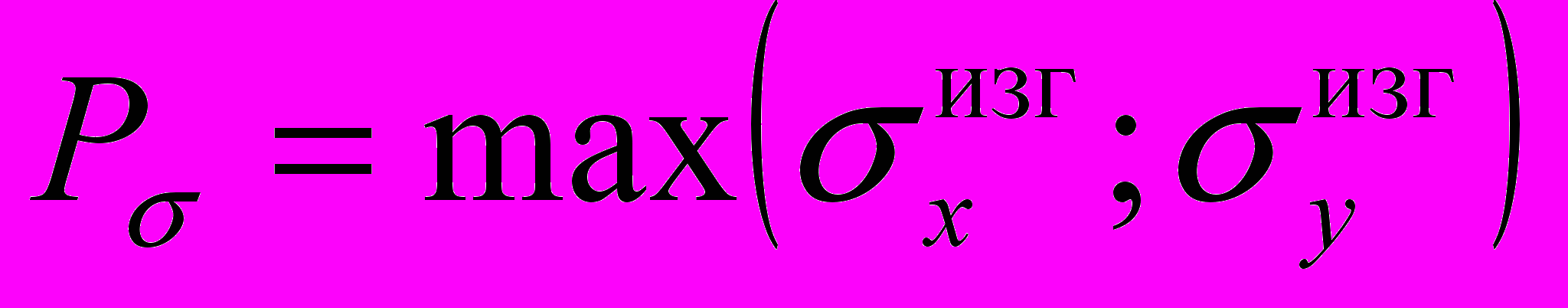. (8)

В качестве критериев качества для данной конструкции выбираем критерий по виброизносу (6) и критерий усталости по амплитудам изгибных колебаний (8). Исходя из возможностей ПЛП-поиска, при решении вопроса оптимизации конструкции трубного пучка в данной работе минимизировались параметры:

Ф1 – максимальный путь трения в за одну секунду движения трубки Lс, м/c;

Ф2 – максимальная нормальная (погонная) сила соударения в опоре FN, Н/м;

Ф3 – максимальная тангенциальная (погонная) сила соударения в опоре Fτ, Н/м;

Ф4 – максимальное изгибное напряжение по оси Х σХ, Па;

Ф5 – максимальное изгибное напряжение по оси Y σY, Па.

Данные параметры определялись при численной реализации предложенной математической модели вибрации трубных пучков с учетом зазоров в промежуточных опорах.

Идеологическая основа ПЛП-поиска состоит в том, что в результате рандомизации процесса проведения N вычислительных экспериментов образуется совокупность значений 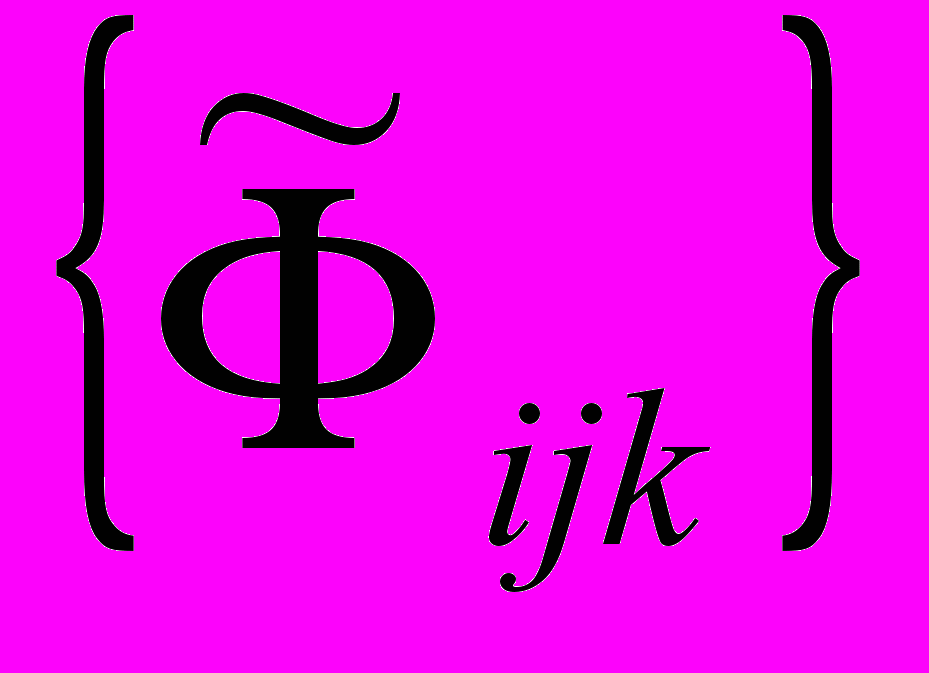, где 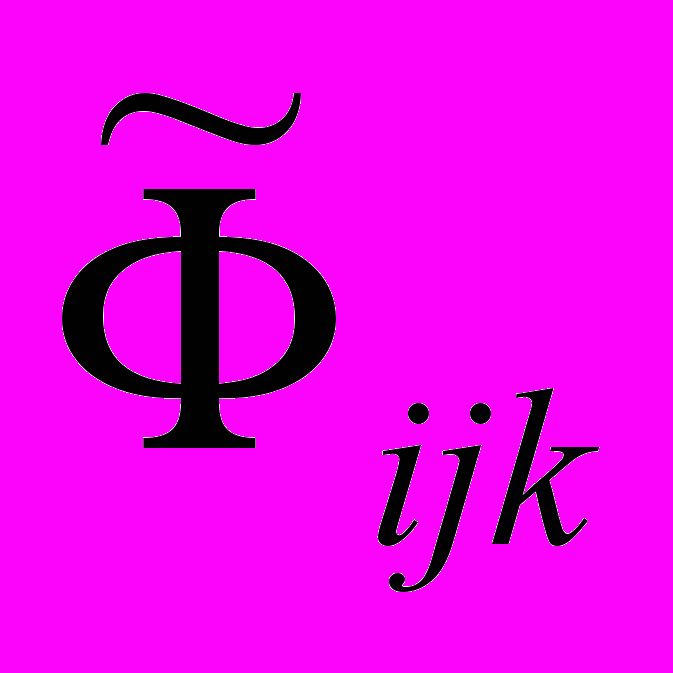– среднее значение k-го критерия качества на i-ом уровне j-го параметра. Совокупности значений 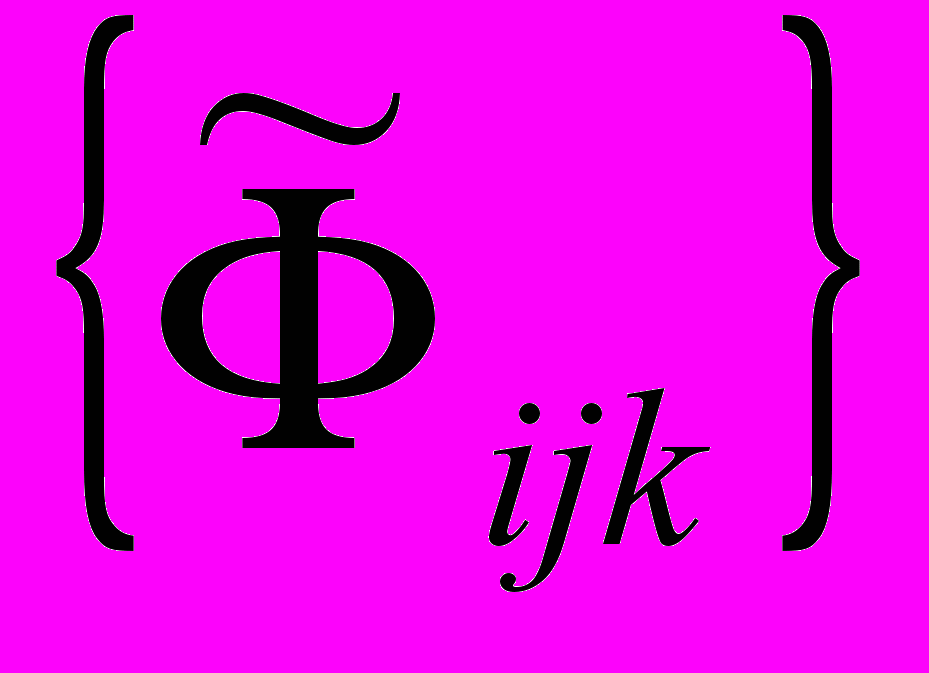позволяют на основе техники дисперсионного, регрессионного и топологического анализа дать ответы на поставленную задачу выбора оптимальной конструкции.

Предложенную методику многомерной оптимизации проиллюстрируем на расчете трубного пучка с двумя промежуточными опорами. К варьируемым параметрам отнесем величины пролетов (расстановку опор) и радиальные зазоры в них. Столь малое количество варьируемых параметров для численного примера взято с целью экономии машинного времени, а также для принятых нами варьируемых параметров можно провести соответствующий анализ и оценить физическую реальность данной методики многомерной оптимизации. Исходные данные исследуемого пучка представлены в таблице 1. Варьируемые параметры можно представить областью G0, содержащей варьируемые параметры:

,

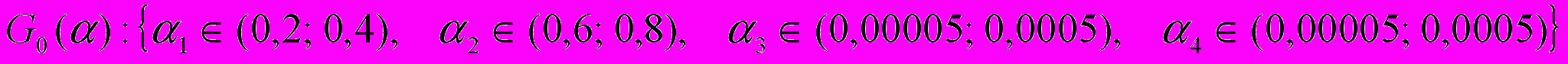где 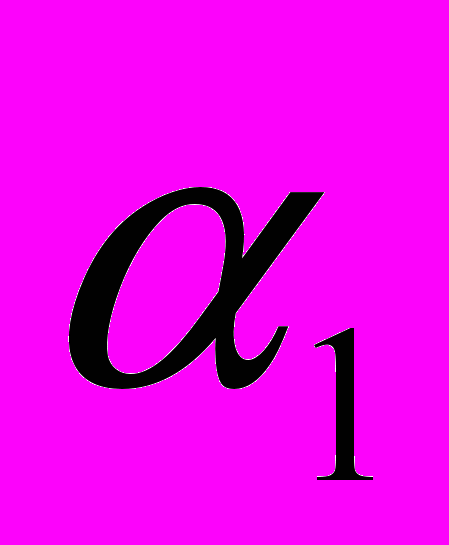, 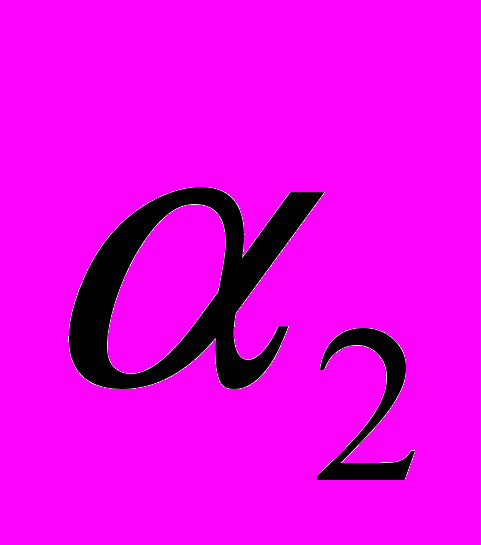– расстояние от начала трубы до первой и второй опоры; ,– радиальный зазор в первой и во второй опорах, соответственно.


Таблица 1. Исходные данные исследуемой трубной системы (фрагмента пучка).


Параметр
Значение

Исследуемый пучок, №
1

Количество опор
2

Количество труб, k
9

Тип пучка
Квадратный

Диаметр трубы d, мм
16

Длина труб L, м
1

Шаг в Х направлении Tх , мм
40

Шаг в Y направлении Tу , мм
40

Относительный шаг, qt = T/d
2,5

Коэффициент лобового сопротивления Сх
0,5*

Коэффициент подъемной силы Су
0,3*

Число Струхаля Sh
0,202**

Коэффициенты гидромеханических связей

***

* Характеристики вихревого возбуждения принимались в соответствии с данными [4].

** Значение принято в соответствии с формулой [1] для коридорного пучка: .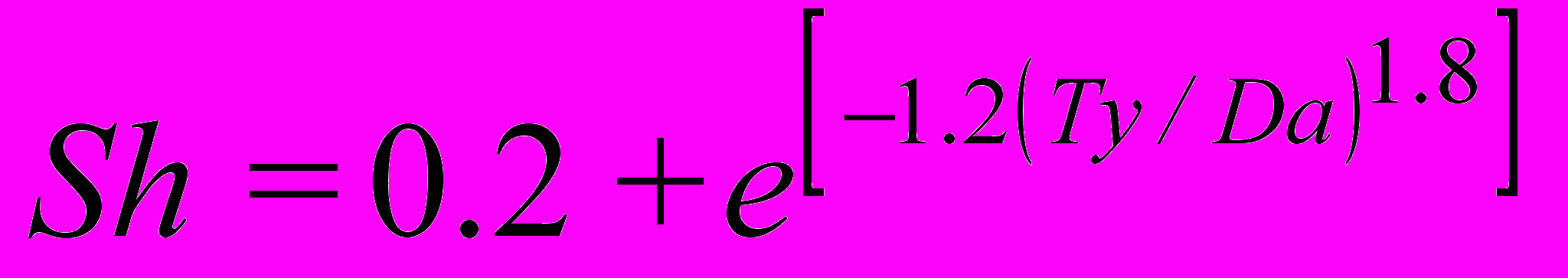

*** Значение коэффициентов гидродинамических связей определяется или вычислено согласно [2]


Было проведено 80 численных экспериментов и для всех уровней определены значения критериев качества. По данным численных экспериментов определялись: максимумы критериев max Фk(), минимумы критериев min Фk(), общие средние значения 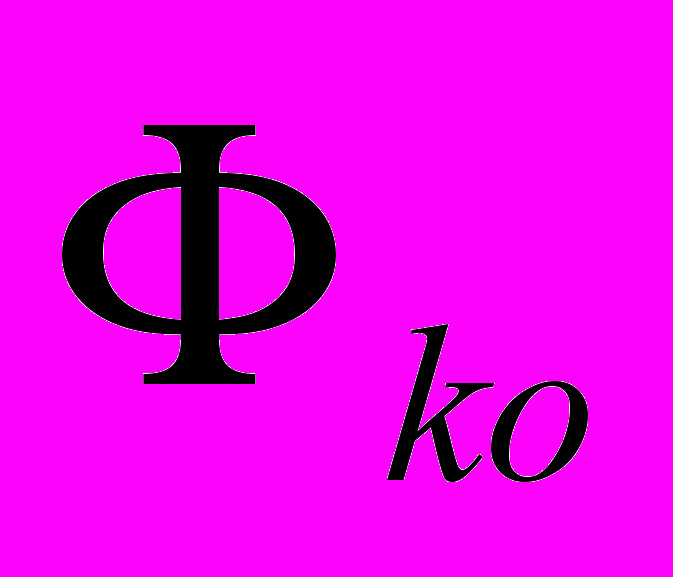, среднеквадратичные отклонения критериев Sk. На основе проведенного дисперсионного анализа построена таблица 2.

Таблица 2

критерии
параметры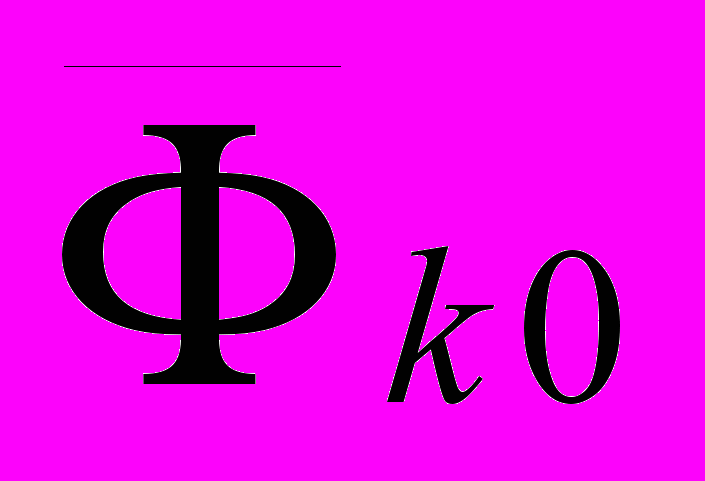


Sk
Степени

свободы
Эмпирич.

значение

критерия

Фишера

F
Уровень

значим.
Доверит.

вероятность.

P = 1 – 

1
2




1
0,00137605
0,00197147
7
72
2,031
0,0625
0,9375

2
7
72
1,059
0,3985
0,6015

3
7
72
14,811
0,0002
0,9998

4
72
7
1,005
0,5580
0,4420




1
5,04491113
6,39459558
7
72
3,1566
0,0057
0,9943

2
7
72
1,8969
0,0823
0,9177

3
7
72
6,4171
0,0002
0,9998

4
7
72
11,5788
0,0002
0,9998




1
3,32755351
4,17755493
7
72
3,5368
0,0024
0,9976

2
7
72
2,1214
0,0519
0,9481

3
7
72
7,6627
0,0002
0,9998

4
7
72
11,3238
0,0002
0,9998




1
1582073,37
769691,11
7
72
1,5048
0,1793
0,8207

2
7
72
2,5995
0,0191
0,9809

3
7
72
5,5415
0,0002
0,9998

4
7
72
4,4334
0,0002
0,9998




1
4183180,53
1736427,81
7
72
1,3816
0,2262
0,7738

2
72
7
1,0097
0,4452
0,5548

3
7
72
8,3414
0,0002
0,9998

4
7
72
8,2470
0,0002
0,9998


На основе данных таблицы 2 дисперсионного анализа можно рекомендовать области наилучших решений по каждому критерию и область компромиссных решений, если придерживаться равнозначности всех критериев. Для данного численного примера области наилучших параметров будут следующие:



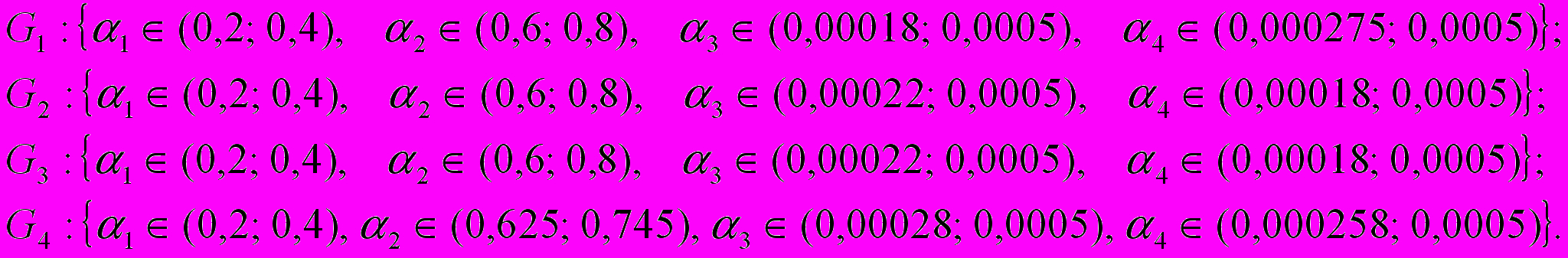
Возможная область поиска компромиссных решений:

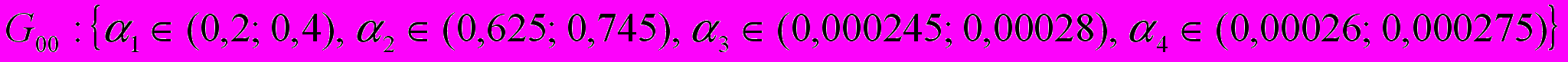Результаты оптимизации показаны на рис. 9. Приведенные результаты численного эксперимента наглядно свидетельствуют о возможностях использования данного метода для автоматического проектирования трубных пучков.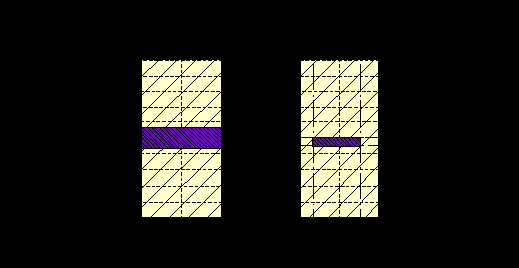



Рис. 9. Выбор диаметральных зазоров для труб заданной длины

с двумя перегородками и соответствующих длин пролетов

из условия обеспечения заданного ресурса.

Заключение



Колебания конструктивных элементов оборудования в потоке жидкого теплоносителя занимают важное место в общей проблеме повышения вибропрочности рассматриваемых конструкций. Решение ее для каждого агрегата или подобных установок не ограничивается только разработкой экспери­ментально-теоретической методики исследования и прогнозирова­ния динамических состояний. Оно включает также прогнозирование ресурса и получение рекомендаций по его продлению.

Представленный в докладе подход по определению гидродинамических нагрузок и силового взаимодействия при обтекании поперечным однофазным турбулентным потоком среды теплоносителя многокомпонентных конструкций трубных пучков является в настоящее время наиболее эффективным и успешно используется не только для определения параметров критического состояния конструкции, но также полезен при получении и анализе параметров нагружения и отклика конструкции на рабочих и форсированных режимах при эксплуатации рассматриваемых агрегатов энергетического оборудования.

Предложенная методика в целом позволяет, в отличие от известных, проводить достаточно оперативную оценку характерных параметров сложных амплитудно-частотных характеристик (особенно для нелинейных систем) колебаний труб в линейной и нелинейной постановках, а также выявлять для исследуемых процессов и различных типов трубных систем (с различными количествами опор с зазорами и величинами пролетов между ними) важные для проектирования, эксплуатации и прогнозирования ресурса параметры. Так как время до разрушения труб определяется виброизносом и циклической прочностью, были сформулированы критерии оптимизации и проведена многомерная оптимизация конструктивных параметров трубных пучков путем минимизации составляющих обоих критериальных параметров. Для оптимизации применен известный метод ПЛП-поиска 16.


Список литературы


1. Фролов К.В., Махутов Н.А., Каплунов С.М., Смирнов Л.В.и др. Динамика конструкций

гидроаэроупругих систем. //Под редакцией С.М.Каплунова и Л.В.Смирнова. М., Наука,

2002, 398 с.

2. Fesenko T.N., Foursov V.N., Forced oscillation of tube bundles in liquid cross- flow. Vibration

problem+s ICOVP 2005., Springer. 2005 - p.205-212.

3. Каплунов С.М., Фесенко Т.Н, Шитова Л.И, Шумилов Б.А. Динамические характеристики

регулярных трубных систем теплообменных аппаратов в поперечном однофазном потоке

теплоносителя. Теплоэнергетика, №4, Энергоатомиздат, 1991. С. 46-51.

4. Чен С.С. Механизм возникновения неустойчивости для группы круглых цилиндров,

подверженных воздействию поперечного потока. Ч. 1// Тр. Амер. общ. инж.-мех.

Конструирование и технология машиностроения. -1983. Т. 105, № 1. С. 16-24.

5. Фергюсон Дж., Паркинсон Н. Явления на поверхности кругового цилиндра и в вихревом

следе при колебаниях цилиндра, возбуждаемых вихрями // Тр. Амер. общ. инж.-мех.

Конструирование и технология машиностроения, -1967. Т. 89. № 4.С. 260-269.

6. Hartlen R.T. Currie T.G. Lift – oscillator model of vortex – induced vibration // J. Eng. Mec.

Div. Proc. Soc. Civ. Eng. 1970. 96, № 5.

7. Griffin O.M., Skop R.A., Koopman G.H. The vortex exident resonant vibration of circular

cylinders. Journal Sound and Vibration. 1973. V.31(2), p.235-249.

8. Девнин С.И. Гидроупругость конструкций при отрывном обтекании. Л.,Судостроение,

1975. 190 с.

9. Чжень И.Н. Колебания подъемной силы, обусловленной вихревыми дорожками Кармана

за одиночными круговыми цилиндрами и в пучках труб. Ч.1, 2, 3. // Тр. Амер. общ. инж.-

мех. Конструирование и технология машиностроения, -1972, Т.94, №2, С.111-139.

10. Вальес Н.Г. Расчет срывного обтекания цилиндра при автоколебаниях в потоке

жидкости. Механика жидкости и газа. 1980. с.174-178.

11.Каплунов С.М., Вальес Н.Г., Горелов Е.В., Шитова Л.И. Метод математического

моделирования гидродинамических механизмов возбуждения вибраций теплообменных

пучков труб. Проблемы машиностроения и надежности машин. 2008. № 3. стр.107-112.

12. Седов Л.И. Плоские задачи гидродинамики и аэродинамики. М.: Наука, 1980. 448с.

13. Ивен В.Д. Колебания элементов конструкций при вихревом возбуждении//

Конструирование и технология машиностроения. 1975, т. 97. № 4. С. 240-245.

14. Bathe K.I., Wilson E.L. Large eigen value problems in dynamics analysis //J. Eng. Mech.

Div., 1972. Vol. 98. N. 6. P. 1471 – 1485.

15. Трение, изнашивание и смазка. Спр. в 2-х книгах/под ред. И.В. Крагельского и

В.В.Алисина. М.: Машиностроение, 1978. Кн. I /В.В. Алисин, А.Я. Алябьев,

А.М.Архаров и др. 400 с.

16. Каплунов С.М., Статников И.Н. «О выборе параметров многопролетных трубных

пучков с учетом их вибронадежности», Energetika, №3, 1991-с. 171-178.