Рабочая программа специальности 100700. Промышленная теплоэнергетика (ПТ) направления 650800. Теплоэнергетика испециальности 330100. Безопасность жизнедеятельности в техносфере (бжт) направления

Вид материала

Рабочая программа

Содержание Кинематический анализ механизмов. Планом механизма План скоростей Динамический анализ. 7.1.4. Синтез механизмов Зубчатые передачи. Общая нормаль к профилям зацепления, проведенная в точке их касания, делит межцентровое расстояние на части, об­ратно пропорцион Эвольвентой окружности Кулачковые механизмы. В 7.2. Сопротивление материалов Внутренние силы 7.2.2. Растяжение и сжатие Контактные напряжения. 7.2.3. Геометрические характеристики поперечных сечений 7.2.4. Сдвиг. Кручение Деформация при кручении определяется углом закручивания

Подобный материал:

• Рабочая программа для студентов VI курса специальности, 350.79kb.
• Рабочая программа для студентов Vкурса специальности 290800. Промышленная теплоэнергетика, 63.46kb.
• Рабочая программа учебной дисциплины сд. 13 Информационные технологии в управлении, 340.61kb.
• Чурикова Екатерина Валериевна рабочая программа, 322.31kb.
• Рабочая программа и задание на курсовую работу с методическими указаниями для студентов, 1673.35kb.
• Рабочая программа для студентов II курса специальности 280101 «Безопасность жизнедеятельности, 279.42kb.
• Рабочая программа учебной дисциплины «промышленная экология региона», 229.54kb.
• К ф. н., доцент Латышева, 547.01kb.
• Рабочая программа для студентов IV курса специальности 100700 промышленная теплоэнергетика, 243.31kb.
• Рабочая программа и задание на контрольную работу с методическими указаниями для студентов, 1598.02kb.

7.1.3. Анализ механизмов

Кинематический анализ механизмов. Основные задачи кинематического анализа механизмов сводятся к следующе­му: определение положений звеньев и построение траекто­рий движения их точек; определение линейных скоростей то­чек и угловых скоростей звеньев; определение линейных ус­корений точек и угловых ускорении звеньев. Эти задачи мо­гут быть решены графическим, графоаналитическим, ана­литическим и экспериментальным методами.

При изучении темы наибольшее внимание следует уде­лить кинематическому анализу рычажно-шарнирных меха­низмов графоаналитическим методом - методом векторных уравнений и их графическим решением в виде планов поло­жений, скоростей и ускорений.

Планом механизма называют выполненную в масшта­бе структурную схему для определенного положения звень­ев. Звенья плоских рычажно-шарнирных механизмов могут совершать поступательное, вращательное или сложное плос­копараллельное движение, которое можно представить как совокупность переносного, поступательного движения звена вместе с его некоторой точкой А и относительного враща­тельного движения вокруг этой же точки.

Учитывая, что скорость и ускорение являются величи­нами векторными, то есть характеризуются не только мо­дулем (численным значением), но и направлением, абсолют­ная линейная скорость любой другой точки звена, например точки В, может быть представлена векторным уравнением: V_B = V_A + V_BA, а абсолютное линейное ускорение - a_B= a_A+ a_BА, где V_A, a_A - абсолютные линейные скорость и ускорение точ­ки А; V_BA, a_BA - относительные линейные скорость и ускоре­ние точки В относительно А.

План скоростей и план ускорений представляют собой графические решения совокупности векторных уравнений, определяющих линейные скорости и ускорения точек звень­ев механизма.

Угловые скорости ускорения звеньев механизма опре­деляются по формулам курса теоретической механики.


Вопросы

1. Назовите основные задачи и методы кинематического анализа механизмов. Укажите их достоинства и недостатки.
   
2. Напишите векторные уравнения для линейных ско­ростей и ускорений, связывающие две точки звена.
   
3. Изложите последовательность построения планов скоростей и ускорений.
   
4. Как определить угловые скорости и угловые уско­рения звеньев механизма?
   

Динамический анализ. Изучая динамический анализ механизмов, обратите внимание на следующее.

Исследование движения механизма под действием активных сил, реакций связей и сил инерции называют динамическим анализом. В том случае, когда влияние инерции невелико, задачу исследования решают методами статистики, при существенном влиянии сил инерции используются методы динамики.

При динамическом анализе часто действительный ме­ханизм заменяют упрощенным эквивалентным механизмом.

За критерий эквивалентности этих механизмов приня­та кинетическая энергия. Условие эквивалентности заклю­чается в равенстве кинетической энергии действительного механизма кинетической энергии механизма эквивалентно­го. Это равенство используется для вычисления так называ­емых приведенной массы или приведенного момента инерции эквивалентного механизма. Изменение кинетической энергии механизма на некотором перемещении равно работе сил, действующих на механизм на том же перемещении. Из это­го условия определяется приведенная сила или приведенный момент силы эквивалентного механизма и составляется об­щее уравнение движения.

Применяя уравнение движения для трех стадий (режи­мов) - пуск, установившееся движение и торможение - мож­но достаточно полно исследовать работу механизма [1...6].


Вопросы

1. Назовите основные задачи и методы динамического исследования механизмов.
   
2. Как классифицируются силы, действующие на зве­нья механизма?
   
3. В какой последовательности производится силовой расчет плоского механизма по методу планов сил?
   
4. Что называют приведенным моментам инерции ме­ханизма и как он определяется?
   
5. Изложите сущность метода приведения масс и сил.
   
6. Объясните принцип, заложенный в основу полного уравновешивания ротора на станке Б. В. Шитикова.
   

7.1.4. Синтез механизмов

Термин "синтез" означает проектирование, создание схем новых механизмов по заданным кинематическим и динамическим параметрам. Следовательно, всякая задача синтеза механизма является обратной по отношению к зада­че анализа.

Зубчатые передачи. В рассматриваемой теме наиболь­шее внимание следует уделить расчетам и проектированию передач с эвольвентными зубчатыми колесами. Для профи­лирования таких колес применяется способ Эйлера (1707- 1783 гг.). Профили зубьев должны удовлетворять определен­ным теоретическим положениям.

Основной закон зацепления (теорема Виллиса, 1841 г.). Общая нормаль к профилям зацепления, проведенная в точке их касания, делит межцентровое расстояние на части, об­ратно пропорциональные угловым скоростям.

При изучении элементов и геометрических параметров зацепления плоских цилиндрических эвольвентных зубчатых колес необходимо усвоить следующие понятия и определения.

Эвольвентой окружности называют кривую, которую описывает любая точка прямой, перекатываемой без сколь­жения по окружности (прямую называют производящей пря­мой, окружность эволютой или основной окружностью).

В соответствии с основной теоремой зацепления, цент­роиды, в относительном движении зубчатых колес, называ­ют начальными окружностями. Они перекатываются одна по другой без скольжения. Расстояние между центрами этих окружностей называют межосевым расстоянием. Дугу на­чальной окружности, вмещающей один зуб, называют окруж­ной толщиной зуба. Толщина зуба и ширина впадины образу­ют окружной шаг. Расстояние между одноименными профи­лями соседних зубьев, измеренное по дуге начальной окруж­ности, называют начальным окружным шагом. Модулем называют линейную величину, в п раз меньшую окружного шага (часть диаметра, приходящаяся на один зуб).

Окружность, для которой модуль соответствует стандартному, называют делительной. У большинства зуб­чатых передач диаметры делительных и начальных окруж­ностей совпадают. Отношение числа зубьев колеса к числу зубьев шестерни называют передаточным числом.


Вопросы

1. В чем заключаются основные задачи синтеза меха­низмов?
   
2. Сформулируйте и докажите основную теорему за­цепления.
   
3. Как определяется общее передаточное число для многоступенчатых передач зацеплением?
   
4. Построите эвольвенту окружности и объясните ее основные свойства.
   
5. Назовите основные элементы и параметры цилинд­рических эвольвентных зубчатых колес.
   
6. Как определить коэффициент перекрытия в зубча­том зацеплении? Объясните, почему он не должен быть мень­ше единицы.
   
7. Назовите параметры цилиндрических косозубых и конических прямозубых колес.
   
8. Объясните основные кинематические и силовые соотношения в передачах зацеплением.
   

Кулачковые механизмы. В структурном отношении кулачковый механизм - трехзвенная кинематическая цепь с высшей парой, ведомое звено которой (толкатель) движет­ся циклически. Эти механизмы преобразуют вращательные или поступательные движения кулачков в любое заданное движение ведомых звеньев, в том числе с остановками тре­буемой продолжительности.

Синтез кулачковых механизмов заключается в постро­ении профиля кулачка по заданному закону движения толка­теля. При этом определяются рациональные размеры кулач­ка, обеспечивающие наиболее благоприятные динамические условия работы механизма.

Изучая кулачковые механизмы, необходимо ознако­миться с видами кулачков, основаниями для выбора закона движения толкателя, с методами расчета или построения про­филя кулачков по заданному, либо выбранному закону дви­жения толкателя [1...6].


Вопросы

1. Назовите достоинства, недостатки и область применения плоских кулачковых механизмов.
   
2. Что называют углом давления (углом передачи)?
   
3. В чем заключается условие заклинивания кулачкового механизма?
   
4. Определите общие предпосылки для выбора закона движения толкателя в плоском кулачковом механизме.
   

5. Какие силы действуют в плоских кулачковых механизмах?


7.2. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

7.2.1. Общие сведения

Сопротивление материалов - наука о методах расчета элементов сооружений и машин на прочность, жесткость и устойчивость. Прочность - способность тел воспринимать нагрузку без разрушения, жесткость - без изменения разме­ров и формы, устойчивость - без нарушения определенной первоначальной формы равновесия.

Основы науки базируются на следующих допущениях и гипотезах: сплошное (непрерывное) строение тела, одно­родность и изотропность материала, справедливость прин­ципа независимости действия сил, отсутствие в теле внут­ренних усилий до приложения нагрузки и др.

Возникновение науки о сопротивлении материалов свя­зывают с именем Галилея (1564-1642 гг.).

Важнейшими положениями, которые надлежит усвоить в этой теме, следует считать понятия о внутренних силах и напряжениях.

Внутренние силы (силы упругости) в соответствии с допущением о непрерывности материала возникают в телах как силы непрерывно распределенные. Для их определения используют метод сечений, суть которого заключается в следующем. Тело, находящееся под действием внешней нагрузки в равновесии, должно оставаться в этом состоянии и после его расчленения на части, если к этим его частям при­ложены соответствующие внешние и внутренние силы. Ина­че говоря, возможность определения внутренних сил по сече­ниям тела возникает из условия равновесия любой мысленно отсекаемой от него части.

Интенсивность распределения внутренних сил характеризуется напряжением, под которым понимают пре­дел отношения равнодействующей внутренних сил, дей­ствующей на бесконечно малый элемент сечения к площа­ди этого элемента. Составляющую такого полного напря­жения, перпендикулярную к сечению, называют нормаль­ным напряжением-σ, лежащую в плоскости сечения на­зывают касательным напряжением - τ. Совокупность напряжений на элементарных площадках кубика, разме­щенного в какой-либо точке тела,, называют наряженным состоянием в данной точке. Если по граням кубика дей­ствуют только нормальные напряжения, то их называют главными напряжениями, а такие грани кубика называют главными площадками. Главные напряжения обозначают обычно σ₁, σ₂, σ₃ и располагают в последовательности σ₁> σ₂> σ₃. Трехосным или объемным напряженным состоянием называют случай, когда действуют все три главные напряжения, двухосным- когда σ₃=0, σ₁> σ₂, и одноосным-когда σ₂= σ₃=0, σ₁= σ.

Напряжения измеряются в паскалях (Па=Н/м², МПа= 10⁶Па), [1; 2; 3; 7; 8; 15].

Вопросы

1. Сформулируйте основные допущения, положенные в основу науки о сопротивлении материалов.
   
2. В чем состоит сущность метода сечений?
   
3. Что называют полным, нормальным и касательным напряжениями?
   

7.2.2. Растяжение и сжатие

Осевое (центральное) растяжение или сжатие возни­кает, когда внешние силы действуют вдоль оси стержня. Растяжение проявляется в удлинении стержня и уменьше­нии его поперечных размеров, сжатие-в укорочении стер­жня и увеличении его поперечных размеров. Приращение длины обычно называют абсолютным удлинением - Δ1. От­ношение абсолютного удлинения к первоначальной длине l носит название относительного удлинения - ε. Абсолют­ную величину отношения относительной поперечной дефор­мации к относительной продольной называют коэффициен­том Пуассона μ.

При растяжении (сжатии) в любом поперечном сечении стержня можно определить равнодействующую внутренних сил N. В соответствии с гипотезой плоских сечений отноше­ние этой равнодействующей к площади поперечного сечения А определяет нормальное напряжение σ=N/A,[ МПа].

Для многих материалов в пределах малых деформа­ций относительные линейные деформации прямо пропорци­ональны нормальным напряжениям, то есть σ=Еε (закон Гука, 1676 г.), где Е модуль упругости первого рода (мо­дуль Юнга, 1807 г.), МПа.

Абсолютное удлинение (укорочение) стержня, как сле­дует из закона Гука, Δl = Nl/(EA). В свою очередь, удлинение стержня постоянного сечения от собственного веса G = γА1 будет:

Δl =Gl/(2EA),

где γ - удельный вес материала стержня.

Рассмотренные положения имеют большое практичес­кое значение.

Приведем основные характеристики прочности, кото­рые определяют при испытаниях материалов на растяжение: предел пропорциональности σ_пц - напряжение, при котором материал перестает следовать закону Гука; предел текучести σ_т - напряжение, при котором в материале появляются заметные удлинения без увеличения нагрузки; предел проч­ности σ_в - напряжение, при котором материал претерпевает разрушение. Условие прочности при растяжении (сжатии) записывают так σ = N/A> [σ], где [σ] = σ_пр /[n] - допускае­мое напряжение, σ_пр = σ_в - ля хрупких и σ_пр = σ_т - для пластичных материалов, [n] - номинальный коэффициент запаса прочности.

Концентрация напряжений. Если контур продольного сечения растягивающегося идя сжимающегося стержня рез­ко меняется, то в местах изменения формы стержня распре­деление напряжений по его поперечному сечению не будет равномерным. Значительное нарастание напряжении в мес­тах резкого изменения геометрической формы стержня назы­вают концентрацией напряжений.

Отношение максимального местного напряжения к но­минальному (определяется расчетами без учета концентра­ции) называют теоретическим коэффициентом концентрации напряжений.

Отношение предела прочности σ_в детали без концент­рации напряжении к пределу прочности σ_вк, к детали с за­данным концентратором напряжении K_s=σ_в/σ_вк, называют эффективным коэффициентом концентрации напряжений. Его вводят для хрупких либо мало пластичных материалов. Надо твердо усвоить, что в расчетах на выносливость K_s учитыва­ют для всех материалов.

Ниже мы увидим, что многие детали машин (шарико­вые подшипники, закрытые зубчатые передачи и др.) рассчитывают на контактную прочность, поэтому вопросу контактных напряжений следует уделить особое внимание.

Контактные напряжения. Деформации и напряжения, возникающие при взаимном давлении двух упругих тел, со­прикасающихся по линии или в точке, называют контактны­ми, соприкасающихся по площадке конечных размеров - деформациями и напряжениями смятия.

Основным критерием работоспособности значительного количества деталей машин является контактная прочность.

Контактные напряжения определяют методами теории упругости, чаще всего по формуле Герца (1882 г.). В случае контакта двух цилиндров формула имеет вид:

σ_Н={E_прq/[2π(1-μ²)ρ_пр]}^1/2

E_пр=2Е₁E₂/(E₁+E₂) - приведенный модуль упругости; E₁ и E₂ - модули упругости контактирующих тел; μ- коэффициент Пуассона;

q - номинальная нагрузка на единицу длины контакт­ной линии;

ρ_np⁼ρ₁ρ₂^/(ρ1+ρ2) - приведенный радиус кривизны; ρ₁;ρ₂- радиусы кривизны контактирующих тел.

Эта формула является исходной для определения межосевого расстояния закрытых зубчатых передач из ус­ловия контактной прочности.

На смятие работают заклепочные соединения, шпоноч­ные соединения и др. (см. раздел 3). Смятие не распространя­ется на большую глубину. Это деформация местная. Усло­вие прочности при смятии:

где F-сила нагружения;

A_см - площадь смятия;

[σ]_см - соответственно расчетное и допускаемое напря­жения смятия.

При контакте одно тело может проникать в другое, оставляя отпечаток (углубление). Свойство тела сопротив­ляться прониканию в него другого (более твердого) тела на­зывают твердостью.

Контактные напряжения имеют важное значение в ра­боте большого количества деталей машин. С теорией расчета по контактной прочности следует ознакомиться по посо­биям [1; 2; 3; 7; 8].

Более подробное изучение деформации растяжения (сжа­тия ) по пособиям [7] и [8] позволит освоить методы расчетов на прочность и жесткость статически определимых и ста­тически неопределимых систем, изучить вопросы о напряже­ниях в наклонных сечениях, познакомиться с обобщенным законом Гука и другими важными вопросами.


Вопросы

1. Сформулируйте закон Гука. Как определяются зна­чения входящих в него величин?
   
2. Какие напряжения называют пределом упругости, пределом пропорциональности, пределом текучести и преде­лом прочности?
   
3. Как определяется удлинение стержня при растяже­нии под действием собственного веса?
   
4. Как определяются нормальные и касательные напря­жения в наклонных сечениях при осевом растяжении стержня?
   
5. В чем сущность методов расчета на прочность при растяжении (сжатии) по допускаемым нагрузкам и предель­ным состояниям?
   

6. Что называют эффективным коэффициентом концентрации напряжений?

7. По каким зависимостям определяют контактные напряжения случае сжатия шаров?


7.2.3. Геометрические характеристики поперечных сечений

Прочность, жесткость, а также и устойчивость нельзя оценить без геометрических характеристик сечений. К ним относят: площадь поперечного сечения - А, статический момент относительно какой-либо оси:



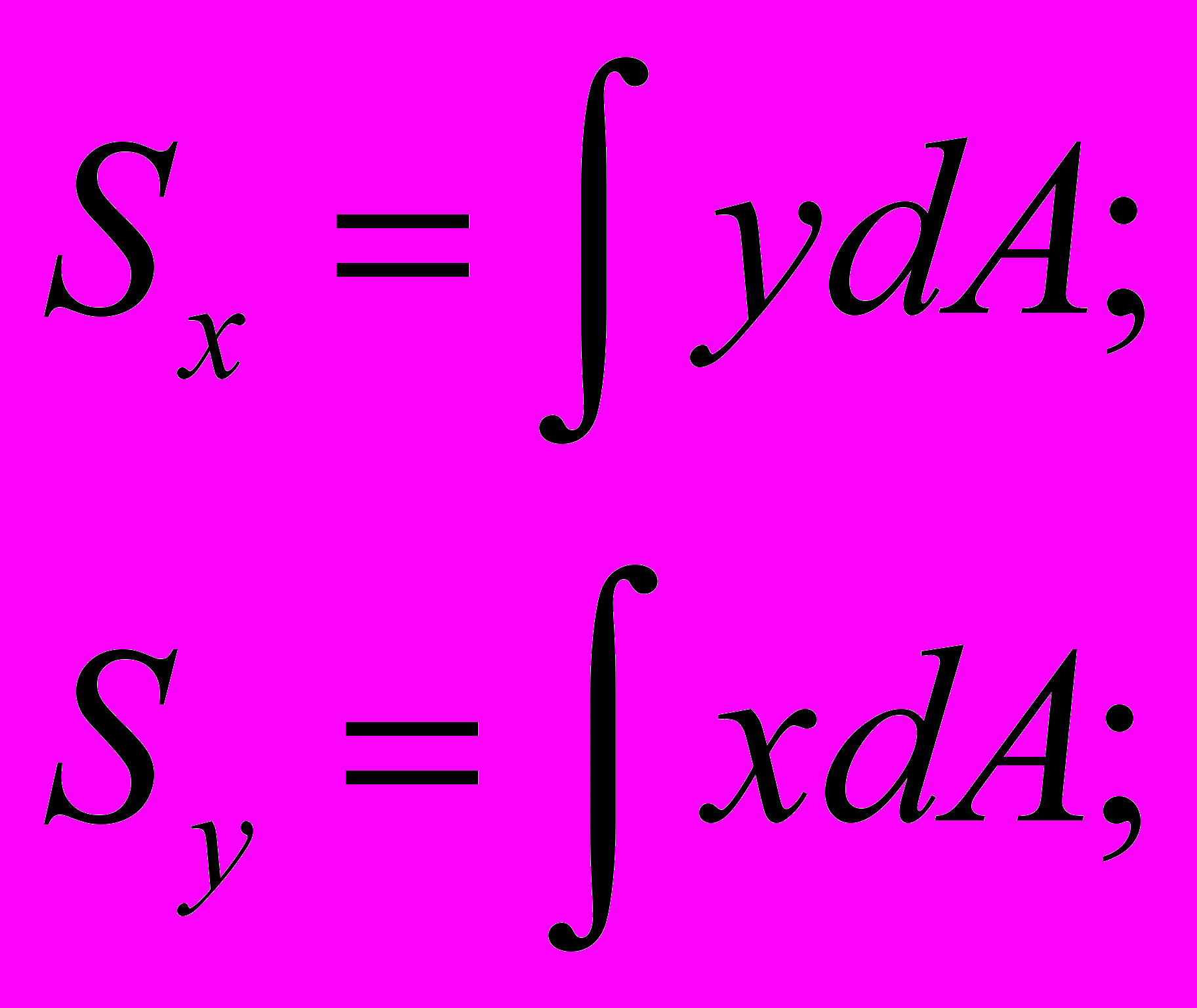
осевые моменты инерции:



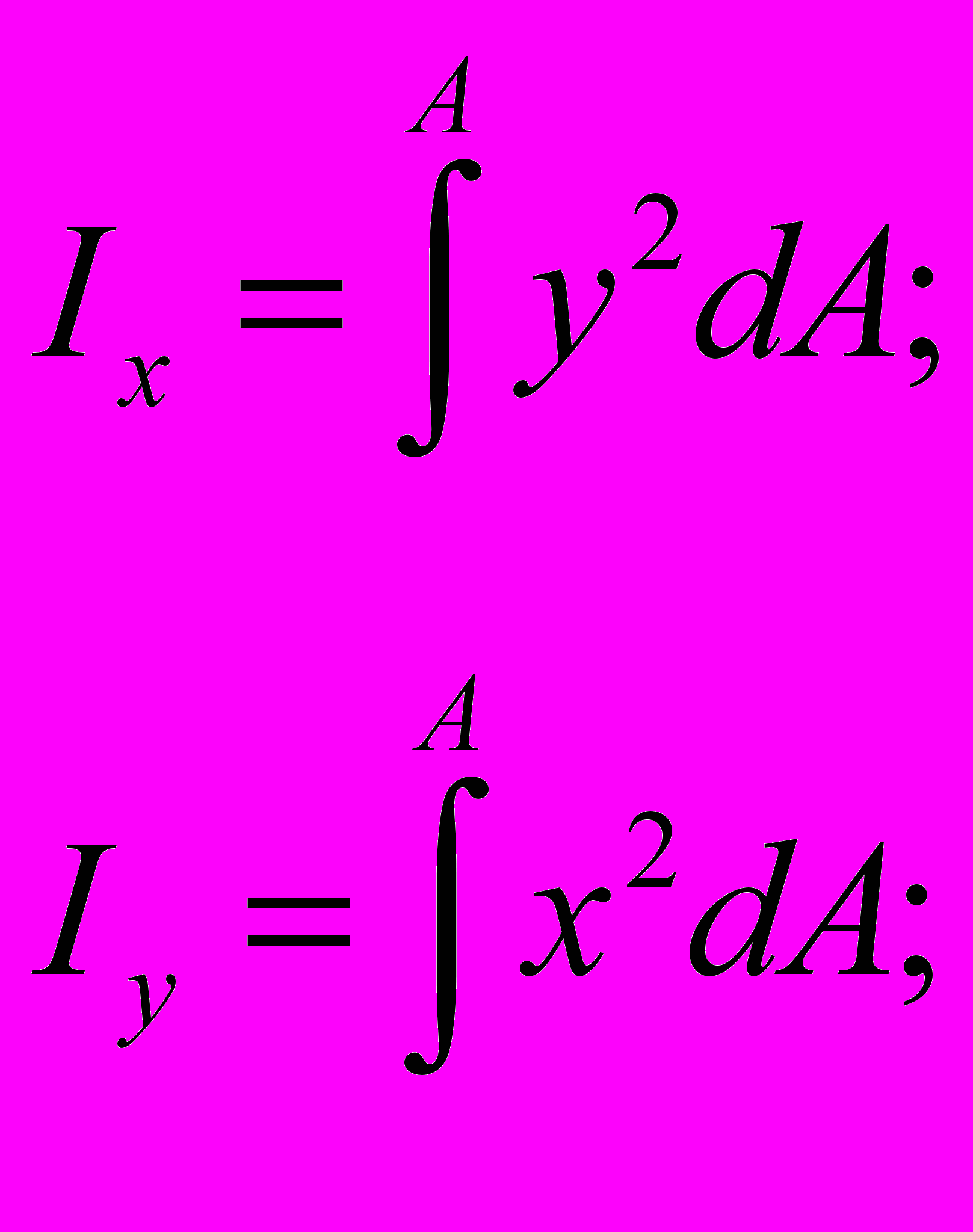
полярный момент инерции:

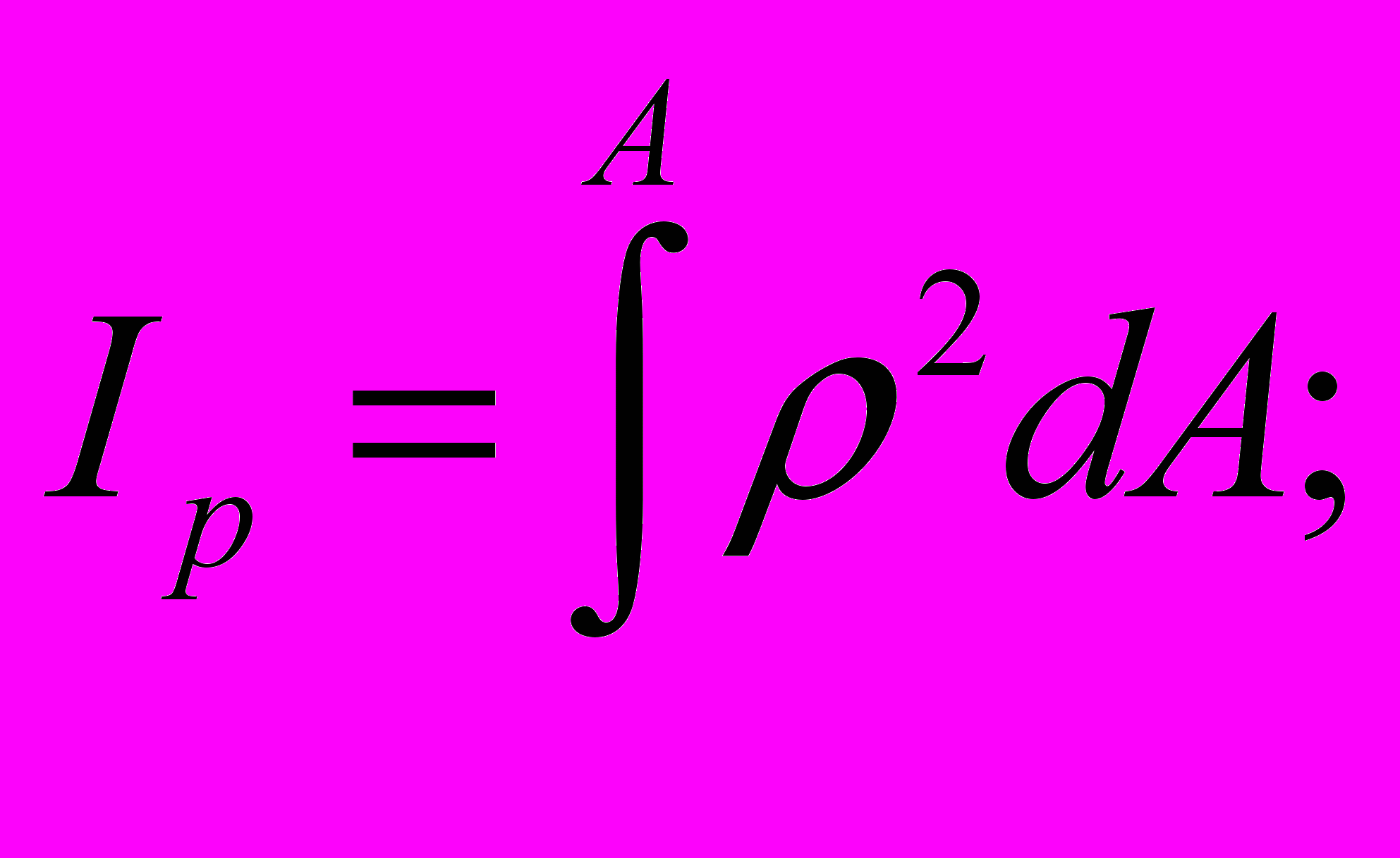
центробежный момент инерции:

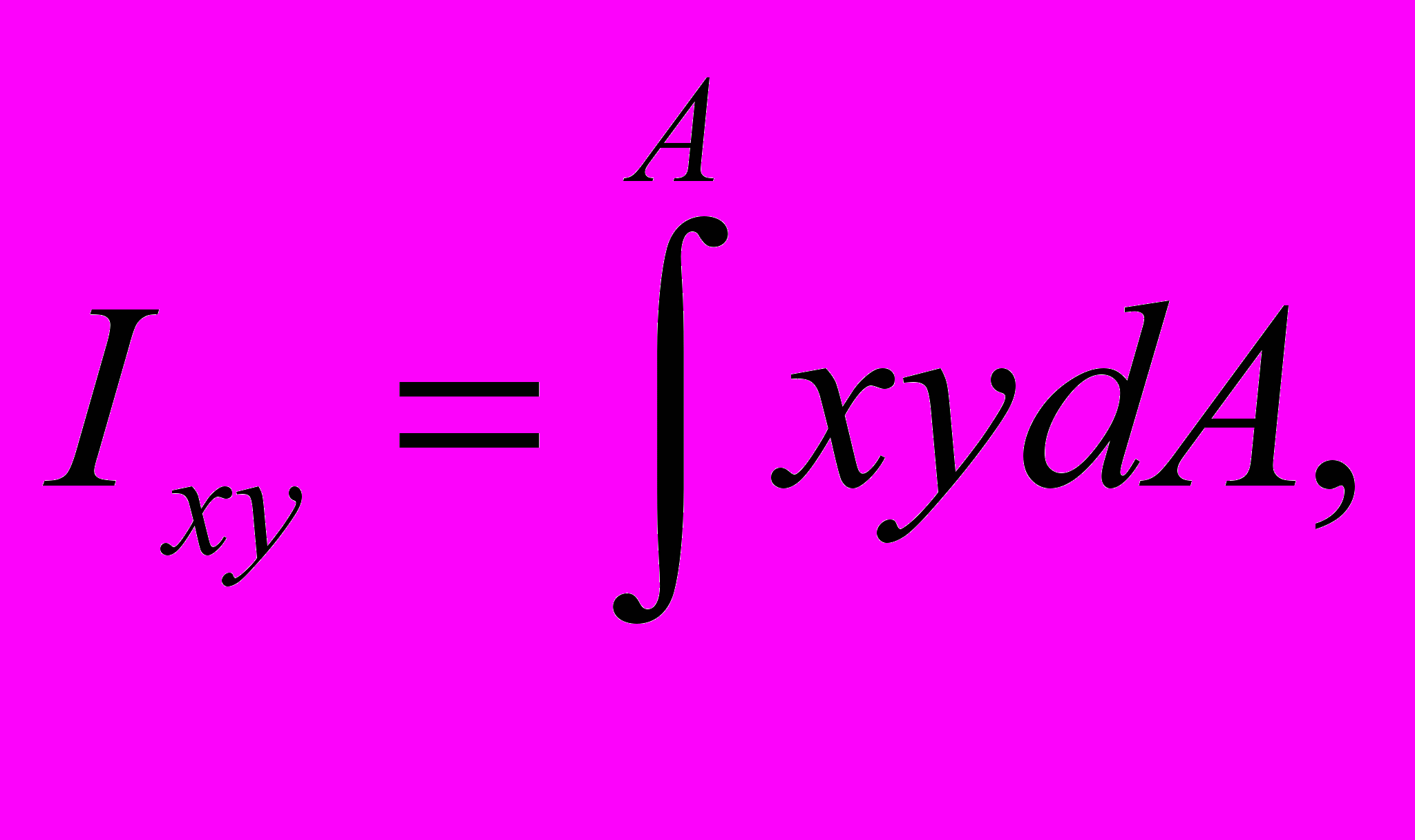
где x и y - расстояния от элементарной площадки dA до начала координат. Очевидно, I_p =I_x + I_y .

Оси, проходящие через центр тяжести сечения, называ­ют центральными осями. Две взаимно перпендикулярные оси, для которых центробежный момент инерции плоской фигу­ры равен нулю, называют главными осями инерции фигуры.

Главные оси инерции в центре тяжести фигуры назы­вают главными центральными осями инерции. Их на­правление относительно осей х и у определяют углом Θ по зависимости: tg2Θ = -2I_xy /(I_x – I_y).

Моменты инерции относительно главных центральных осей инерции называют главными моментами инерции

Момент инерции относительно любой оси равен момен­ту инерции относительно центральной оси, ей параллельной, плюс произведение площади фигуры на квадрат расстояния между осями [1; 2; 3; 7; 8].

Вопросы

1. Как вычисляют моменты инерции сложных фигур?
   
2. Что называют осевым, полярным и центробежным мо­ментами инерции и как их определяют для простейших фи­гур?
   
3. Как определяют координаты центров тяжести состав­ных сечений?
   

7.2.4. Сдвиг. Кручение

Деформацию сдвига или среза можно наблюдать, ког­да стальную полосу перерезают ножницами. Действующие по поверхности среза касательные силы Р вызывают по се­чению касательные напряжения т. Случай, когда на гранях элемента действуют только касательные напряжения, назы­вают чистым сдвигом.

В качестве относительной деформации при сдвиге принимают угловую деформацию γ - угол сдвига. Закон Гука для сдвига имеет вид: τ = Gγ, где G - модуль упруго­сти при сдвиге, G = E/[2(1 + μ)].

Заклепочные, болтовые и сварные соединения (см. раз­дел 3) рассчитывают на срез. Условие прочности τ = F/A≤[τ], где А - площадь поперечного сечения; [т] - допускаемое на­пряжение на срез. Для заклепочных соединений τ = F/(An)≤ [τ], где A = πd²/4 - площадь поперечного сечения заклепки диа­метром d , n - общее число срезов заклепок; F - действую­щая сила.

Стержень испытывает кручение, если в его поперечном сечении действует крутящий момент (момент сил, лежащих в плоскости сечения) - T_к. При кручении касательные напря­жения прямо пропорциональны расстоянию от центра тяжес­ти сечения.

Крутящий момент, действующий в любом сечении стер­жня, как момент внутренних сил численно равен моменту внешних сил. действующих по одну сторону от сечения.

Условие статической прочности стержня при круче­нии τ_max = Т_к/W_p ≤[τ], где W_p -полярный момент сопротивле­ния (для круглого сечения W_{p =}πd³/16, [τ] - допускаемое каса­тельное напряжение.

Деформация при кручении определяется углом закручивания φ=T_kl/(GI_p) и относительным углом закручи­вания Θ = T_к/ GI_p). где GI_p - жесткость стержня при круче­нии; I_p - полярный момент инерции сечения; l-длина стер­жня.

Диаметр стержня из условия прочности можно опреде­лить по формуле: d = (16Т_к/π[τ] )^1/3 = 1,72(Т_к/[τ] )¹/3, из усло­вия жесткости по формуле d = {Т_k /(0,1G[Θ]}^1/4, где [Θ] - от­носительный угол закручивания, [рад]. Очевидно, за исполнительное значение диаметра принимают наибольшее его значение.

Изменение крутящих моментов и углов закручивания по сечениям будет наглядным, если построить эпюры T_к и φ. Изучение темы по пособиям [1; 2; 3; 7; 8; 15] позволит освоить основы теории.