Определение момента инерции тел методом крутильных колебаний
| Вид материала | Лабораторная работа |
СодержаниеПорядок выполнения работы Контрольные вопросы |
- Решение дифференциального уравнения затухающих колебаний, график затухающих колебаний,, 68.04kb.
- Автоматизированный комплекс для определения механических характеристик асинхронных=, 146.19kb.
- Лабораторная работа №29, 38.23kb.
- Определение удельной поверхности материалов (твердых тел) газохроматографическим методом, 114.43kb.
- 1564-1642 итальянский ученый, физик, механик и астроном, один из основоположников, 157.31kb.
- Н. Э. Баумана кафедра химии овчаренко Л. П., Татьянина И. В., Горячева В. Н. Определение, 217.5kb.
- Химический анализ водорастворимых солей, 388.64kb.
- Механические колебания и волны, 25.91kb.
- Колебания и волны, 42.79kb.
- Урок 12. Тема: Механика Ньютона, 49.88kb.
Лабораторная работа № 6 а
Определение момента инерции тел методом крутильных колебаний
Выполнил студент гр. ________________ Ф.И.О. _____________________
Подпись преподавателя _______________ Дата _____________________
Цель работы – изучить метод крутильных колебаний для рассчета момента инерции тел разной формы. Сравнить экспериментальные значения моментов инерции этих тел с теоретическими расчетами.
Описание лабораторной установки.
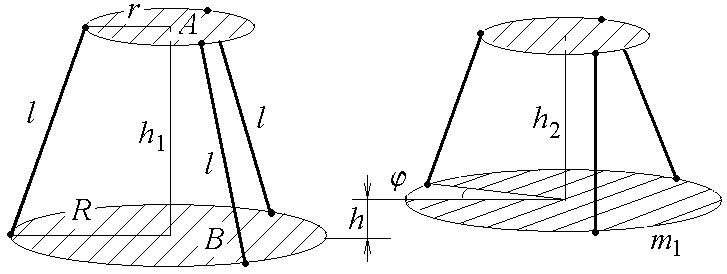 Моменты инерции различных тел могут быть измерены методом крутильных колебаний с помощью так называемого трифилярного подвеса. Трифилярный подвес состоит из диска В массой
Моменты инерции различных тел могут быть измерены методом крутильных колебаний с помощью так называемого трифилярного подвеса. Трифилярный подвес состоит из диска В массой 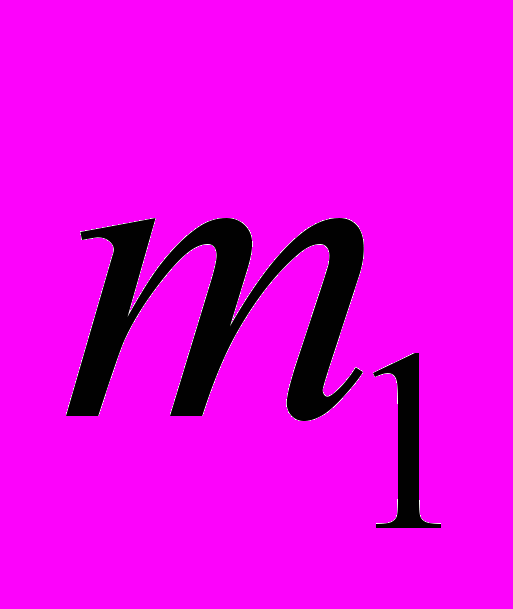 радиуса R, подвешенного на трёх симметрично расположенных нитях длины
радиуса R, подвешенного на трёх симметрично расположенных нитях длины 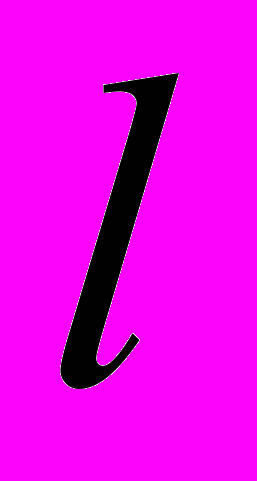 (см.рис.). Наверху эти нити симметрично закреплены по краям диска А меньшего радиуса r. При повороте верхнего диска А на небольшой угол вокруг вертикальной оси, перпендикулярной плоскости диска и проходящей через центр, все три нити принимают наклонное положение, центр тяжести системы несколько приподнимается. Нижний диск начинает совершать крутильные колебания.
(см.рис.). Наверху эти нити симметрично закреплены по краям диска А меньшего радиуса r. При повороте верхнего диска А на небольшой угол вокруг вертикальной оси, перпендикулярной плоскости диска и проходящей через центр, все три нити принимают наклонное положение, центр тяжести системы несколько приподнимается. Нижний диск начинает совершать крутильные колебания.Порядок выполнения работы
1. Измерить линейкой радиусы дисков R1 и r, а также длину нити l. Занести данные в Таблицу 1.
2. Резко повернуть рукой диск
 до упора и отпустить. При этом нижний диск В должен совершать крутильные колебания, а верхний диск А должен остаться в покое из-за трения в оси.
до упора и отпустить. При этом нижний диск В должен совершать крутильные колебания, а верхний диск А должен остаться в покое из-за трения в оси.3. С помощью секундомера определить время
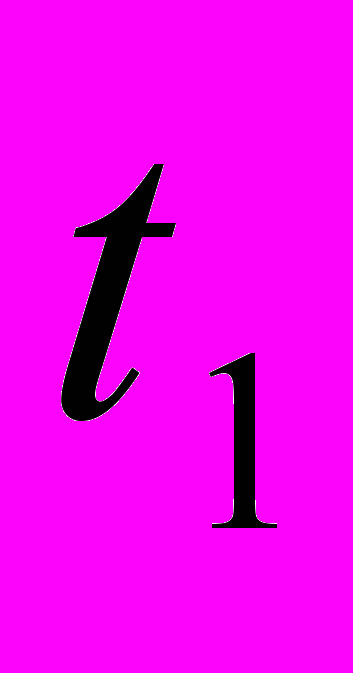 полных n =20 колебаний ненагруженного диска. Опыт повторить три раза. Вычислить среднее значение
полных n =20 колебаний ненагруженного диска. Опыт повторить три раза. Вычислить среднее значение 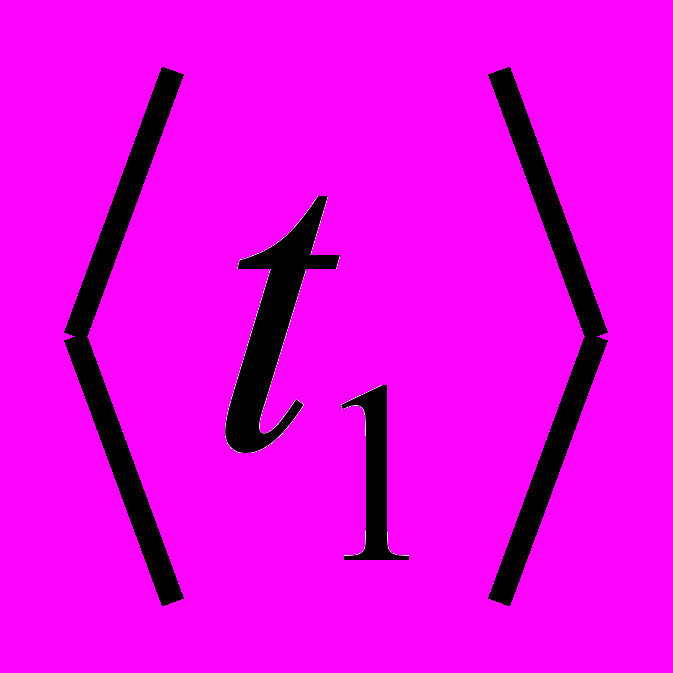 и среднее значение периода колебаний
и среднее значение периода колебаний 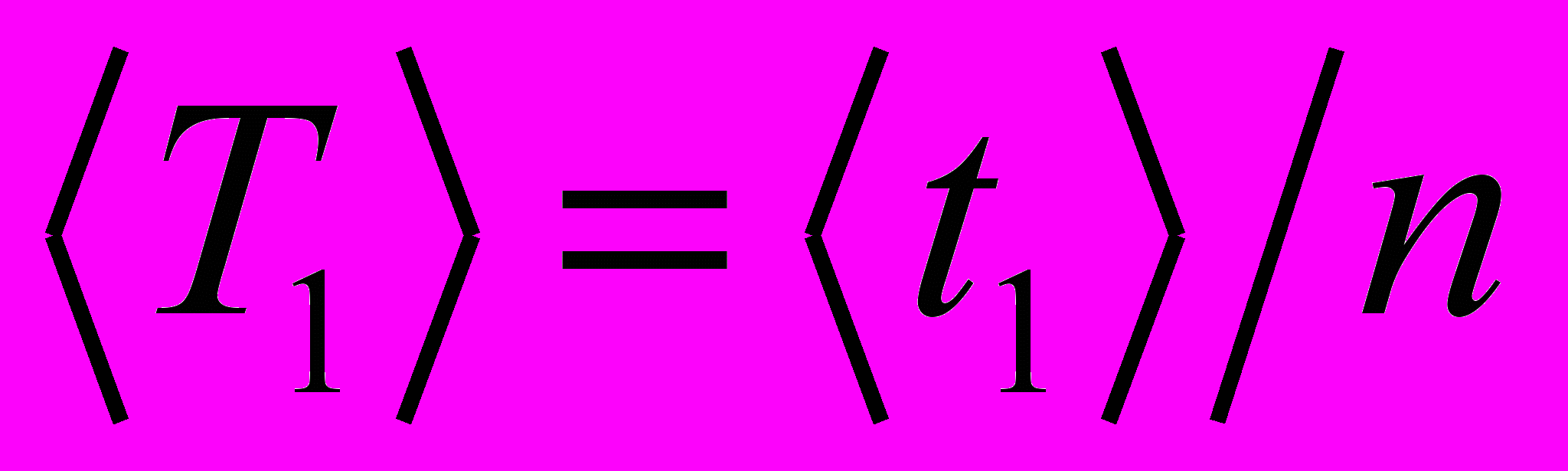 . Результаты измерений и вычислений занести в таблицу 1.
. Результаты измерений и вычислений занести в таблицу 1.Таблица 1.
| m1, кг | R1, м | r, м | l, м | t1, с | 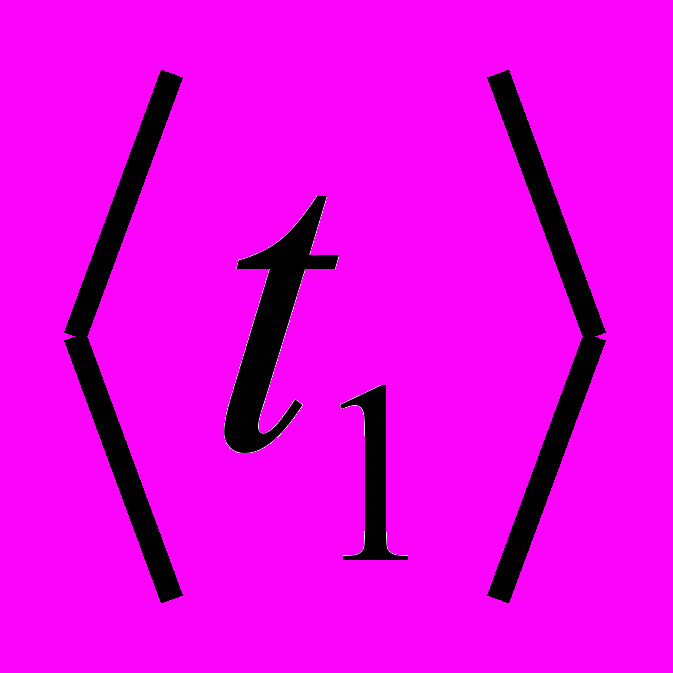 ,с ,с | <T1>, с |
| | | | | | | |
| | ||||||
| |
4. Положить на нижний диск исследуемое тело так, чтобы центры масс тела и диска были на одной оси. Масса
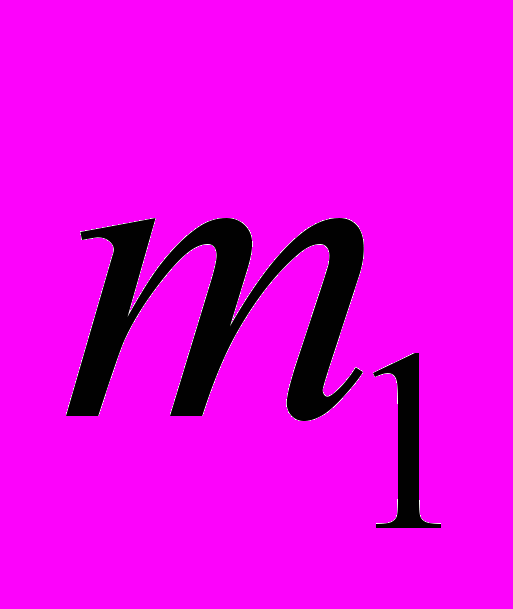 диска В и масса исследуемого тела m2 указаны на установке.
диска В и масса исследуемого тела m2 указаны на установке. 5. Определить время
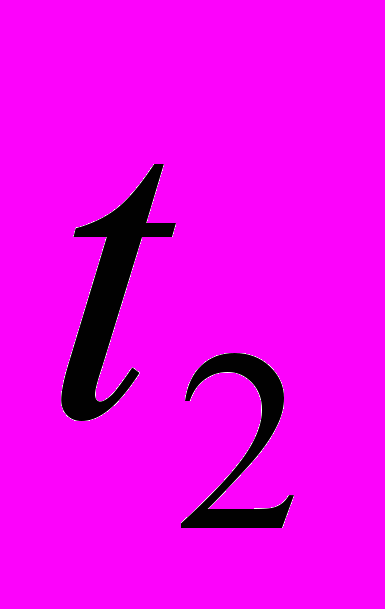 полных n=20 колебаний нагруженного диска. Опыт повторить три раза. Вычислить среднее значение
полных n=20 колебаний нагруженного диска. Опыт повторить три раза. Вычислить среднее значение 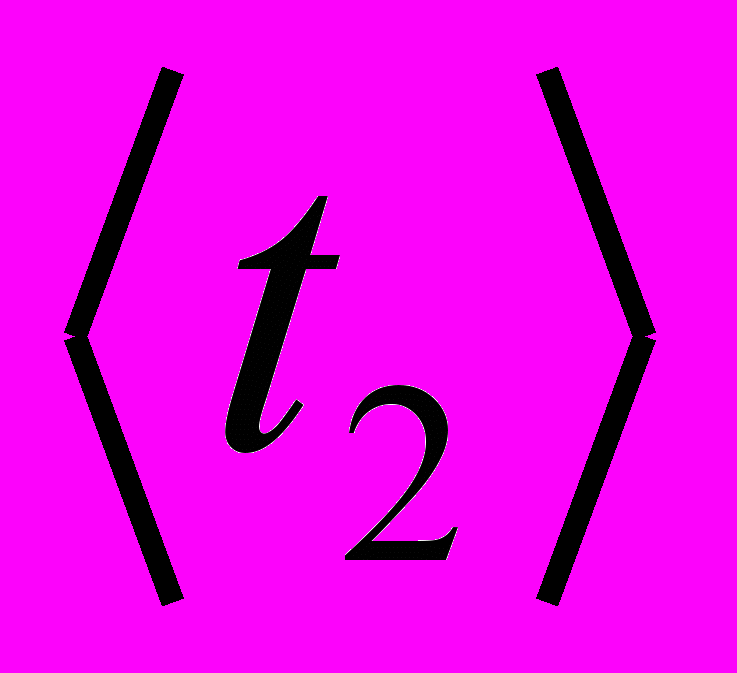 и среднее значение периода колебаний
и среднее значение периода колебаний 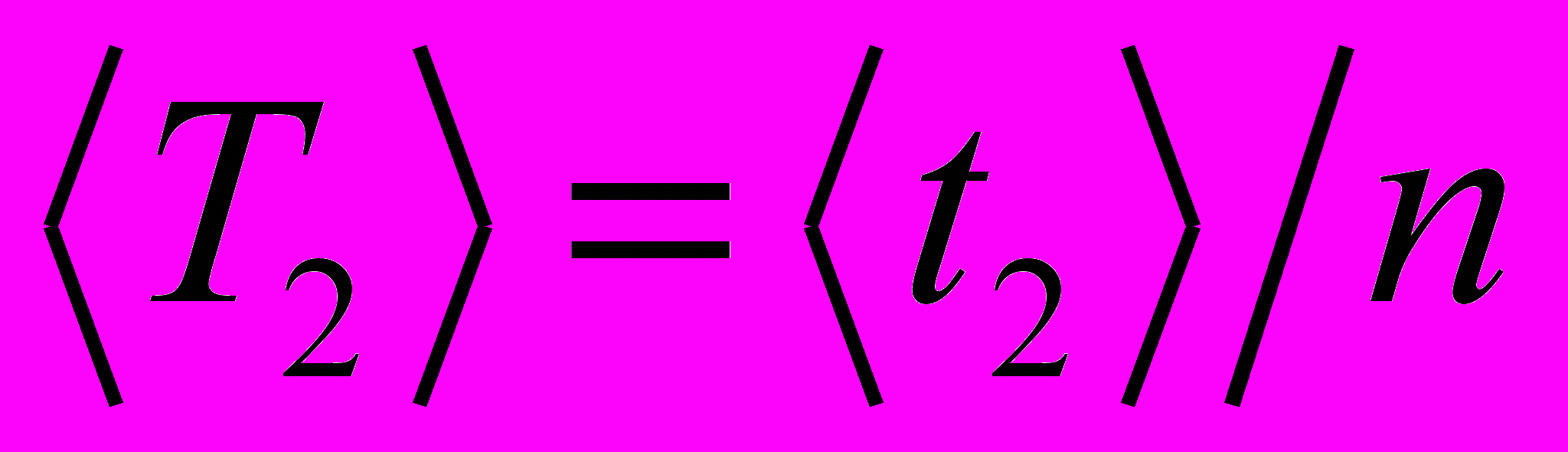 . Результаты измерений и вычислений занести в таблицу 2.
. Результаты измерений и вычислений занести в таблицу 2.6. Используя экспериментальные данные, вычислить момент инерции Iэксп исследуемого тела по формуле
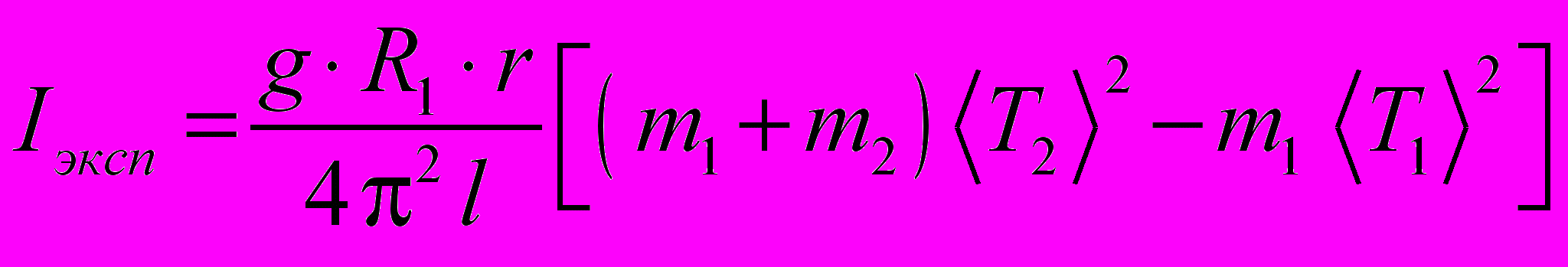 .
.7. Измерить размеры исследуемого тела и из таблицы 3 для данной формы тела вычислить теоретический момент инерции Iтеор тела относительно той же оси, что и при эксперименте.
8. Сравнить теоретическое Iтеор и экспериментальное Iэксп значения момента инерции. Для этого вычислить относительное отклонение по формуле
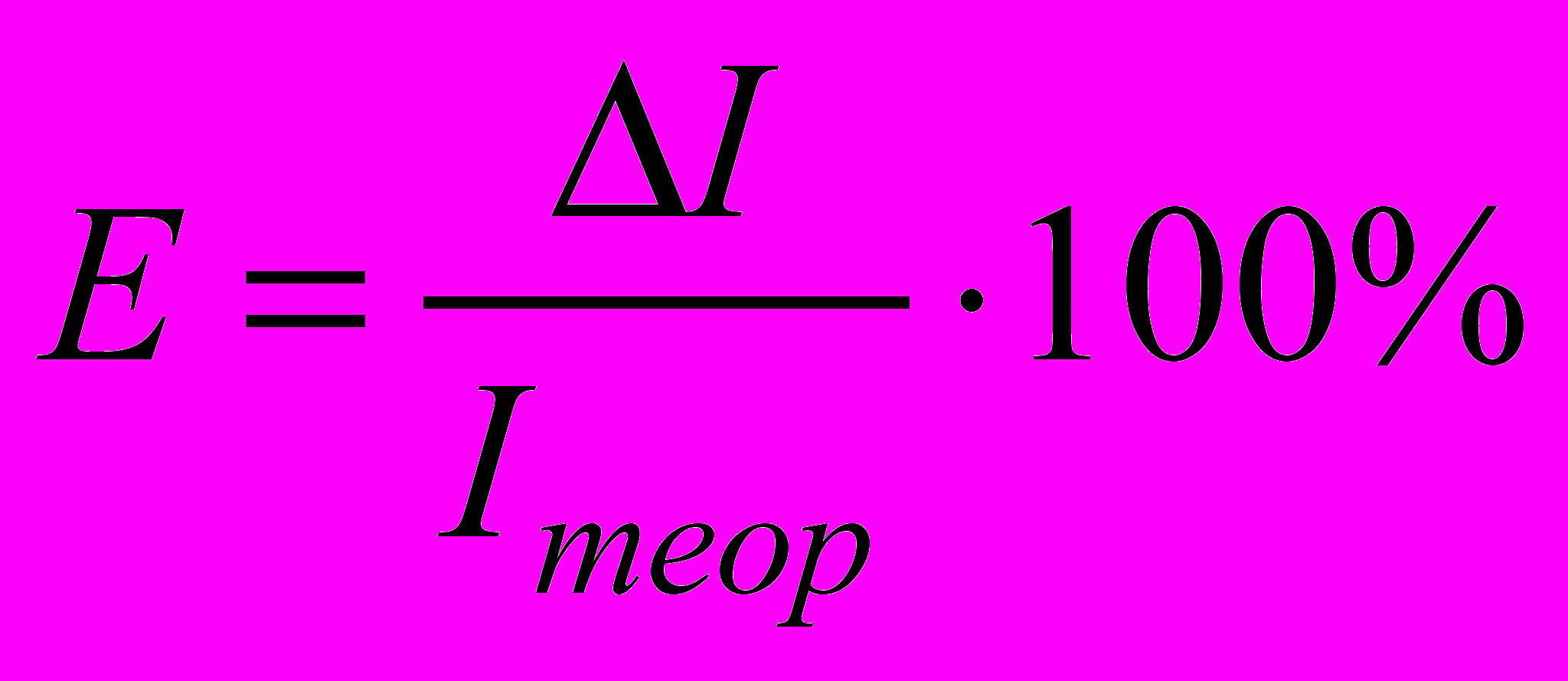 , где
, где 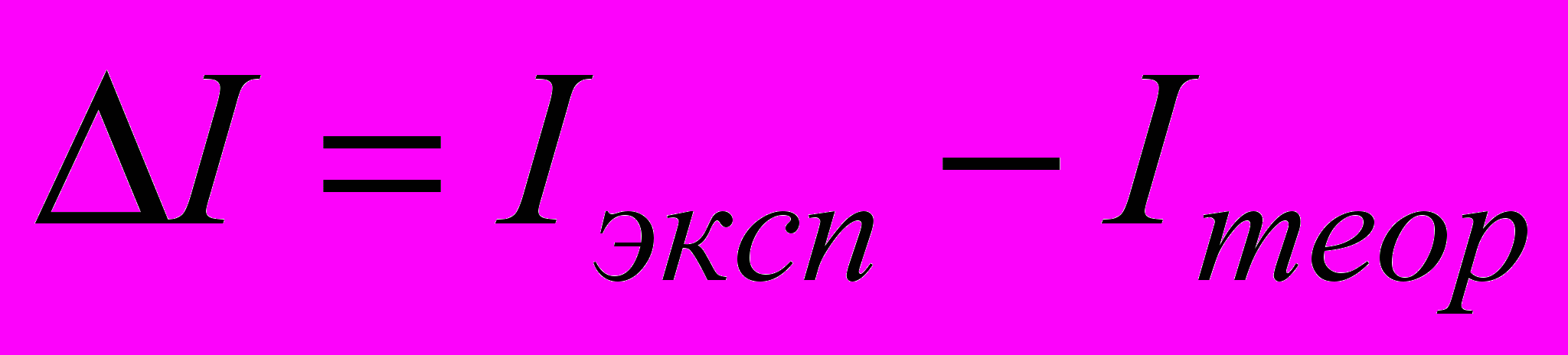
9. С пункта 3 по 8 проделать аналогично измерения и вычисления с другими телами .
Таблица 2.
| Вид тела и его размеры | m2, кг | t2, с | 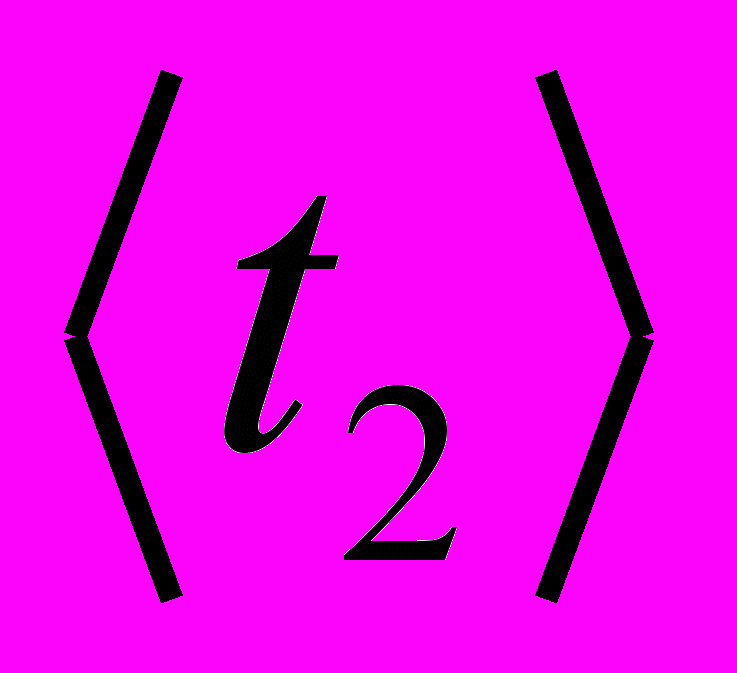 , ,с | <T2>, с | Iэксп, кгм2 | Iтеор, кгм2 | I = Iэксп– Iтеор, кгм2 | 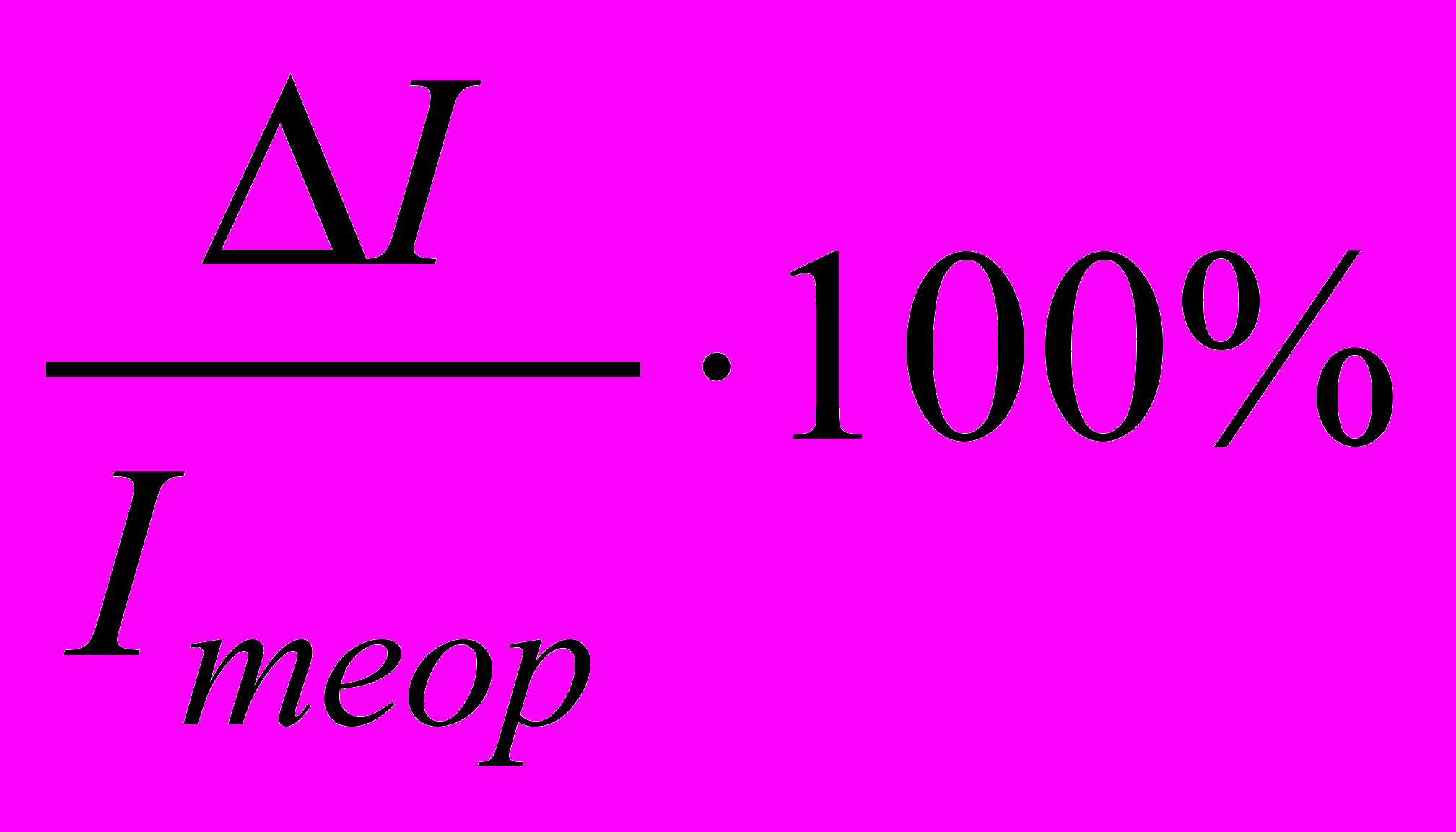 |
| диск Rд = м | | | | | | | | |
| | ||||||||
| | ||||||||
| Прямоугольник a = м b = м | | | | | | | | |
| | ||||||||
| | ||||||||
| Треугольник a = м | | | | | | | | |
| | ||||||||
| |
Таблица 3. Моменты инерции плоских тел относительно оси, проходящей через центр масс перпендикулярно их плоскости.
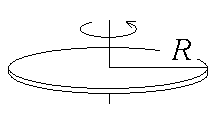
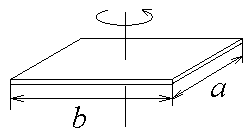
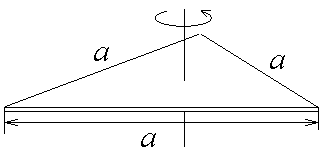
Диск Прямоугольник Равносторонний треугольник
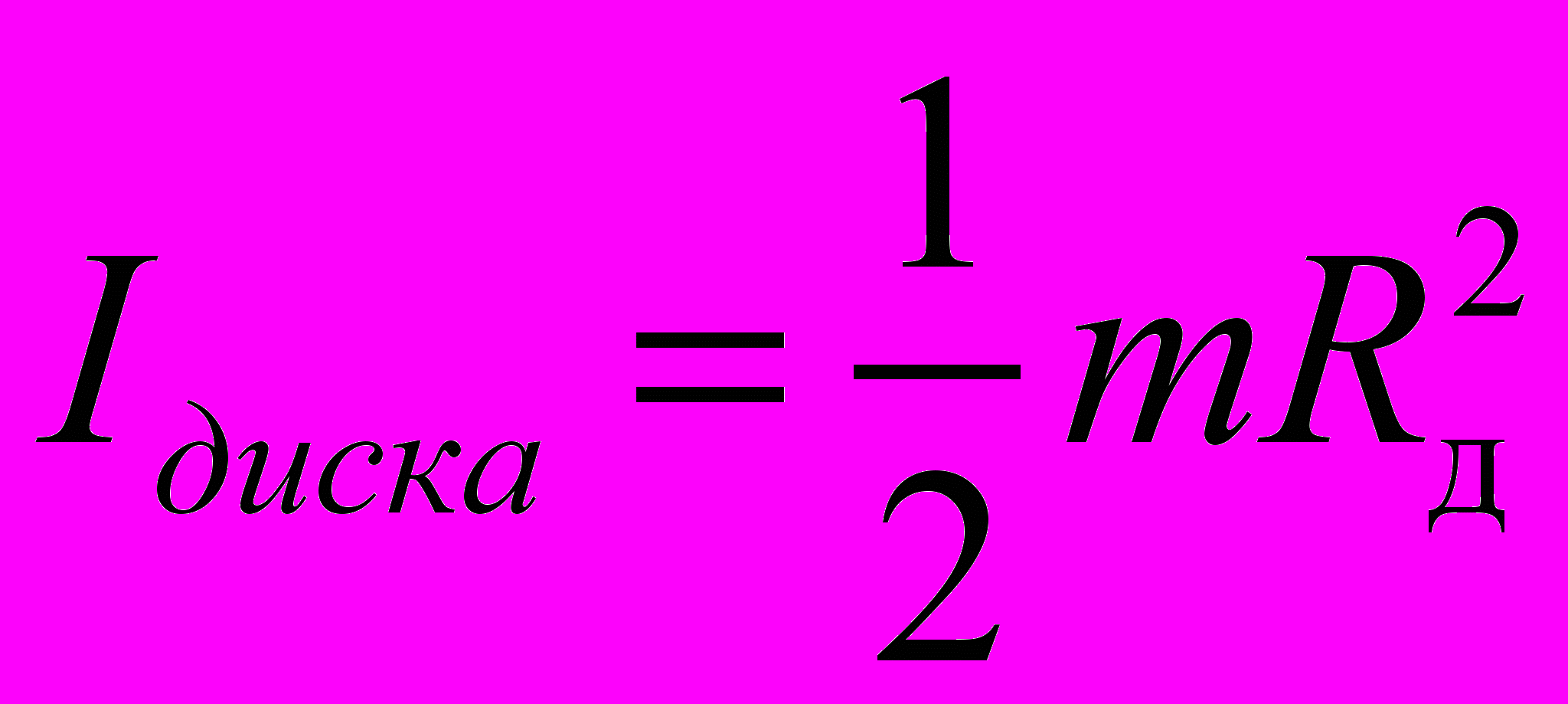
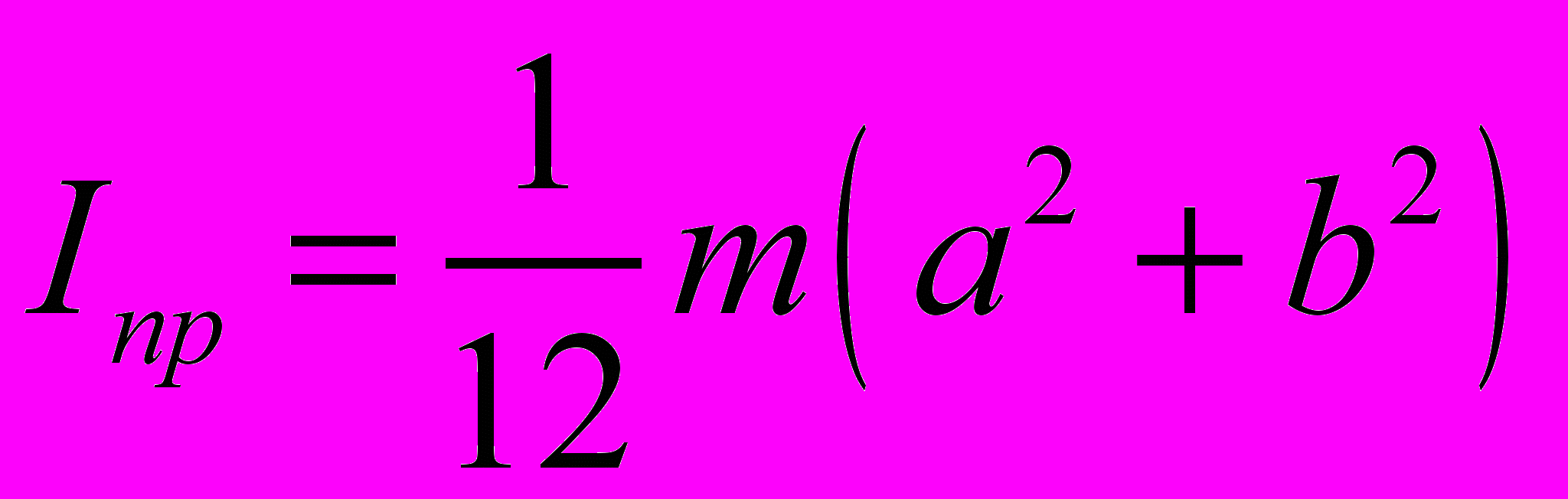
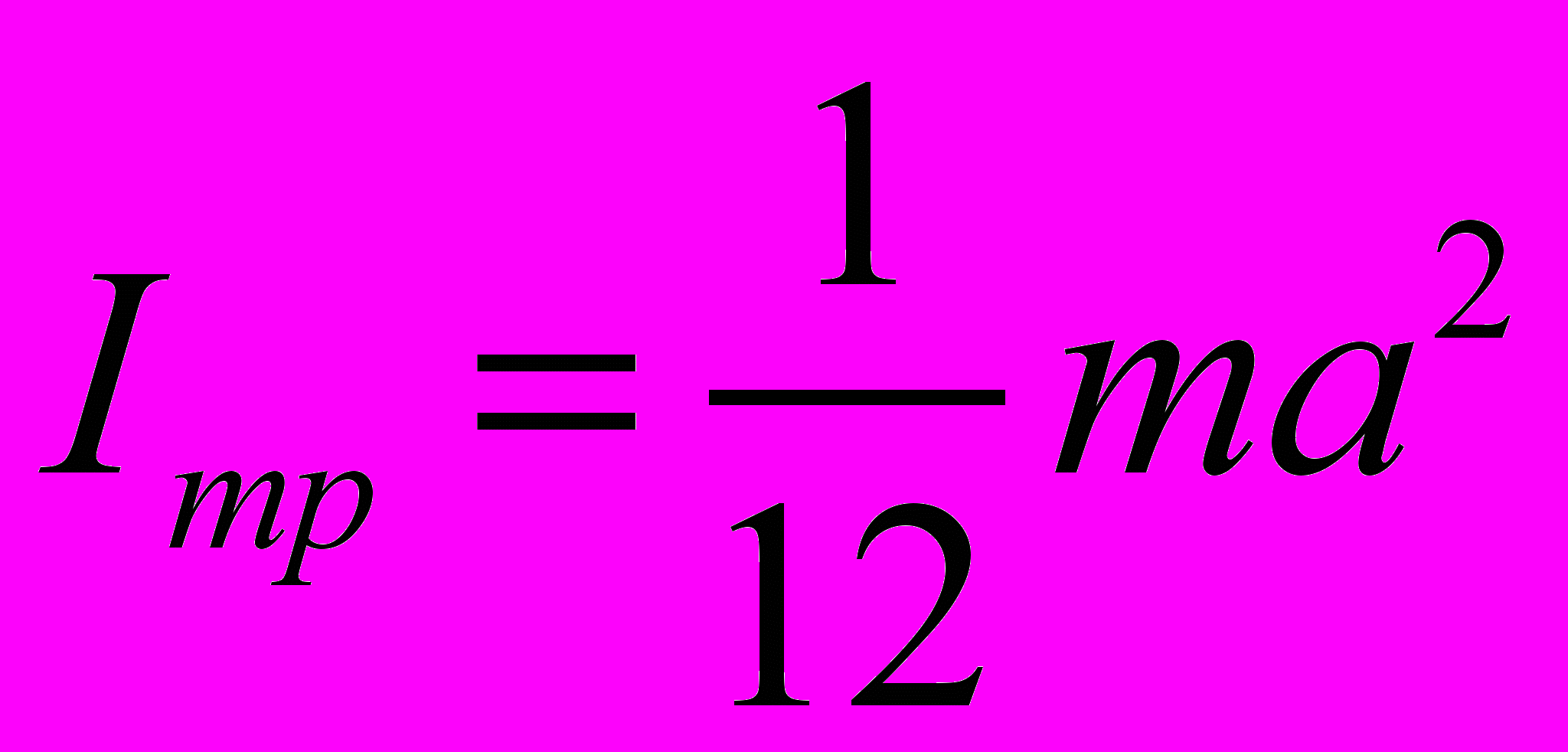
Контрольные вопросы
1. В чем заключается физический смысл момента инерции?
2. От чего зависит момент инерции?
3. Сформулируйте теорему Штейнера.
4. С помощью теоремы Штейнера объясните, относительно какой оси момент инерции тела минимален (максимален)?
5. Получите расчетную формулу для момента инерции плоской прямоугольной пластины относительно оси, проходящей через центр масс, и лежащей в плоскости пластины.
6. Получите расчетную формулу для момента инерции пластины в форме равностороннего треугольника относительно оси, лежащей в плоскости пластины и проходящей через одну из его сторон.
7. Как нужно проводить эксперимент в данной работе, чтобы расчетные формулы, которыми вы пользовались, были справедливы?
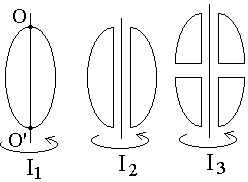 8. Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали: одну - пополам вдоль оси симметрии, а вторую - на четыре одинаковые части. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси OO' (см. рис.). Выберите правильное соотношение между моментами инерции этих деталей относительно оси OO'.
8. Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали: одну - пополам вдоль оси симметрии, а вторую - на четыре одинаковые части. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси OO' (см. рис.). Выберите правильное соотношение между моментами инерции этих деталей относительно оси OO'.а)
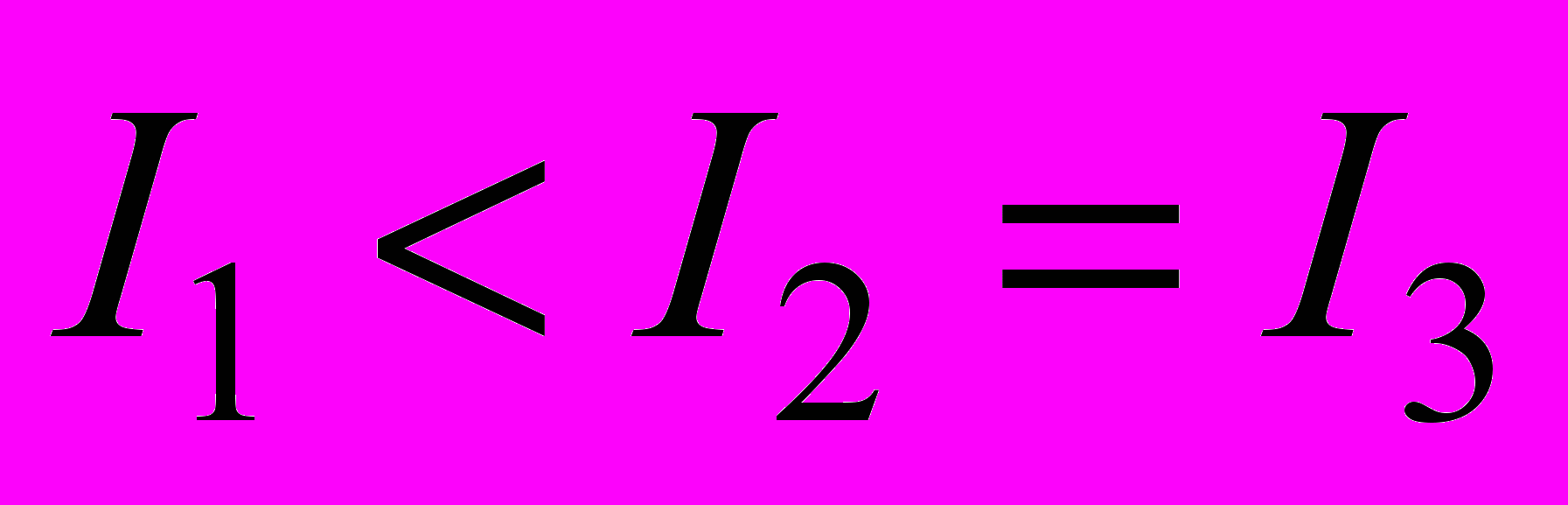 б)
б) 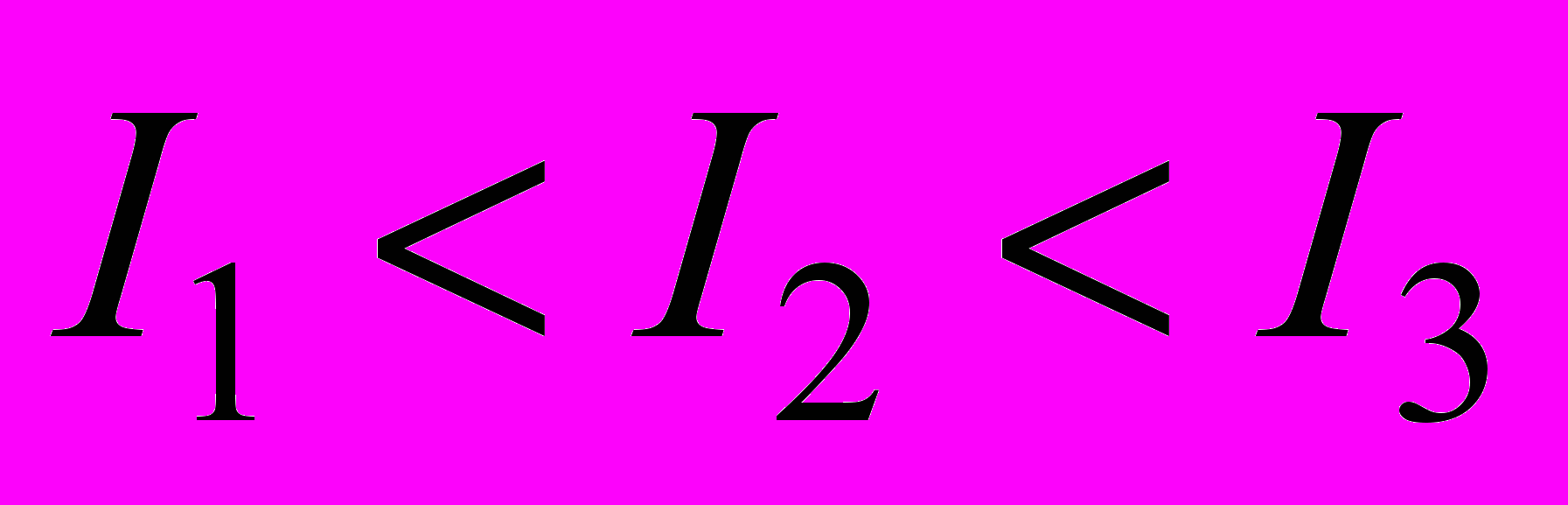 в)
в) 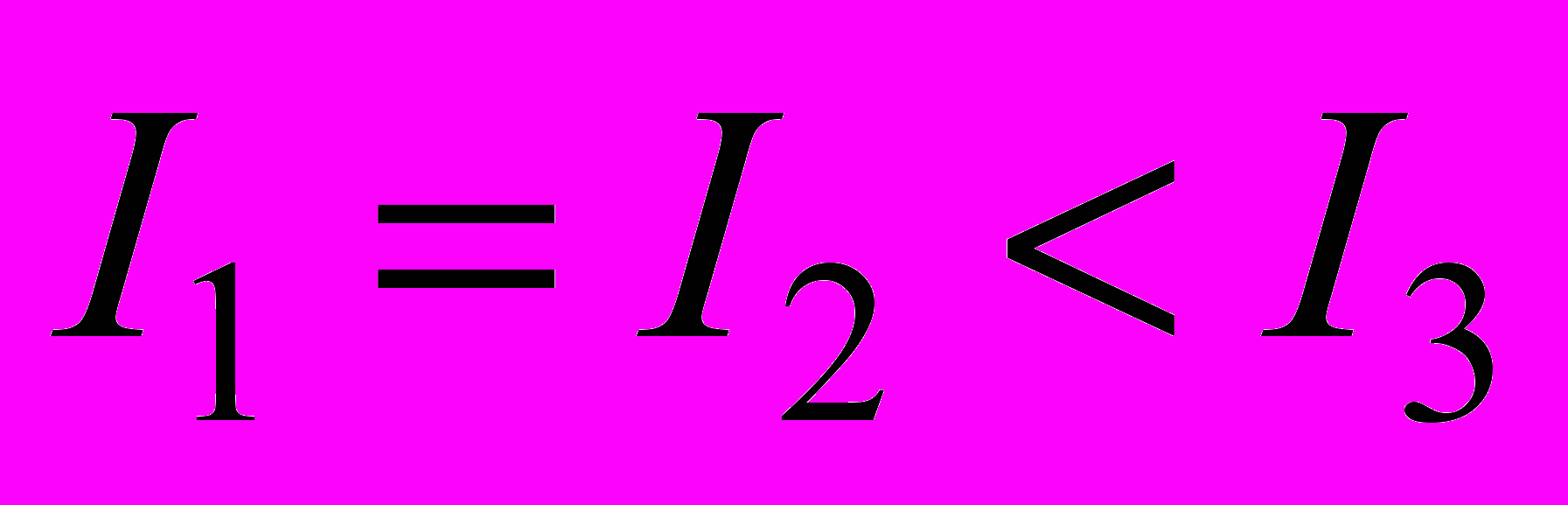 г)
г) 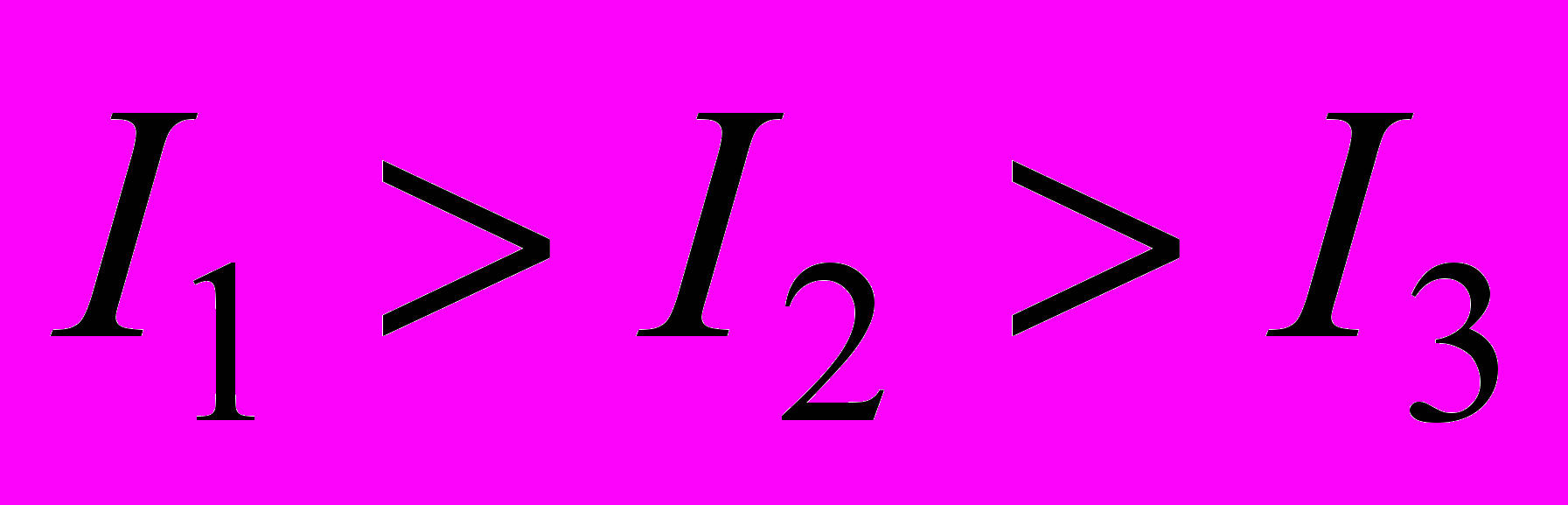
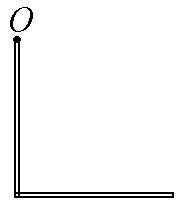 9. Два одинаковых однородных тонких стержня массой m = 1 кг и длиной l = 1 м каждый приварили концами перпендикулярно друг к другу. Через конец одного из стержней проходит ось О, перпендикулярная плоскости стержней. Найти момент инерции получившейся детали относительно оси О.
9. Два одинаковых однородных тонких стержня массой m = 1 кг и длиной l = 1 м каждый приварили концами перпендикулярно друг к другу. Через конец одного из стержней проходит ось О, перпендикулярная плоскости стержней. Найти момент инерции получившейся детали относительно оси О.
