Применение дифференциального и интегрального исчисления к решению физических задач (11 класс, 2 часа)

Вид материала

Урок

Содержание Ход урока. V. Актуализация физических знаний (путь и скорость, сила и работа, плотность жидкости и гидростатическое давление) (5-7 мин). VI

Подобный материал:

• Факультативный курс «Применение дифференциального и интегрального исчисления к решению, 69.62kb.
• 1. Общекультурное и практическое значение парадигмы непрерывности и дифференциального, 2182.36kb.
• Календарно-тематическое планирование элективного курса " методы решения физических, 107.87kb.
• Практикум по решению физических задач Учащиеся лицея №1580, 59.5kb.
• Правила дифференцирования, исследование функций; ( в 1 сем) основы интегрального исчисления:, 10.67kb.
• Программа элективного курса по информатике «Программируем на языке Паскаль», 104.96kb.
• Год издания, 77.56kb.
• Учетно-экономический факультет ростовского государственного экономического университета, 17.04kb.
• Лейбниц (Leibniz) Готфрид Вильгельм (1646-1716), немецкий философ, математик, физик,, 201.35kb.
• Темы ученических исследований Применение комплексных чисел к решению задач. Решение, 36.07kb.

МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«ЛИЦЕЙ №3»


Интегрированный урок по теме

«Применение дифференциального и интегрального исчисления к решению физических задач»

(11 класс, 2 часа)


Учитель физики

Клапчук Т.С.


г. Старый Оскол

2005

Тема урока: Применение дифференциального и интегрального исчисления к решению физических задач» (11 класс, 2 часа)

Цель урока: - вооружить обучающихся ранее не использовавшимися методами решения задач;

- показать на конкретных примерах связь физики с математикой;

- развивать умения переноса имеющихся знаний из одной научной области в другую.

Оборудование: компьютер с мультимедийным сопровождением.


Ход урока.

I. Организация класса (2 мин)

II. Актуализация математических знаний (нахождение наибольшего и наименьшего значения функции, теорема косинусов) (5 мин)

III. Решение задач.

Задача №1 (8-10 мин). Дождевая капля падает под действием силы тяжести, равномерно испаряясь так, что ее масса меняется по закону m (t) = 1 - 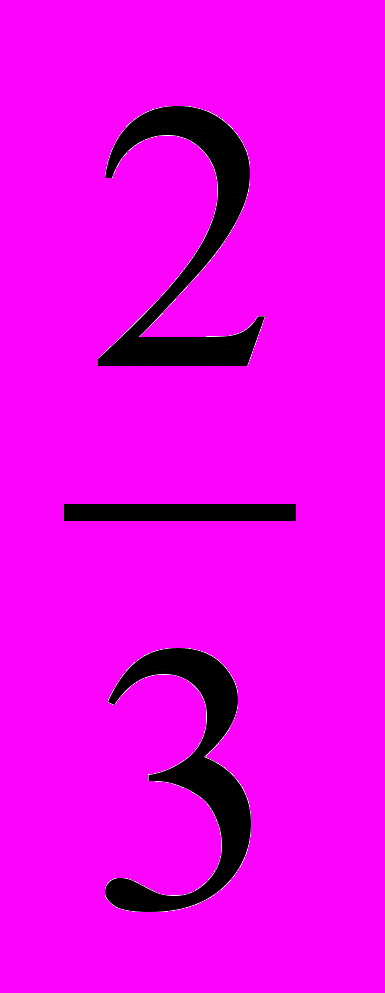t . (m – измеряется в граммах, t - в секундах). Через какое время после начала падения кинетическая энергия капли будет наибольшей?

Обсуждается физический способ решения и доказывается нецелесообразность его применения, т.к. речь идет о произведении двух переменных величин.

Решение (схематично). Е_к = ; ; ;

.

;

;

; .

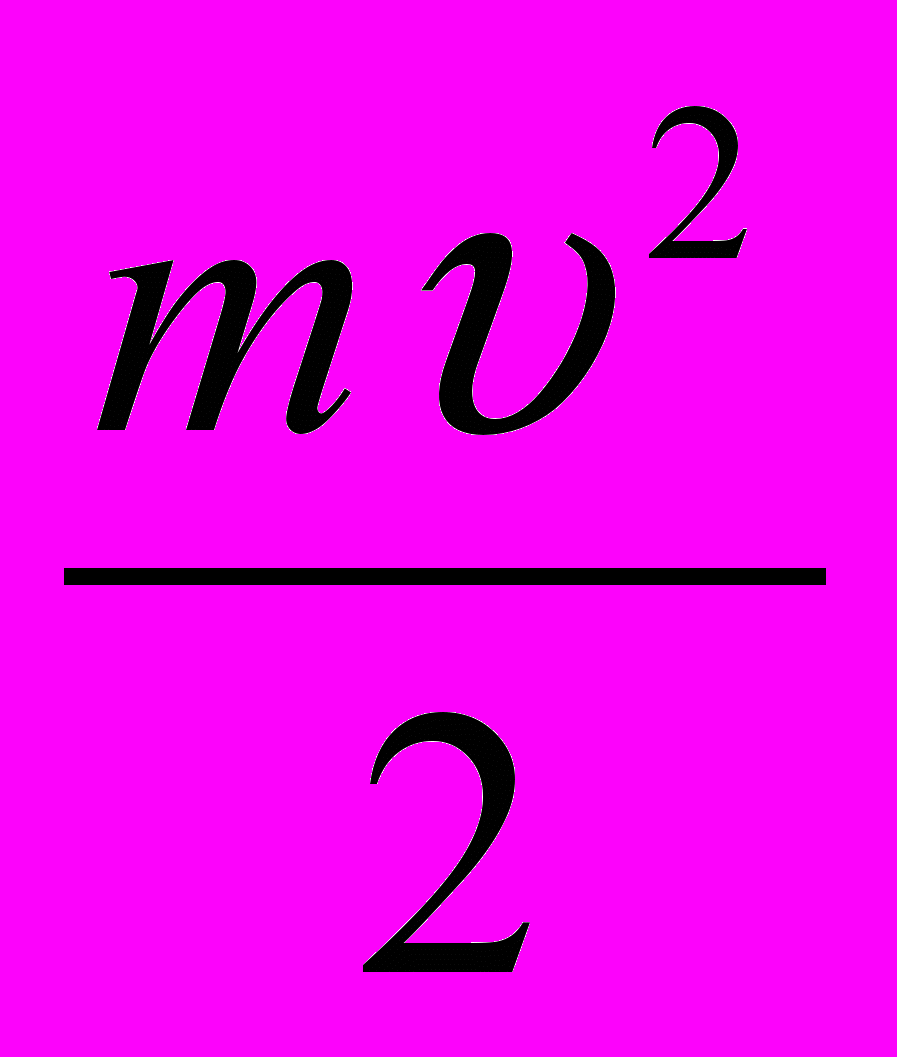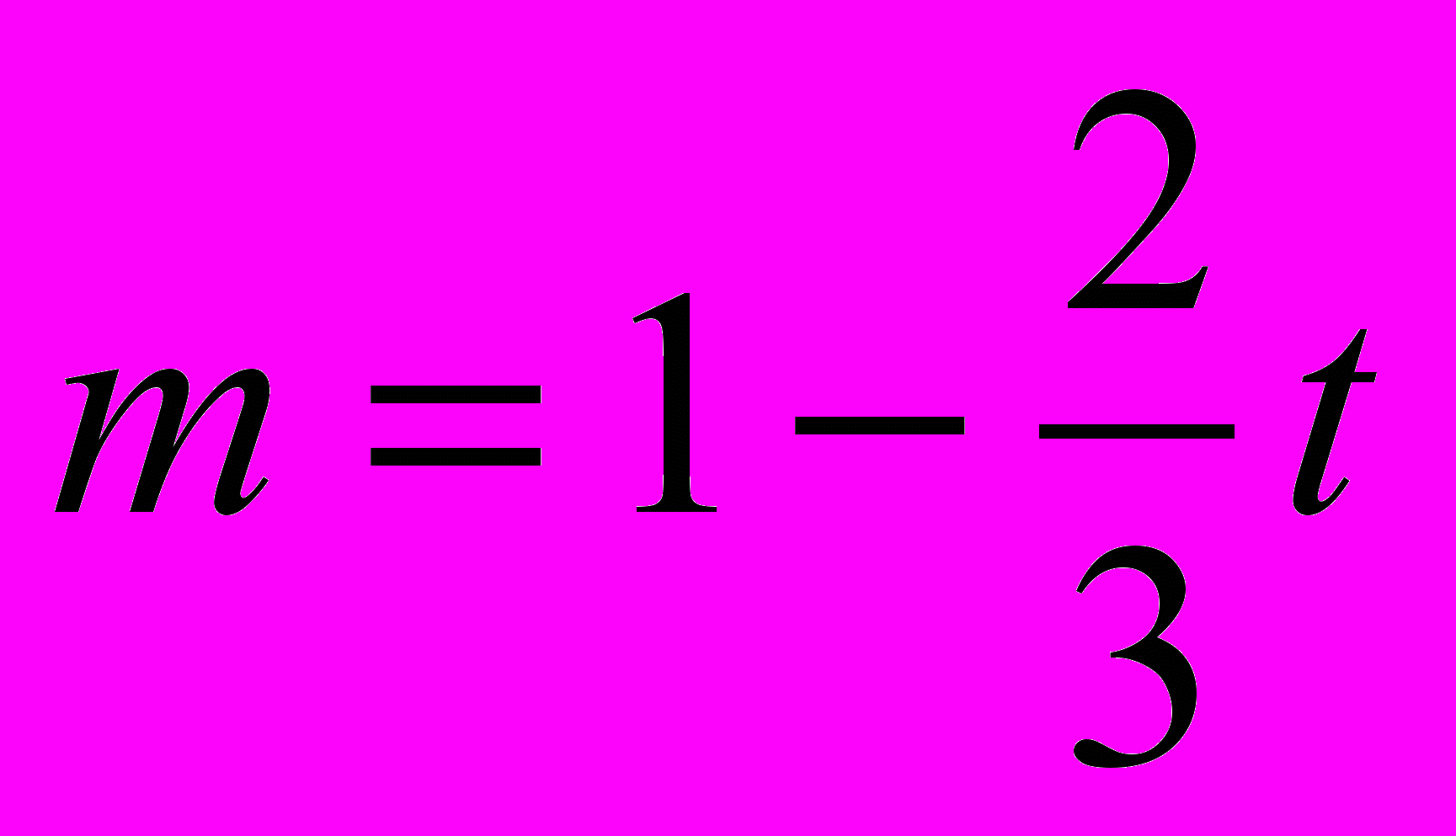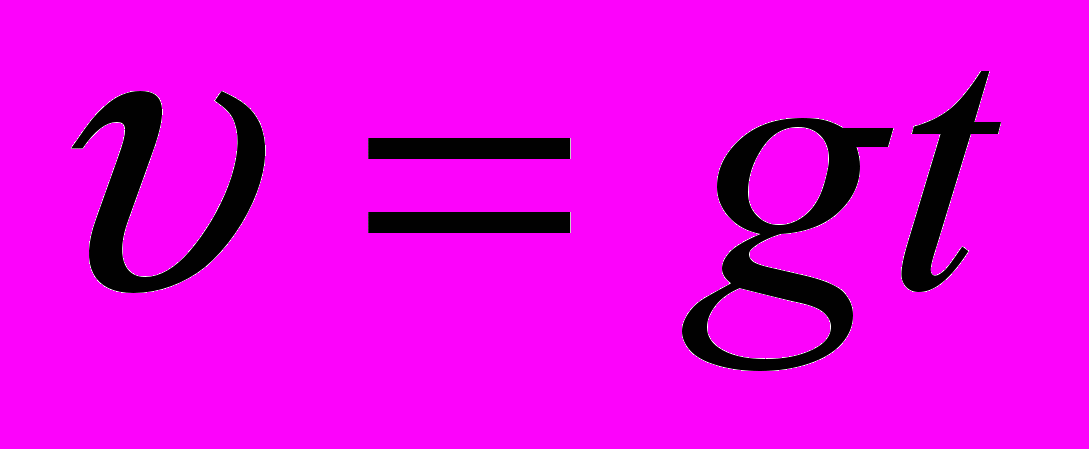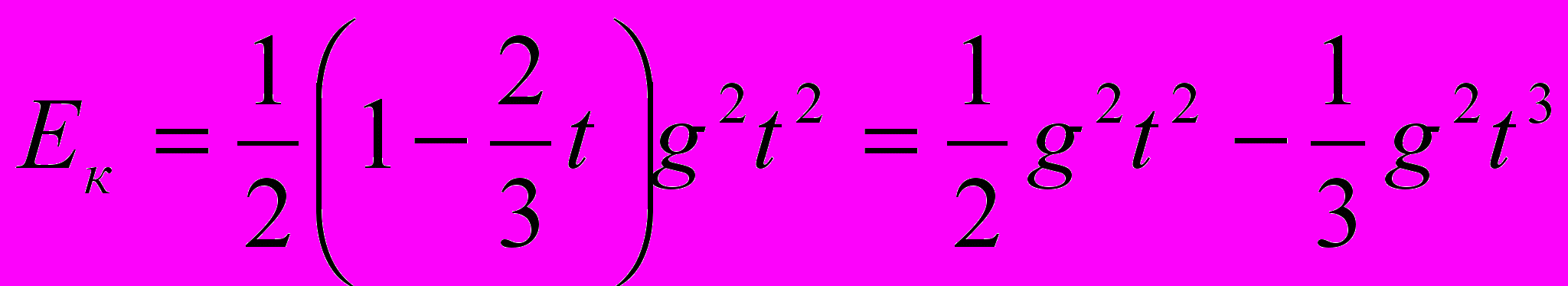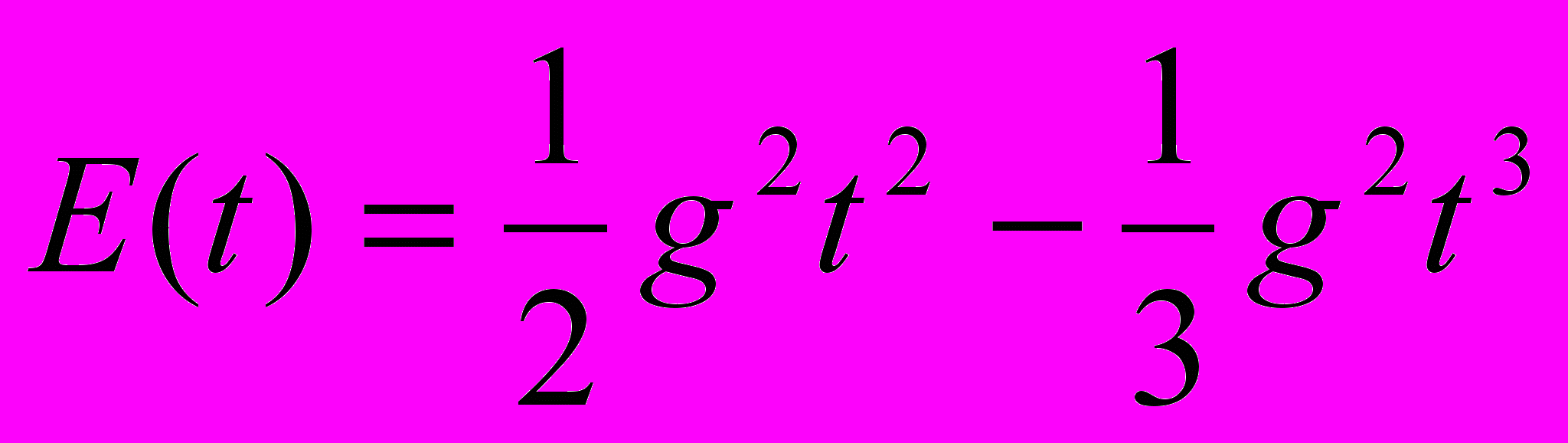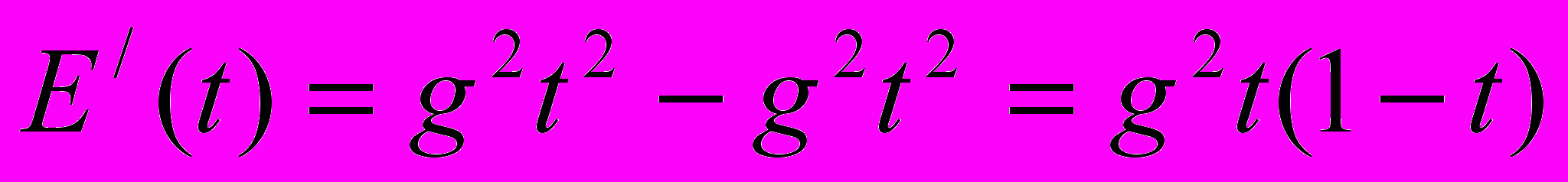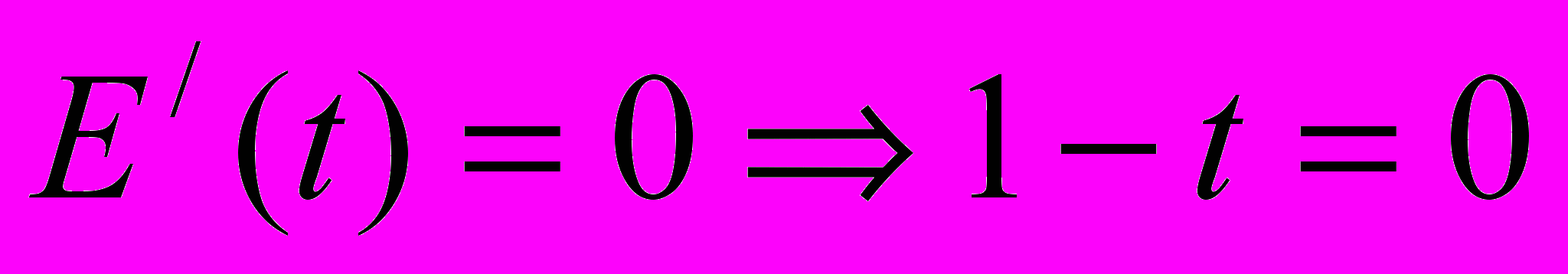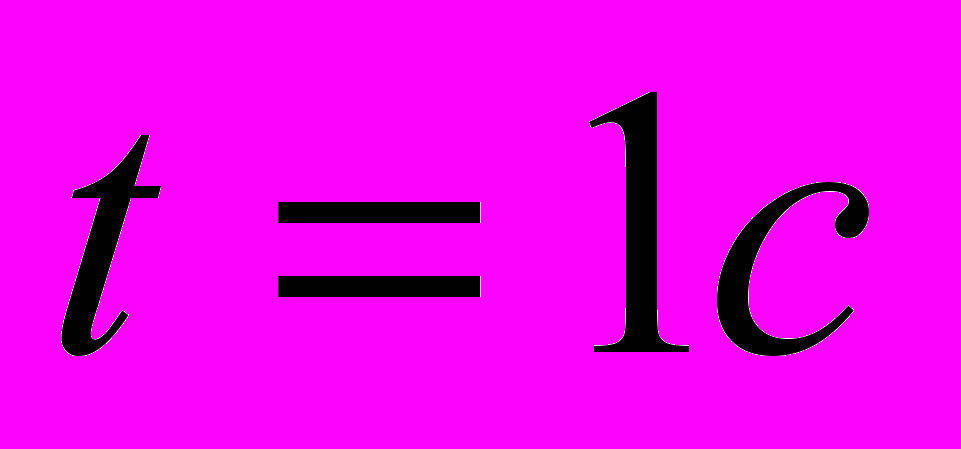Ответ: через 1 секунду после начала падения.

Задача №2 (5-7 мин). Источник тока с электродвижущей силой 220 В и внутренним сопротивлением 50 Ом подключен к прибору сопротивлением R. Чему должно быть равно сопротивление R потребителя, чтобы потребляемая мощность была наибольшей?

Решение. ; ; . .

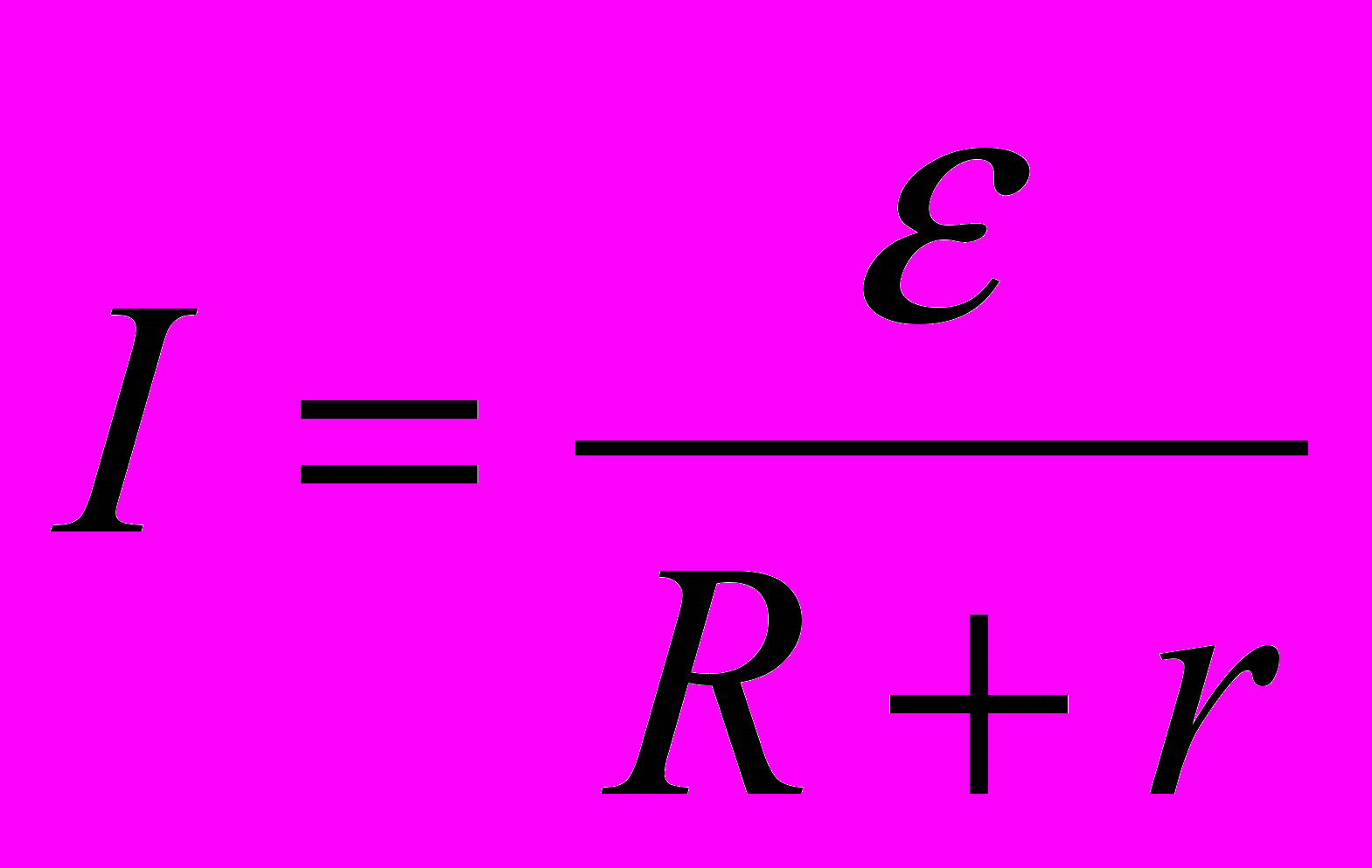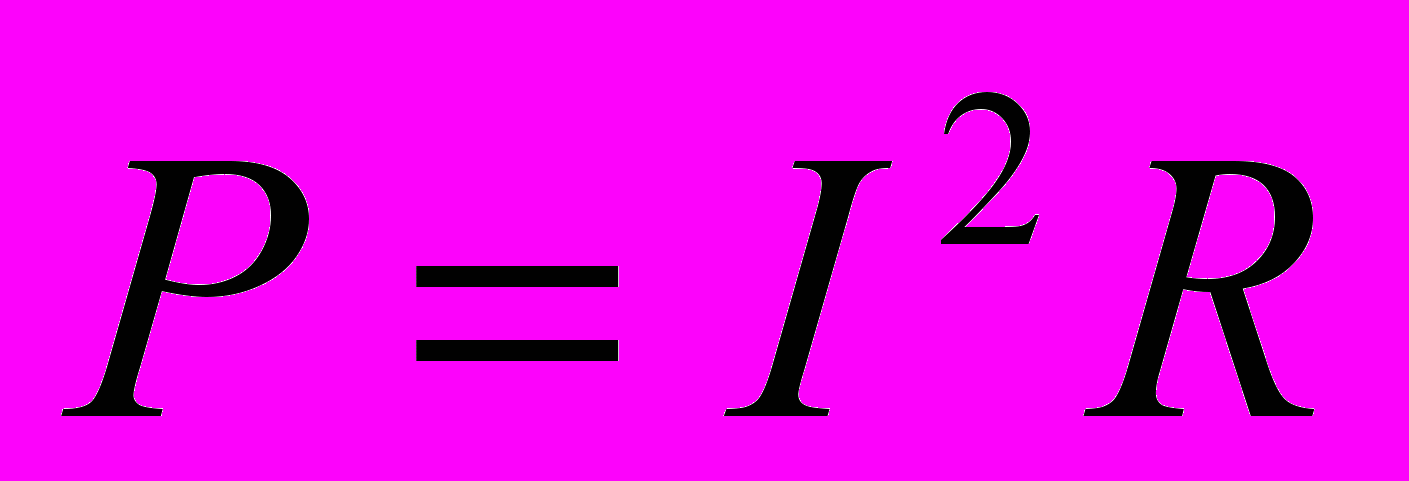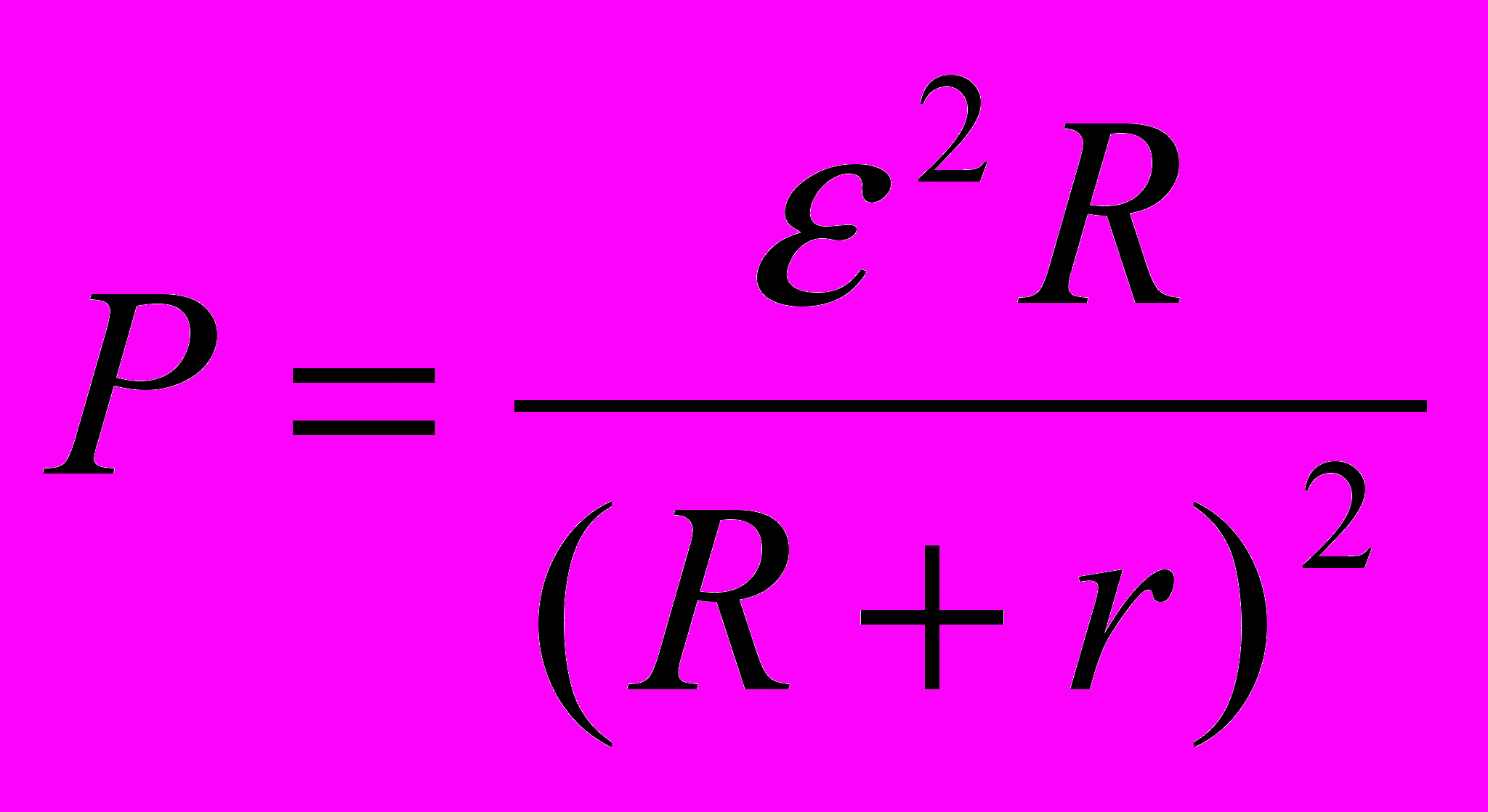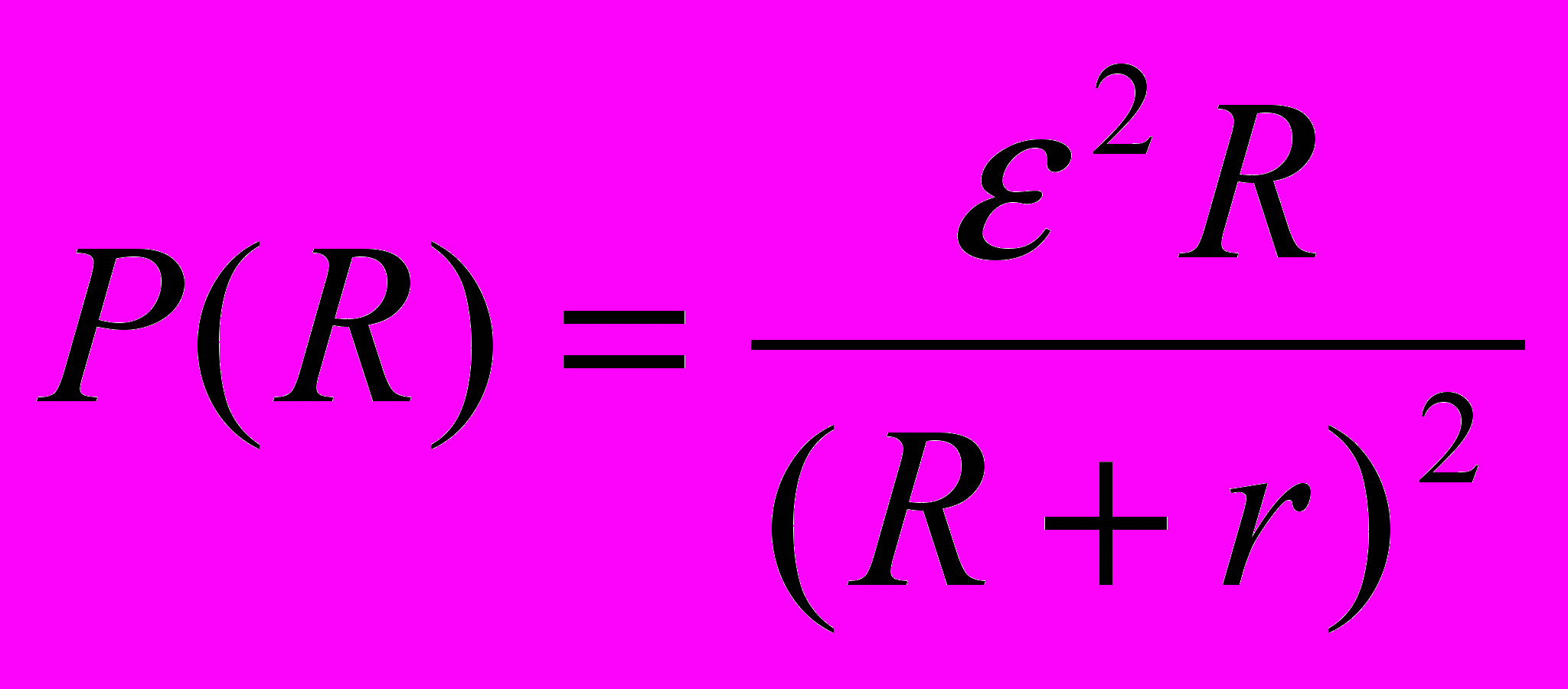Применяем правило дифференцированной дроби и получаем R = r = 50 Ом.

Задача №3 (10 мин). Два корабля плывут со скоростями 20 км/ч и 30 км/ч по прямым, угол между которыми равен 60 ^о, в направлении точки пересечения этих прямых. Найдите наименьшее расстояние между кораблями, если в начальный момент времени расстояния кораблей от точки пересечения прямых были соответственно 10 км и 20 км.

Решение. После использования теоремы косинусов

;

.

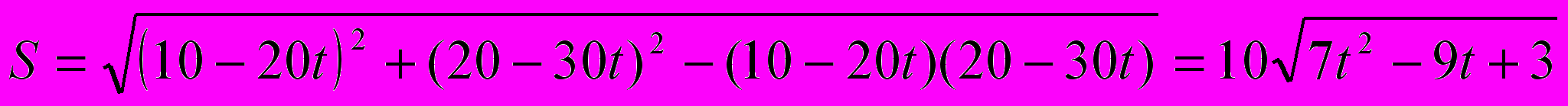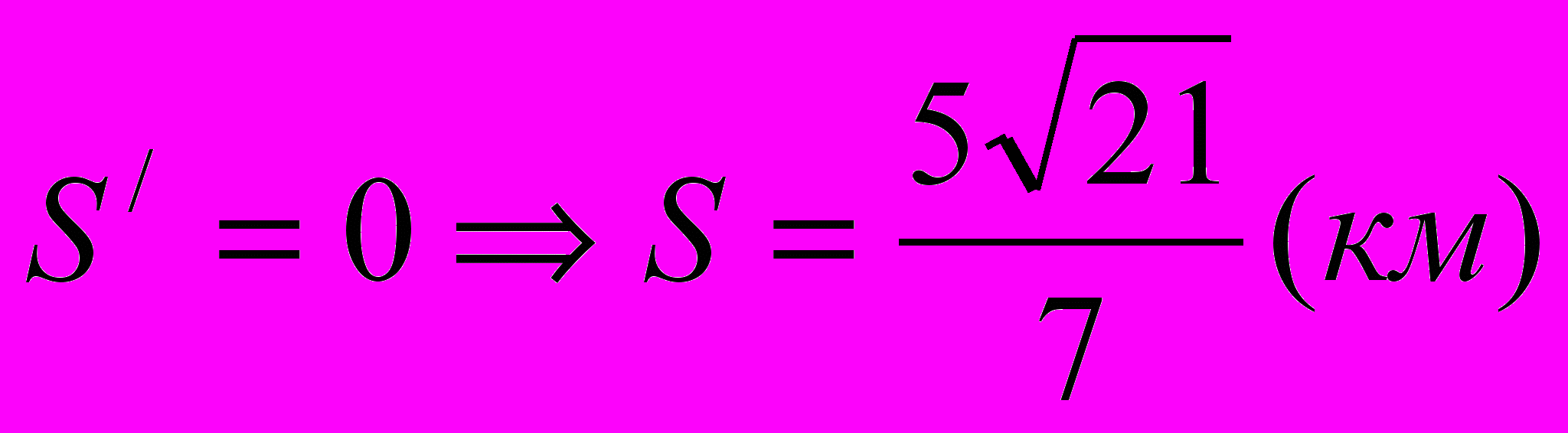Ответ: 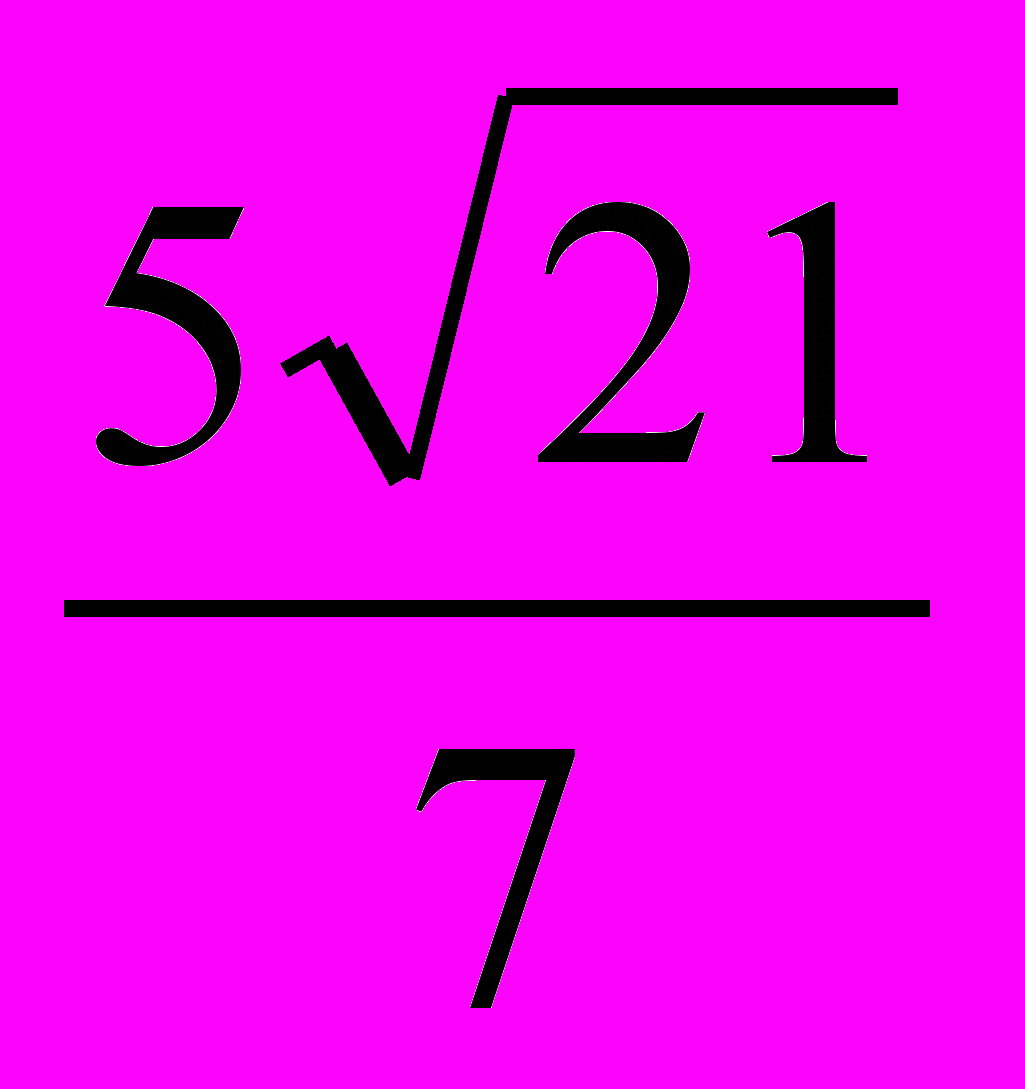км.

IV. Итоги решения задач и формулировка вывода о целесообразности применения дифференциального исчисления к решению задач по физике (определить тип задач). (5-7 мин).

V. Актуализация физических знаний (путь и скорость, сила и работа, плотность жидкости и гидростатическое давление) (5-7 мин).

VI. Решение задач.

Задача №4 (8-10 мин). Тело брошено с поверхности Земли вертикально вверх со скоростью 39,2 м/с. Найти наибольшую высоту подъема тела.

Решение. 1) Физический способ.

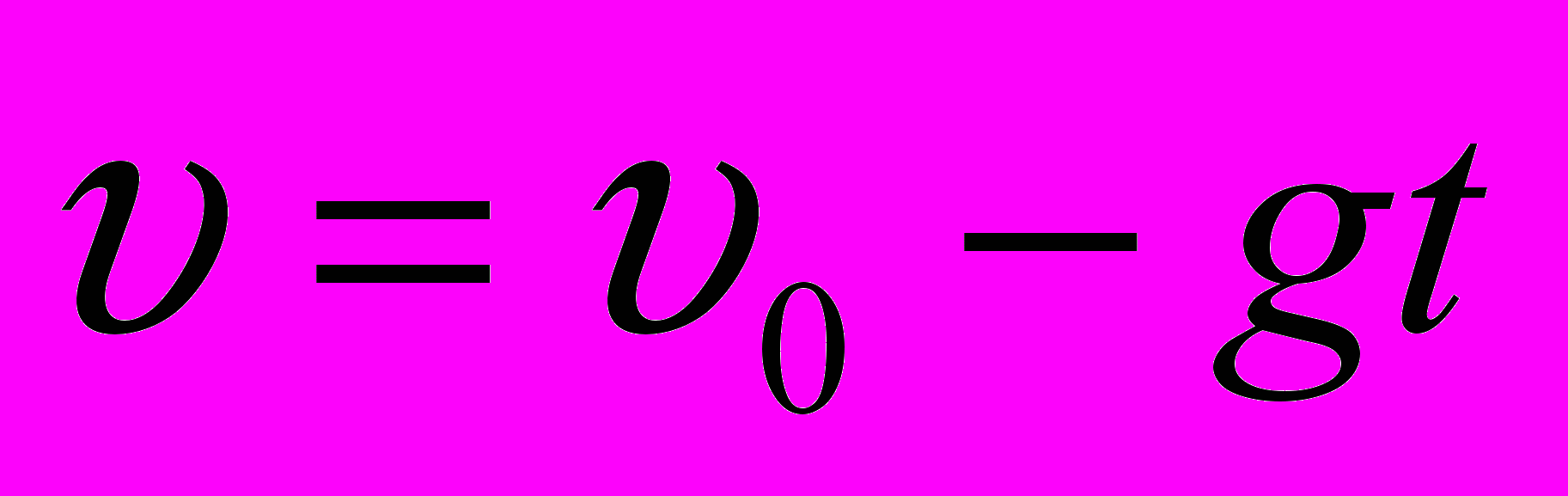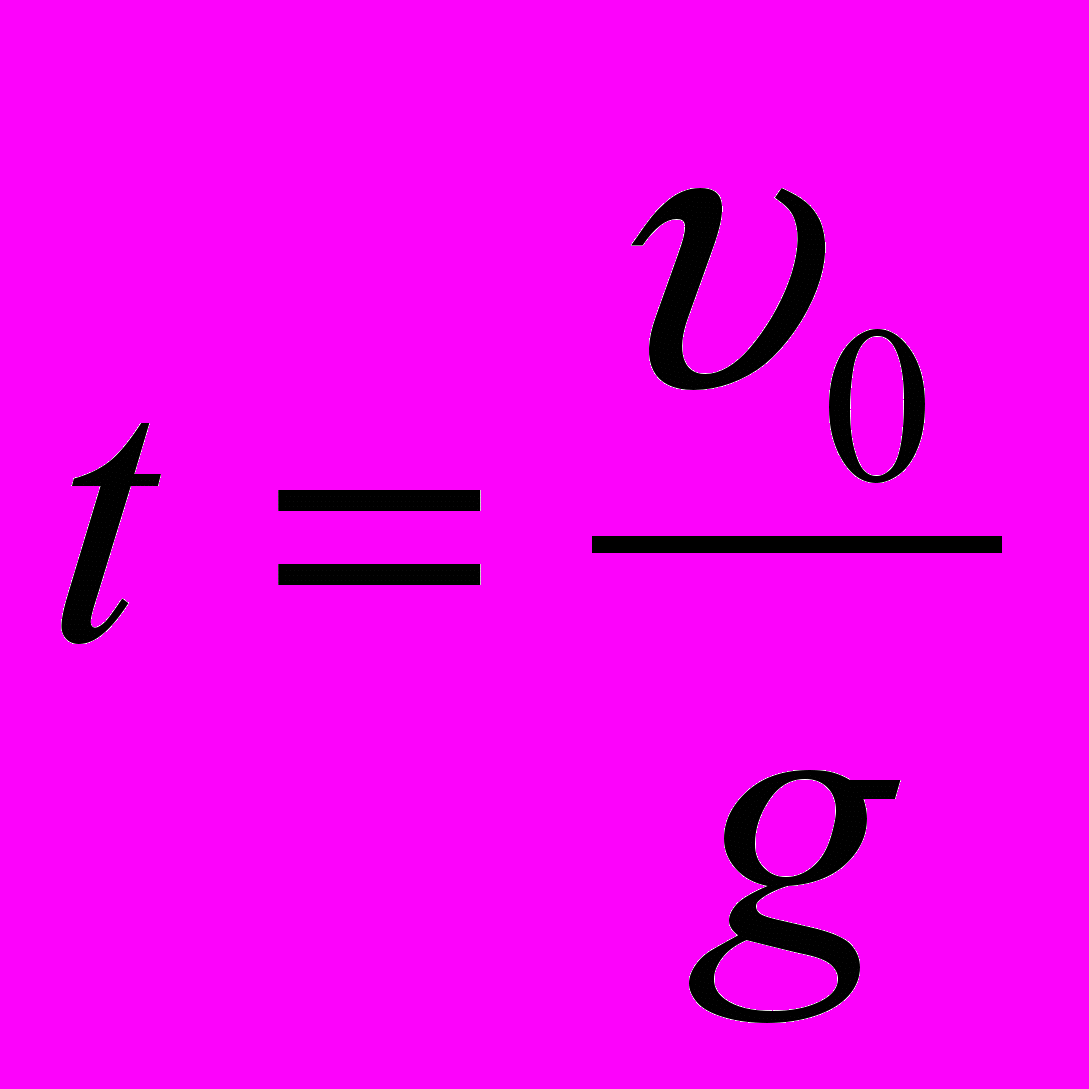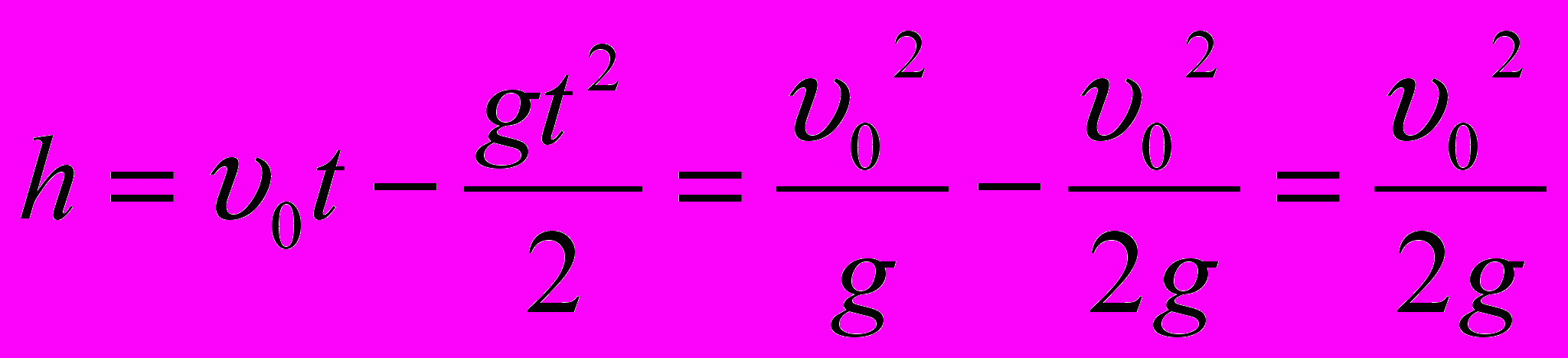; ; ; . h = 78,4 м.

2) Математический способ решения.

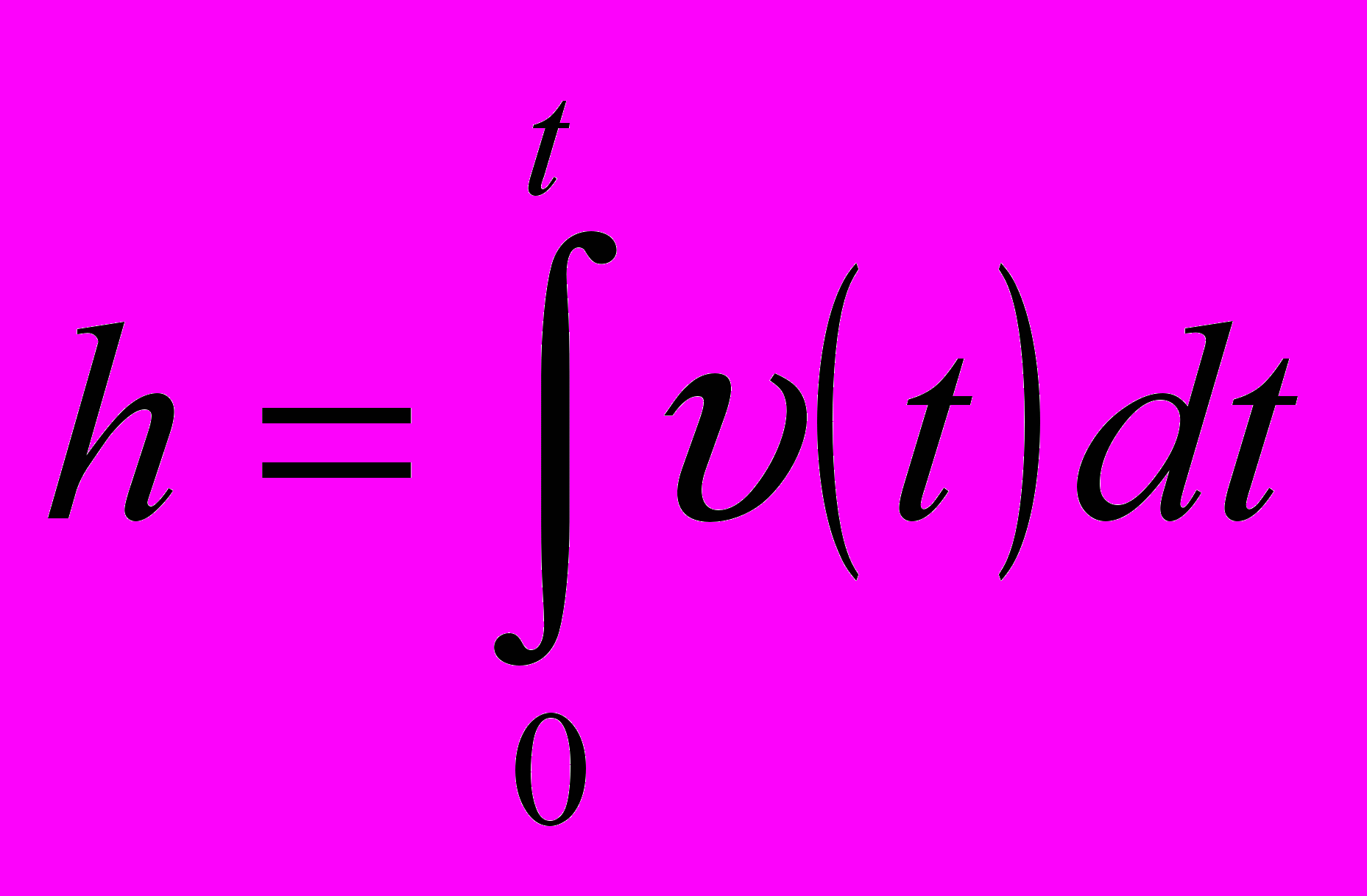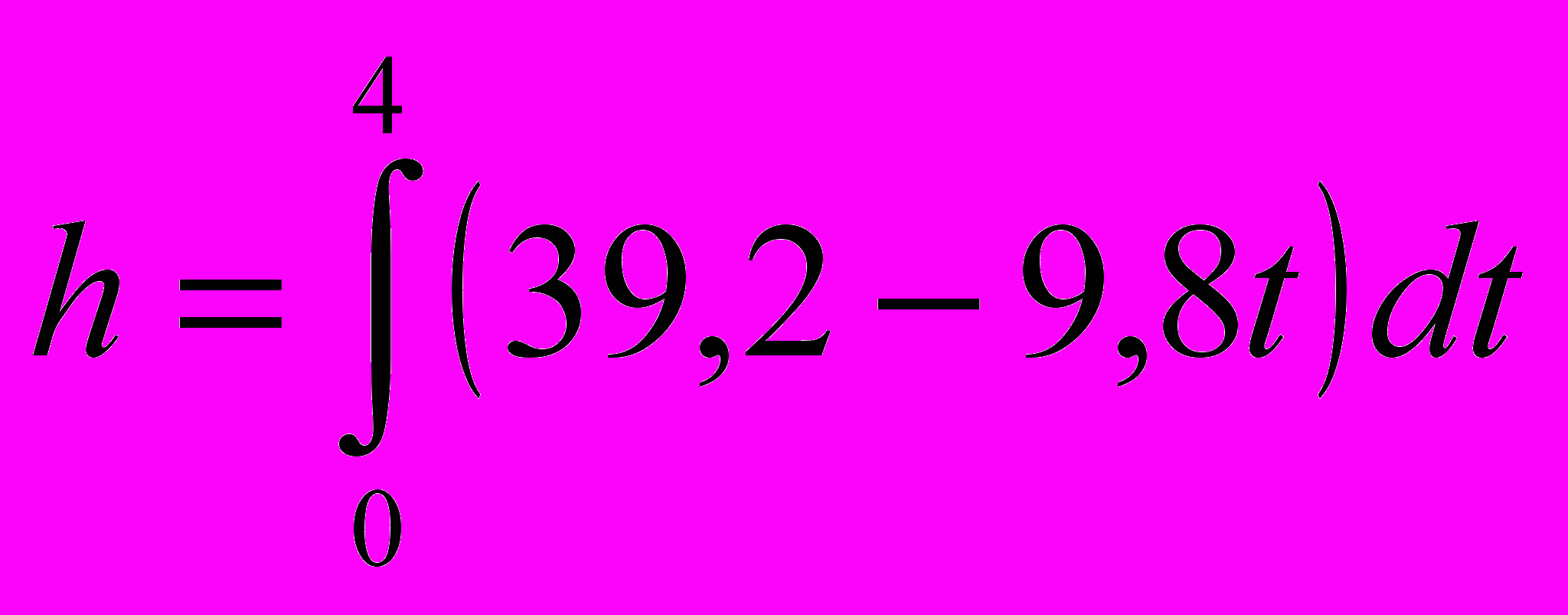; ; h = 78,4 м.

Задача №5 (5 мин). Для растяжения пружины на 0,04 м необходимо совершить работу 20 Дж. На какую длину можно растянуть пружину, совершая работу 80 Дж? Какова жесткость пружины?

Решение. .

.

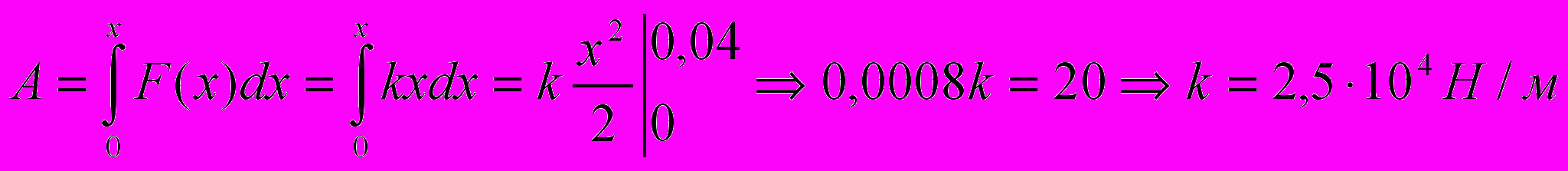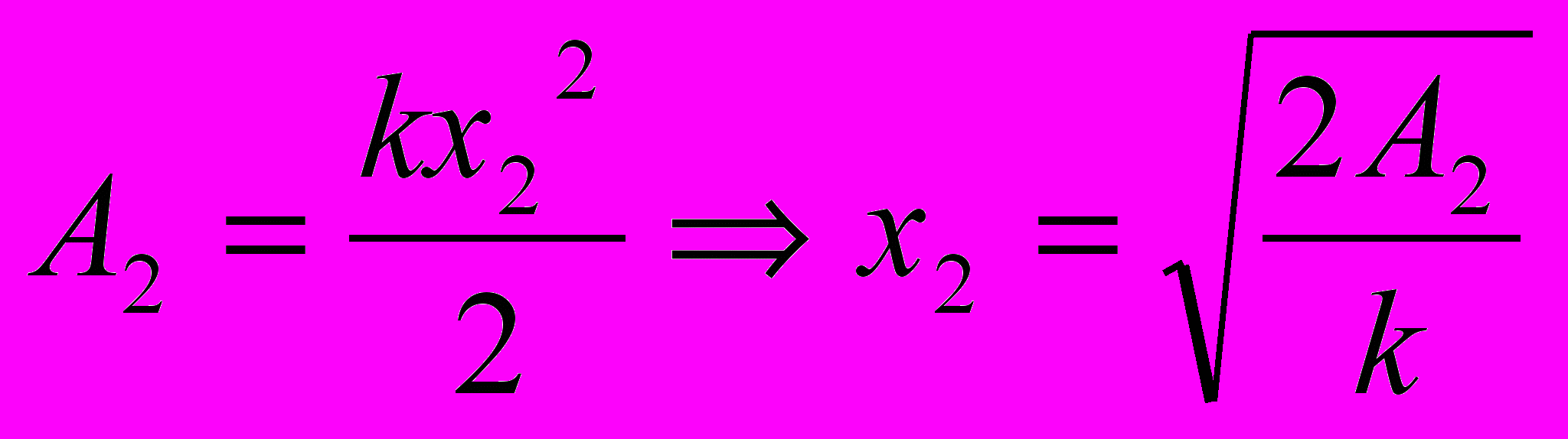Ответ: 0,16 м; 2,5 ^. 10⁴ Н/м

Задача №6 (10-12 мин). Вычислить силу давления воды на вертикально погруженную треугольную пластину АВС с основанием АС = 9 см и высотой ВД = 2 м, если вершина В лежит на свободной поверхности жидкости, а АС параллельна ей.

Решение.

Пусть МК – поперечное сечение пластины на уровне ВЕ = х. Найдем зависимость длины МК от х. Из подобия треугольников ВМК и АВС имеем, МК:АС=ВЕ:ВД или МК: 9 = х : 2, откуда МК = f (x) = 4,5x.

На основании этого и формулы гидростатического давления р =

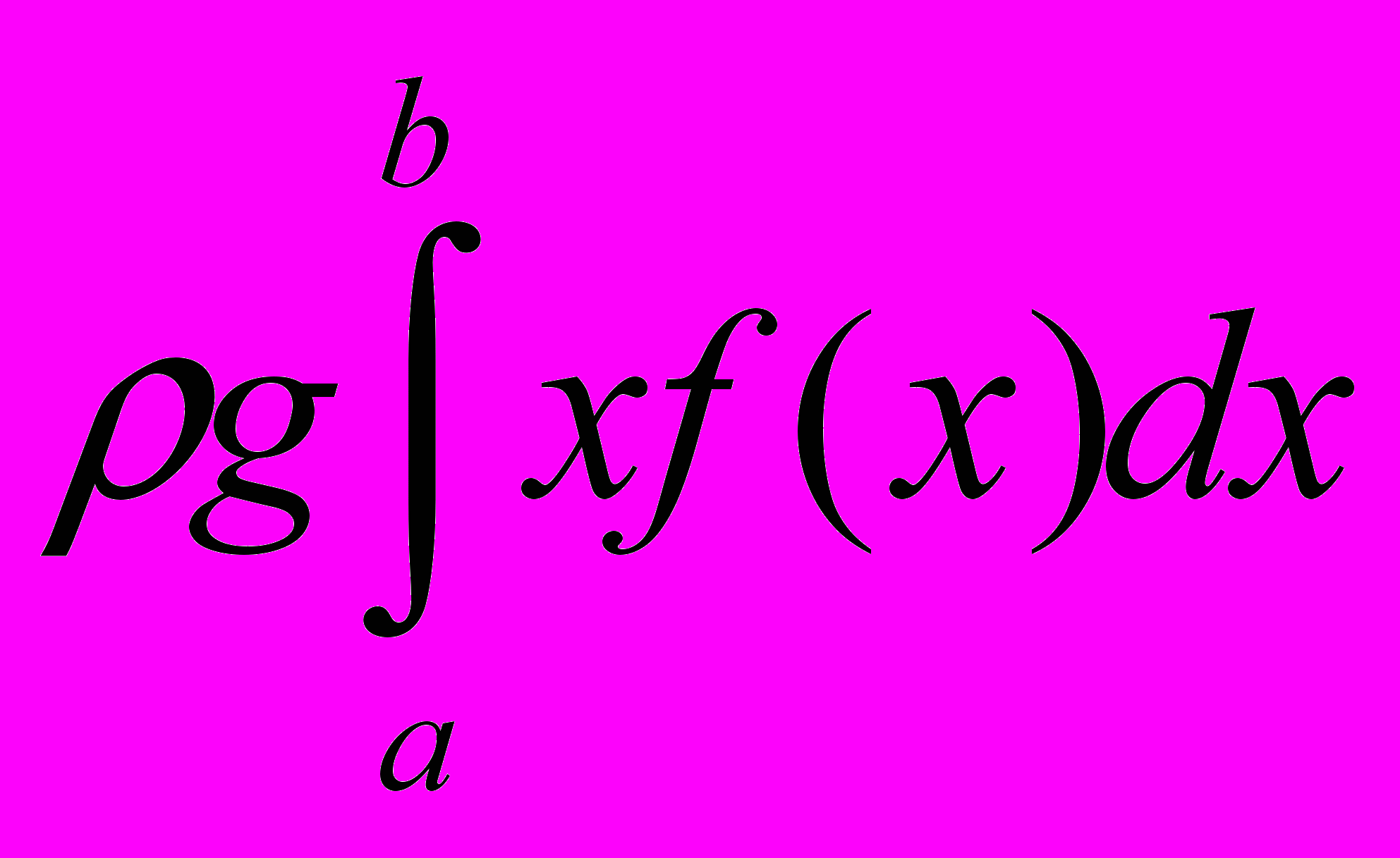
получим .

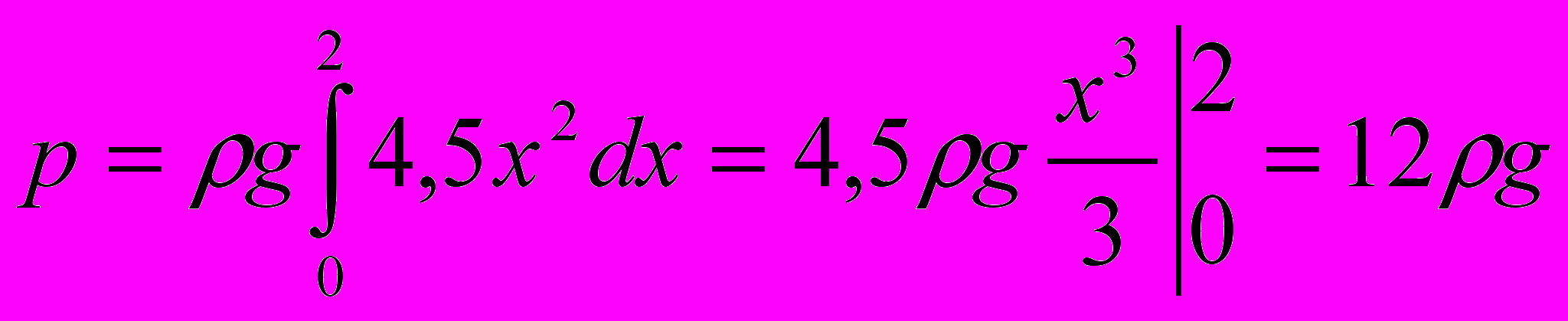Ответ: 1,2 ^. 10⁵ Н.

VII. Анализ решенных задач и определение критерия необходимости применения интегрального исчисления к решению физических задач (обратить особое внимание на задачу №6) (7-8 мин).

VIII. Домашнее задание.

Задача №1. На стене висит картина. Нижний край ее на 75 см, а верхний на 3 м выше уровня глаз наблюдателя. На каком расстоянии от стены должен стать наблюдатель, чтобы рассмотреть картину под наибольшим углом?

Задача №2. Пружина растягивается на 0,02 м под действием силы в 60 Н. Какая работа производится при растяжении пружины на 0,12 м?

IX. Итоги урока (2-3 мин)