Geum.ru

Теоретическое дополнение к практическому разделу

Вид материалаДокументы

Содержание


Решить уравнение
Теорема о целых корнях
Разложение многочлена на множители группировкой.
Метод подстановки.
Подобный материал:
1. Теоретическое дополнение к практическому разделу.

Общие сведения.

А
n-1

n-2
лгебраическим многочленом n-ой степени называют выражение вида:

a0 xn +а1х + a2 x + …+аn-1х + an , (1)

где n принадлежит Z ,n≥0 , a 0 , a1 ,...an принадлежат R и a0≠0, и обозначают его через Pn (х).

Равенство Pn (х)=0 называют алгебраическим уравнением n-ой степени. (2)

Число α называют корнем многочлена (1) , а также корнем (решением) уравнения (2) , если α удовлетворяет уравнению (2) ,

т.е. если верно числовое равенство Pn(ɑ) =0 .

Решить уравнение (2) −значит найти множество всех его корней (решений).

Если n=1 , то уравнение (2) называют уравнением 1-ой степени, а при n=2 – квадратным уравнением. Формулы для решения таких уравнений хорошо известны и они достаточно просты. Однако для уравнений выше 2-ой степени таких простых формул нет. Для уравнений третьей степени существуют формулы Кардано и Феррари, выражающие корни этих уравнений через радикалы. Но эти формулы слишком громоздки и неудобны. Поэтому на практике ими редко пользуются. Таким образом, если n≥3, а коэффициенты многочлена (1) −произвольные действительные числа, отыскание корней уравнения (2) −задача непростая.

Тем не менее, во многих частных случаях эта задача решается до конца. Остановимся на некоторых из них.
  1. Теорема Безу. Остаток от деления многочлена Pn (х) на двучлен x- α равен Pn (х).

Докажем эту теорему для случая, когда n=3. Для этого разделим многочлен P3 (х) на двучлен x- αn уголком.



a0 x³ + a1 x² + a3
x- α

a0 x³ - αa 0 x²
a0x²+(a1+ αa0)x + (a2+ α(a1+ αa0))

(a1+ αa0)x² + a2 x + a3

(a1+ αa0)x² - α(a1 + αa0)x

(a2 + α(a1 + αa0))x+a3

(a2+ α(a1+ αa0))x- α(a2+ α(a1+ +αa0))

a3+ α(a2+ α(a1+ αa0))-остаток

Обозначим остаток от деления P3(х) на x- α через r. Тогда:

r=a3+ α (a2 + α(a1 + αa0))=a3+ αa2+ α²a1 + α³+a0=a0a³+ a1 α² + a2 α +a3=P3(α) ,

т.е. остаток r=P3(∞)

Из теоремы Безу вытекают следующие практические следствия:

Следствие 1. Если многочлен Pn(x) делится без остатка на двучлен x- α,(т.е.r=0) то α является корнем многочлена Pn(x) ,т.е. Pn(α) =0. поэтому решения уравнения Pn (x)=0 сводится к решению уравнения Pn-1(x) =0 , на единицу меньшей степени.

Следствие 2. Если число α является корнем многочлена Pn (x) , то Pn (x) делится без остатка на двучлен x- α , т.е. в этом случае справедливо разложение: Pn (x)=(x- α)∙Pn-1 (x) .

Следствие 3. Если многочлен Pn-1 (x) делится без остатка на двучлен x- α , то Pn (x)=(x- α)² ∙Pn-2 (x)

Если при этом многочлен Pn-2 (x) не делится на x- α, то число α называют двукратным корнем многочлена (1) или уравнения (2).

Число α называется m-кратным корнем многочлена Pn (x) если Pn (x)=Pn-m (x) ∙(x- α) в m-ой степени и многочлена Pn-m (x) не делится на x- -α .

Однократные корни называются простыми, m-кратные корни, при m>1 называются кратными.

Особо отметим: Теорема о целых корнях, заключающая в себе

Если целое число α - корень многочлена с целыми коэффициентами, то α - делитель его свободного члена.

Доказательство. Пусть:

P (x)=a0xⁿ +a1xⁿֿ¹ +…+an-1x +an−многочлен с целыми коэффициентами и целое число α −его корень.

Тогда по определению корня выполняется равенство P (α)=0;

a0 αⁿ+a1 αⁿֿ¹+…+an-1 α +an=0

Вынося общий множитель α за скобки, получим равенство:

α(a0 αⁿֿ¹ +a1 αⁿֿ² +…+an-1)+ad=0, откуда

an= -α(a0 αⁿֿ¹ + a1 αⁿֿ² +…+ αn-1)

Так как числа a0, a1,…an-1, an и α −целые, то в скобке стоит целое число, и, следовательно, an делится, на α, что и требовалось доказать.

Доказанная теорема может быть сформулирована и следующим образом: всякий целый корень многочлена с целыми коэффициентами является делителем его свободного члена.

2.Дополнительная теорема о целых корнях

Если целое число α−корень многочлена P(x) с целыми коэффициентами, то α-1−делитель числа P(1), α+1−делитель числа P(-1)

Доказательство. В самом деле, при a=1, P (α)-P (1),а значит, и P(1) делится на α-1. Аналогично рассматривается второй случай.

На теореме (1) основан алгоритм поиска целых корней многочлена с целыми коэффициентами: выписать все делители свободного члена и поочерёдно выписать значения многочленов этих чисел.

В то же время проведение этого алгоритма с вычислительной точки зрения может показаться достаточно трудным, однако он может быть существенно упрощён, если применить дополнительное утверждение, основанное на одной из известных формул сокращённого умножения.

Именно: из тождества

xⁿ-yⁿ=(x-y)(xⁿֿ¹+xⁿֿ²y+…+ xyⁿֿ²+yⁿֿ¹)

вытекает, что для целых чисел b и c число bⁿ-cⁿ делится на b∙c. Но для любого многочлена P разность

P (b)-P(c)= (a0bⁿ+a1bⁿֿ¹+…+an-1b+an)-(a0cⁿ+a1cⁿֿ¹+…+an-1c+an)=a0(bⁿ- cⁿ)+a1(bⁿֿ¹-cⁿֿ¹)+…+an-1(b-c)

и, следовательно, для многочлена P с целыми коэффициентами и целых чисел b и c разность P(b)-P(c) делится на b-c.

Очень частным, но весьма полезным случаем этого утверждения является теорема 2

Итак, задача нахождения целых корней многочлена с целыми коэффициентами полностью решена −с помощью теоремы делимости целых чисел.

2. Схема Горнера.

Так называют способ деления многочлена Pn (x)=a 0xⁿ+a 1xⁿֿ¹+a 2xⁿֿ²+…+a n-1x+an на двучлен x- α, довольно легко позволяет выразить коэффициенты неполного частного

b 0xⁿֿ¹+b 1xⁿֿ²+b 2xⁿֿ³+…+bn-1 и остаток r через коэффициенты многочлена Pn(x) и число α (смотри доказательство теоремы Безу):

b0=a0, b1= αb0+a1, b2= αb1+a2,…,bn-1= αbn-2+an-1 и r = αbn-1+an

Вычисления по схеме Горнера в виде следующей таблицы:
a0
a1
a2
…
an

α
b0=a0
b1= αb0+a1
b2= αb1+a2
…
r= αbn-1+an

Поскольку r=Pn(α), то α−корень уравнения (2). Для того, чтобы проверить не является ли α кратным корнем, схему Горнера можно применить уже к частному b 0x+b 1x+…+bn-1 по таблице. Если в столбце под bn-1 получится снова ноль, значит α−кратный корень.
  1. Разложение многочлена на множители группировкой.

Разложение многочлена на множители может проводиться разными способами: с помощью формул сокращённого умножения, метода группировки. Подробнее они будут рассмотрены на примерах в следующем разделе.

4. Метод подстановки.

Суть этого метода состоит в следующем. Пусть требуется решить уравнение g(φ(x))=0. Заменим φ(x)=t. Тогда g(t)=0.

Пусть последнее уравнение имеет корни t1, t2,…t n. Тогда уравнение g(φ(x))=0 равносильно совокупности уравнений:

φ(x)=t1, φ(x)=t2,…, φ(x)=tn. Множество решений этой совокупности и есть множество решений исходного уравнения.

Как правило, для произвольно данного уравнения функции g и φ сразу не видны. Поэтому на первом этапе необходимо внимательно присматриваться к данному уравнению и увидеть (догадаться), какие преобразования следует сделать, чтобы привести уравнение к виду g(φ(x))=0


2. Различные методы решения алгебраических уравнений высших степеней.


  1. Теорема Безу. Поиск целых корней многочлена.

Примеры:

1.Решим уравнение x³-x²-3x-1=0

Если данное уравнение имеет целый корень, то он является делителем числа -1, т.е. равен 1 или -1. Проверка убеждает нас, что число -1− корень уравнения. Значит, в силу доказанной теоремы, его левую часть можно представить в виде произведения (x+1)P(x), где P(x)−многочлен второй степени.

Для того, чтобы найти многочлен P(x), разделим x³-x²-3x-1 на (x+1).

x³-x²-3x-1
x+1

x³+x²
x²-2x-1

-2x²-3x

-2x²-2x



-x-1



-x-1



0

Деление многочленов выполняется «уголком»


Итак,

x³-x²-3x-1=(x+1)(x²-2x-1)

Из уравнения

(x+1)(x²-2x-1)=0

Получаем

‌‌‌‌‌‌x+1=0‌ ИЛИ x²-2x-1=0

Решив этИ уравнениЯ, найдём, что данное уравнение третьей степени имеет три корня:

x1=-1, x2=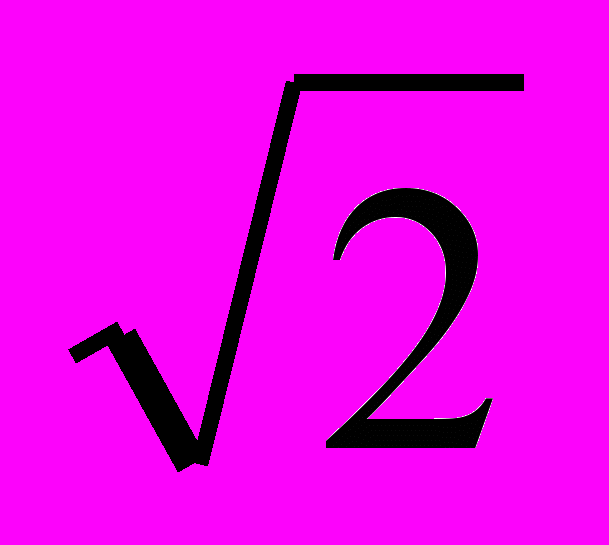, x3=1+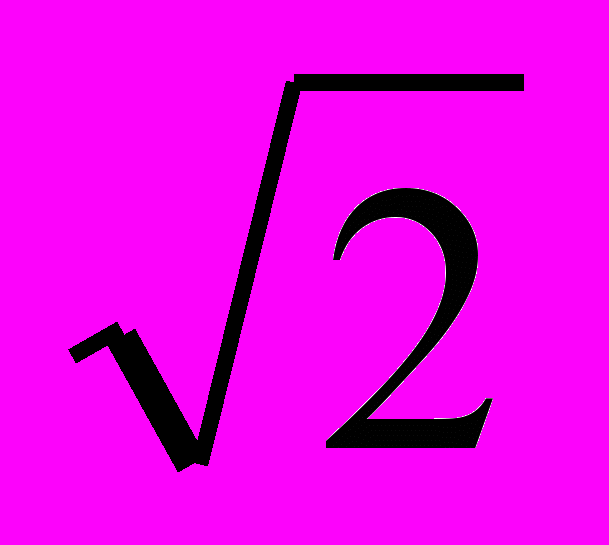

Ответ: -1, 1+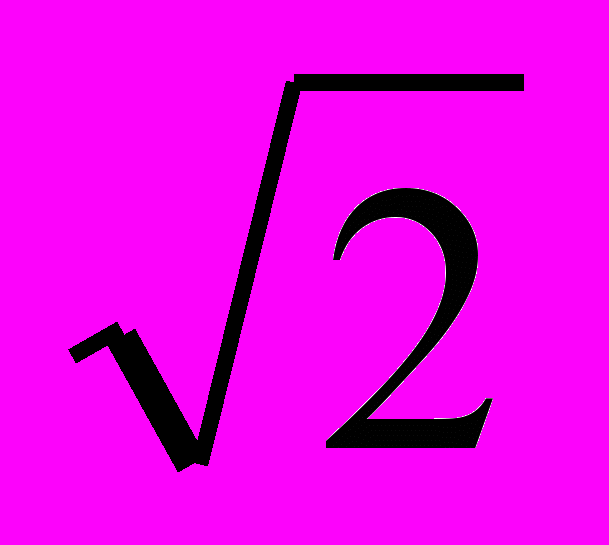, 1-.
  1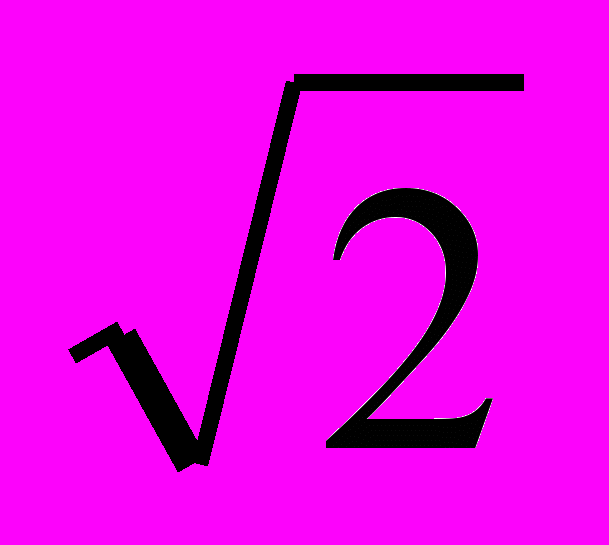. Найдём целые корни уравнения:

2x+x³-9x²-4x-4=0

Делителями свободного члена являются числа -1, 1, -2, 2,-4, 4.

Подставляя эти числа в уравнение, находим, что левая часть уравнения обращается в нуль лишь при x1=-2 и x2=2.
  1. Решим уравнение

x-x³-5x²+3x+2=0

Делители свободного члена− числа -1, 1, -2, 2.

Подставляя эти числа в уравнение, находим, что x1=1, x2=-2.

Значит, левую часть уравнения можно представить в виде (x-1)(x+2)(x²+px+q) или (x²+x-2)(x²+px+q), где p и q −неизвестные нам числа. Методом неопределённых коэффициентов находим, что -2q=2 и p+1=-1.

Отсюда q=-1, p=-2.

Приравняв к нулю трёхчлен x²-2x-1, найдём остальные корни данного уравнения:

x²-2x-1=0

x3=1-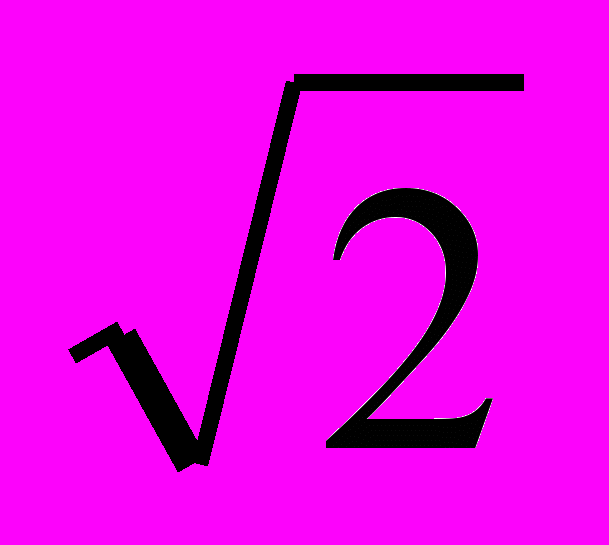, x4=1+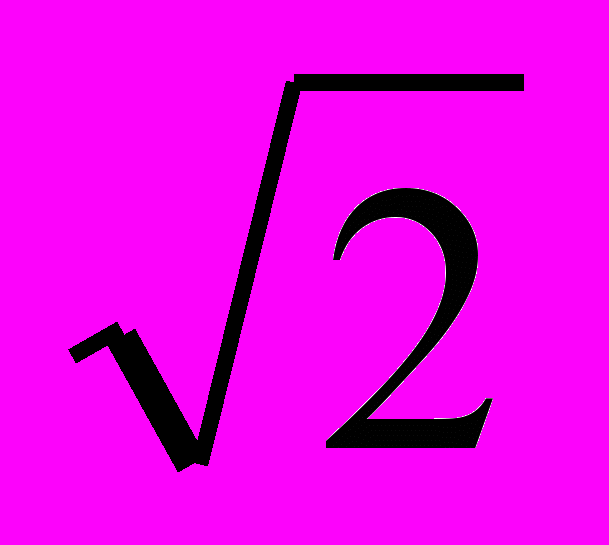

Ответ:x1=1, x2=-2, x3=1-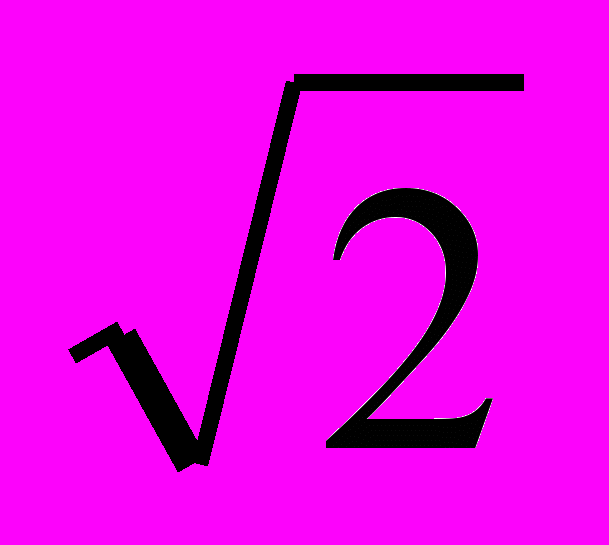, x4=1+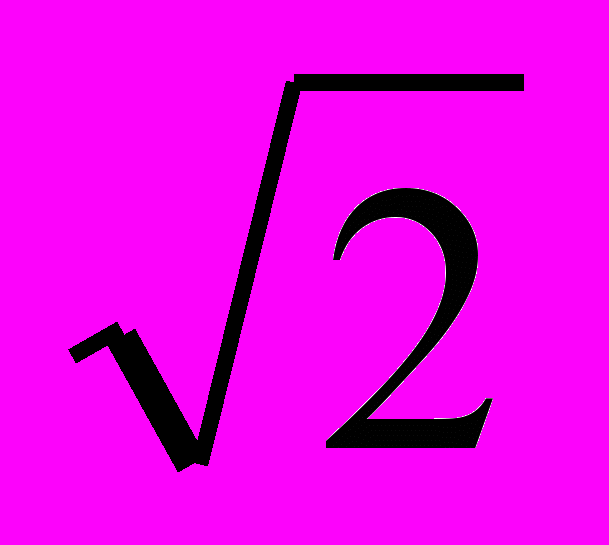

  1. Схема Горнера.

Поиск рациональных корней по схеме Горнера. Примеры:

  1. Решить уравнение:

x⁸-6x⁷+9x⁶-x²+6x-9=0 (5)

Так как в уравнении a0=1, то рациональными корнями уравнения могут быть только целые числа.
1
-6
9
0
0
0
-1
6
-9
Выводы:

1
1
-5
4
4
4
4
3
9
0
1-корень

1
1
-4
0
4
8
12
15
24≠0



1-простой корень

-1
1
-6
10
-6
10
-6
9
0



-1-корень

-1
1
-7
17
-23
33
-39
48≠0






-1-простой корень

3
1
-3
1
-3
1
-3
0






3-корень

3
1
0
1
0
1
0









3-простой корень

Делители свободного члена: ±1;±3;± 9. Если это уравнение имеет целые корни, то все они находятся среди этих чисел. Найдём эти корни по схеме Горнера.

Как видно из таблицы:

(x-1)(x+1)(x-3)² (x+x²+1)=0 , x∊{-1;1;3}

Ответ: {-1;1;3}

2.Решить уравнение 4x+8x³+x²-3x-1=0 (6)

Делители a0=4;±1;±2;±4;делители a4=±1.

Значит, возможно, рациональные корни нужно искать среди чисел:±1;±0.5;±0.25. По теореме других рациональных корней быть не может. Ясно, что числа ±1 не удовлетворяют уравнению (6). Проверим остальные числа по схеме Горнера:
4
8
1
-3
-1
Выводы

-½
4
6
-2
-2
0
-½-корень

-½
4
4
-4
0



-½-кратный корень

Дальше схему Горнера можно приостановить, так как после двукратного деления левой части (6) на (x+½) мы получим в частном квадратный трёхчлен, корни которого легко найти. Итак, из таблицы видно, что

(6)↔(x+½)²(4x²+4x-4)=0 ↔x=-½∨x=(-1±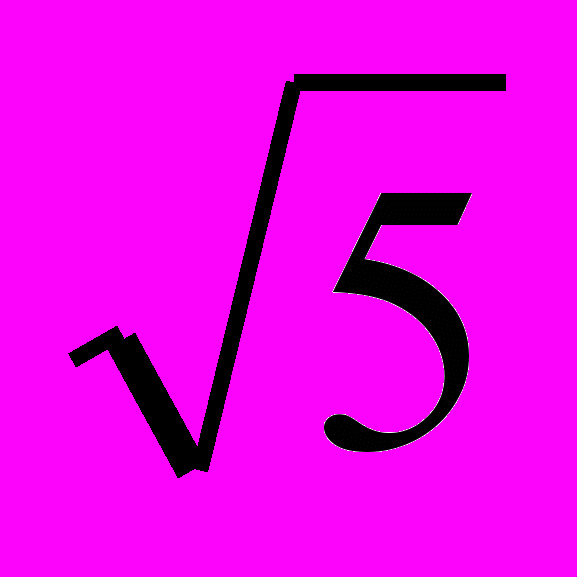)/2

Ответ: {-½;(-1±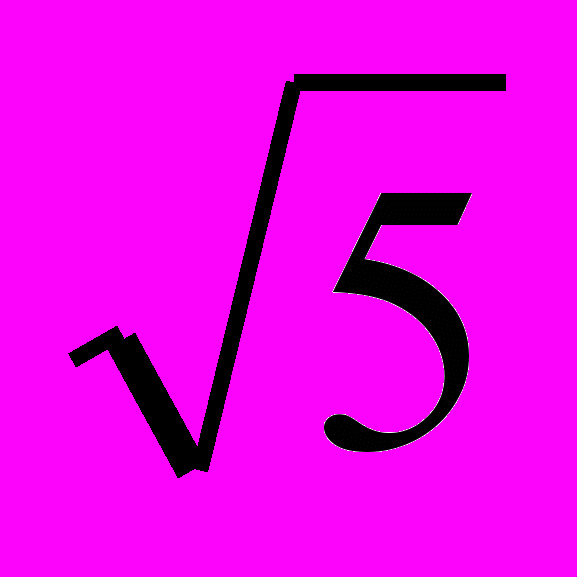)/2}
  1. Методы группировки и разложения на множители.

Примеры.

  1. Решить уравнение 2x+3x²-14=0

Квадратный трёхчлен 2y²+3y-14 имеет корни 2 или -3.5 и поэтому равен произведению (y-2)(2y+7), а данный многочлен равен (x²-2)(2x²+7)

Ответ:±;-
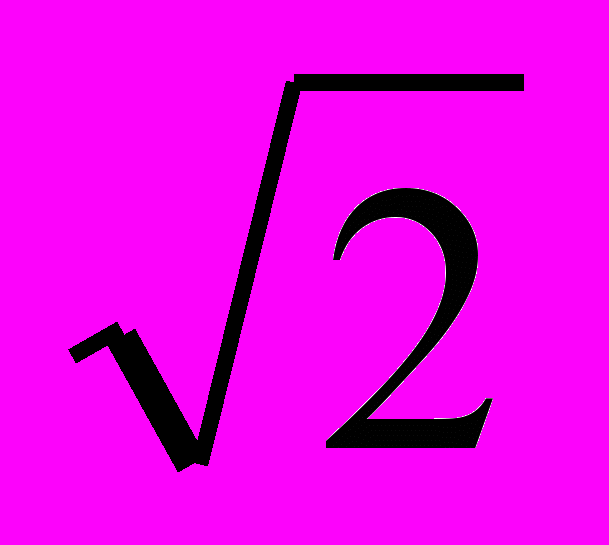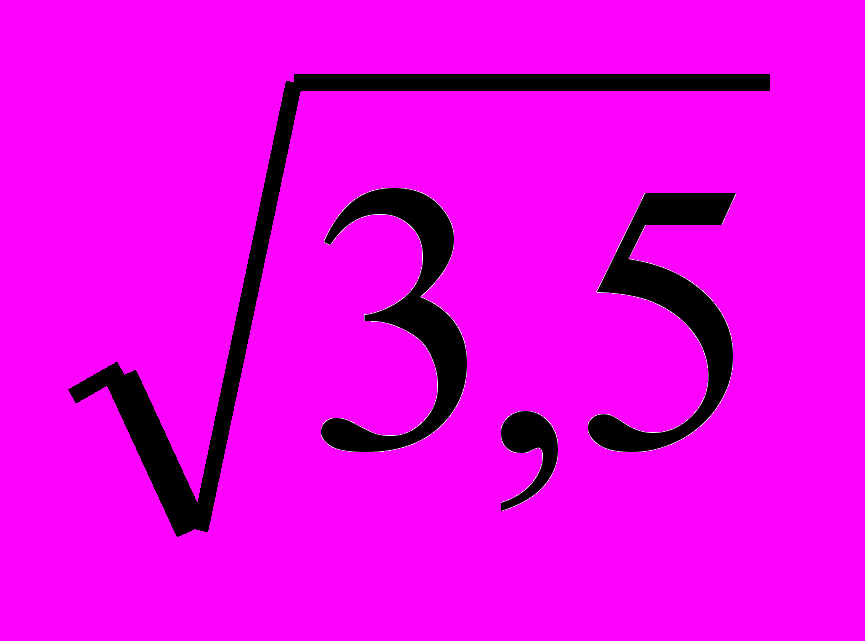
  1. Решить уравнение (5)

Внимательно посмотрев и подумав, нетрудно сообразить, что:

x⁸-6x⁷+9x⁶-x²+6x-9=0 ⇔(x²-6x+9)(x⁶-1)=0 ⇔(x-3)³((x²)³-1)=0 ⇔

⇔ (x-3)²(x²-1)((x²)²+x²+1)=0⇔(x-3)²(x+1)(x-1)=0⇔x=3∨x=-1∨x=1 ,Х ∊{3;-1;1}

Ответ: {3;-1;1}

3.Решить уравнение

2x³+3x²-3x-2=0

Коэффициенты этого уравнения (нечётной степени), одинаково удалены от старшего и свободного членов, противоположные числа. Такие уравнения можно назвать кососимметрическими Ясно, что 1 – корень такого уравнения. Степень уравнения можно было показать по схеме Горнера. Но проще решить это уравнение методом группировки разложения по множителям.

Имеем:

2х³ + 3х ²- 3х – 2 = 0 ⇔(2х³- 2) + ( 3х² - 3х ) =0⇔2(х³ - 1) + 3х( х – 1)=0 ⇔ (х-1)(2(х²+ х + 1) +3х)=0

х=1 ∨ х=(-5± 3) / 4 , х∊{ 1; -2; -½ }

Ответ: { 1; -2; -½ }
  1. 3х³ - 7х² -7х + 3 =0

Здесь уже коэффициенты одинаково удаленные от концов многочлена равны. Такие уравнения принято называть симметрическими. Здесь 1 – очевидный корень. Решаем это уравнение разложением на множители.

3х³ - 7х² - 7х + 3=0 ⇔ (3х³ +3) – (7х² + 7х)=0 ⇔

⇔ (3(х+1)(х² - х + 1) -7х(х+1)=0 ⇔ (х+1)(3х²-3х +3-7х)=0 ⇔

⇔ (х+1)(3х²-10х+3)=0 ⇔ х=-1 ∨ х=( 5 ±4) / 3

х∊{ -1; 3; ⅓ }

Ответ: { -1; 3; ⅓ }
  1. Метод подстановки.

Примеры.


  1. Решить уравнение

х - 5х³ +6х² -5х+1=0 (10)

Это уравнение – симметрическое уравнение четной степени. Такие уравнения решаются подстановкой. Но сразу не видно, что принять в качестве переменной t. Очевидно, что 0 не является корнем уравнения (10). Поэтому, если все члены (10) разделить на х², то получим уравнение равносильное (10).

(10) ⇔ х²-5х +6 – 5/х + 1/х²=0 ⇔ (х² + 1/х²)-5(х+1/х)+6=0 (11)

Теперь ясно, что целесообразна подстановка t= х+1/х

Отсюда t²=х²+2+1/х² ↔ х²+1/х²=t²-2

При такой замене переменной уравнение (11) принимает вид:

t²-2+5t+6=0 ⇔ t² -5t+4=0 ⇔ t=1∨ t=4

Таким образом,

(10) ⇔ х+1/х =1 ∨ х+1/х=4 ⇔ х² -х+1=0 ∨ х²-4х+1=0 (4)

х ∊Ø ∨ х=2± 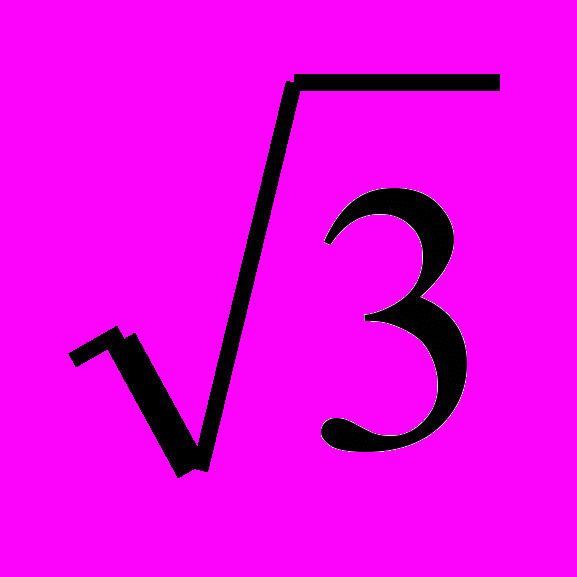, х=2±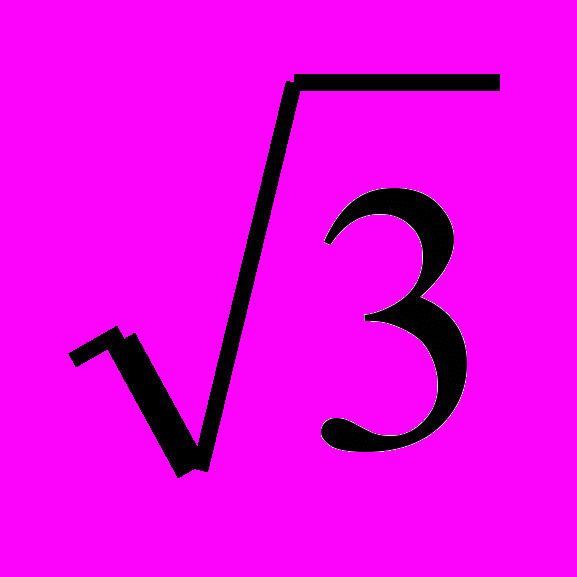

Ответ: {2±}

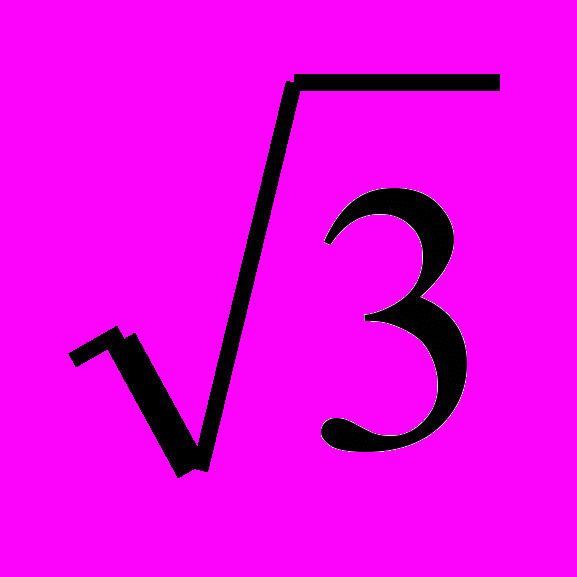2.Решить уравнение.

(х+4)+(х+4)=16 (12)

(х+4+х+2)/2=х+3. Пусть х+3=1. Тогда х=t-3 и уравнение (11) принимает вид:

(t+1) +(t-1)=16

Решаем (13) методом «прибавить-вычесть». Идея состоит в том, чтобы двучлен, расположенный в левой части (13), дополнить до полного квадрата. Имеем:

(t+1) -2(t+1)²(t-1)² +(t-1) + 2(t+1)²(t-1)²=16 ⇔

⇔((t+1)²(t-1)²)²+2((t+1)(t-1))²=16 ⇔

⇔ (((t+1)-(t-1))((t+1)+(t-1)))² +2(t²-1)²=16

(2-2t)²+2(t²-1)²=16

16t²-16+2(t²-1)²=0 ⇔ (t²-1)²+8(t²-1)=0 ⇔

(t²-1)(t²+7)=0 , t=±1

Следовательно

(12) ⇔х=1-3 ∨ х=-1-3 , х=-2 ∨ х=-4

Ответ: {-2; -4}

3.Решить уравнение.

(х+1)(х+2)(х+3)(х+4)=120 (17)

Присмотревшись к этому примеру, видим, что сумма свободных членов в 1-ой и 4-ой скобках равна сумме свободных членов во 2-ой и 3-ей скобках. Это наводит на мысль, что целесообразны следующие преобразования:

(17) ⇔ [(x+1)(x+4)][(x+2)(x+3)]=120 ⇔

⇔ (х²+5х+4)(х²+5х+6)=120

Теперь уже нет сомнений, что разумна подстановка: t=x²+5x+4.

При этом получим:

t(t+2)-120=0 ⇔ t²+2t-120=0 ⇔ t=-12 ∨ t=10

Таким образом,

(17) ⇔ х² +5х+4=-12 ∨ х²+5х+4=10

х² +5х +16=0 ∨ х² 5х-6=0 ⇔ х∊Ø ∨ (х=-6 ∨ х=1) , х=-6 ∨ х=1

Ответ: {-6; 1}


3.Практическая часть работы.


1. x³+x²+x=-

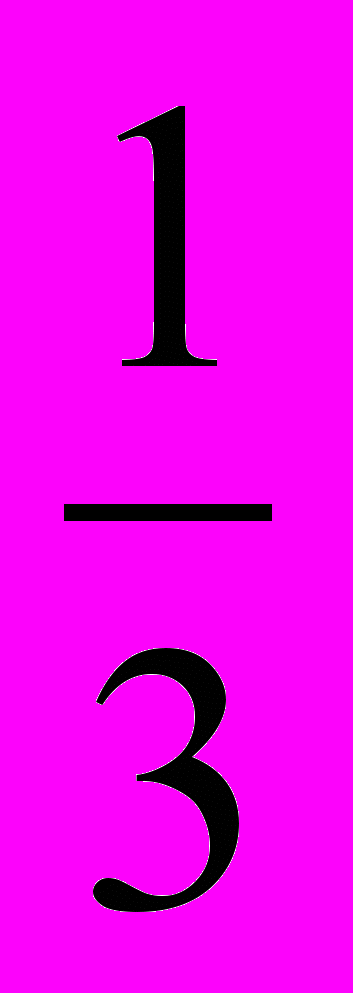
3x³+3x²+3x+1=0

x³+x²+3x+1=-2x³

(x+1)³=-2x³


x+1=-х∛2

Ответ: -

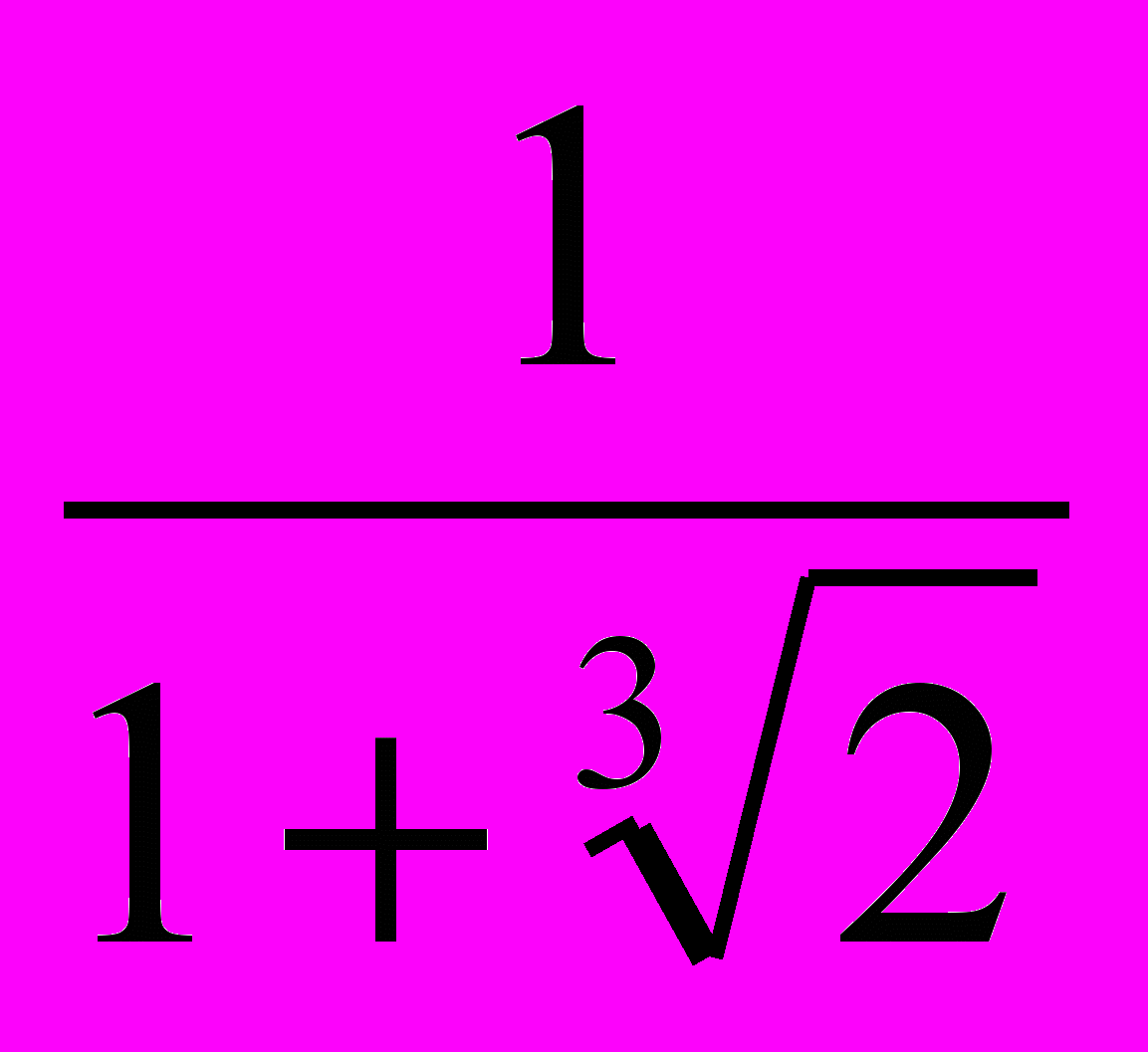
2. x-2x²-12x-8=0

x-2x²-12x-8= x+2x²+1-4x²-12x-9= (x²+1)² –(2x+3)²=

( x²+1-2x-3)( x²+1+2x+3) . x²-2x-2=0 (1) ∨ x²+2x+4=0 (2)

Решим (1). Решим (2).

x²-2x-2=0 x²+2x+4=0

D1=3 D<0, корней нет.

x12=1±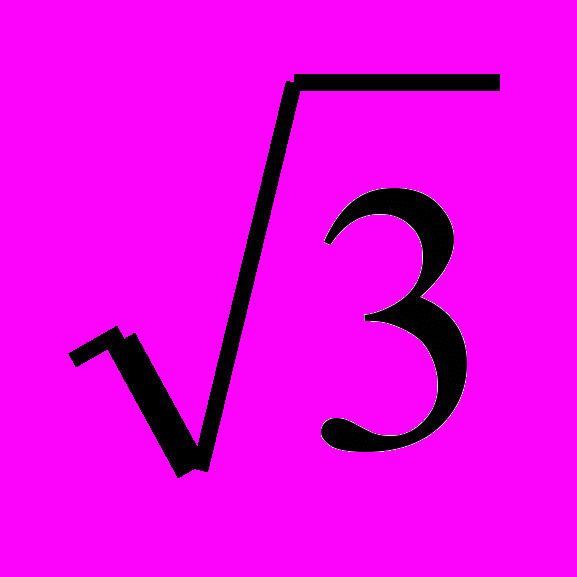↔ x1=1+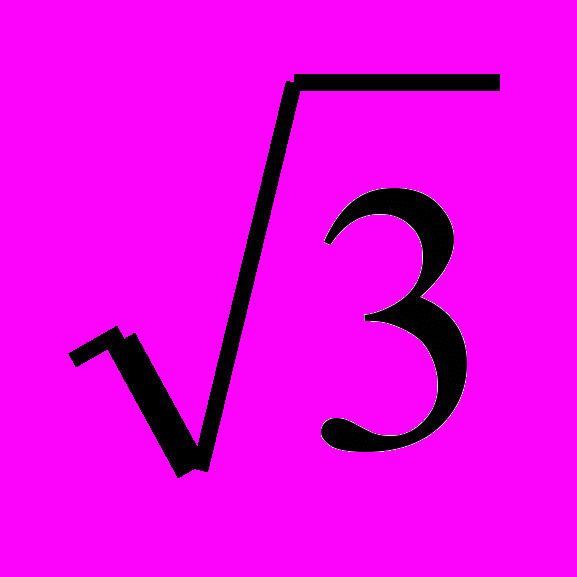; x2=1-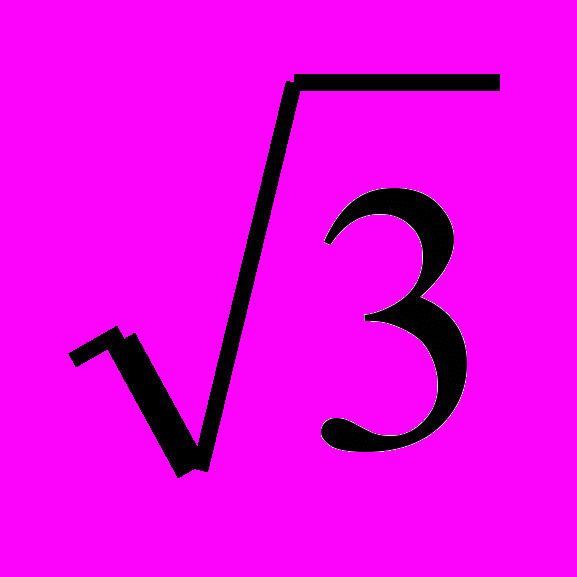

Ответ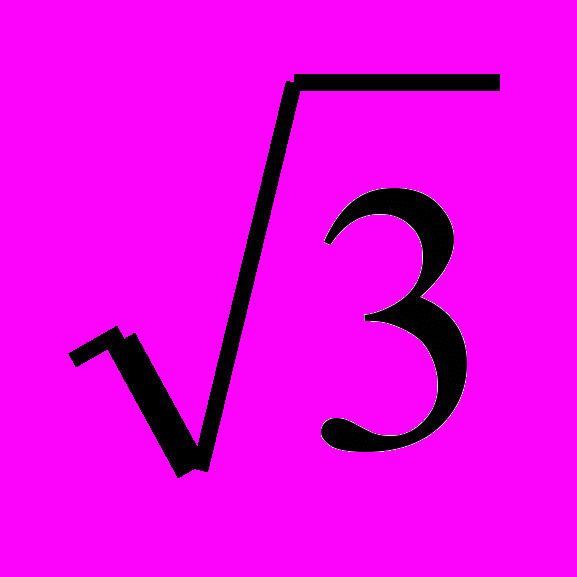: 1+; 1-.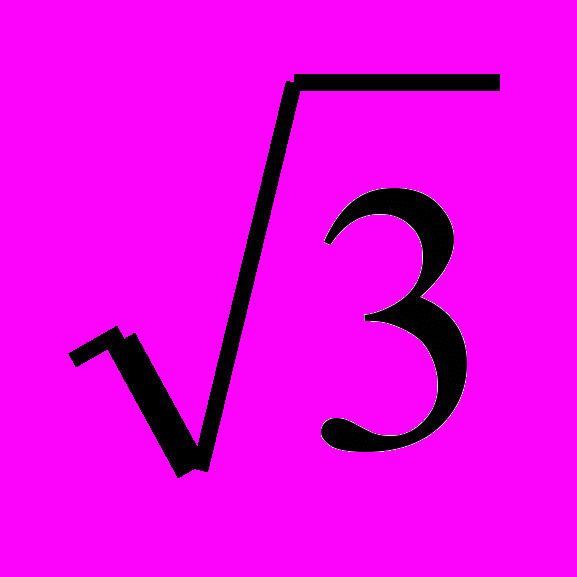

3. x-2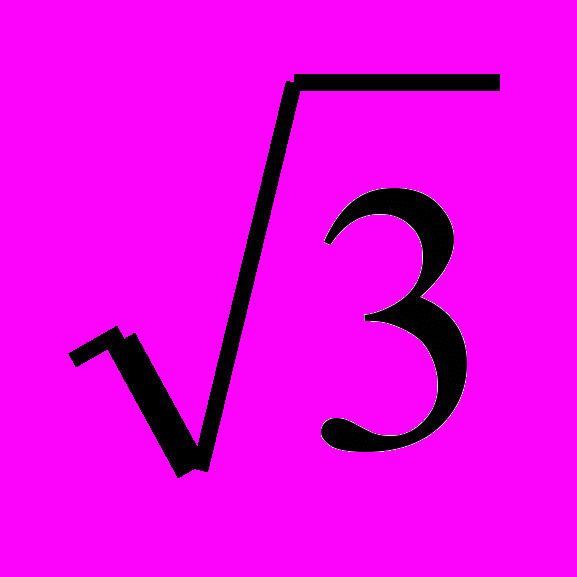x²-x+3-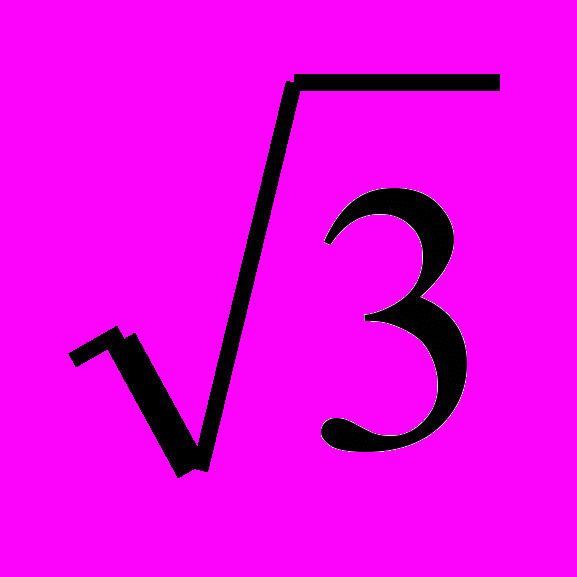-=0

Пусть a=,

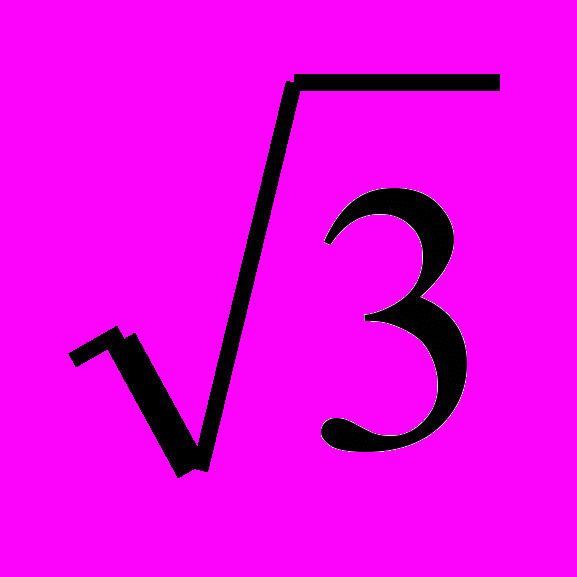x-2ax²-x+a²-a=0

x-2ax²-x+a²-a=( -x²+x+a)( -x²-x+a-a)

Поскольку a=,

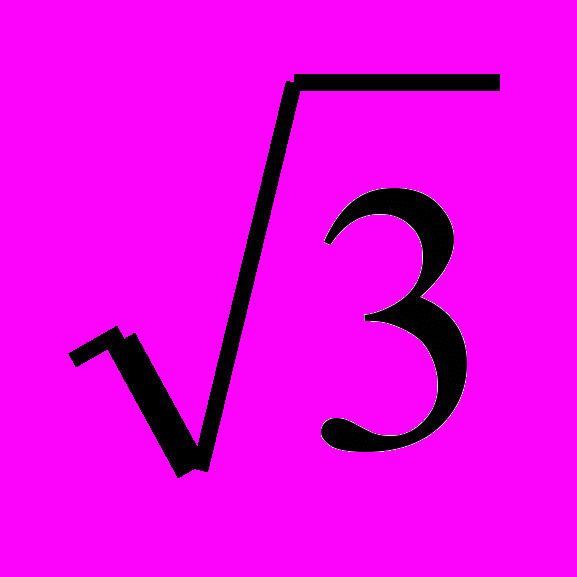x-2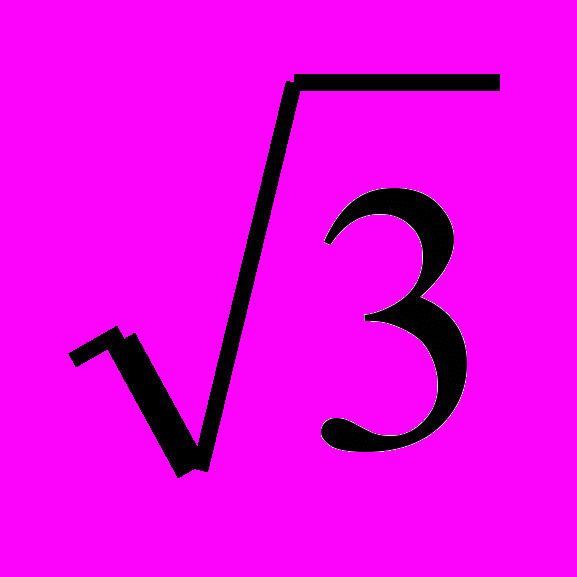x²-x+3-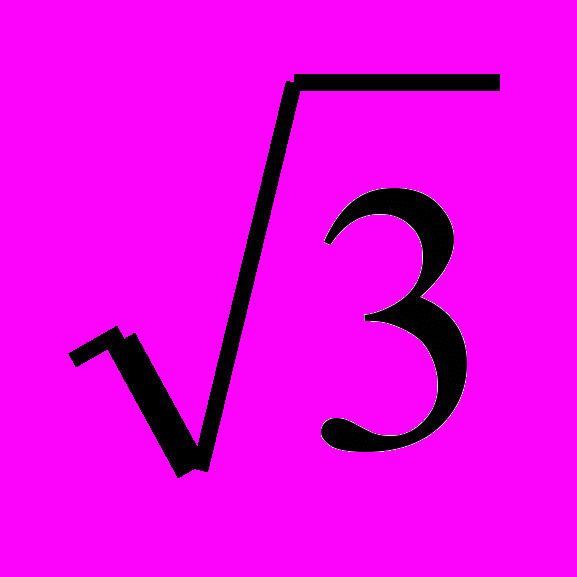=(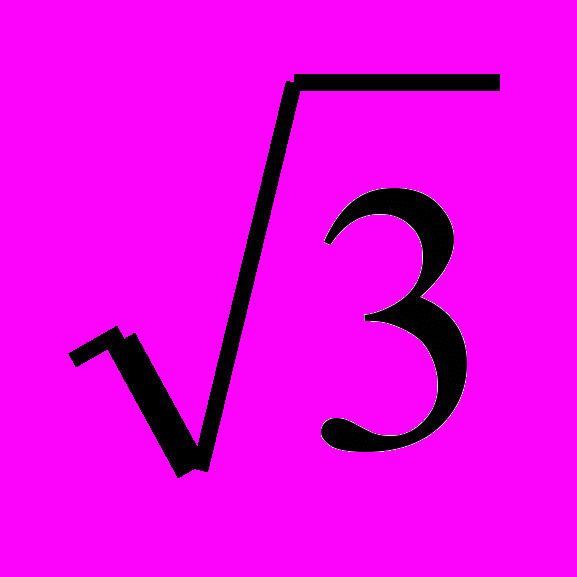-x²+x)(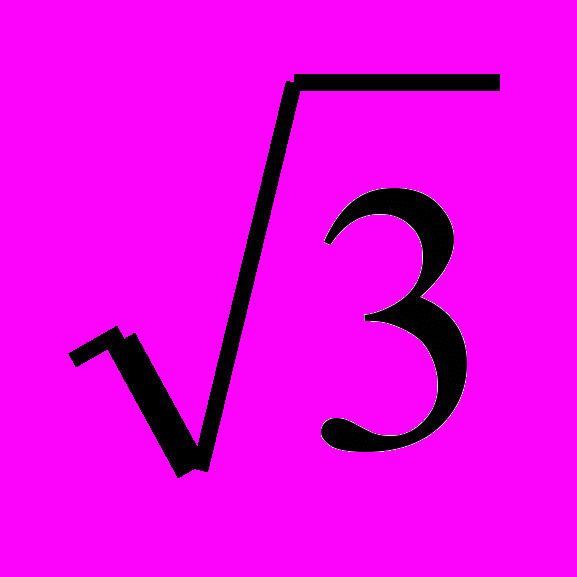-x²-x-1)

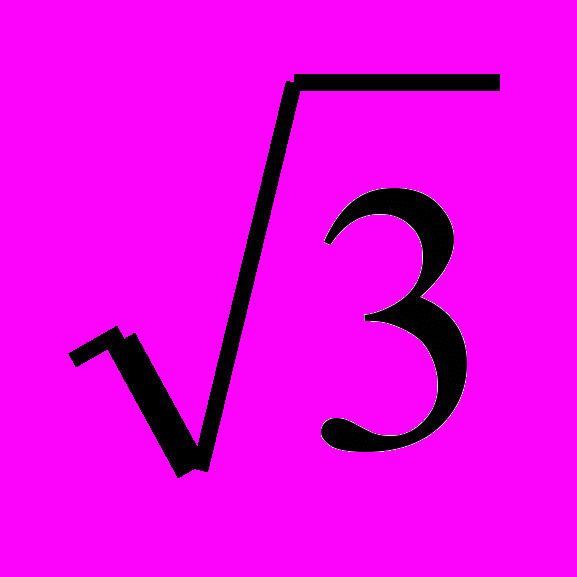-x²+x=0 ∨ 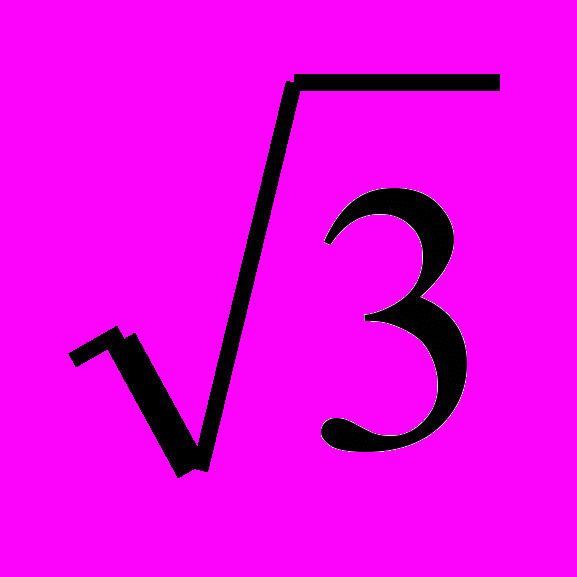-x²-x-1=0

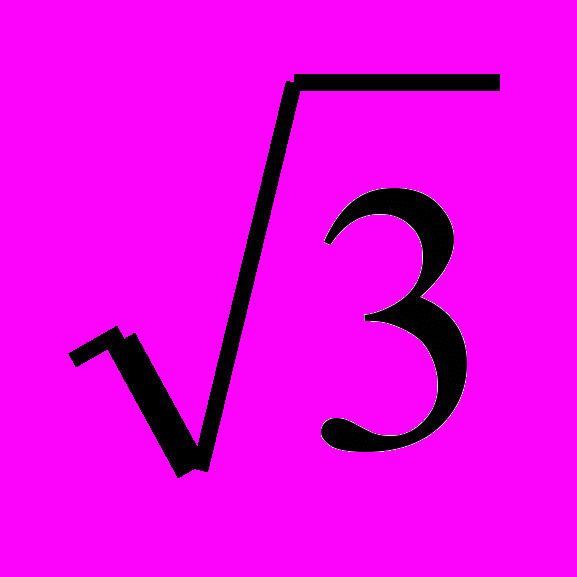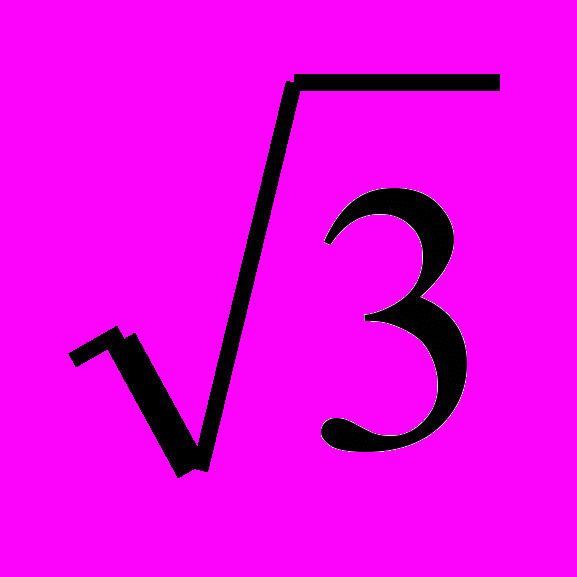D=1+4 D=4-3

x12=1± 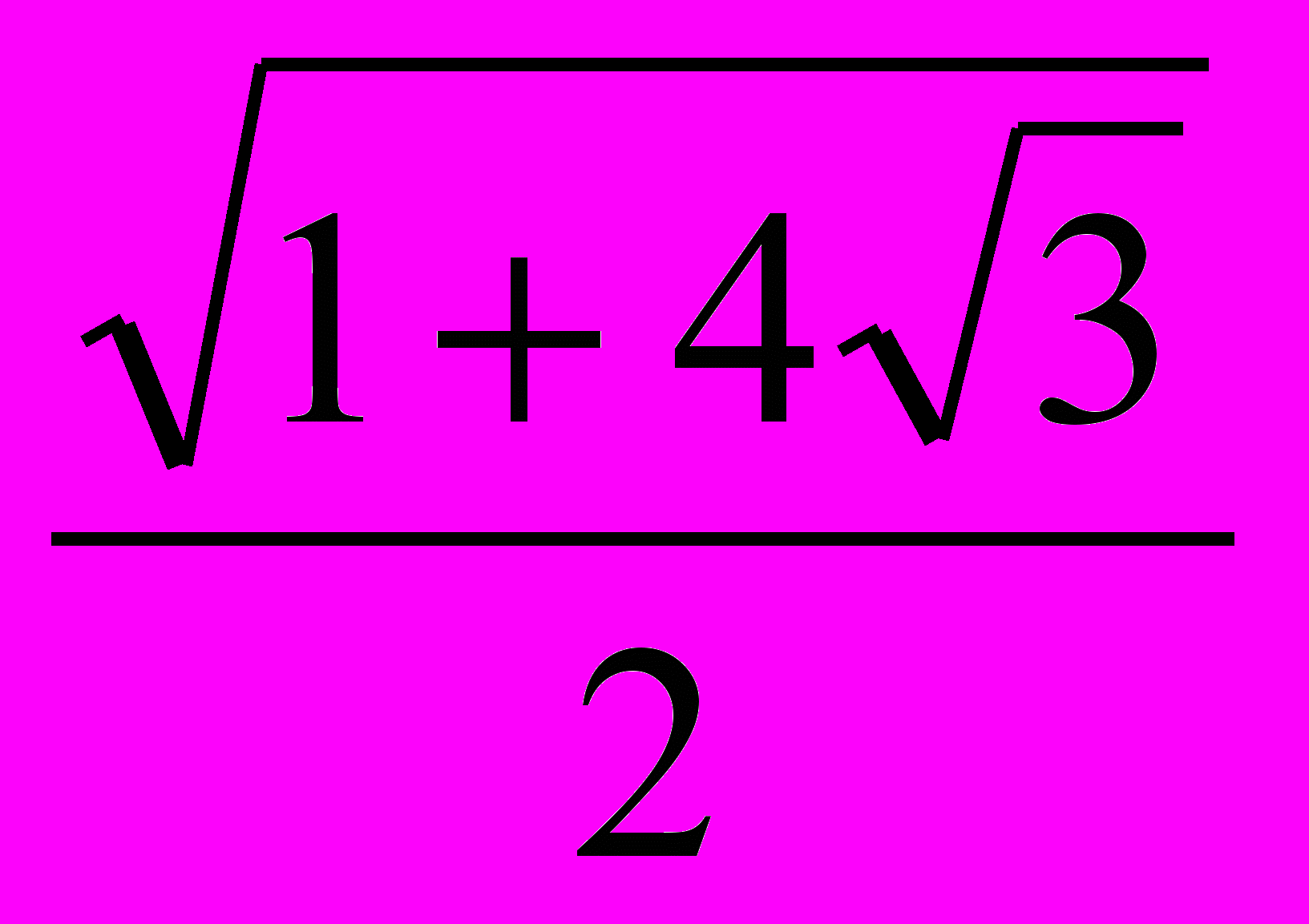x12=-1±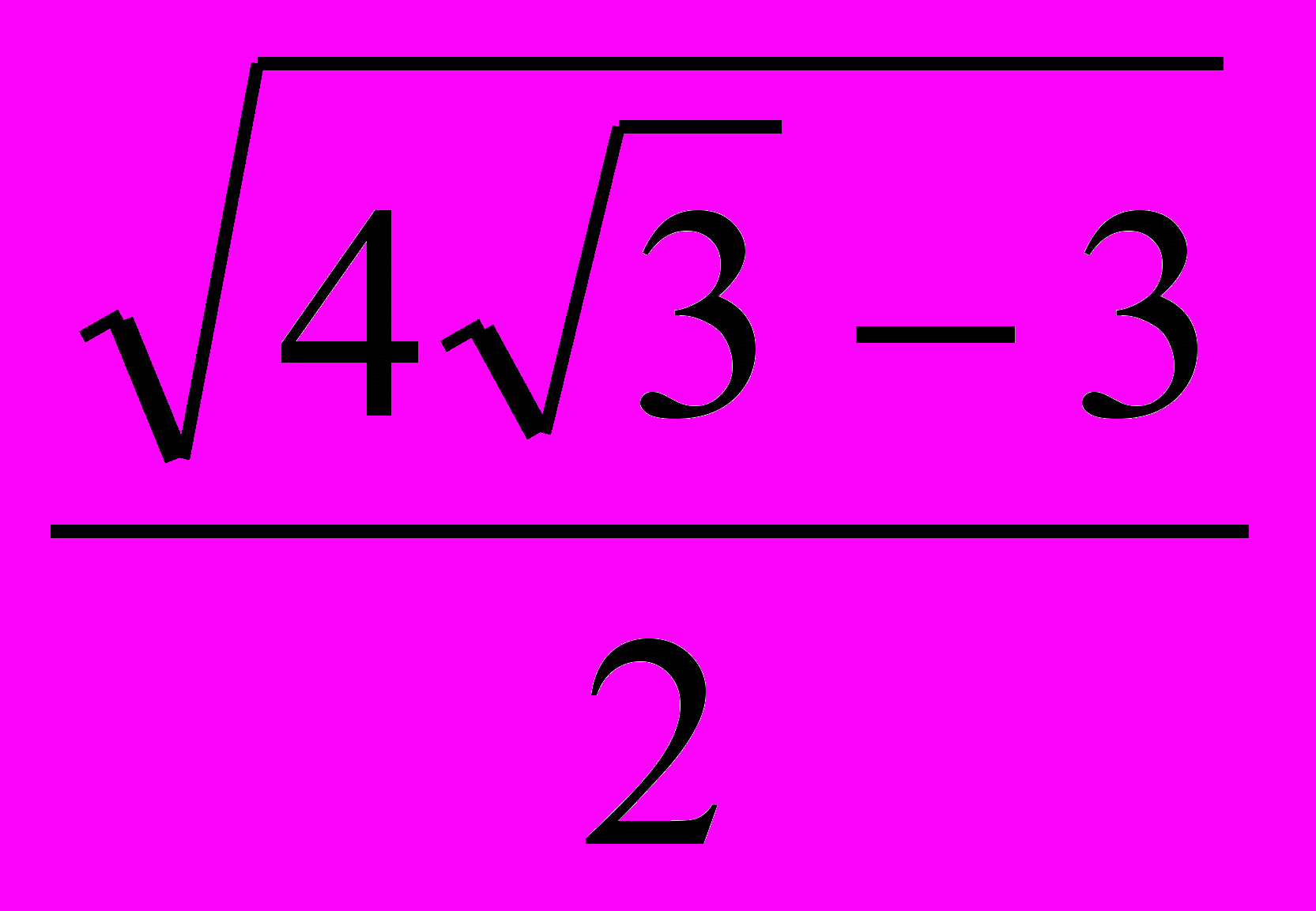

Ответ:x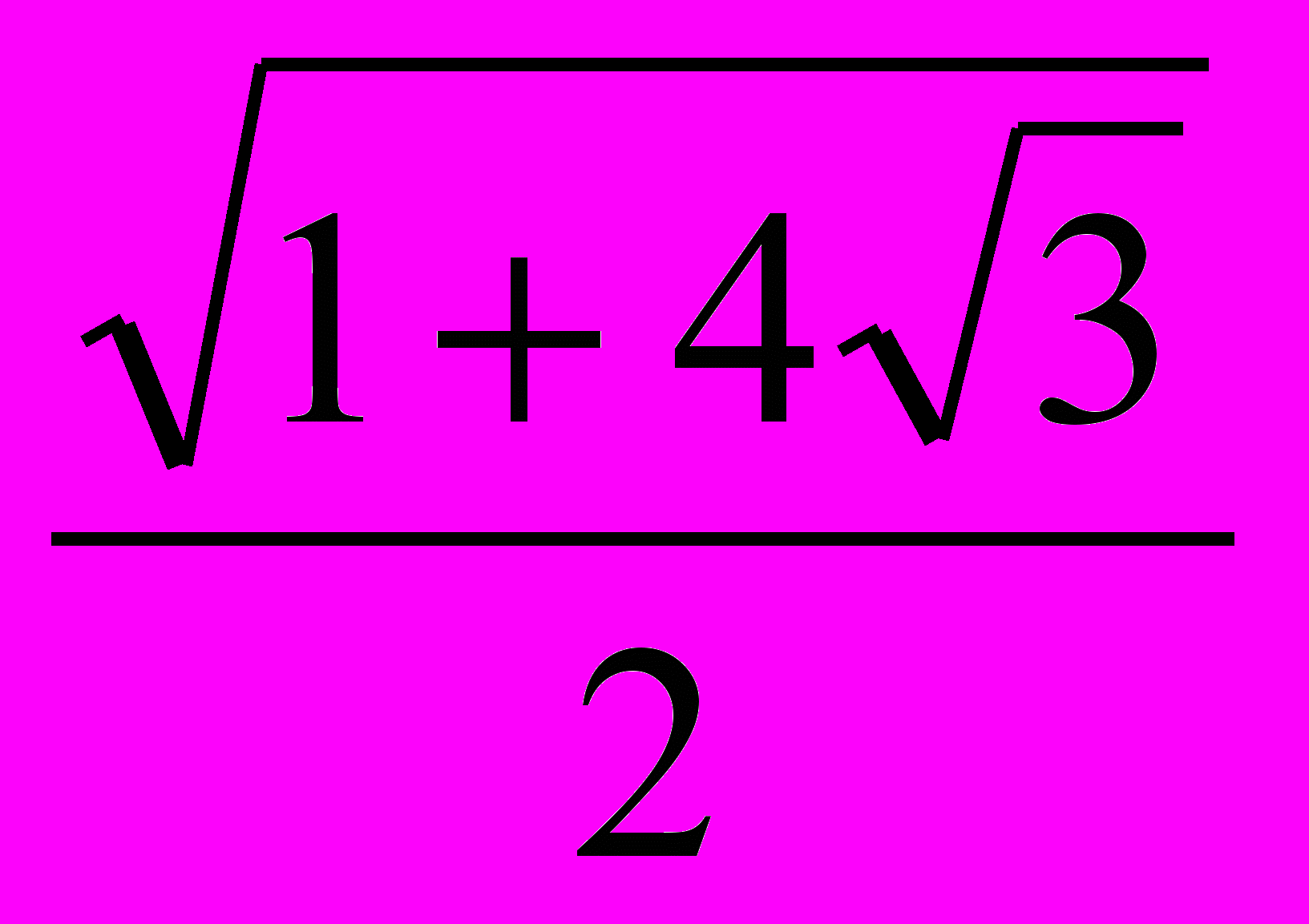=1±;-1±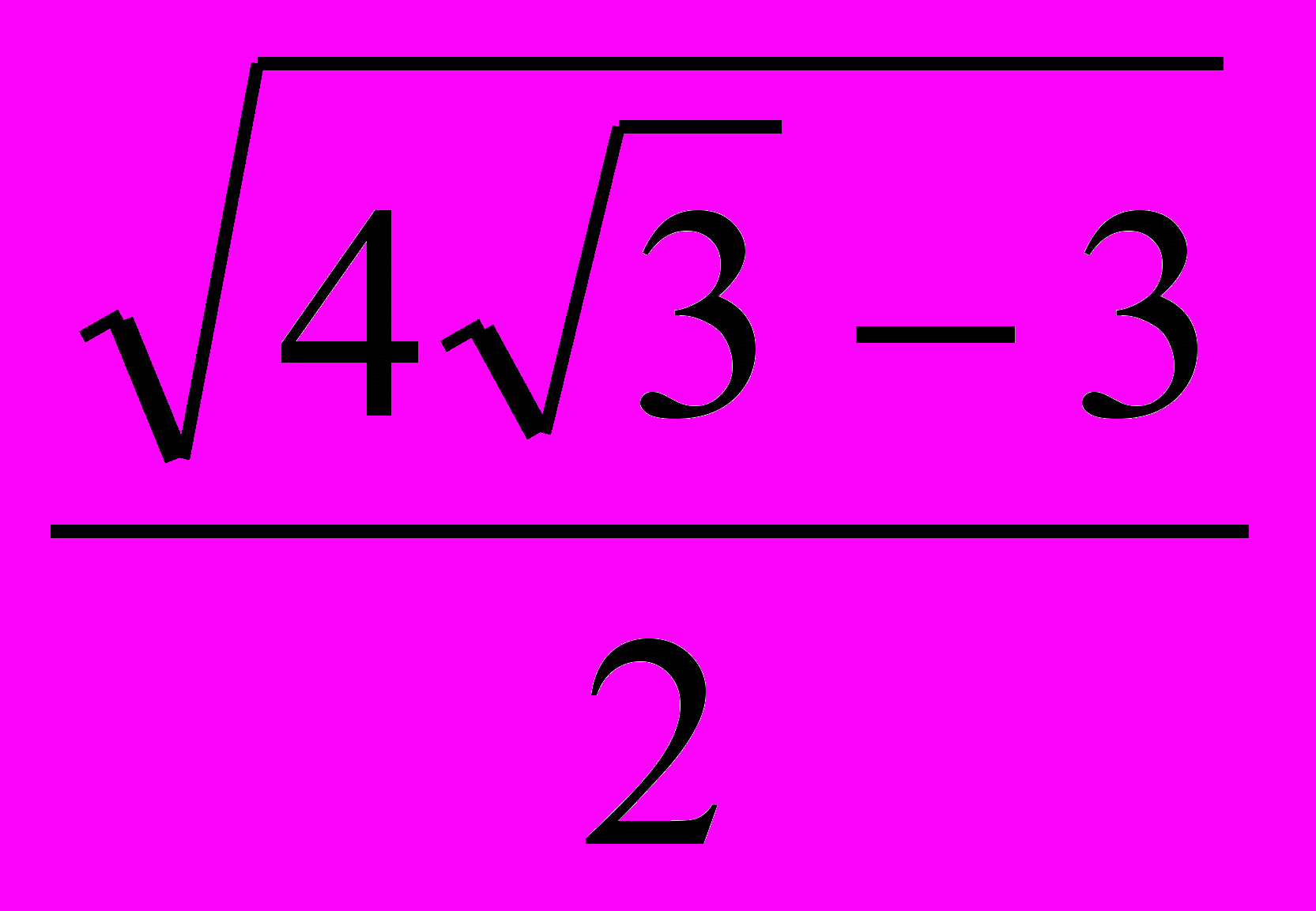

4. 3x³+4x²+4x+3=0

3x³+4x²+4x+3=3(x³+1)+4x(x+1)=(x+1)(3x³-3x+3+4x).

(x+1)(3x³+x+3)=0

x+1=0 ∨ 3x²+x+3=0

x=-1 D<0, корней нет.

Ответ: -1.


5. x-5x³+8x²-5x+1=0

Т.к. x=0 не корень,

x-5x³+8x²-5x+1=0| :x²

-5x+8+ x²-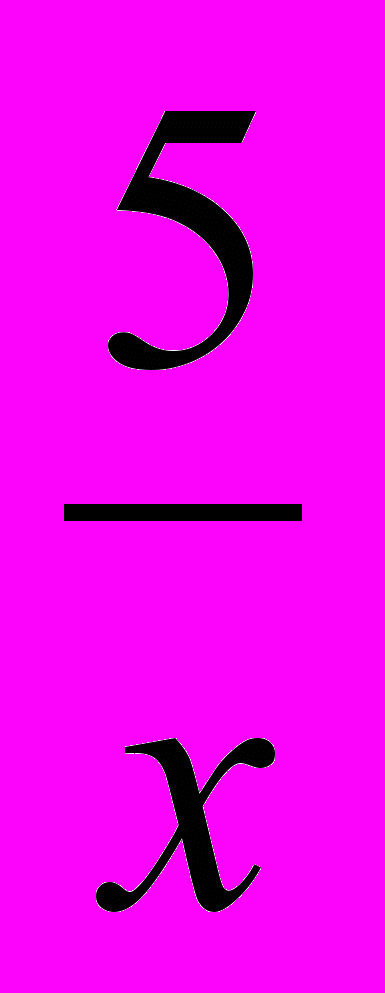+(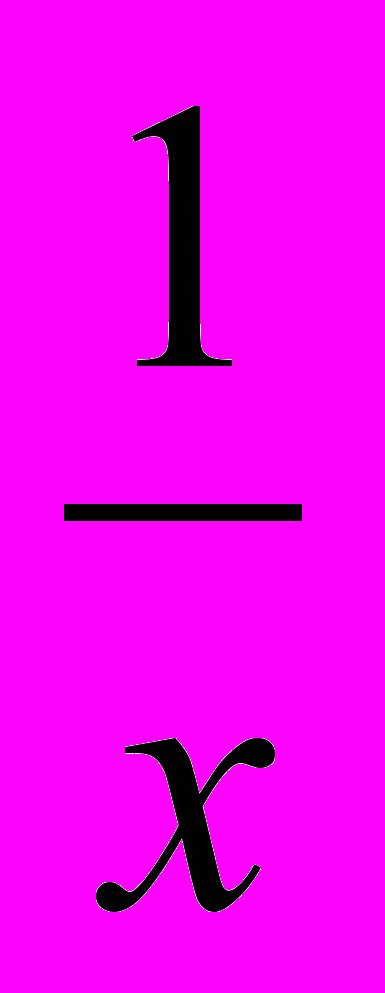)2=0

+ x²-5(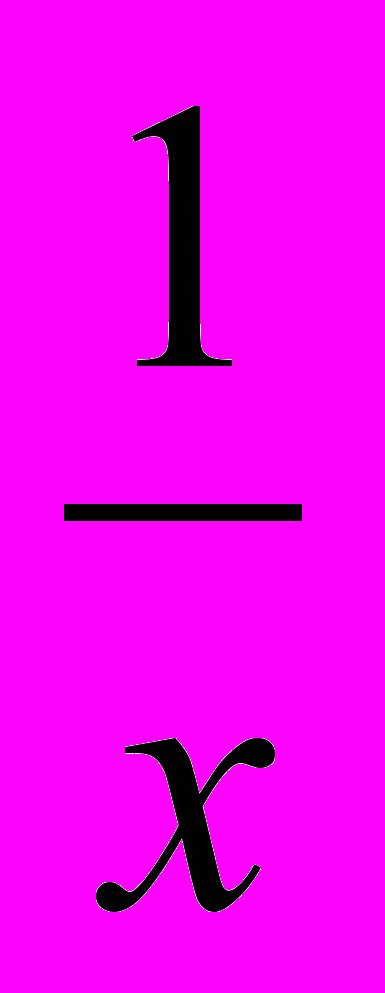+x)+8 +(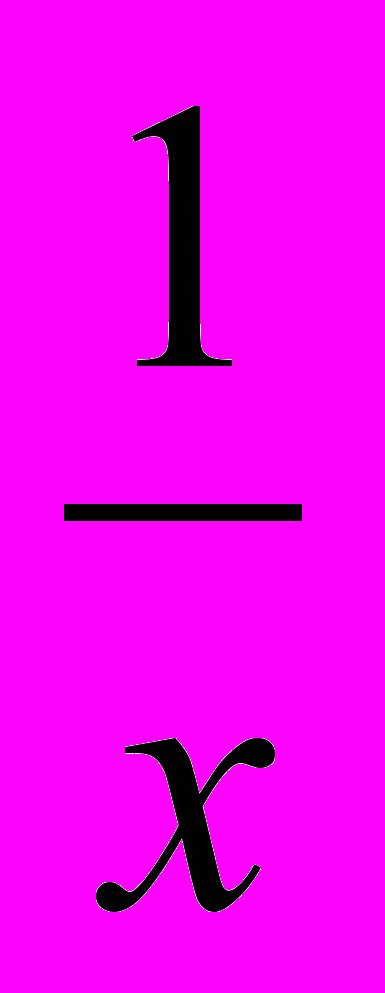)2=0

(x+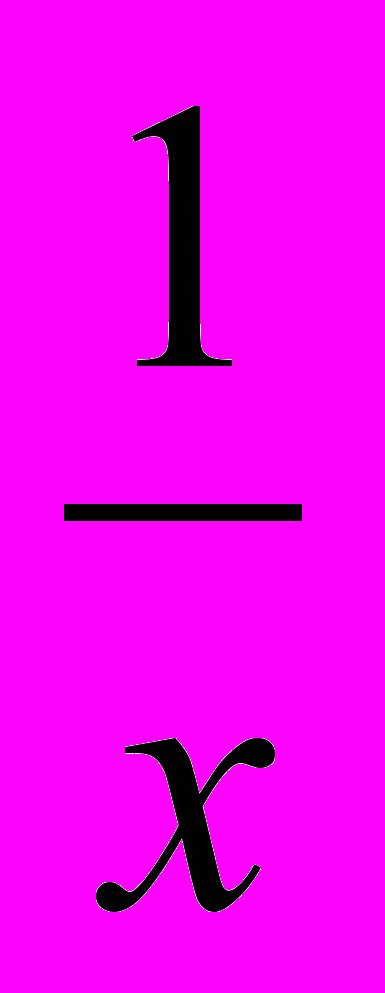)²-5(x+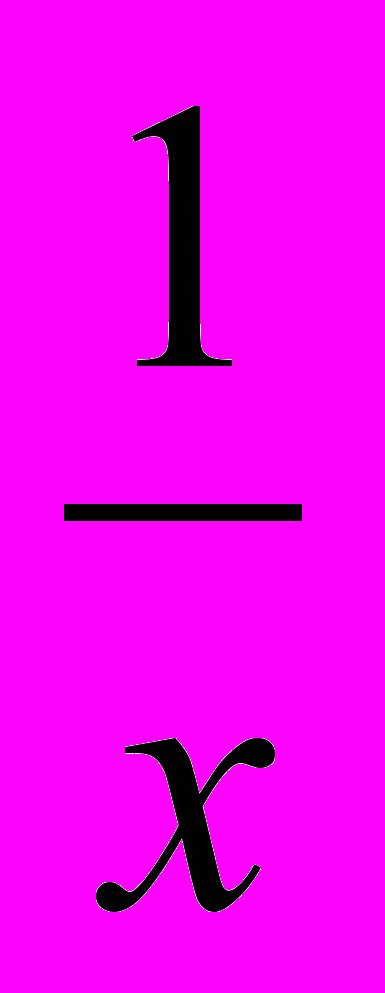)+6=0

Введём новую переменную x+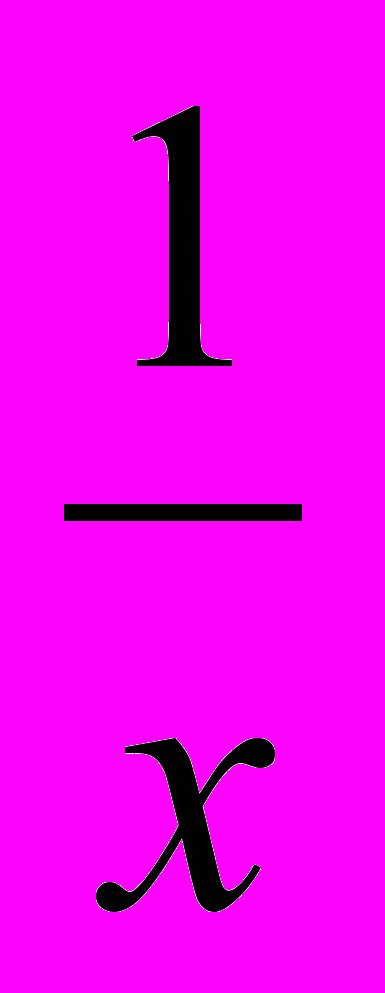=m

m²-5m+6=0

D=25-24=1

m12= 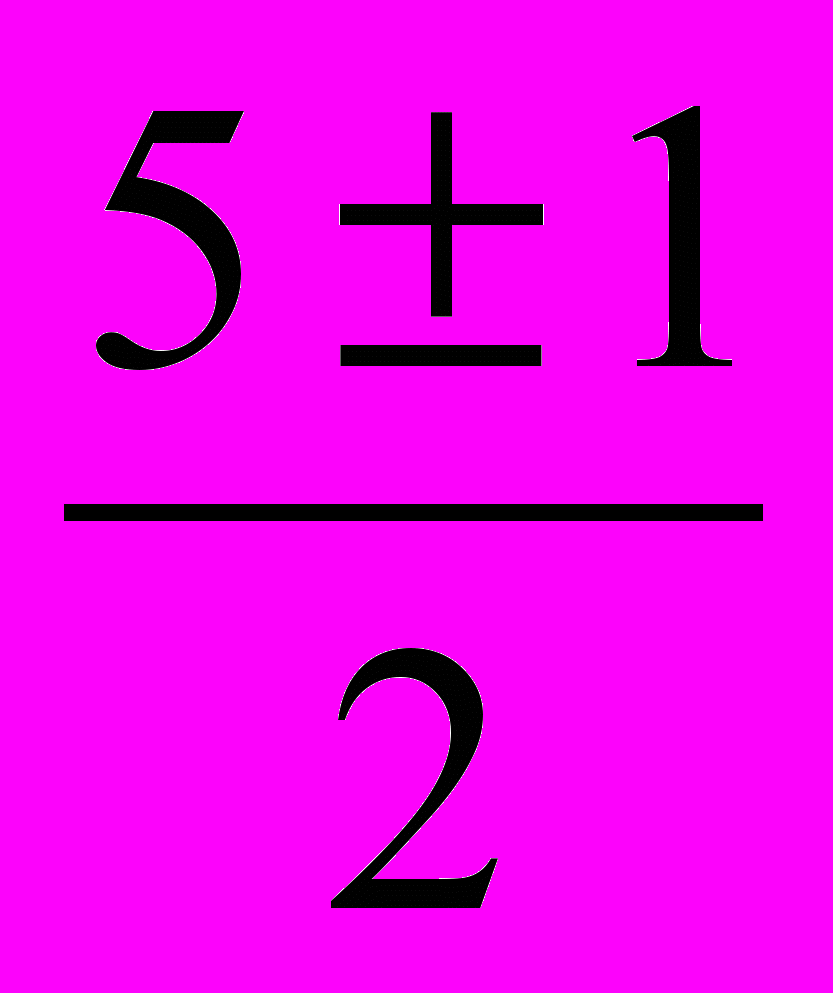, m1=3, m2=2

x+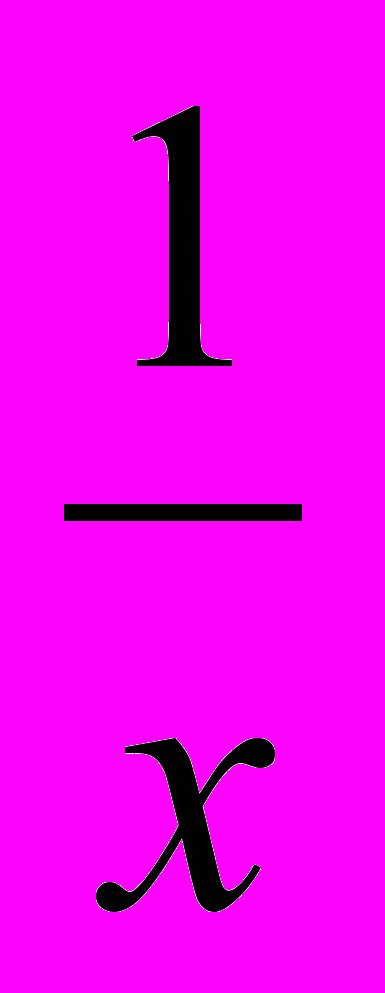=3 (1) ∨ x+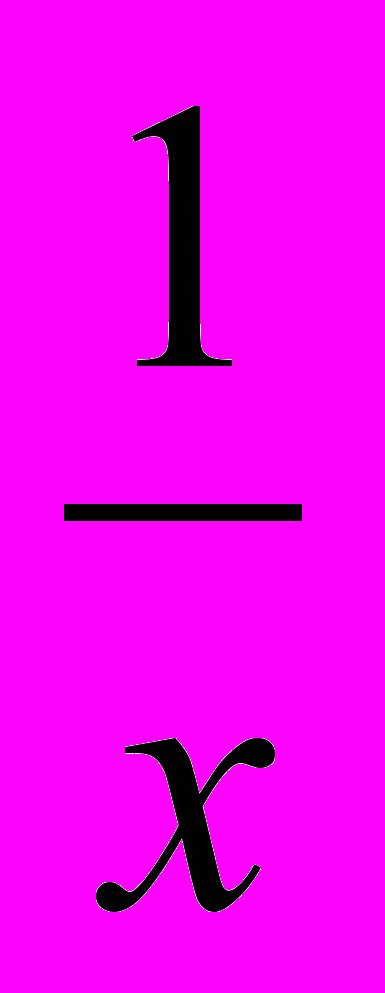=2 (2)

Решим уравнение (1)

x²-3x+1=0 x²-2x+1=0

D=9-4=5 (x-1)²=0

x12= 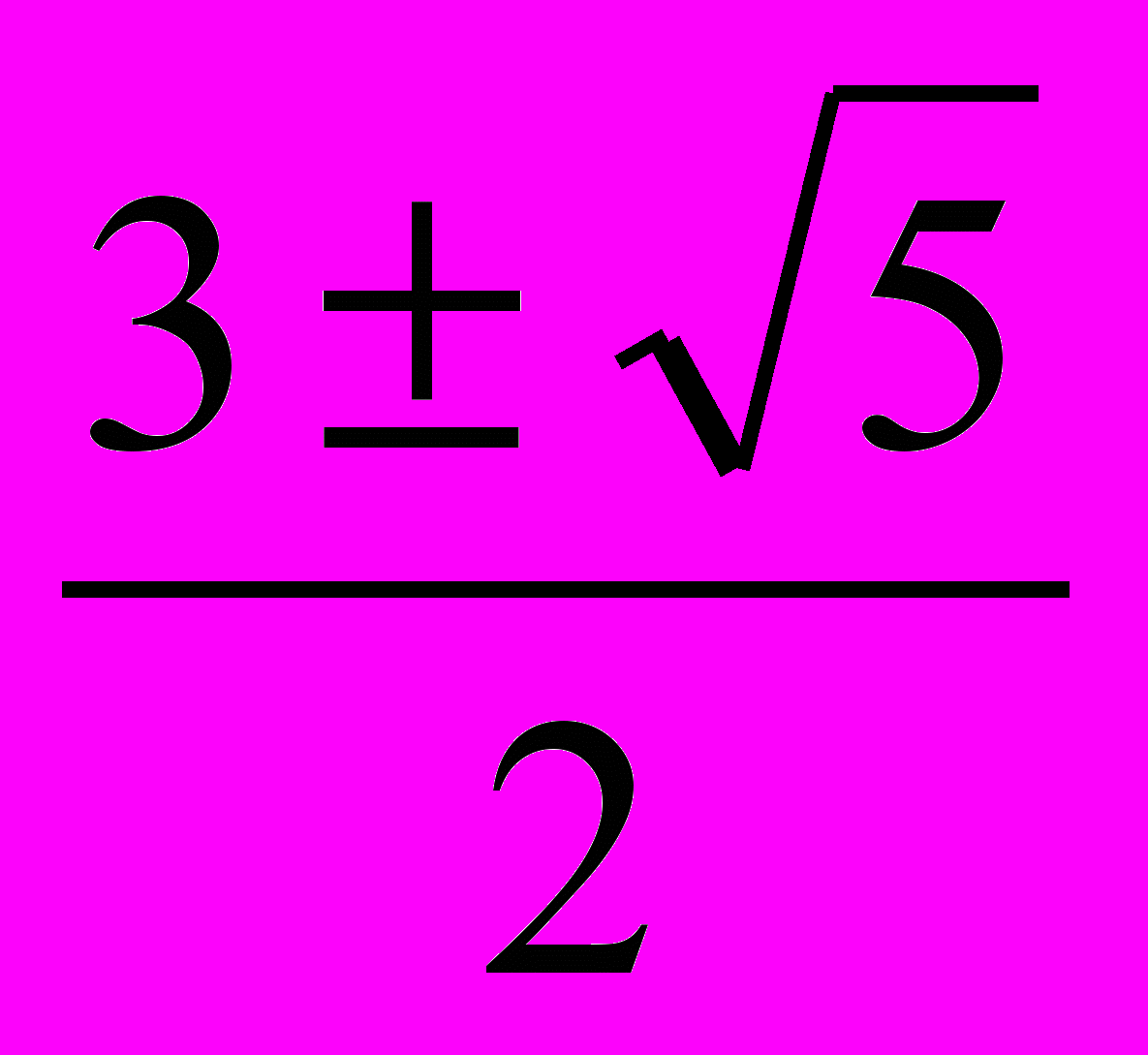x=1

Ответ:x=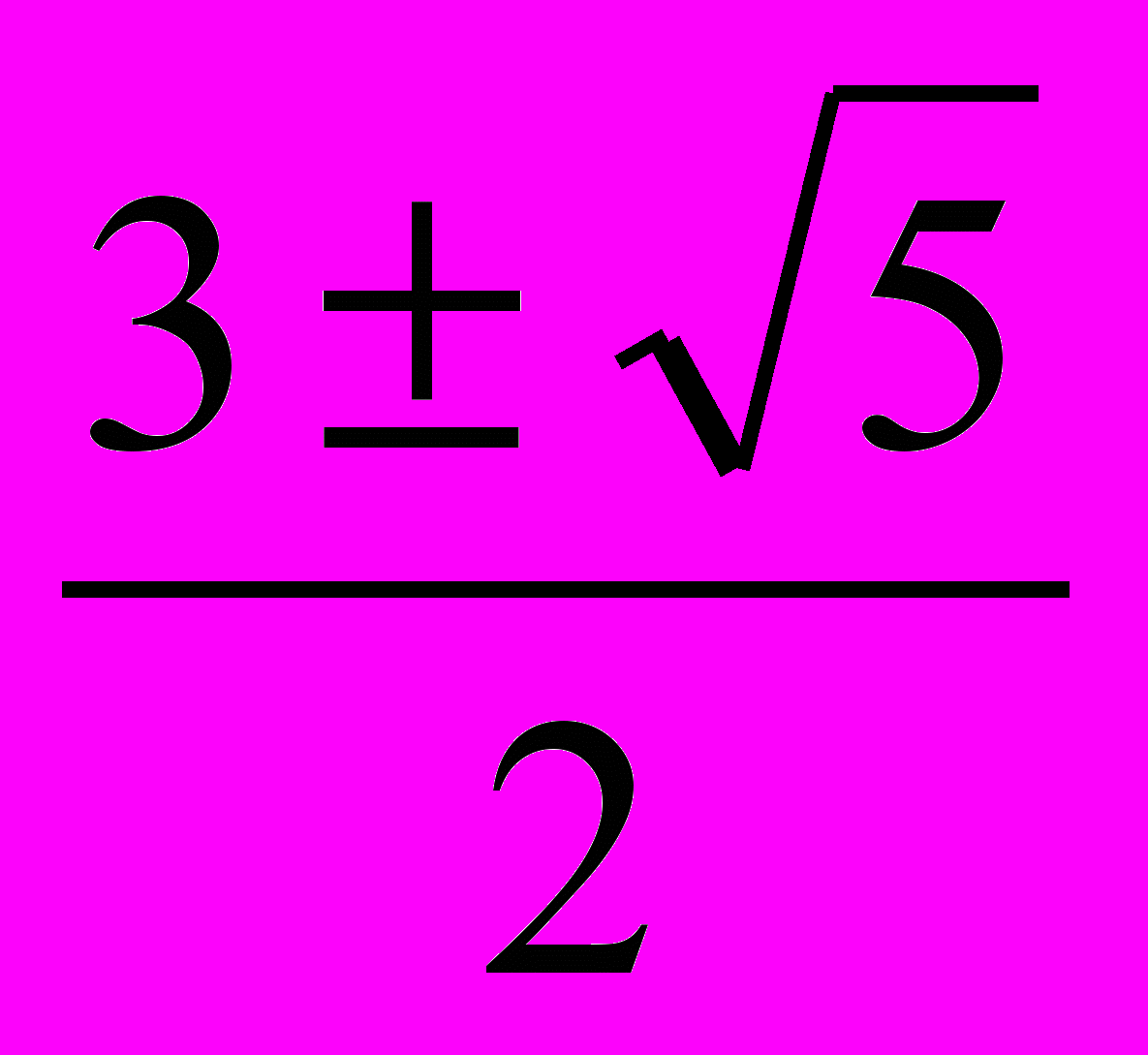;1.


6. x⁸-x⁶+x-x²+1=0

Умножим левую и правую части уравнения на многочлен x²+1, не имеющий корней, и:

(x+1)( x⁸-x⁶+x-x²+1)=0

x¹°-x⁸+x⁶-x+x²+ x⁸-x⁶+x-x²+1=0

x¹°+1=0

Нет решений

Ответ: нет решений.

7. 6x³-x²-20x+12=0

Умножим обе части уравнения на многочлен x+0.5, и

6x+2x³-20.5x²+2x+6=0 |:2x² ,т.к. х=0 не корень уравнения.

3x²+3/x²+x+1/x-41/4=0

Введём новую переменную:y=x+1/x

3y²+y-65/4=0

D=1+195=196

y12=(-1±14)/6∨y1=-2.5∨y2=13/6

x+1/x=-2.5 (1) ∨ x+1/x=13/6 (2)

Решим (1) Решим (2)

6x²-13x+6=0 2x²+5x+2=0

D=25 D=9

x12=(13±5)/12↔x1=1.5∨x2=2/3 x34=(-53)/4,x3=-2∨x4=-0.5

x=-0.5 –посторонний корень.

Ответ: x=1.5;2/3;-0.5.

8. (6x+7)²(3x+4)(x+1)=1 | ∙12

Введём новую переменную 6x+6=z, следовательно

(z+1)²(z+2)z=12

(z+1)²(z²+2z)=12

Введём новую переменную z²+2z=u

(u+1)u=0

u²+u-12=0

D=49

u12=(-1±7)/2⇔u1=3∨u2=-4

z²+2z=3 (1) z²+2z=-4 (2)

Решим (1) Решим (2)

z²+2z-3=0 z²+2z+4=0

D1=4 D<0, нет решений.

z12=(-1±2)/1, z1=-3∨ z2=1

6x+6=-3 6x+6=1

6x=-9 6x=-5

x=-1.5 x=-5/6

Ответ:-1.5, -5/6.

9. (x²+x+2)( x²+2x+2)= 2x²

x=0 не корень

(x²+x+2)( x²+2x+2)= 2x² ∣ :x²

(x+1+2/x)( x+2+2/x)= 2

Введём новую переменную m=x+2/x

(m+1)(m+2)=2

m²+2m+m+2= 0

m(m+3)=0

m=0;-3

x+2/x=0 x+2/x=-3

x²=-2, нет решения x²+3x+2=0

D=1

x12=(-3±1)/2 , x1=-2∨ x2=-1

Ответ: =-2;-1.

10. 3(x²+2x-1) ²-2(x²+3x-1)²+ 5x²=0

x=0 не корень

3(x²+2x-1) ²-2(x²+3x-1)²+ 5x²=0 |:x²

3(x+2-1/x)²-2(x+3-1/x)²+5=0

Введём новую переменную x-1/x=y,

3(y+2)²-2(y+3)²+5=0

3y²+12y+12-2y²-12y-18+5=0

y²-1=0

y=±1 ⇔ x-1/x=1 ∨ x-1/x=-1

x²-x-1=0 x²+x-1=0

D=5 D=5

x12=(1±√5) x34=(-1±√5)/2

Ответ: (1±√5)/2; (-1±√5)/2.

11. 1/x+1/(x+1)+1/(x+2)+1/(x+3)+1/(x+4)=0

( 1/x+ 1/(x+4))+( 1/(x+1)+ 1/(x+3))+1(x+2)=0

2(x+2)/( x²+4x)+ 2(x+2)/( x²+4x+3)+1(x+2)=0

x=-2 не корень , →

2(x+2)/( x²+4x)+ 2(x+2)/( x²+4x+3)+1(x+2)=0 |:2(x+2)

1/( x²+4x)+ 1/( x²+4x+3)+1(x²+4x+4)=0


Введём новую переменную x²+4x=u

1/u+1/(u+3)+1/2(u+4)=0

(5u²+25u+24)/2u(u+3)(u+4)=0

5u²+25u+24=0

D=145

u12=(-25±√145)/10⇔ u1=(-25+√145)/10 (1)∨ u2=(-25-√145)/10 (2)→

Решим(1) Решим (2)

x²+4x=(-25+√145)/10 x²+4x=(-25-√145)/10

D1=(15+145)/10 D1=(15-145)/10

x12=-2±√(15+145)/10 x1,2=-2±√(15-145)/10

Ответ: -2±√(15+145)/10 ; -2±√(15-145)/10.

12.

(x+4)/(x-1) +(x-4)/(x+1)-(x+8)/(x-2)-(x-8)/(x+2)=-8/3

1+5/(x-1)+1-5(x+1)=1+10/(x-2)+1-10/(x+2)-8/3

(5/(x-1)-5/(x+1))=(10/(x-2)-10/(x+2))-8/3

10/(x²-1)-40/(x²-4)+8/3=0

Введём новую переменную x²=u,

10/(u-1)-40/(u-4)+8/3=0

(4u-65u+16)/(u-1)(u-4)=0 ОДЗ:u≠1;4

4u²-65u+16=0

D=3969

u12=(65±63)/8⇔ u1=16 ∨ u2=1/4

x²=16 x²=1/4

x=±4 x=±1/2

Ответ: ±4; ±1/2.

13. 4x/(4x²-8x+7)+3x/(4x²-10x+7)=1

x=0 не корень ,

4x/(4x²-8x+7)+3x/(4x²-10x+7)=1 |:x

4/(4x-8+7/x)+3/(4x-10+7/x)=1

Введём новую переменную 4x+7/x=y,

4/(y-8)+3/(y-10)=1

4y-40+3y-24=y²-10y-8y+80

y²-25y+144=0

D=49

y12=(25±7)/2⇔y1=16 ∨ y2=9

4x+7/x=16 4x+7/x=9

4x²-16x+7=0 4x²-9x+7=0

D=36 D=81-112<0, корней нет

x12=(8±6)/4⇔ x1=3,5∨x2=0,5

Ответ: 3,5;0,5.