Geum.ru

Методическое сопровождение: дидактические материалы для учащихся Ход мастер-класса I

Вид материалаДокументы
Подобный материал:
Муниципальное общеобразовательное учреждение Судиславская средняя общеобразовательная школа Судиславского муниципального района Костромской области


Выступление на районном методическом объединении учителей математики по теме


«Решение алгебраических уравнений высших степеней»


Провела учитель математики Зайцева Татьяна Евгеньевна


ноябрь 2009


Место и время проведения : Районный методический кабинет

Ноябрь 2009 года


Цель проведения: представление опыта работы в профильных классах

Методическое сопровождение: дидактические материалы для учащихся


Ход мастер-класса

I Вступительное слово учителя о месте темы «Алгебраические уравнения высших степеней в курсе алгебры и начал анализа»

В 2008-2009 и 2009-2010 учебных годах мне довелось работать в старших класса, обучающихся по технологическому профилю. Этот профиль предполагает 4 часа алгебры и начал анализа в 10 и 11 классе. Сейчас я работаю в двух одиннадцатых классах с таким профилем. Обучение ведётся по учебнику А.Г.Мордковича «Алгебра и начала математического анализа» для 11 кл. с профильным обучением. В содержание учебного материала добавлена дополнительная глава «Многочлены от одной и нескольких переменных. Решение уравнений высших степеней» С этой темы и начинается обучение в 11 классе. Рассматриваются разные виды многочленов, способы разложения на множители (вспоминаются и даются новые), и как следствие этой темы осуществляется переход к решению уравнений. Такое начало учебного года оправдано тем, что позволяет учащимся начать процесс обучения с повторения алгебры 7-9 класса, восстановить в памяти известные понятия и алгоритмы.

Глава «Многочлены. »направлена на систематизацию знаний, с которыми ученик пришел из основной школы. Учащиеся вспоминают, как решаются квадратные и дробно-рациональные уравнения, в чем заключается замена переменной. Однако учащиеся не только будут повторять пройденный материал, но и изучать много нового: исследование квадратных уравнений, квадратные уравнения с параметром.

От линейных и квадратных уравнений учащиеся переходят к алгебраическим уравнениям общего вида Рn(x)=0, где Рn(x) многочлен степени n. В связи с этим вводятся понятия степени многочлена. Решение уравнений опирается на теорему Безу: если х1 – корень уравнения Рп (х)=0, то многочлен Рп (х) делится нацело на (х-х1).Эта теорема демонстрируется на конкретных примерах. Рассматривается способ нахождения целых корней алгебраического уравнения с целыми коэффициентами.

Среди уравнений, сводящихся к алгебраическим, рассматриваются возвратные, рациональные, однородные..

Умение решать алгебраические уравнения первой и второй степени входит в “прожиточный” минимум любого выпускника средней общеобразовательной школы. А как быть с уравнениями выше второй степени? Такие уравнения называются уравнениями высших степеней, изучение их в общем виде выходит за рамки программы средней школы. На самом деле для уравнений третьей и четвертой степени есть формулы корней (формулы Кордано и Феррари), выведенные итальянскими математиками в 1545 году, но в силу своей громоздкости эти формулы используют очень редко в школьной программе. После того, как были выведены формулы корней для уравнений третьей и четвёртой степени, на протяжении почти 300 лет, учёные-математики пытались вывести формулы для нахождения корней уравнений пятой степени и выше, но труды их оказались безуспешными. В 1826 году норвежский математик Абель доказал, что нельзя вывести формулы для решения уравнений пятой степени и выше. Но всё же есть хорошие уравнения, которые решаются различными методами и способами.

Сегодня мы рассмотрим некоторые способы.

Но начать нам стоит с разложения многочленов на множители, вспомнить основные способы.

II Учителям предлагается карточка с заданиями. И даётся время не работу.

Разложите многочлен на множители:
  1. х2-ху3+у2-х3у
  2. х2-3ху+2у2
  3. 5х2-8ху+3у2
  4. 4х2-у2-8х+4у
  5. 2х2-7ху+5у2-3х+3у

Решить уравнение:
  1. х4-4х3+4х2=(7х+1)2
  2. х3-3х2-х+3=0
  3. х3-2х2+х=(х2-2х+1)2
  4. х3-4х2+х+6=0
  5. 2х3+7х2+5х+1=0


III Затем идет разбор способов в решении заданий

  1. х2-ху3+у2-х3у=( х2+ у2)+( -ху3-х3у)= ( х2+ у2)-ху(х2+ у2)= ( х2+ у2)(1- ху) используется способ группировки
  2. х2-3ху+2у2= х2- ху-2ху+2у2=( х2- ху)+( -2ху+2у2)=х(х-у)-2у(х-у)=(х--у)(х-2у) также используется способ группировки
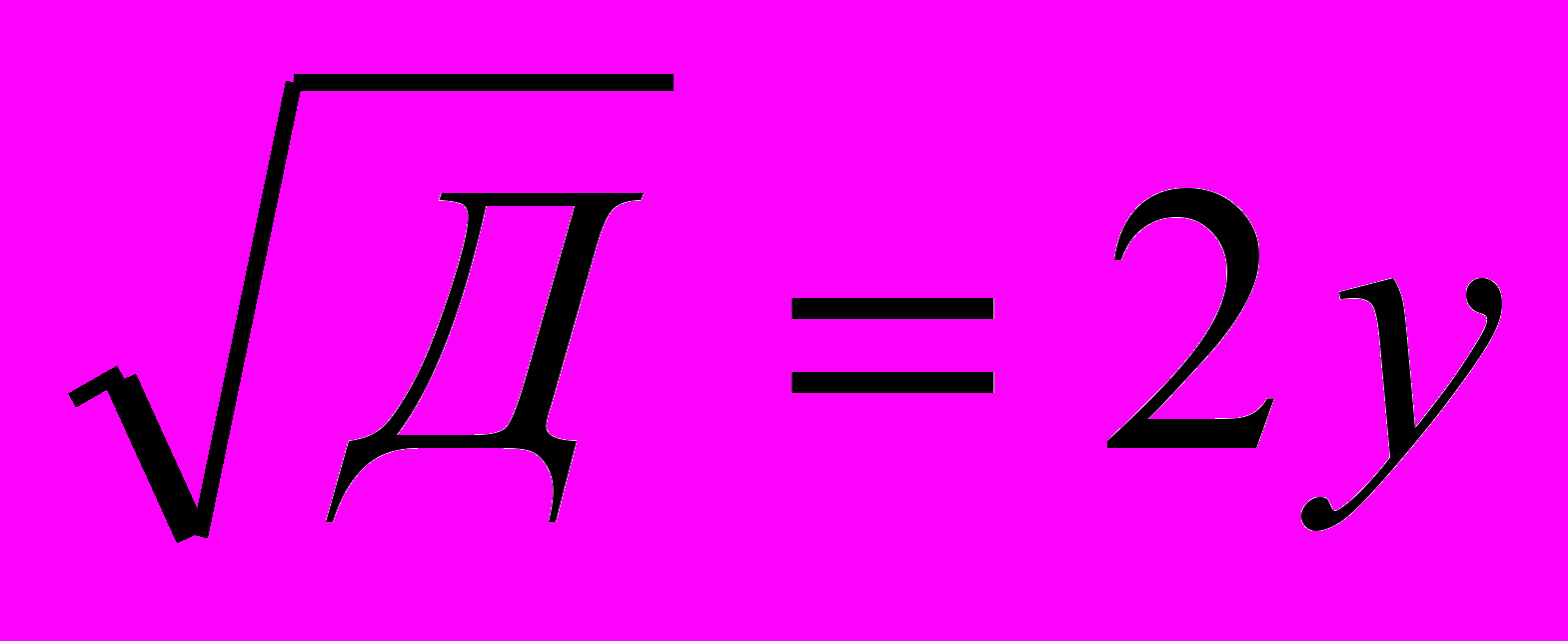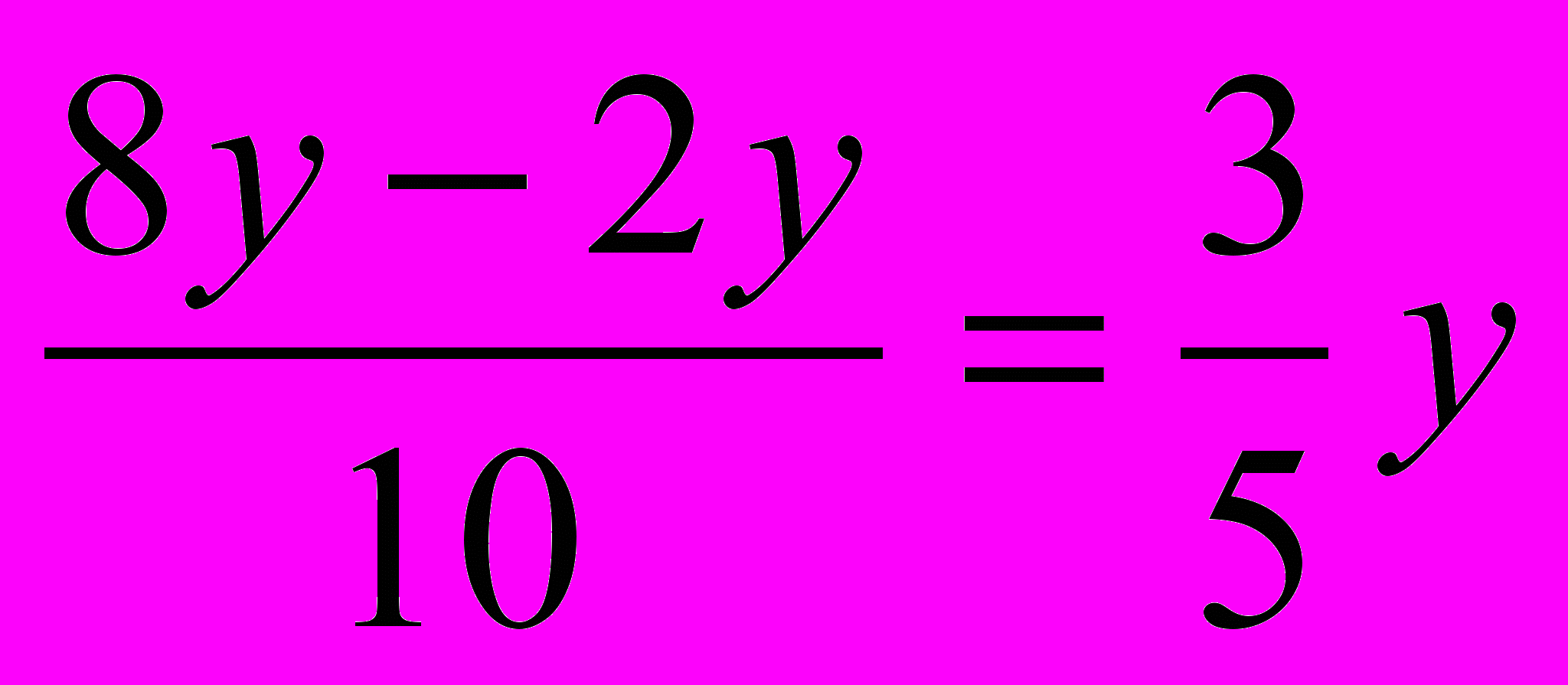  3. 5х2-8ху+3у2 применяем формулу разложения квадратного трёхчлена на множители. 5х2-8ху+3у2=0 и решаем уравнение относительно х. Д=(-8у)2-4·5·3у2 =64у2-60у2 =4у2 х1= х2= 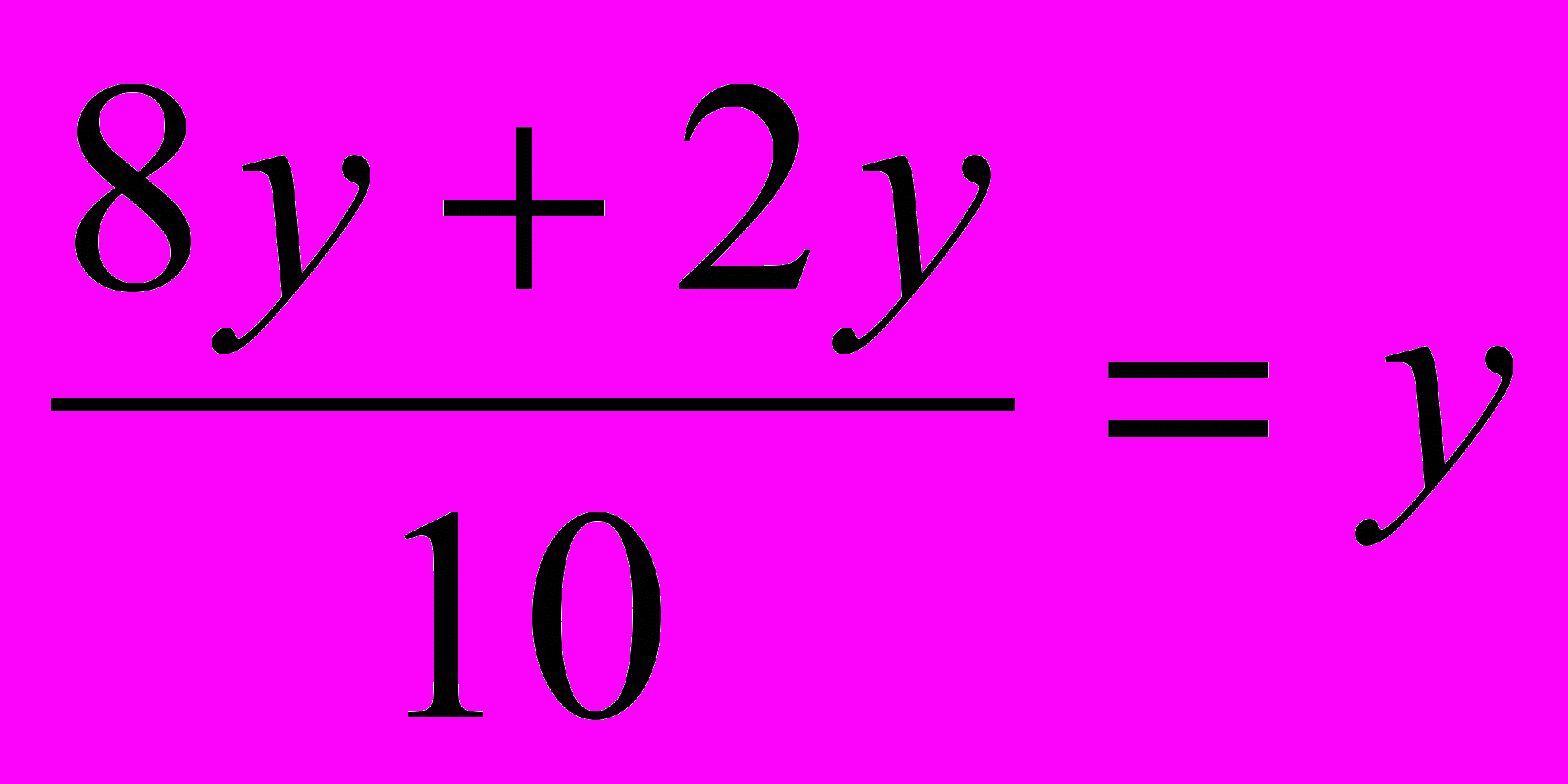Тогда 5х2-8ху+3у2=5(х-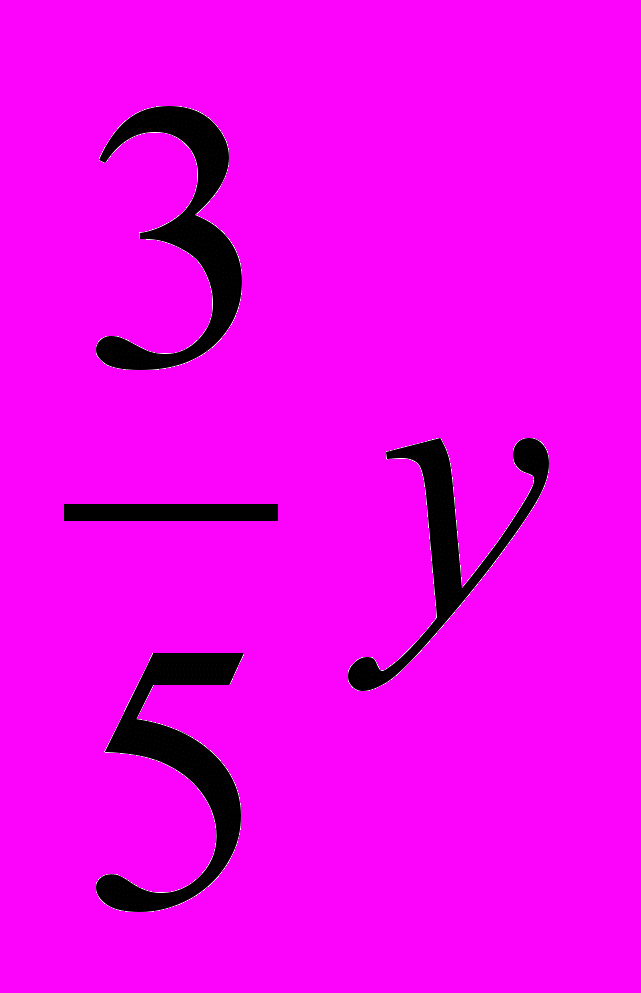)(х-у)=(5х-3у)(х-у)
  4. 4х2-у2-8х+4у=(4х2-у2)+(-8х+4у)=(2х-у)(2х+у)-4(2х-у)=(2х-у)(2х+у-4) Способ группировки, применяется формула разность квадратов
  5. 2х2-7ху+5у2-3х+3у=(х -у)(2х-5у)-3(х-у)=(х-у)(2х-5у-3)



Решаем уравнения
  1. х4-4х3+4х2=(7х+1)2; х2(х2-4х+4)=(7х+1)2; х2(х-2)2= (7х+1)2; х2(х-2)2--(7х+1)2=0; (х(х-2)- (7х+1)) (х(х-2)+ (7х+1))=0; (х2-2х-7х-1) (х2--2х+7х+1)=0; (х2-9х-1)( х2+5х+1)=0
  2. х3-3х2-х+3=0 ; (х3-3х2)+( -х+3)=0; х2(х-3)-(х-3)=0; (х-3)(х2-1)=0; (х-3)(х-1)(х+1)=0; х-3=0 или х-1=0 или х+1=0; х=3; х=1; х=-1
  3. х3-2х2+х=(х2-2х+1)2; х(х2-2х+1) =(х2-2х+1)2; х(х2-2х+1)- (х2-2х+1)2=0; (х2-2х+1)(х- х2+2х-1)=0; (х-1)2(- х2+3х-1)=0; (х-1)2=0 или - х2+3х-1=0; х=1; х=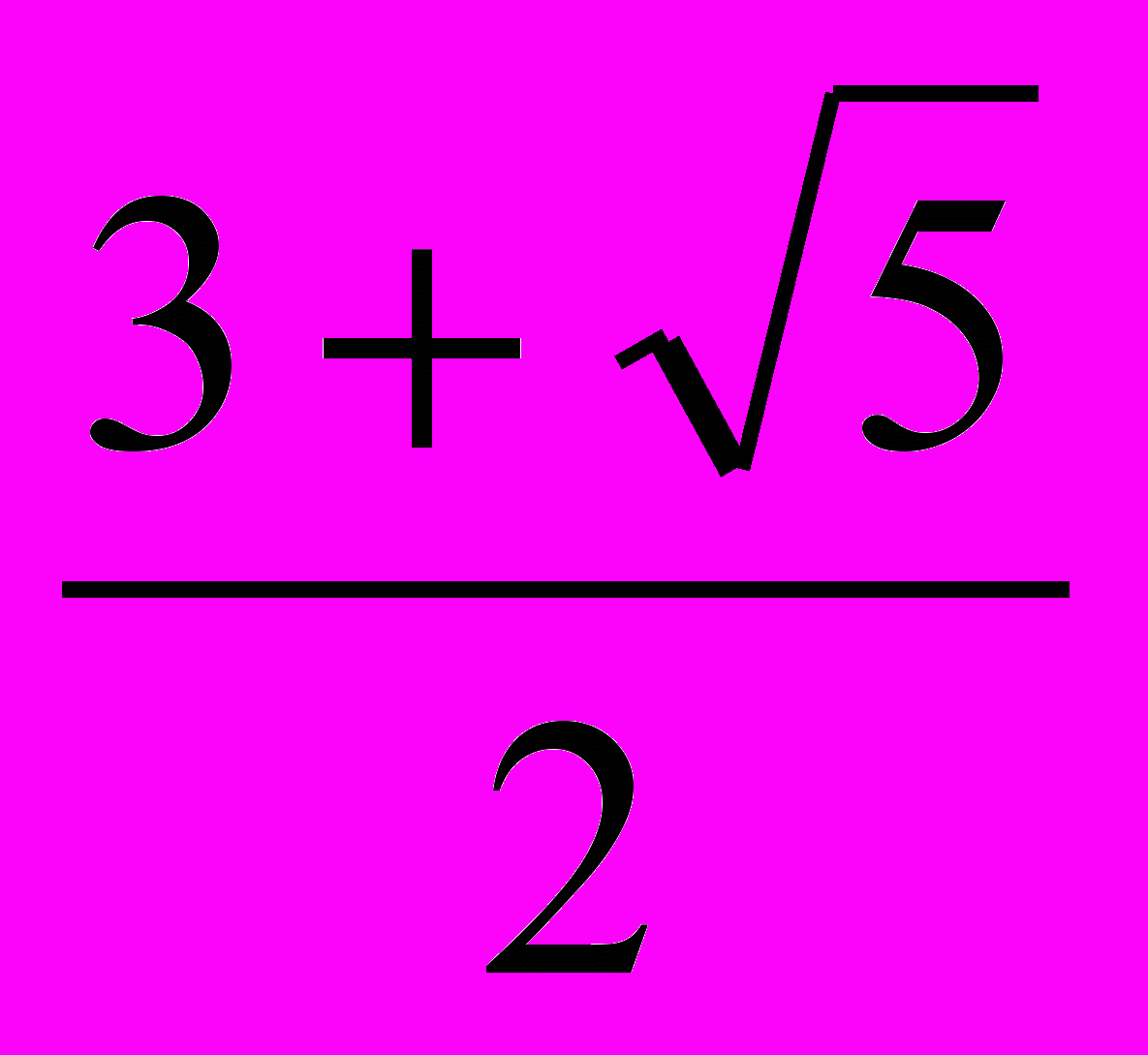; х=-
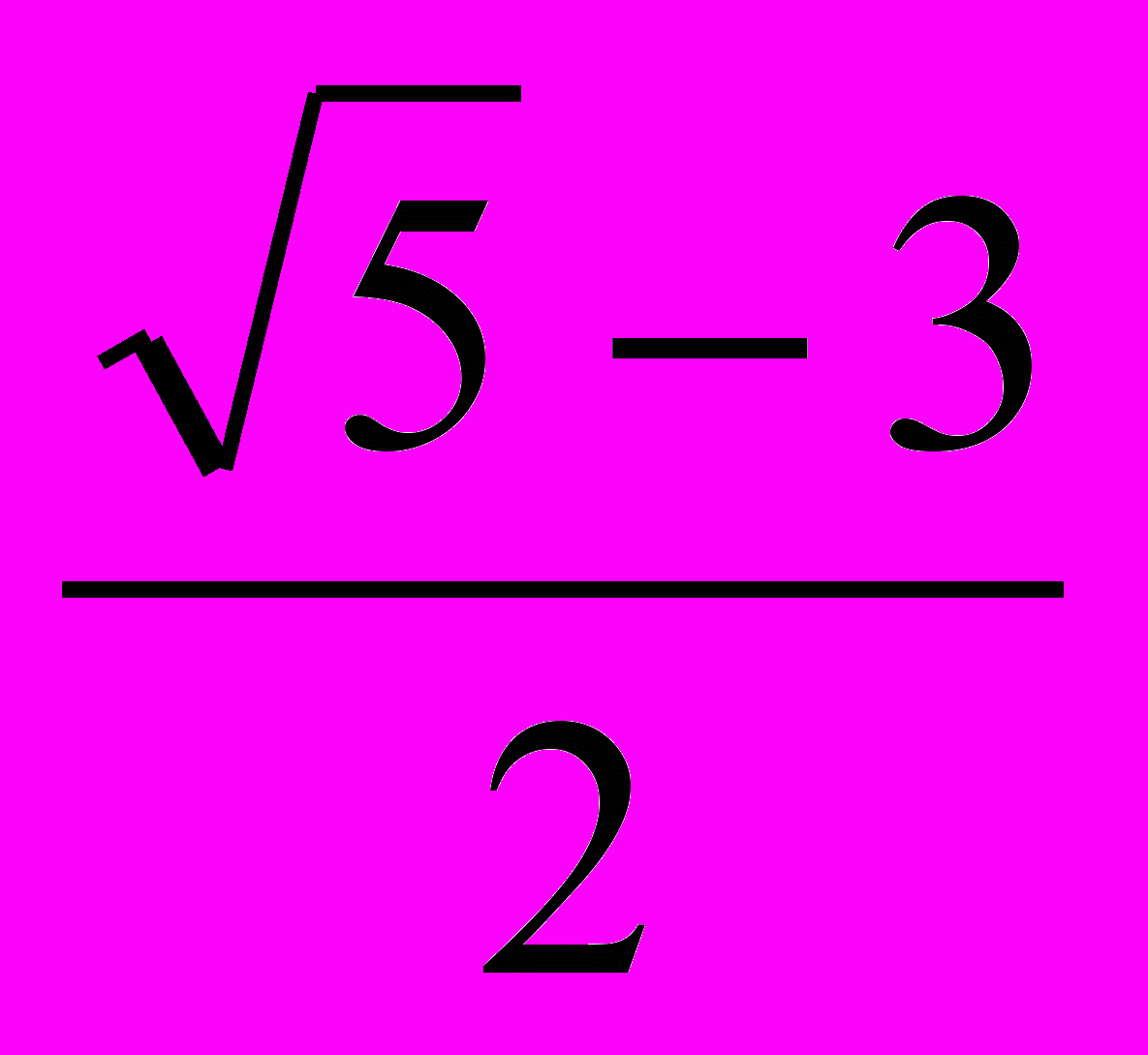
  4. х3-4х2+х+6=0; Применяется теорема Безу. Ищем целый корень среди делителей свободного члена . Это число -1. Делим многочлен на х+1.Записываем многочлен в виде произведения (х+1)(х2-5х+6)=0; х+1=0 или х2-5х+6=0; х=-1;х=2; х=3
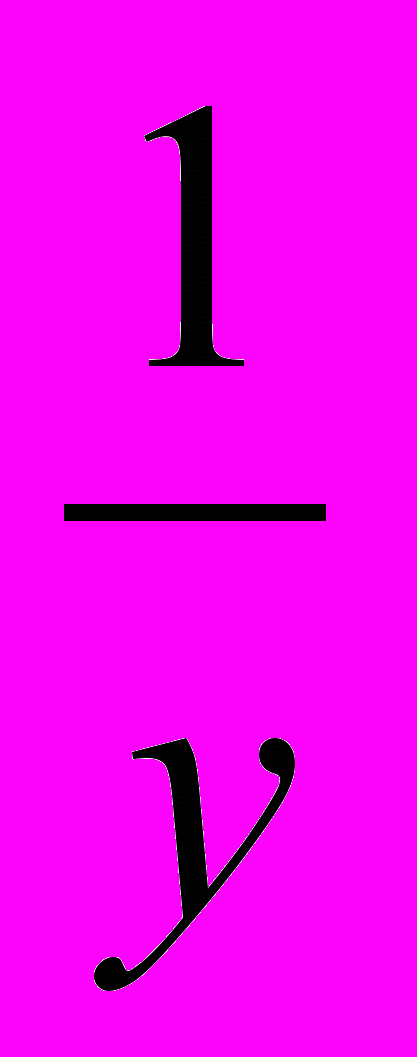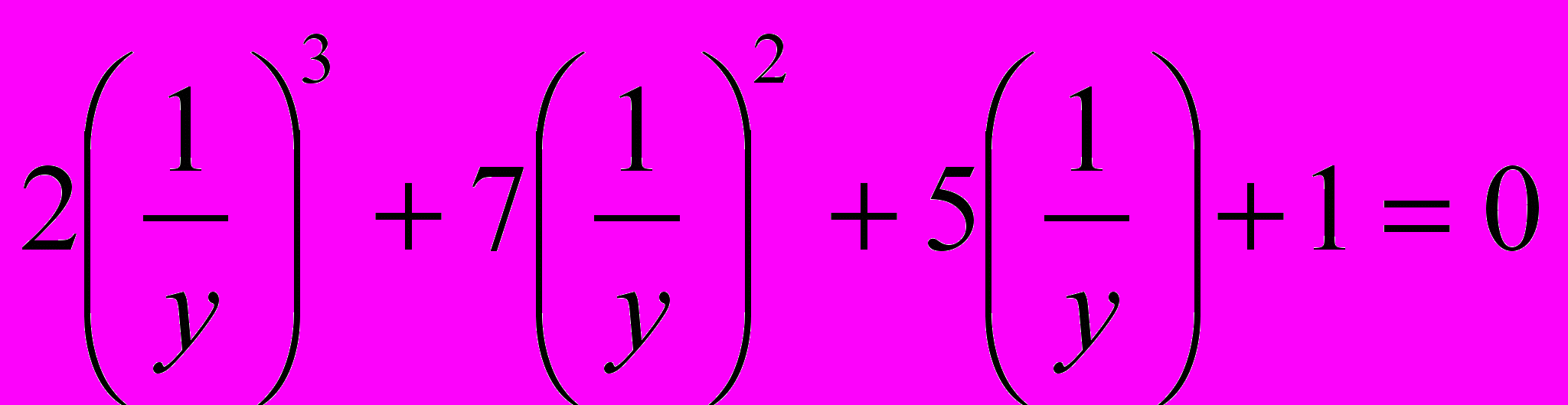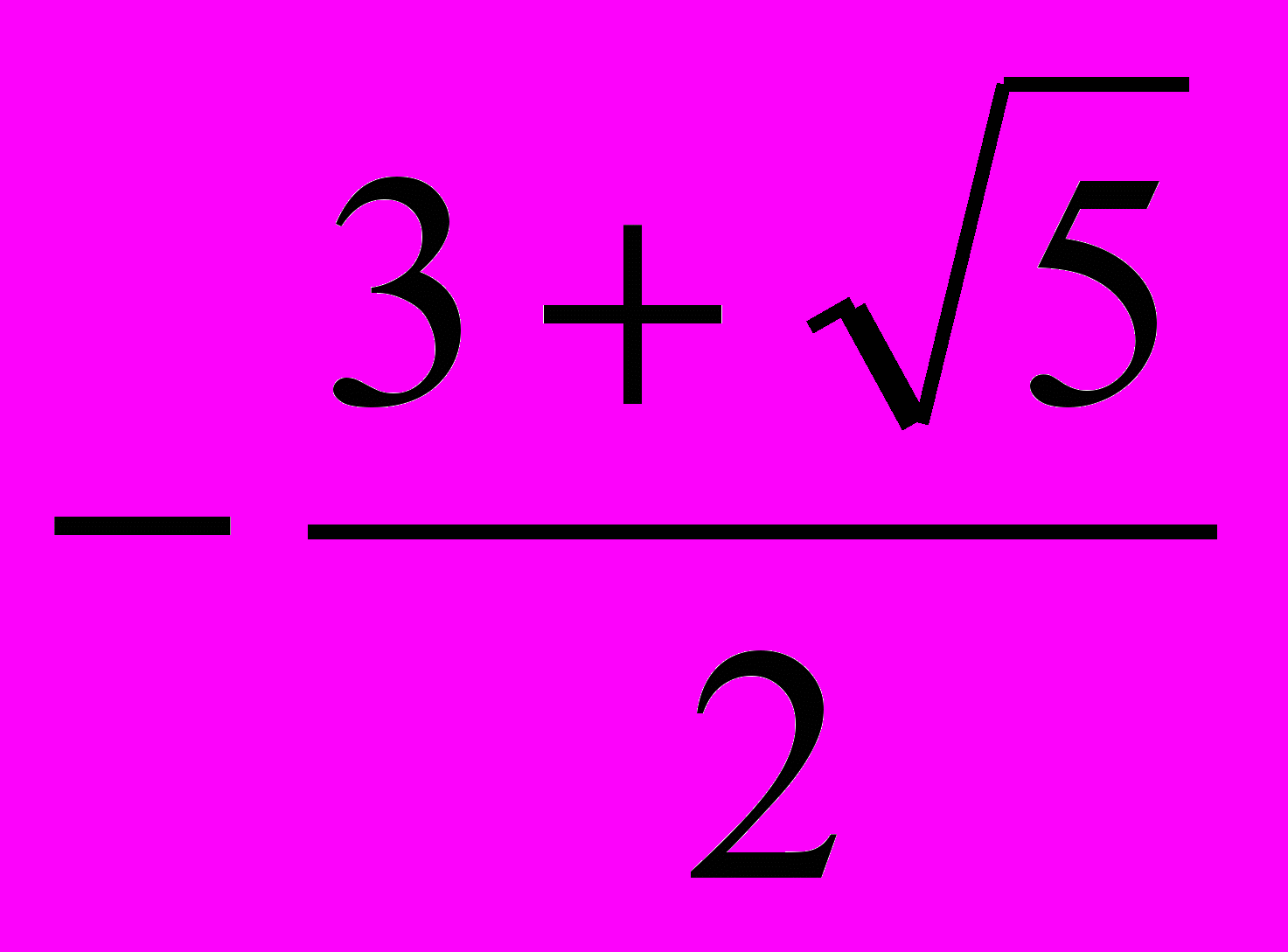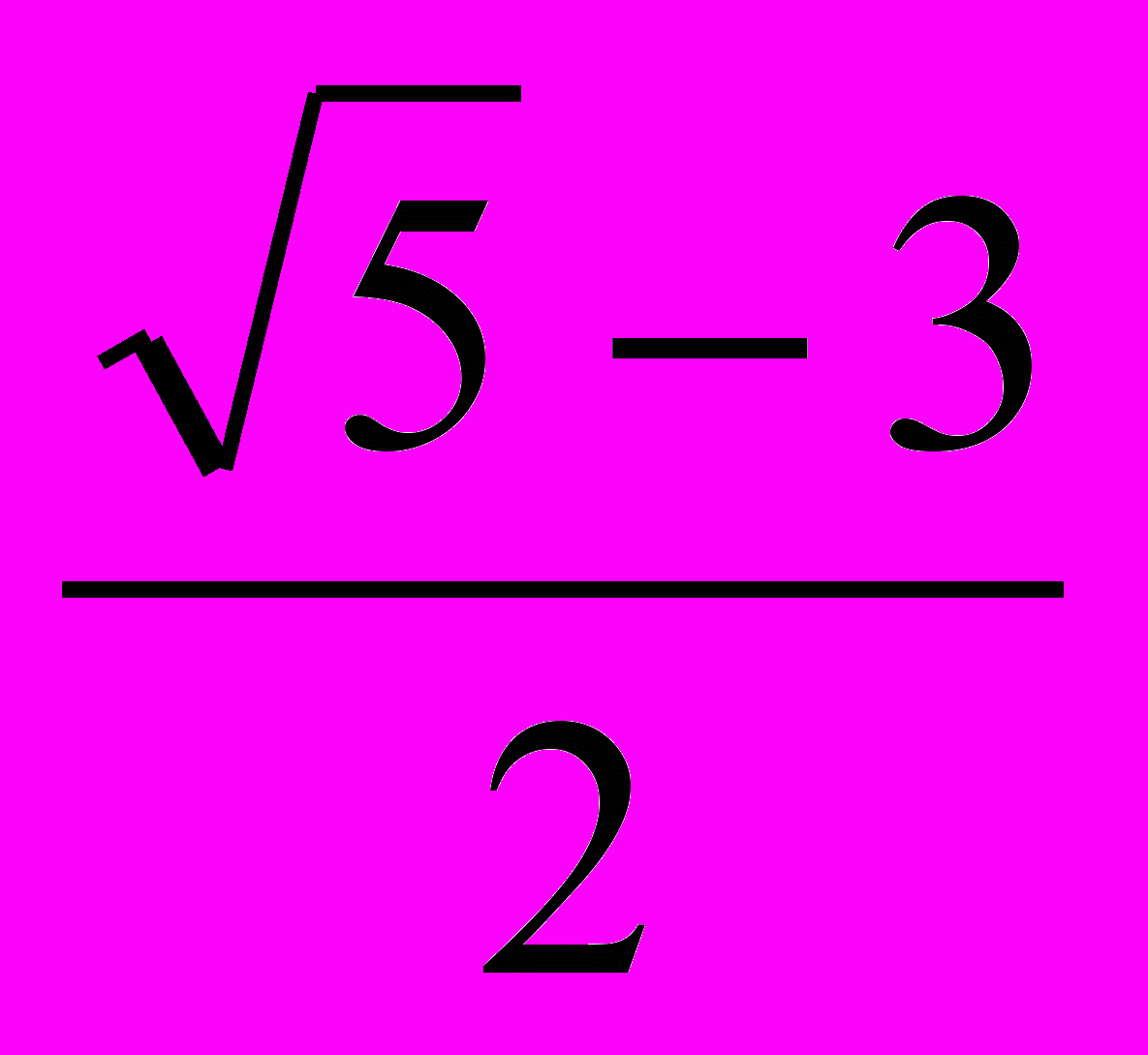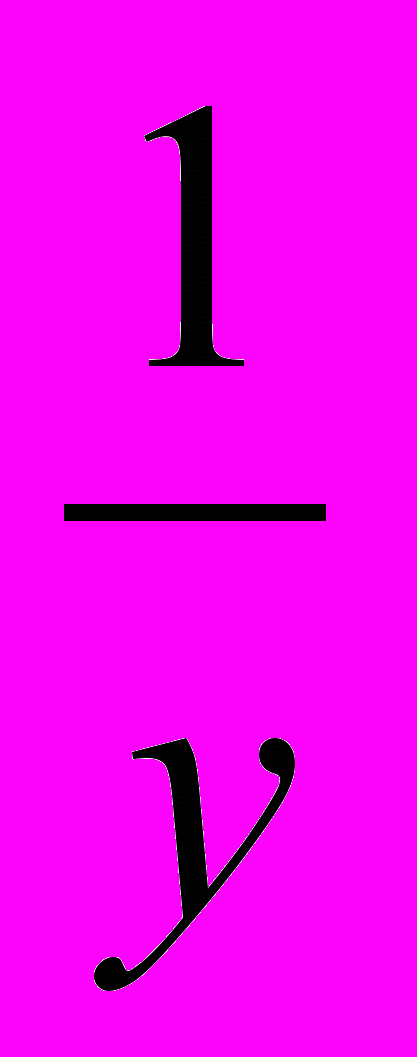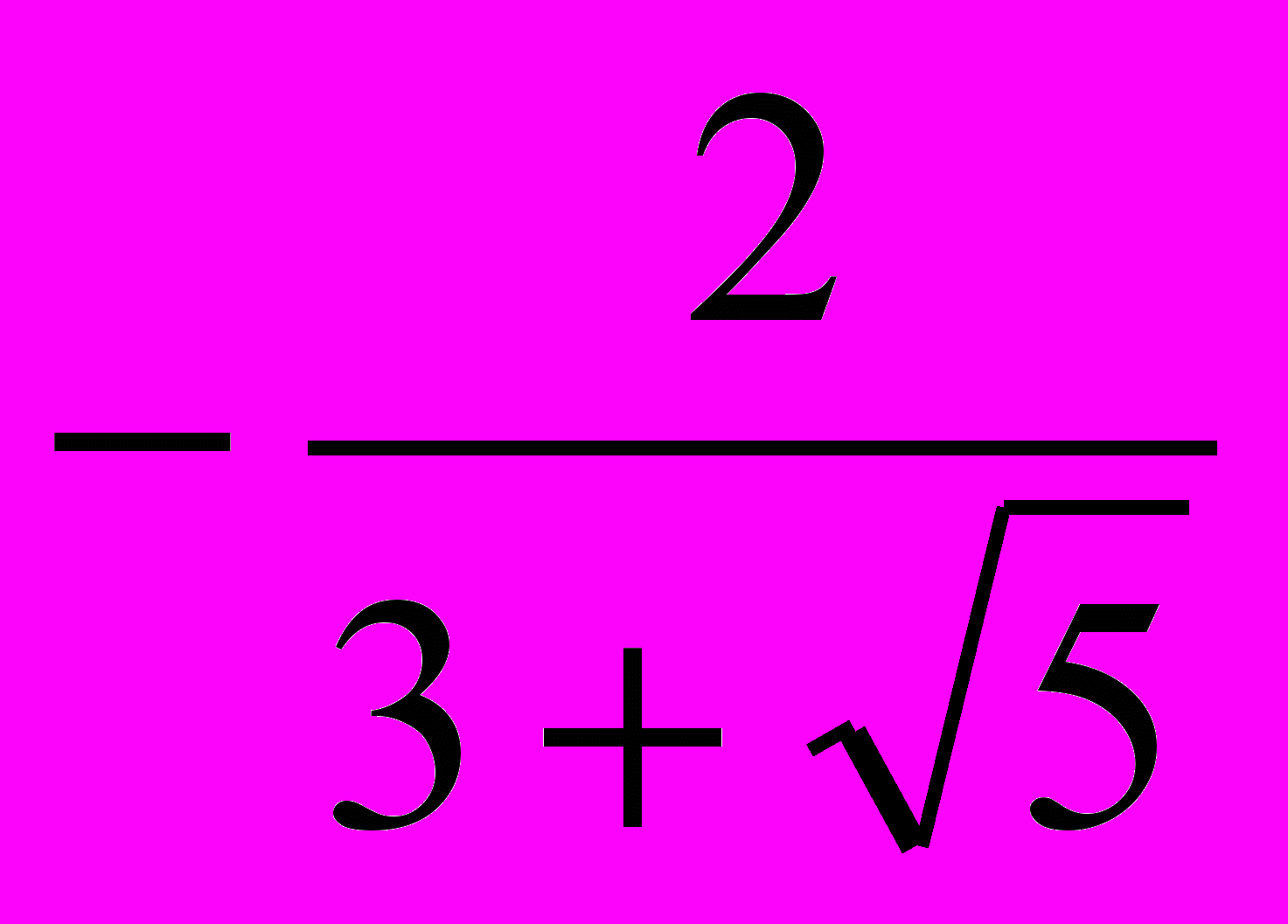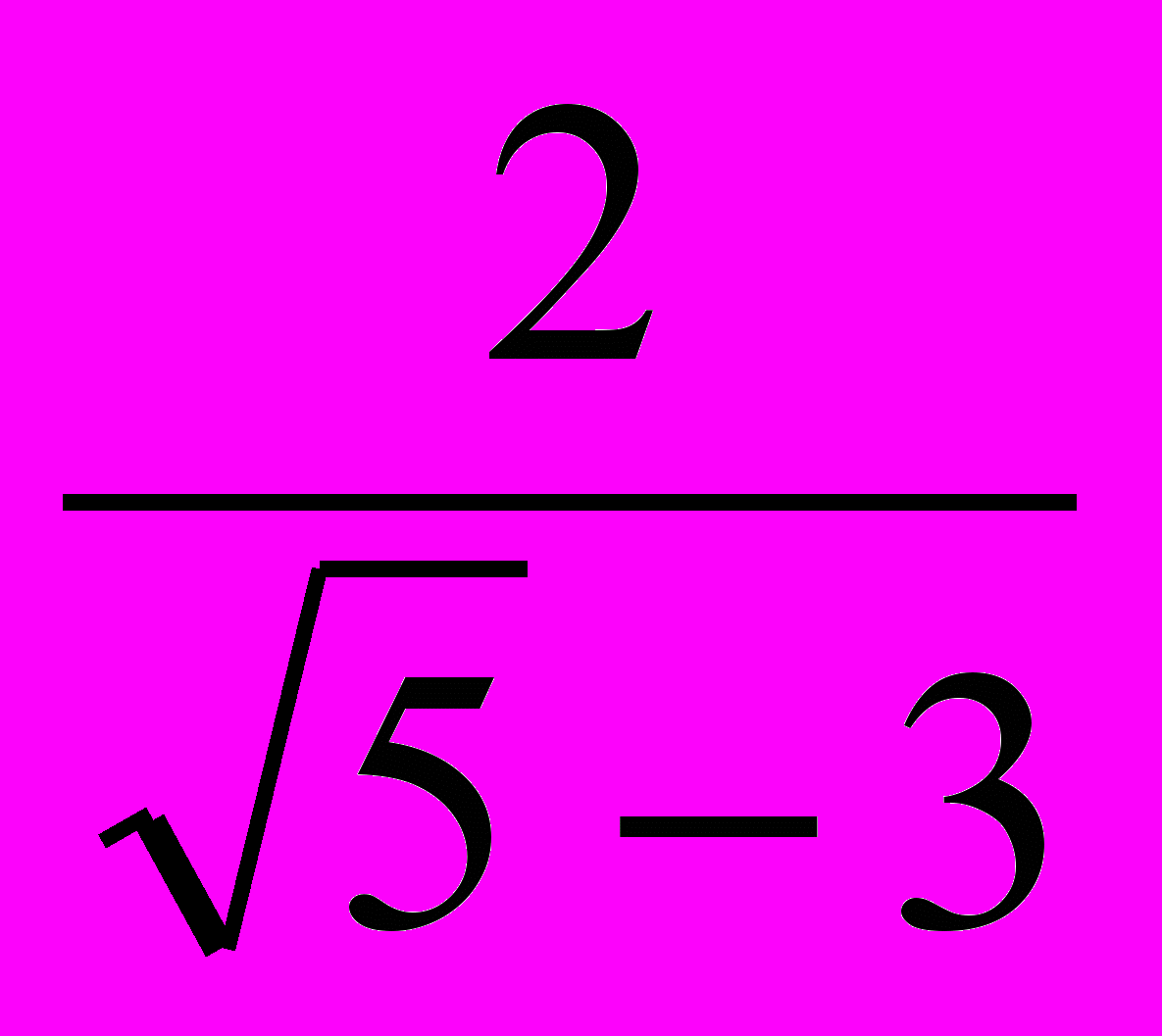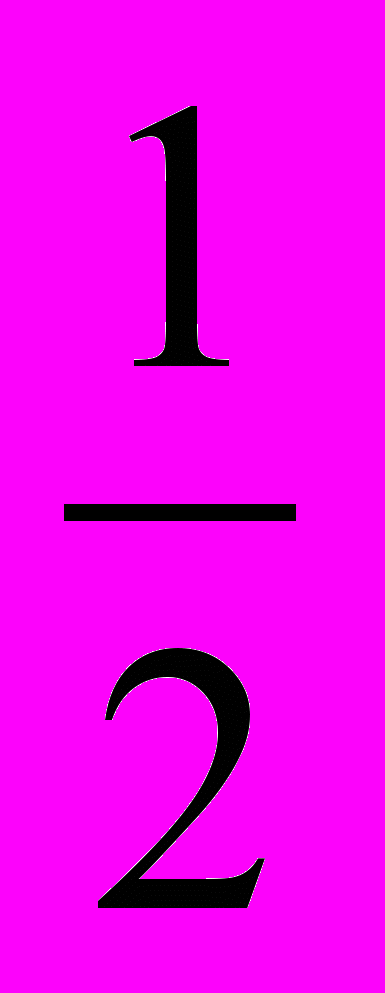
  5. 2х3+7х2+5х+1=0; Делаем замену х =. Тогда ; 2+7у+5у2+у3=0. Применяем метод из примера №5. -2-корень многочлена, делим многочлен на у+2. Получаем (у+2)(у2+3у+1)=0; у=-2; у=; у=. Возвращаемся к замене х =. х =; х =; х=Ответ: ;
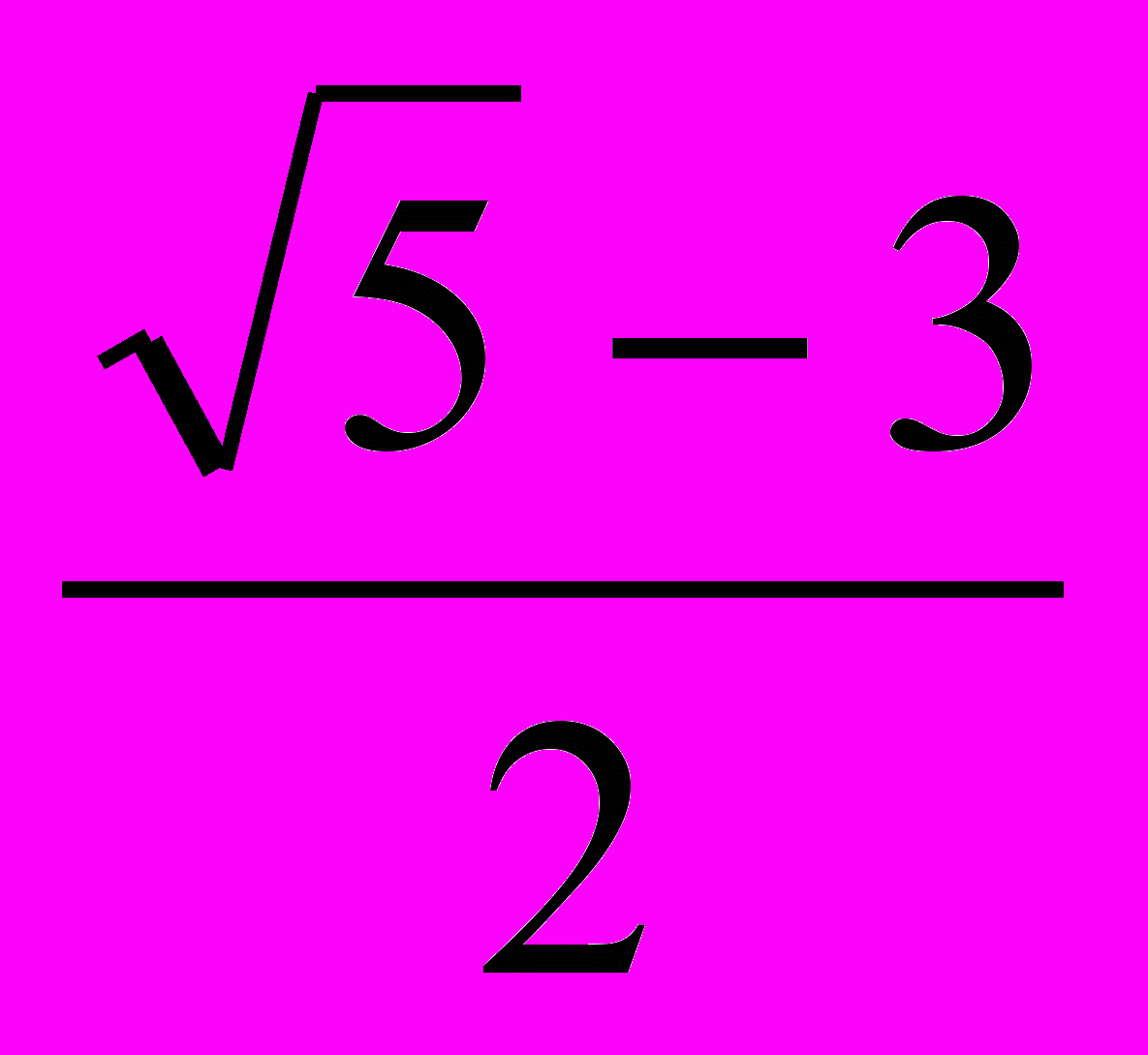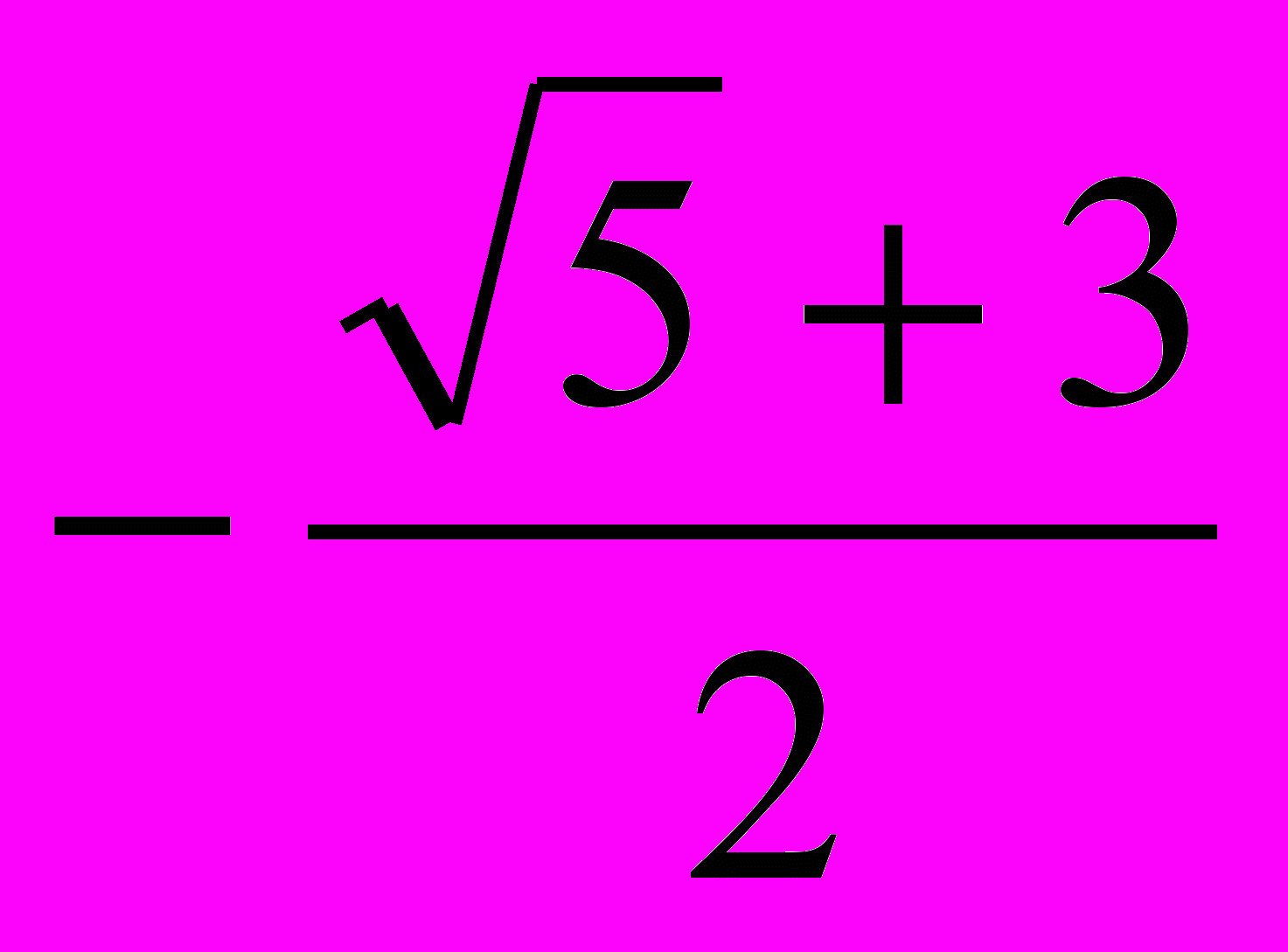
  6. Также рассматриваются ещё примеры

(х – 4)(х2 + 15 + 50)(х – 2) = 18х2

Решение. Разложим на множители х2 + 15 + 50.

х2 + 15 + 50 = 0, х1 = -5, х2 = -10, тогда х2 + 15х + 50 = (х + 5)(х + 10). Уравнение примет вид: (х – 4)(х + 5)(х + 10)(х – 2) = 18х2

Так как (-4)•5 = -20, 10•(-2) = -20, то перемножая первую скобку со второй, третью с четвертой, будем иметь: (х2 + х – 20)( х2 + 8х – 20) = 18х2

Поскольку х = 0 не корень, разделим обе части уравнения на х2 ? 0. Получим:

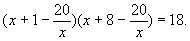
Вводим замену: 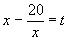, тогда (t+1)(t+8)=18, т.е. t2+9t-10=0, t1= -10, t2 = 1.

Вернемся к исходной переменной:



Решим первое уравнение х2 + 10х – 20 = 0, D = 180,



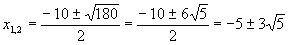
Решим второе уравнение х2 - х – 20 = 0, D =81, х3 = - 4, х4 = 5.

Ответ: 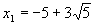, , 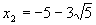х3 = - 4, х4 = 5.


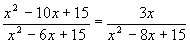, используя основное свойство дроби.

Р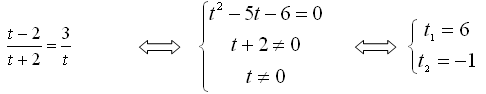ешение. х = 0 не является корнем уравнения, поэтому числитель и знаменатель каждой дроби делим на х 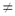0. 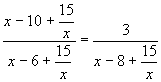, вводим замену: 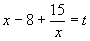, тогда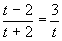

Решим это уравнение

 

 

Вернемся к “старой” переменной:



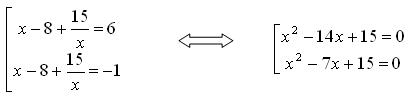
Решаем первое уравнение х2 – 14х + 15 = 0

; .

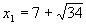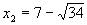Второе уравнение не имеет действительных корней.

Ответ: ;




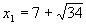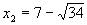
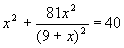
выбирает способ выделения квадрата двучлена. Приведу решение этого уравнения.

Решение. В левой части выделим полный квадрат разности:

 



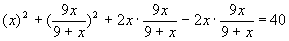
Сгруппируем первый, второй и четвертый члены:





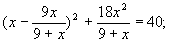
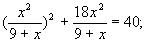
Вводим замену: 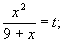t2 + 18t – 40 = 0; t1 = -20, t2 = 2.

Вернемся к “старой” переменной, получим:



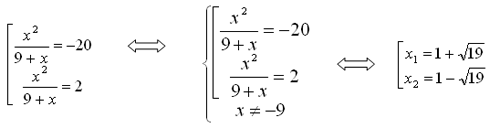
Ответ: , .
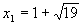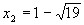