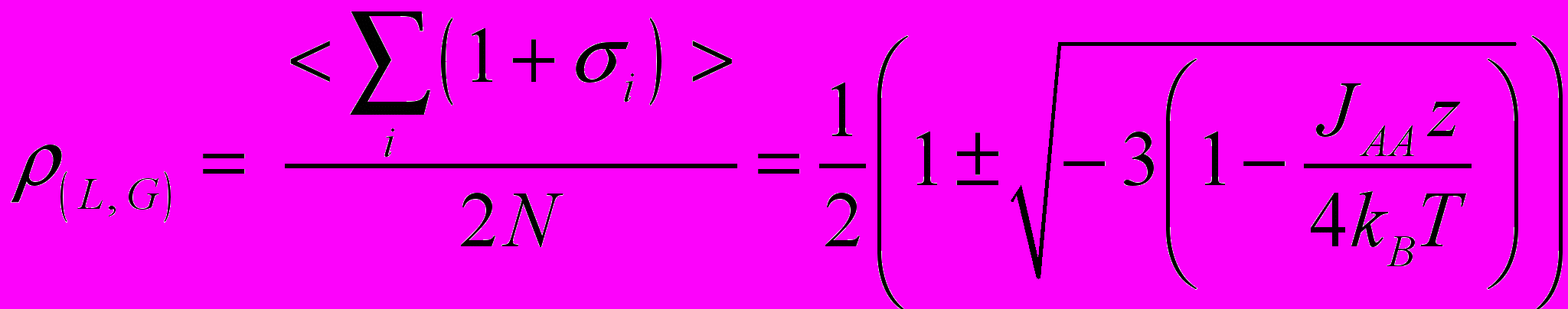Geum.ru

Лекция №6

Вид материалаЛекция

Содержание


Повторим то, что было сказано про модель Изинга в первой лекции
Подобный материал:
Лекция №6

Модель Изинга




До сих пор наше рассмотрение основывалось, фактически, на уравнениях состояния, которые сами по себе имели сугубо эмпирический характер. Возникает вопрос, насколько их можно обосновать. Проблема обоснования того или иного уравнения состояния – это проблема статистической физики. Забегая вперед, следует сказать, что задача обоснования уравнения состояния до сих пор весьма далека от своего окончательного решения. Целью настоящей лекции является проиллюстрировать статистический подход на примере простейшей системы – уже упоминавшейся в первой лекции модели Изинга. Спецификой этой модели является то, что несмотря на свою простоту, она не только ухватывает сам факт фазового перехода, но и способна описать все основные особенности поведения измеряемых величин в критической области.

Повторим то, что было сказано про модель Изинга в первой лекции

Модель Изинга представляет собой несжимаемую решетку, в каждом узле которой находится магнитные стрелки. Эти стрелки могут быть направлены или вверх, или вниз. Соседние стрелки взаимодействуют таким способом что силы, действующие между этими стрелками, стремятся расположить их параллельно друг другу. Энергия взаимодействия такой системы стрелок может быть записана в виде


.

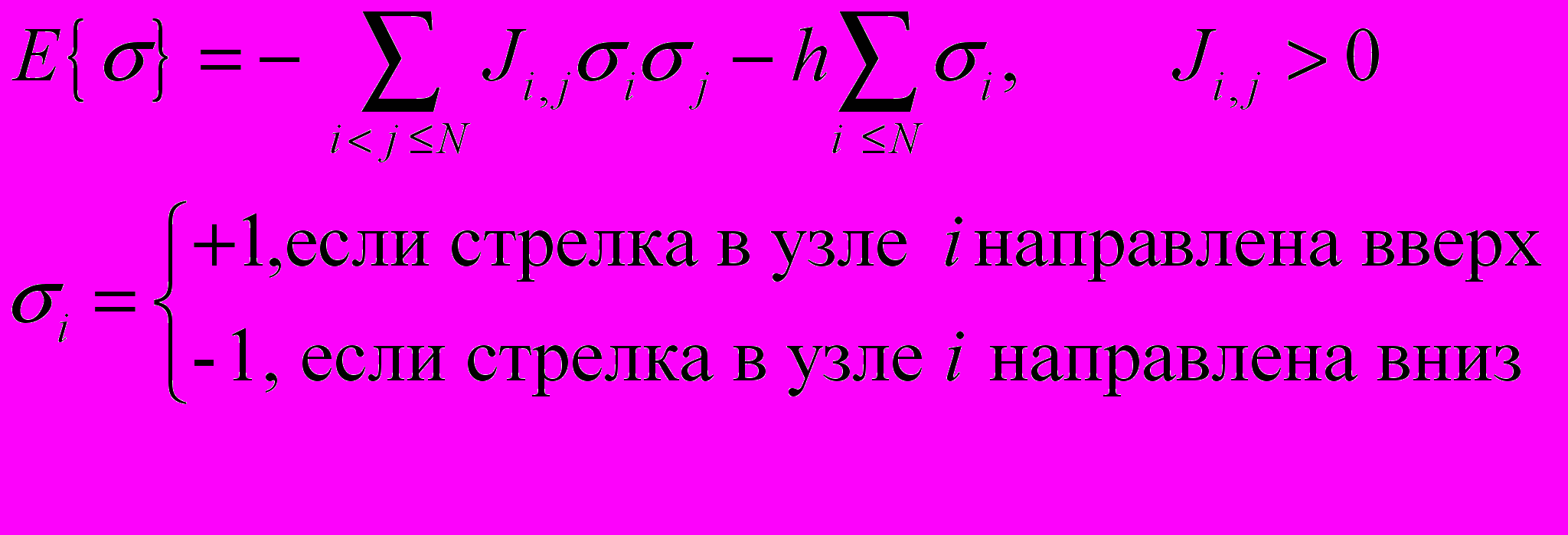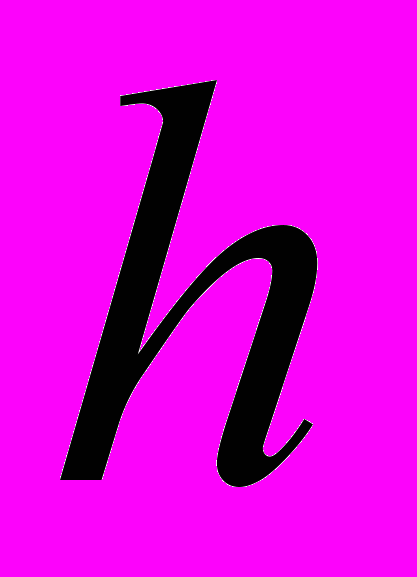Здесь число узлов решетки, внешнее магнитное поле (тоже имеет только два направления: либо вверх, либо вниз.






Из статистической физики имеем для свободной энергии



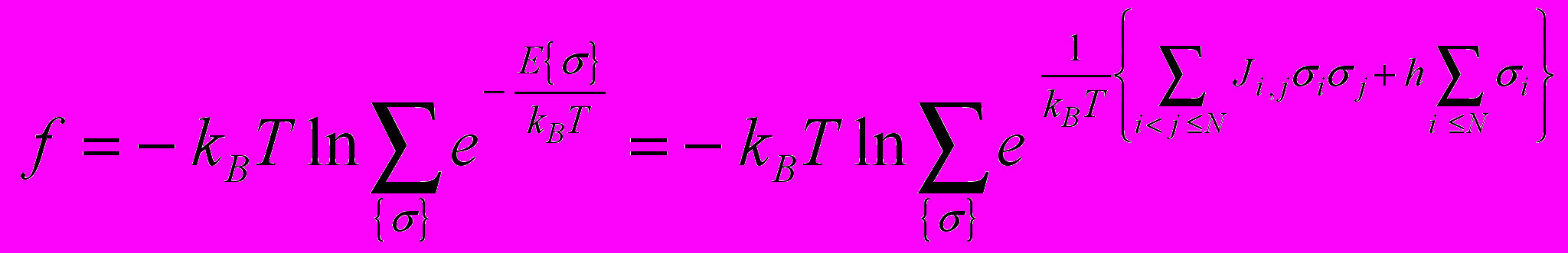
В общем случае вычисление стоящей под знаком логарифма суммы по всем возможным конфигурациям стрелок эадача совершенно невыполнимая. Следует сказать, что модель Изинга отнюдь не сводится только к модели магнитной системы, а лежит в основании самых фундаментальных и важных задач теоретической физики. Поэтому в последние десятилетия были потрачены огромные усилия для создания теоретических методов вычисления этой суммы. В определенном смысле развилась специальная ветвь теоретической физики – физика решеточных систем. Однако, точного решения задачи так и не получено. Тем не менее существуют более или менее сложные приближенные методы решения этой задач. Мы остановимся на самом простом из этих приближенных методов.

Давайте перепишем произведение 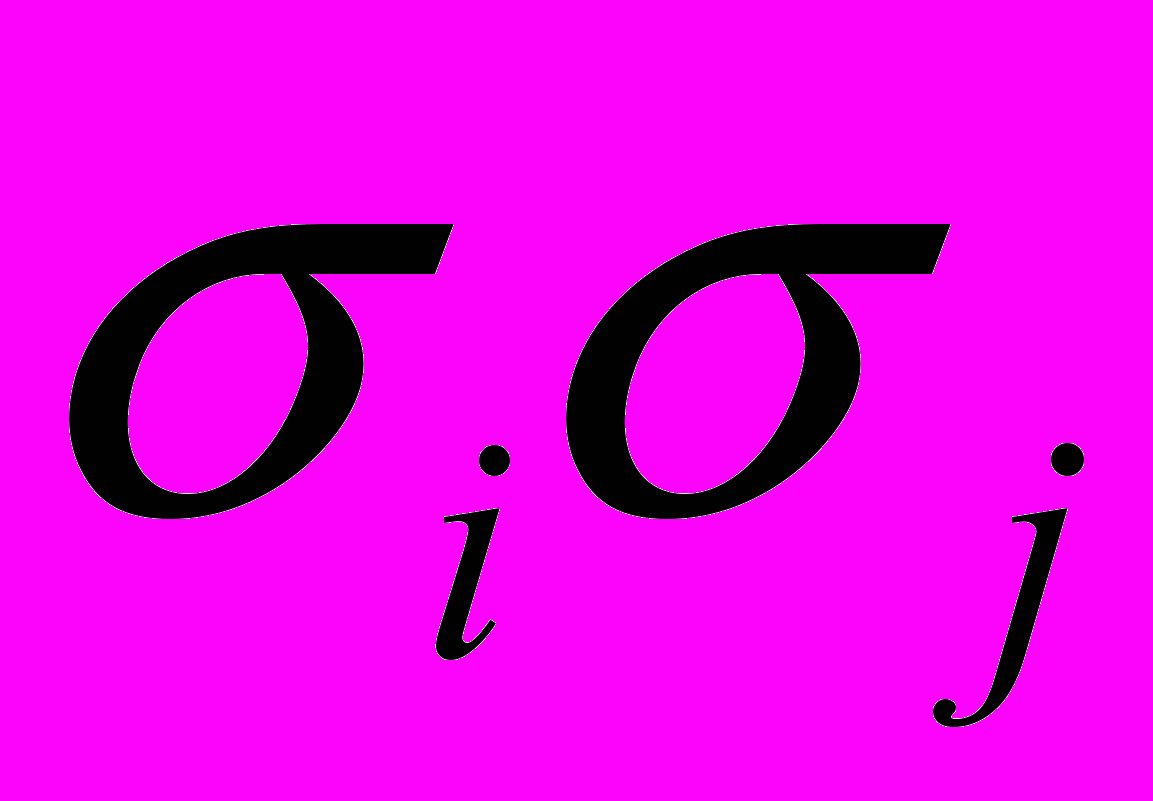в виде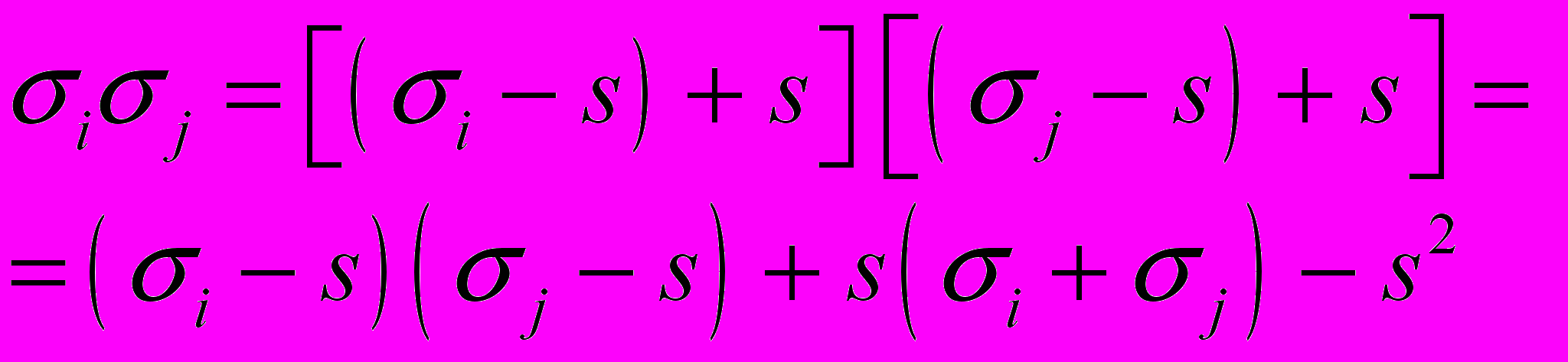





Наши преобразования, разумеется, являются тождественными. Мы всего лишь добавили и вычли некоторую величину , про которую пока вообще ничего не знаем. Впоследствии мы будем интерпретировать эту величину как среднее значение намагниченности, что позволит нам написать уравнение для определения этой величины.

Первый член в правой стороне выписанного выше тождества описывает взаимодействие между магнитными стрелками в узлах 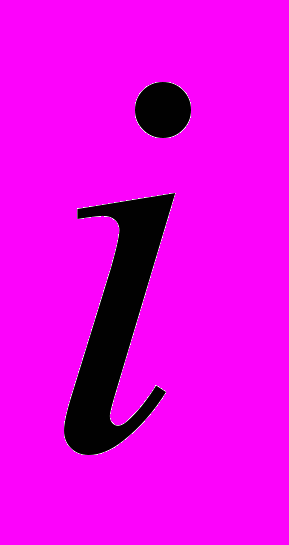и 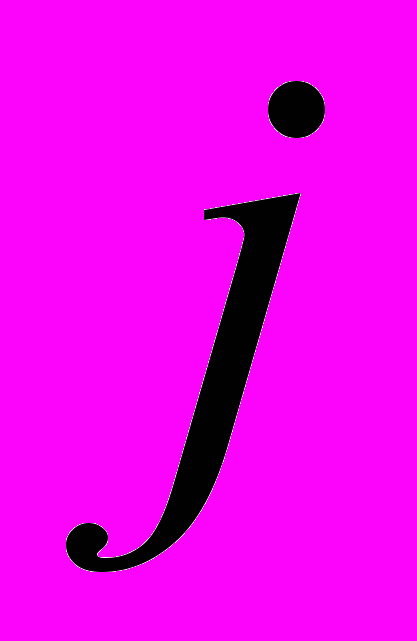. Второй член описывает влияние поля, создаваемого средней намагниченностью на магнитные стрелки в узлах 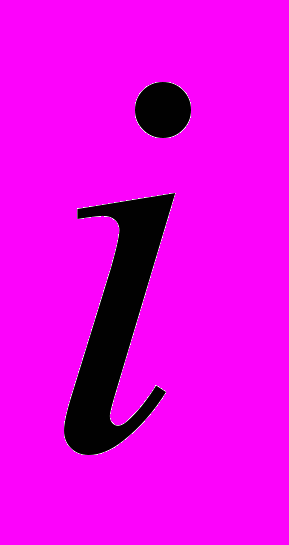и 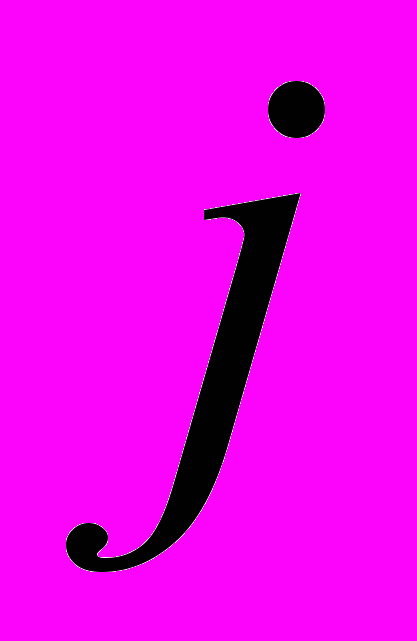. Теперь можно сформулировать наше основное приближение.

Мы предполагаем, что член 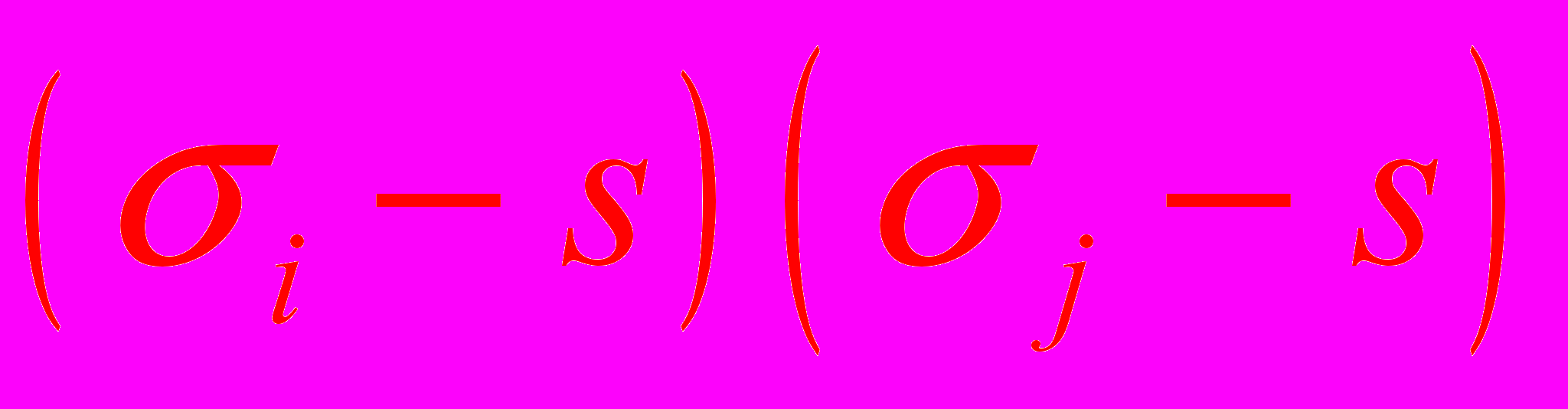мал и будем в дальнейшем им пренебрегать.

Это приближение принципиально. Оно означает, что спин 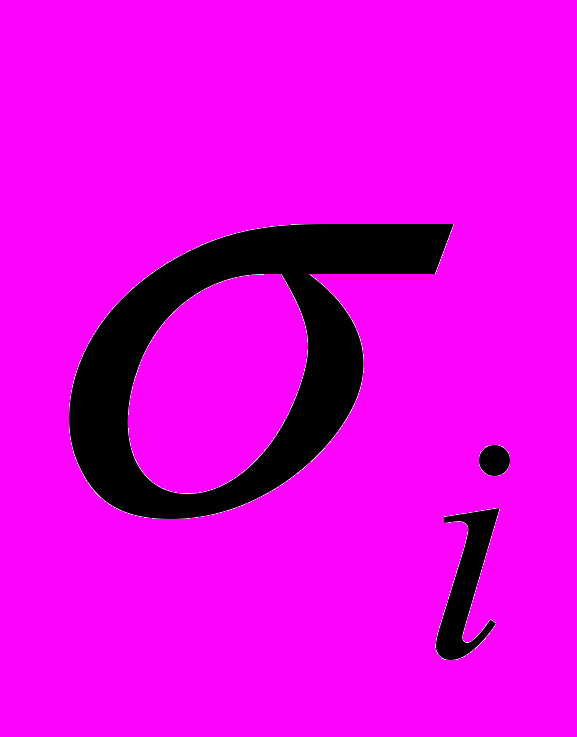взаимодействует только с полем, создаваемым средней намагниченностью, но не взаимодействует с соседним спином . Выражение для энергии системы теперь может быть переписано в виде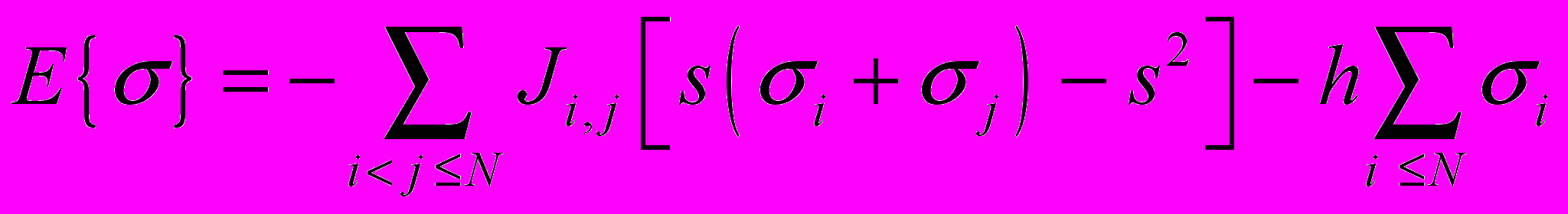



Принципиальным моментом является отсутствие в выражении для энергии члена с произведением спинов в различных узлах решетки. Последующие приближения уже не носят принципиального характера, однако, несколько упрощают расчеты. Предположим, в частности, что взаимодействуют только спины, находящиеся в ближайших узлах рассматриваемой решетки.

Другими словами предположим, что




Энергия данной конфигурации стрелок при этом равна




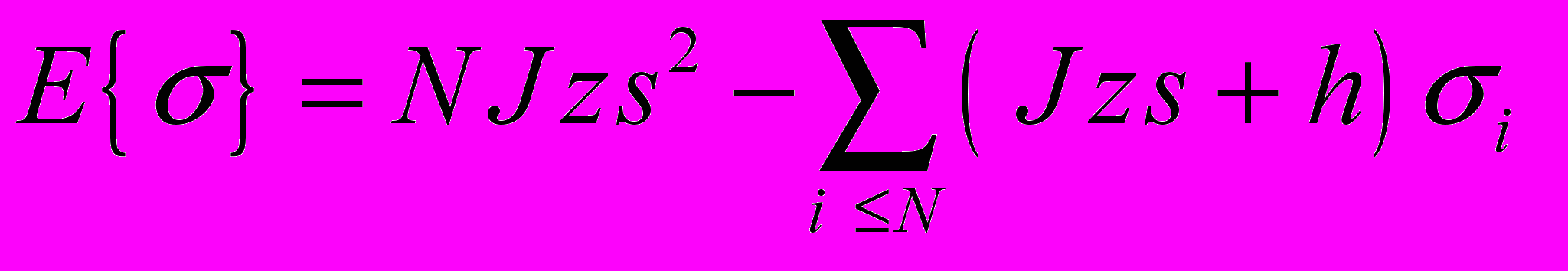
Здесь z – число ближайших соседей в рассматриваемой решетке. Теперь легко вычислить свободную энергию системы

.




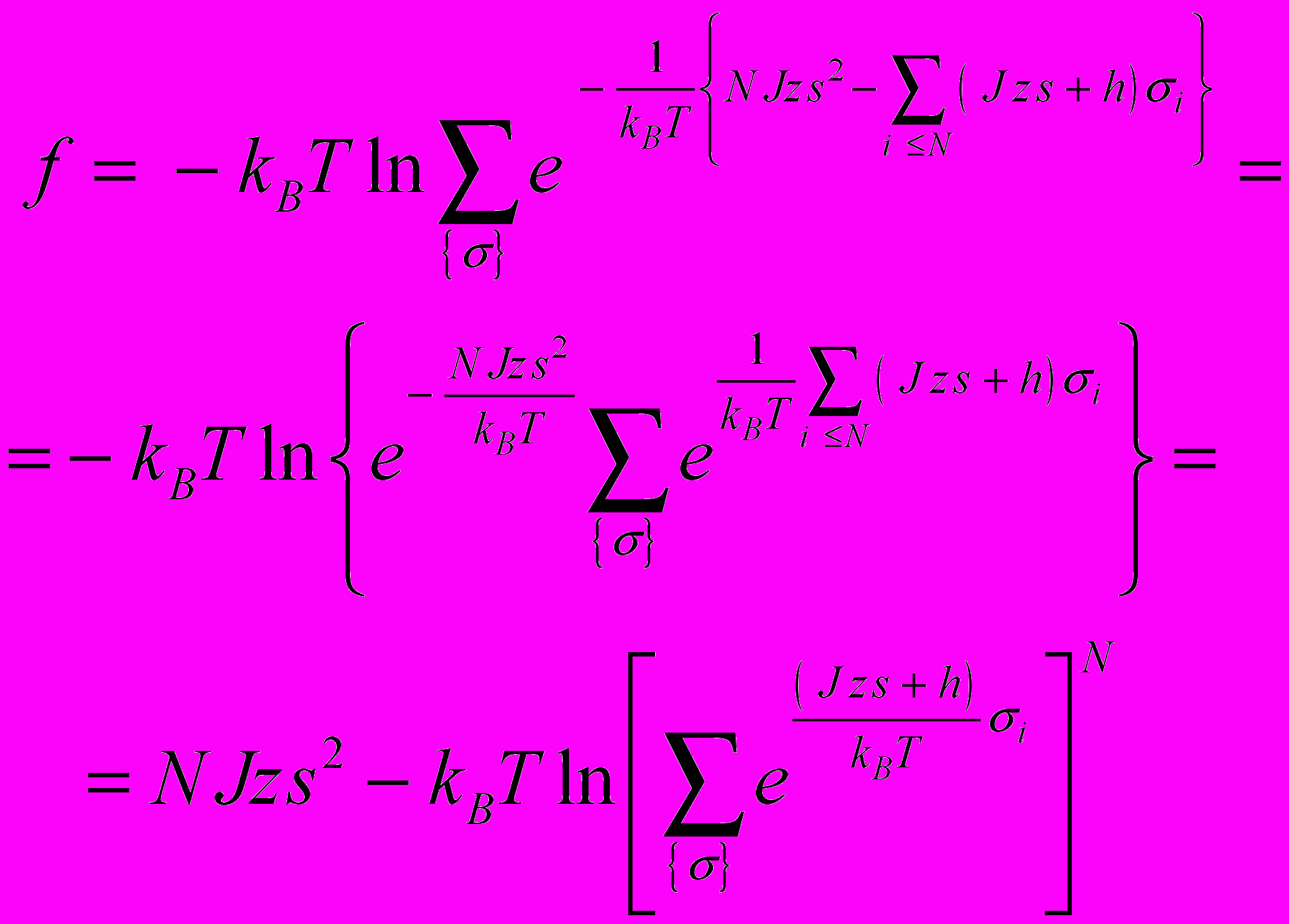
Принимая во внимание, что переменная , т.е может иметь только два значения, и проводя суммирование по этим двум значениям в каждом узле решетки, получим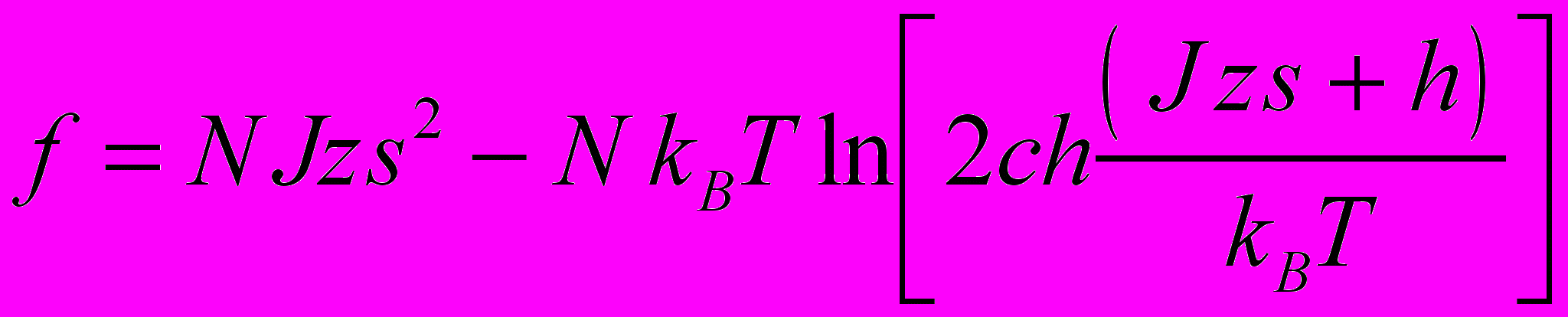





Давайте вспомним теперь, что величина до сих пор не определена. Выберем таким образом, чтобы свободная энергия при выбранном имела минимум. Т.е. наложим дополнительное условие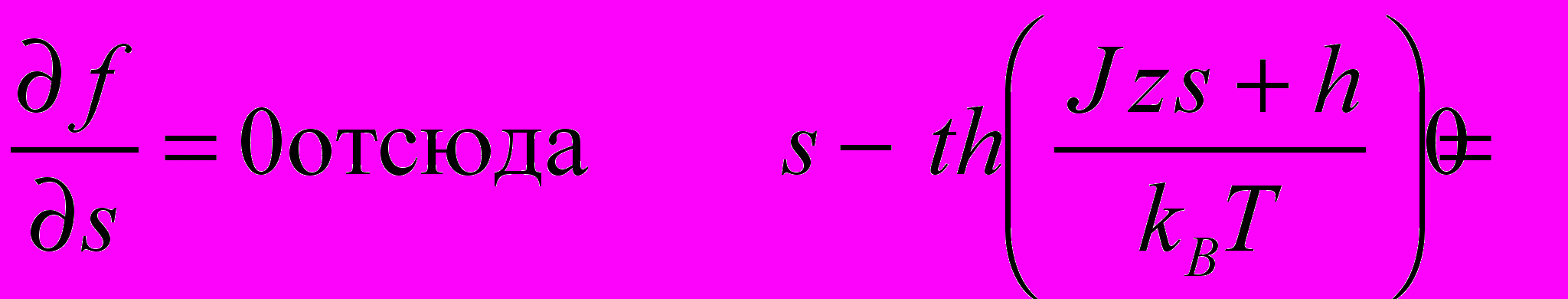


.

Решение этого уравнения может быть записано в форме.

(*)

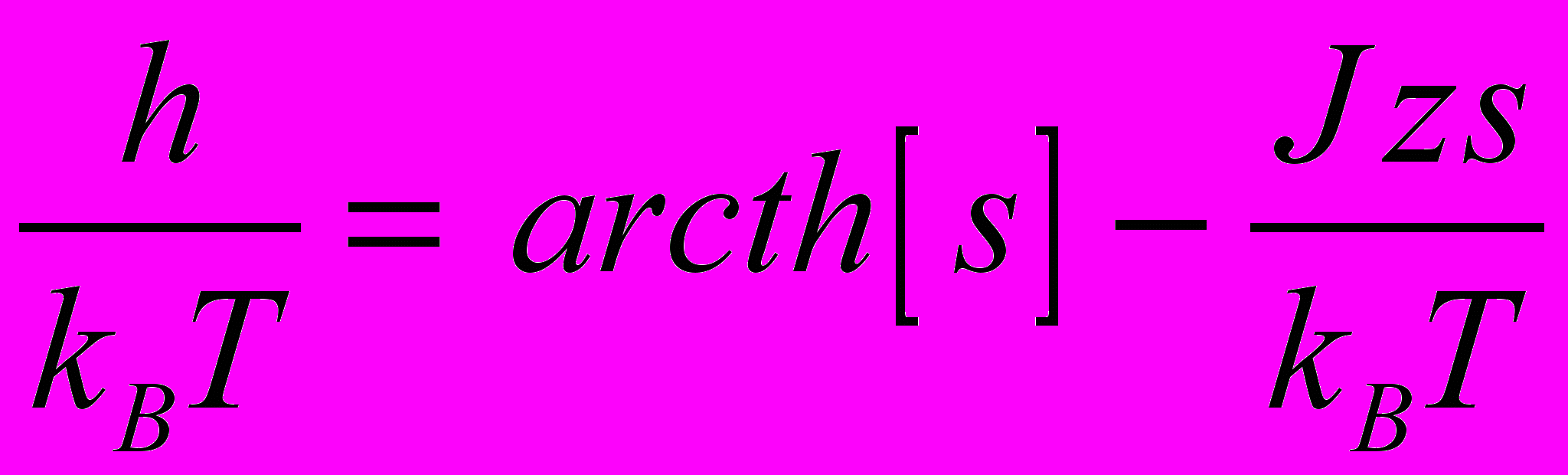Это уравнение совершенно фнфлогично уравнению состояния ван-дер-Ваальса. В частности, легко видеть, что при малых это уравнение полностью совпадает с разложением, получаемым из уравнения ван-дер-Ваальса и оба они совпадают с разложением Ландау. Действительно, для малых имеем




откуда уравнение состояния принимает вид


,


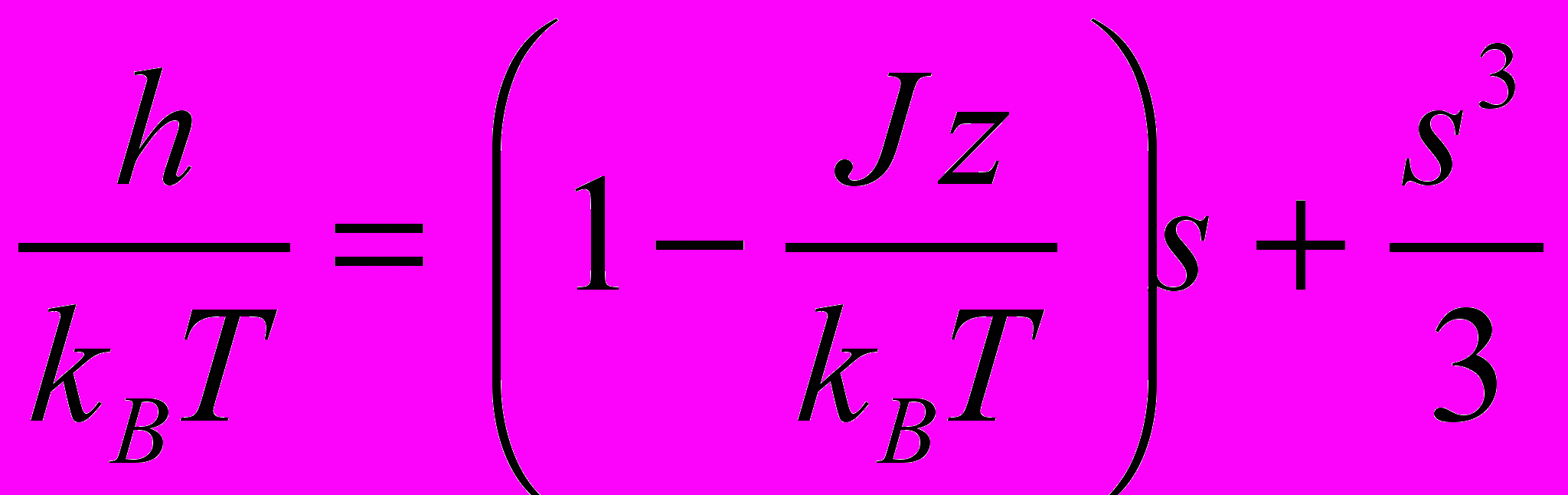что дословно совпадает с соответствующим уравнением теории Ландау.

Рассмотрим частный случай нулевого магнитного поля 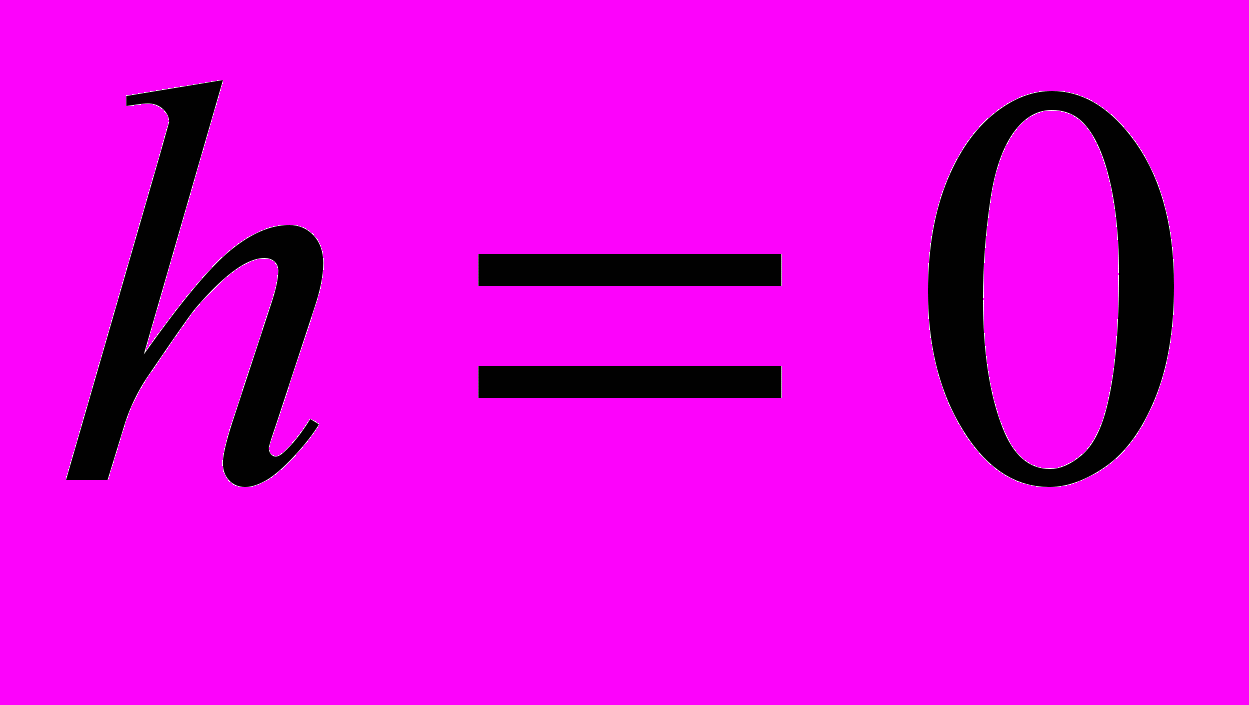. Для высоких температур 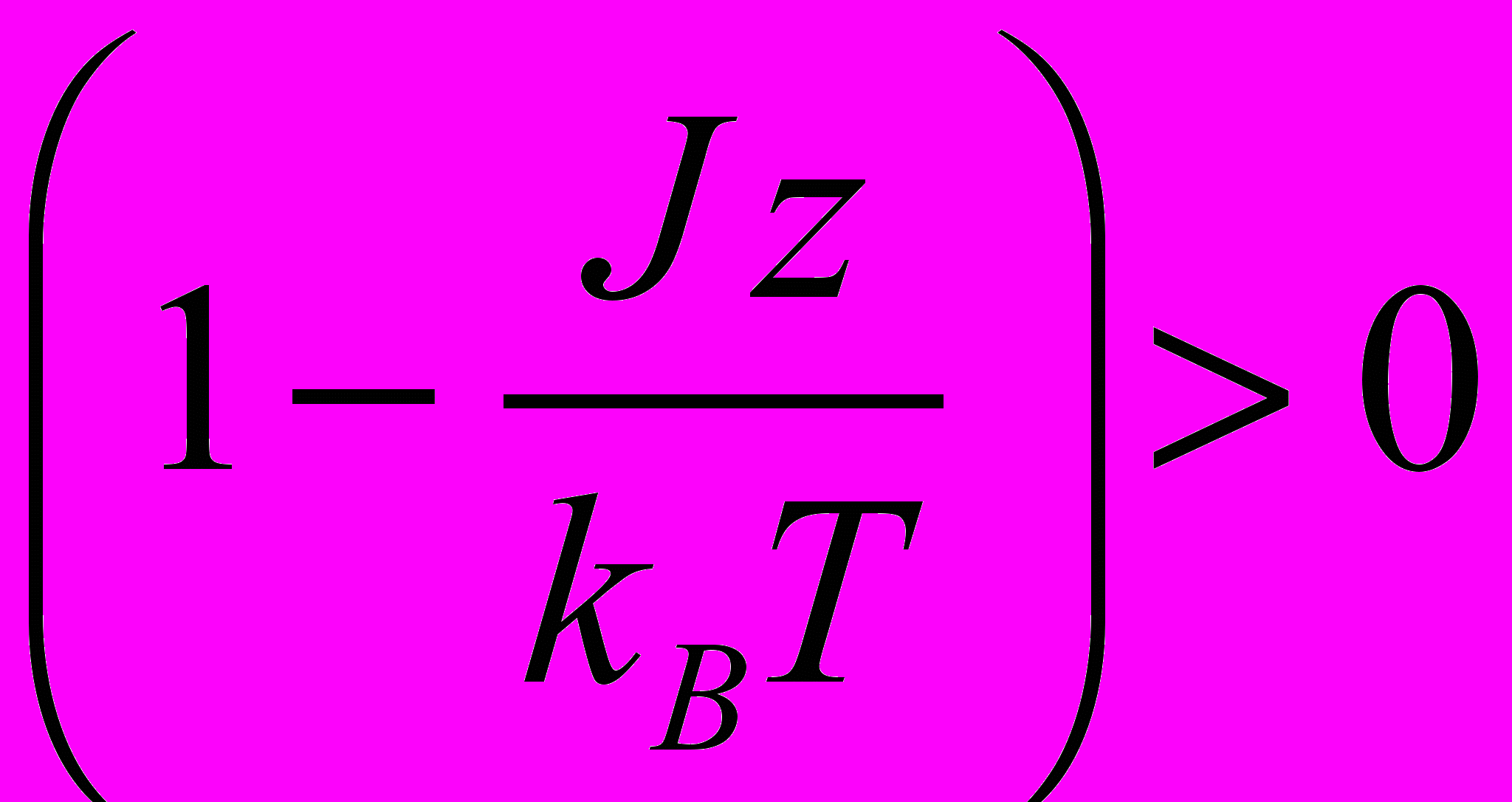и уравнение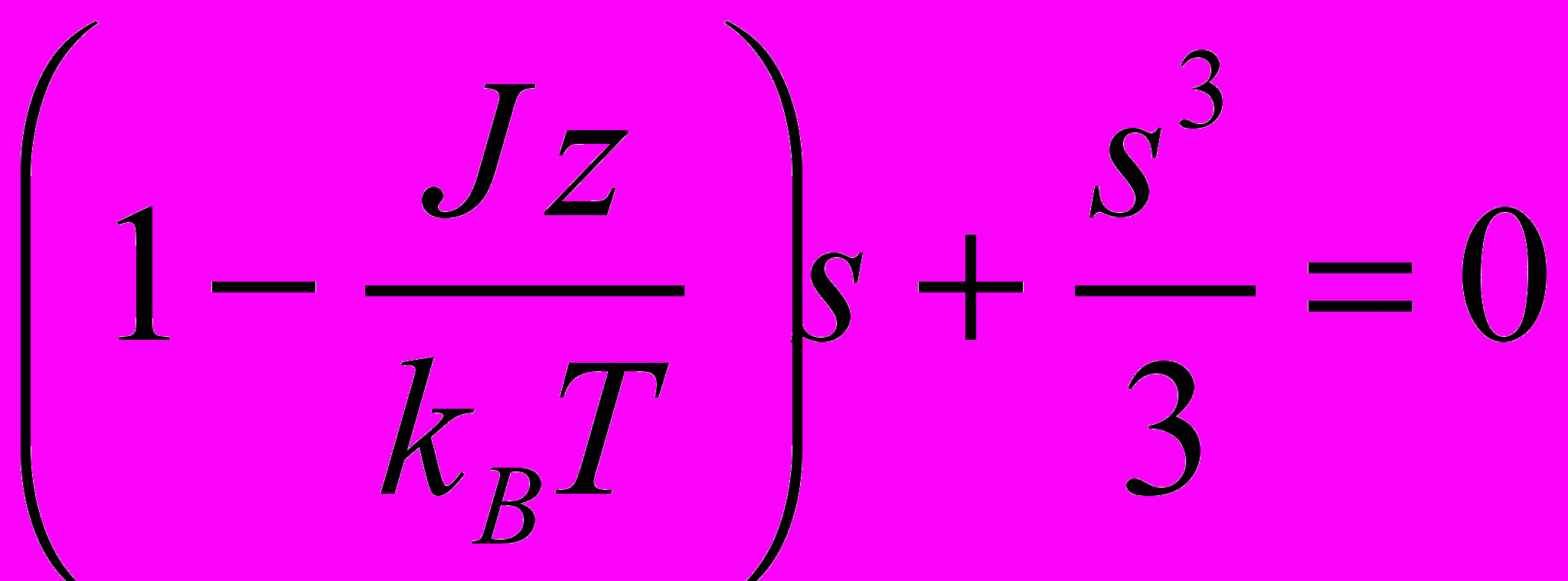





имеет единственный корень 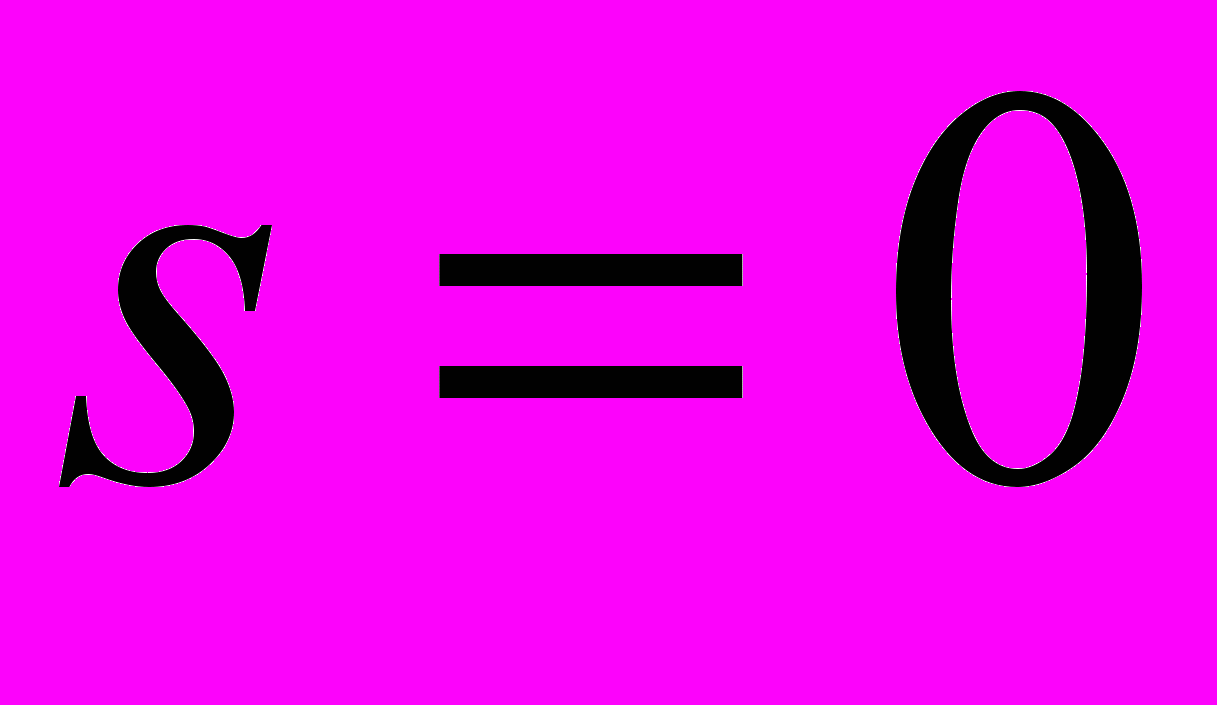. Для низких температур 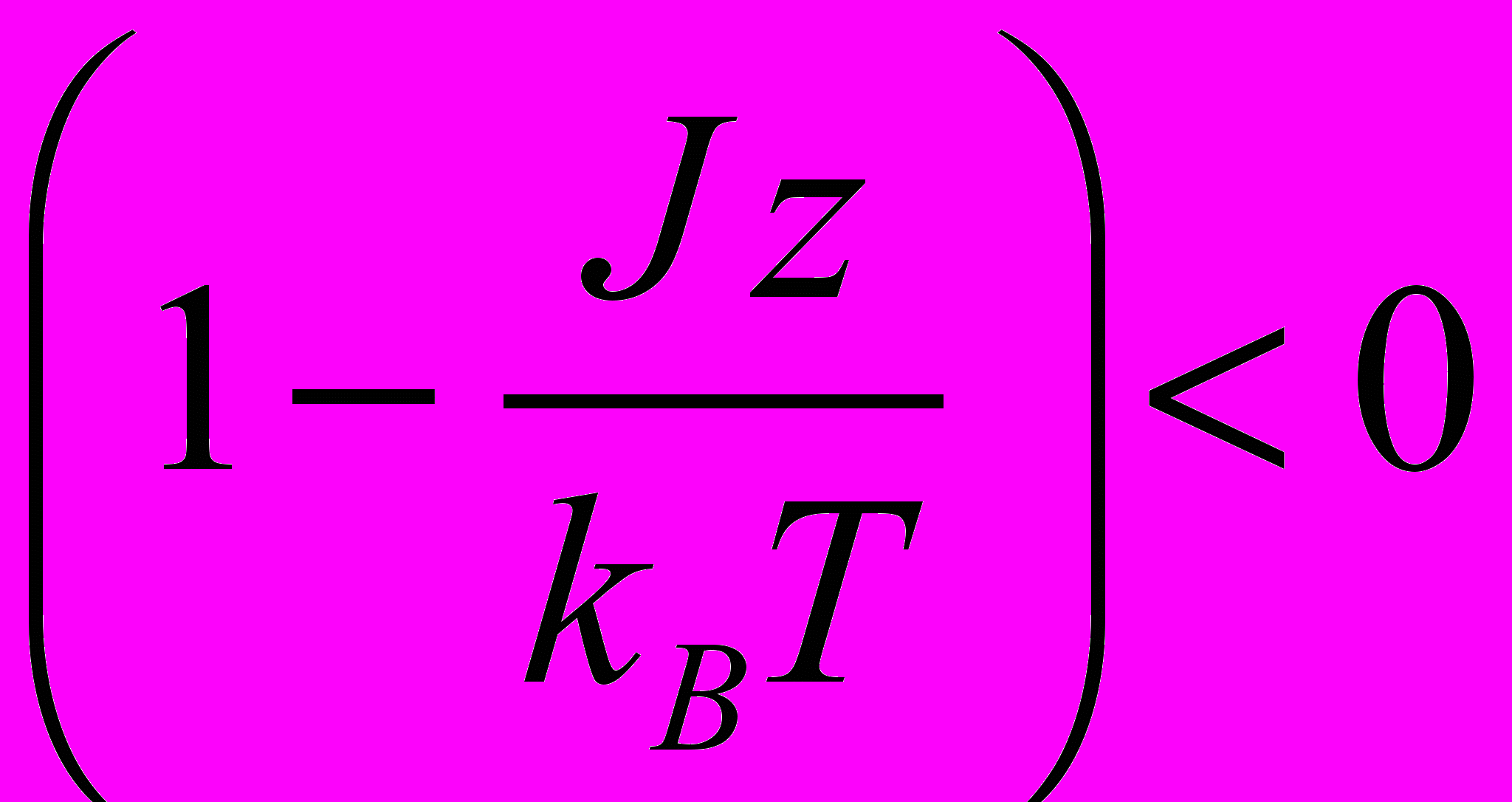и, наряду с корнем 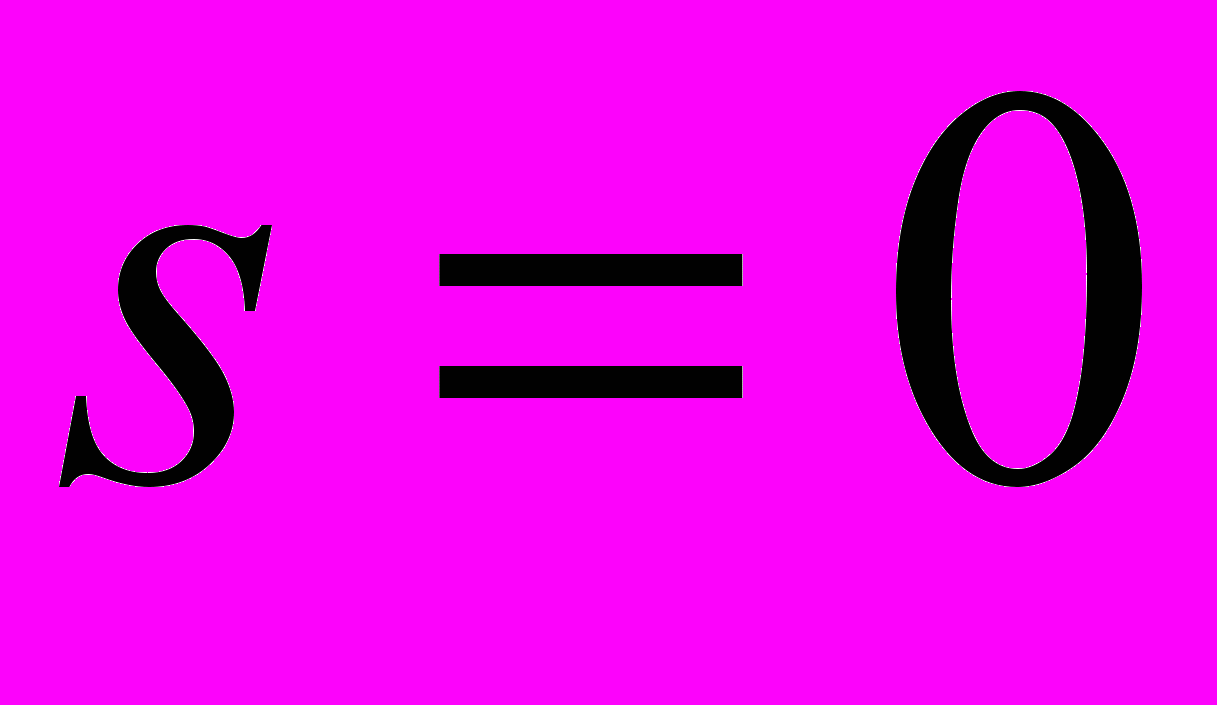, появляются еще два корня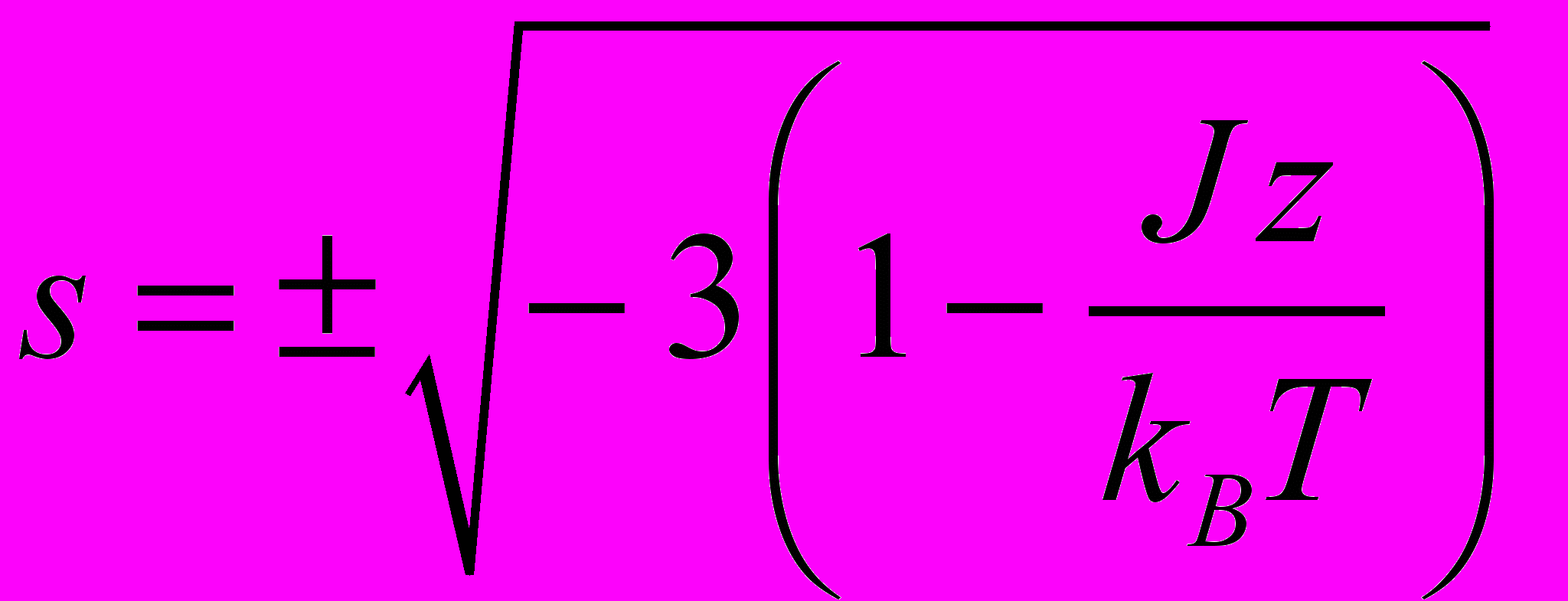





Другими словами, критическая температура этой в системе магнитных стрелок в рассмотренном приближении оказывается равной 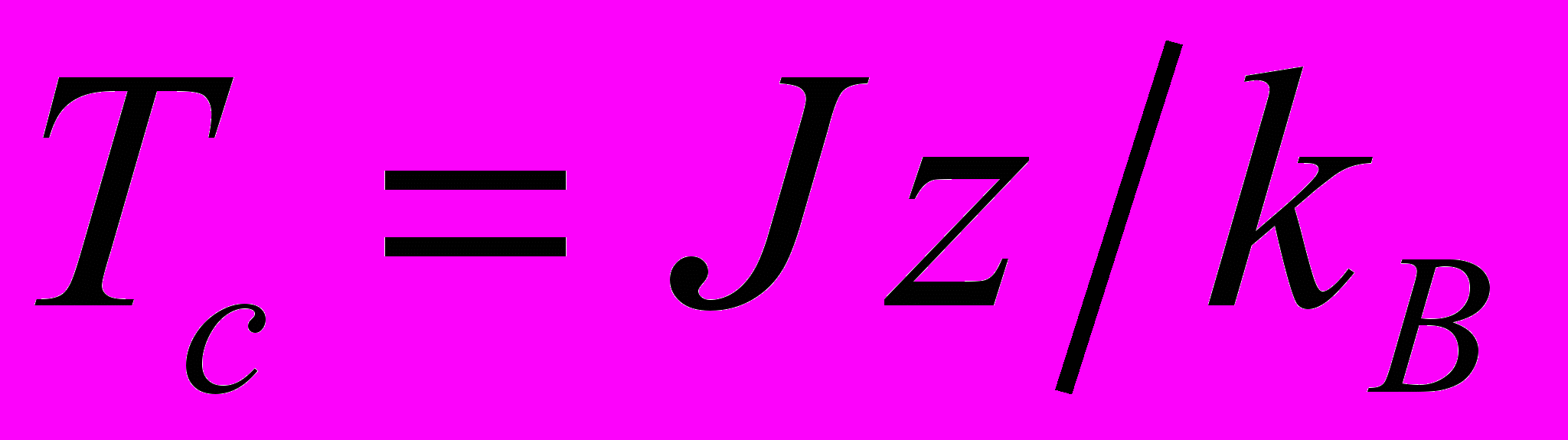. При этом очевидно, что магнитное поле в данном случае является упорядочивающим поле. (Действительно, при 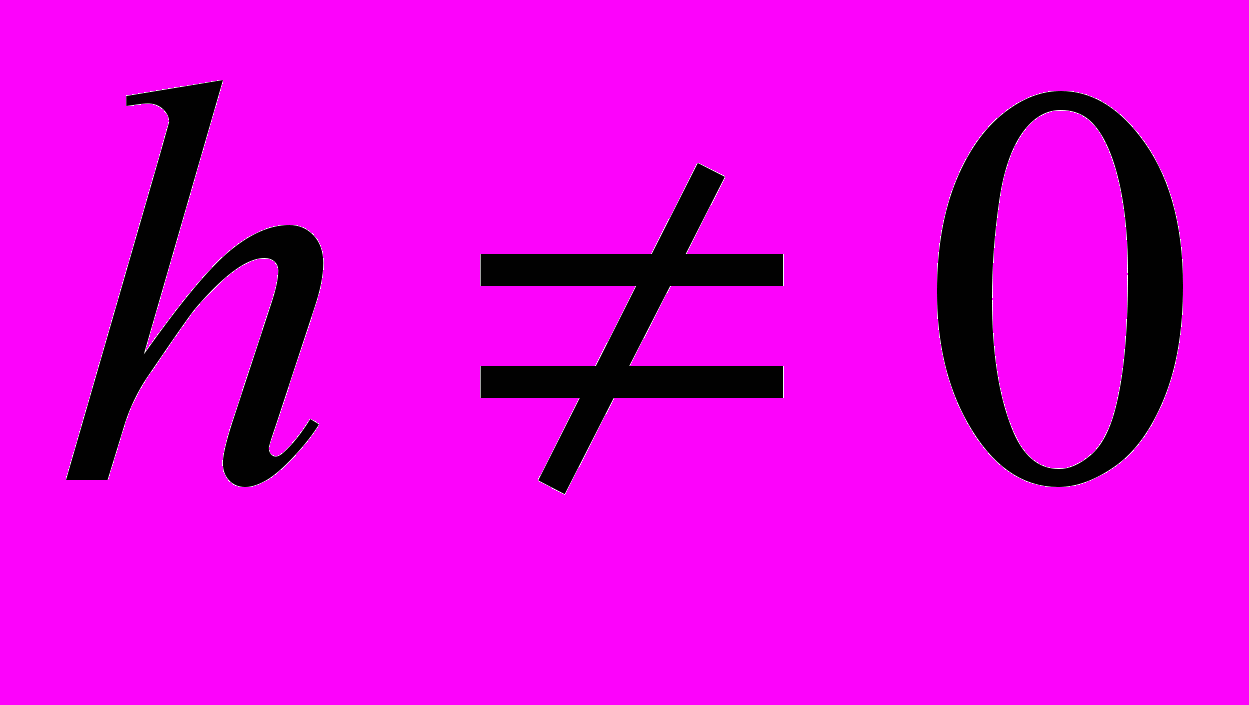решение 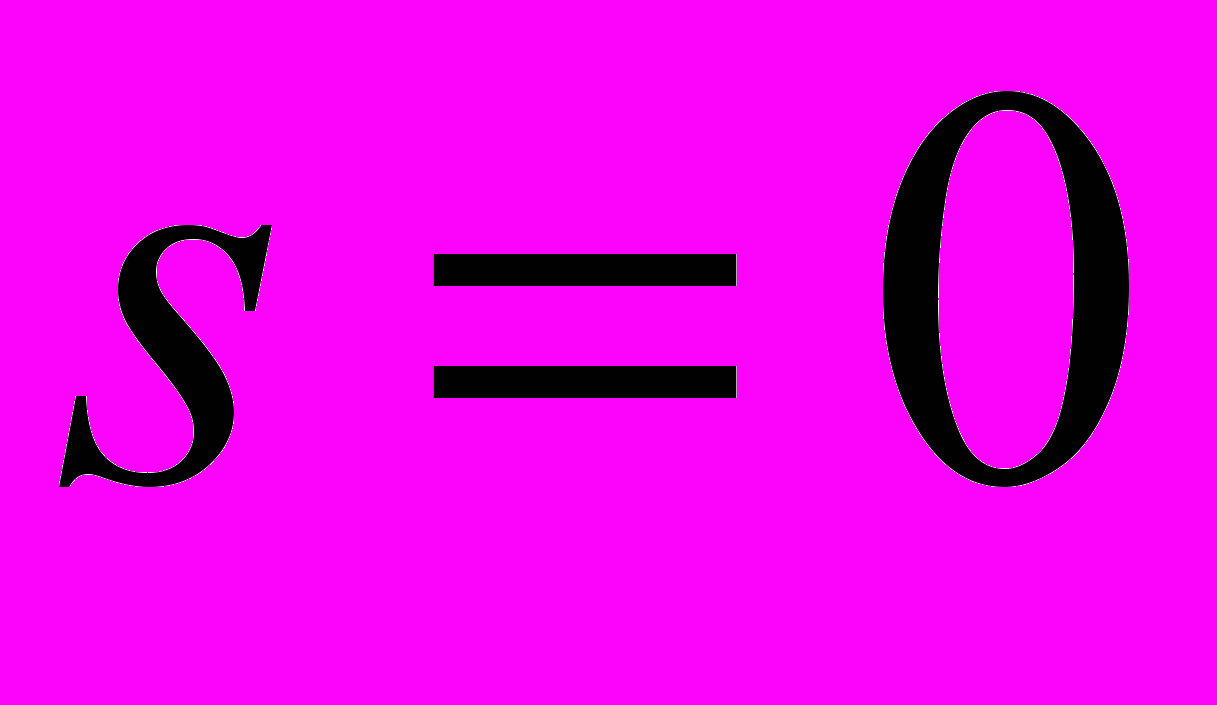отсутствует при сколь угодно высоких температурах. А это означает, что и фазовый переход в этом случае отсутствует


Решеточный газ. Общий случай.

Ранее уже отмечалось, что модель Изинга описывает не только магнитные системы, является существенно более общей моделью. Действительно, в наиболее общем виде модель Изинга может быть сформулирована следующим образом: есть набор идентичных ячеек, каждая из которых может находиться только в двух состояниях.

Обозначим эти состояния как и 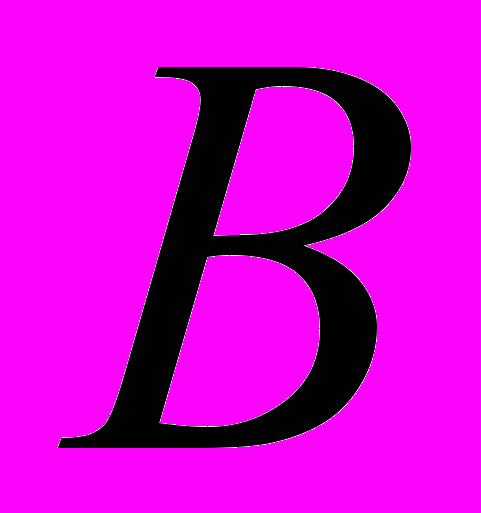. Введем переменную , такую, что





Энергия такой системы может быть записана в виде





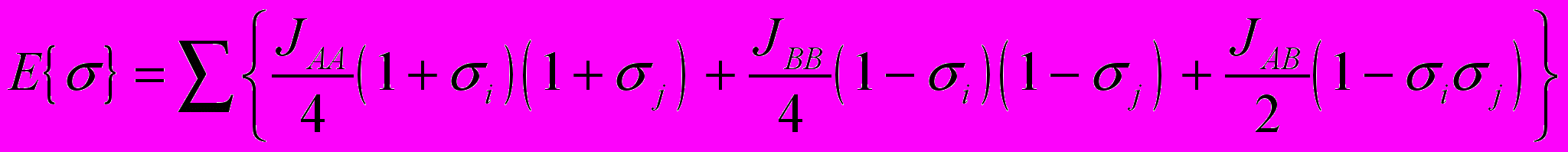
Мы ввели константы взаимодействия между ячейкам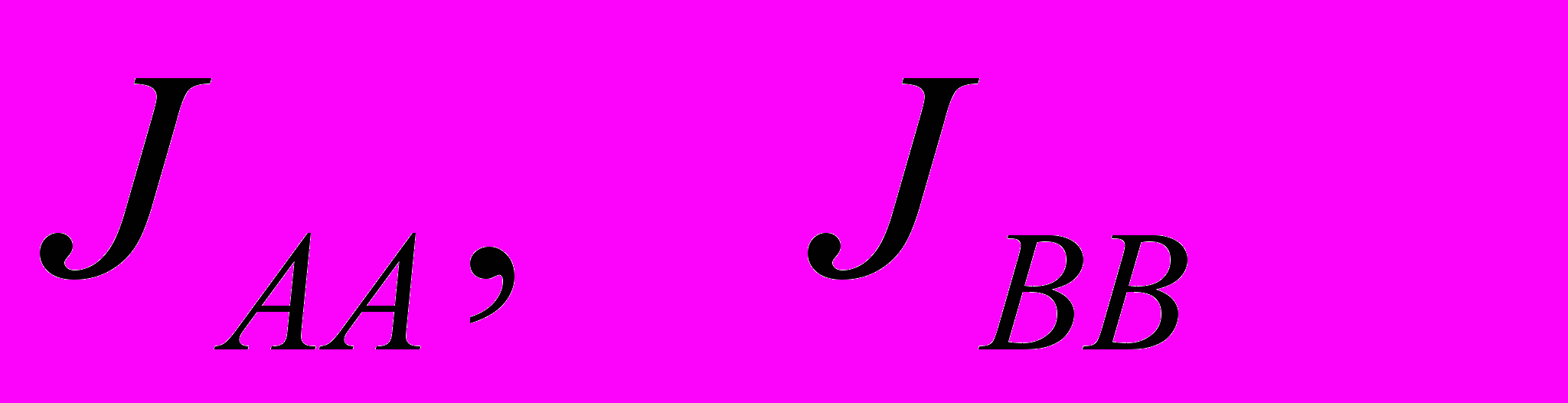и и . Для магнитной системы, рассмотренной выше, состояние соответствует стрелке, направленной вверх, состояние - стрелке, направленной вниз, а для энергий взаимодействия ячеек имеют место соотношения 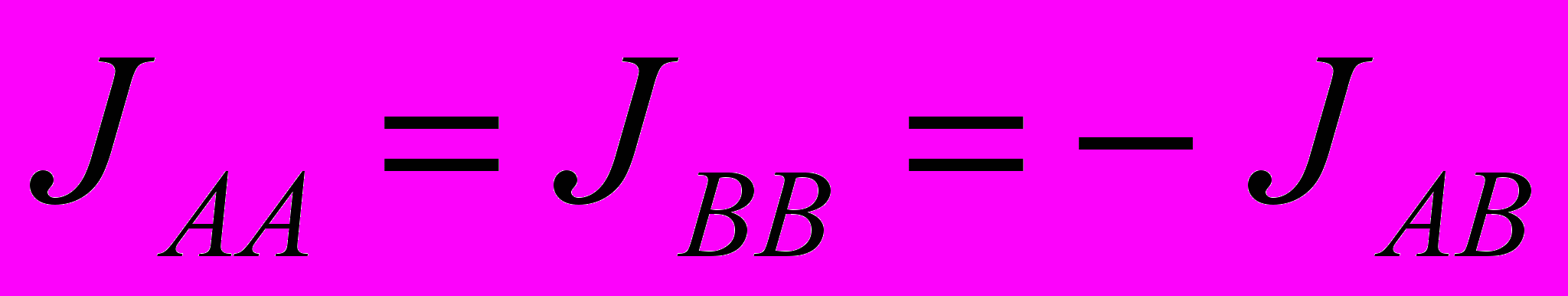. В общем случае эти константы различны. Кроме того сушествуют две возможности: есть или нет закон сохранения числа ячеек в состояниях А и В. Для магнитной системы такой закон сохранения отсутствует. Однако могут быть и другие ситуации. Рассмотрим две из них. Первая – это, так называемая, модель решеточного газа. Вновь рассмотрим несжимаемую решетку, но каждый узел теперь либо занят частицей (состояние А), либо пустой (состояние В). - энергия взаимодействия между частицами. Очевидно, что 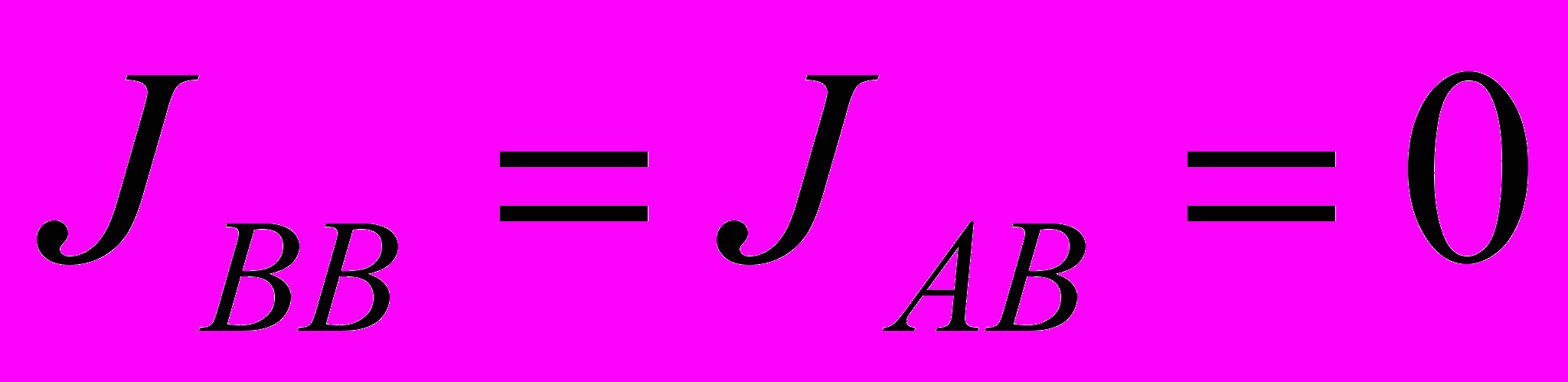. Число частиц (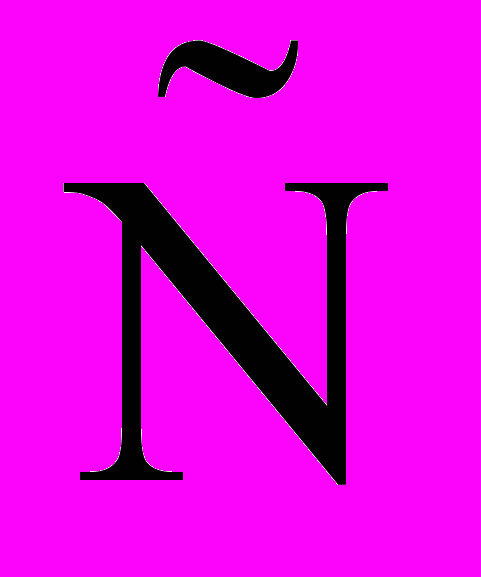) равно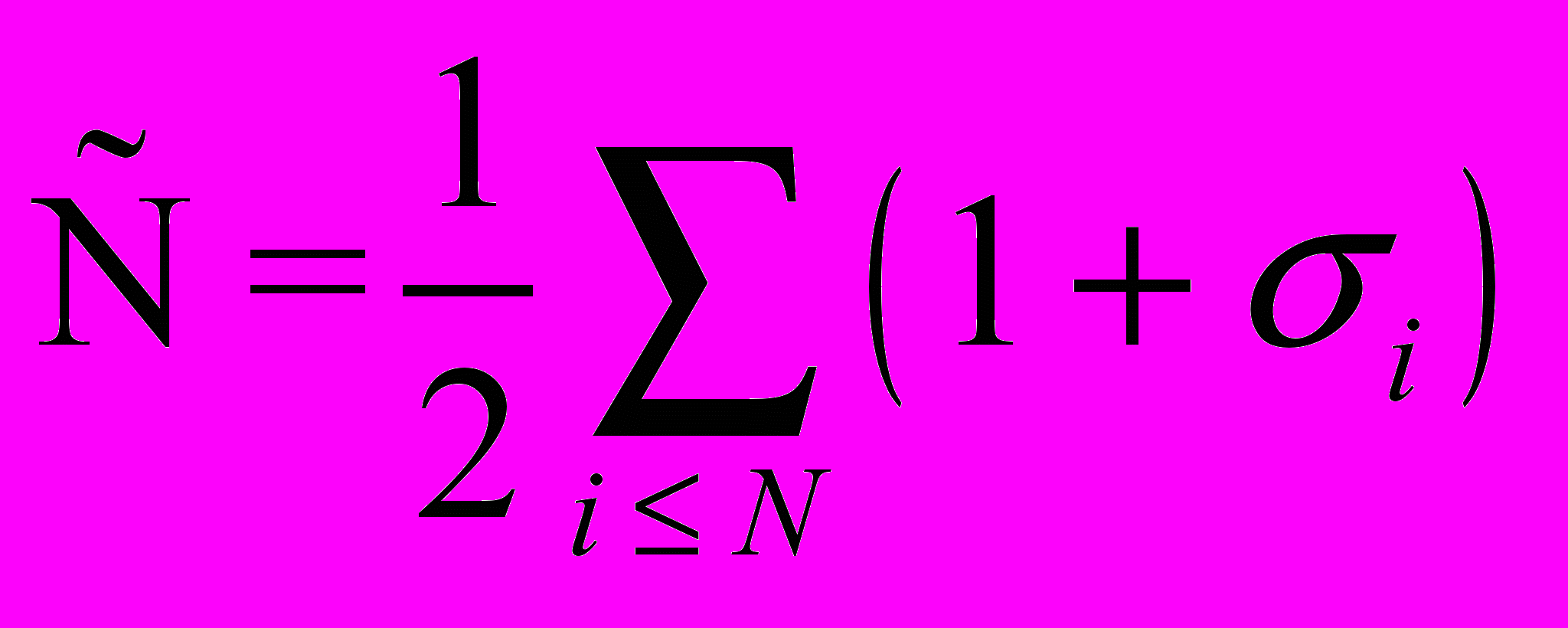



Легко найти среднюю плотность системы


.


Различные конфигурации переменной соответствуют различному числу частиц в системе и, соответственно, различной плотности. Для описания такой системы необходимо использовать большой термодинамический потенциал . Из статистической физики имеем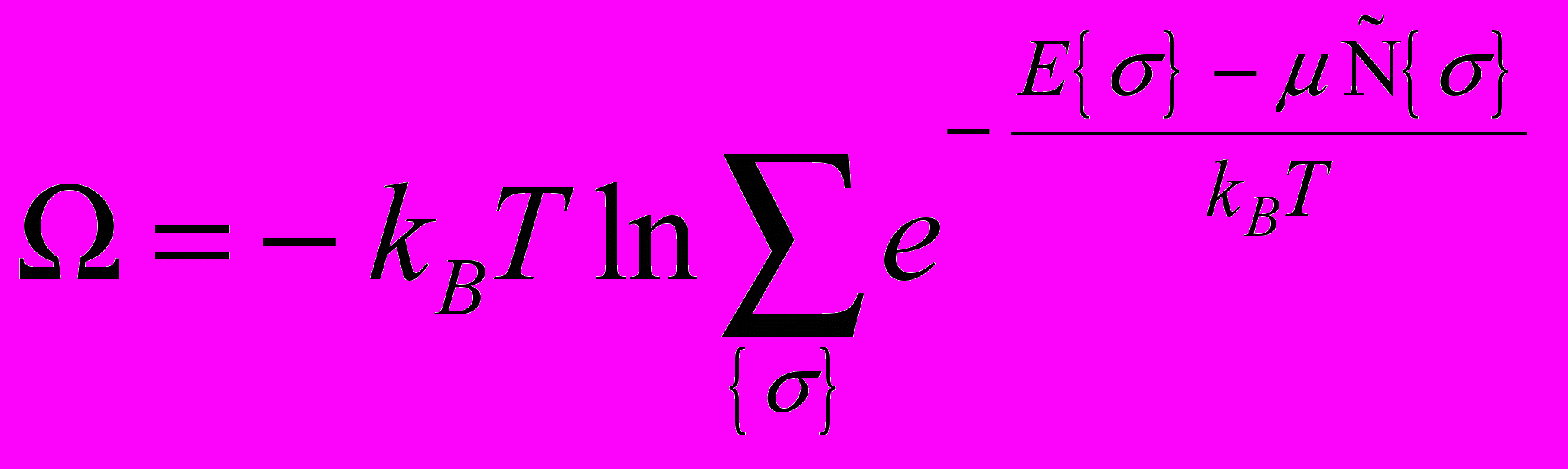





где химический потенциал.. Вычислим выражение, стоящее в показателе входящей под знак суммы экспоненты.





где число ближайших соседей в рассматриваемой решетке и несущественная константа.

Из сравнения экспонент для решеточного газа и магнитной системы очевидно, что эти системы эквивалентны.

В таблице приведены изоморфные друг другу физические свойства магнитной системы и решеточного газа.






Магнитные

системы
Решеточный газ

Энергия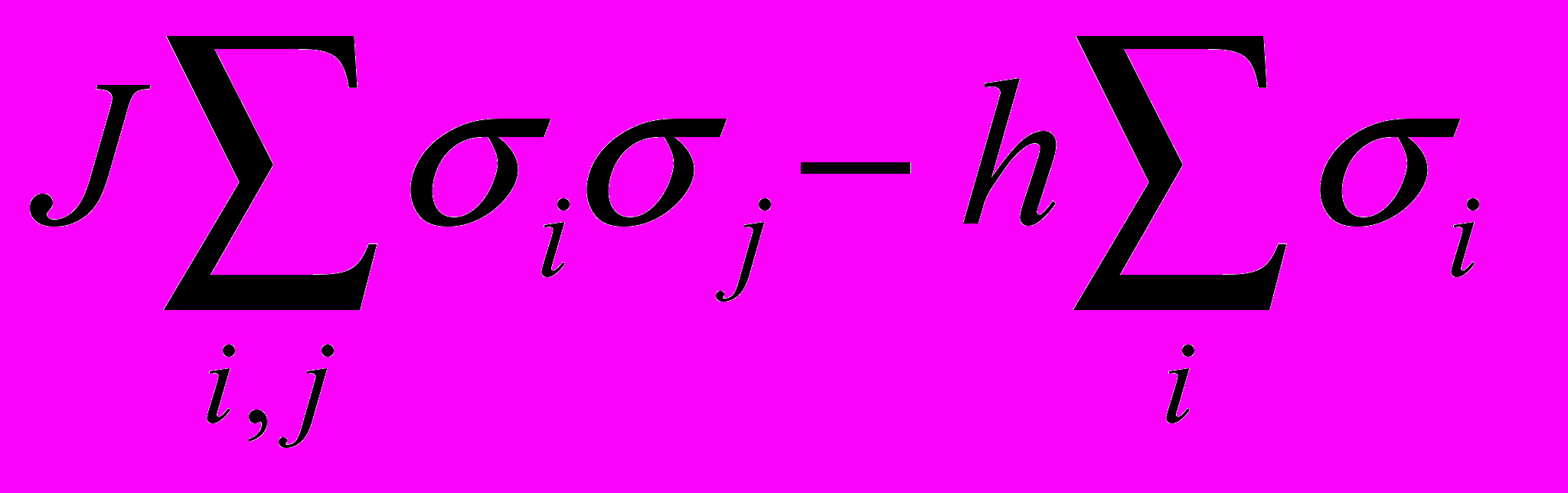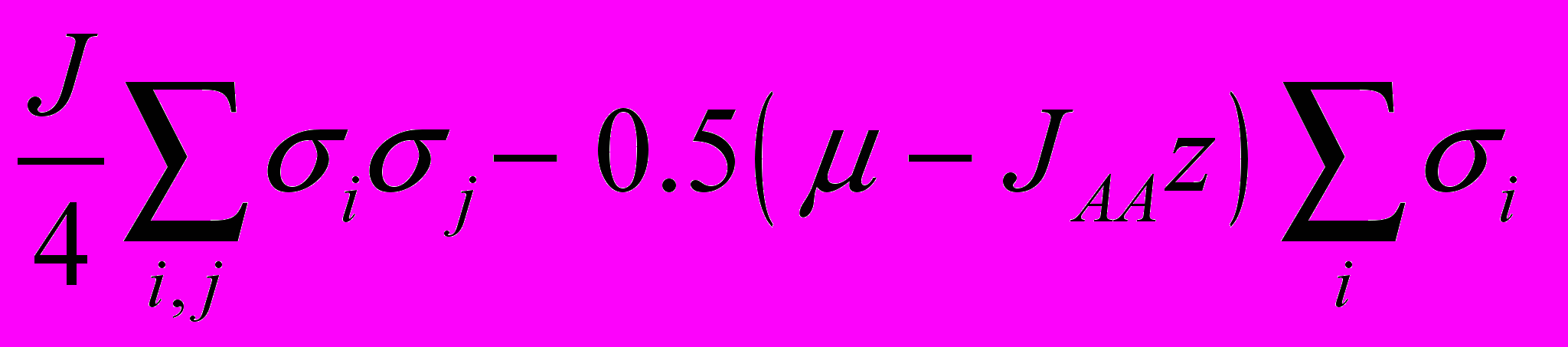





Критическая

температура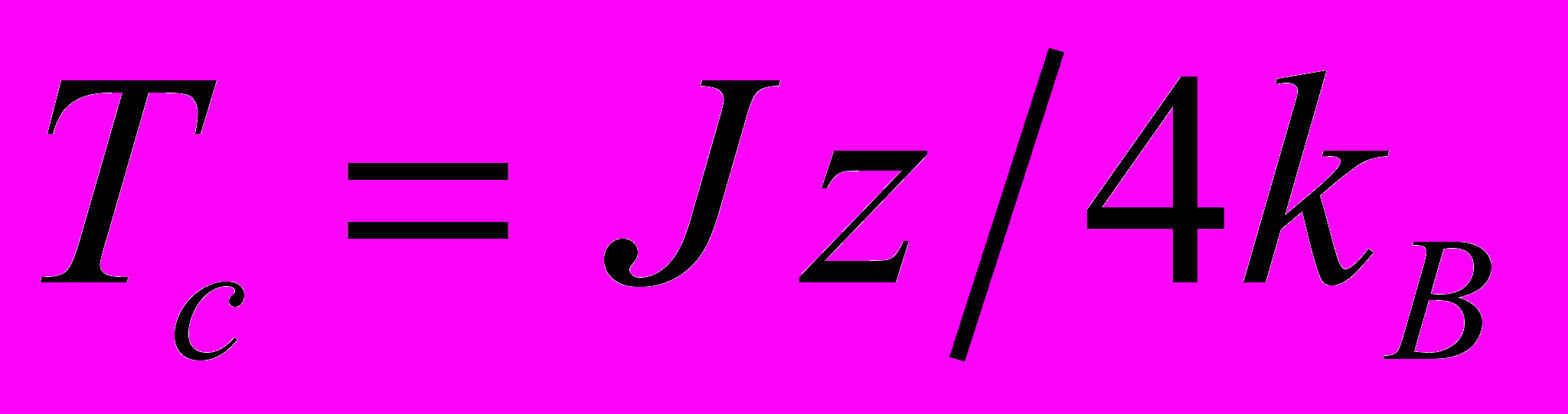




Упорядочивающее

поле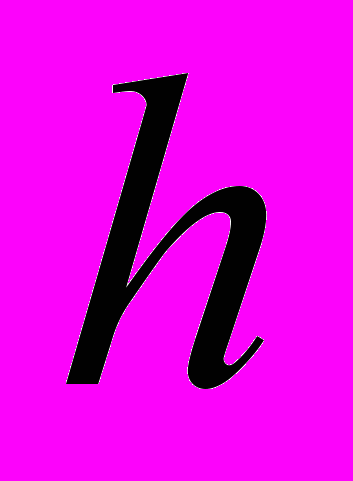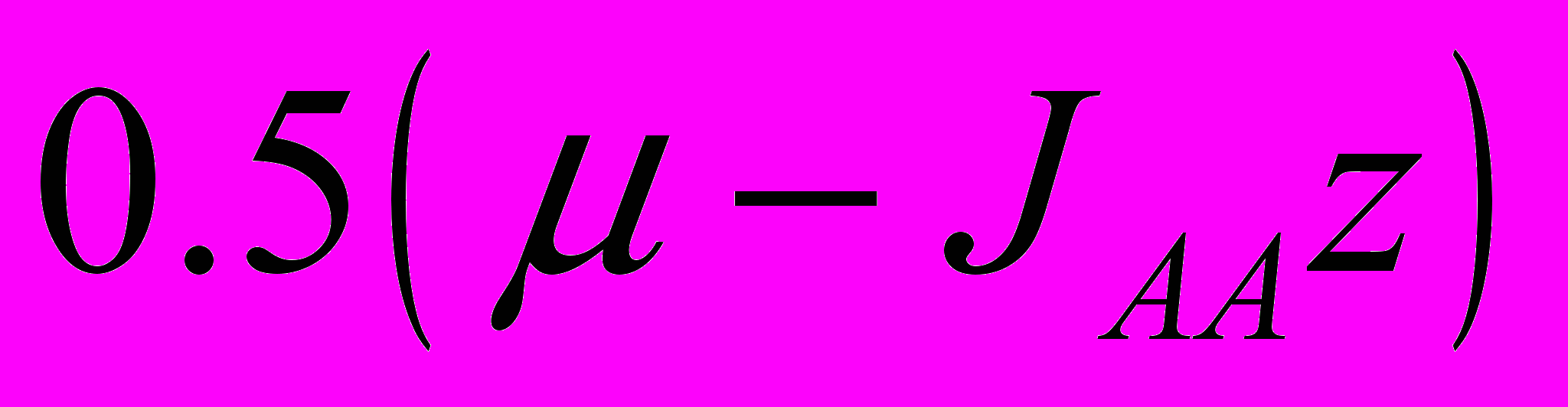




Намагниченность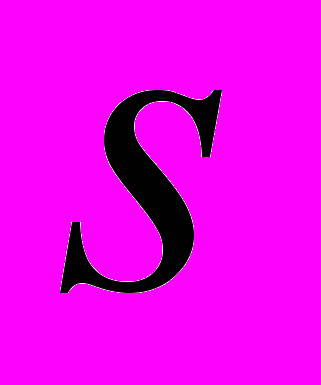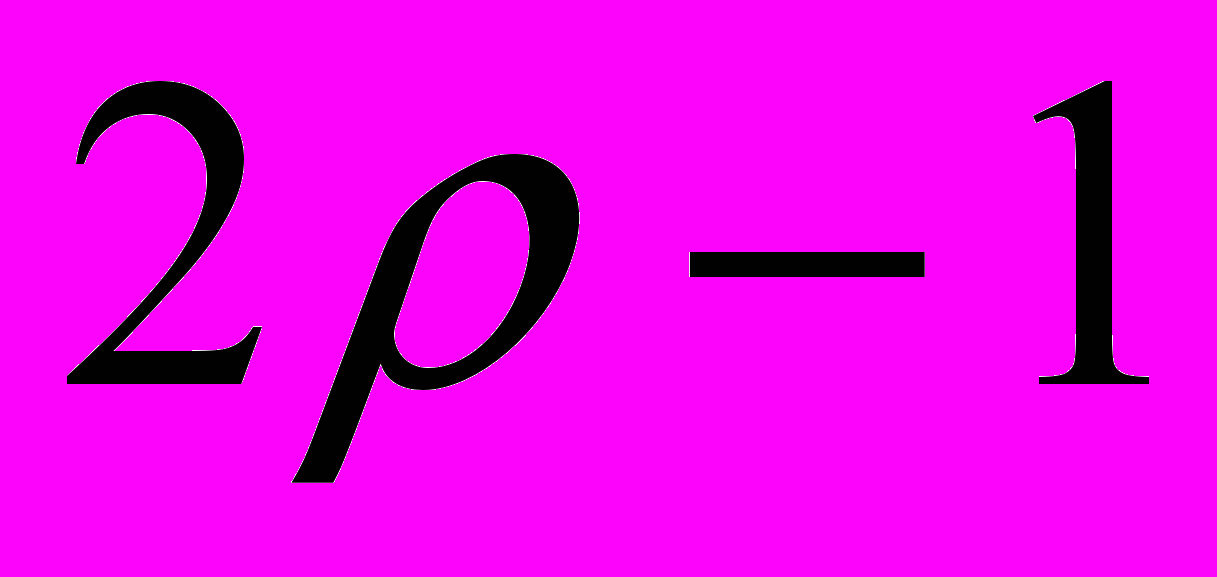





Уравнение

состояния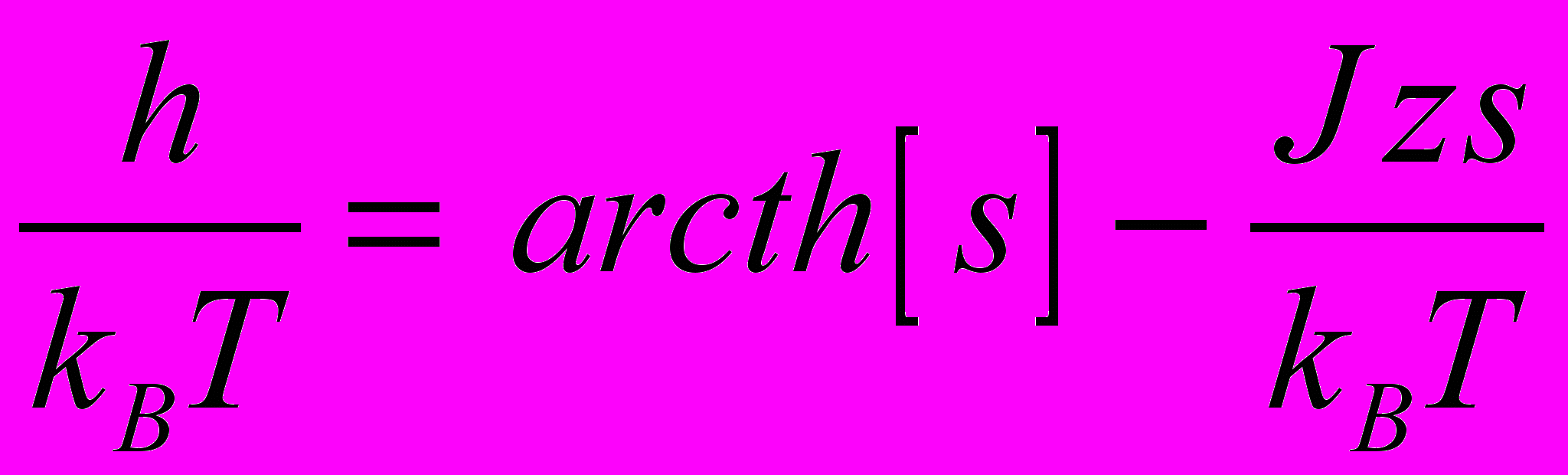





Для случая

и 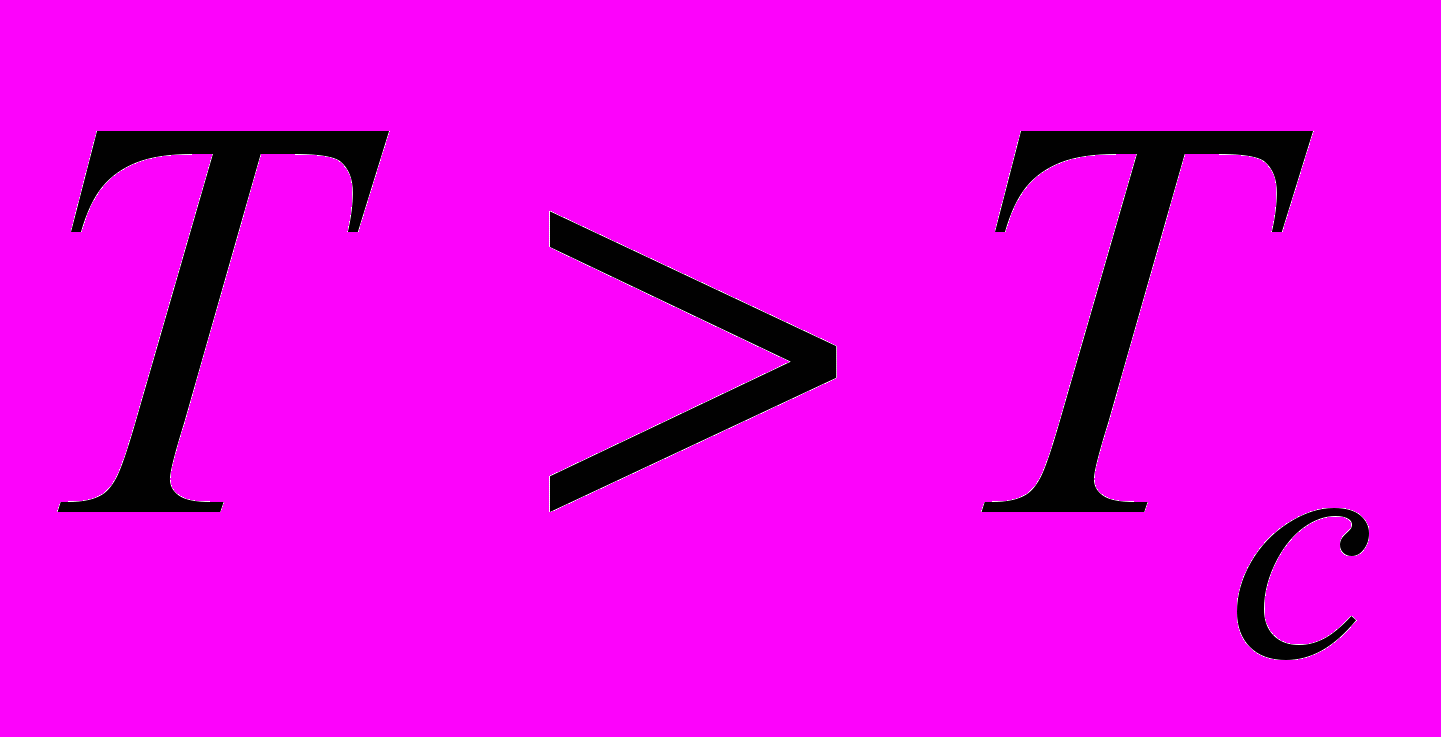мы имеем . Легко найти плотность газа в этом случае.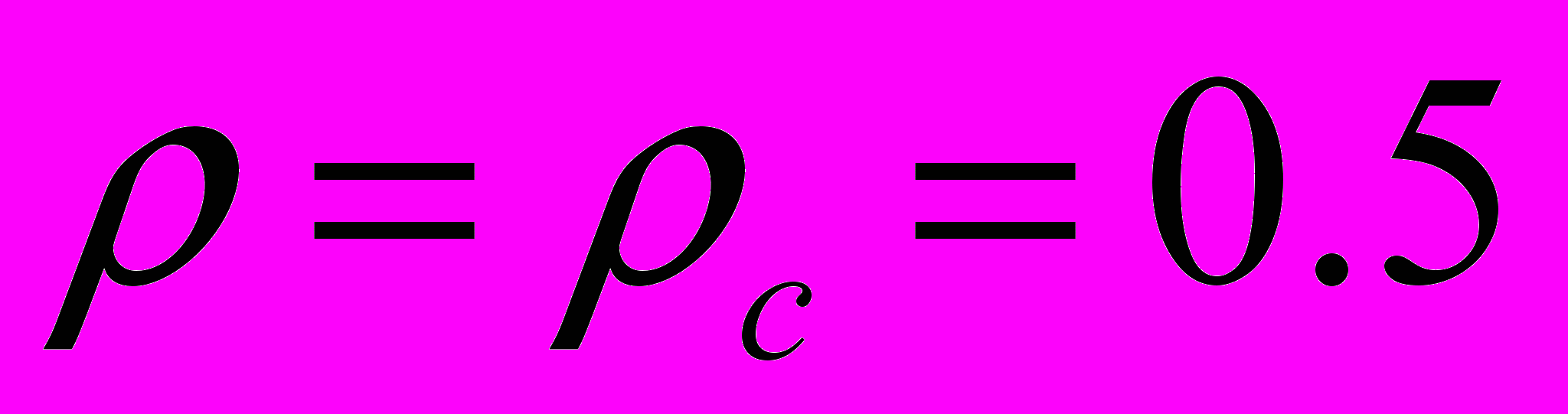

.


Это критическая плотность.

Для случая 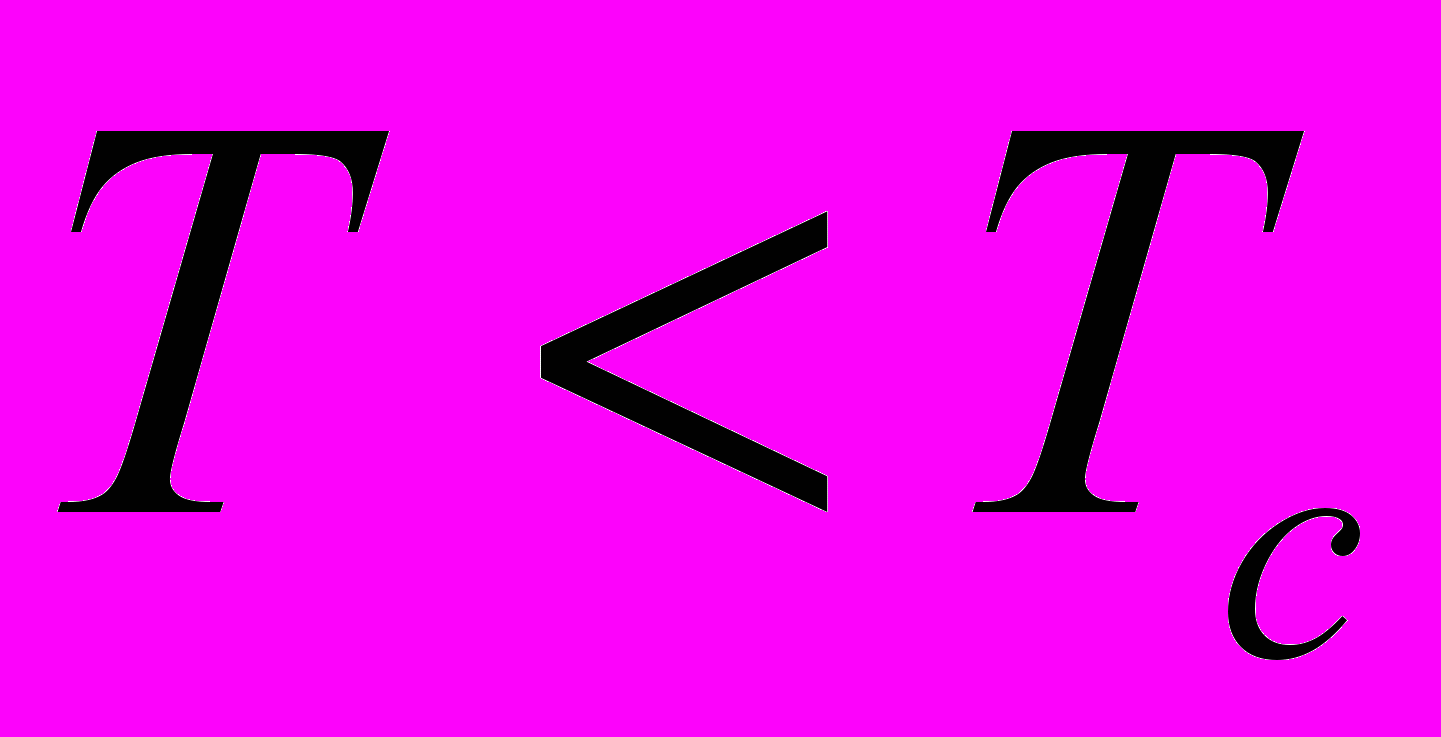имеем два значения переменной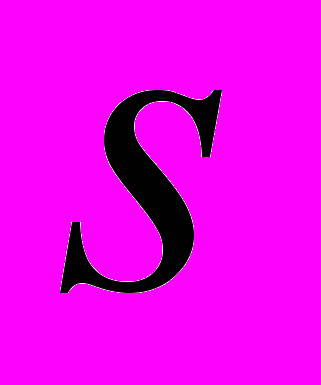





Эти два значения переменной 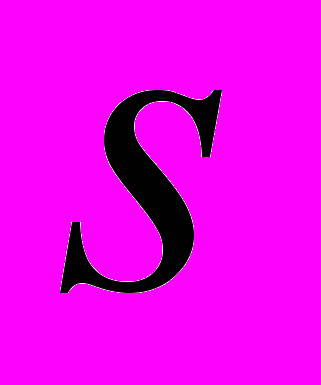соответствуют двум различным плотностям сосуществующих фаз (жидкости и газа)