Программа дисциплины компьютерное моделирование в физике Направление 540200 Физико-математическое образование
| Вид материала | Программа дисциплины |
- Учебная программа курса для направления 540200 физико-математическое образование 540202М, 259.65kb.
- Программа вступительного испытания по дисциплине Физика с теорией и методикой обучения, 388.78kb.
- Аннатационная программа дисциплины интегральные преобразования и операционное исчисление, 30.41kb.
- Учебное пособие для студентов высших учебных заведений, обучающихся по направлению, 1100.02kb.
- Аннатационная программа дисциплины стохастический анализ направление подготовки 010200., 38.6kb.
- Программа вступительных испытаний для лиц, поступающих в магистратуру на направление, 220.49kb.
- Магистерская программа 540204м информатика в образовании Разработчики программы, 115.3kb.
- Рабочая программа дисциплины (модуля) асимптотические методы решения дифференциальных, 19.29kb.
- Рабочая программа дисциплины «Математическое моделирование» од. А. 08; цикл од., 124.08kb.
- Учебная программа дисциплины опд. Р. 05. Математическая логика Направление: 050200, 71.65kb.
Министерство образования московской области
Московский государственный областной Университет
Кафедра вычислительной математики
и методики преподавания информатики
| | Утверждена на заседании кафедры _______________2008 г. |
ПРОГРАММА ДИСЦИПЛИНЫ
компьютерное моделирование в физике
Направление 540200 Физико-математическое образование
Степень (квалификация) – магистр физико-математического образования
Магистерская программа 540204М Информатика в образовании
| | Разработчик программы: доктор технических наук, профессор А.Л. Бугримов |
Москва 2008
СОДЕРЖАНИЕ
ВВЕДЕНИЕ ……………………………………………………………..1. ВЫПИСКА ИЗ ГОСУДАРСТВЕННОГО ОБРАЗОВАТЕЛЬНОГО СТАНДАРТА ……………………………. 2. УЧЕБНАЯ ПРОГРАММА ………………………………………….. 2.1. содержание дисциплины ……………………………………….. 2.2. Тематический план лекционного курса ………………………..2.2. Тематический план семинарских занятий ……………………..2.4. Тематический план самостоятельных занятий ………………. 2.5. Список рекомендуемой литературы ..………………………… 2.5.1. Основная литература …………………………………….. 2.5.2. Дополнительная литература …………………………….. 2.5.3. Перечень ключевых слов ………………………………... 3. ОРГАНИЗАЦИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ …………….. 4. ТЕМЫ КУРСОВЫХ РАБОТ ……………………………………….. 5. ТРЕБОВАНИЯ К ЗАЧЕТУ И ЭКЗАМЕНУ СПИСОК ВОПРОСОВ 5.1. Требования к зачету ……………………………………………. 5.2 Требования к экзамену ………………………………………….. 5.3. Список вопросов к экзамену …………………………………… 6. МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ …………... 6.1. Методические рекомендации к семинарским занятиям и лабораторным работам ………………………………………. 6.2. Методические рекомендации по осуществлению текущего, самостоятельного и итогового контроля ………….. 6.3. Методические рекомендации по организации самостоятельной работы студентов …………………………… 7. ДОПОЛНИТЕЛЬНЫЕ МАТЕРИАЛЫ …………………………….. 7.1. Методические рекомендации по организации изучения дисциплины …………………………………………... 7.2. Образцы практических заданий ……………………………….. 8. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ РЕАЛИЗАЦИИ ПРОГРАММЫ УЧЕБНОЙ ДИСЦМПЛИНЫ …... 8.1. Программы, пособия, литература (в т.ч. в библиотеке МГОУ) 8.2. Технические средства обучения ……………………………….. | 4 5 5 5 6 7 7 8 8 8 9 10 10 10 10 11 11 12 12 12 13 13 13 13 14 14 15 |
ВВЕДЕНИЕ
Закономерности реального мира познаются идеальными методами. Невозможно познать какое-либо явление во всей его исчерпывающей полноте. Чтобы получить достаточные для практики результаты необходимо ограничить изучаемое явление с точки зрения его главных особенностей. Остальными приходится пренебрегать. В этом состоит существо моделирования.
В этом смысле вся физическая наука являет собой пример поистине грандиозного моделирования самых различных явлений природы.
Идеальной является модель, которая допускает аналитическое описание. Это бывает редко. Чаще приходится сталкиваться с ситуацией, когда аналитическое решение получить невозможно, или эксперимент является дорогостоящим, или ... опасным. В таких случаях проанализировать явление становится возможным с помощью современных компьютерных технологий. Поэтому одной из важнейших составных частей современного моделирования является моделирование компьютерное.
Компьютерное моделирование - имитация, численный эксперимент, компьютерная графика сейчас уверенно теснят описательные методы научного исследования и даже классические способы использования математики (количественные сопоставления, расчет).
Следует показать, что в отличие от обычной расчетной схемы, из которой предполагается извлечь интересующие исследователя расчетные показатели, математическая или компьютерная модель демонстрирует само явление, освобождая исследователя от анализа промежуточных состояний, в ряде случаев ненужного. Показательным примером может служить модель массового обслуживания, которая позволяет игнорировать индивидуальные предпочтения клиентов.
Необходимо обратить внимание на все увеличивающееся значение таких моделей в экономике, медицине (модель развития эпидемии, процесс старения, модели эволюционных процессов).
Конкретные примеры предлагается иллюстрировать рабочими компьютерными программами с непосредственным проигрыванием их в лаборатории.
1. ВЫПИСКА ИЗ ГОСУДАРСТВЕННОГО
ОБРАЗОВАТЕЛЬНОГО СТАНДАРТА
Данная дисциплина Государственным образовательным стандартом не предусмотрена. Она является более углубленным продолжением дисциплины «Компьютерное моделирование», изучаемой бакалаврами как дисциплины по выбору из раздела ДНМ.В.
Учебная дисциплина предназначена для студентов магистратуры 540204М – «Информатика в образовании» в рамках проблемного поля направления 050200.68 – «Физико-математическое образование».
Дисциплина изучается в XI семестре. На ее изучение отводится 150 час, из которых на аудиторные занятия планируется 72 час из расчета: лекции – 36 час, лабораторные занятия – 36 час.
2. УЧЕБНАЯ ПРОГРАММА
2.1. Содержание дисциплины
Тема 1. Моделирование как метод познания
Понятия: «модель» и «макет». Моделирование как метод познания. Натурные и абстрактные модели. Виды моделирования в естественных и технических науках. Компьютерная модель. Моделирование в физике.
Тема 2. Математическое моделирование
Физическая основа формулирования математической модели. Имитационное моделирование. Модели динамических систем. Инструментальные программные средства для моделирования динамических систем.
Тема 3. Численный эксперимент
Численные, натурные эксперименты и их взаимосвязь с теорией. Достоверность численной модели. Анализ и интерпретация модели.
Тема 4. Избранные модели в механике
Моделирование движения тел в поле сил тяготения. Полет тела, брошенного под заданным углом к горизонту с заданной начальной скоростью. Свободное падение шарика с упругим отражением от горизонтальной поверхности. Модель движения планет вокруг Солнца. Механические колебания. Математический маятник. Физический маятник. Маятник с трением. Независимые колебания. Фигуры Лиссажу.
Тема 5. Световые явления
Эффекты смешения цветов движущихся (вращающихся) объектов. Прохождение света через границу двух сред. Принцип Гюйгенса. Принцип минимума времени прохождения светом расстояния между двумя точками, лежащими по разные стороны границы раздела.
Тема 6. Квантование уравнение Шредингера
Одномерное стационарное уравнение Шредингера и его анализ. Алгоритм квантования. Разработка программы.
Тема 7. Фракталы в физике
Объекты и явления, породившие создание фрактальных моделей. Понятие меры Хаусдорфа – Безековича. Традная кривая Кох. Снежинка Кох. Ковер Серпинского. Кластеры. Экспериментальный метод идентификации фрактальных свойств. Ограниченная диффузией агрегация частиц.
2.2. Тематический план лекционного курса
| №№ п/п | Тема или содержание | Время, час |
| 1 | Введение в математическое и компьютерное моделирование | 2 |
| 2 | Моделирование как метод познания. Основные этапы моделирования. | 2 |
| 3 | Физическая основа формулирования математической модели. | 2 |
| 4 | Численный эксперимент. Численные, натурные эксперименты и их взаимосвязь с теорией. Достоверность численной модели. Анализ и интерпретация модели. | 2 |
| 5 | Моделирование движения тел в поле сил тяготения. Полет тела, брошенного под заданным углом к горизонту с заданной начальной скоростью. | 2 |
| 6 | Моделирование падения шарика с отражением. | 2 |
| 7 | Модель движения планет вокруг Солнца. | 2 |
| 8 | Механические колебания. Математический маятник. Физический маятник. Маятник с трением. | 2 |
| 9 | Независимые колебания. Фигуры Лиссажу. | 2 |
| 10 | Световые явления. Эффекты смешения цветов движущихся (вращающихся) объектов. | 2 |
| 11 | Прохождение света через границу двух сред. Принцип Гюйгенса. | 2 |
| 12 | Прохождение света через границу двух сред. Принцип минимума времени прохождения светом расстояния между двумя точками, лежащими по разные стороны границы раздела. | 2 |
| 13 | Квантование уравнение Шредингера | 2 |
| 14 | Фрактальное моделирование. Понятие фрактала. Триадная кривая Кох. | 2 |
| 15 | Самоподобие и фрактальная размерность. Ковер Серпинского. | 2 |
| 16 | Реализация самоподобия с помощью рекурсии. | 2 |
| 17 | Моделирование случайных величин | 2 |
| 18 | Кластеры. Ограниченная диффузией агрегация частиц. | 2 |
| | ИТОГО | 36 |
2.3. Тематический план практических (лабораторных) занятий
| №№ п/п | Тема или содержание | Время, час |
| 1 | Полет тела, брошенного под заданным углом к горизонту с заданной начальной скоростью. | 2 |
| 2 | Моделирование падения шарика с отражением. | 2 |
| 3 | Модель движения планет вокруг Солнца. | 2 |
| 4 | Математический маятник. Физический маятник. Маятник с трением. | 4 |
| 5 | Фигуры Лиссажу. | 2 |
| 6 | Эффекты смешения цветов при наблюдении за вращающихся дисками с окрашенными секторами. | 4 |
| 7 | Прохождение света через границу двух сред. Принцип Гюйгенса. | 2 |
| 8 | Прохождение света через границу двух сред. Принцип минимума времени прохождения светом расстояния между двумя точками, лежащими по разные стороны границы раздела. | 4 |
| 9 | Квантование уравнение Шредингера | 2 |
| 10 | Триадная кривая Кох. | 4 |
| 11 | Ковер Серпинского. | 2 |
| 12 | Моделирование случайных величин | 2 |
| 13 | Модель ограниченной диффузией агрегация частиц. | 4 |
| | ИТОГО | 36 |
Примечание. Лабораторная работа «Квантование уравнение Шредингера» проводится демонстрационным способом.
2.4. Тематический план практических самостоятельных занятий
| №№ п/п | Тема или содержание | Время, час |
| 2 | Моделирование падения шарика с отражением.. Разработка модели. Проект программы. | 2 |
| 3 | Модель движения планет вокруг Солнца. Изучение темы из астрономии. Вывод основных соотношений. | 2 |
| 4 | Математический маятник. Физический маятник. Маятник с трением. Краткие сведения из теоретической физики. | 4 |
| 5 | Фигуры Лиссажу. | 2 |
| 6 | Эффекты смешения цветов при наблюдении за вращающихся дисками с окрашенными секторами. | 4 |
| 7 | Прохождение света через границу двух сред. Принцип Гюйгенса. | 2 |
| 8 | Прохождение света через границу двух сред. Принцип минимума времени прохождения светом расстояния между двумя точками, лежащими по разные стороны границы раздела. | 4 |
| 9 | Квантование уравнение Шредингера (сведения из теоретической физики) | 4 |
| 10 | Триадная кривая Кох (ознакомление с основами физики фракталов) | 4 |
| 11 | Ковер Серпинского (ознакомление с основами физики фракталов) | 2 |
| 12 | Моделирование случайных величин | 2 |
| 13 | Модель ограниченной диффузией агрегация частиц (ознакомление с основами физики фракталов) | 4 |
| | ИТОГО | 36 |
2.5 Список рекомендуемой литературы
2.5.1. Основная литература
1. Бугримов А.Л., Мельников С.А. Методичкеские рекомендации по
проведению практикума по решению задач на ЭВМ и оформлению
отчетов по выполненным работам. – М.: МГОУ, 2005. - 16 с.
2. Бугримов А.Л., Тихонова Е.А., Мельников С.А. Математическое
моделирование процессо в экологических системах. – М.: МГОУ,
2006. – 16 с.
3. Могилев А.В., Пак Н.И., Хеннер Е.К. Информатика: Учеб. Пособие для
студ. Пед. ВУЗов. М.: Изд. центр «Академия», 200. - 816 с.
4. Самсонов Б.Б. и др. Компьютерная математика. Ростов-на-Дону:
«Феникс», 2002. - 512 с.
2.5.2. Дополнительная литература
1. Вычислительные комплексы и моделирование сложных систем. Сб. На-
учных трудов факультета вычислительной математики и кибернетики
МГУ/ Под ред. Л.Н.Королева, П.С.Краснощекова. М.: Изд-во МГУ.
1989. 215 с.
2. Дульнев.Г.Н., Парфенов В.Г., Сигалов А.И. Применение ЭВМ для реше-
ния задач теплообмена. М.: Высшая школа. 1990. 206 .
3. Чернышев М.К., Гаджиев М.Ю. Математическое моделирование
иерархических систем (с приложениями к биологии и экономике). М.:
Наука, 1983. - 182 с.
2.5.3. Перечень ключевых слов
Вербальная модель
Дескриптивные модели
Детерминированная система
Динамическая система
Дискретная случайная величина
Имитация
Информационная модель
Компьютерная графика
Линейное программирование
Макет
Массовое обслуживание
Многокритериальные модели
Модель
Объект
Оптимизационные модели
Популяция
Последовательностей независимых случайных испытаний
Распределенные параметры
Сосредоточенные параметры
Статистические испытания
Стохастическая система
Хаотическое поведение
Численный эксперимент
3. ОРГАНИЗАЦИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Тематический план практических самостоятельных занятий приведен в разделе 2.4.
Специфика дисциплины «Компьютерное моделирование в физике» ориентирует студентов на активную самостоятельную работу:
- овладение терминологией;
- приобретение навыков в постановке задач;
- приобретение навыков в проектировании расчетов;
- привитие навыков четких рассуждений;
- практика в анализе связей между процессами;
- самостоятельная разработка алгоритма решаемой задачи;
- практика в написании программ для ЭВМ;
- самостоятельная работа с книгой.
4. ТЕМЫ КУРСОВЫХ РАБОТ
В данном разделе приведены примерные темы курсовых работ. Естественно, темы курсовых работ должны постоянно обновляться с тем, чтобы учесть быстрые изменения в информационных науках.
1. Моделирование в экологии.
2. Математические модели в экономике.
3. Моделирование прогноза курса валют.
4. Модели сложных физических явлений.
5. Логические модели.
6. Моделирование равновесия в природе.
7. Моделирование азартных игр.
8. Фрактальные модели.
9. Бифуркация Ферхюльста.
5. ТРЕБОВАНИЯ К ЗАЧЕТУ И ЭКЗАМЕНУ
СПИСОК ВОПРОСОВ
5.1. Требования к зачету
Для сдачи зачета по дисциплине «Компьютерное моделирование в физике» необходимо выполнить все требуемые практические задания (получить допуск к зачету или экзамену у преподавателя, проводившего семинарские занятия). Существенным моментом является посещаемость занятий (в случае пропусков занятий предполагается более подробный опрос по темам пропущенных занятий).
На зачет выносится материал, излагаемый в лекционном курсе и рассматриваемый на семинарских занятиях. Для получения зачета надо правильно ответить на несколько поставленных вопросов и решить предложенные несложные задачи. В затруднительных ситуациях (в отдельных случаях) допускается на зачете воспользоваться тетрадью с записью материалов лекций и семинаров в присутствии преподавателя. При этом преподаватель может убедиться, в какой степени студент ориентируется в «своих» материалах и по ряду дополнительных вопросов (по тетради) решить вопрос о зачете.
5.2 Требования к экзамену
К экзамену допускаются магистранты, отчитавшиеся по семинарским занятиям сдавшие зачет. На экзамен выносится материал, излагаемый в лекционном курсе и рассматриваемый на семинарских занятиях. Обязательным требованием является умение формулировать высказывания, грамотно применять логические связки, четко и быстро ориентироваться в истинностных значениях логических формул.
Предварительно магистранты знакомятся с программой курса и содержанием экзаменационных вопросов, а также с набором элементарных задач, которые предлагаются на экзамене. В экзаменационном билете дается задача и теоретический вопрос. При ответах рекомендуется сначала отчитаться по задаче, а затем - по теоретическому вопросу.
5.3. Список вопросов к экзамену
Введение в математическое и компьютерное моделирование
Моделирование как метод познания. Основные этапы моделирования.
Физическая основа формулирования математической модели.
Моделирование падения шарика с отражением.
Основы теории подобия в моделировании. Понятие критериев.
Фрактальное моделирование. Понятие фрактала. Триадная кривая Кох.
Самоподобие и фрактальная размерность. Ковер Серпинского.
Реализация самоподобия с помощью рекурсии.
Кластеры. Ограниченная диффузией агрегация частиц.
Математические модели в биологии и экологии. Нормальное размножение.
Моделирование неограниченного роста.
Зарождение равновесия при размножении.
Влияние конкуренции на равновесие.
Вмешательство в равновесие. Абсолютные квоты отлова.
Вмешательство в равновесие. Относительные квоты отлова.
Моделирование равномерно распределенной случайной величины.
Моделирования случайной величины с произвольной плотностью.
Статистическое моделирование числа .
Имитационное моделирование. Задача о разорении игрока.
Математические модели в экономике. Задача о плане производства.
Математические модели в экономике. Прямая и двойственная задачи
линейного программирования.
Математические модели в экономике. Задача о производстве хлебозавода.
Математические модели в экономике. Задача о рационе.
Математические модели в экономике. Транспортная задача.
6. МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
6.1. Методические рекомендации к семинарским занятиям
и лабораторным работам
Для эффективного овладения дисциплиной «Компьютерное моделирование в физике» рекомендуется:
- освоить фундаментальные понятия дисциплины;
- овладеть элементарными приемами составления программ;
- усвоить язык физики моделирования;
- получить практические навыки в выводе формул;
- регулярно прорабатывать изученный материал.
6.2. Методические рекомендации по осуществлению
текущего, самостоятельного и итогового контроля
Текущий контроль следует осуществлять по направлениям: посещаемость занятий; выполнение текущих заданий. Самоконтроль студенты могут проводить по результатам решения задач, по результатам пробных попыток самостоятельной разработки несложных задач моделирования отдельных процессов. При этом крайне целесообразно вести краткий конспект, а также дополнять основной конспект сведениями, полученными и усвоенными в результате самостоятельной работы. Итоговый контроль проводится с помощью отчетов по выполненным заданиям, зачетам и экзаменам.
6.3. Методические рекомендации по организации
самостоятельной работы студентов
Виды самостоятельной работы магистрантов отмечены в разделе (3) настоящего УМК. Самостоятельную работу магистрантов можно также организовать за счет выбора ими индивидуального задания. На семинарских занятиях - самостоятельное решение поставленных задач. На лекциях - дискуссия, обсуждение мнений магистрантов. На экзамене - проверка ознакомления магистрантов с литературой.
7. ДОПОЛНИТЕЛЬНЫЕ МАТЕРИАЛЫ
7.1. Методические рекомендации по организации
изучения дисциплины
Дисциплина изучается информатиками в XI-м семестре. На ее изучение отводится 150 час, из которых на аудиторные занятия планируется 72 час из расчета: лекции – 36 час, лабораторные занятия – 36 час.
7.2. Образцы практических заданий
Какие природные процессы можно моделировать с помощью соотношения
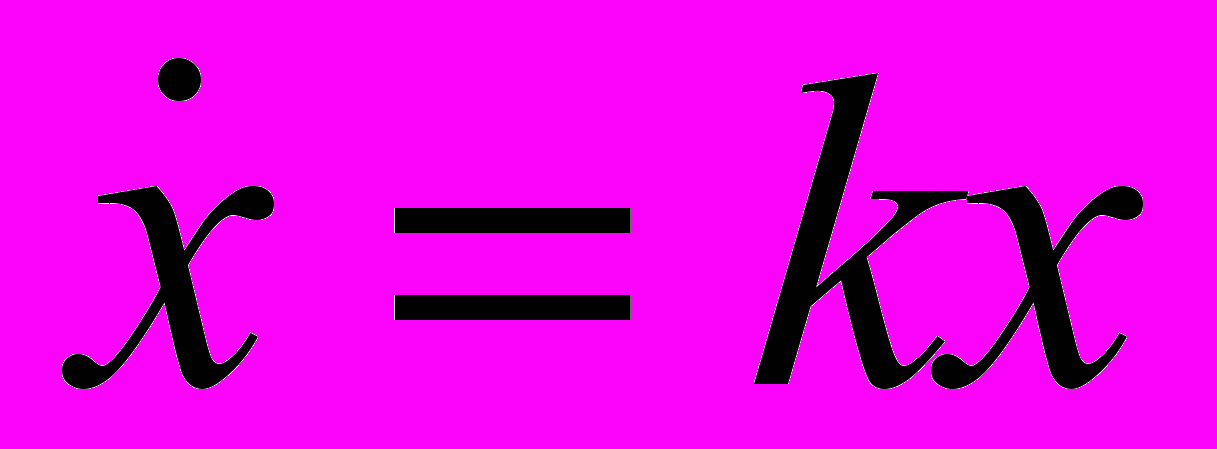, k > 0 ?Дать обоснованное решение.
Какие природные процессы можно моделировать с помощью соотношения
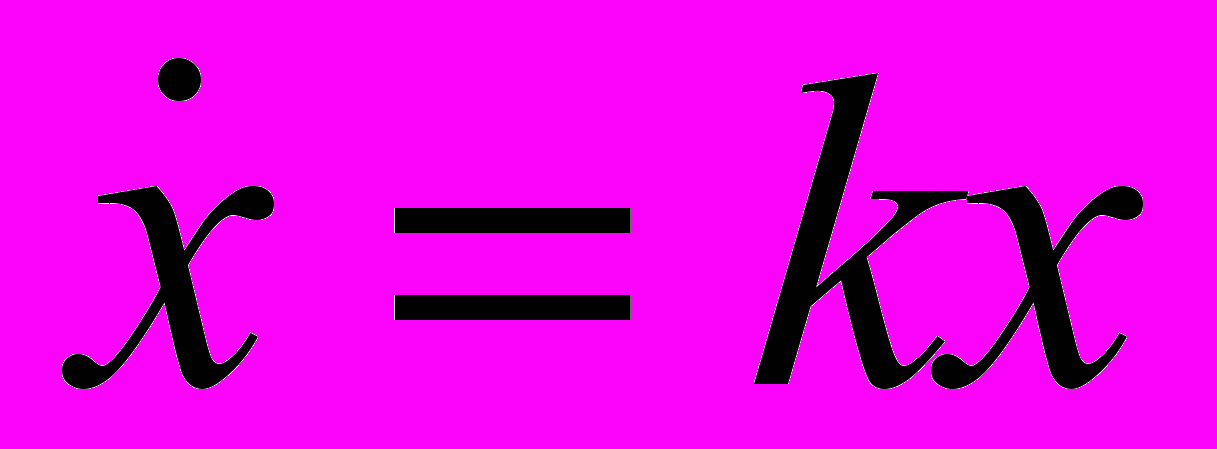, k < 0 ?Дать обоснованное решение.
14
Какие природные процессы можно моделировать с помощью соотношения
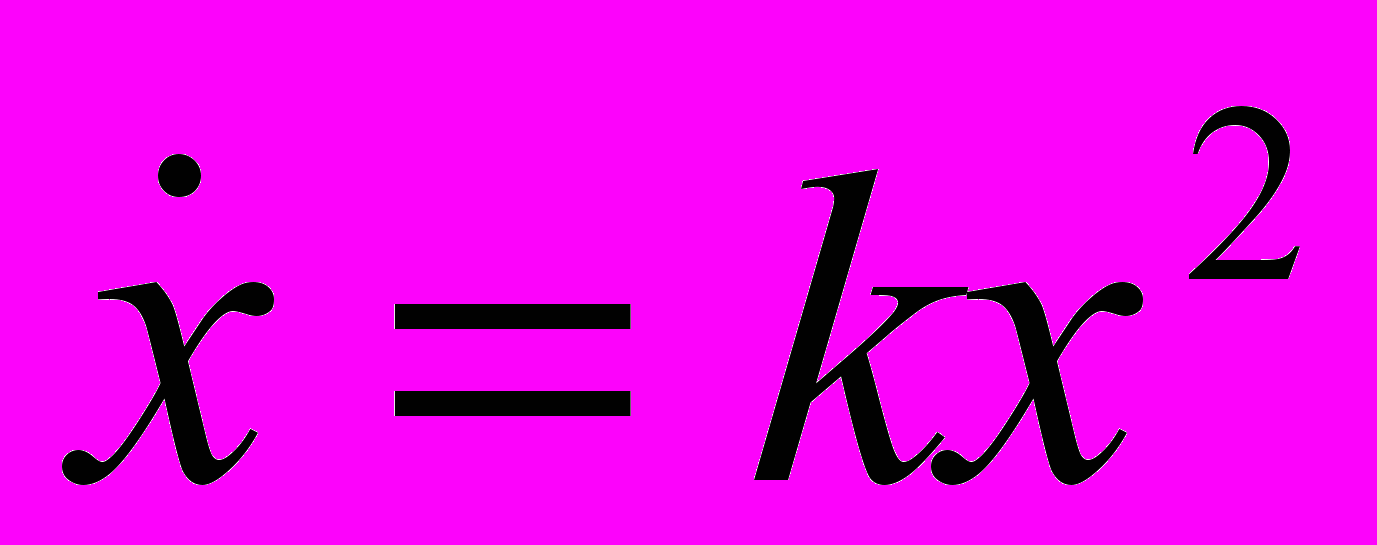?Дать обоснованное решение.
В 1800 г. на счету одного человека было 2$. Смоделировать рост банковского вклада на текущий год из расчета 2% годовых. Дать обоснованное решение.
Местность заражена распылением 1 кг радиоактивного материала. Смоделировать изменение количество материала, если период его полураспада равен 1620 лет
Завод выпускает в сутки велосипедов в четыре раза больше, чем мотоциклов. Стоимость мотоцикла в два раза выше стоимости велосипеда. На складе можно разместить не более 70 единиц продукции. Смоделировать оптимальный план работы завода для достижения максимальной прибыли.
8. МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ ОБЕСПЕЧЕНИЕ РЕАЛИЗАЦИИ
ПРОГРАММЫ УЧЕБНОЙ ДИСЦИПЛИНЫ
8.1. Программы, пособия, литература (в т.ч. в библиотеке МГОУ)
Библиотека МГОУ обеспечивает дисциплину «Компьютерное моделирование в физике» в полном объеме. В ней имеется следующая литература.
1. Бугримов А.Л., Мельников С.А. Методичкеские рекомендации по
проведению практикума по решению задач на ЭВМ и оформлению
отчетов по выполненным работам. – М.: МГОУ, 2005. - 16 с.
2. Бугримов А.Л., Тихонова Е.А., Мельников С.А. Математическое
моделирование процессо в экологических системах. – М.: МГОУ,
2006. – 16 с.
3. Вычислительные комплексы и моделирование сложных систем. Сб. На-
учных трудов факультета вычислительной математики и кибернетики
МГУ/ Под ред. Л.Н.Королева, П.С.Краснощекова. М.: Изд-во МГУ.
1989. 215 с.
4. Дульнев.Г.Н., Парфенов В.Г., Сигалов А.И. Применение ЭВМ для реше-
ния задач теплообмена. М.: Высшая школа. 1990. 206 .
5. Могилев А.В., Пак Н.И., Хеннер Е.К. Информатика: Учеб. Пособие для
студ. Пед. ВУЗов. М.: Изд. центр «Академия», 200. - 816 с.
6. Самсонов Б.Б. и др. Компьютерная математика. Ростов-на-Дону:
«Феникс», 2002. - 512 с.
7. Чернышев М.К., Гаджиев М.Ю. Математическое моделирование
иерархических систем (с приложениями к биологии и экономике). М.:
Наука, 1983. - 182 с.
8.2. Технические средства обучения
На факультете средства вычислительной техники имеются в достаточном количестве: 3 компьютерных класса с современными персональными компьютерами.
Некоторые занятия по компьютерному моделированию целесообразно проводить в игровом варианте.
Предусмотрено проведение игровых занятий по статистическому определению числа , по моделированию вероятности встречи, по моделировнию равновесия в живой природе. Имеются соответствующие методические разработки:
1. Бугримов А.Л., Мельников С.А. Методичкеские рекомендации по
проведению практикума по решению задач на ЭВМ и оформлению
отчетов по выполненным работам. – М.: МГОУ, 2005. - 16 с.
2. Бугримов А.Л., Тихонова Е.А., Мельников С.А. Математическое
моделирование процессо в экологических системах. – М.: МГОУ,
2006. – 16 с.
Министерство образования московской области
Государственное образовательное учреждение
высшего профессионального образования
Московский государственный областной Университет
(МГОУ)
ФИЗИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ
Кафедра вычислительной математики
и методики преподавания информатики
компьютерное моделирование в физике
Учебно-методический комплекс
Направление 050200.68 «Физико-математическое образование»
Степень (квалификация) – магистр физико-математического образования
Магистерская программа 540204М – «Информатика в образовании»
Москва 2010
Министерство образования московской области
Государственное образовательное учреждение
высшего профессионального образования
Московский государственный областной Университет
(МГОУ)
ФИЗИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ
Кафедра вычислительной математики
и методики преподавания информатики
| | УТВЕРЖДАЮ Декан физико-математического факультета профессор А.Л. Бугримов 10.05.2010 |
| | УТВЕРЖДЕНА на заседании кафедры от 10.05.2010 № 3 |
компьютерное моделирование в физике
Учебно-методический комплекс
Направление 050200.68 «Физико-математическое образование»
Степень (квалификация) – магистр физико-математического образования
Магистерская программа 540204М – «Информатика в образовании»
Форма обучения: очная
| | Разработчик: доктор технических наук, профессор А.Л. Бугримов |
Москва 2010
| УДК 348.146 | Печатается по решению ученого совета физико-математического факультета и редакционного совета МГОУ |
Рабочая программа дисциплины «Компьютерное моделирование в физике» / Составитель А.Л. Бугримов. - М.: МГОУ, 2010. – 16 с.
Рабочая программа предназначена для руководства в преподавании дисциплины по выбору «Компьютерное моделирование в физике» студентам очной формы обучения направления подготовки 050200.68 «Физико-математическое образование» в 11 семестре.
Рабочая программа составлена с учетом Государственного образовательного стандарта Высшего профессионального образования по направлению подготовки 050200.68 «Физико-математическое образование», утвержденного Министерством образования Российской Федерации от 31.01.2005.
© Московский государственный университет, 2010
© Издательство МГОУ, 2010
©Бугримов А.Л., 2010