Geum.ru

Урок изучения нового материала Цель урока : расширить понятие «окружности»

Вид материалаУрок

Содержание


Организационный момент.
II. Изучение нового материала.
О окружности. Д С пределение.
Диаметр – это наибольшая из хорд окружности!
L равна удвоенному произведению числа π
Подобный материал:

Тема: «Длина окружности и площадь круга».


Тип урока: урок изучения нового материала

Цель урока: расширить понятие «окружности» и ее элементов, установить связь между ними и начать формирование понятий длины окружности и площади круга.

Задачи урока: образовательные:
  1. вспомнить первоначальные сведения об окружности, полученные в начальной школе;
  2. ввести понятие длины окружности;
  3. ввести понятие площади круга;
  4. познакомить учащихся с постоянной величиной π;
  5. отработать навыки проведения эксперимента и с помощью экспериментальных данных делать выводы;
  6. отработать навыки соотнесения экспериментальных данных с данными, полученными в результате вычислений;
  7. отработать навыки решения текстовых задач на нахождение длины окружности и площади круга;

воспитательные:
  1. воспитание чувства взаимопомощи и самоконтроля;
  2. воспитание уважения к мнению каждого ученика;
  3. воспитание терпимости к критике (поощрять критику, касающуюся существа дела, но не критику личности).

развивающие:
  1. развитие логического мышления;
  2. развитие внимательности;
  3. развитие познавательного интереса к математике.

Оборудование: Компьютер, проектор для демонстрации кроссворда и геометрического материала (для закрепления материала), раздаточный материал; для практической работы: предмет с круглым дном, нитки, ножницы, циркуль, линейка, карандаш.

Форма работы: групповая.

Ход урока:


«Истина не рождается в голове отдельного человека, она рождается между людьми, совместно ищущими, в процессе их диалогического общения»

Бахтин М.М.
    1. Организационный момент.

1. Стадия вызова.(5 минут)

Вступительное слово учителя:

- Ребята, подумайте и скажите, о чем сегодня на уроке пойдет речь: «это замкнутая кривая, все точки которой одинаково удалены от данной точки (центра О)»? (Окружность).

- Итак, речь пойдет об окружности.

Сообщение темы.

- Что вы уже знаете по этой теме? (ответы учащихся).

Сообщение цели урока.

II. Изучение нового материала.

2. Стадия осмысления. (10 минут)

Каждому ученику выдается текст под определенным номером, ученик знакомится с теоретическим материалом, выделяет главное, составляет в тетради опорный конспект. Учитель выступает в роли наблюдателя (практическое задание пока не выполняется). Выполнив работу, ученик сам себя оценивает (лист оценивания «Мои успехи» лежит у каждого на парте).

Текст № 1

Что такое окружность?


О
окружности.

Д


С
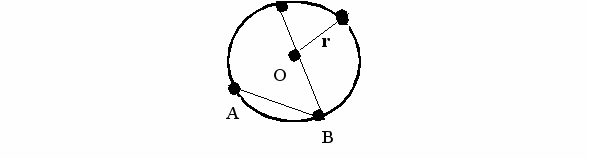
пределение. Окружность – это замкнутая кривая линия, все точки которой находятся на равном расстоянии от данной точки плоскости, называемой центром


Точка О – центр окружности.

ОД = r – радиус окружности (это отрезок, соединяющий центр окружности с любой ее точкой). По-латыни radius – это спица колеса.

АВ – хорда окружности (это отрезок, соединяющий любые две точки на окружности).

СВ = d – диаметр окружности (это хорда, проходящая через центр окружности). С греческого диаметр – это «поперечник».

Диаметр – это наибольшая из хорд окружности!

Диаметр окружности d и ее длина радиуса r связаны между собой следующей формулой: d = 2* r.

Окружность – удивительно гармоничная фигура, древние греки считали ее самой совершенной, так как окружность – единственная кривая, которая может «скользить сама по себе», вращаясь вокруг центра. Основное свойство окружности дает ответ на вопросы, почему для ее вычерчивания используют циркуль и почему колеса делают круглыми, а не квадратными. Колесо – одно из самых великих изобретений человечества.

Окружность можно начертить с помощью циркуля. Для этого надо:
  1. Отметить точку на плоскости.
  2. Ножку циркуля с острием совместить с отмеченной точкой, а ножкой с грифелем вращать вокруг этой точки.
  3. Получилась геометрическая фигура – окружность.



Задание: Начертите окружность, укажите центр окружности, ее радиус, диаметр, хорду. Сделайте соответствующие обозначения. Измерьте длину радиуса и диаметра окружности. Сделайте вывод.

Текст № 2

Практическая работа

«Измерение длины окружности»


Вы знаете, что длину отрезка можно измерить с помощью линейки. А как измерить длину окружности, если сама окружность – кривая линия?

Есть несколько способов измерения длины окружности. И вот один из них:
  1. Возьми предмет с круглым дном и обведи это дно карандашом в тетради.
  2. Оберни дно предмета ниткой (один раз) так, чтобы конец нитки совпал с началом в одной и той же точке окружности, оставшуюся часть нитки отрежь.
  3. Выпрями эту нитку и по линейке измерь ее длину, это и будет длина окружности.

Длину окружности обозначают буквой L. Запиши в тетради свои измерения: L = … см.
  1. Измерь диаметр дна предмета. Обозначив его букой d, запиши, чему равен диаметр: d = … см.
  2. Вычисли отношение L : d (с точностью до сотых) и результат запиши в тетрадь.

Текст № 3

«Знакомство с числом π»


Число π – обозначение отношения длины окружности L к ее диаметру d.

Многие ученые – математики пытались доказать, что это отношение есть число постоянное, не зависящее от размеров окружности. Впервые это удалось сделать древнегреческому математику Архимеду. Он нашел довольно точное значение этого отношения. Архимед жил на Сицилии с 287 г. до 212 г. до н.э. Используя рассуждения, он доказал, что

π ≈ 22/7 ≈ 3, 14

На самом деле число π не может быть выражено точной дробью. Математик 16 века Лудольф имел терпение вычислить его с 35 десятичными знаками. В 1946 – 1947 гг. два ученых независимо друг от друга вычислили 808 десятичных знаков числа π.

Приближенное значение π с точностью до пяти десятичных знаков можно запомнить по следующей строчке (по числу букв в слове):


π ≈ 3, 14159 - «это я знаю и помню прекрасно»


Итак, число π можно найти по формуле: π = L : d.


Текст № 4

Длина окружности и площадь круга.


Длина окружности L равна произведению числа π (пи) на ее диаметр d:


L = π d

π ≈ 3, 14 (постоянная величина)


Длину окружности можно выразить и через ее радиус. Тогда Длина окружности L равна удвоенному произведению числа π на ее радиус r:

L = 2π r

Так как d = 2 r.


Площадь круга S равна произведению числа π на квадрат радиуса r:


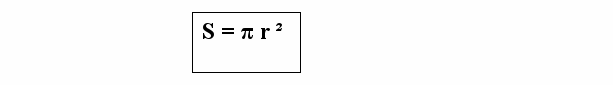
Задание:
  1. Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
  2. Найдите длину окружности, диаметр которой равен 40 дм.
  3. Найдите площадь круга, радиус которого 10 см.






3. Стадия размышления. (20 минут)

ШАГ 1.

Учащиеся пересаживаются в рабочие группы с одинаковыми текстами. В

группе происходит обмен информацией, разбираются все затруднения, непонятные моменты. Выполняются практические задания. Учитель выступает в роли консультанта. После проделанной работы учащиеся оценивают друг друга.

ШАГ 2.

Учащиеся возвращаются в свои группы для взаимообучения, они по очереди знакомят друг друга с изученным материалом. Задача группы: чтобы каждый овладел всей темой целиком. Каждый ученик выступает в роли учителя, остальные же делают записи в тетради. После выступления всех членов группы, ее участники снова оценивают друг друга и ставят оценку в сводную ведомость. Учитель – координатор.

III. Подведение итогов урока. 4. Стадия рефлексии. Осуществляется с использованием компьютера и проектора (см. Приложение). (5 минут)

Вопросы учителя:
  • Что нового вы узнали на уроке?
  • Что показалось наиболее интересным?
  • Проверка полученных знаний: решение кроссворда с картинками. Оно сопровождается повторением определений хорды, радиуса, диаметра, круга, формул длины окружности и площади круга. И как результат – ключевое слово: «ОКРУЖНОСТЬ» (по горизонтали).

Выставление оценок, комментарии по выполнению домашнего задания.

IV. Домашнее задание.

п. 24, № 867, № 868.