Теория функций действительных переменных

Вид материала

Документы

Содержание Тема 2. Мера Лебега. Тема 3. Функции измеримые по Лебегу. Тема 5. Интеграл Римана.

Подобный материал:

• Лекция 19. Предел и непрерывность функции нескольких переменных, 34.61kb.
• Программа междисциплинарного государственного экзамена по специальности 090102 Компьютерная, 116.53kb.
• Повторение. Аналитические методы оптимизации функций одной и нескольких переменных, 250.23kb.
• Программа дисциплины «Математический анализ», 500.52kb.
• Программа дисциплины «математический анализ», 432.47kb.
• Высшая математика II иттф (тф 9…13), эл-16, 2004-2005 уч год, 50.97kb.
• Рабочая программа учебной дисциплины «Теория функций комплексной переменной» Специальность, 57.58kb.
• Позволяющий с помощью компьютерной техники интерполировать функции одной и многих переменных, 6.93kb.
• Высшая математика, 34.34kb.
• Значение формулы логики предикатов, 9.17kb.

ТЕОРИЯ ФУНКЦИЙ ДЕЙСТВИТЕЛЬНЫХ ПЕРЕМЕННЫХ


Кафедра математического анализа и теории функций.

Факультет физико-математических и естественных наук.

Обязательный курс

Объем учебной нагрузки: лекции – 72 час., практические занятия – 72 час.

Цель курса:

Познакомить с идеями и обучить методам исследования задач действительного анализа.


Содержание курса:


Тема 1. Топология в евклидовом пространстве.

Открытые и замкнутые множества в евклидовом пространстве, диадические кубы. Компактные множества, критерии компактности.

Тема 2. Мера Лебега.

Пример функции, не интегрируемой по Риману. Мера на кольце .

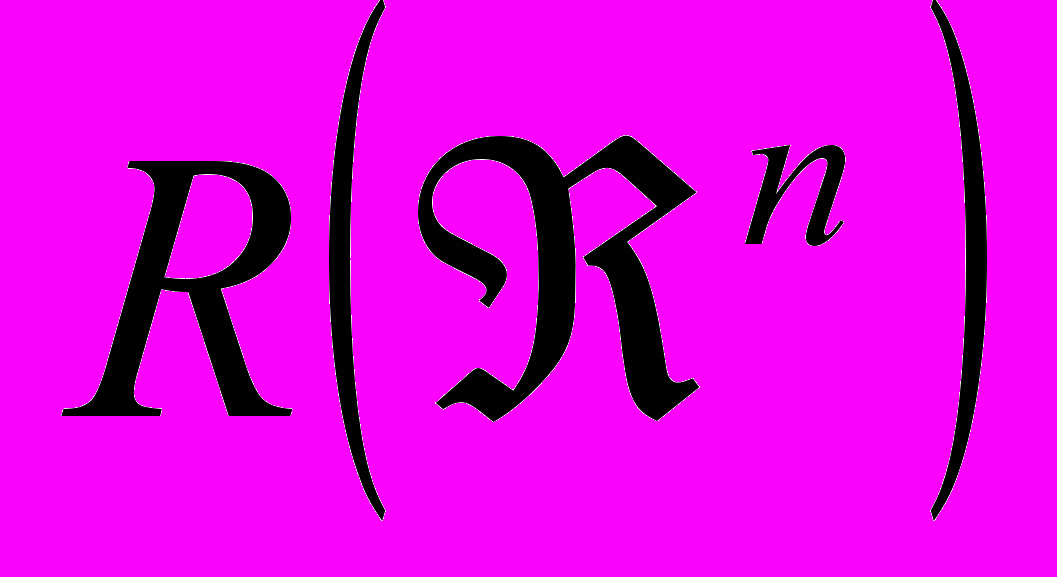Внешняя мера на 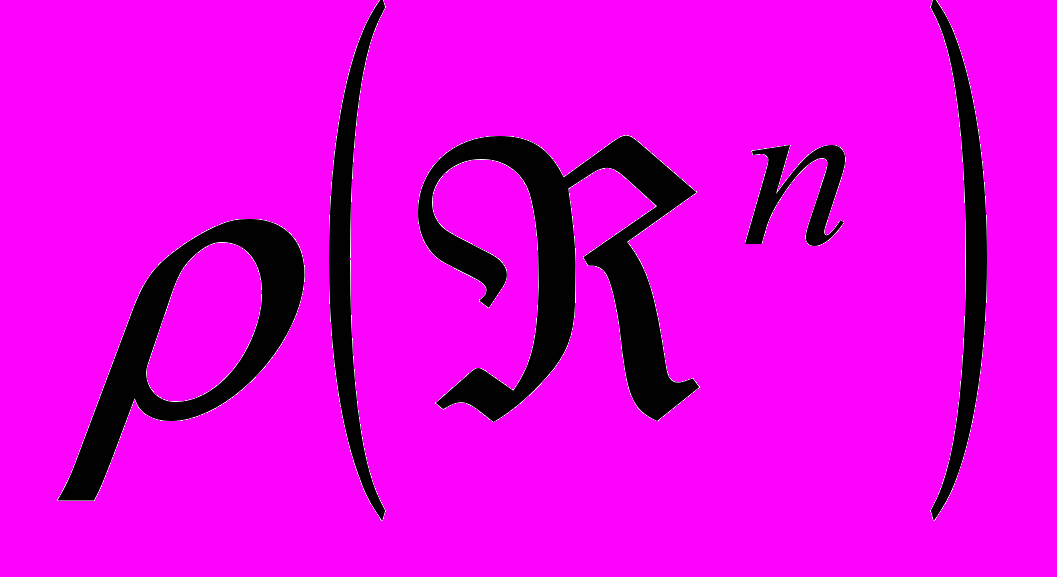. Мера Лебега. Свойства мер, эквивалентные счетной аддтивности. Борелевские множества. Внутренняя мера. Неизмеримое множество.

Тема 3. Функции измеримые по Лебегу.

Определения и простейшие свойства. Сходимость последовательностей измеримых функций.

Тема 4. Интеграл Лебега.

Определение интеграла Лебега и корректность определения. Основные свойства интеграла Лебега. Абсолютная непрерывность интеграла Лебега. Плотность непрерывных функций в пространстве 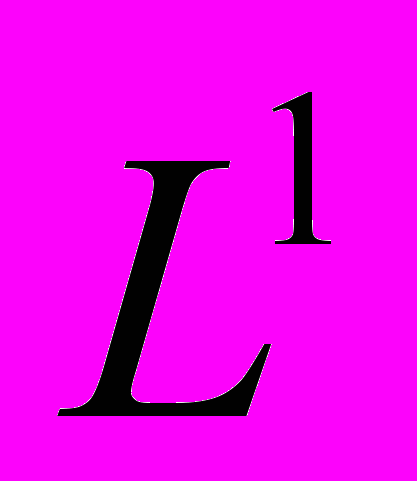. Сходимость по мере. Теорема Б. Леви. Теорема Фату. Теорема Лебега о мажорируемой сходимости. Теорема Фату в форме Либа. Представление интеграла Лебега через функцию распределения.

Тема 5. Интеграл Римана.

Определения. Критерий интегрируемости по Риману ограниченных функций.

Интеграл Римана-Стилтьеса. Критерий существования интеграла Римана.

Тема 6. Теорема Лебега о дифференцировании.

Функция Вейерштрасса. Теорема Харди-Литтлвуда о максимальной функции. Теорема Лебега о дифференцировании и ее следствия.

Тема 7. Пространства последовательностей.

Нормированные пространства. Пространство l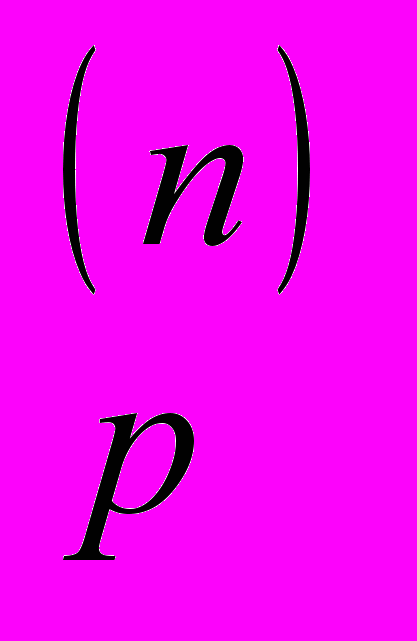. Пространство l.

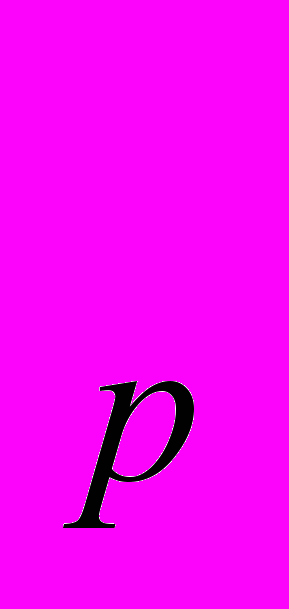Тема 8. L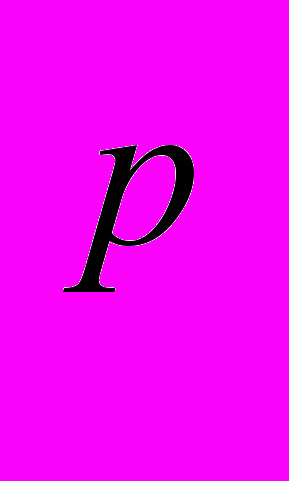- пространства.

Неравенство Гельдера и его применения. Неравенства Минковского для интегралов. Неравенство Йенсена. Полнота L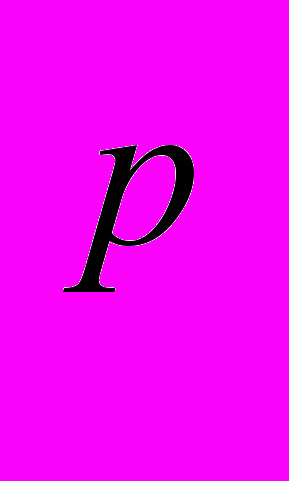- пространств. Характеризация компактных множеств в L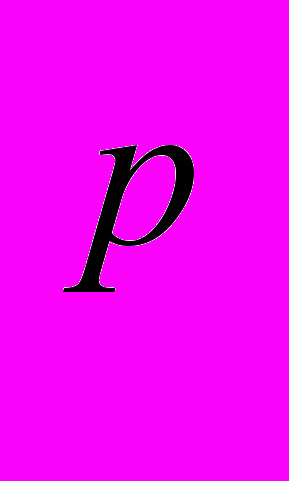-пространствах. L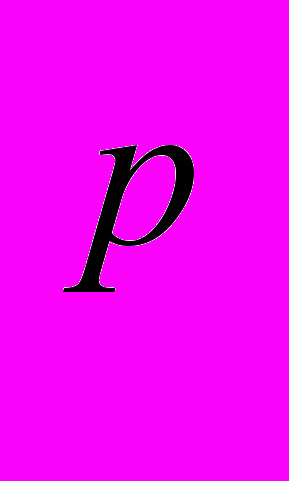- пространства при 0 < p < 1.

Тема 9. Элементы абстрактной теории меры.

Лебегово расширение меры. Знакопеременные меры. Теорема Хана. Абсолютная непрерывность мер. Теорема Радона-Никодима. Теорема Лебега о разложении меры.

Тема 10. Теорема Фубини.

Меры на декартовом произведении. Теорема Фубини.


Литература:


Обязательная


1. Дьяченко М.И., Ульянов П.Л., Мера и интеграл, 1998.

2. Ульянов П.Л. и др. Действительный анализ в задачах, 2005


Дополнительная

1. Колмогоров А.Н., Фомин С.В., Элементы теории функций и функционального анализа, 1976
   

2. Rudin W., Real and complex analysis, McGRAW-HILL, London, 2000.


Программу составил

Степанов В.Д. – д.ф.м.н., профессор кафедры математического анализа и теории функций