Нормальный закон распределения

Вид материала

Содержание

Правило 3-х  (трех “сигм”)
Совместное распределение двух случайных величин.

Подобный материал:

Тема 11

Нормальный закон распределения.

_{Если плотность распределения случайной величины  определяется формулой}

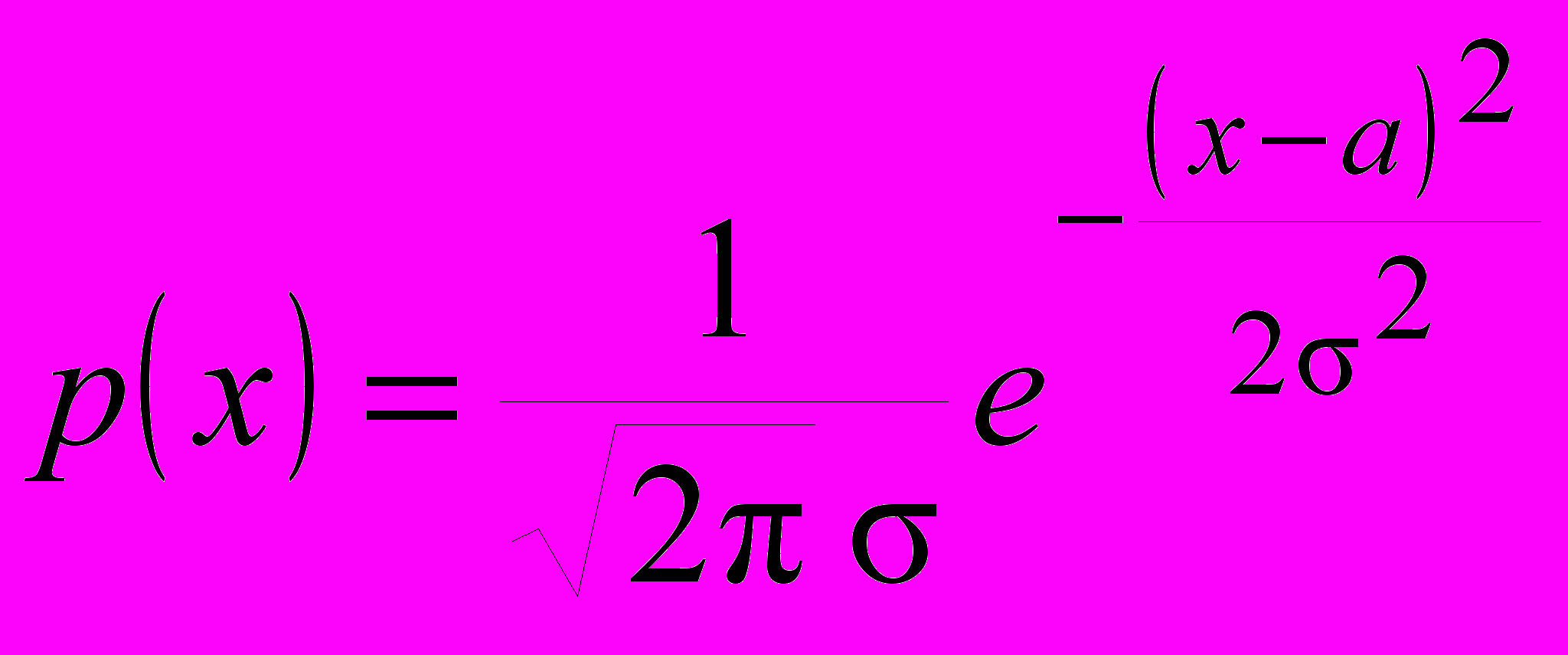_{, (1)}

где а – произвольное число, а  – положительное число, то говорят, что  распределена по нормальному закону или что  “нормальная” случайная величина.

_{Значения а и  полностью определяют функцию р(х). Для неё иногда вводится обозначение: p(x) = n(x;a;).}

_{График плотности распределения нормальной случайной величины при н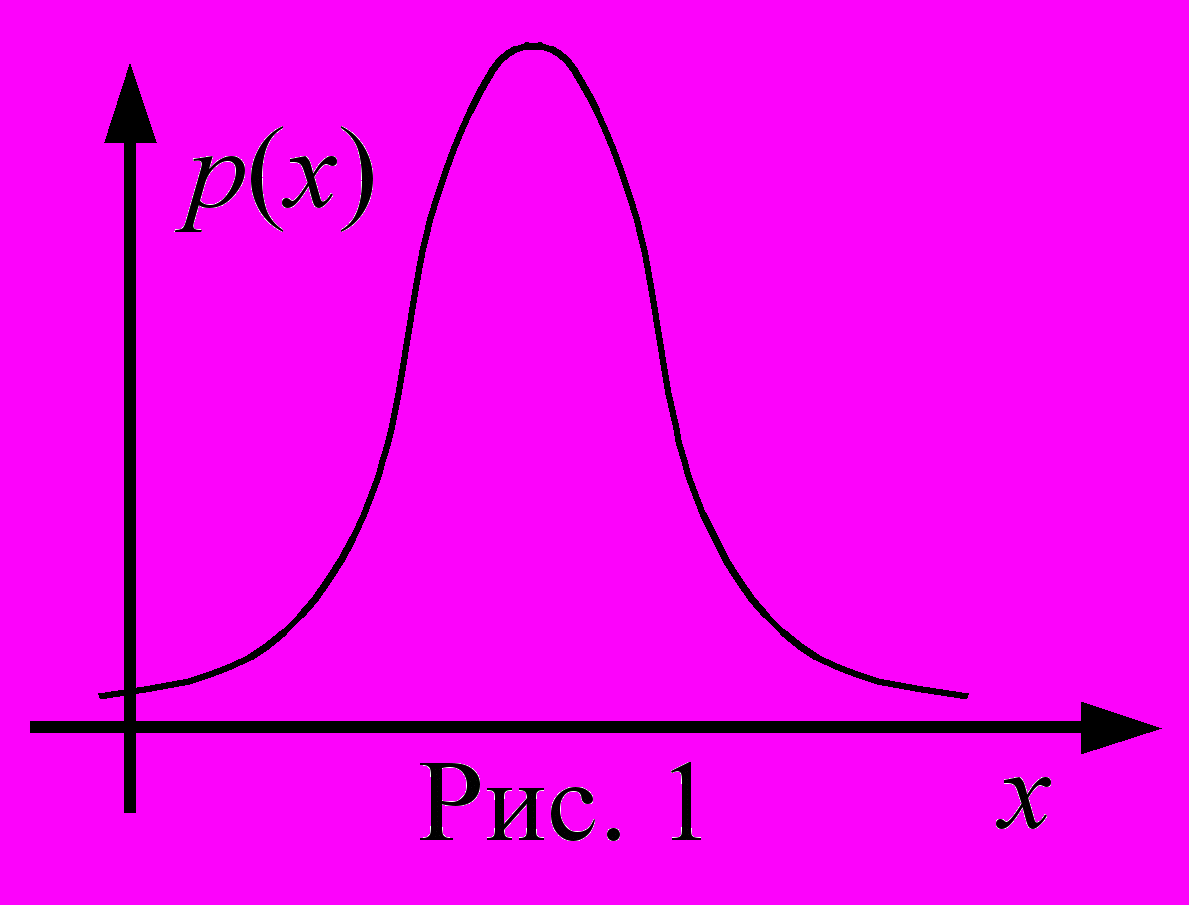екоторых значениях а и  представлен на рисунке 6. График симметричен относительна прямой х = а, и выполняются условия: р(х)  0 при х  . Если а увеличивать, оставляя  неизменной, то график будет перемещаться вправо, а если а уменьшать, то – влево, не изменяя формы.}

_{Е
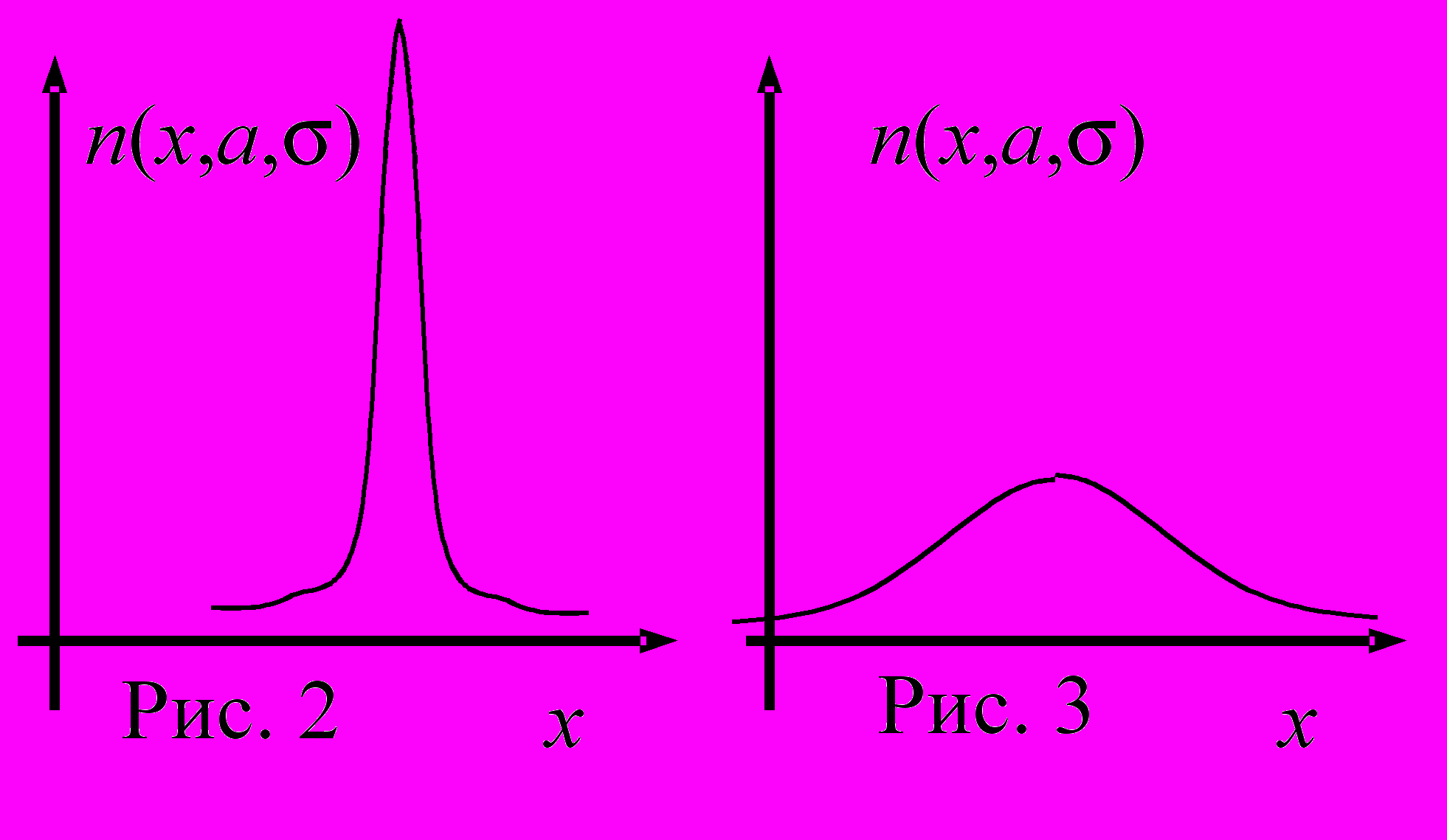
сли значение а неизменно, то относительно малому значению  будет соответствовать график р(х) с выраженным пиком, как на рисунке 2. При относительно большом значении  график р(х) представляет собой пологую кривую, как изображено на рисунке 3.}

_{Функция распределения F(x) нормальной случайной величины  иногда обозначается N(x;a;). Она обычным образом получается из плотности распределения :}

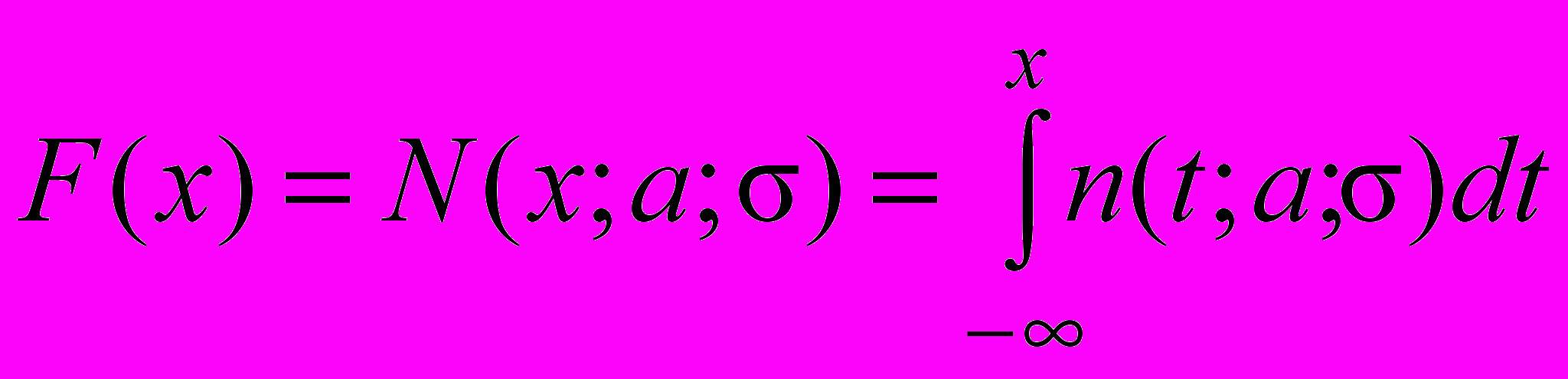
_{Г
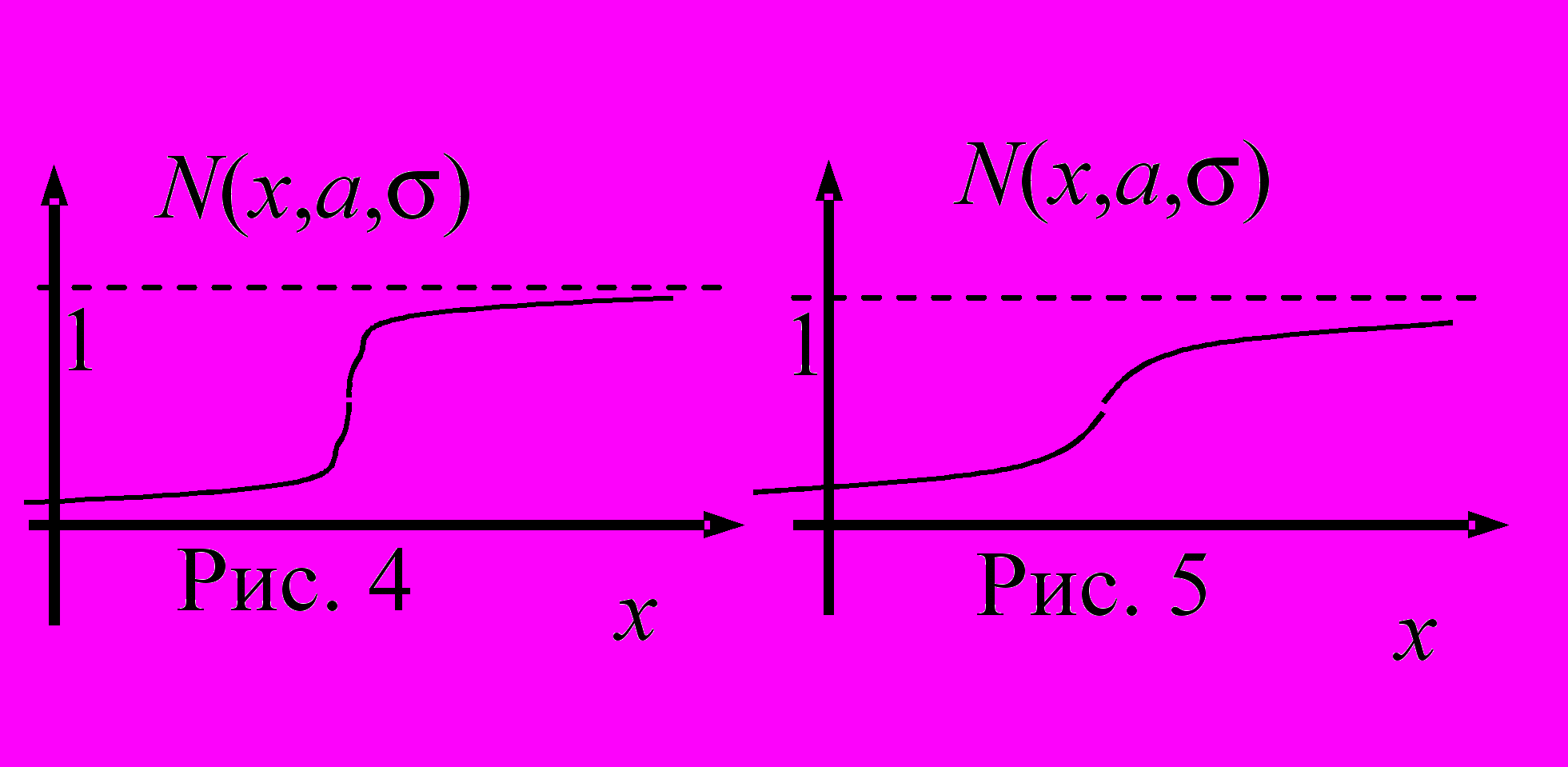
рафики функции F(x) для нормально распределённых случайных величин при относительно малых и относительно больших значениях 
изображены, соответственно, на рисунках 4 и 5.}

_{Из симметрии графика функции плотности распределения р(х) нормально распределённой случайной величины  относительно прямой х = а следует, что М = а.}

_{Если вычислить дисперсию D нормально распределённой случайной величины, то оказывается, что она равна 2.}

_{Таким образом, параметры а и  в формуле для плотности распределения случайной величины, распределённой по нормальному закону, приобретают смысл: а – математическое ожидание, 2 – дисперсия.}

_{Вероятность того, что нормально распределённая случайная величина  примет значение из промежутка (х1, х2) рассчитывается по формуле}

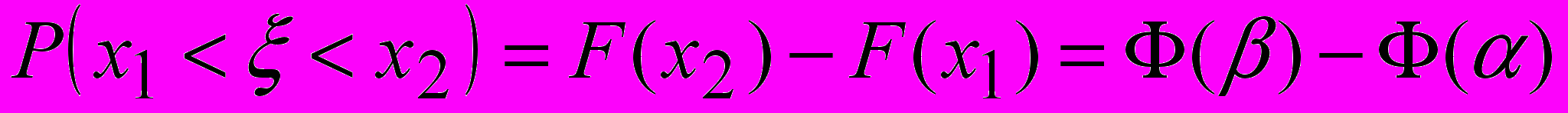
Здесь

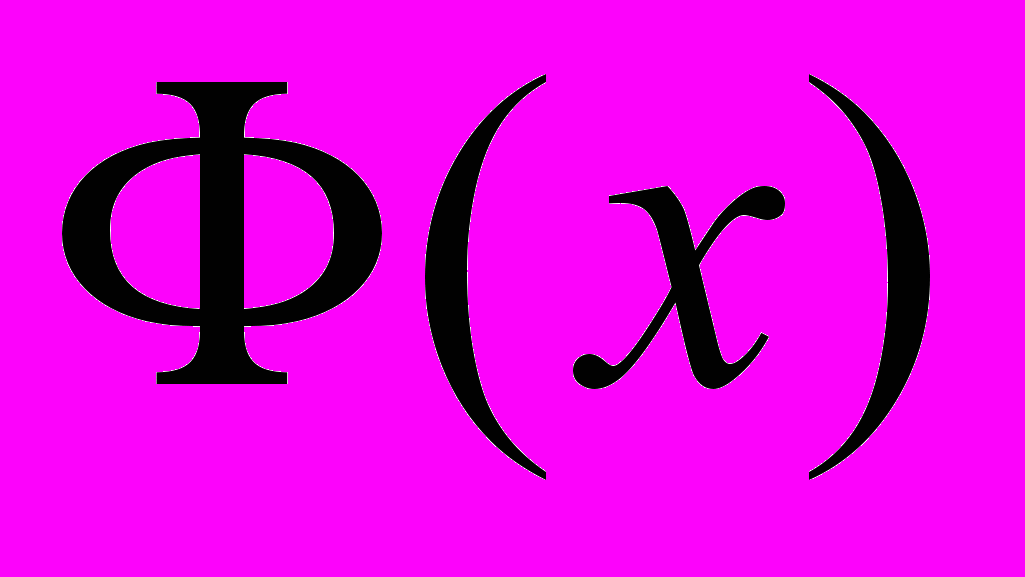– интегральная функция Лапласа –

;

.

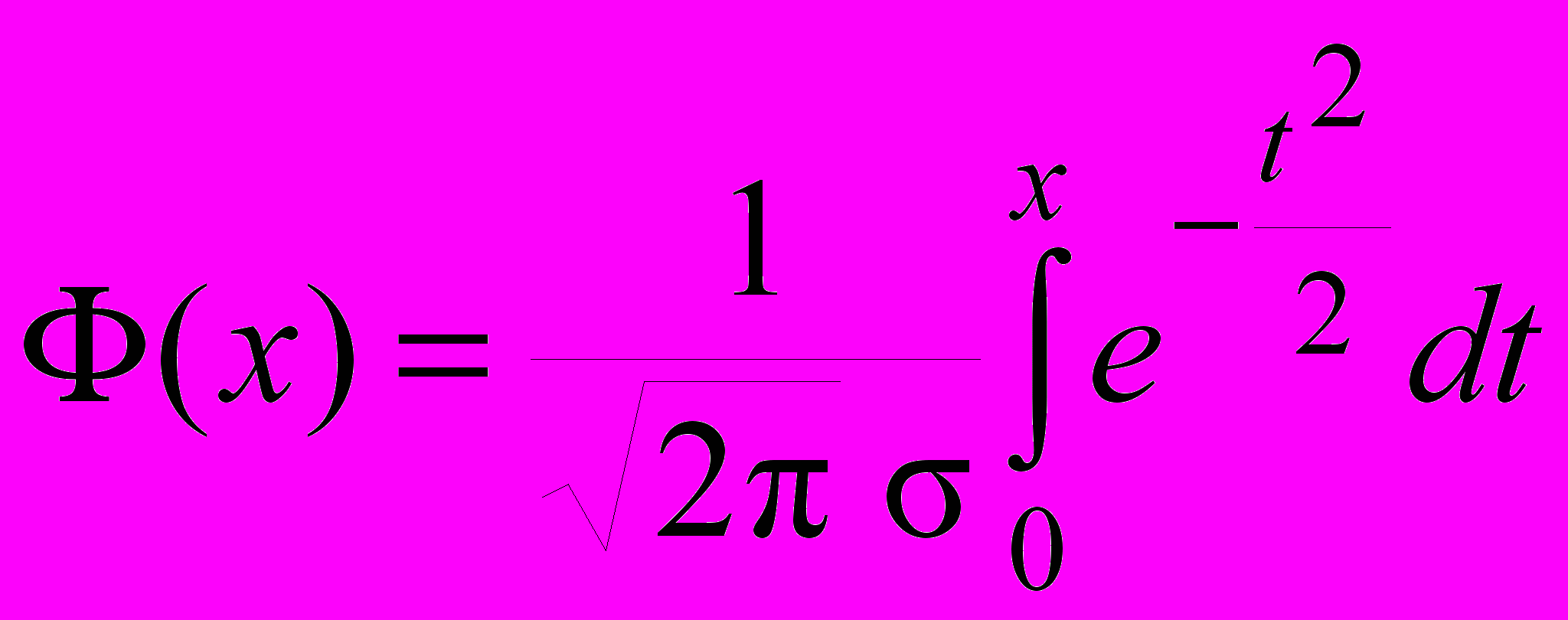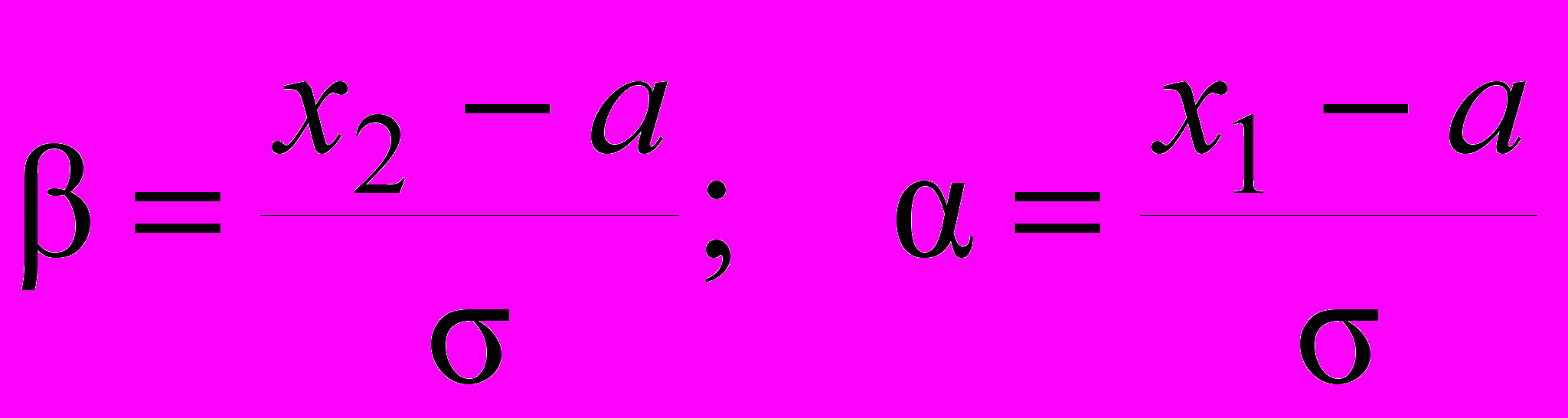_{Значения (х) определяются из таблиц, как это показывалось ранее.}

_{Если случайная величина  имеет плотность распределения, выражающуюся функцией n(x;0;1), то есть  – нормально распределённая случайная величина с математическим ожиданием, равным нулю, и дисперсией, равной единице, то}

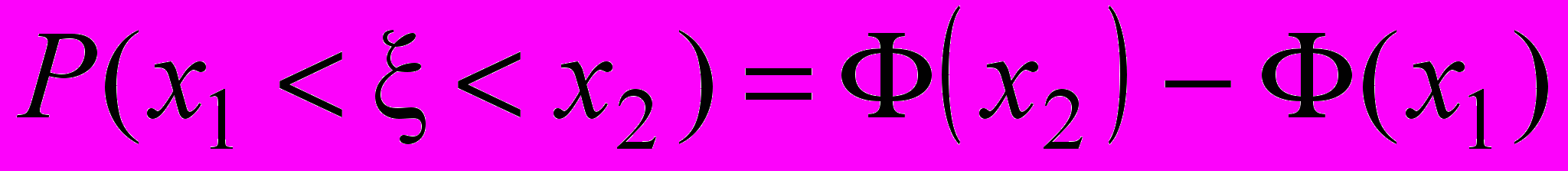
Случайную величину с плотностью распределения n(x;0;1) можно принять за некоторый эталон для случайных величин, распределённых по нормальному закону. График плотности распределения такой случайной величины симметричен относительно оси ординат.

_{Пусть  и  – независимые нормально распределённые случайные величины, при этом М = а1, D = 12, М = а2, D = 22. Тогда случайная величина , равная сумме с1 + с2 (с1 и с2 – любые числа), тоже распределена по нормальному закону. Её математическое ожидание и дисперсия определяются формулами: М = с1а1 + с2 а2, D = с1212 + с2222.}

_{Задача. Масса ящика, вмещающего 12 бутылок – нормально распределённая случайная величина с математическим ожиданием 2 кг и среднеквадратическим отклонением 0,01 кг. Масса бутылки с пивом – тоже нормально распределённая случайная величина с математическим ожиданием 0,8 кг и среднеквадратическим отклонением 0,04 кг. Найти вероятность того, что масса ящика с 12-ю бутылками пива будет находиться в пределах от 11 до 11,5 килограммов.}

_{Правило 3-х  (трех “сигм”).}

_{Пусть имеется нормально распределённая случайная величина  с математическим ожиданием, равным а и дисперсией 2. Определим вероятность попадания  в интервал (а – 3; а + 3), то есть вероятность того, что  принимает значения, отличающиеся от математического ожидания не более, чем на три среднеквадратических отклонения.}

_{P(а – 3<  < а + 3)=Ф(3) – Ф(–3)=2Ф(3)}

_{По таблице находим Ф(3)=0,49865, откуда следует, что 2Ф(3) практически равняется единице. Таким образом, можно сделать важный вывод: нормальная случайная величина принимает значения, отклоняющиеся от ее математического ожидания не более чем на 3.}

_{(Выбор числа 3 здесь условен и никак не обосновывается: можно было выбрать 2,8, 2,9 или 3,2 и получить практически тот же вероятностный результат. Учитывая, что Ф(2)=0,477, можно было бы говорить и о правиле 2–х “сигм”.)}

Совместное распределение двух случайных величин.

_{Пусть пространство элементарных исходов  случайного эксперимента таково, что каждому исходу ij ставиться в соответствие значение случайной величины , равное xi и значение случайной величины , равное yj.}

1. Представим себе большую совокупность деталей, имеющих вид стержня. Эксперимент заключается в случайном выборе одного стержня. Этот стержень имеет длину, которую будем обозначать  и толщину— (можно указать другие параметры—объем, вес, чистота обработки, выраженная в стандартных единицах).

2. Если рассмотреть акции двух различных корпораций, то в данный день биржевых торгов они каждая из них характеризуется определённой доходностью. Случайные величины  и  –это доходности акций этих корпораций.

_{В этих случаях мы можем говорить о совместном распределении случайных величин  и  или о “двумерной” случайной величине.}

_{Если  и  дискретны и принимают конечное число значений ( – n значений, а  – k значений), то закон совместного распределения случайных величин  и  можно задать, если каждой паре чисел xi, yj (где xi принадлежит множеству значений , а y j—множеству значений ) поставить в соответствие вероятность pij, равную вероятности события, объединяющего все исходы ij (и состоящего лишь из этих исходов), которые приводят к значениям  = xi;  = y j.}

_{Такой закон распределения можно задать в виде таблицы:}

_ _	_y1	_y2	_	_yj	_	_yk
_x1	_р11	_р12	_	_р1j	_	_р1k	_P1
_	_	_	_	_	_	_	_
_xi	_рi1	_рi2	_	_рij	_	_рik	_Pi	_(*)
_	_	_	_	_	_	_	_
_xn	_рn1	_рn2	_	_рnj	_	_рnk	_Pn
	_P1	_P2	_	_Pj	_	_Pk	_

_{Очевидно}

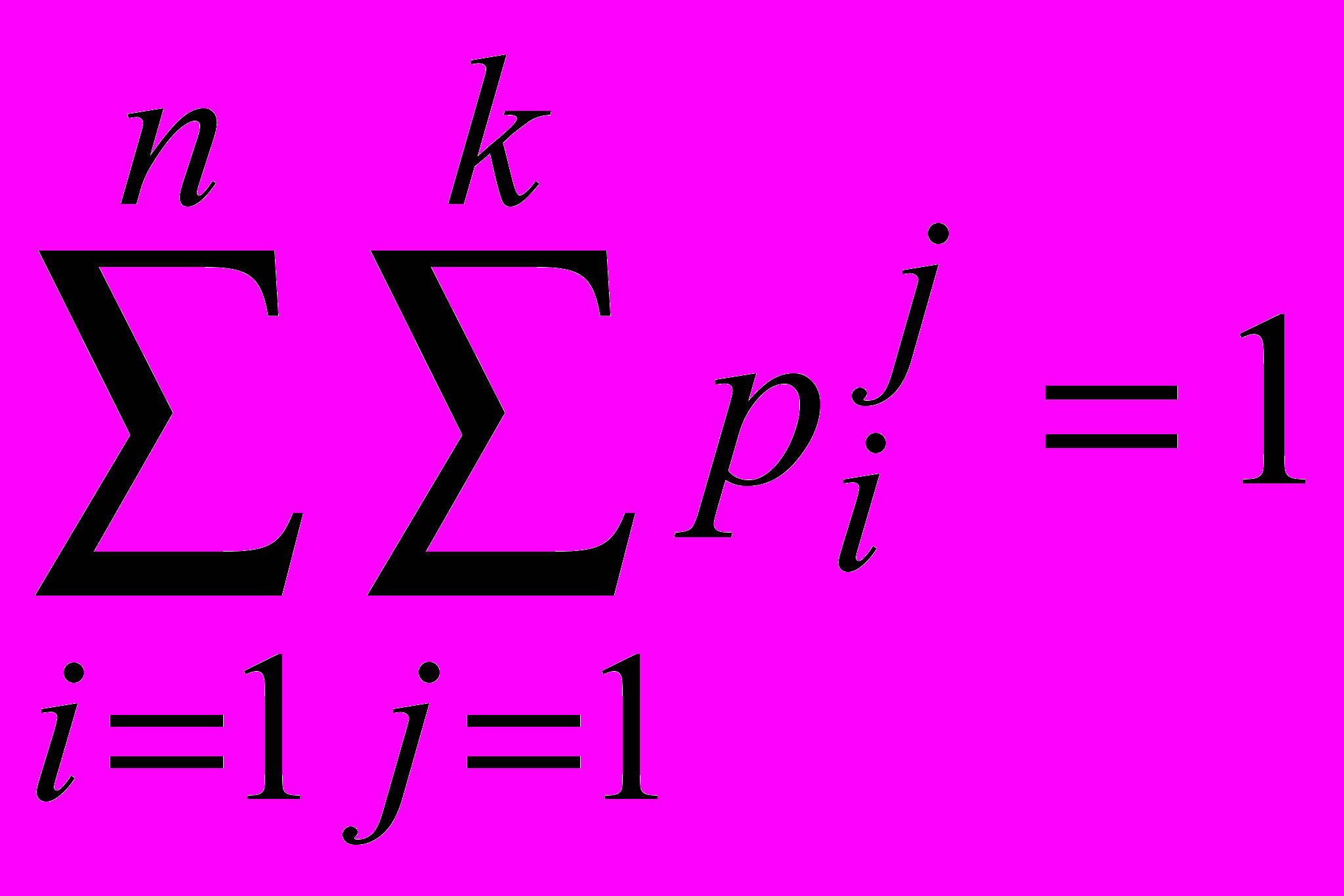
_{Если просуммировать все рij в i–й строке, то получим 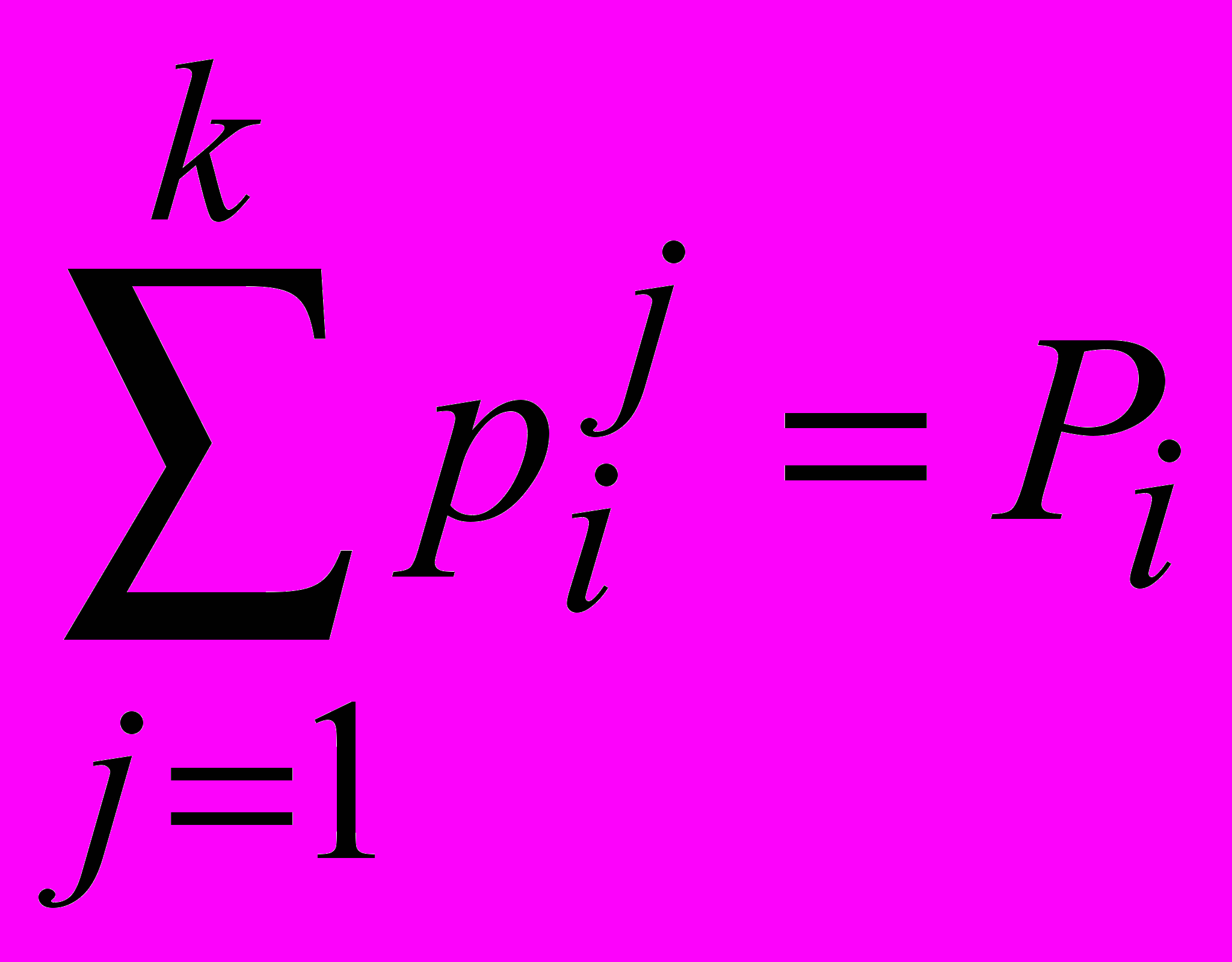– вероятность того, что случайная величина  примет значение xi. Аналогично, если просуммировать все рij в j–м столбце, то получим}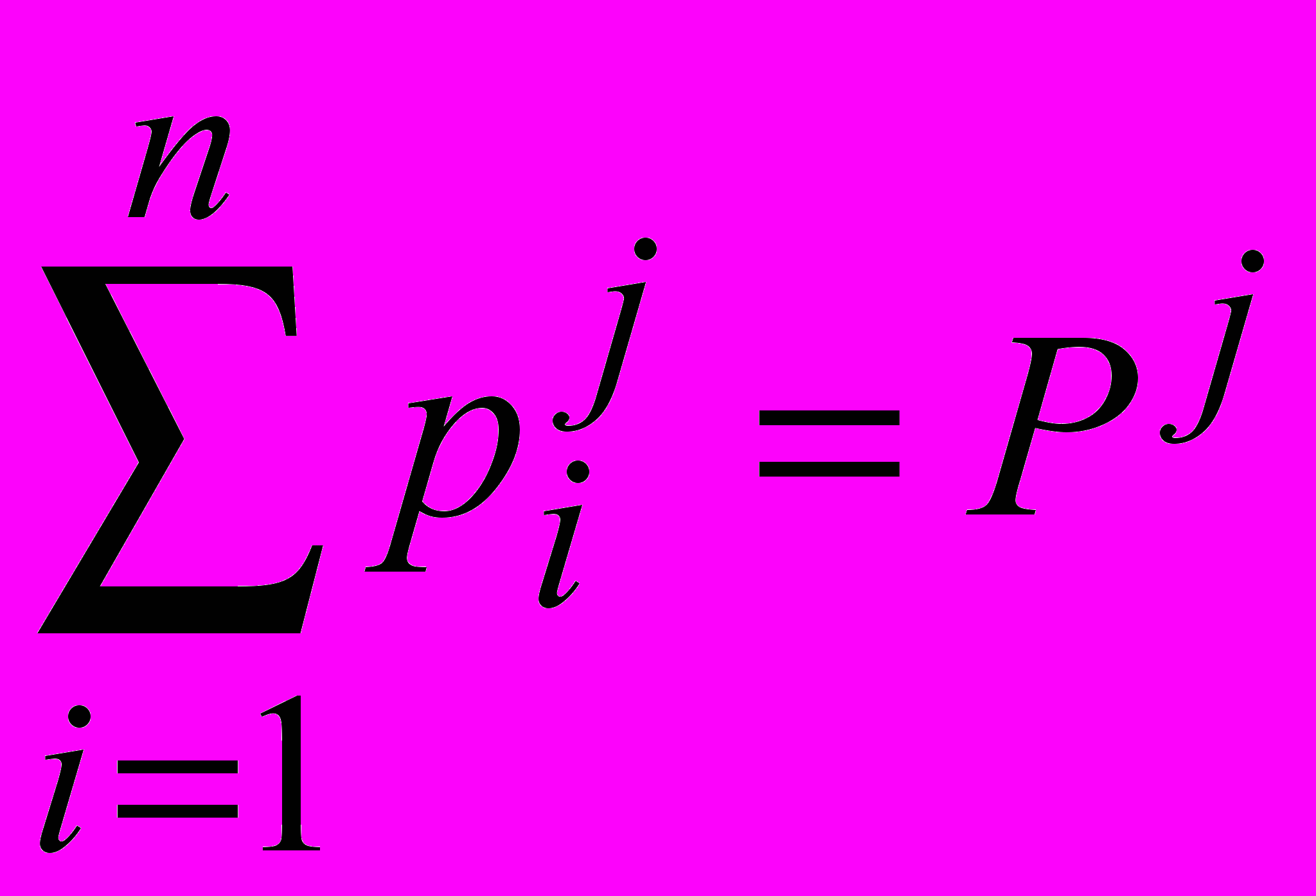

_{вероятность того, что  принимает значение y j.}

_{Соответствие xi  Pi (i = 1,2,,n) определяет закон распределения , также как соответствие yj  P j (j = 1,2,,k) определяет закон распределения случайной величины .}

_{Очевидно , .}

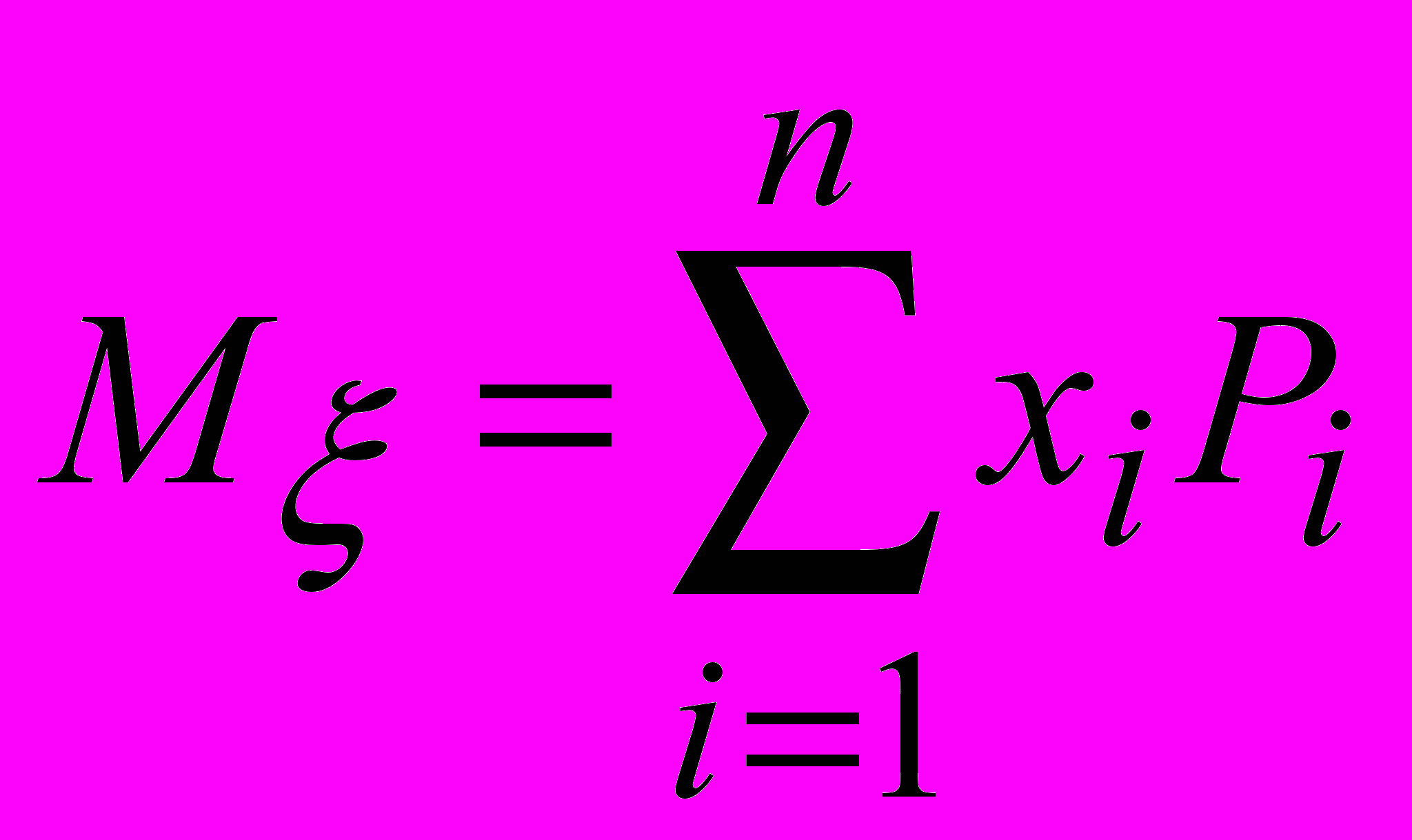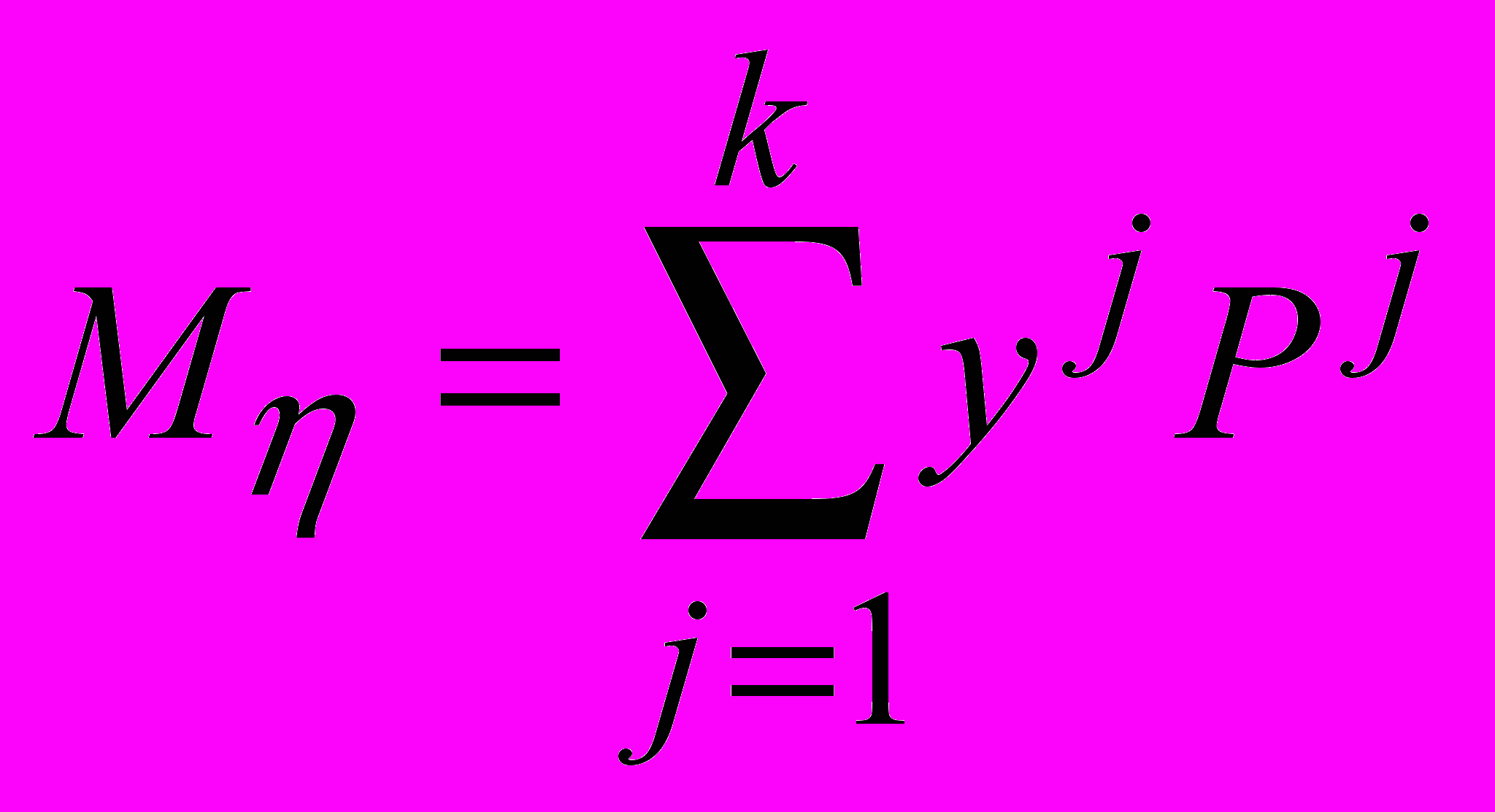_{Раньше мы говорили, что случайные величины  и  независимы, если}

_{pij=PiP j (i=1,2,,n; j=1,2,,k).}

_{Если это не выполняется, то  и  зависимы.}

_{В чем проявляется зависимость случайных величин  и  и как ее выявить из таблицы?}

_{Рассмотрим столбец y1. Каждому числу xi поставим в соответствие число}

_{pi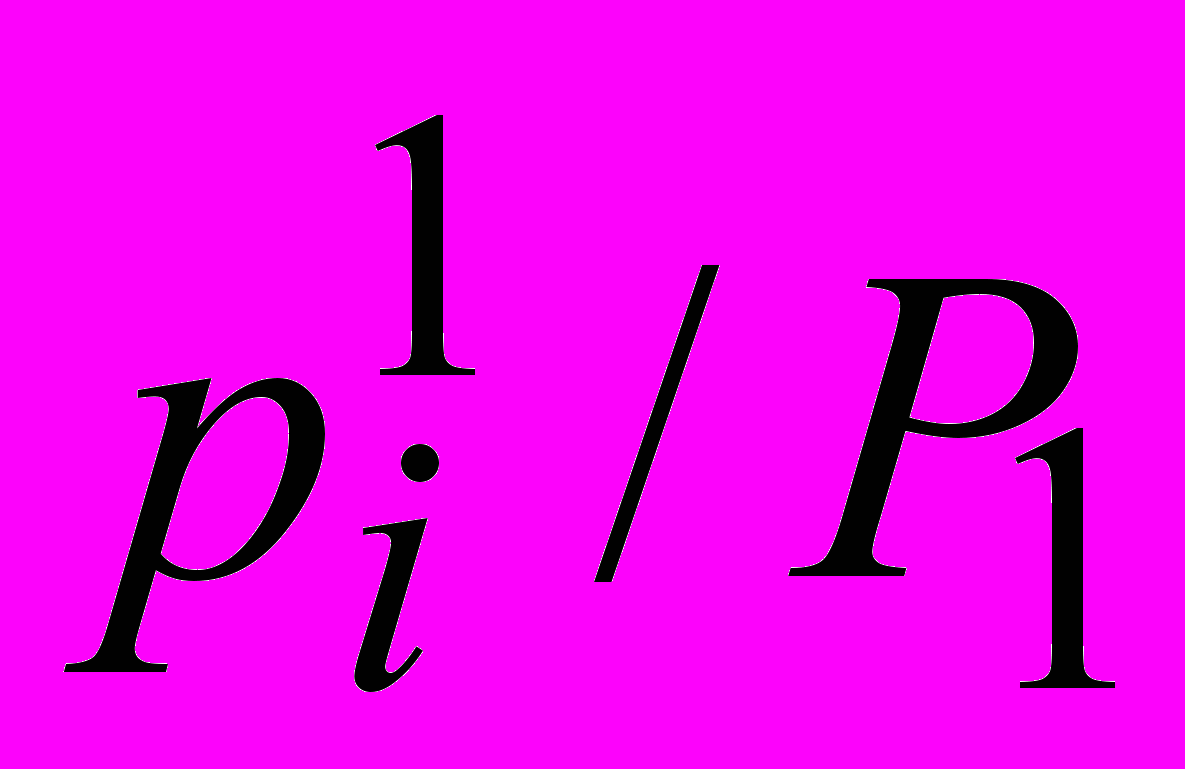/1 = (1)}

_{которое будем называть условной вероятностью = xi при =y1. Обратите внимание на то, что это не вероятность Pi события = xi, и сравните формулу (1) с уже известной формулой условной вероятности .}

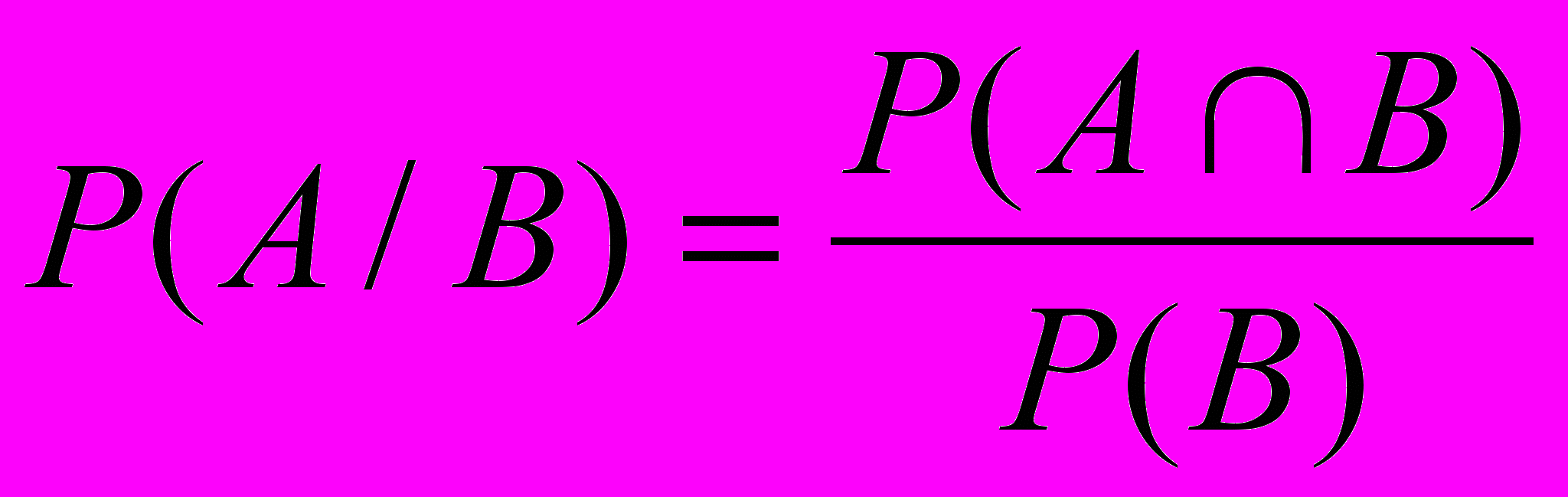_{Соответствие}

_{xiрi/1, (i=1,2,,n)}

_{будем называть условным распределением случайной величины  при =y1. Очевидно .}

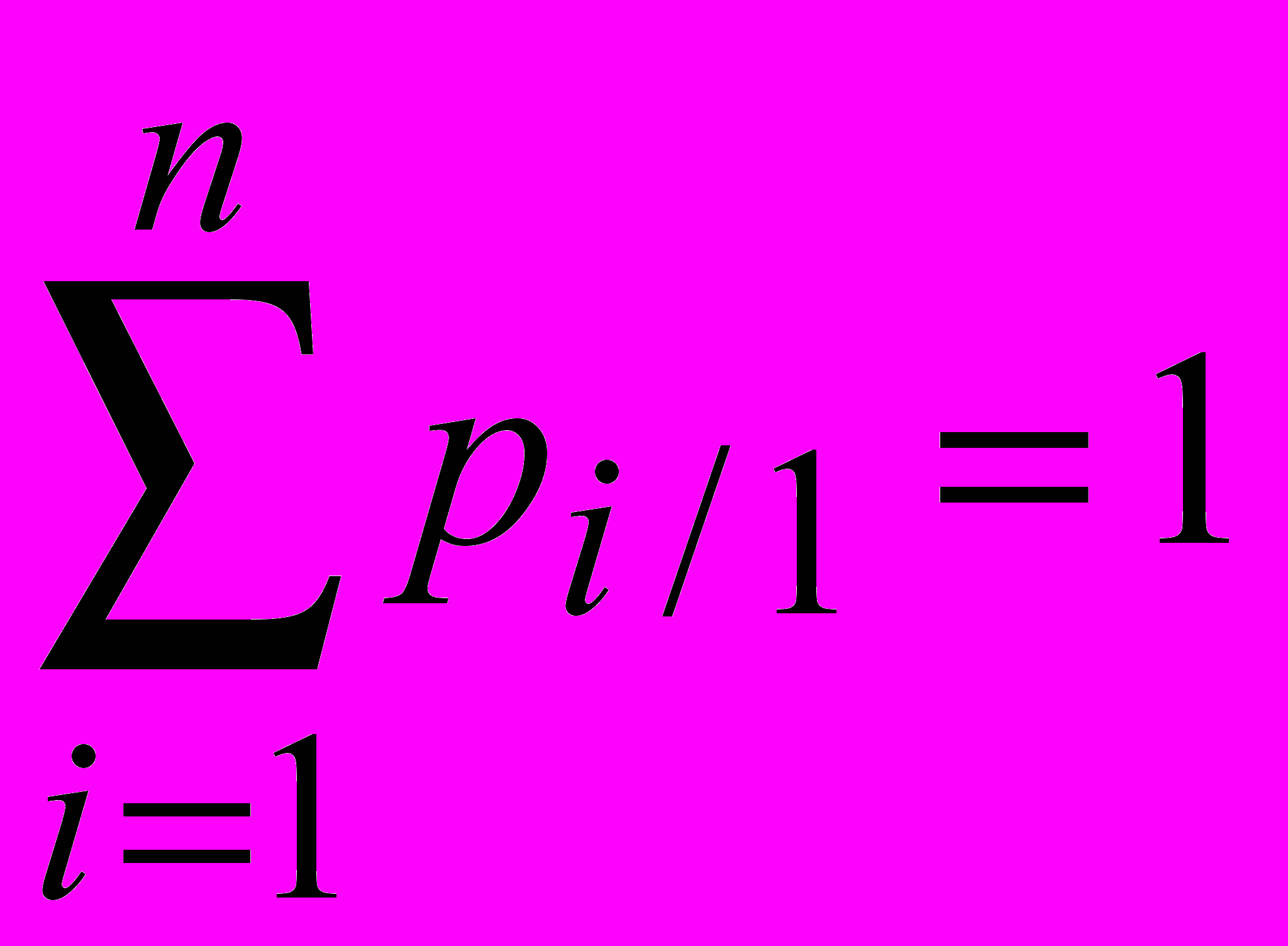_{Аналогичные условные законы распределения случайной величины  можно построить при всех остальных значениях , равных y2; y3,, yn ,ставя в соответствие числу xi условную вероятность pi/j = ().}

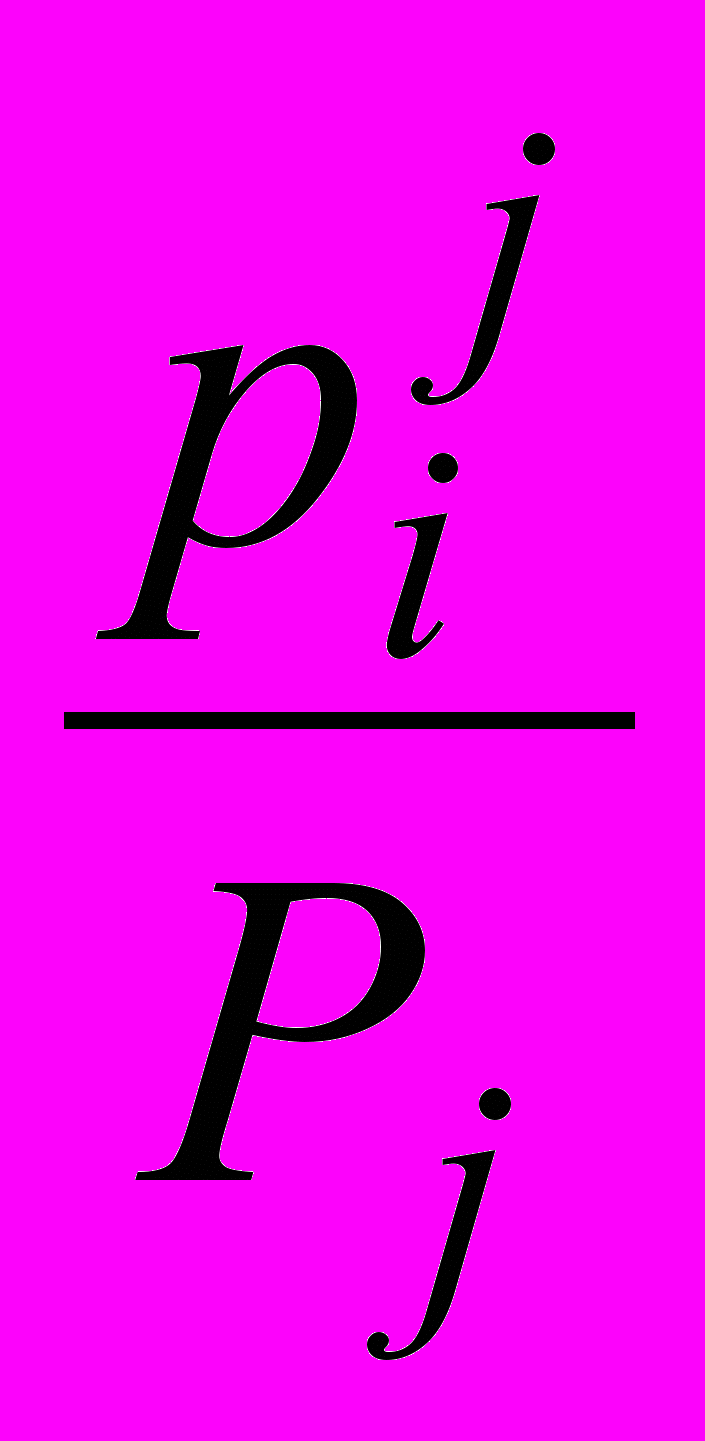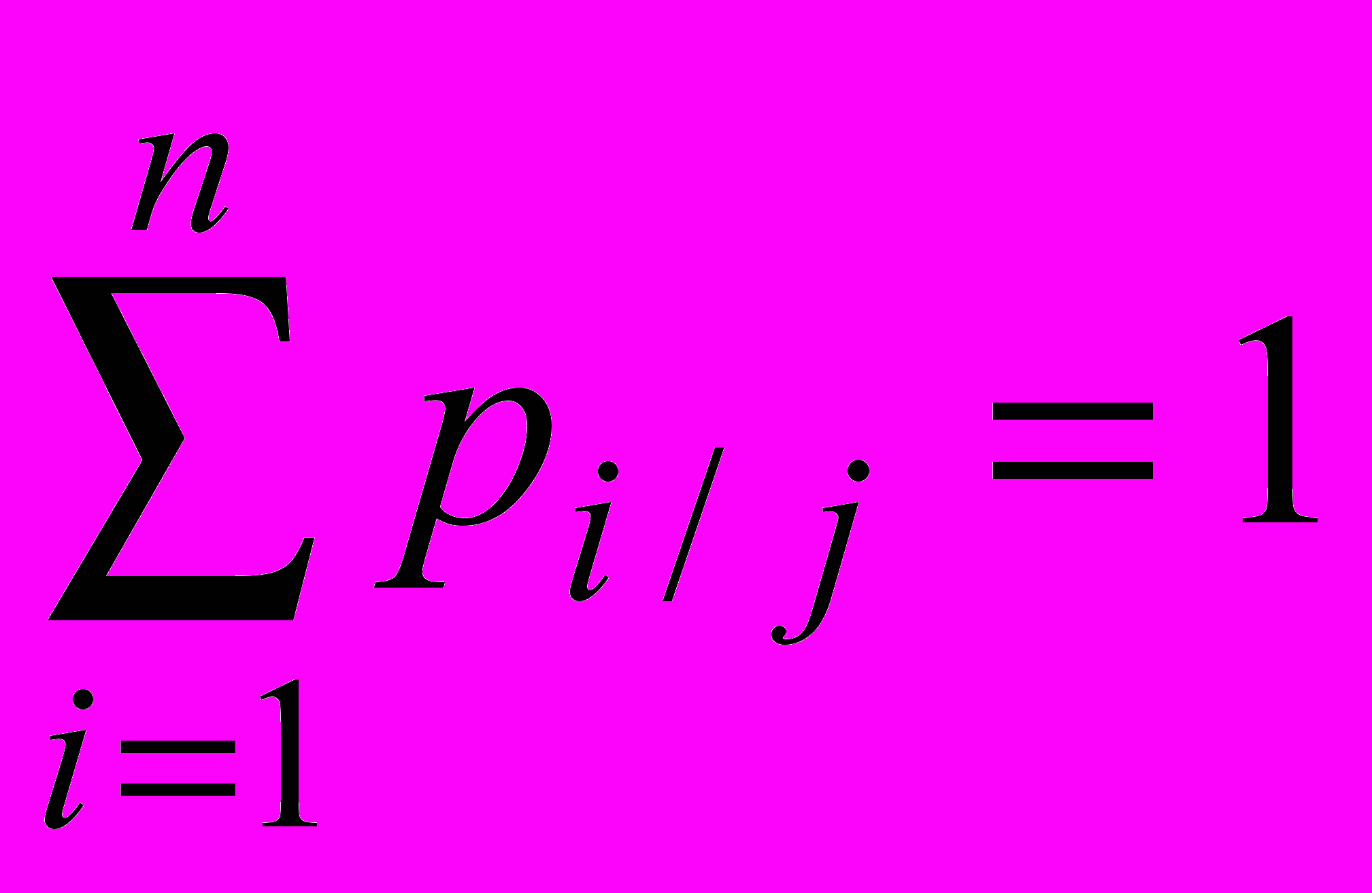_{В таблице приведён условный закон распределения случайной величины  при =yj}

_	_x1	_x2	_	_xi	_	_xn
_pi/j			_		_

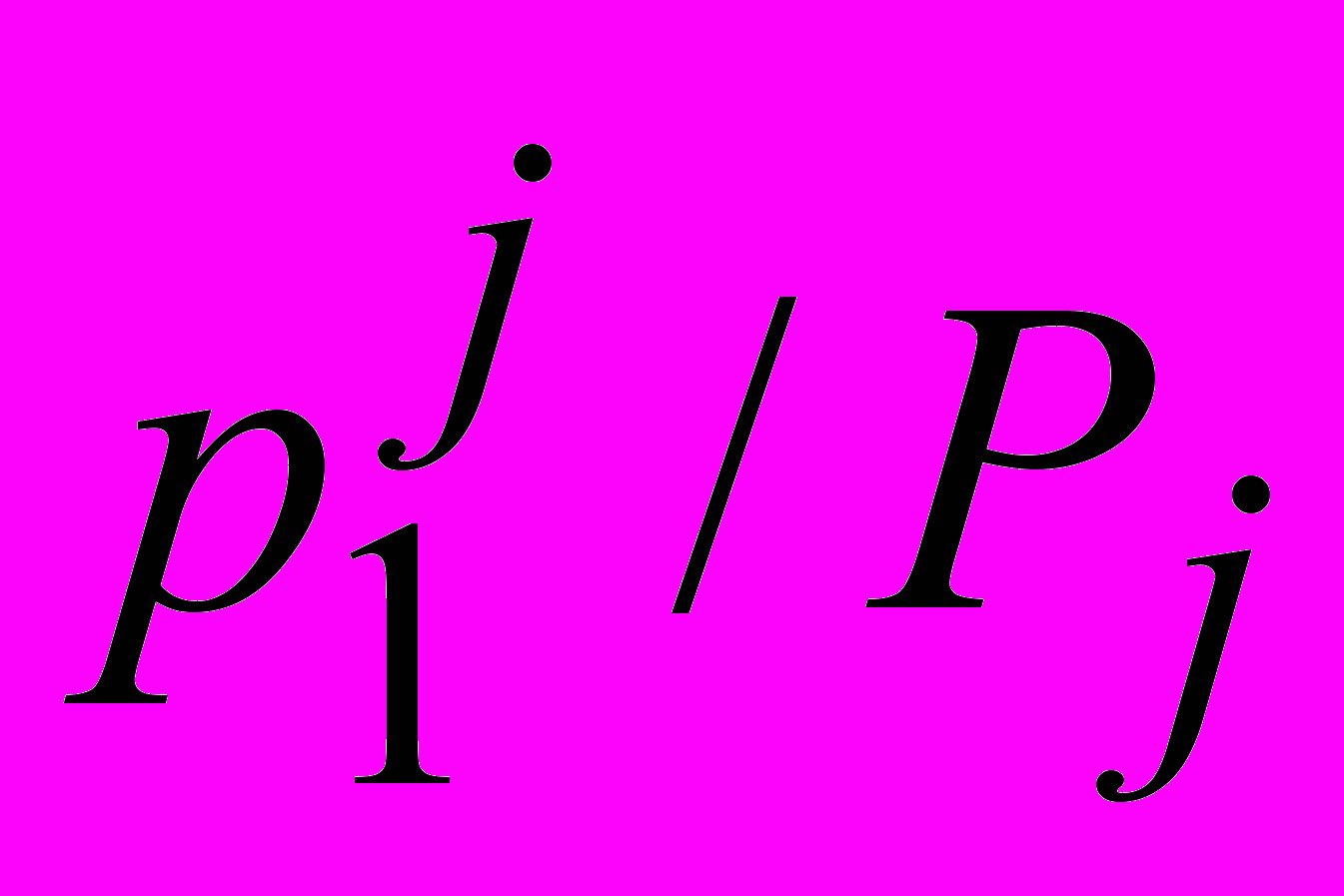
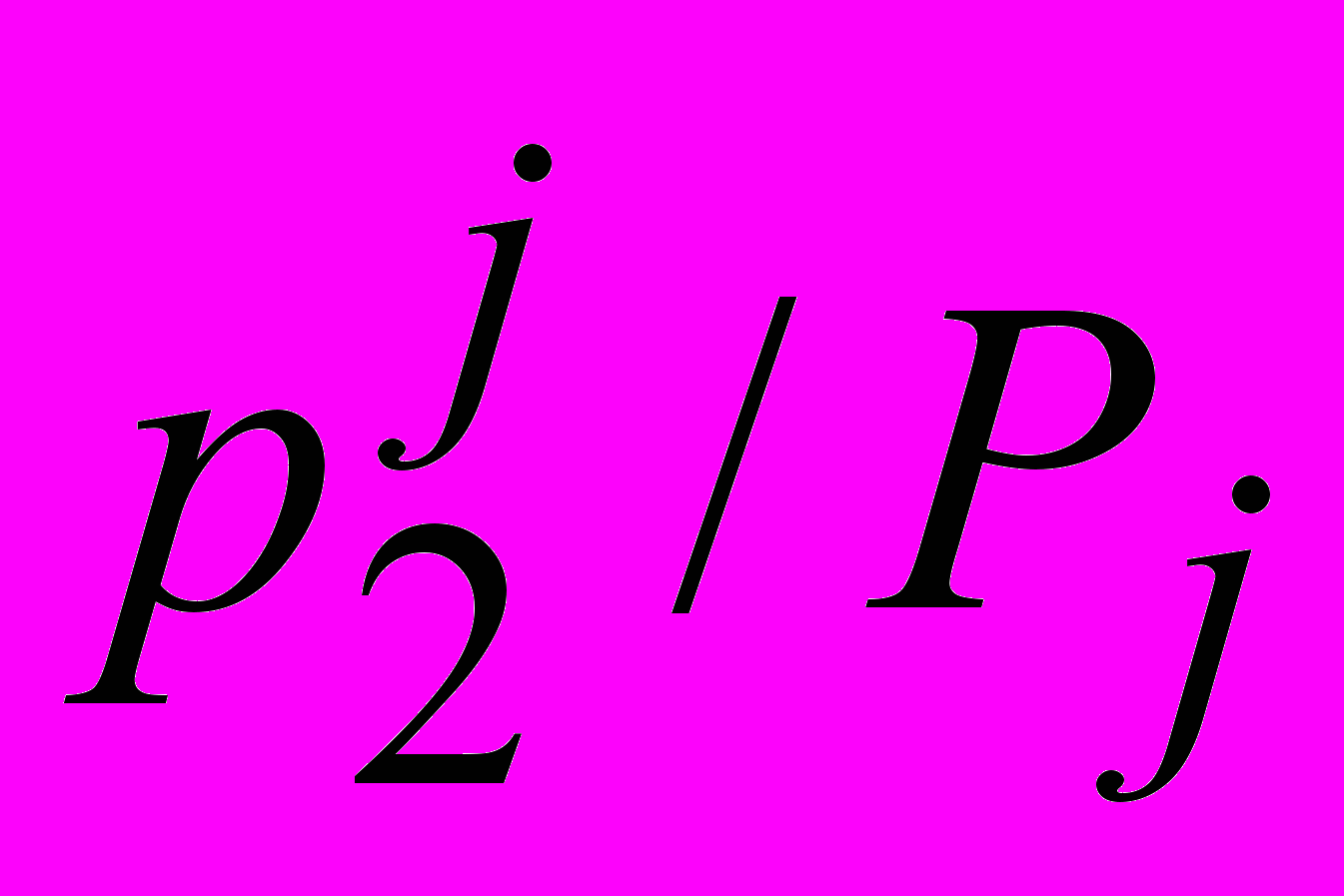
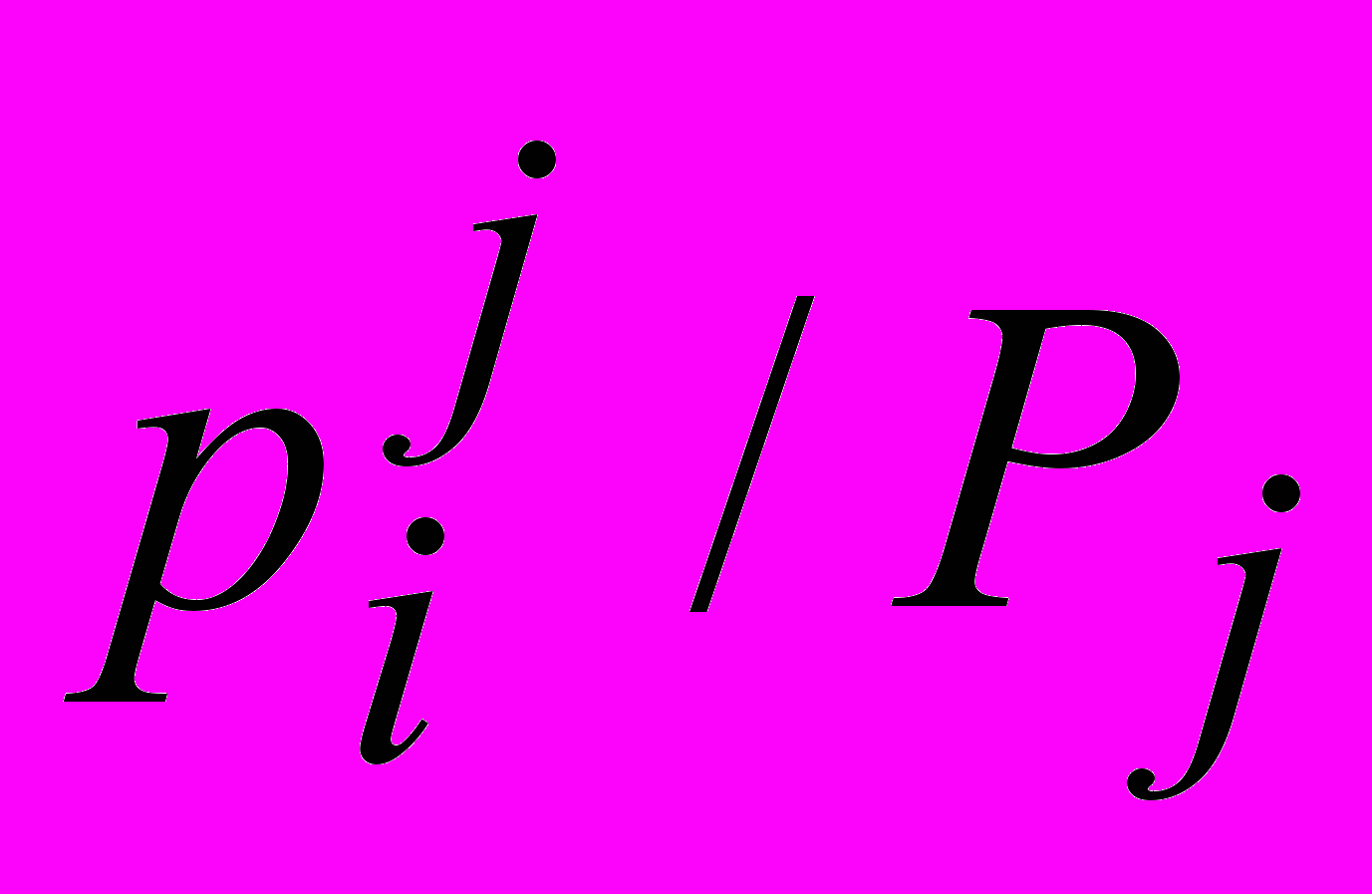
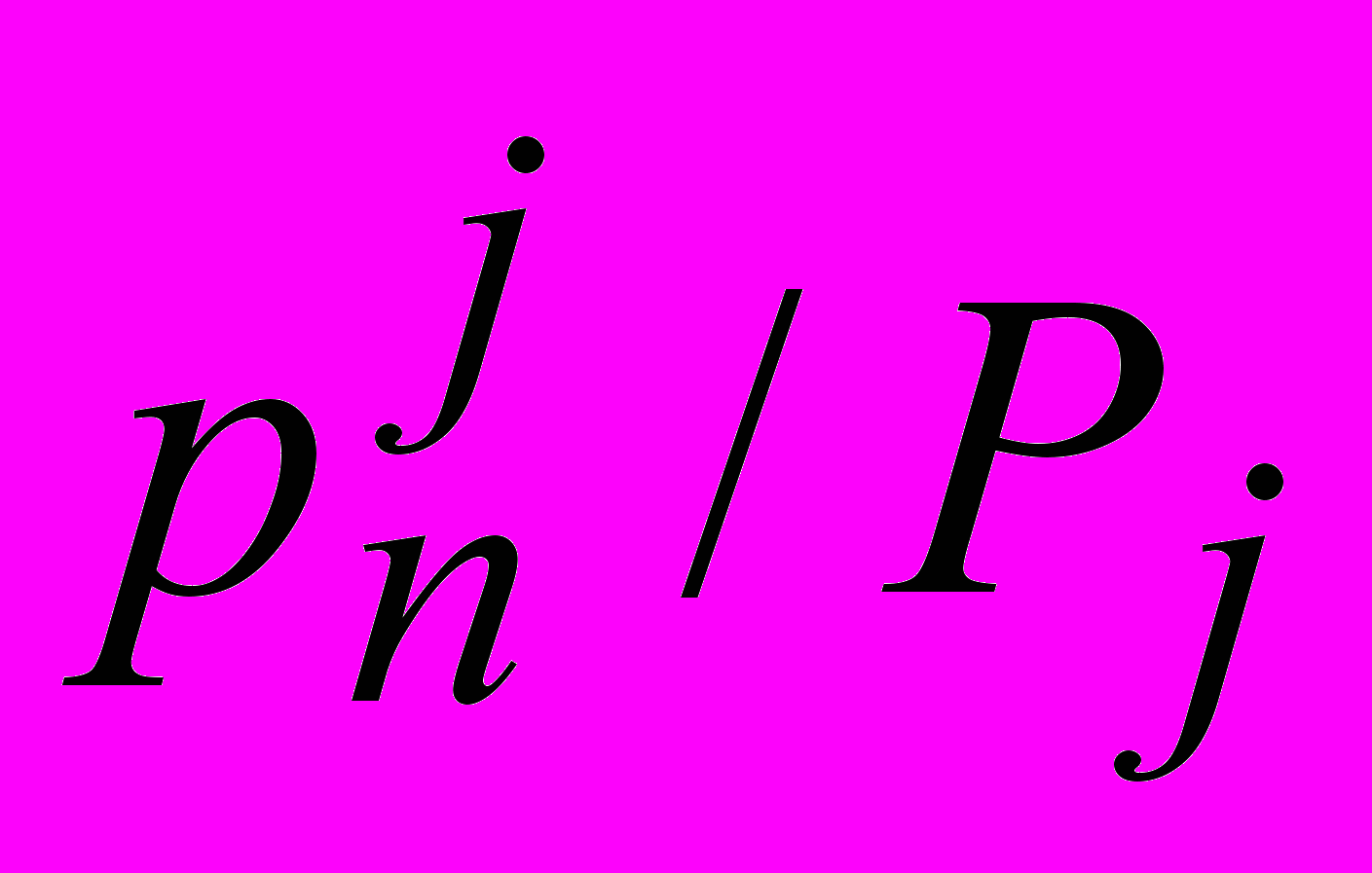
_{Можно ввести понятие условного математического ожидания  при  = yj}

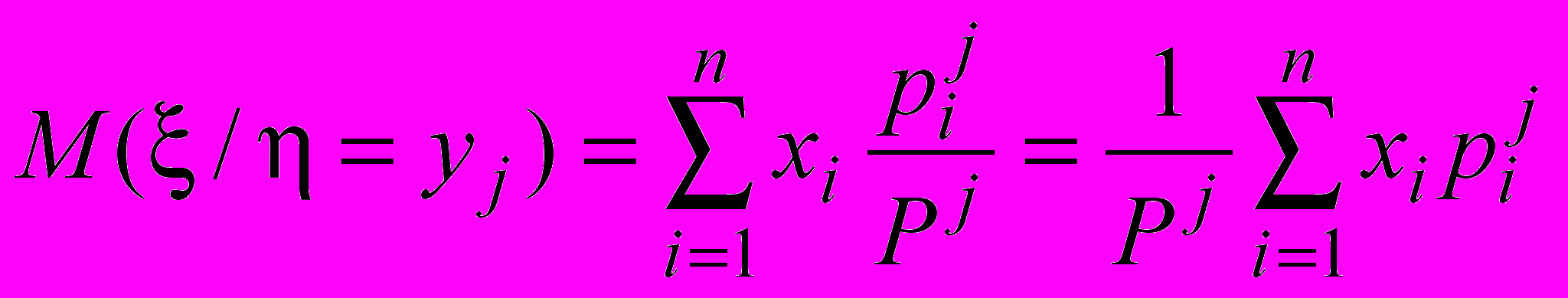
_{Заметим, что  и  равноценны. Можно ввести условное распределение  при =xi соответствием}

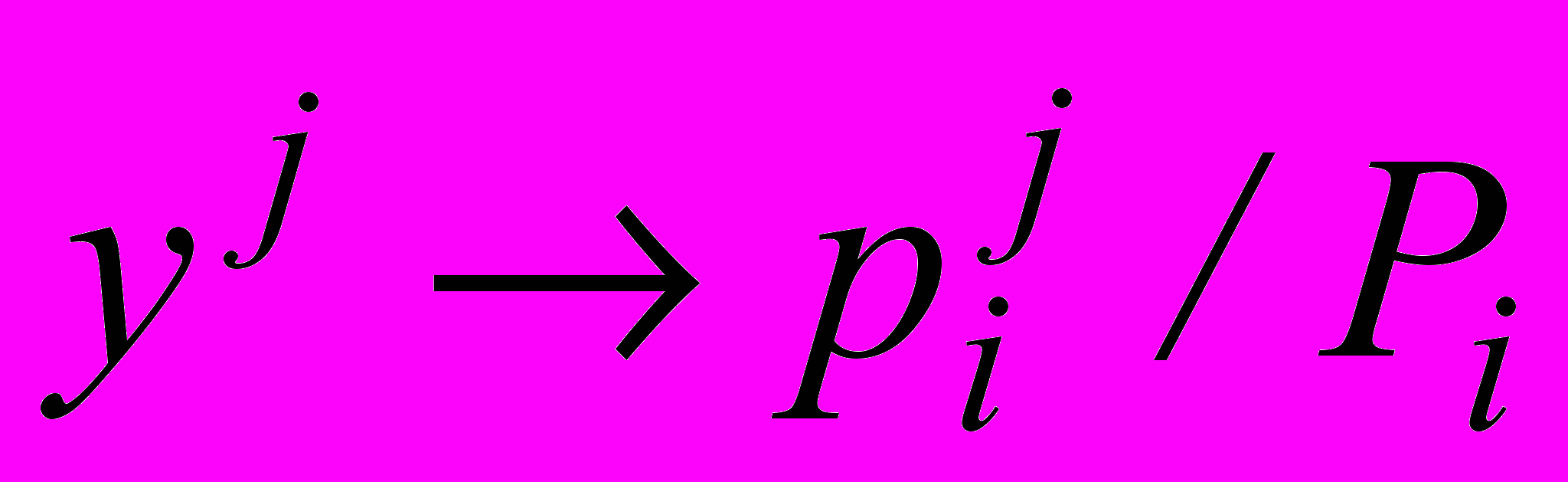_{(j = 1,2,,k)}

_{Также можно ввести понятие условного математического ожидания случайной величины  при =xi :}

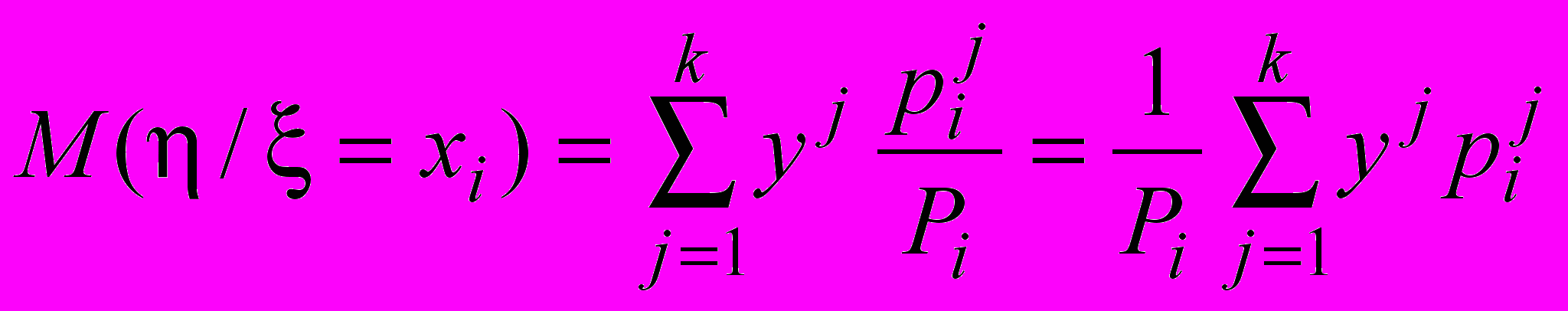
_{Из определения следует, что если  и  независимы, то все условные законы распределения одинаковы и совпадают с законом распределения  (напоминаем, что закон распределения  определяется в таблице (*) первым и последним столбцом). При этом очевидно, совпадают все условные математические ожидания М(/ = yj) при j = 1,2,,k, которые равны М.}

_{Если условные законы распределения  при различных значениях  различны, то говорят, что между  и  имеет место статистическая зависимость.}

_{Пример I. Пусть закон совместного распределения двух случайных величин  и  задан следующей таблицей. Здесь, как говорилось ранее, первый и последний столбцы определяют закон распределения случайной величины , а первая и последняя строки – закон распределения случайной величины .}

_ _	₁	₂	₃
₁₀	_1/36	₀	₀	_1/36
₂₀	_2/36	_1/36	₀	_3/36
₃₀	_2/36	_3/36	_2/36	_7/36
₄₀	_1/36	_8/36	_16/36	_25/36
	_6/36	_12/36	_18/36

_{Полигоны условных распределений можно изобразить на трехмерном графике (рис. 1).}

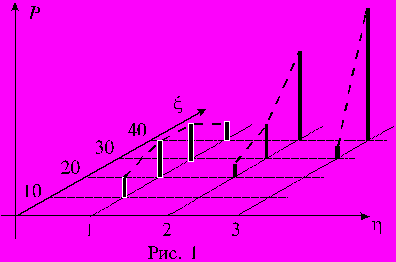
_{Здесь явно просматривается зависимость условного закона распределения  от величины .}

_{Пример II. (Уже встречавшийся).}

_{Пусть даны две независимые случайные величины  и  с законами распределения}

_	₀	₁		_	₁	₂
_Р	_1/3	_2/3		_Р	_3/4	_1/4

_{Найдем законы распределений случайных величин =+ и =}

_	₁	₂	₃		_	₀	₁	₂
_Р	_3/12	_7/12	_2/12		_Р	_4/12	_6/12	_2/12

_{Построим таблицу закона совместного распределения  и .}

_ _	₀	₁	₂
₁	_3/12	₀	₀	_3/12
₂	_1/12	_6/12	₀	_7/12
₃	₀	₀	_2/12	_2/12
	_4/12	_6/12	_2/12

_{Чтобы получить =2 и =0, нужно чтобы  приняла значение 0, а  приняла значение 2. Так как  и  независимы, то}

_{Р(=2; =0)= Р(=0; =2)=Р(=0)Р(=2)=1/12.}

_{Очевидно также Р(=3; =0)=0.}

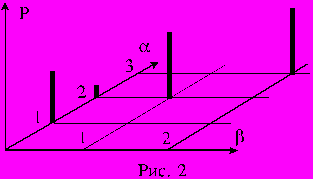
_{Построим полигоны условных распределений. Здесь зависимость  от  довольно близка к функциональной: значению =1 соответствует единственное =2, значению =2 соответствует единственное =3, но при =0 мы можем говорить лишь, что  с вероятностью 3/4 принимает значение 1 и с вероятностью 1/4 – значение 2.}

_{Пример III.}

_{Рассмотрим закон совместного распределения  и , заданный таблицей}

_ _	₀	₁	₂
₁	_1/30	_3/30	_2/30	_1/5
₂	_3/30	_9/30	_6/30	_3/5
₃	_1/30	_3/30	_2/30	_1/5
	_1/6	_3/6	_2/6

_{В этом случае выполняется условие P(=xi; =yj)=P(=xi)P(=yj), i, j =1,2,3}

_{Построим законы условных распределений}

_	₁	₂	₃
_{р=1()=р=2()=р=3()=р=4()}	_1/5	_3/5	_1/5

_{Законы условных распределений  не отличаются друг от друга при =1,2,3 и совпадают с законом распределения случайной величины . В данном случае  и  независимы.}

_{Характеристикой зависимости между случайными величинами  и  служит математическое ожидание произведения отклонений  и  от их центров распределений (так иногда называют математическое ожидание случайной величины), которое называется коэффициентом ковариации или просто ковариацией.}

_{cov(; ) = M((–M)(–M))}

_{Пусть  = x1, x2, x3,, xn,  = y1, y2, y3,,yk. Тогда}

_{cov(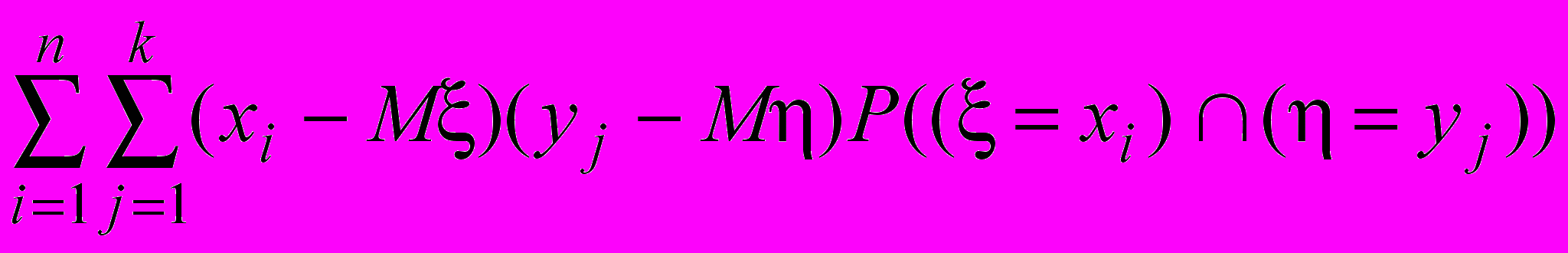; )= (2)}

_{Эту формулу можно интерпретировать так. Если при больших значениях  более вероятны большие значения , а при малых значениях  более вероятны малые значения , то в правой части формулы (2) положительные слагаемые доминируют, и ковариация принимает положительные значения.}

_{Если же более вероятны произведения (xi – M)(yj – M), состоящие из сомножителей разного знака, то есть исходы случайного эксперимента, приводящие к большим значениям  в основном приводят к малым значениям  и наоборот, то ковариация принимает большие по модулю отрицательные значения.}

_{В первом случае принято говорить о прямой связи: с ростом  случайная величина  имеет тенденцию к возрастанию.}

_{Во втором случае говорят об обратной связи: с ростом  случайная величина  имеет тенденцию к уменьшению или падению.}

_{Если примерно одинаковый вклад в сумму дают и положительные и отрицательные произведения (xi – M)(yj – M)pij, то можно сказать, что в сумме они будут “гасить” друг друга и ковариация будет близка к нулю. В этом случае не просматривается зависимость одной случайной величины от другой.}

_{Легко показать, что если P(( = xi)∩( = yj)) = P( = xi)P( = yj) (i = 1,2,,n; j = 1,2,,k), то cov(; )= 0.}

_{Действительно из (2) следует}

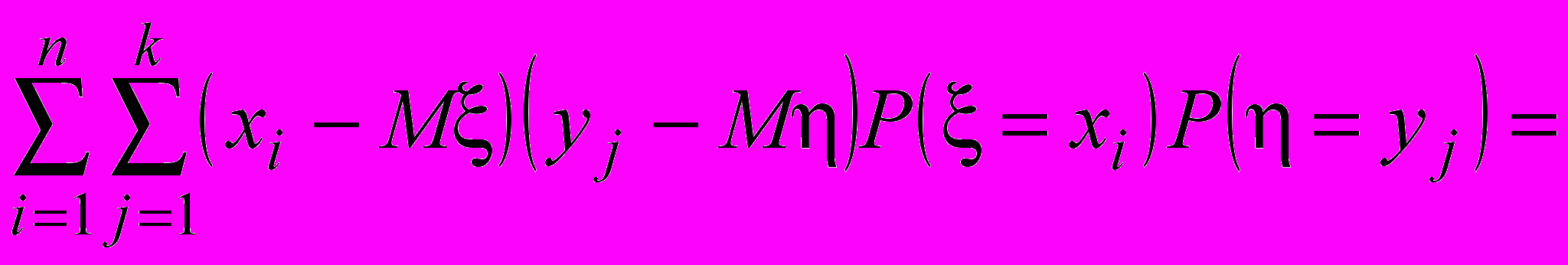
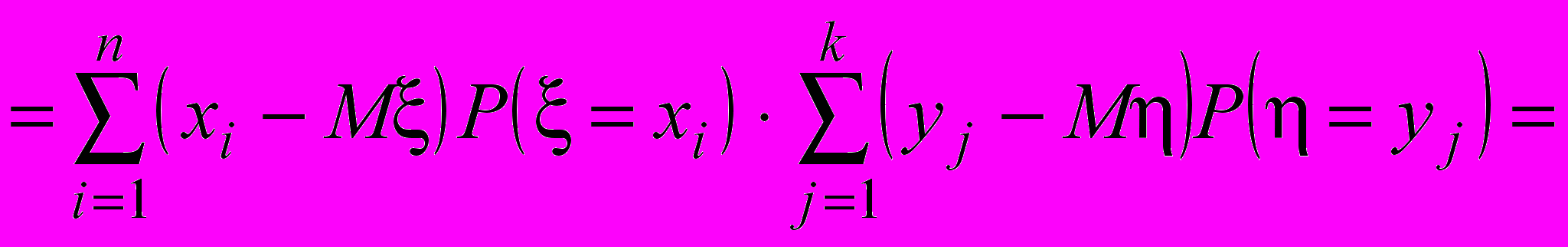
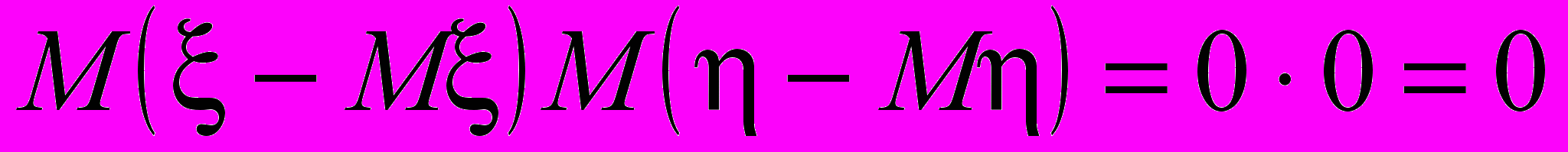
_{Здесь использовано очень важное свойство математического ожидания: математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю.}

_{Доказательство (для дискретных случайных величин с конечным числом значений).}

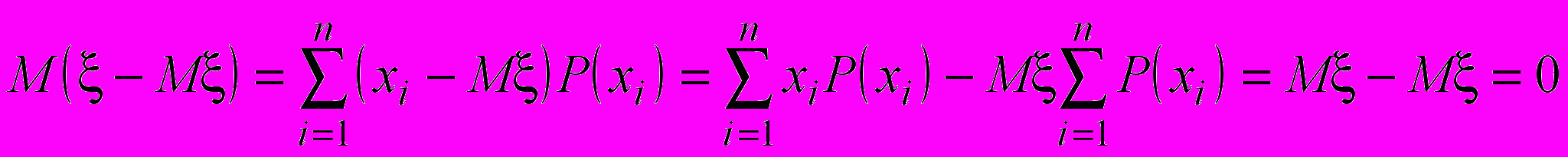
_{Ковариацию удобно представлять в виде}

_{cov(; )=M(–M–M+MM)=M()–M(M)–M(M)+M(MM)=}

_{=M()–MM–MM+MM=M()–MM}

_{Ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение математических ожиданий.}

_{Легко доказывается следующее свойство математического ожидания: если  и —независимые случайные величины, то М()=ММ. (Доказать самим, используя формулу M() = )}

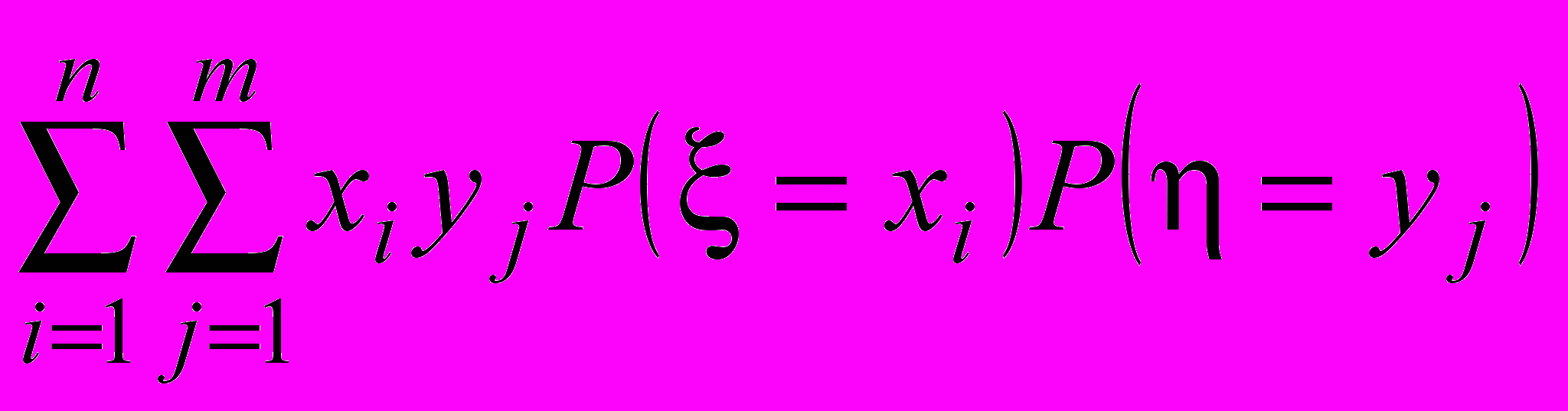_{Таким образом, для независимых случайных величин  и  cov(;)=0. Задачи. 1. Монету подбрасывают 5 раз. Случайная величина  – число выпавших гербов, случайная величина  – число выпавших гербов в последних двух бросках. Построить совместный закон распределения случайных величин, построить условные законы распределения  при различных значениях . Найти условные математические ожидания и ковариацию  и .}

_{2. Две карты наудачу извлекаются из колоды в 32 листа. Случайная величина  – число тузов в выборке, случайная величина  – число королей в выборке. Построить совместный закон распределения  и , построить условные законы распределения  при различных значениях . Найти условные математические ожидания и ковариацию  и .}

Blog

Нормальный закон распределения

Содержание

Нормальный закон распределения.

Совместное распределение двух случайных величин.