Урок рассказ для учащихся 11-х классов

Математика - самая древняя из наук, она была и остается необходимой людям. Слово «математика» греческого происхождения. Оно означает «наука», «размышление». В древности полученные знания, открытия часто старались сохранить в тайне. Например, в школе Пифагора запрещено было делиться своими знаниями с пефигорейцами. За нарушение этого правила один из учеников, требовавший свободного обмена знаниями, - Гиппас был изгнан из школы. Сторонников Гиппаса стали называть математиками, то есть приверженцами науки.

Основы математики все без исключения начинают изучать уже с первых классов школы, потому что эта наука нужна всем, особенно сейчас, когда математика проникла во все отрасли знаний - физику и химию, науки о язьш и медицину, астрономию и биологию и так далее.

Математики учат вычислительные машины сочинять стихи и музыку, измерять размеры атомов и проектировать плотины электростанций.

Математика необходима в любой профессии, какую бы вы ни выбрали для себя. Но кроме того, вы могли заметить: это и очень интересная и увлекательная наука. Любите ее.

Рене Декарт

Декарт (1596-1650)родил­ся на юге Франции в семье, принадлежащей знатному, но обедневшему роду. Когда Рене исполнилось восемь лет, отец отправил его в коллеж Ла-Флеш. Вспоминая годы учебы, Декарт писал: «Я изучал там всё, что изучали другие, и, не довольствуясь преподаваемы­ми сведениями, пробегал все попадавшие мне под руки кни­ги* трактовавшие о наиболее . редкостных и любопытнейших науках... Особенно нравилась мне математика вер­ностью и очевидностью своих рассужде­ний*.

Окончив коллеж, юноша обдумывал план дальнейшей жизни. В путешестви­ях, наблюдениях, экспериментах, размыш­лениях он видел путь, который приведет его к познанию тайн природы. Но внача­ле» оказавшись в Париже, он ведет обыч­ную для молодого и знатного дворянина светскую жизнь. Затем наступает пере­лом — он уединяется в предместье Пари­жа Сен-Жермен и предается занятиям на­укой. Но ненадолго. В 22 года он вступает добровольцем в армию и три года служит офицером под знаменами французской ко­роны, принимает участие в сражениях. Ос­тавив военную службу, Декарт посвящает себя занятиям философией, много путеше­ствует: он побывал в Швейцарии, Голлан­дии, Италии, в полной мере осуществив задуманный в юности план общеобразова­тельных путешествий.

Снова обосновавшись в Париже, Декарт разрабатывает основы своего научного ме­тода, «позволяющего направить свой ра­зум и отыскивать истину в науках»; о нем заговорили как о создателе новой фило­софской системы. Слава молодого ученого быстро растет. Он чувствует необходимость полного уединения, чтобы завершить ис-

следования, и решает «уда­литься от всех мест, где мог иметь знакомства».

Декарт переезжает в Гол­ландию. Здесь он прожил двад­цать лет, наполненных непре­рывным трудом. Его время распределяется так: утром — продолжительные размышле­ния и решение математиче­ских задач, затем опыты по оп­тике, анатомии, медицине, бо­танике, вечерами — письма. Он ведет обширную переписку с выдаю­щимися учеными Европы.

Математические труды Декарта собраны в книге «Геометрия», в которой он изложил основы, аналитической геометрии и алгеб­ры. Он ввел в математику ряд обозначе­ний, которые применяются и по сей день. Декарт положил начало исследованию ал­гебраических уравнении. Так, он установил, что число действительных и мнимых кор­ней алгебраического уравнения равняется степени неизвестного. Это важнейшая тео­рема алгебры (доказана она была значитель­но позднее Гауссом). Его труды оказали ре­шающее влияние на дальнейшее развитие математики, в частности, на основе дости­жений Декарта были разработаны принци­пы дифференциального исчисления.

О великом ученом была наслышана и шведская королева Христина, которая за­интересовалась его философской системой и пожелала изучить ее под руководством самого Декарта. Для этого она пригласи­ла философа в «страну медведей, снегов и льдов» (так писал о Швеции Декарт). За­нятия Христина назначила на пять утра, что было тяжело для ученого, привыкше­го к иному распорядку жизни. К тому же зима в этот год выдалась на редкость хо­лодной. Вскоре Декарт простудился и за­болел воспалением легких. 11 февраля 1650 г. он умер.

Декартова система координат

Декарт переделал геометрию и сделал возможным существование современной геометрии.

Основная идея, как и все истинно вели­кие идеи математики, проста до очевид­ности. Начертим на плоскости две пересе­кающиеся прямые. Не теряя общности, можем предположить, что они образуют прямой угол. Вообразим теперь город, в котором проспекты идут на юг и на север, а улицы — на восток и запад. План горо­да может быть описан полностью, если вы­брать некоторый проспект и некоторую улицу в качестве осей, пересекающихся в точке, называемой началом, от которой последовательно отсчитываются номера проспектов и улиц. Эти номера дают ад­рес, по которому сразу же представляем соответствующее место. Такая идея позво­ляет нам однозначно .определить положе­ние любой точки относительно осей, зада­вая пару чисел, которые измеряют ее уда­ление от осей на восток или запад и на север или юг; эта пара чисел называется координатами точки (относительно осей).

Теперь предположим, что точка движет­ся по плоскости. Координаты (х; у) любой точки кривой, по которой перемещается точка, будут связаны между собой уравнением, которое называется уравнением кри­вой. Предположим теперь для простоты, что наша кривая является окружностью. Мы имеем ее уравнение. Что можно извлечь из него? Вместо этого конкретного уравнения мы можем написать более общее уравне­ние того же вида, а затем исследовать его с помощью алгебры. В конце концов, все результаты алгебраических преобразований переходят в свои эквиваленты в термина координат точек кривой, о чем все это время мы намеренно забывали.

У'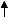
	4	А(2;4)
		2	х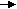

Для прямых линий и окружностей это не кажется очень поразительным: мы знали раньше, как с ними обращаться пользуясь другим, древнегреческим способом. Истинная сила метода проявляется лишь тогда, когда мы начинаем иметь дело с уравнениями любой степени и любой сложности и интерпретируем их алгебраические и аналитические свойства геометрически.

То, к чему Декарт все время стремился было применение метода координат hi только к представлению уравнениями уж< определенных геометрически кривых, н< и к взгляду с совершенно противоположной точки зрения, к определению все бо лее и более сложных кривых.

Все, что мы проделали, может быть распространено на пространство любого чаем измерений; на плоскости нам нужны две координаты, в обычном пространстве -три, в механике и теории относительное три — четыре и, наконец, в «пространстве», которое по нраву математикам, — п коор­динат, или столько координат, сколько су­ществует всех натуральных чисел.

Как Декарт проводил касательные

В «Геометрии» Декарт приводит общий метод проведения касательных — так на­зываемый «метод нормалей». Нормалью линии в данной ее точке называется пря­мая, проходящая через эту точку перпен­дикулярно к касательной. В частности, если данная линия — окружность, то нор­маль есть прямая, идущая вдоль радиуса, имеющего концом точку касания. Понят­но, что если нам удастся построить нор­маль, мы без труда построим и касатель­ную. Именно так поступает Декарт: он строит сначала нормаль, а затем касатель­ную (отсюда и название его метода).

Покажем, как методом Декарта найти касательную к эллипсу в данной его точ­ке. Уравнение эллипса имеет вид:





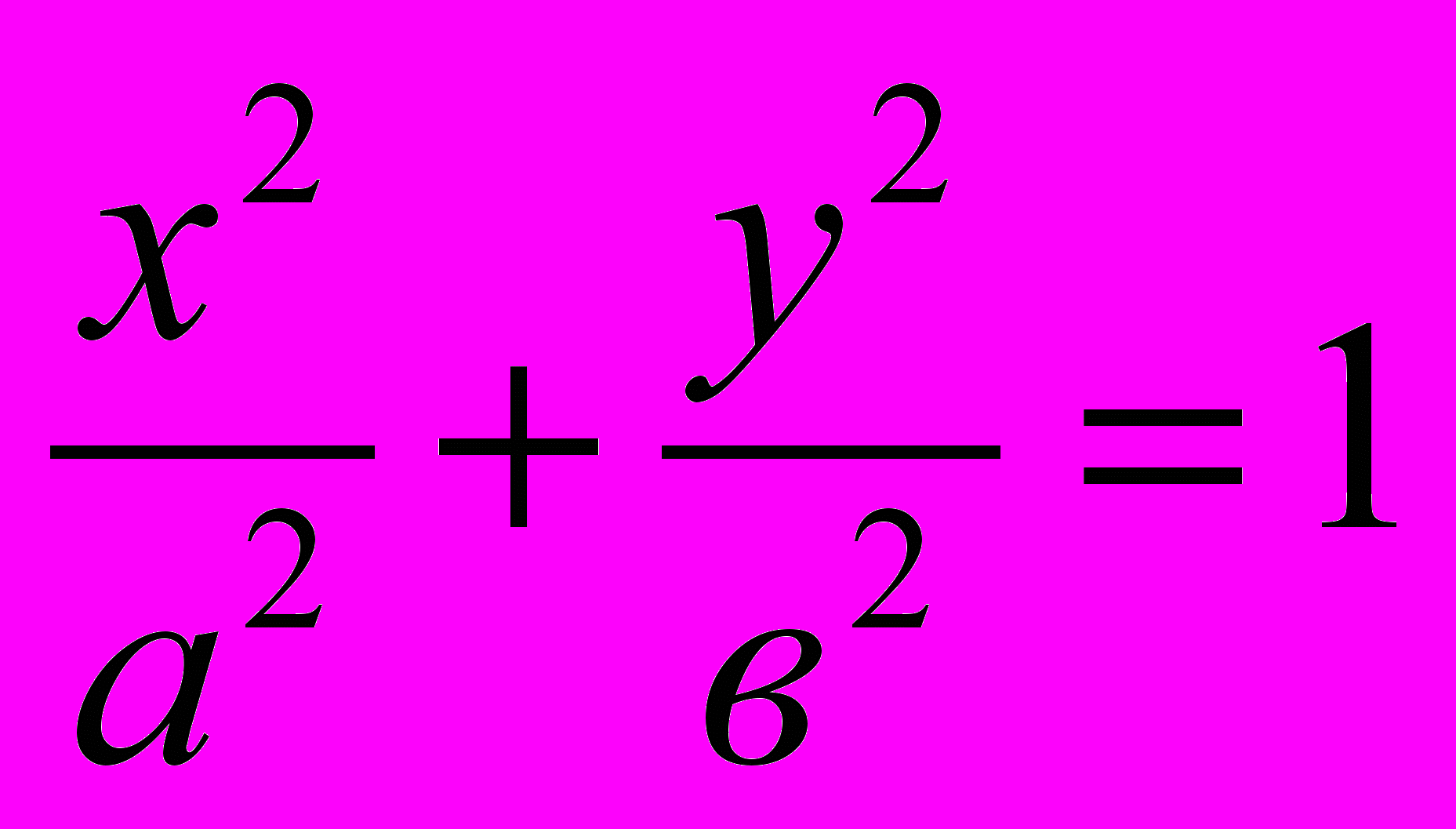
Возьмем эллипс, заданный уравнением





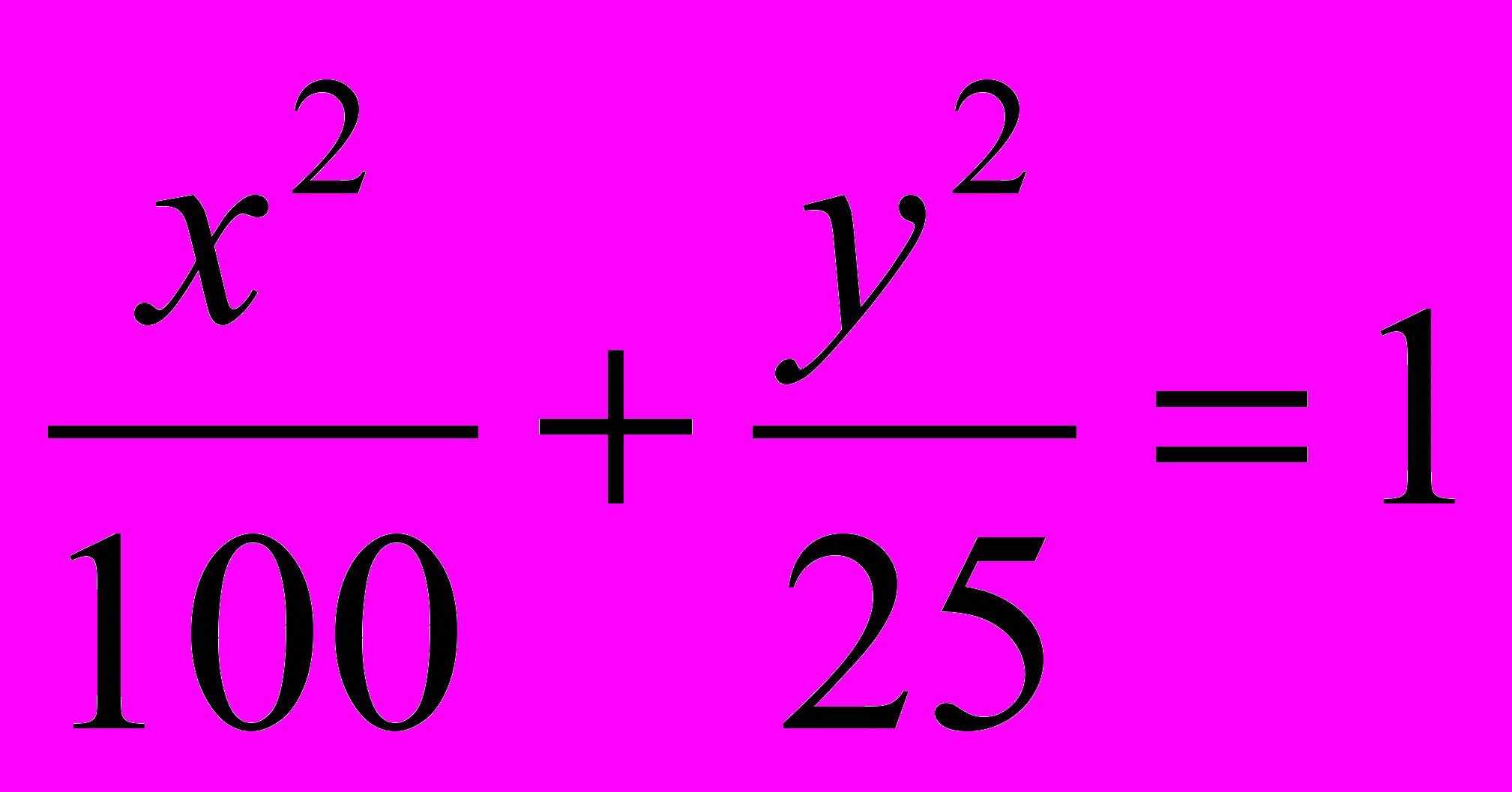
и какую-нибудь точку на нем, например Р(8; 3). Нормаль эллипса в точке Р пере­сечет ось абсцисс в некоторой точке Q(c; 0). Если мы найдем число с, то сможем записать уравнение нормали и затем урав­нение касательной. Для нахождения чис­ла с построим вспомогательную окруж­ность с центром в точке Q, которая каса­ется эллипса в двух симметричных отно­сительно оси абсцисс точках.



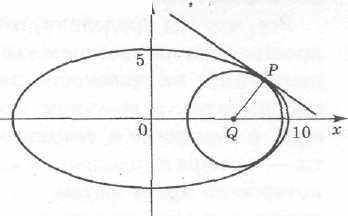
Напишем уравнение окружности:

(х – с)² + у² = (8 - с)² + 9, и преобразуем его к виду

х² + у² = 2хс - 16с + 73.

Теперь запишем уравнение эллипса в виде

х² + 4у² = 100 и решим систему





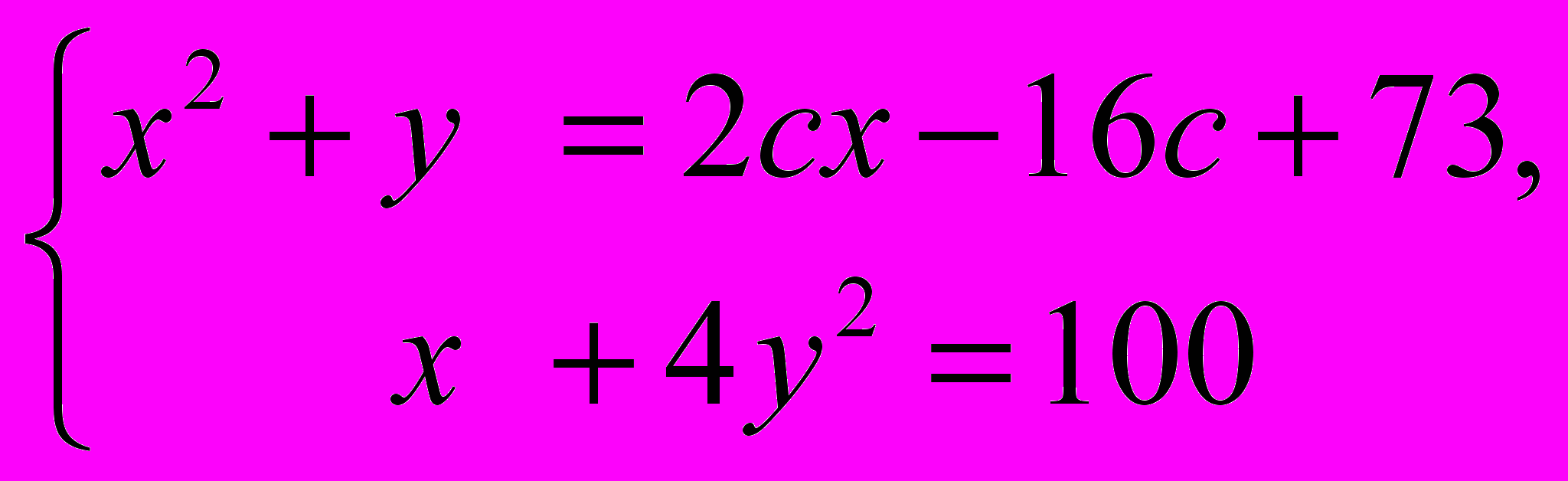
Исключив неизвестное у, придем к квад­ратному уравнению

Зх² - 8хс + 64с - 192 = 0,

которое должно иметь единственное реше­ние, поскольку точки касания окружнос­ти с эллипсом имеют одну и ту же абсцис­су. Значит, дискриминант уравнения

16с² - 3(64с - 192)

должен быть равен нулю. Отсюда получим, что с = 6.

Теперь, зная две точки Р(8; 3) и Q(6; 0) нормали, нетрудно на писать ее уравнение:

У=3/2х-9. Так как произведение угловых коэффициентов перпендикулярных пря­мых (непараллельных осям координат) равно —1, то угловой коэффициент касательной равен -2/3. Запишем уравнение касательной:


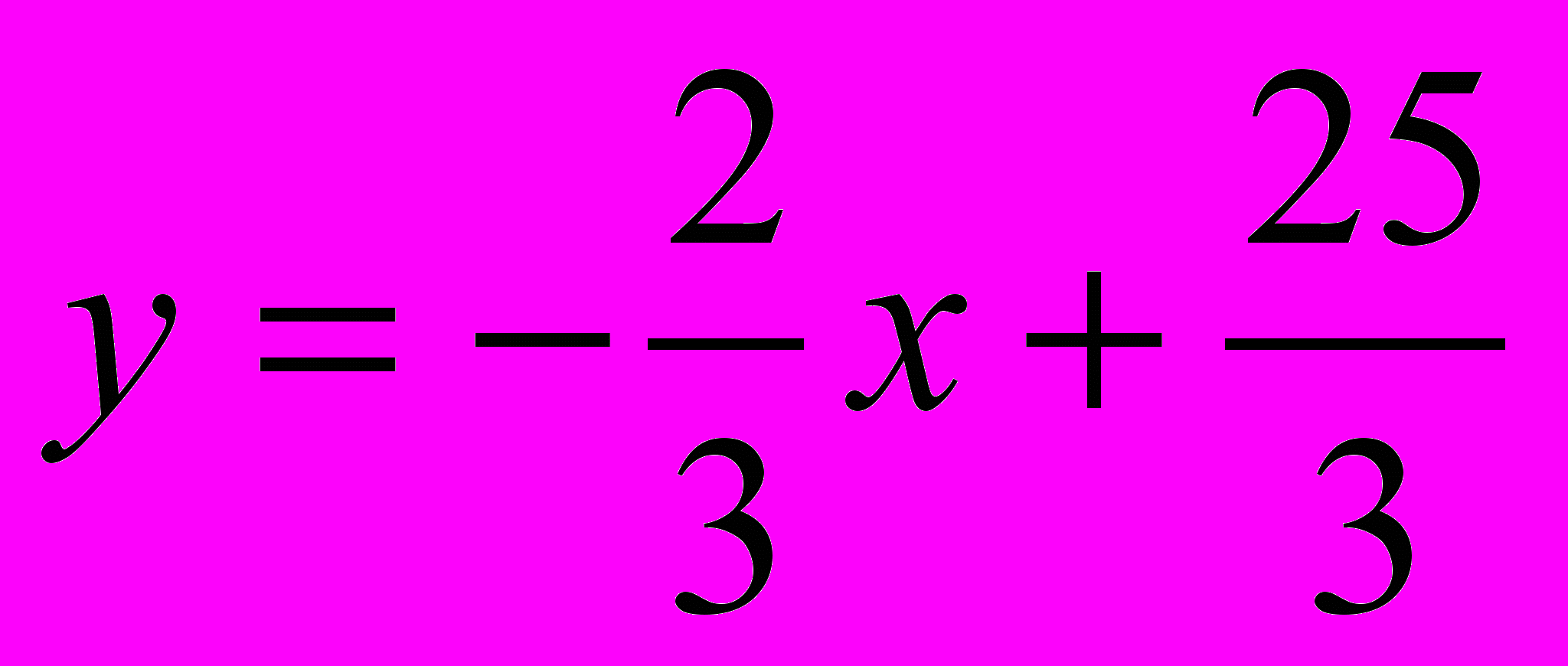или 2х + 3y = 25.

Задача 1. Пользуясь методом Декарта, найдите уравнение касательной к эллипсу





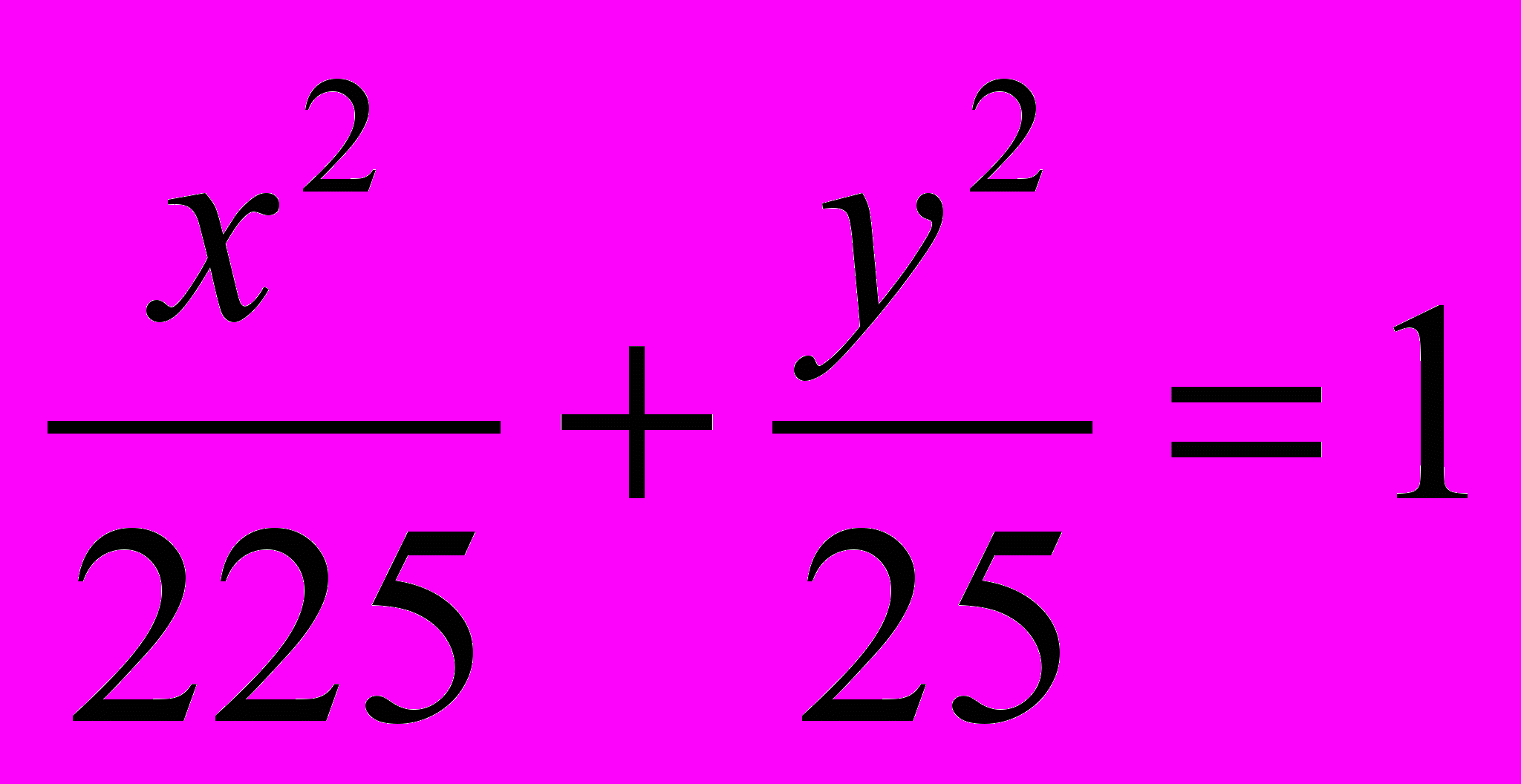
в точке Р(9; 4).

Задача 2. С помощью производной по­кажите, что уравнение касательной к эл­липсу в точке (х₀; у₀) имеет вид





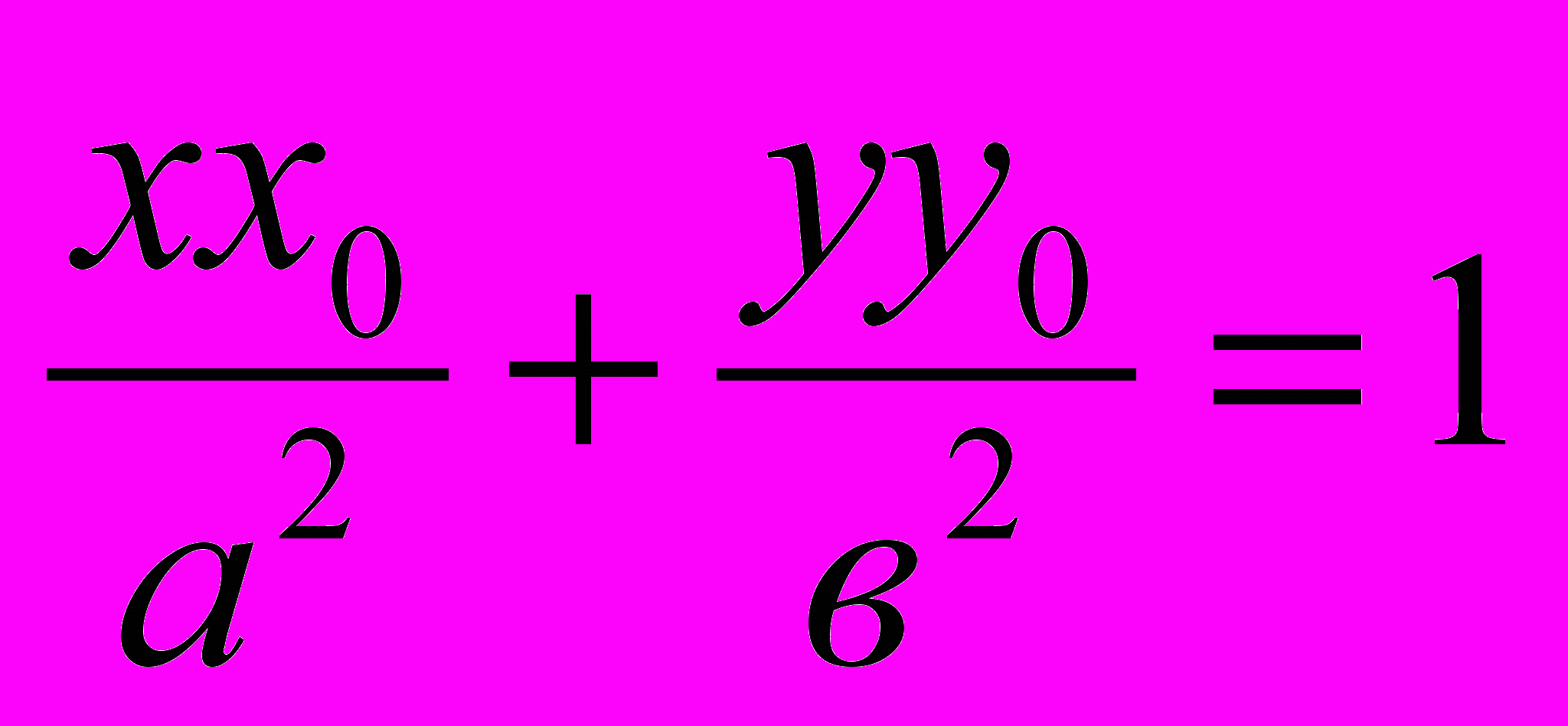
Франсуа Виет

Будущий преобразователь алгебры Франсуа Виет (1540-1603) появился на свет в ма­леньком французском городке Фонтене ле Конт, что находит­ся недалеко от крепости Ла-Ро-шель (где сражались бравые мушкетеры — Атос, Портос и Арамис и их друг Д'Артаньян).

В 1560 году Ф. Виет окончил Парижский университет и начал адвокатскую практику, через не­сколько лет перешел на государ­ственную службу, став сначала советником короля Генриха III, а затем рекетмейстером — до­кладчиком по ходатайствам. В 1589 году покровитель Виета — король Генрих Ш — был убит, и Виет стал служить новому королю — знаменитому Генриху IV. Жизнь его проходила на фоне кровавых со­бытий войны, которую вели две мощные ре­лигиозные группировки католиков и проте­стантов-гугенотов. Достаточно сказать, что он пережил Варфоломеевскую ночь.

Но был небольшой промежуток време­ни, когда из-за происков врагов Виет был отставлен от государственной службы и получил неожиданный досуг.

Сейчас нам трудно представить матема­тику без формул и уравнений, но именно такой была она до Виета. Виет завершил создание буквенного исчисления, введя обо­значения не только для неизвестного и его степеней (что делали и до него), но и для параметров. Это позволило записывать це­лые классы задач, которые можно решать с помощью одного правила. А над форму­лами стало возможным проводить операции и получать новые формулы и соотношения, то есть буквенное исчисление позволило за­менить часть рассуждений механическими операциями (выкладками) и, как говорил Лейбниц, «разгрузить воображение».

Именно тогда Виет пришел к выводу, что «должна существовать общая, неизвестная пока наука, обнимающая и остроумные раз

мышления новейших алгебраи­стов, и глубокие геометрические рассуждения древних». Он встал у истоков создания новой на­уки — тригонометрии. Многие тригонометрические формулы, которые ныне изучают в курсе математики средней школы, впервые были записаны Виетом. Еще в Средние века матема­тики изучали треугольники, но у Виета методы решения тре­угольников приняли закончен­ный вид. В 1593 году он пер­вым сформулировал в словесной форме теорему косинусов, исчер­пывающе разобрал известный ранее своей трудностью случай решения тре­угольника по двум данным сторонам и од­ному из углов, не лежащих между ними, ясно сказав, что в этом случае решение не всегда возможно, а если оно есть, то их мо­жет быть два.

Разрабатываемая Виетом, но еще дале­ко не законченная тригонометрия щедро от­благодарила ученого. Например, применяя тригонометрию, удалось научиться выра­жать корни кубического уравнения через тригонометрические функции.

Четыре года опалы оказались необычай­но плодотворными для Виета. Он работал самозабвенно. По рассказам современников, Виет мог просиживать за письменным сто­лом по трое суток подряд, только иногда забываясь сном на несколько минут. В тот период он начал большой труд, который на­звал «Искусство анализа, или Новая алгеб­ра». Книгу он не завершил, но главное, что определило развитие всей математики Но­вого времени, было написано.

В мемуарах современников Виета есть указания на то, что он был женат, что у него была дочь, единственная наследница имения, по которому Виет именовался «се­ньор де ла Биготье». А наследство, которое он оставил нам с вами, и сейчас служит поводом для восхищения и поклонения.

^{Теорема Виета}

Школьный вариант теоремы Виета был известен задолго до Виета. Заслуга Виета состоит в том, что он выявил соот­ношения между корнями и коэффициен­тами уравнения для уравнений, по край­ней мере, 5-й степени. Вот, например, те­орема Виета для кубического уравнения.

Если числа a, b и с — корни кубиче­ского уравнения х³ + рх² + qx + s = 0, то



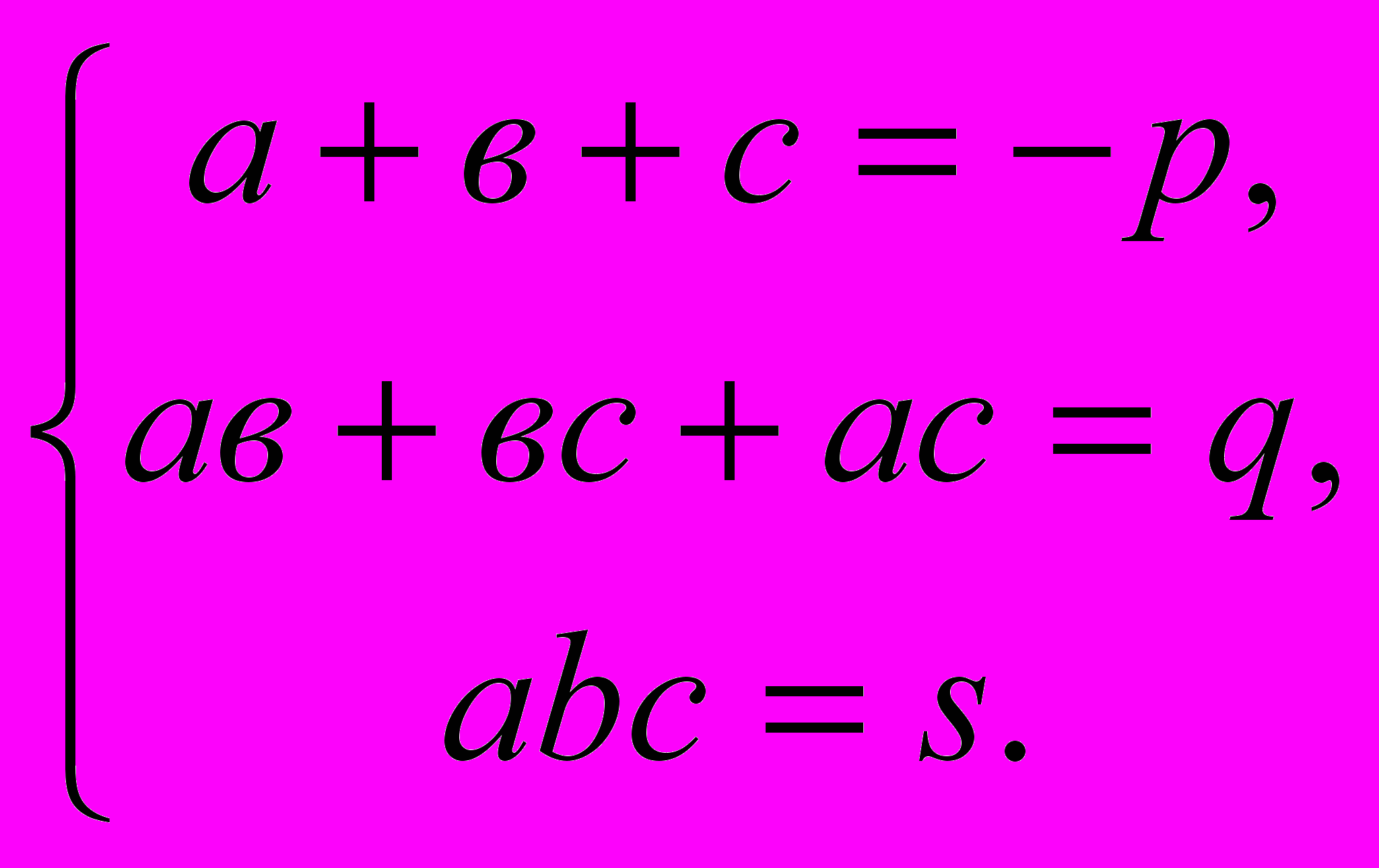
Впоследствии теорема была доказана для уравнений произвольных степеней.

Для случая квадратного уравнения Виет формулировал свою теорему так:

«если В + D, умноженное на А минус А², равно BD, то А равно В и равно D»

Виет прописными гласными буквами обозначал неизвестные величины (то, что мы обозначаем х, у него — А), а коэффи­циенты уравнения — прописными соглас­ными буквам (В и D).

Следовательно, в современных обозна­чениях утверждение Виета формулирует­ся следующим образом:

Если имеет место уравнение

(b + d)x - х² = bd,

то его корни равны b u d.

Теперь обозначим b + d = -p, bd = q и, после преобразований, получим

х² + рх + q = 0.

Эта теорема в современном школьном учебнике называется «обратной теоремой Виета».

А после этого уже недалеко до «прямой теоремы» из школьного учебника:

Сумма корней приведенного квадратно­го уравнения равна второму коэффициен­ту, взятому с противоположным знаком, а произведение корней равно свободному члену.


Две истории

История первая «Научный вызов Ван Ромена»

Однажды в ноябре 1594 г. при дворе Генриха IV нидерландский посланник рас­сказал об известной задаче знаменитого ма­тематика Адриена ван Ромена (1561-1615). Это был вызов математикам всего мира. Речь шла о решении уравнения 45-й сте­пени:

45х — 3795x³ + 9534х⁵ - ... - 12 300x³⁹ + 945х⁴¹ - 45⁴³ + х⁴⁵ = а,


где а =


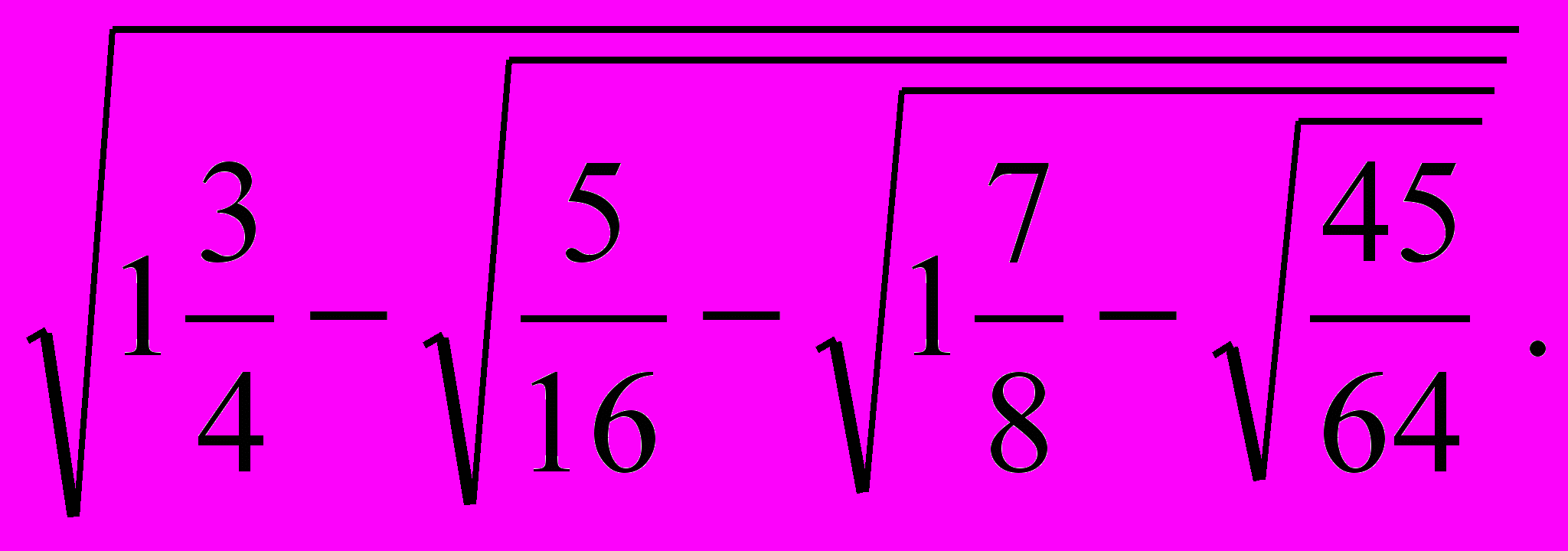
В списке тех, кому следовало направить его научный вызов, Ван Ромен не указал ни одного француза, и посланник заметил, что, по-видимому, во Франции нет матема­тиков. «Но почему же? — возразил ко­роль. — У меня есть математик, и весьма выдающийся». И он послал за Виетом.

Один корень Виет нашел сразу, а на сле­дующее утро — еще 22. Как же ему уда­лось сделать это так быстро?

Дело в том, что, занимаясь разложением sin nx и cos nx по степеням sin x и cos x, Виет установил связь некоторых алгебраи­ческих уравнений и задачи о делении угла на равные части. Он увидел, что предло­женное значение параметра а является сто­роной вписанного в круг правильного 15-угольника, то есть хордой, стягивающей дугу в 24°. Коэффициенты при д*⁵, х⁴³, ..., х показывали, что речь идет о делении этого угла на 45 равных частей, значит, одно из решений предложенного уравнения


2sin


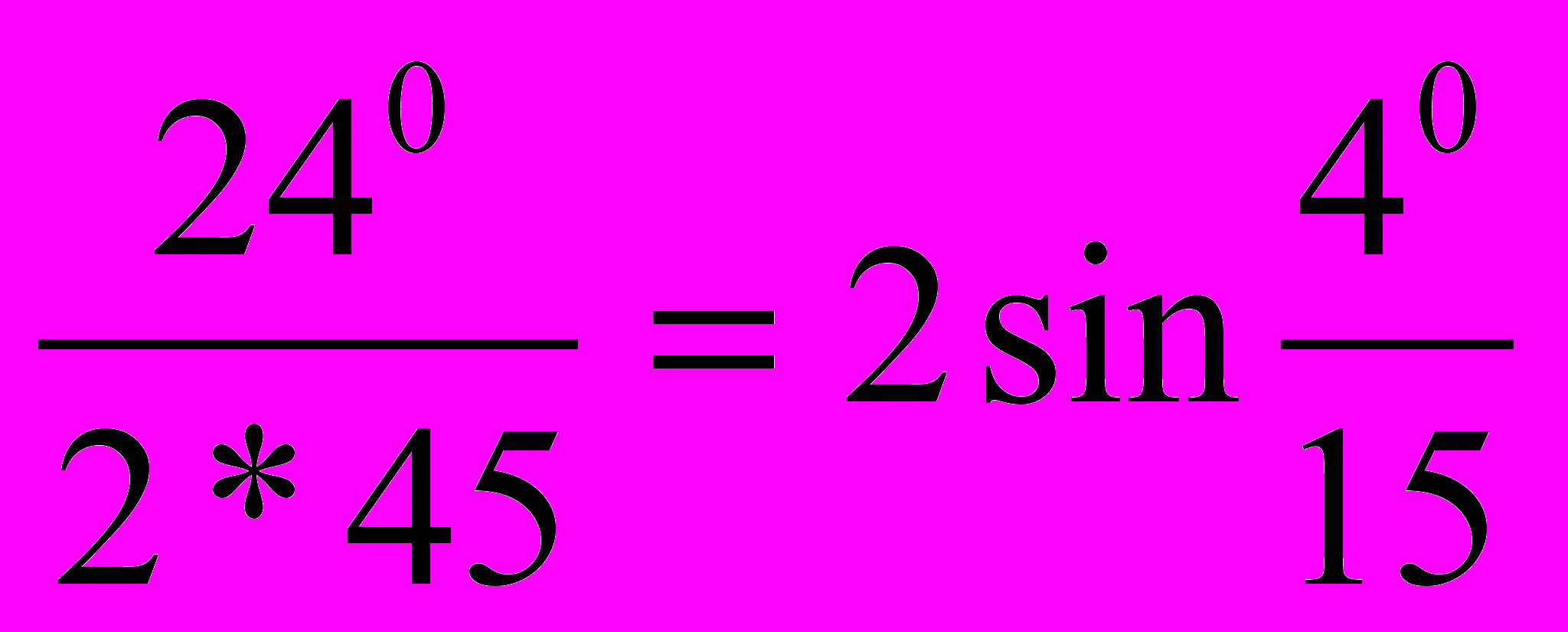
Остальные положительные решения будут


иметь вид 2sin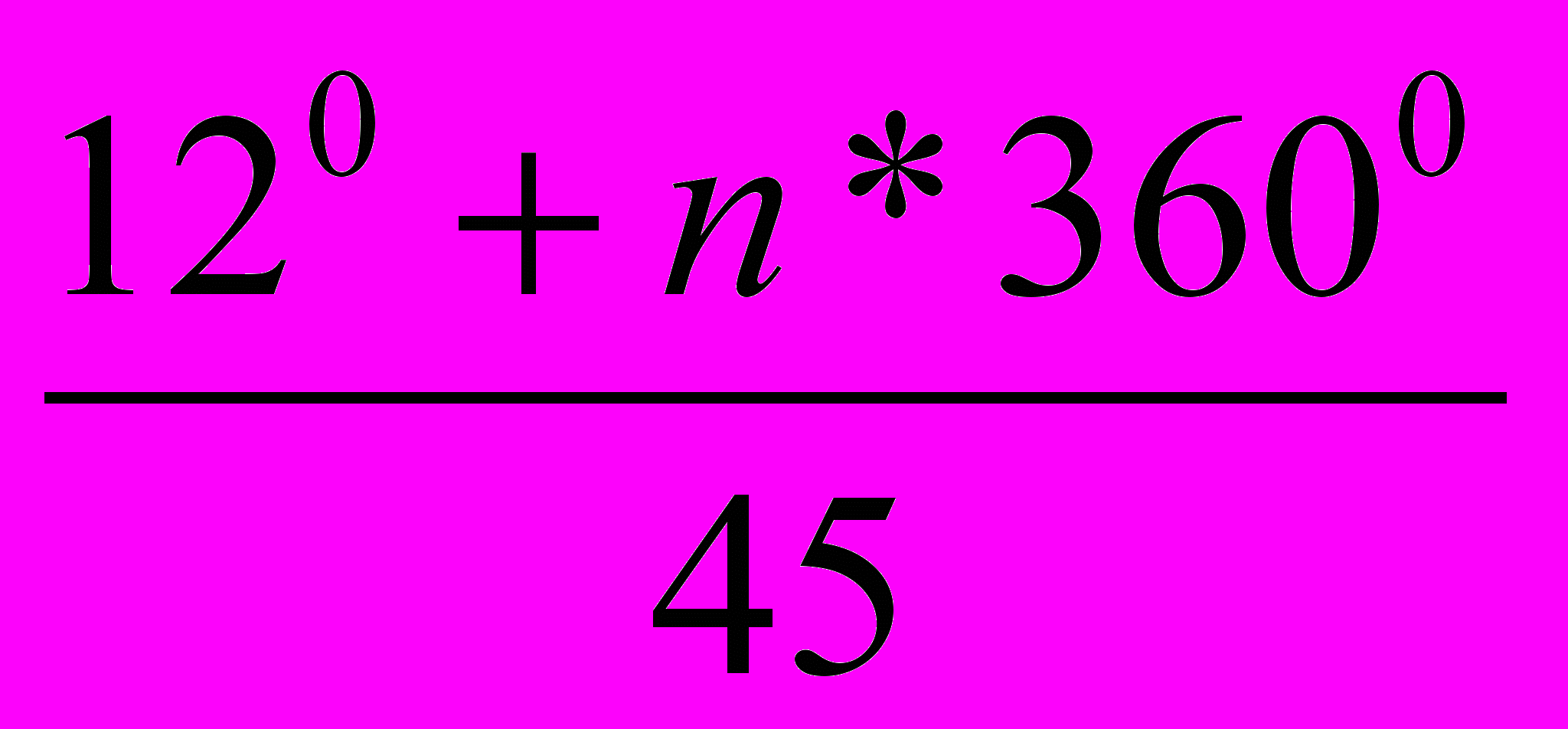, n=1,2, …, 22


Еще 22 решения — отрицательные, по традиции того времени Виет их не учи­тывал.

Ответ Виета был вскоре опубликован и принес ученому мировую славу.

История вторая «Расшифровка кода»

В XVI веке обострились отношения меж­ду соседями Франции на юге и на севере. На юге католический король Испании Фи­липп II вел жесткую политику против ряда государств. Особенно от нее страдали Ни­дерланды — области к северу от Франции. Когда-то эти области перешли в собствен­ность испанской короны. А население этих мест, почти сплошь протестантское, терпе­ло страшные бедствия от налогов, которы­ми его задавил испанский король. Нача­лась революция.

В этих условиях королю Франции Ген­риху III приходилось вести очень взвешен­ную дипломатию. А дипломатия тем более успешна, чем глубже знания о противни­ках.

Мечтая вернуть ускользающую власть над Нидерландами, Филипп II посылал туда и войска, и своих эмиссаров. Понятно, что ему приходилось вести обширную перепис­ку, чтобы руководить этими посланцами. Боясь, что секретные письма, которым предстоит пересекать не одну границу, бу­дут перехвачены, испанцы зашифровыва­ли их очень сложным кодом. Он содержал до 500 различных знаков, которые перио­дически менялись.

Но когда переписка действительно ока­залась перехваченной, задача её расшиф­ровки встала перед ответственным пра­вительственным чиновником и матема­тиком Виетом. С этой задачей он успеш­но справился. После этого авторитет Ви­ета при дворе еще более упрочился, ведь благодаря расшифровке кода француз­ский король смог прочесть всю перепис­ку Филиппа II, поэтому был полностью в курсе всех важнейших европейских событий.

Когда стало известно, что код расшиф­рован, испанцы не смогли в это поверить и обвинили французского короля в связи с нечистой силой.

_Фалес

Фалес считается одним из семи мудрецов, оказавших большое влияние на жизнь древних греков. И это пер­вый древнегреческий мысли­тель, имя которого дошло до нас. Его основная деятель­ность связана с городом Ми-летом в Малой Азии. По имени родного города его стали называть Фалес Ми­летский. Население там было неоднородным, много было греков, финикийцев, и некоторые историки утвер­ждают, что Фалес происходил из зажиточ­ной финикийской семьи. Долгие годы он провел по торговым делам в Египте и этим пребыванием воспользовался для получе­ния от египетских жрецов доступа к выс­шим тайнам их науки, прежде всего, к математике и астрономии.

Временной период жизни Фалеса дати­руют 624-547 годами до н.э. Это подтвер­ждается косвенными данными: известно, что Фалес предсказал полное солнечное затмение, которое произошло 28 мая 585 года до н.э. Отец истории Геродот рас­сказывает, что затмение случилось во вре­мя битвы между персами и войсками ионийских городов, в число которых вхо­дил и Милет. Воины были так напуганы, что не захотели продолжить битву. При­шлось договариваться о мире.

Предсказание солнечного затмения про­извело большое впечатление на современ­ников, а вообще, Фалес дальновидно сове­товал согражданам не вмешиваться в вой­ны могущественных соседей. Политические прогнозы философа чаще оправдывались, что способствовало распространению его славы как мудрого общественного деятеля. Но более всего Фалес известен тем, что ввел в геометрию доказательства. Вдумай­тесь: убеждая людей в чем-то при помощи доказательств, человек обра­щается только к разуму, верит только в разум, что было в древности далеко не ординарным. Верили во что угодно и кому угодно: ора­кулу, жрецу, колдуну. Они казались существами особен­ными, наделенными благо­словением богов. Но чтобы обыкновенный смертный че­ловек вдруг брался с уверен­ностью судить о том, чего нельзя непосредственно по­трогать, — это было совер­шенно непостижимо! Можно назвать вели­чайшие цивилизации, которые обогатили мир ценнейшими изобретениями и знани­ями, но до доказательств так я не додума­лись.

Появление доказательств у Фалеса не должно нас удивлять. Ведь греки воспри­няли геометрические знания из Египта и Месопотамии. Но в массе геометрических фактов, накопленных ко времени Фалеса, попадались и противоречивые. Например, для вычисления площади круга в Месопо­тамии пользовались одним способом, а в Египте — другим. Причем не было ника­кой возможности восстановить ход мысли жрецов, которые когда-то получили эти ре­зультаты. Их рассуждения нигде не фик­сировались, и их безнадежно забыли.

Оценить факты, полученные его пред­шественниками, отделить верные знания от неверных было проще всего с помощью доказательства.

Фалес начал строить геометрию на ло­гических основаниях, постепенно перехо­дя при помощи доказательств от одного положения к другому. Ему принадлежит только начало этой системы, но ее продол­жение оказалось настолько грандиозным, что можно говорить о Фалесе как о родо­начальнике науки.

Три истории

История первая «О практической сметке»

Размышляя, главным образом, над во­просами устройства мира, философ почти не обращал внимания на обыденную жизнь. Однажды, например, засмотревшись в небо, он упал в ров. Такие события не могли не вызывать насмешек окружающих. Видев­шая это некая прекрасная рабыня сказа­ла, что Фалес хотел увидеть происходящее на небесах, но не заметил того, что нахо­дится у него под ногами. И однажды Фа­лес захотел доказать своим состоятельным друзьям, что у него тоже есть практиче­ская сметка.

Он взял у них громадный кредит и ску­пил на эти деньги все маслодавильни в окру­ге, поскольку предвидел хороший урожай оливок. А оливковое масло, будучи одним из основных продуктов питания в Древнем мире, служило еще и главным предметом экспор­та, поэтому урожаи плодов оливковых дере­вьев регулярно приносили доход как мелким крестьянам, так и собственникам крупных оливковых рощ. Когда благоприятный про­гноз оправдался, владельцам урожая ничего не оставалось делать, как везти свои оливки к «монополисту» Фалесу и платить за отжим масла хорошие деньги. Так философ не толь­ко вернул долг своим кредиторам (их же день­гами), но и сам разбогател.

История вторая «Об измерении высоты пирамиды»

Египетские жрецы, желая испытать Фа-леса, предложили ученому измерить высо­ту пирамиды. Он дождался, когда длина его собственной тени стала равна его росту, и в этот момент измерил длину тени, кото­рую отбрасывала пирамида. Эта измерен­ная длина тени и равна высоте пирамиды.

История третья «Морская»

Рассказывают, что Фалесу принадлежит первое доказательство шарообразности Зем­ли. Оно состоит в том, что человек, смотря­щий в морскую даль, сначала замечает вер­хушку мачты приближающегося к берегу корабля, потом ее нижнюю часть и только в последнюю очередь видит сам корабль. Ситуация такая же, как будто объект вы­ныривает из-за бугорка.

А как определить, на какое расстояние от наблюдателя, находящегося на суше, удален корабль, видимый в открытом море? Метод определения, применявшийся в те времена, был основан на признаке равен­ства треугольников по стороне и двум при­лежащим углам, который, как известно, был доказан Фалесом.




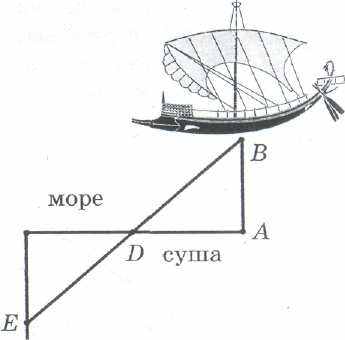
Пусть наблюдатель находится на суше, в точке А, а корабль — в море, в недоступ­ной точке В. Проведем к отрезку АБ пер­пендикуляр АС произвольной длины и раз­делим его пополам точкой D. Из точки С проведем перпендикуляр к отрезку АС, а затем проведем прямую BD до пересечения ее с этим перпендикуляром в точке Е. Тре­угольники EDC и BDA равны, а значит, равны и отрезки СЕ и АВ. Задача сводится к измерению на суше длины отрезка СЕ.