Полевая калибровочно-инвариантная модель гравитации

Вид материала

Документы

Содержание U через потенциал  согласно (6), и имея в виду соотношение (5), из (14) получаем нелинейное уравнение для 4-вектора напряженнос 6. Чёрная дыра U через ограничивающую центральное тело сферу S

Подобный материал:

• Ый подход к решению проблемы единого поля электромагнетизма и гравитации в рамках классической, 219.01kb.
• Единая теория электродинамики и гравитации  Абрамов А. П., 2006, 103.9kb.
• Учебная рабочая программа по дисциплине «военно-полевая терапия» V курс, 2075kb.
• Лекция 5 Методы построения математических моделей асу, 53.76kb.
• Александра Гордона «Релятивистская теория гравитации», 243.83kb.
• Законы эволюции вселенной часть движение фотонов вблизи тел, 227.77kb.
• Примеры моделей дискретных элементов рэа. Модель пленочного резистора. Модель диффузного, 131.9kb.
• «Бюллетень Министерства образования и науки рф», 369.69kb.
• Татарников К. В. Русская полевая армия 1700-1730. Обмундирование и снаряжение / Под, 14315.67kb.
• Программа зачетной работбы по модулю 2 дисциплины «Микроэкономика», 28.39kb.

ПОЛЕВАЯ КАЛИБРОВОЧНО-ИНВАРИАНТНАЯ МОДЕЛЬ ГРАВИТАЦИИ

А.Н.Сердюков


Развивается калибровочно-инвариантная модель гравитационного поля, порождаемого локальным масштабным преобразованием функции Лагранжа. В рамках этого подхода строится теория гравитационного взаимодействия в электродинамике.

1. Формулировка проблемы
   

Тривиальной особенностью лагранжева формализма является неизменность уравнений движения при умножении лагранжиана физической системы на произвольную положительную постоянную [^1,2]. Таким образом, в физике реализуется симметрия уравнений движения относительно своеобразного глобального калибровочного преобразования – масштабного преобразования лагранжиана  → '  U ² при постоянном U. Следуя принципу локальной калибровочной инвариантности, от такого глобального преобразования можно перейти к локальному, сделав U зависящим от четырехмерных координат x_. Такой переход означает введение калибровочного скалярного поля U(x_). Универсальность взаимодействия этого поля со всеми видами материи, обеспечиваемая его мультипликативным подключением к функции Лагранжа любой физической системы, дает основание рассматривать U(x_) как потенциальную функцию гравитационного поля.

Несмотря на имеющиеся хорошо разработанные релятивистские модели тяготения с тензорным потенциалом, исследование гравитации в рамках открывающегося подхода представляется оправданным, если иметь в виду те надежды, которые возлагаются на принцип локальной калибровочной инвариантности в создании будущей единой теории фундаментальных взаимодействий. Построение модели тяготения как классического поля актуально так же и в свете нефизического характера общей теории относительности, в которой отсутствуют основные законы сохранения [³].

Немаловажным, на наш взгляд, обстоятельством является и то, что в сегодняшних представлениях фундаментальной физики место линейного скалярного безмассового поля считается вакантным. Такая расточительность вряд ли свойственна самой природе, и возникает соблазн положительно решить эту проблему. В предлагаемом подходе данную вакансию заполняет гравитационное поле.

Первая попытка последовательно релятивистского (в рамках СТО) обобщения гравистатики Ньютона в духе классической теории поля была предпринята еще Нордстрёмом [^4–6] накануне создания ОТО. В основе модели Нордстрёма лежит предположение о том, что гравитационный потенциал является скалярным полем, который определен в плоском четырехмерном пространстве, а источником поля является инвариант Лауэ – след тензора энергии-импульса гравитирующей системы, включая и само гравитационное поле. Однако при таком выборе релятивистской формы «гравитационного заряда» электромагнитное поле с нулевым инвариантом Лауэ лишено гравитационных свойств. Данная «патология» теории Нордстрёма в значительной степени скомпрометировала саму идею построения адекватной скалярной модели тяготения [^{7, 8}]. С позиций современной теоретико-полевой идеологии теория Нордстрёма обладает ещё одним принципиальным недостатком – в ней отсутствует калибровочная инвариантность. Полевые уравнения этой теории неустранимым образом включают гравитационный потенциал, который определен через наблюдаемые – силовые характеристики поля с точностью до аддитивной константы.

Указанные недостатки теории Нордстрёма можно преодолеть, сохранив для потенциала гравитационного поля тензорную размерность 4-скаляра, если отказаться от инварианта Лауэ как релятивистской формы «гравитационного заряда», а в качестве одного из правил отбора допустимых релятивистских обобщений теории Ньютона использовать принцип калибровочной инвариантности. Такой подход приводит к новой полевой модели скалярного гравитационного поля, реализуемой в рамках СТО [⁹]. Эта модель описывает гравитационное взаимодействие в электродинамике, и оказывается достаточно привлекательной благодаря своей простоте при высокой эвристической ценности.

2. Частица в гравитационном поле
   
3. 
   

Применяя к функции Лагранжа свободной релятивистской частицы локальное масштабное преобразование, получим

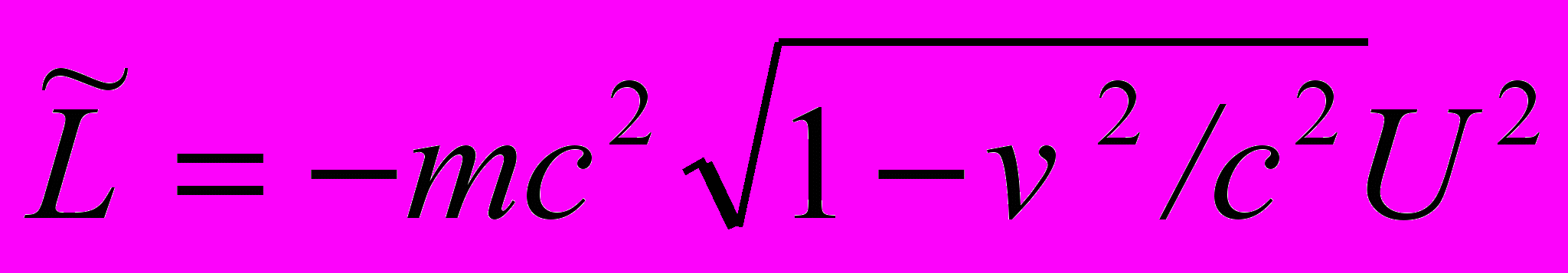. (1)

На основе (1) рассмотрим релятивистское движение частицы в поле U  U(x_μ) Уравнение Эйлера – Лагранжа

,

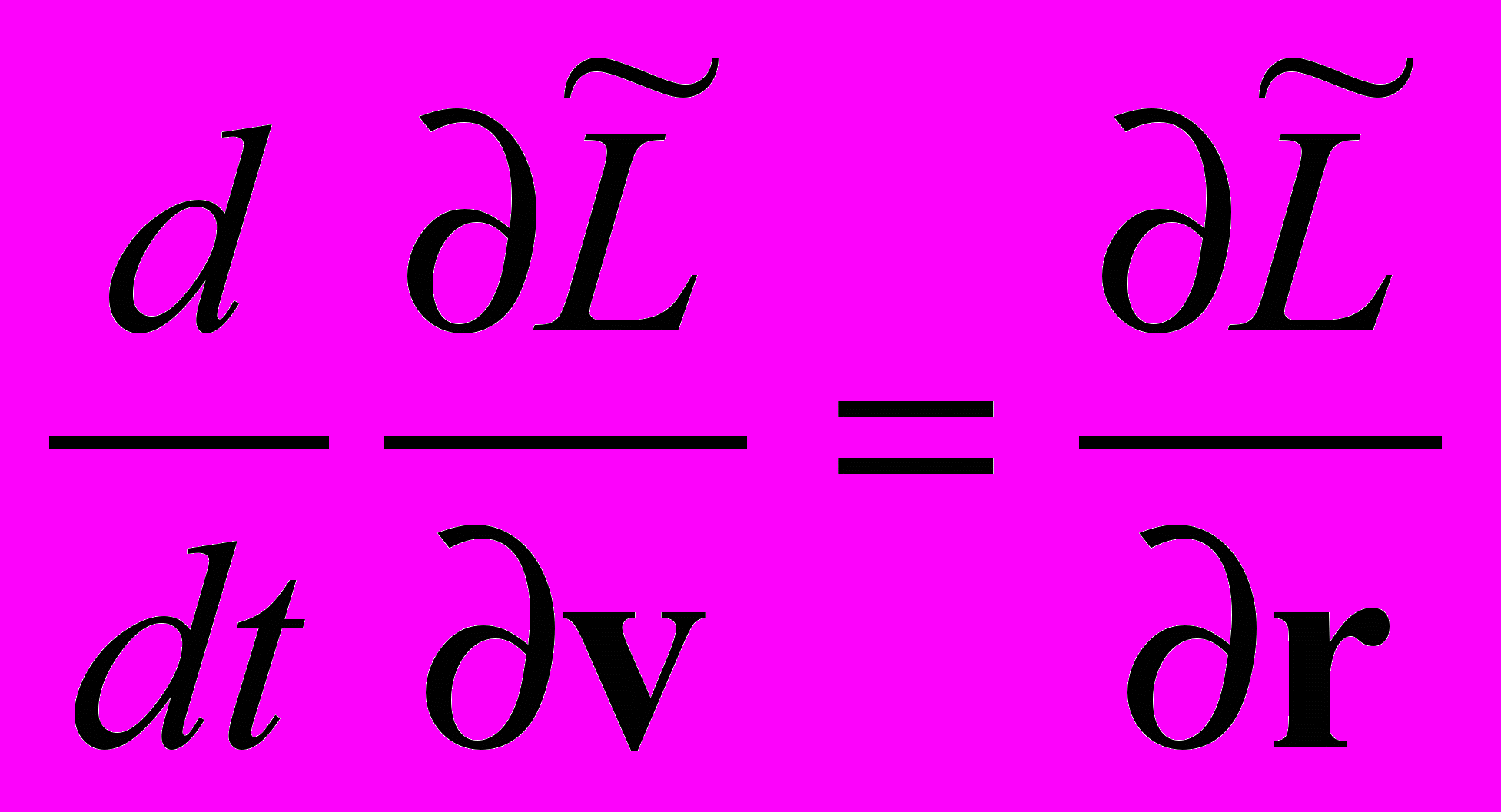и уравнение для энергии

,

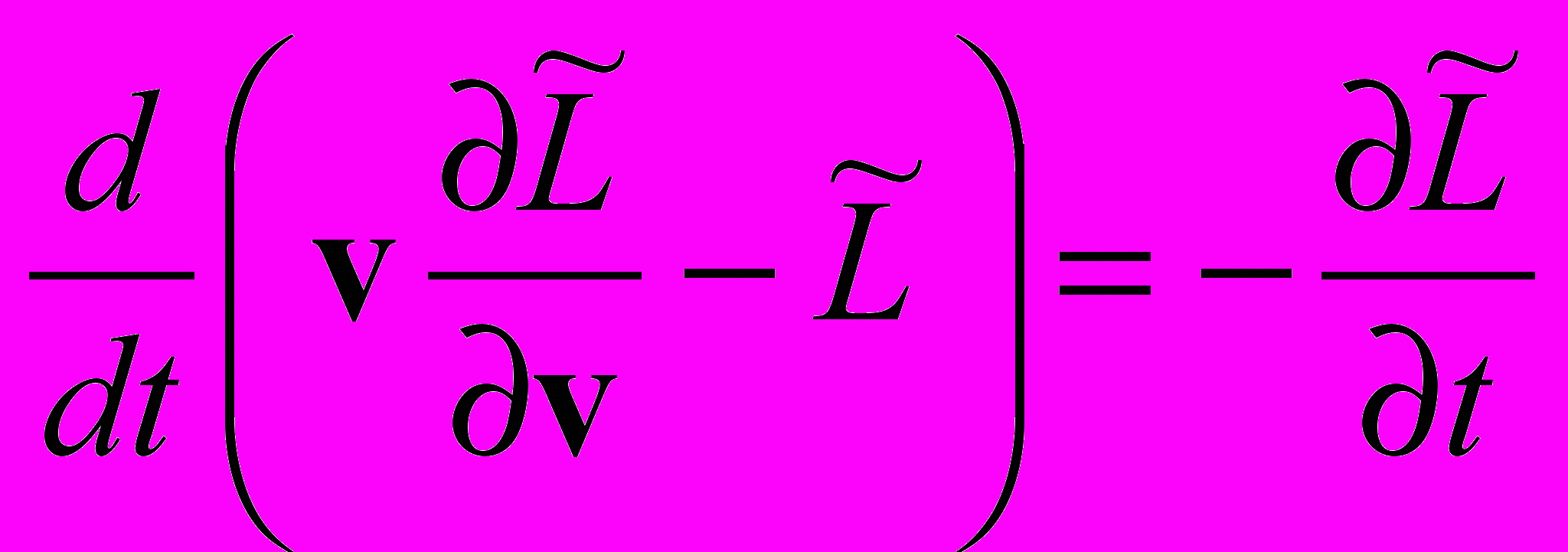в случае функции Лагранжа (1) образуют четырехмерное уравнение

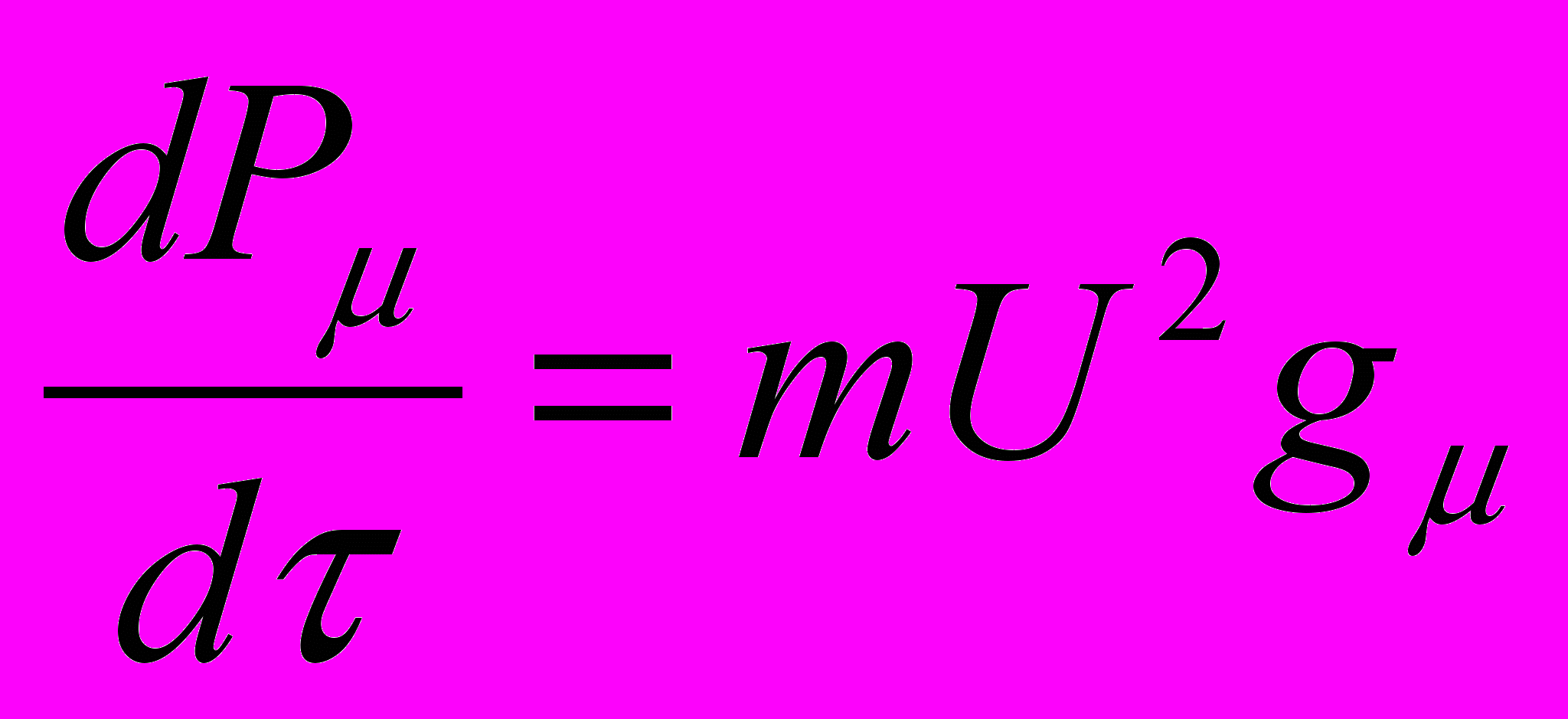. (2)

Здесь 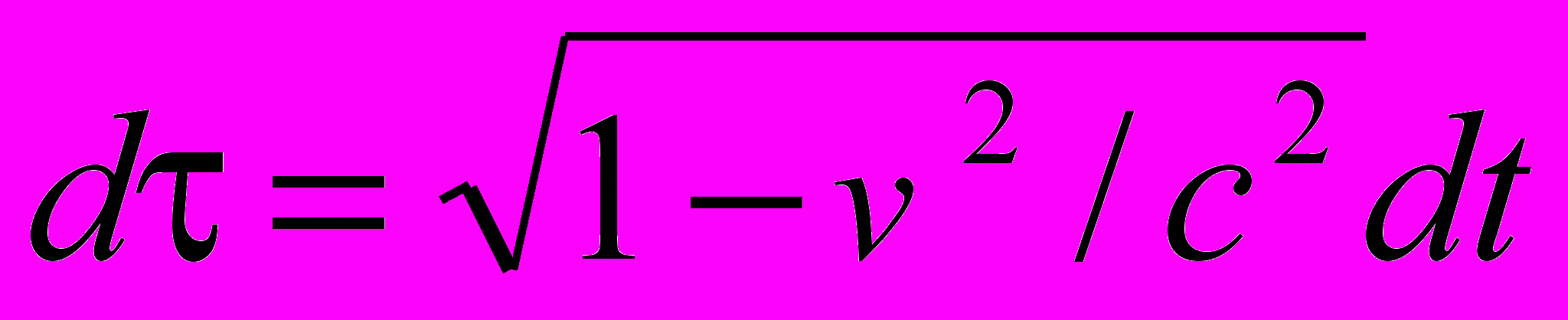; 4-вектор 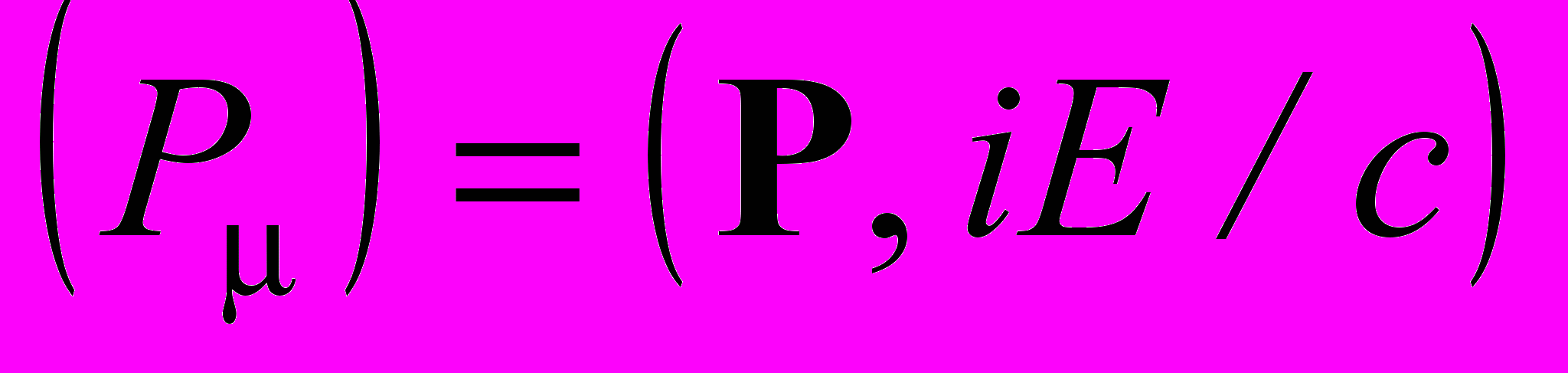составлен из обобщенного импульса 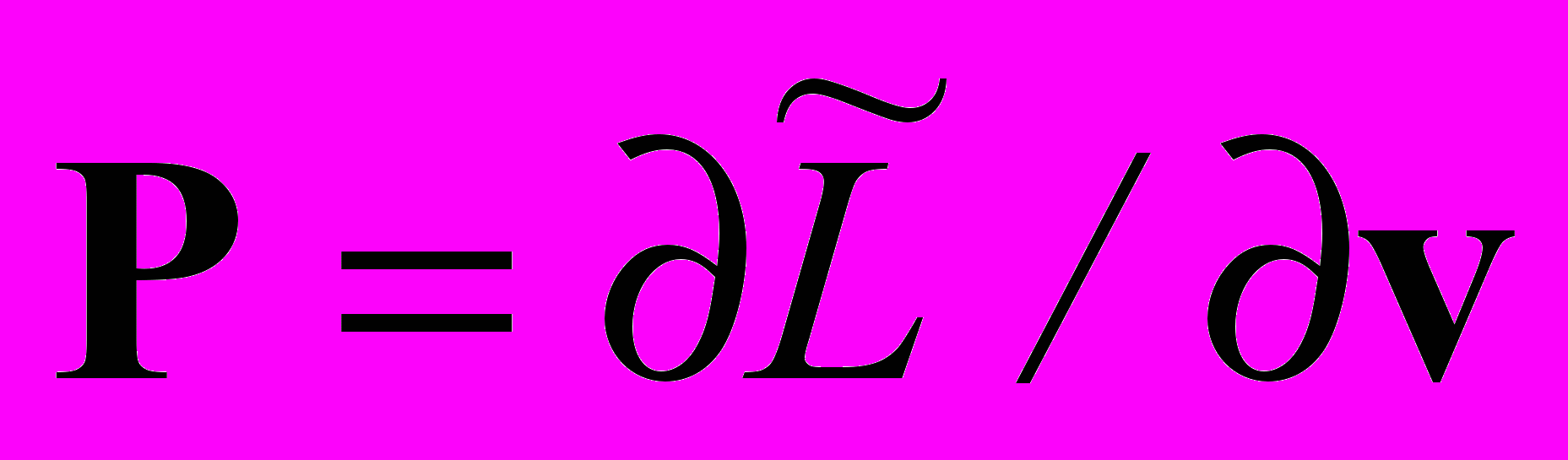и энергии частицы в поле, при этом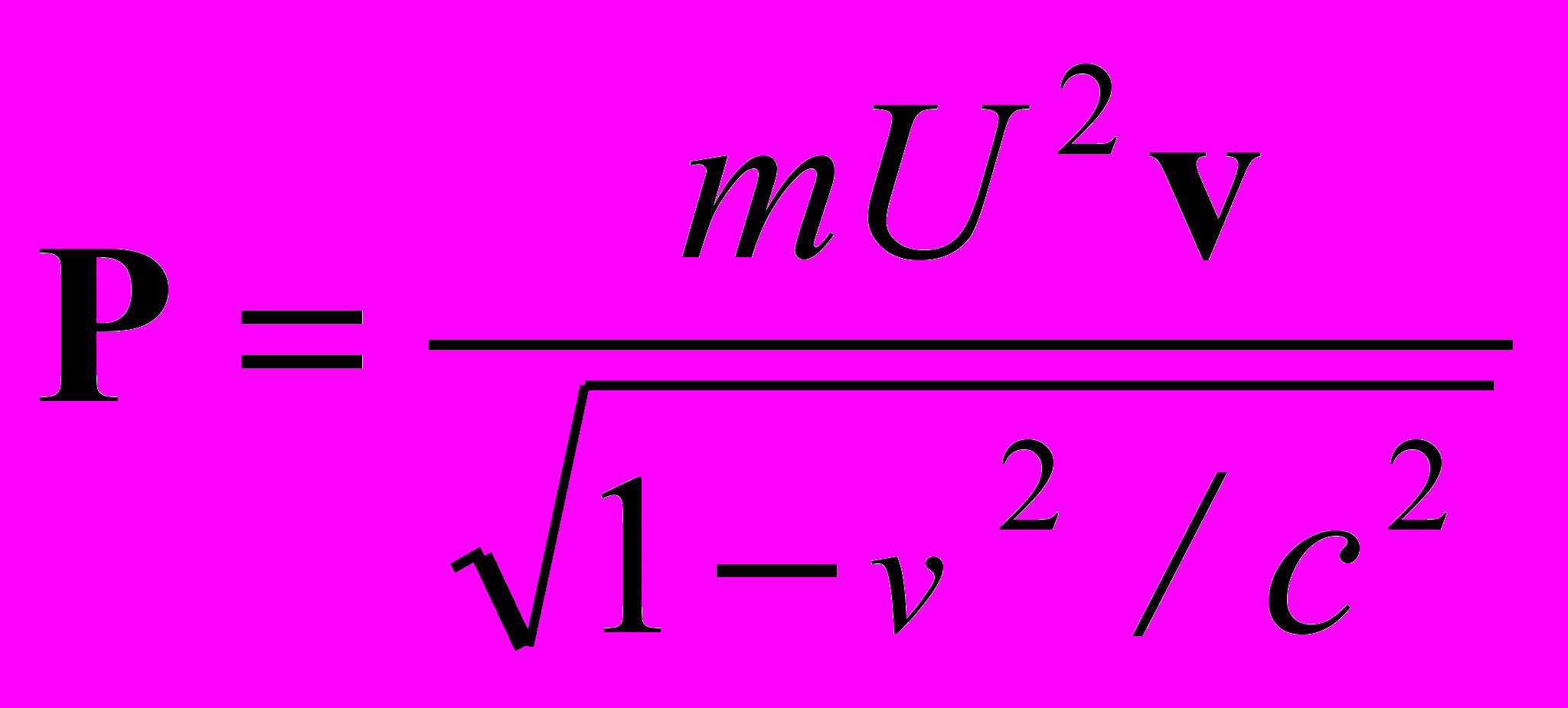

, (3)

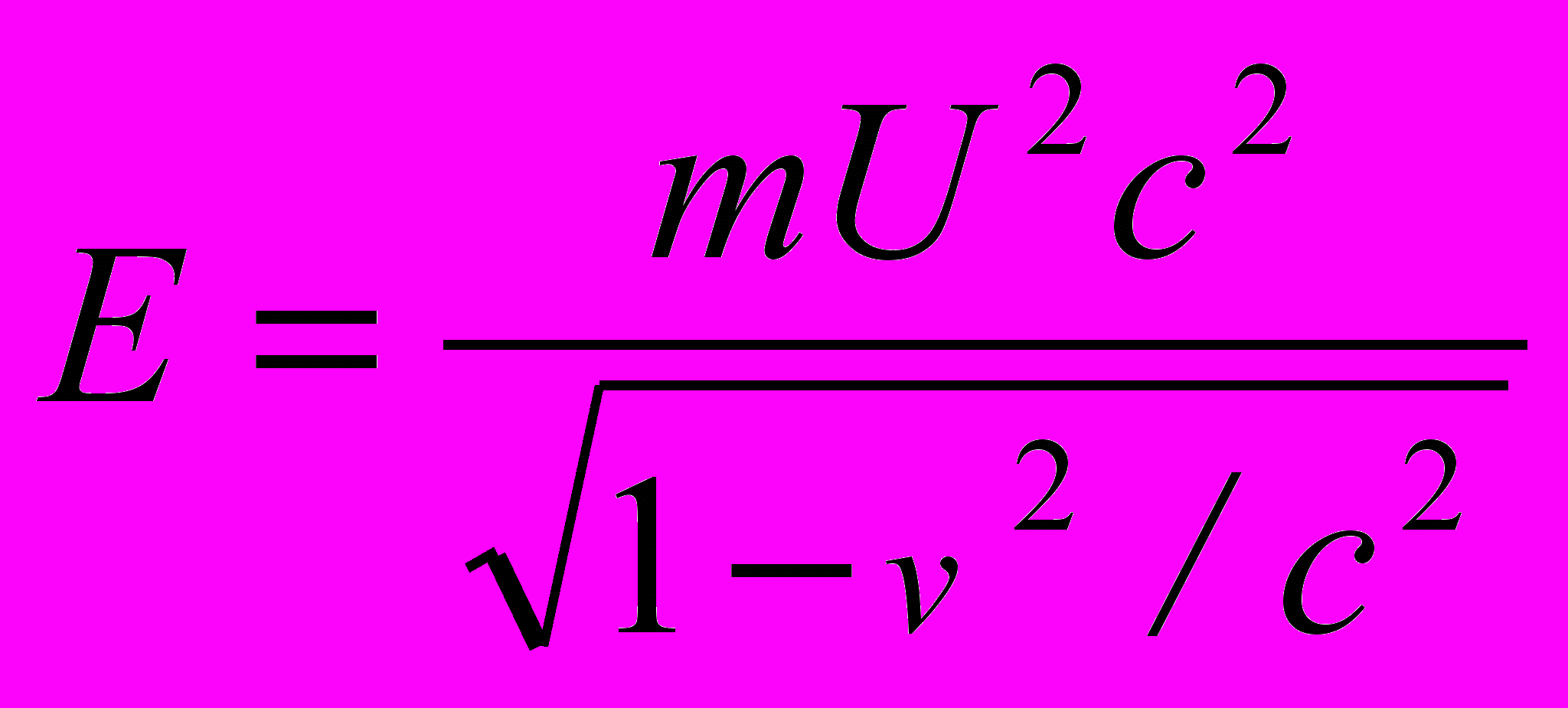. (4)

Поле g_μ в (2) является потенциальным:

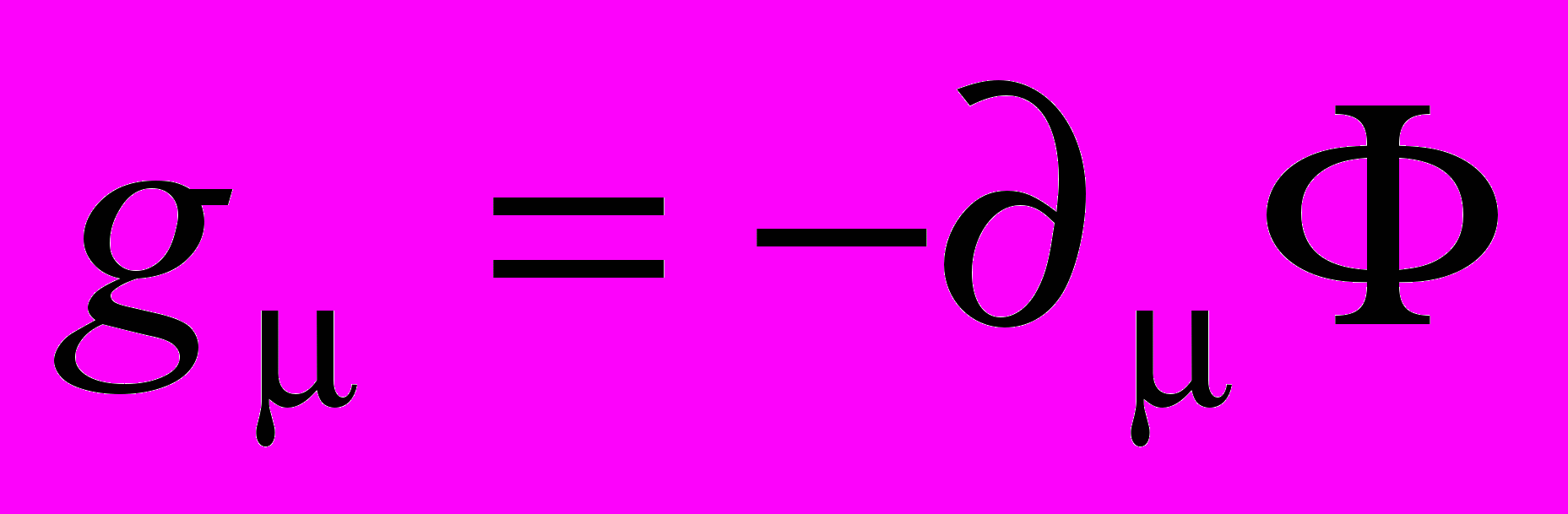, (5)

причем потенциал  связан с полевой функцией U соотношением

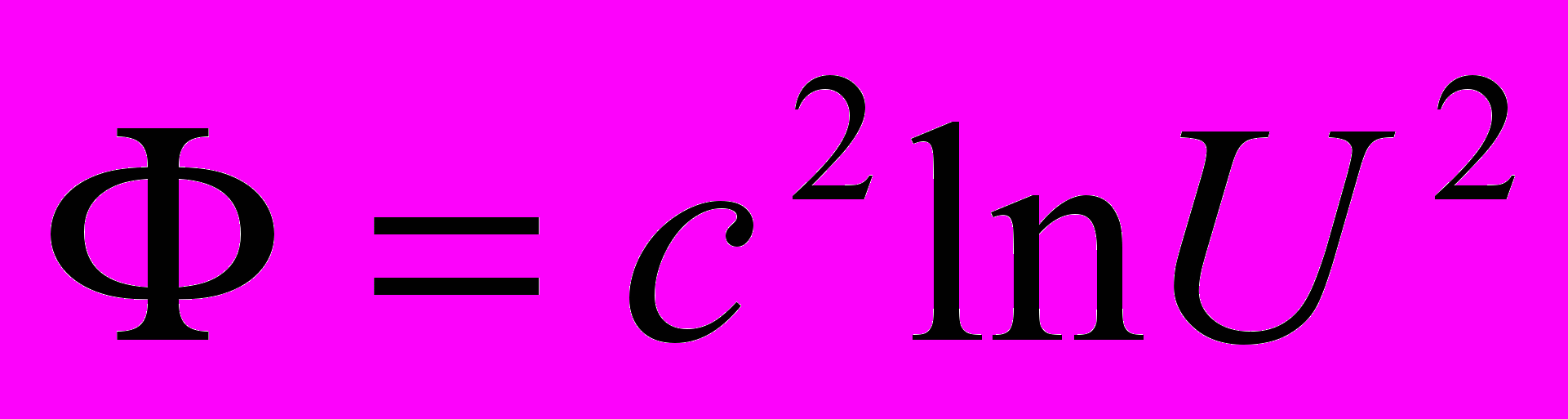. (6)

Из (2) в результате элементарных преобразований вытекает уравнение

.

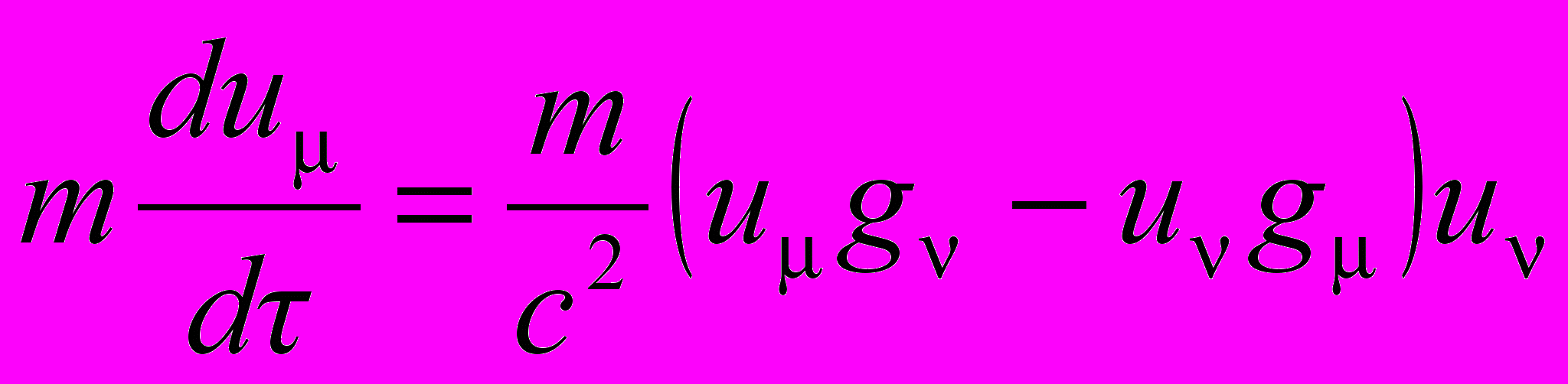Отсюда, в частности имеем уравнение для динамического импульса частицы

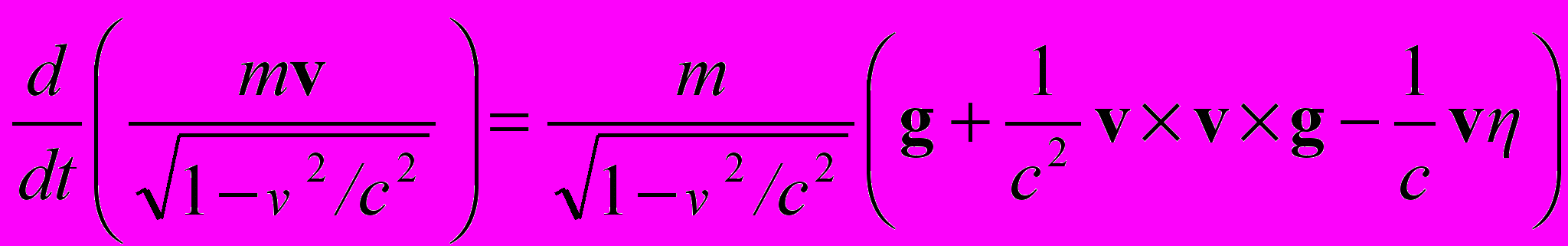. (7)

Здесь силовые характеристики гравитационного поля – трёхмерный вектор g и трёхмерный скаляр η образуют 4-вектор напряженности 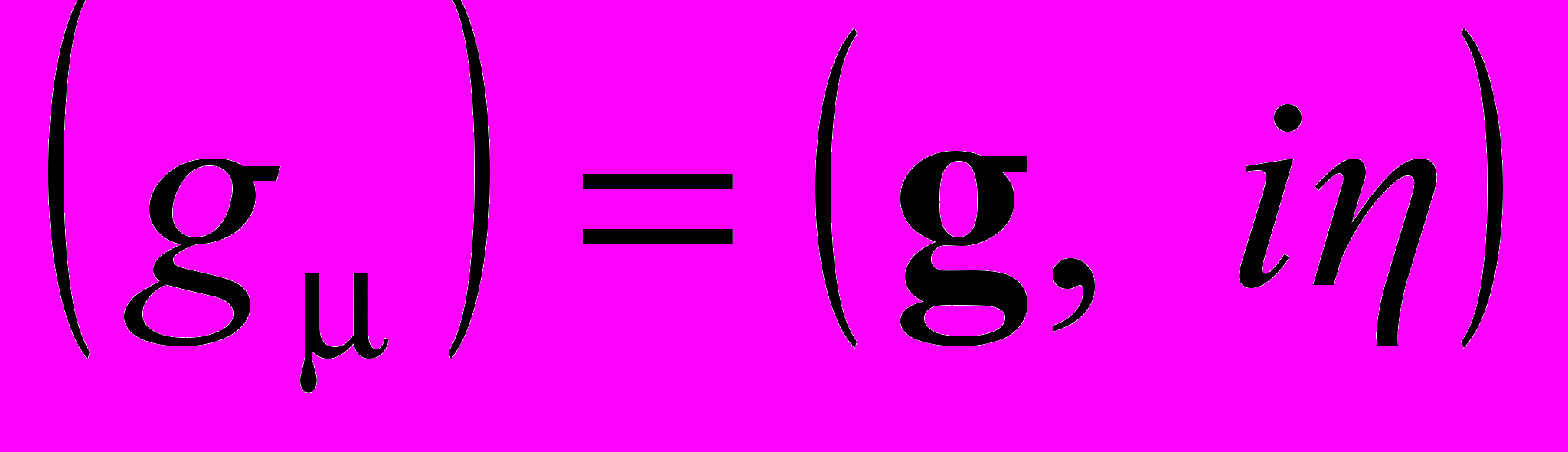. Согласно (5),

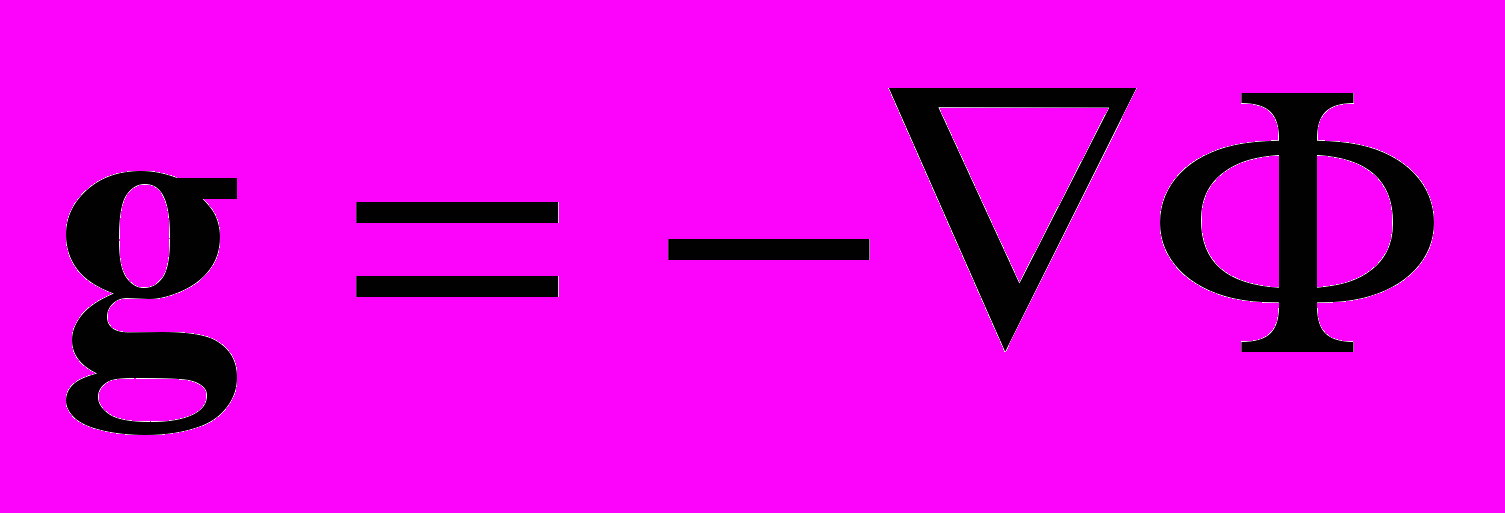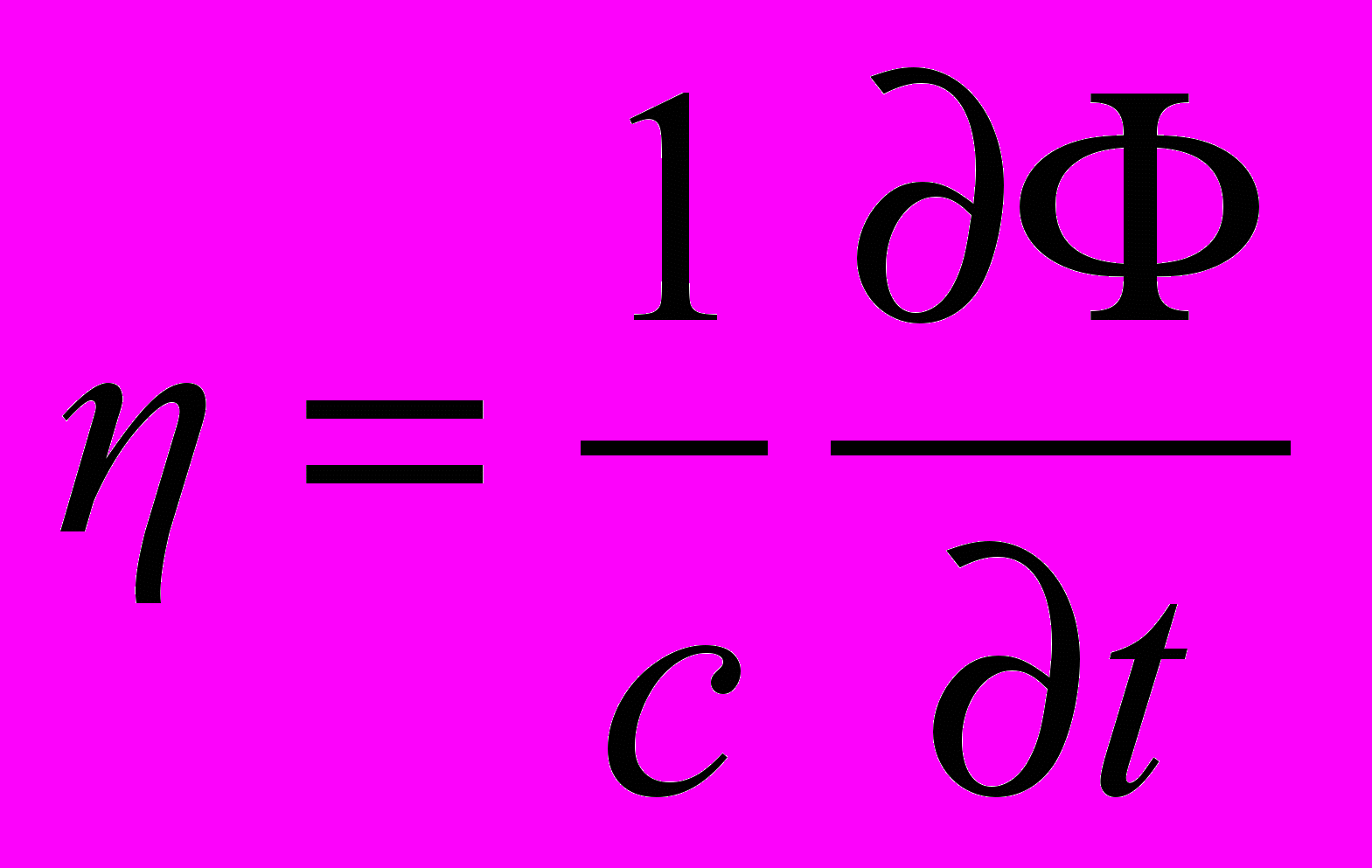, . (8)

Как видно из уравнения (7), действие гравитационного поля на частицу полностью определяется наблюдаемыми – напряжённостями g(r, t) и η(r, t). Что же касается потенциала (r, t), то эта величина задается посредством соотношения (5) с точностью до аддитивной постоянной. При этом как само поле, так и описывающие его уравнения должны оставаться инвариантными относительно калибровочного преобразования потенциала  и полевой функции U

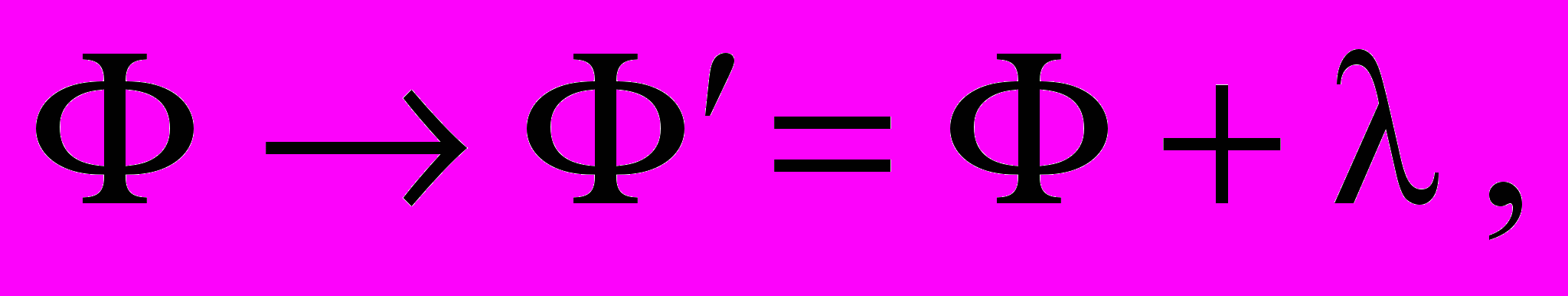
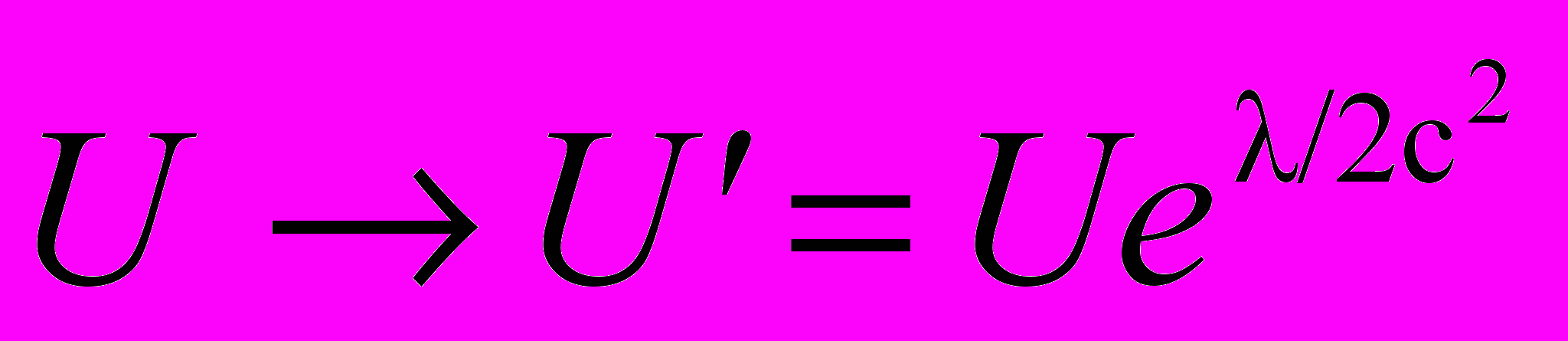. (9)

с произвольным постоянным параметром .


3. Уравнения гравитационного поля


Из соотношения (5) очевидным образом вытекает тензорное полевое уравнение для 4-вектора напряженности g_μ:

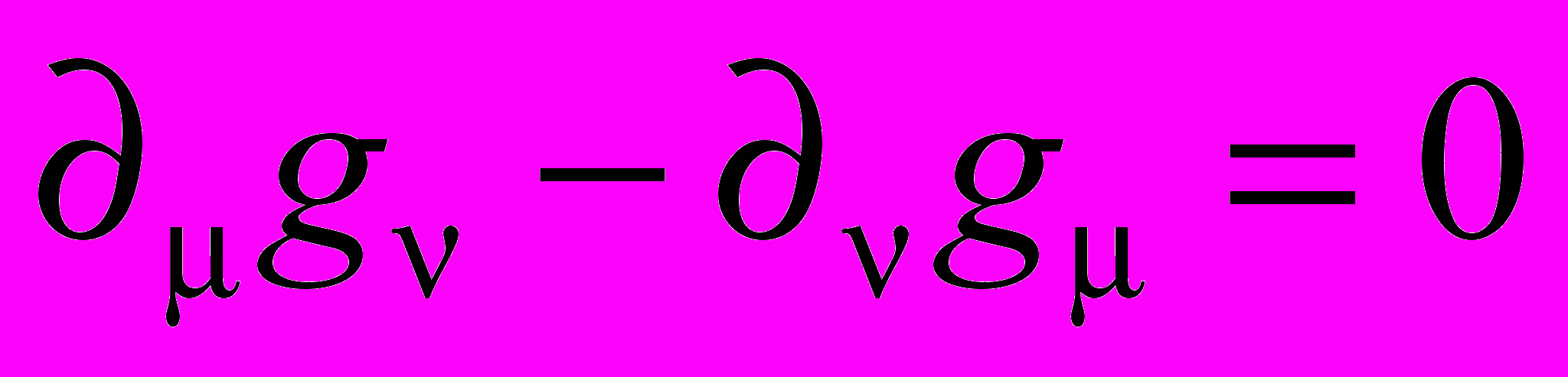. (10)

Четырехмерный ротор 4-вектора g_μ в левой стороне данного равенства является антисимметричным тензором второго ранга, и, следовательно, содержит всего шесть независимых компонент, не равных нулю тождественно. Уравнение (10) объединяет, таким образом, шесть различных уравнений, которые в трехмерных обозначениях можно записать в виде двух векторных уравнений для наблюдаемых g и η

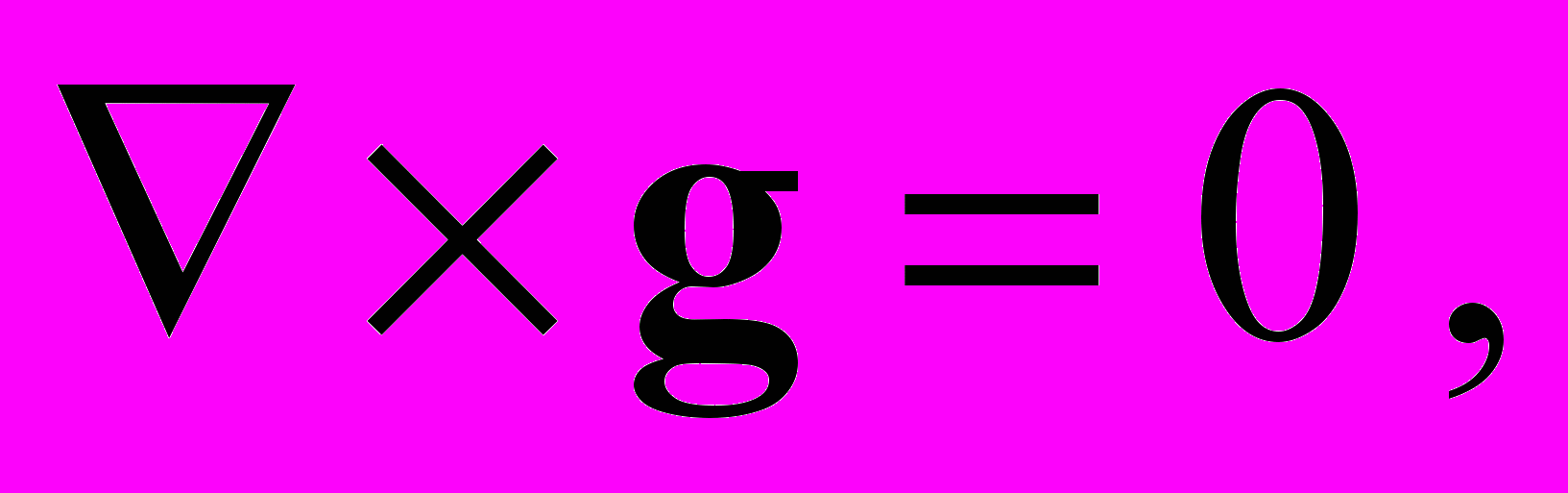
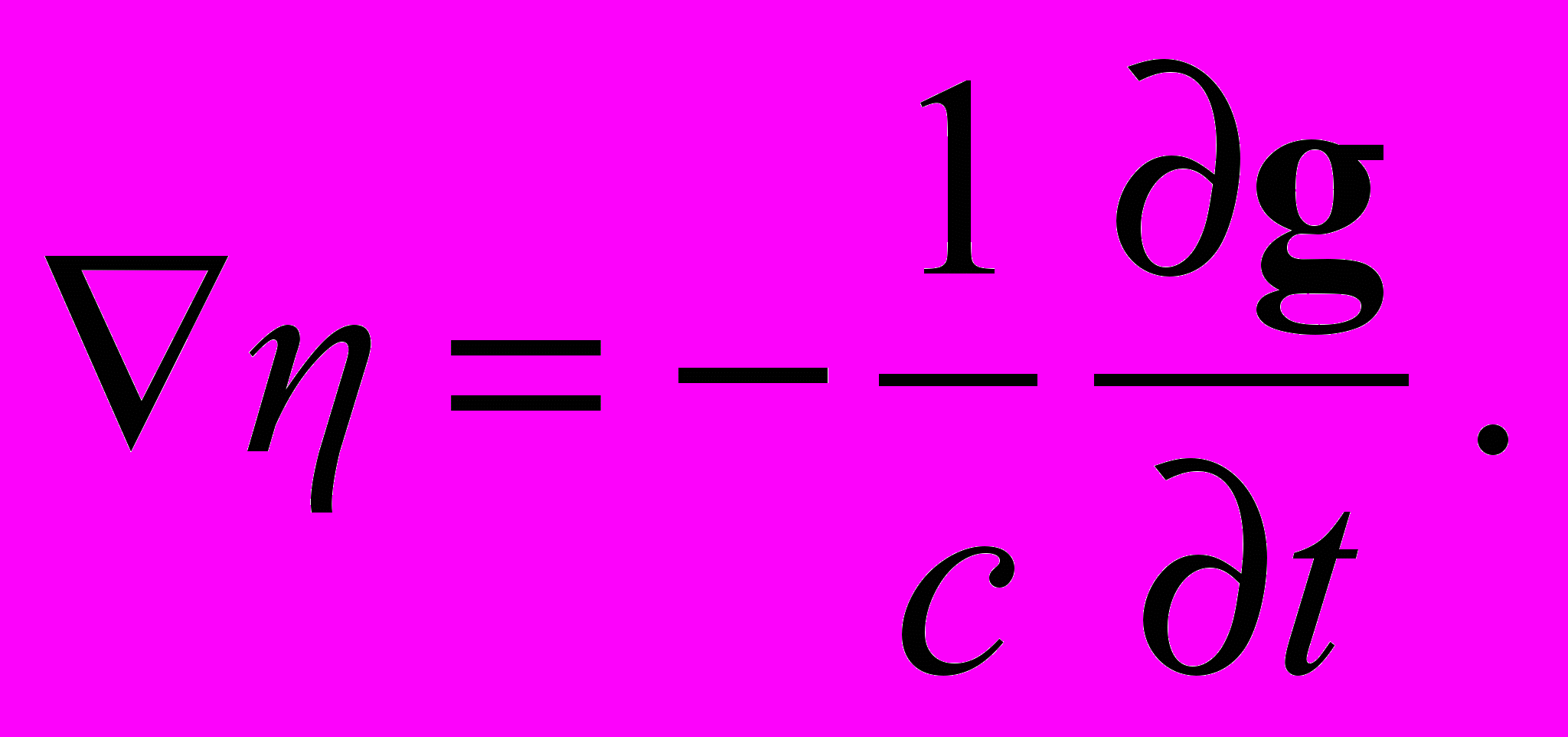(11)

Используя вариационный принцип, построим далее уравнение, которое определяло бы закон формирования гравитационного поля движущейся весомой материей. Рассмотрим пылевидную гравитирующую материю – систему точечных частиц, взаимодействующих между собой только посредством гравитационного поля. Поскольку взаимодействие частиц с полем, согласно (1), подключается к функции Лагранжа мультипликативно, то плотность функции Лагранжа L системы взаимодействующих между собой частиц и поля будет содержать только два члена:

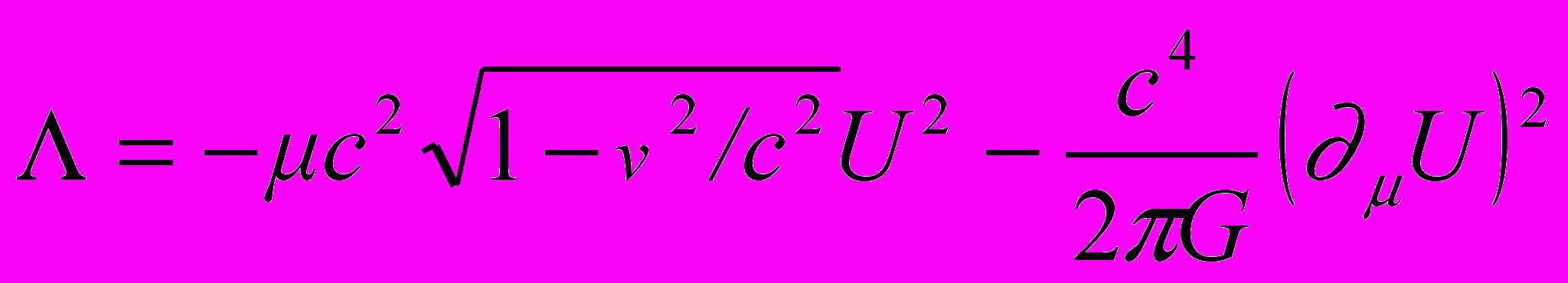. (12)

Первый из них соответствует функции Лагранжа (1) взаимодействующих с полем точечных частиц, когда плотность массы

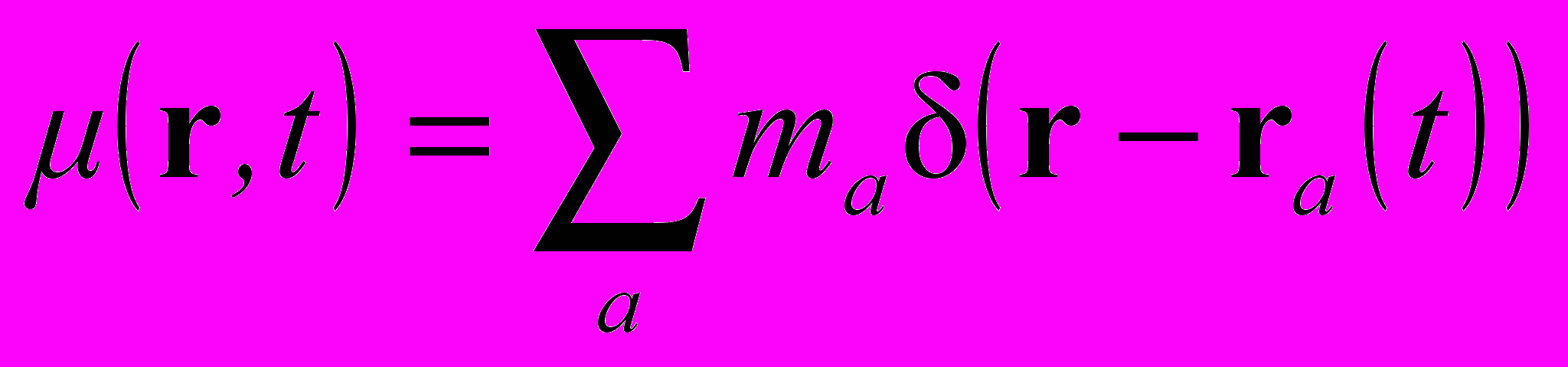. (13)

Для полевой части лагранжиана (второй член в (12)) мы постулируем минимальное выражение, характерное для линейного скалярного безмассового поля. Коэффициент в (12), включающий гравитационную постоянную G, подобран с тем расчетом, чтобы уравнение поля, вытекающее из (12), соответствовало единицам, используемым в ньютоновской теории тяготения.

Уравнение Эйлера – Лагранжа

,

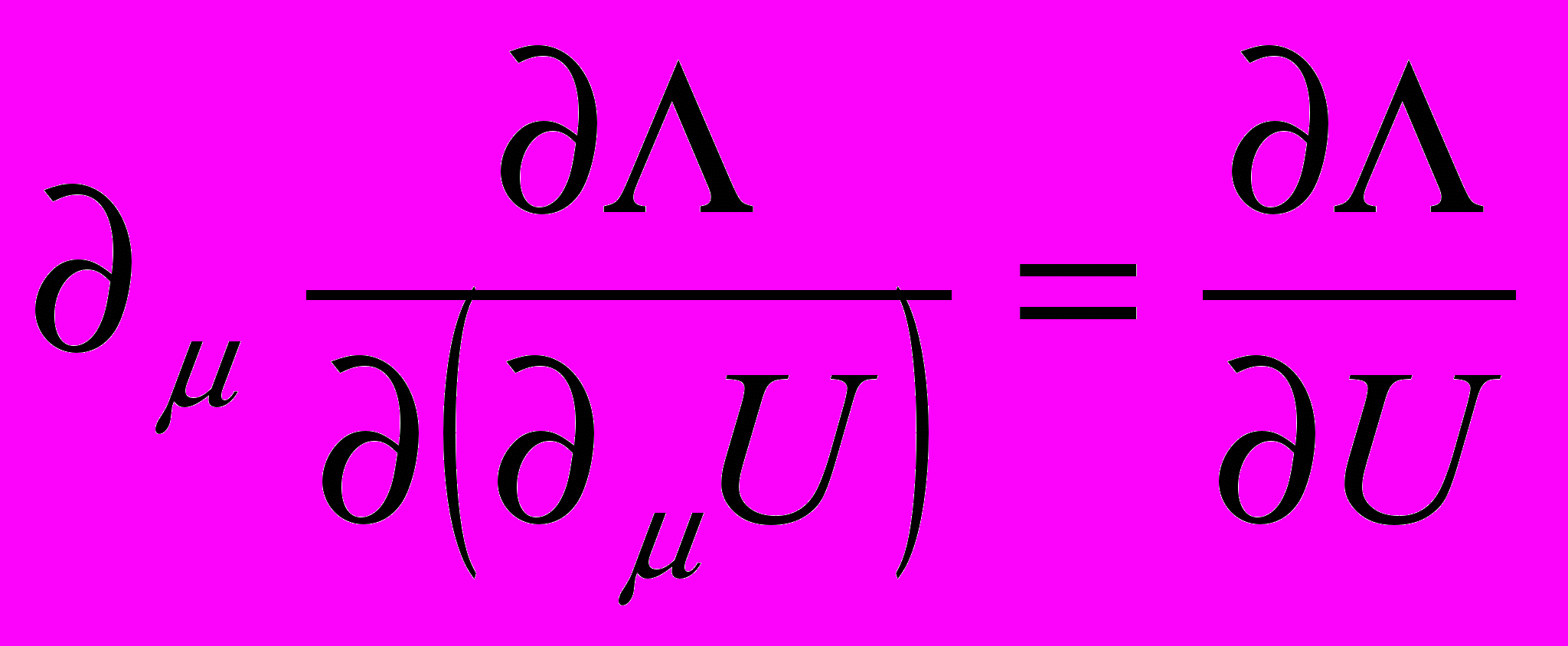получающееся при варьировании в интеграле действия (12) полевой переменной U, для лагранжиана (12) дает скалярное уравнение поля

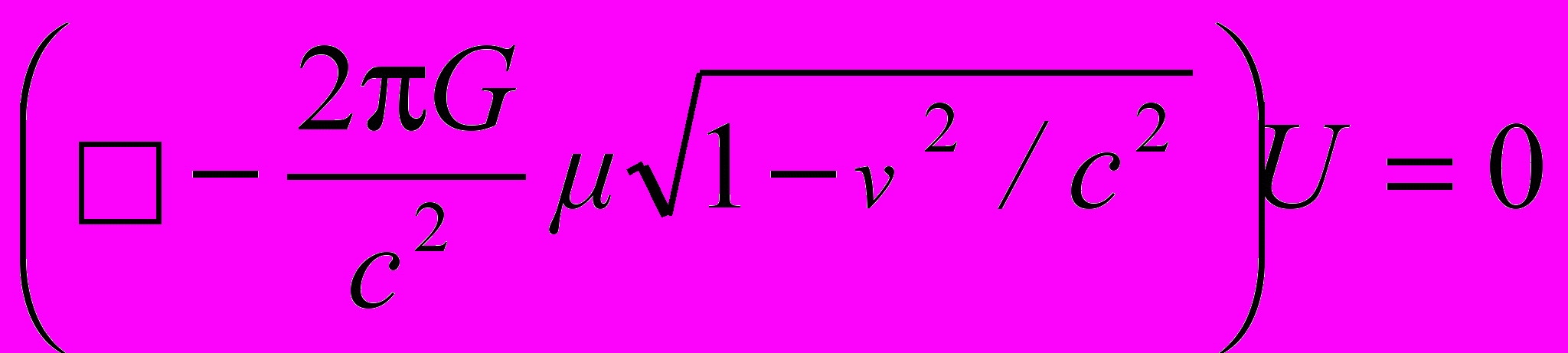. (14)

Выражая полевую функцию U через потенциал  согласно (6), и имея в виду соотношение (5), из (14) получаем нелинейное уравнение для 4-вектора напряженности поля g_

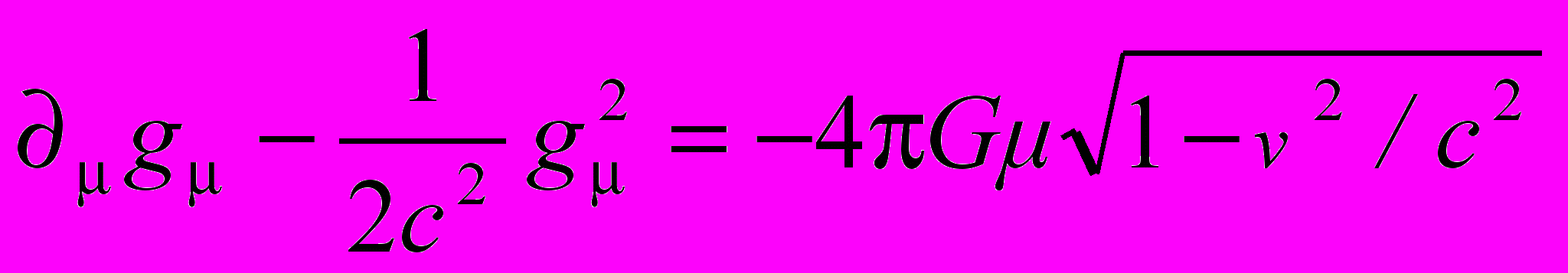, (15)

или в трехмерных обозначениях

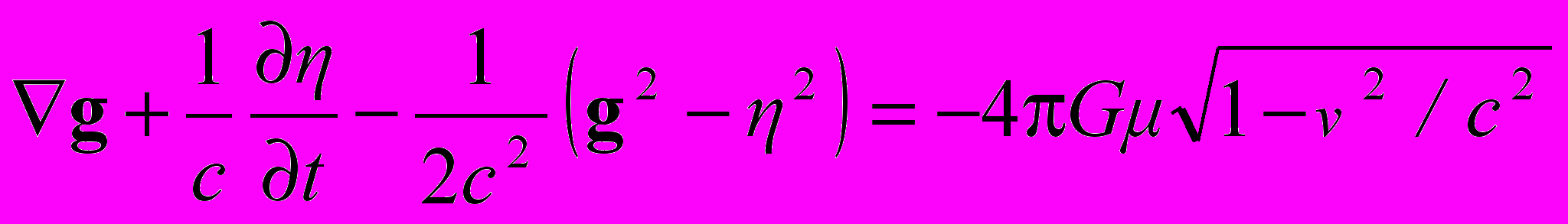. (16)

В статическом пределе в приближении слабого поля из (16) следует уравнение

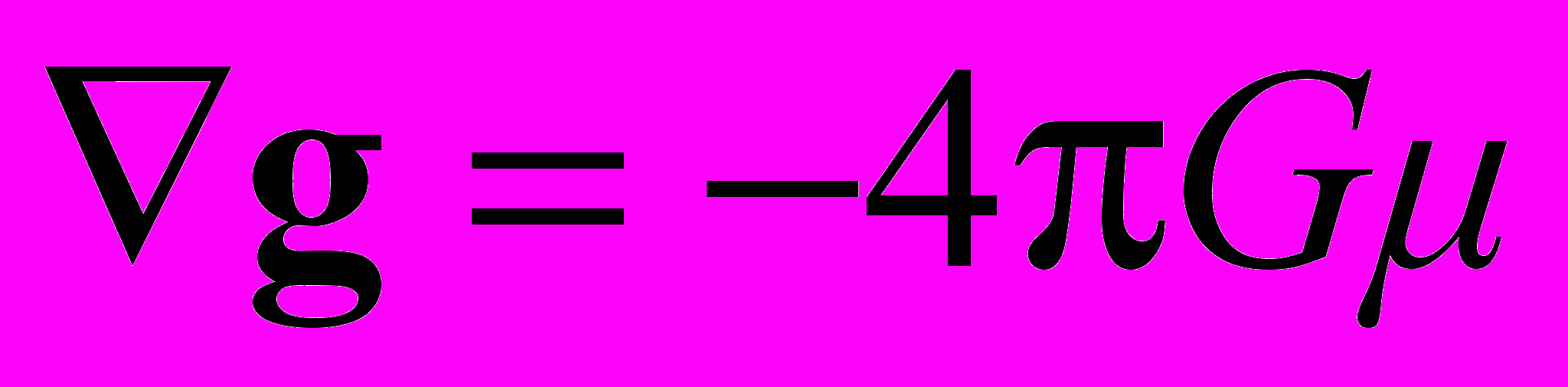, (17)

которое является дифференциальной формой закона тяготения Ньютона.

4. Тензор энергии-импульса
   
5. 
   

Общее выражение для тензора энергии-импульса скалярного поля имеет вид

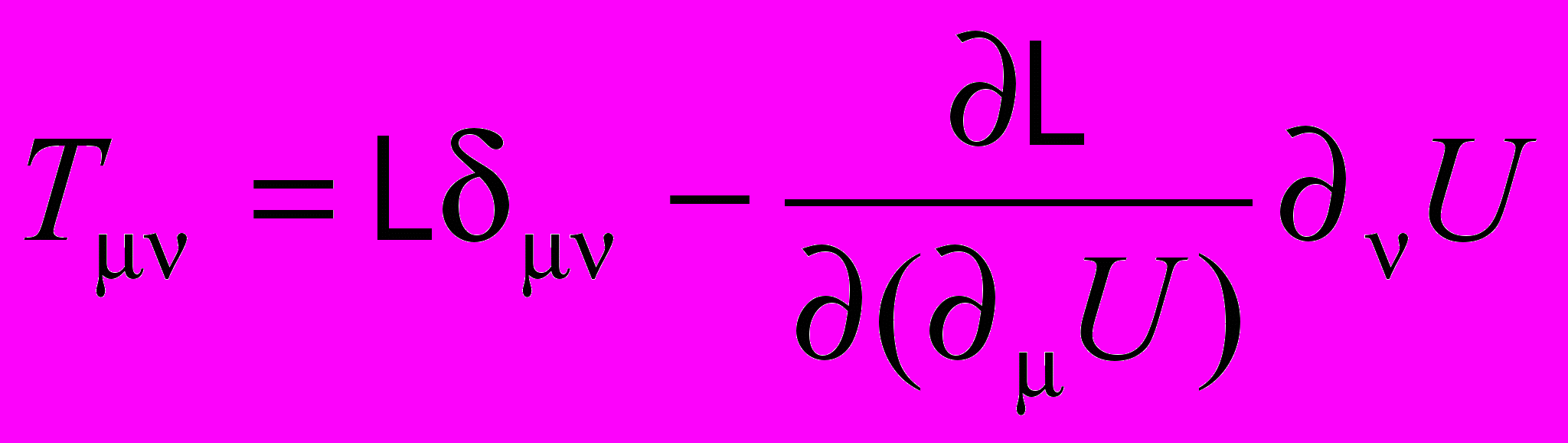. (18)

Подставляя в (18) полевую часть лагранжиана (12), получим

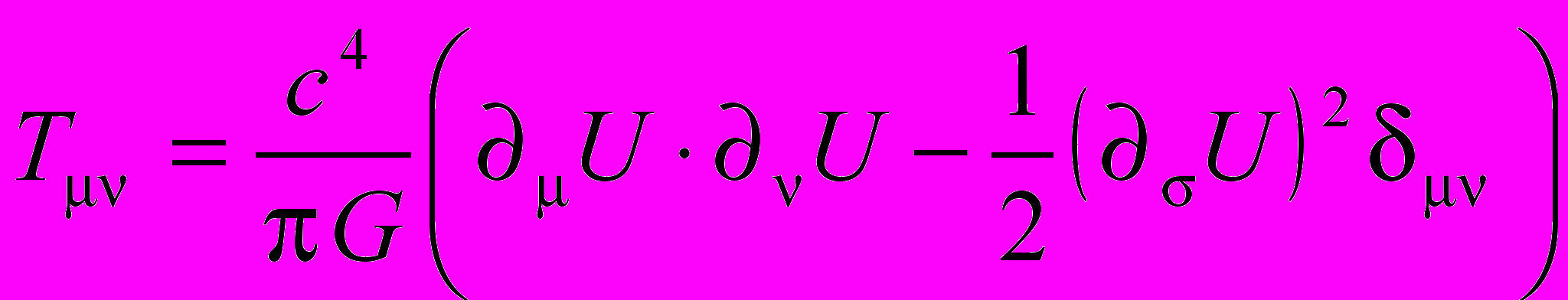. (19)

Тензор (19) симметричен и в отсутствие частиц удовлетворяет закону сохранения энергии и импульса поля в виде уравнения непрерывности _μT_μν  0. При наличии взаимодействующего с полем вещества четырехмерная дивергенция тензора (19) уже не равна нулю, что обусловлено обменом энергией и импульсом между частицами и полем. В этом случае, как легко убедиться, имеет место соотношение

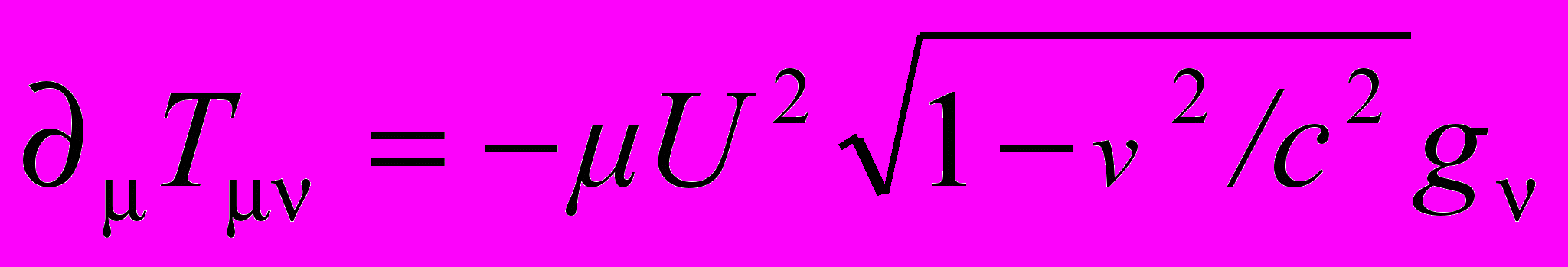. (20)

Однако для замкнутой системы, состоящей из частиц и поля, законы сохранения энергии и импульса, разумеется, в точности выполняются. Чтобы это показать, проинтегрируем равенство (20) по некоторому объему V, ограниченному гладкой поверхностью Σ. Применяя теорему Гаусса и учитывая (13) и (2), находим

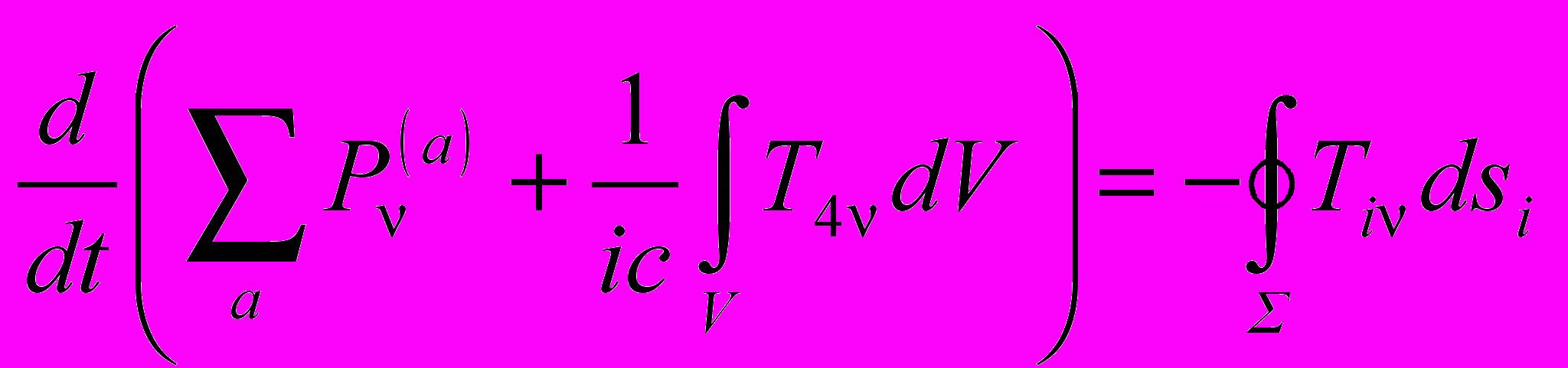. (21)

Здесь P_^(a) – 4-вектор энергии-импульса находящейся в поле частицы с номером a. Очевидно, левая сторона равенства (21) представляет скорость изменения -ой компоненты 4-импульса всей системы из частиц и поля в выделенном объеме V. Это изменение компенсируется стоящим справа потоком энергии-импульса поля через ограничивающую объем V поверхность . Следовательно, 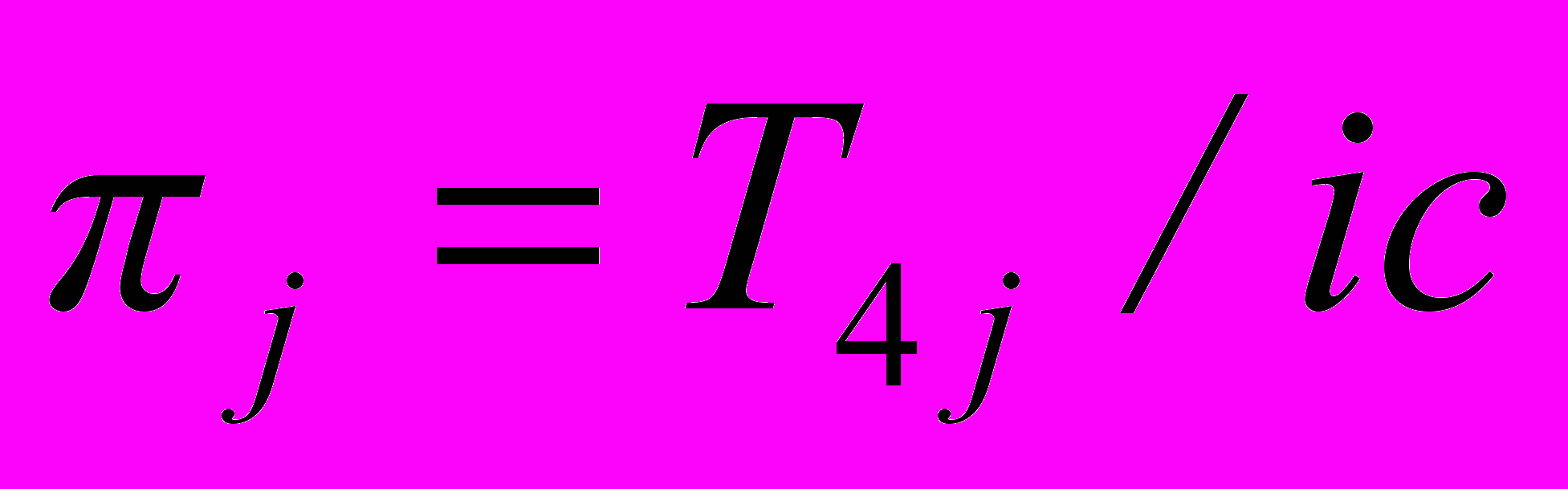есть j-я компонента плотности импульса, а T_ij – компонента трехмерного тензора T плотности потока импульса поля. Из (19) находим

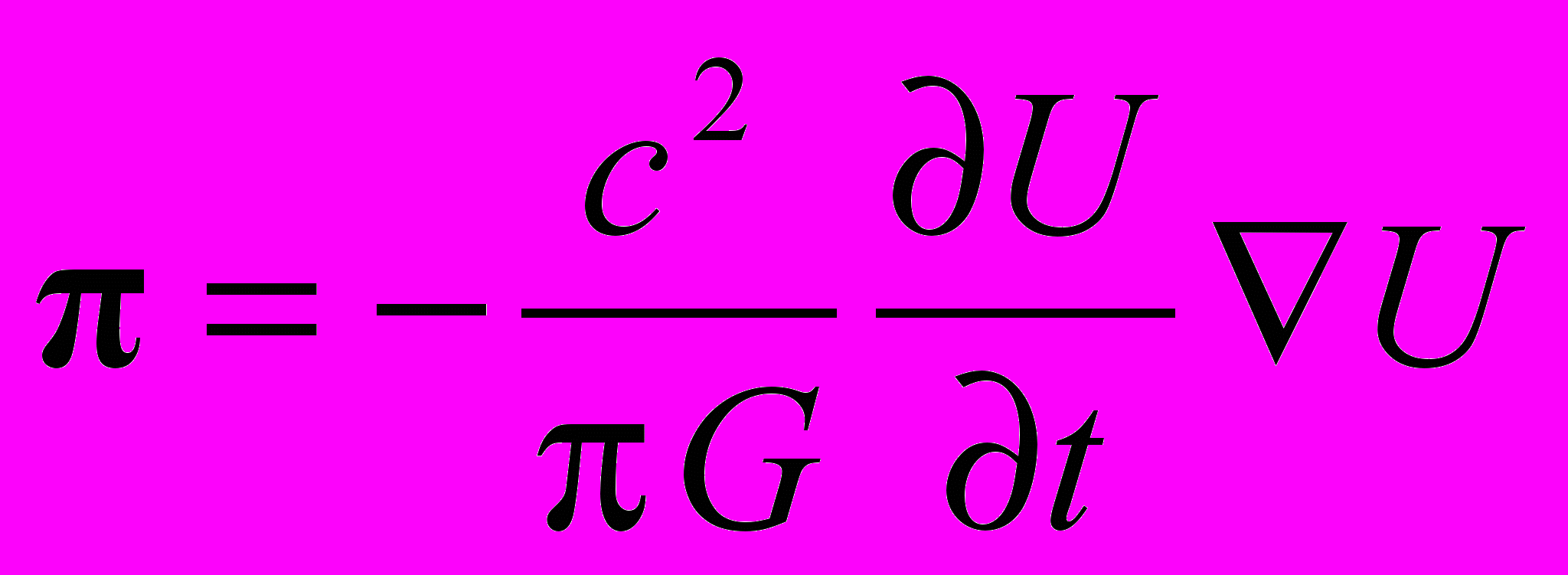, (22)

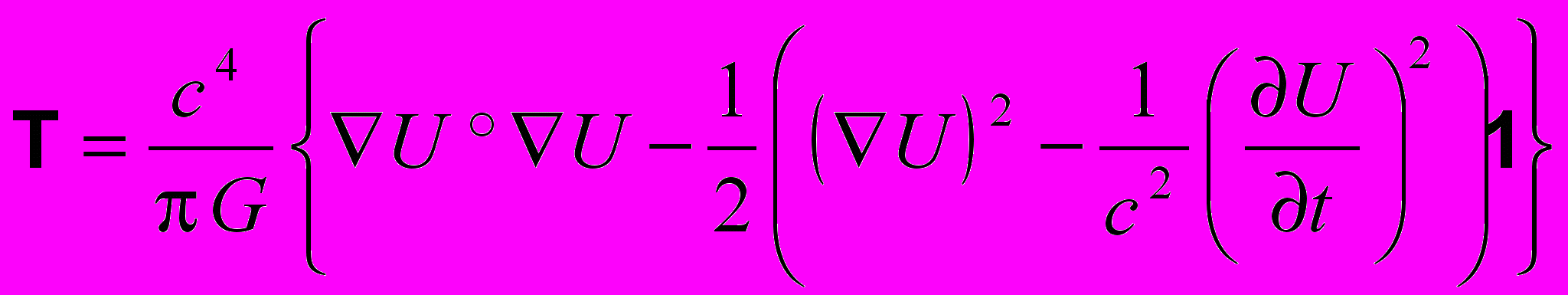. (23)

Временная составляющая равенства (21) дает энергетическое соотношение

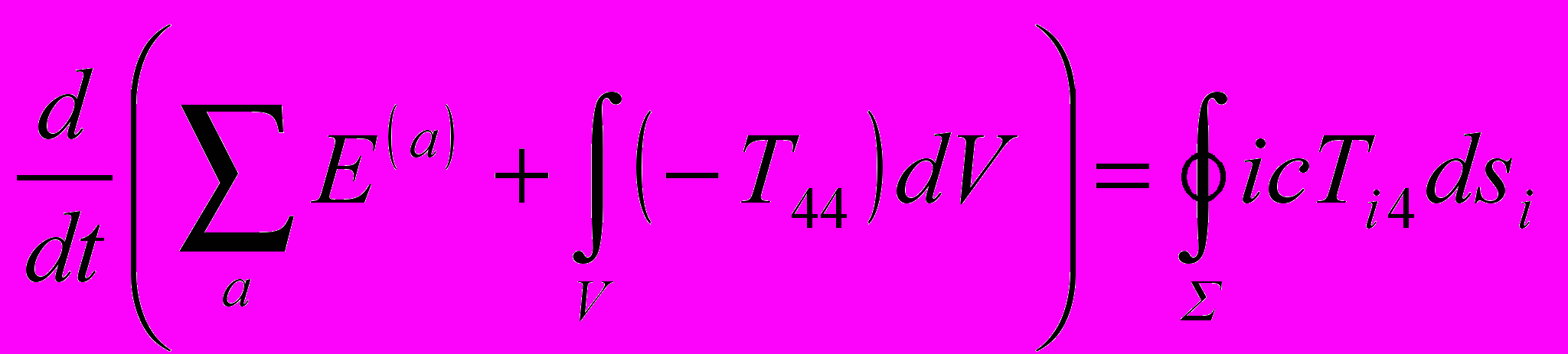, (24)

где W =  T₄₄  плотность энергии поля, а S_i =  icT_i4 – вектор плотности потока энергии. Из (19), таким образом, находим

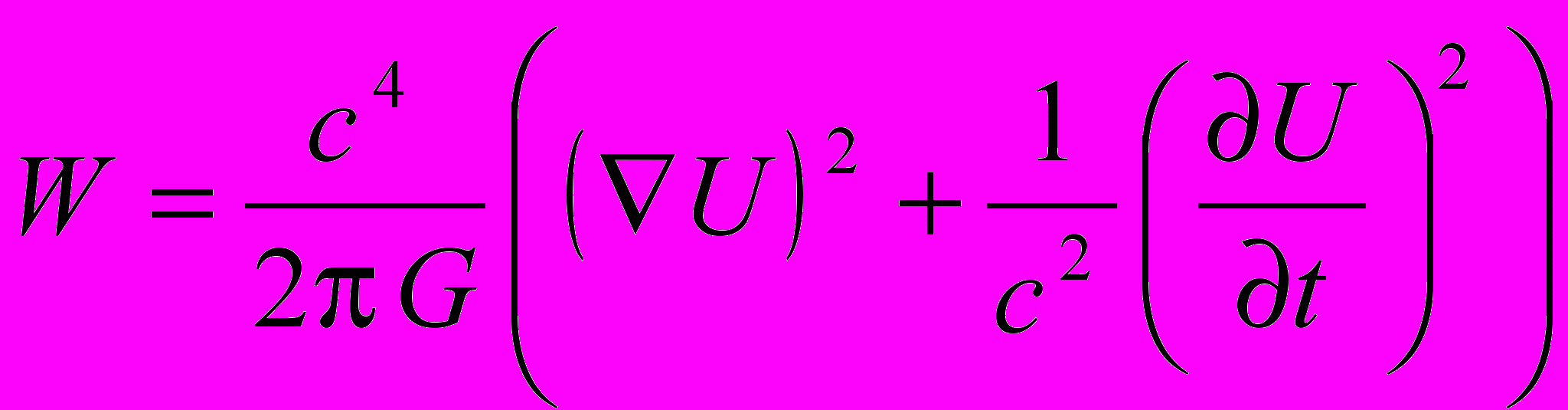, (25)

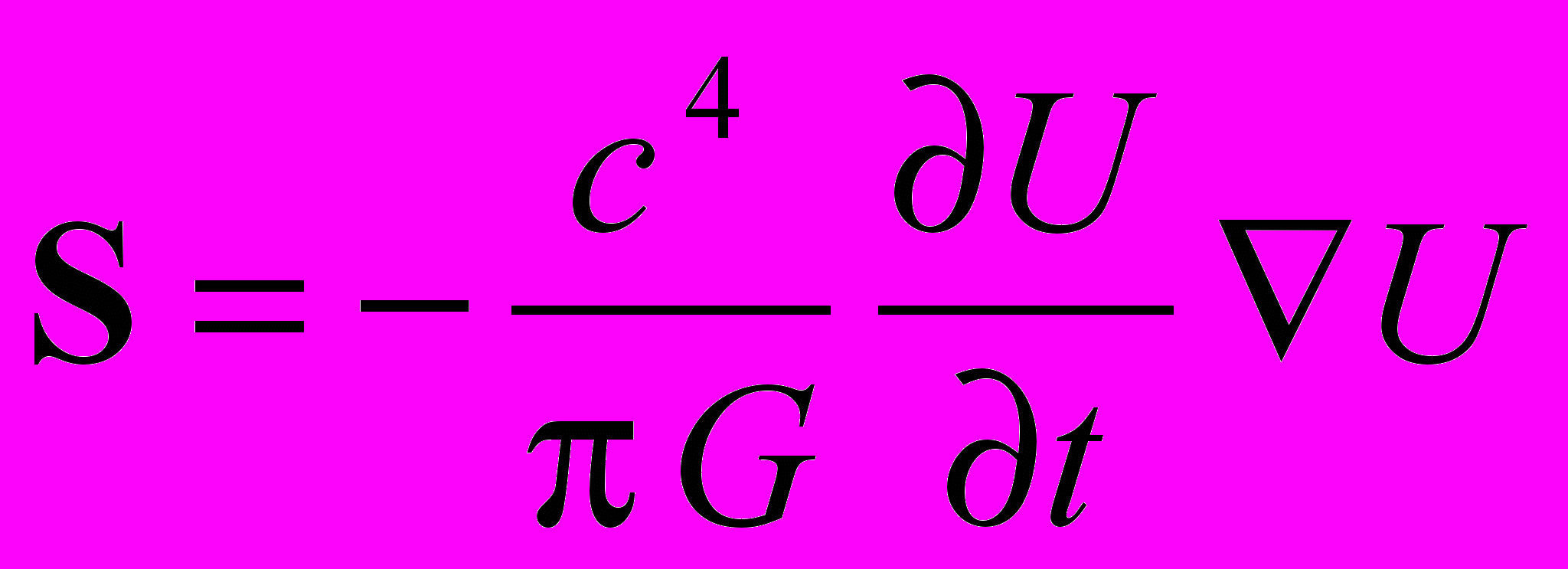. (26)

Компоненты тензора T_μν полезно выразить через силовые характеристики и потенциал гравитационного поля. Используя соотношения (5) – (9), найдем

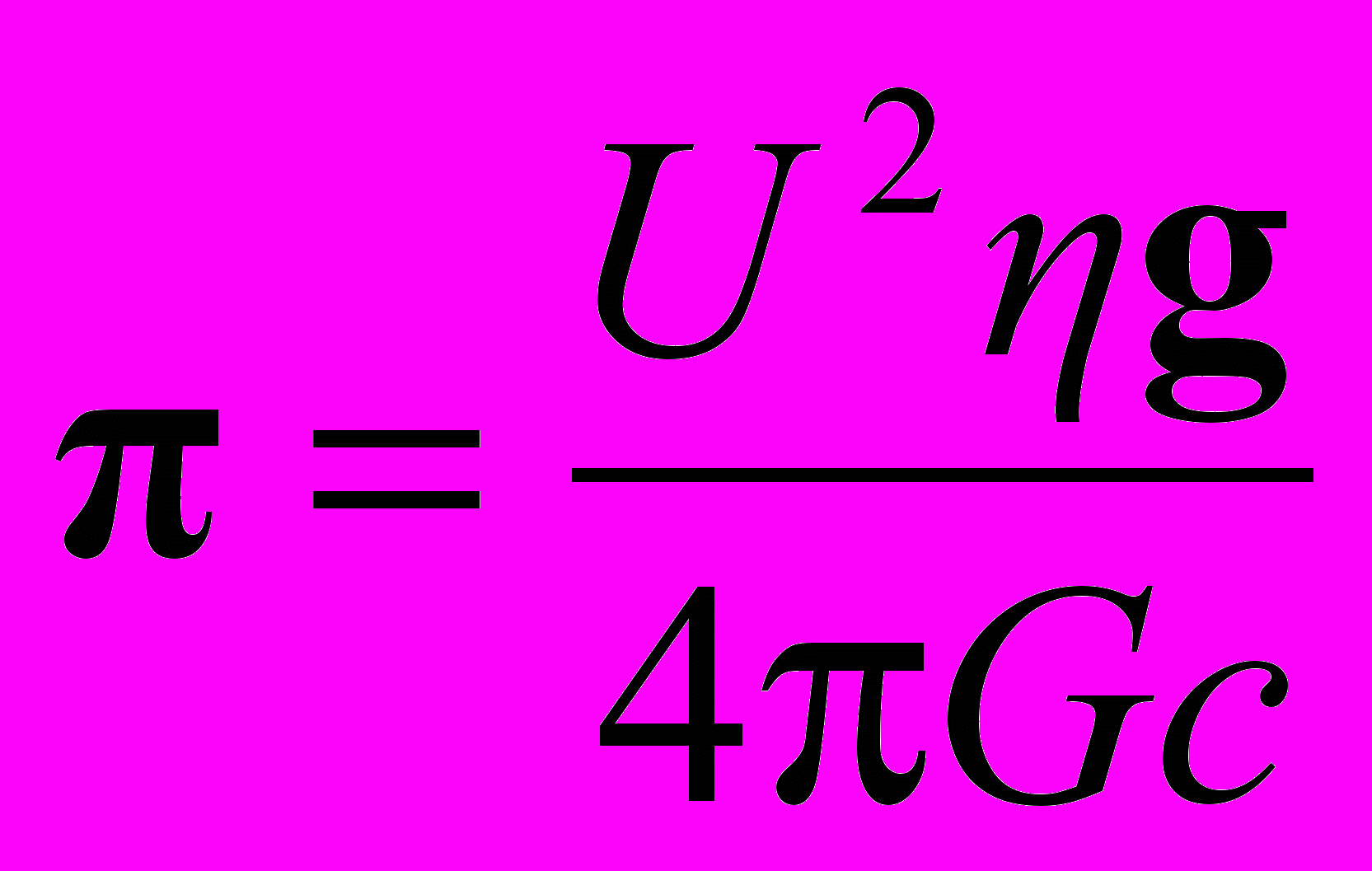, (27)

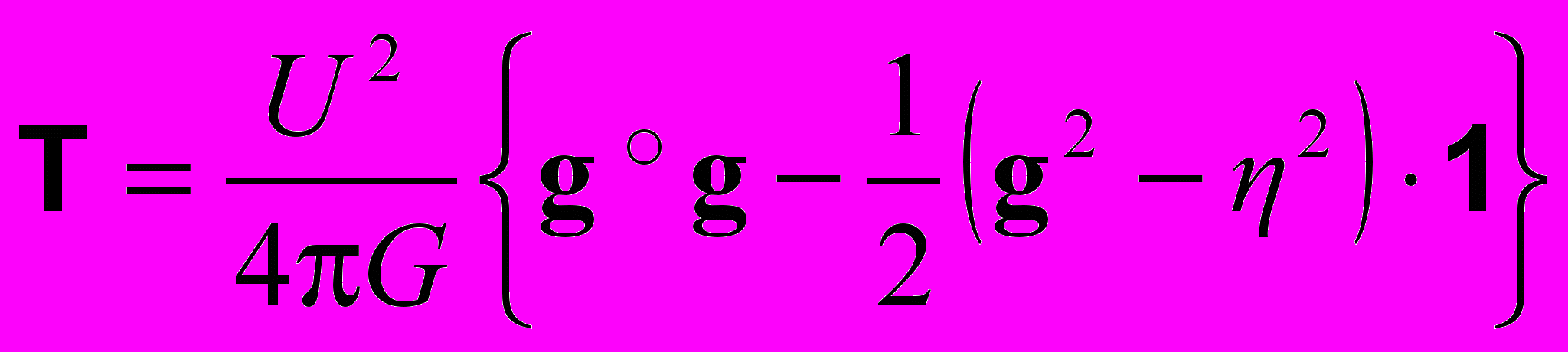, (28)

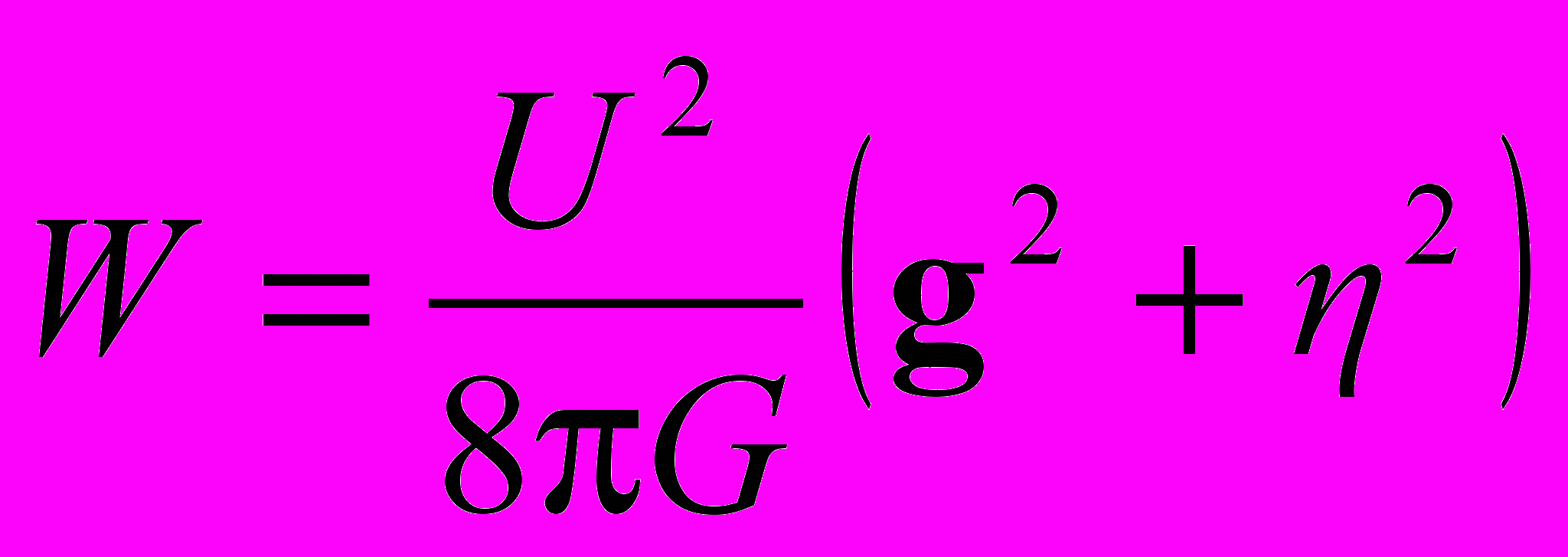, (29)

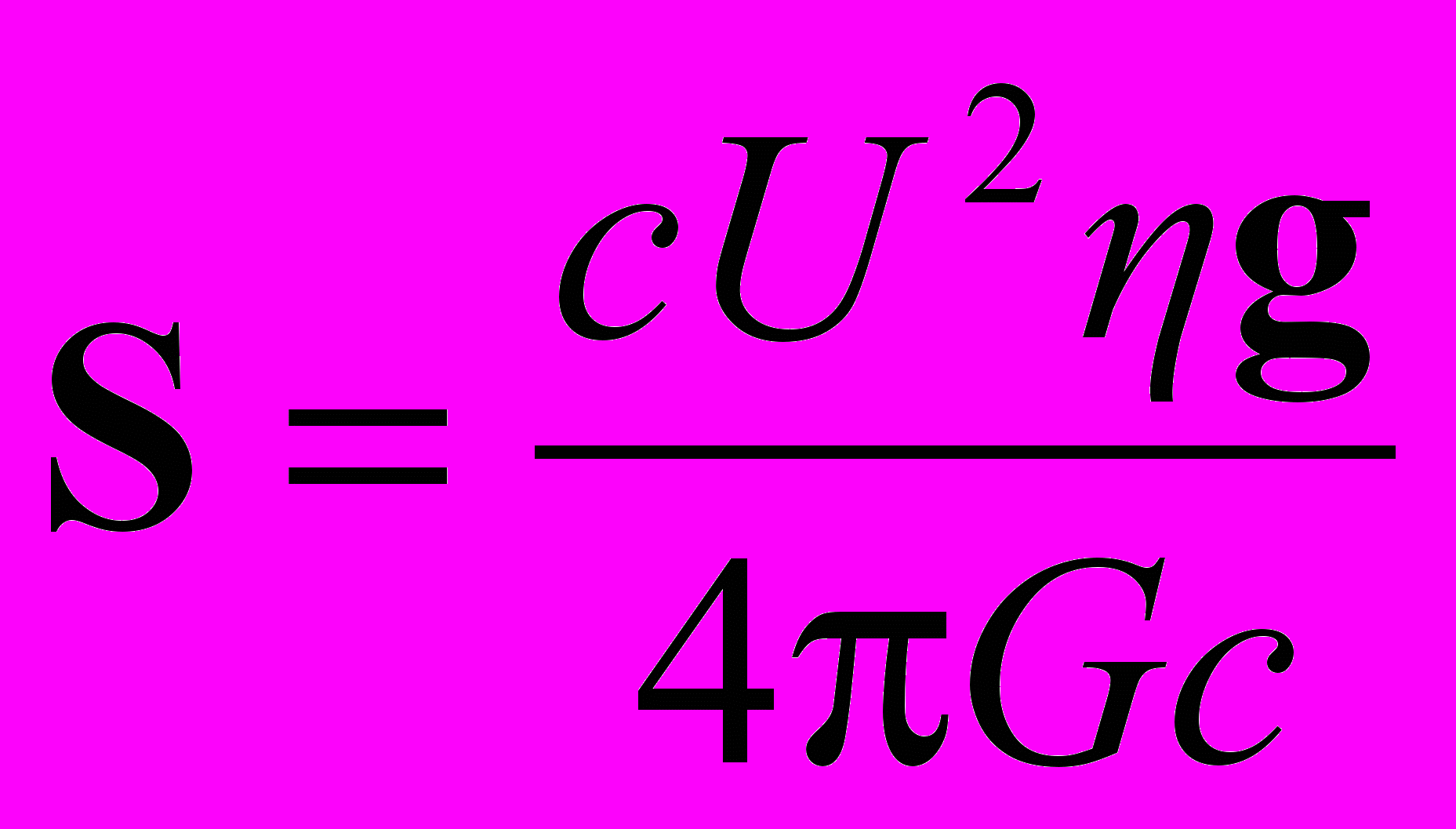. (30)

6. Статическое поле тяготения
   
7. 
   

Из общих полевых уравнений (11), (11), (16) следует, что поле напряжённости g  g(r), создаваемое неподвижной гравитирующей пылевидной материей с плотностью массы 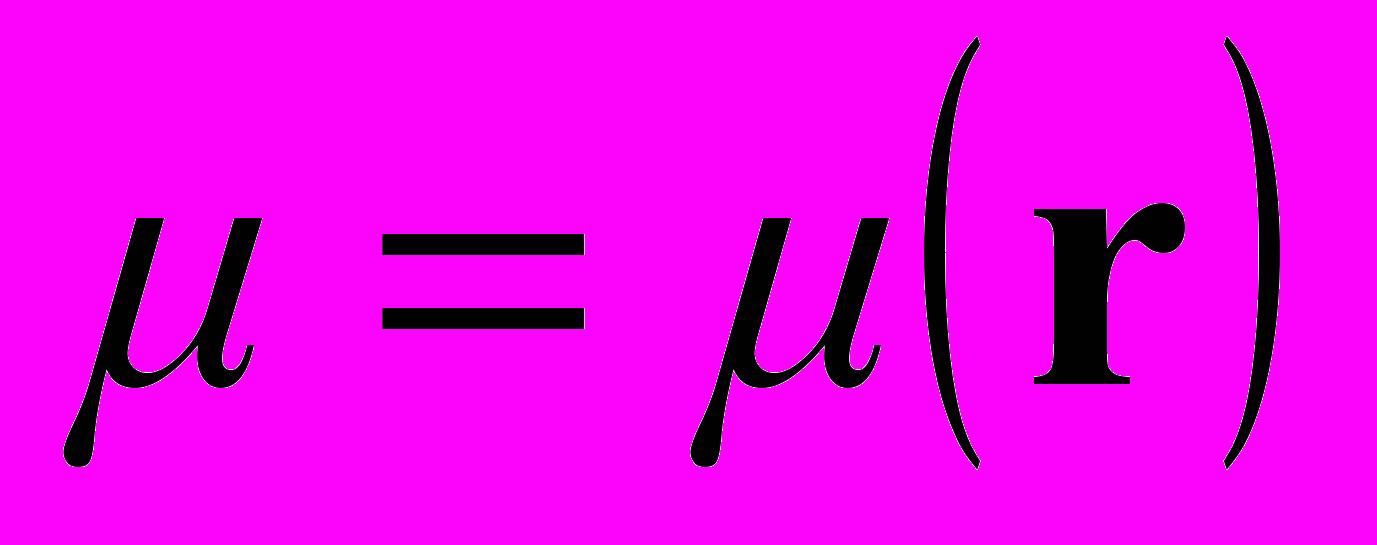, удовлетворяет нелинейному уравнению гравистатики Бриллюэна [¹¹]

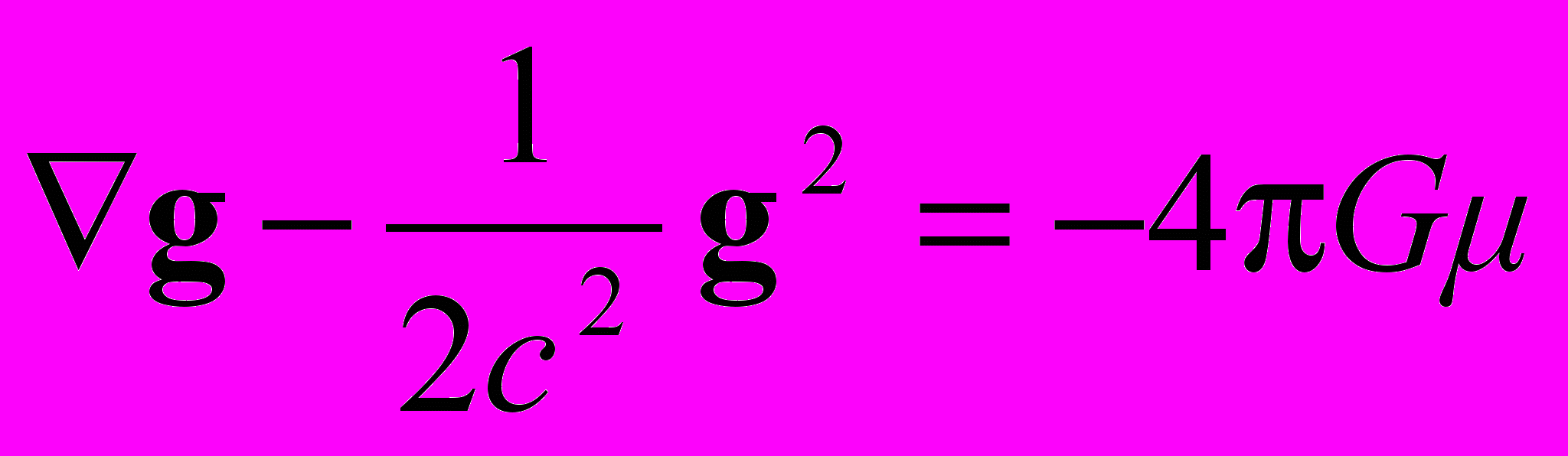. (32)

Уравнение (14) для функции U = U(r) статического поля принимает вид

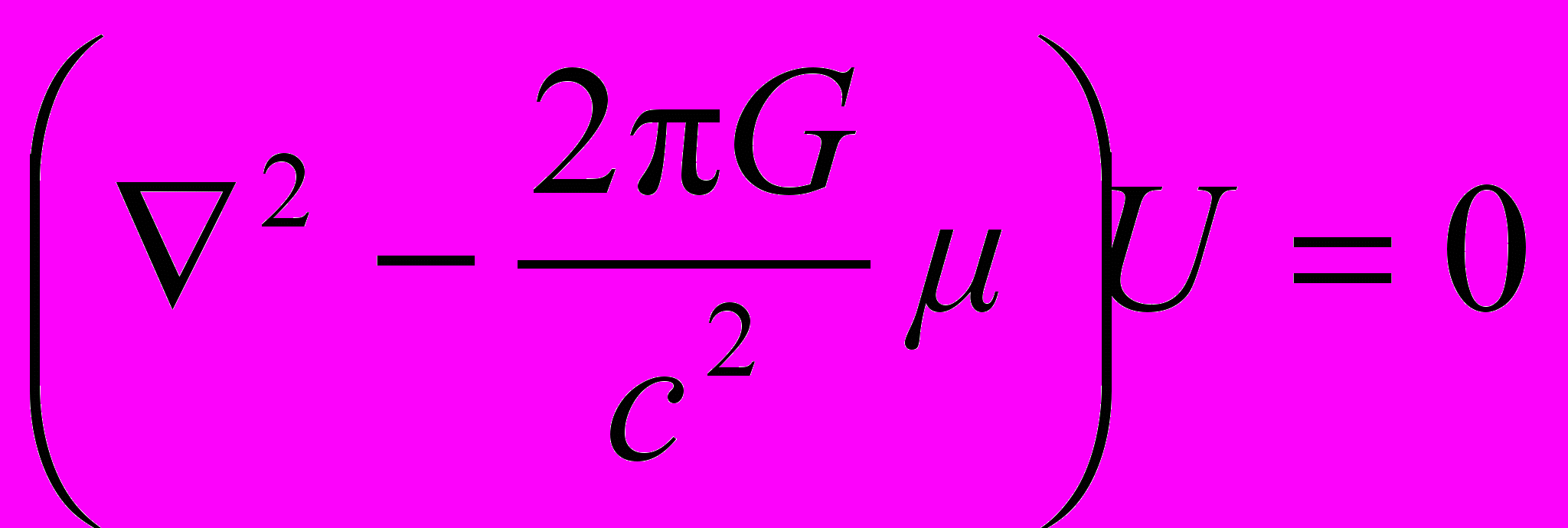. (33)

Сферически симметричное внешнее решение этого уравнения для области пространства вне центрального гравитирующего тела со сферически симметричным распределением массы запишем в виде

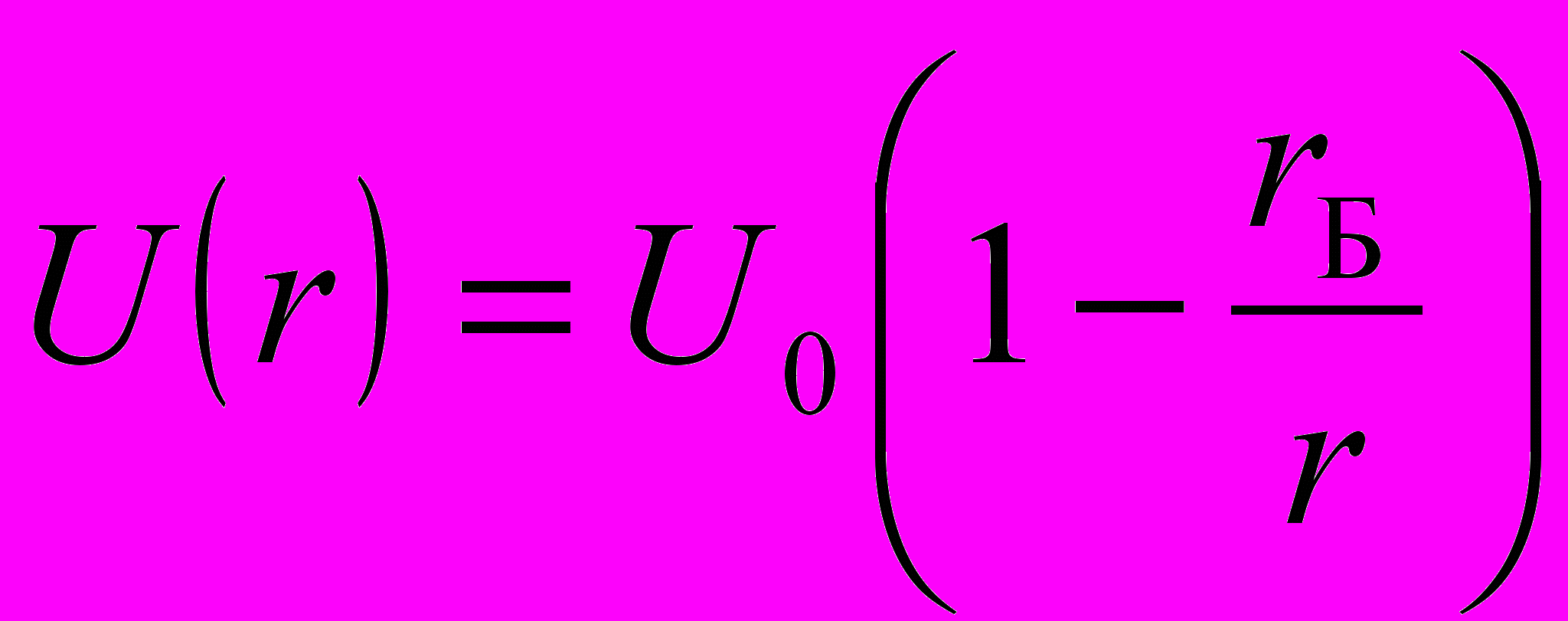, (34)

где U₀ и r_Б – постоянные интегрирования. Из (6), (8) (34) находим центральное поле напряженности

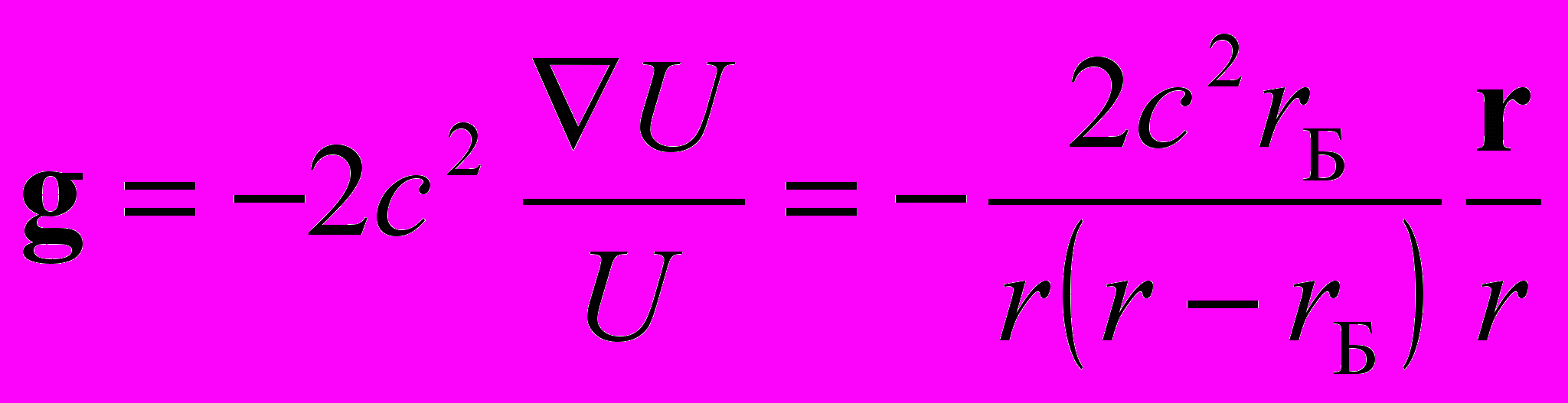. (35)

Установим теперь физический смысл критического радиуса Бриллюэна r_Б, при котором напряжённость g обращается в бесконечность. С этой целью умножим уравнение (32) на U ² и преобразуем его к виду

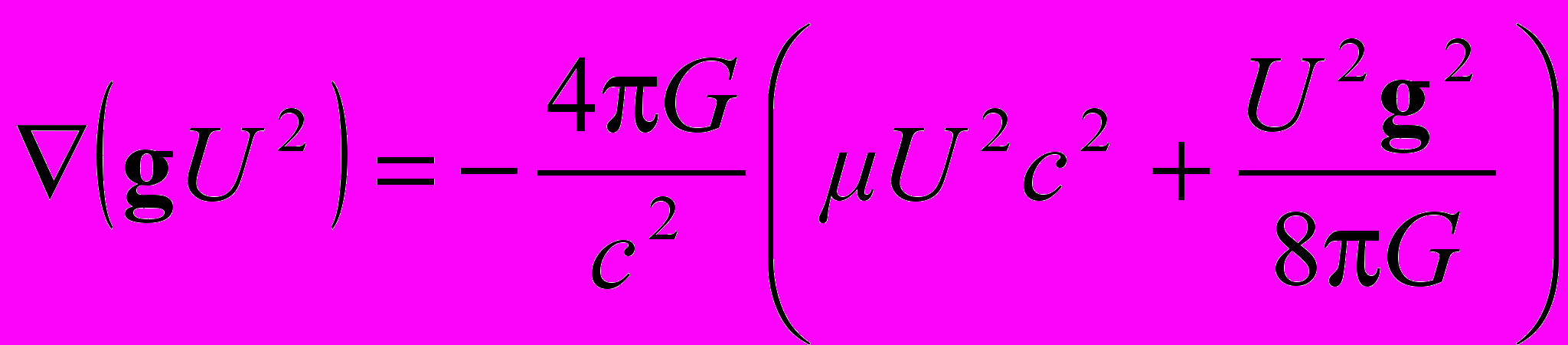. (36)

Выражение в скобках в правой части (36) включает два члена, первый из которых, согласно (4), равен плотности энергии покоящегося вещества в гравитационном поле, а второй представляет положительно определенную плотность энергии (29) статического поля тяготения, у которого скалярная напряженность η отсутствует. Проинтегрируем (36) по всему пространству. Левую часть получающегося при этом равенства представим как поток вектора gU² через сферическую поверхность бесконечно большого радиуса. Подсчёт этого потока для внешнего решения (34), (35) при калибровке   0 на бесконечности, то есть при U₀ = 1, дает значение 8с²r_Б. В то же время в правой части получим величину 4GM, где

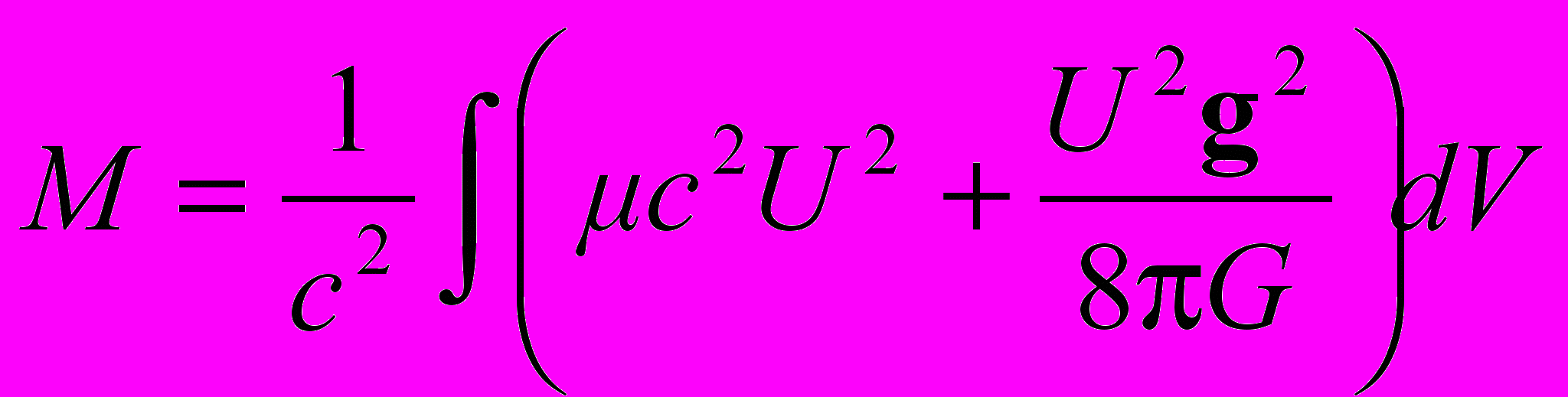(37)

 деленная на c² полная энергия всей системы, то есть её инертная масса по определению. В результате находим

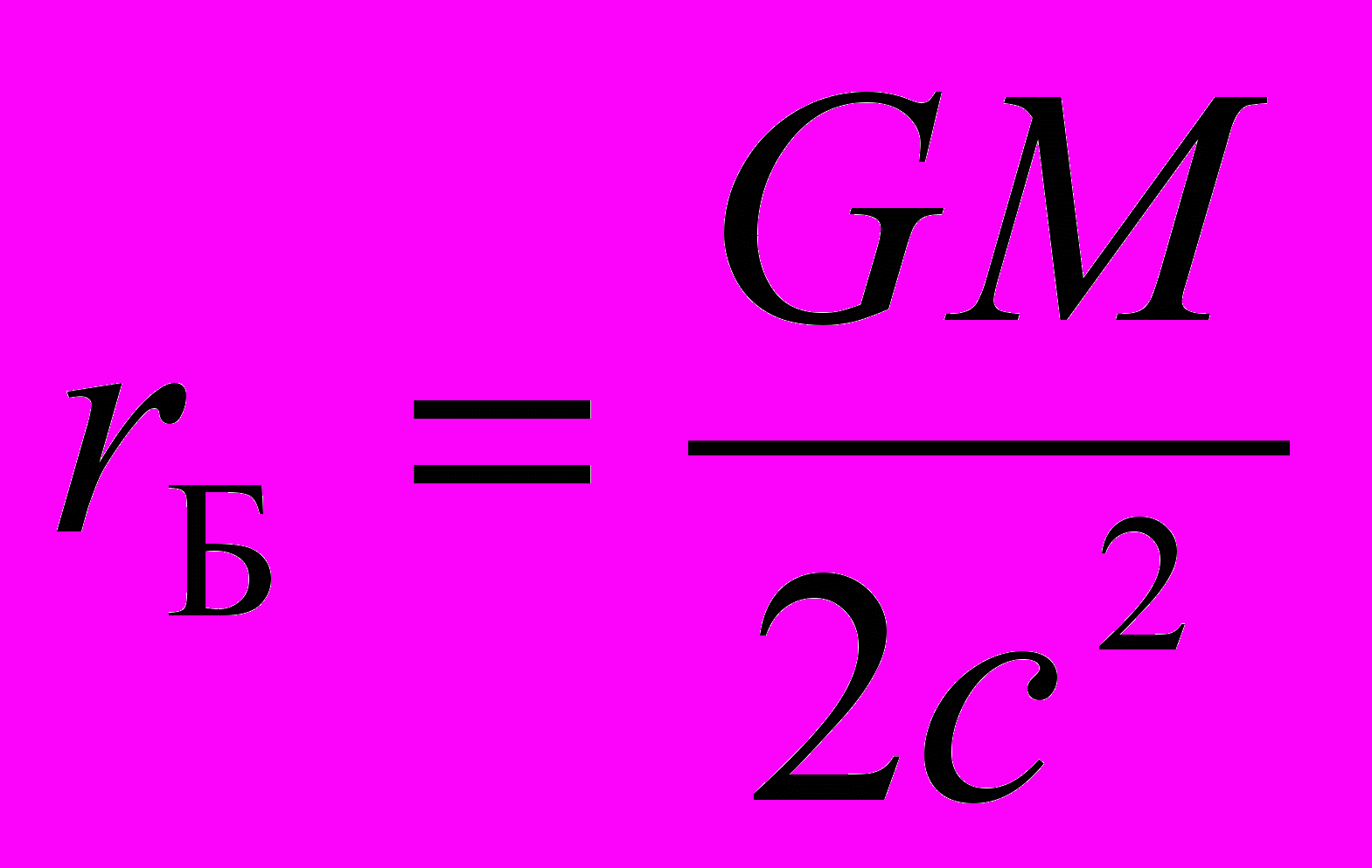. (38)

Установив связь радиуса Бриллюэна r_Б в решениях (34), (35) с полной массой системы, можем переписать выражение для напряженности внешнего поля

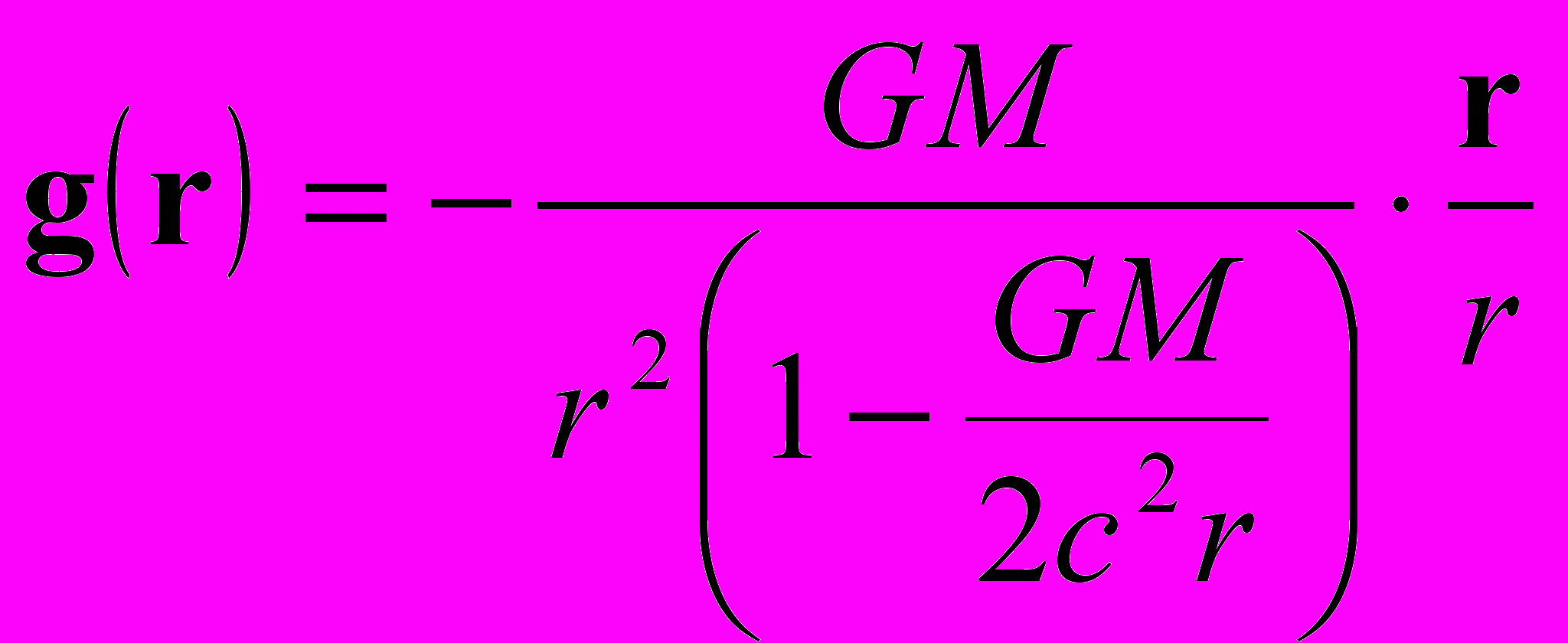, (39)

Данное решение нелинейного уравнения (32) представляет релятивистское обобщение закона тяготения Ньютона. На больших расстояниях, когда r r_Б, поле (39) асимптотически переходит в ньютоновское.

6. Чёрная дыра


В то время как в гравистатике Ньютона представление о точечном источнике поля тяготения вполне допустимо, в развиваемом здесь подходе, строго говоря, нельзя полагать размеры пространственной области, которую занимает гравитирующая масса, сколь угодно малыми. Чтобы в этом убедиться, рассмотрим шарообразный источник статического гравитационного поля – центральное тело с массой, распределенной сферически симметрично в шаровом объеме V. Полная масса 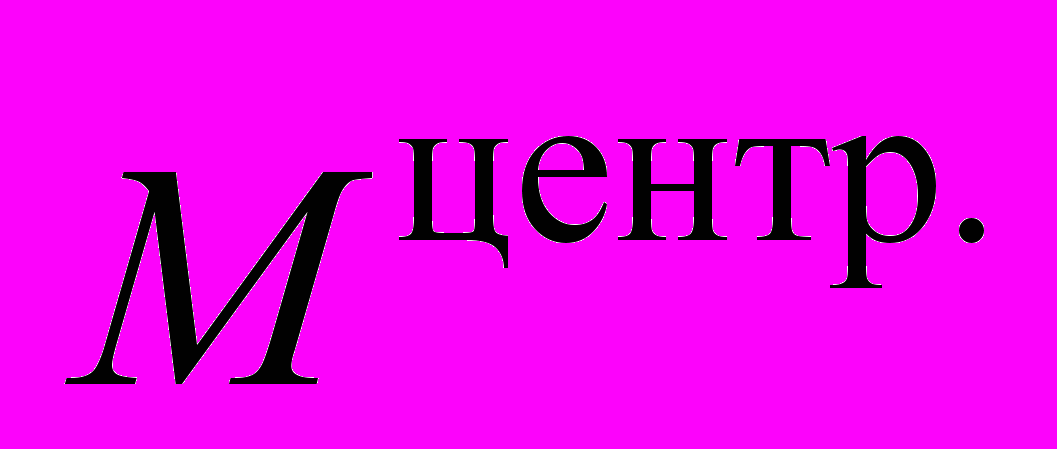, сосредоточенная в объёме центрального тела, будет равна интегралу (37) по объему V от положительно определенной полной плотности массы вещества и поля. При этом из (36) следует связь между и потоком вектора g U² через ограничивающую центральное тело сферу S радиуса R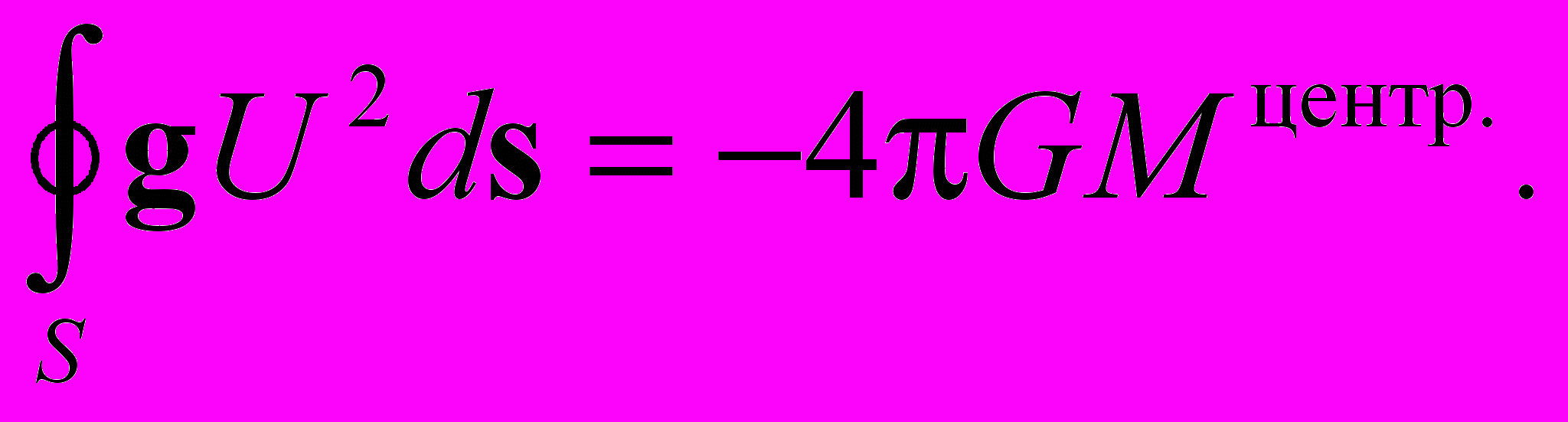

(40)

Выполняя непосредственное интегрирование в левой части (40) с использованием внешних решений (39), (34) при калибровке U = 1 на бесконечности, также получаем

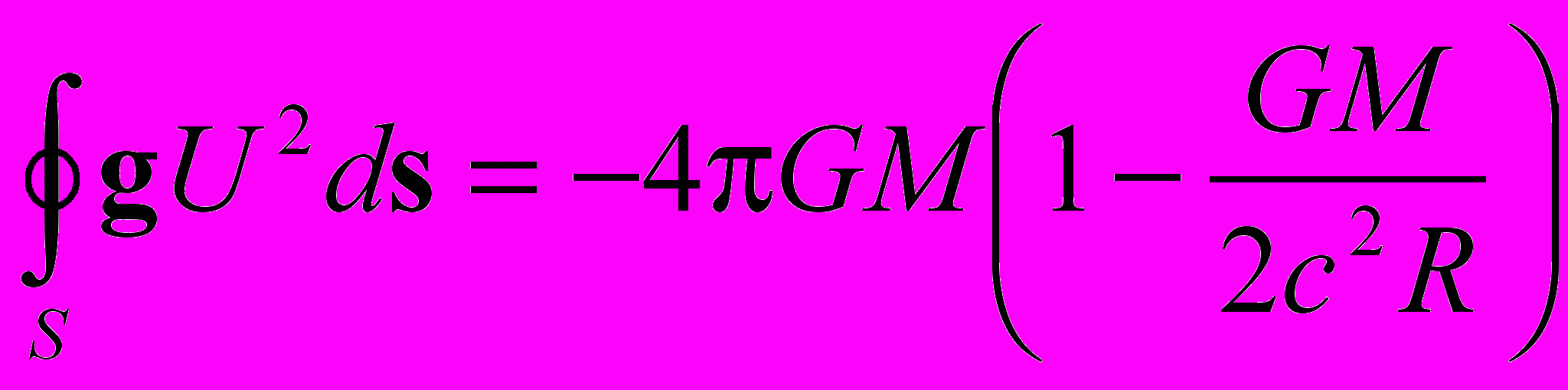, (41)

где M полная масса (37) гравитирующей системы. Сравнивая (40) и (41), приходим к выражению для массы, заключённой в объёме центрального тела

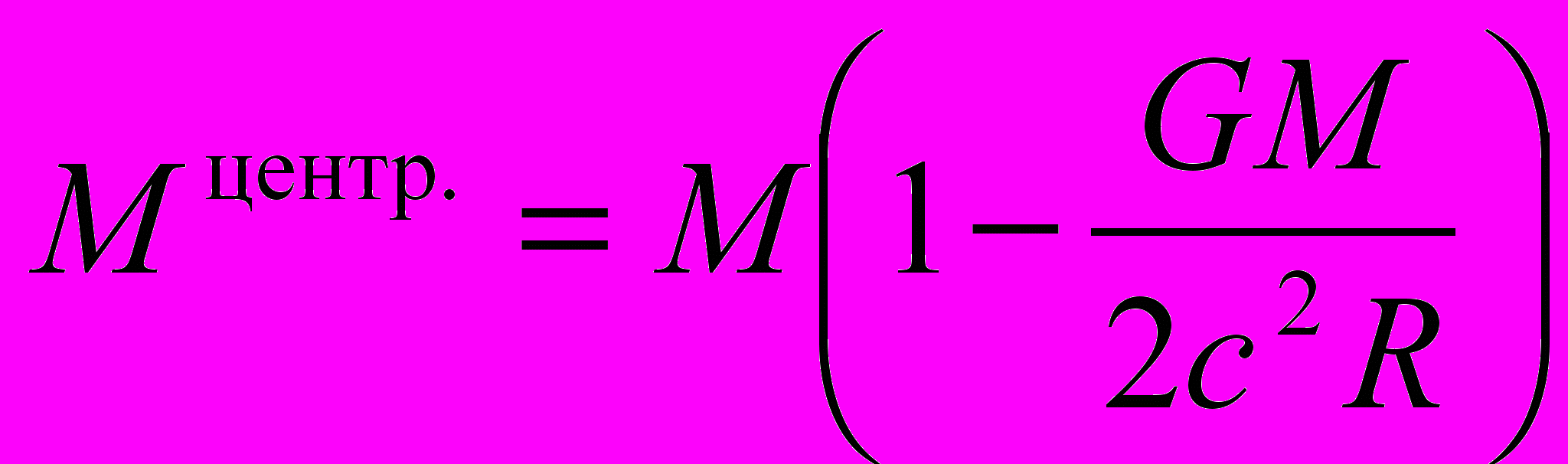. (42)

Из (37) вытекает положительная определенность массы в объёме центрального тела и полной массы: , M  0. Согласно (42), это приводит к ограничению минимальных размеров центрального тела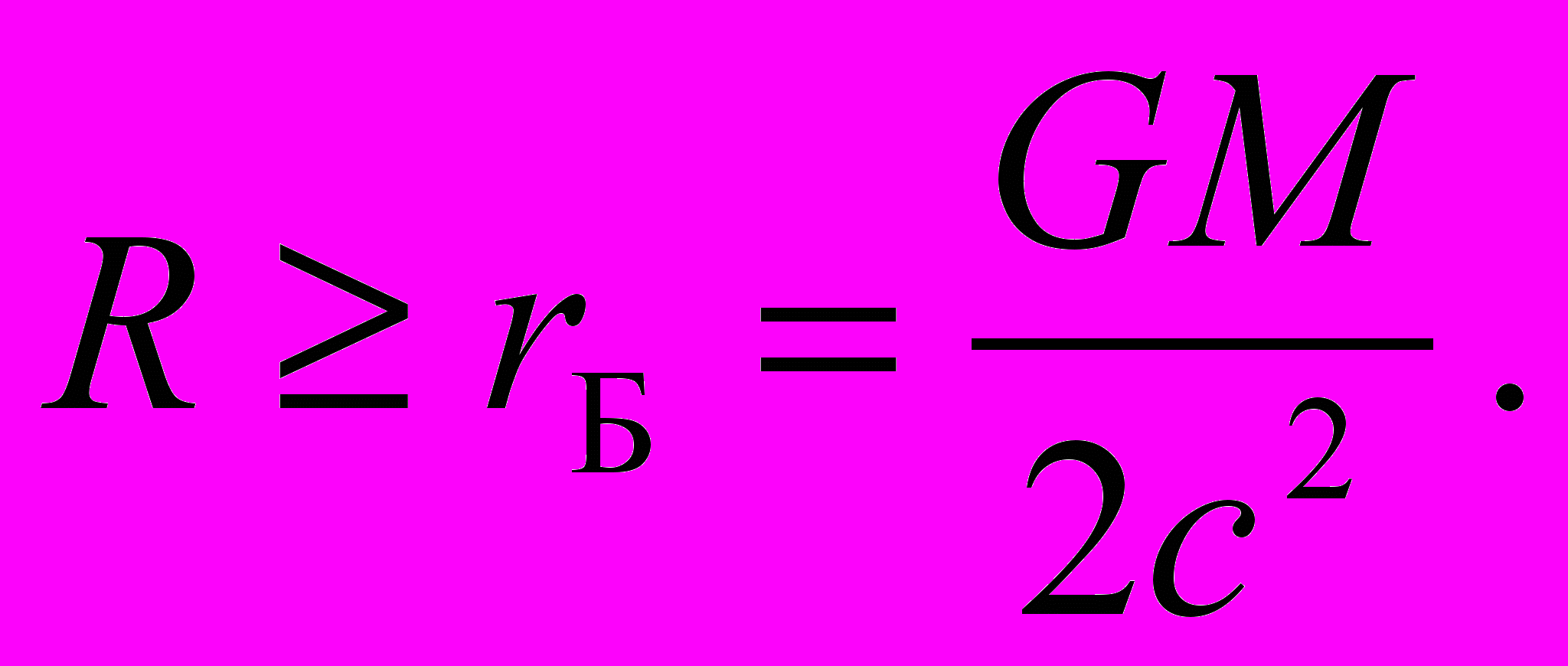

(43)

Данное неравенство показывает, что понятие точечной частицы как источника поля тяготения лишено физического смысла. В самом деле, неограниченное уменьшение размеров тяготеющего тела означало бы, согласно (43), в такой же степени неограниченное уменьшение массы всей гравитирующей системы, что равносильно исчезновению самого объекта гравитации. Здесь, однако, следует оговорить, что сделанный вывод не относится к точечной электрически заряженной частице, как источнику поля тяготения. У такой частицы существует неисчезающая гравитирующая масса электромагнитного происхождения, распределенная во всём пространстве

Требование (43) допускает равенство радиуса центрального тела критическому радиусу: R  r_Б  GM / 2c². Такая система, имеющая при заданной полной массе M минимальный радиус центрального тела r₀, соответствует известным в ОТО решениям для так называемых чёрных дыр. Из соотношения (42) видно, что при достижении критического радиуса масса центрального тела оказывается равной нулю, так что вся масса черной дыры имеет полевое происхождение. Таким образом, гравитационный дефект массы центрального тела достигает ста процентов.

Заметим также, что существование чёрных дыр совместимо с положительно определённой плотностью энергии гравитационного поля. Противоположное утверждение (см. обзор [⁸]) основано на недоразумении, возникающем из-за пренебрежения гравитационным дефектом массы.

Согласно (39), напряжённость g поля тяготения на поверхности чёрной дыры при r  r₀ обращается в бесконечность. Используя закон сохранения энергии, рассчитаем скорость, которую приобретёт массивная частица, достигая поверхности чёрной дыры. Приравнивая энергию (4) покоящейся частицы в точке r₀, с которой начинается падение, её энергии в некоторой точке r, с учётом (34) получим

,

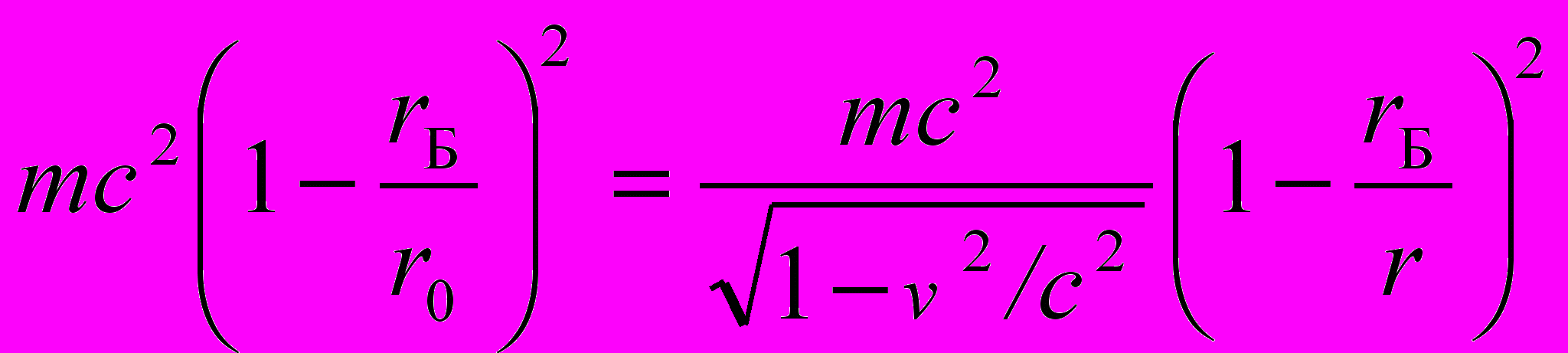откуда



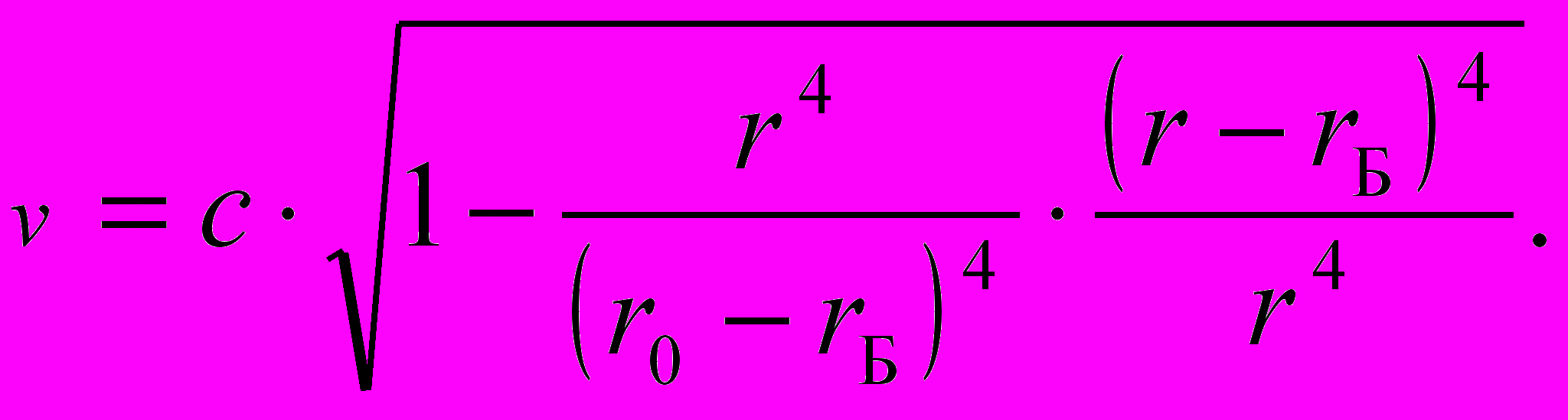
Как видим, при свободном падении частица, достигает поверхности черной дыры, где r = r_Б, имея скорость, равную скорости света c независимо от значения r₀. Это оказывается возможным, поскольку эффективная масса покоя частицы



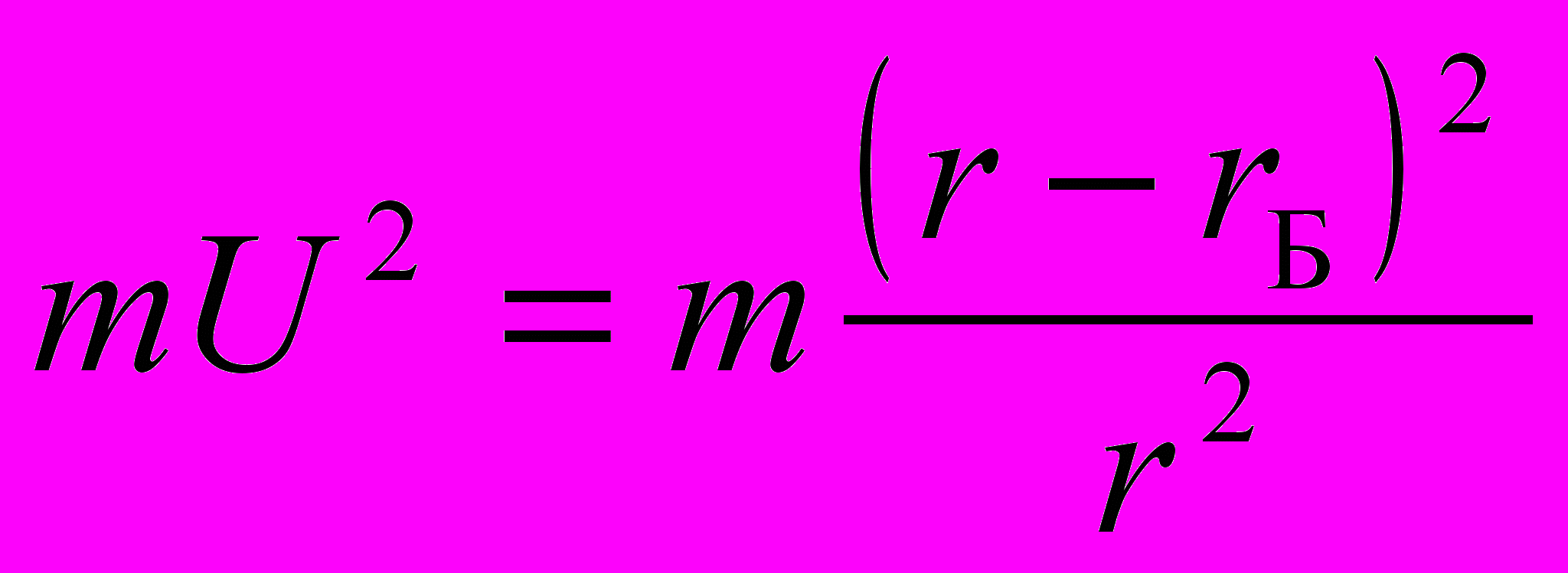
при этом становится равной нулю. Время такого ускоряющегося падения по часам внешнего покоящегося наблюдателя будет, очевидно, конечным.


Список литературы

1. Ландау Л. Д., Лифшиц Е. М. Механика. М., Физматгиз. 1958.
   
2. Гельфанд И. М. и др. Представления группы вращений и группы Лоренца. М., Физмат
   

гиз, 1960.

3. Логунов А. А. Лекции по теории относительности и гравитации: современный анализ
   

проблемы. М., Наука, 1987.

4. Nordström G. // Phys. Zeitschrift, 1912, Bd. 13, S. 1126.
   
5. Nordström G. // Ann. d. Phys., 1913, Bd. 40, S. 856.
   
6. Nordström G. // Ann. d. Phys., 1913, Bd. 42, S. 533.
   
7. Thirring W. E. // Annals of Physics. 1961. Vol. 16. P. 96 – 117.
   
8. Барышев Ю. В. // Гравитация. 1996. Т. 2, вып.2. С. 5.
   
9. Сердюков А. Н. Калибровочная теория скалярного гравитационного поля. Гомель, ГГУ,
   

2005.

10. Ландау Л. Д., Лифшиц Е. М. Теория поля. М., Физматгиз, 1960.
    
11. Бриллюэн Л. Новый взгляд на теорию относительности. М., Мир, 1972.