Единая теория электродинамики и гравитации Абрамов А. П., 2006
| Вид материала | Документы |
- Александра Гордона «Релятивистская теория гравитации», 243.83kb.
- Высокочастотная электродинамика, 84.33kb.
- Программа учебной дисциплины "Компьютерная математика в задачах электродинамики" (СД., 337.47kb.
- Обзор [18-21]. Единая голографическая информационна теория вселенной егитв, 3252.63kb.
- Ый подход к решению проблемы единого поля электромагнетизма и гравитации в рамках классической, 219.01kb.
- Лекция Квантово-полевая картина мира (кпкм), 110.07kb.
- Книга рассказывает о самых знаменитых из богов, которым поклонялись в прошлом, а отчасти, 447.08kb.
- «Единая Европа», 227.43kb.
- Законы эволюции вселенной часть движение фотонов вблизи тел, 227.77kb.
- Квантовые Флуктуации Вакуума в Искривленном Пространстве и Теория Гравитации, доклад, 340.83kb.
ЕДИНАЯ ТЕОРИЯ ЭЛЕКТРОДИНАМИКИ И ГРАВИТАЦИИ
Абрамов А.П., 2006
Санкт-Петербург, Е-mail: arabramov @ yandex.ru
Показана возможность единого описания гравитации, классической механики и электродинамики. Объединение взаимодействий проведено в системе единиц метр, килограмм, секунда в пространстве Минковского в рамках специальной теории относительности. 4-потенциал электродинамики в Единой теории преобразован в 4-импульс материального поля. При этом в Единой теория поля гравитация и электромагнетизм отличаются только константой связи. Высказано предположение об электромагнитной природе гравитации. В Единой теории поля смещение перигелия Меркурия получено с использованием запаздывающего потенциала гравитационного поля, аналогичного запаздывающему потенциалу электромагнитного поля.
Abramov A.P. Unified Theory of electrodynamics and gravitation. The opportunity of the uniform description of gravitation, classical mechanics and electrodynamics is shown. Unification of interactions is carried out in system of units meter, kg, second in Minkowski space within the framework of the special theory of relativity (SRT). The 4-potential of electrodynamics in the unified theory is transformed into a 4-momentum of a material field. Thus in Unified theory of a field (UFT) gravitation and electromagnetism differ only with a constant of interaction. The assumption of the electromagnetic nature of gravitation is stated.
Несмотря на разработанную А.Эйнштейном в 1915 году для описания гравитации общую теорию относительности (ОТО), проблема Единой теории поля и сегодня продолжает занимать умы исследователей. . Сам Эйнштейн так и не нашёл пути объединения гравитационного и электромагнитного взаимодействий. Его геометрическая интерпретация тяготения не связывается в общую теорию с уравнениями электромагнитного поля Дж. Максвелла и с квантовой механикой. Неоправданно сложный математический аппарат и немногочисленные предсказания ОТО не позволяют считать эту теорию действительно физической теорией гравитации.
Между тем общеизвестно, что ещё со времён Дж. Максвелла предпринимались попытки [1–3] описания гравитации с помощью уравнений очень похожих на уравнения электродинамики
В настоящей работе проведено объединение электродинамики, гравитации и механики на основе уравнений электромагнитного поля Дж. Максвелла и специальной теории относительности (СТО). Как известно, постулаты относительности и постоянства скорости света приводят к инвариантности всех законов природы относительно группы Лоренца. Потенциалы теории Лоренца, скалярный j и векторный
 , как впервые было отмечено Минковским, могут быть соединены в один вектор четырёхмерного мира – четырёхмерный потенциал Аm = (j,А). Однако, этот потенциал, несмотря на его полезность, не имеет в теории Лоренца никакого физического смысла [5], а в классической механике и в классической теории гравитации нет аналогичного электродинамике четырёхмерного потенциала.
, как впервые было отмечено Минковским, могут быть соединены в один вектор четырёхмерного мира – четырёхмерный потенциал Аm = (j,А). Однако, этот потенциал, несмотря на его полезность, не имеет в теории Лоренца никакого физического смысла [5], а в классической механике и в классической теории гравитации нет аналогичного электродинамике четырёхмерного потенциала.Вместе с тем, анализ уравнений Максвелла позволяет прийти к выводу о возможности их применения и для описания гравитации и в механике. Единая теория может быть построена в системе единиц, в которой основными величинами являются длина (м), масса (кг) и время (сек). Чтобы записать уравнения Максвелла в такой системе единиц, необходимо переопределить напряжённость электрического поля. Предлагается в качестве пробного заряда взять электрон, обладающий одновременно наименьшей величиной заряда е и наименьшей массой me – реальную частицу, существующую в природе. Тогда напряжённость электрического поля
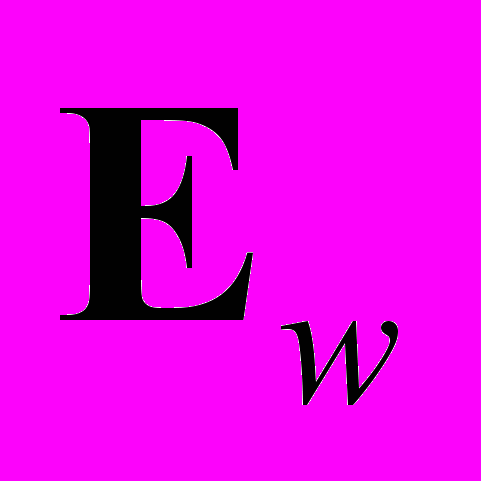 можно определить как силу, действующую на электрон, находящийся в данной точке силового поля электрического заряда Q = Ne, (где N – целое число, e – заряд электрона):
можно определить как силу, действующую на электрон, находящийся в данной точке силового поля электрического заряда Q = Ne, (где N – целое число, e – заряд электрона):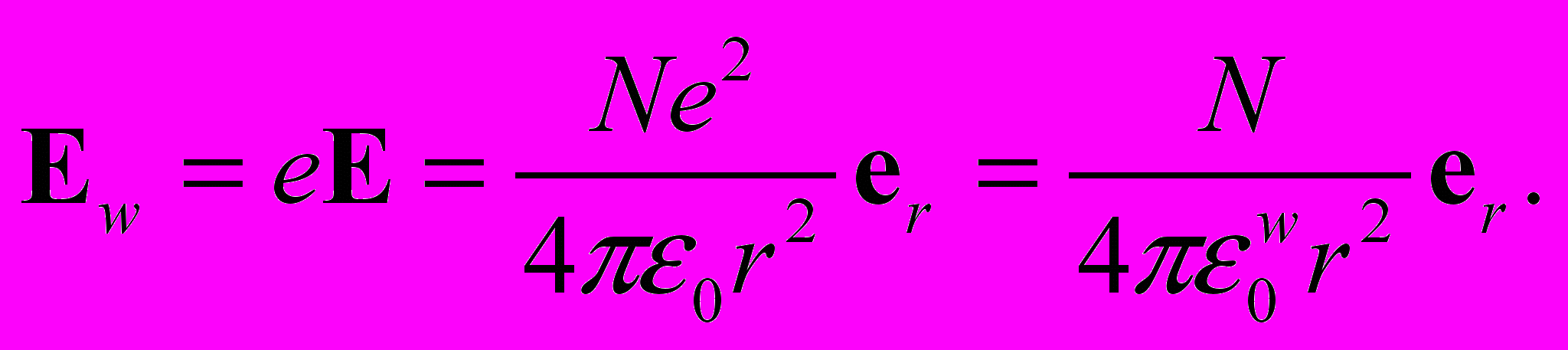 (1)
(1)Здесь eо – электрическая постоянная,
 – общепринятая напряженность электрического поля,
– общепринятая напряженность электрического поля, 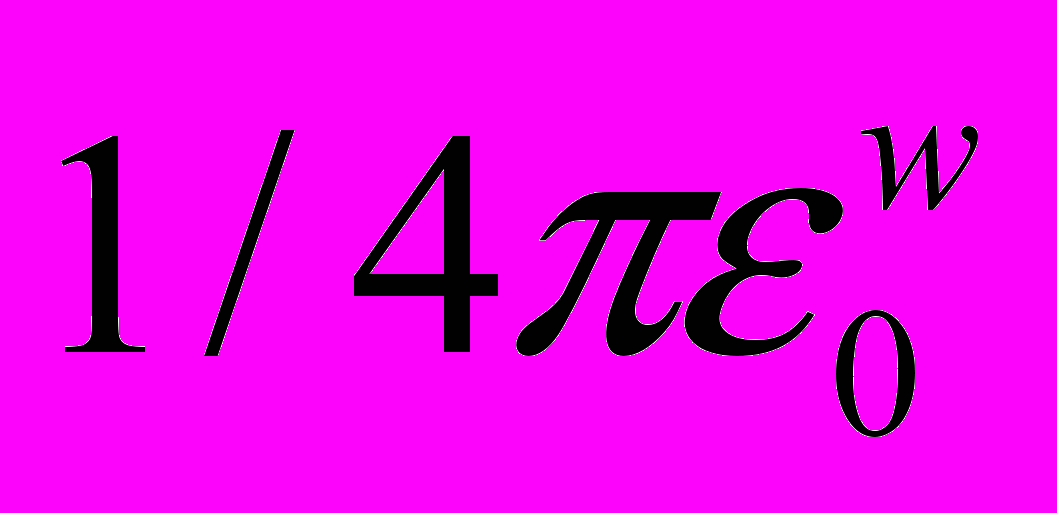 = e²/4peо – константа электромагнитного взаимодействия,
= e²/4peо – константа электромагнитного взаимодействия, 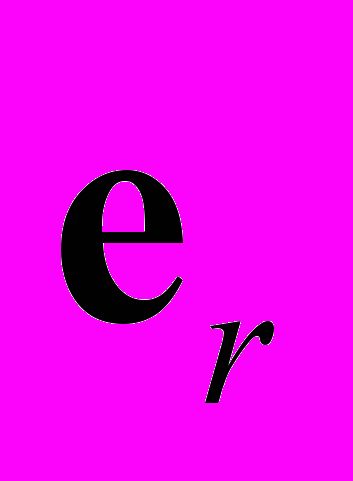 – единичный вектор, имеющий направление силового поля. Здесь и далее значком w будем обозначать преобразованные величины модифицированной теории.
– единичный вектор, имеющий направление силового поля. Здесь и далее значком w будем обозначать преобразованные величины модифицированной теории.Воспользуемся известным соотношением из квантовой теории:
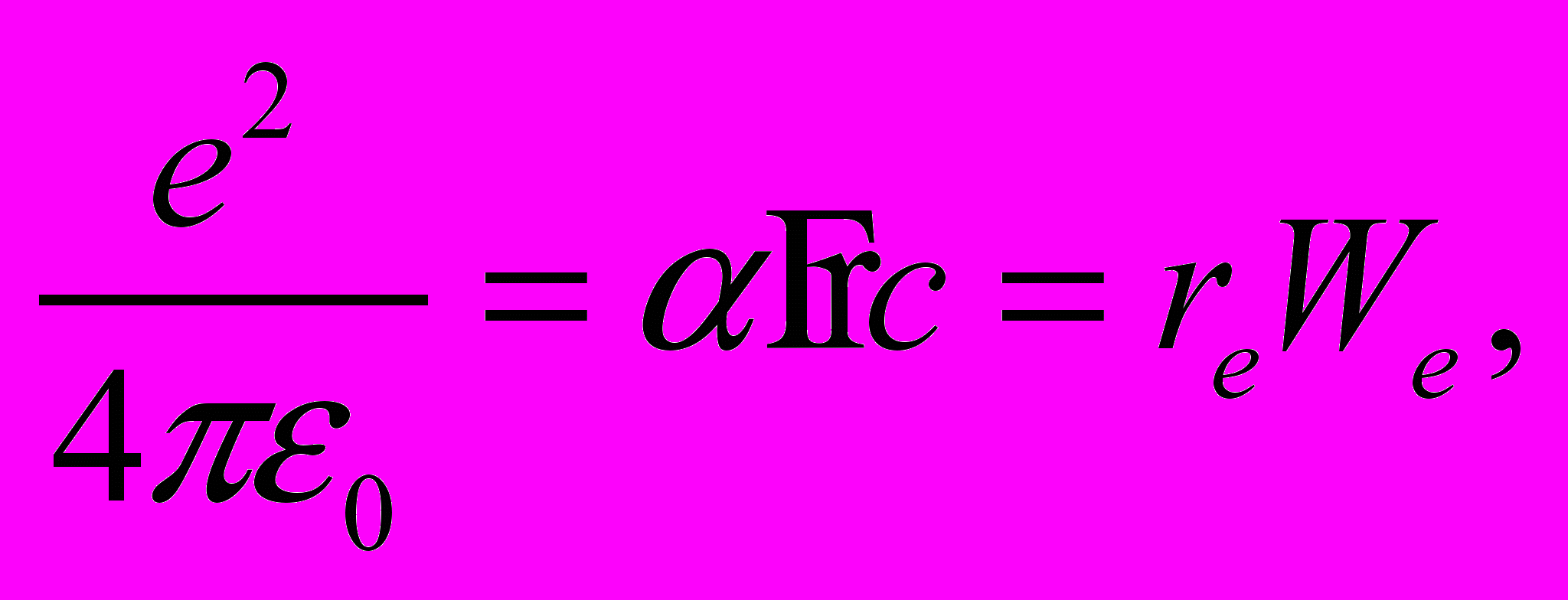 (2)
(2)где a – постоянная тонкой структуры, h – постоянная Планка (h = h/2p), rе – классический радиус электрона, We = mec2 – энергия электрона, и перепишем (1) в виде:
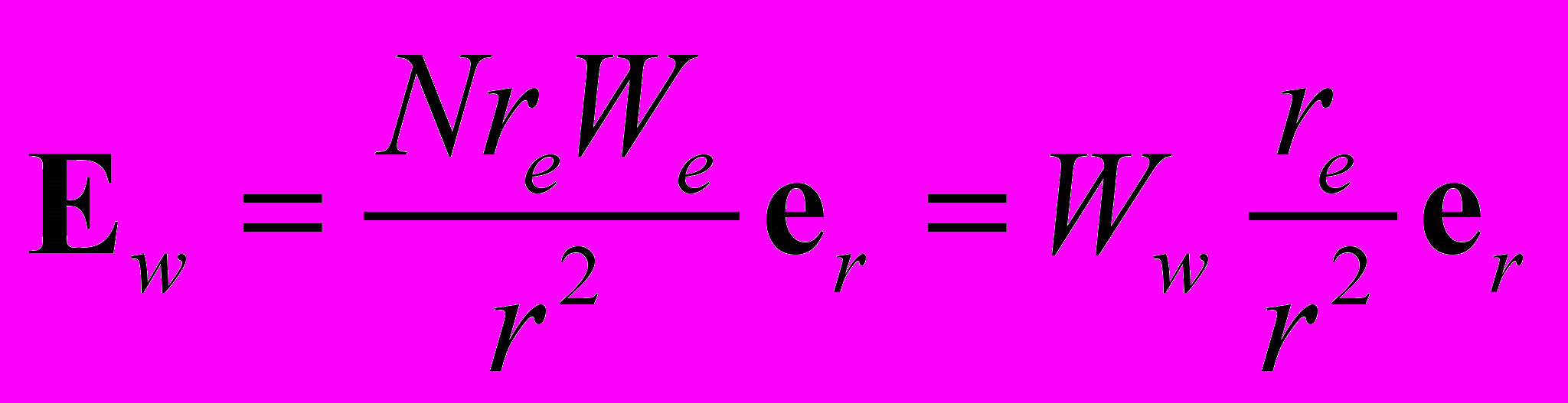 (3)
(3)В этом выражении величина Ww = NWe – полная энергия заряда Ne.
Напряженность силового электрического поля, как видим, имеет размерность силы (или Дж/м).
Используя известное выражение, связывающее напряжённость электрического поля со скалярным и векторным потенциалом электродинамики
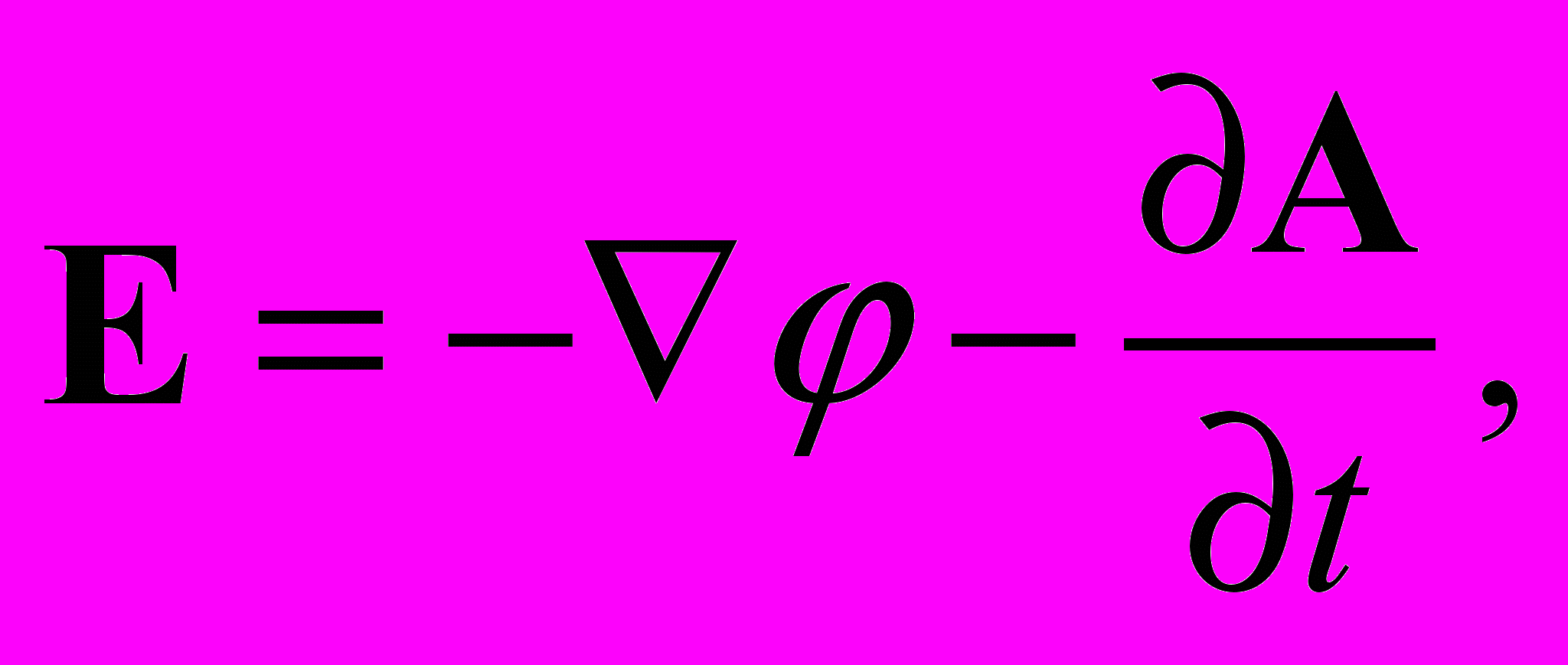 (4)
(4)преобразуем это выражение, умножив его на величину е заряда электрона:
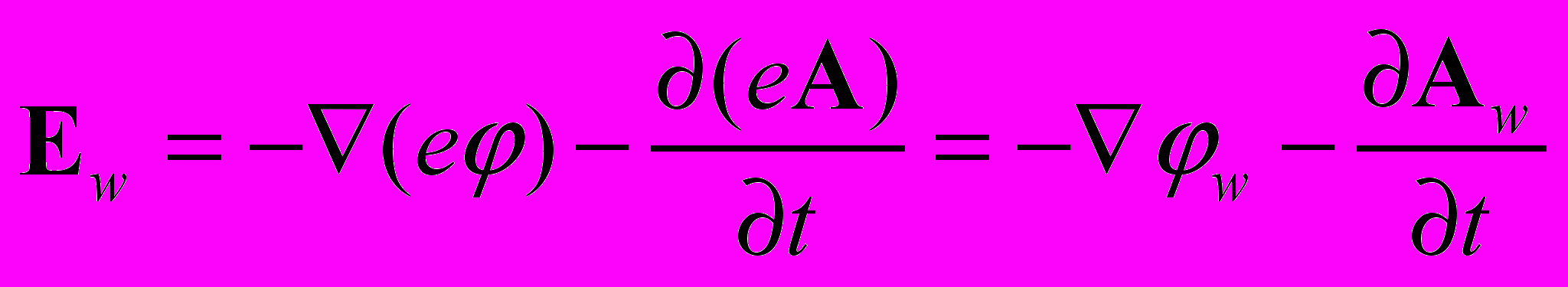 . (5)
. (5)Скалярный потенциал модифицированной теории имеет размерность энергии (Дж) и дает представление о работе, которую нужно совершить, чтобы пробную частицу – электрон переместить из заданной точки силового поля на бесконечность. Скалярный потенциал в нашей теории – это потенциальная энергия пробной частицы в момент времени t, находящейся в точке 1 в поле заряда Ne, расположенного в точке 2:
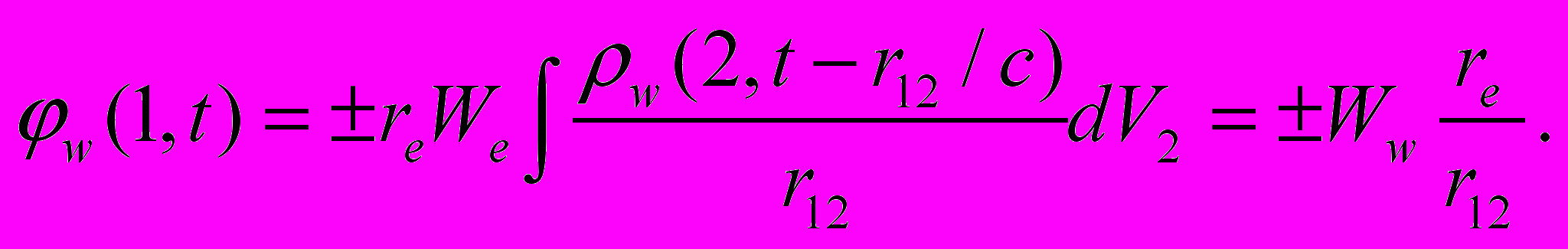 (6)
(6)Здесь
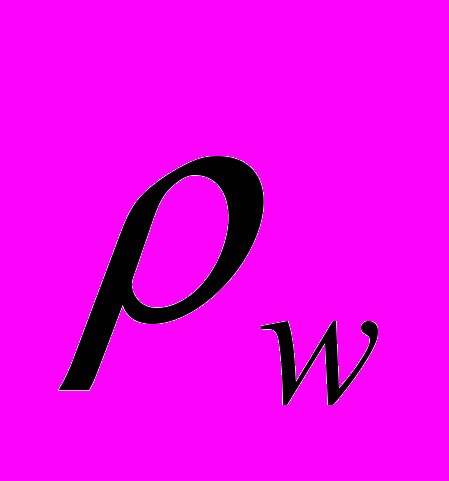 = r/е – плотность заряженных частиц, r – общепринятая плотность заряда. Знак “минус” соответствует притяжению заряда и пробной частицы – электрона.
= r/е – плотность заряженных частиц, r – общепринятая плотность заряда. Знак “минус” соответствует притяжению заряда и пробной частицы – электрона.Как видим, в выражения для напряжённости силового поля и потенциальной энергии заряд в явном виде не входит. Вместо него введена безразмерная величина N = Q/e, которая, впрочем, как и заряд, является инвариантом преобразований Лоренца. Интенсивность электромагнитного взаимодействия определяется константой
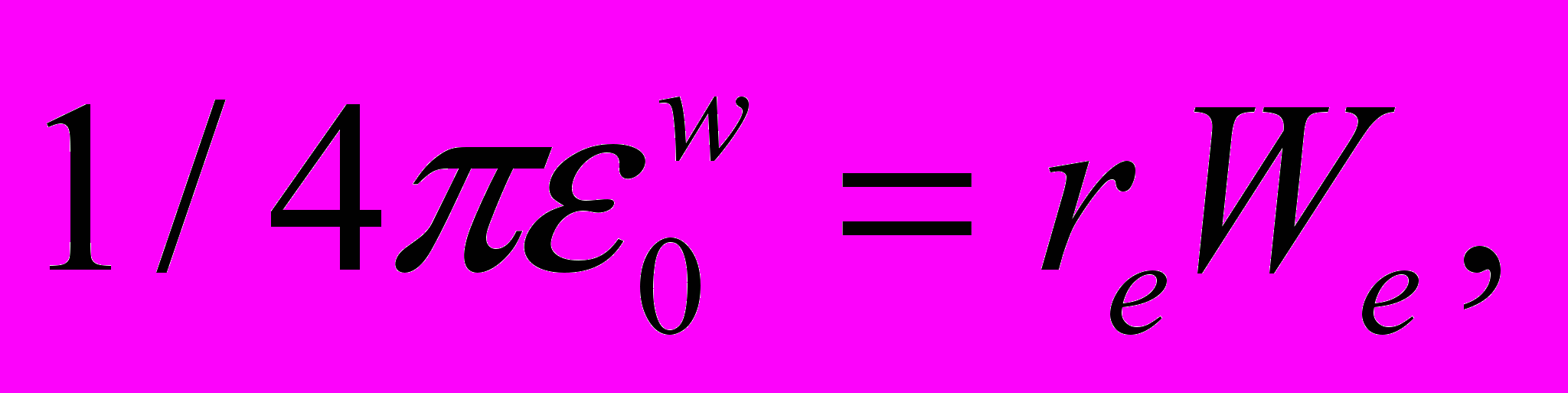 которая также является инвариантом преобразований Лоренца.
которая также является инвариантом преобразований Лоренца.Векторный потенциал электродинамики А, после умножения его на е, преобразуется к виду
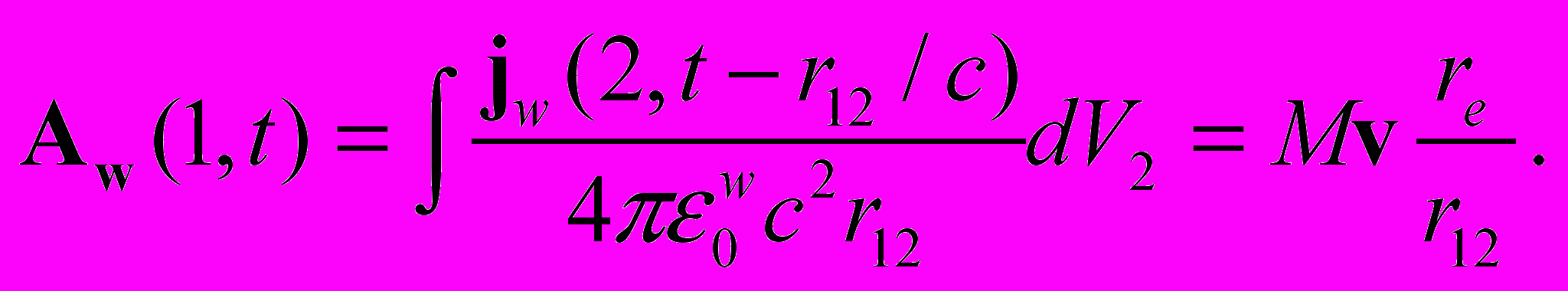 (7)
(7)Здесь jw = rwv – плотность потока заряженных частиц (электронов), М – масса движущихся заряженных частиц (при v << c). Векторный потенциал нашей теории имеет размерность импульса (кгм/с) и приобрёл новый физический смысл: вокруг движущегося заряда имеется импульс электромагнитного поля (7). Таким образом, в нашей теории мы заменили 4-потенциал электромагнитного поля 4-импульсом
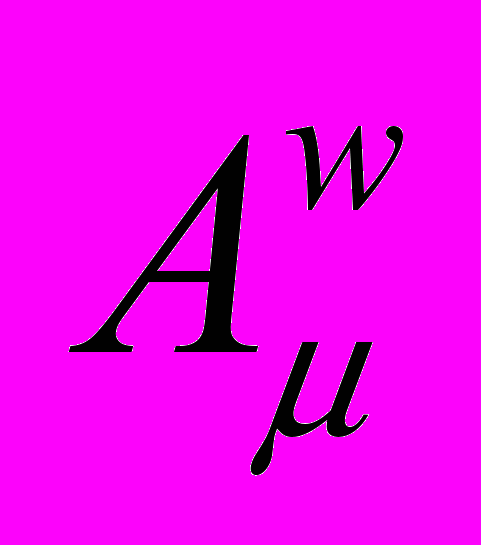 = (jw, Aw), компоненты которого являются функциями координат и времени. Функция Лагранжа для пробного заряда – электрона в электромагнитном поле примет вид
= (jw, Aw), компоненты которого являются функциями координат и времени. Функция Лагранжа для пробного заряда – электрона в электромагнитном поле примет вид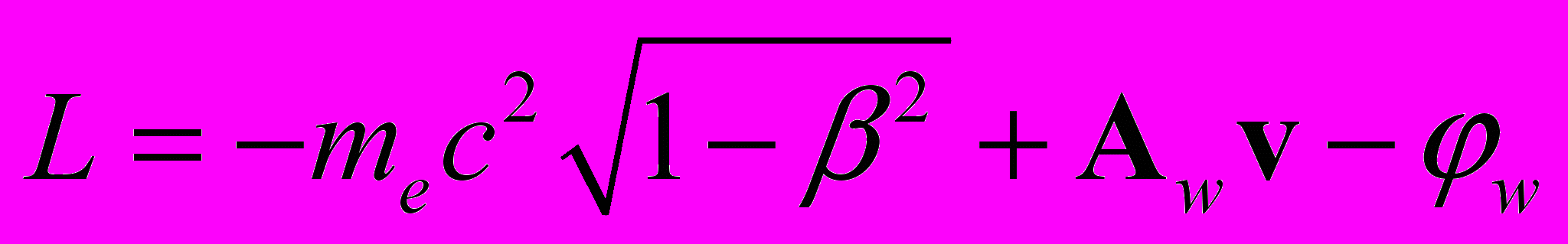 , (8)
, (8)и уравнение движения пробного заряда в электромагнитном поле будет
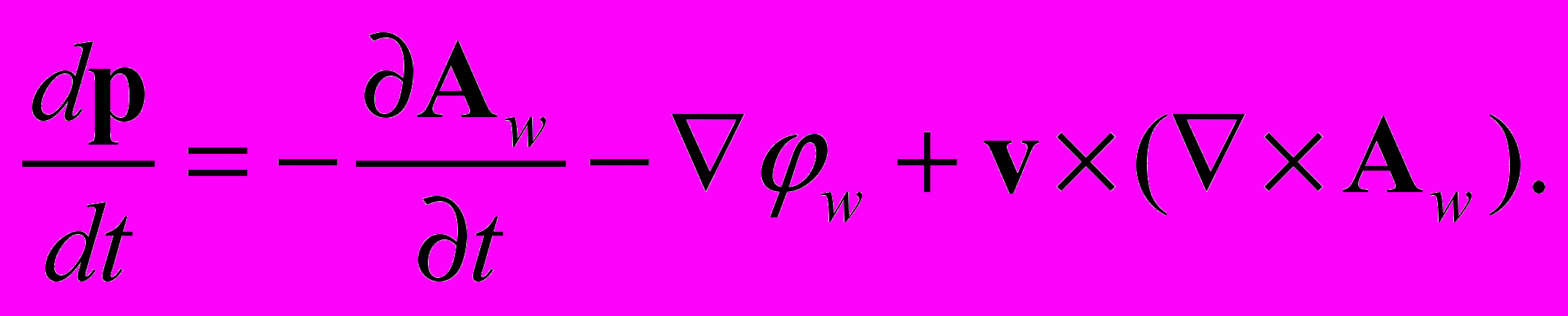 (9)
(9)Если в электромагнитном поле движется заряд, состоящий из N электронов, последнее уравнение необходимо умножить на N. В выражении (9) вектор Bw = eB
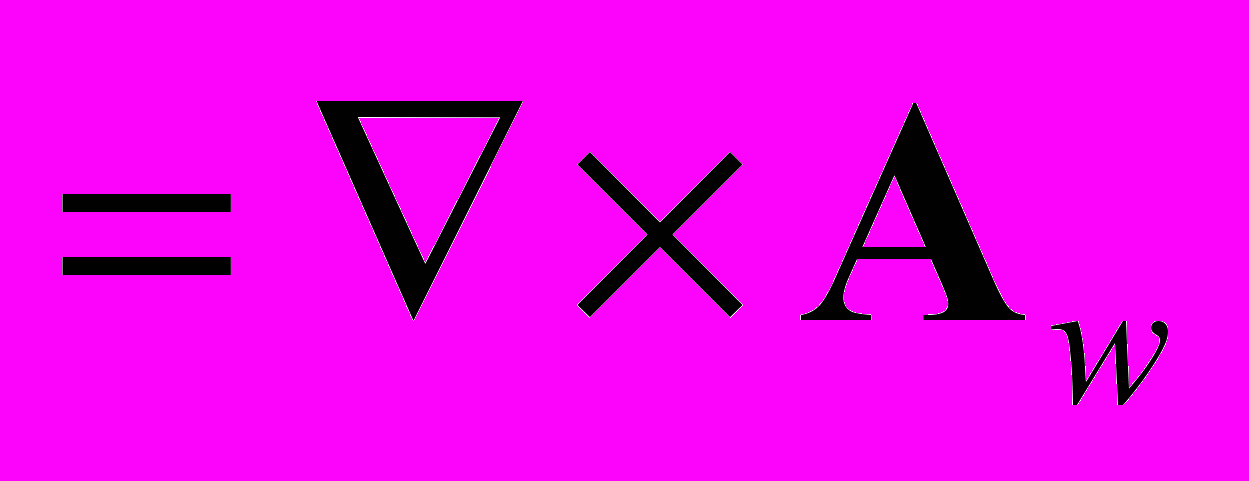 в отличие от вектора В магнитного поля, назовём вектором кинетического поля. Вектор Вw характеризует пространственные изменения импульса электромагнитного поля, а также определяет силу, действующую на электрон, движущийся со скоростью v в кинетическом поле. Уравнение движения пробного заряда в электромагнитном поле теперь будет иметь вид
в отличие от вектора В магнитного поля, назовём вектором кинетического поля. Вектор Вw характеризует пространственные изменения импульса электромагнитного поля, а также определяет силу, действующую на электрон, движущийся со скоростью v в кинетическом поле. Уравнение движения пробного заряда в электромагнитном поле теперь будет иметь вид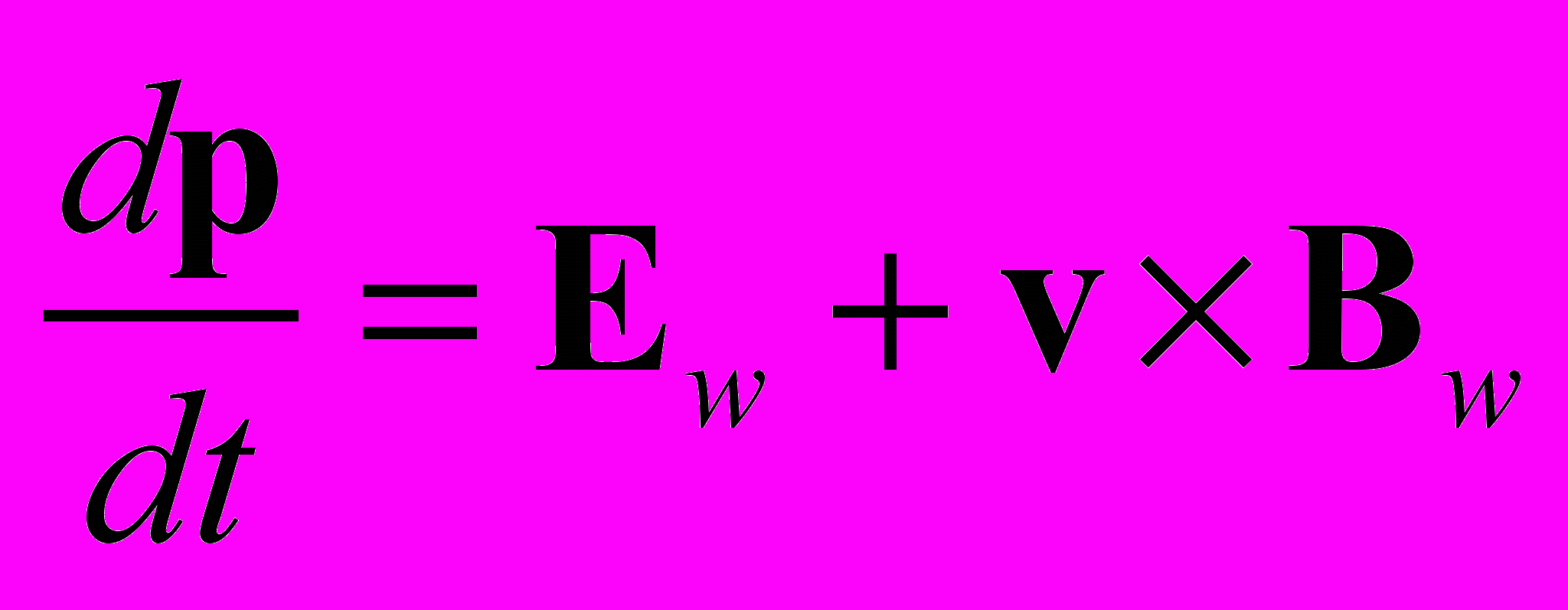 . (10)
. (10)Здесь стоящее справа выражение является силой Лоренца. Уравнения для потенциалов электромагнитного поля, с учётом (2), переходят в уравнения энергии – импульса электромагнитного поля:
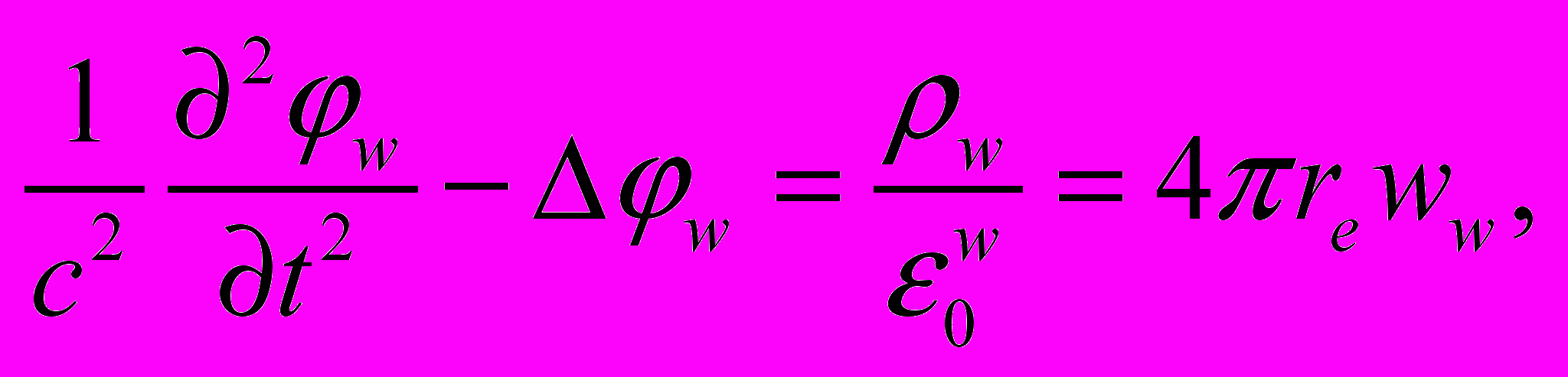 (11)
(11)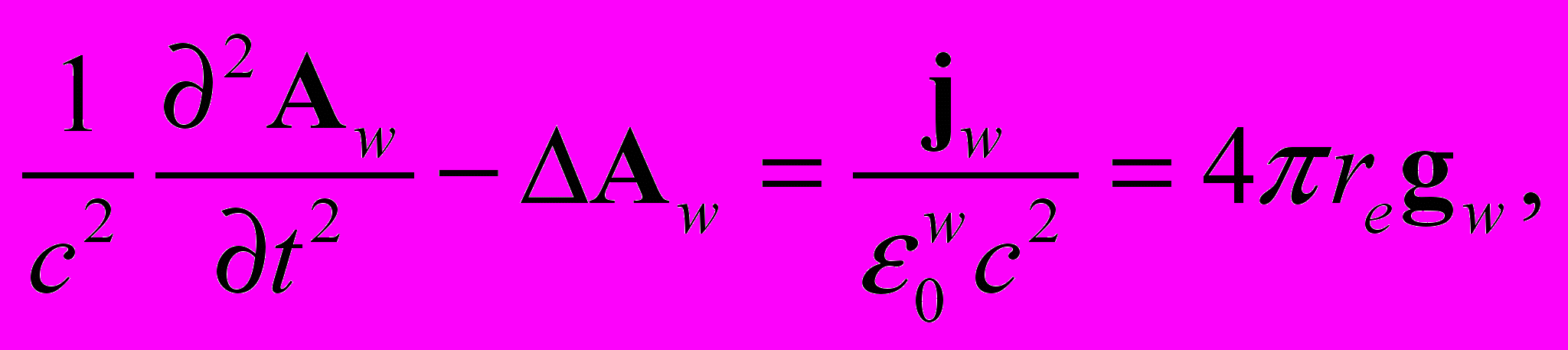 (12)
(12)где ww = rwWe – плотность энергии заряда – источника электромагнитного поля, gw – плотность импульса источника электромагнитного поля.
В четырёхмерных обозначениях уравнение для 4-импульса электромагнитного поля получит вид
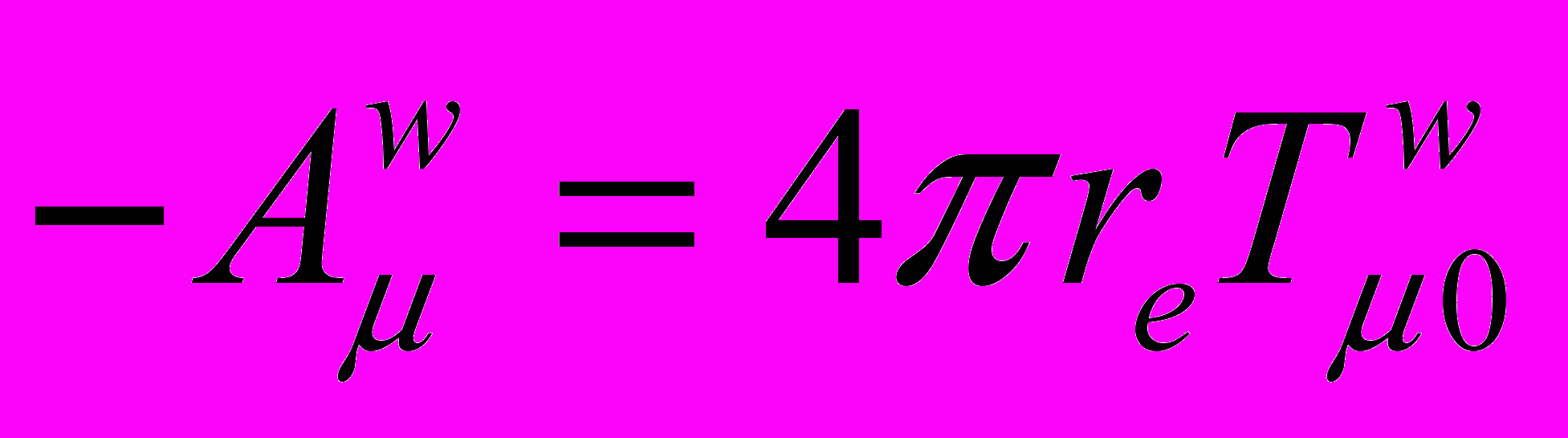 , (13)
, (13)где
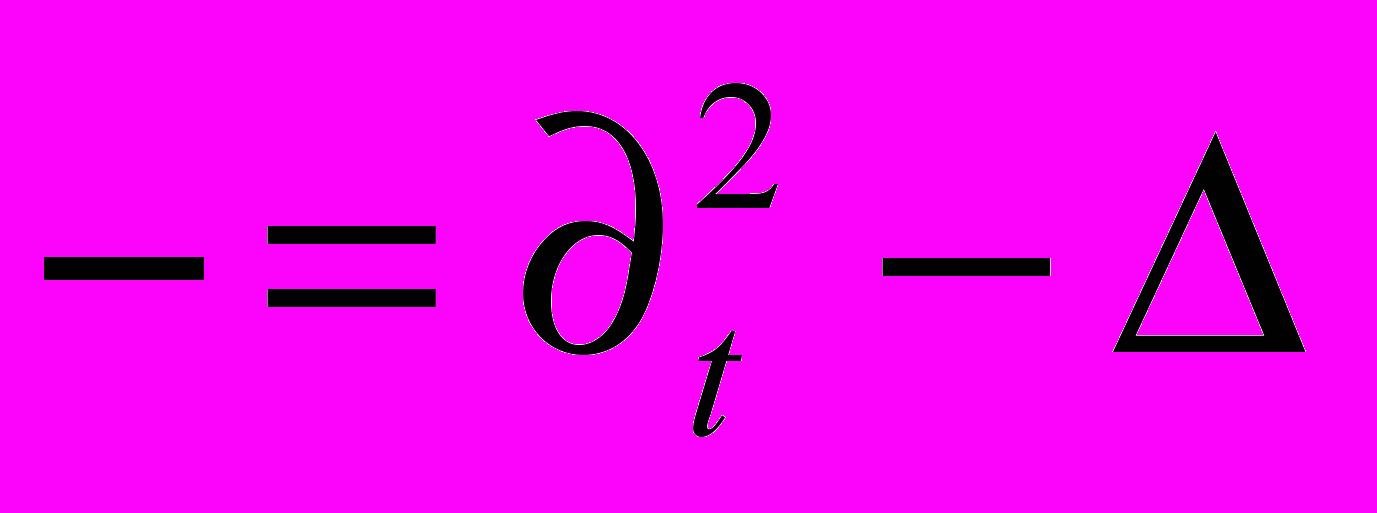 – оператор Даламбера
– оператор Даламбера 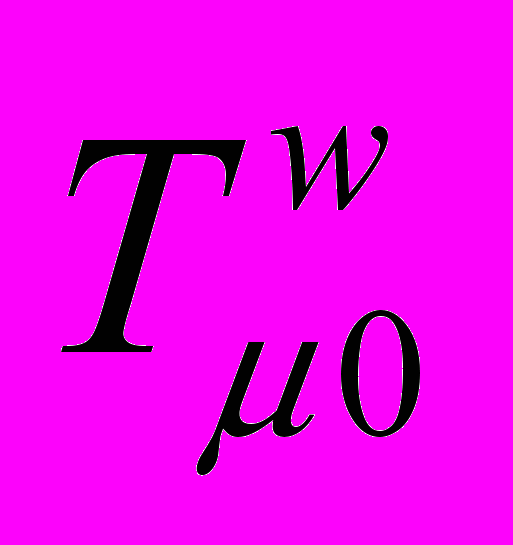 – компонента тензора
– компонента тензора  энергии – импульса источника электромагнитного поля, m,n = 0,1,2,3.
энергии – импульса источника электромагнитного поля, m,n = 0,1,2,3.В модифицированной теории электромагнитного поля, в системе единиц метр, килограмм, секунда, уравнения Максвелла будут выглядеть следующим образом:
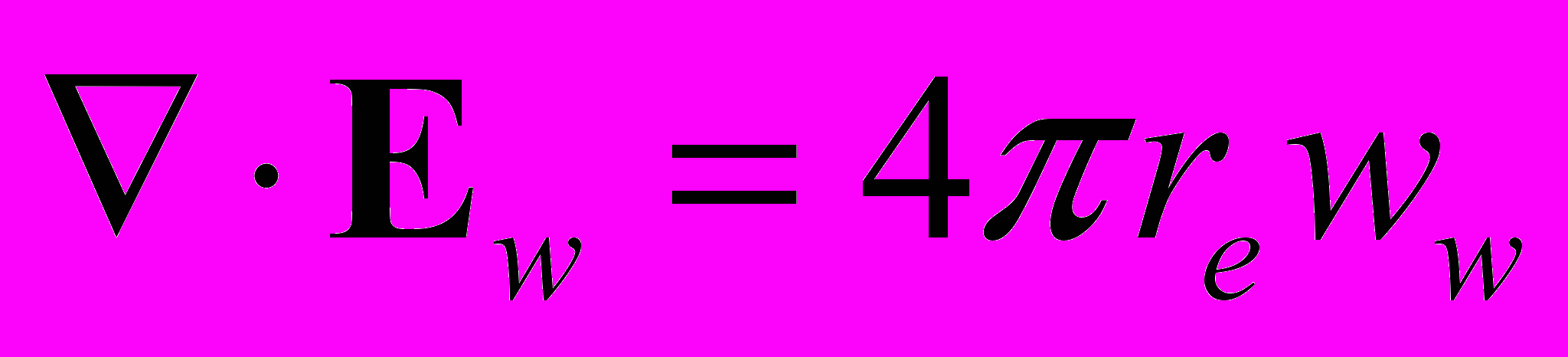 (14)
(14)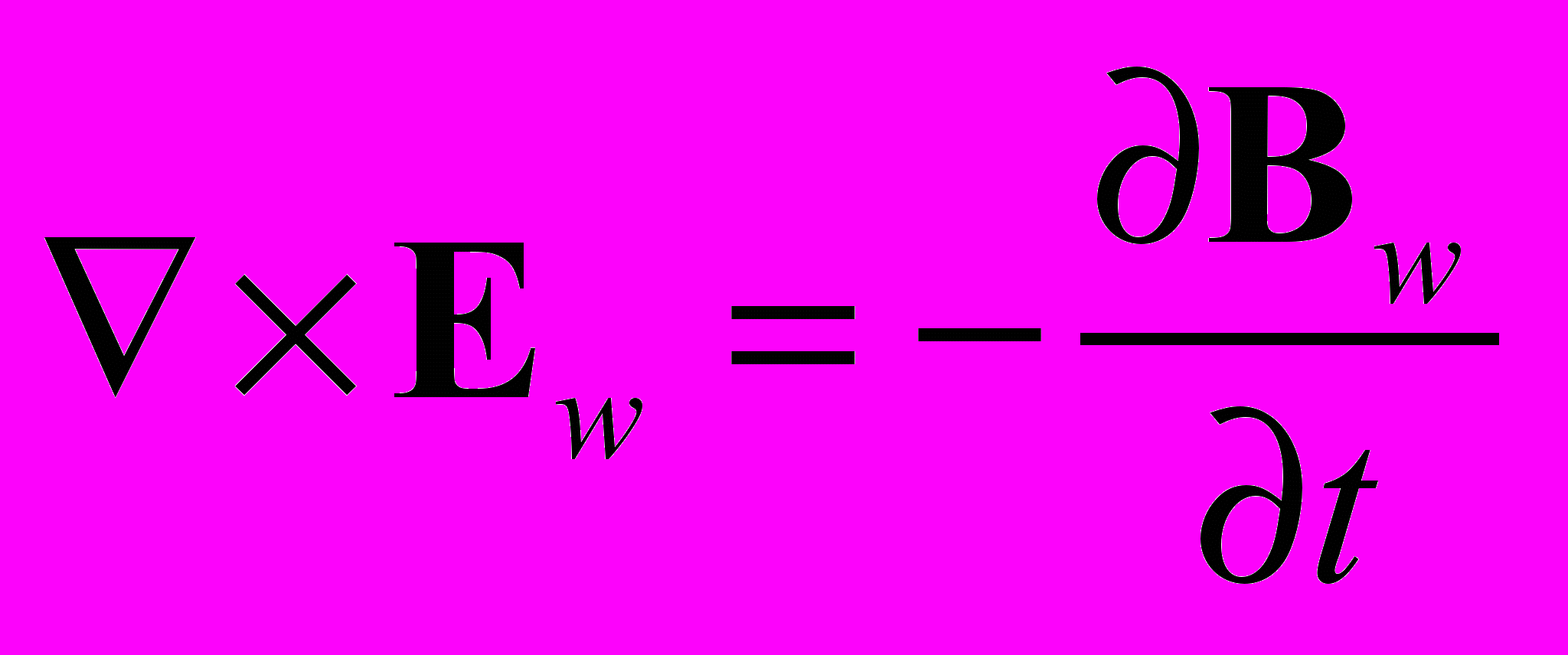 (15)
(15)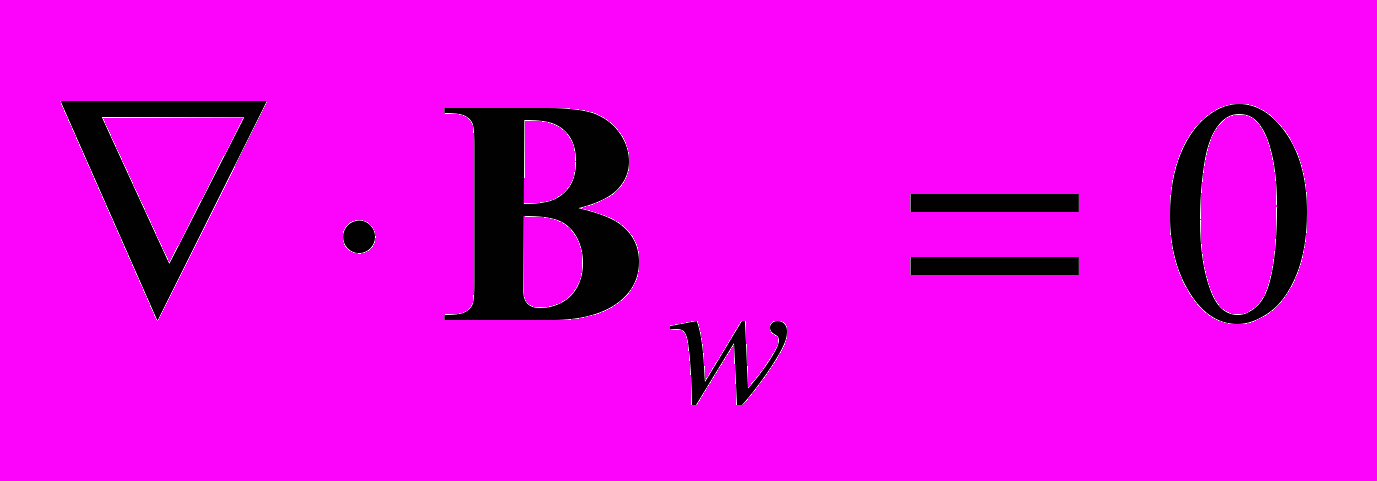 (16)
(16)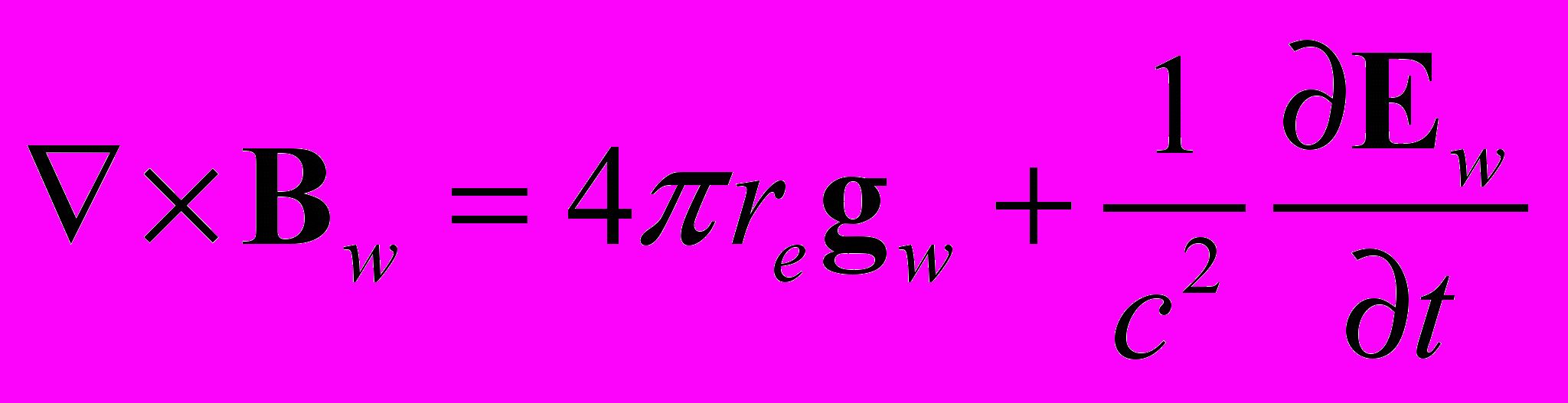 (17)
(17)Уравнения (14 – 17) записаны в инерциальной системе отсчёта, источниками электромагнитного поля являются энергия и импульс зарядов. Необходимо заметить, что эти уравнения получены из обычных уравнений Максвелла путём умножения последних на величину е заряда электрона.
Рассмотрим теперь гравитационное поле тела, массу которого будем измерять в единицах массы электрона: М = Nme. Введём напряжённость силового гравитационного поля как силу, действующую на неподвижный электрон, находящийся в гравитационном поле.
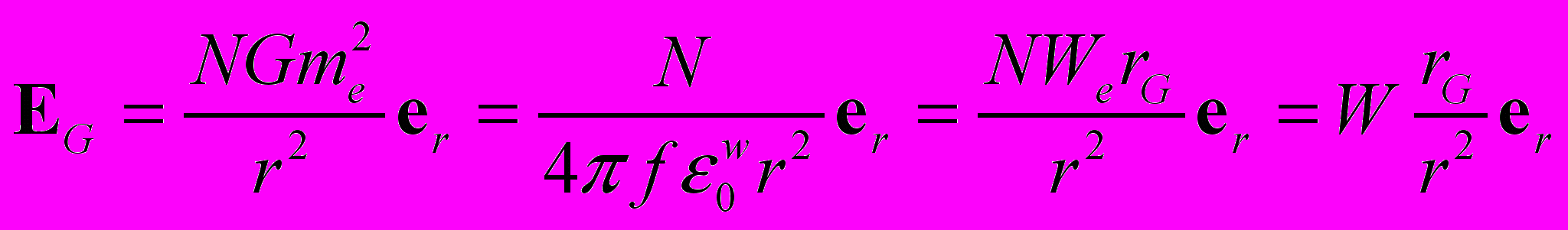 . (18)
. (18)Здесь G – гравитационная постоянная, rG = Gme/c2 – гравитационный радиус электрона, f = re/rG =
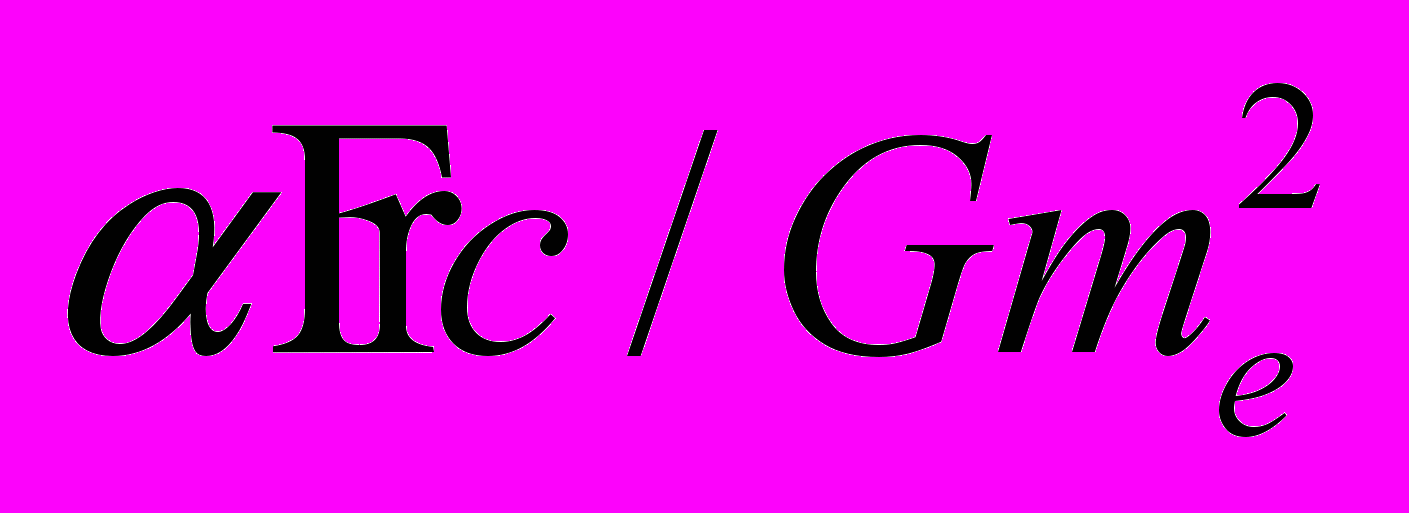 = 4,167.1042 – отношение электромагнитного и гравитационного взаимодействия двух электрон. Из сравнения выражений (1), (3) и (18) видно, что напряжённости силовых электрического и гравитационного полей записаны в одних единицах и отличаются только константой связи (
= 4,167.1042 – отношение электромагнитного и гравитационного взаимодействия двух электрон. Из сравнения выражений (1), (3) и (18) видно, что напряжённости силовых электрического и гравитационного полей записаны в одних единицах и отличаются только константой связи (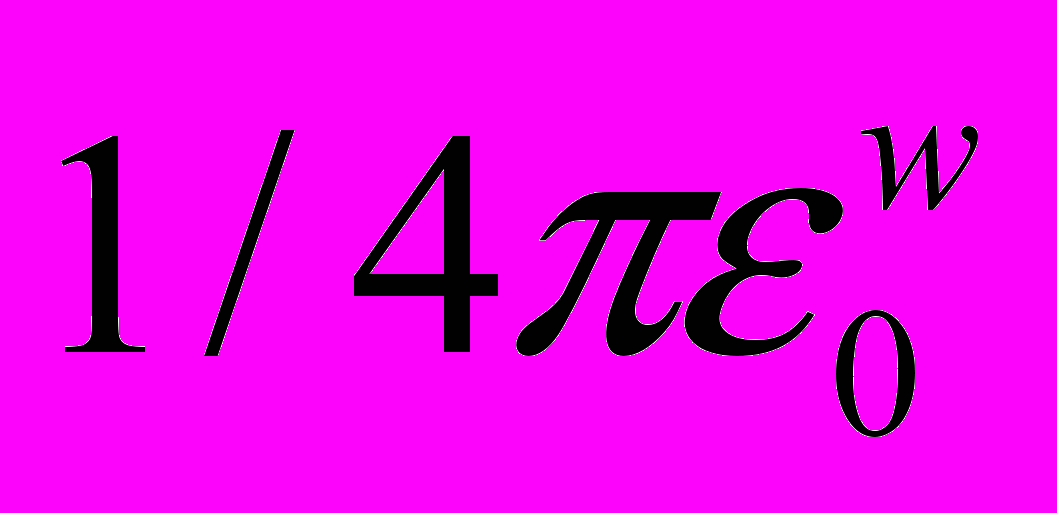 – для электродинамики,
– для электродинамики, 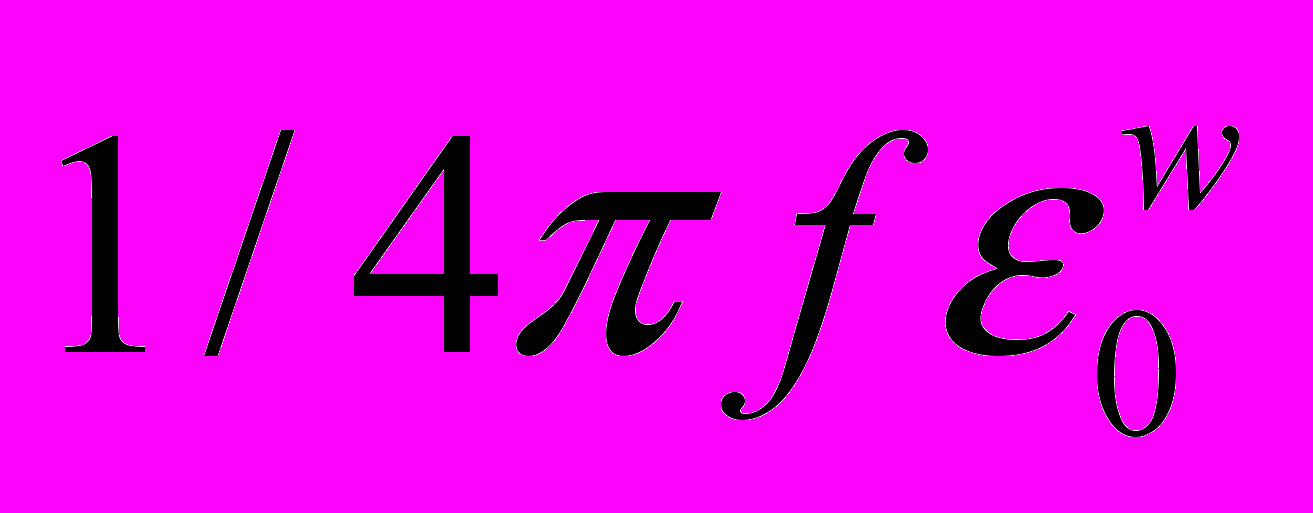 – для гравидинамики). При этом оба числителя инвариантны относительно преобразований Лоренца, а в знаменателе стоит квадрат расстояния. Это означает, что явления аналогичные магнитным обязаны существовать и в гравитационном поле [4]. Источником электрического поля является энергия зарядов, а источником гравитационного поля может быть любая энергия. Потенциальная энергия электрона в гравитационном поле массы М, имеющей энергию W = Mc2
– для гравидинамики). При этом оба числителя инвариантны относительно преобразований Лоренца, а в знаменателе стоит квадрат расстояния. Это означает, что явления аналогичные магнитным обязаны существовать и в гравитационном поле [4]. Источником электрического поля является энергия зарядов, а источником гравитационного поля может быть любая энергия. Потенциальная энергия электрона в гравитационном поле массы М, имеющей энергию W = Mc2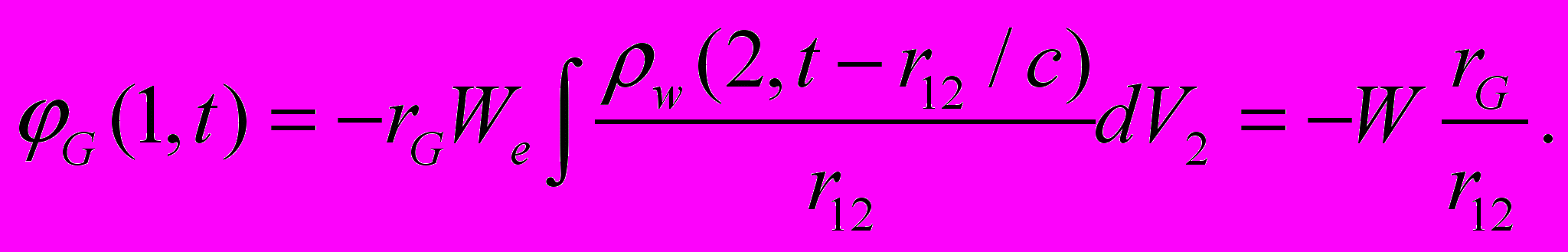 (19)
(19)При движении заряда или массы, вместе с ними движется их силовое поле, которое, как известно, обладает плотностью энергии
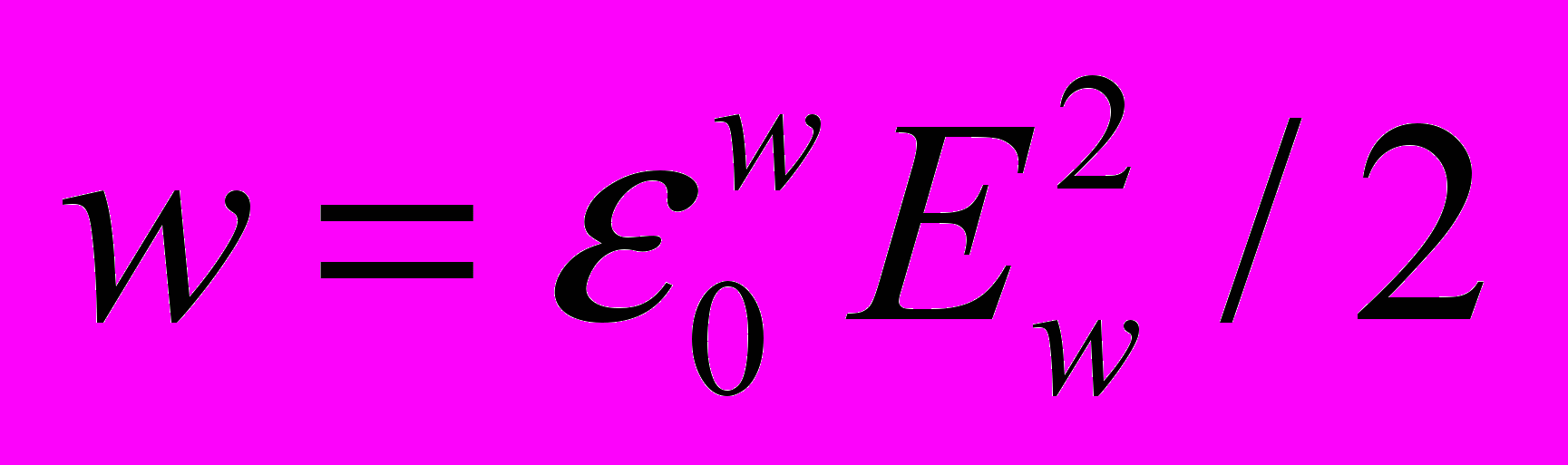 (электрическое поле), или
(электрическое поле), или 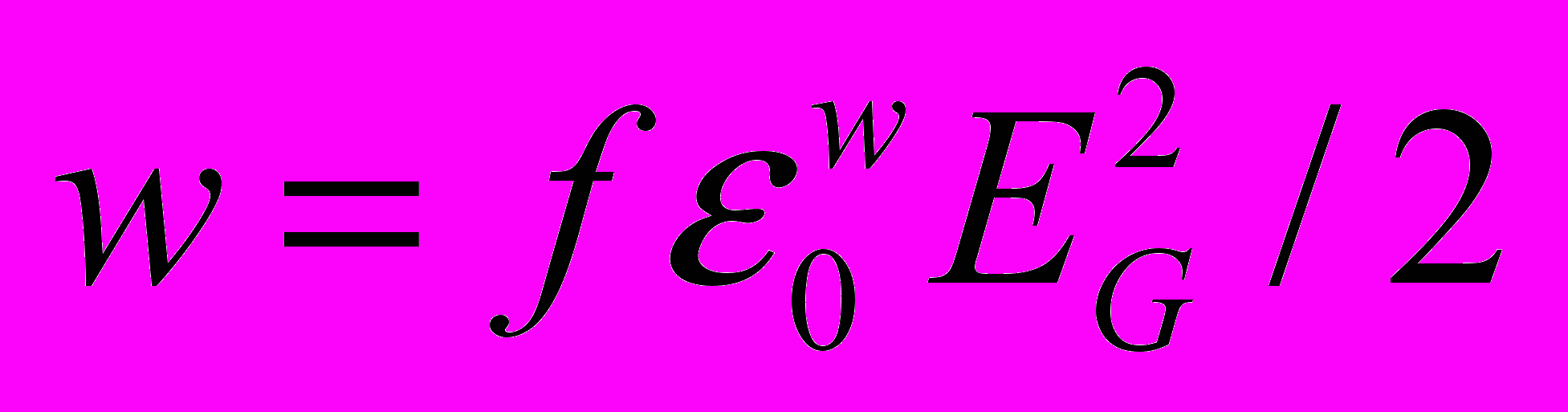 (гравитационное поле). В пространстве, окружающем движущийся заряд или массу, возникает импульс соответственно электромагнитного или гравитационного поля. В гравидинамике импульс поля будет иметь вид аналогичный импульсу поля (7) электродинамики
(гравитационное поле). В пространстве, окружающем движущийся заряд или массу, возникает импульс соответственно электромагнитного или гравитационного поля. В гравидинамике импульс поля будет иметь вид аналогичный импульсу поля (7) электродинамики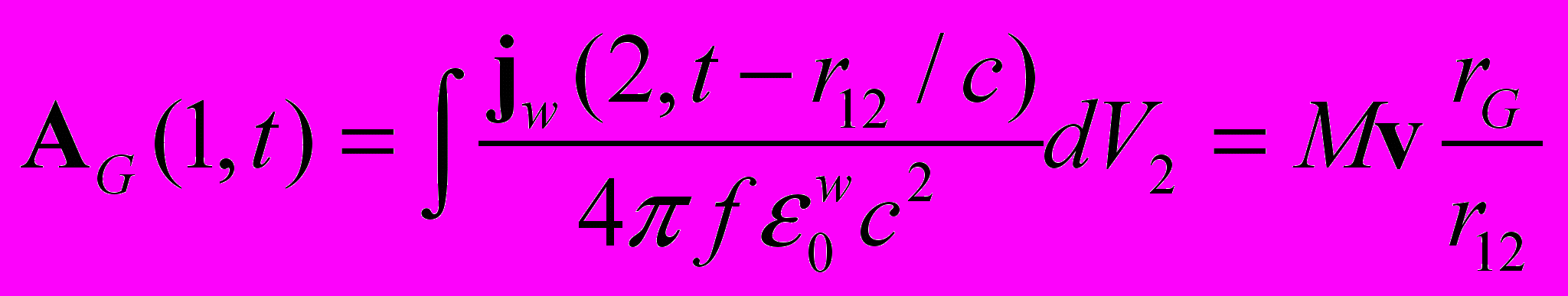 , (20)
, (20)где jw – плотность потока незаряженных частиц, имеющих массу электрона, М – масса движущегося тела (при v << c). Таким образом, мы обнаруживаем полную аналогию в описании электромагнитного и гравитационного полей (по крайней мере для слабых гравитационных полей, когда
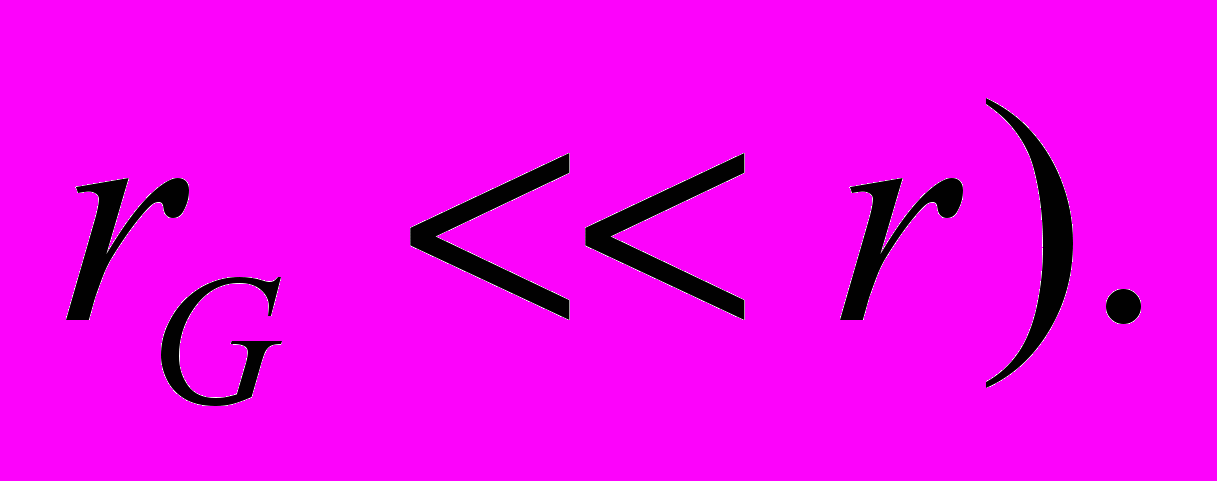 Так же, как и в электродинамике, гравитационное поле может быть описано 4-импульсом
Так же, как и в электродинамике, гравитационное поле может быть описано 4-импульсом  Отсюда, как и в электродинамике, гравитационное и кинетическое поля можно представить частью антисимметричного тензора
Отсюда, как и в электродинамике, гравитационное и кинетическое поля можно представить частью антисимметричного тензора 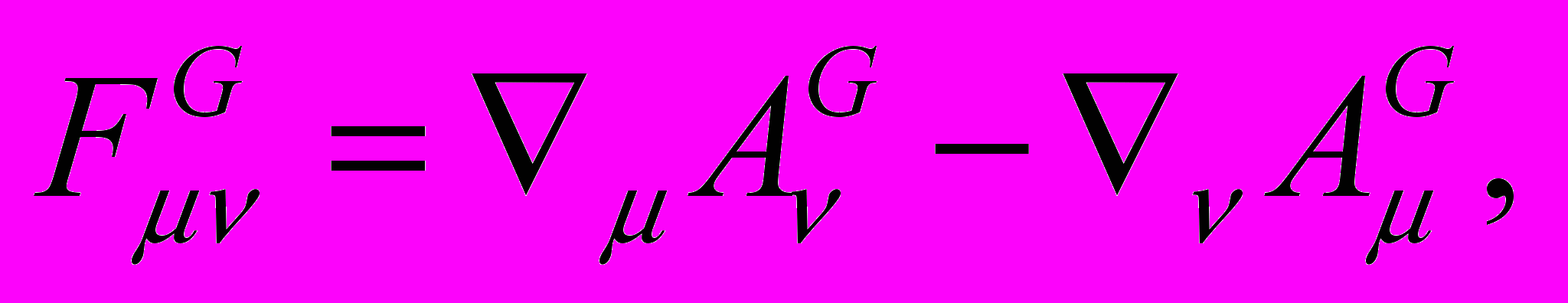 из которого, как и в электродинамике [5], может быть образован тензор
из которого, как и в электродинамике [5], может быть образован тензор 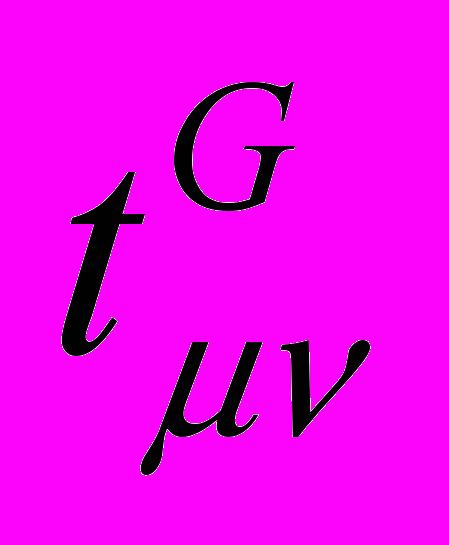 энергии – импульса гравикинетического поля
энергии – импульса гравикинетического поля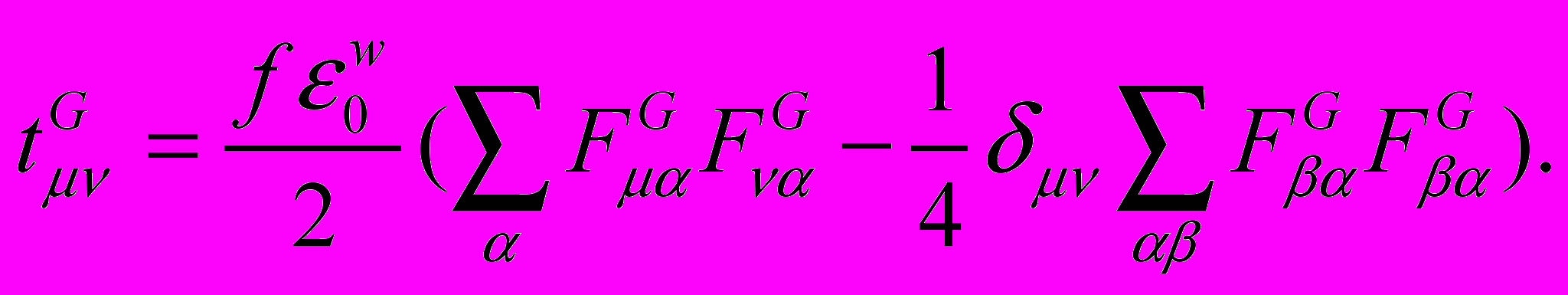 (21)
(21)Уравнение движения нейтральной частицы в гравикинетическом поле будет иметь тот же вид, что и уравнение движения заряженной частицы в электромагнитном поле:
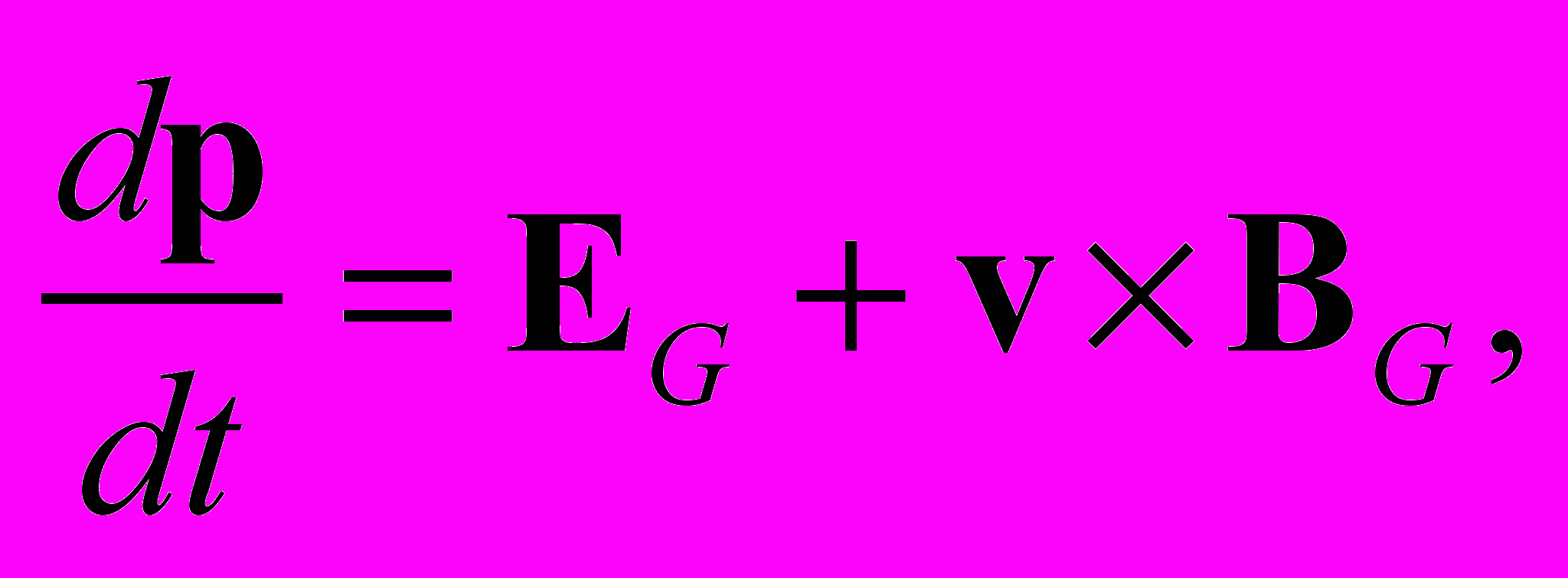 (22)
(22)где
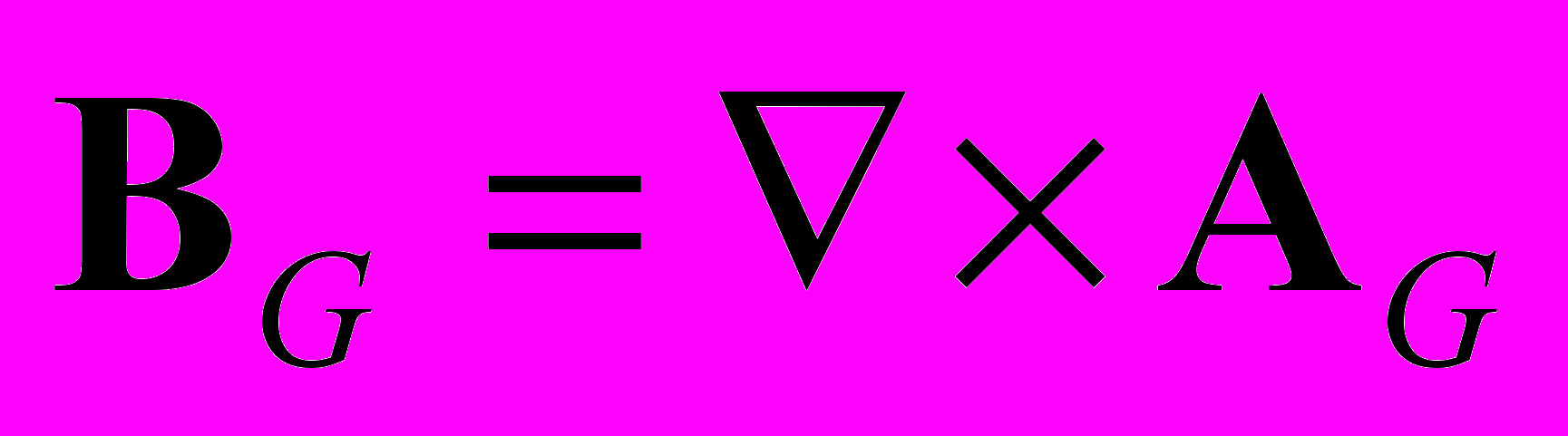 – вектор кинетического поля гравитации,
– вектор кинетического поля гравитации, 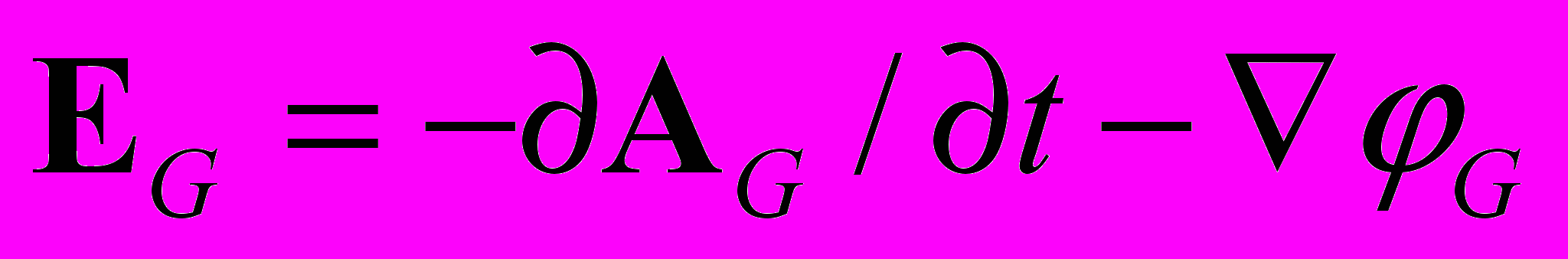 – напряжённость силового гравитационного поля. В последнем выражении заключён принцип эквивалентности: невозможно отличить гравитационное поле гравитирующей массы от индуцированного гравитационного поля, возникающего при изменении импульса. В гравитации, как и в электродинамике, имеется гравитационная сила Лоренца, действующая на нейтральную массу. Уравнения гравидинамики полностью аналогичны уравнениям (14–17) электродинамики и отличаются только константой связи. Такая аналогия позволяет предположить электромагнитную природу гравитации. Уравнение для слабых гравитационных полей в четырёхмерных обозначениях запишем по аналогии с (13)
– напряжённость силового гравитационного поля. В последнем выражении заключён принцип эквивалентности: невозможно отличить гравитационное поле гравитирующей массы от индуцированного гравитационного поля, возникающего при изменении импульса. В гравитации, как и в электродинамике, имеется гравитационная сила Лоренца, действующая на нейтральную массу. Уравнения гравидинамики полностью аналогичны уравнениям (14–17) электродинамики и отличаются только константой связи. Такая аналогия позволяет предположить электромагнитную природу гравитации. Уравнение для слабых гравитационных полей в четырёхмерных обозначениях запишем по аналогии с (13)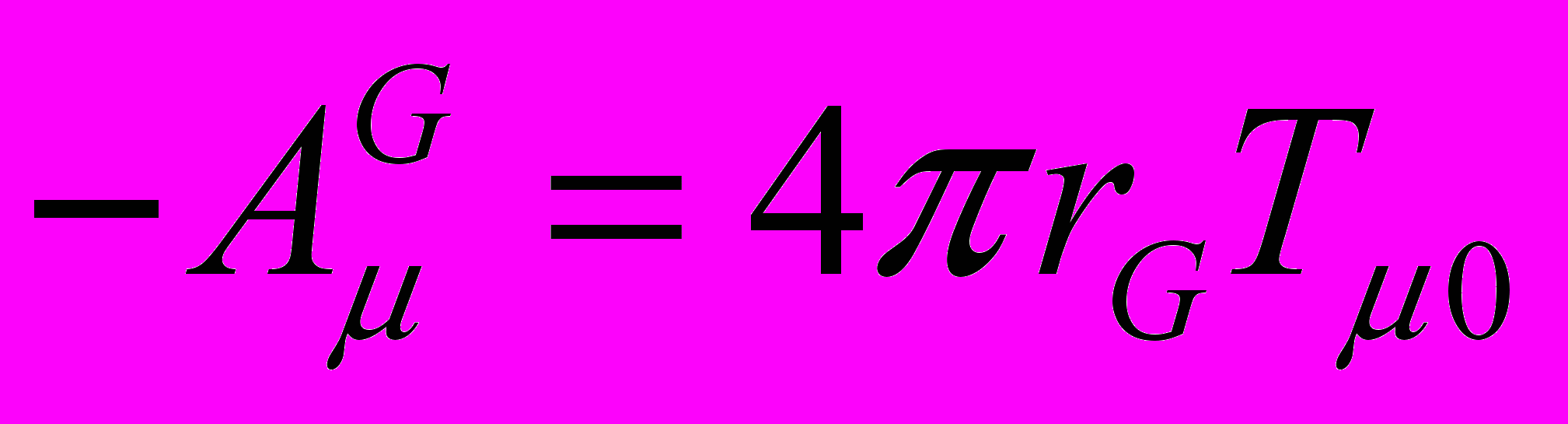 , (23)
, (23)где
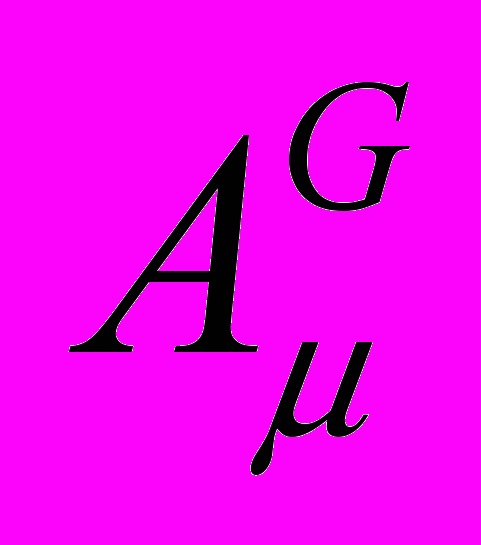 – 4-импульс гравитационного поля,
– 4-импульс гравитационного поля, 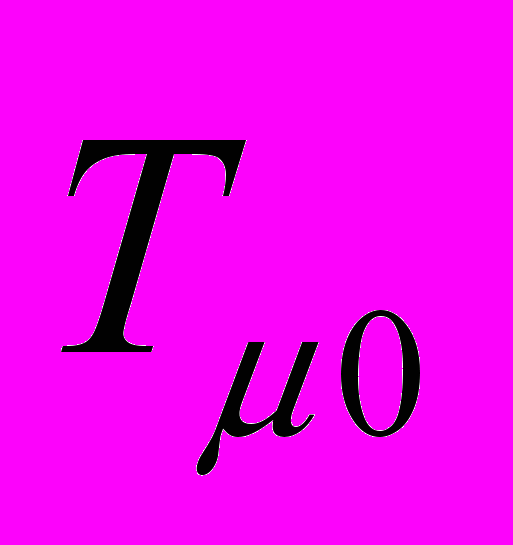 – компонента тензора
– компонента тензора 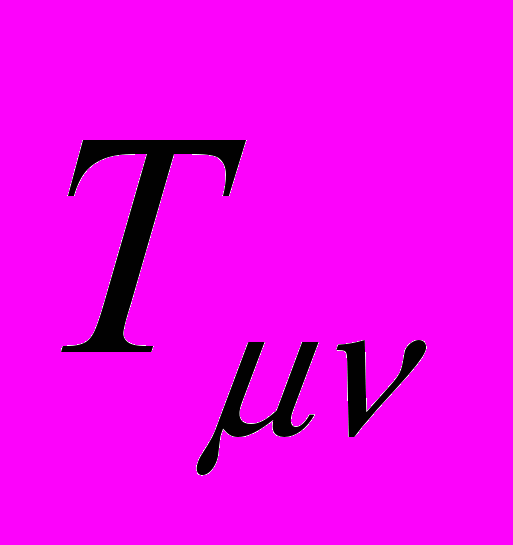 энергии – импульса источника гравитационного поля. Это уравнение предполагает существование гравитационных волн, также как уравнение (13) предполагает существование электромагнитных волн. Теория слабого гравитационного поля (применимая в масштабах Солнечной системы) полностью аналогична теории электромагнитного поля
энергии – импульса источника гравитационного поля. Это уравнение предполагает существование гравитационных волн, также как уравнение (13) предполагает существование электромагнитных волн. Теория слабого гравитационного поля (применимая в масштабах Солнечной системы) полностью аналогична теории электромагнитного поляТаким образом, в Единой теории поля гравитация и электродинамика существуют в неискривлённом пространстве Минковского.
В единой теории поля, следуя аналогии между гравидинамикой и электродинамикой, смещение перигелия Меркурия можно получить, используя запаздывающий потенциал гравитационного поля, аналогичный запаздывающему потенциалу электромагнитного поля. Как известно [6], в электродинамике потенциал движущегося заряда определяется выражением
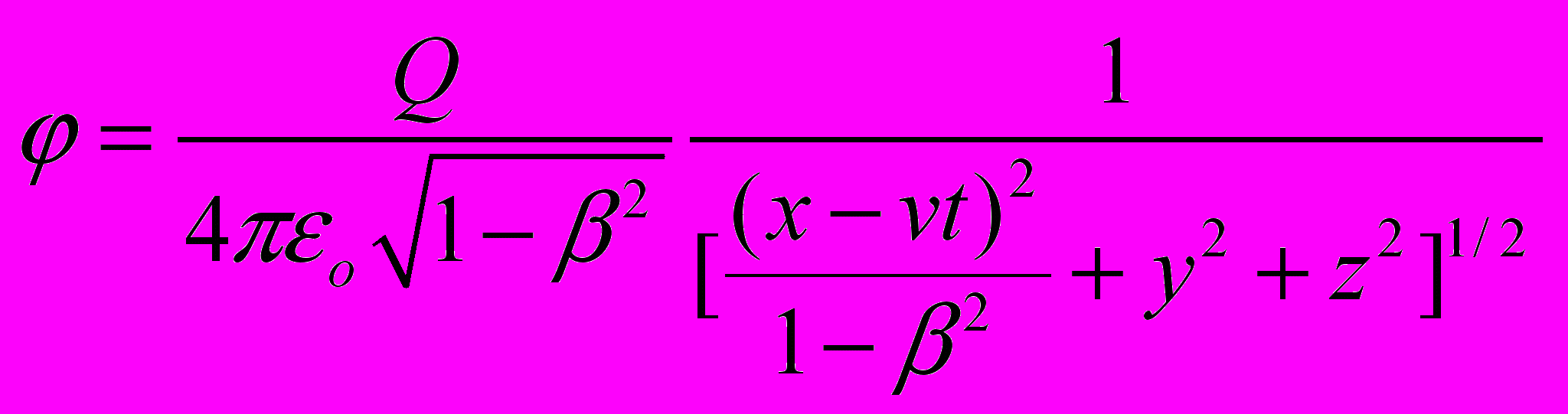 .
. (24)
(24)
где b =
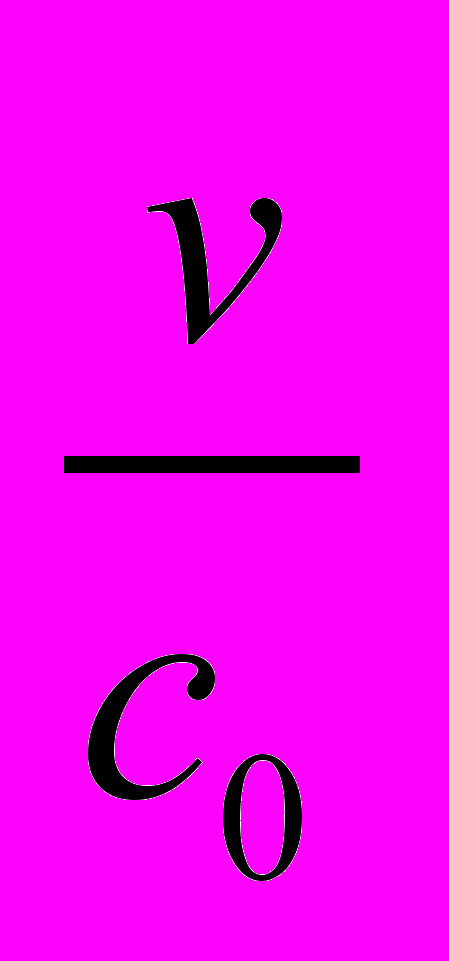 .
.В единой физической теории [2] потенциал примет вид
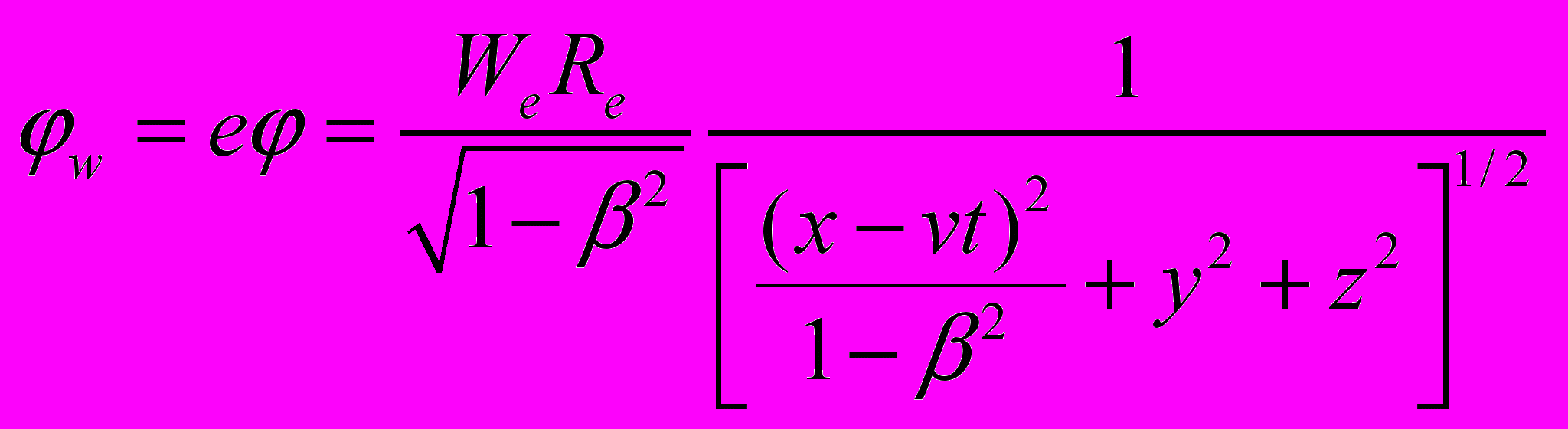 .
. (25)
(25)
Э
(26)
то потенциальная энергия пробной частицы – электрона. По аналогии с (2) гравитационный потенциал движущегося гравитирующего тела можно записать как
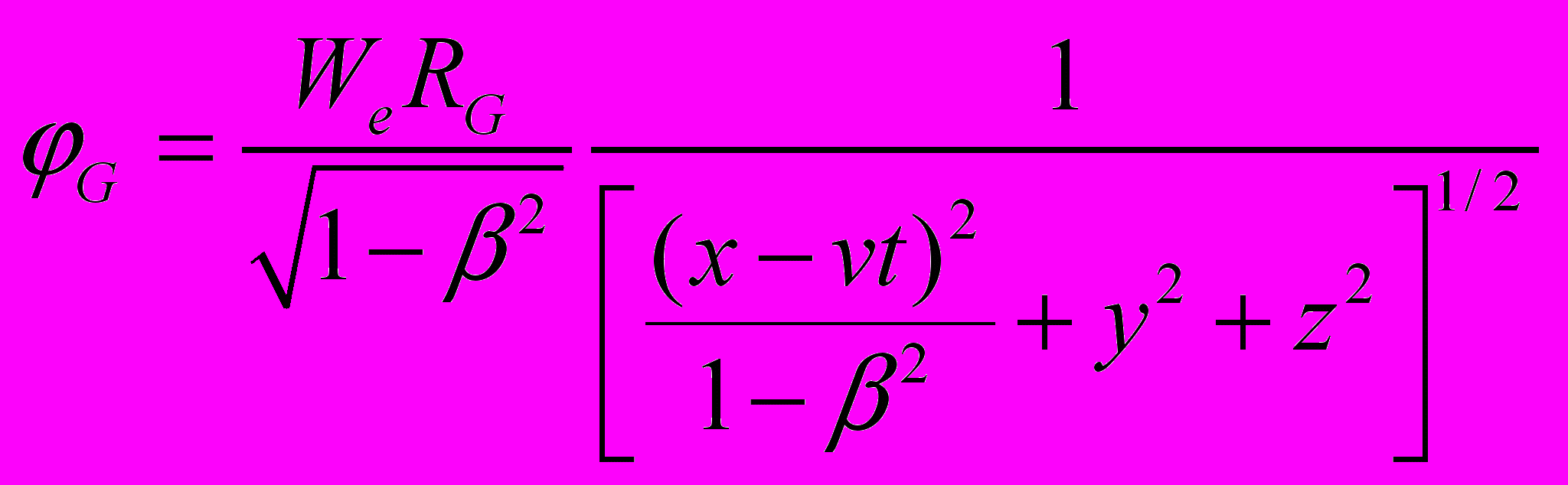 . (26)
. (26)В системе двух гравитирующих тел, когда одно тело обращается вокруг другого (например, Меркурий вокруг Солнца), потенциальная энергия взаимодействия, с учетом (3) может быть представлена как
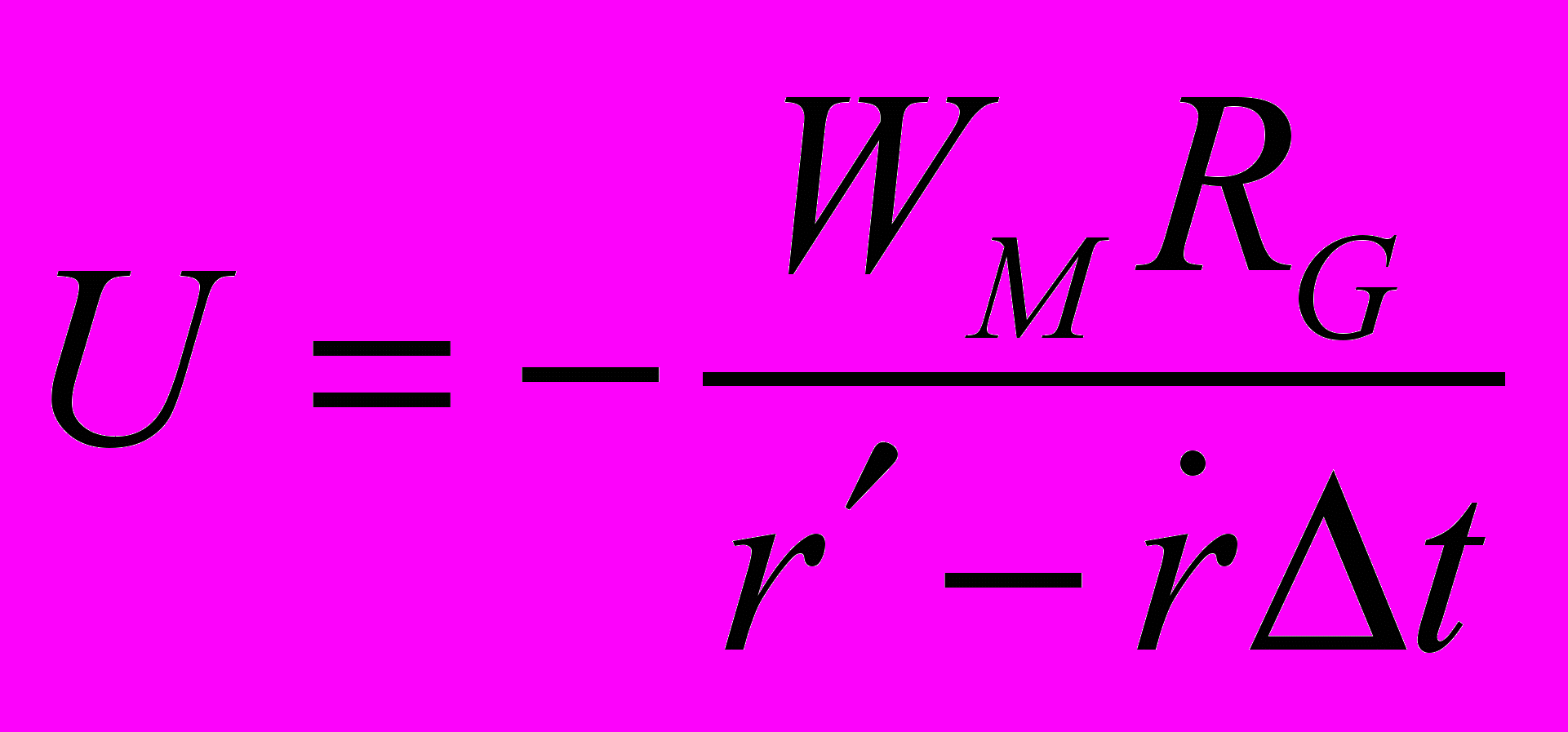 .
. (27)
(27)
Здесь r' – расстояние между телами в запаздывающий момент (рис. .1),
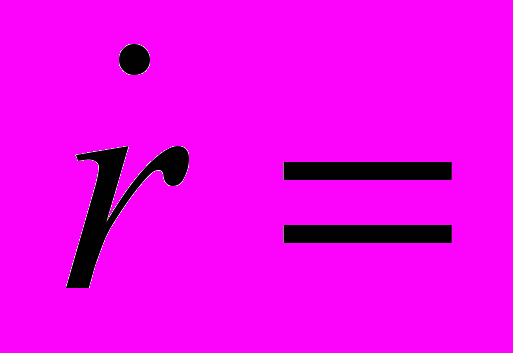 dr / dt – скорость взаимного сближения тел,
dr / dt – скорость взаимного сближения тел,Wм = Mм co2 – полная энергия Меркурия,
RG – гравитационный радиус Солнца,
Dt – время распространения взаимодействия.
Предполагается, что взаимодействие устанавливается после того, как информация о положении движущейся планеты Меркурий доходит до Солнца со скоростью света с, а ответная реакция возвращается от Солнца к планете также со скоростью света. Время Dt распространения взаимодействия из положения планеты в точке А через S в точку В равно
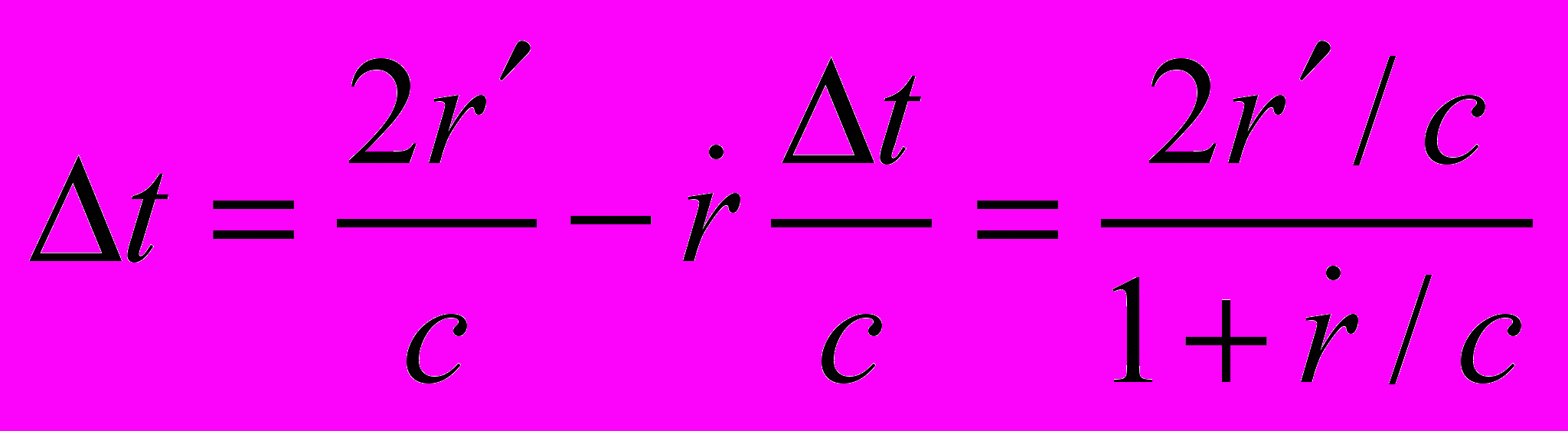 (28)
(28)П
29)
одставляя Dt из (28) в (27), получим
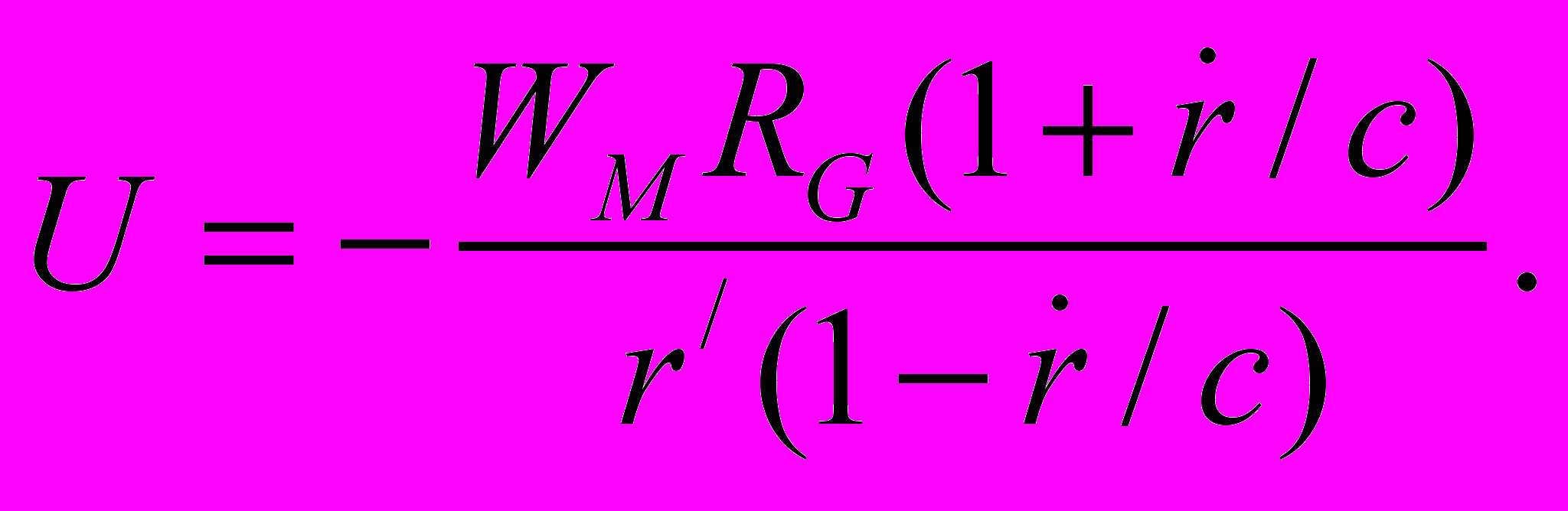
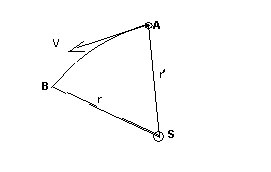
Рис.1
С достаточной степенью точности, учитывая, что
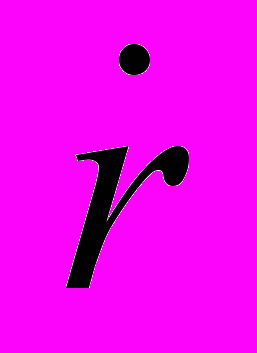 << c, последнее выражение можно записать в виде
<< c, последнее выражение можно записать в видеU = –

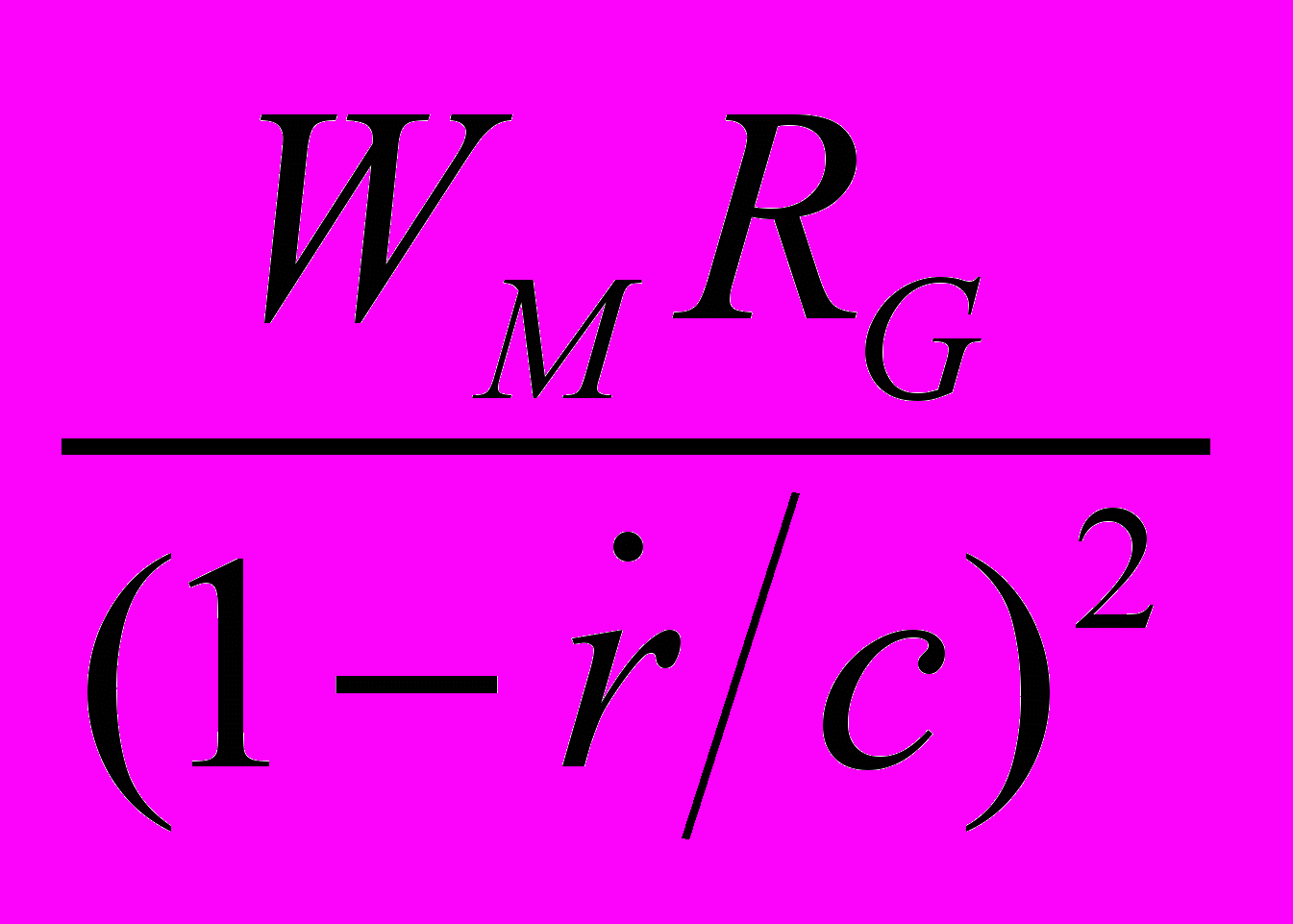 (29)
(29)и
(30)
ли
U = –
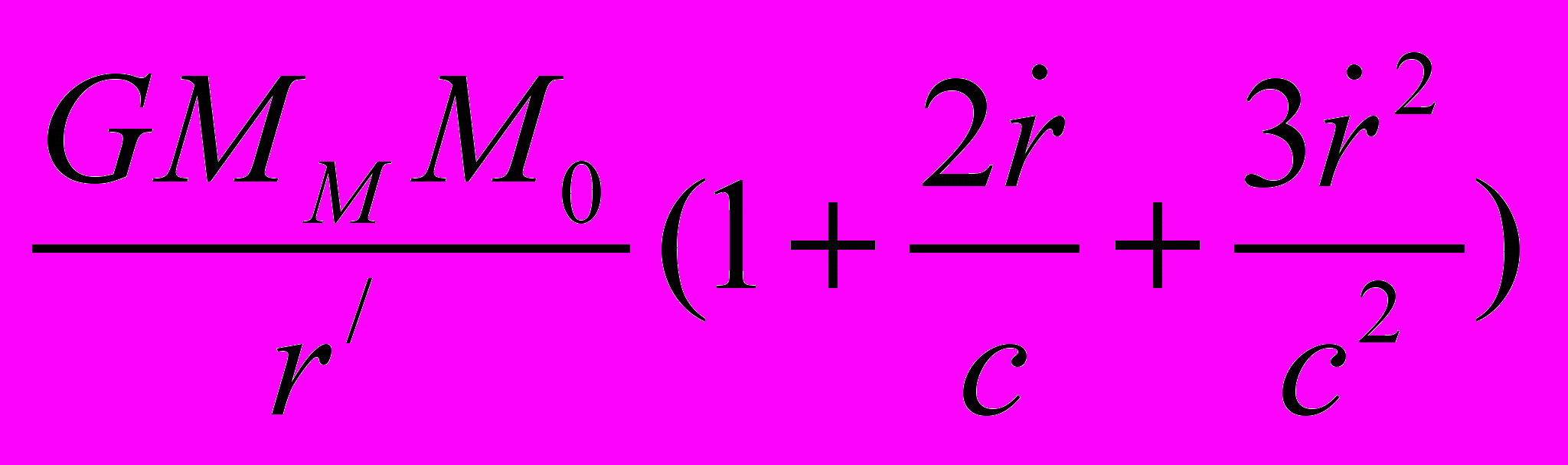 (30)
(30)Полученное выражение совпадает с известным потенциалом Гербера [13], дающего с применением уравнения Лагранжа движение перигелия Меркурия такое же, как и в ОТО.
Потенциал вида (29) был также получен в 1962 году М. А. Сурдиным [14]. Однако Сурдин вывел его, не учитывая аналогию с потенциалом движущегося электрического заряда, для которого уже учтена релятивистская поправка [см. выражения (25), (26)], и не посмел записать свой потенциал в виде (30), т.к. не знал, куда девать дополнительное смещение перигелия, получающееся за счет релятивистского эффекта изменения массы. В результате он представил свой потенциал в виде
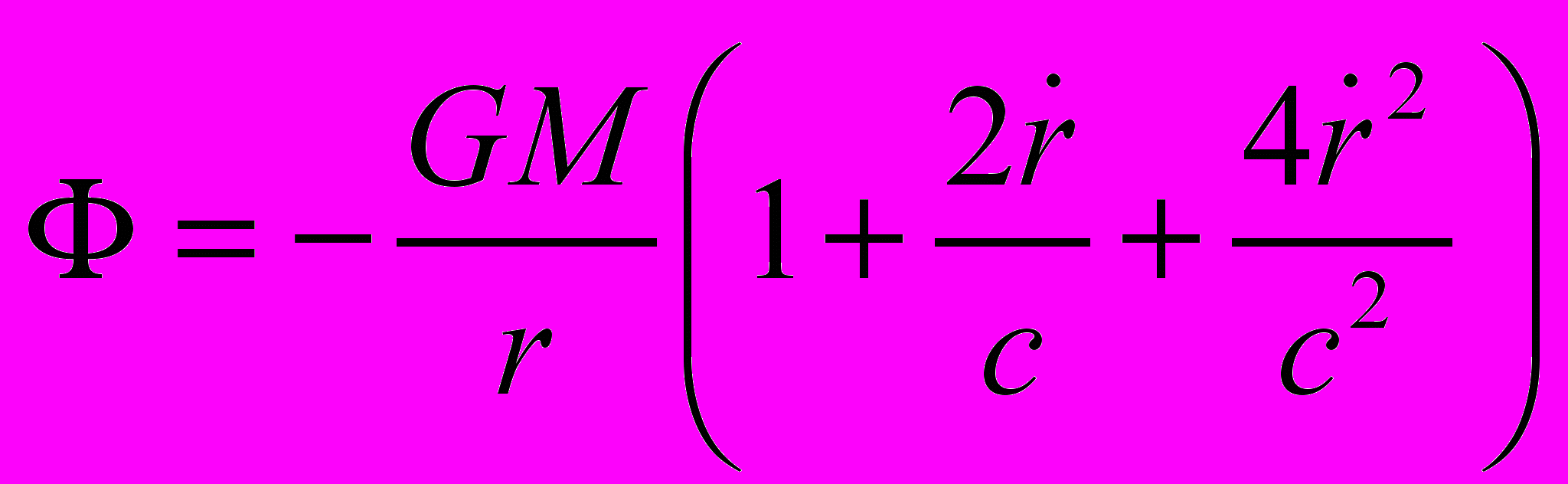
и получил смещение перигелия Меркурия меньшее, чем дает потенциал (30) и ОТО.
Здесь необходимо заметить, что если бы скорость распространения гравитационного взаимодействия отличалась от скорости света, применение потенциала (30), давало бы неверное движение перигелия.
ЛИТЕРАТУРА
1. O. Heaviside, Electromagnetic Theory, New York, (1893).
2. J. Carstoiu, Compt. Rend.,268,201 (1969).
3. М.Боулер, Гравитация и относительность, Мир, Москва, (1972).
4. Э. Парселл. Электричество и магнетизм. Берклеевский курс физики. Наука, Москва,(1983), с.173.
5. В.Паули, Теория относительности, Наука, Москва, (1983), с.118.
6. Р. Фейнман, Р.Лейтон, М.Сэндс, Фейнмановские лекции по физике, Мир, Москва, (1977), т.6.
7. А.П. Абрамов, Новые аналогии между уравнениями электродинамики и механики в сб. “Электрические машины и электромашинные системы”, ППИ, Пермь, (1990), с. 137-149.
8. А.П. Абрамов, Законов природы не отражает. “Наука Урала”, (1991), № 49.
9. А.П. Абрамов, Две ошибки Эйнштейна. “Наука Урала”, (1992), № 6.
10. А.П. Абрамов, К объединению электромагнитного и гравитационного взаимодействий, в сб. Проблемы современных материалов и технологий. Вестник ПГТУ. Пермь, (1997), с. 182-193.
11. А.П. Абрамов, Описание гравитации по аналогии с электродинамикой. Труды Конгресса 2000 “Фундаментальные проблемы естествознания и техники”, Санкт-Петербург, (2000),т.1, с 7 – 14.
12. А.П. Абрамов, Гравитация и электродинамика. Труды Конгресса – 2004 “Фундаментальные проблемы естествознания и техники”, Санкт-Петербург, (2004), ч.1, с 6 –12.
13. Роузвер Н.Т. Перигелий Меркурия от Леверье до Эйнштейна. Пер. с англ., М.: Мир, 1985.
14. Surdin M. A note on time-varying gravitational potentials. Proc. Camb. phil. Soc., 58, 550-553.
