Урок как способ пробуждения интереса ученика к математике
| Вид материала | Урок |
- Осипова Надежда Петровна. Тверь 2010. пояснительная записка, 156.53kb.
- Развитие интереса к математике, 42.37kb.
- Тема «Игровая технология как средство развития познавательного интереса к математике», 253.3kb.
- Элективный курс по выбору Чтение и творчество, 132.88kb.
- Аннотированный список ресурсов Интернет по теме: «Развитие познавательного интереса, 60.1kb.
- Математический вечер, посвященный Дню Победы, 80.36kb.
- Программа золотое сечение (элективный курс по математике для учащихся 9 класса) Автор, 53.42kb.
- Исторический материал как средство развития у младших школьников познавательного интереса, 64.65kb.
- Интегрированный урок как средство формирования мотивов учения школьников в процессе, 79.87kb.
- Урок- сказка «Теремок» по математике, 74.01kb.
Нестандартный урок как способ
пробуждения интереса ученика к математике.
Автор: Домникова Наталья Владимировна,
учитель математики школы №37.
«Надо прогнать с уроков бога сна Морфея
и чаще приглашать бога смеха Момуса».
Ш.А.Амонашвили.
Урок, оставаясь основной формой учебного процесса в школе, в новых условиях стал «тесен» для некоторых видов практической деятельности учащихся. В своей работе с некоторых пор я стала испытывать потребность в создании оптимальных условий обучающимся для реализации их учебного потенциала, стремления помогать друг другу, возникла необходимость избегать перегрузок учащихся.
Работаю я в общеобразовательных классах, состав которых очень неоднороден: есть очень способные ученики, которые «все схватывают на лету», ученики – «почемучки», ученики, «плывущие по течению», есть очень сложные ученики. И очень мало таких ребят, которым математика нравится изначально.
Одной из форм повышения интереса к предмету и развития способностей учащихся является проведение нестандартных уроков, которая помогает систематически воспитывать интерес учащихся к математике. Нестандартный урок – это импровизированное учебное занятие, имеющее нетрадиционные: подготовку и проведение урока; структуру урока; взаимоотношение и распределение ролей, обязанности между учителем и учениками; подбор и критерии оценки учебных материалов; методику оценки деятельности учащихся.
При планировании нестандартных уроков я ставлю следующие целевые ориентации:
- Дидактические
Расширение кругозора,
Познавательная деятельность,
Применение ЗУН в практической деятельности,
Развитие общеучебных умений и навыков.
- Воспитывающие
Формирование определенных подходов, позиций и мировоззренческих установок.
- Развивающие
Развитие внимания, воображения, фантазии, рефлексии, умения сравнивать,
сопоставлять; развитие мотивации учебной деятельности.
В 5–м классе уже на первых уроках я стараюсь показать не только красоту математики, но и ее занимательность. У пятиклассников интерес легко возникает, но и легко угасает. Учитывая это, я провожу разнообразные уроки: урок – путешествие по теме «Действия с десятичными дробями», урок – сказка по теме «Обыкновенные дроби», урок – практическая работа по теме «Прямоугольный параллелепипед», бинарный урок математика – история «Действия с натуральными числами» и другие.
Для шестиклассников важен не только сам факт игры, но и содержание урока, поэтому в системе нестандартных уроков большее внимание уделяется следующим формам: урок – экскурсия по истории космонавтики «Рациональные числа», урок с компьютером «Координаты на плоскости», интегрированный урок математика и экология «Длина окружности и площадь круга», «Защита органов дыхания» и др.
Для семиклассников характерно критическое отношение к преподаванию, стремление преодолеть трудности. Первый урок алгебры в 7 классе я провожу в игровой форме с повторением материала 6–го класса. После такого итогового повторения можно смело переходить к новым темам. Наряду с игровыми формами нестандартных уроков я провожу уроки тестирования, уроки – зачеты в группах, уроки – исследования.
У восьмиклассников появляется стремление к успеху. Детям этого возраста свойственны многосторонние интересы, частая их смена, желание попробовать свои возможности в разных областях знаний. В 8 классе чаще провожу уроки – практикумы по различным темам, проблемные беседы, например, по теме «Теорема Пифагора». Не забываю и об игровых формах урока: урок – игра «Морской бой» по теме «Преобразование выражений, содержащих арифметические корни» и др.
При подготовке к урокам в 5 – 8 классах я часто использую дополнительные исторические сведения, прелагаю различные числовые ребусы, решив которые можно получить дополнительные оценки.
К нестандартным урокам в старших класса я подхожу более осторожно. Считаю возможным включать уроки – лекции, уроки – практикумы, уроки – зачеты, уроки – семинары, уроки – конференции. Иногда возникает необходимость провести нестандартный урок, близкий по форме к уроку – игре. Такой урок я и хочу представить на суд зрителей.
Урок алгебры и начал анализа в 11 классе.
Тема: «Первообразная и интеграл».
Цель:
- Образовательная: повторить и закрепить материал по темам «Площадь криволинейной трапеции», «Интеграл», выявить пробелы и постараться ликвидировать их.
- Воспитательная: активизация познавательного интереса, развитие внимания, содействие формированию понимания и оценки прекрасного, расширение кругозора учащихся.
- Развивающая: развитие памяти, преодоление трудностей, повышение интереса к математике.
Форма урока: урок – игра «Рыцарский турнир»
Оборудование: Плакат с анаграммой, кодоскоп, чистая кодопленка, кодопленка с готовым кроссвордом, карточки с интегралами, плакат с интегралами, плакат с ответами, отличительные знаки «рыцарь красной розы».
Ход урока.
Слышны звуки скрипки. В средние века жили на земле благородные рыцари. Все мальчики мечтали стать рыцарями. Но сначала они становились пажами, т.е. слугами рыцарей, в возрасте 8 лет. В обязанности пажа входило носить воду для умывания, поддерживать порядок в замке, помогать на кухне, прислуживать за столом. Одновременно мальчик учился фехтовать, стрелять из лука, ездить верхом. В 14 лет пажей «повышали в должности» и они становились оруженосцами: чистили оружие и рыцарские доспехи, учились владеть копьем и щитом. В возрасте 21 года их ожидало посвящение в рыцари. Поэты рыцарских времен воспевали семь добродетелей, семь искусств, которыми должен владеть каждый рыцарь. Рыцарь должен был уметь: фехтовать, ездить верхом, владеть копьем, плавать, играть в шашки, охотиться, сочинять и петь стихи. Сегодня мы проведем своеобразное посвящение в рыцари на нашем уроке. Вы будете защищать, отстаивать эти умения.
В качестве разминки разрешите вам предложить анаграмму. Здесь зашифровано имя рыцаря, славного и храброго. Он сражался и побеждал на страницах романа знаменитого английского писателя.
 Задание записано на большом плакате, на доске. (Ответ: Айвенго).
Задание записано на большом плакате, на доске. (Ответ: Айвенго).Только что вы доказали, что владеете искусством слова. Теперь вам необходимо доказать, что вы умеете фехтовать. Каждый верный ответ на вопрос будет засчитан как точный укол шпагой (ученики отвечают по очереди, работа устная).
1.Дать определение интеграла.
2. Найти первообразную для функции f(х)=х2.
3.Верно ли равенство
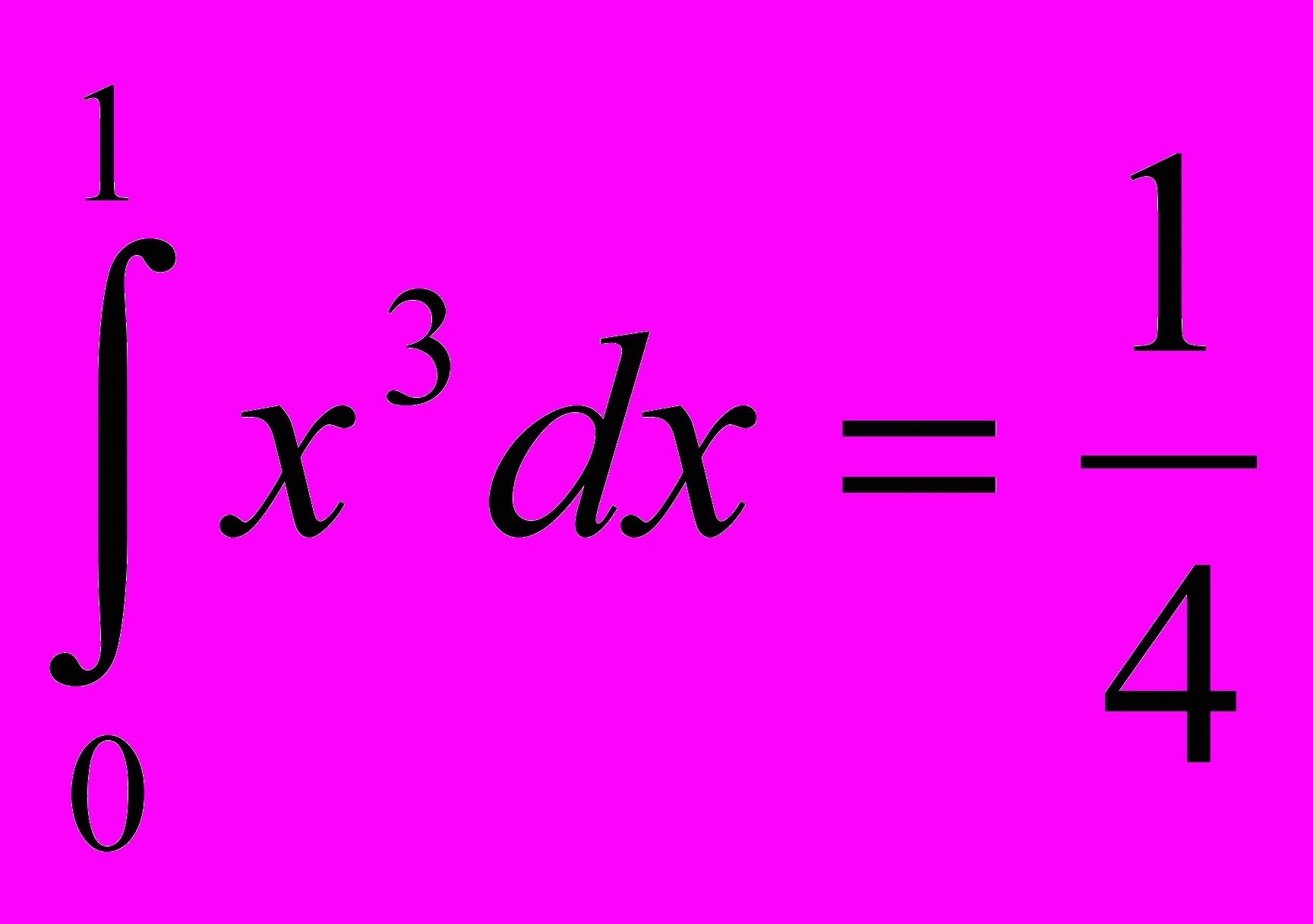 ?
?4. Что называется первообразной F(х) для функции f(х) на х
 I?
I?5. Найти первообразную для функции f(х)=sinx.
6. Верно ли равенство
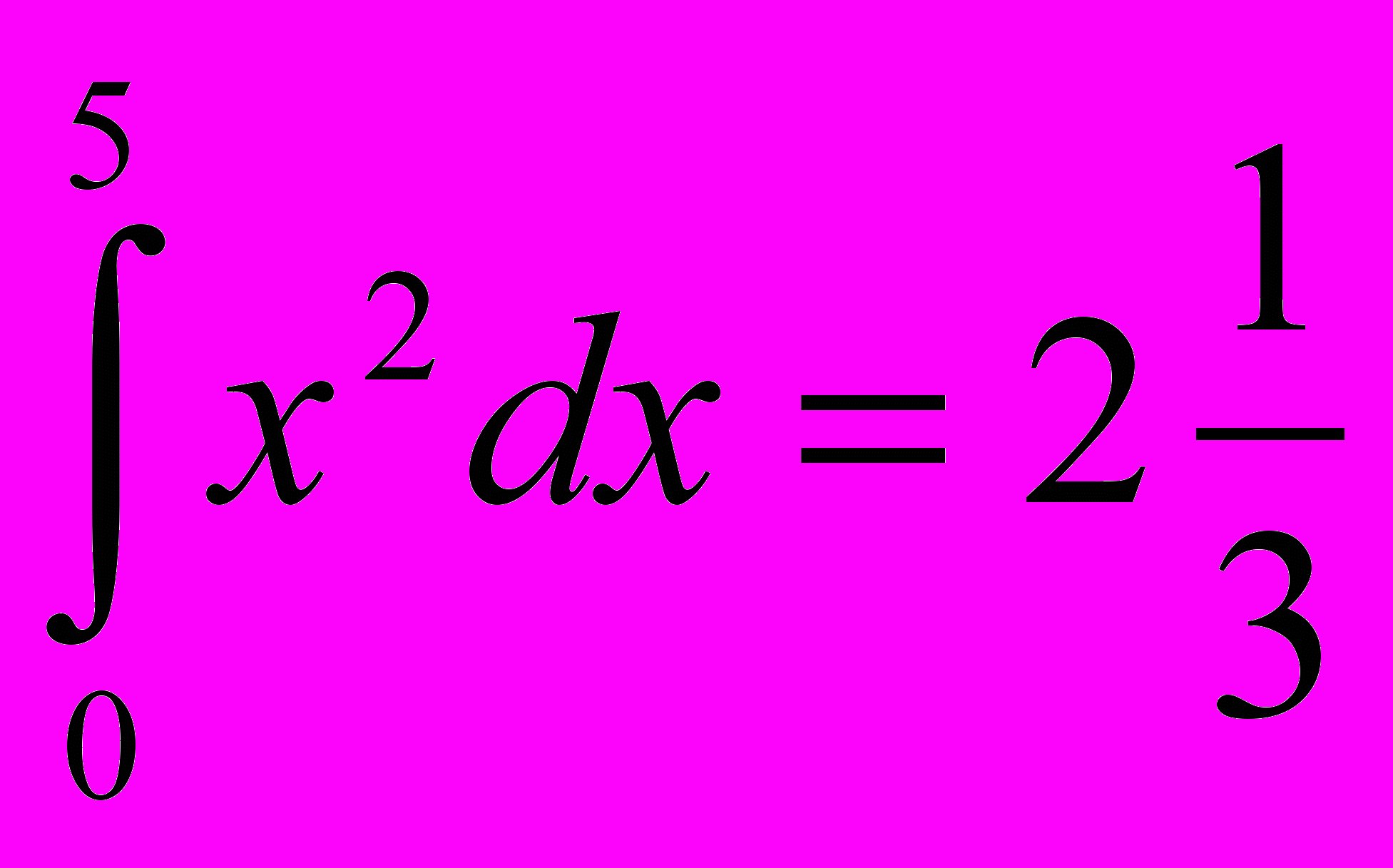 ?
?7. В чем заключается основное свойство первообразной?
8. Найти первообразную для функции f(х)=х4.
9. Верно ли равенство
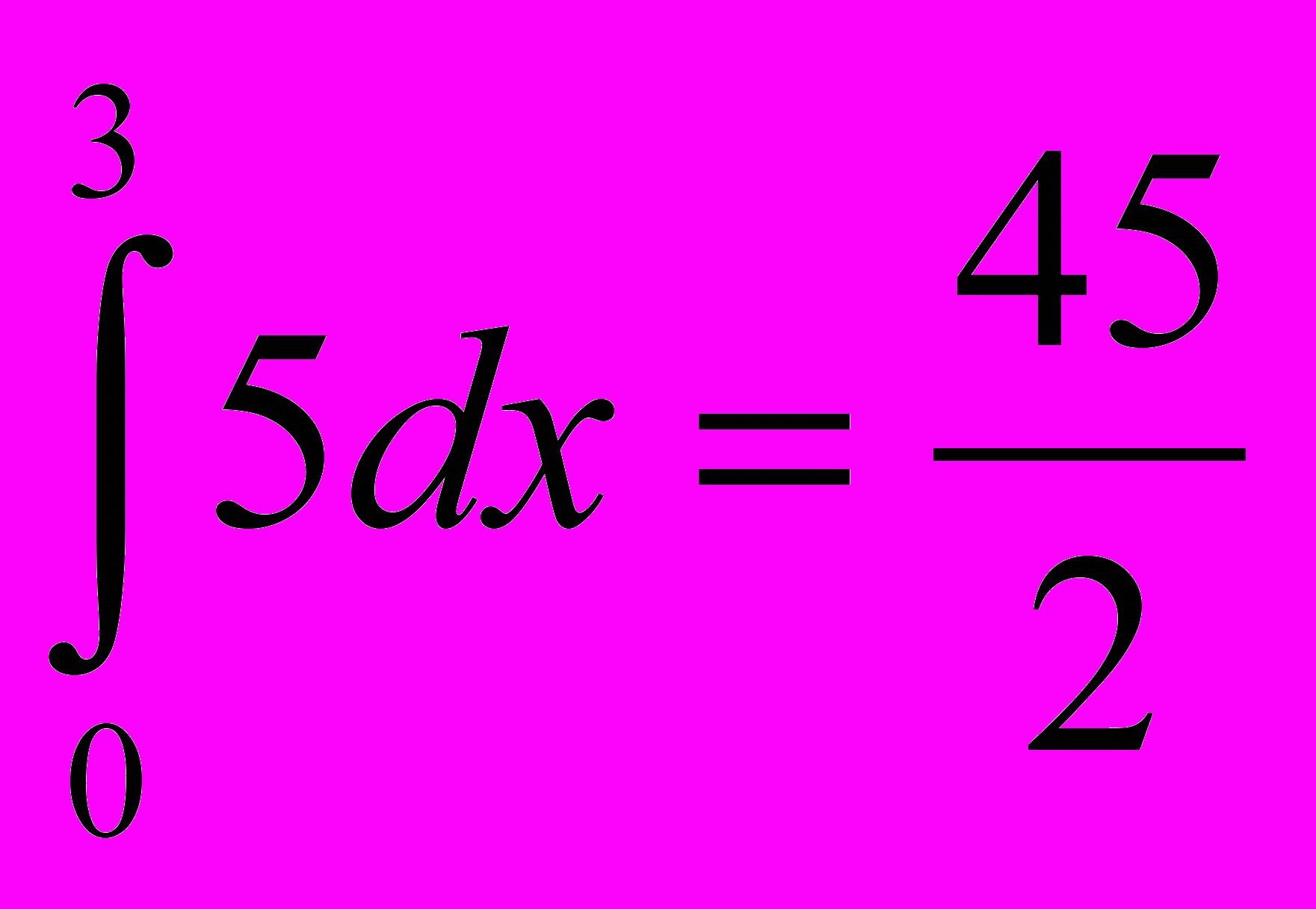 ?
?10. Что называется криволинейной трапецией?
11. Найти первообразную для функции f(х)=10х.
12. Верно ли равенство
 ?
?Каждый рыцарь должен был уметь ездить верхом. Для этого необходимо оседлать коня, т.е. вам нужно изобразить фигуру, ограниченную линиями (участники получают карточки с заданиями).
Карточка 1. Построить фигуру, ограниченную линиями у=(х+1)2, у=0, у=1 – х.
Карточка 2. Построить фигуру, ограниченную линиями у=4х - х2, у=0, у=4 – х.
Карточка 3. Построить фигуру, ограниченную линиями у=4 - х2, у=0, у=4 – х.
Учащиеся выполняют задания на кодопленке, проверка через кодоскоп.
Следующее испытание – метание копья. Участнику турнира нужно было точно попасть в цель. Докажите, что вы тоже можете это сделать (учащиеся получают карточки с заданиями, выполняют письменно на местах, проверка фронтально).
Карточка 1. Вычислить х1, если х1=
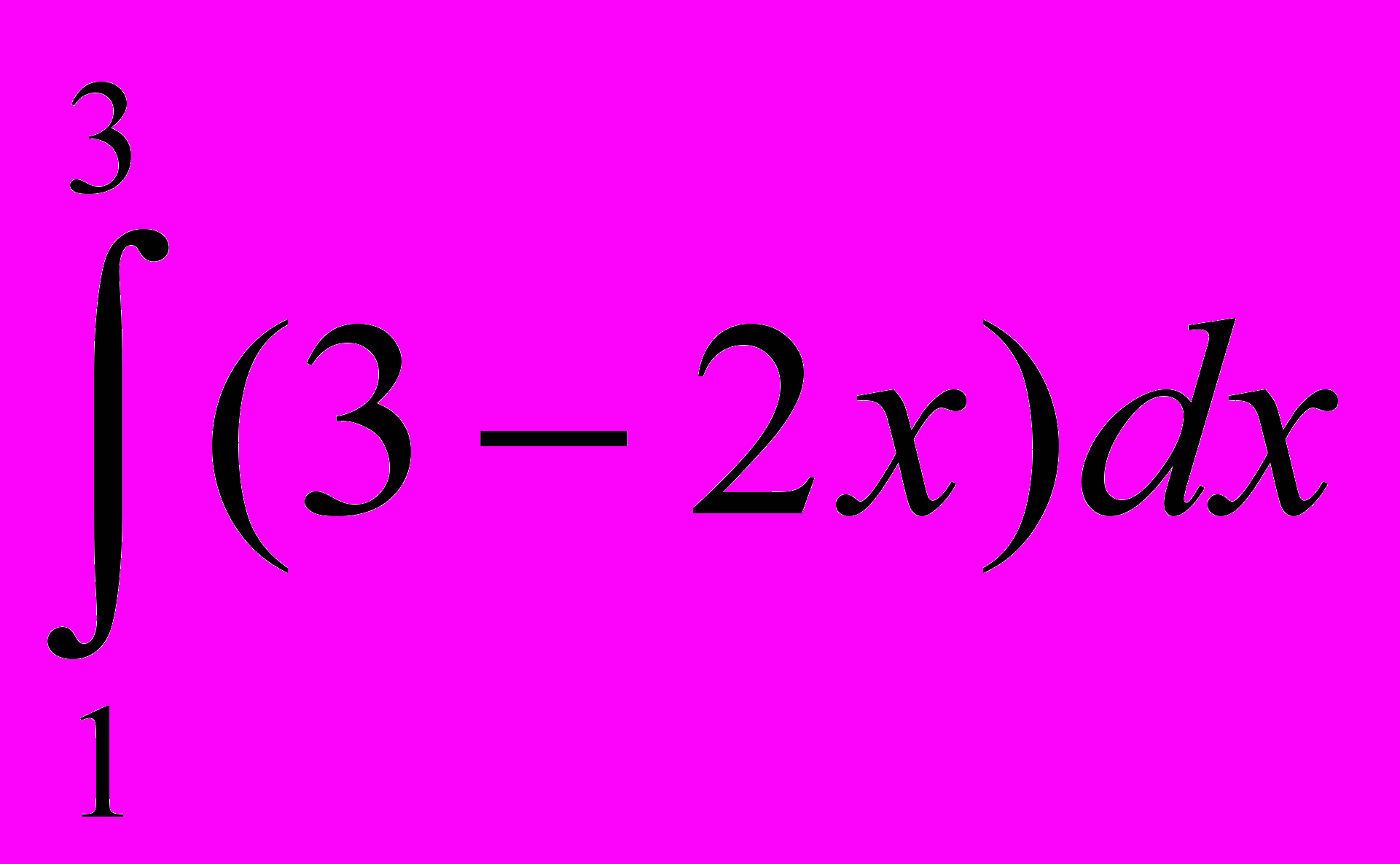 ; х2, если х2=
; х2, если х2=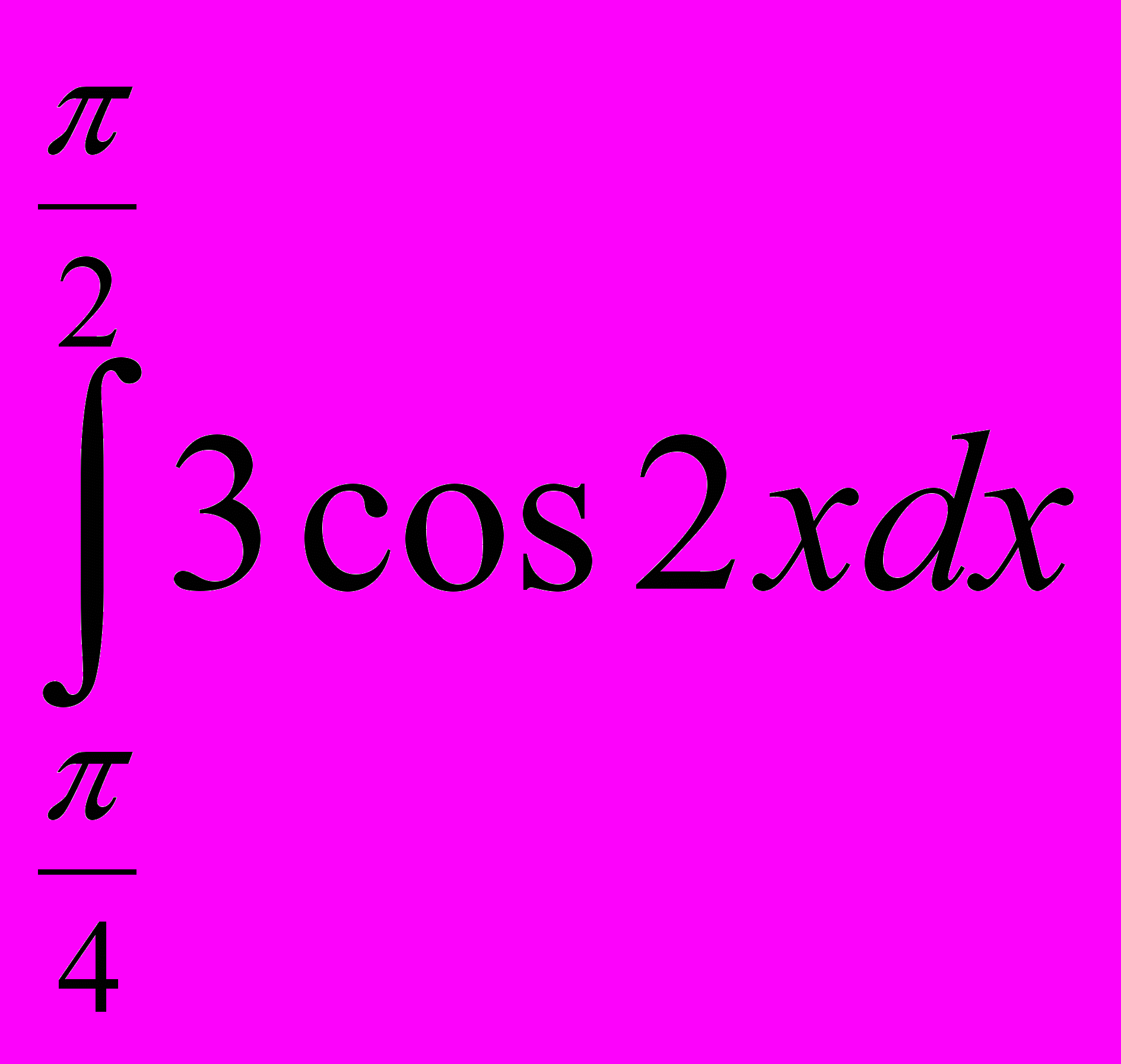 ; х3, если х3 – площадь фигуры, ограниченной линиями у=4-х2, у=х+2, у=0. В равенство х1 –2·х2+6·х3=38 подставьте вместо х1, х2 и х3 числа так, чтобы равенство было верно.
; х3, если х3 – площадь фигуры, ограниченной линиями у=4-х2, у=х+2, у=0. В равенство х1 –2·х2+6·х3=38 подставьте вместо х1, х2 и х3 числа так, чтобы равенство было верно.Карточка 2. Вычислить х1, если х1=
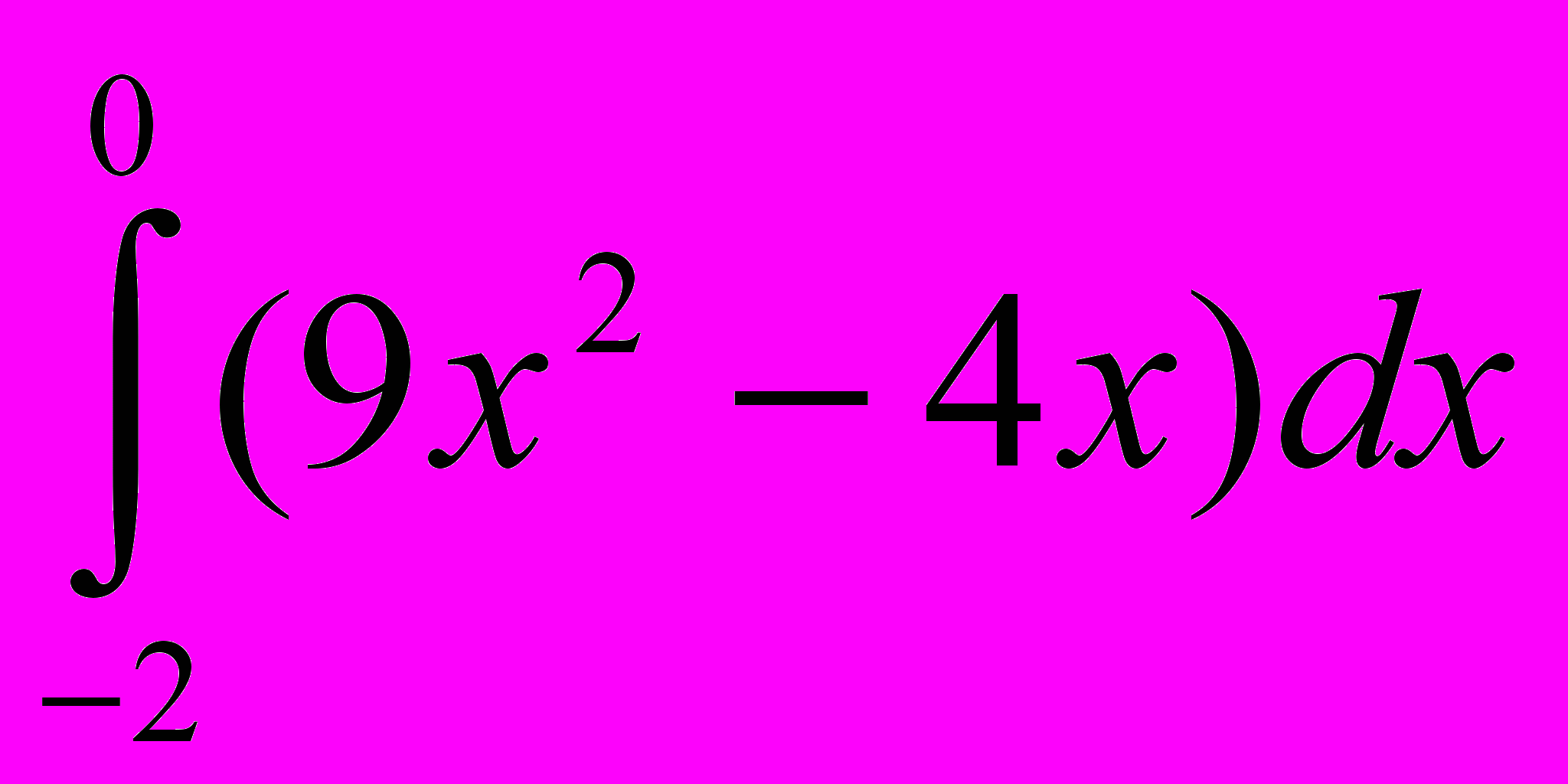 ; х2, если х2=
; х2, если х2=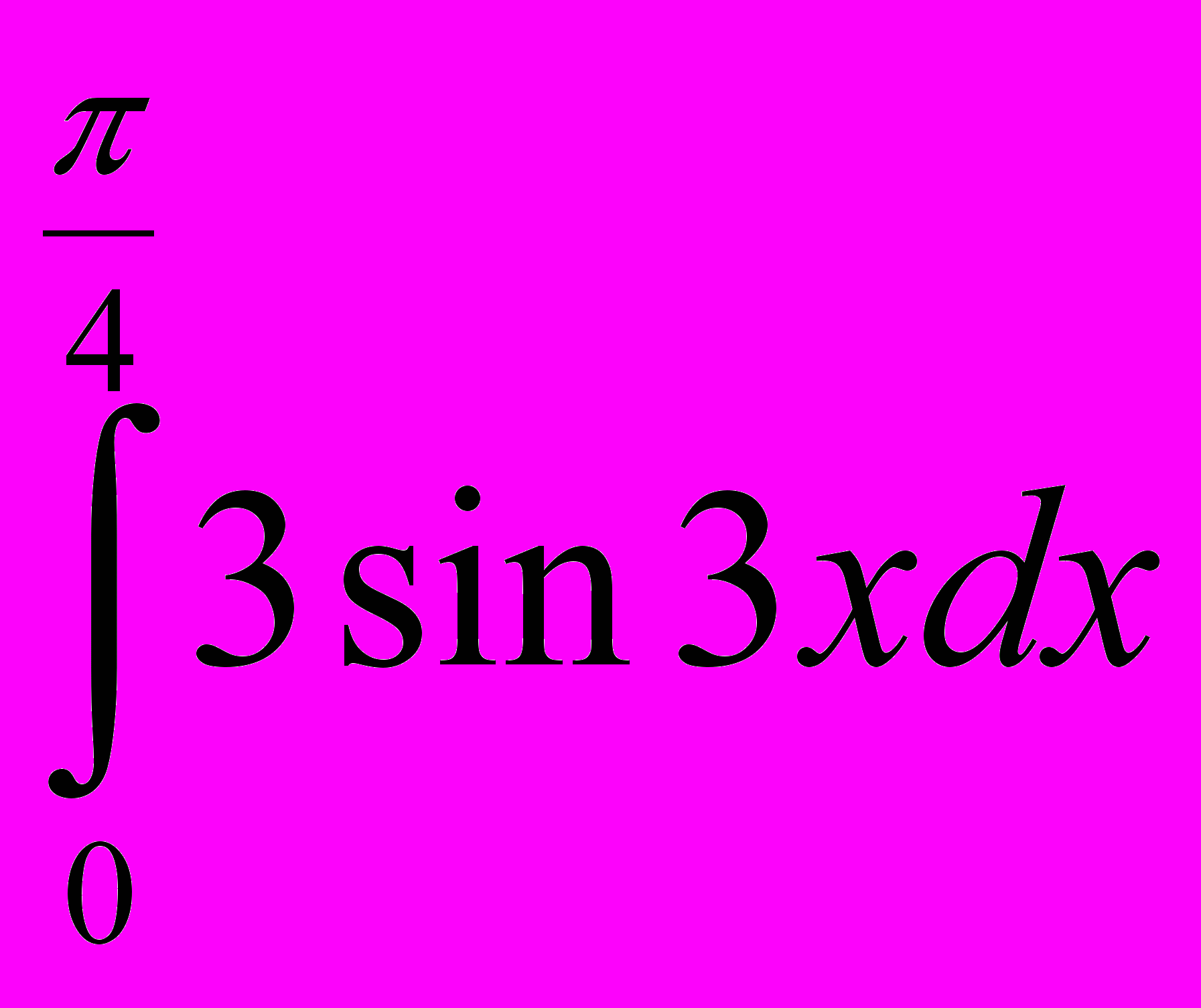 ; х3, если х3 – площадь фигуры, ограниченной линиями у=х2, у=6 – х, у=0. В равенство х1+х2 – 3·х3= - 2 подставьте вместо х1, х2 и х3 числа так, чтобы равенство было верным.
; х3, если х3 – площадь фигуры, ограниченной линиями у=х2, у=6 – х, у=0. В равенство х1+х2 – 3·х3= - 2 подставьте вместо х1, х2 и х3 числа так, чтобы равенство было верным.Карточка 3. Вычислить х1, если х1=
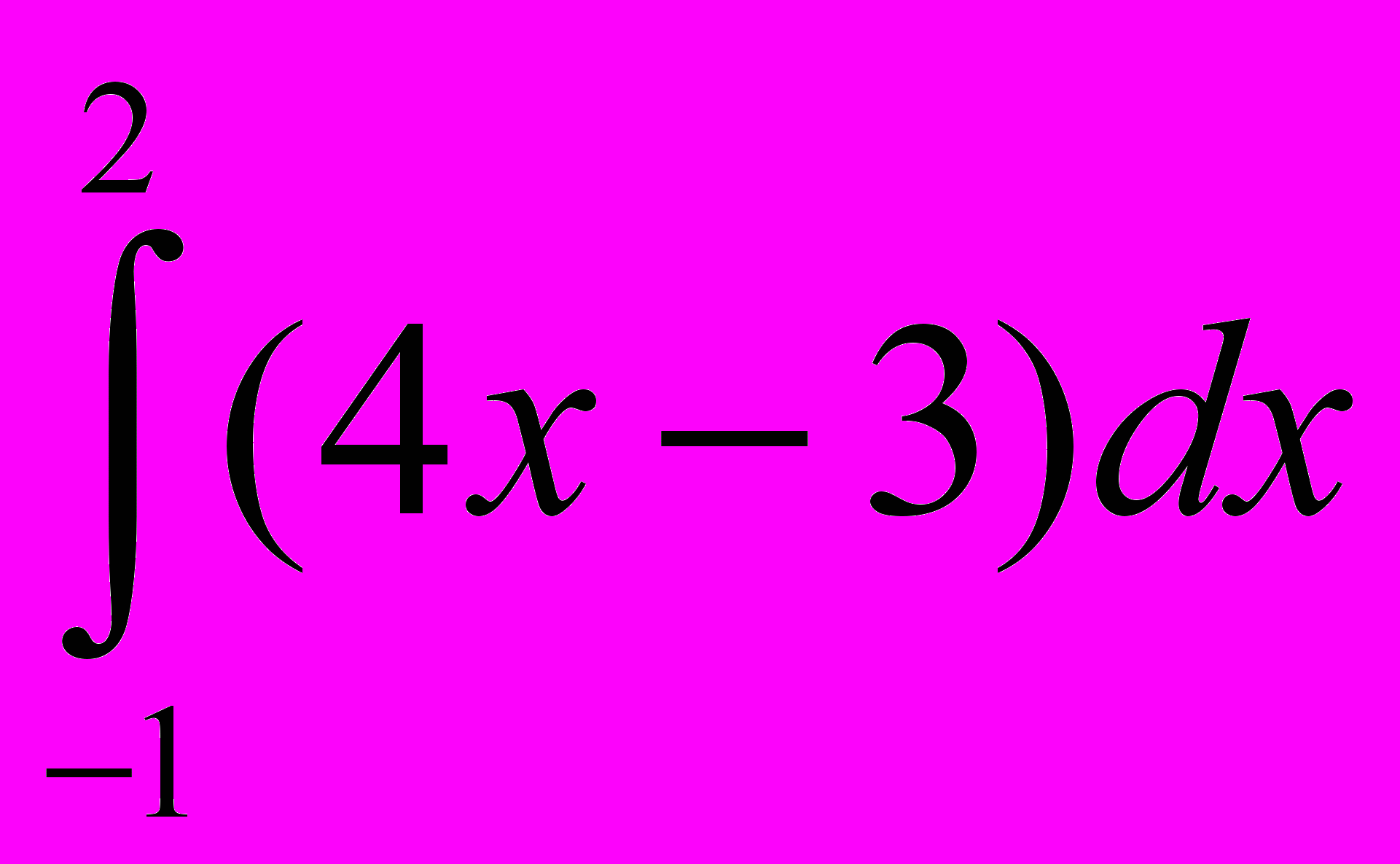 ; х2, если х2=
; х2, если х2=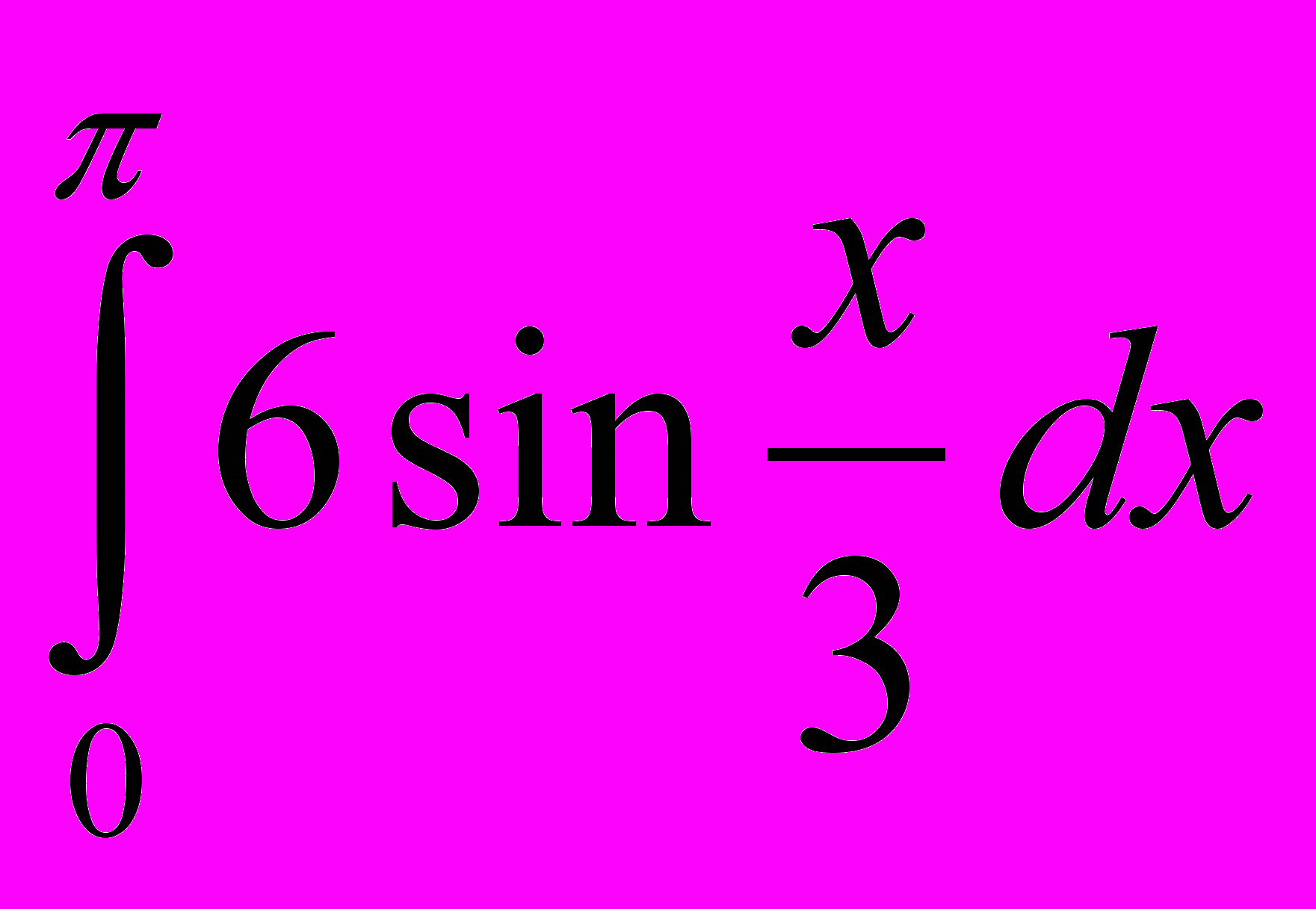 ; х3, если х3 – площадь фигуры, ограниченной линиями у=х2+1, х= - 2, х=2, у=0. В равенство 3·х1+х2+3·х3=28 подставьте числа так, чтобы равенство было верным.
; х3, если х3 – площадь фигуры, ограниченной линиями у=х2+1, х= - 2, х=2, у=0. В равенство 3·х1+х2+3·х3=28 подставьте числа так, чтобы равенство было верным.Одно из искусств, которым должен владеть рыцарь – умение играть в шашки. Вам, как претендентам на рыцарский титул, нужно делать только верные шаги (участники разгадывают кроссворд, который спроектирован на доску с помощью кодоскопа).
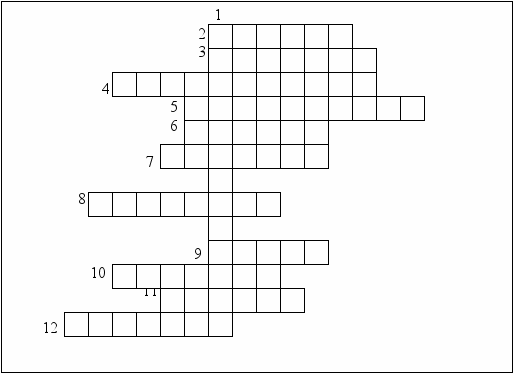
1.Чем является функция F(х) для функции f(х). 2. Графиком функции у=kх+b. 3. Самая низкая школьная оценка. 4. Какой урок проходит обычно перед зачетом? 5. Синоним слова «дюжина». 6. Есть в каждом слове, у растения и может быть у уравнения. 7. Что можно вычислить при помощи интеграла? 8. Одно из важнейших математических понятий. 9. Форма урока, на котором проводится проверка знаний. 10. Немецкий ученый, в честь которого названа формула, связывающая площадь криволинейной трапеции и интеграл.
11. конь – лошадь – жеребенок, бык – корова – теленок, король – королева – принц, граф – графиня - ? 12. Зависимость между множествами х и у, при которой каждому значению из множества х соответствует единственное значение из множества у называется …
Одним из важнейших искусств есть охота. Сейчас вы будете охотиться за фразой. Вам нужно вычислить интегралы и около каждого из них написать букву, соответствующую полученному ответу. (Должна получиться фраза: «жизнь и доверие теряют один раз».
Каждый ученик получает несколько карточек, решает их и записывают буквы около соответствующих заданий.)
| а | в | д | е | ж | з | и | к | л | н | о | р | т | ь | ю | Я |
| 6 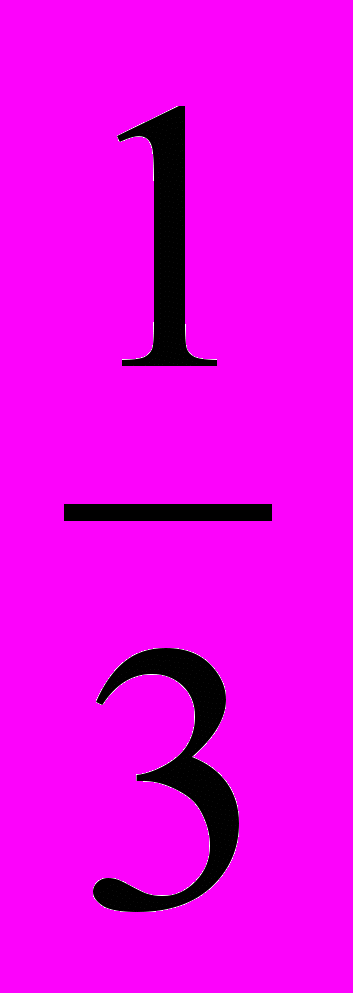 | - 2 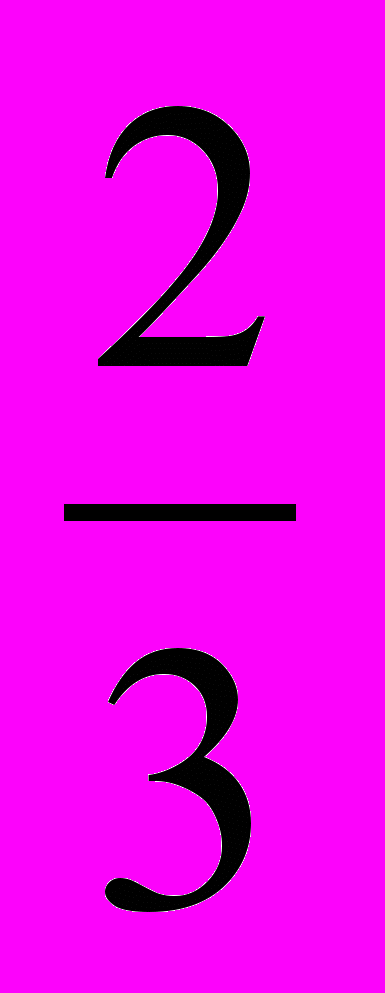 | 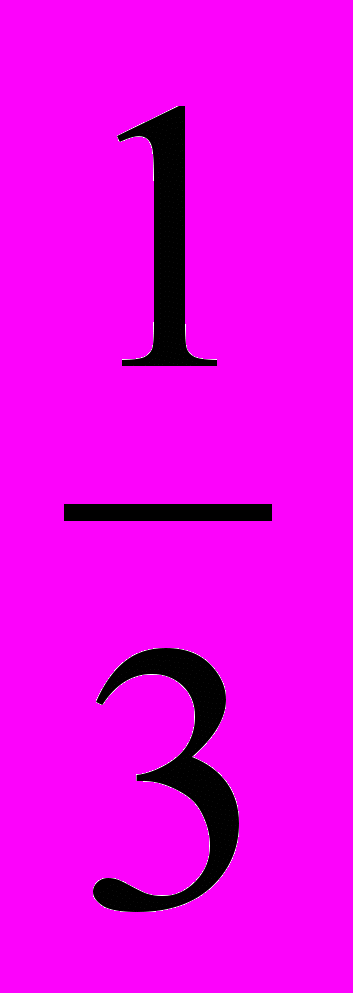 | 18 | 6,2 | - 2 | 6 | 24,2 | 48 | 10,5 | 4 | 2 | 0 | 9 | 21 | 16 |
1.
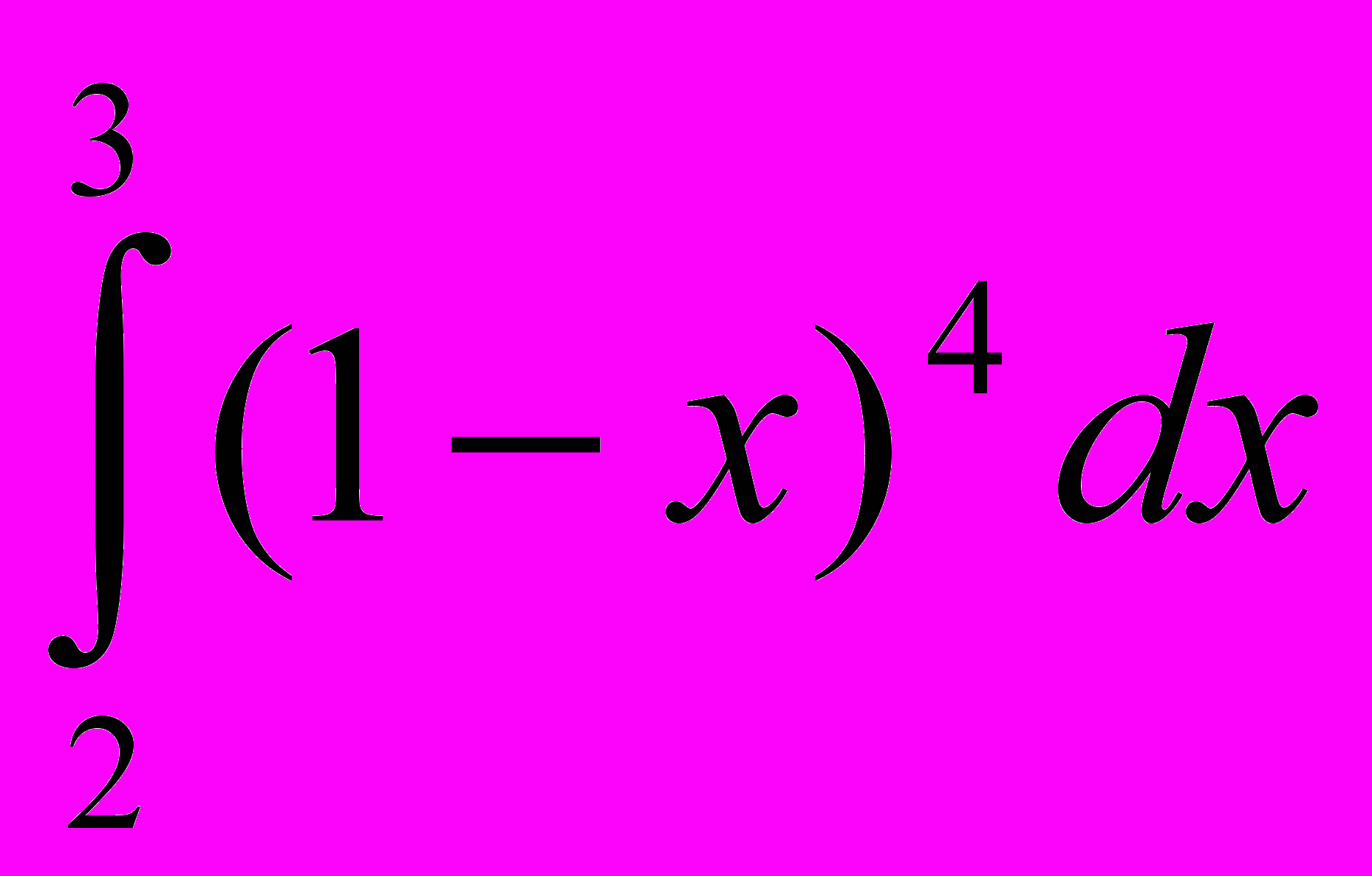 ; 2.
; 2. 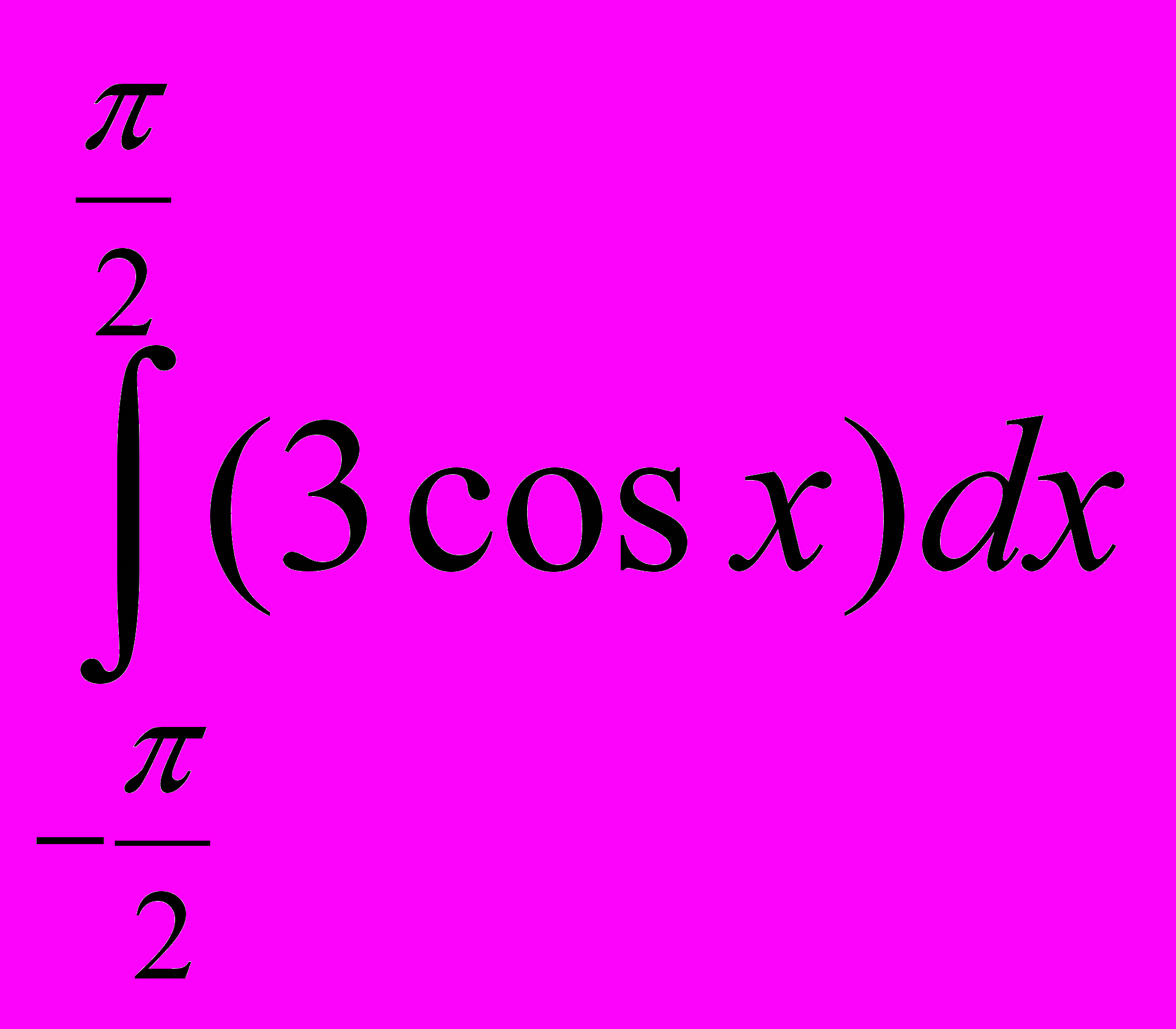 ; 3.
; 3. 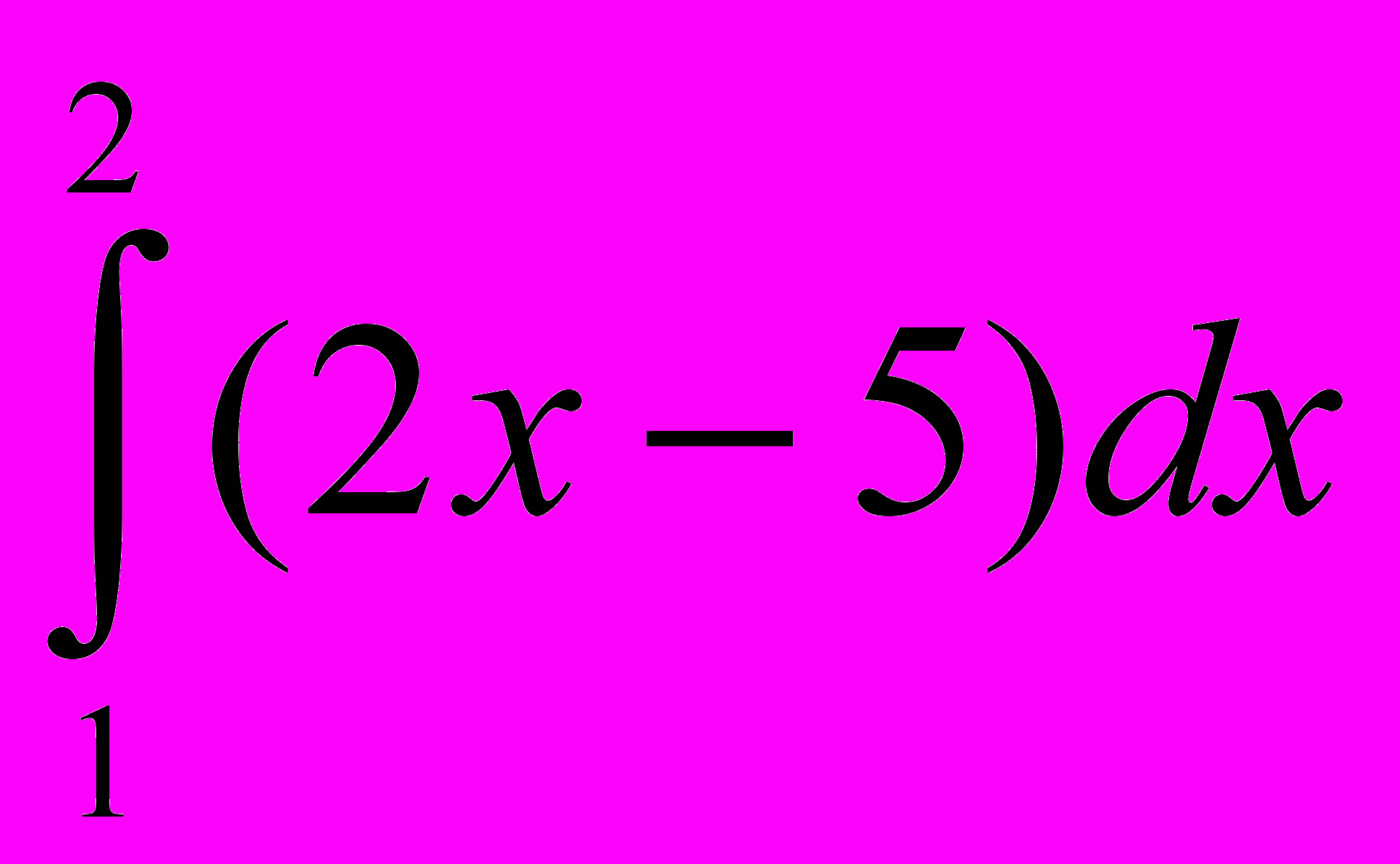 ; 4.
; 4. 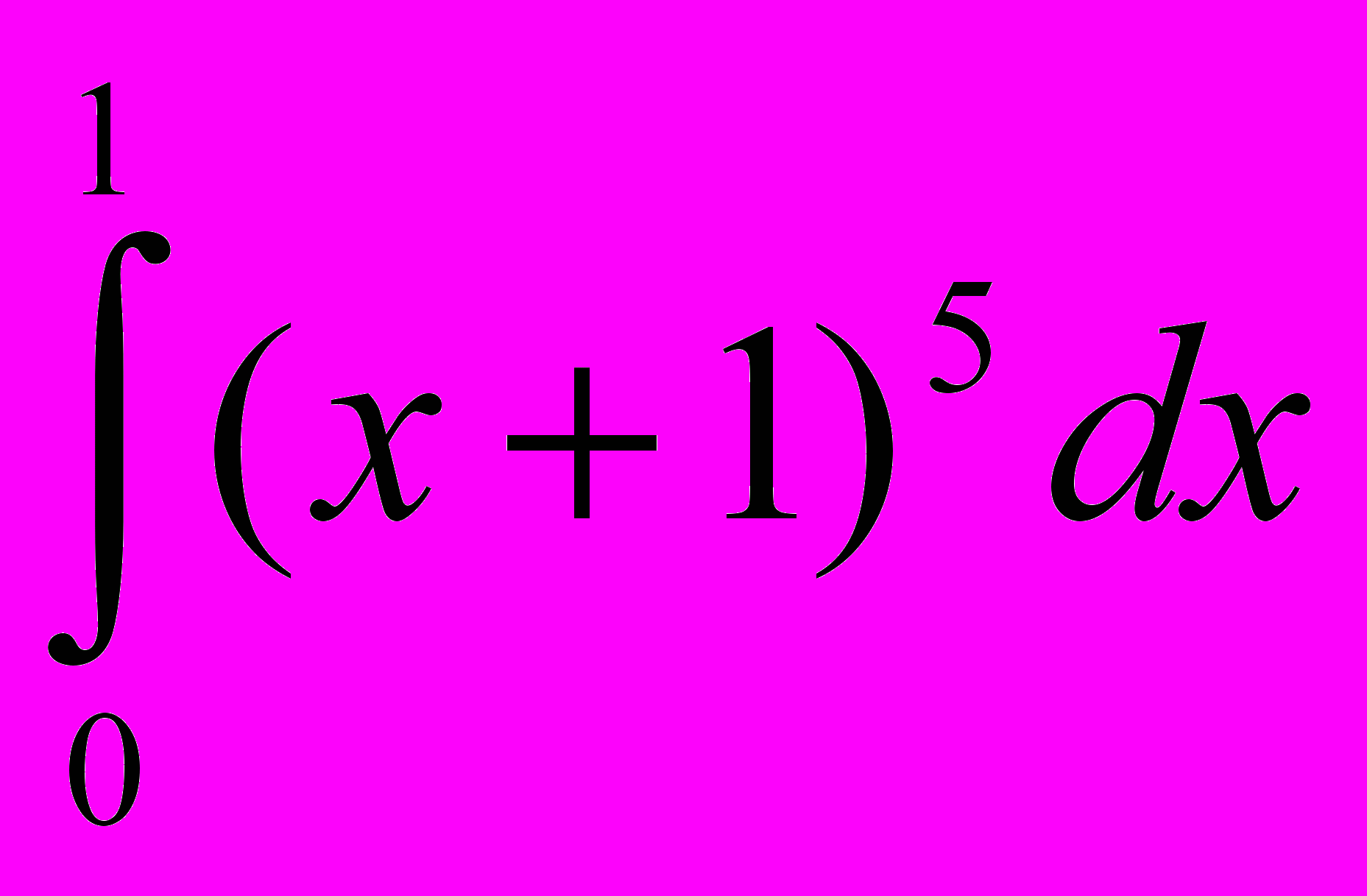 ; 5.
; 5. 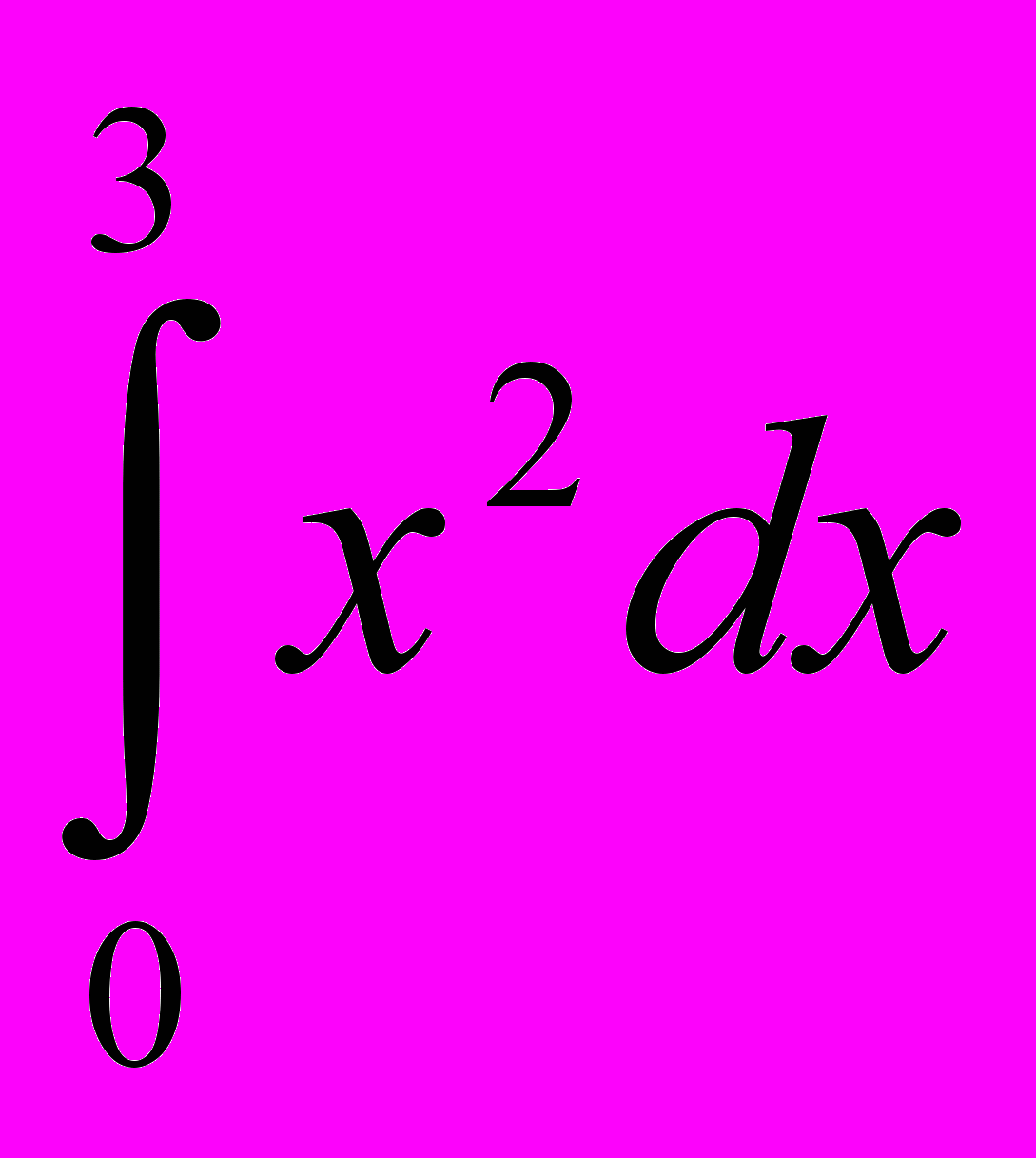 ; 6.
; 6. 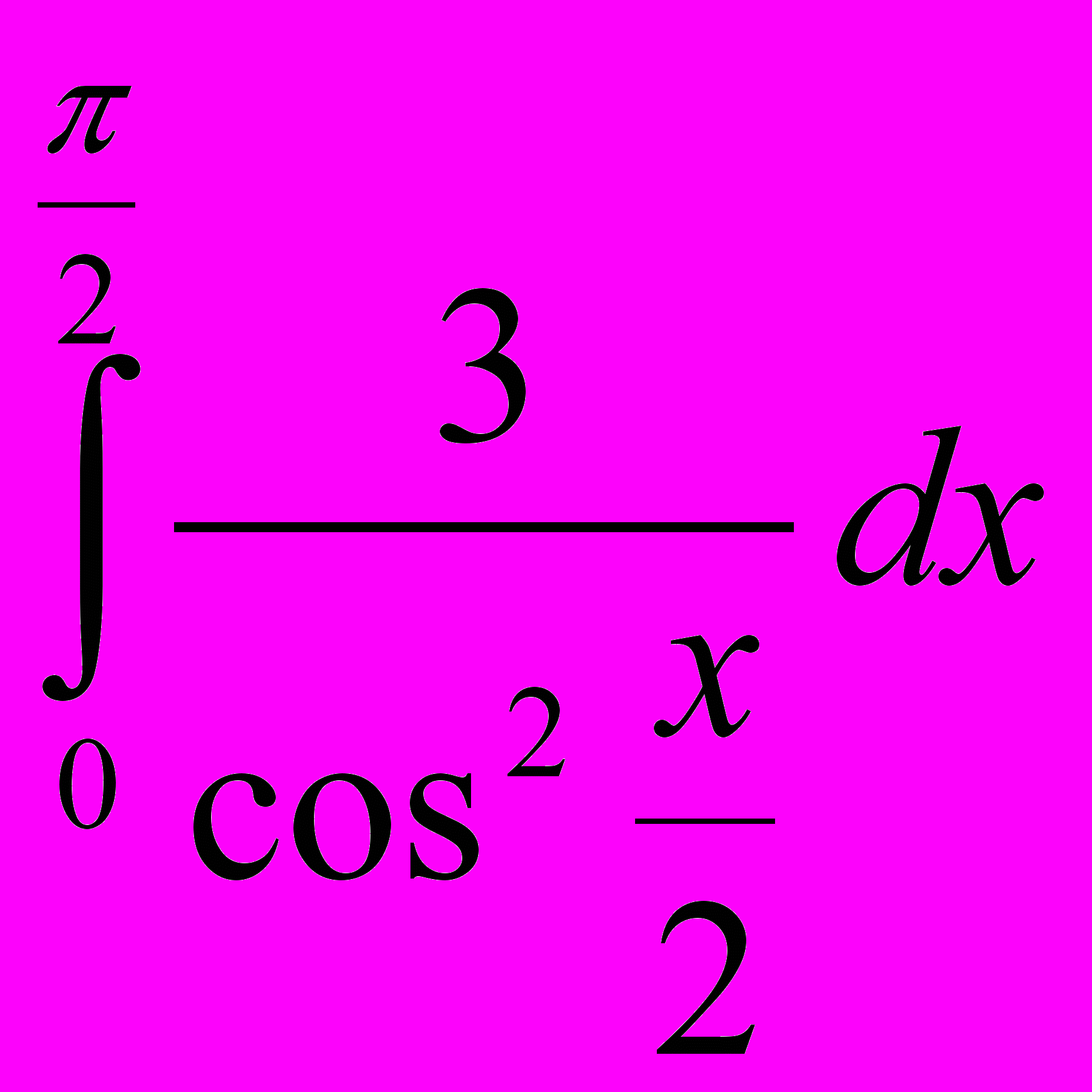 ;
;7.
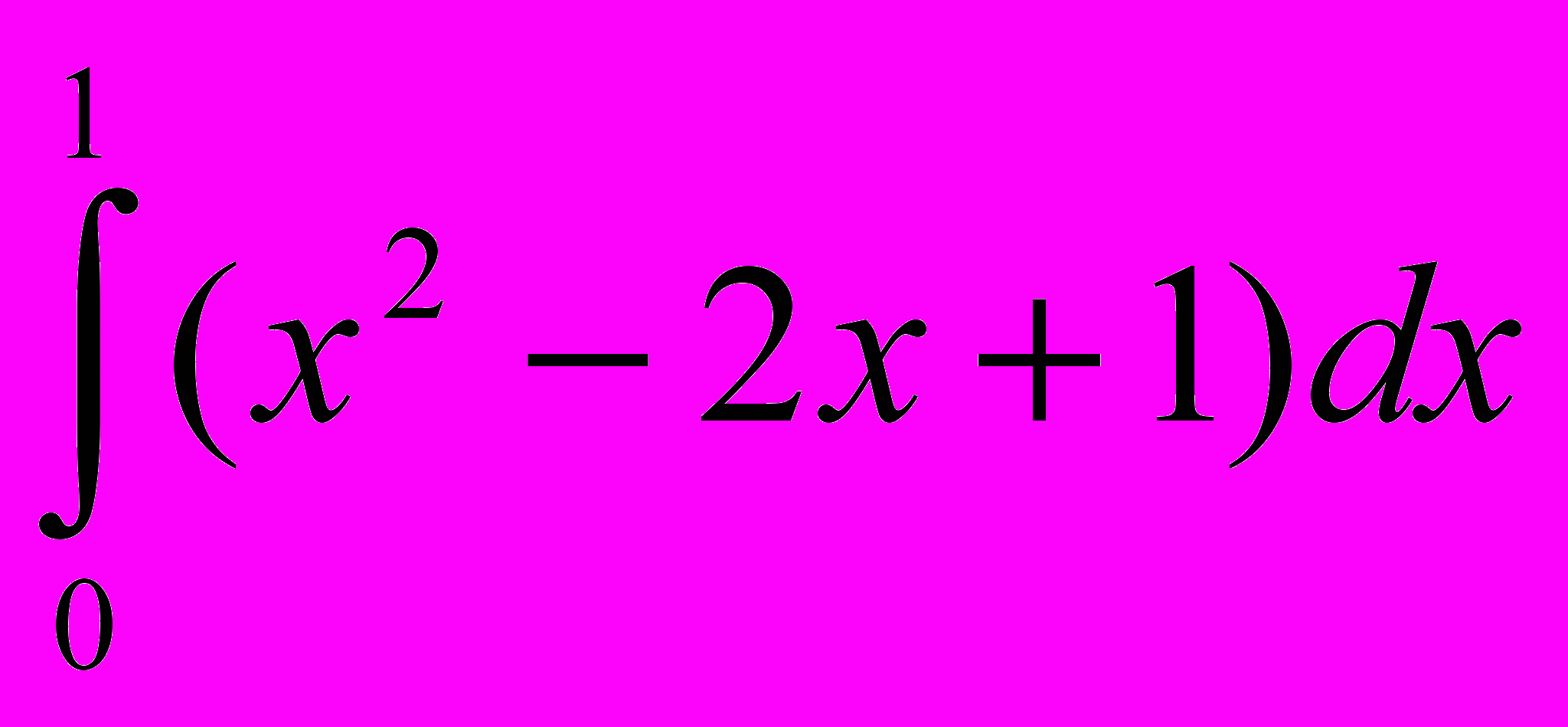 ; 8.
; 8.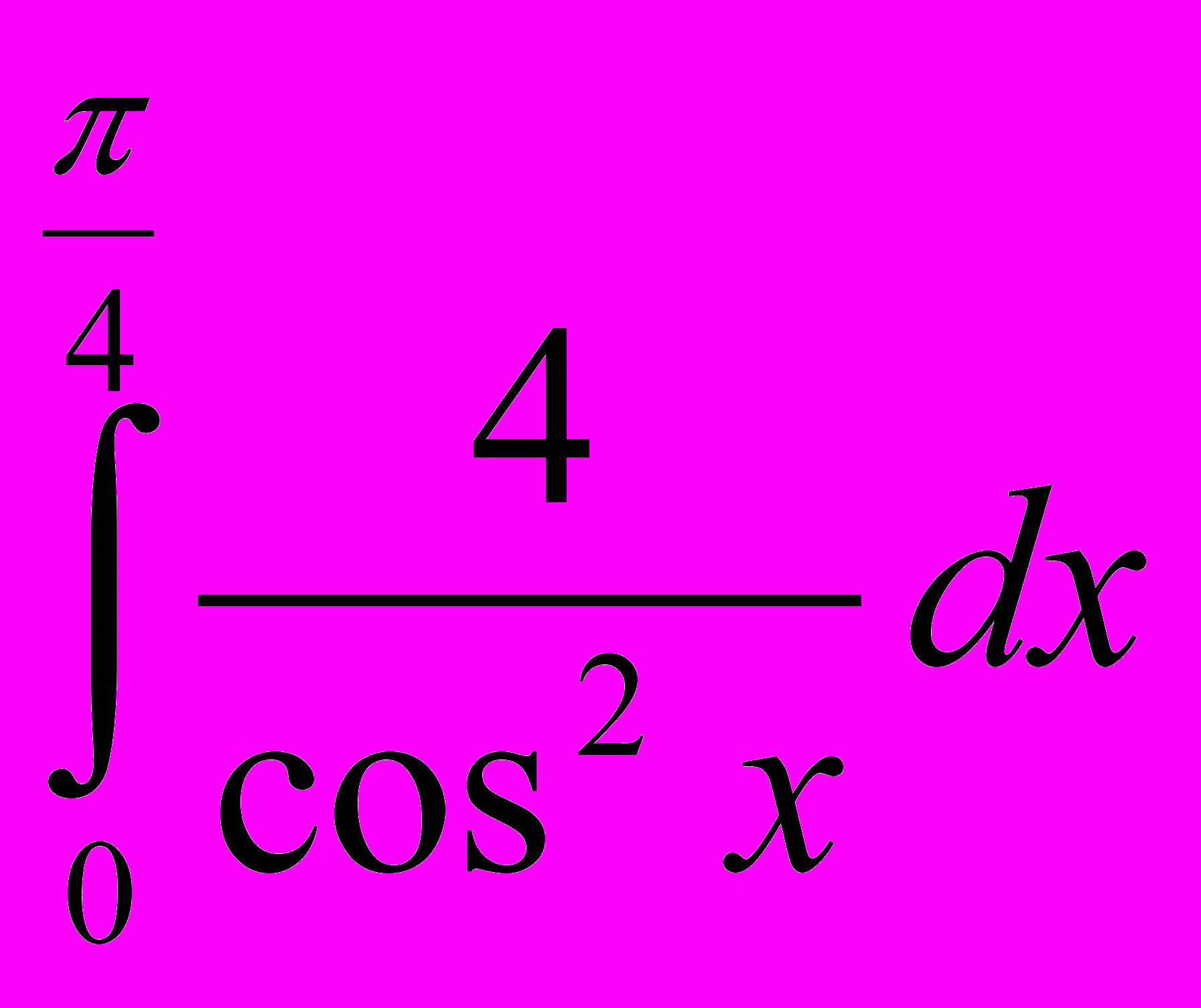 ; 9.
; 9.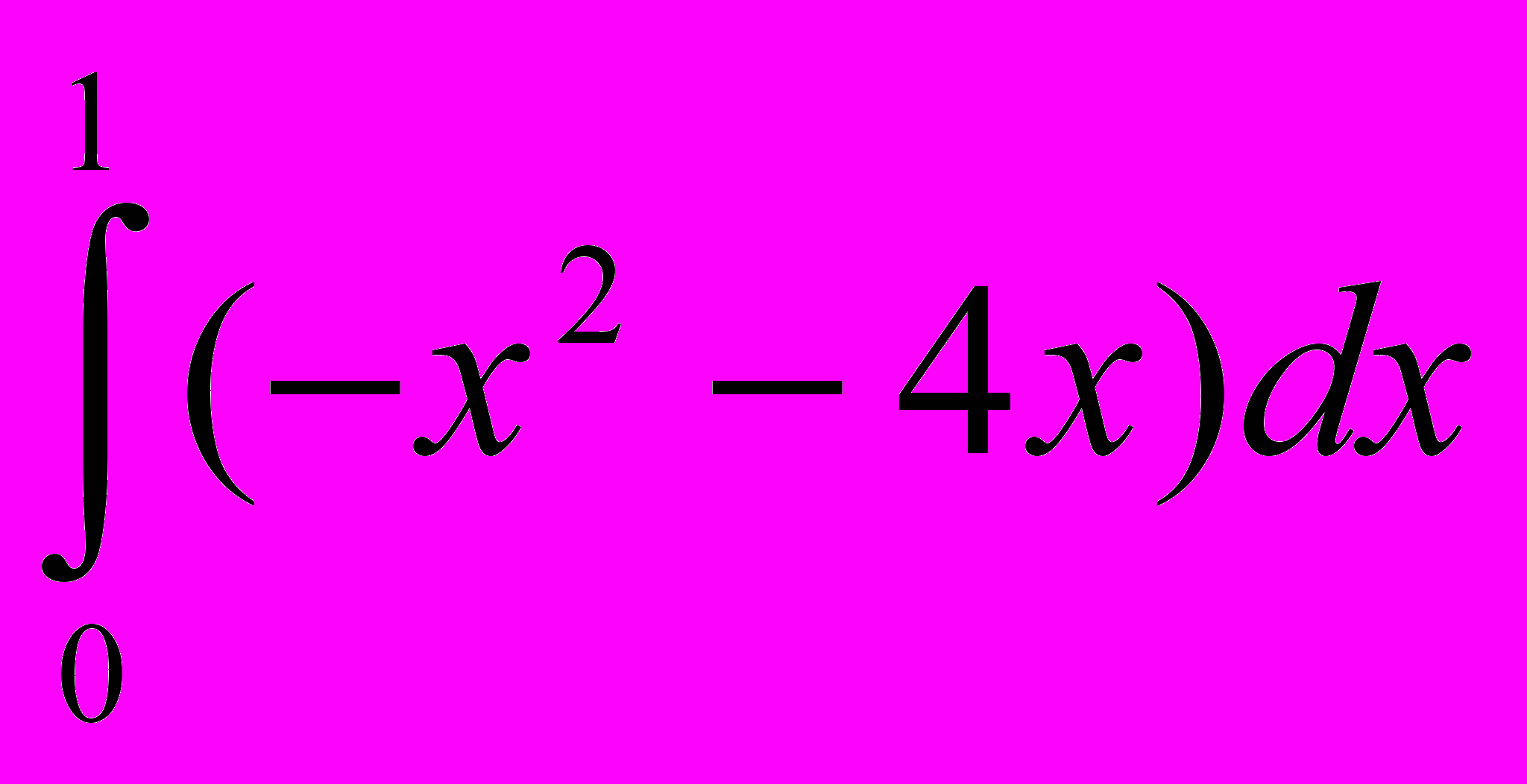 ; 10.
; 10.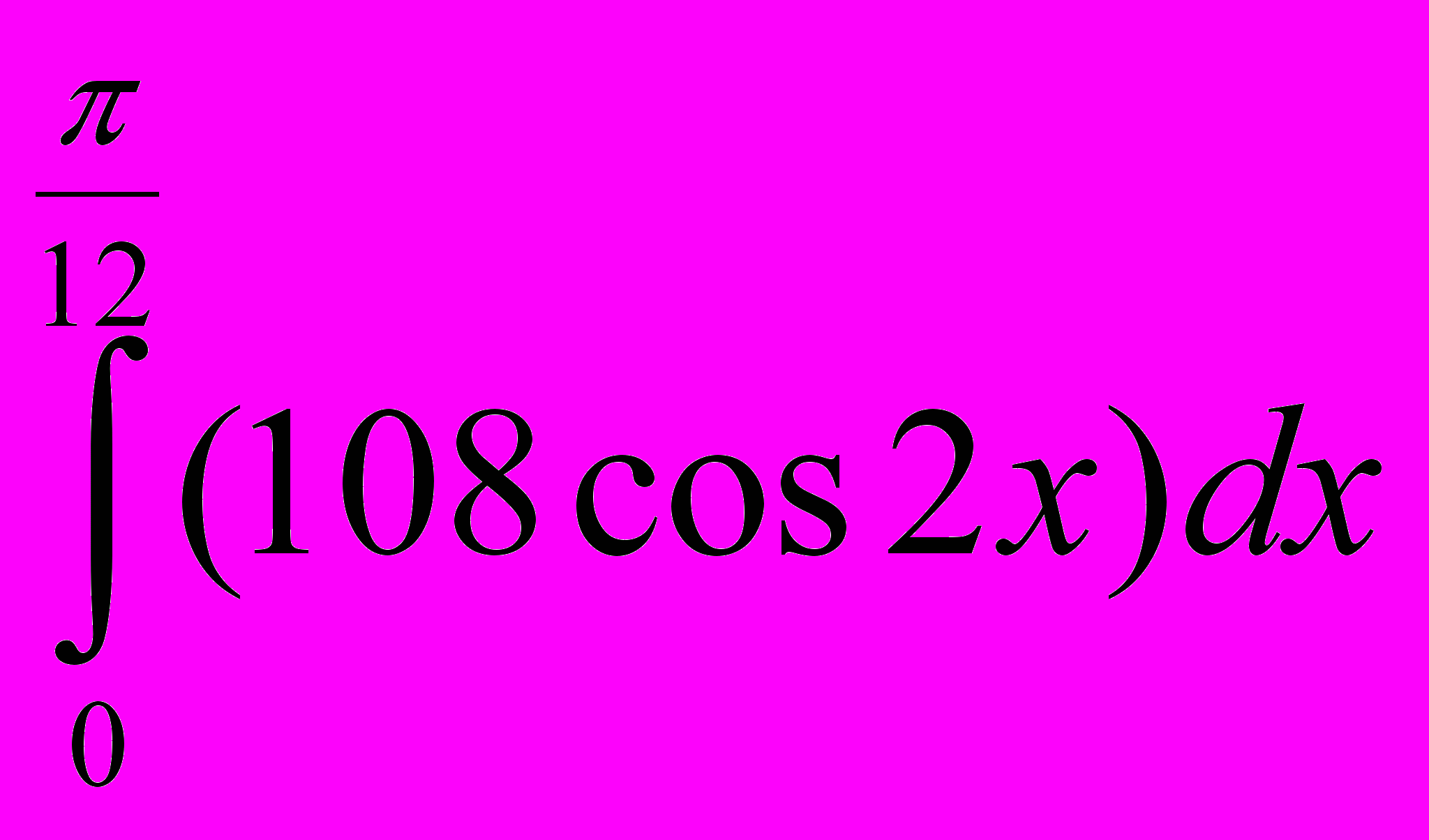 ; 11.
; 11.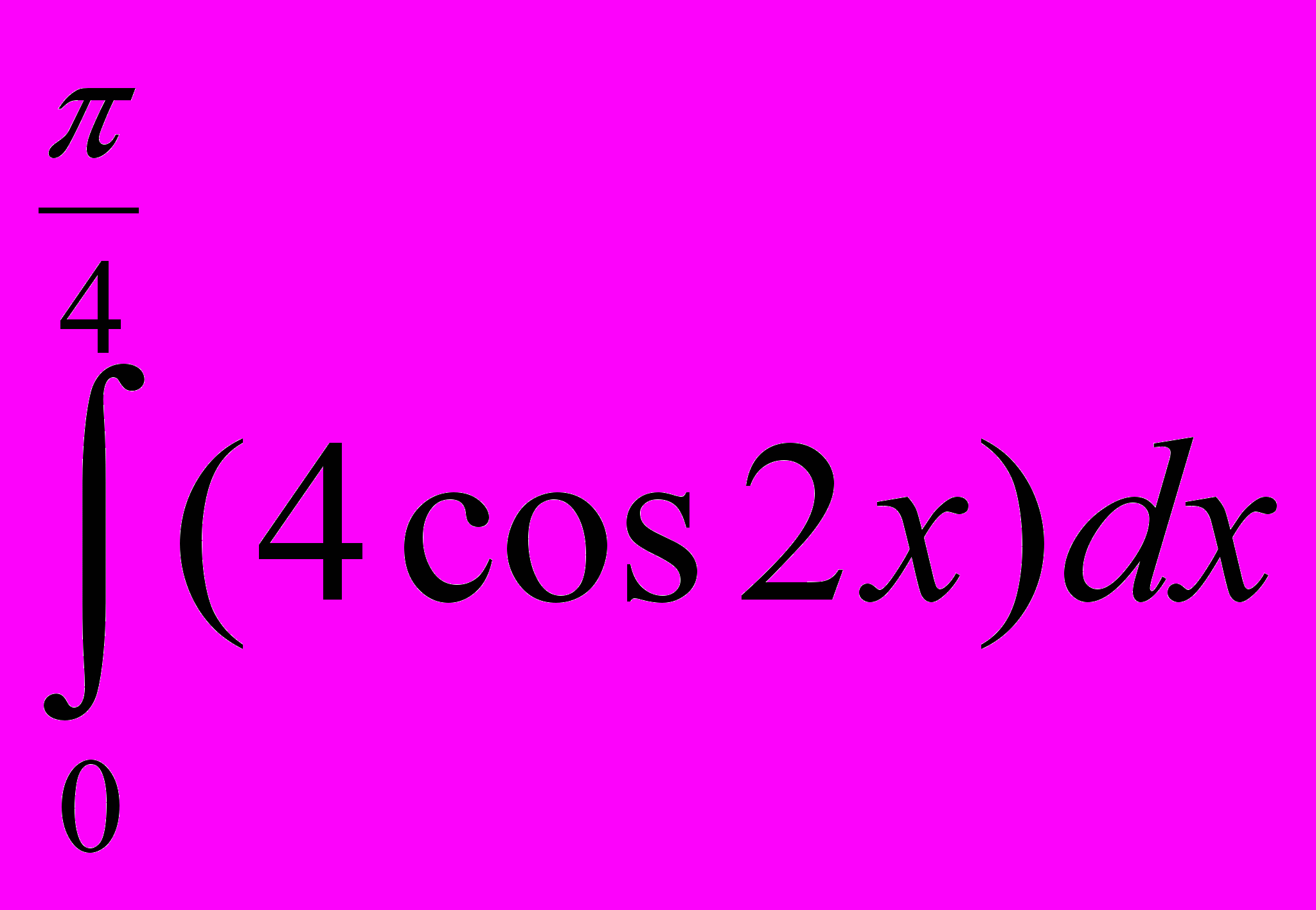 ;
;12.
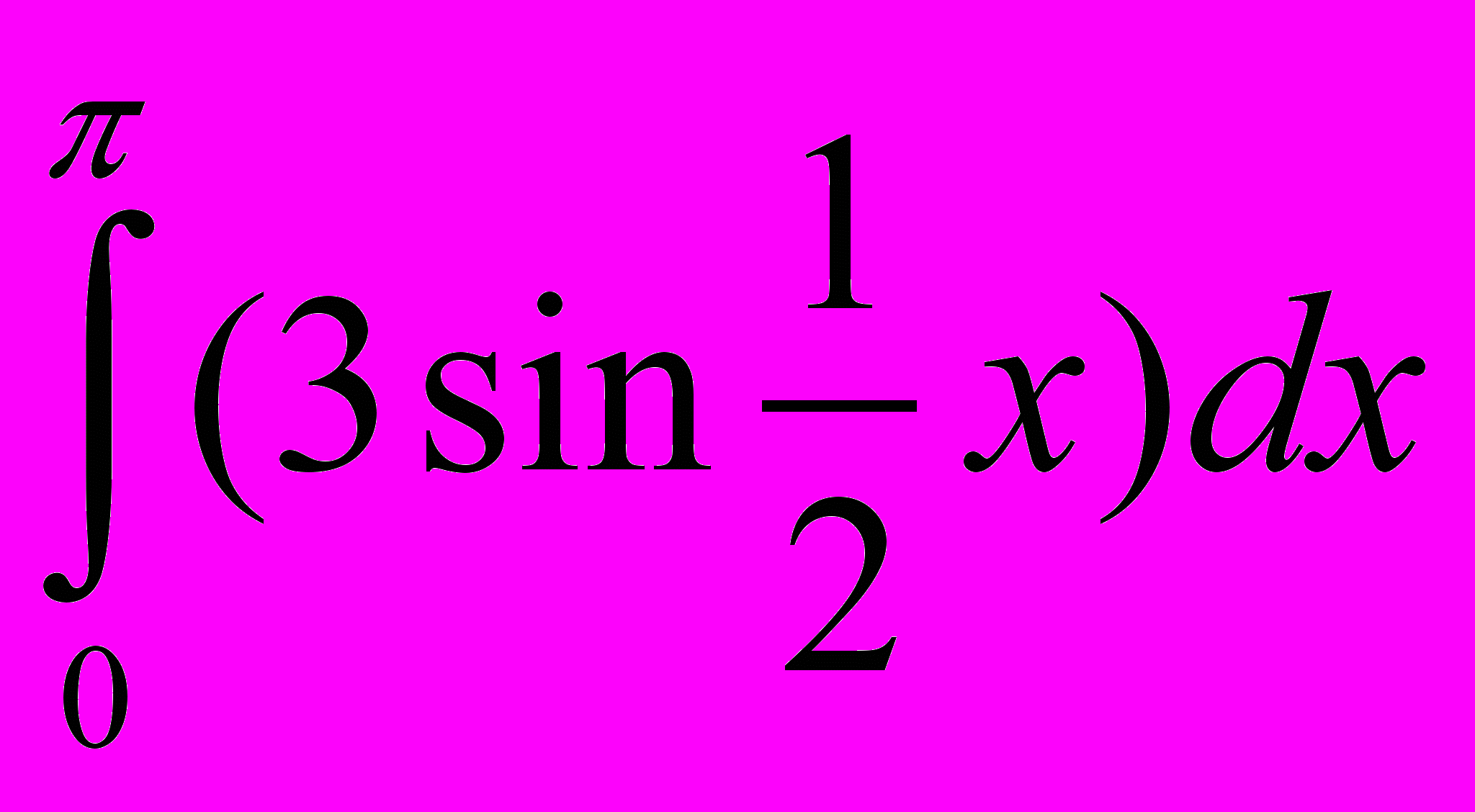 ; 13.
; 13.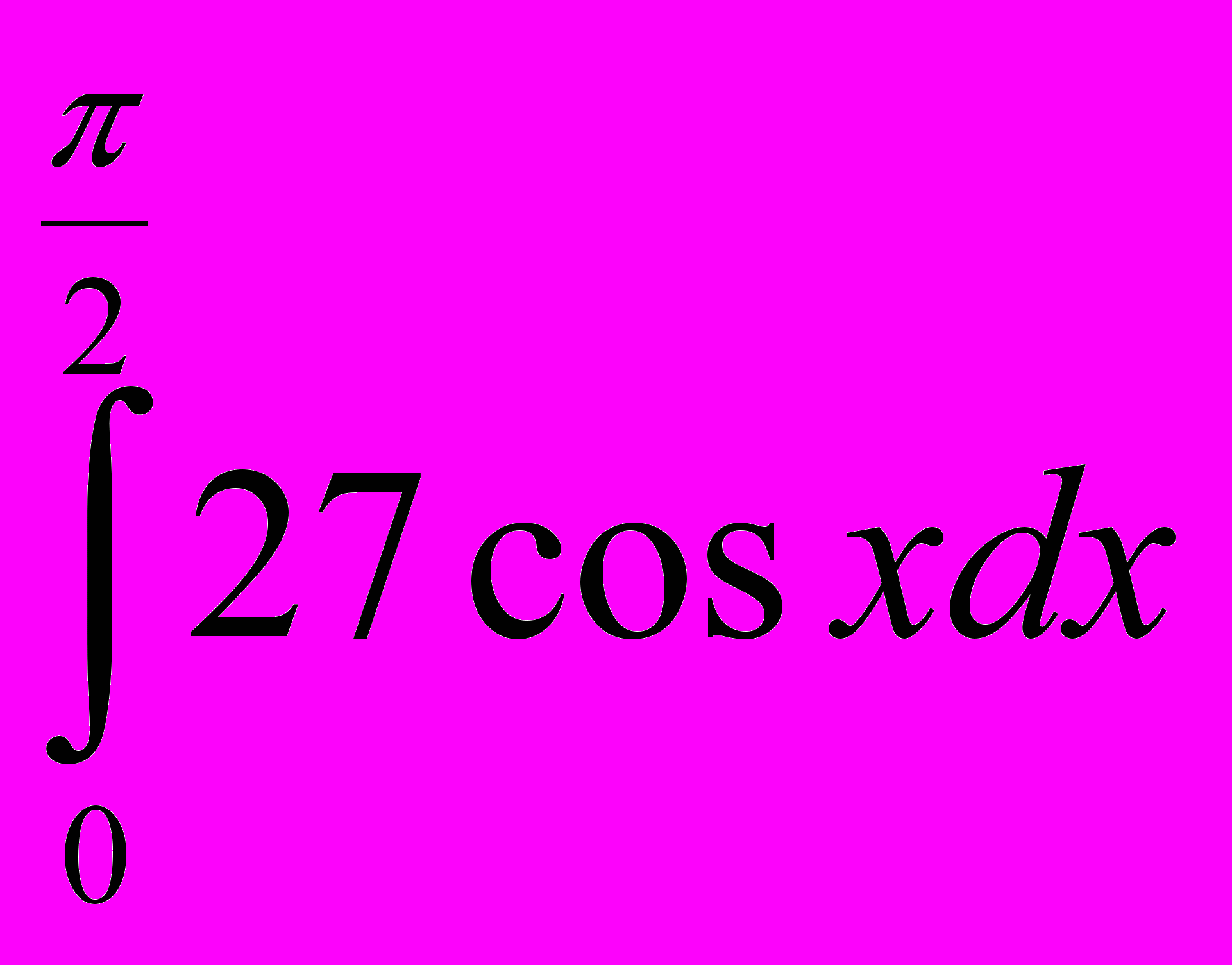 ; 14.
; 14.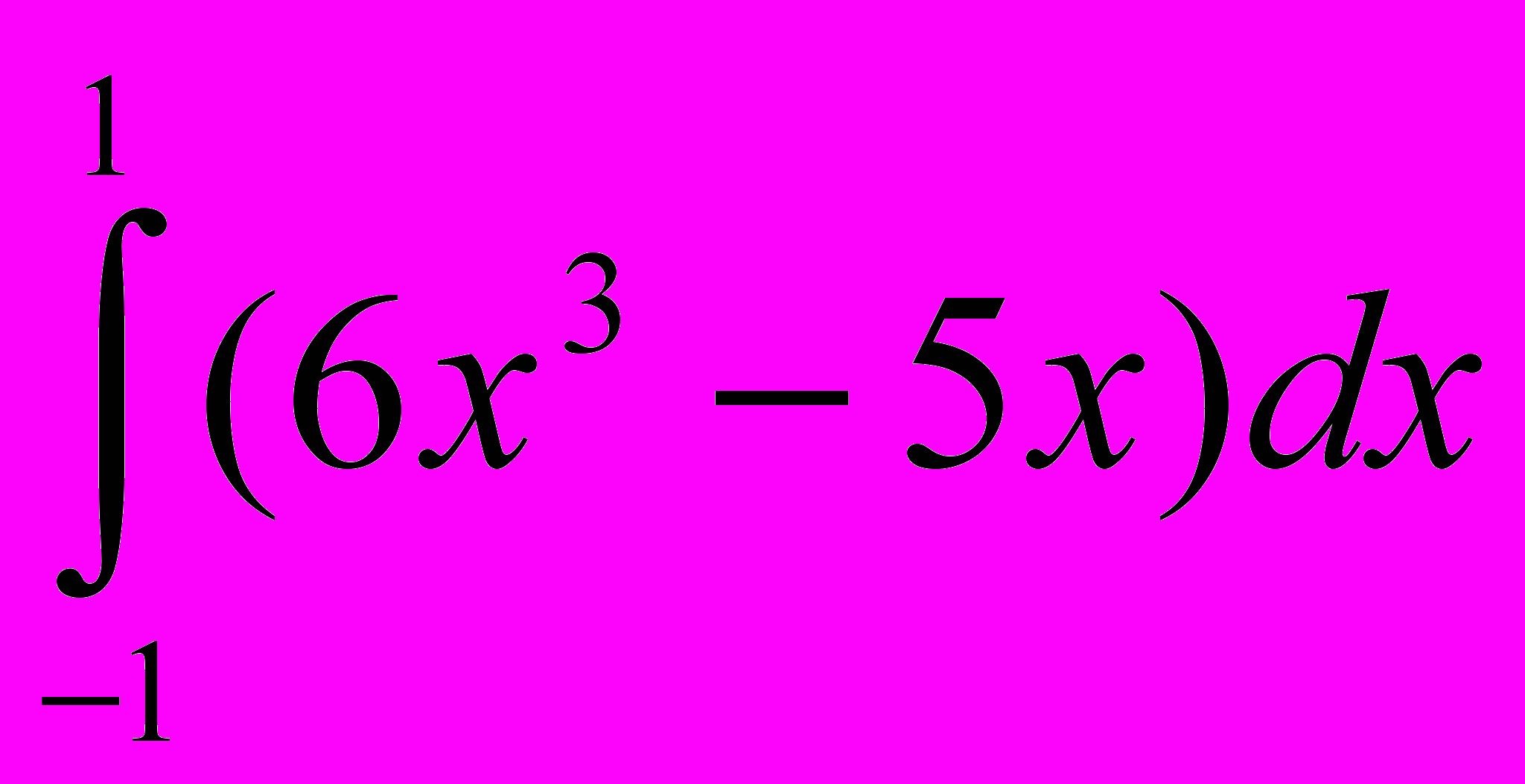 ; 15.
; 15.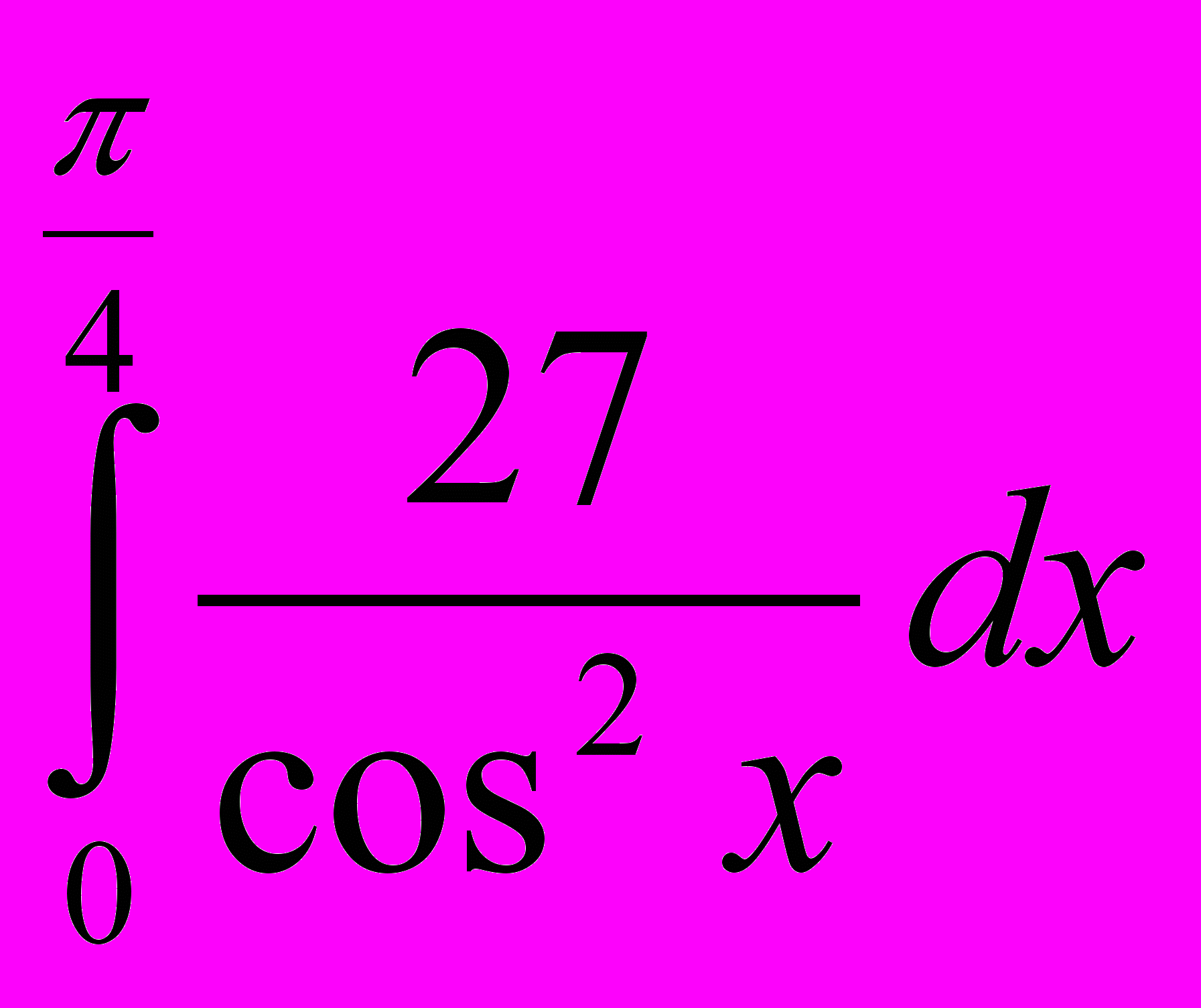 ; 16.
; 16.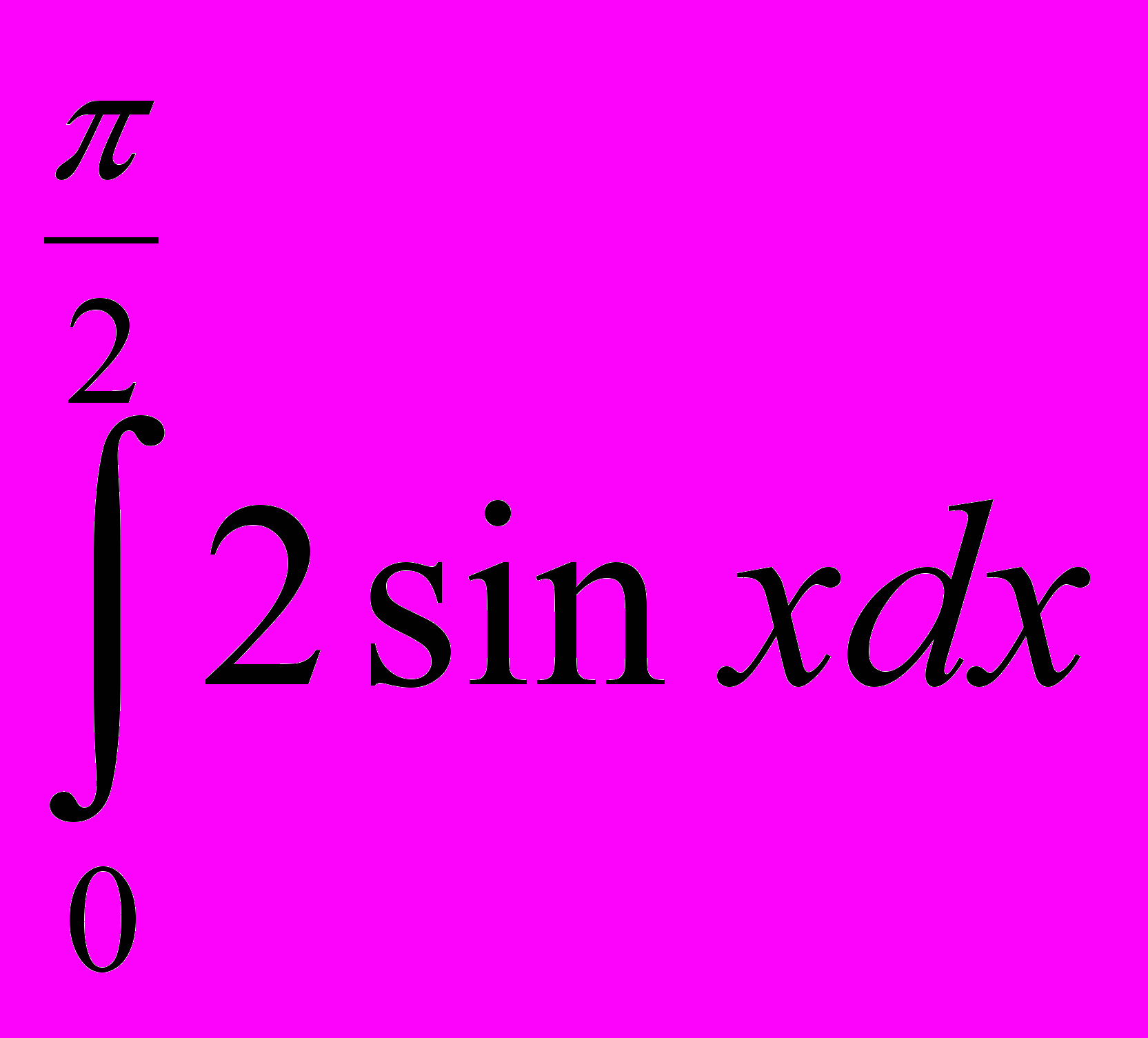 ;
;17.
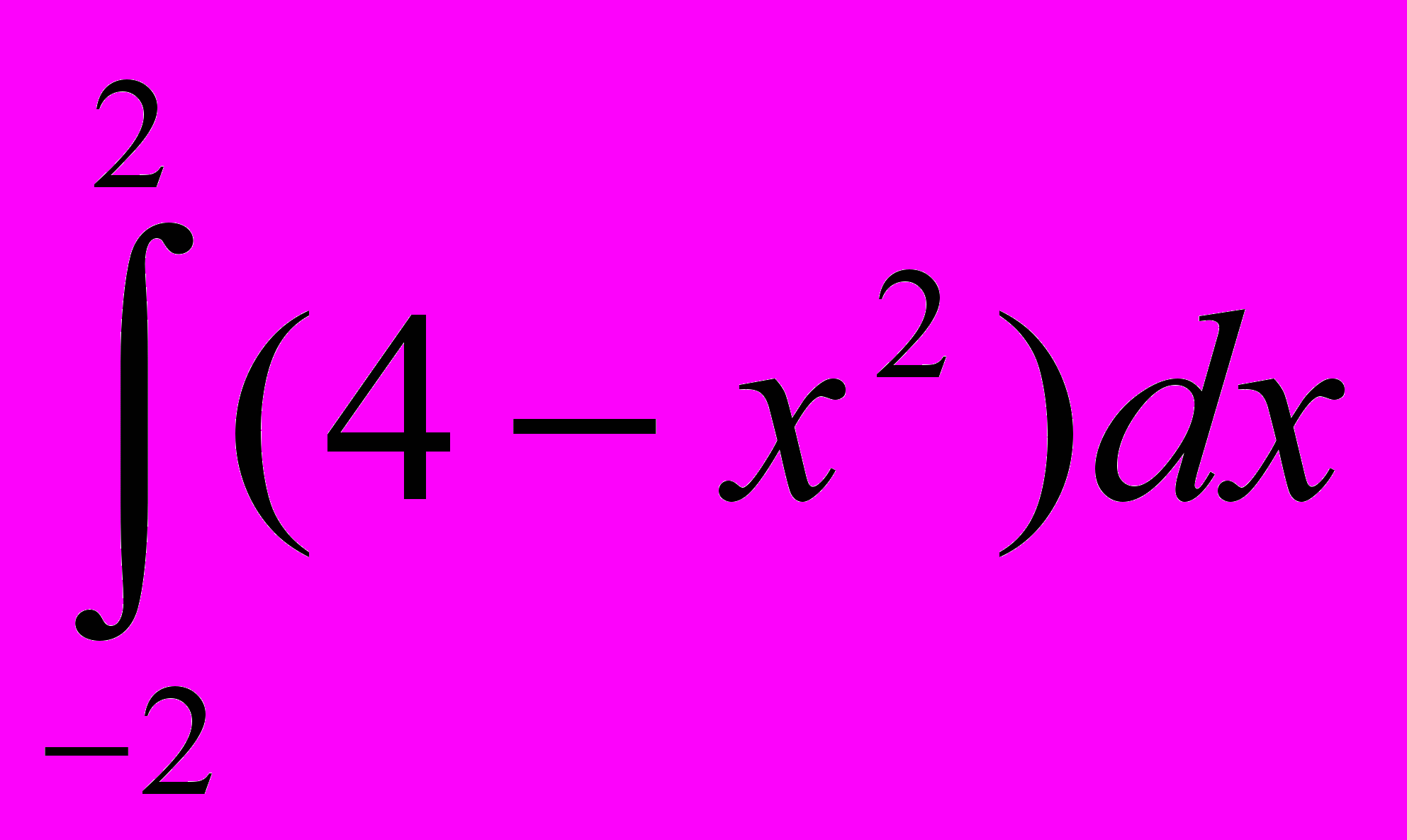 ; 18.
; 18.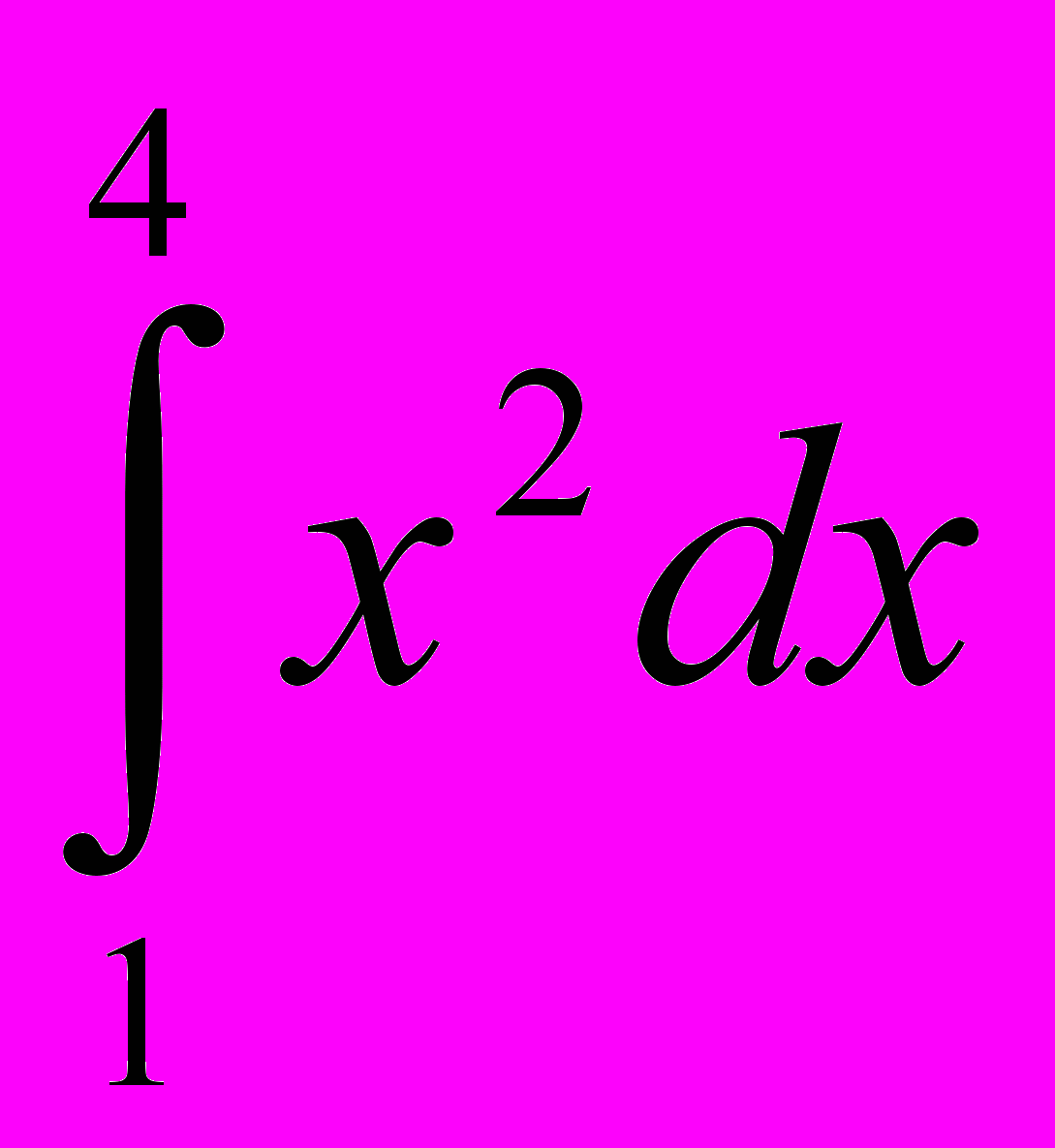 ; 19.
; 19.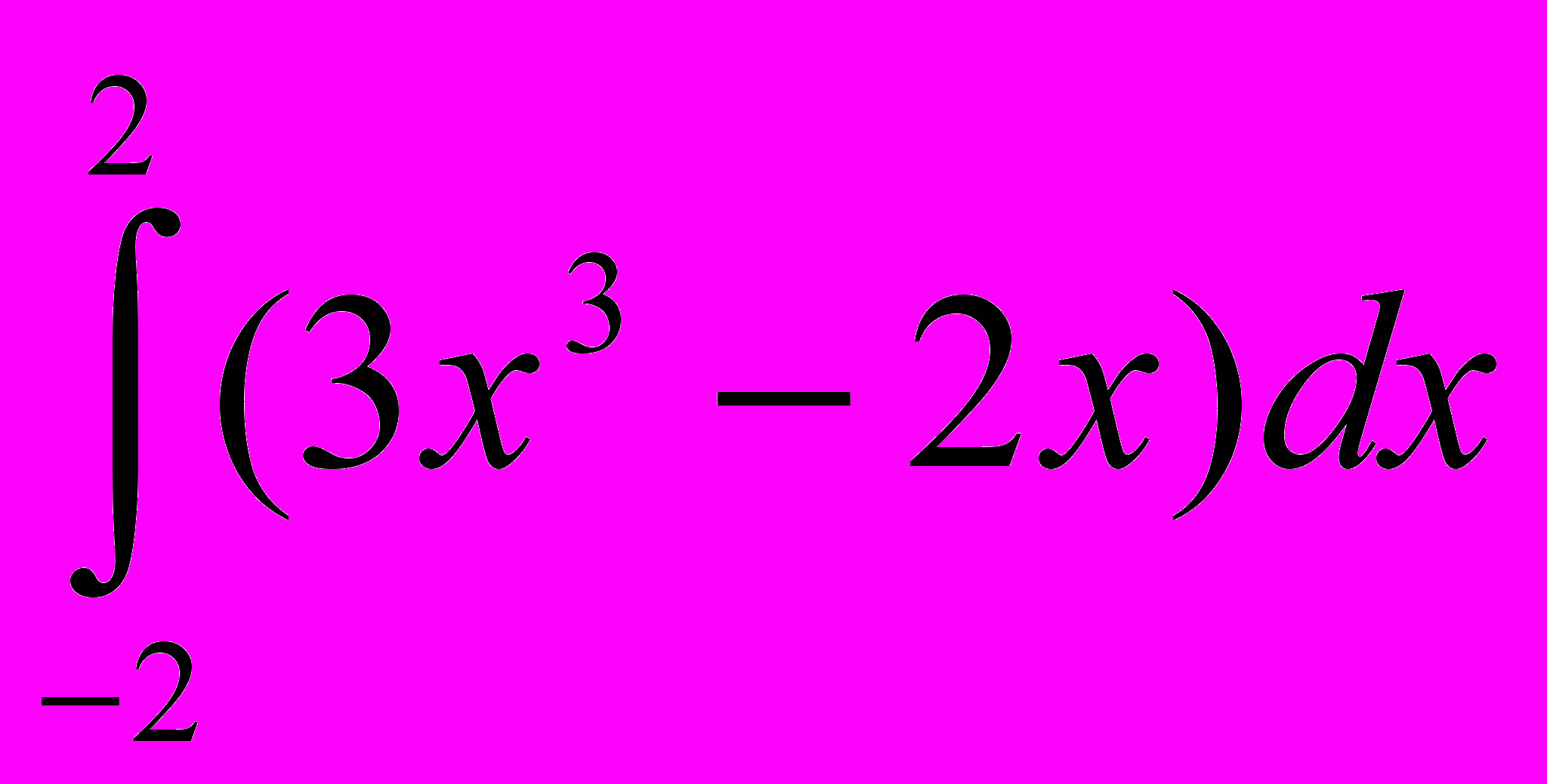 ; 20.
; 20.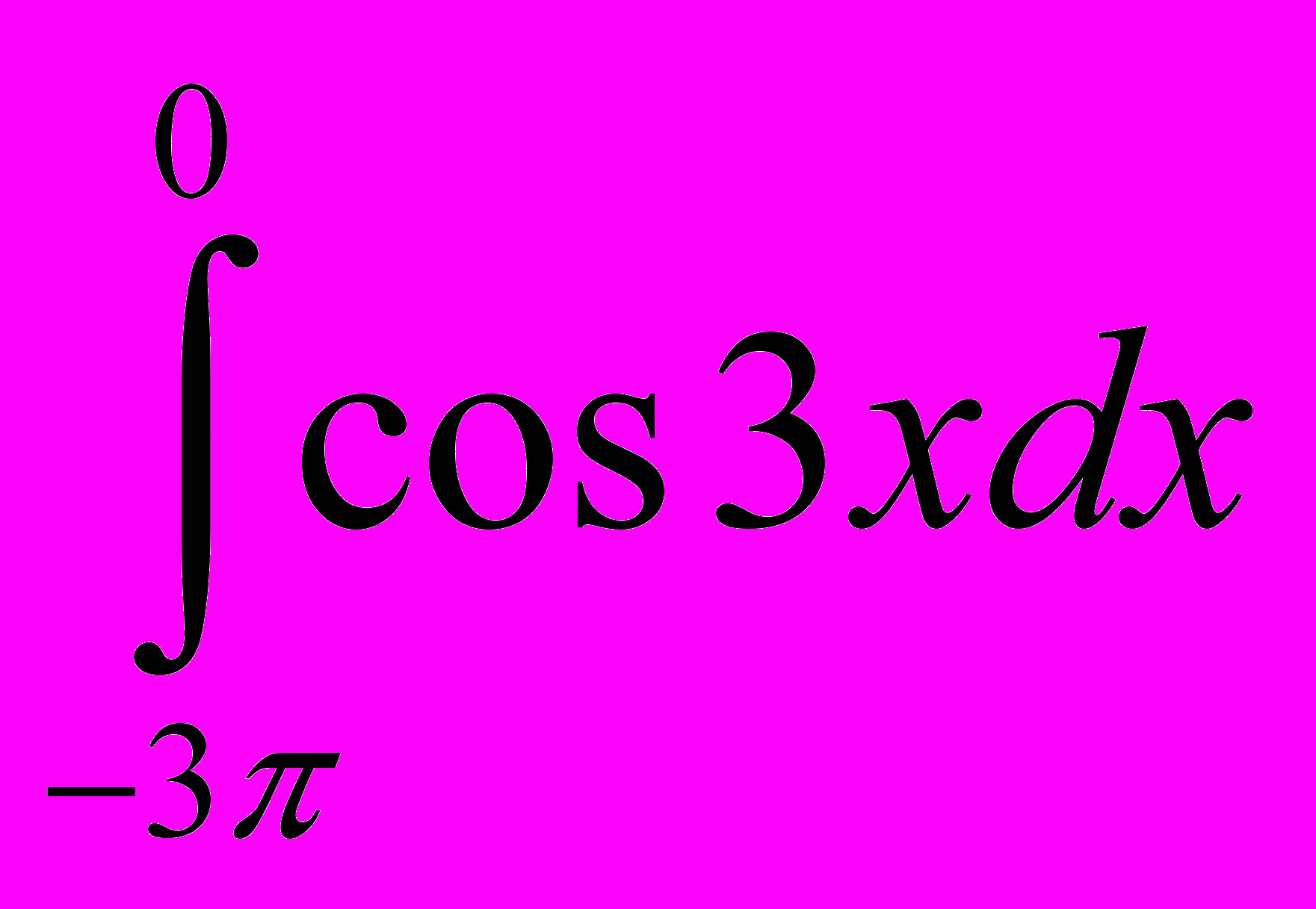 ; 21.
; 21.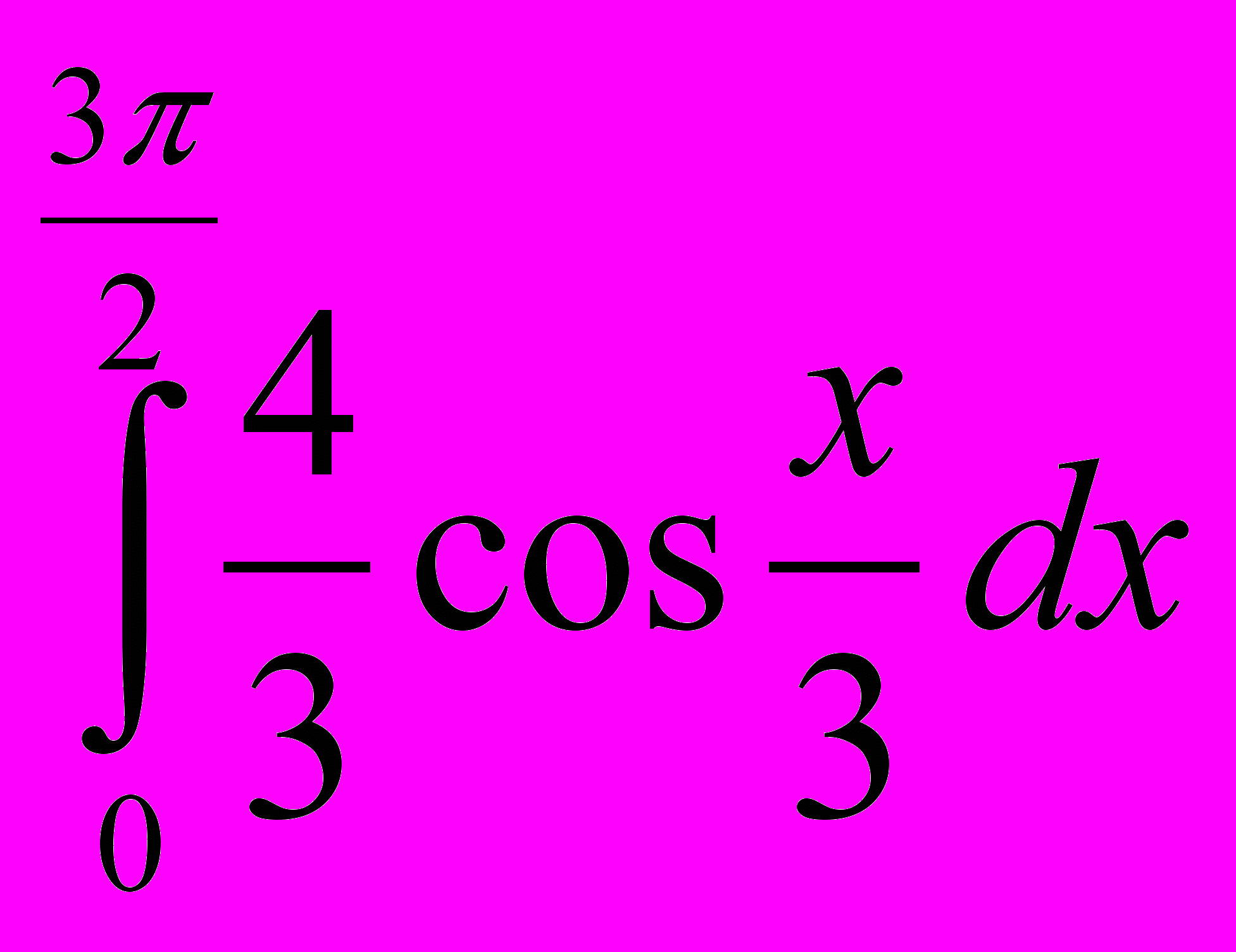 ;22.
;22.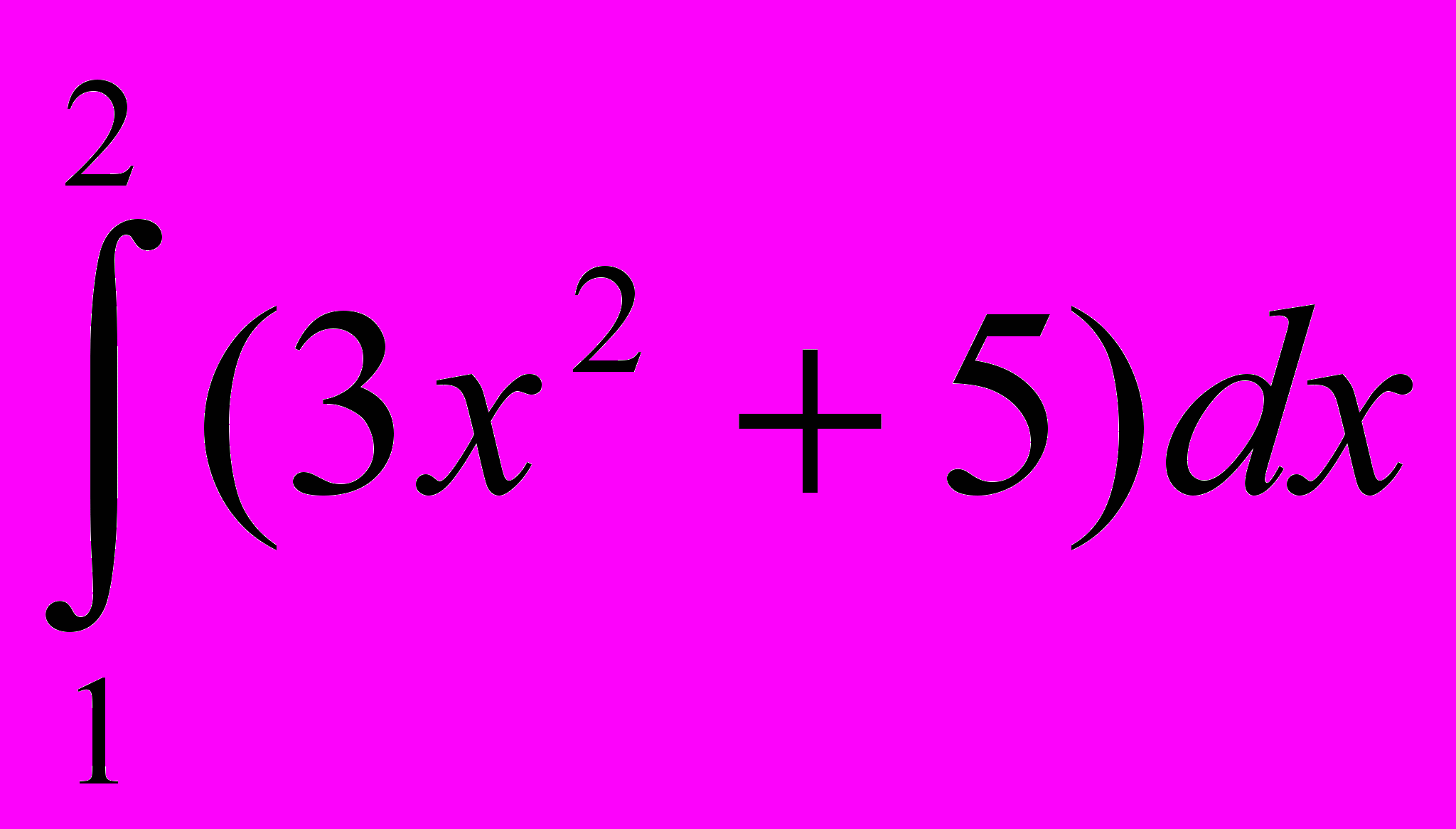 ; 23.
; 23.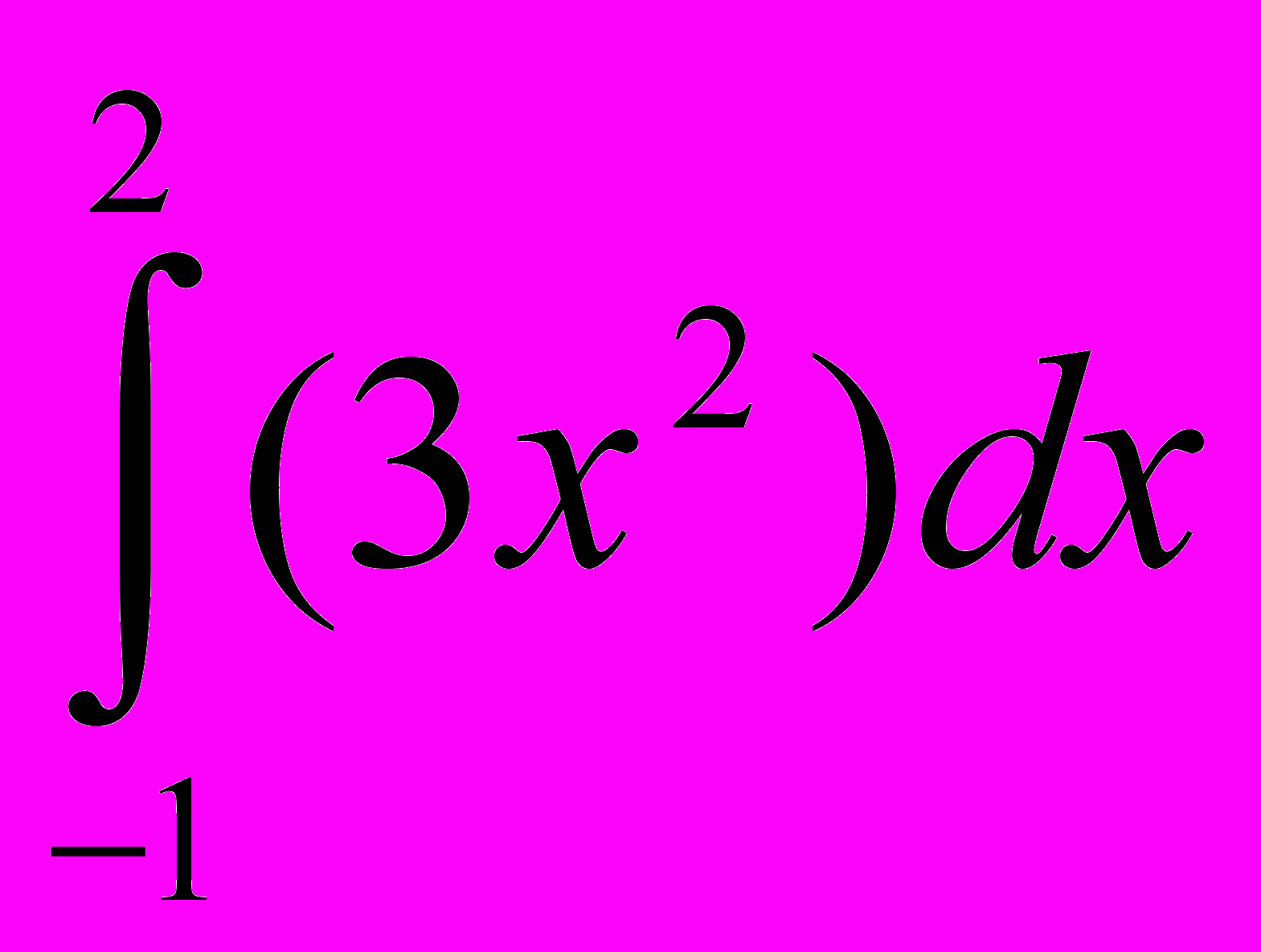 ; 24.
; 24.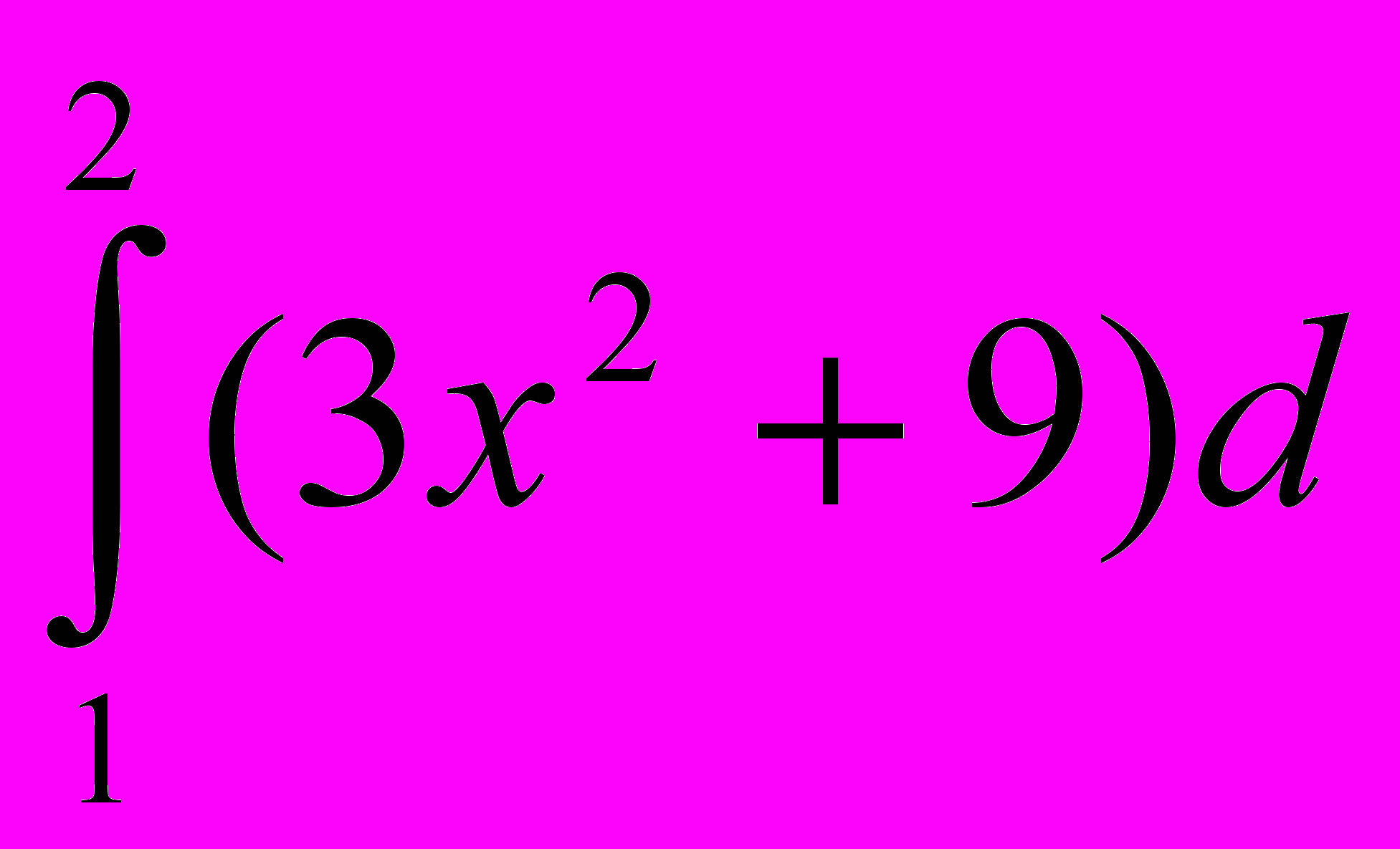 ; 25.
; 25.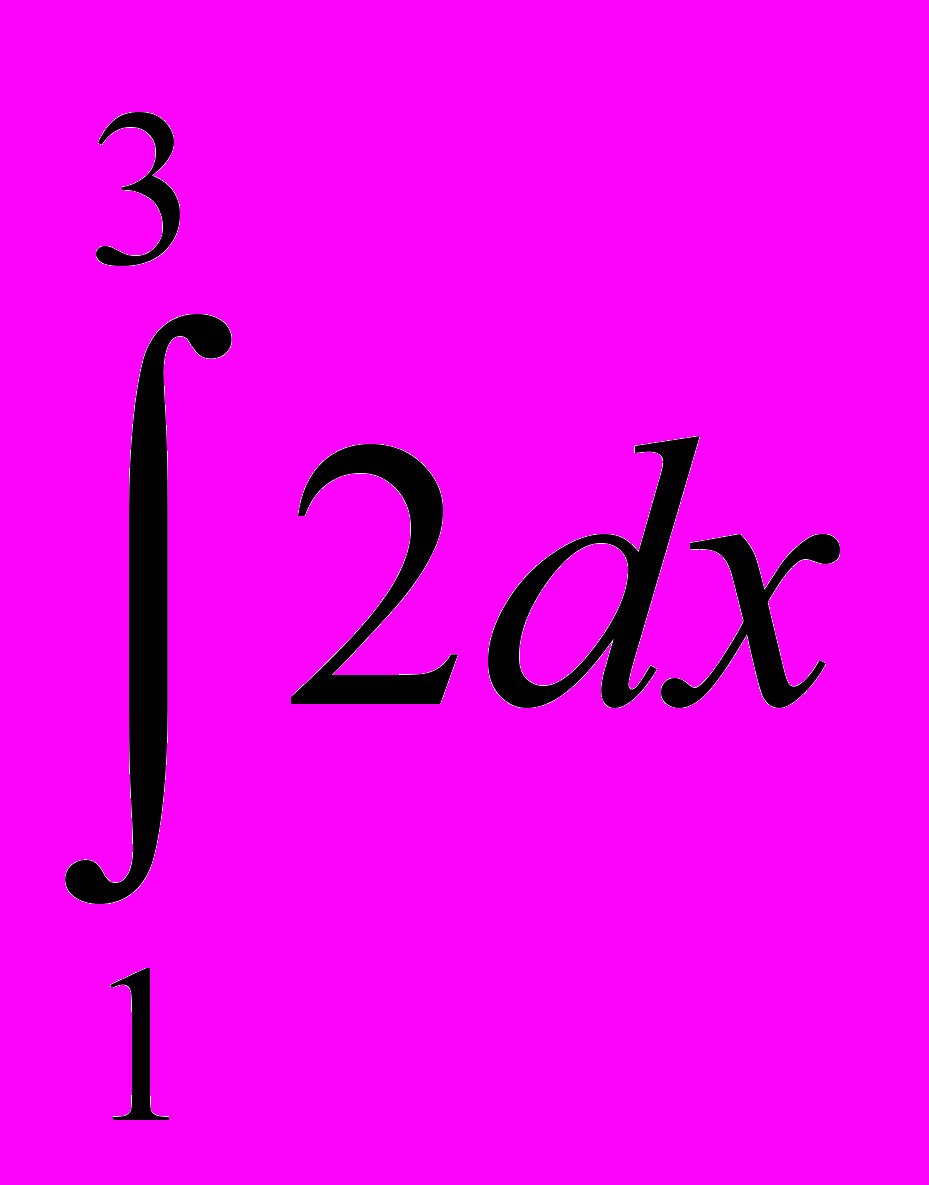 ; 26.
; 26.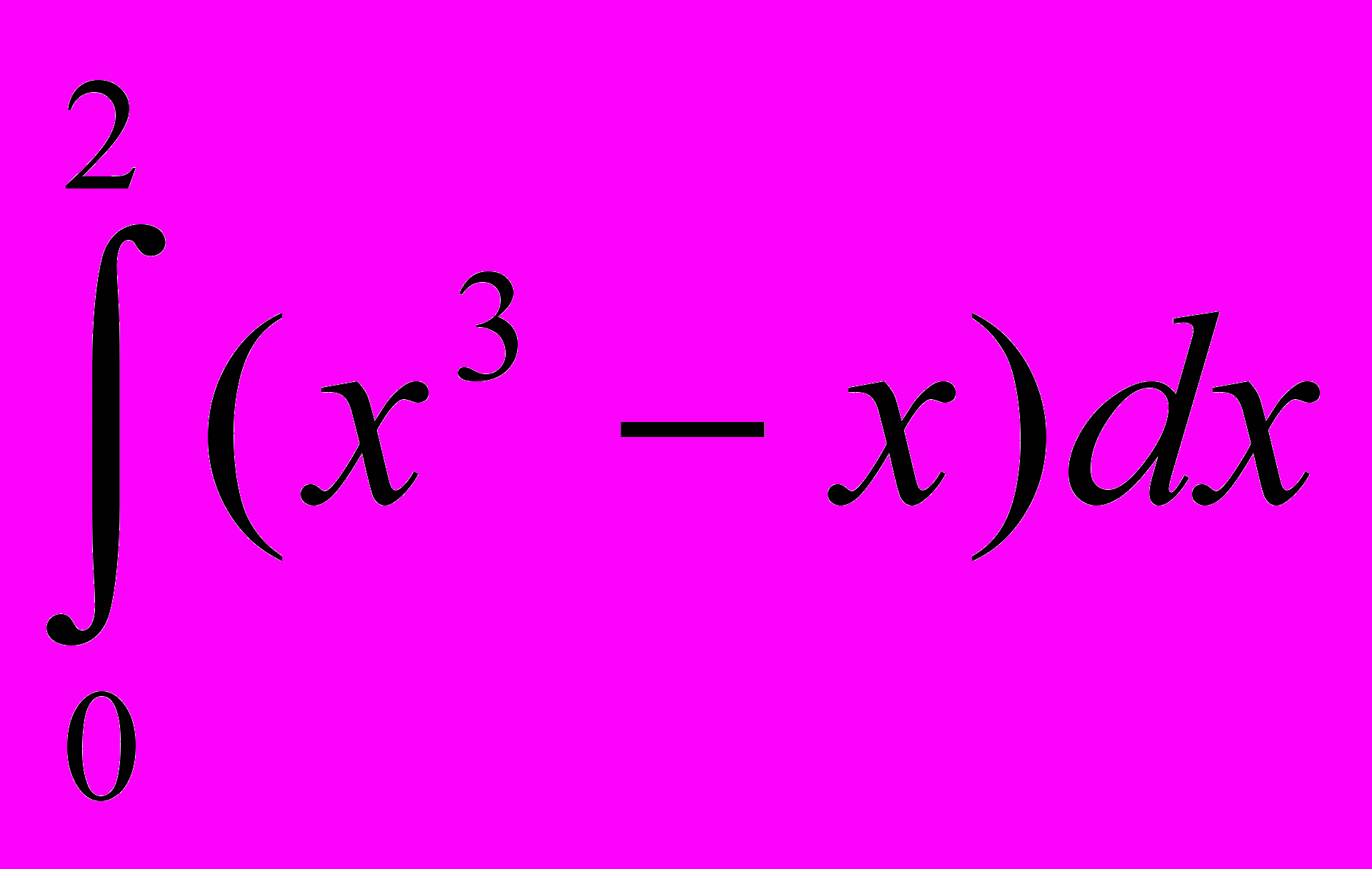 ; 27.
; 27.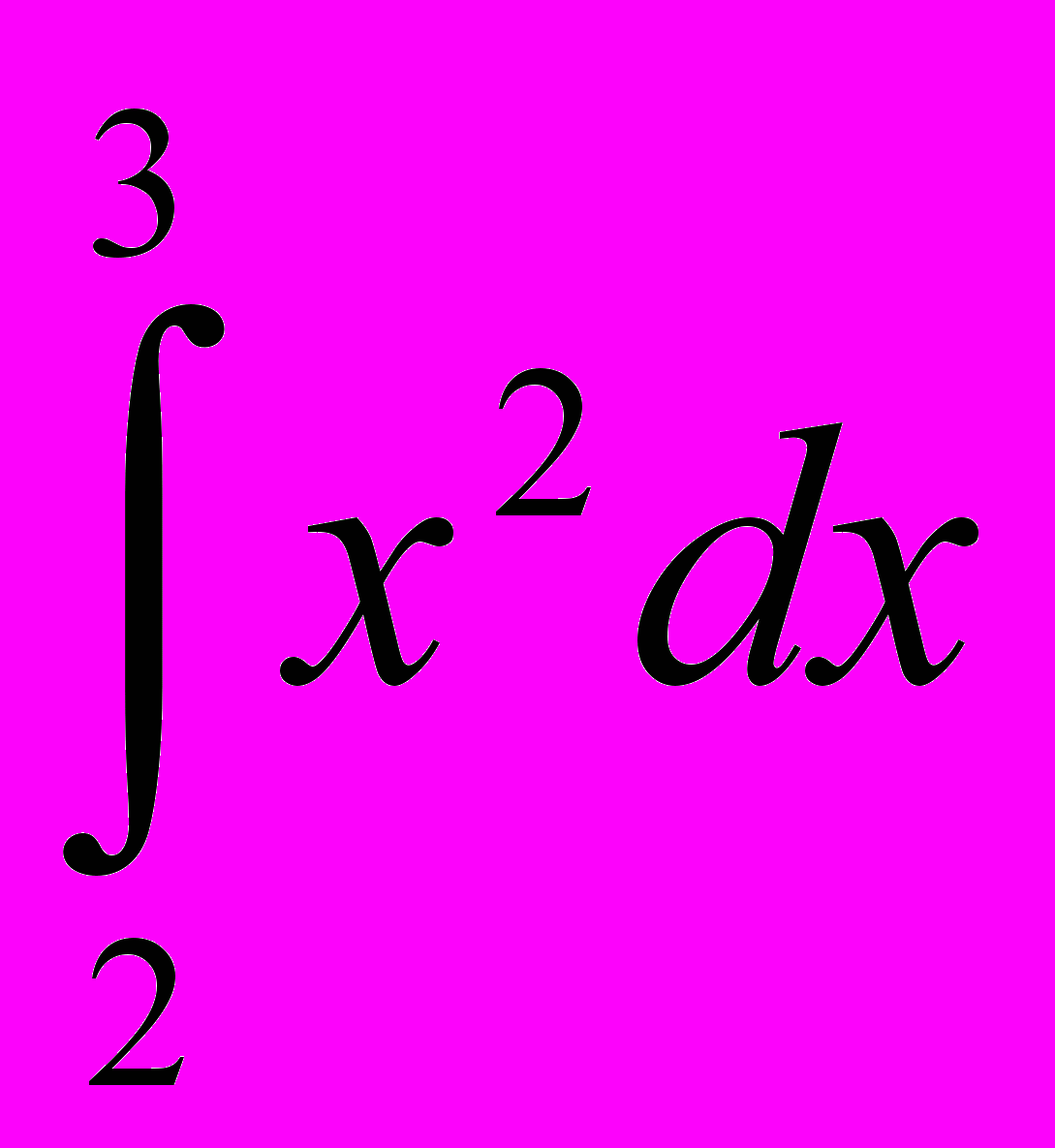 ; 28.
; 28.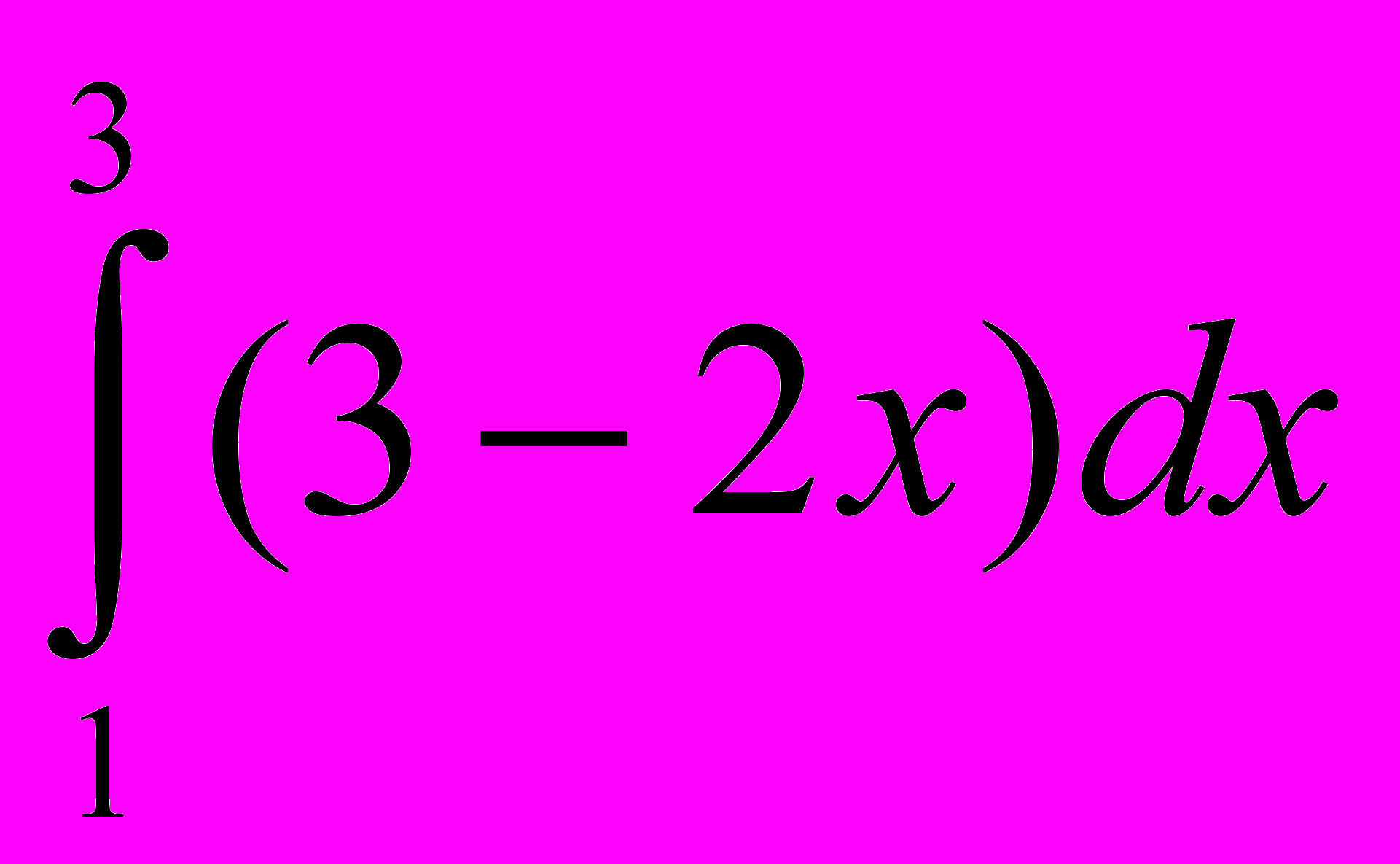 .
.Вы все успешно справились с испытаниями и всех вас решено принять в общество рыцарей красной розы.
Звучит музыка.
Чтобы пробудить у современного ученика интерес к математике, учитель должен постоянно искать, применять новые методы, приемы, новые формы урока. Конечно, нестандартные уроки, необычные по замыслу, методике проведения больше нравятся ученикам, чем будничные занятия со строгой структурой и установленным режимом работы. Поэтому практиковать такие уроки следует всем учителям. Но превращать нестандартные уроки в главную форму работы, вводить их в систему нецелесообразно из – за большой потери времени, отсутствия серьезного познавательного труда, невысокой результативности и т.п. Такие уроки можно проводить как обобщающие уроки по разделам. В 5 – 6 классах следует как можно чаще проводить нестандартные уроки, т.к. в этом возрасте ребята постоянно ощущают потребность в игре, игровом общении. В 7 – 9 классах применение нестандартных уроков позволяет не только повысить интерес к предмету, но и расширяет и углубляет знания учащихся. Использование нестандартных форм на уроках является эффективным средством активизации познавательной деятельности учащихся, положительно влияющим на повышение качества знаний, умений и навыков, развитие умственной деятельности.
Литература:
1. Минскин Е.М. От игры к знаниям. М.; Просвещение, 1982.
2. Элькоин Д.Б. Психология игры. М.; Педагогика, 1978.
3. Усатова Е.В. Соревнования на уроках математики. //Математика в школе, №6, 1993.
4. Горностаев П.В. Играть или учиться на уроке. //Математика в школе, №1, 1999.
