Geum.ru

Рабочая программа математический анализ наименование дисциплины Специальность 010400-Физика, направление 510400-Физика Факультет

Вид материалаРабочая программа

Содержание


Рабочая программа курса
II. Содержание учебного материала
III. Тематическое планирование
V. Примерные задачи математического практимума.
VI. Необходимый минимум подготовки студента для итоговой положительной оценки.
Подобный материал:


ИВАНОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ


УТВЕРЖДАЮ

Декан физического_ факультета


_ _ _ _ _ _ _ _ _ _ _ _ _Е.В. Сметанин__

подпись Ф. И О

«______» _____________200__г.


РАБОЧАЯ ПРОГРАММА


__Математический анализ__

наименование дисциплины


Специальность 010400-Физика, направление 510400-Физика


Факультет физический__________________

Курс_1–2______Семестр_I, II, III_______

Кафедра геометрии____________________

Общая трудоемкость дисциплины _480_________________

В том числе:

Лекции_162________________

Практические занятия_144__________

Лабораторные занятия__—_______________________

Самостоятельная работа_174_________


Рабочая программа принята на заседании кафедры геометрии

«___»__________200__г.


Заведующий кафедрой _________________ _М.А. Паринов____

подпись Ф. И О


РАБОЧАЯ ПРОГРАММА КУРСА


Математический анализ

(Наименование курса)


I. Объяснительная записка

Цель курса, соотнесенная с общими целями образовательной профессиональной программы: обеспечить базовую математическую подготовку студентов младших курсов в разделе математического анализа, необходимую для дальнейшего изучения предметов как математического так и физического цикла.

Задачи курса: Усвоение студентами теоретического материала: теории вещественных функций, теории пределов и непрерывных функций, дифференциального и интегрального исчисления функций одной и нескольких переменных, теории числовых рядов, элементов теории обобщенных функций. Создание навыка применения студентами указанного выше материала для решения математических и физических задач. Воспитание математической культуры; способности к постановке, решению и грамотному оформлению решений математических задач.

Нормативно-методические материалы, на основании которых составлена рабочая программа: государственный стандарт, сборник программ по курсам Высшая математика.

Формы организации учебного процесса и самостоятельной работы студентов:

Аудиторные занятия: лекции, практические занятия (в том числе проверочные самостоятельные и контрольные работы). Самостоятельная работа студентов: решение задач математического практикума (список примерных задач см. п. V), усвоение материала лекций, решение задач при подготовке к практическим занятиям, выполнение домашних контрольных работ.

Требования к уровню освоения содержания курсов: Студент должен уметь: формулировать определения курса, теоремы (в том числе формулы); применять их на практике для решения задач, давать доказательства теорем в объеме и с уровнем строгости, соответствующем лекционному курсу (необходимый минимум вопросов для положительной оценки по всем темам приведен в п. VI).

II. Содержание учебного материала

2.1. Разделы курса

Раздел I. Дифференциальное и интегральное исчисление функций одной вещественной переменной.

Раздел II. Дифференциальное и интегральное исчисление функций нескольких переменных.

Раздел III. Числовые и функциональные ряды. Несобственные интегралы.


2.2. Краткое описание разделов (по темам).


Введение.

Предмет математики. Физические явления как источник математических понятий.


I. Дифференциальное и интегральное исчисление функций одной вещественной переменной.


1. Пределы последовательностей и функций. Непрерывность функции. Свойства непрерывных функций. Элементарные функции.

Элементы теории множеств. Основные сведения о вещественных числах; точные грани числовых множеств. Числовые последовательности; основные теоремы о пределах последовательностей. Предел монотонной последовательности. Предельные точки последовательности, критерий Коши сходимости последовательности. Функция и ее предел; основные теоремы о пределах функций; критерий Коши; сравнение величин. Непрерывность функции; точки разрыва. Основные теоремы о свойствах непрерывных функций. Равномерная непрерывность функции. Монотонные функции. Элементарные функции: определение и непрерывность.

2. Производная функции.

Понятие производной. Основные правила и формулы дифференцирования (арифметические свойства, производная сложной и обратной функции). Производные элементарных функций. Производная вектор-функции. Дифференциал. Производные и дифференциалы высшего порядка.

3. Основные теоремы о дифференцируемых функциях.

Возрастание и убывание функции в точке. Теоремы о нуле производной. Формулы конечных приращений. Методы приближенного решения нелинейных уравнений и оценки погрешностей этих методов. Формула Тейлора; остаточный член в формах Лагранжа, Коши и Пеано. Разложение по формуле Тейлора основных элементарных функций. Применение формулы Тейлора в приближенных вычислениях. Правило Лопиталя раскрытия неопределенностей.

4. Исследование функции и построение ее графика.

Условие монотонности функции. Экстремумы. Направление выпуклости и точки перегиба графика функции. Асимптоты графика функции.

5. Неопределенный интеграл.

Понятие неопределенного интеграла. Основные методы и формулы интегрирования. Комплексные числа, многочлены, интегрирование рациональных дробей и некоторых других классов функций.

6. Определенный интеграл Римана.

Понятие определенного интеграла. Верхние нижние суммы. Необходимое и достаточное условие интегрируемости функции. Классы интегрируемых функций. Свойства определенного интеграла. Формулы среднего значения. Связь с неопределенным интегралом. Геометрические и физические приложения. Приближенное вычисление интегралов и оценки погрешностей.

7. Несобственный интеграл.

Несобственный интеграл I и II-го рода: определение, сходимость, критерий Коши. Абсолютная и условная сходимость. Признаки сходимости.


II. Дифференциальное и интегральное исчисление функций нескольких вещественных переменных.


1. Функции нескольких переменных.

Действительное n-мерное пространство. Последовательности точек n-мерного пространства. Понятие функции нескольких переменных. Предел функции нескольких переменных. Непрерывность. Свойства непрерывных функций. Частные производные. Дифференцируемость функции нескольких переменных. Касательная плоскость и нормаль к поверхности. Дифференцируемость сложной функции. Замена переменных. Первый дифференциал. Производная по направлению. Градиент. Производные и дифференциалы высших порядков. Формула Тейлора. Экстремум функции нескольких переменных. Неявные функции. Понятие зависимости функций. Условный экстремум. Метод множителей Лагранжа.

2. Геометрические приложения Дифференциального исчисления.

Понятие об особых точках кривых. Порядок касания кривых. Соприкасающаяся окружность. Огибающая семейства кривых. Кривизна и кручение пространственной кривой.

3. Кратные интегралы.

Двойной интеграл: критерий существования, основные свойства. Вычисление двойных интегралов: повторное интегрирование и замена переменных. Тройные и n-кратные интегралы. Их свойства и способы вычисления. Геометрические приложения.

4. Криволинейные и поверхностные интегралы. Геометрические свойства поверхностей.

Длина дуги кривой. Криволинейные интегралы первого и второго рода. Понятие поверхности. Внутренние координаты на поверхности. Первая квадратичная форма. Измерение длин, углов, площадей на поверхности. Вторая квадратичная форма. Главные кривизны, полная и средняя кривизна поверхности. Поверхностные интегралы первого и второго рода.


III. Ряды и несобственные интегралы.


1. Числовые и функциональные ряды.

Числовые ряды. Абсолютная и условная сходимость. Признаки сходимости. Функциональные последовательности и ряды. Равномерная сходимость. Признаки равномерной сходимости и свойства равномерно сходящихся функциональных последовательностей и рядов. Почленное дифференцирование и интегрирование. Сходимость в среднем. Степенные ряды.

2. Интегралы, зависящие от параметра. Кратные несобственные интегралы.

Интегралы, зависящие от параметра. Признаки равномерной сходимости несобственных интегралов, зависящих от параметра. Эйлеровы интегралы. Асимптотика интегралов, зависящих от параметра. Кратные несобственные интегралы, зависящие от параметра. Ньютонов потенциал.

3. Ряды Фурье. Интеграл Фурье

Евклидовы пространства. Понятие гильбертова пространства. Ряды Фурье по ортогональной системе элементов евклидова пространства. Неравенство Бесселя и равенство Парсеваля. Полные и замкнутые системы. Полнота и замкнутость тригонометрической системы. Разложение функций в ряд Фурье по тригонометрической системе функций. Сходимость и равномерная сходимость тригонометрического ряда Фурье.Свойства рядов Фурье по тригонометрической системе. Комплексная форма ряда Фурье. Интеграл Фурье. Преобразования Фурье. Формулы обращения. Дискретное преобразование Фурье.

4. Элементы теории обобщенных функций.

Понятие обобщенной функции. Основные операции над обобщенными функциями.

d-функция.


III. Тематическое планирование



№

п/п

Наименование разделов, тем
Всего часов (общая трудоем-кость
Аудиторные занятия

Самосто –ятельная работа

Лекции
Семинары, практичес-кие занятия

1
Пределы последовательностей и функций. Непрерывность функции. Свойства непрерывных функций. Элементарные функции
60
26
16
18

2
Производная функции
32
10
10
12

3
Основные теоремы о дифференцируемых функциях
32
12
8
12

4
Исследование поведения функций и построение ее графика
24
4
10
10

5
Неопределенный интеграл
38
12
16
10

6
Определенный интеграл Римана
44
14
12
18

7
Несобственный интеграл
10
2
4
4

8
Функции нескольких переменных
58
22
18
18

9
Геометрические приложения дифференциального исчисления
14
4
4
6

10
Кратные интегралы
38
8
16
14

11
Криволинейные и поверхностные интегралы. Геометрические свойства поверхностей
30
10
10
10

12
Числовые и функциональные ряды
30
14
6
10

13
Интегралы, зависящие от параметра. Кратные несобственные интегралы
20
8
4
8

14
Ряды Фурье. Интеграл Фурье
30
10
6
14

15
Элементы теории обобщенных функций
20
6
4
10






















Итого
480
162
144
174


IV. Формы промежуточного и итогового контроля.

1. Аудиторные самостоятельные работы (10-15 мин).

2. Контрольные работы (по завершению раздела).

3. Проверка задач математического практикума (выполняемых студентами вне аудиторных занятий).

4. Зачет.

5. Экзамен.

V. Примерные задачи математического практимума.

1. Символьные методы решения алгебраических уравнений до четвертой степени включительно.

2. Численное решение уравнений вида  f(x) = 0  методами деления пополам, простой итерации, хорд, касательных.

3. Численные и символьные методы нахождения локального экстремума функций одной и нескольких переменных.

4. Численное и символьное интегрирование.

5. Численные и символьные методы в задачах суммирования рядов и разложения в ряды.

VI. Необходимый минимум подготовки студента для итоговой положительной оценки.

I. Дифференциальное и интегральное исчисление функций одной вещественной переменной.

1. Два определения предела функции (по Коши и по Гейне). Пример функции, не имеющей предела в некоторой точке.

2. Определение непрерывности функции в точке. Примеры функций, имеющих разрывы: устранимый, 1 рода, 2 рода.

3. Определение производной и дифференциала функции. Таблица производных основных элементарных функций.

4. Понятие первообразной и неопределенного интеграла. Таблица основных неопределенных интегралов. Формула интегрирования по частям. Формула замены переменной.

5. Определение равномерной непрерывности функции. Примеры функций, равномерно непрерывных и не являющихся таковыми на некотором промежутке.

6. Формула Лагранжа конечных приращений. Достаточное условие монотонности функции на промежутке.

7. Формула Тейлора с остаточным членом в форме Пеано. Пять основных разложений по формуле Маклорена: ex, sin x, cos x, ln(1+x), (1+x)a.

8. Понятие экстремума функции. Необходимое условие экстремума. Достаточное условие экстремума.

9. Понятие направления выпуклости графика функции. Достаточное условие определенного направления выпуклости. Точка перегиба графика функции. Необходимое условие перегиба графика в данной точке. Графики элементарных функций.

10. Понятие определенного интеграла. Необходимое и достаточное условие интегрируемости функции на сегменте.

11. Формула Ньютона-Лейбница. Формула замены переменной в определенном интеграле.

12. Вычисление длин кривых и площадей плоских фигур с помощью определенного интеграла.


II. Дифференциальное и интегральное исчисление функций нескольких вещественных переменных.

1. Два определения предела функции многих переменных. Пример функции, не имеющей предела в точке.

2. Непрерывность функции по совокупности переменных и по отдельным переменным. Связь между ними. Примеры.

3. Определение частных производных и дифференцируемости функции. Связь между этими понятиями. Примеры.

4. Производная по направлению и градиент; формула связывающая их. Уравнение касательной плоскости к поверхности z=F(x, y);

5. Понятие неявной функции. Формула производной неявной функции.

6. Понятие экстремума функции многих переменных. Необходимое условие экстремума. Достаточное условие экстремума. Понятие условного экстремума.

7. Вычисление двойных и тройных интегралов с помощью повторного интегрирования. Формулы замены переменных в двойных и тройных интегралах. Переход к цилиндрическим и сферическим координатам.

8. Вычисление криволинейных интегралов первого и второго рода с помощью определенного интеграла.

9. Формула Грина. Условия независимости криволинейного интеграла на плоскости от пути интегрирования.

10. Формула площади поверхности, заданной: а) уравнением z=F(x, y); б) параметрически.

11. Вычисление поверхностных интегралов первого и второго рода с помощью двойного интеграла.

12. Формула Остроградского, ее физический смысл.

13. Формула Стокса, ее физический смысл.

14. Потенциальные и соленоидальные векторные поля, их свойства.

III. Ряды и несобственные интегралы

1. Понятие сходимости числового ряда. Сходимость (расходимость) ряда 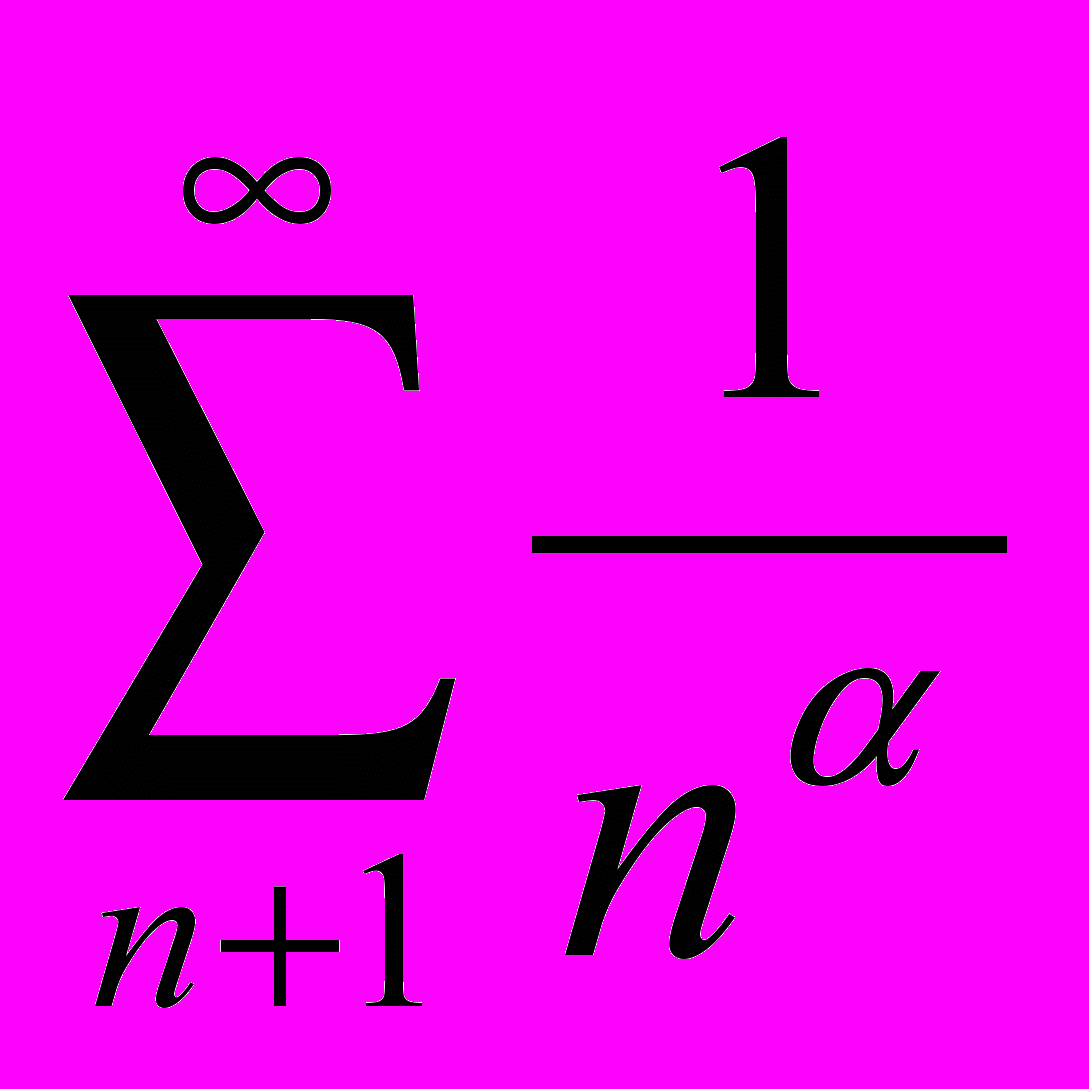при различных .

2. Понятие равномерной сходимости функциональных последовательностей и рядов. Примеры.

3. Понятие сходимости в среднем.

4. Понятие несобственных интегралов 1 и 2 рода. Сходимость (расходимость) интегралов 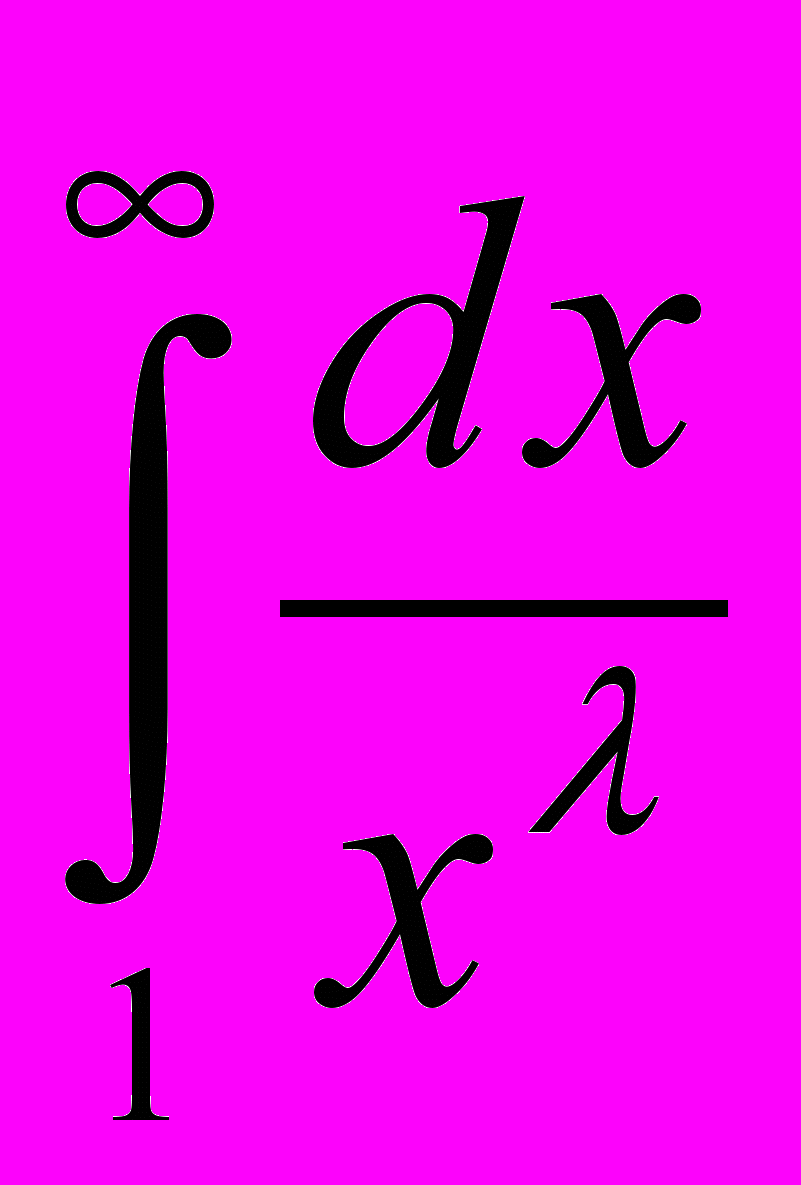и 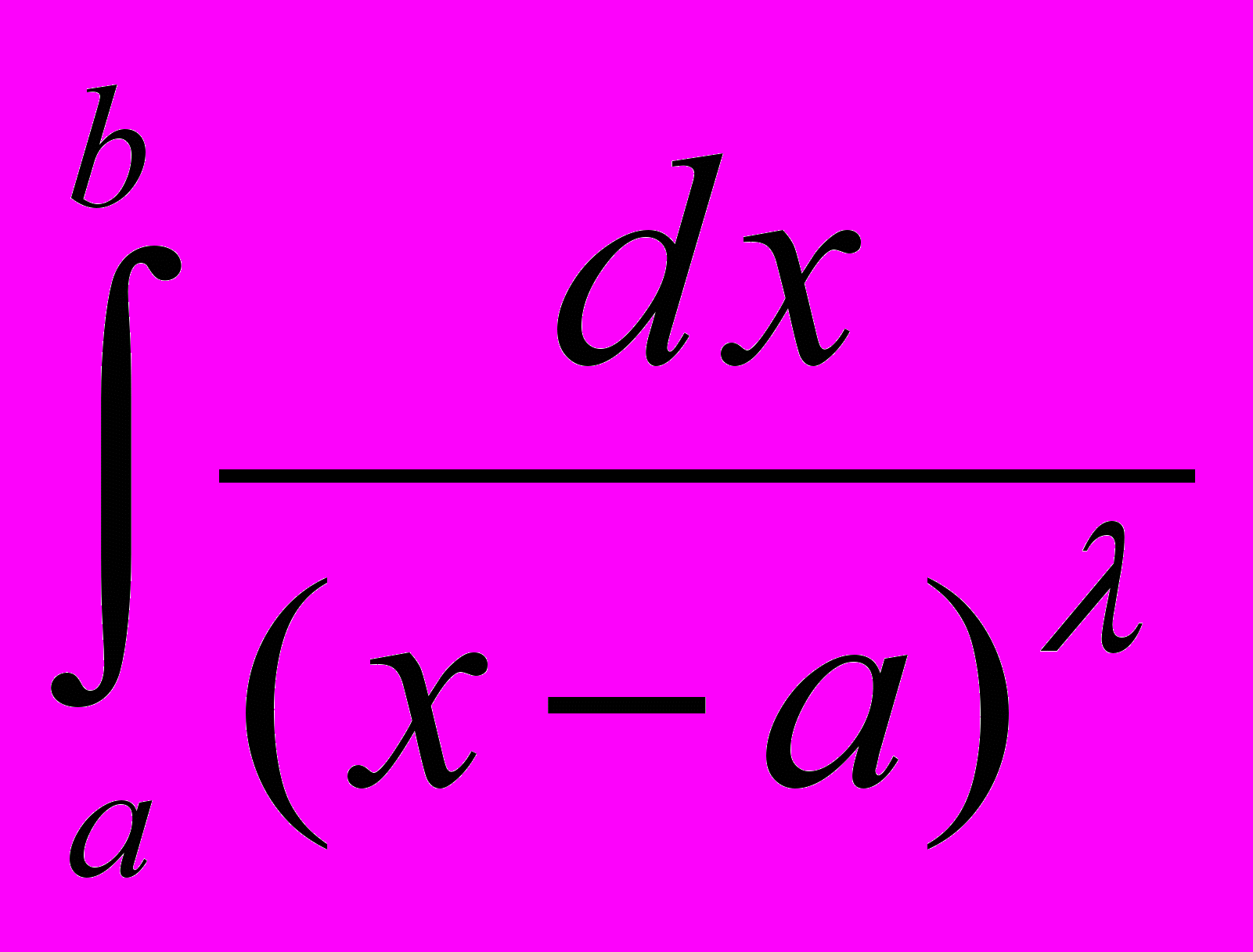при различных .

5. Понятие равномерной сходимости несобственных интегралов, зависящих от параметра. Примеры.

6. Тригонометрический ряд Фурье. Формулы для вычисления коэффициентов ряда Фурье.

7. Формулы преобразования Фурье и обратного преобразования.

8. Понятие -функции.


V. Учебно-методическое обеспечение.

5.1. Рекомендуемая литература (основная).

1. Ильин В.А., Позняк Э.Г. Основы математического анализа, ч.I, ч.II М.:Наука, 1998.

2. Кудрявцев Л.Д. Краткий курс математического анализа. М.: Высшая школа, т.1,2 1998, т.3 1999.

3. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: Наука, 1999.

5.2. Рекомендуемая литература (дополнительная).

1. Никольский С.М. Курс математического анализа, Т.1,2 М.: Наука., 1990.

2. Фихтенгольц Г.М. Основы математического анализа, ч.1,2 «Лань», 2002.

3. Виноградова И.А., Олехник С.Н., Садовничий В.А. Задачи и упражнения по математическому анализу. В 2 кн. — М.: Высш. шк. 2002.

4. Бутузов В.Ф., Крутицкая Н.Ч., Медведев Г.Н., Шишкин А.А. Математический анализ в вопросах и задачах. Изд. 3-е. М.: Физматлит, 2000.

............................................................................................................................................................


Автор - составитель программы __________________ П.Г. Кононенко______

подпись Ф. И. О.