Лекция 13. Исследование функции, график функции
| Вид материала | Лекция |
СодержаниеТеорема 3. (необходимое условие перегиба) |
- Элективный курс «Функции и их графики» (9 класс), 62.92kb.
- Лекция Производная функции, 30.86kb.
- Урок алгебры в 10 классе Тема: «Логарифмы, логарифмическая функция, её свойства и график», 66.6kb.
- Программа вступительного экзамена в аспирантуру цэми ран по специальности 08. 00., 84.35kb.
- Курс лекций. Лекция Финансы и их функции. План. Сущность финансов и их функции. Роль, 1021.27kb.
- Лекция 11. Индивидуальный и рыночный спрос, 58.12kb.
- Лекция 1 Среднеквадратичное приближение функции, 58.12kb.
- Тема: «Квадратичная функция, её свойства и график», 103.05kb.
- Лекция Виртуальные функции. Дружественные функции, 70.17kb.
- Лекция Дифференцирование функций, 25.58kb.
Лекция 13. Исследование функции, график функции.
П.1 Выпуклость функции.
ОПР. Функция
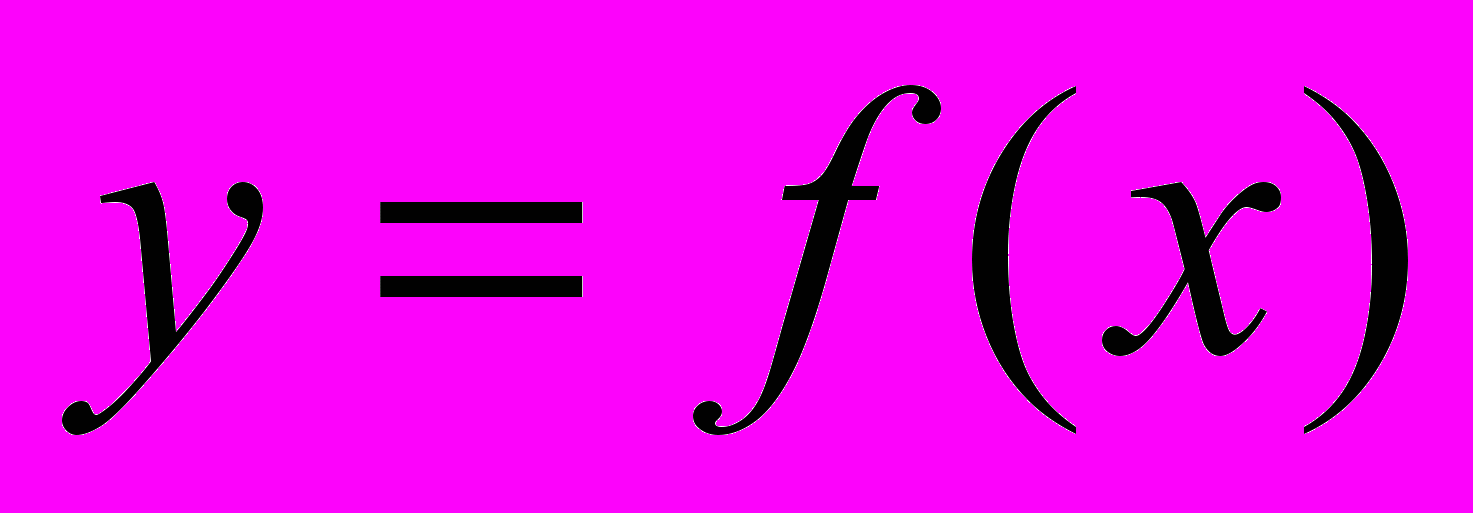 в точке
в точке 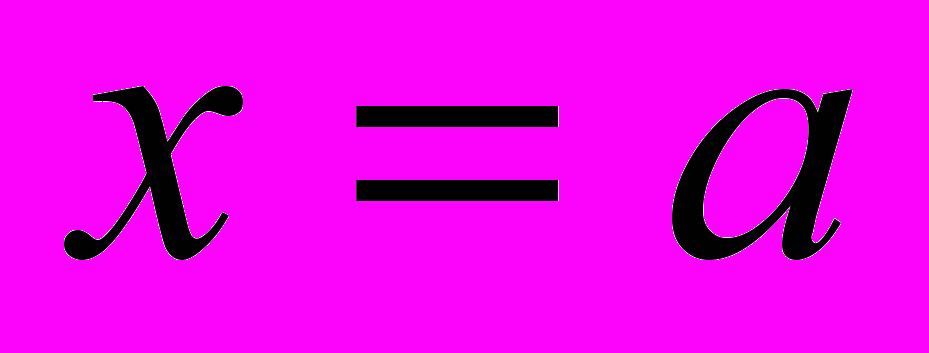 называется выпуклой (вниз), если выражение
называется выпуклой (вниз), если выражение 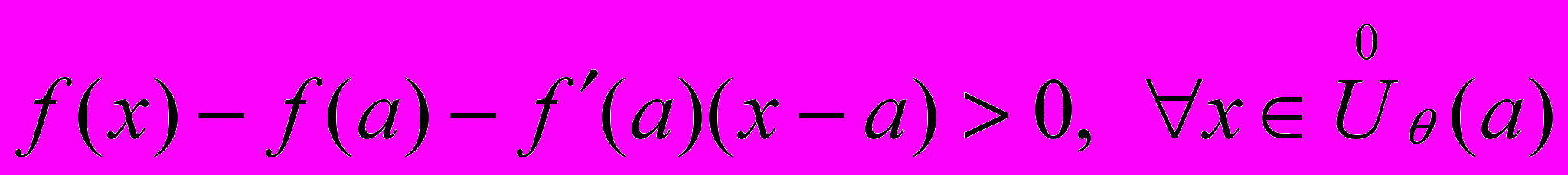 .
.ОПР. Функция
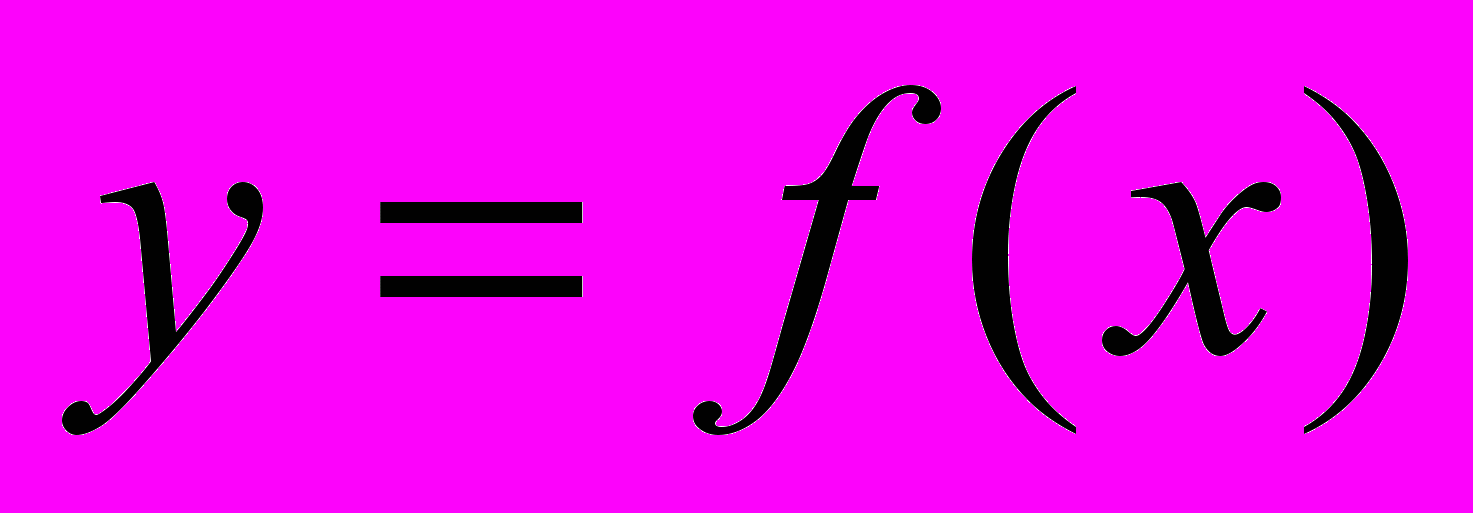 в точке
в точке 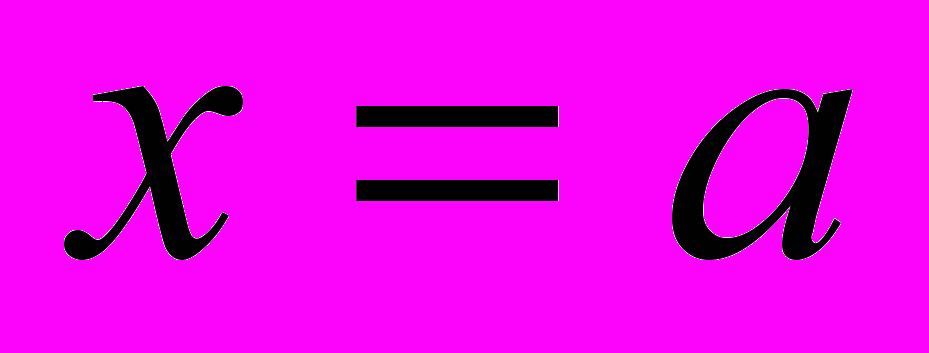 называется выпуклой (вверх), если выражение
называется выпуклой (вверх), если выражение 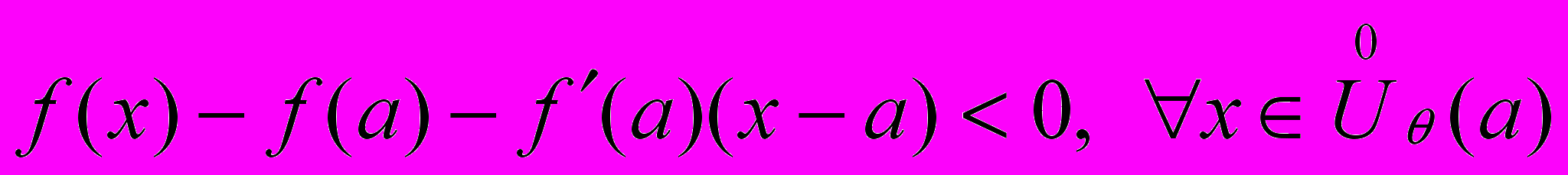
ОПР. Функция
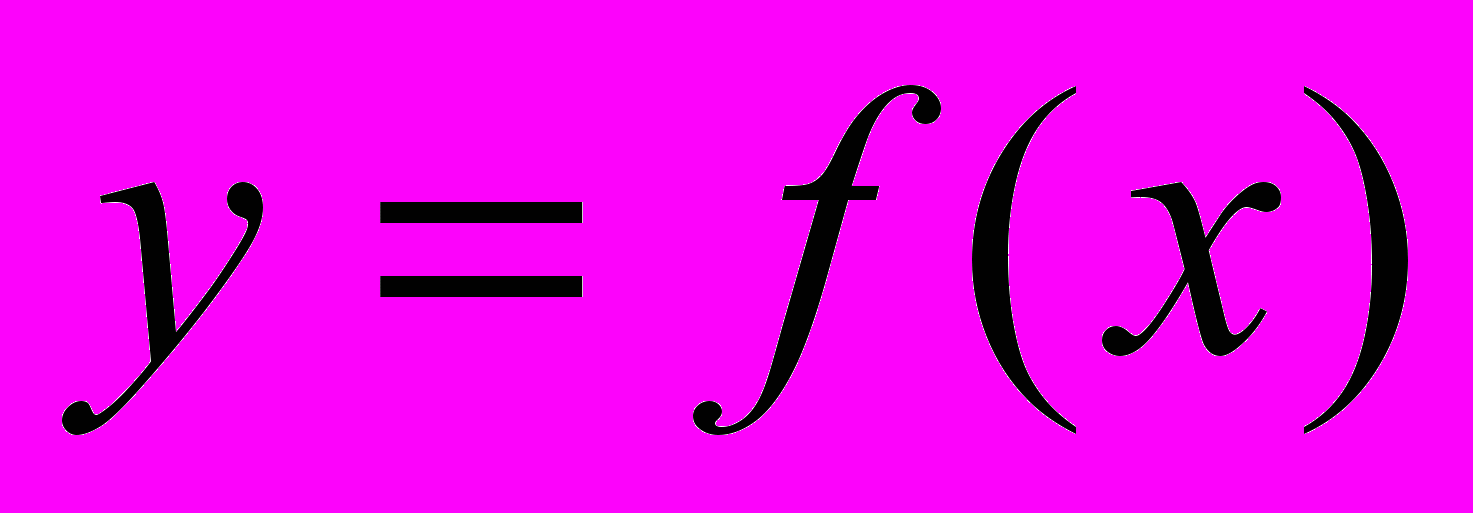 называется выпуклой (вниз или вверх) на интервале
называется выпуклой (вниз или вверх) на интервале 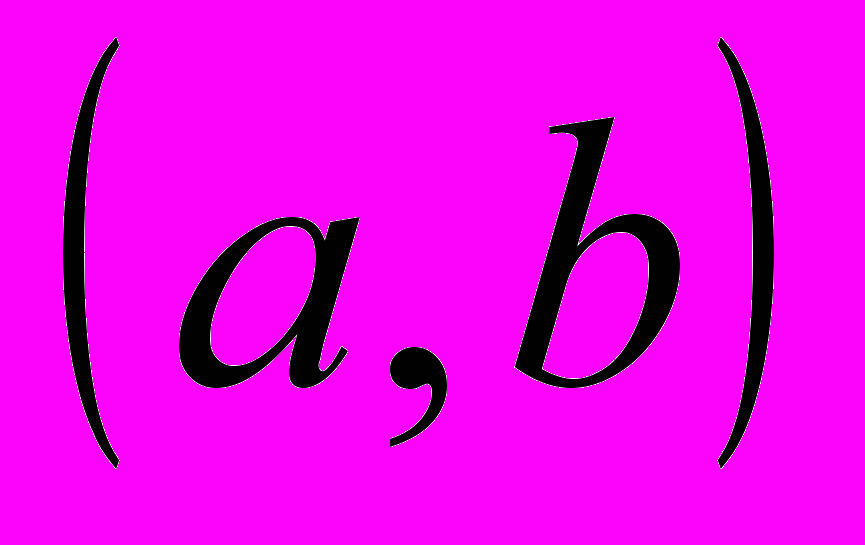 , если она выпукла (вниз или вверх) в каждой точке этого интервала.
, если она выпукла (вниз или вверх) в каждой точке этого интервала.ТЕОРЕМА 1 (ДОСТАТОЧНЫЕ УСЛОВИЯ ВЫПУКЛОСТИ по первой производной)
(1) Если при всех
 и при всех
и при всех  , то функция выпукла (вверх) в точке
, то функция выпукла (вверх) в точке 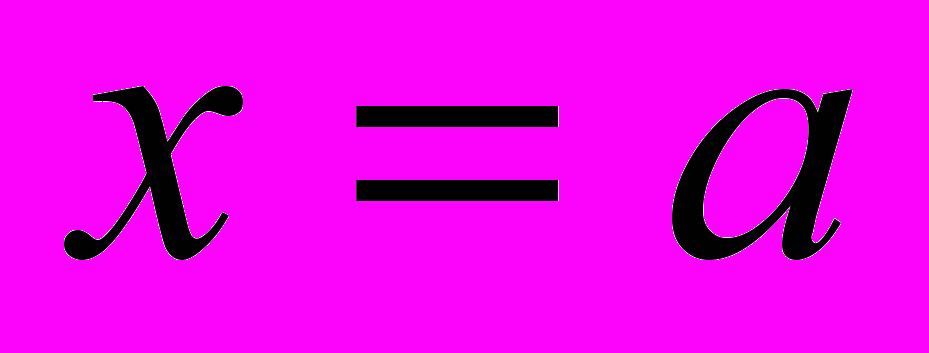 ,(2) Если при всех
,(2) Если при всех  и при всех
и при всех 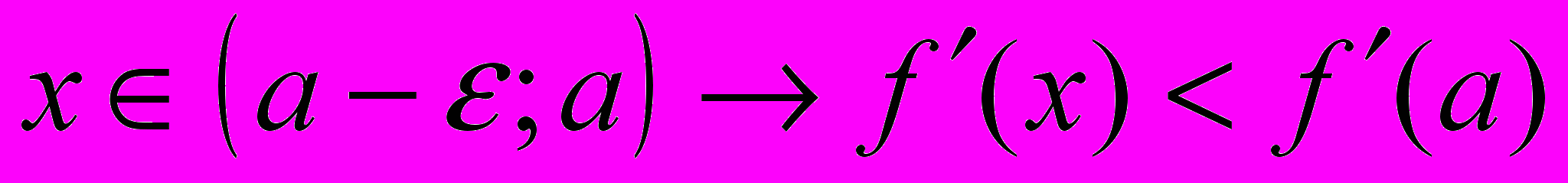 ,то функция выпукла (вниз) в точке
,то функция выпукла (вниз) в точке 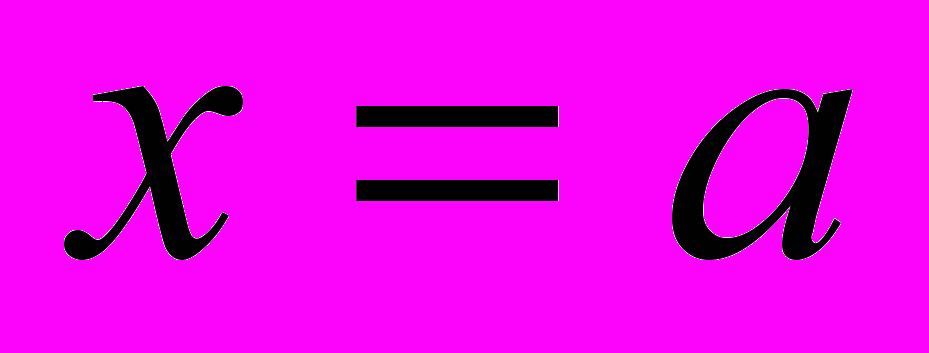 .
.ДОК.(1) На отрезке
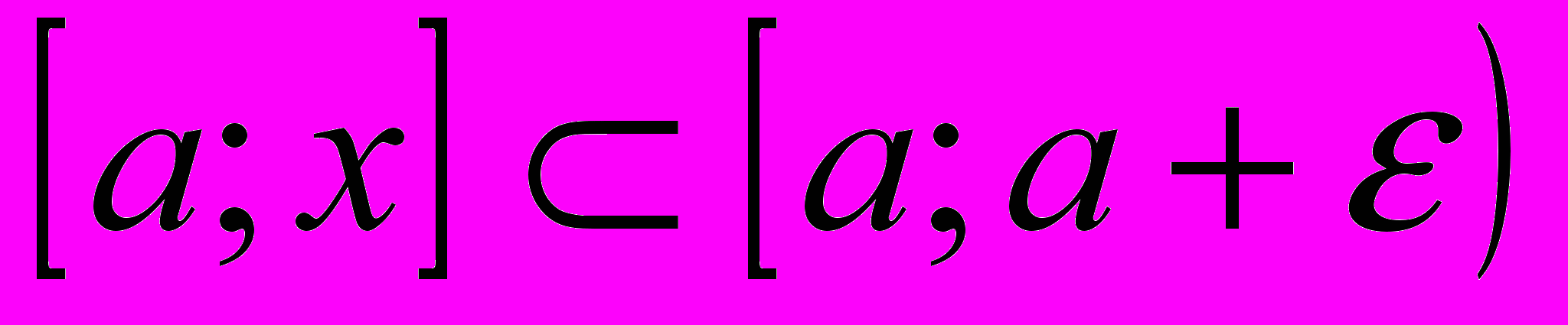 применим к функции теорему Лагранжа :
применим к функции теорему Лагранжа : 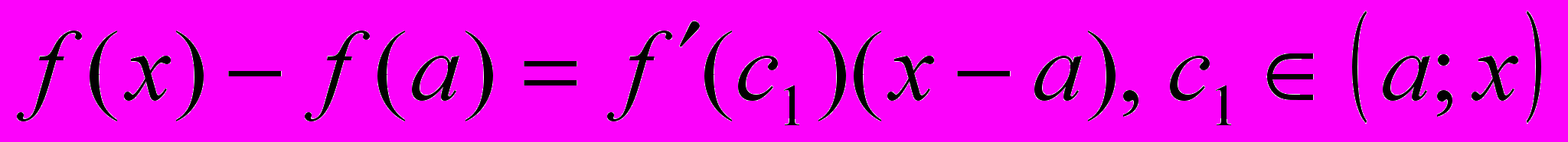 . Тогда
. Тогда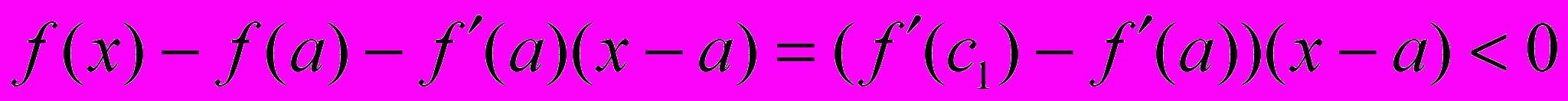 .
.На отрезке
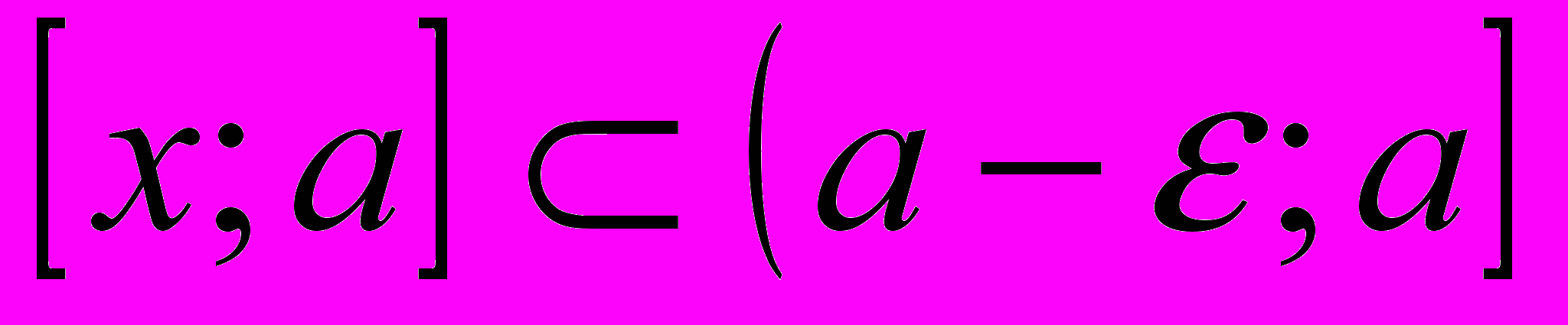 применим к функции теорему Лагранжа:
применим к функции теорему Лагранжа: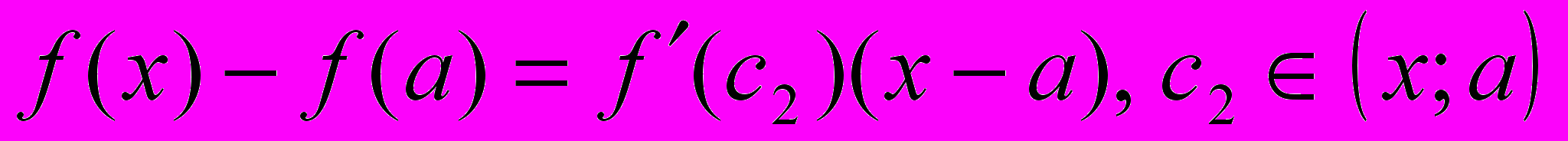 .
.Тогда
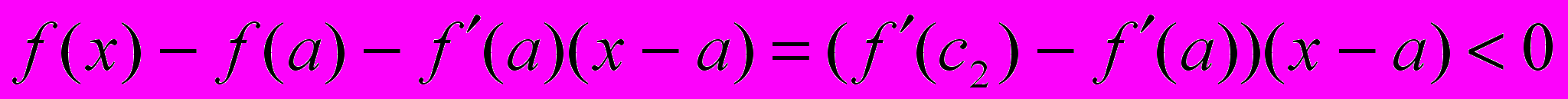 .
.Доказательство (2) самостоятельно.
ТЕОРЕМА 2. ( ДОСТАТОЧНЫЕ УСЛОВИЯ ВЫПУКЛОСТИ по второй производной)
(1) Если для всех
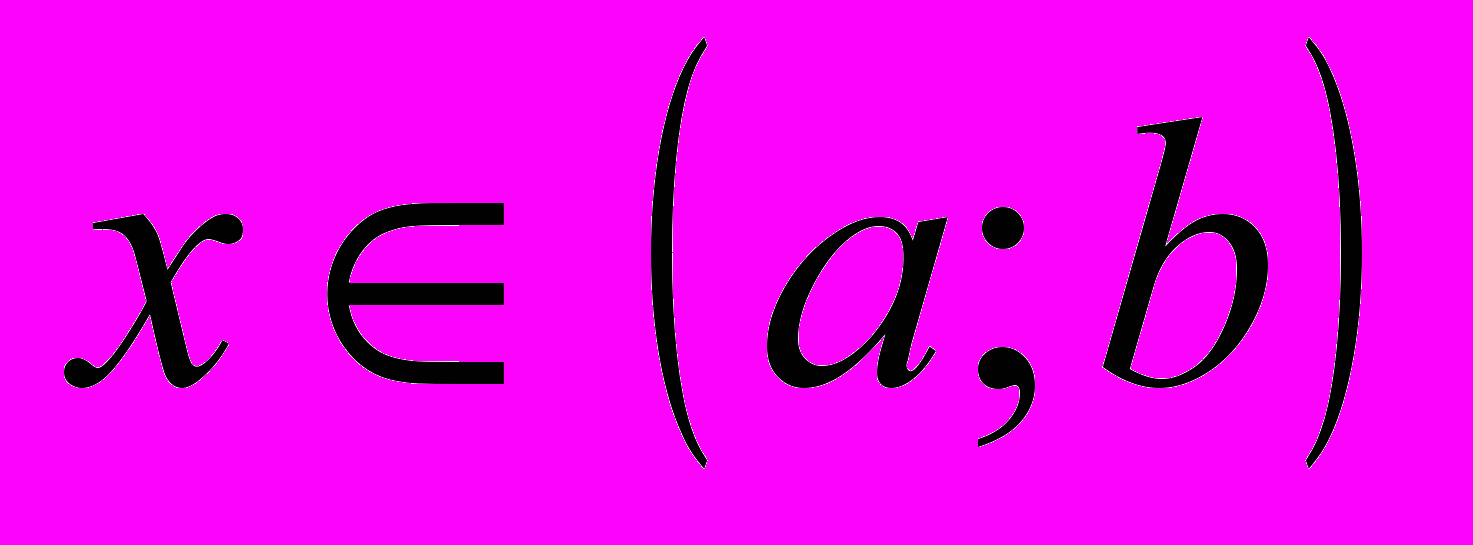
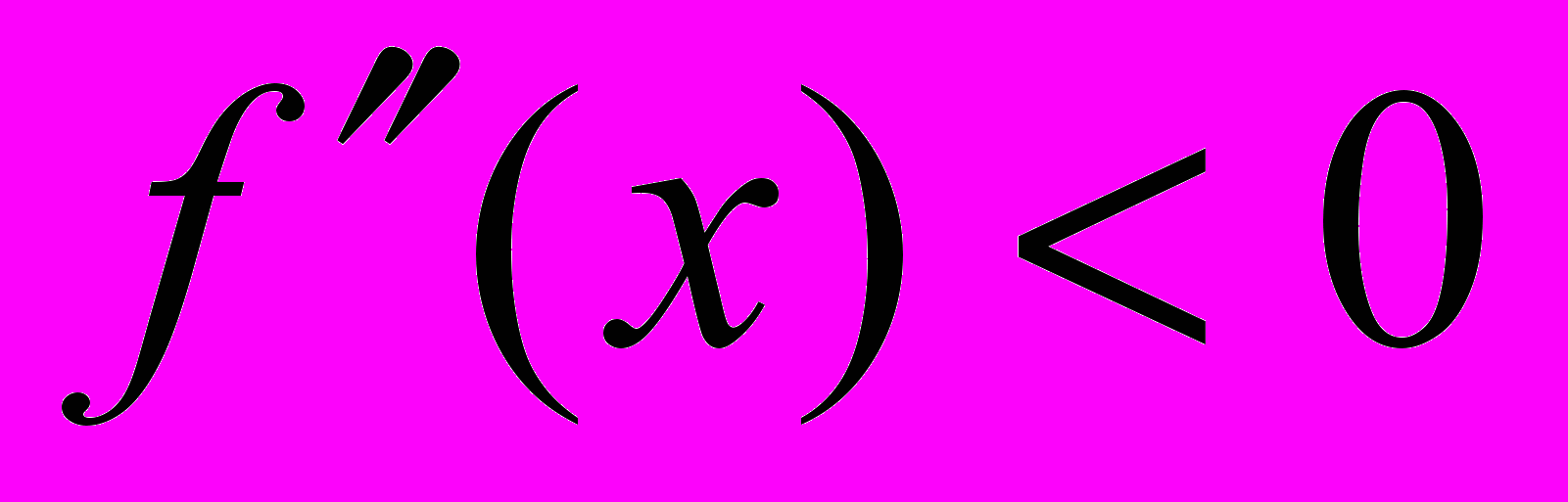 , то функция выпукла (вверх) на интервале
, то функция выпукла (вверх) на интервале 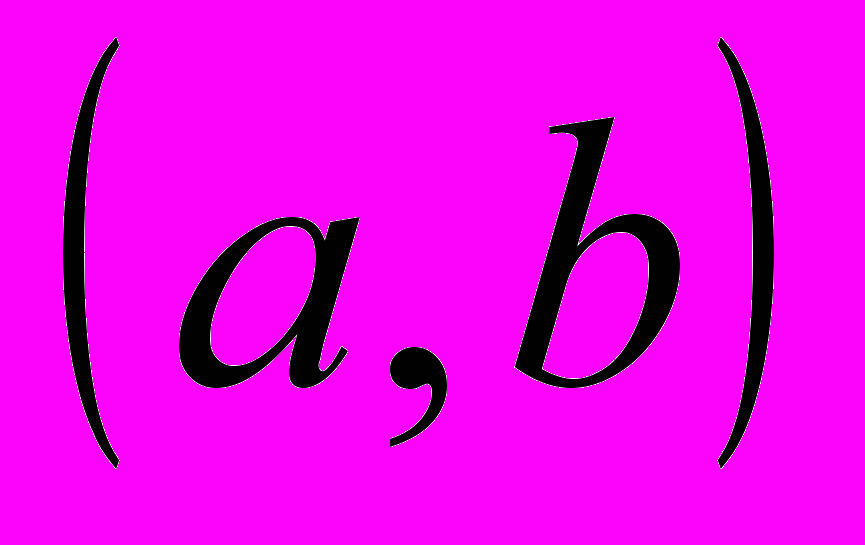 .
.(2) Если для всех
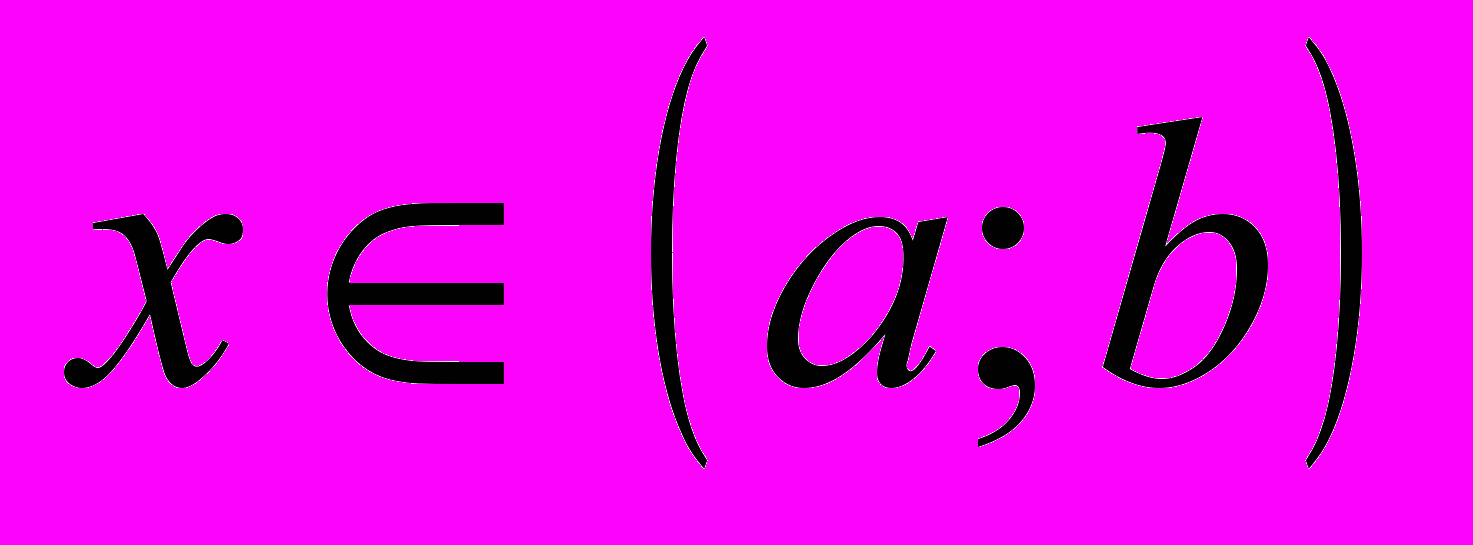
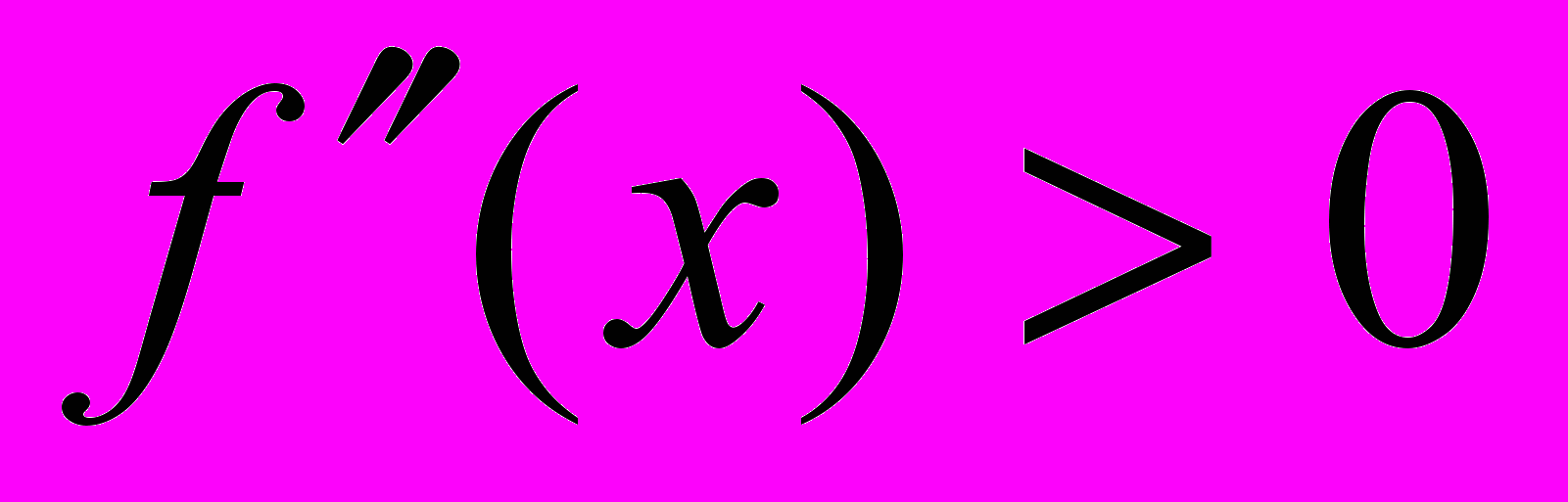 , то функция выпукла (вниз) на интервале
, то функция выпукла (вниз) на интервале 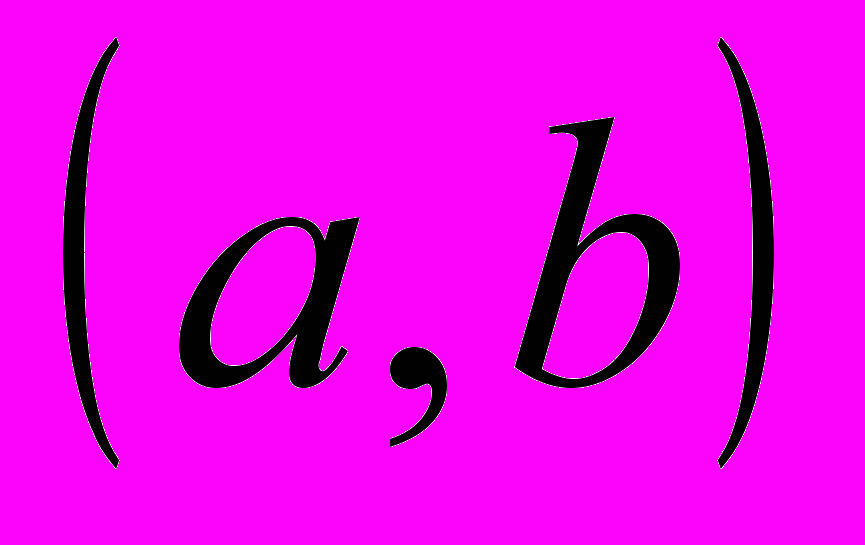 .
. ДОК. (1) Пусть
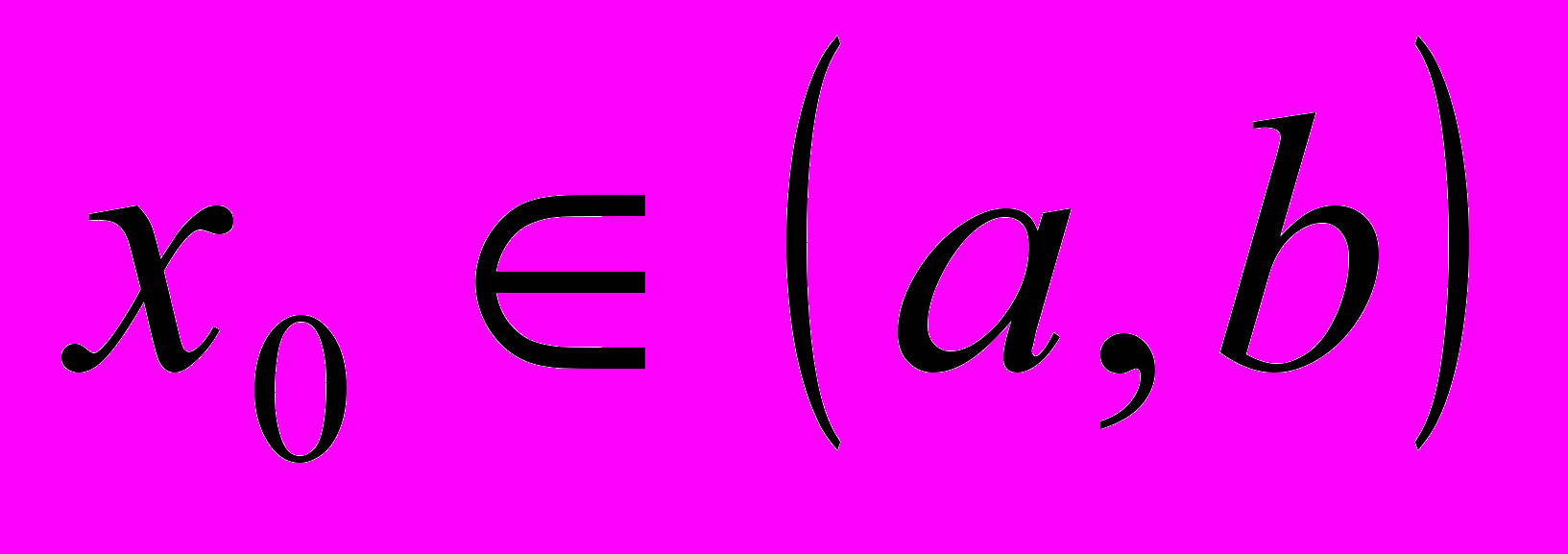 - произвольная точка интервала
- произвольная точка интервала 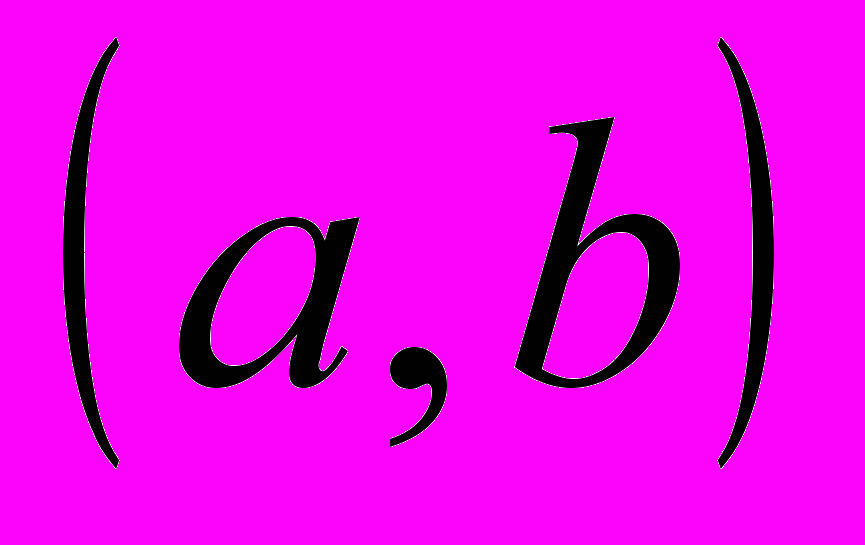 .
. По формуле Тейлора:
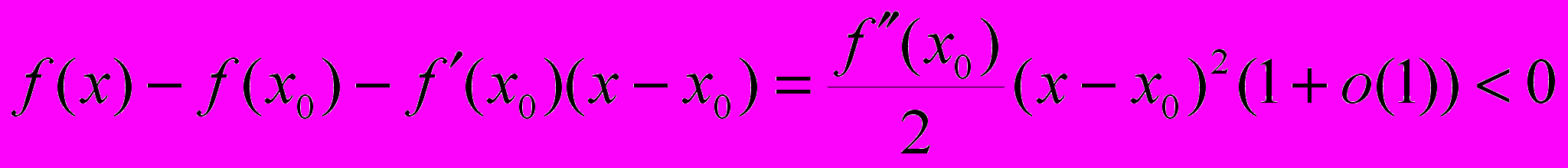
для всех
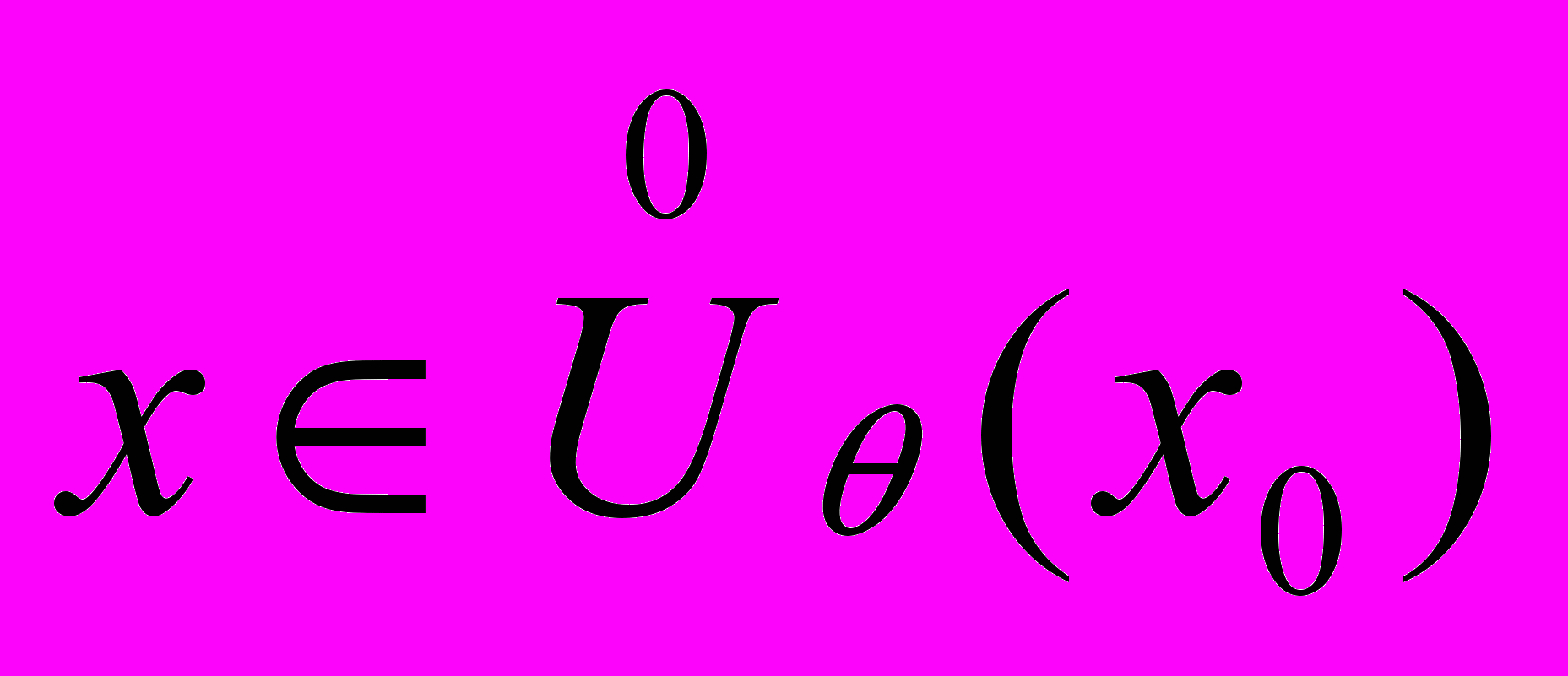 , т.е. функция выпукла (вверх) в точке
, т.е. функция выпукла (вверх) в точке 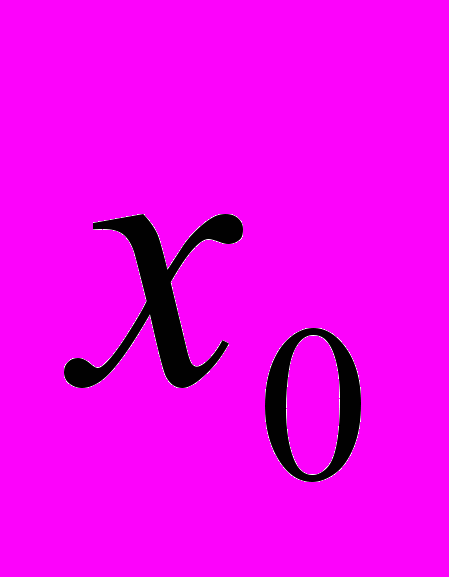 .
.(2) доказать самостоятельно.
Для нахождения интервалов выпуклости необходимо: 1) найти вторую производную функции ; 2) определить критические точки второго рода, т.е. точки в которых вторая производная равна нулю, либо не существует ; 3) расположить критические точки на числовой оси (на области определения функции) и разбить ее на интервалы, границами которых являются критические точки второго рода ;4) выяснить знак второй производной на каждом из интервалов и определить характер выпуклости.
П.2 Точка перегиба.
ОПР. Точка
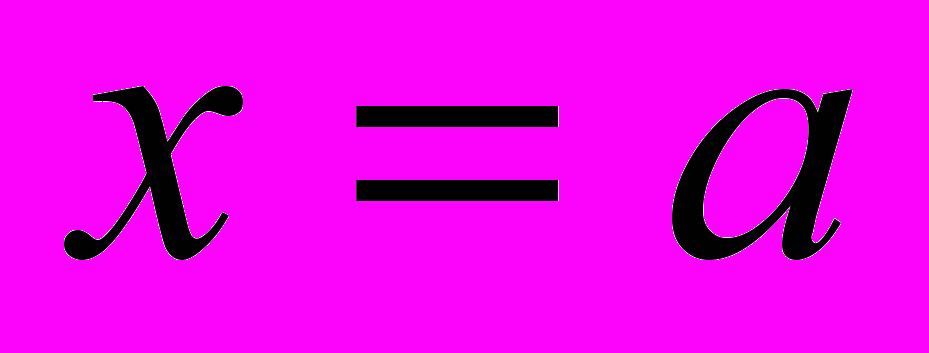 называется точкой перегиба функции
называется точкой перегиба функции 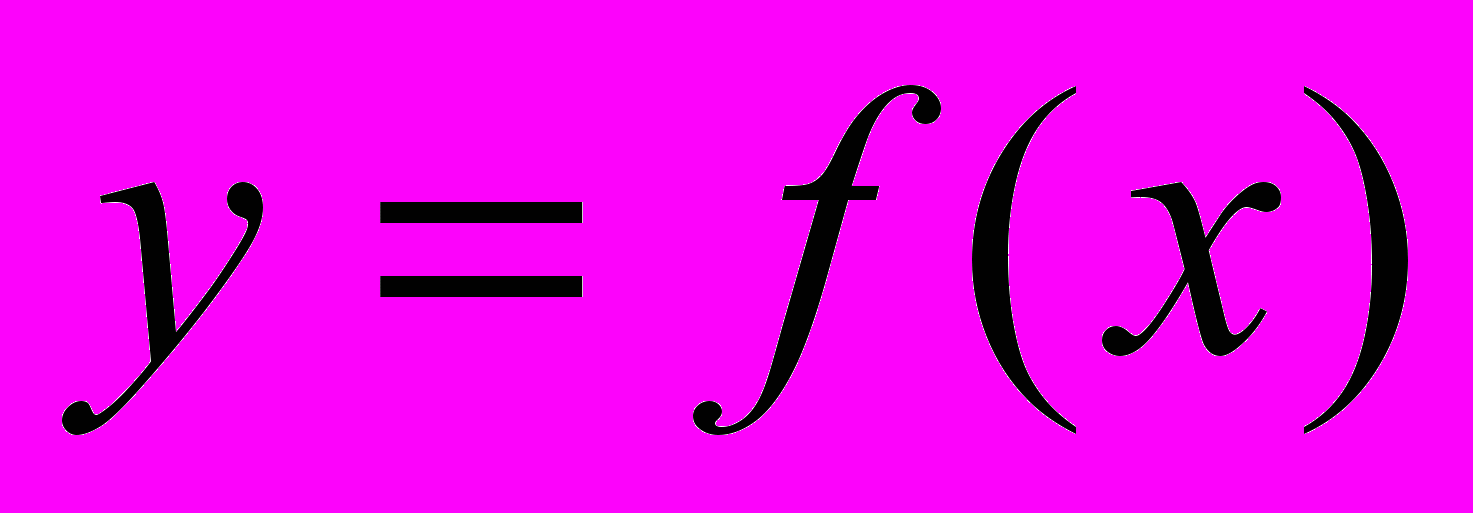 , если производная
, если производная 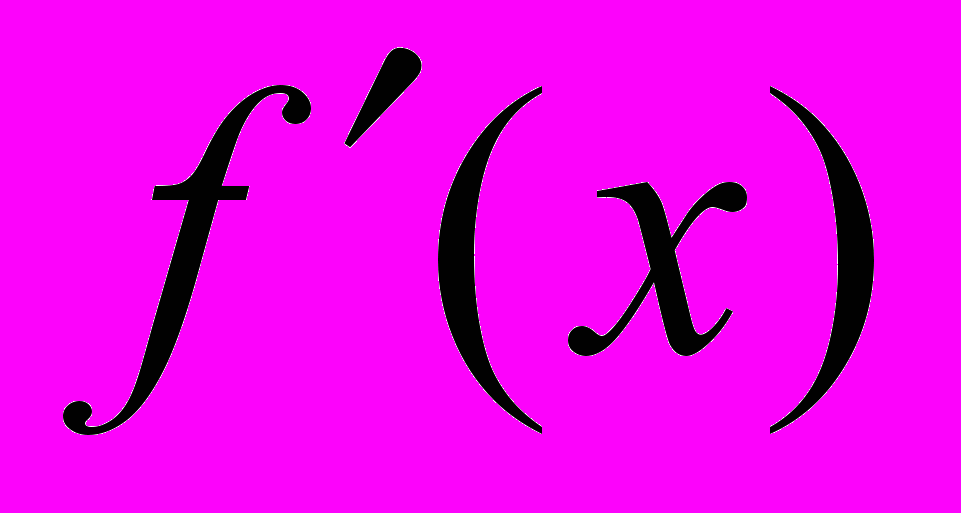 функция непрерывна в этой точке и
функция непрерывна в этой точке и 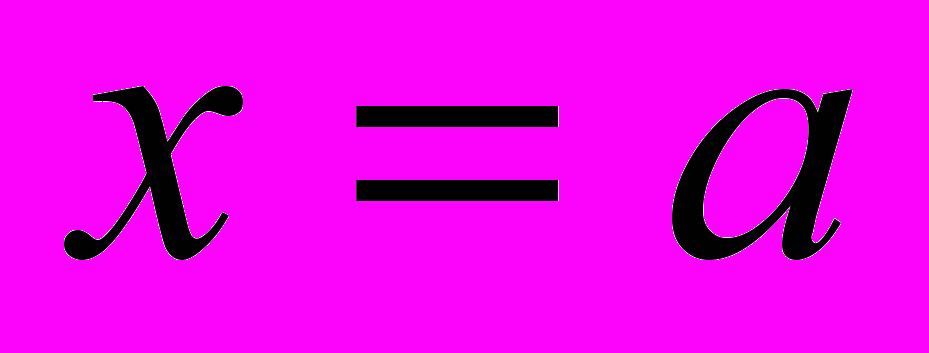 является границей двух различных интервалов выпуклости (вверх и вниз).
является границей двух различных интервалов выпуклости (вверх и вниз).ТЕОРЕМА 3. (НЕОБХОДИМОЕ УСЛОВИЕ ПЕРЕГИБА)
Если
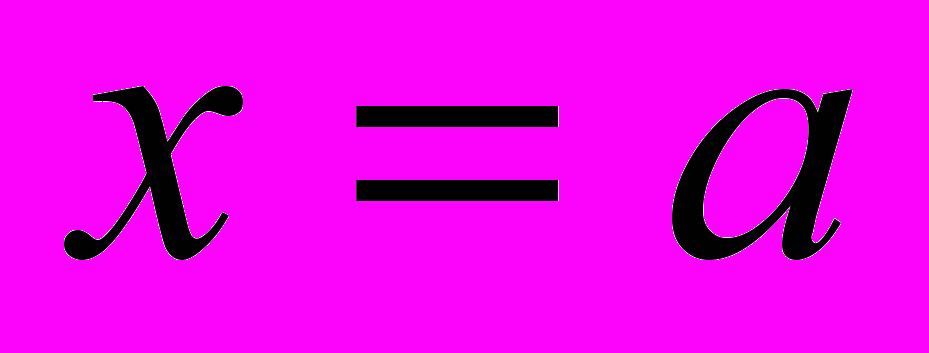 точка перегиба, то либо
точка перегиба, то либо 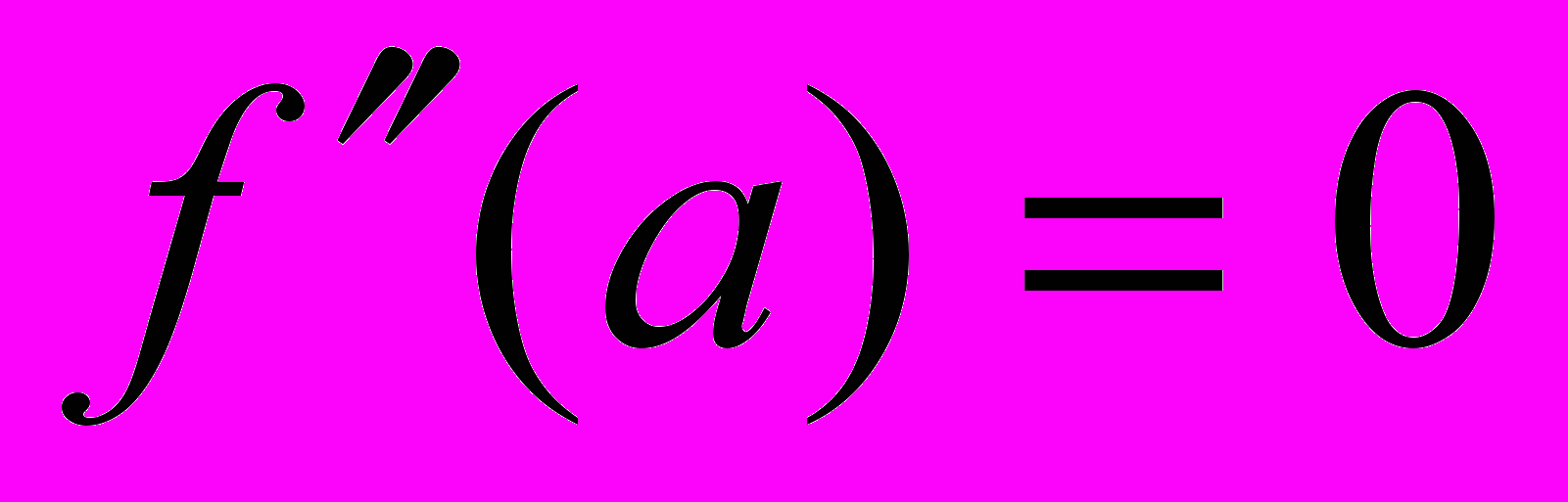 , либо вторая производная в точке
, либо вторая производная в точке 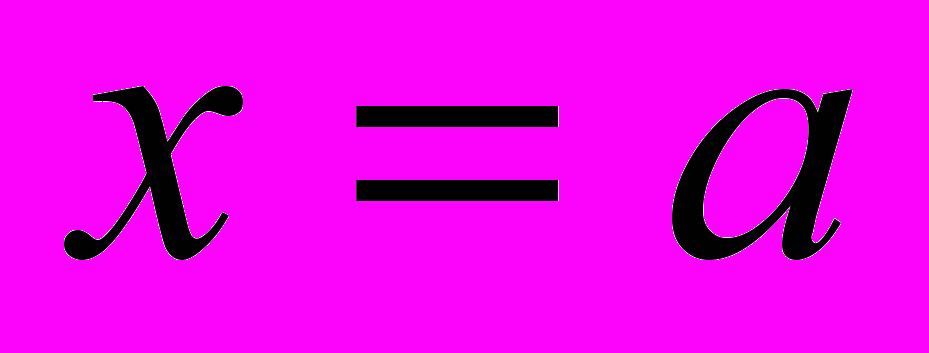 не существует.
не существует.ДОК. Если вторая производная не существует, то теорема доказана. Если она существует, но не равна нулю, то выражение
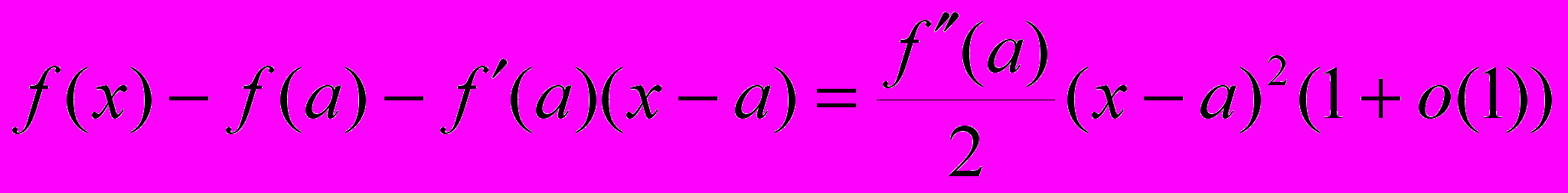
сохраняет знак в малой окрестности
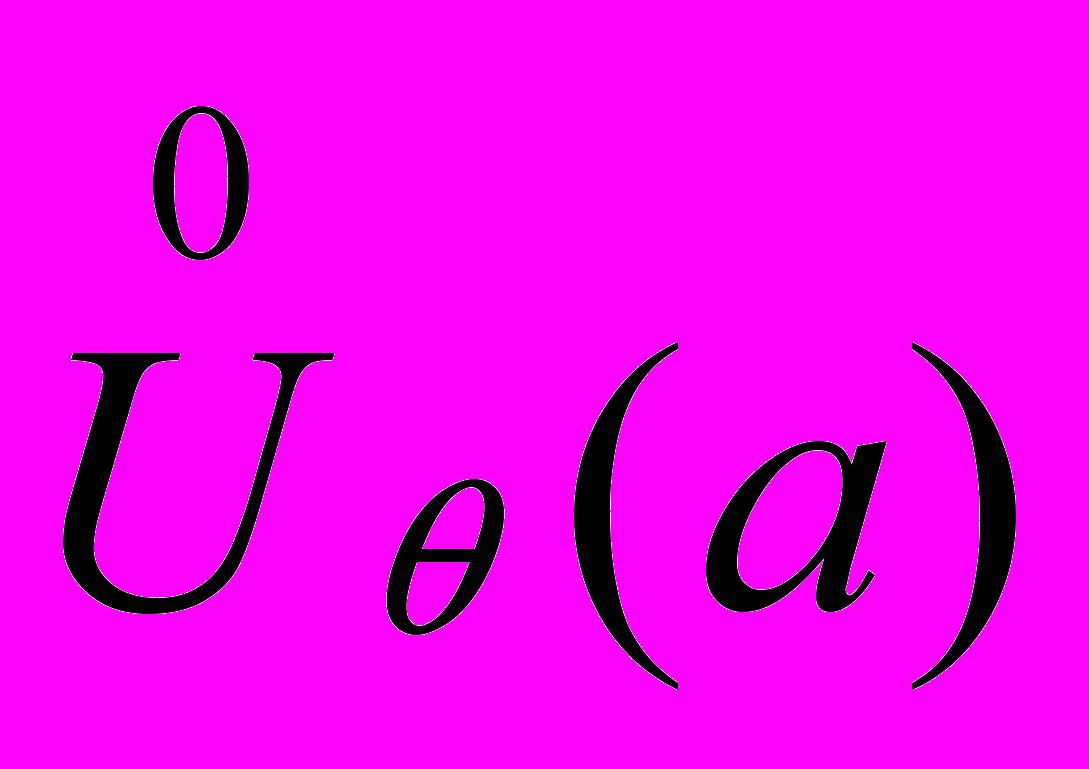 , т.е. функция выпукла (вверх или вниз) в точке
, т.е. функция выпукла (вверх или вниз) в точке 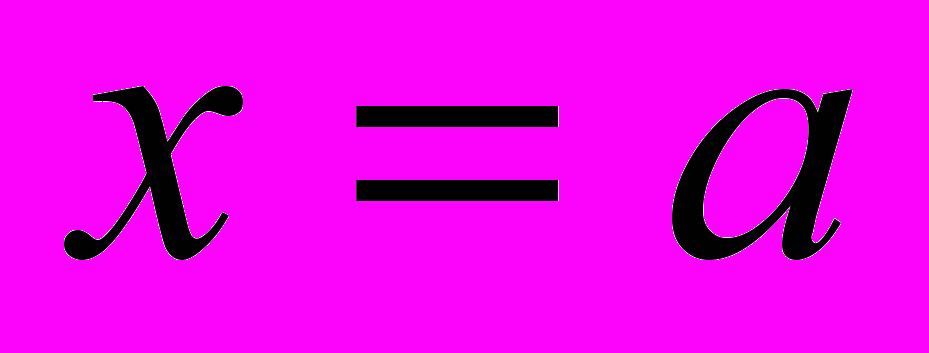 и она точкой перегиба не является.
и она точкой перегиба не является.ТЕОРЕМА 4 (ДОСТАТОЧНОЕ УСЛОВИЕ ПЕРЕГИБА по второй производной)
Пусть функция
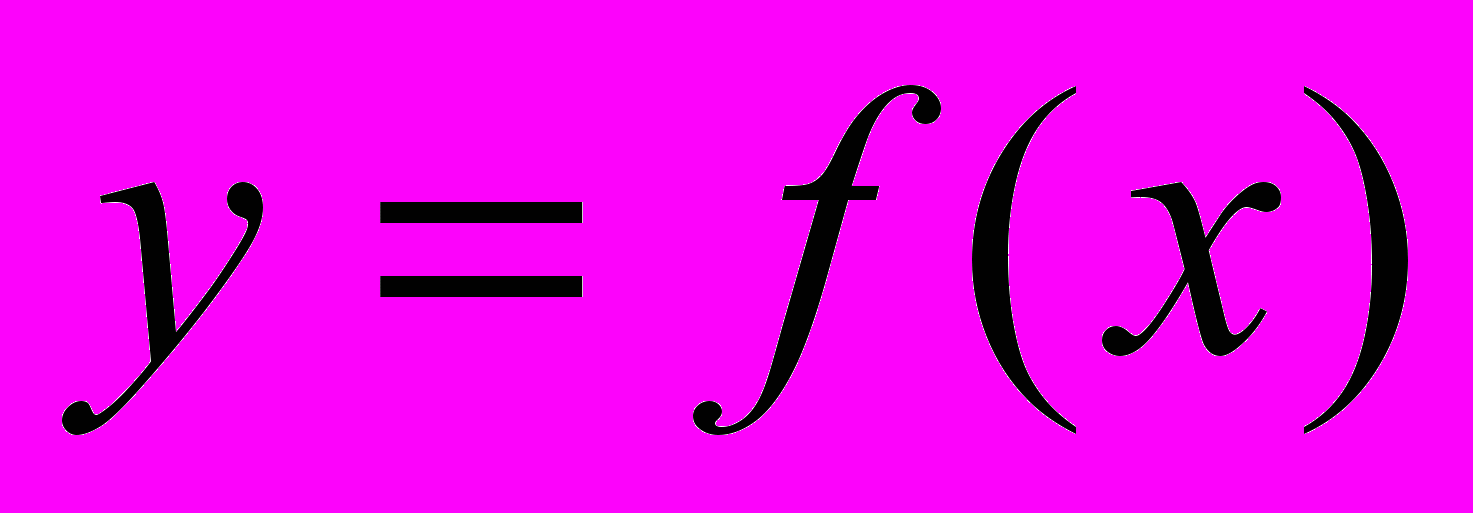 в окрестности точки
в окрестности точки 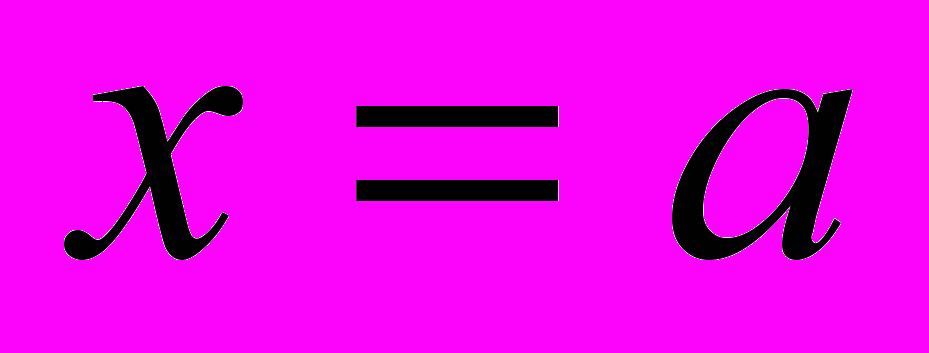 удовлетворяет условиям :1) существует
удовлетворяет условиям :1) существует 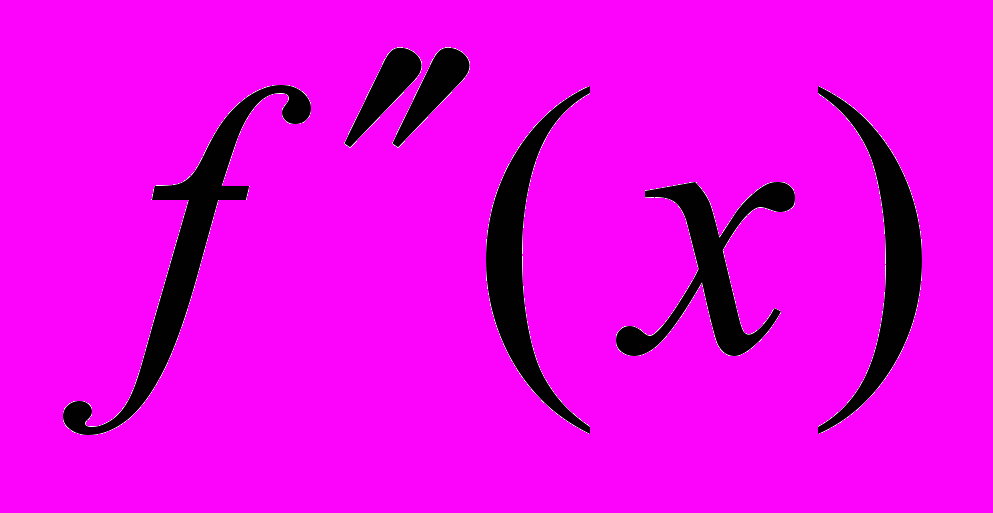 для всех
для всех 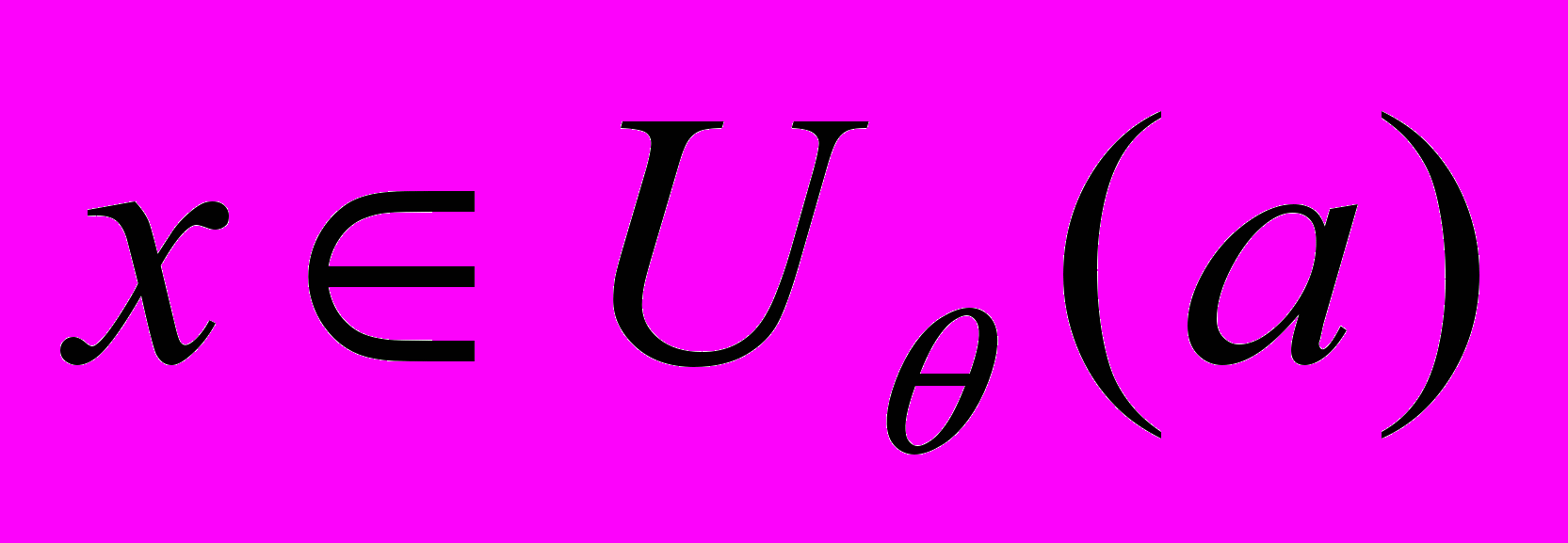
2)
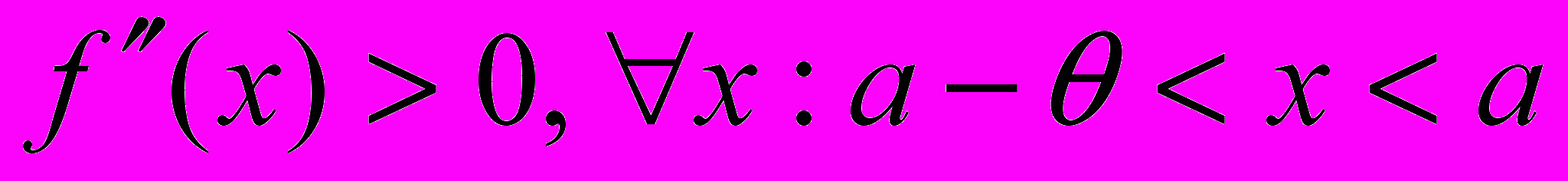 и
и 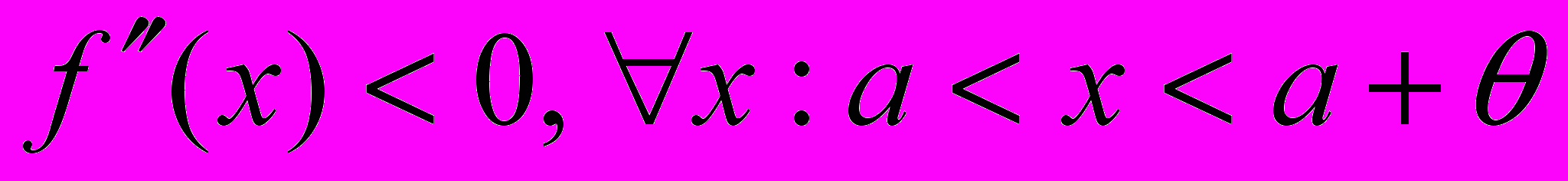
( или
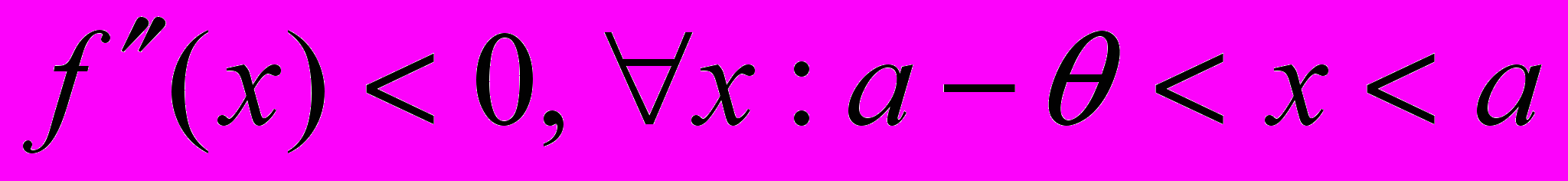 и
и 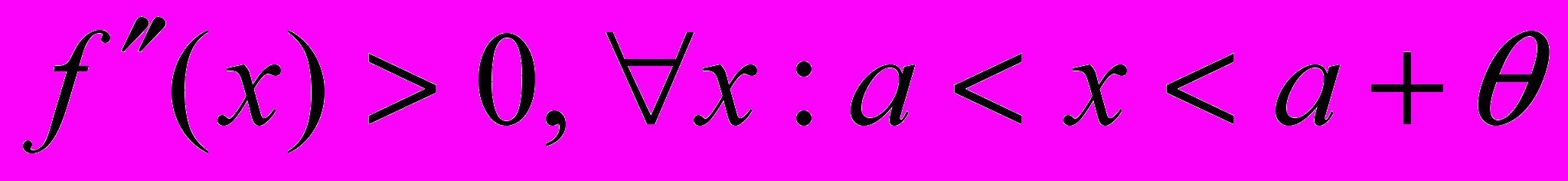 )
) Тогда в точке
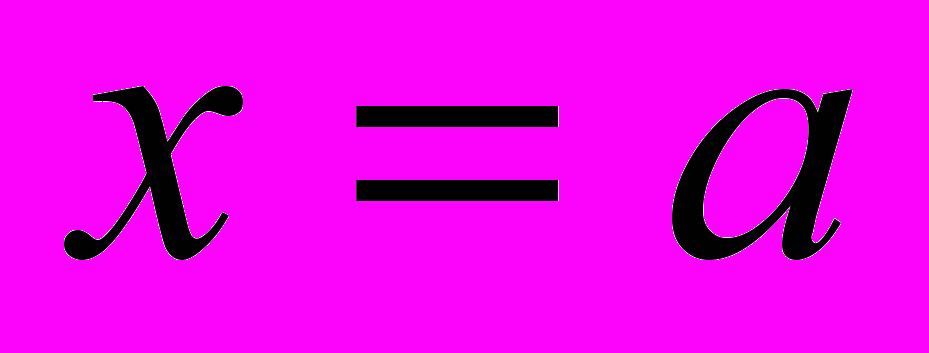 перегиб.
перегиб.ДОК. Из условия 1) теоремы следует, что
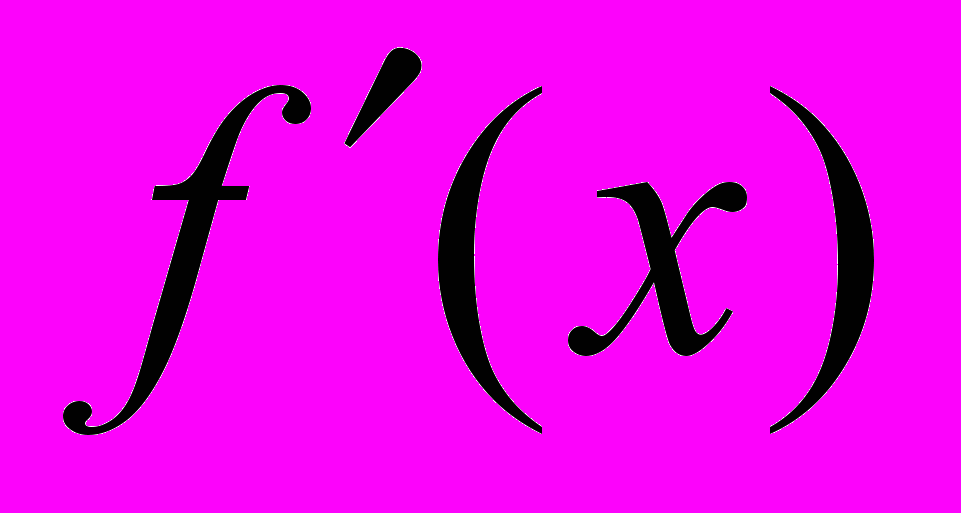 непрерывна в точке
непрерывна в точке 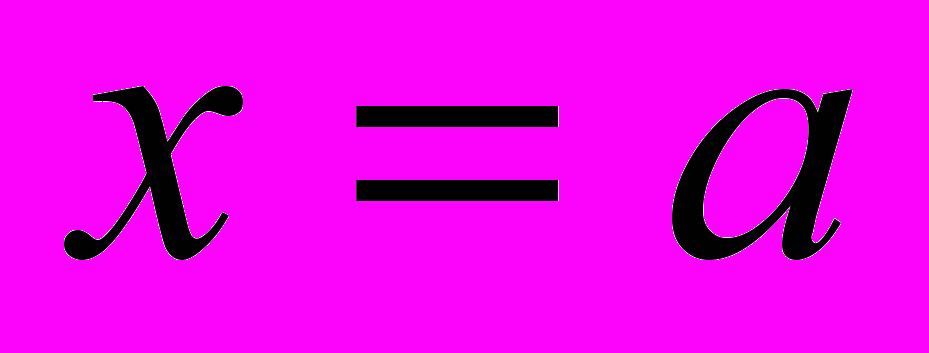 .Из условия 2) и теоремы 2 следует, что интервалы
.Из условия 2) и теоремы 2 следует, что интервалы 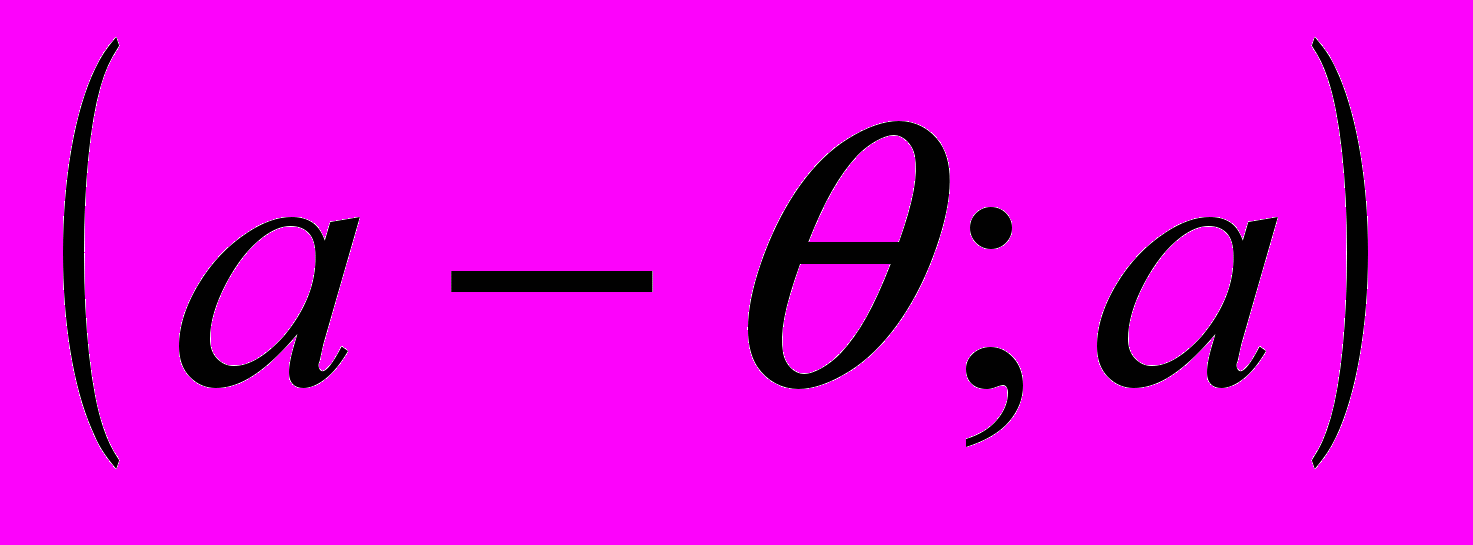 и
и 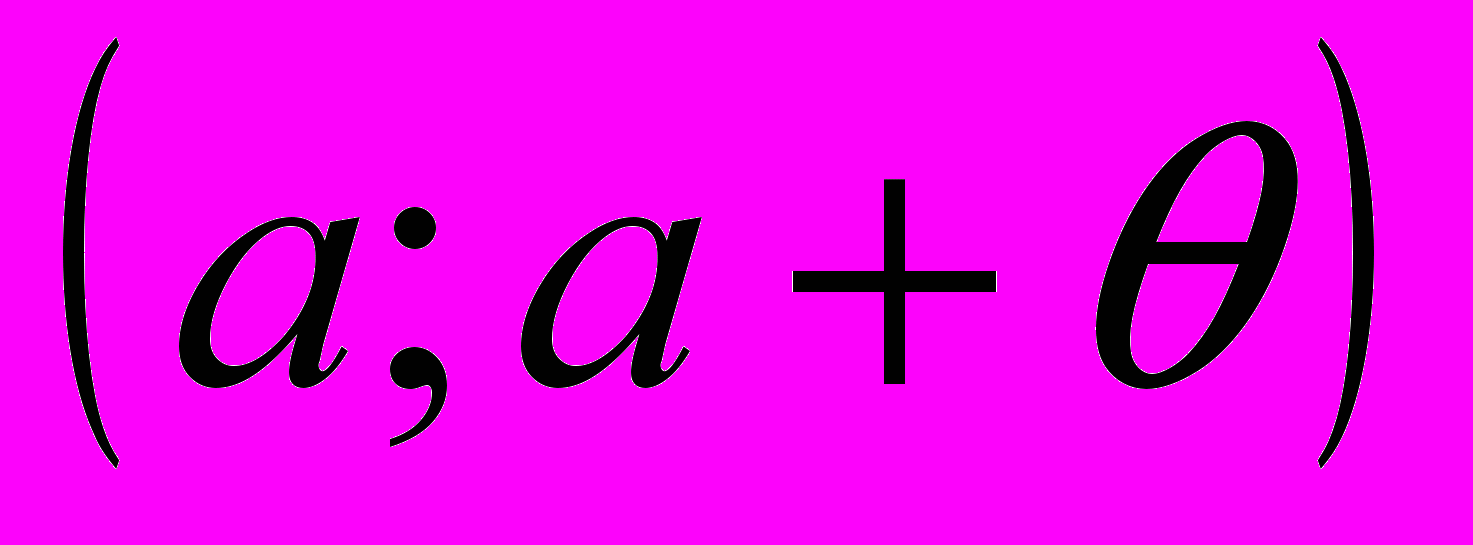 являются интервалами выпуклости функции
являются интервалами выпуклости функции 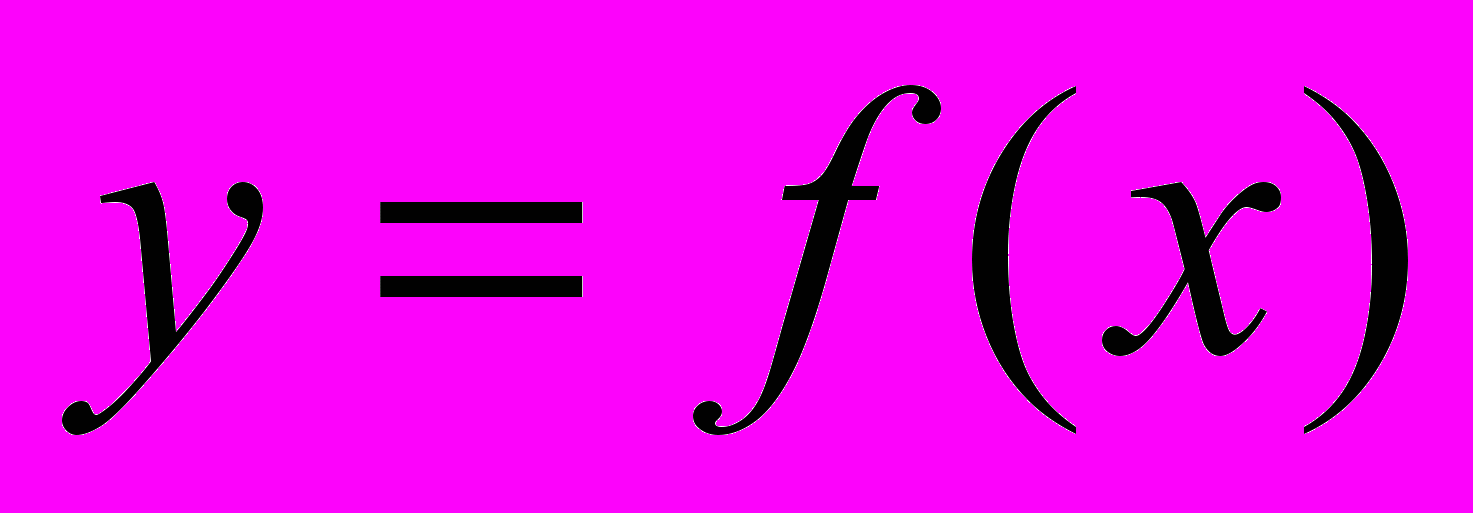 вверх и вниз или наоборот.Тогда
вверх и вниз или наоборот.Тогда 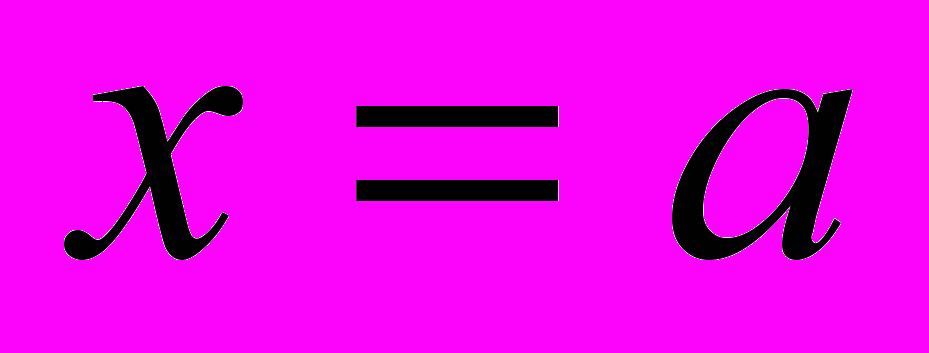 - точка перегиба.
- точка перегиба.П 3. Асимптоты графика функции.
ОПР. Прямая
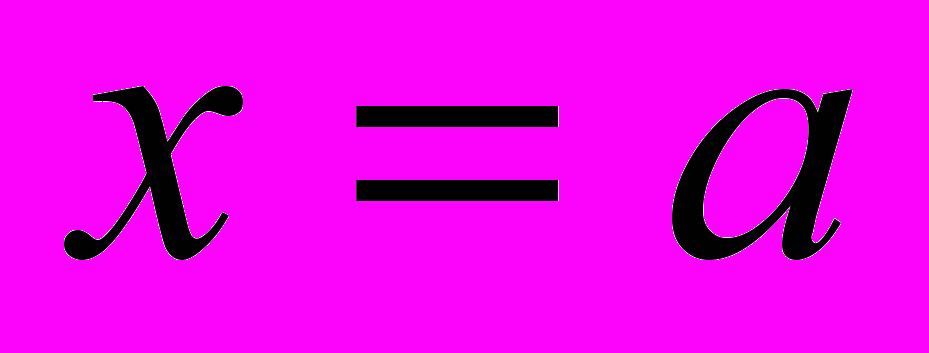 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 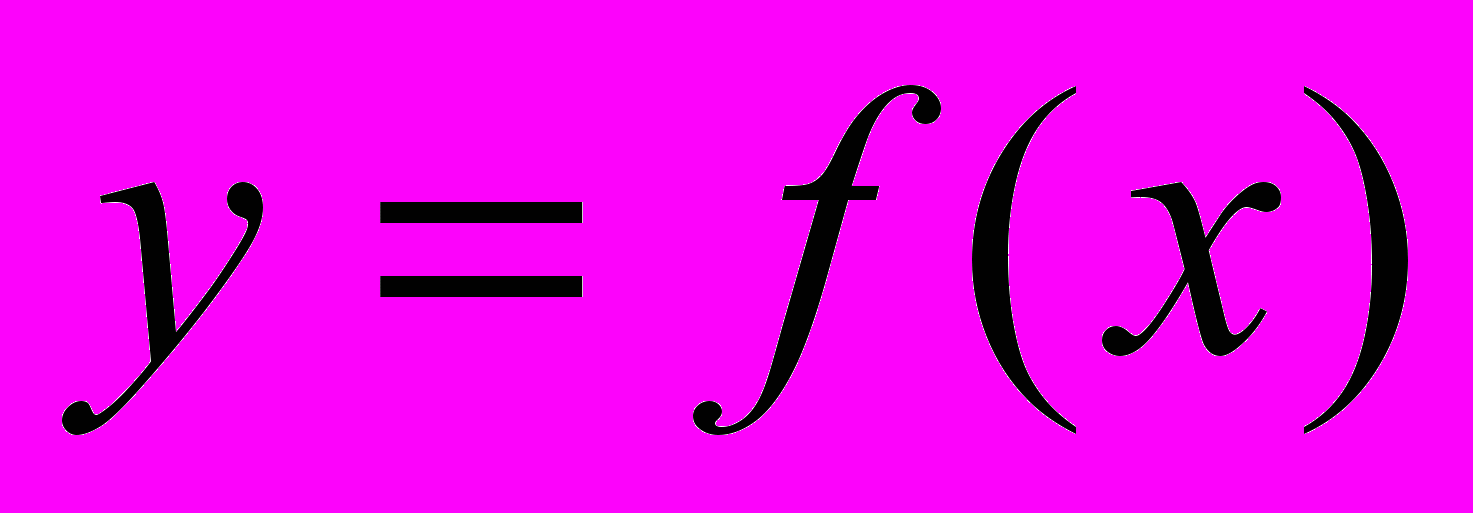 , если функция является бесконечно большой в точке
, если функция является бесконечно большой в точке 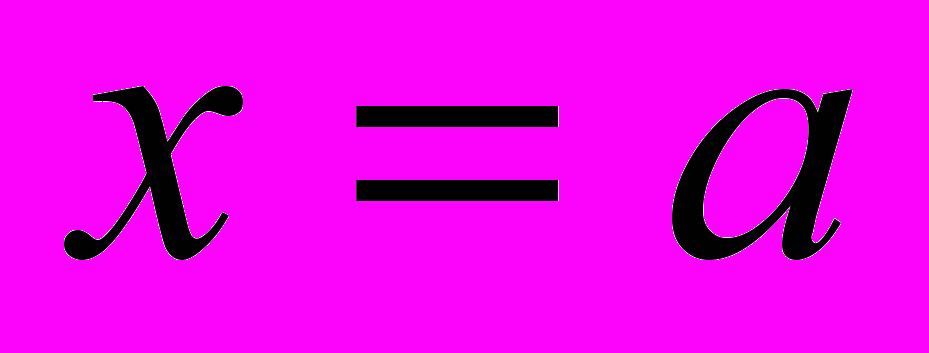 .
.ПРИМЕР 1. Для функции
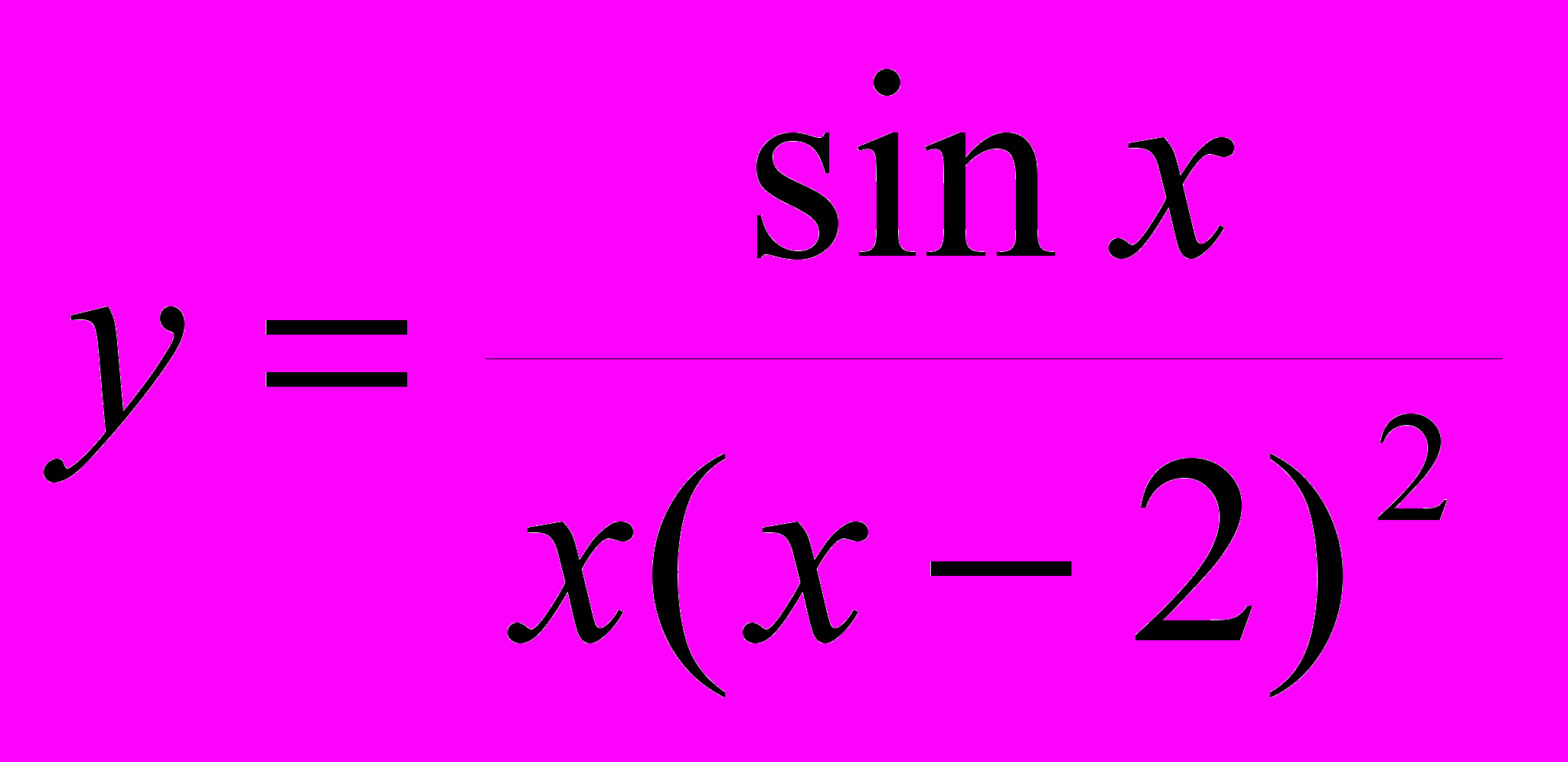 прямая
прямая 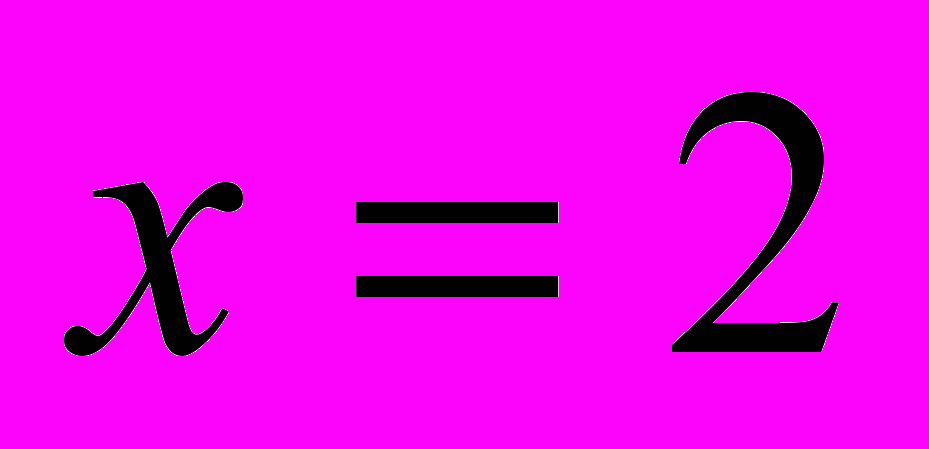 является вертикальной асимптотой, а прямая
является вертикальной асимптотой, а прямая 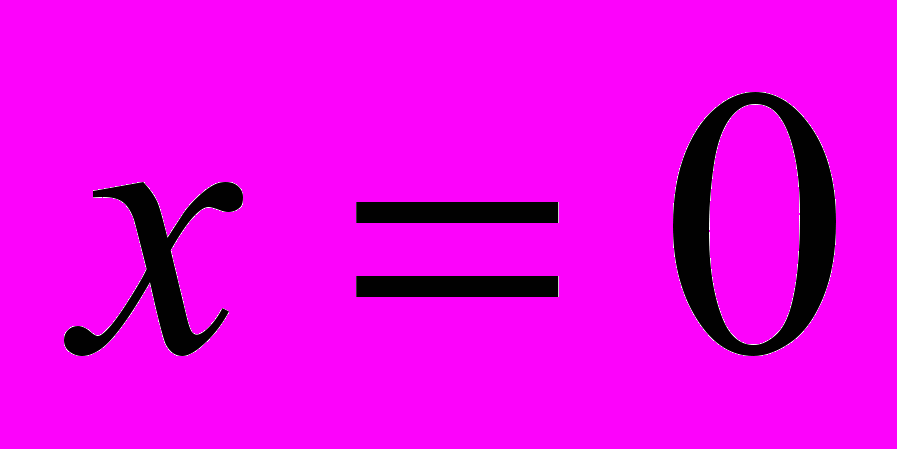 асимптотой не является.
асимптотой не является.ОПР. Прямая
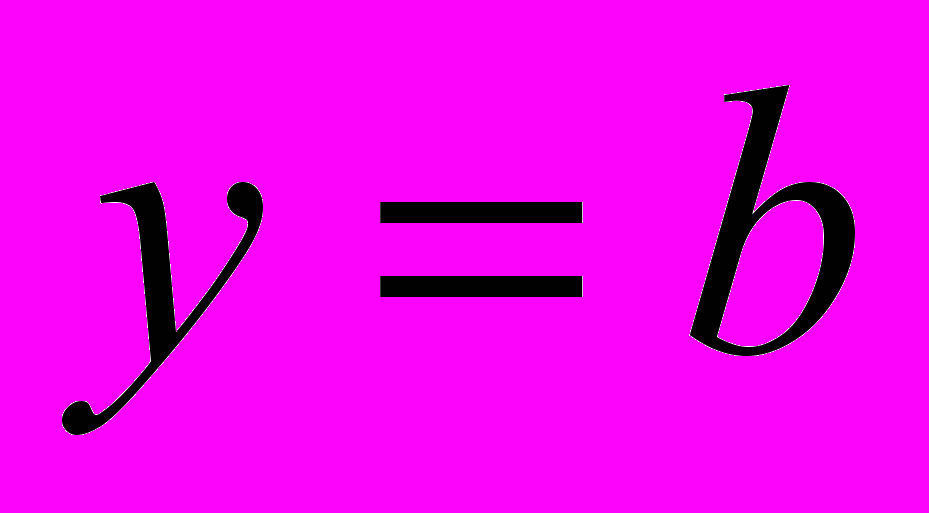 называется горизонтальной асимптотой графика функции
называется горизонтальной асимптотой графика функции 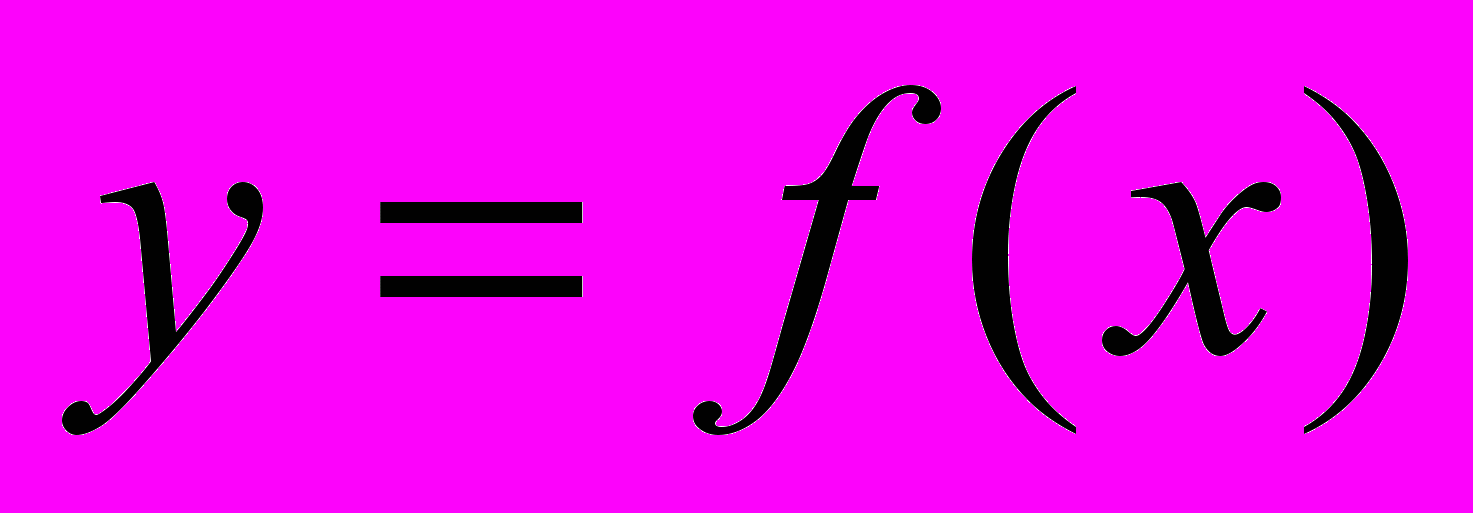 на бесконечности, если
на бесконечности, если 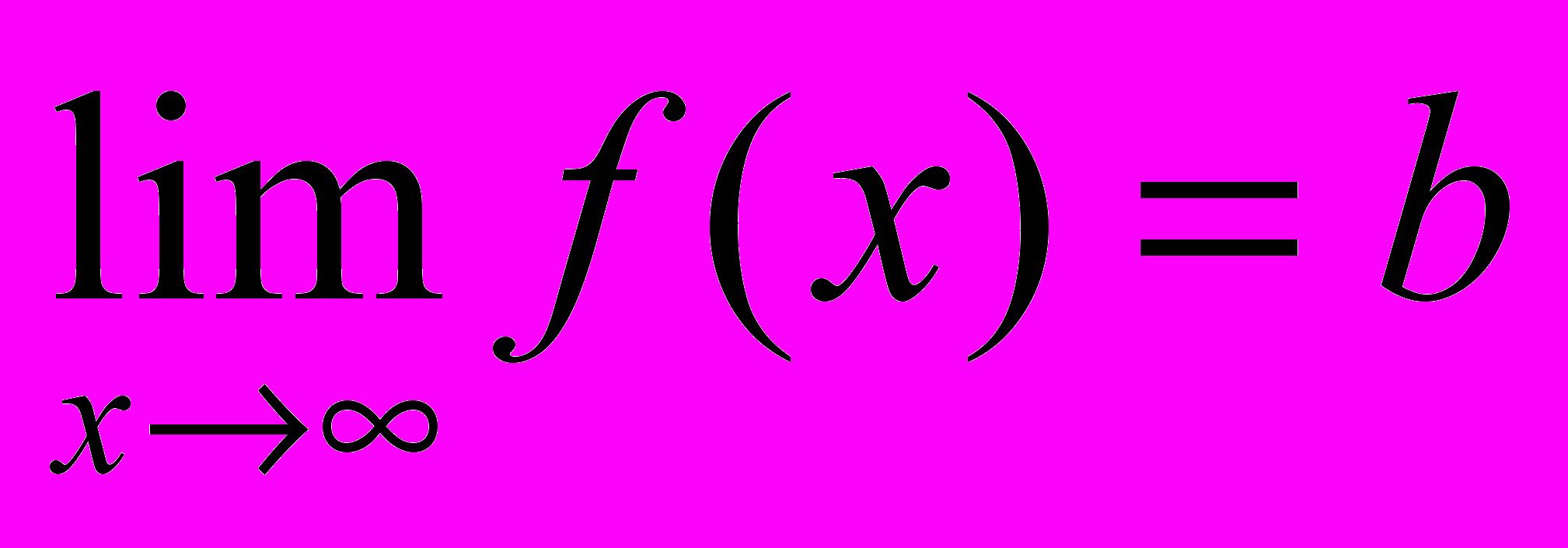 .
.ПРИМЕР 2. Прямая
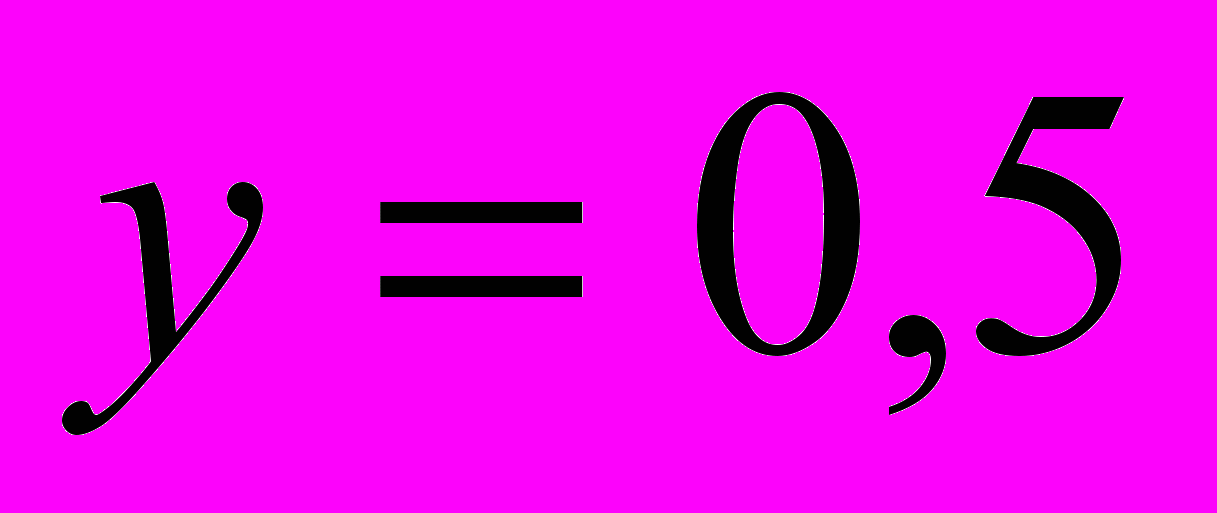 является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции 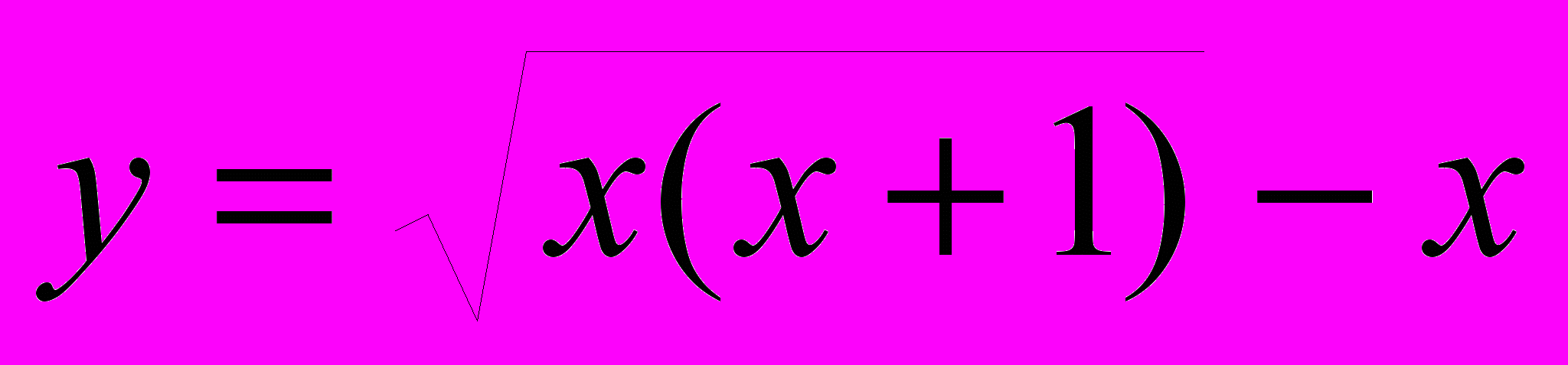 на
на  , поскольку
, поскольку 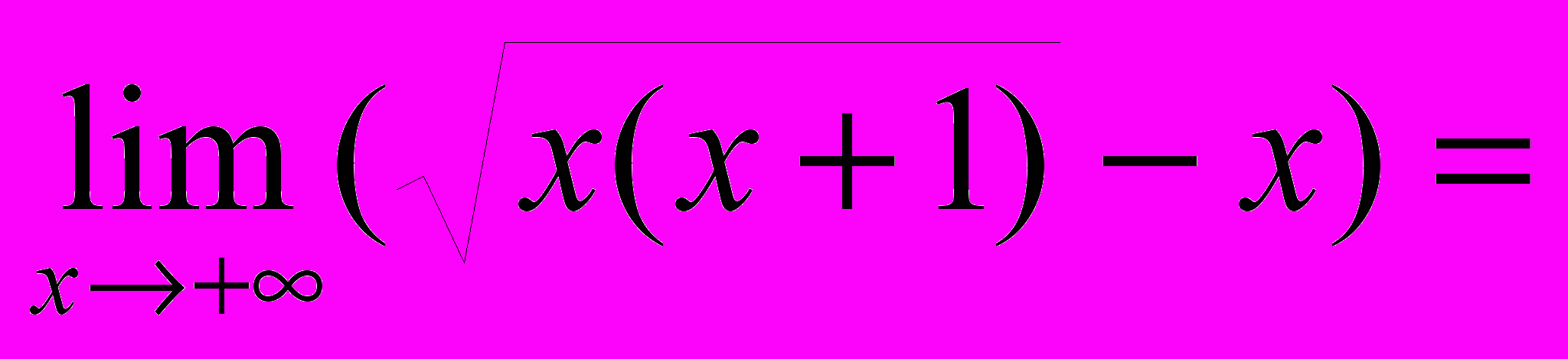
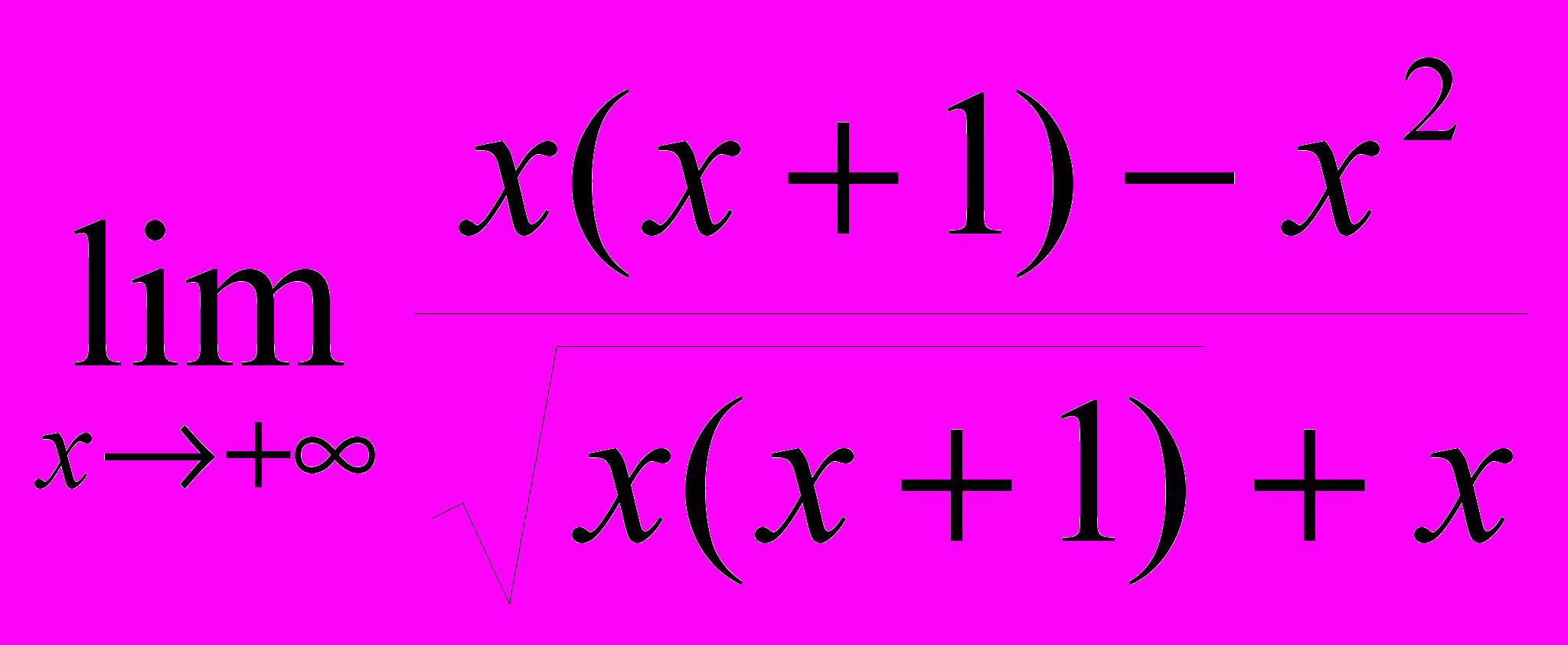 ==
==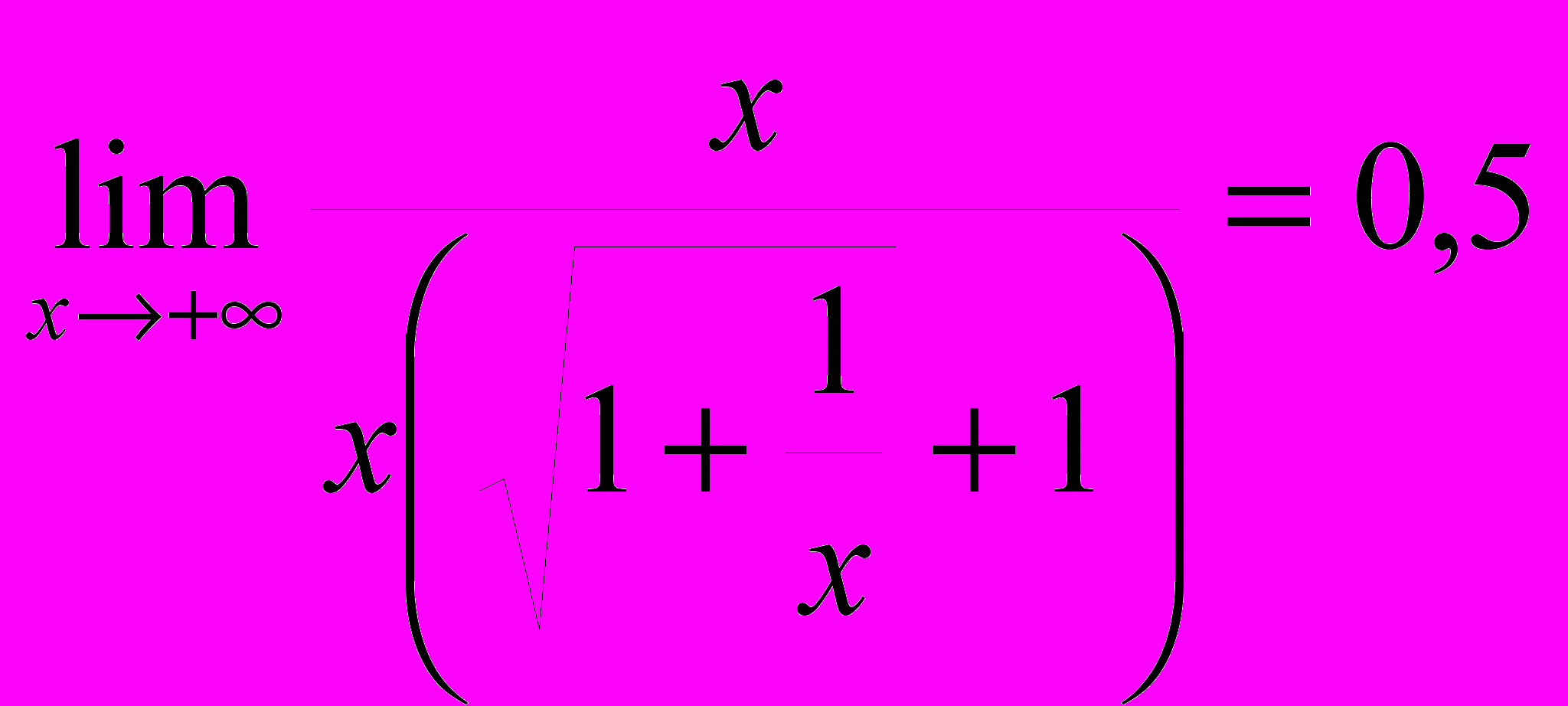 .
. Заметим, что на
 функция не имеет горизонтальной асимптоты.
функция не имеет горизонтальной асимптоты.ОПР. Прямая
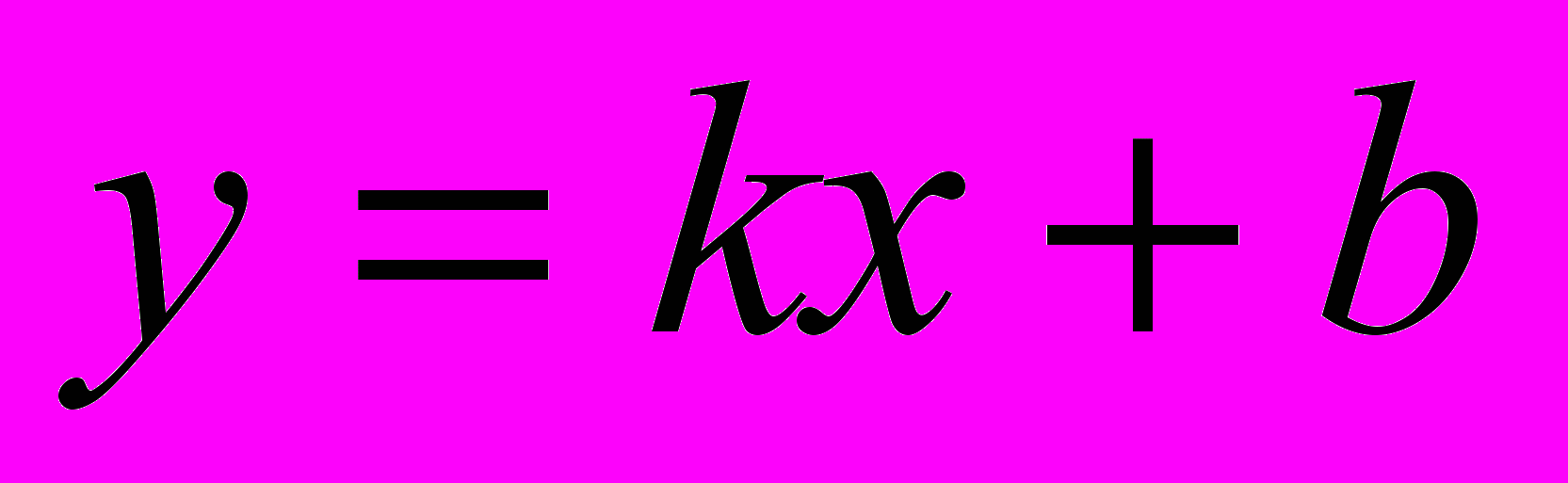 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 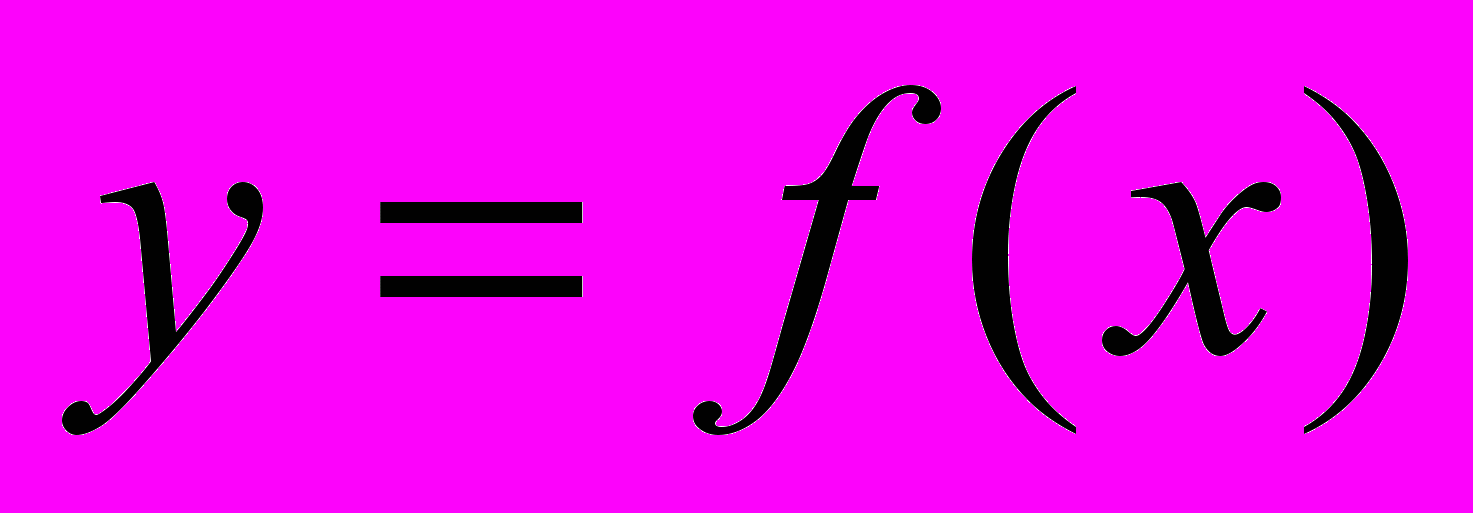 на бесконечности, если
на бесконечности, если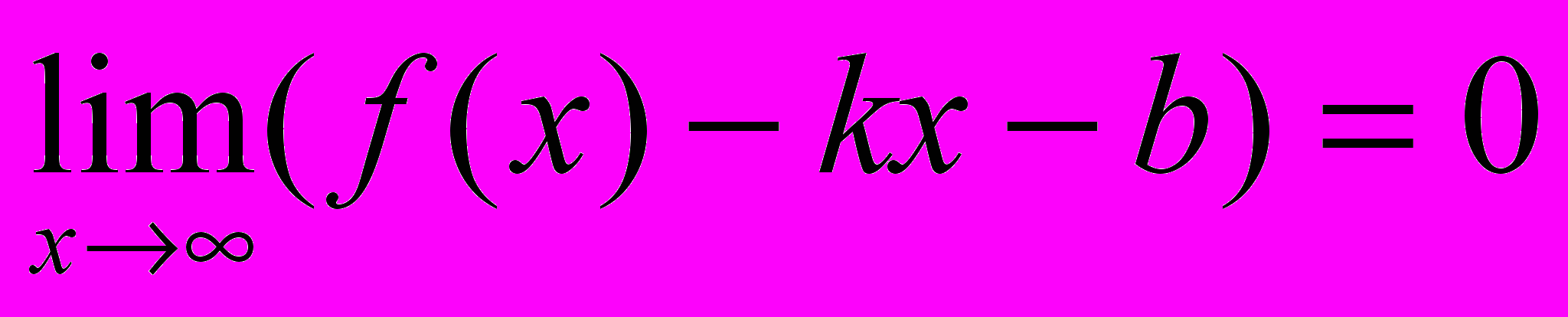 .
.ТЕОРЕМА 5. Если график функции
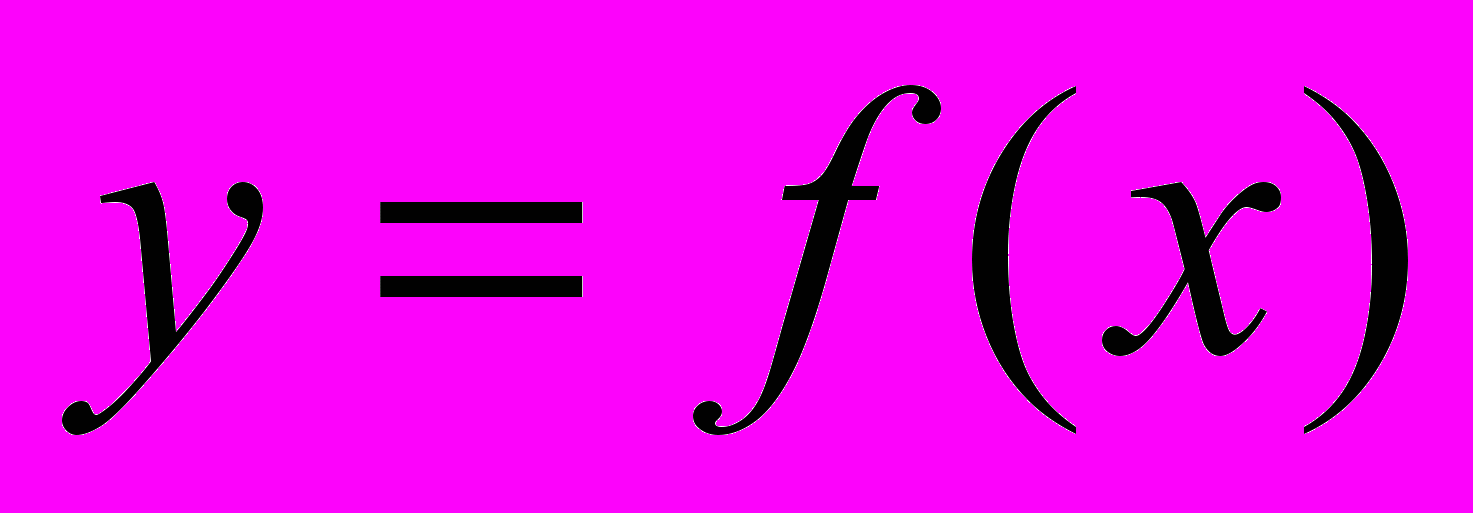 имеет прямую
имеет прямую 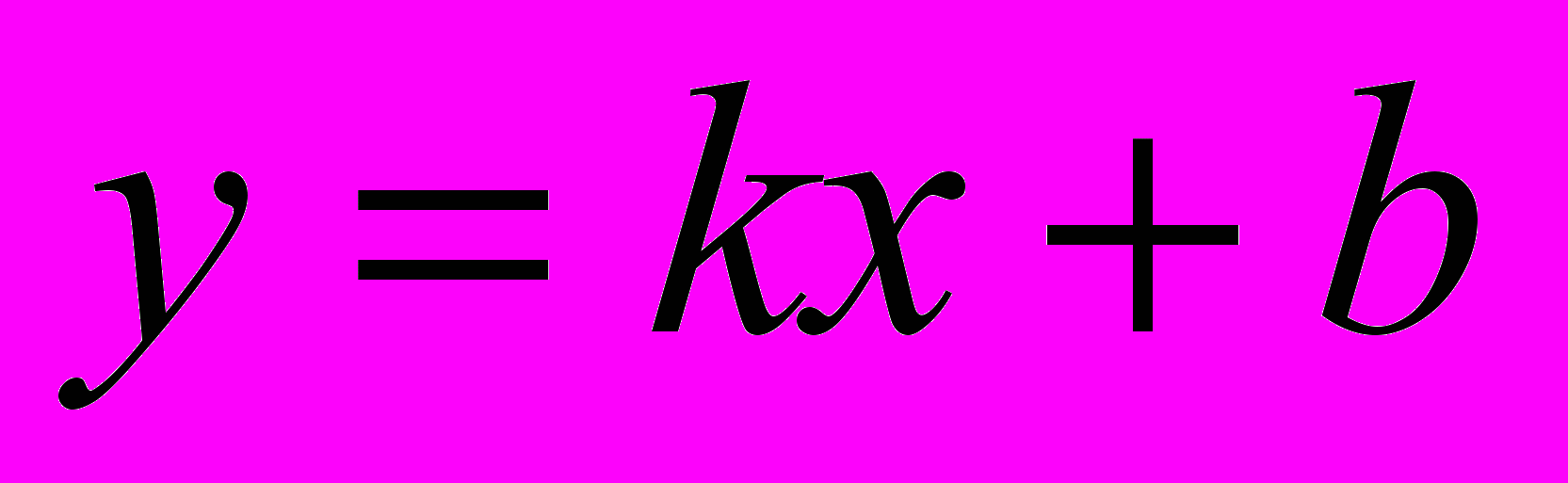 своей наклонной асимптотой, то
своей наклонной асимптотой, то 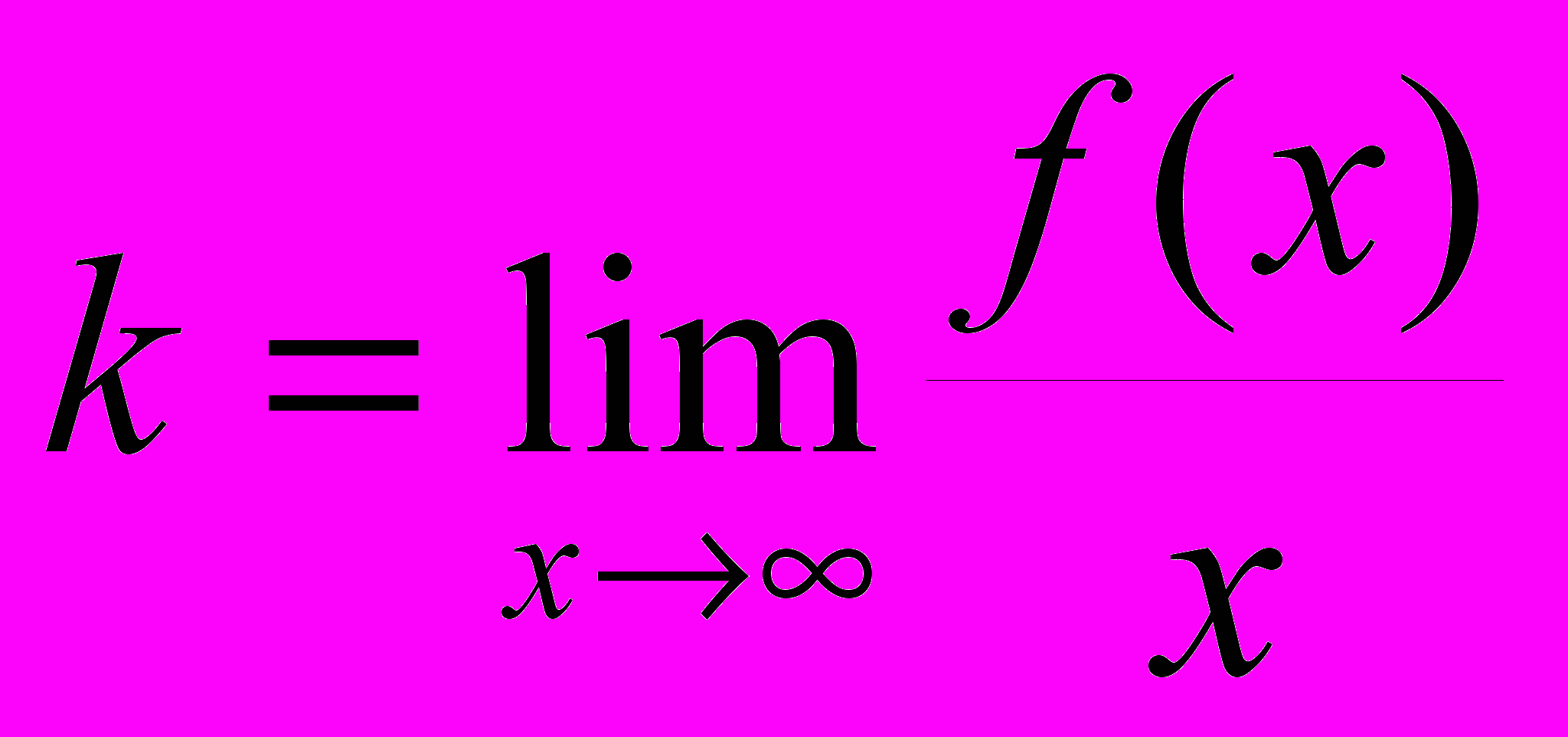 ,
, 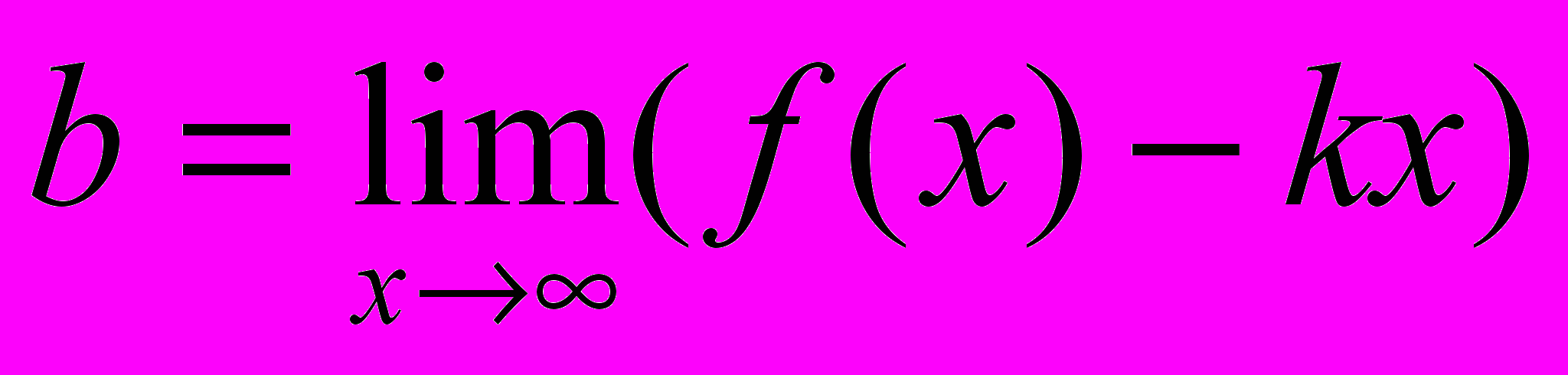 .
.ДОК. По условию
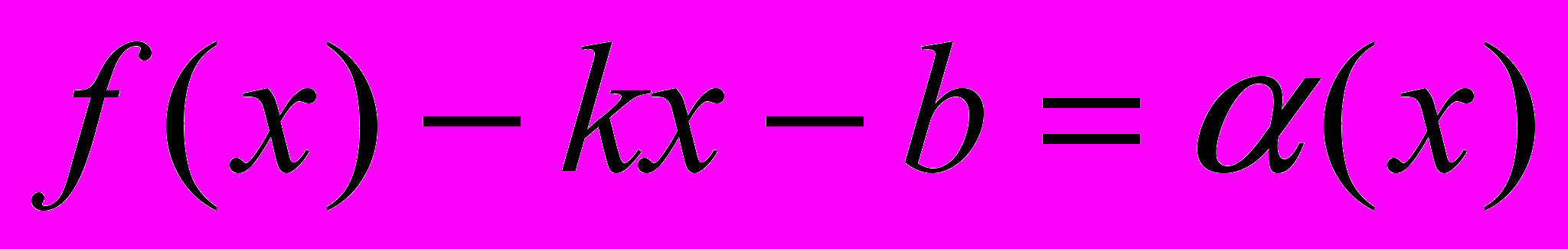 , где
, где 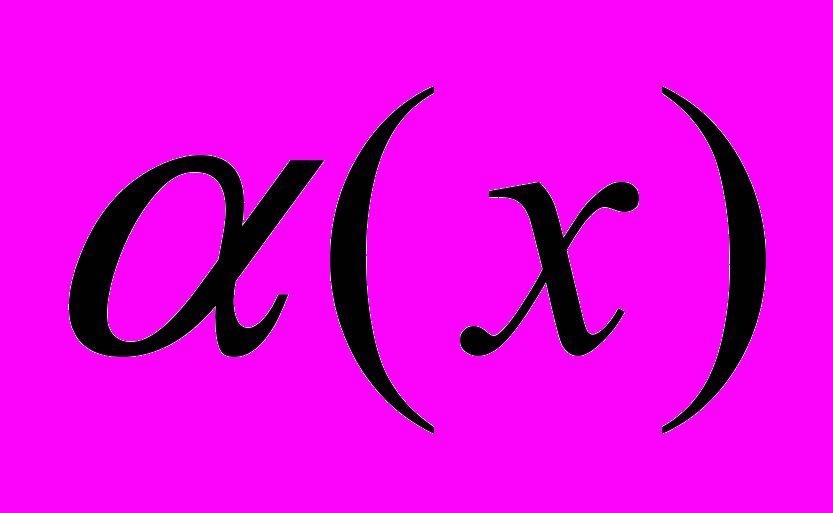 - бесконечно малая функция на бесконечности и
- бесконечно малая функция на бесконечности и 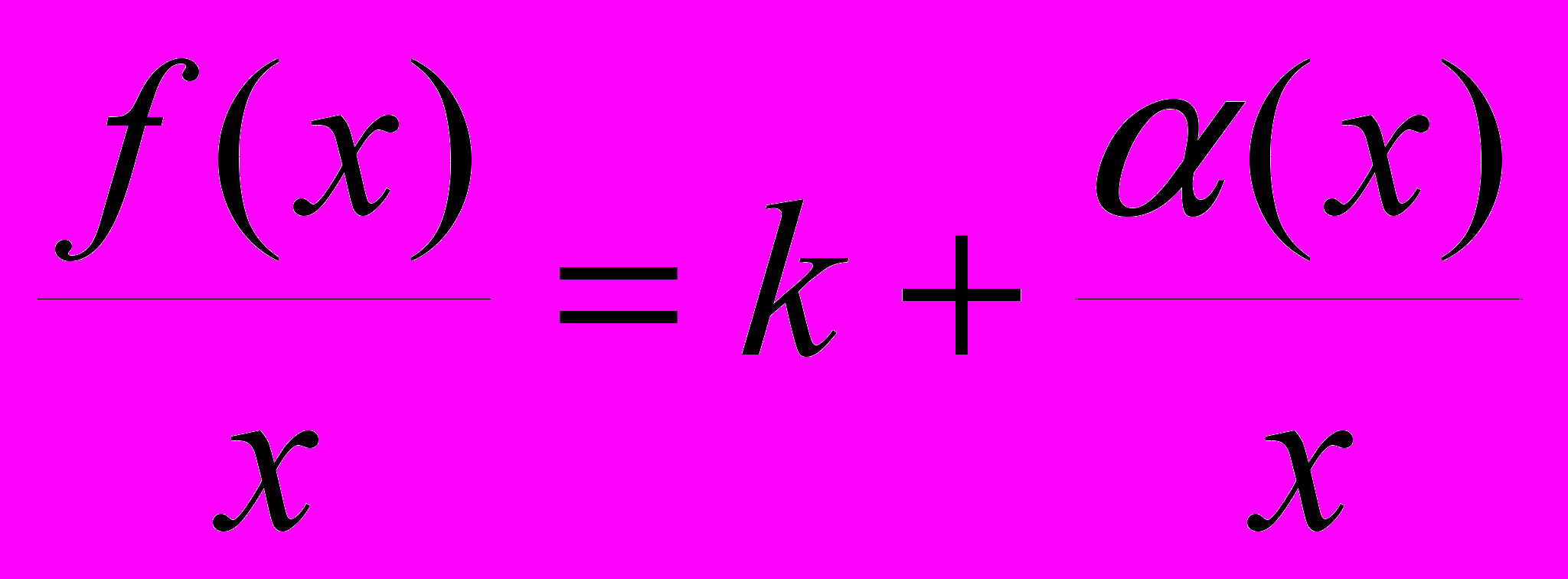 . Поскольку
. Поскольку 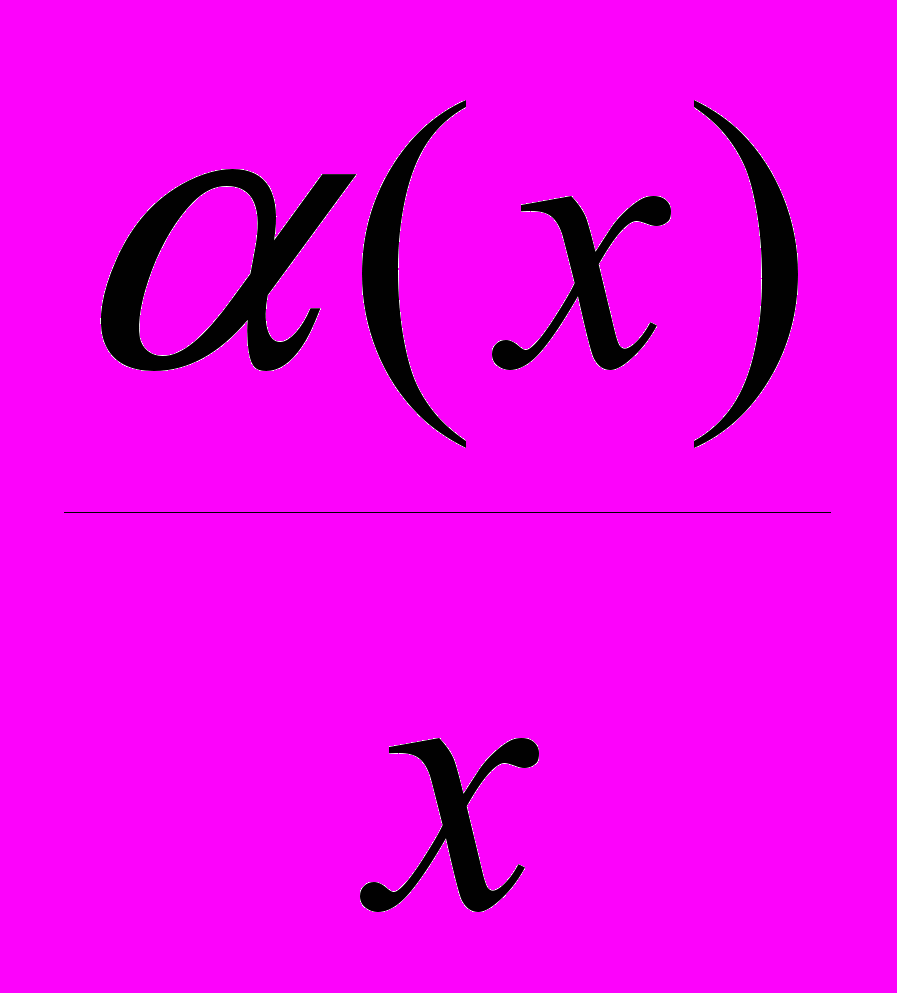 - бесконечно малая функция на бесконечности, то
- бесконечно малая функция на бесконечности, то 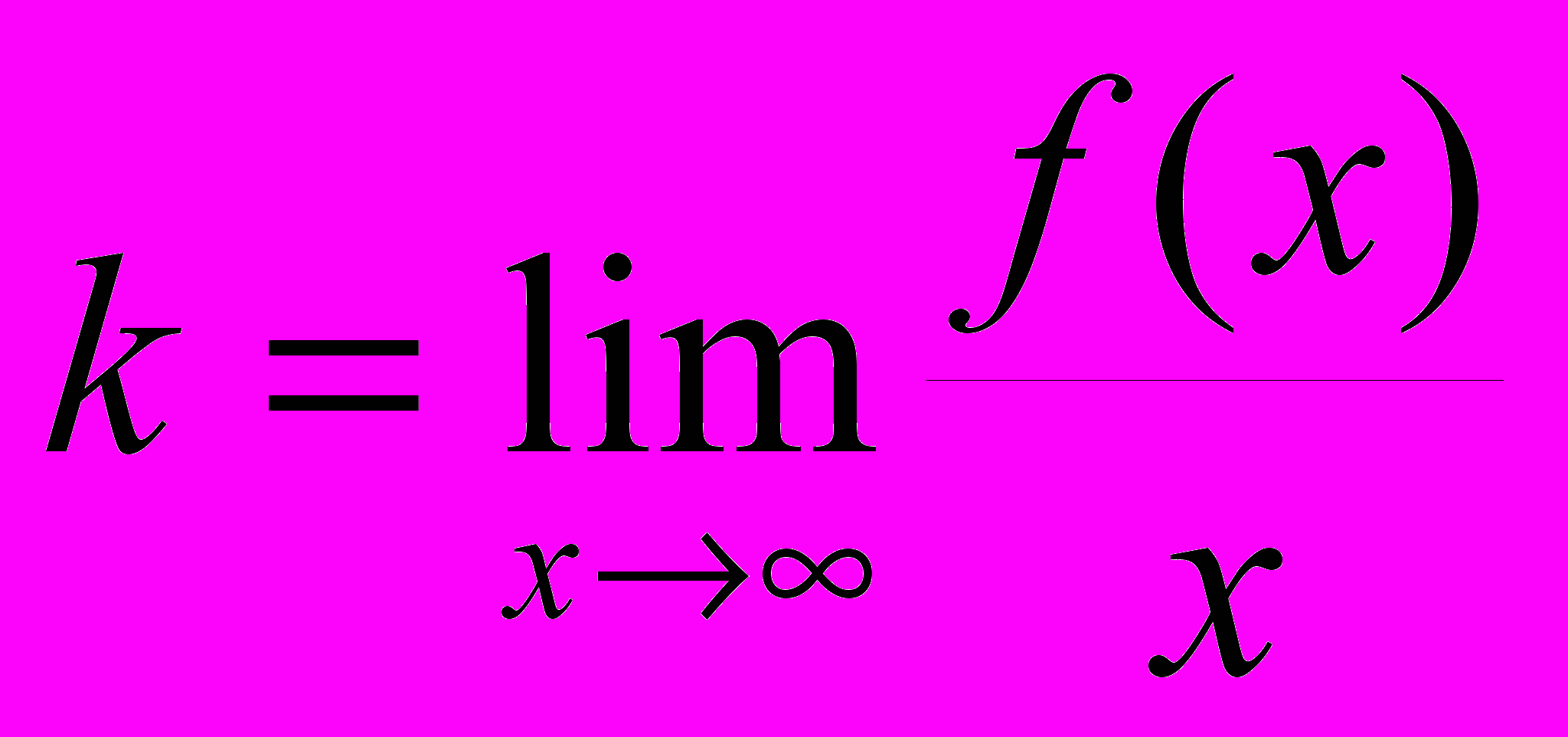 . По условию
. По условию 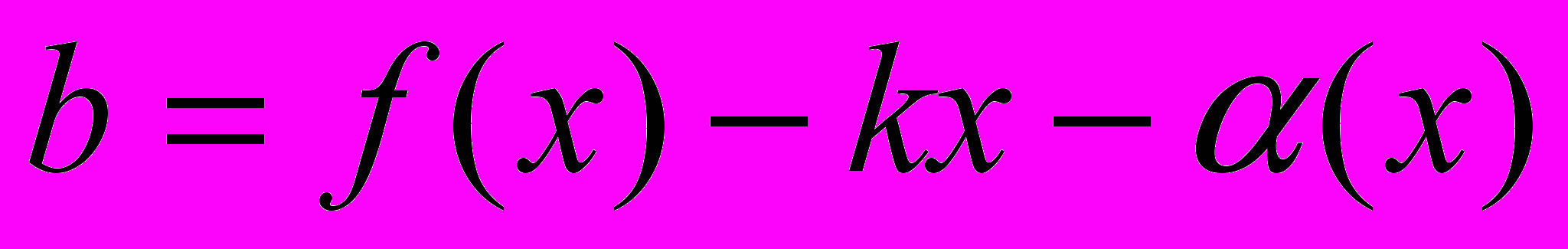 и по теореме
и по теореме 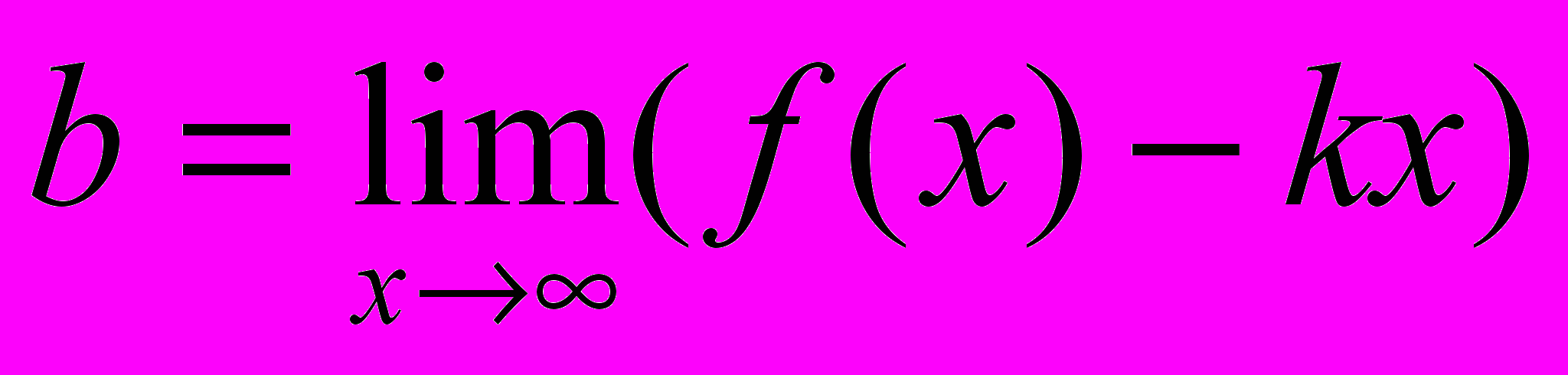 .
.ТЕОРЕМА 6. Если для функции
 существуют пределы
существуют пределы 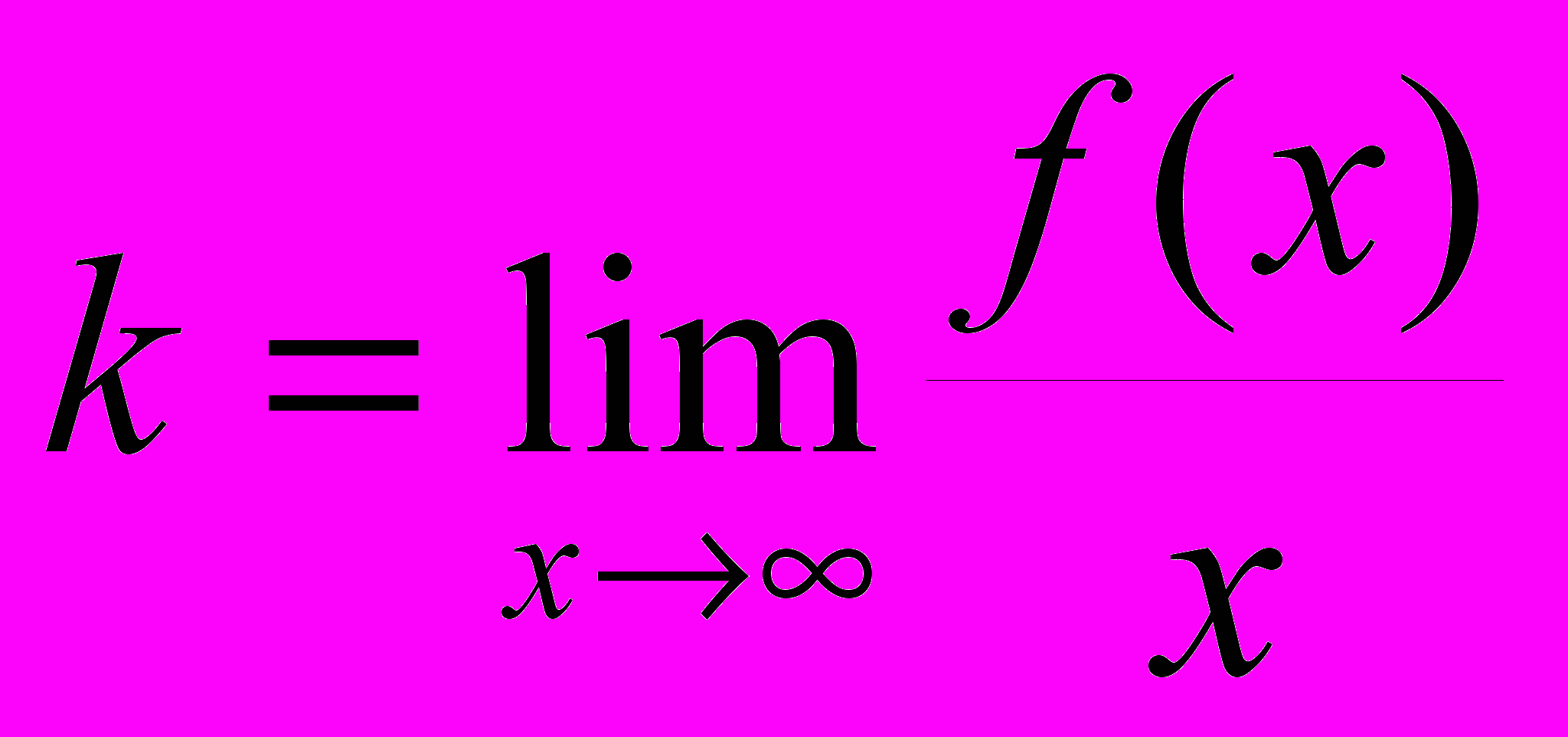 и
и 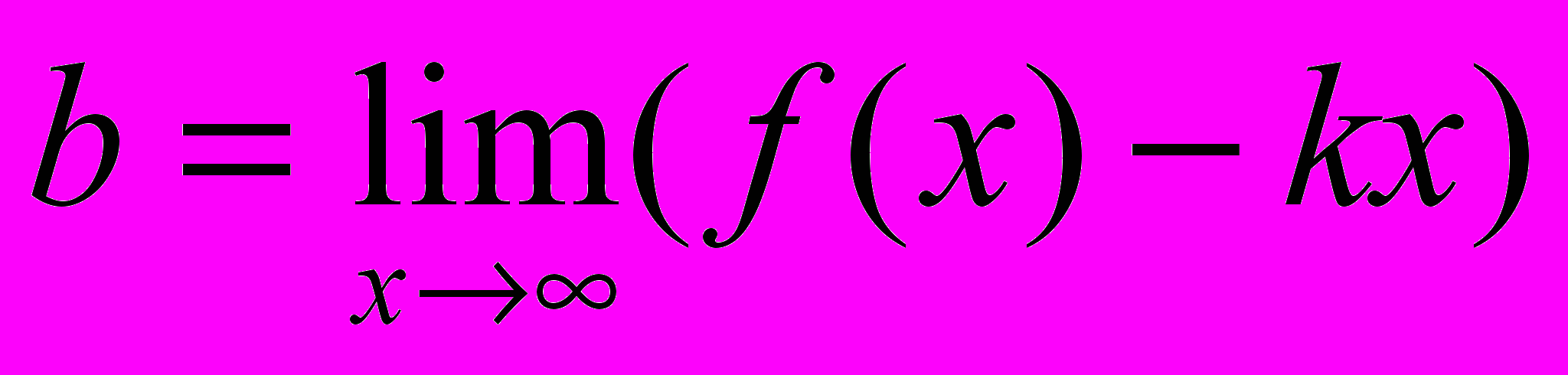 , то прямая
, то прямая 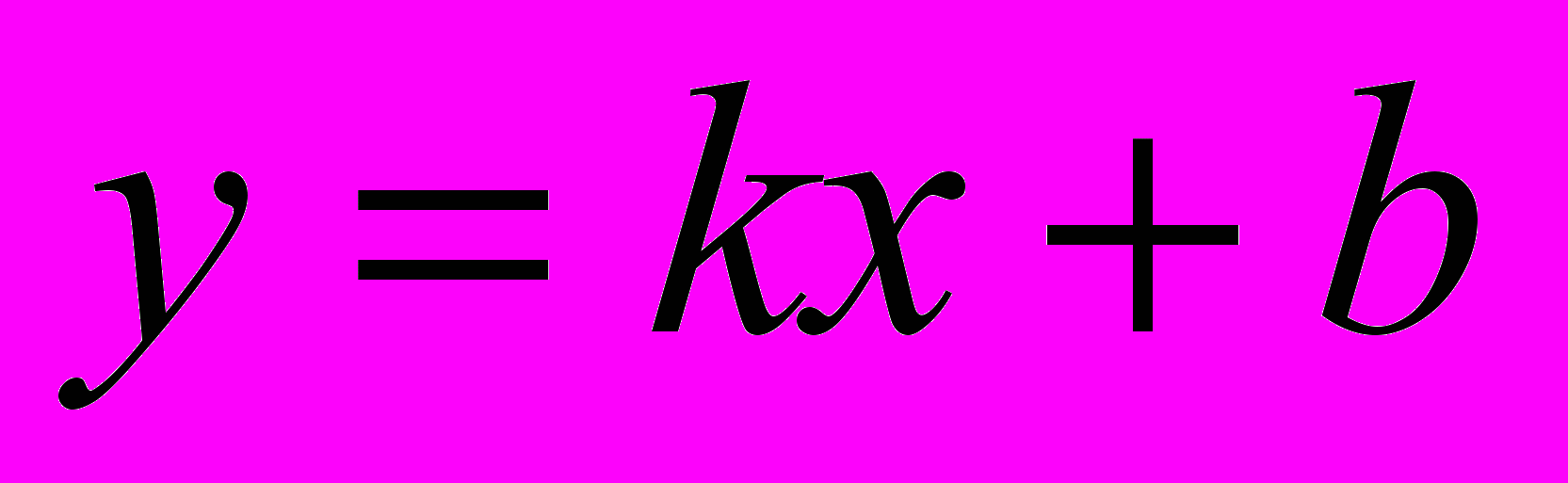 является наклонной асимптотой ее графика.
является наклонной асимптотой ее графика.ДОК. По условию
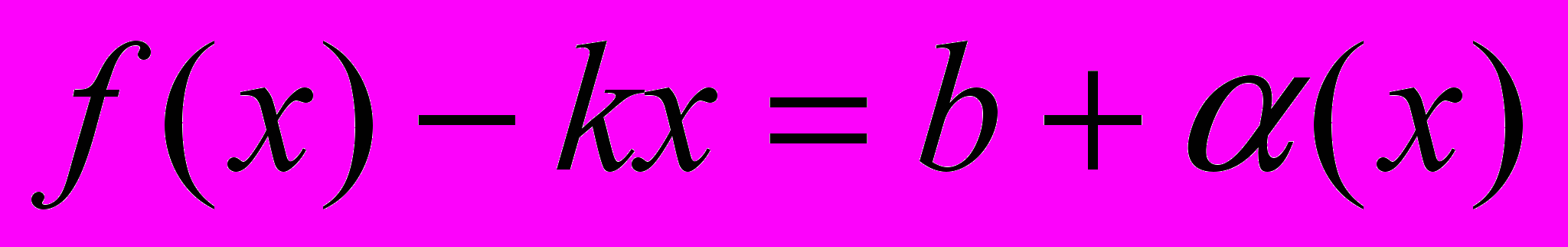 . Тогда
. Тогда 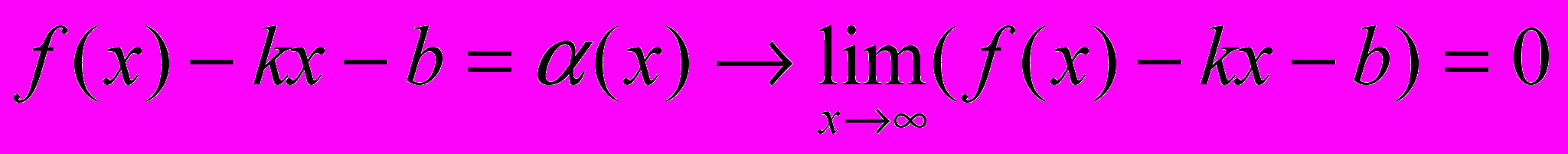
ПРИМЕР 3. Функция
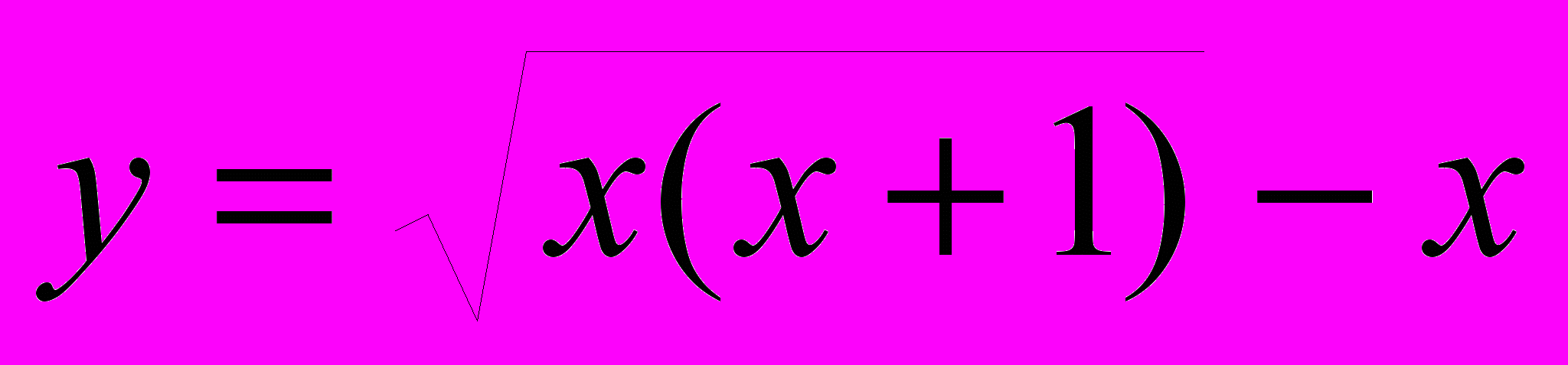 имеет на
имеет на 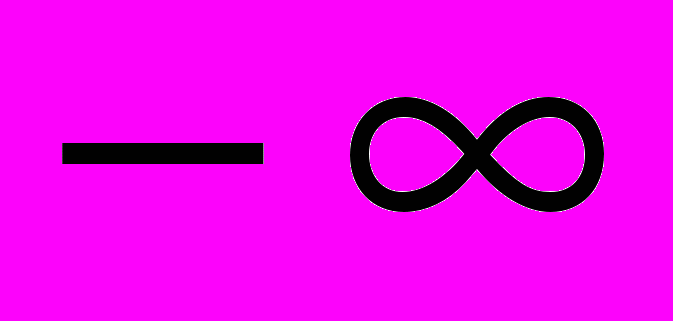 прямую
прямую 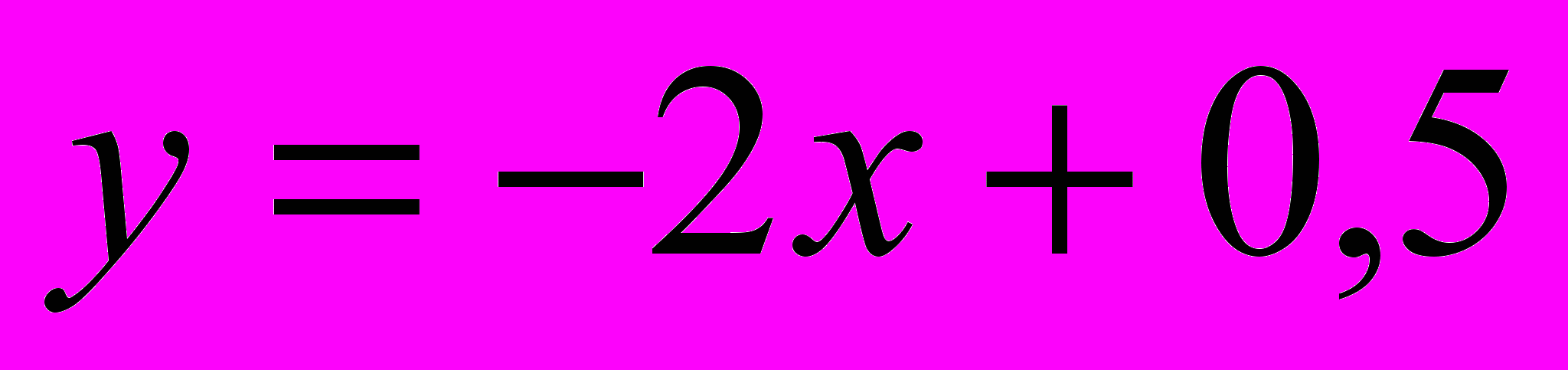 своей наклонной асимптотой. Действительно,
своей наклонной асимптотой. Действительно, 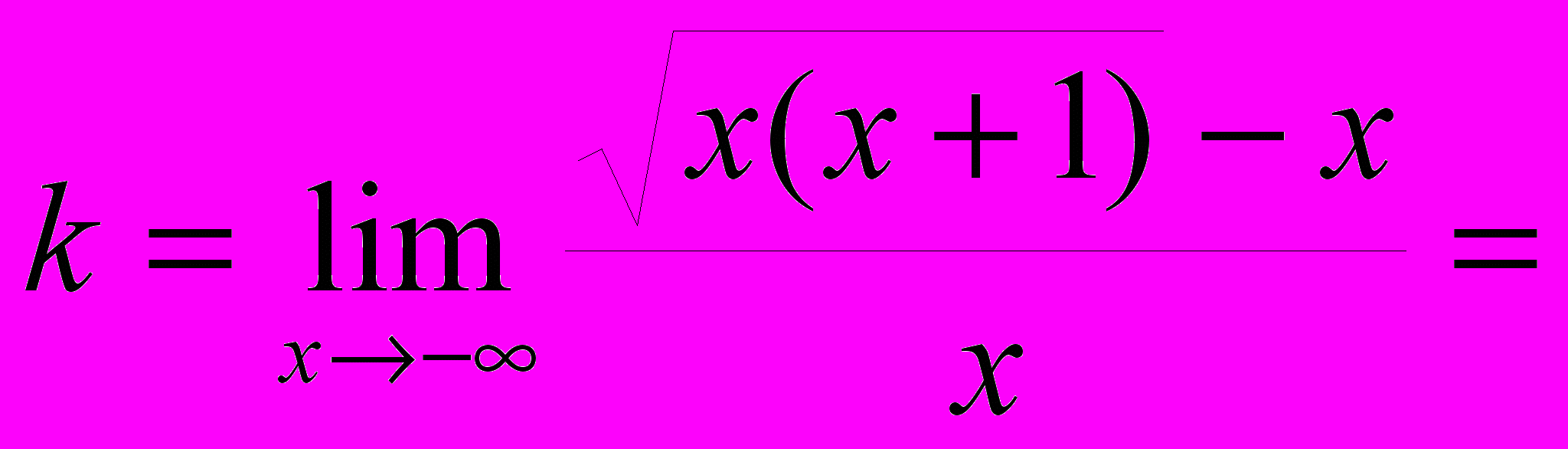
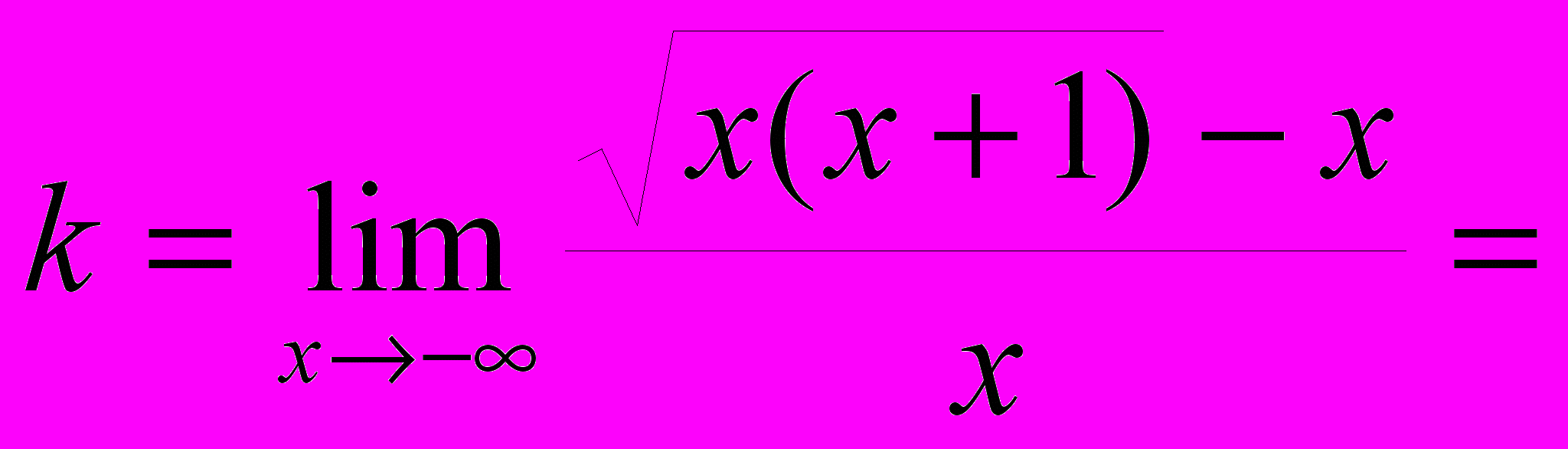
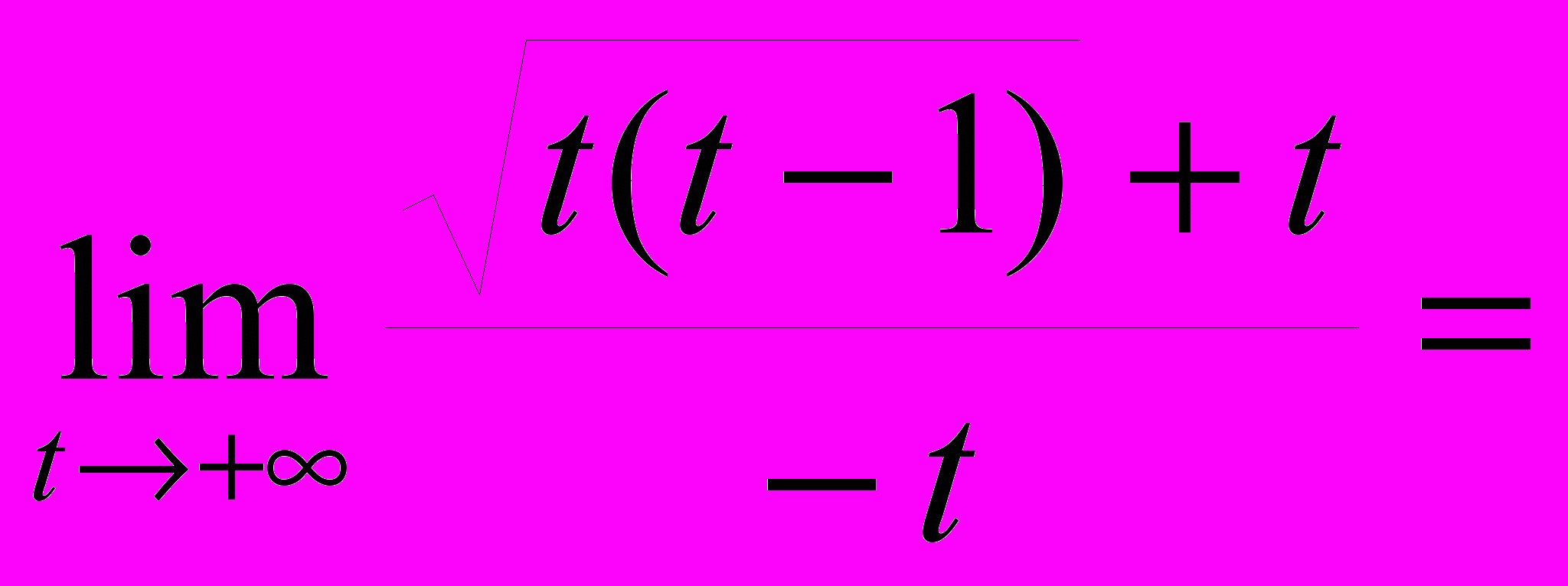
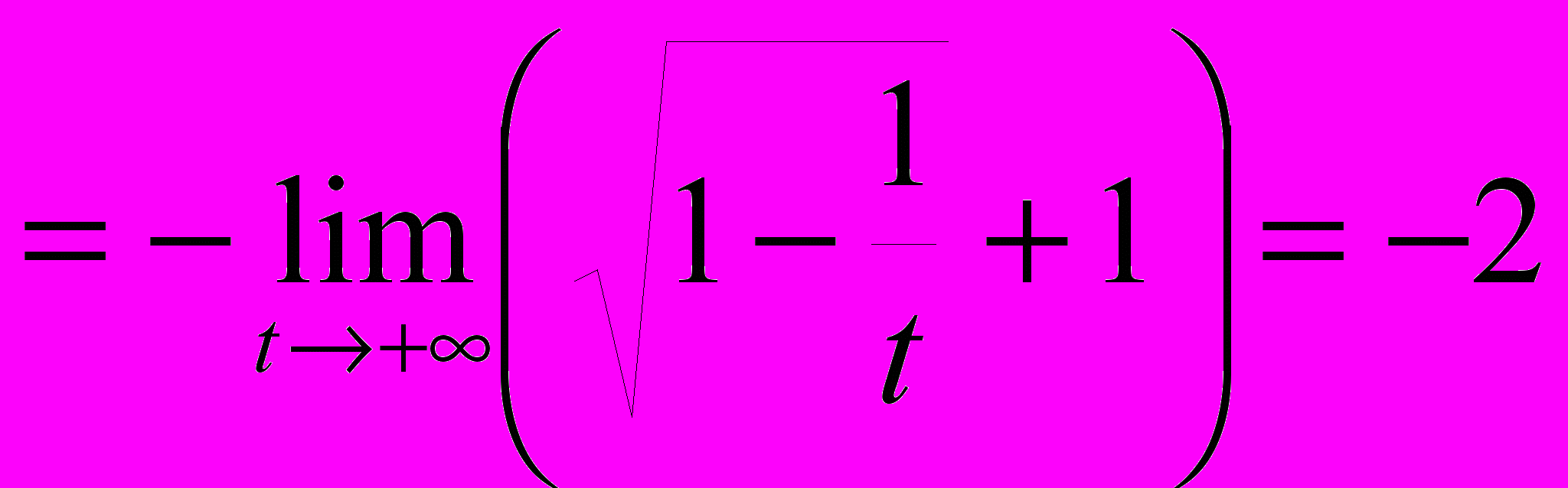 и
и 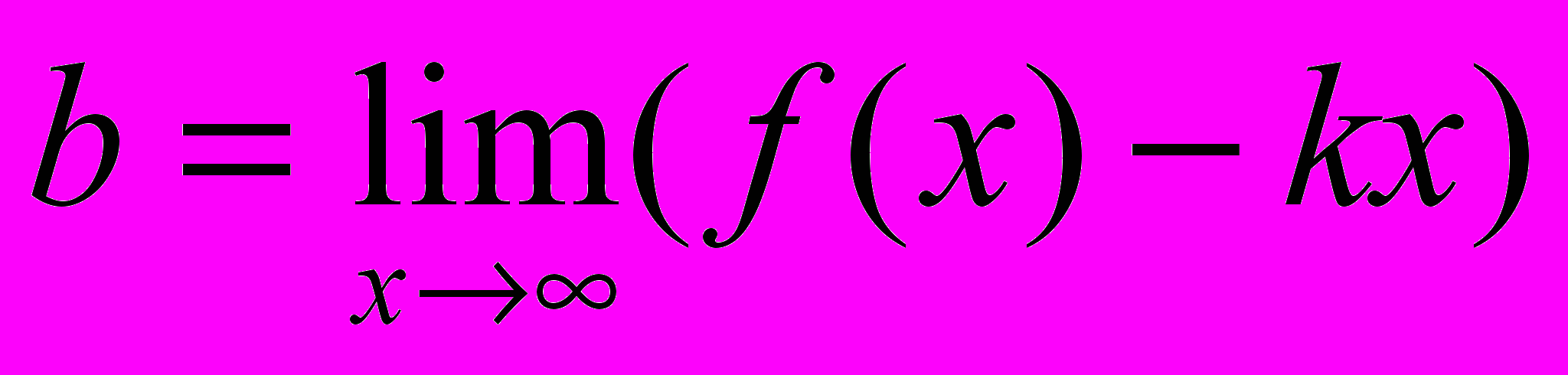 =
=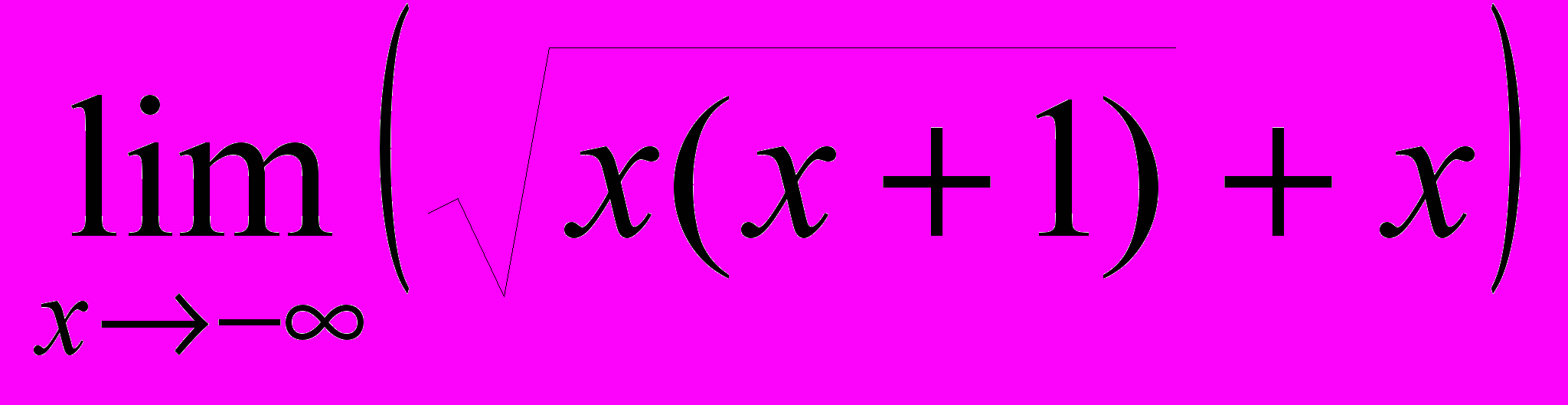
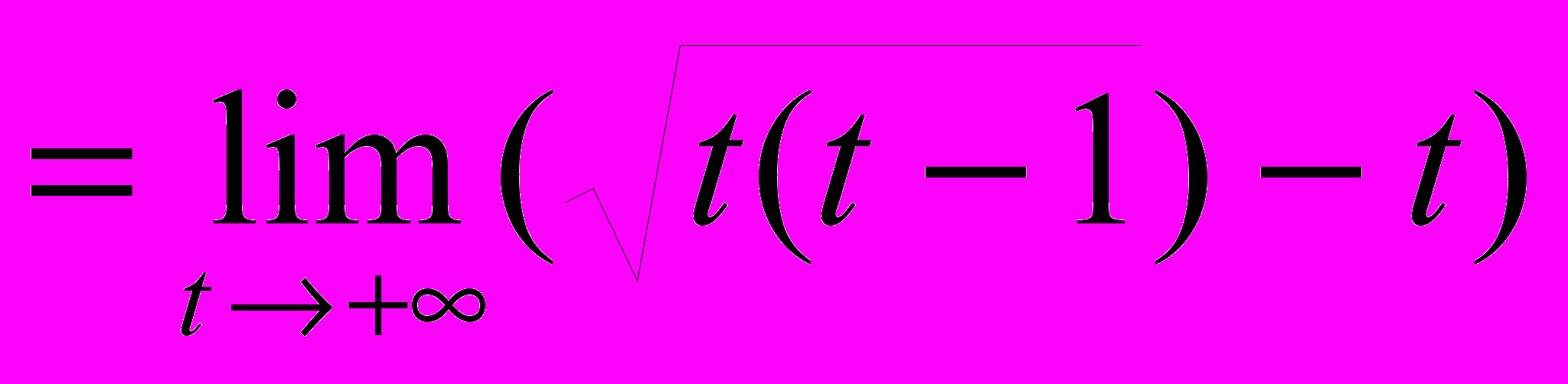 =0,5.
=0,5.П.4 Схема построения графика функции.
При построении графика функции полезно следовать следующей схеме:1) Найти область определения функции.2) Определить особенности функции: четность, нечетность, периодичность или его отсутствие.3) Вычислить первую производную функции.
4) Отметить на области определения функции критические точки первого рода, отметить интервалы монотонности и определить характер монотонности (возрастание или убывание).
5) Среди критических точек отметить точки экстремума (максимума или минимума).6) Вычислить вторую производную функции.7) Отметить на области определения функции критические точки второго рода, отметить интервалы выпуклости и определить характер выпуклости (вниз или вверх).
8) Среди критических точек второго рода отметить точки перегиба.9) Установить асимптоты графика функции (вертикальные, горизонтальные, наклонные ).10) Построить график функции с учетом обнаруженных в пунктах 1)-9) особенностей.
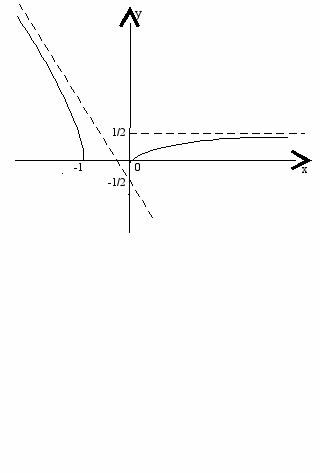
ПРИМЕР 4. Построить график функции
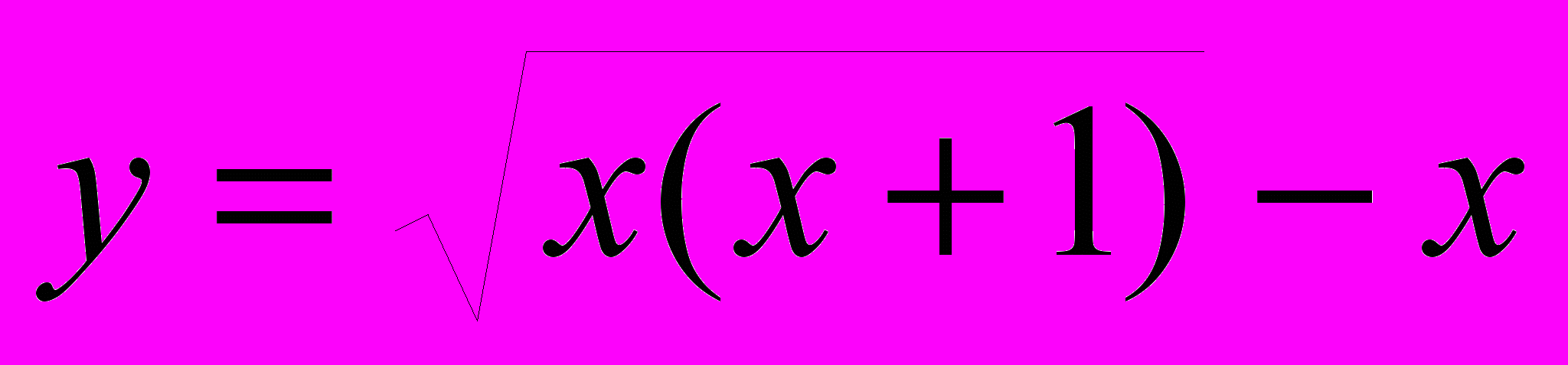 .
.Решение. 1)
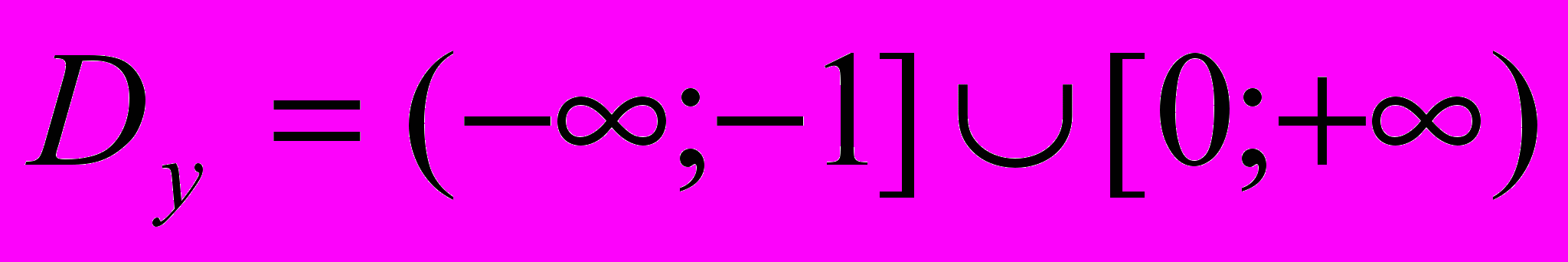 2) общего вида 3)
2) общего вида 3)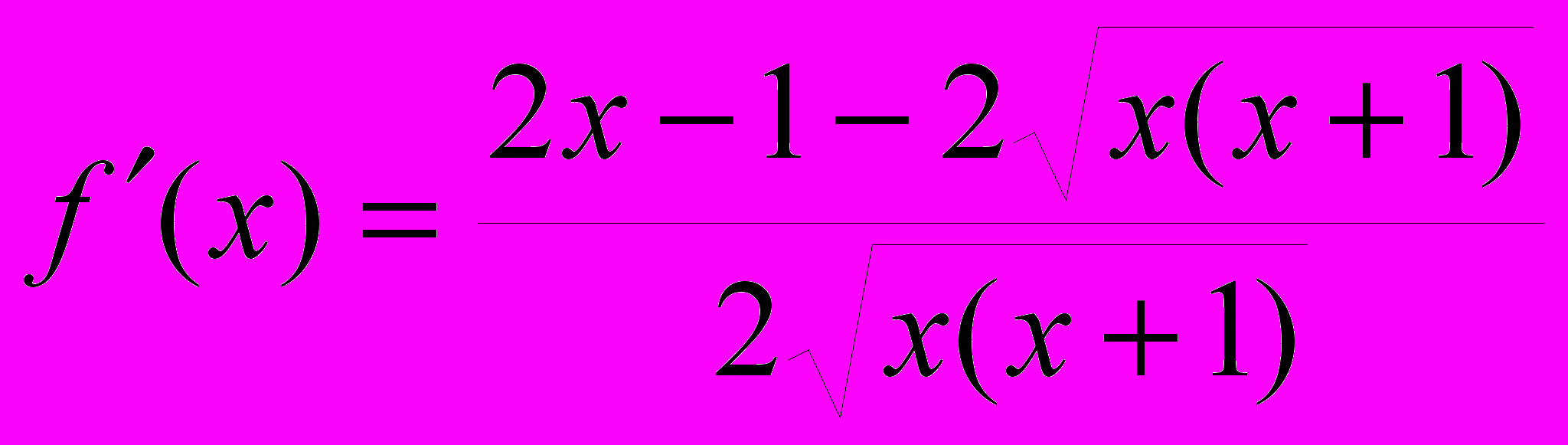 4)
4) 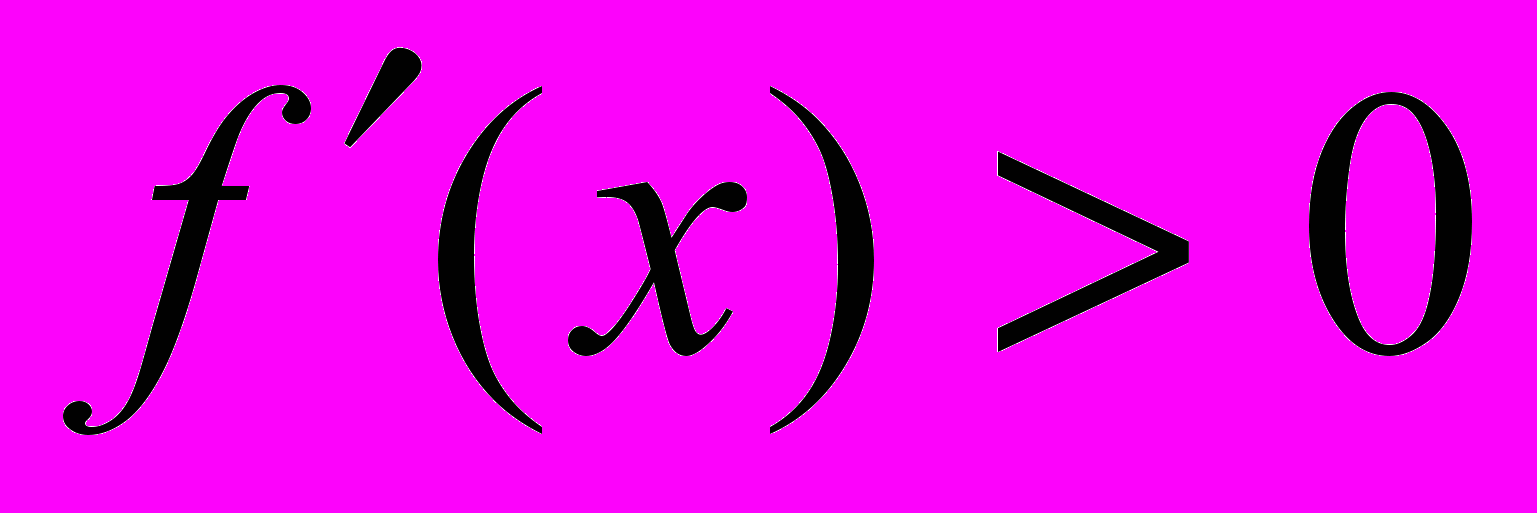 при
при 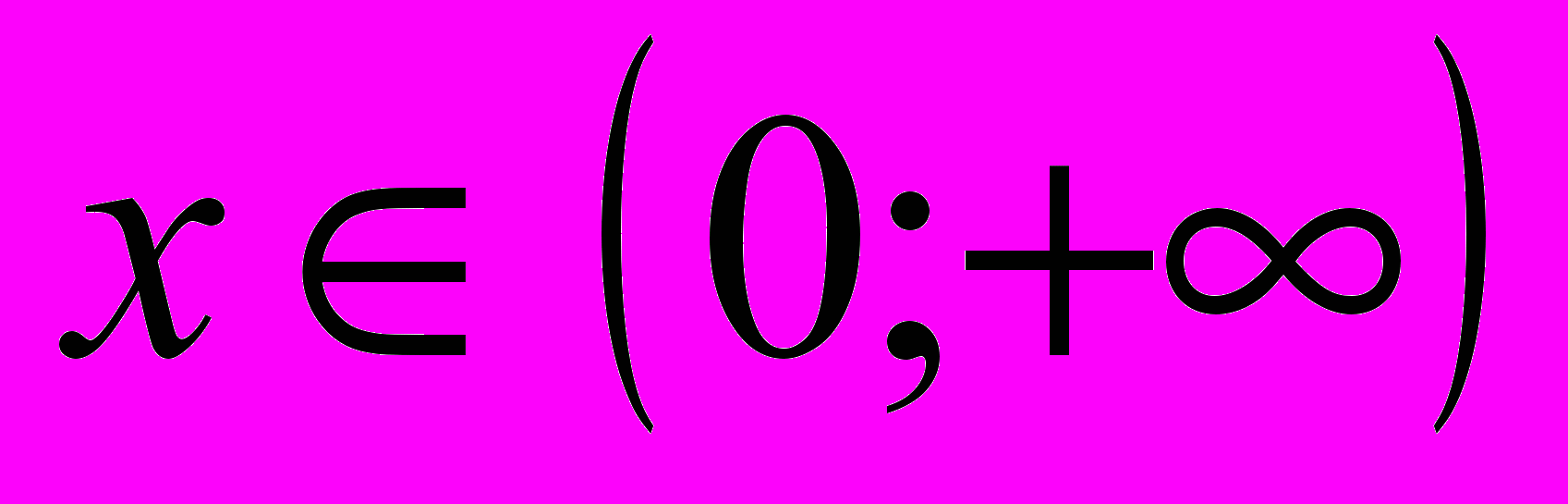 и
и 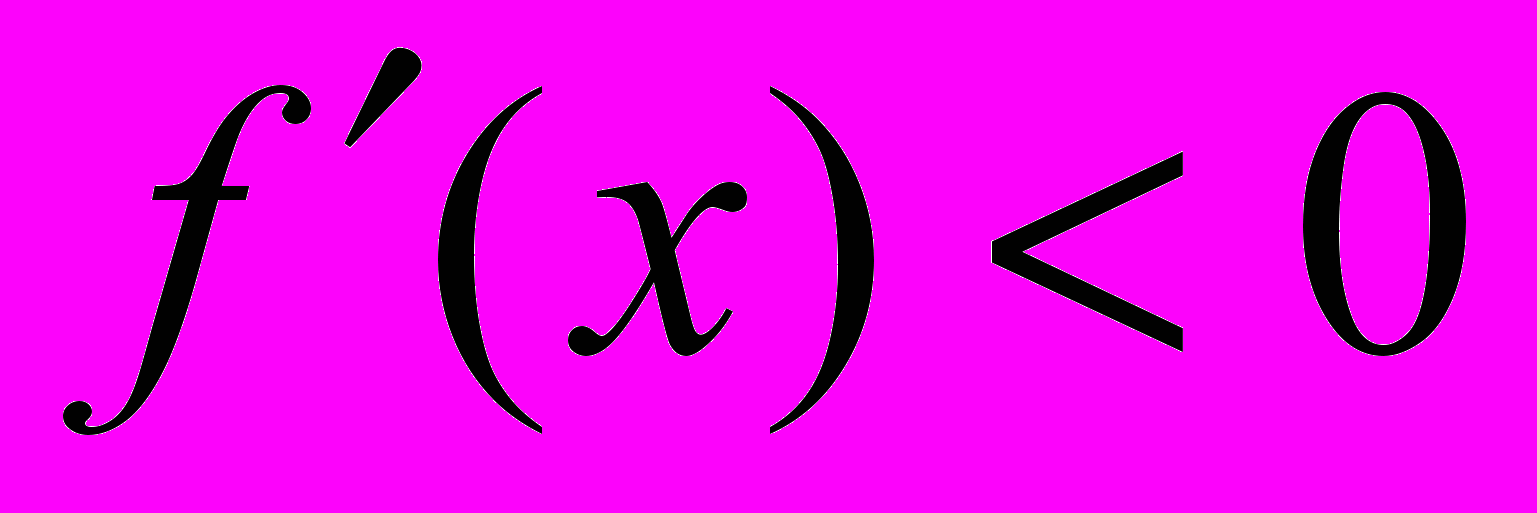 при
при 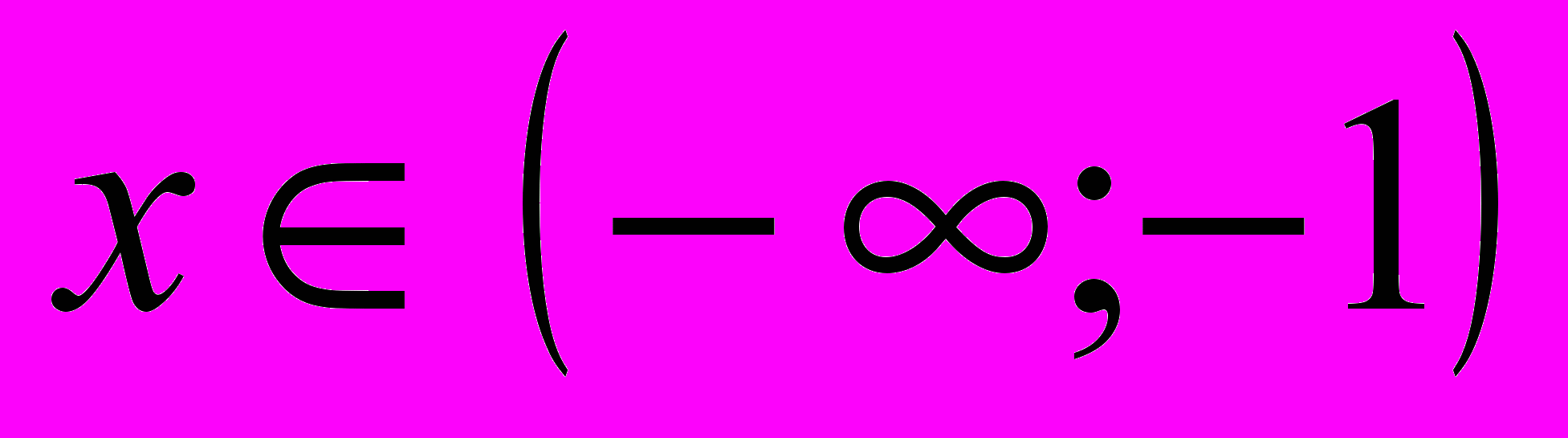 . Критические точки первого рода
. Критические точки первого рода 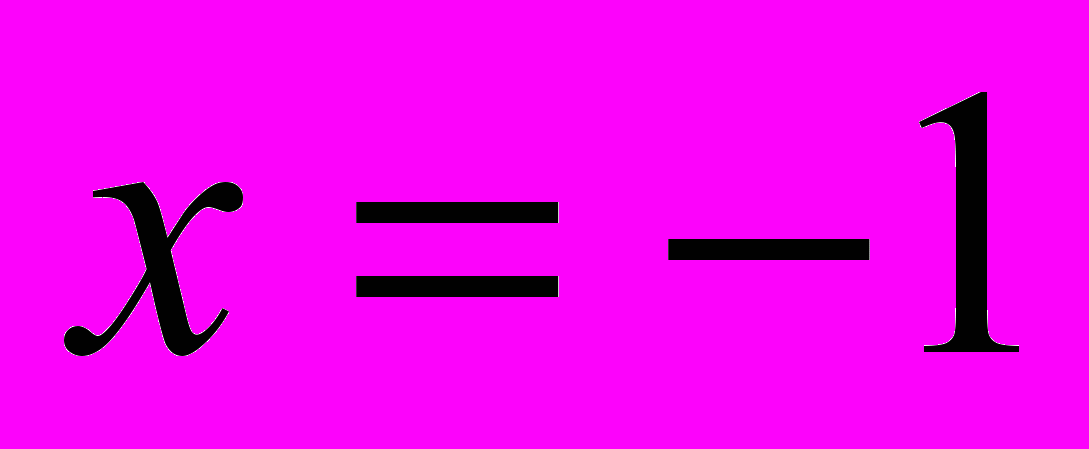 и
и 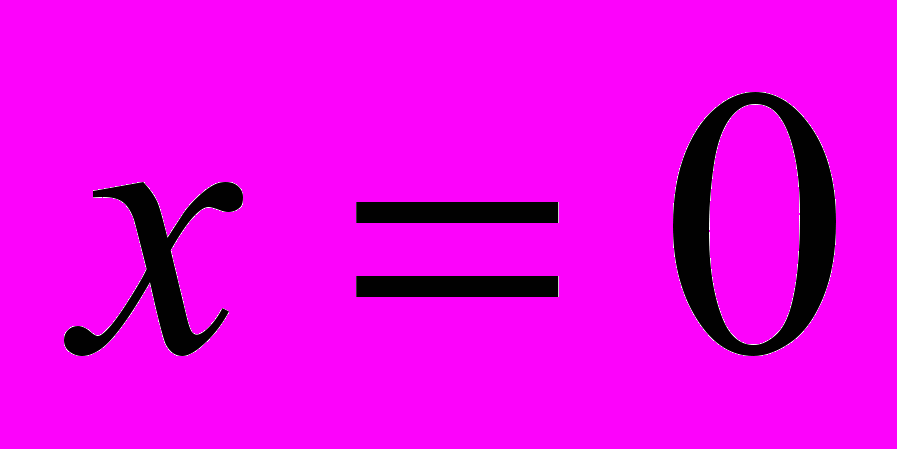 , в них производной нет ( она бесконечно большая, вертикальная касательная) 5) точек экстремума нет.
, в них производной нет ( она бесконечно большая, вертикальная касательная) 5) точек экстремума нет.6)
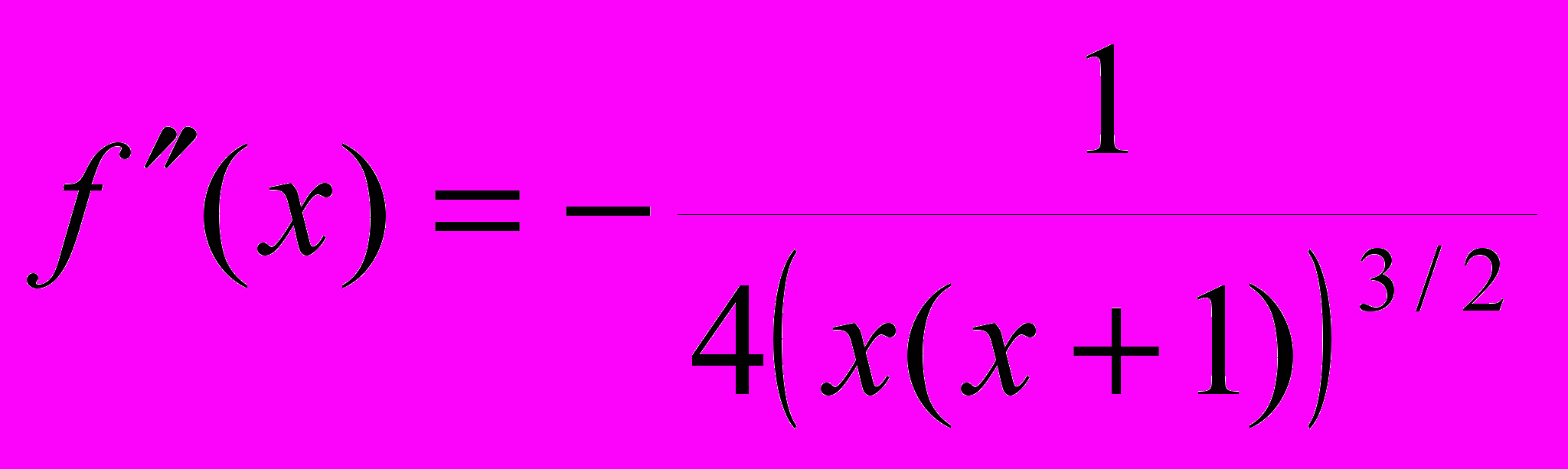 7) Критические точки второго рода
7) Критические точки второго рода 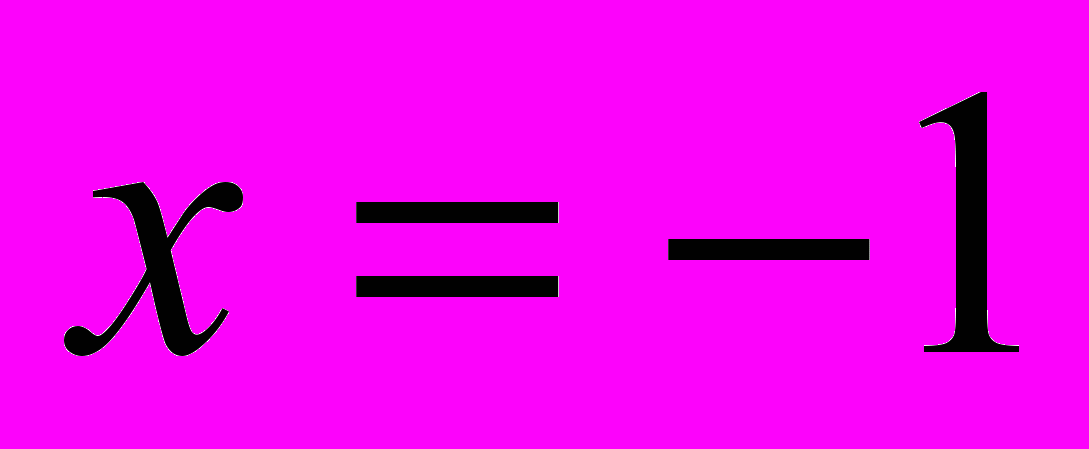 и
и 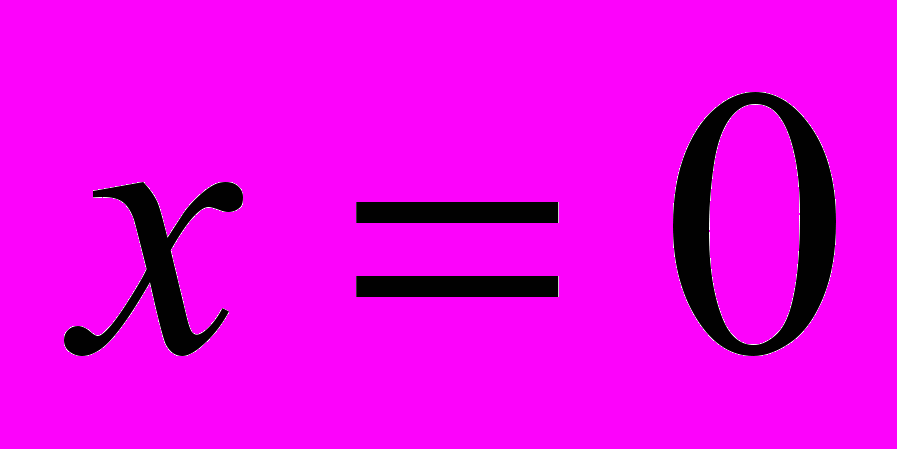 , в них производной нет, функция на области определения выпукла вверх. 8) точек перегиба нет.
, в них производной нет, функция на области определения выпукла вверх. 8) точек перегиба нет. 9) Вертикальных асимптот нет, прямая
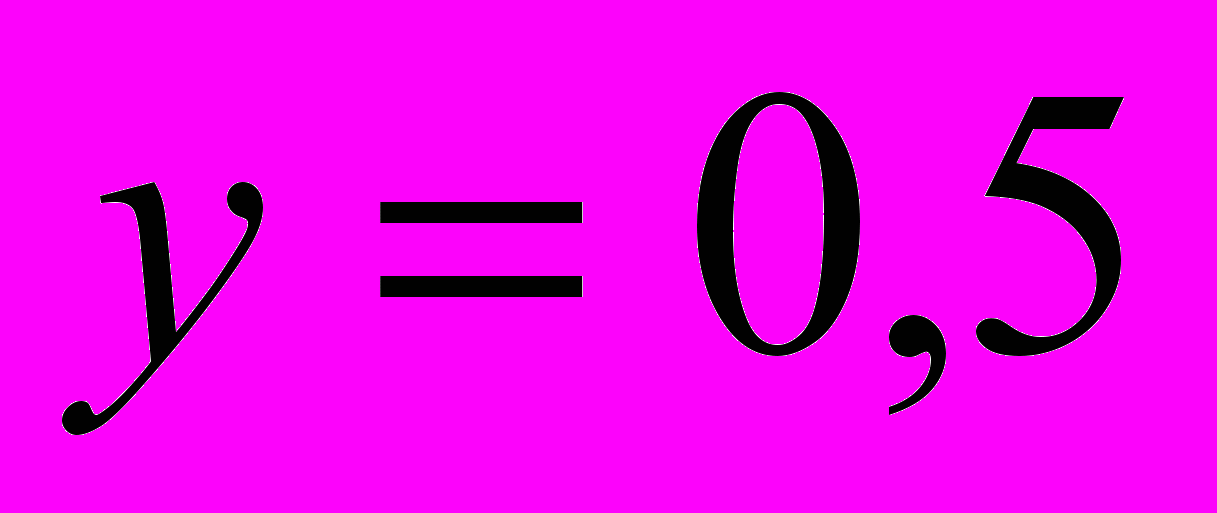 -горизонтальная асимптота на
-горизонтальная асимптота на 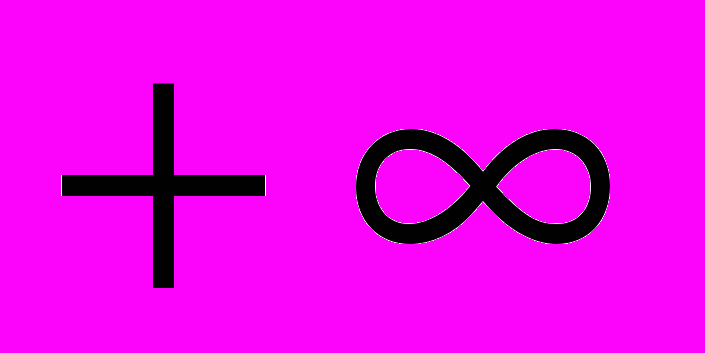 и прямая
и прямая 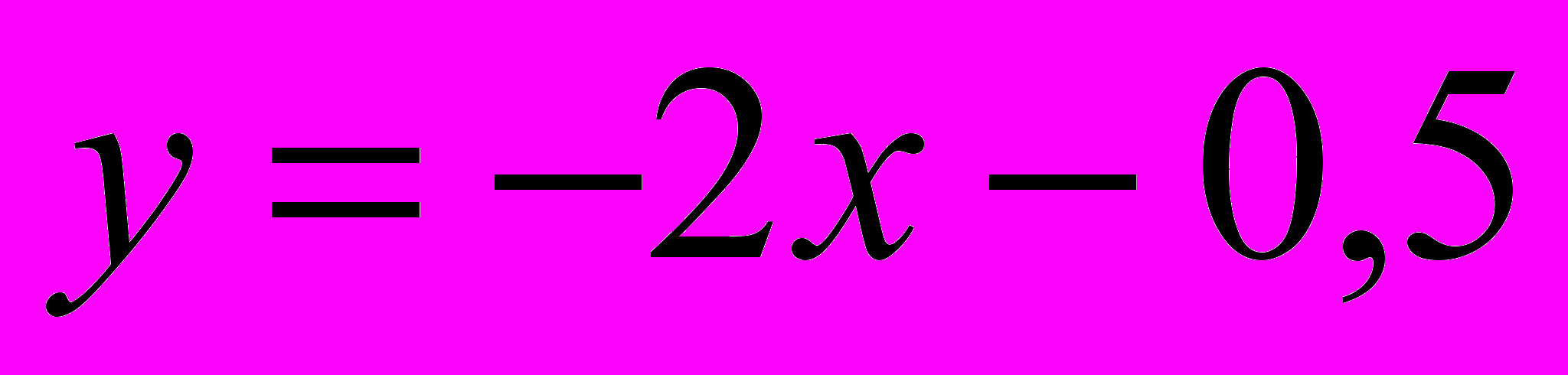 является наклонной асимптотой на
является наклонной асимптотой на 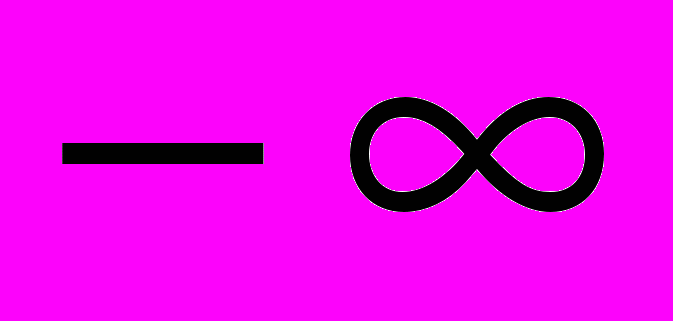 .
.
ВОПРОСЫ К ЭКЗАМЕНУ.
1) Выпуклость функции, достаточное условие выпуклости по первой производной, достаточное условие выпуклости по второй производной.
2) Точка перегиба, необходимое условие перегиба, достаточное условие перегиба.
3) Асимптоты графика функции : вертикальные, горизонтальные, наклонные. Необходимое и достаточное условие существования наклонной асимптоты.
4) Общая схема исследования функции и построения ее графика. Проиллюстрировать схему на примере по выбору.
