Нахождение наибольшего и наименьшего значений функции непрерывной на отрезке

Вид материала

Документы

Подобный материал:

• В. И. Афанасьева 01 марта 2011 г. Программа, 116.92kb.
• Программа междисциплинарного государственного экзамена по специальности 090102 Компьютерная, 116.53kb.
• Решение логических задач, 273.53kb.
• Лекция 11. Исследование функций с помощью производной, 168.49kb.
• Метод решения функциональных уравнений, 173.74kb.
• Правила нахождения первообразных. Понятие определенного интеграла. Формула Ньютона-Лейбница., 67.43kb.
• Игра Отборочный тур. Перечислите виды спорта по числу играющих, начиная с наименьшего:, 176.68kb.
• Назначение программы. Данная программа предназначена для исследования функции. Всостав, 270.6kb.
• Лекция Дифференцирование функций, 25.58kb.
• Свойства функций, непрерывных на отрезке Теорема, 9.02kb.

Нахождение наибольшего и наименьшего значений функции

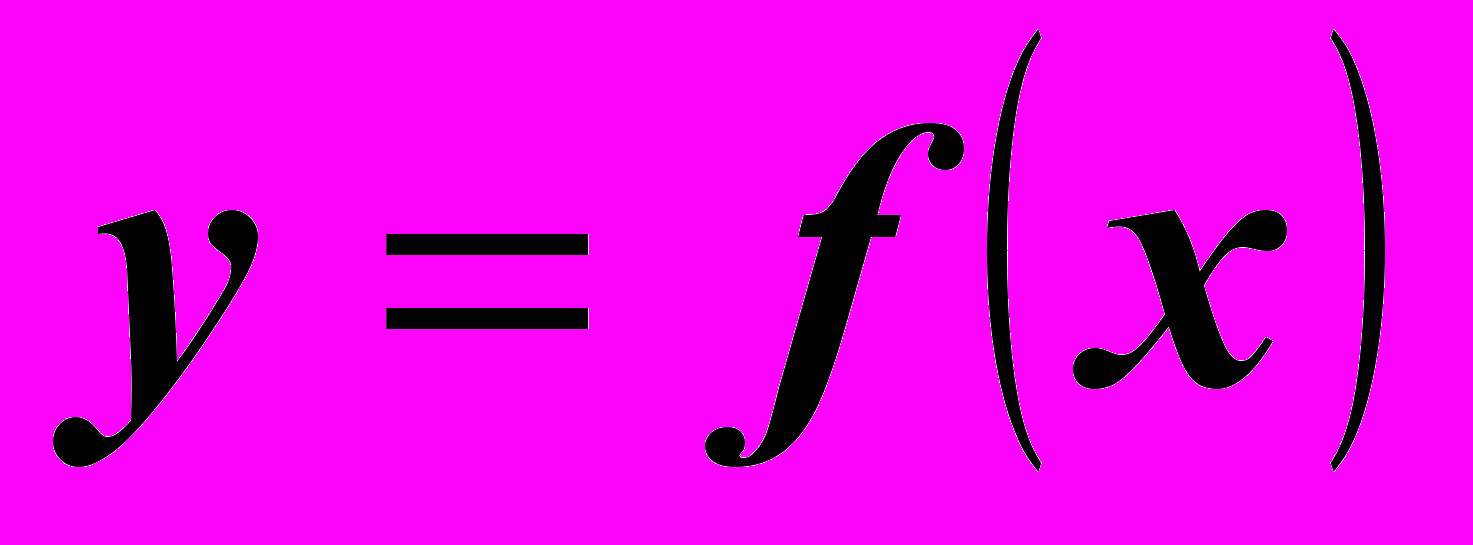непрерывной НА отрезке


Теорема 1. Функция 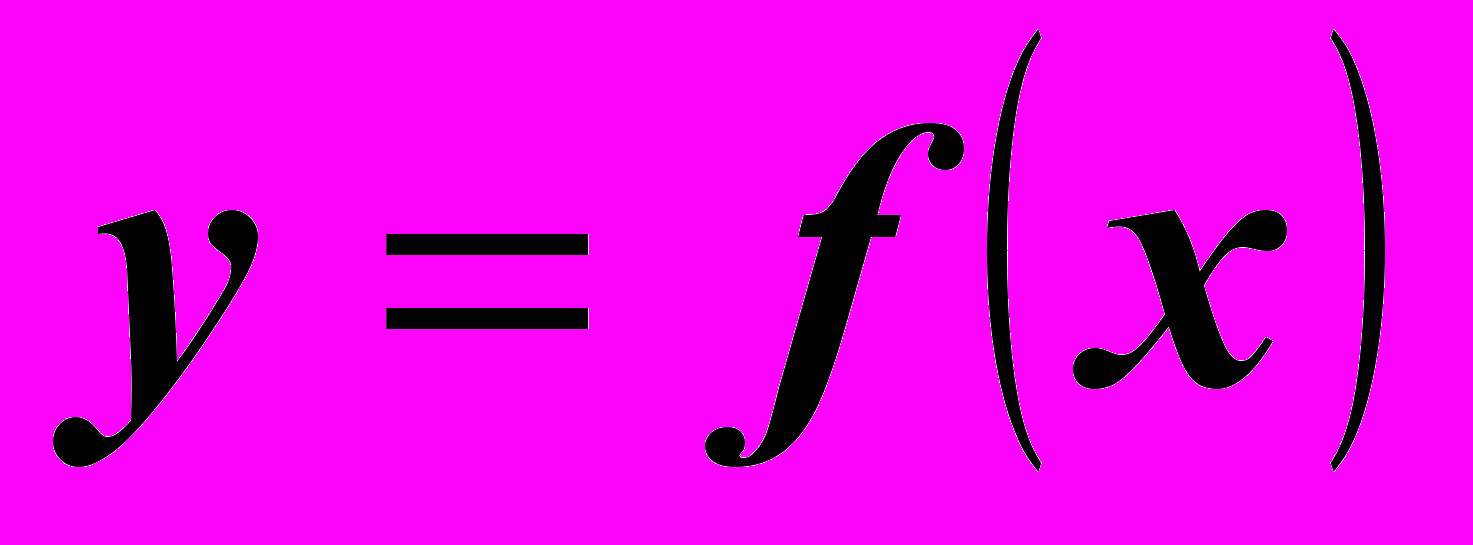, непрерывная на отрезке , достигает на нем наибольшего и наименьшего значений.

Теорема 2. Областью значений функции 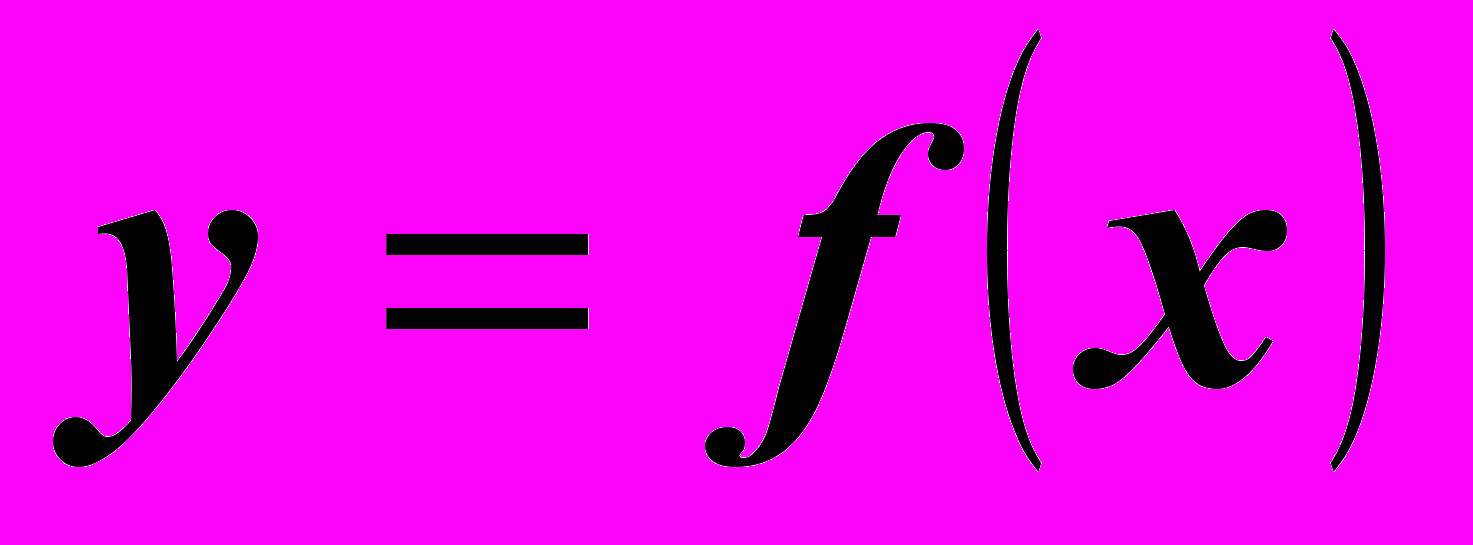, непрерывной на , является отрезок

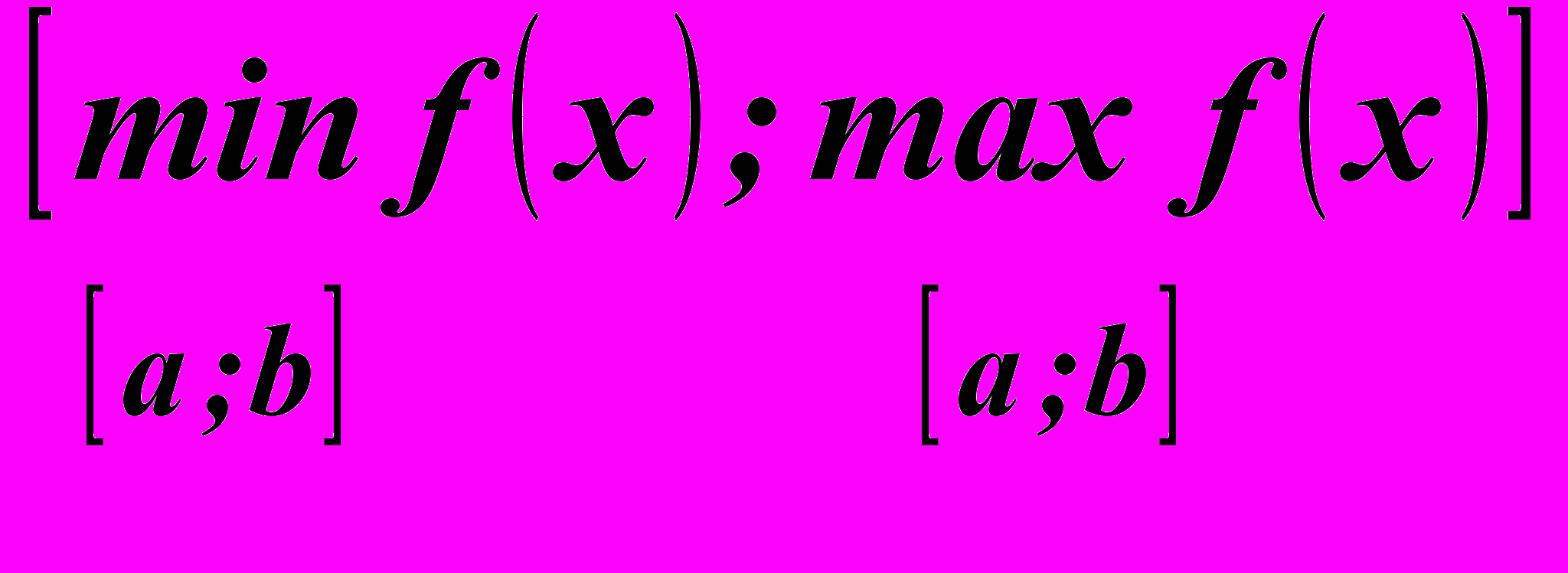
Алгоритм

1. Найти критические точки функции 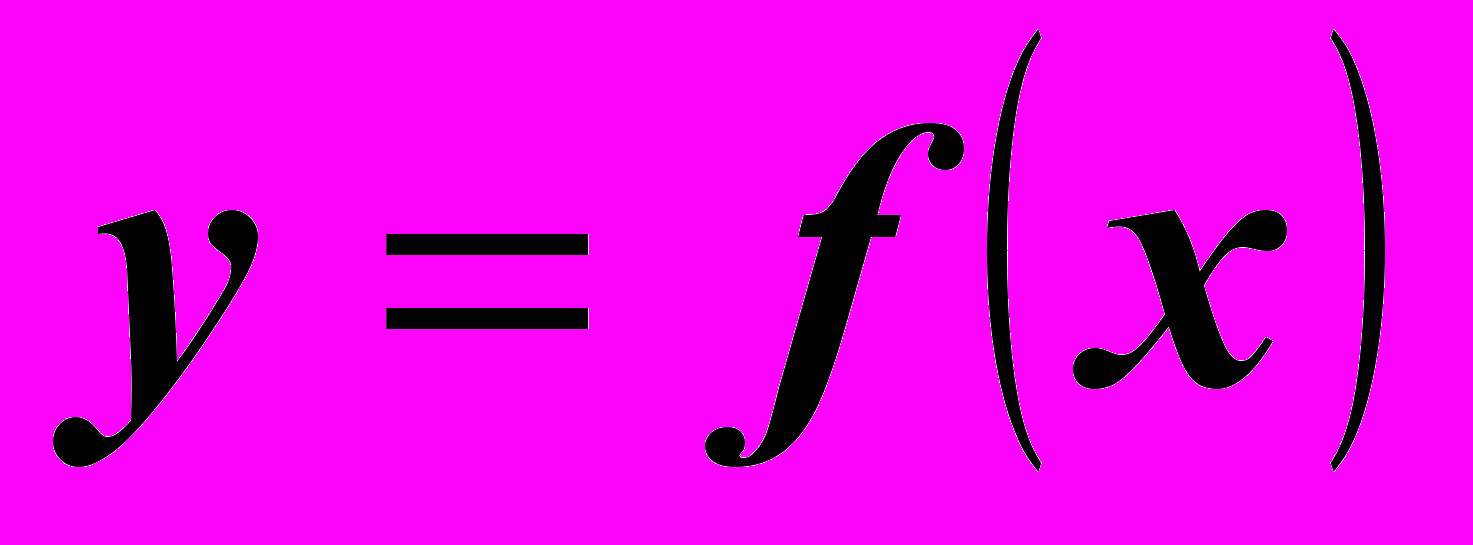(внутренние точки из области определения функции, в которых производная равна нулю или не существует).

2. Выбрать из них те, которые лежат внутри .

3. Вычислить значение функции 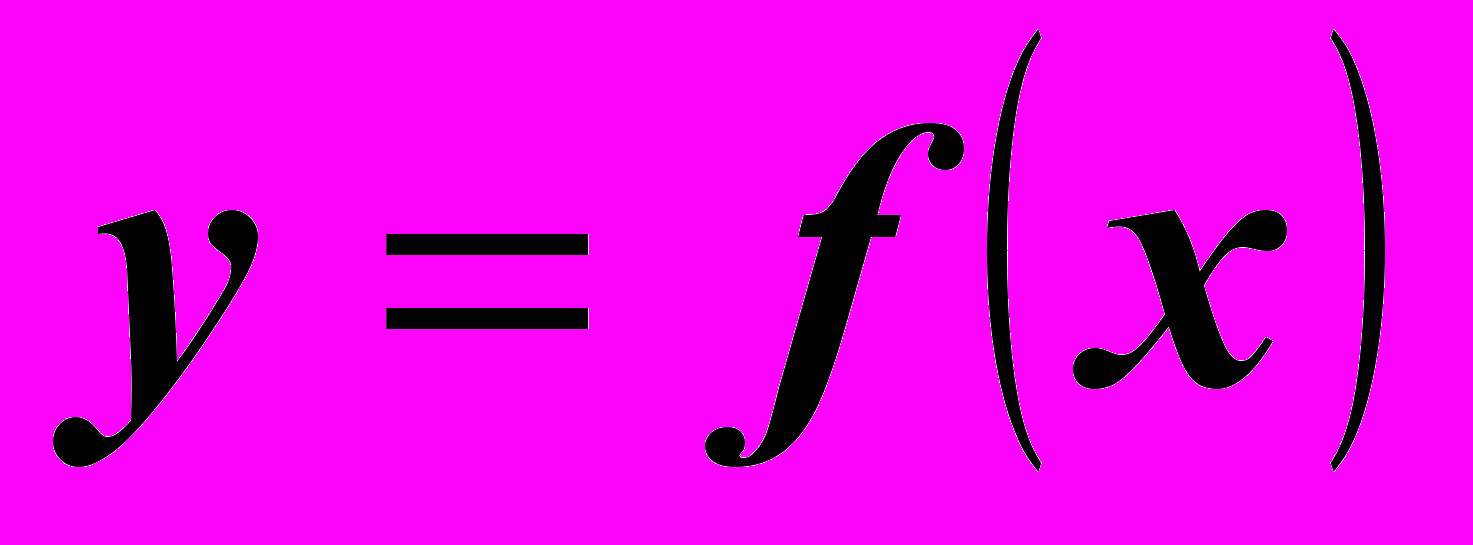в точках и 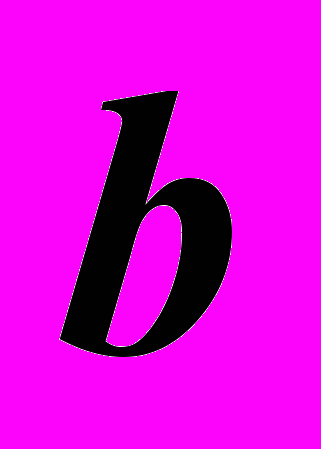, а также в критических точках функции , лежащих внутри .

4. Выбрать из полученных чисел наименьшее (это будет 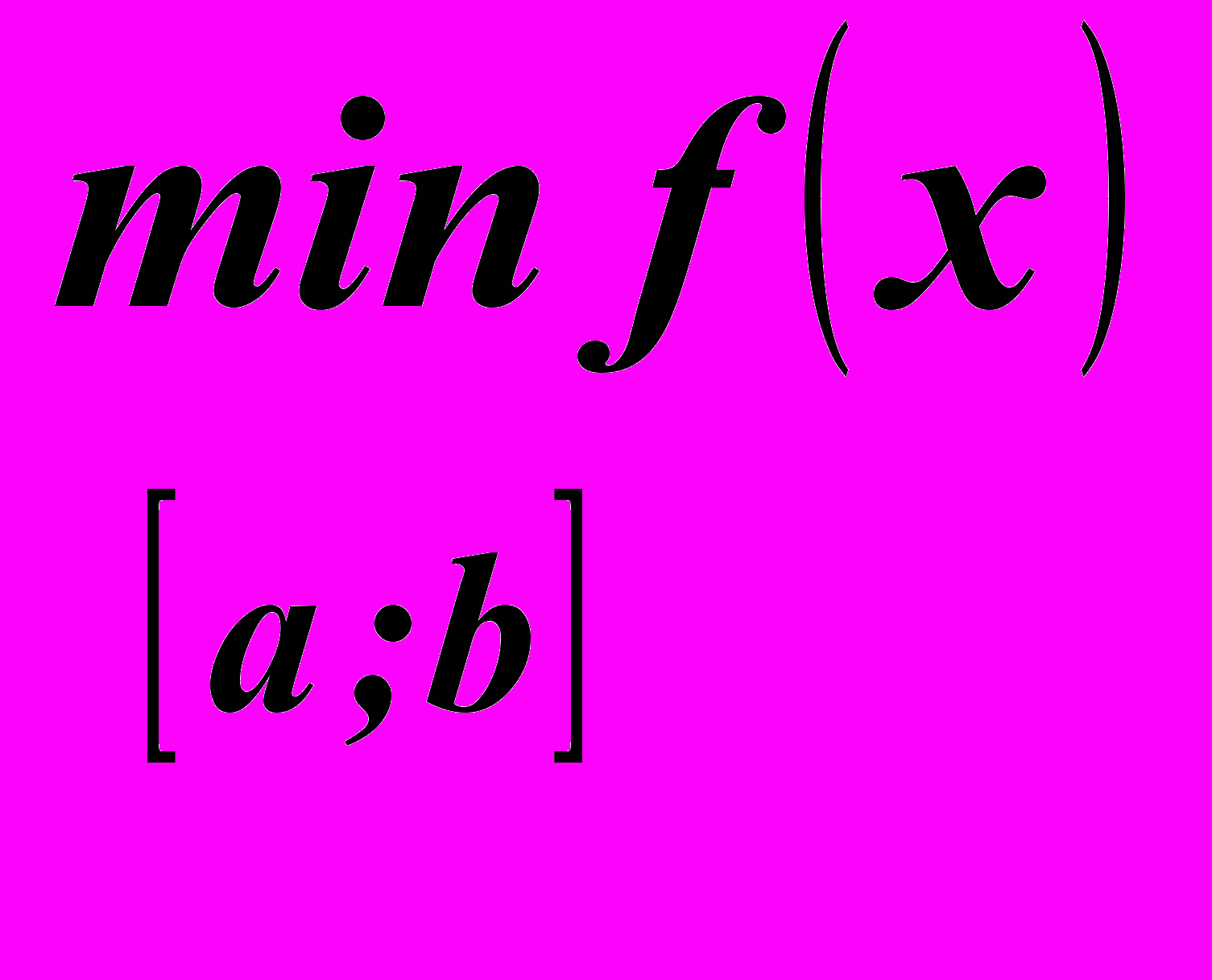) и наибольшее (это будет ).


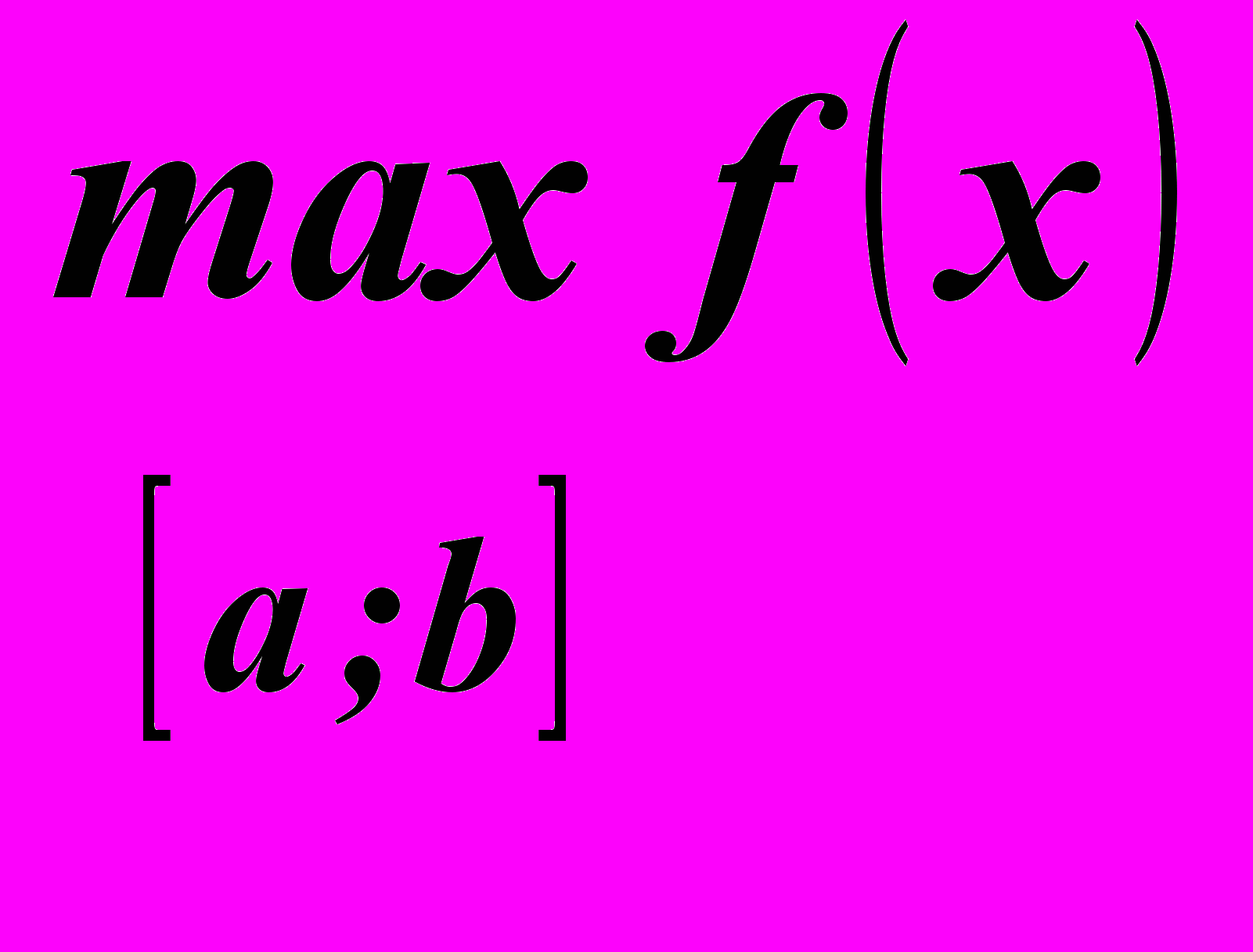Нахождение наибольшего и наименьшего значений функции

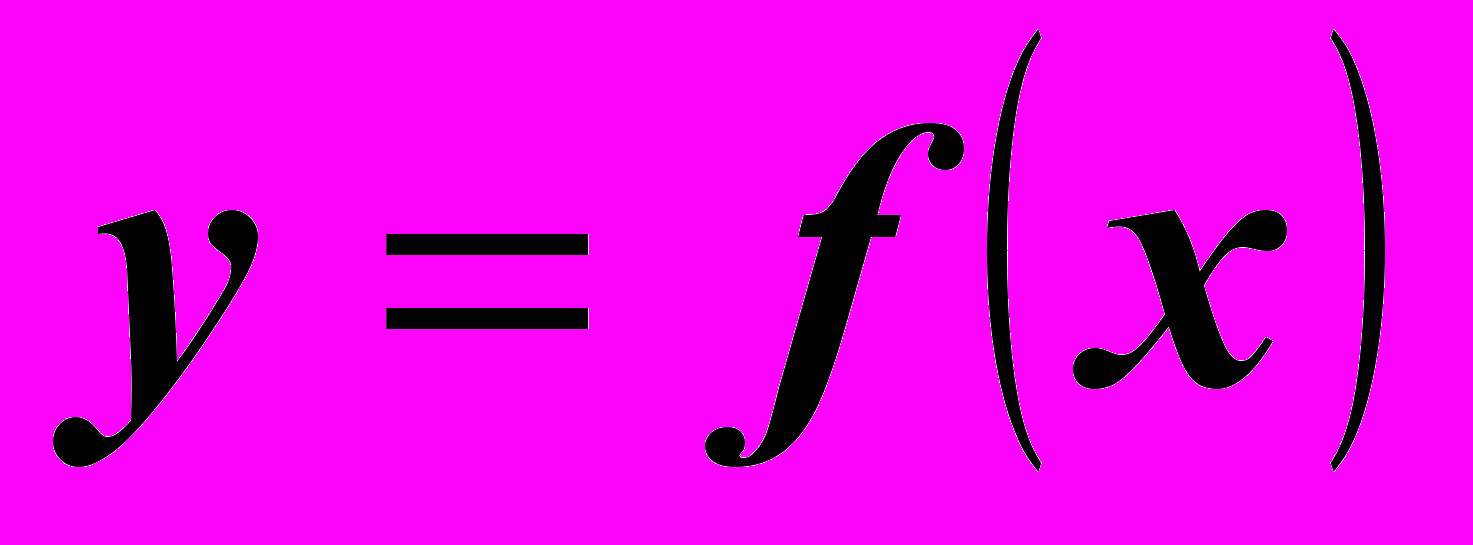непрерывной НА интервале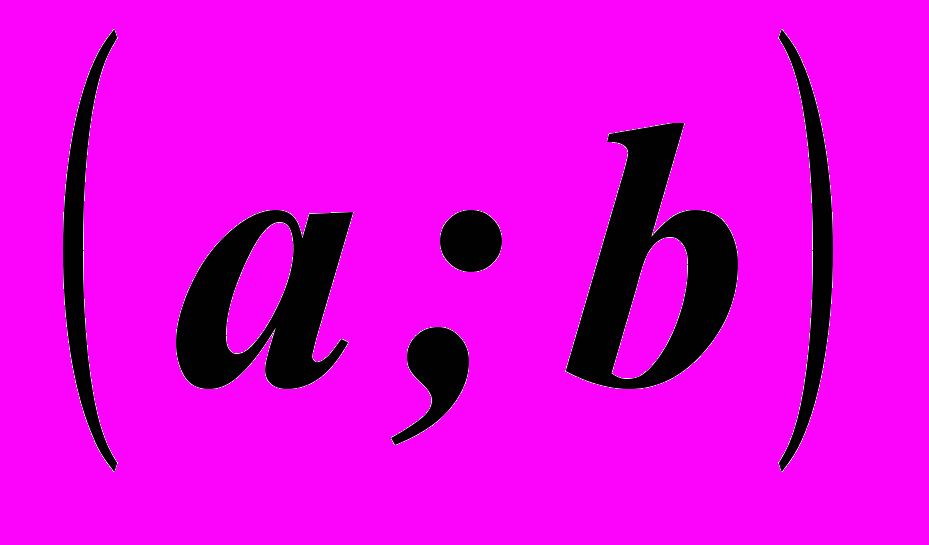


1. Чтобы исследовать функцию на наибольшее (наименьшее) значение на интервале 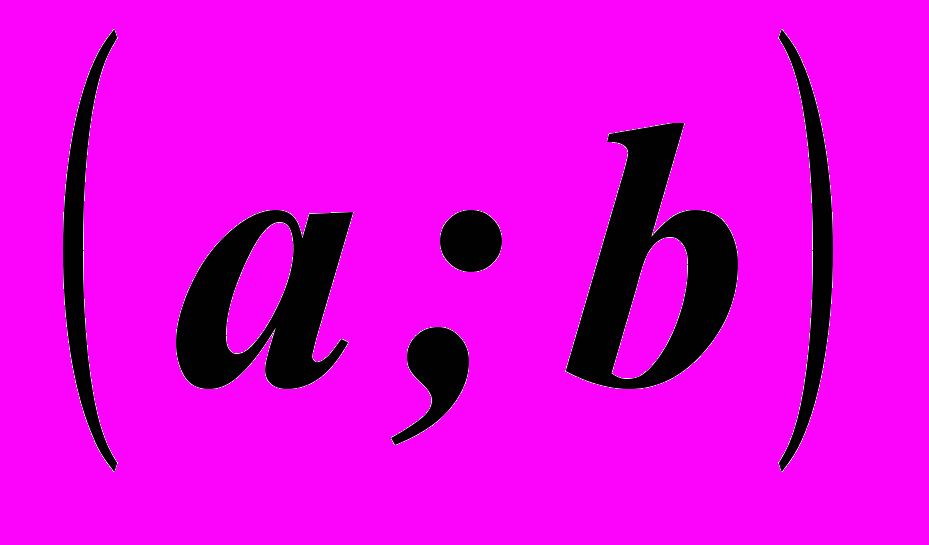, надо исследовать ее, если это возможно, на отрезке . Если наибольшее (наименьшее) значение достигается функцией во внутренней точке отрезка , то оно будет наибольшем (наименьшим) значением и на интервале 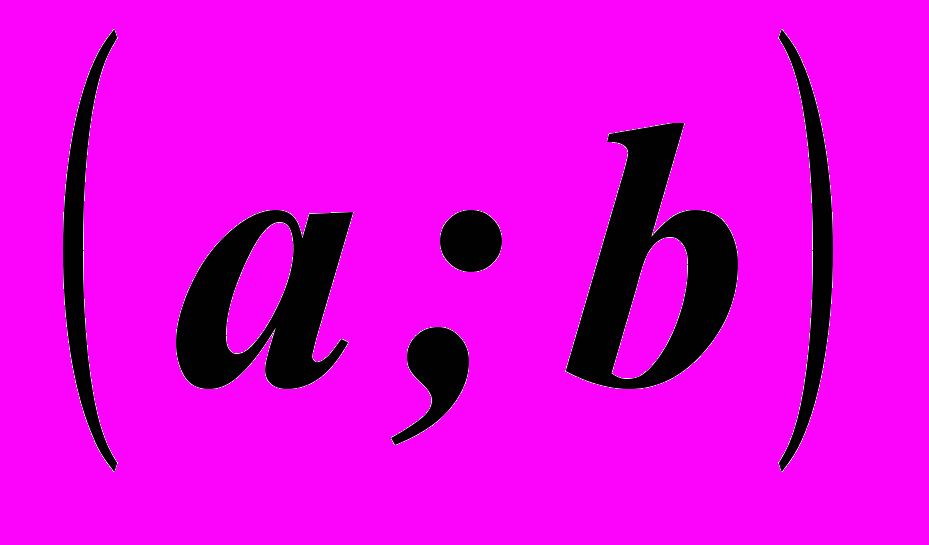, а если на конце отрезка , то на интервале 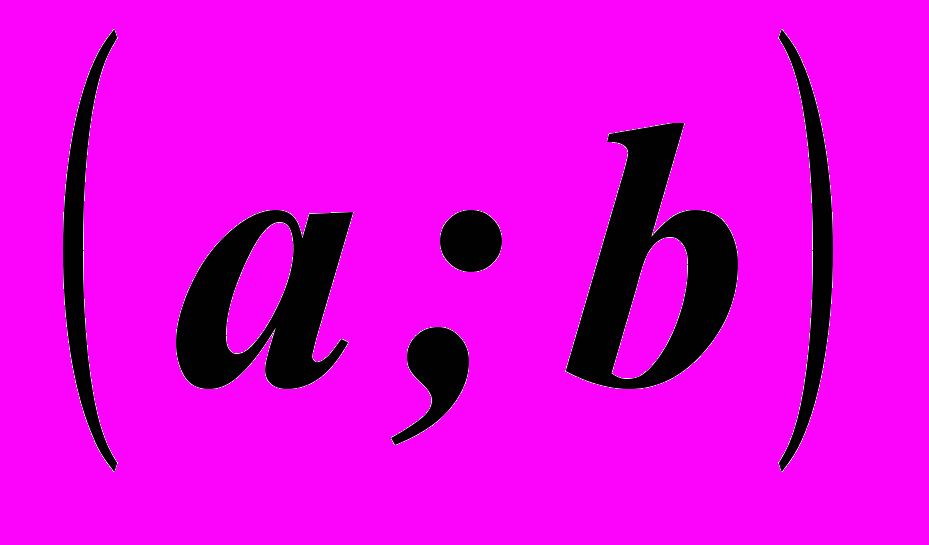наибольшего (наименьшего) значения функция не имеет.


2. На практике часто встречается такой случай, когда внутри интервала 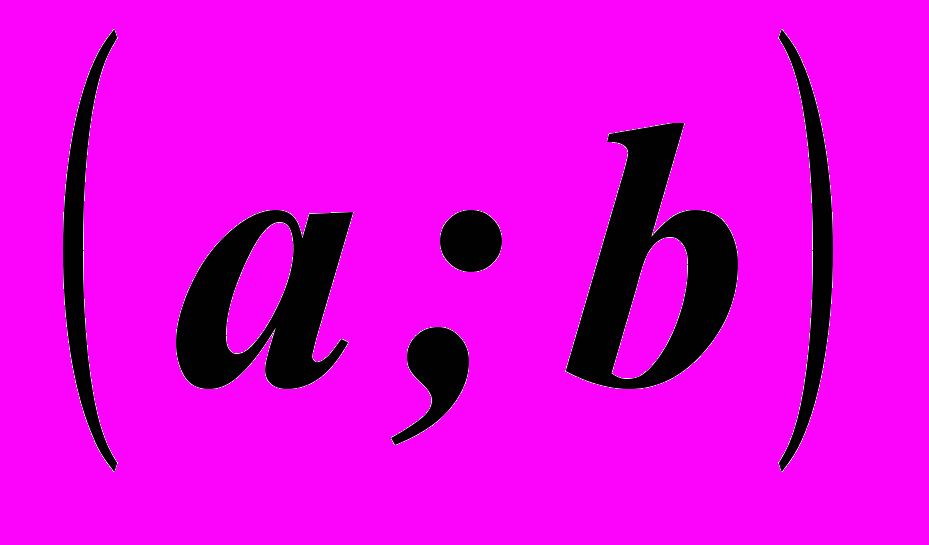заданная непрерывная функция имеет только одну точку экстремума. Тогда помогает следующая теорема.

Теорема

Пусть функция 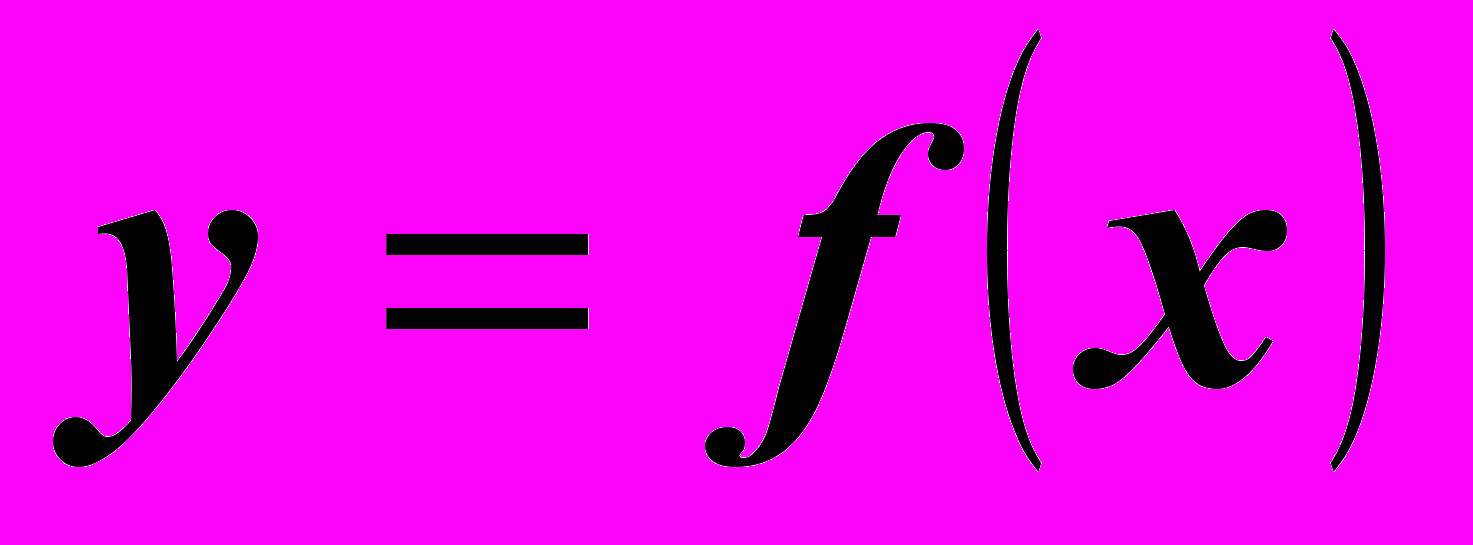, непрерывная на интервале 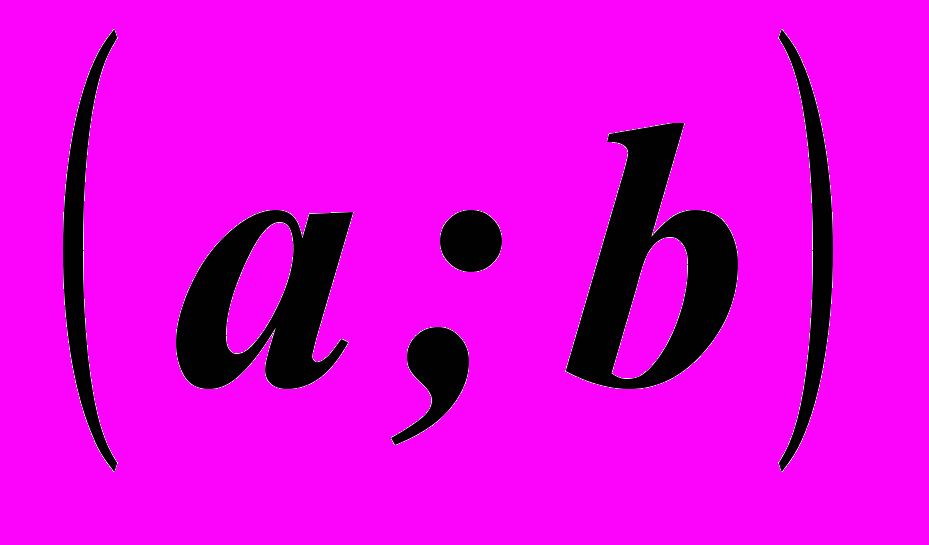, имеет на этом интервале только одну точку экстремума – точку 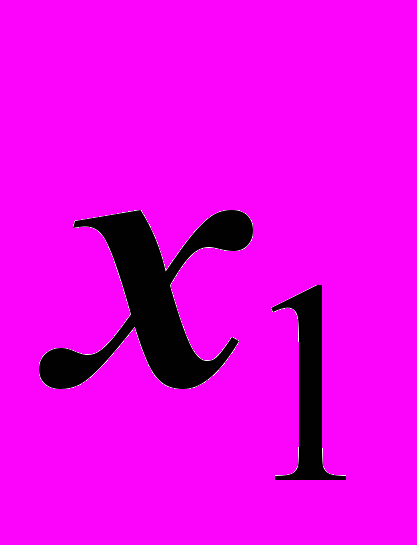. Тогда если 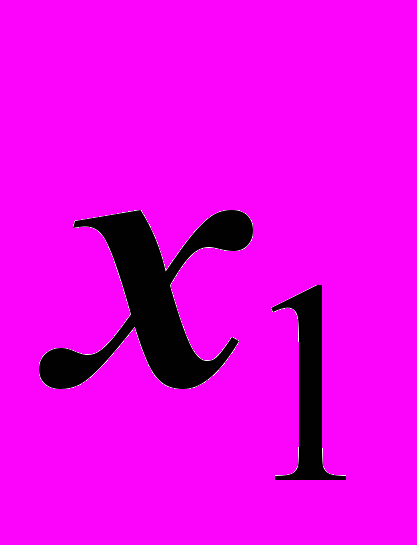- точка максимума, то 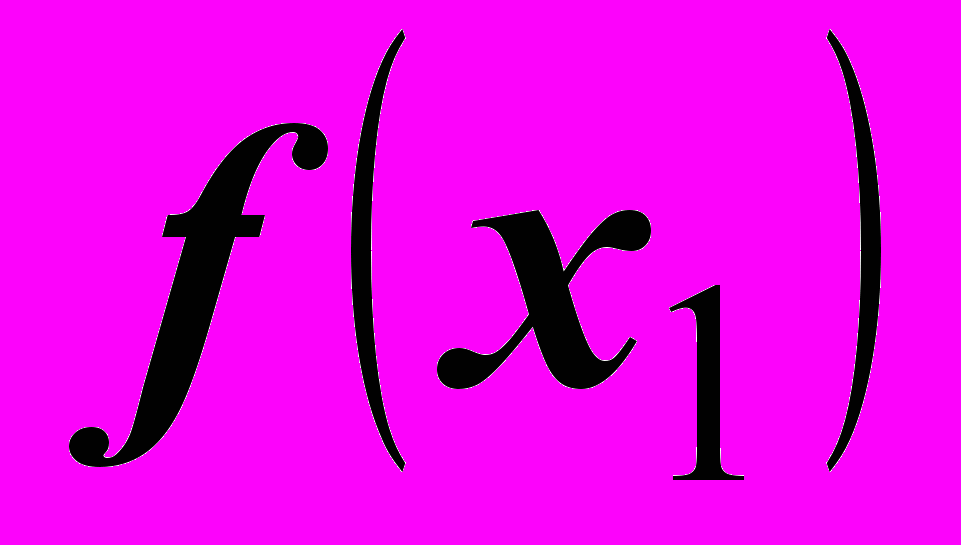- наибольшее значение функции 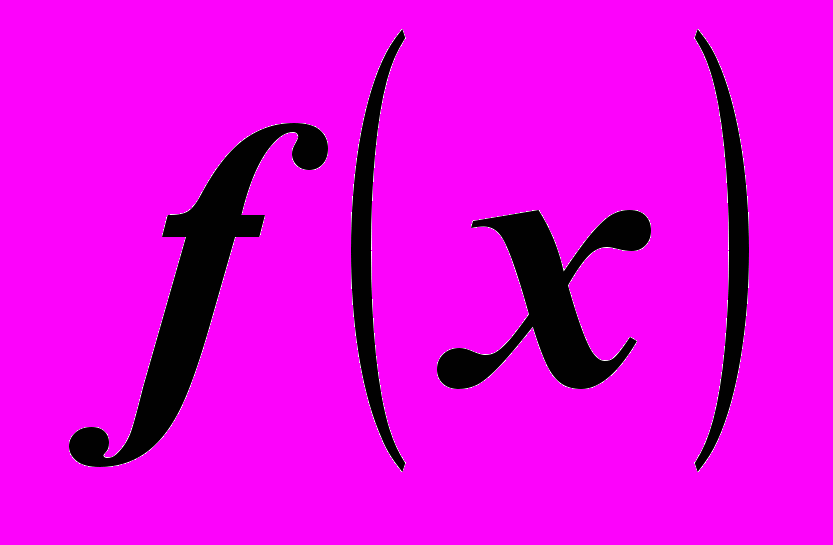на интервале 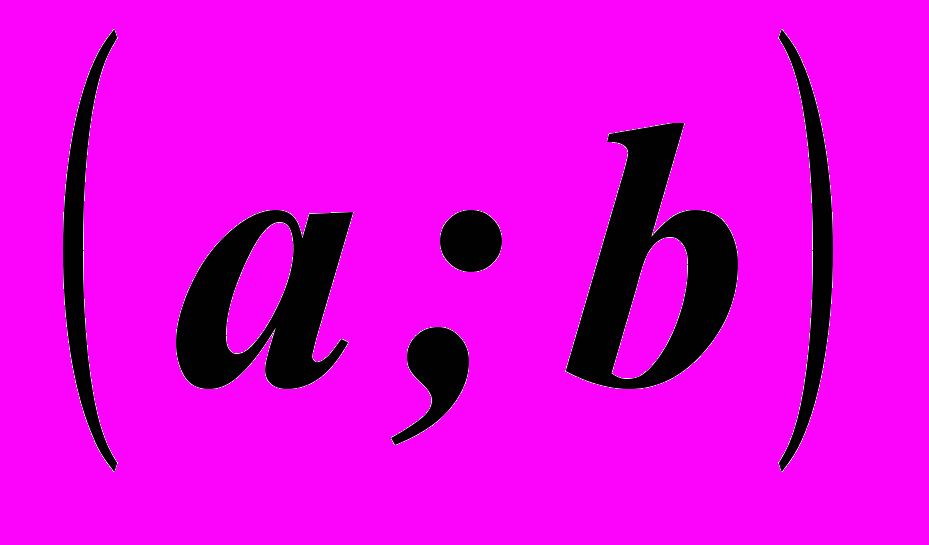; если же 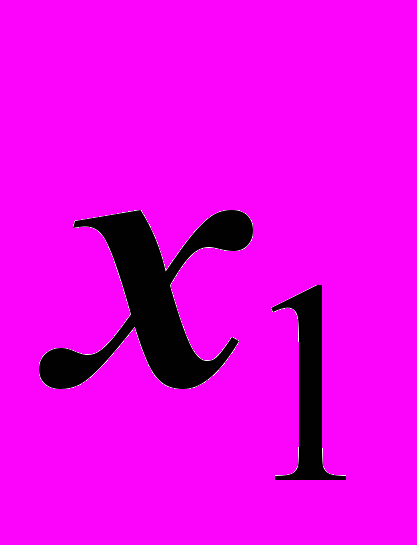- точка минимума, то 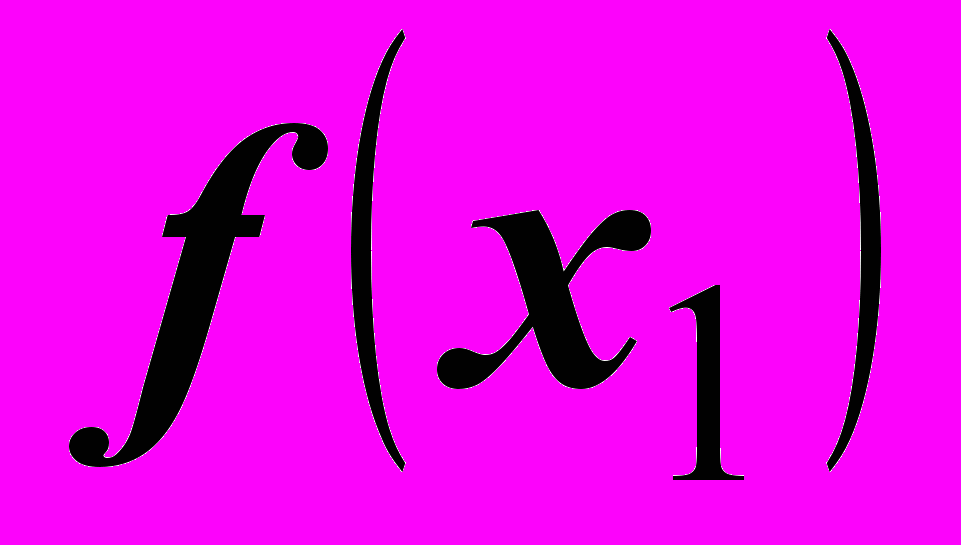- наименьшее значение функции 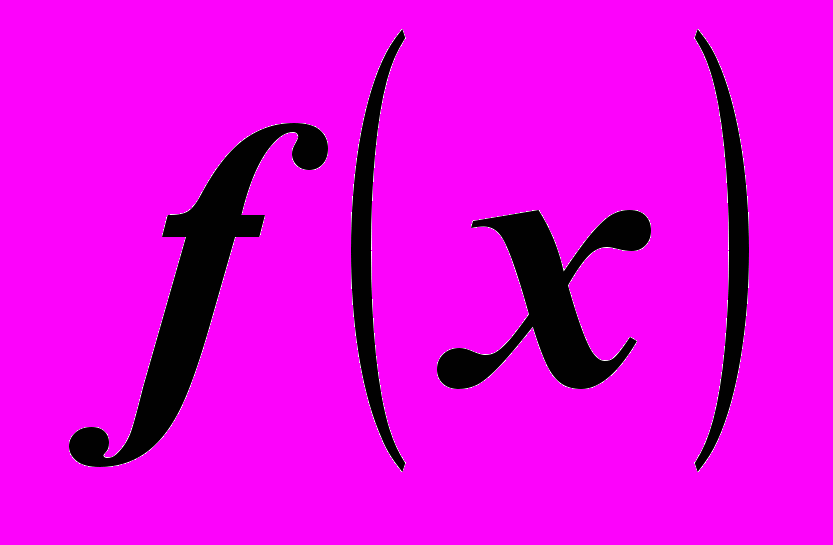на интервале .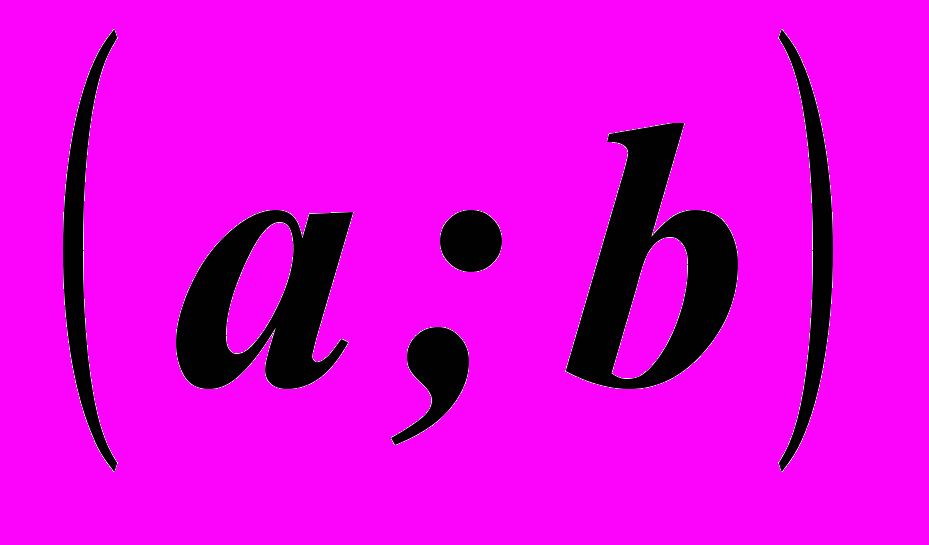