Свойства функций, непрерывных на отрезке Теорема
| Вид материала | Документы |
- Программа междисциплинарного государственного экзамена по специальности 090102 Компьютерная, 116.53kb.
- Лекция 11. Исследование функций с помощью производной, 168.49kb.
- Метод решения функциональных уравнений, 173.74kb.
- Нахождение наибольшего и наименьшего значений функции непрерывной на отрезке, 17.47kb.
- В. И. Афанасьева 01 марта 2011 г. Программа, 116.92kb.
- Реферати наукових праць І тези виступів гліба несторовича саковича Некоторые свойства, 84.85kb.
- Тема. Тригонометрические функции любого угла, 58.27kb.
- Программа для аттестационных испытаний по дисциплине: «математический анализ и линейная, 77.58kb.
- Аннотация программы учебной дисциплины «Дискретная математика и математическая логика», 59.2kb.
- Програма н/к "Основи мсс" курс- 3, семестр-1, 54год лекц, 28.91kb.
Свойства функций, непрерывных на отрезке
Теорема. Пусть функция
 непрерывна на отрезке
непрерывна на отрезке 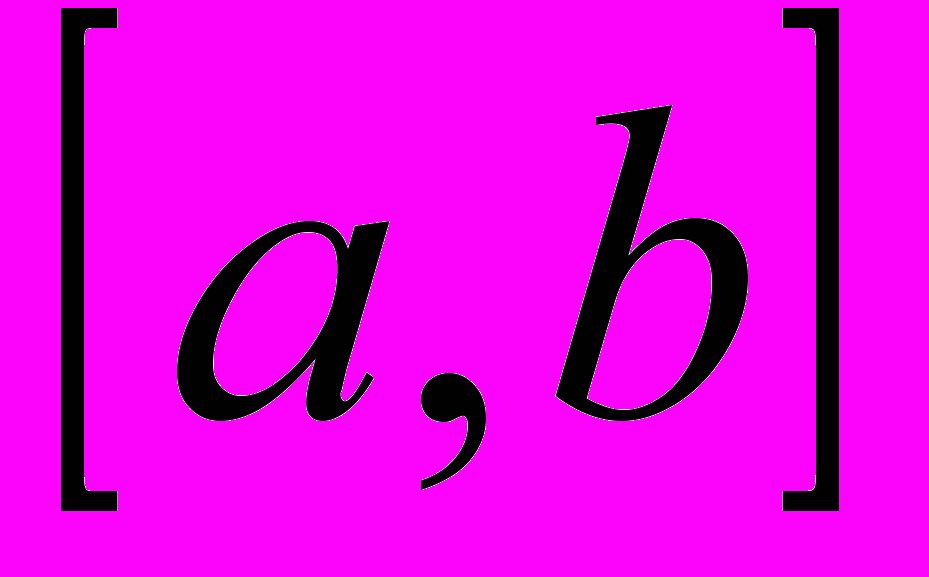 . Тогда справедливы следующие утверждения:
. Тогда справедливы следующие утверждения:(1) она достигает на этом отрезке своего наибольшего и своего наименьшего значения, т.е.
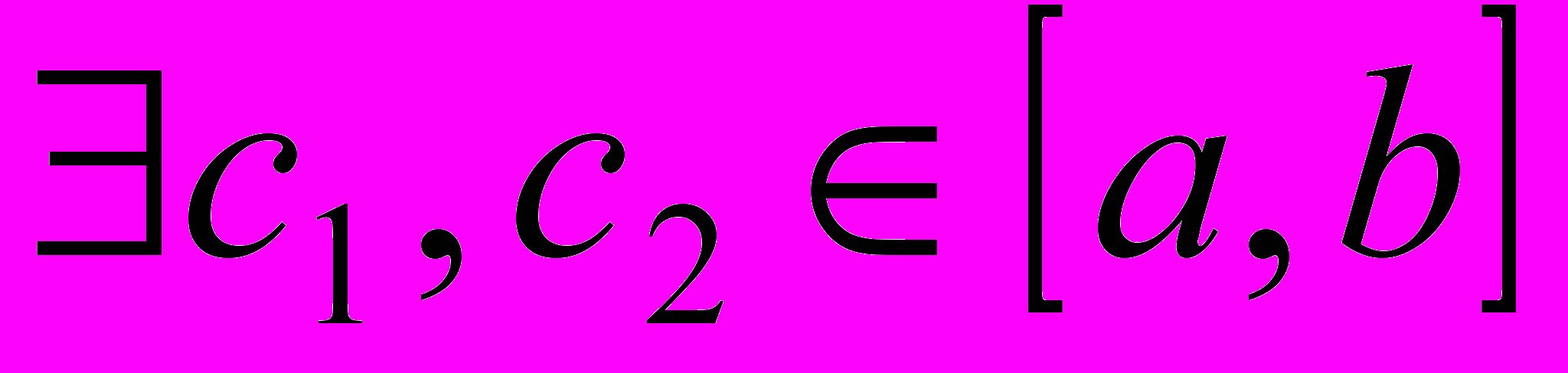 такие, что
такие, что 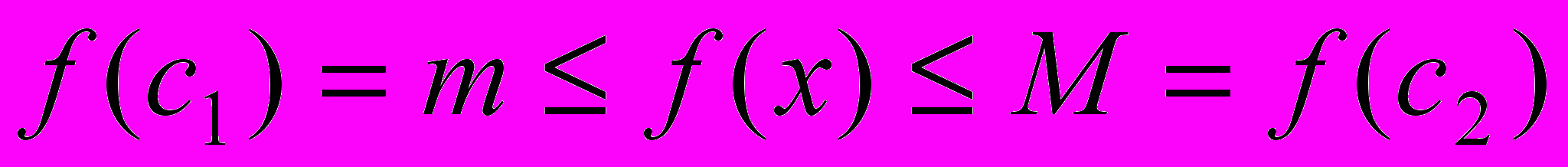 для
для  ;
;(2) функция
 достигает на отрезке любое промежуточное значение, т.е. если m – наименьшее, а M – наибольшее значение
достигает на отрезке любое промежуточное значение, т.е. если m – наименьшее, а M – наибольшее значение  на этом отрезке и
на этом отрезке и  – любое число, удовлетворяющее неравенствам:
– любое число, удовлетворяющее неравенствам: 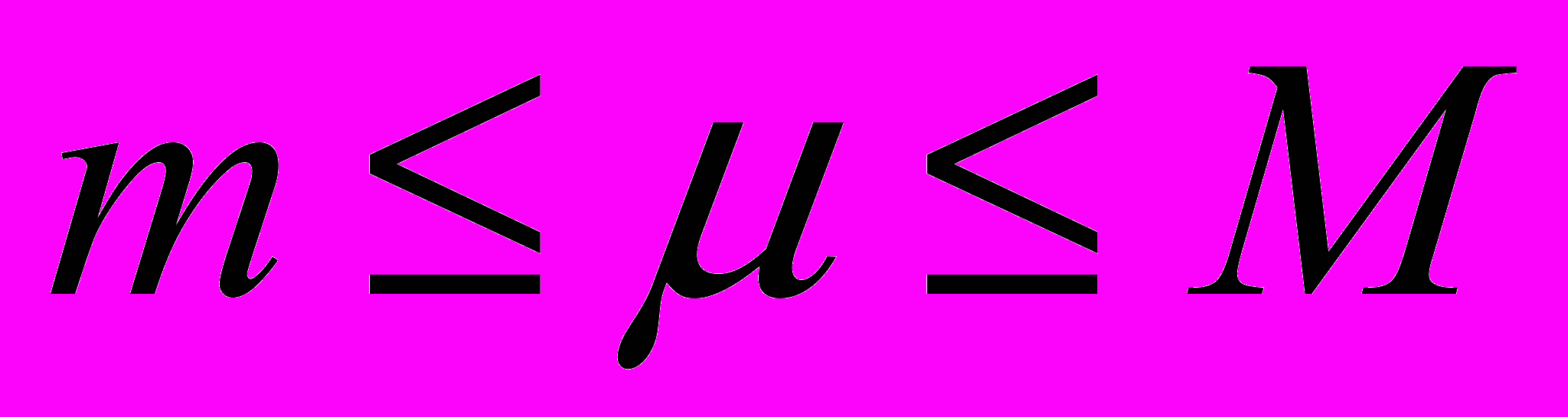 , то
, то  такая, что
такая, что 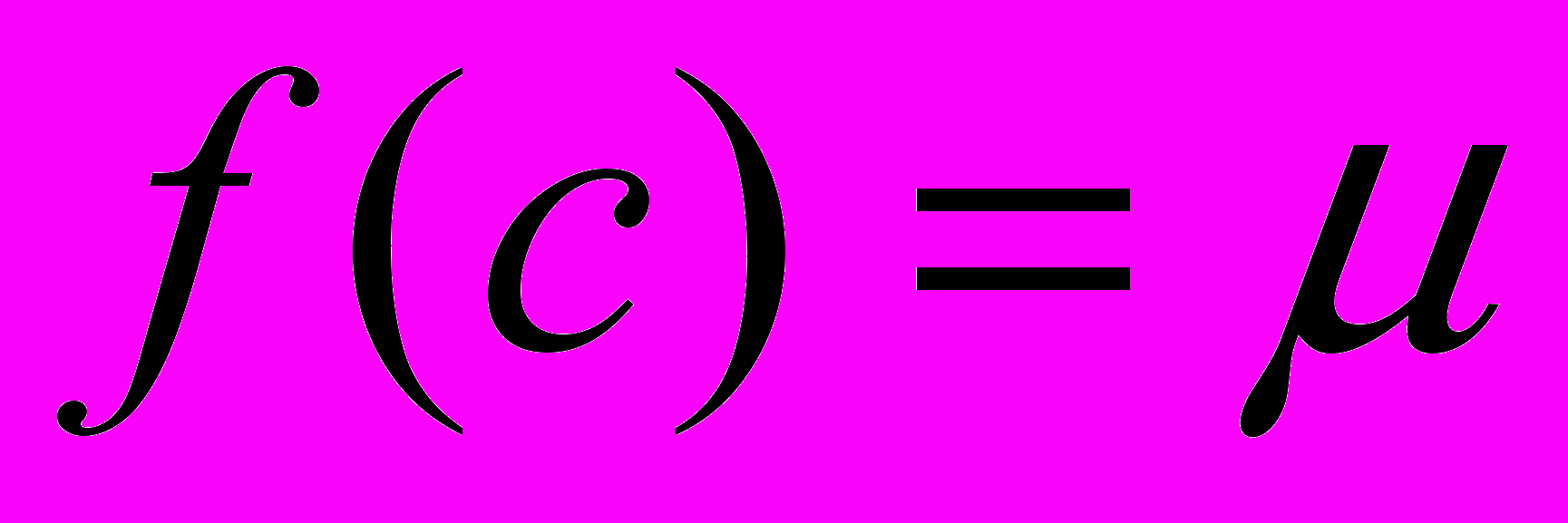 ;
;(3) если функция на концах отрезка
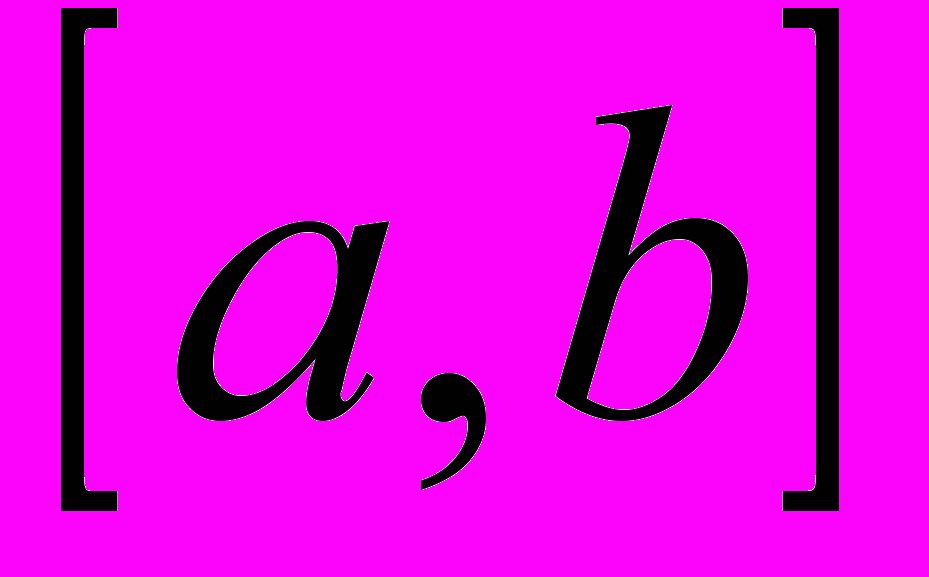 принимает значения разных знаков, т.е.
принимает значения разных знаков, т.е. 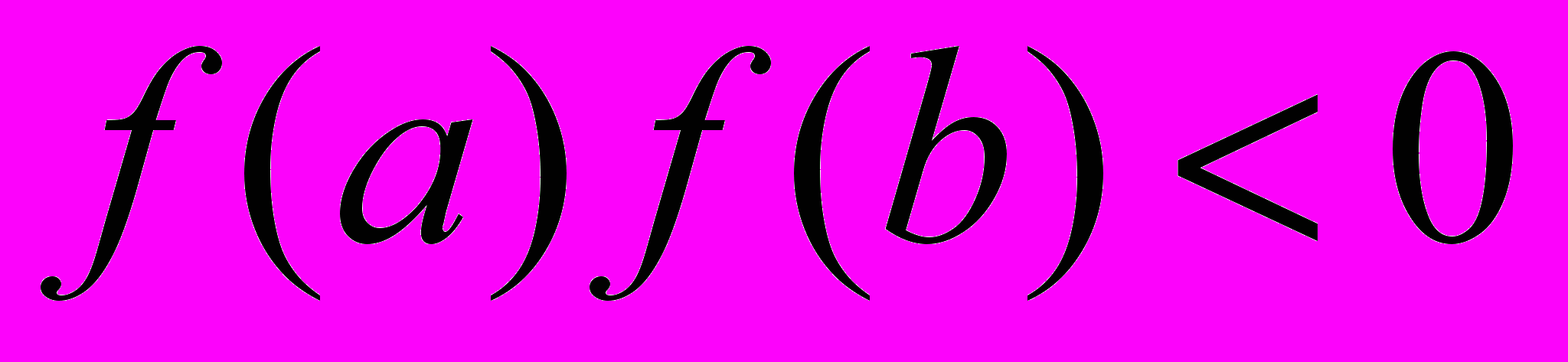 , то внутри отрезка найдется такая точка
, то внутри отрезка найдется такая точка 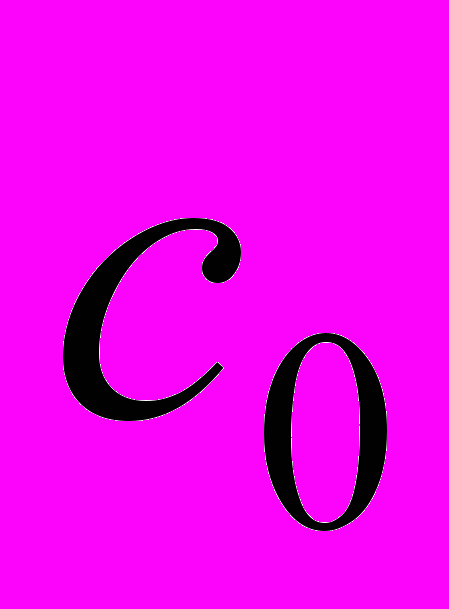 (
(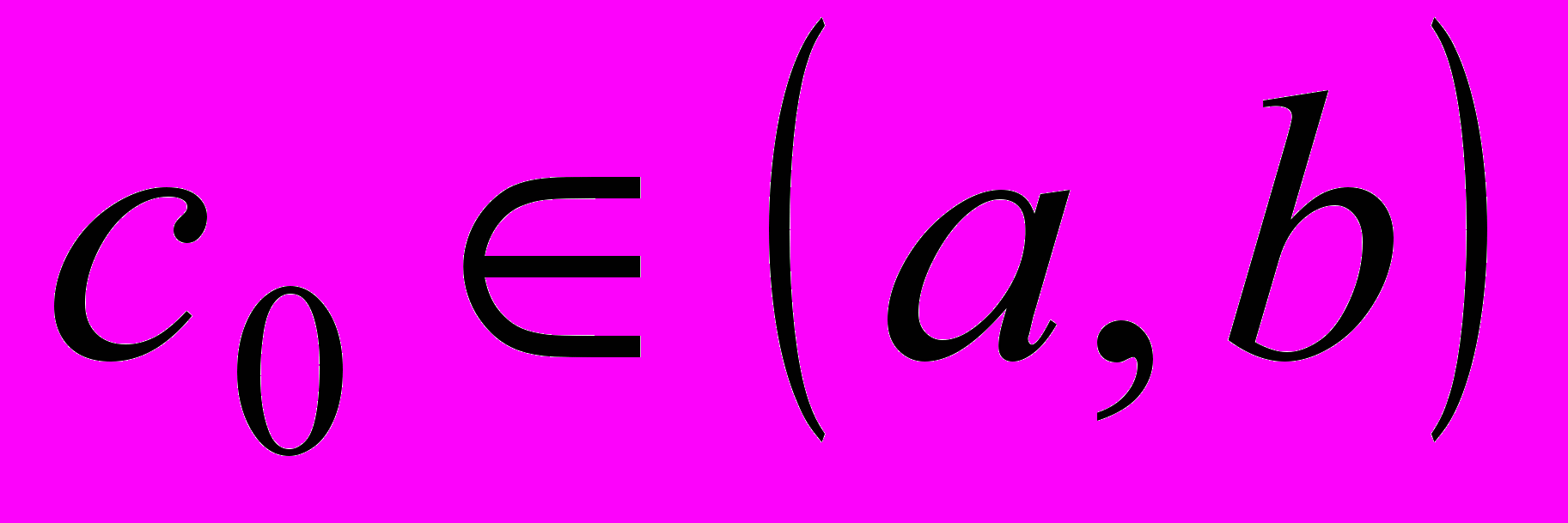 ), что
), что 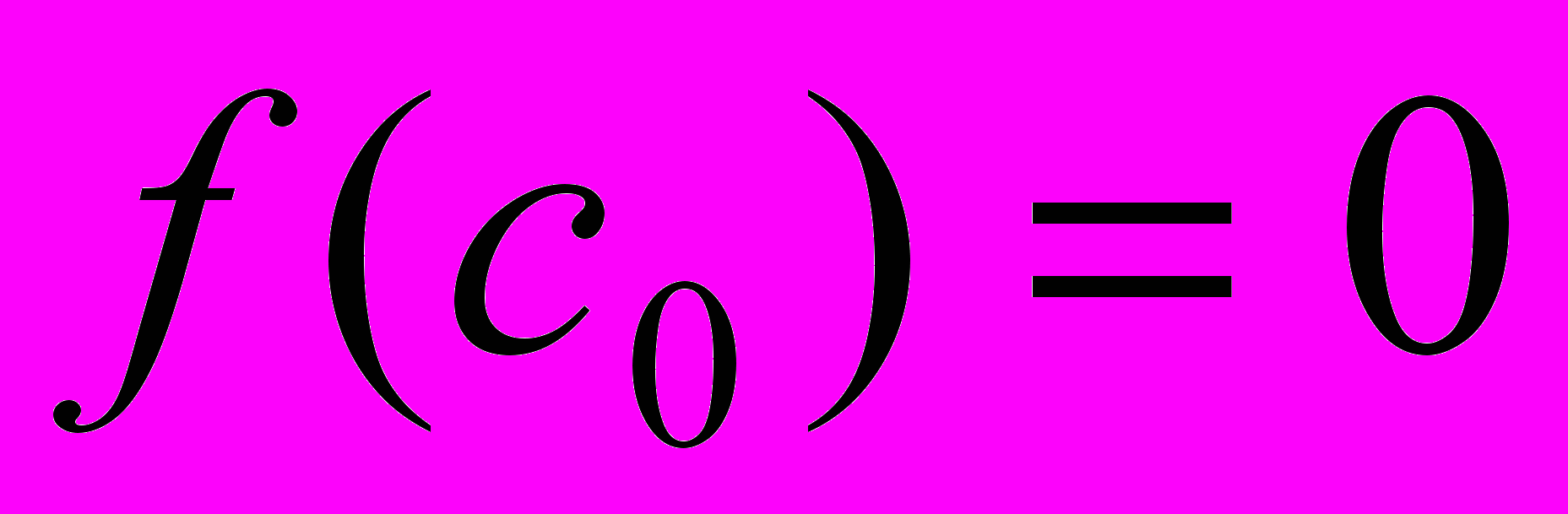 .
.Иллюстрации к теореме приведены на следующем рисунке.
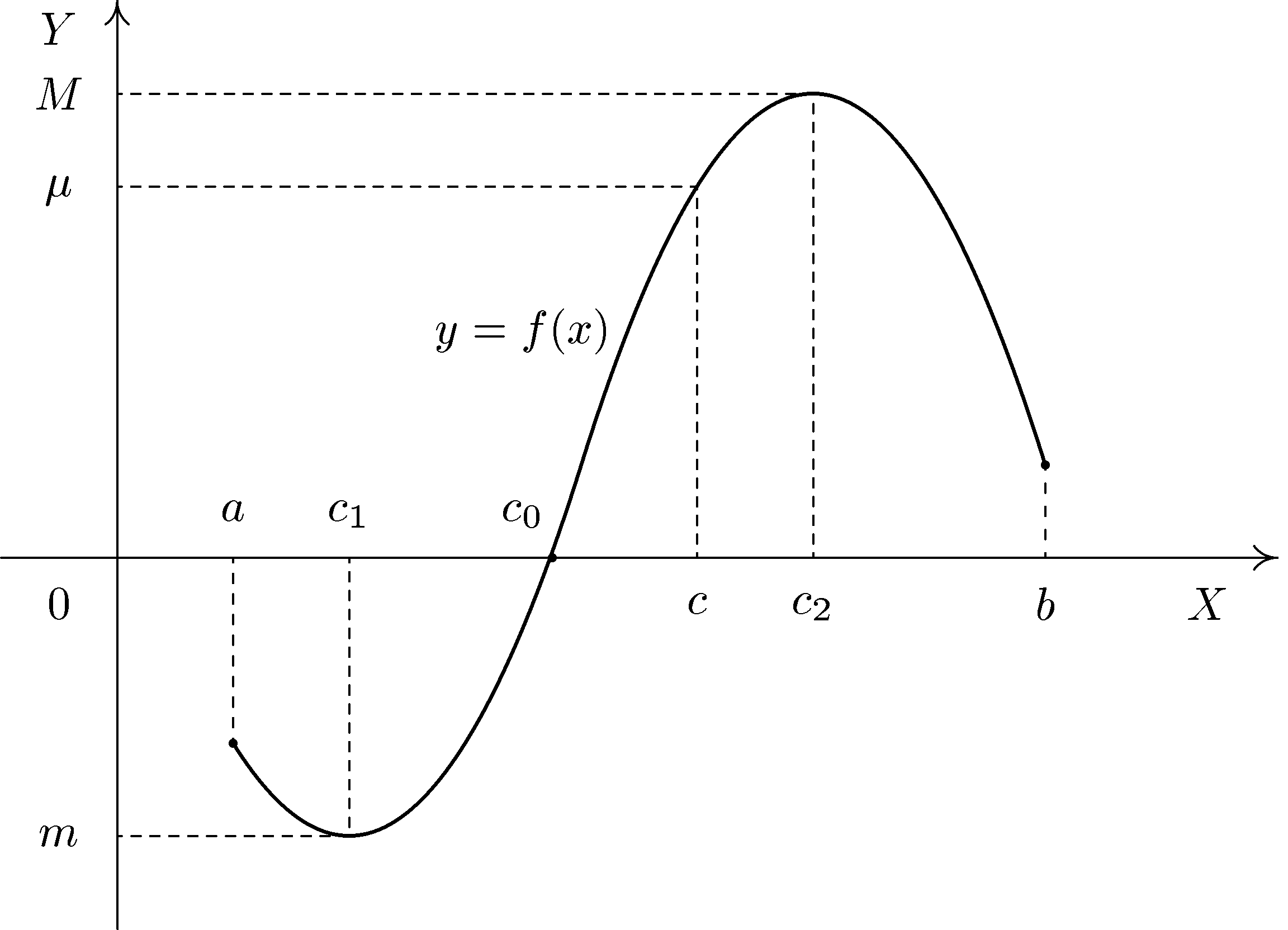
Свойства непрерывных на отрезке функций широко используются в математическом анализе, в частности, утверждение (3) данной теоремы лежит в основе метода половинного деления для нахождения приближенного значения корня уравнения вида
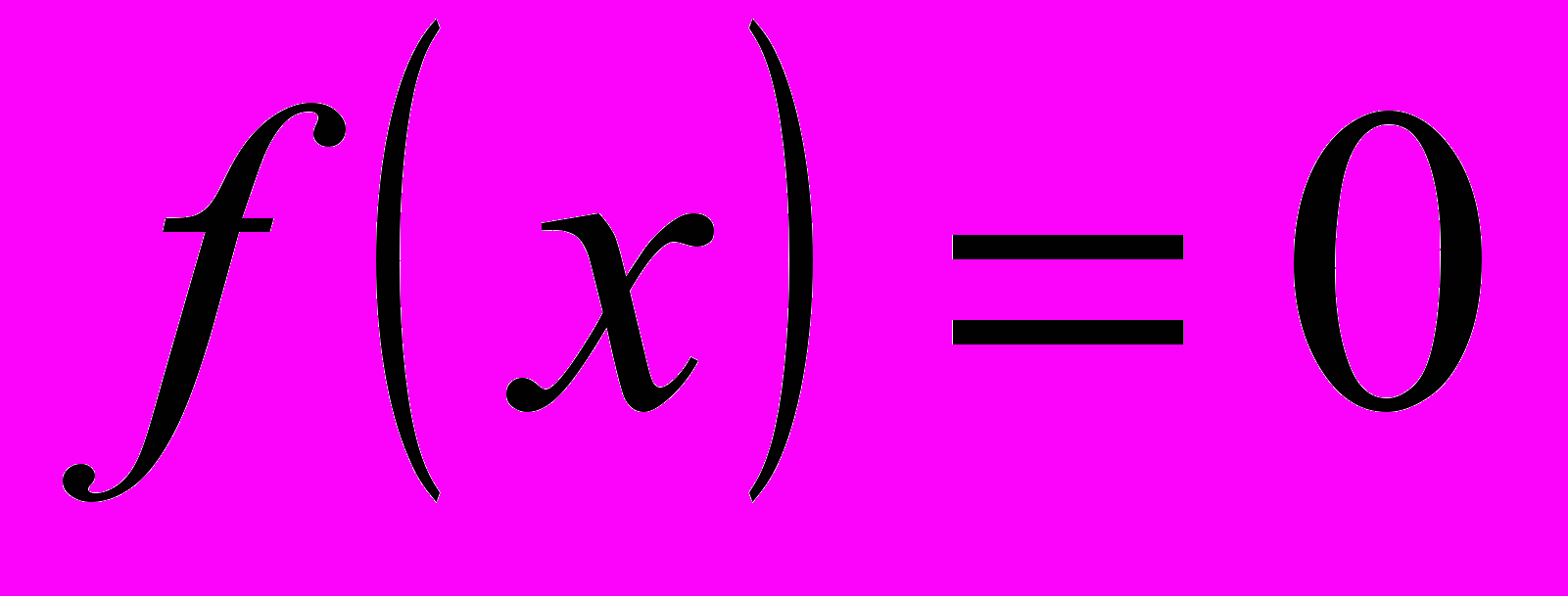 .
..
