Робоча програма з дисципліни комплексний аналіз для спеціальностей: 010100 пмсо. Математика > 080200 Інформатика Форма навчання
| Вид материала | Документы |
- Робоча програма затверджена на засіданні кафедри філософії Протокол №14 від "24" червня, 1203.01kb.
- Робоча навчальна програма з дисципліни " Інформатика та комп’ютерна техніка" для професійного, 660.32kb.
- Робоча програма учбової дисципліни «менеджмент» для економічних спеціальностей всіх, 946.31kb.
- Навчальна І робоча програма дисципліни за вибором студента "Наближені методи обчислень", 100.2kb.
- Робоча програма, методичні вказівки та індивідуальні завдання до вивчення дисципліни, 539.78kb.
- Робоча програма, методичні вказівки та індивідуальні завдання до вивчення дисципліни, 446.22kb.
- Програма навчальної дисципліни робоча програма навчальної дисципліни кваліфкаційні, 680.22kb.
- Робоча програма навчальної дисципліни " міжнародний менеджмент" (для студентів магістерської, 664.33kb.
- Робоча програма, методичні вказівки та індивідуальні завдання до вивчення дисципліни, 427.94kb.
- Робоча програма дисципліни Лекційні заняття та розділи дисципліни, що пропонуються, 1010.34kb.
Мелітопольський державний педагогічний університет
ім. Б. Хмельницького
ЗАТВЕРДЖЕНО: Кафедра математики
Декан факультету математики та фізики
та інформатики,
к.п.н. ____________ Бєльчев П.В.
“___” ____________ 2010 р.
РОБОЧА ПРОГРАМА
з дисципліни КОМПЛЕКСНИЙ АНАЛІЗ
для спеціальностей: 6.010100 ПМСО. Математика
6.080200 Інформатика
| Форма навчання | Курс, спец. | Семестр | Лекції (год) | Практики (год) | Самост. робота (год) | Всього (год) | Залік (семестр) | Екзамен (семестр) |
| денна | ІІІ | І | | | | | | |
| матем. | ІІ | 22 | 36 | 104 | 153/4,25 | | + | |
| заочна | ІІІ | І | 12 | 8 | 133 | 153/4,25 | | + |
| матем. | ІІ | | | | | | | |
| заочна | ІІІ | І | 4 | 4 | 127 | 135/3,75 | + | |
| інформ | ІІ | | | | | | |
Мелітополь 2010 р.
Робоча програма розроблена на основі навчальної програми дисципліни «Комплексний аналіз», затверджено вченою радою (протокол № __ від «__» __________ 2010р.).
Розробник: ст. викладач Титаренко Н.Є.
Робоча програма ухвалена рішенням кафедри (протокол № 1 від 30 серпня 2010)
Завідувач кафедри
Модуль . Комплексний аналіз.
Змістовий модуль 1. Комплексні числа, основи ТФКЗ.
Тема 1. Комплексні числа та дії над ними.
Історія виникнення комплексних чисел. Операції над комплексними числами. Форми представлення комплексних чисел
Тема 2. Стереографічна проекція. Сфера Рімана. Геометричне зображення комплексних чисел.
Геометричне зображення комплексних чисел на площині. Нескінченно віддалена точка. Стереографічна проекція. Сфера Рімана.
Тема 3. Послідовності комплексних чисел. Числові ряди. Топологія комплексної площини.
Границя послідовності комплексних чисел Збіжні, розбіжні послідовності. Рівномірна збіжність числової послідовності. Дослідження числових рядів на збіжність. Абсолютна та умовна збіжність. Ознаки збіжності числових рядів.
Тема 4. Функції комплексної змінної: загальні поняття про функції, границя і неперервність функції.
Границя функції в точці і на нескінченності. Неперервність функції.
Тема 5. Елементарні функції комплексної змінної.
Дробово-лінійна функція та її властивості, степенева функція
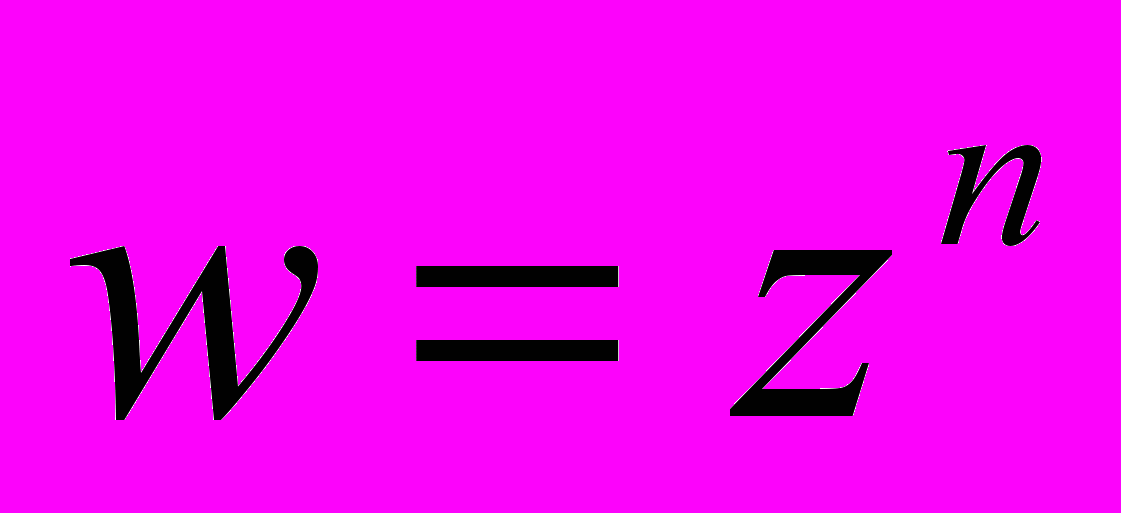
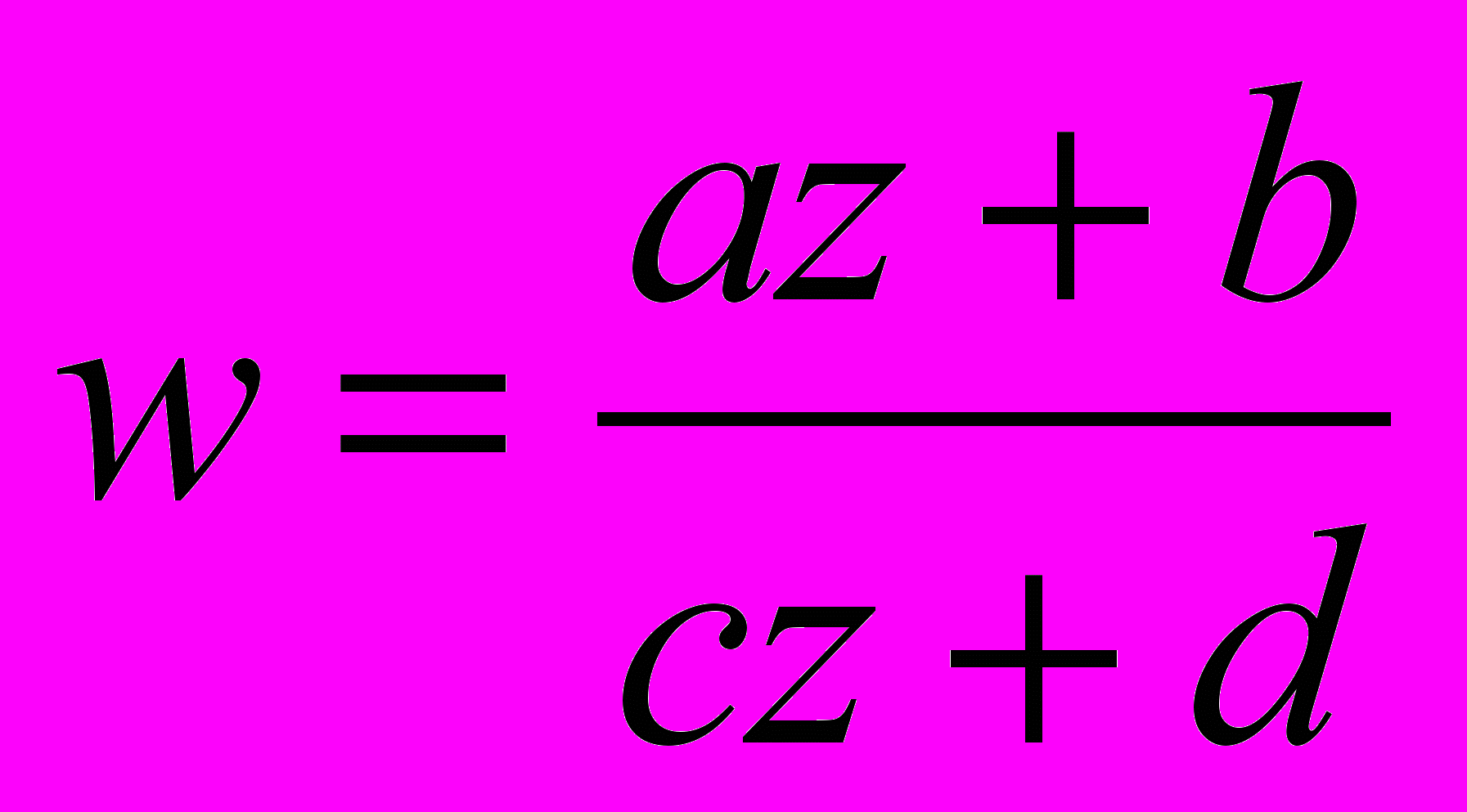, функція Жуковського 
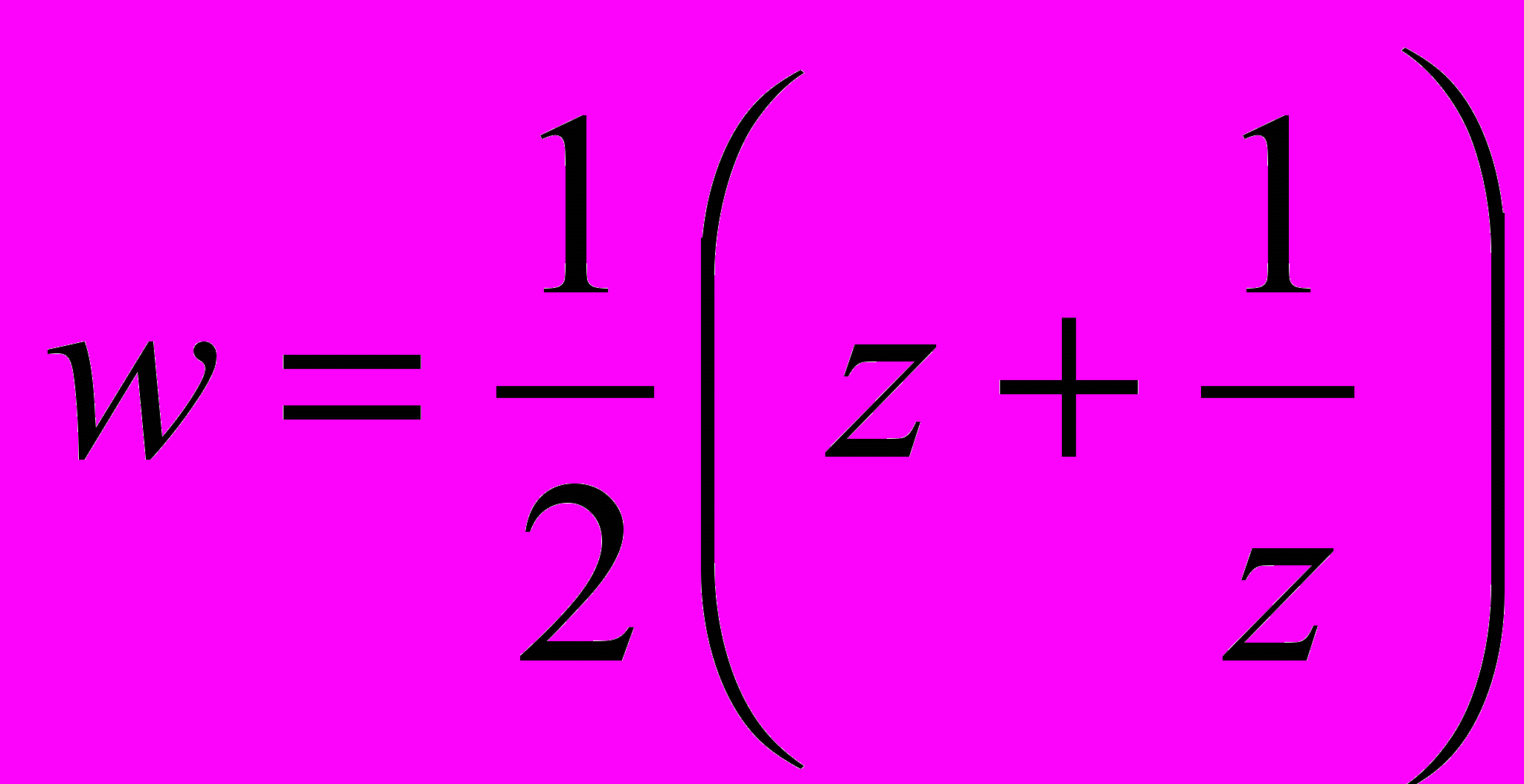, показникові функція 
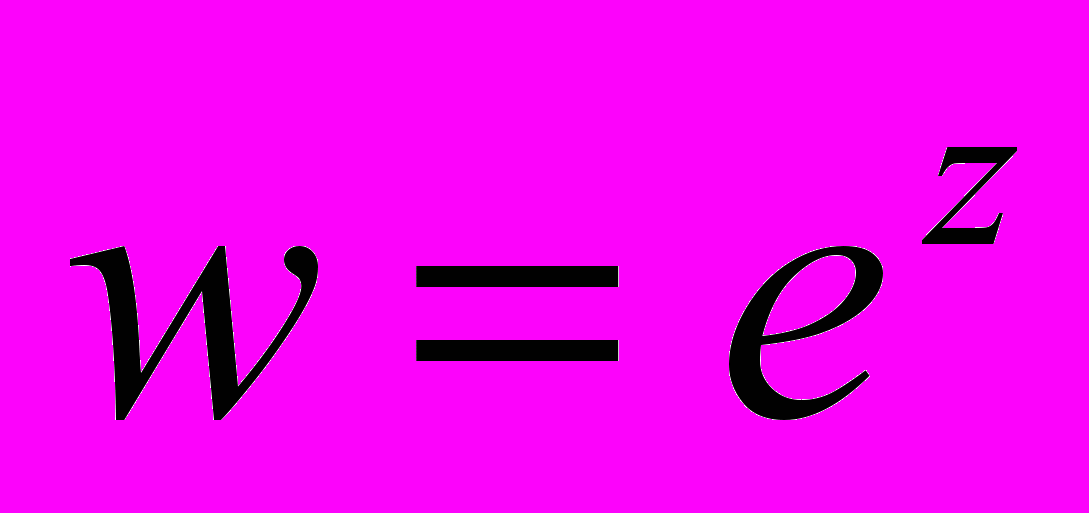, тригонометричні функції, функція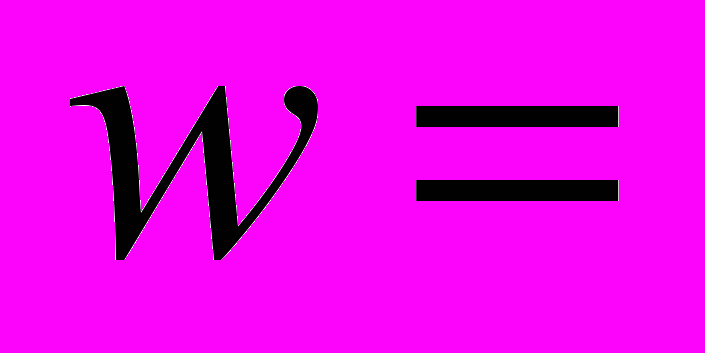 
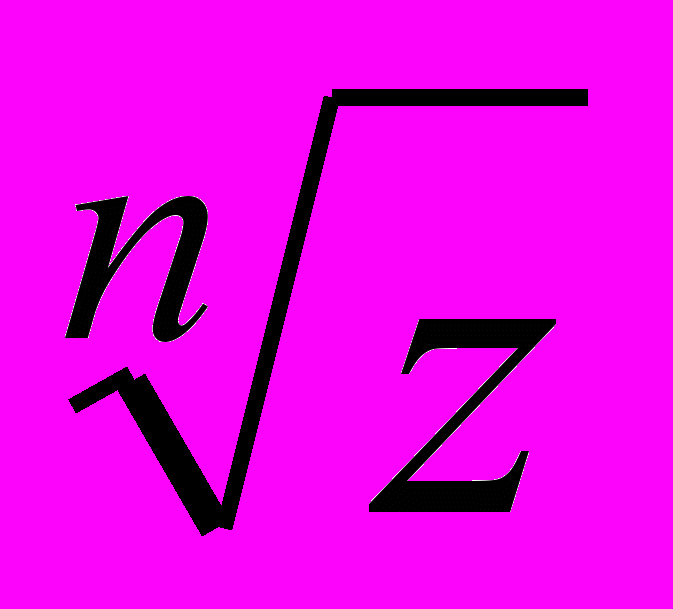, логарифмічна функція, обернені тригонометричні функції Змістовий модуль 2. Диференціальне та інтегральне числення ФКЗ.
Тема 6. Диференційованість ФКЗ: неперервні криві, аналітичність функції, правила диференціювання.
Неперервні криві. Похідна та диференціал Правила диференціювання. Необхідні і достатні умови диференційованості функції у внутрішній точці області. Гармонічні фунції.
Тема 7. Інтегрування функції комплексної змінної.
Інтеграл від ФКЗ, його властивості. Зведення до обчислення звичайного інтеграла.
Тема 8. Інтегральна теорема Коші, інтегральна формула Коші.
Інтегральна теорема Коші, її застосування до обчислення визначених інтегралів. Інтегральна формула Коші.
Змістовий модуль 3. Ряди, лишки.
Тема 9. Функціональні ряди. Степеневі ряди. Інтеграли, залежні від параметру.
Степеневі ряди, розвинення аналітичної функції в ряд Тейлора. Функціональні ряди. Інтеграли, залежні від параметра..
Тема 10. Ряди Лорана. Ізольовані особливі точки однозначного характеру.
Ряд Лорана. Ізольовані особливі точки однозначного характеру. Випадок нескінченно віддаленої точки. Зв’язок рядів Лорана з рядами Фур’є
Тема 11. Лишки та їх застосування.
Основна теорема про лишки та її застосування до обчислення визначених інтегралів. Лишок відносно нескінченно віддаленої точки. Принцип аргументу та його наслідки.
Тематичне планування
| №, п/п | Теми | Види занять | Літ-ра | Види контролю | |||
| л | пр | сам | мод | ||||
| | Модуль 1. | 12 | 18 | 48 | | | |
| 1. | Комплексні числа та дії над ними. | 2 | 3 | 8 | | 1, 3 | поточний, періодичний, екзамен |
| 2. | Стереографічна проекція. Сфера Рімана. Геометричне зображення комплексних чисел | 2 | 3 | 8 | | 1, 5 | поточний, періодичний, екзамен |
| 3. | Послідовності комплексних чисел. Числові ряди. Топологія комплексної площини | 2 | 3 | 8 | | 3, 6 | поточний, періодичний, екзамен |
| 4. | Функції комплексної змінної: загальні поняття про функції, границя і неперервність функції | 2 | 3 | 8 | | 4, 5 | поточний, періодичний, екзамен |
| 5 | Елементарні функції комплексної змінної | 2 | 3 | 8 | | 7, 8 | поточний, періодичний, екзамен |
| 6. | Диференційованість ФКЗ: неперервні криві, аналітичність функції (правила диференціювання) | 2 | 3 | 8 | | 5, 7 | поточний, періодичний, екзамен |
| | Модуль 2. | 10 | 18 | 47 | | | |
| 7. | Інтегрування функції комплексної змінної. | 2 | 3 | 9 | | 3, 5 | поточний, періодичний, екзамен |
| 8. | Інтегральна теорема Коші, інтегральна формула Коші. | 2 | 3 | 9 | | 4, 6 | поточний, періодичний, екзамен |
| 9. | Функціональні ряди. Степеневі ряди. Інтеграли, залежні від параметра | 2 | 4 | 10 | | 2, 8 | поточний, періодичний, екзамен |
| 10 | Ряди Лорана. Ізольовані особливі точки однозначного характеру | 2 | 4 | 9 | | 1, 2 | поточний, періодичний, екзмен |
| 11. | Лишки та їх застосування | 2 | 4 | 10 | | 4, 6 | поточний, періодичний, екзамен |
Теми практичних занять
-
№
Тема
Питання до практичного заняття
Літ-ра
1
Комплексні числа та дії над ними.
Історія виникнення комплексних чисел. Операції над комплексними числами. Форми представлення комплексних чисел
[3], c.175-190 [1], c.18-25
2
Стереографічна проекція. Сфера Рімана. Геометричне зображення комплексних чисел
Геометричне зображення комплексних чисел на площині. Нескінченно віддалена точка. Стереографічна проекція. Сфера Рімана.
[1], c. 25-41
[2], c.48-58
3
Послідовності комплексних чисел. Числові ряди. Топологія комплексної площини
Границя послідовності комплексних чисел Збіжні, розбіжні послідовності. Рівномірна збіжність числової послідовності. Дослідження числових рядів на збіжність. Абсолютна та умовна збіжність. Ознаки збіжності числових рядів.
[1], c. 41-55
[2], c.85-92
4
Функції комплексної змінної: загальні поняття про функції, границя і неперервність функції
Границя функції в точці та на нескінченності. Неперервність функції. Обчислення границь ФКЗ
[1], c.60-71
5
Елементарні функції комплексної змінної
а) дробова – лінійна функція та ії властвості
б) степенева функція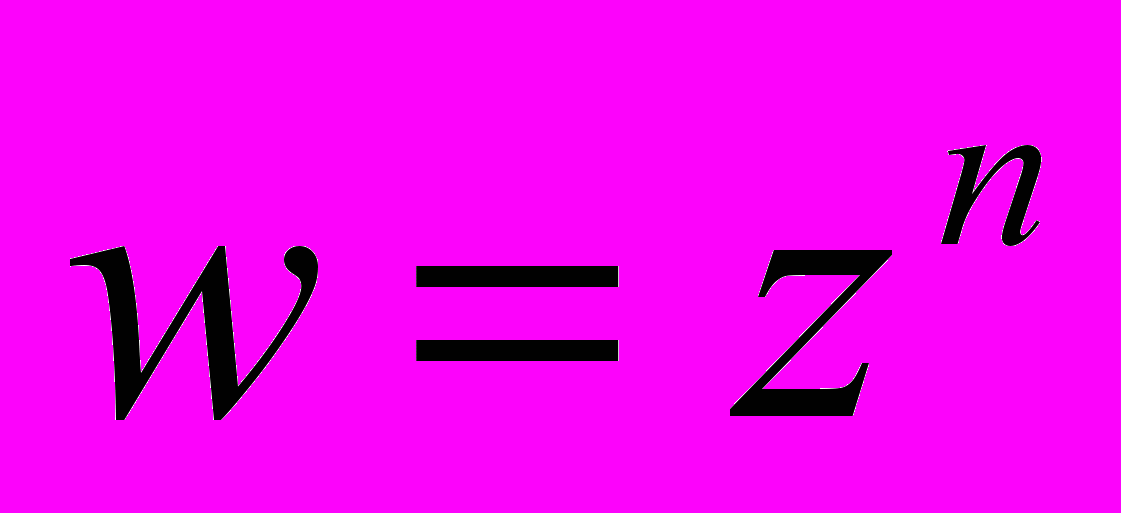
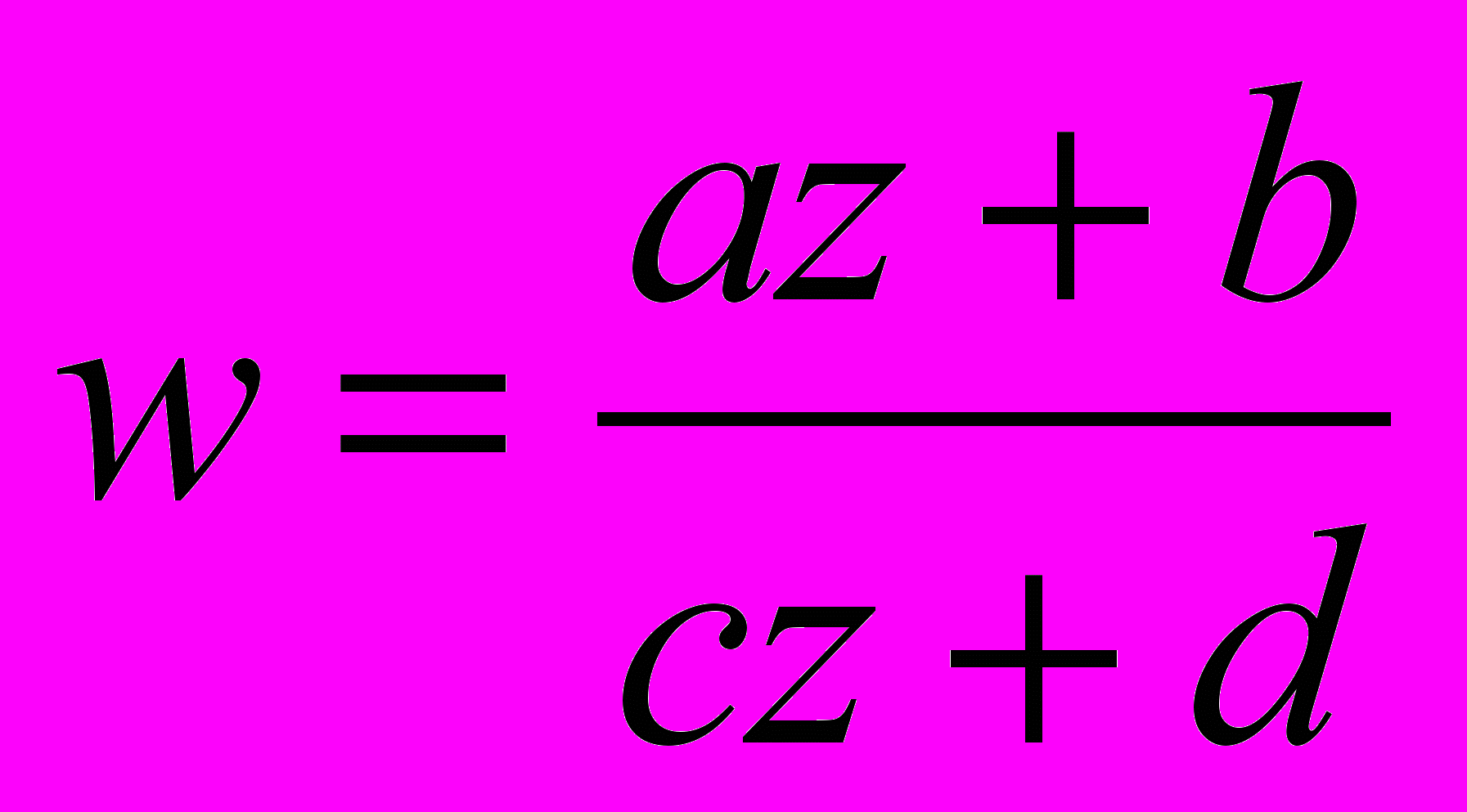
в) функція Жуковського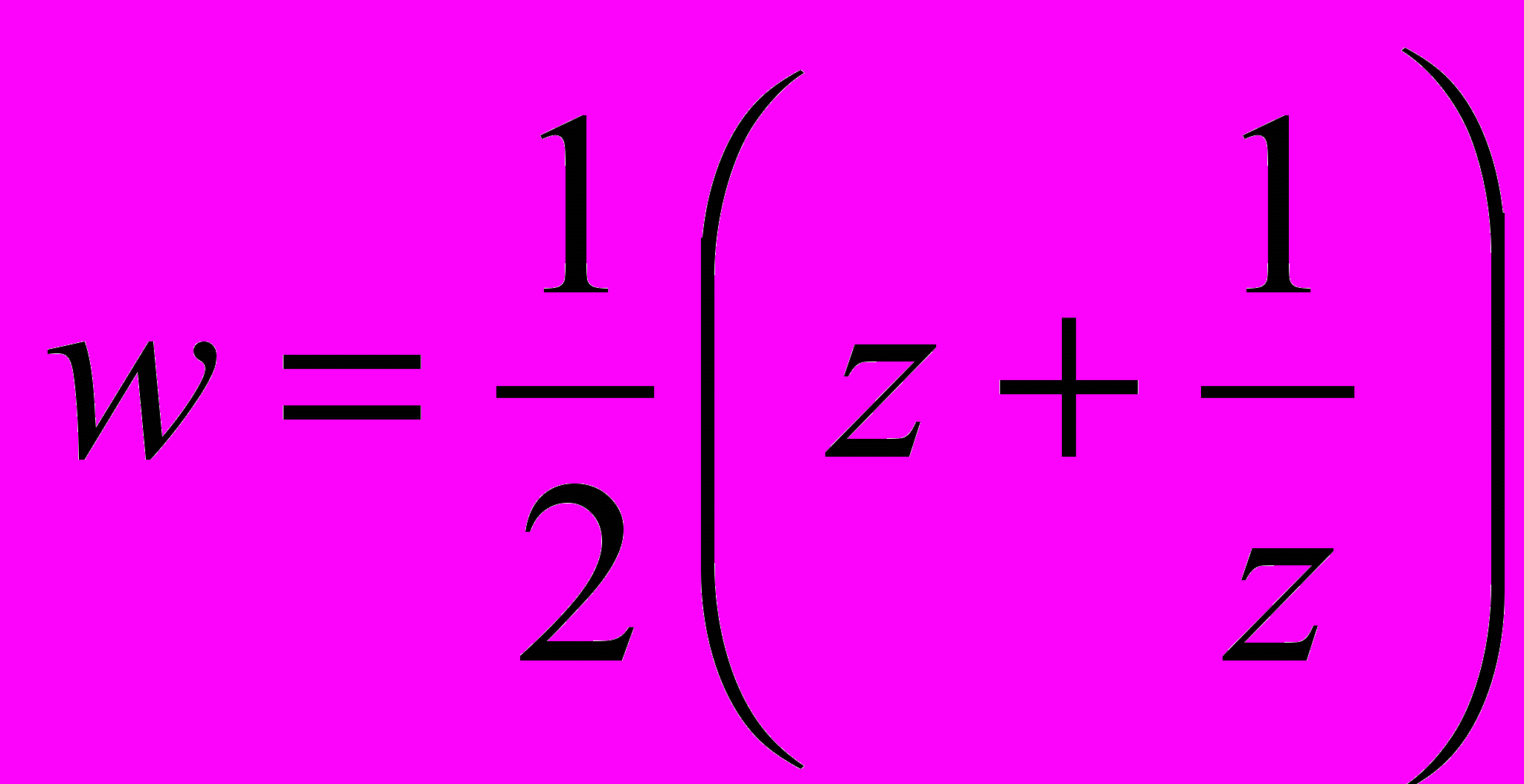
г) показникова функція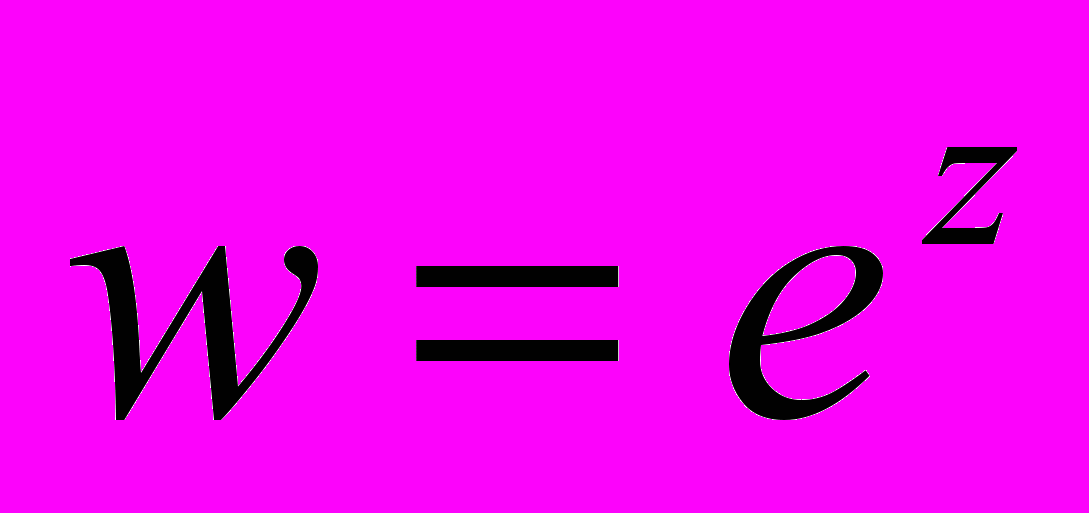
д) тригонометричні функції
е) функція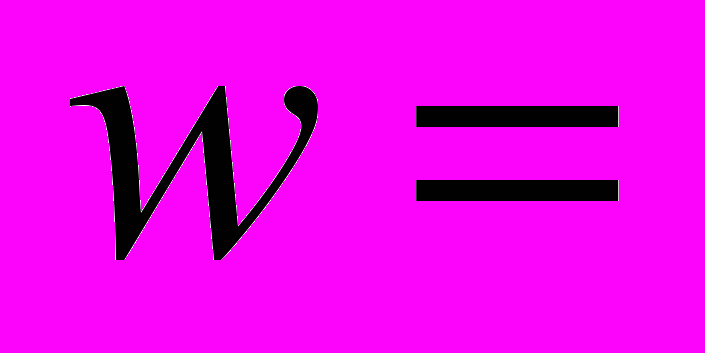
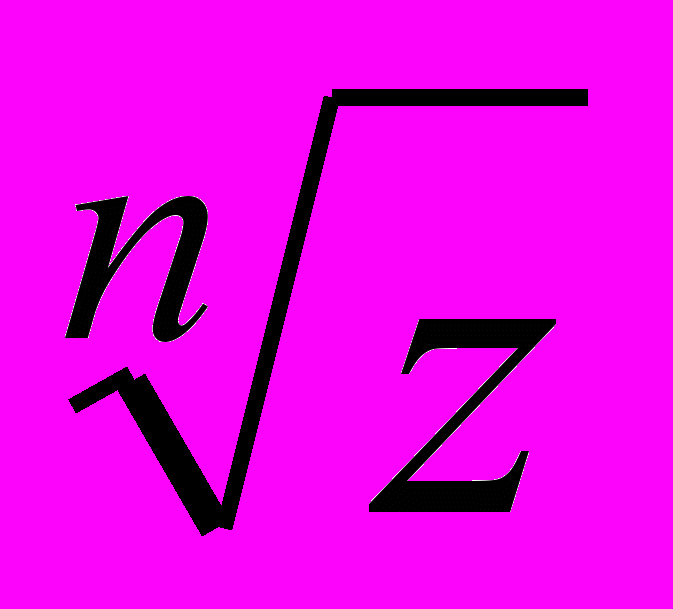
ж) логарифмічна функція
з) обернені тригонометричні функції
[1], c.71-82
6
Диференційованість ФКЗ: неперервні криві, аналітичність функції (правила диференціювання)
Неперервні криві. Похідна та диференціал Правила диференціювання. Необхідні і достатні умови диференційованості функції у внутрішній точці області. Гармонічні фунції.
[2], c. 58-67
[2], c.67-72
7
Інтегрування функції комплексної змінної.
Інтеграл від ФКЗ, його властивості. Зведення до обчислення звичайного інтеграла.
[3], c.175-190
8.
Інтегральна теорема Коші, інтегральна формула Коші.
Інтегральна теорема Коші, її застосування до обчислення визначених інтегралів. Інтегральна формула Коші.
[3], c.175-190
9
Функціональні ряди. Степеневі ряди. Інтеграли, залежні від параметра
Степеневі ряди, розвинення аналітичної функції в ряд Тейлора. Функціональні ряди. Інтеграли, залежні від параметра.
[3], c.175-190
10
Ряди Лорана. Ізольовані особливі точки однозначного характеру
Ряд Лорана. Ізольовані особливі точки однозначного характеру. Випадок нескінченно віддаленої точки. Зв’язок рядів Лорана з рядами Фур’є
[3], c.175-190
11
Лишки та їх застосування
Основна теорема про лишки та її застосування до обчислення визначених інтег-ралів. Лишок відносно нескінченно віддаленої точки. Принцип аргумента та його наслідки.
Список літератури.
- А.И. Маркушевич. Краткий курс теории аналитических функций. М. Наука.–1978. – 416 c.
- В. И. Смирнов. Курс высшей математики. Т.III, ч.2. М. Гос. изд-во технико-теоретической лит-ры. –1951. – 676с.
- А. Г. Свешников, А.Н. Тихонов. Теория функций комплексной переменной.
- А. В. Бицадзе. Основы теории аналитических функций комплексного переменного.
- М. А. Лаврентьев, Б. В. Шабат. Методы теории функций комплексного переменного.
- Б. А. Фукс, Б.В. Шабат. Функции комплексного переменного.
- Ю. В. Сидоров, М.В. Федорюк, М.И. Шабунин. Лекции по теории функций комплексного переменного.
- И. И. Привалов. Введение в теорию функций комплексного переменного.