Приложения дискретного эргодического метода к арифметике бинарных и изотропных тернарных квадратичных форм 01. 01. 06 математическая логика, алгебра и теория чисел

Вид материала

Автореферат

Содержание Основное содержание диссертационной работы изложено в следующих публикациях

Подобный материал:

• Программы кандидатского экзамена по специальности 01. 01. 06 "Математическая логика,, 50.44kb.
• Программа вступительного экзамена в аспирантуру по специальной дисциплине 01. 01., 67.09kb.
• Состав рабочих групп по разработке основных образовательных программ на основе требований, 497.64kb.
• Алгебра и теория чисел, 52.79kb.
• Алгебра, логика и теория чисел, 14.13kb.
• Вопросы по курсу: Математическая логика и теория алгоритмов (2 курс), 30.21kb.
• Аннотация программы учебной дисциплины «Дискретная математика и математическая логика, 55.65kb.
• Рабочая программа по дисциплине в 2-Математическая логика и теория алгоритмов шифр, 316.78kb.
• Рабочей программы учебной дисциплины дв2 Математическая логика и теория алгоритмов, 50.1kb.
• Рабочая учебная программа по дисциплине «Математическая логика и теория алгоритмов», 69.99kb.

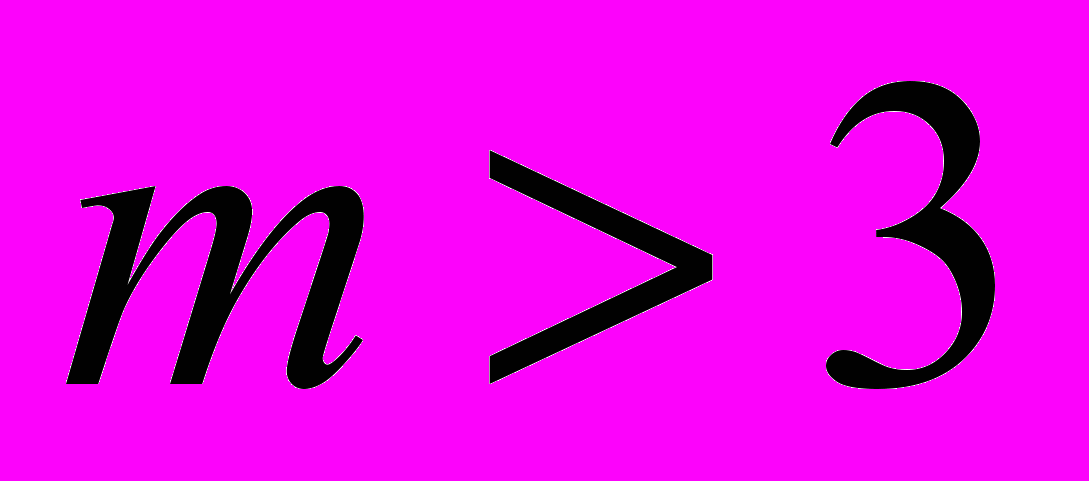Теорема 4.4. Пусть и 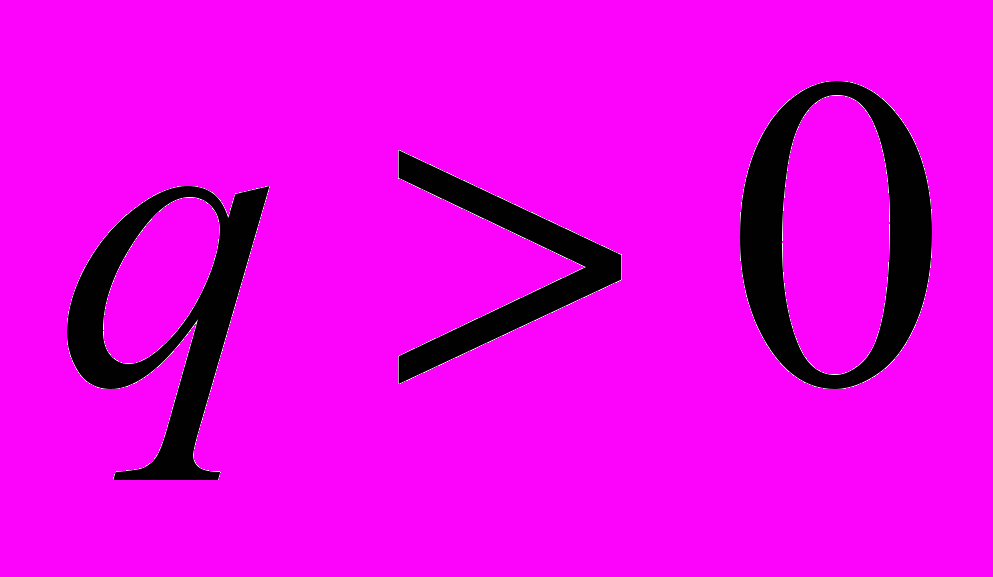- целые числа, причем НОД и

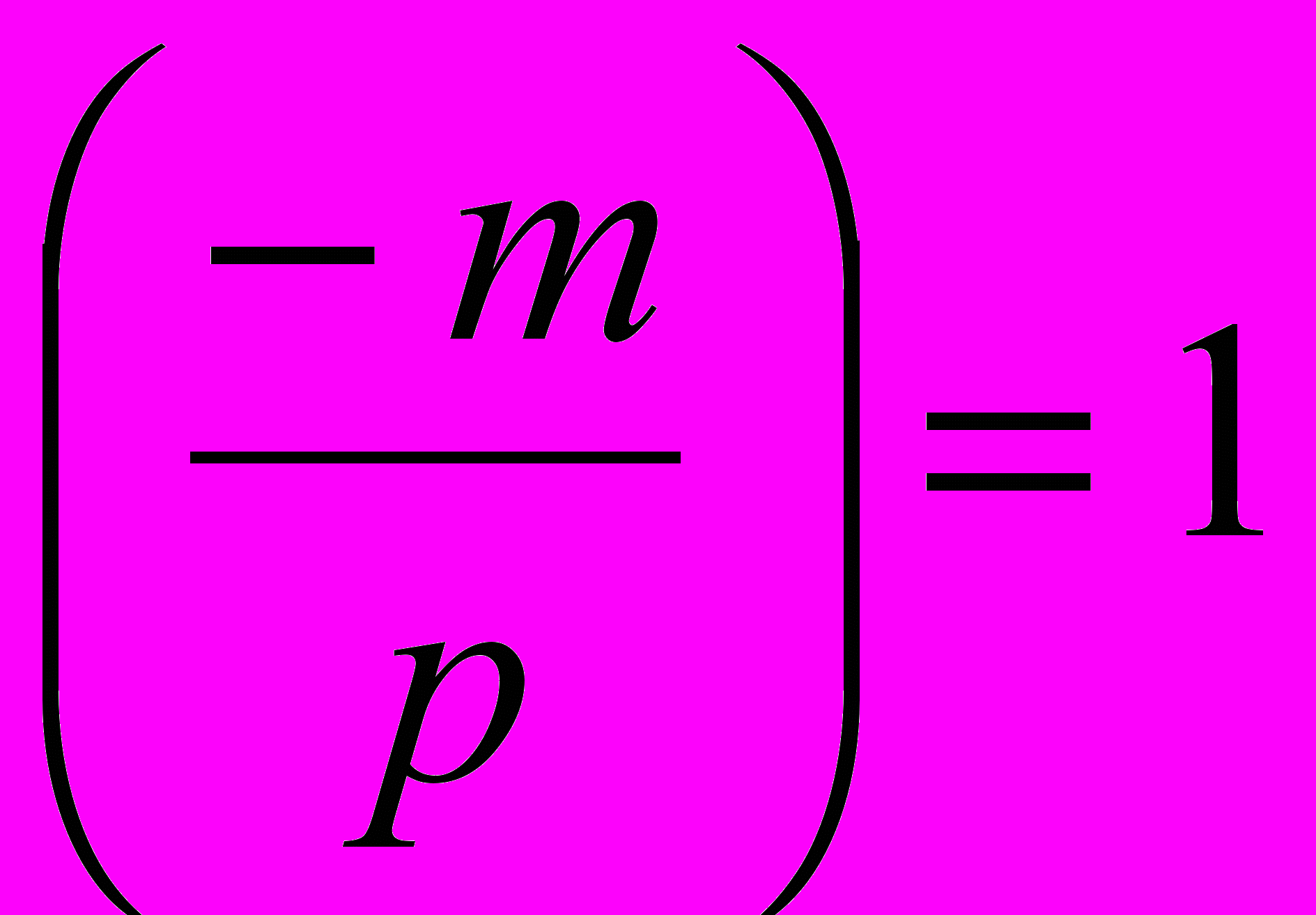, (23)

для всех простых делителей числа q.

Обозначим через число классов целочисленных положительных бинарных квадратичных форм гауссового рода G определителя m, арифметический минимум которых делится на .

Тогда при

~ , (24)

где 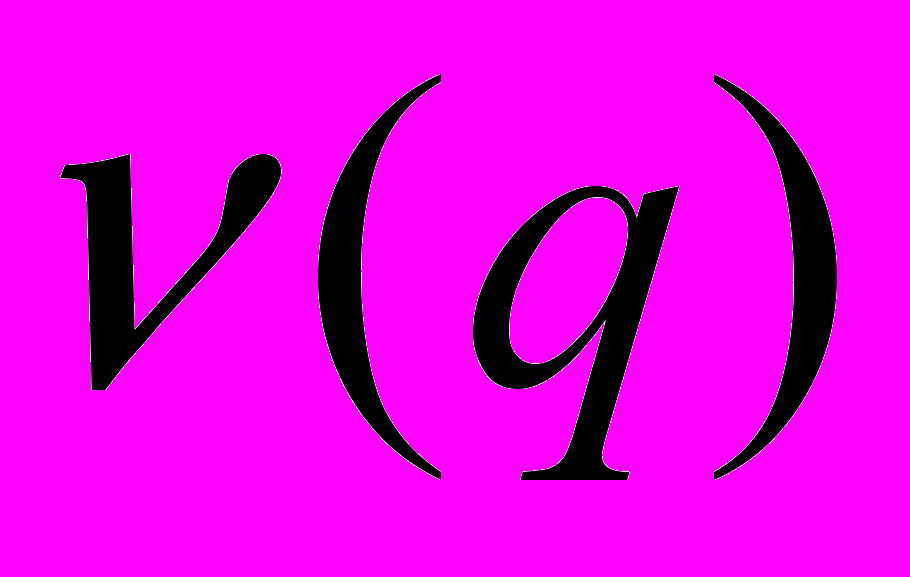– число различных простых делителей числа q; постоянные, входящие в асимптотическую формулу (24), зависят только от q.

Частный случай нашего результата при 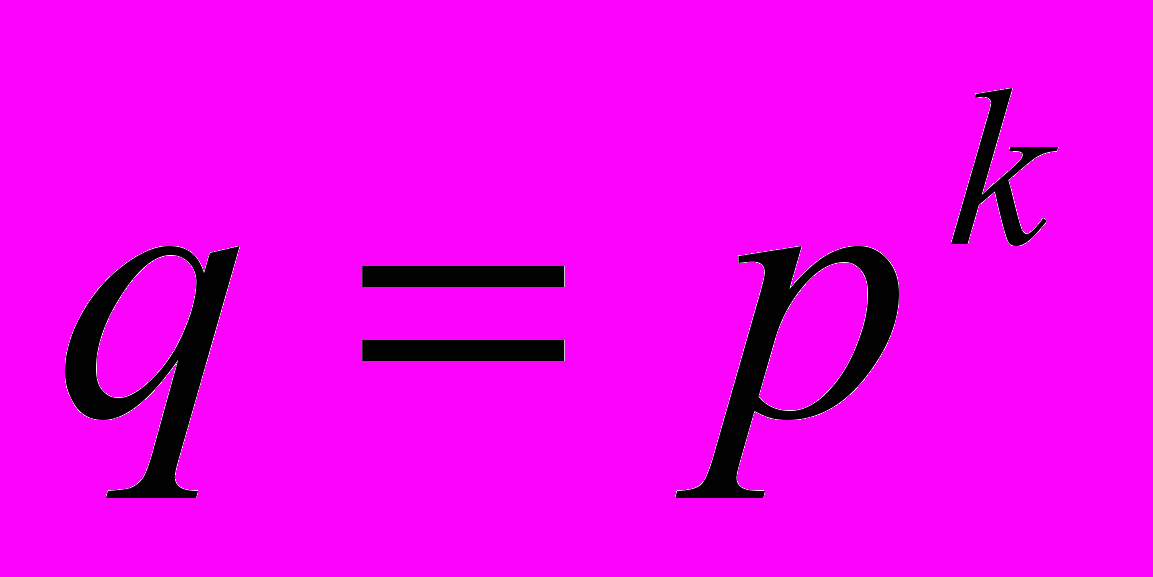, где 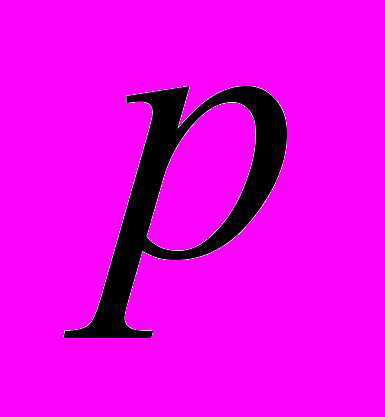– простое число, был ранее получен Ю.В. Линником. Результат теоремы 4.4 относится к малоизученному интересному на наш взгляд вопросу о величине 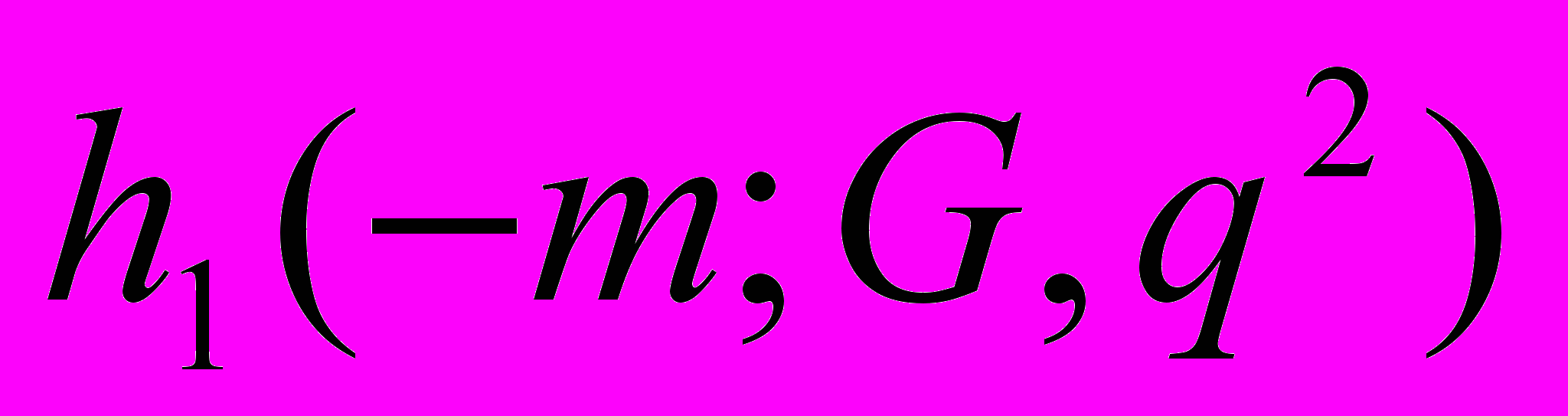, когда арифметический минимум классов гауссового рода G делятся на произвольное заданное нечетное число q.

Предполагаем, что в общем случае будет иметь место асимптотика 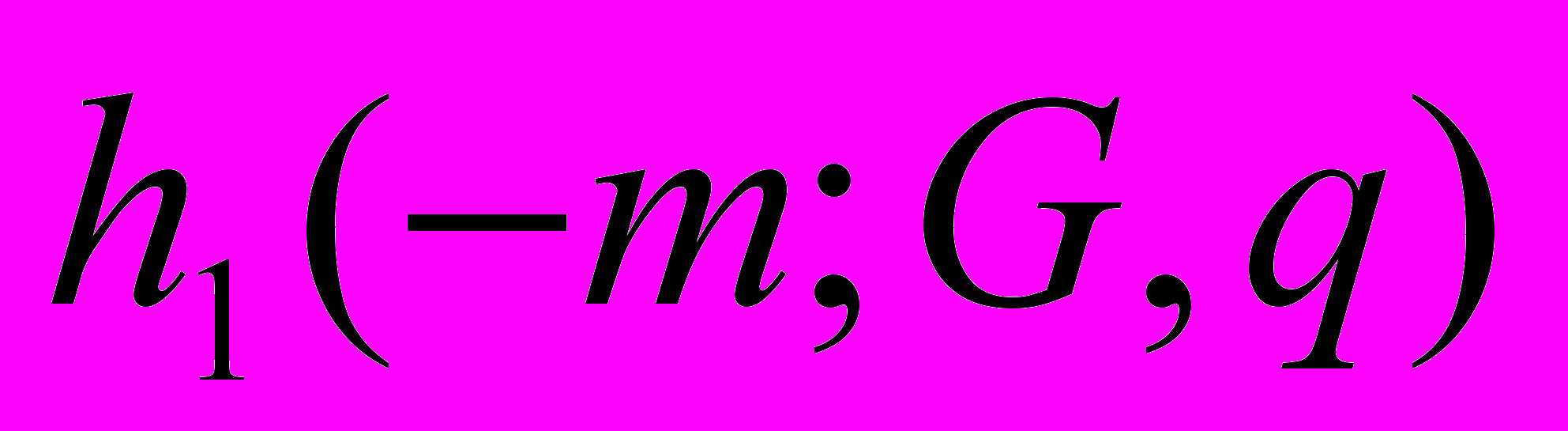~ при любом нечетном .

Вполне возможно, что теорему 4.4 не удастся доказать другими аналитическими методами, используемыми в арифметике квадратичных форм.

Следующий основной результат диссертации, опубликованный в [4], значительно расширяет возможности приложения ДЭМ к арифметике бинарных квадратичных форм. Он касается асимптотического поведения числа бинарных квадратичных форм с условием делимости произведения крайних коэффициентов на заданное нечётное число (см. [4]).

Теорема 4.7. Пусть 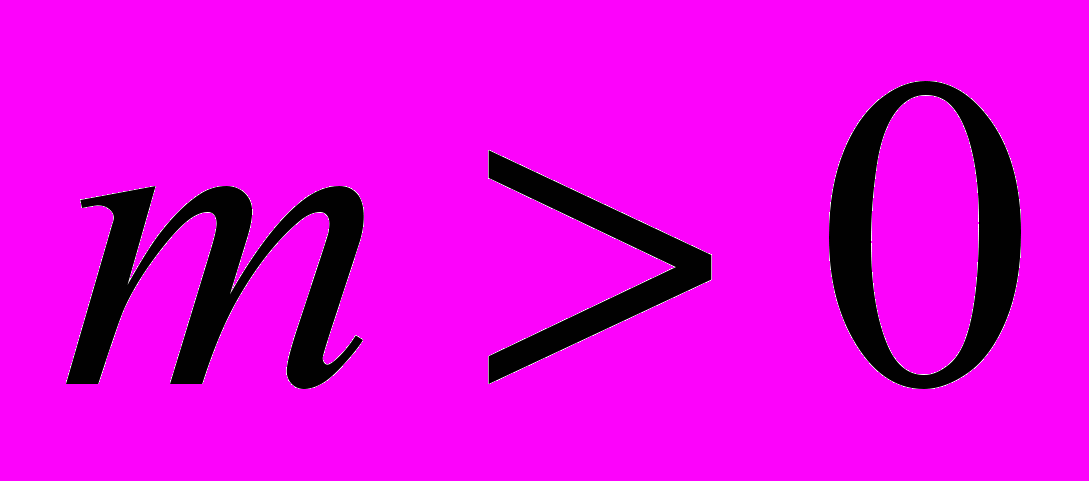– целое число, – взаимно простые нечетные числа, НОД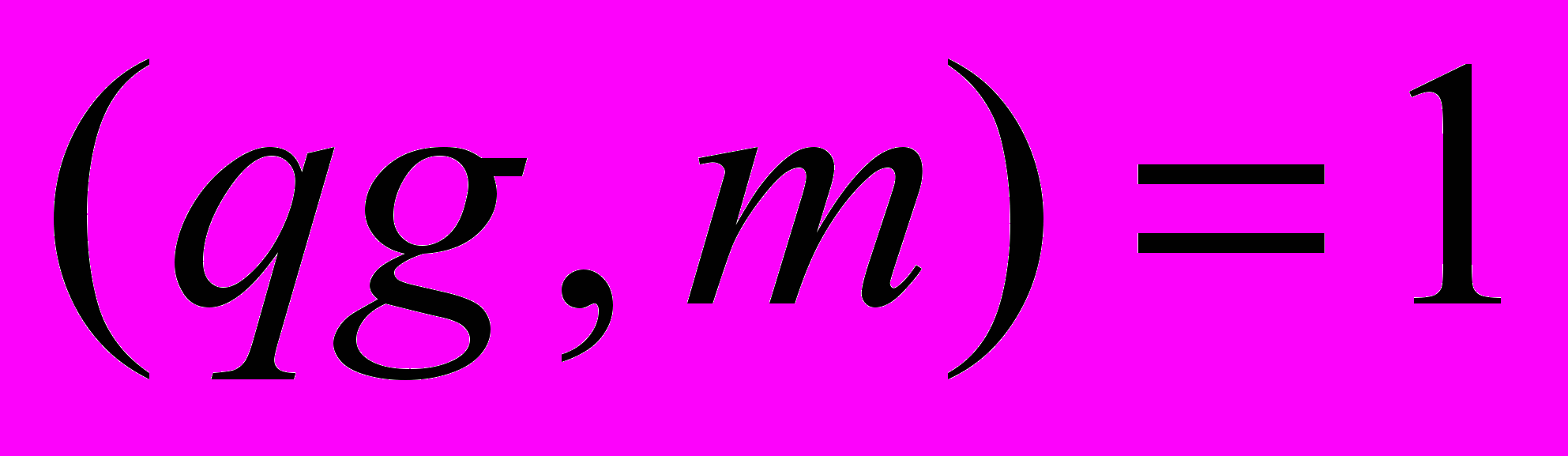, 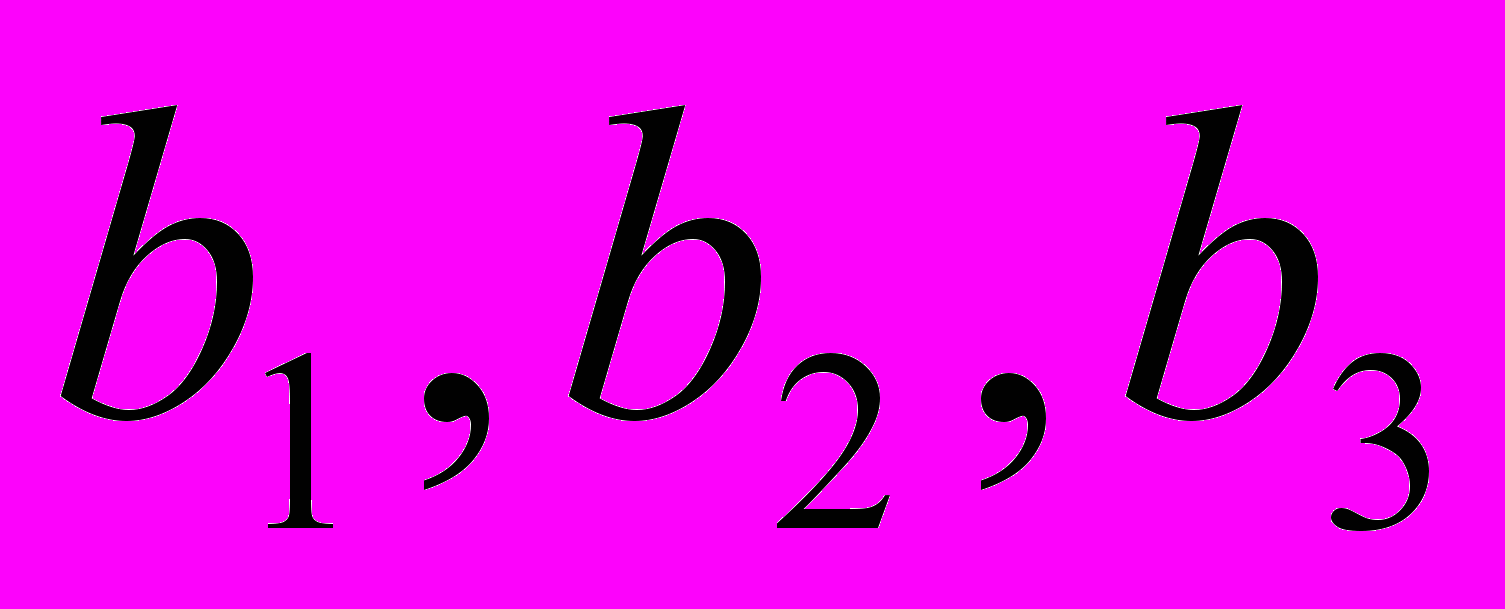– целые числа, удовлетворяющие условиям 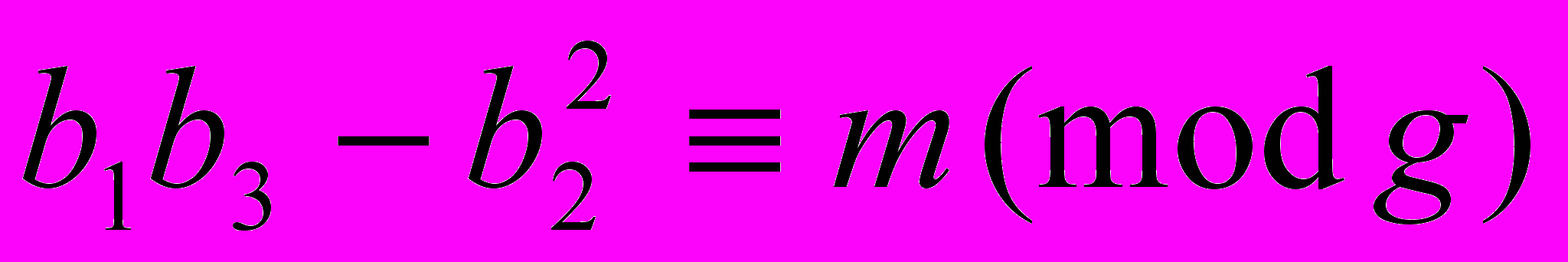, НОД,

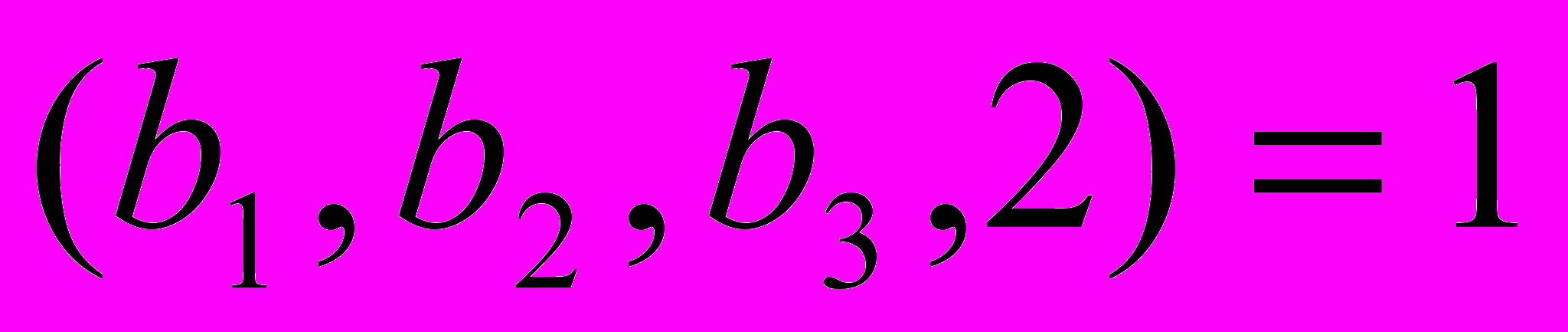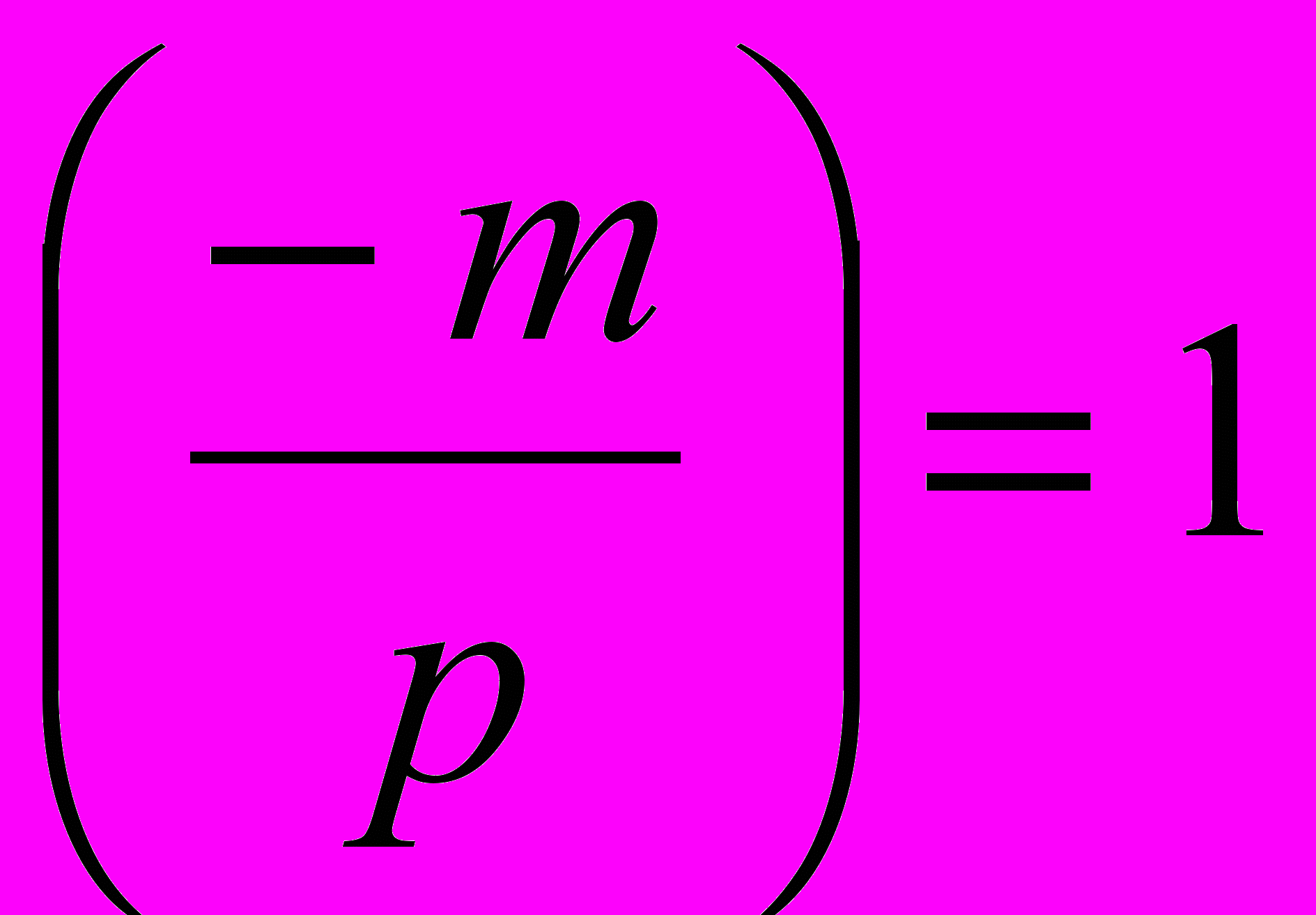для всех .

Пусть – ограниченная квадрируемая область на поверхности двуполостного гиперболоида , 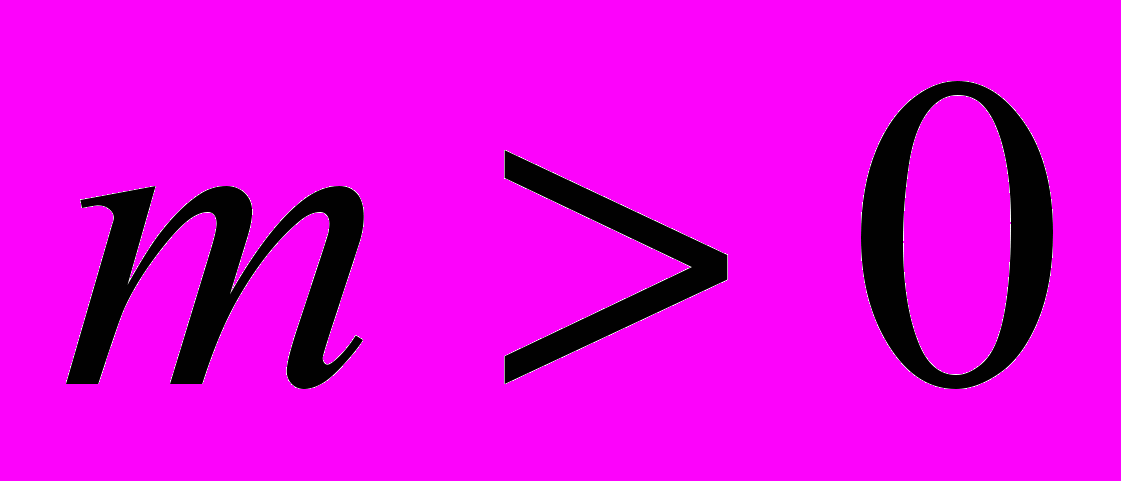с 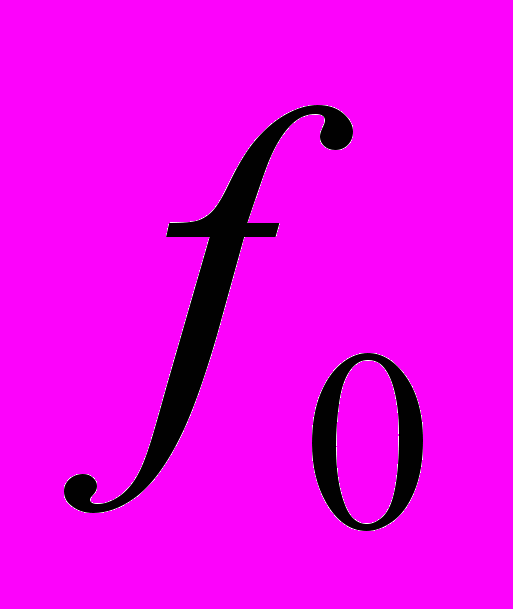-гиперболическим телесным углом. Обозначим через 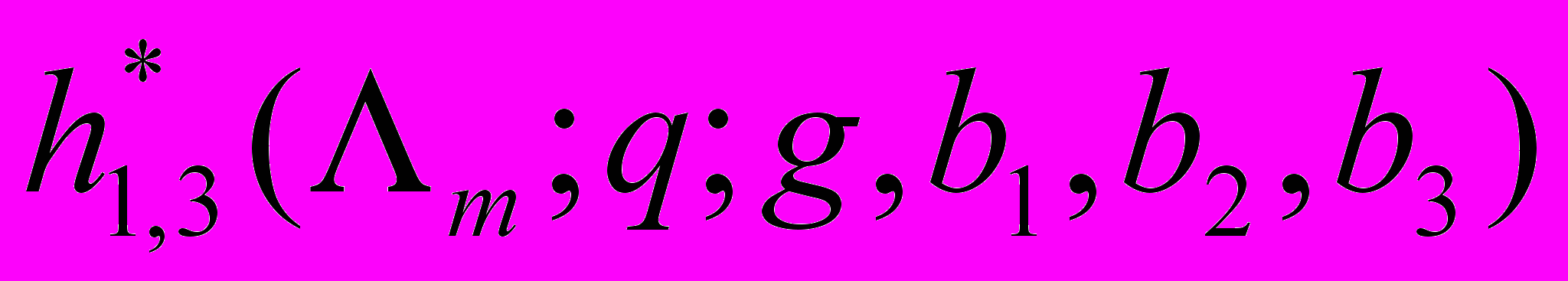число классов собственно примитивных положительных бинарных квадратичных форм определителя 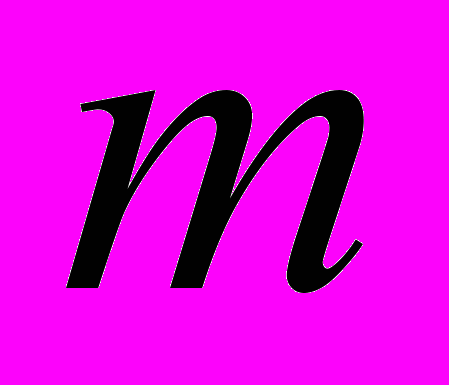, представители 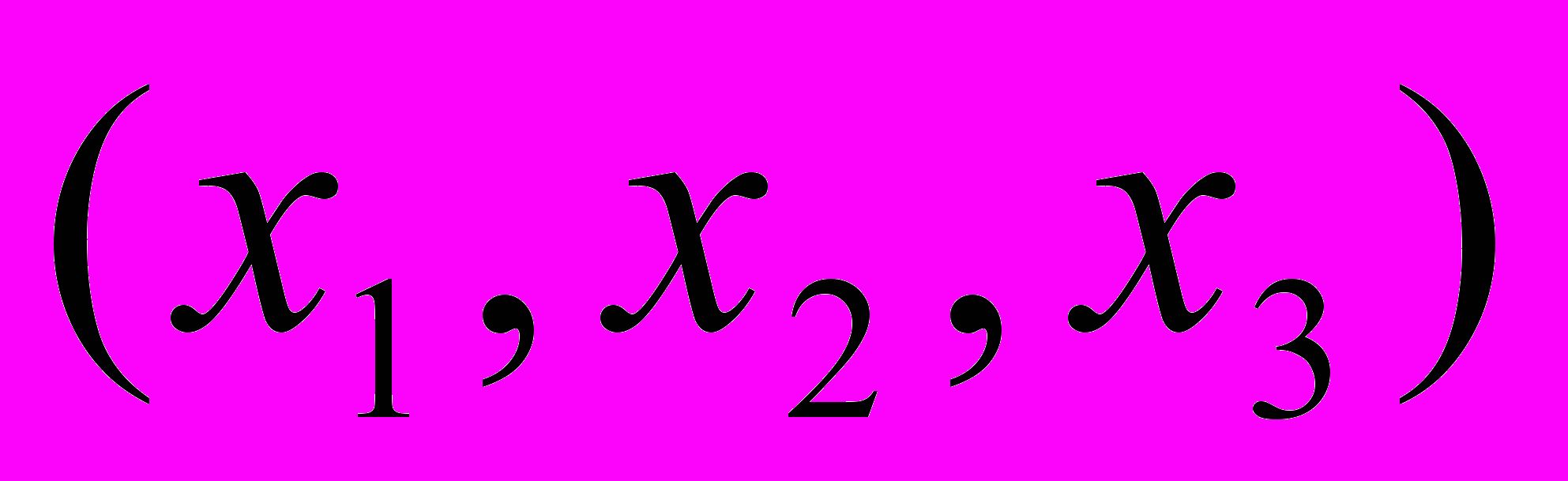которых удовлетворяют условиям

, , .

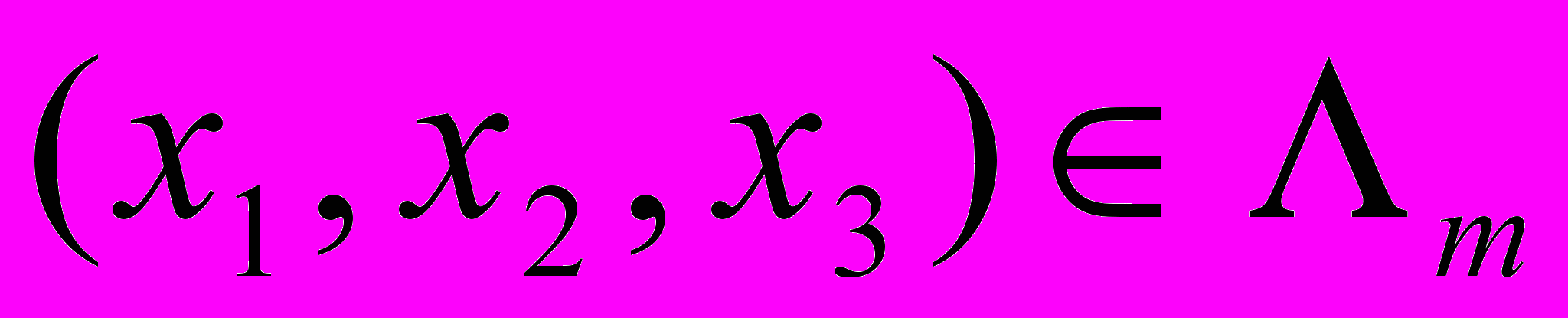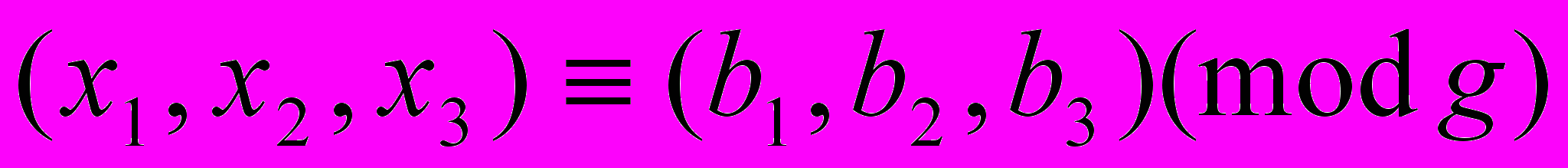Тогда при

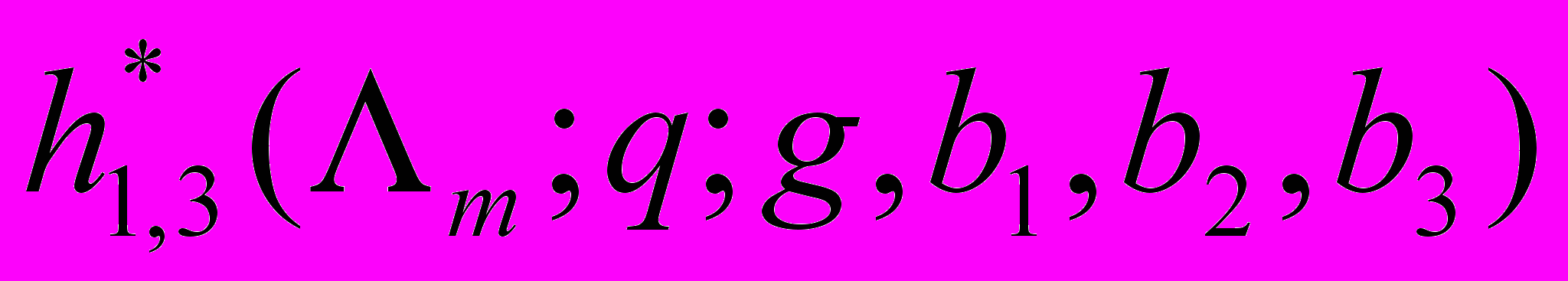~ , (25)

где – число делителей числа ;

постоянные, входящие в асимптотическую формулу (25), зависят только от 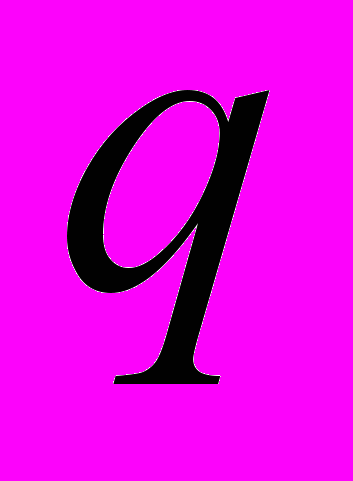, 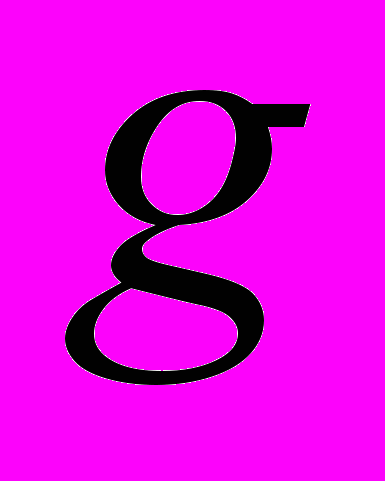и центральной проекции 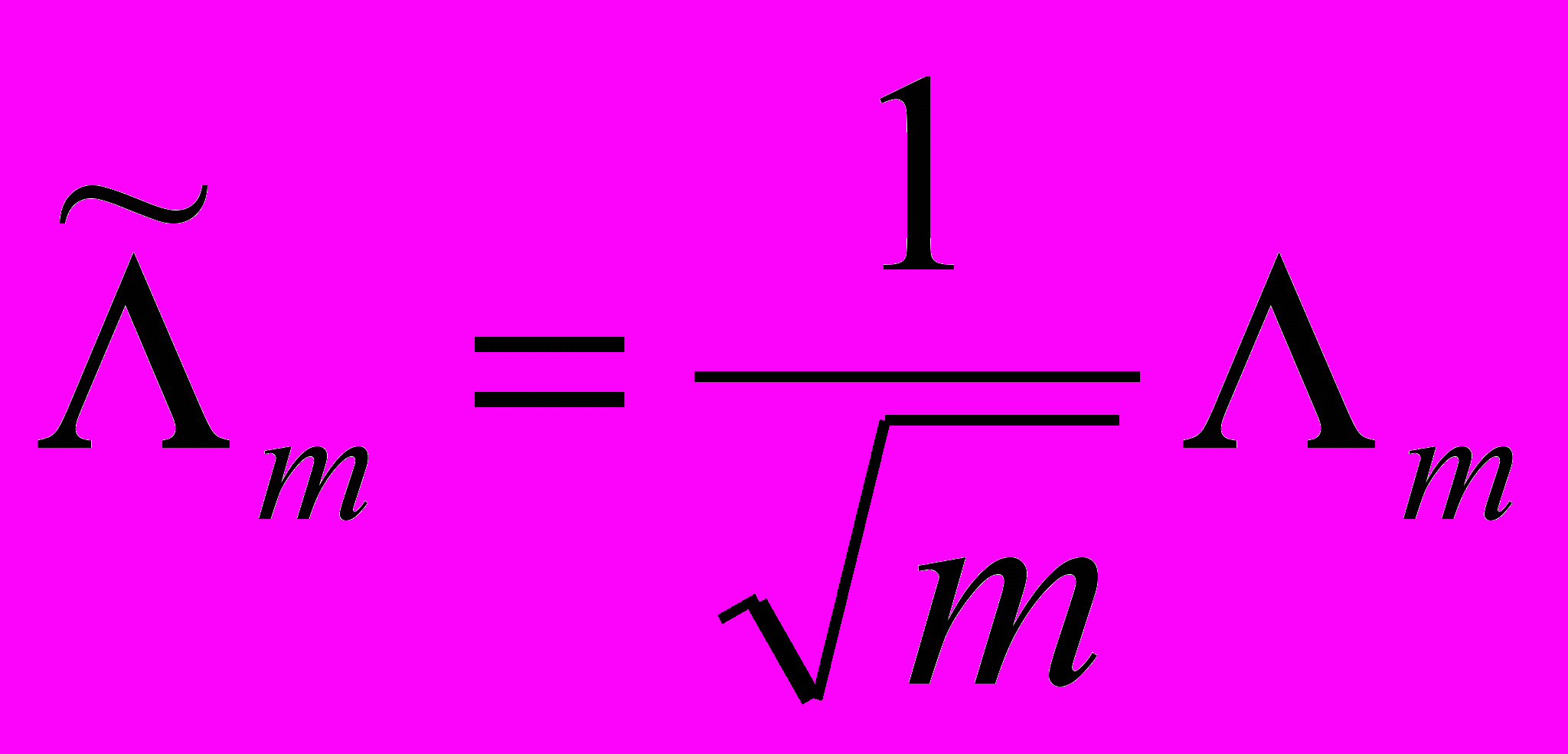области 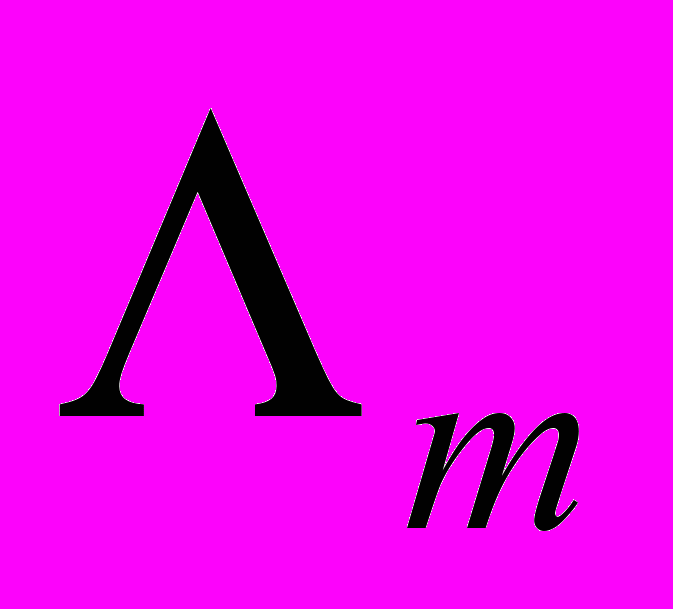на нормированный гиперболоид.

Результат теоремы 4.7 дает решение в частном случае n=2 поставленного Ю.В. Линником общего вопроса о существовании решений одной системы диофантовых уравнений специального вида, удовлетворяющих предписанным сравнениям по модулю q.

Наконец, в § 5 главы IV подводится итог изучению асимптотического поведения числа приведённых целочисленных бинарных квадратичных форм с условием делимости первых коэффициентов на заданное число (основные результаты опубликованы в [2]).

Впервые исследования по асимптотическому подсчёту числа классов положительных бинарных квадратичных форм с указанным условием были проведены Ю.В. Линником в связи с приложениями ДЭМ к вопросу о представлении целых чисел неопределёнными тернарными квадратичными формами.

Основными результатами главы IV являются теоремы 4.11 – 4.13, которые обобщают и уточняют результаты Ю.В. Линника и Б.Ф. Скубенко.

Теорема 4.11. Пусть 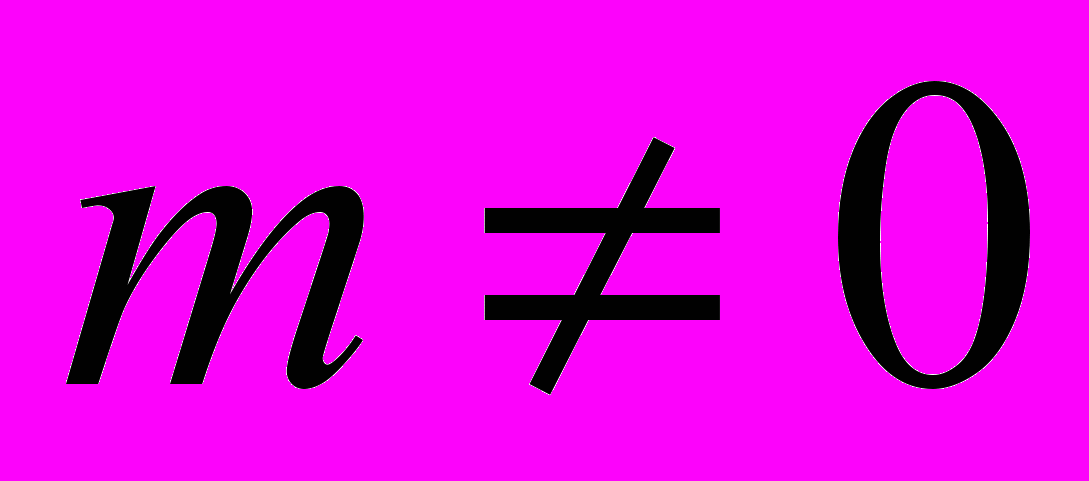– целое число, 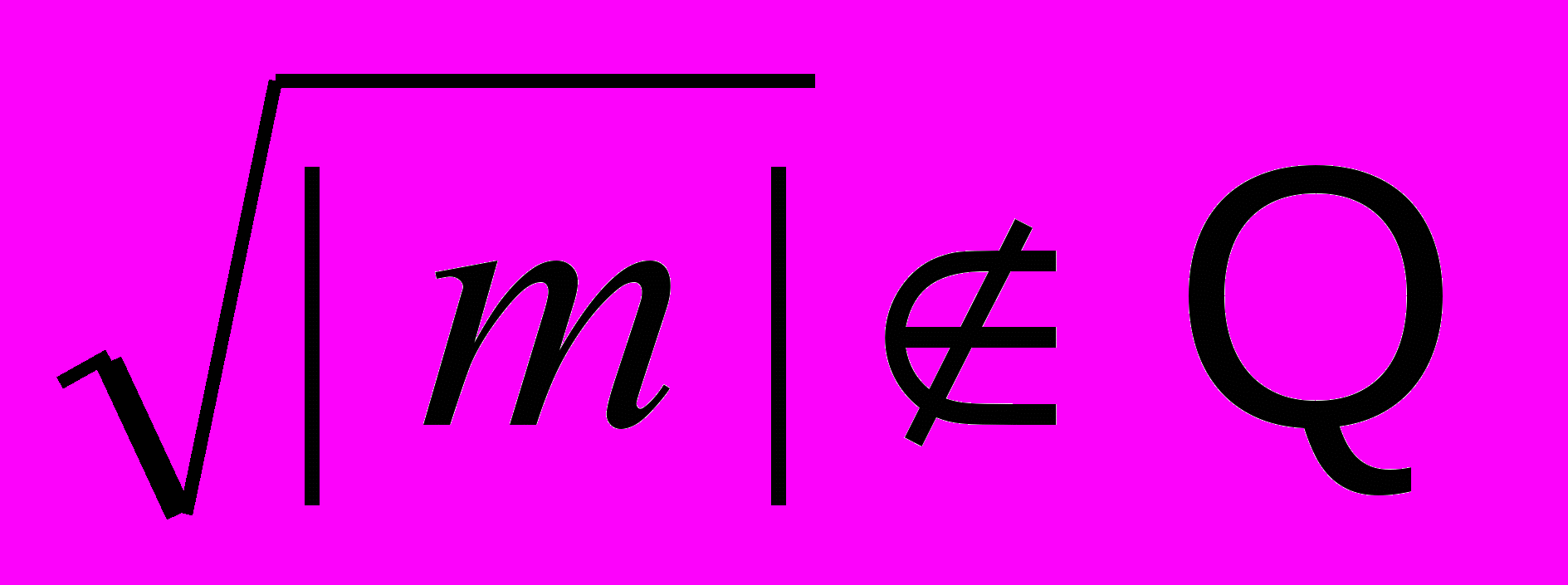, 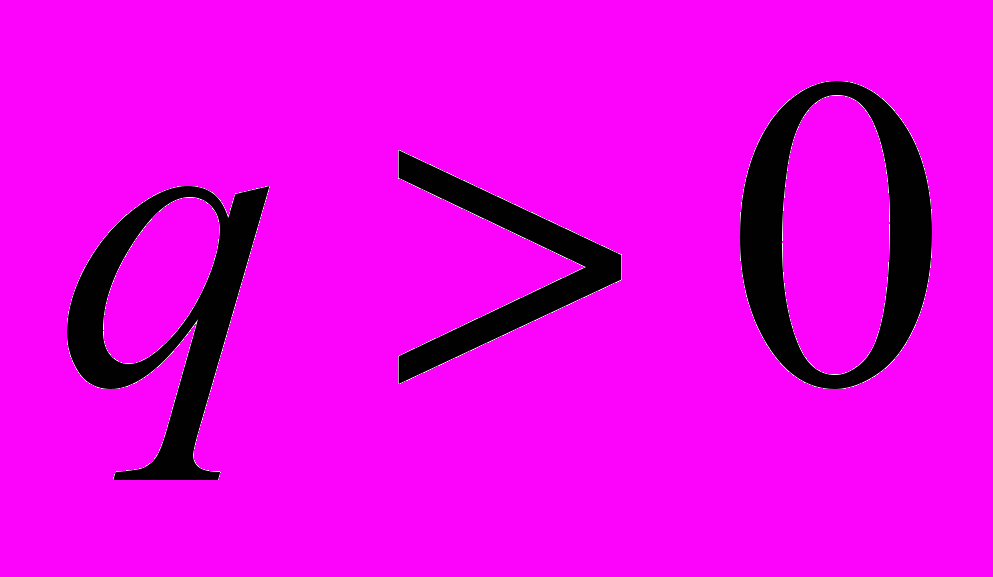– целое число, причем НОД, 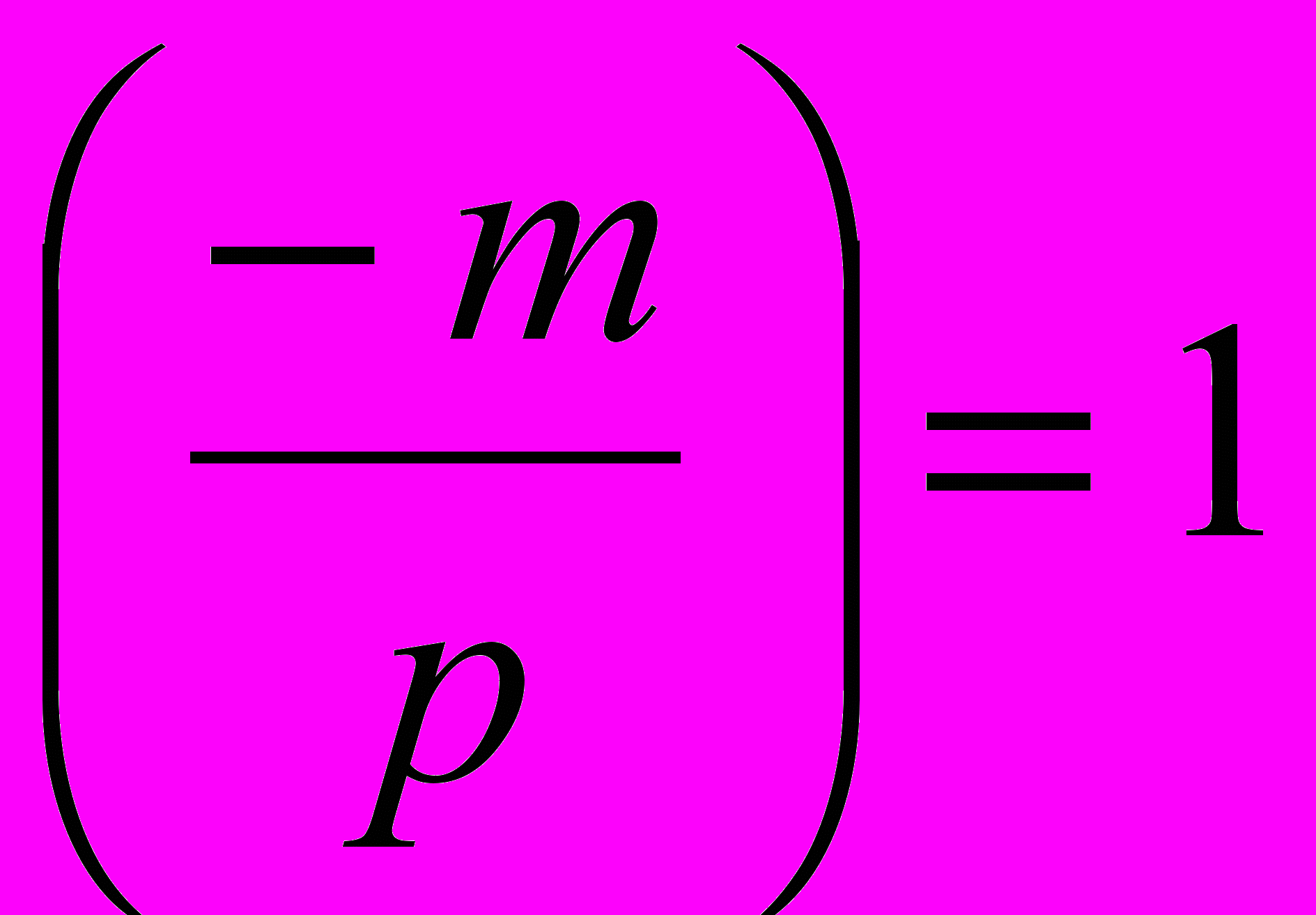для всех .

Обозначим через 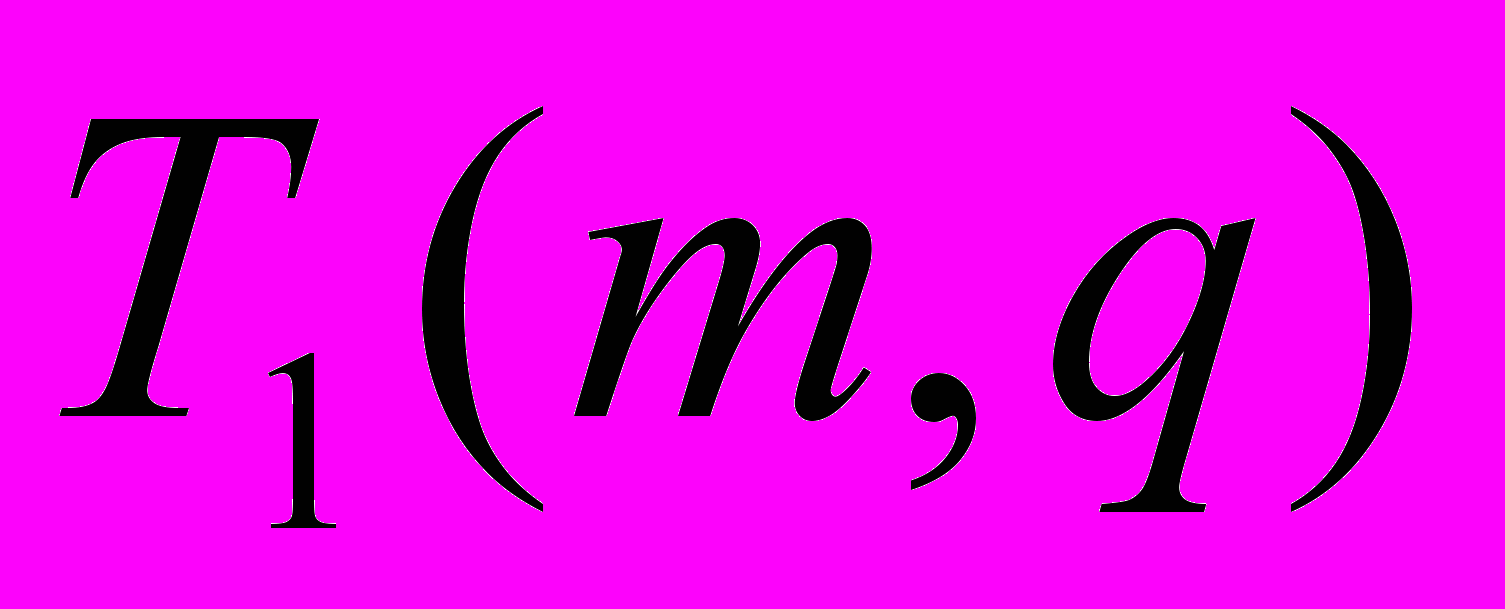число целочисленных приведенных бинарных квадратичных форм определителя m, первые коэффициенты которых делятся на заданное нечетное число q.

Тогда при



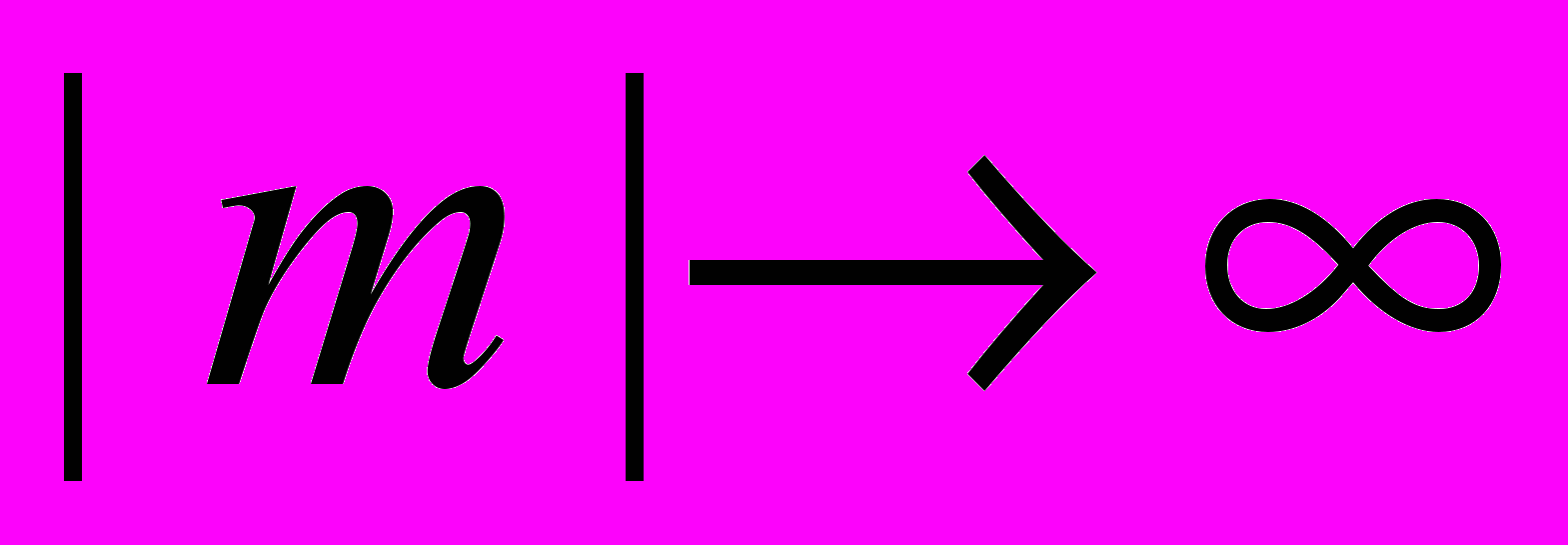
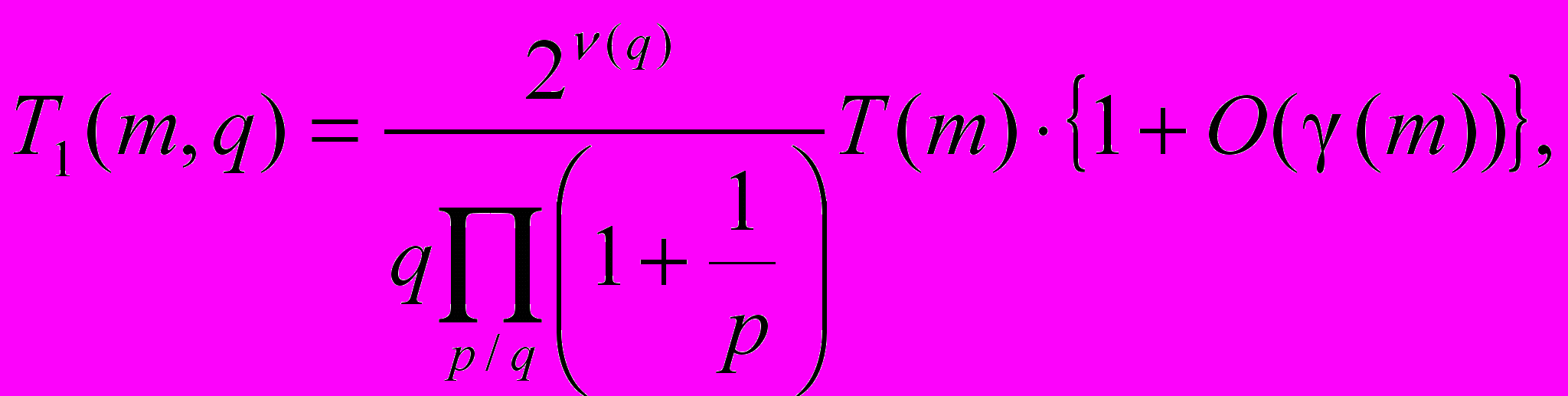(26)

где 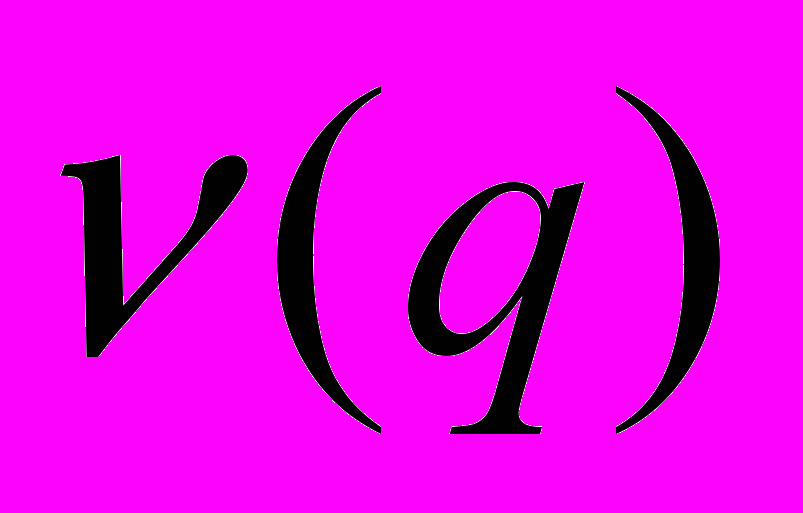– число различных простых делителей числа 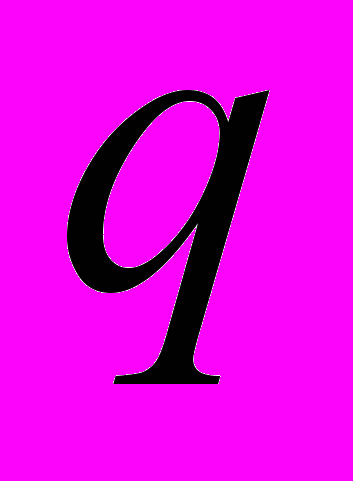; постоянная входящая в символ O, зависит только от .

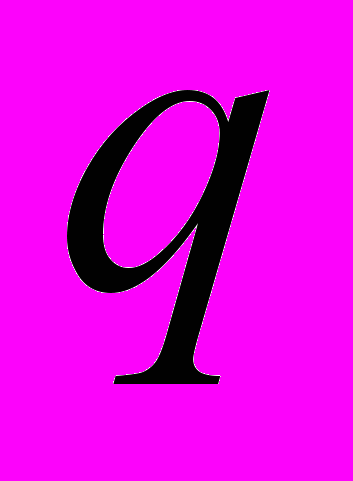Частным случаем теоремы 4.11 являются результаты Ю.В. Линника и Б.Ф. Скубенко при 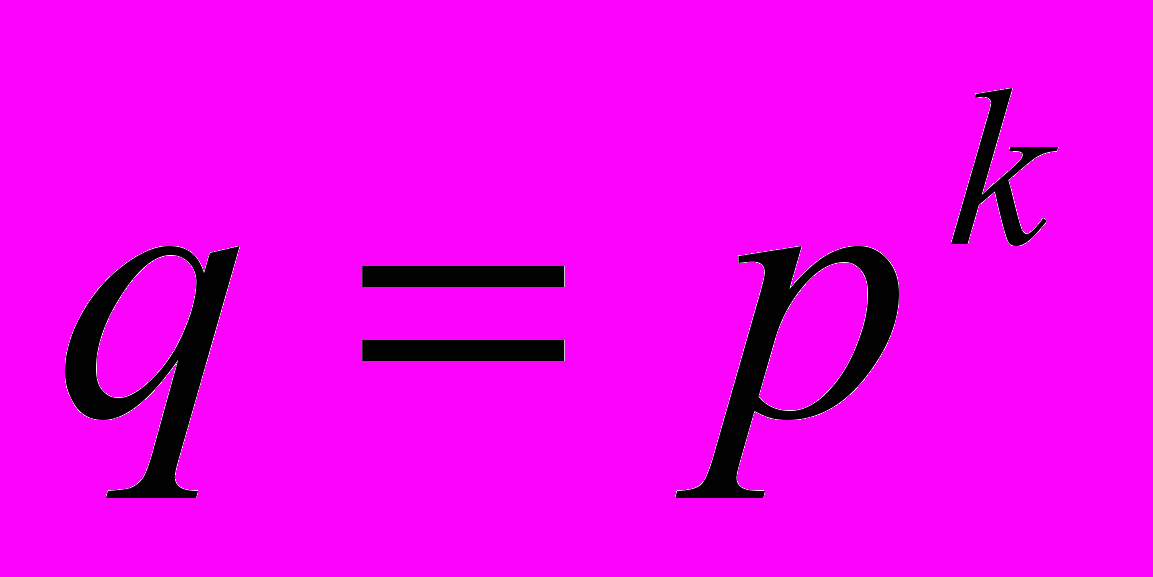, где 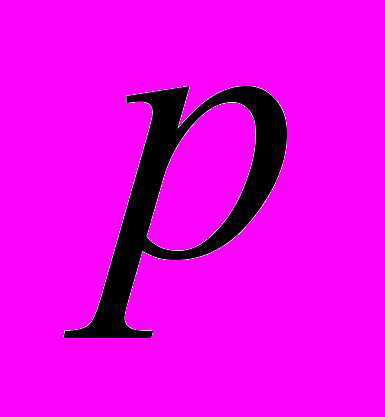– нечетное простое число.

Следующие два основных результата для величины с остаточными членами основаны на гипотезах о поведении 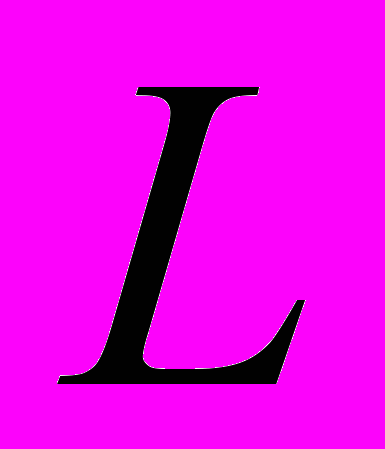-функции Дирихле.

Теорема 4.12. В условиях теоремы 4.11 пусть выполнена гипотеза (K), т.е. 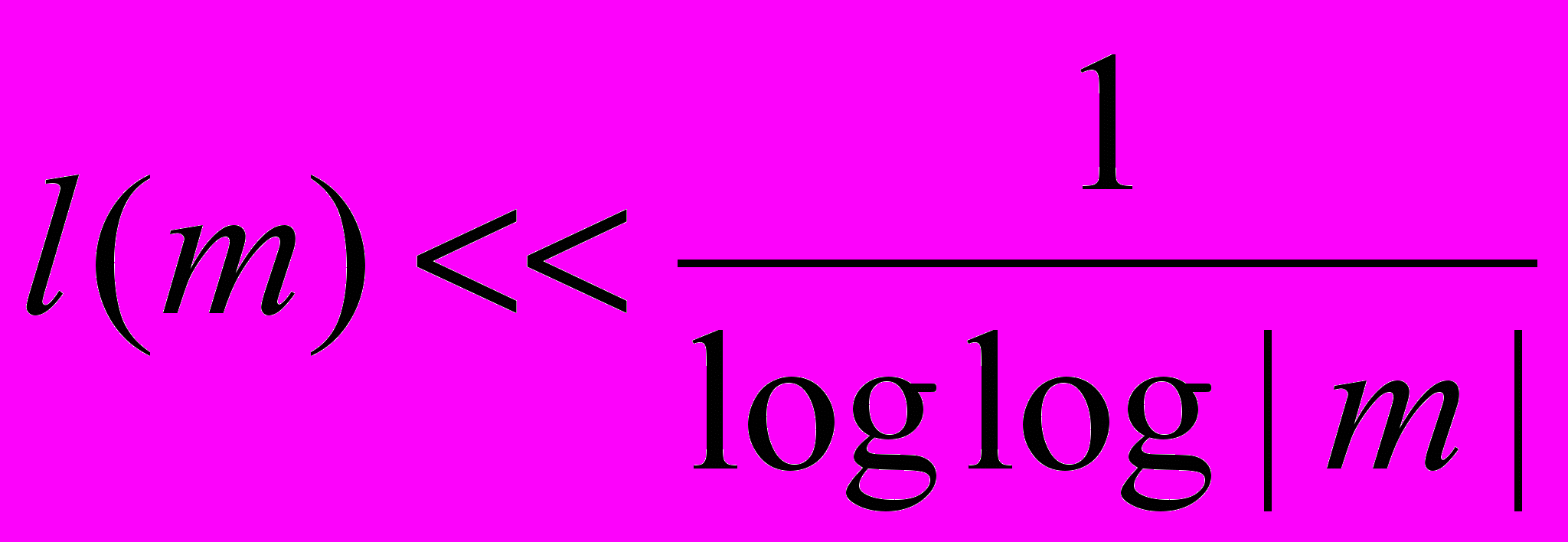. Тогда при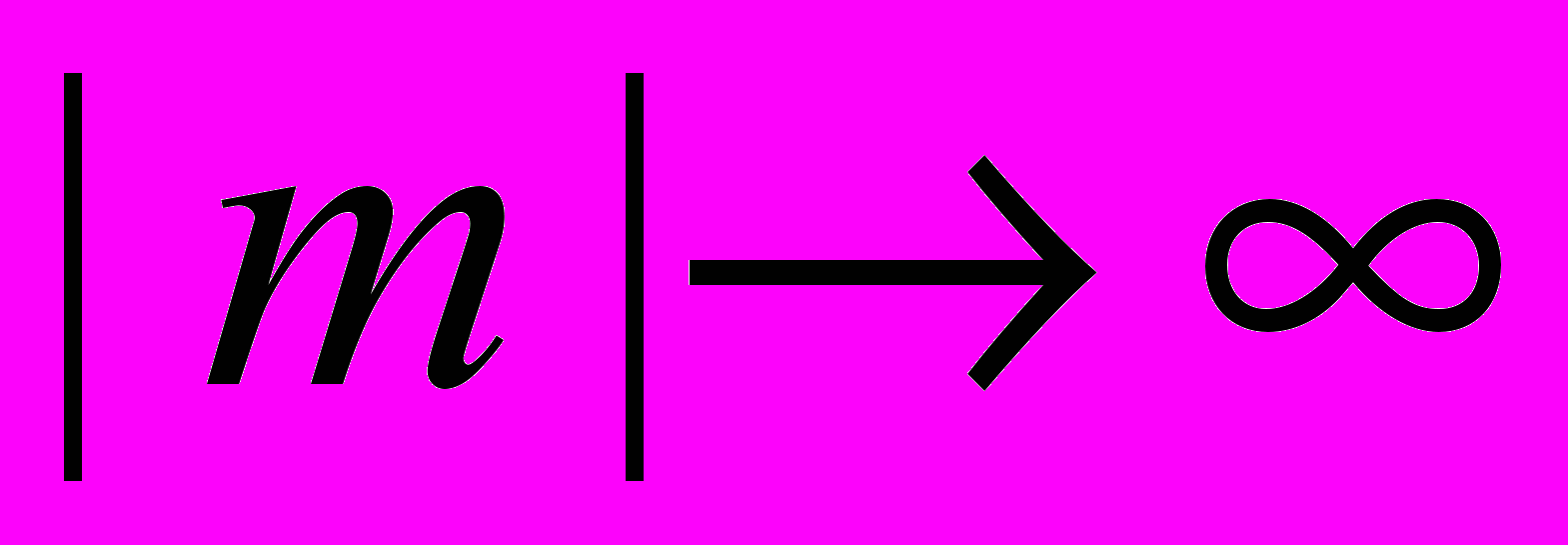

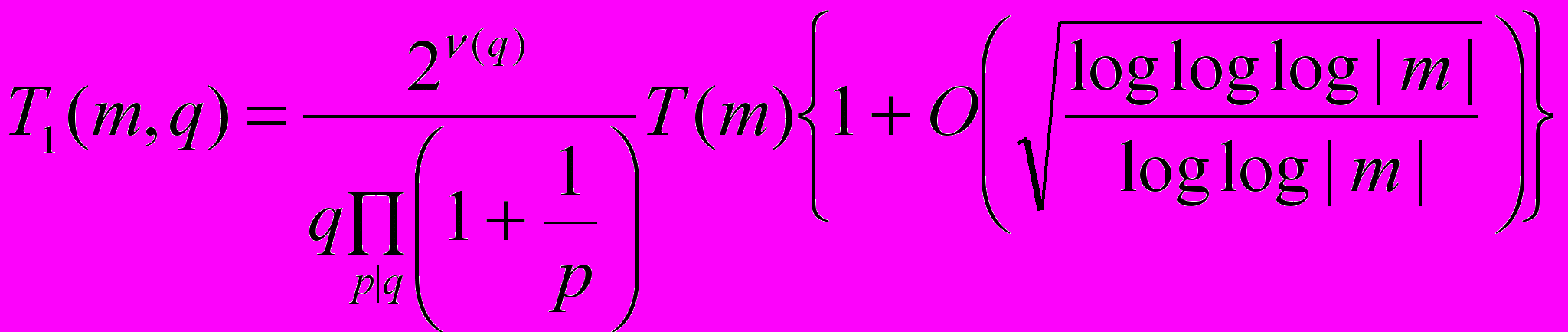, (27)

постоянные, входящие в (27), зависят только от .

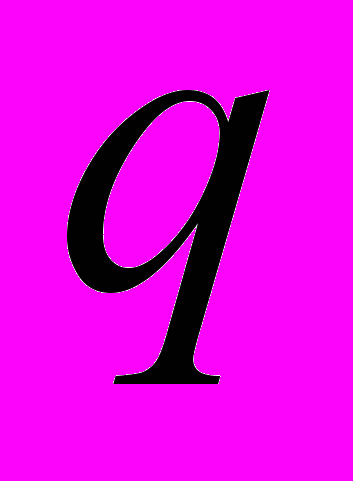Теорема 4.13. Пусть в условиях теоремы 4.11 выполнена гипотеза (Y ), т.е. в области 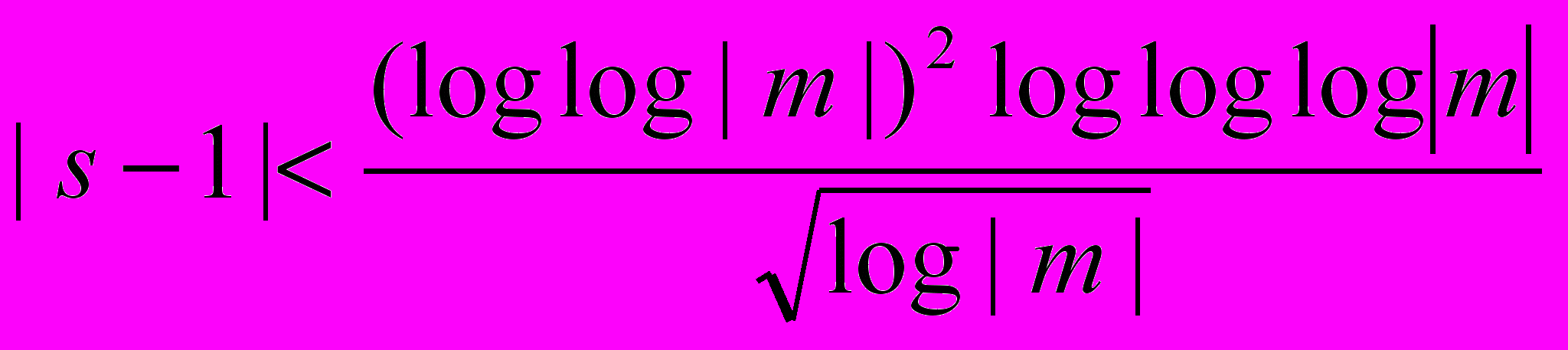комплексной переменной 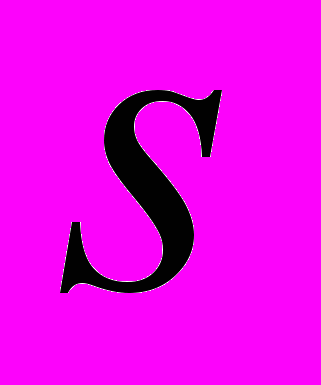нет нулей 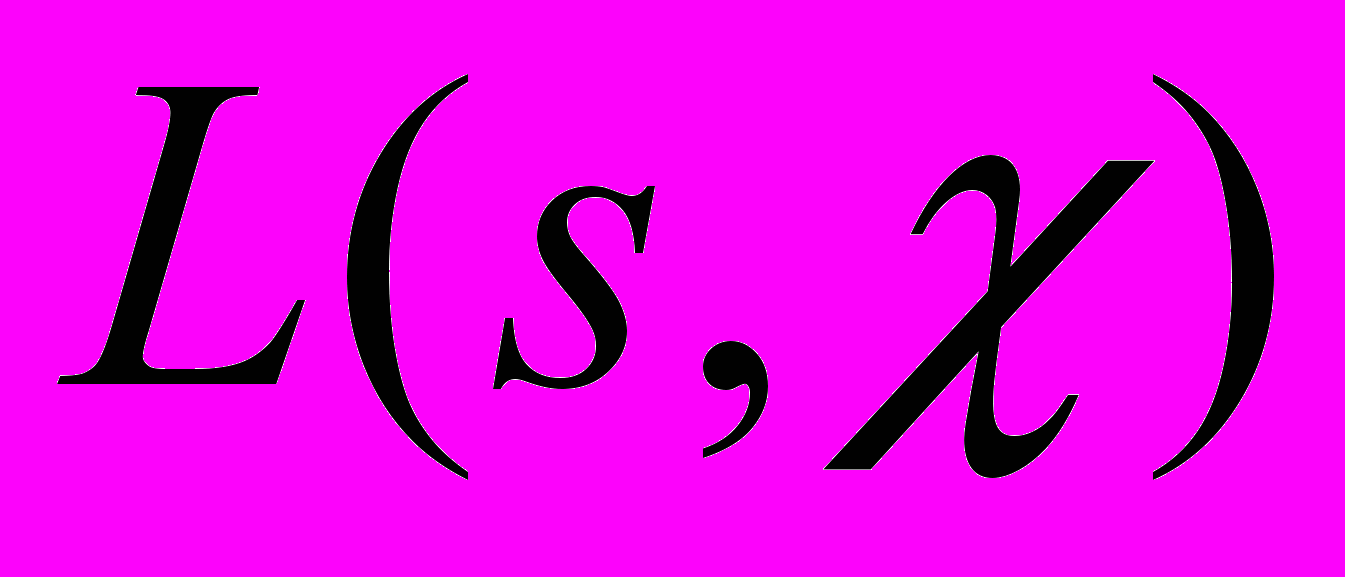. Тогда при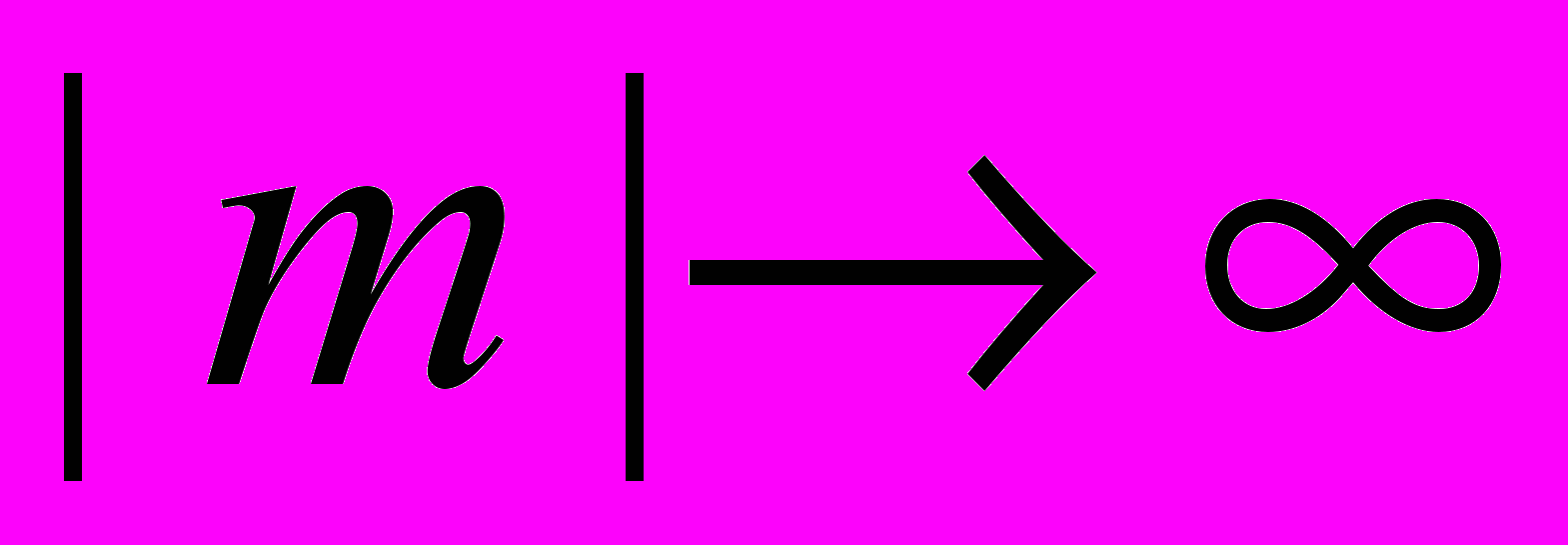

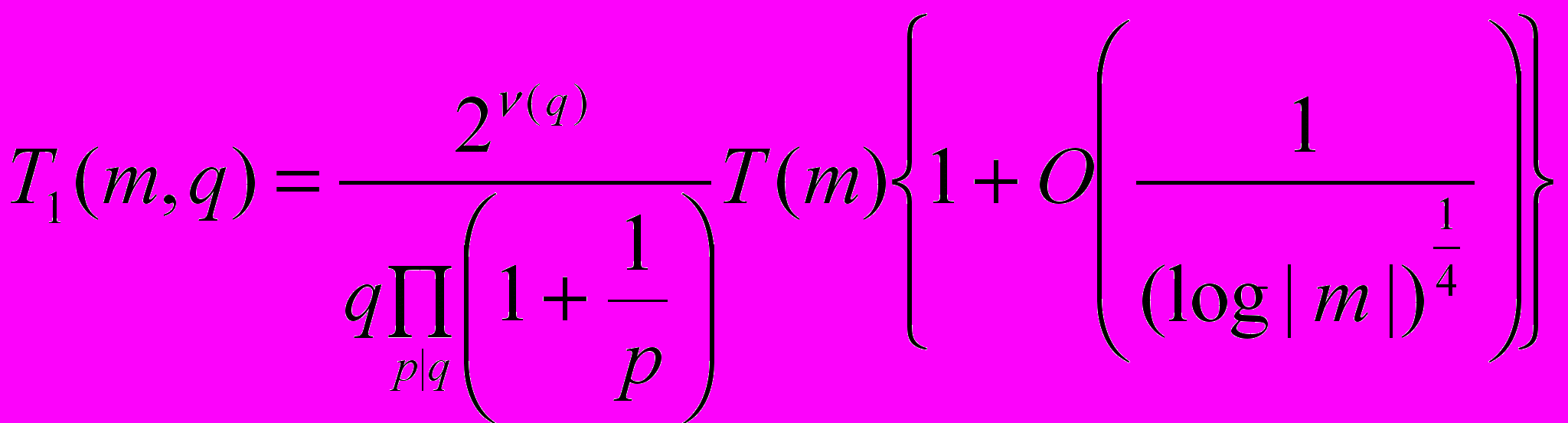, (28)

постоянные, входящие в (28), зависят только от .

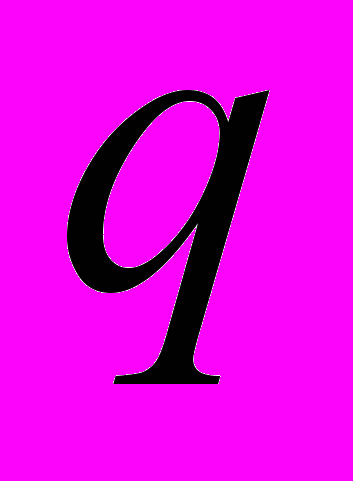Используемые в этих теоремах гипотезы, представляют собой ослабления расширенной гипотезы Римана для L-функции Дирихле.

Заметим также, что безусловные оценки остаточных членов для , если не считать оценки (26), до сих пор не установлены, хотя в работе W. Duke получена безусловная оценка остаточного члена со степенным понижением в асимптотической формуле для числа целых точек на простейшем двуполостном гиперболоиде.

Но до сих пор результат Дьюка не распространён на .

Основное содержание диссертационной работы изложено в следующих публикациях:

1. Пачев У. М. Представление целых чисел изотропными тернарными квадратичными формами [Текст] // Известия РАН, Серия Математическая. -2006. -Т. 70. -№3. –С. 167-184.- 1,12 п. л.

2. Пачев У. М. Об асимптотике числа приведенных бинарных квадратичных форм с условием делимости первых коэффициентов [Текст] // Сибирский математический журнал. -2007. –Т. 48. -№2. –С. 376-388.- 0,81 п. л.

3. Пачев У. М. О числе классов гауссового рода, арифметический минимум которых делится на квадрат заданного нечетного числа [Текст] // Математические заметки. -1994.–Т. 55. -№2. –С. 118-127.- 0,62 п. л.

4. Пачев У. М. Асимптотическое распределение классов положительных бинарных квадратичных форм с условием делимости коэффициентов [Текст] //Фундаментальная и прикладная математика. -2005. –Т. 11. -№6. –С. 123-130.- 0,5 п. л.

5. Пачев У. М. Эргодические свойства потоков классов положительных бинарных квадратичных форм в гауссовых родах [Текст] // Записки научных семинаров. ПОМИ РАН. - 1997. –Т. 236. –С. 149-161. - 1,2 п. л.

6. Пачев У. М. О распределении целых точек на некоторых двуполостных гиперболоидах [Текст] // Записки научных семинаров. ЛОМИ. -1980. –Т. 83. – С 87-141.- 4,3 п. л.

7. Пачев У. М. Об арифметике матриц второго порядка [Текст] / Пачев У. М., А.В.Малышев // Записки научных семинаров. ЛОМИ. -1980. –Т. 83. –С. 41-86. - 3,6 п. л. (авт. вклад 70%).

8. Пачев У. М. О представлении целых чисел положительными тернарными квадратичными формами (новый вариант дискретного эргодического метода) [Текст] / Пачев У. М., А.В.Малышев // Записки научных семинаров. ЛОМИ. -1979. –Т. 82. – С. 33-87.- 3,4 п. л. (авт. вклад 50%).

9. Пачев У. М. Эргодические теоремы и теоремы перемешивания для потоков целых точек на некоторых изотропных гиперболоидах [Текст] // Актуальные проблемы теории чисел. -2002. –ч.III. –МГУ. –С. 133-151 - 1,2 п. л.

10. Пачев У. М. О числе приведенных целочисленных неопределенных бинарных квадратичных форм с условием делимости первых коэффициентов [Текст] // Чебышевский сборник. -2003. –Т. 4. –№3(7). – С. 92-105. - 0,8 п. л.

11. Пачев У. М. Об уточнении ключевой леммы дискретного эргодического метода для вектор-матриц второго порядка [Текст] // Чебышевский сборник. -2004. –Т. 5. –№2(10). –С. 89-97.- 0,5 п. л.

12. Пачев У. М. Асимптотическое распределение гауссовых родов [Текст] // Автоморфные функции и теория чисел. Межвузовский сборник. -1987. –С. 32-40. - 0,5 п. л.

13. Пачев У. М. О числе классов целочисленных положительных бинарных квадратичных форм, арифметический минимум которых делится на заданное число [Текст] / Пачев У. М., А.В.Малышев// Алгебра и теория чисел. -1979. -№4. –С. 53-67. - 0,95 п. л. (авт. вклад 70%).

14. Пачев У. М. Об остаточных членах в эргодических теоремах для целых точек на некоторых двуполостных гиперболоидах [Текст] / Пачев У. М., А.В.Малышев// Аналитическая теория чисел, Межвузовский сборник. -1986. –С. 32-40.- 0,32 п. л. (авт. вклад 80%).

15. Пачев У. М. Об остаточных членах в эргодических теоремах для потоков в гауссовых родах [Рукопис.] // Деп. ВИНИТИ. -1992. -№ 3246. –С. 29. - 1,8 п.л.

16. Пачев У. М. Эргодические свойства целых точек на некоторых двуполостных гиперболоидах [Рукопис.] / Пачев У. М., А.В.Малышев// Деп. ВИНИТИ. -1984. -№6127. – С. 43.- 2,7 п. л. (авт. вклад 80%).

17. Пачев У. М. Эргодическая теорема для целых точек на двуполостных гиперболоидах [Текст] // Структурные свойства алгебраических систем. -1981. – С. 84-90. - 0,4 п. л.

18. Пачев У. М. Эргодические свойства целых точек на двуполостных гиперболоидах рода 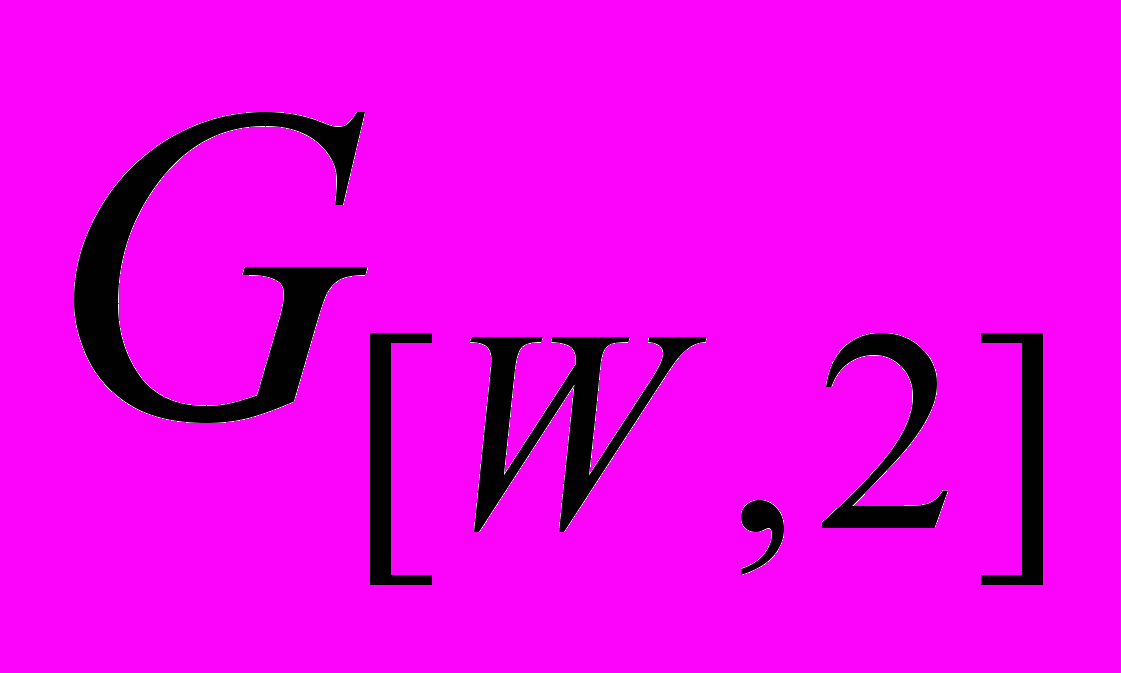[Текст] / Пачев У. М., А.В.Малышев// Тезисы докладов всесоюзной конференции. –Тбилиси: 1985. –С. 147-149.- 0,19 п.л. (авт. вклад 50%).

19. Пачев У. М. Асимптотическое распределение классов бинарных квадратичных форм по гауссовым родам [Текст] // Тезисы докладов всесоюзной конференции. –Тбилиси: 1985. –С. 197-198. - 0,12 п. л.

20. Пачев У. М. Об остаточном члене в асимптотической формуле для гауссовых родов [Текст] // Тезисы докладов всесоюзной школы. –Минск: 1989. – С. 118.- 0,06 п. л.

21. Пачев У. М. Эргодическая теорема для потоков классов бинарных квадратичных форм в гауссовых родах [Текст] // Тезисы докладов международной конференции. –Тула: 1993. – С. 126. - 0,06 п.л.

22. Пачев У. М. Теорема о перемешивании для гауссовых родов [Текст] // Тезисы докладов международной конференции, посвященной 100-летию со дня рождения Н.Г. Чеботарева. –Казань: 1994. –С. 74-75. - 0,12 п. л.

23. Пачев У. М. О числе классов положительных бинарных квадратичных форм с некоторым условием делимости коэффициентов [Текст] // Тезисы докладов III международной конференции. –Тула: 1996. –С. 113. - 0,06 п.л.

24. Пачев У. М. Эргодическая теорема для потоков целых точек на некоторых гиперболоидах [Текст] // Тезисы докладов IV международной конференции, посвященной 180-летию П.Л. Чебышева и 110-летию И.М. Виноградова. –Тула: 2001. –С. 91-92. - 0,13 п. л.

25. Пачев У. М. О числе приведенных неопределенных бинарных квадратичных форм с условием делимости первых коэффициентов [Текст] // Тезисы докладов V международной конференции. – Тула: 2003. –С. 176-177. - 0,13 п. л

26. Пачев У. М. Об асимптотике с остаточным членом для числа бинарных квадратичных форм с условием делимости первых коэффициентов [Текст] // Тезисы докладов VI международной конференции, посвященной 100-летию Н.Г. Чудакова. – Саратов: 2004.–С. 90-91. – 0,12 п. л.