Geum.ru

Приложения дискретного эргодического метода к арифметике бинарных и изотропных тернарных квадратичных форм 01. 01. 06 математическая логика, алгебра и теория чисел

Вид материалаАвтореферат
Подобный материал:
1   2   3
Теорема 3.3 (эргодическая теорема для потоков целых точек на изотропном гиперболоиде)

Пусть – род примитивной изотропной тернарной квадратичной формы 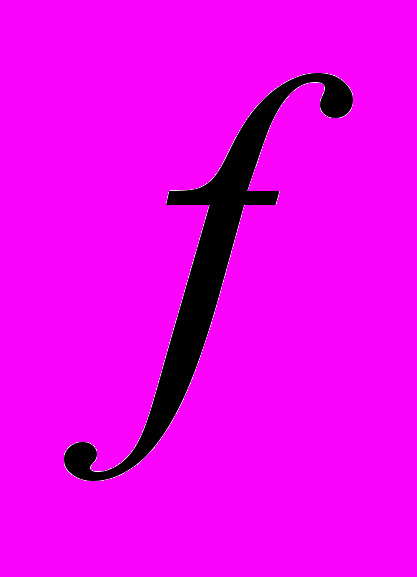=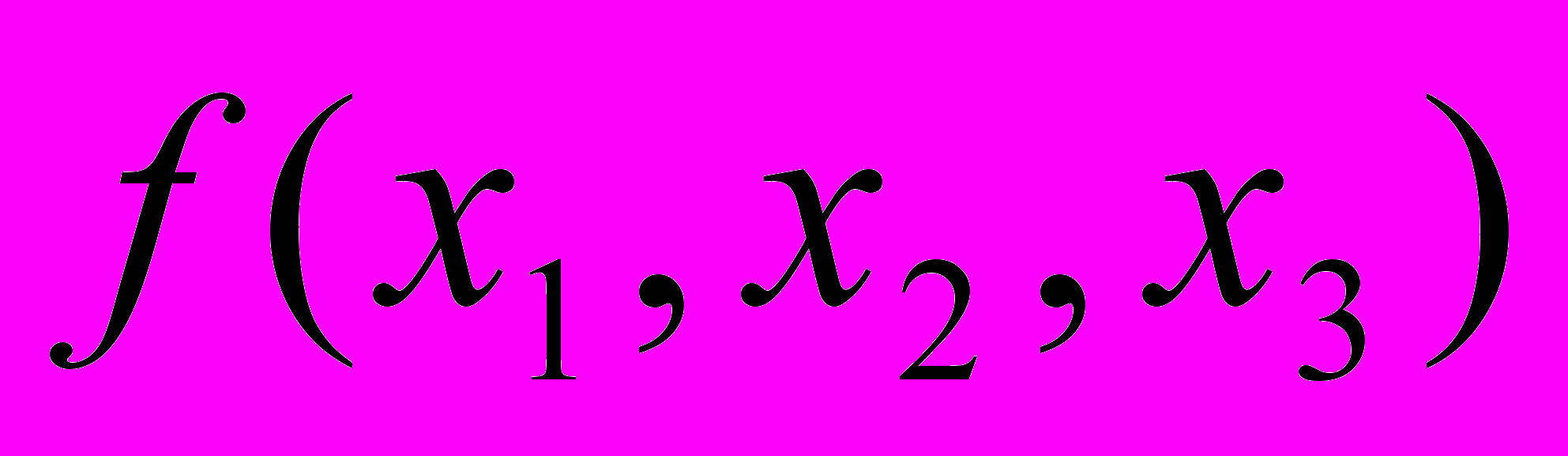, имеющей вид

,

где 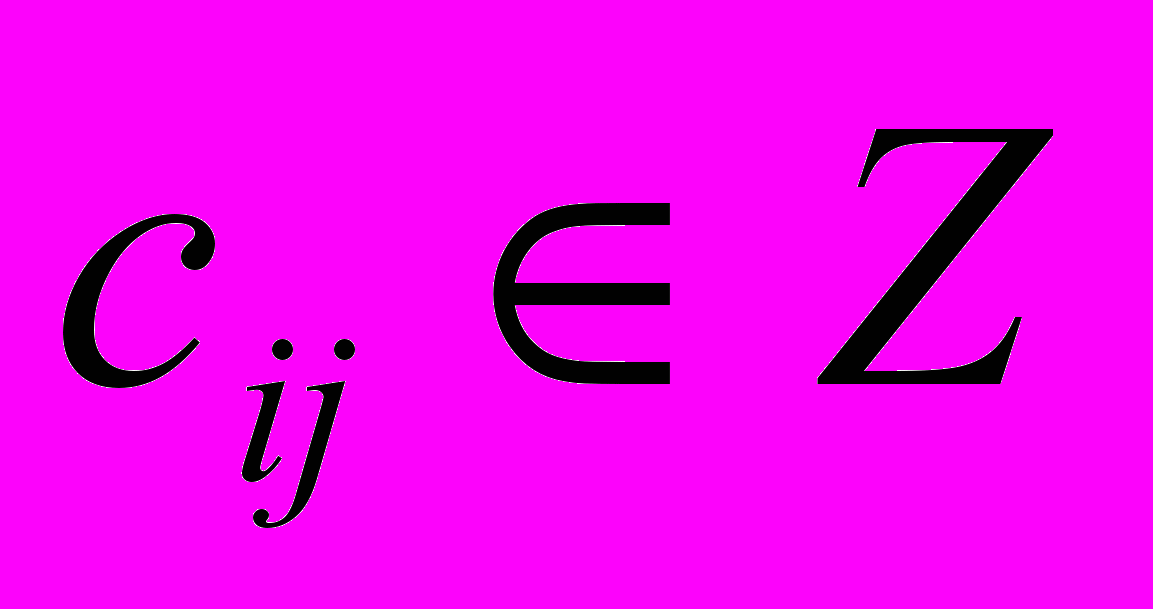, , 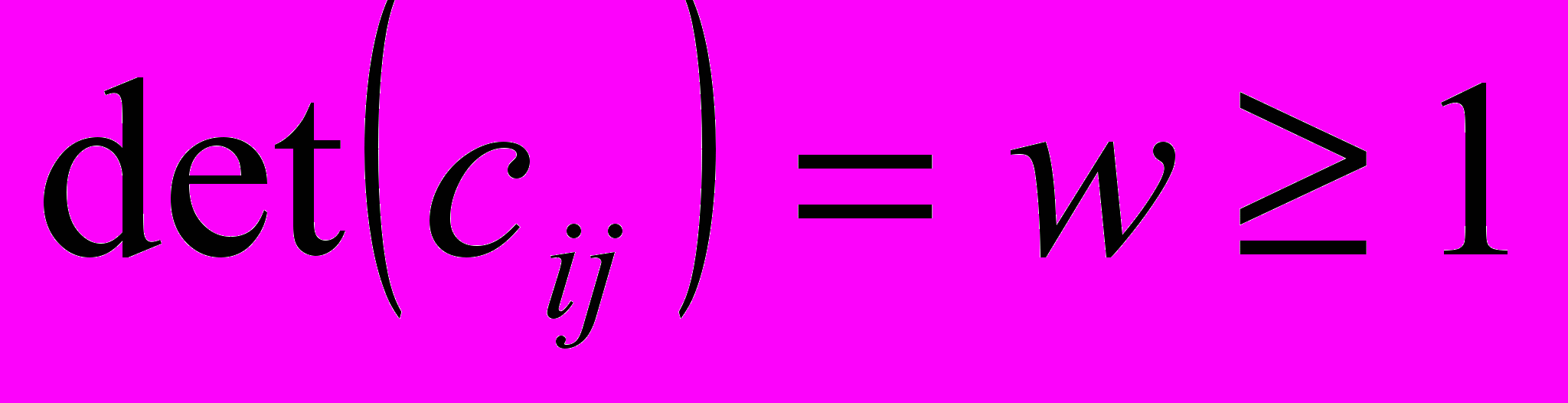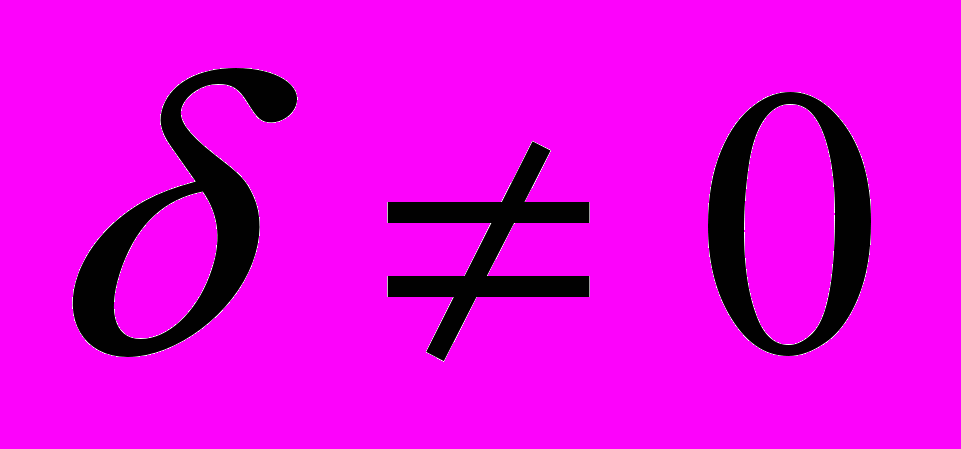– целое число, причем 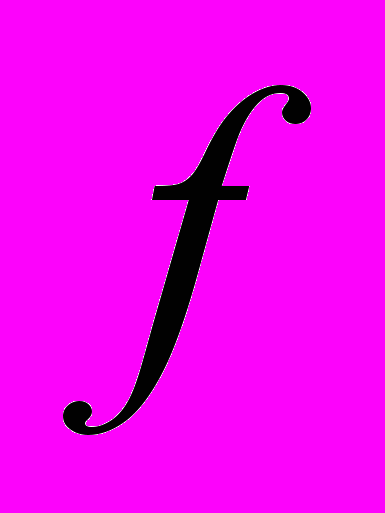принадлежит набору представителей рода ; .

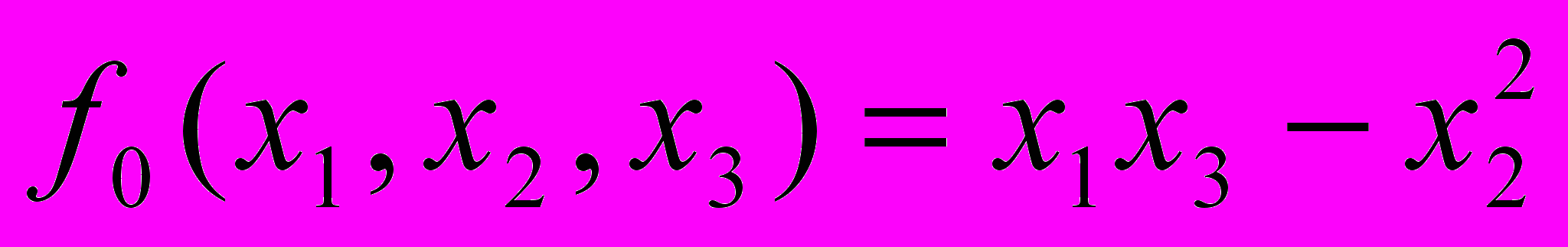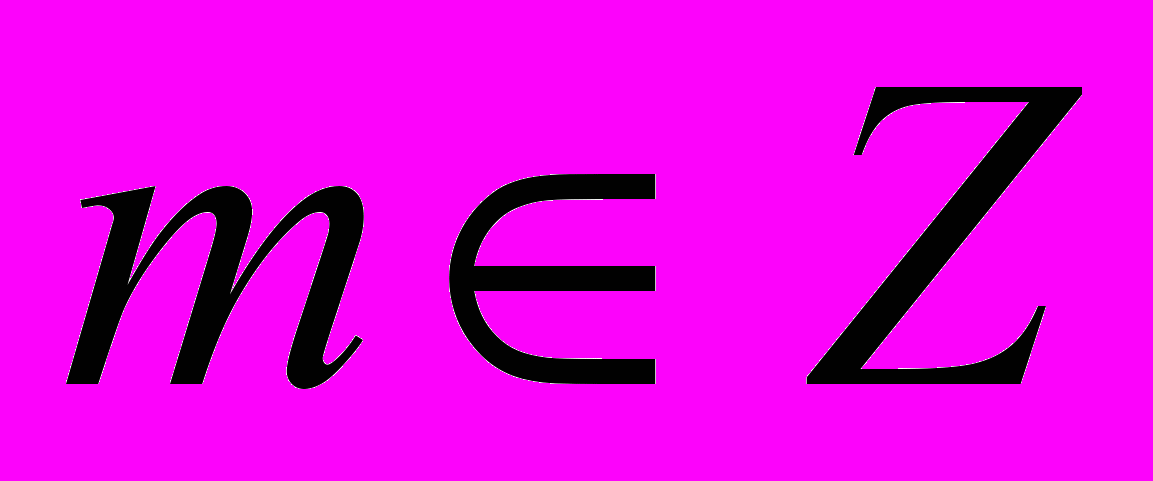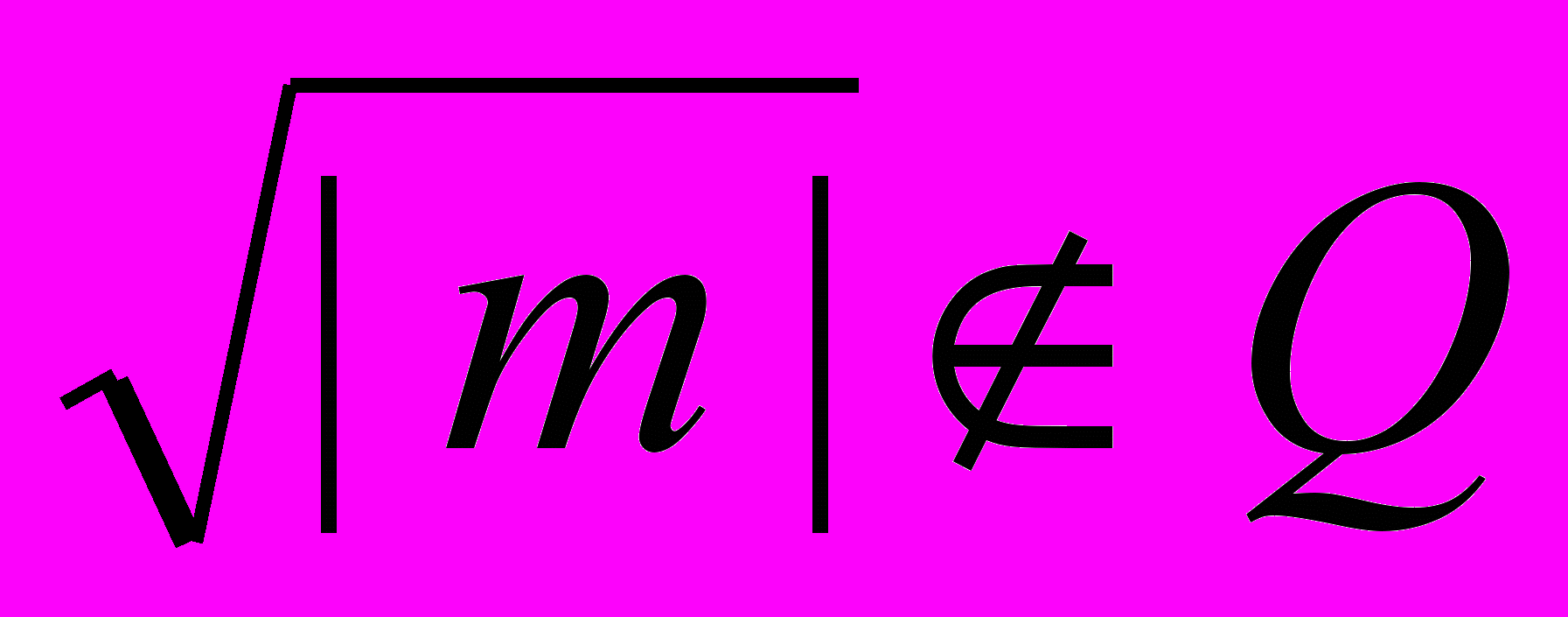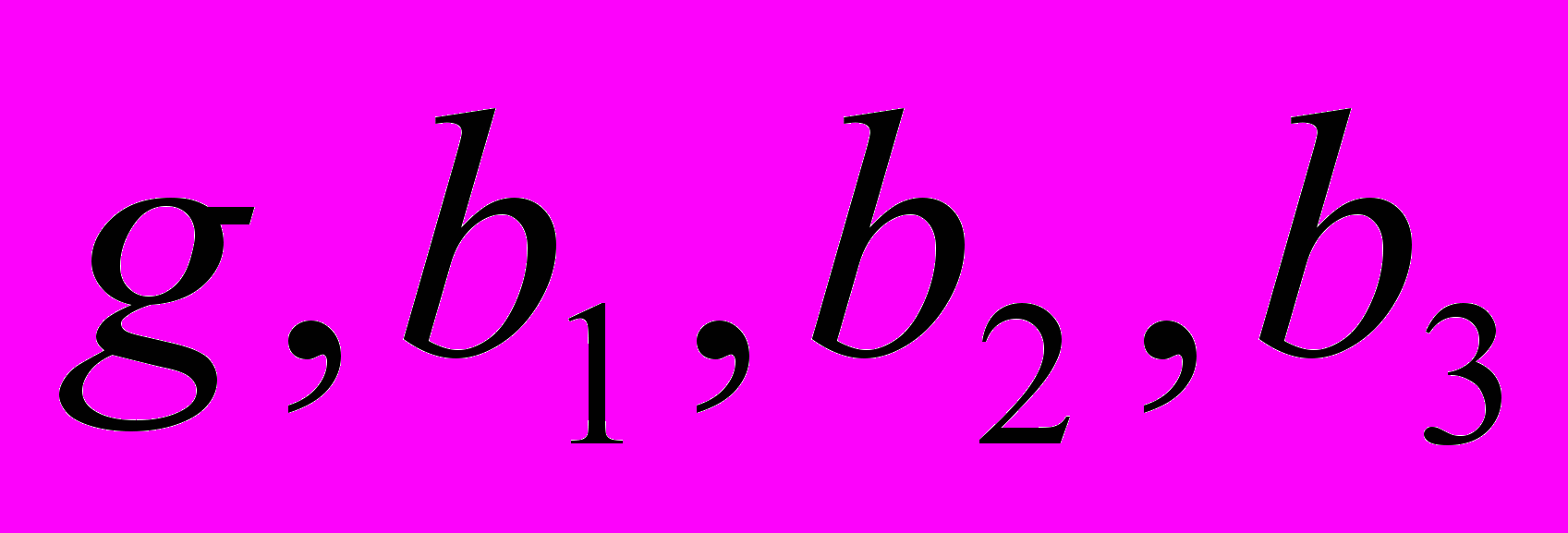Пусть – простое число, , , – целые числа, удовлетворяющие условиям

Н.О.Д.,

,

.

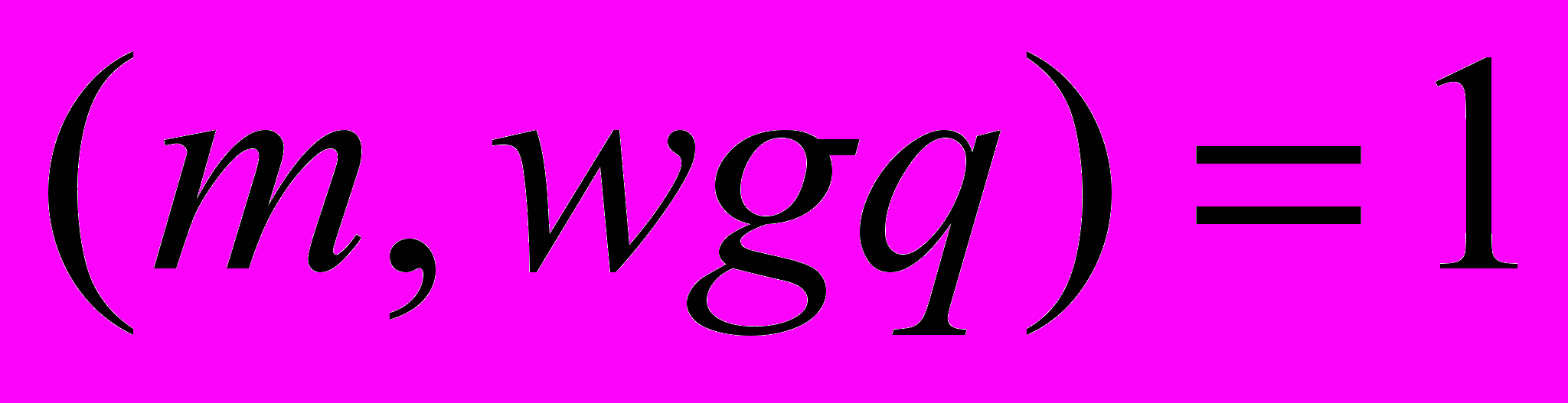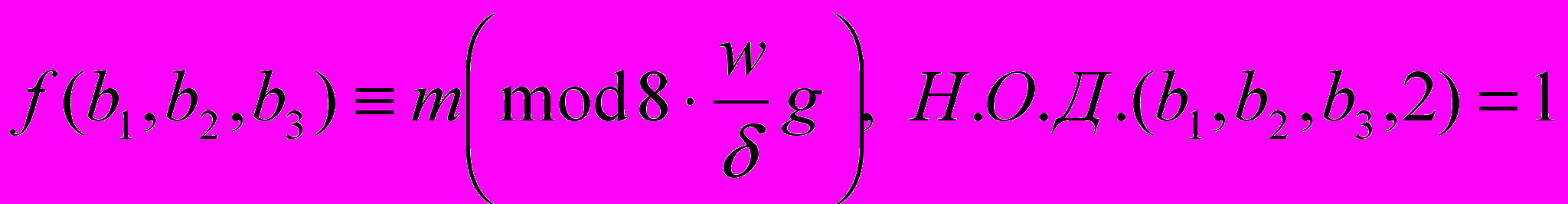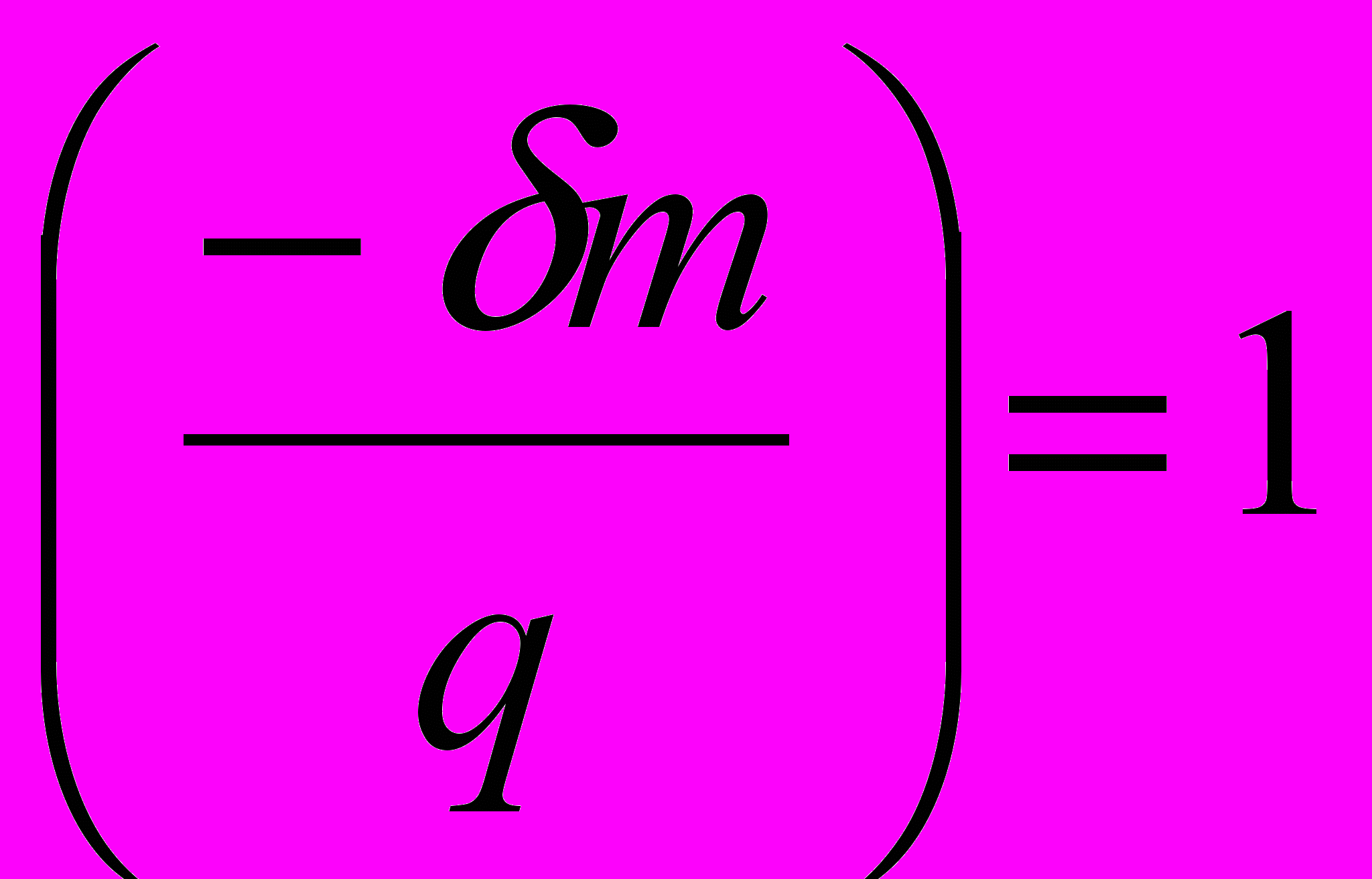Пусть 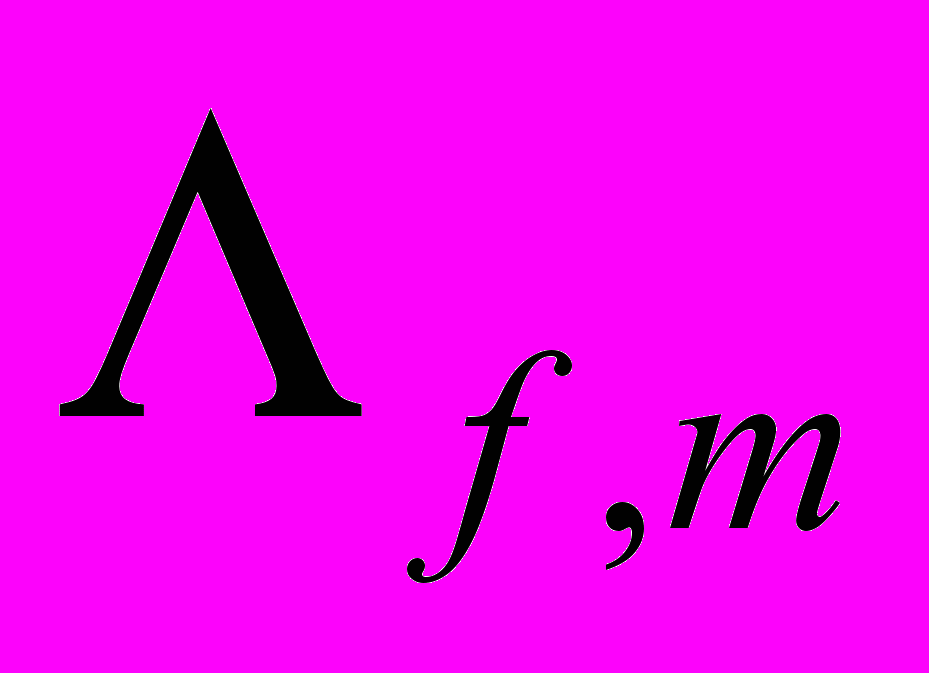– ограниченная квадрируемая область на поверхности гиперболоида

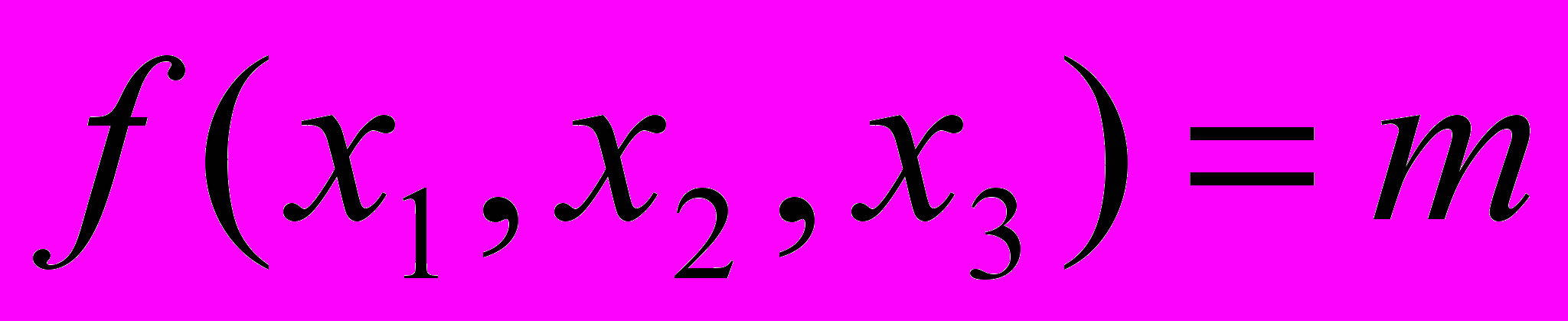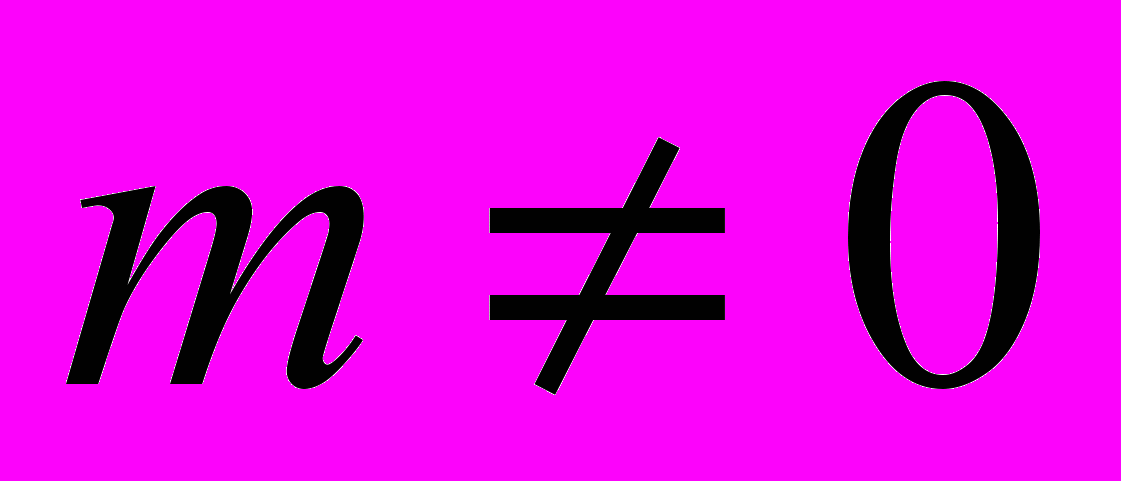, (12)

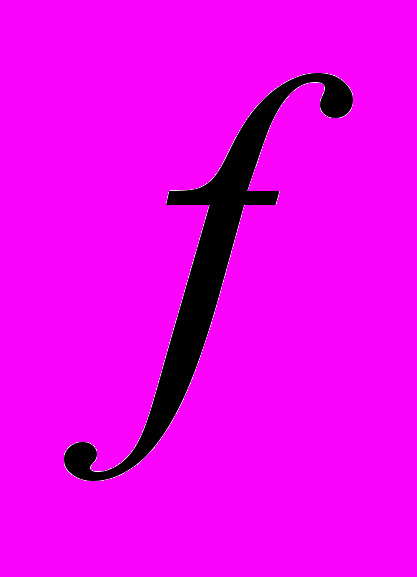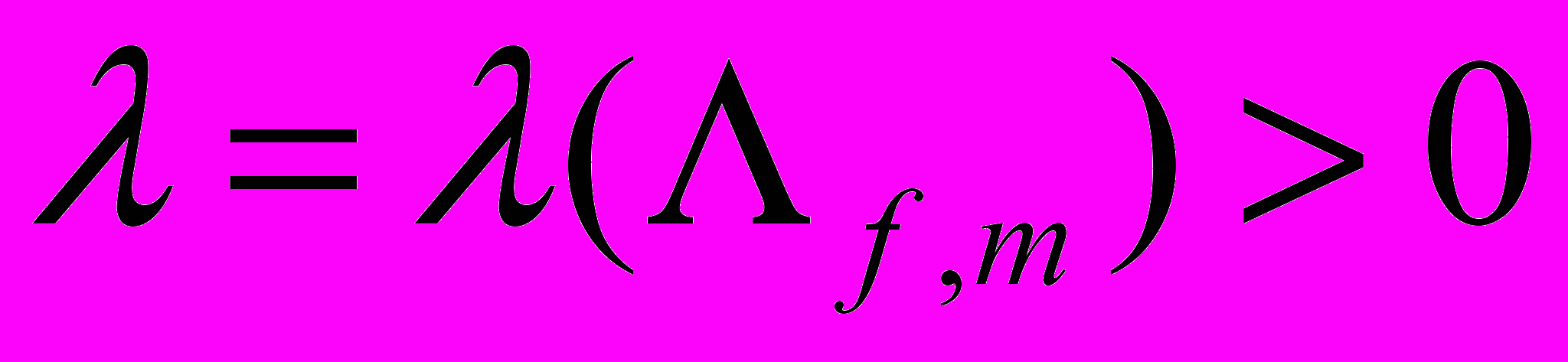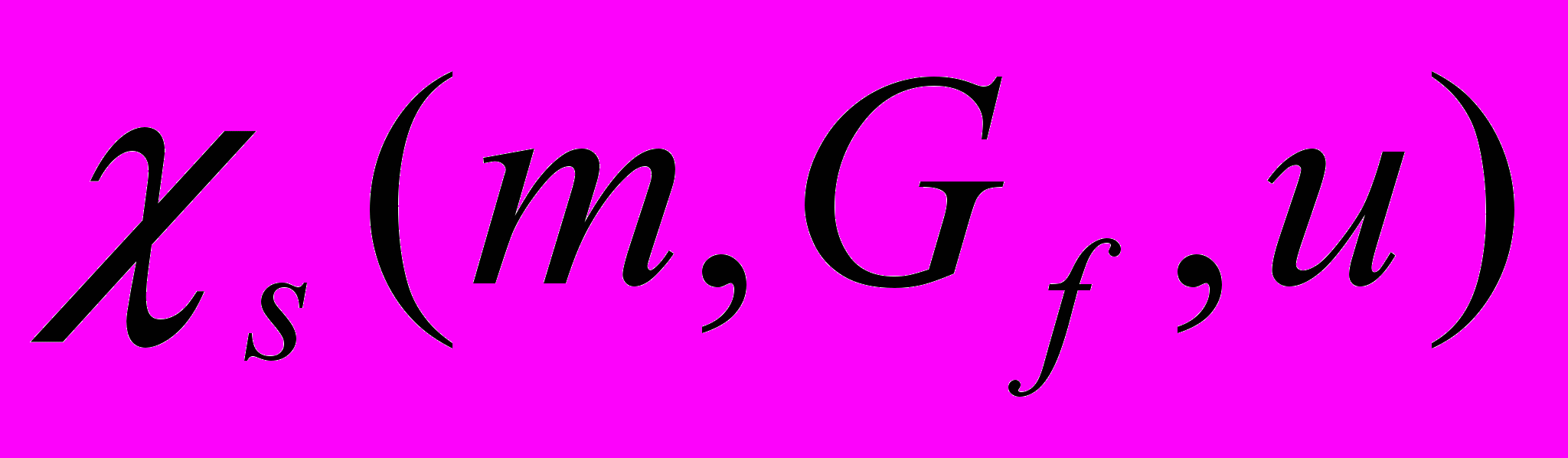с -гиперболической площадью . Рассмотрим часть потока примитивных точек поверхности (3.18), состоящую из цепочек длины .

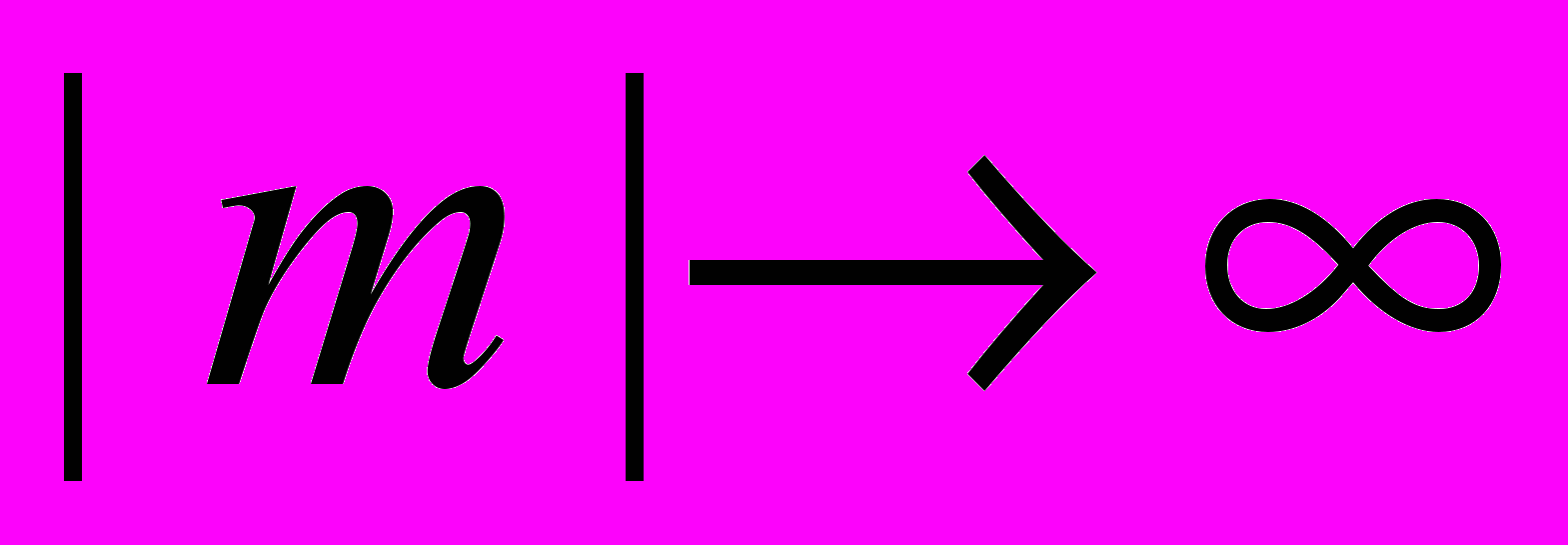
Тогда, если при , где 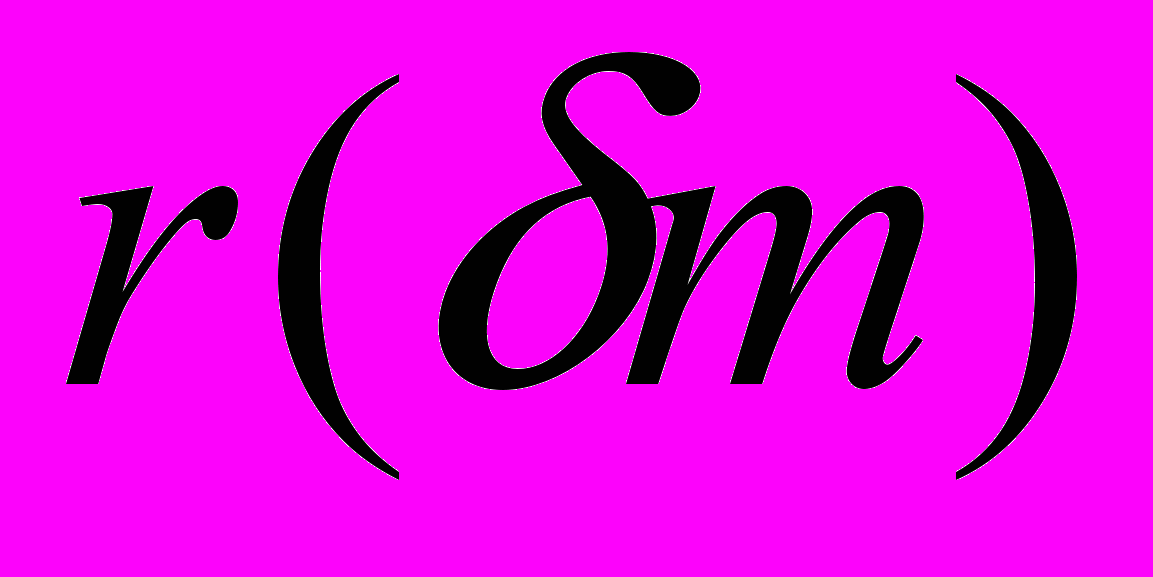– число примитивных приведенных бинарных квадратичных форм определителя , то цепочки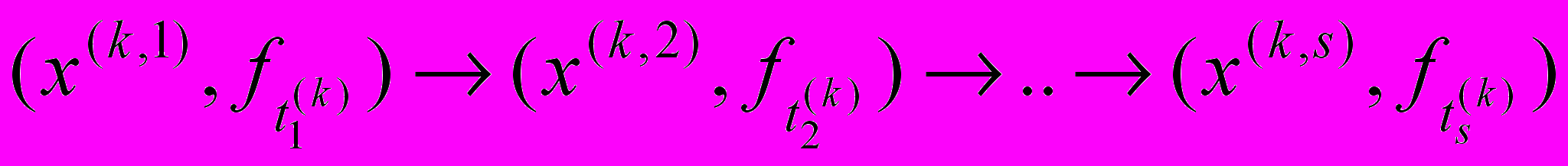

, (13)

() можно разбить на две категории:

а) «хорошие» эргодические цепочки, для которых



=#

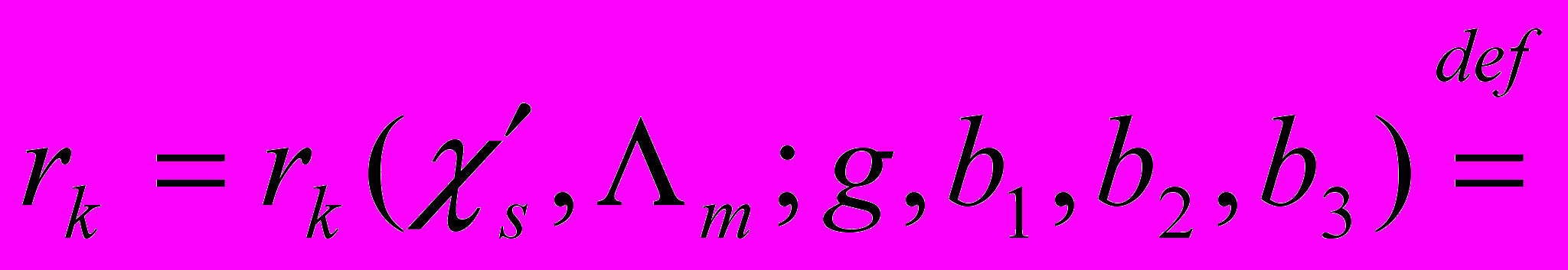
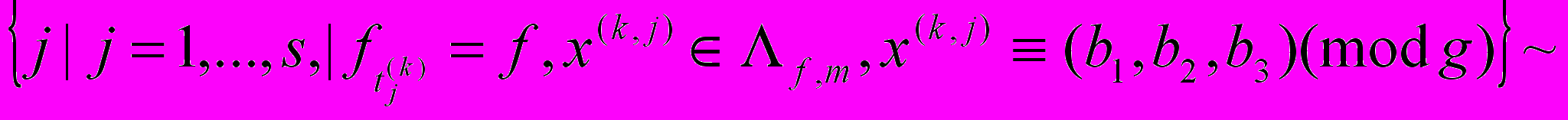
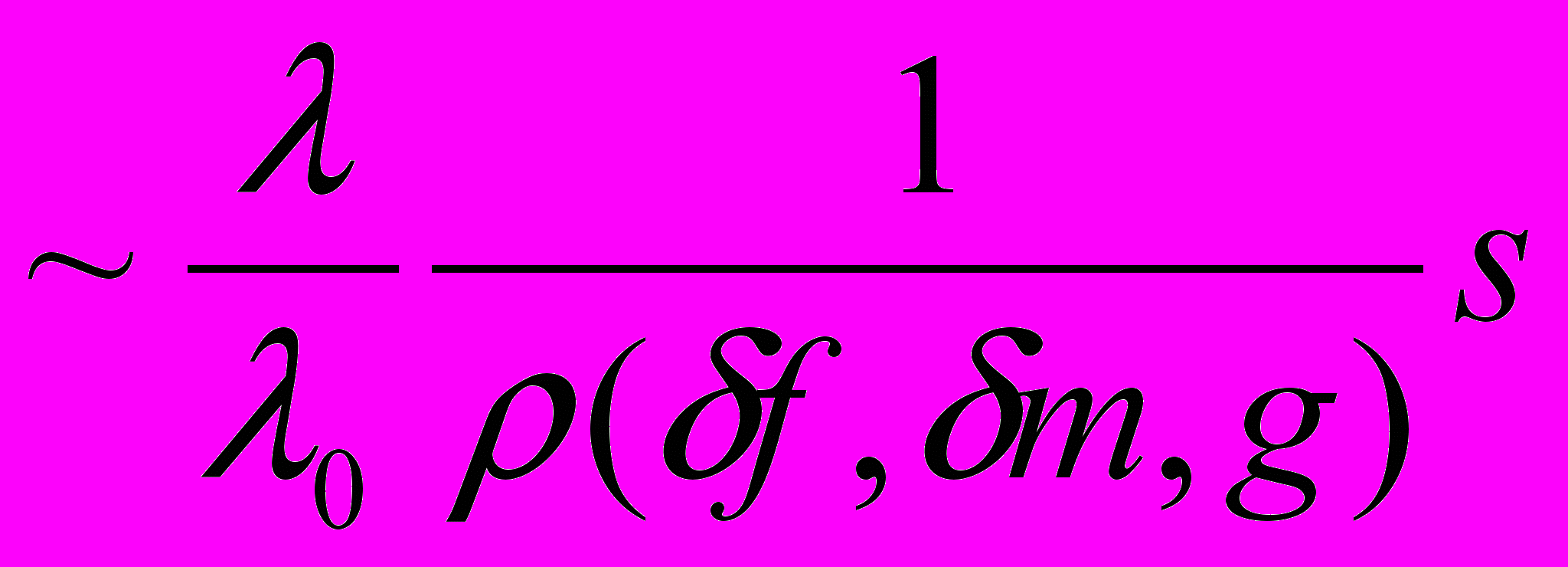, (14)

где - число решений сравнения ; 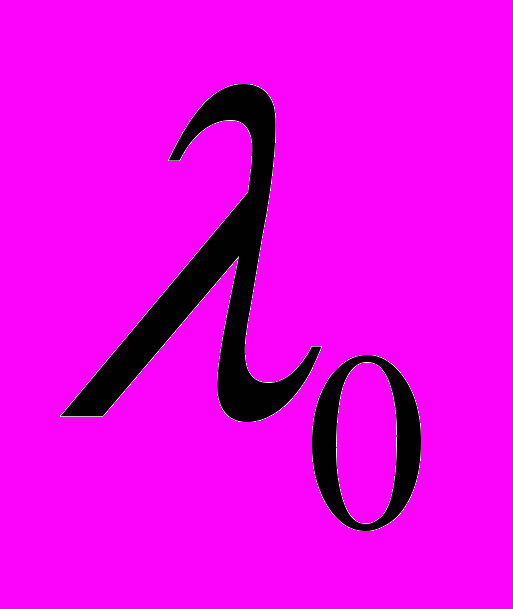– полный 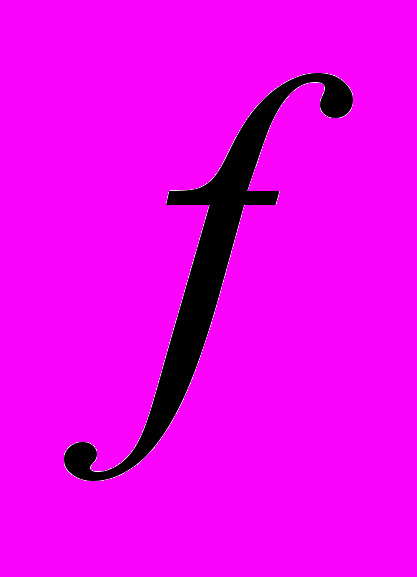-гиперболический телесный угол на поверхности гиперболоида (12)

б) «плохие» цепочки в количестве 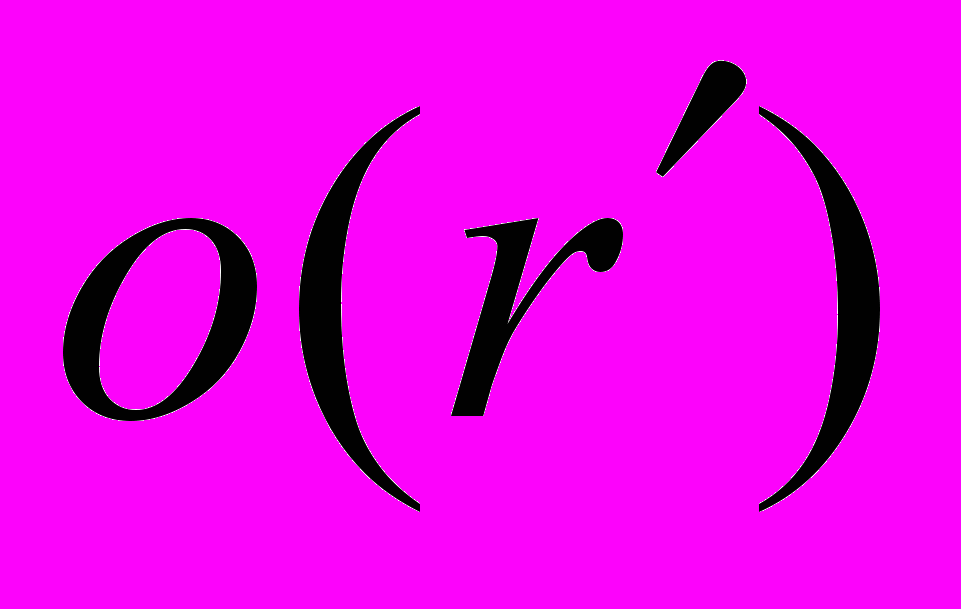, для которых не выполняется (14); постоянные, входящие в (14), зависят только от и .

Эргодическая теорема 3.3 для целых точек на изотропном гиперболоиде в частных случаях пр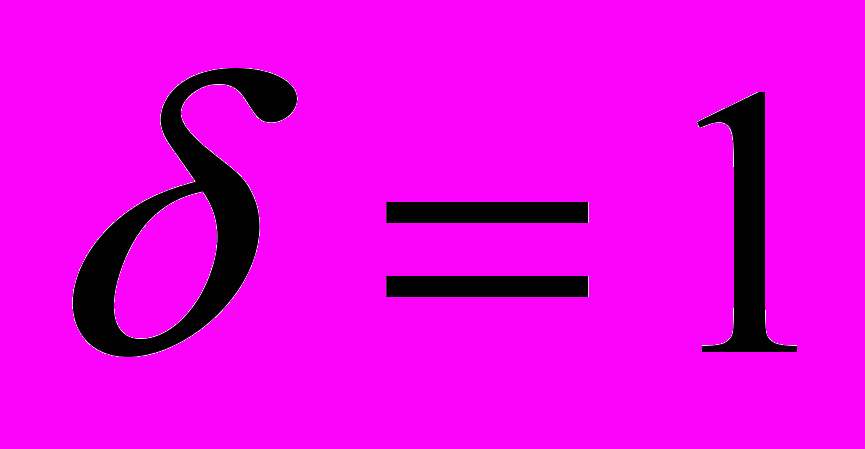и и и 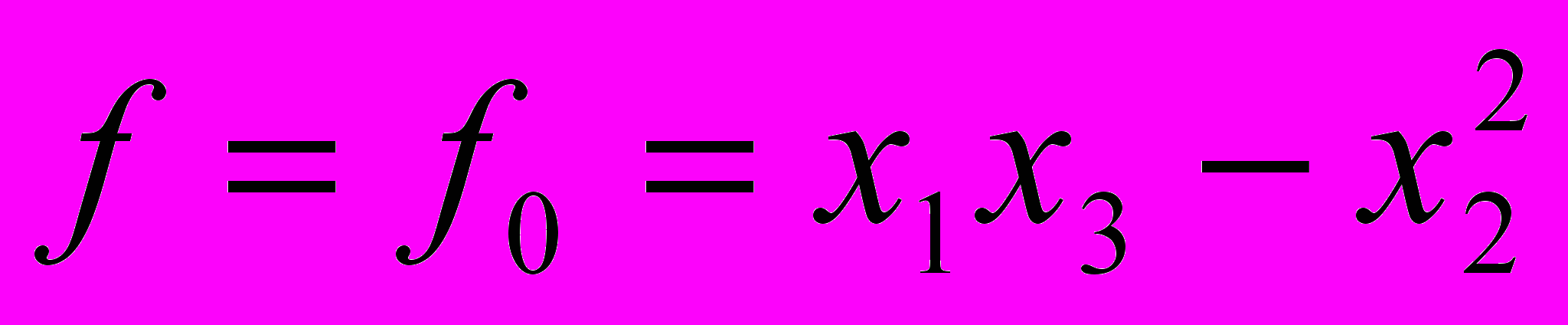дает соответствующие результаты Ю.В. Линника и Б.Ф. Скубенко, а при 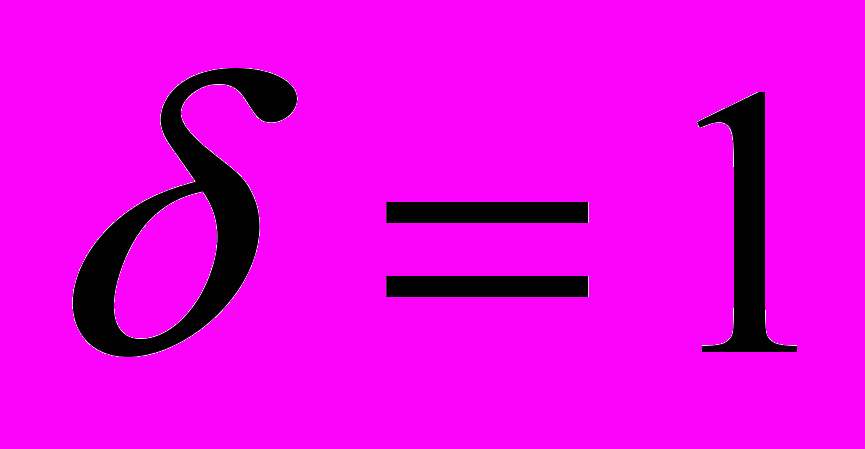и когда форма 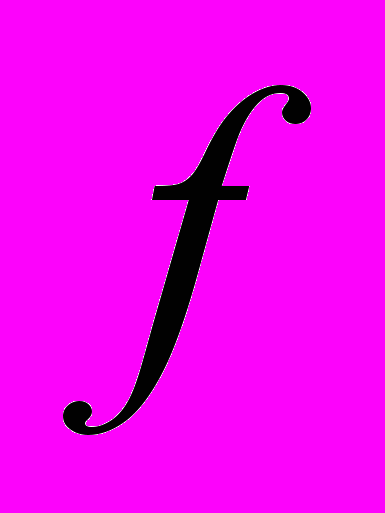имеет сигнатуру [1, 2] (случай двуполостного гиперболоида) из нее получается результат А.В. Малышева1).

На важность рассмотрения эргодических теорем в аналитической теории чисел указывал еще Ю.В. Линник, поскольку помимо их самостоятельного интереса из них как частный случай следуют теоремы об асимптотически равномерном распределении целых точек в смысле соответствующей меры на алгебраических многообразиях, а в применениях к алгебраическим числовым полям такие теоремы дают представление об эргодическом поведении идеалов последовательности алгебраических полей данной степени.

Теорема 3.3 обобщает также результат автора [11], опубликованный в кн. «Актуальные проблемы теории чисел», МГУ, 2002 на случай изотропных тернарных форм произвольного рода, используя при этом построение потока точек не на отдельном гиперболоиде, а на роде изотропных гиперболоидов.

Из эргодической теоремы 3.3 следует так называемая теорема перемешивания для целых точек, занимающая промежуточное положение между эргодической теоремой и теоремой об асимптотической равномерной распределенности целых точек на изотропных гиперболоидах общего вида.

Более того, теорема перемешивания дает усиление теоремы об асимптотическом равномерном распределении целых точек как по областям на поверхности изотропного гиперболоида, так и по классам вычетов по заданному модулю.

В подтверждение сказанного приведем формулировку этого второго основного результата диссертации.

Теорема 3.4. (теорема о перемешивании)

В обозначениях и условиях теоремы 3.3 индексы в цепочках (3.19) можно разбить на две категории:

а) “хорошо перемешивающие” индексы 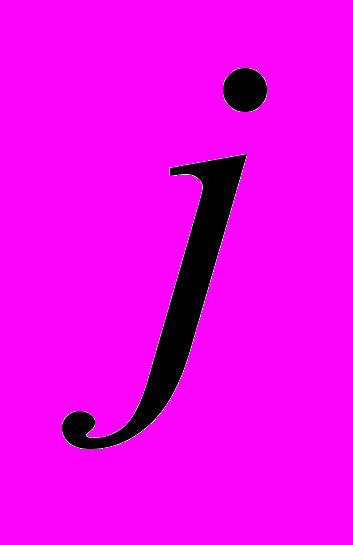, для которых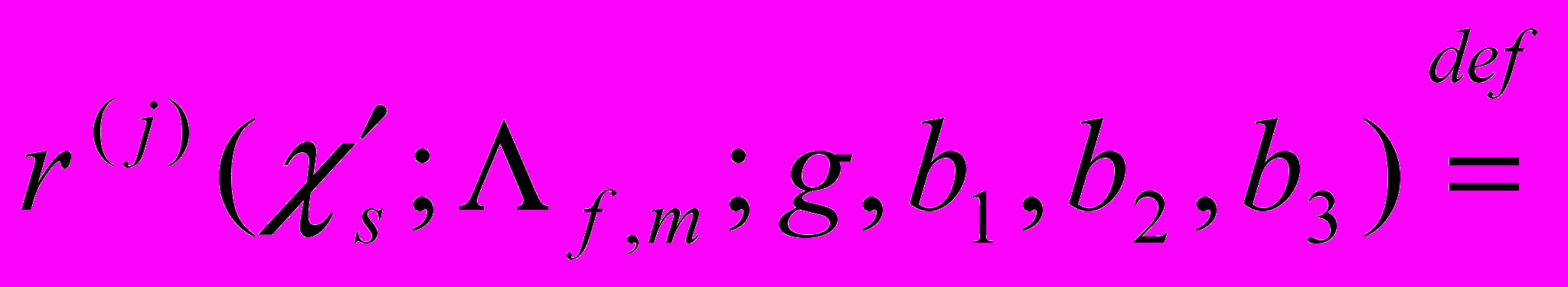



= #~

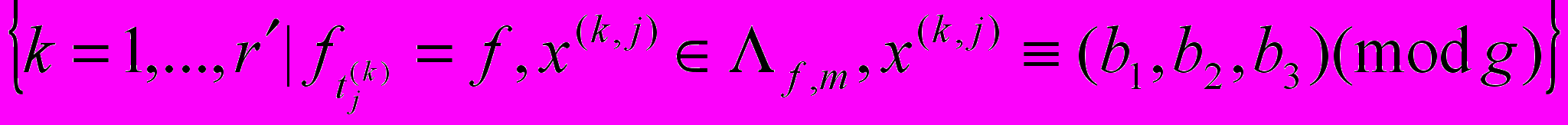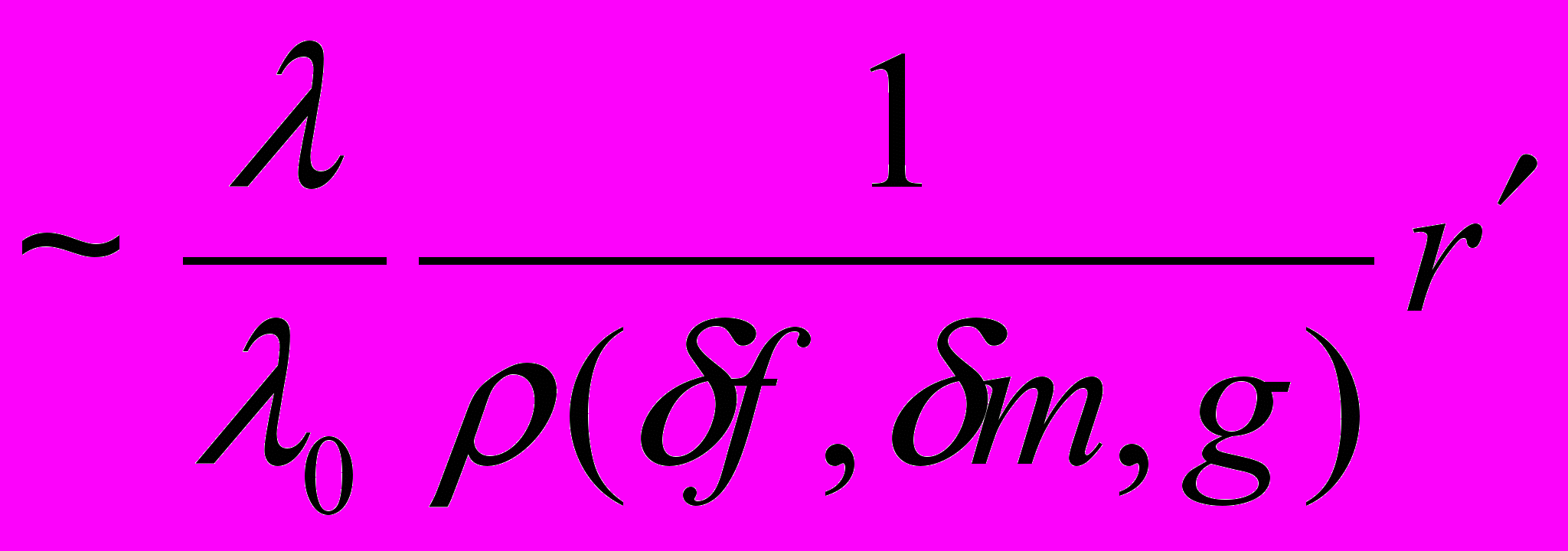, (15)

б) “плохие” индексы 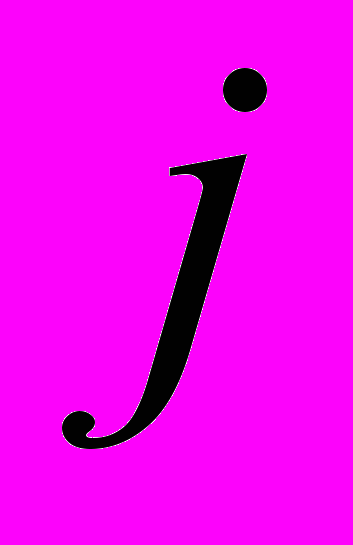в количестве 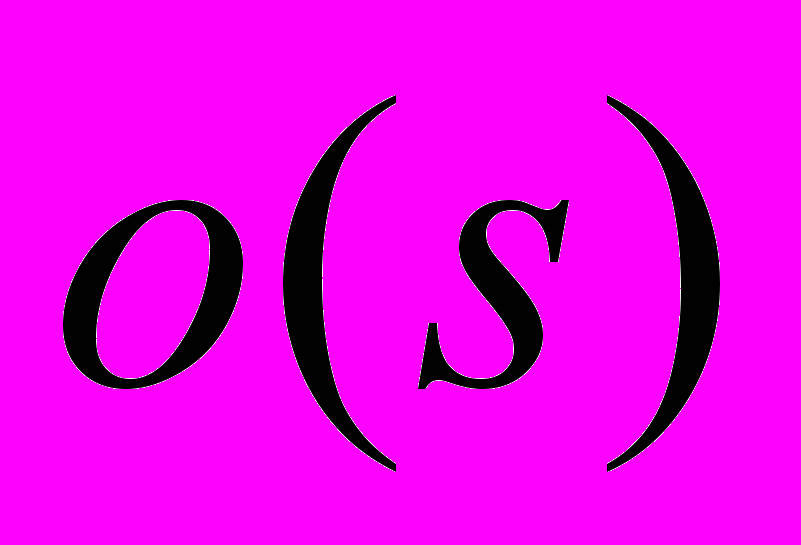, для которых не выполняется (15).

Смысл теоремы 3.4 состоит в том, что число целых точек на изотропном гиперболоиде, содержащихся в j-ом «сечении» цепочек (13) пропорционально числу цепочек в этом потоке, если (коэффициент пропорциональности указывается в (15)).

Теорема 3.4 о перемешивании является более общей теоремой распределения целых примитивных точек на изотропном гиперболоиде, т.к. из нее уже непосредственно выводится теорема об асимптотически равномерном распределении целых точек на таком гиперболоиде как по областям на его поверхности, так и по классам вычетов по заданному модулю. Действительно, фиксируя в теореме 3.4 «хорошо перемешивающий» индекс 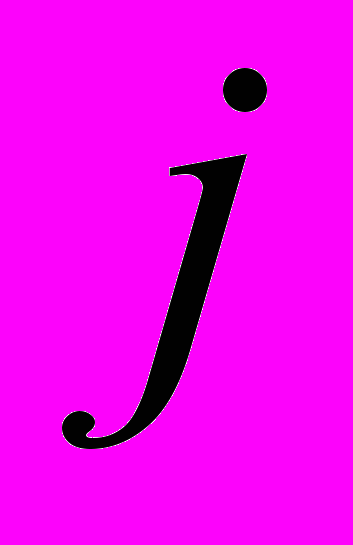, и применяя ее к потоку (13) и к множеству примитивных точек изотропного гиперболоида, отображающихся в область приведения на простейшем гиперболоиде и обозначая 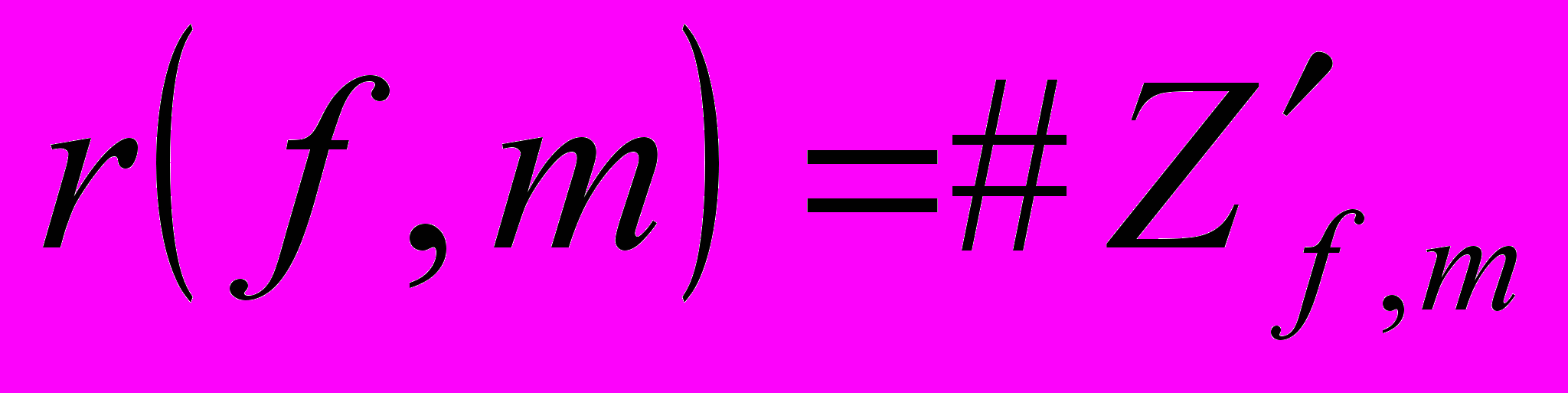, то с учетом инвариантности множества относительно операции Т, производящей повороты целых примитивных точек в цепочках потока (13), получаем следующие основные результаты (теоремы 3.5 и 3.6) об асимптотически равномерном распределении целых точек на изотропном гиперболоиде из статьи [1].

Теорема 3.5. (о равномерном распределении целых точек на изотропном гиперболоиде).

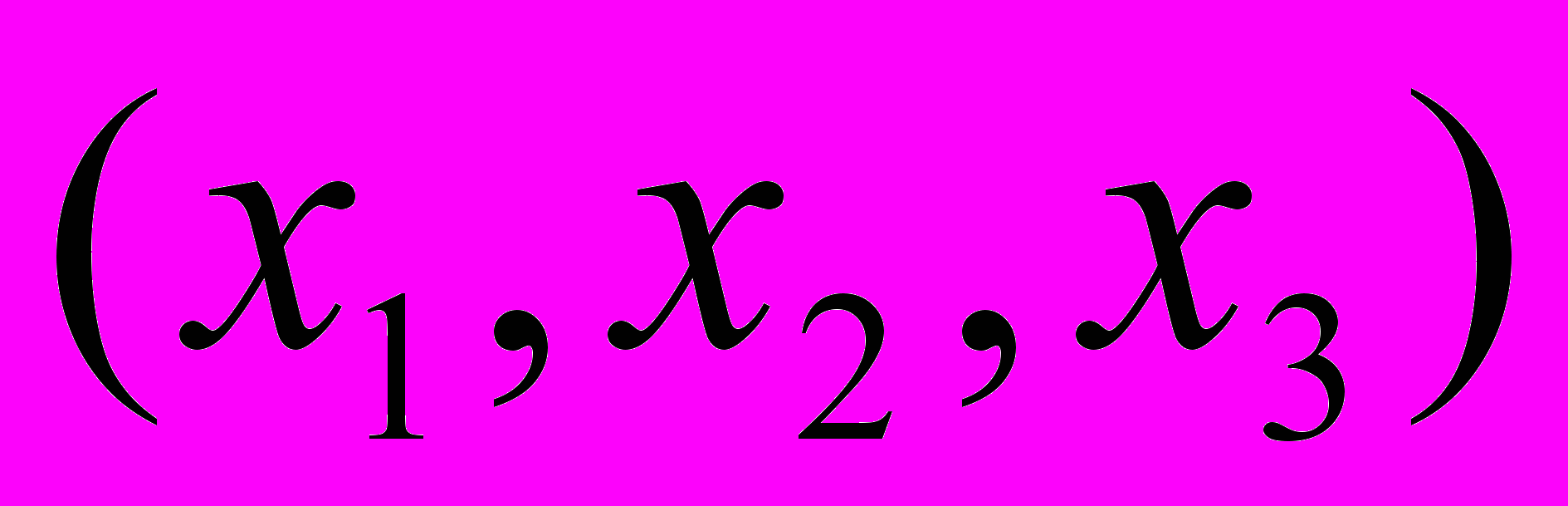В условиях теорем 3.3 и 3.4 пусть - число всех целых примитивных точек на изотропном гиперболоиде , удовлетворяющих условиям

.

Тогда при

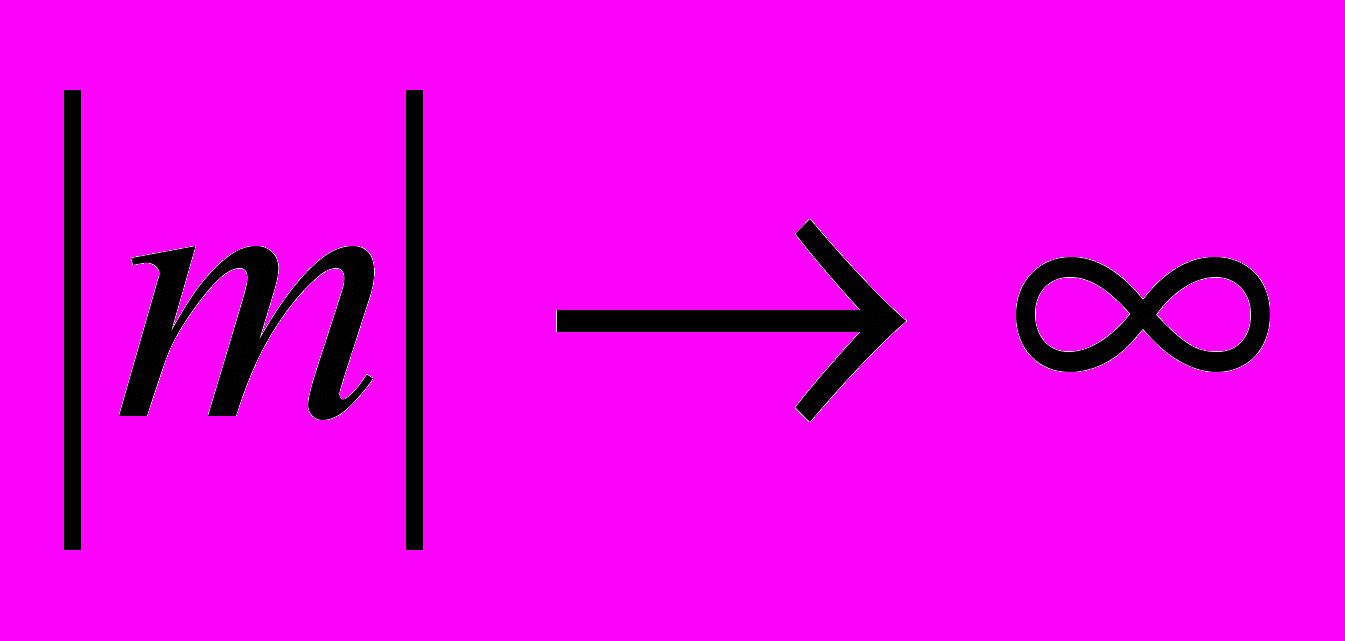
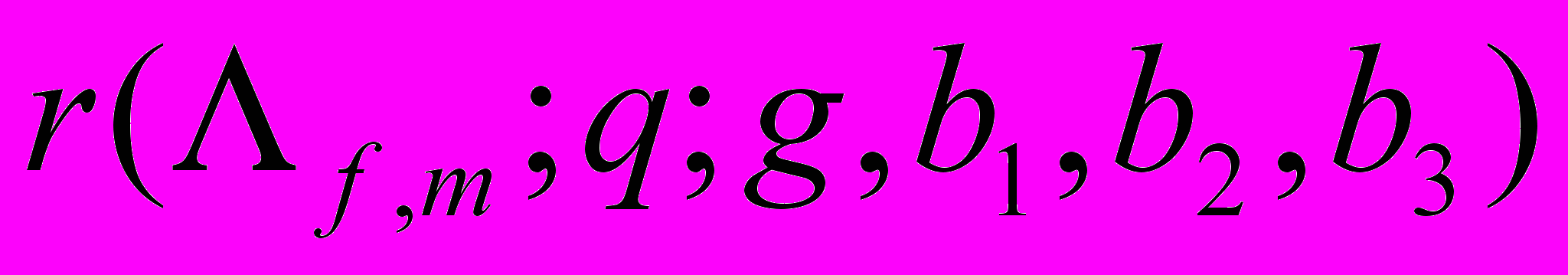~ , (16)

где 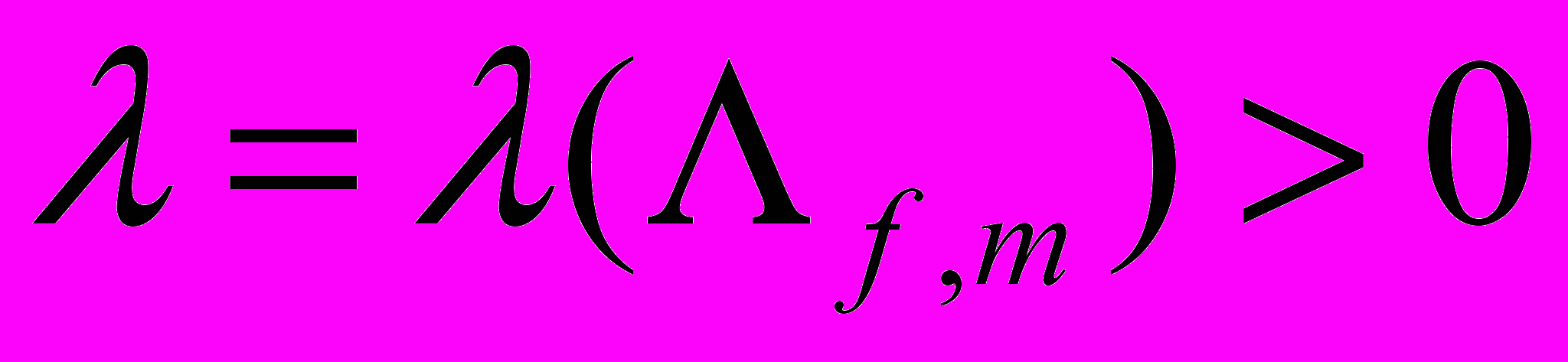– 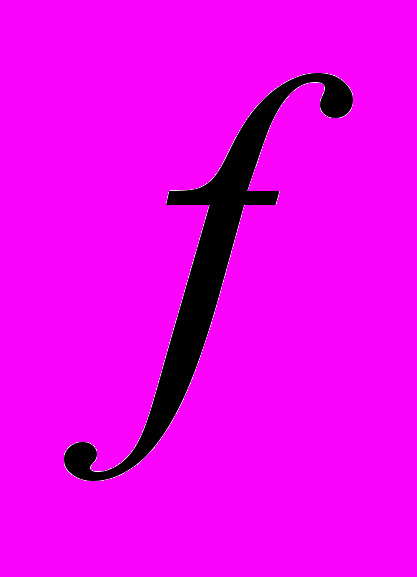-гиперболическая мера (площадь) области 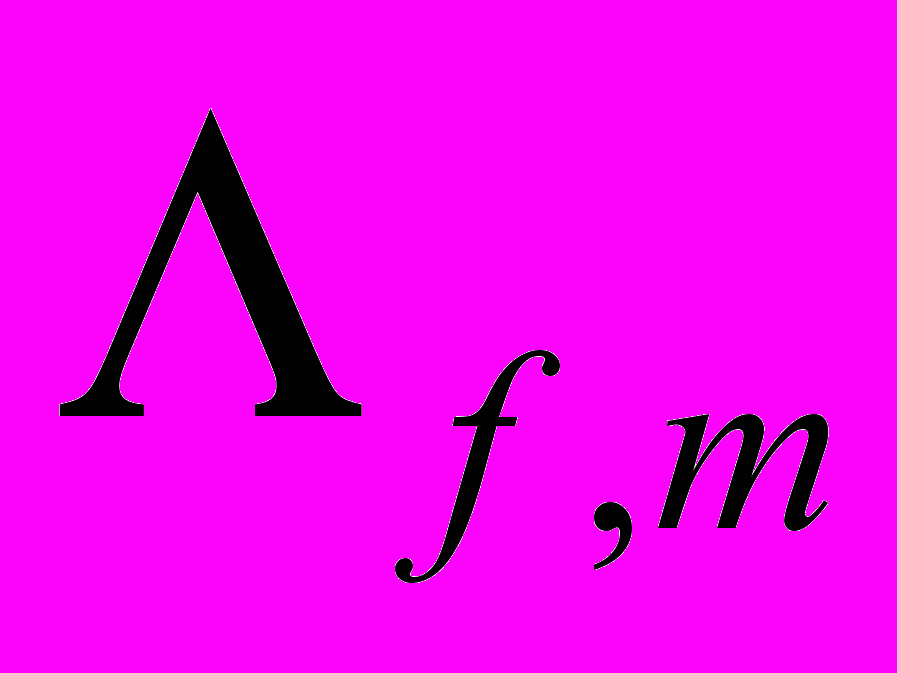; 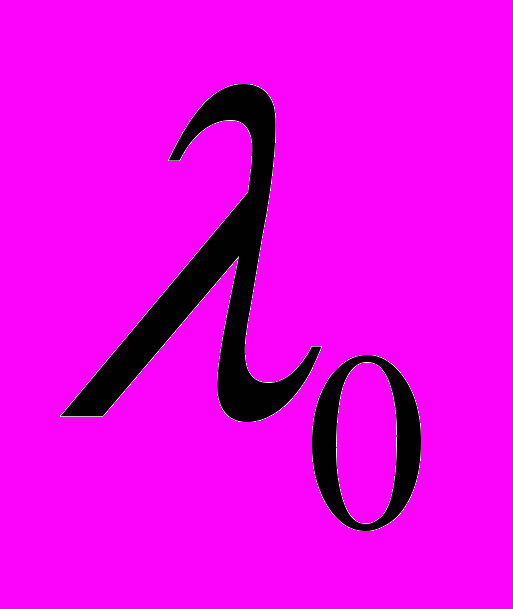– полный 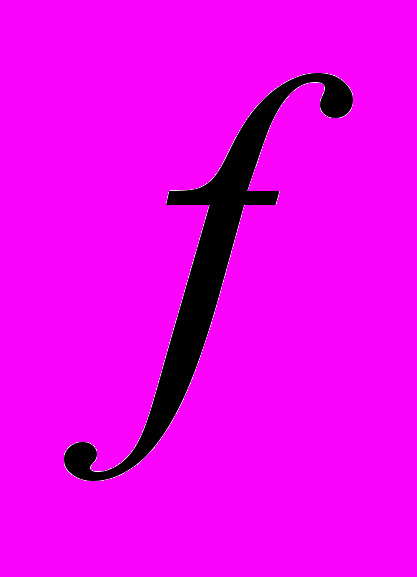-гиперболический телесный угол; 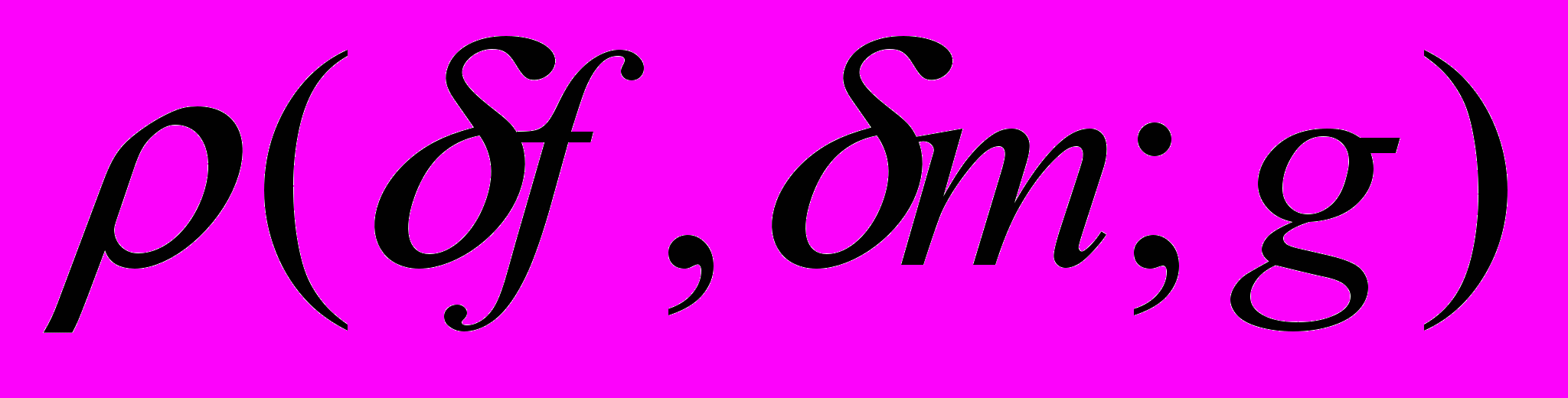– число решений сравнения 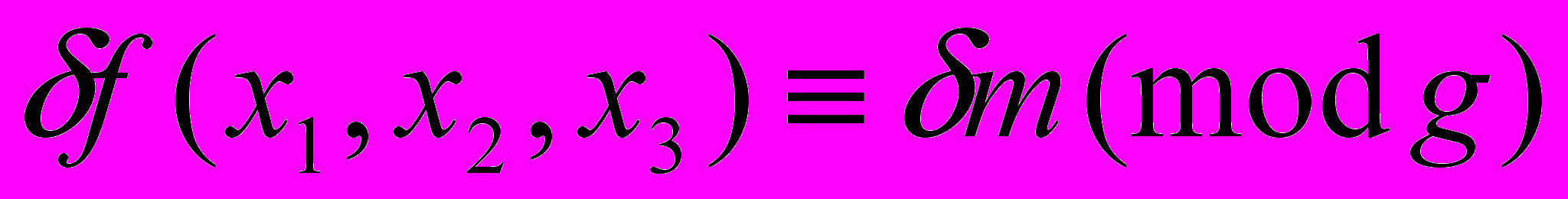; ; 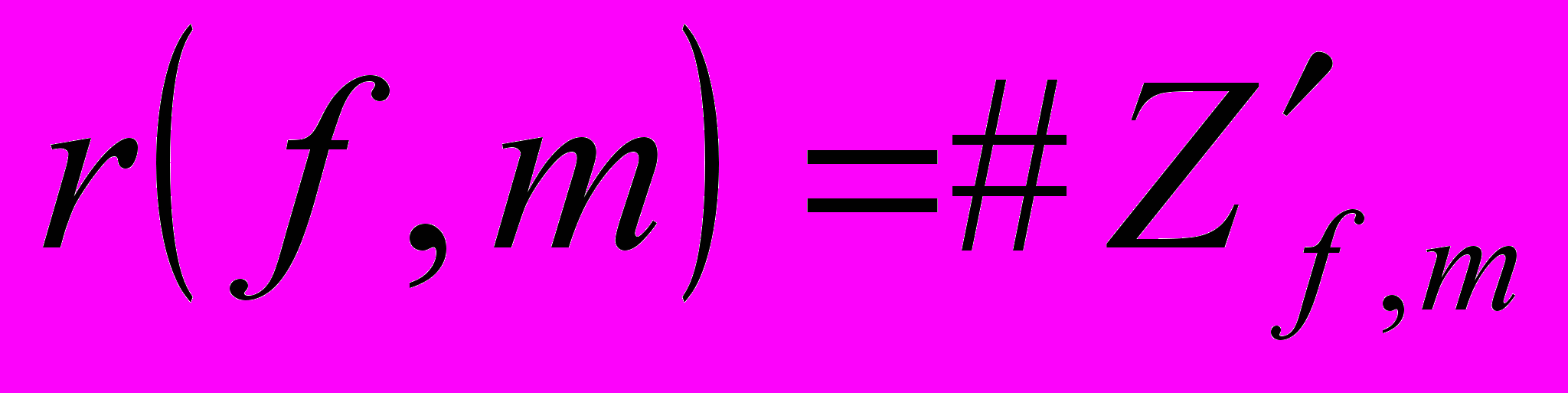постоянные, входящие в асимптотическую формулу (16), зависят только от и .

Теорема 3.5 обобщает результаты Ю.В. Линника (случай 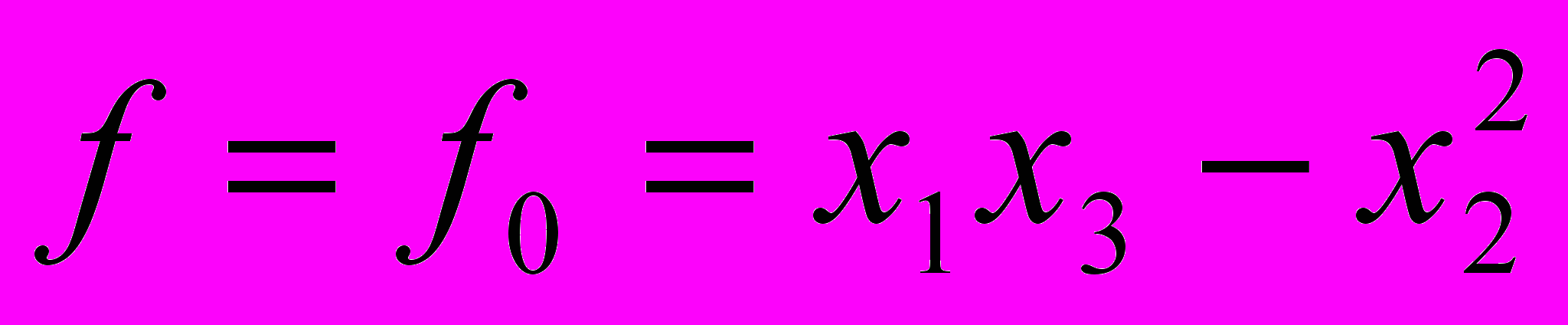, , 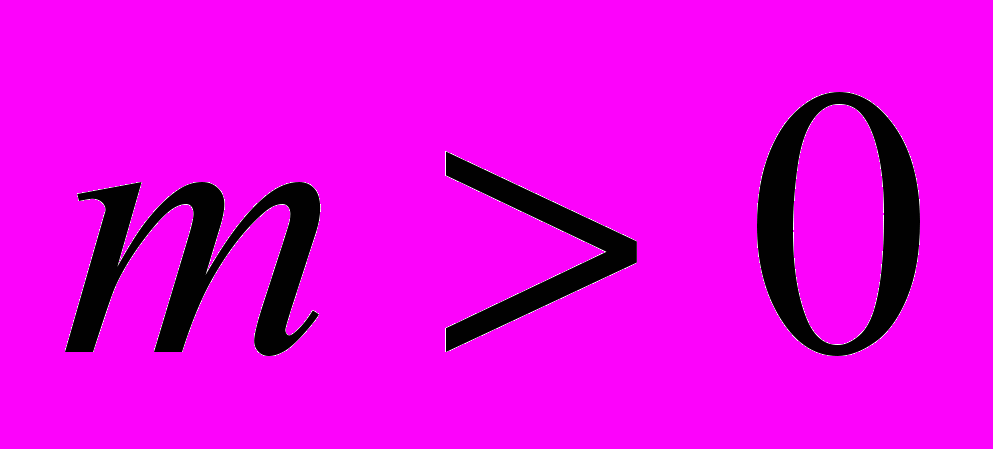, 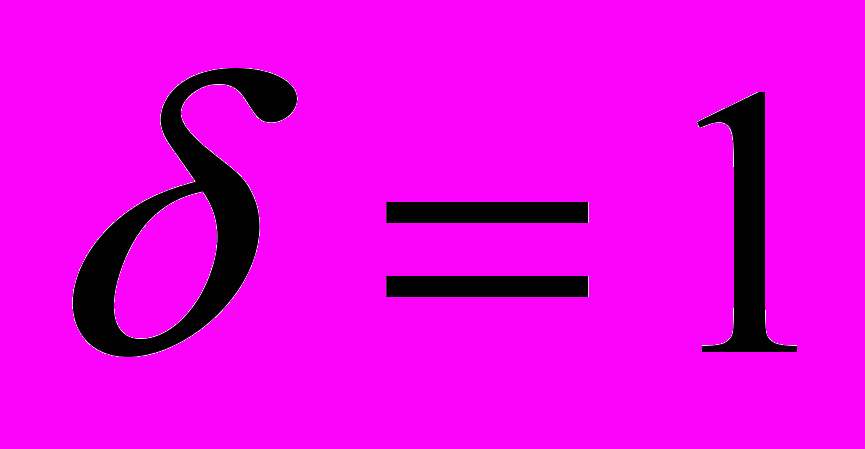), Б.Ф. Скубенко (случай 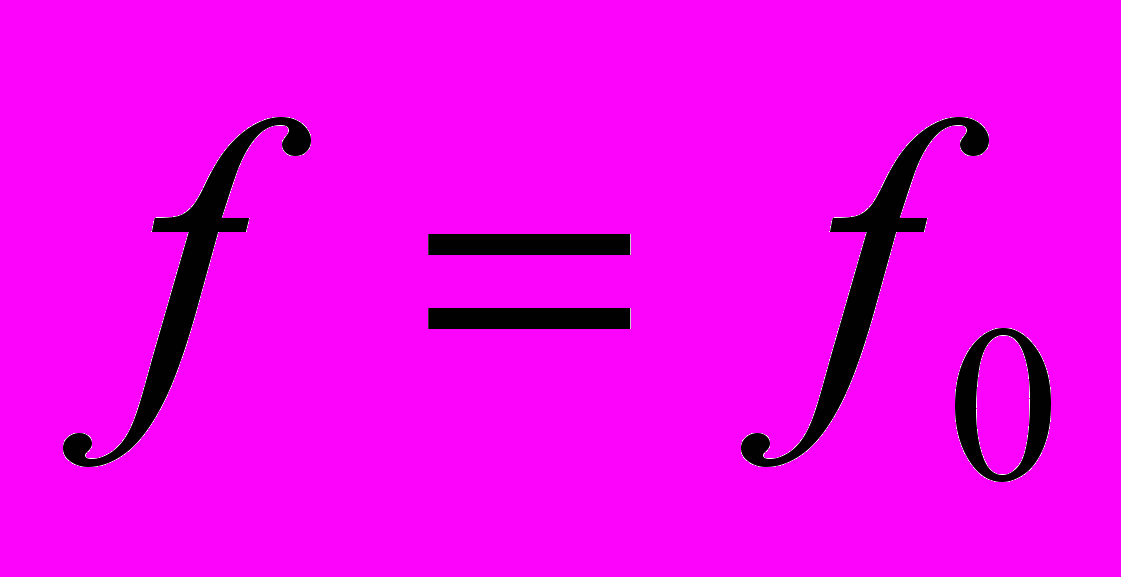, , 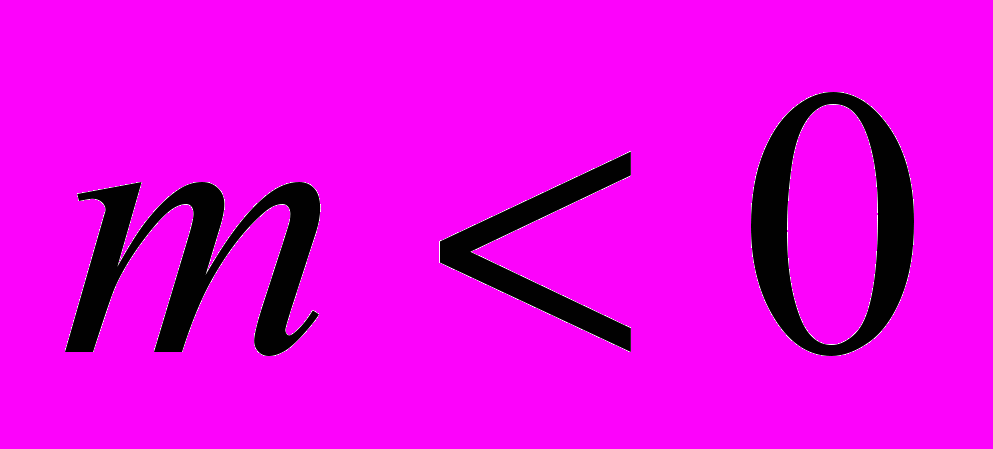, 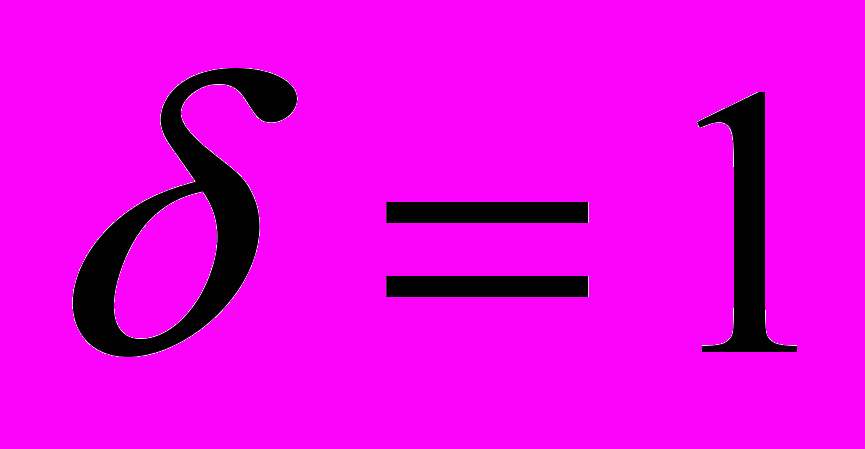), А.В. Малышева (случай 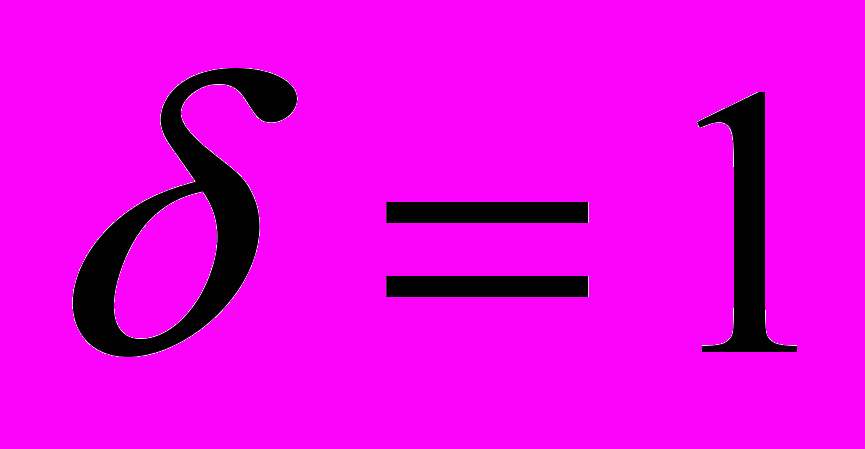, двуполостный гиперболоид, 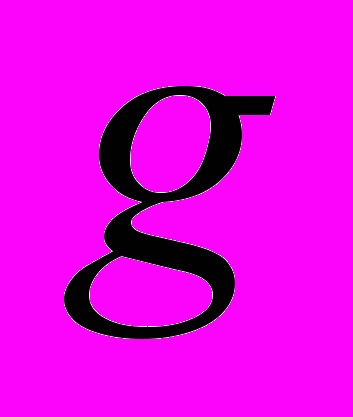– любое нечетное число, взаимно простое с 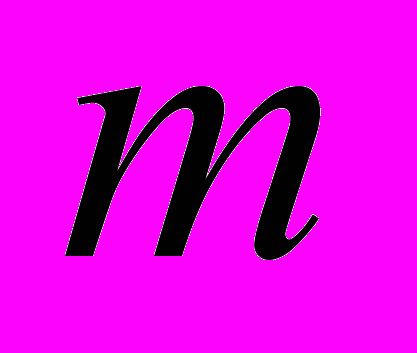) и его учеников Нгуен Нгор Гой1) и Карпова А.Н.2) (случай 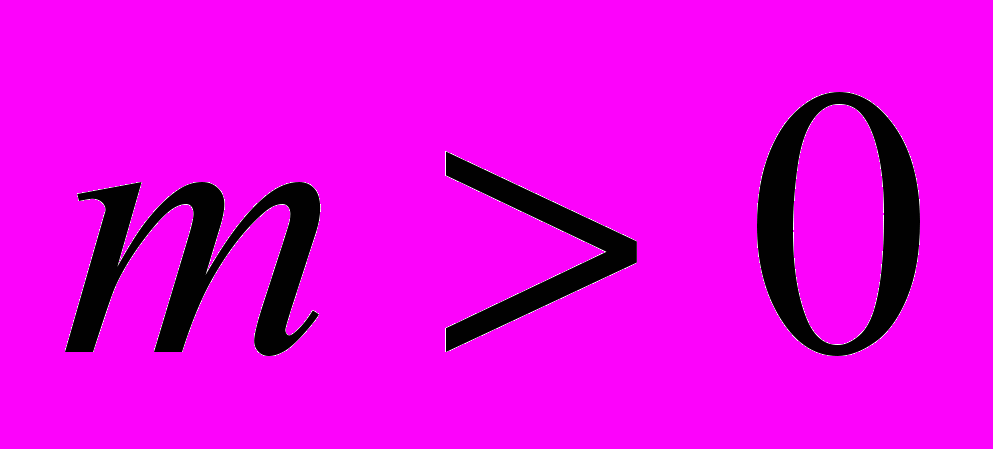, т.е. только двуполостного гиперболоида).

Успех в получении полного решения вопроса о представлении целых чисел изотропными тернарными квадратичными формами общего вида связан в первую очередь с использованием соотношения, характеризующего любую изотропную форму, а также с нашим построением потока примитивных точек на наборе гиперболоидов рода изотропной тернарной квадратичной формы 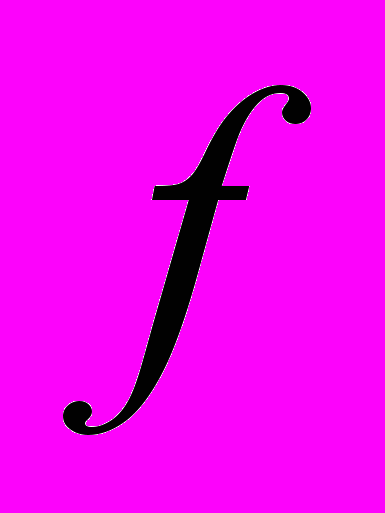и наконец, с использованием ключевой леммы дискретного эргодического метода (ДЭМ) для вектор-матриц второго порядка любой нормы , охватывающей оба случая простейших гиперболоидов.

Другой вариант теоремы 3.5, имеющий более развернутый вид, получен нами также независимо от рассуждений, использованных в доказательстве теоремы 3.5 (см. [1]).

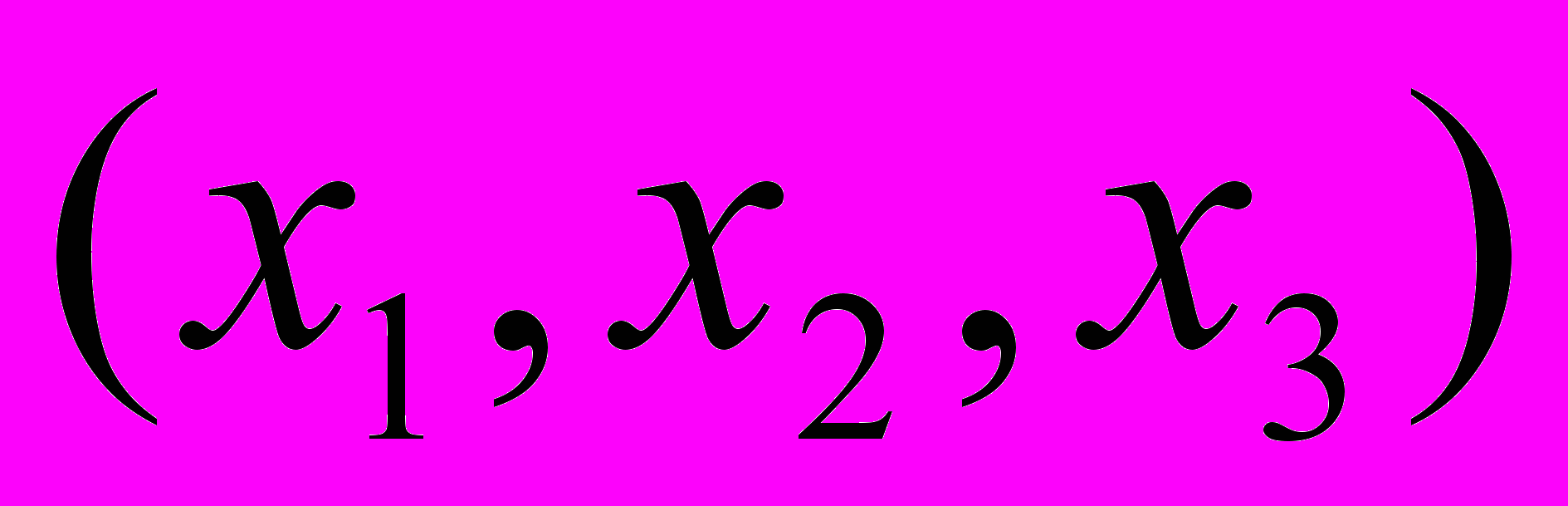Теорема 3.6. В условиях теорем 3.3 и 3.4 пусть – число всех целых примитивных точек на изотропном гиперболоиде , удовлетворяющих условиям

. (17)

Тогда при

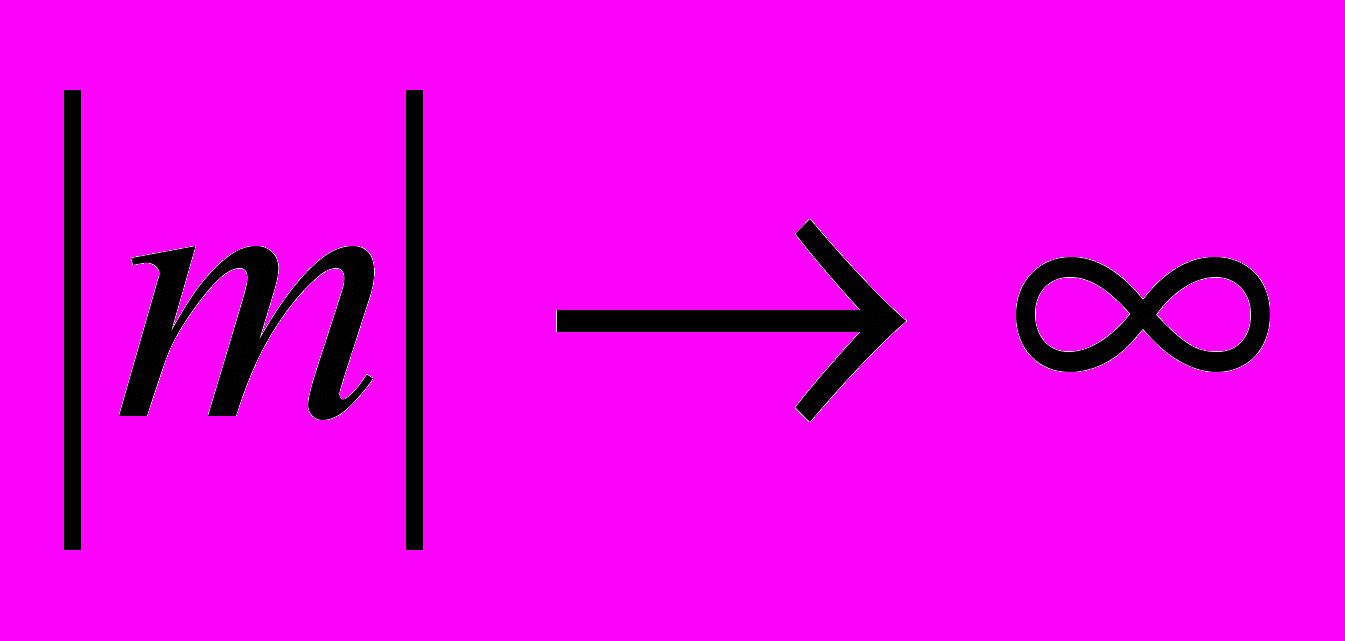
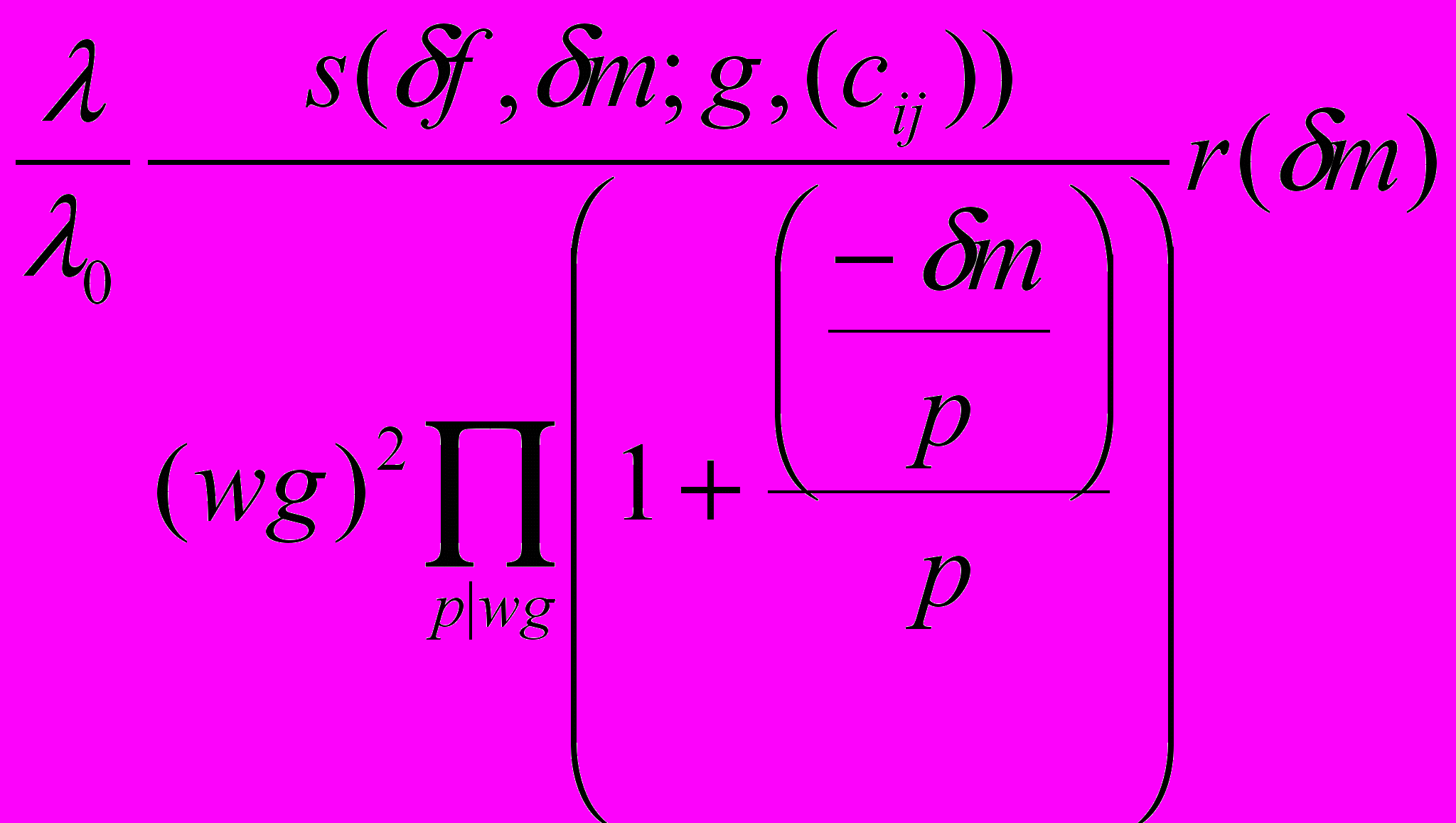~ , (18)

где 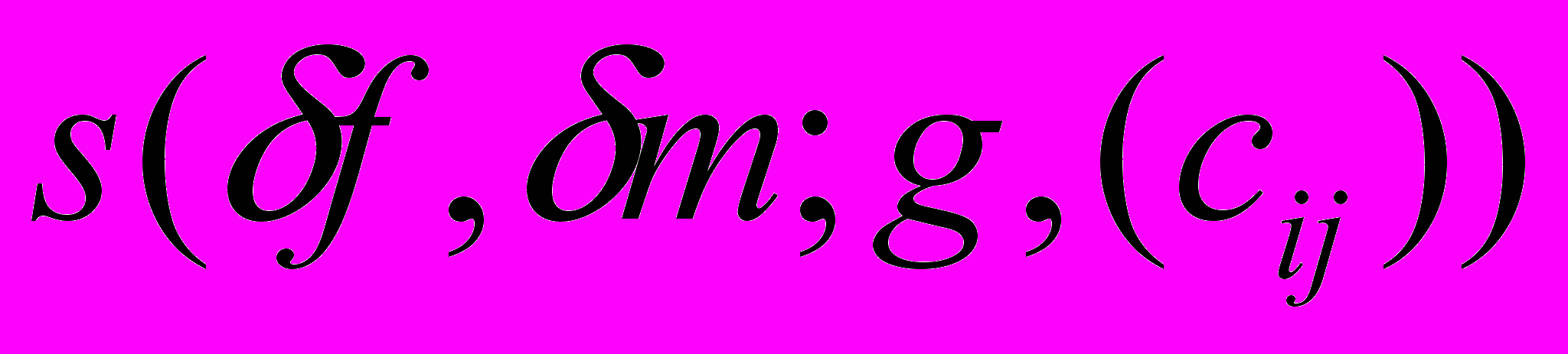равно числу решений 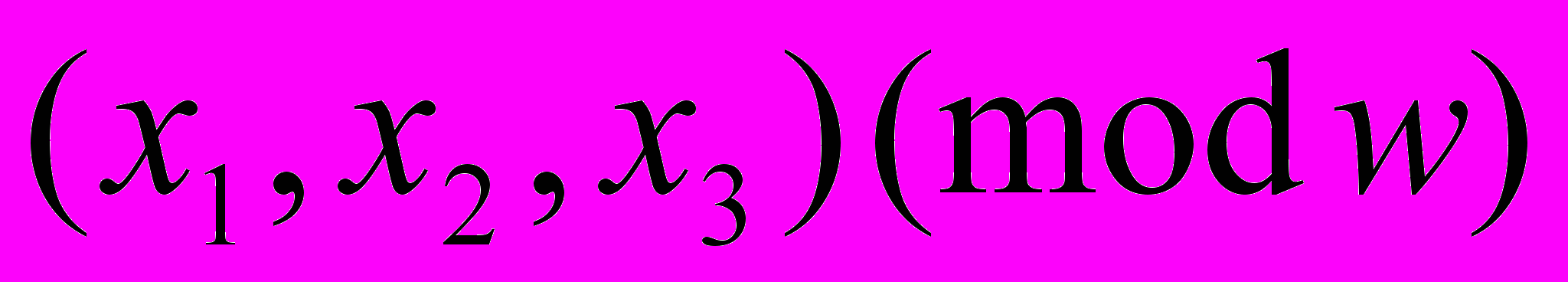сравнения

,

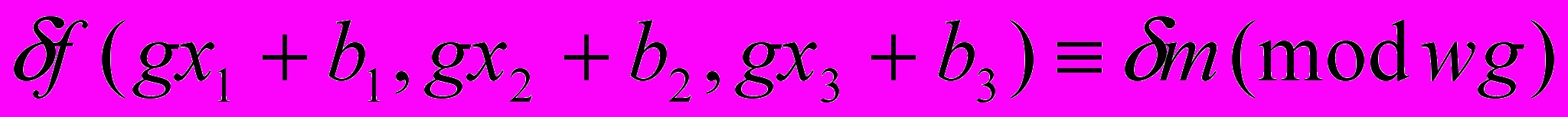для которых точки 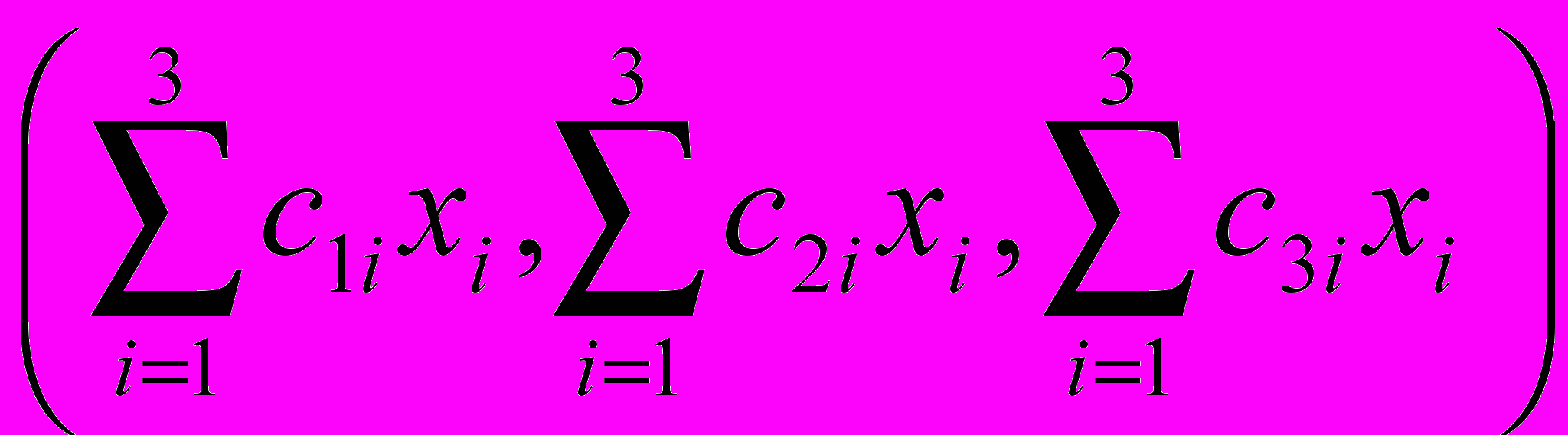различны 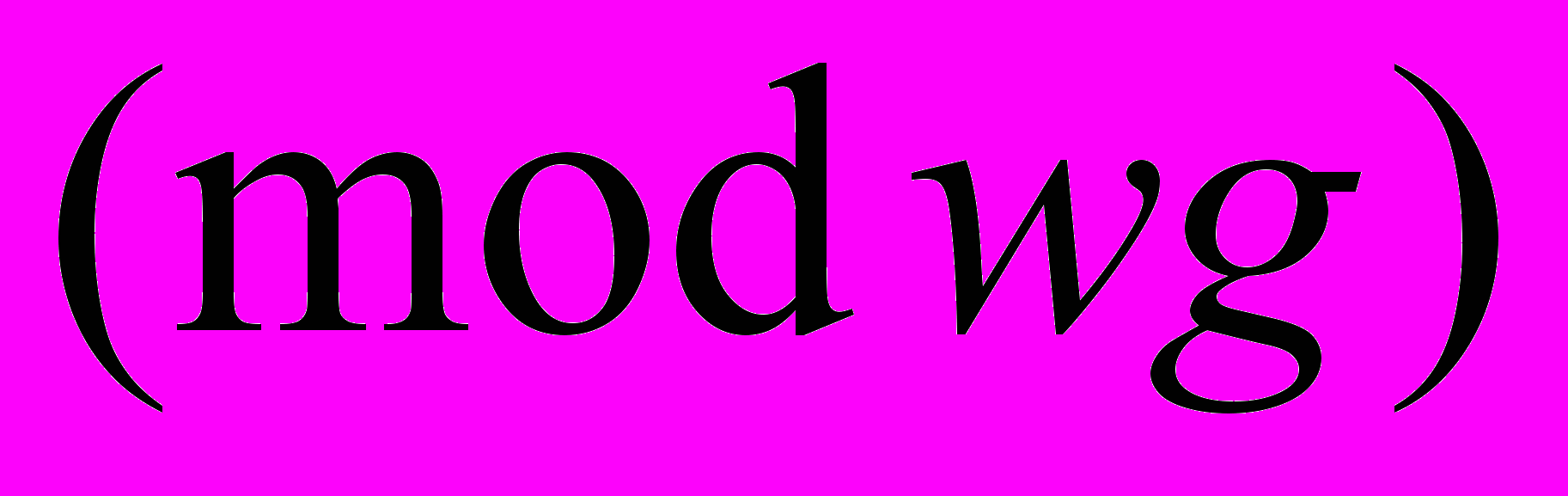, 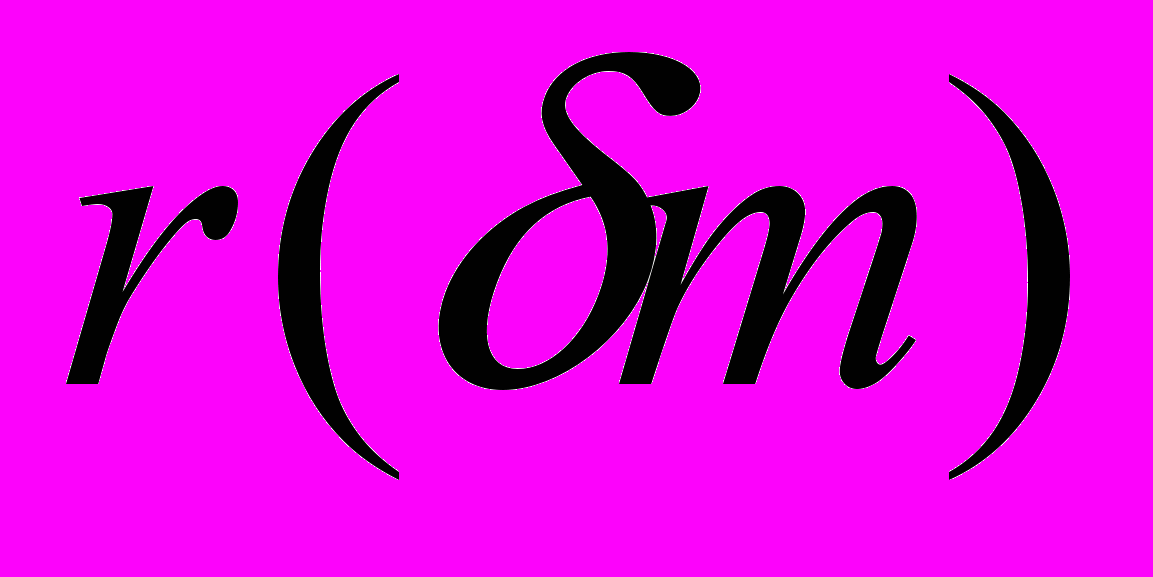– число приведенных примитивных бинарных квадратичных форм определителя 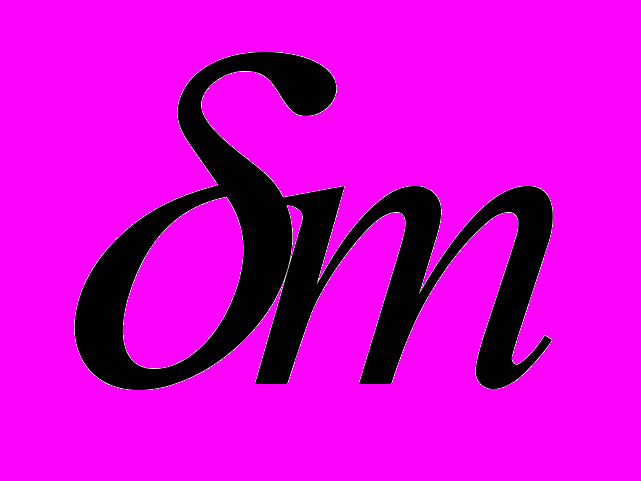; постоянные, входящие в (18), зависят только от и .

Эти две основные теоремы 3.5 и 3.6, результаты которых содержатся в статье [1], дают полное решение вопроса об асимптотике числа примитивных представлений целых чисел произвольной целой изотропной формой как по областям на соответствующей гиперболической поверхности так и по классам вычетов по заданному модулю (исследованного другими специалистами не в самом полном виде).

Из зарубежных специалистов по квадратичным формам исследования по представлению чисел неопределёнными тернарными квадратичными формами проводил американский математик W. Duke1), который, опираясь на результаты H.Iwaniec2), получил степенное понижение остаточного члена в асимптотической формуле для распределения целых точек только на простейшем двуполостном гиперболоиде 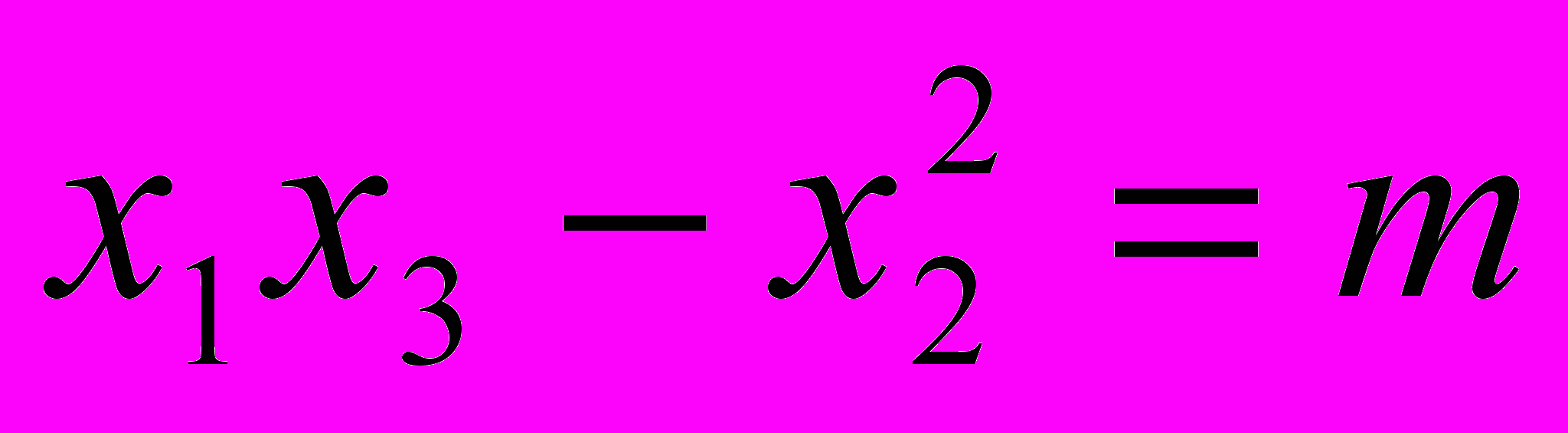, 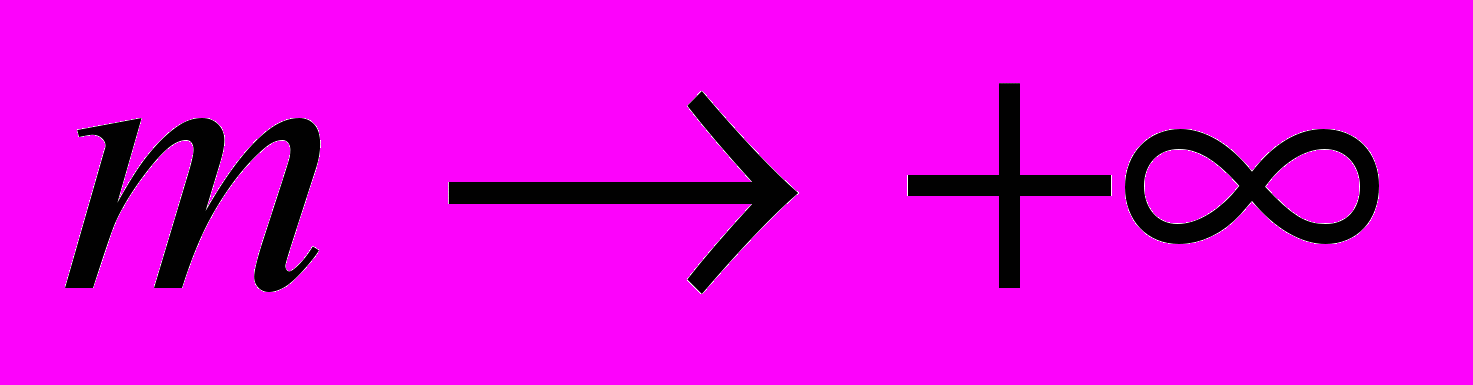. Но как показано в работе Е.П. Голубевой3) из результатов W. Duke невозможно вывести такой же закон распределения целых точек даже на простейшем однополостном гиперболоиде. При этом отметим также, что в работе W. Duke не рассматривалось распределение целых точек простейшего гиперболоида по арифметическим прогрессиям.

Всё это свидетельствует в пользу того, что ДЭМ ещё не исчерпал своих возможностей.

Перейдём теперь к описанию основных результатов главы IV диссертации, в которой содержатся новые применения ДЭМ к аналитической арифметике бинарных квадратичных форм. Что касается основных результатов главы IV, то такие асимптотические результаты не были получены или нашими, или зарубежными специалистами.

Первый основной результат этой главы представляет собой теорема перемешивания для гауссовых родов положительных бинарных квадратичных форм заданного определителя m. Чтобы ее получить строим поток классов гауссового рода через поток соответствующих им вектор-матриц нормы m >0:

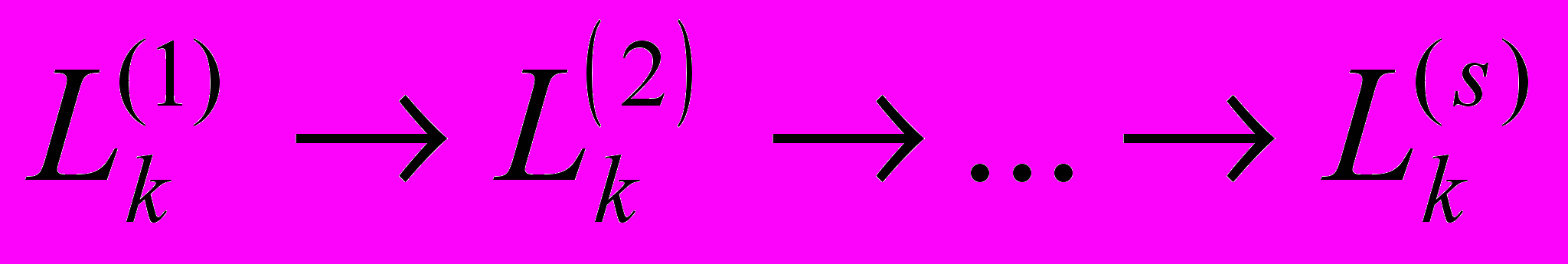, (19)

где 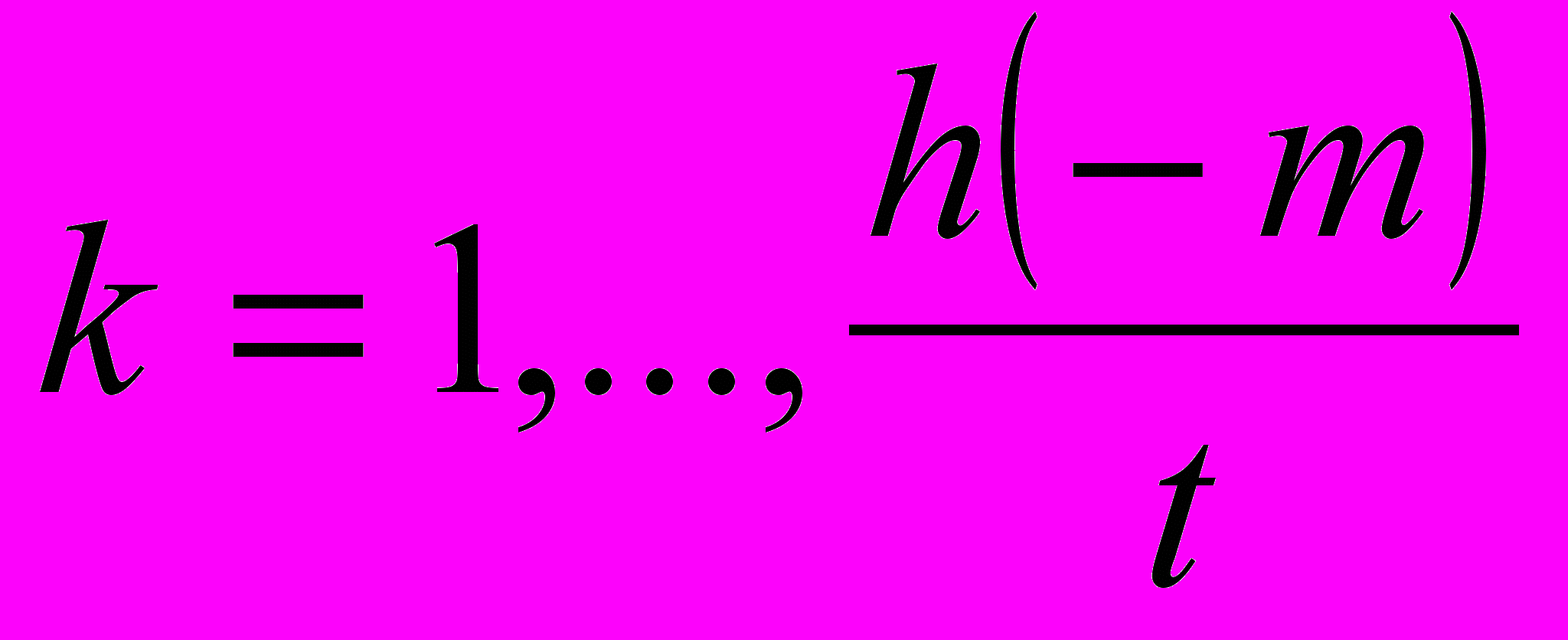, 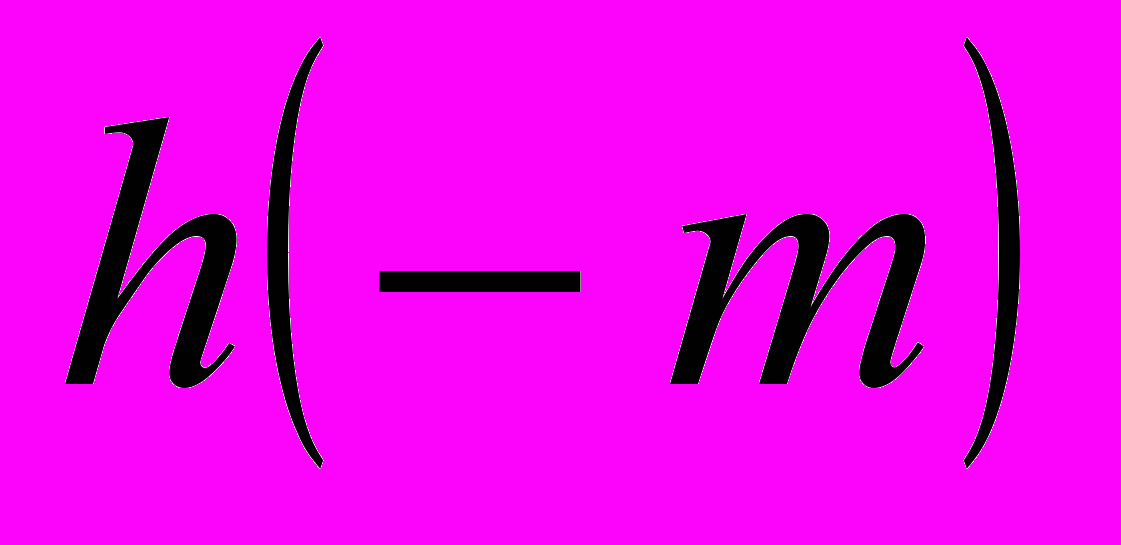– число классов положительных бинарных квадратичных форм определителя 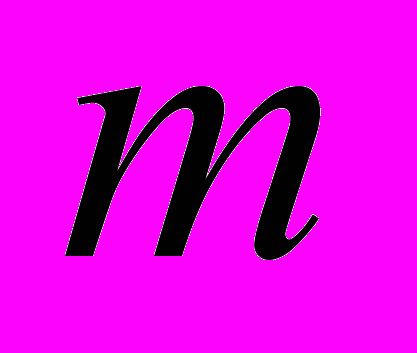; 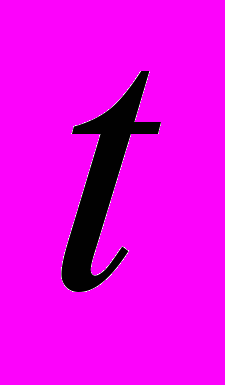– число гауссовых родов.

Сделаем нужные обозначения, прежде чем сформулировать основной результат второго параграфа главы IV.

Обозначим через множество всех приведенных собственно примитивных вектор-матриц второго порядка нормы 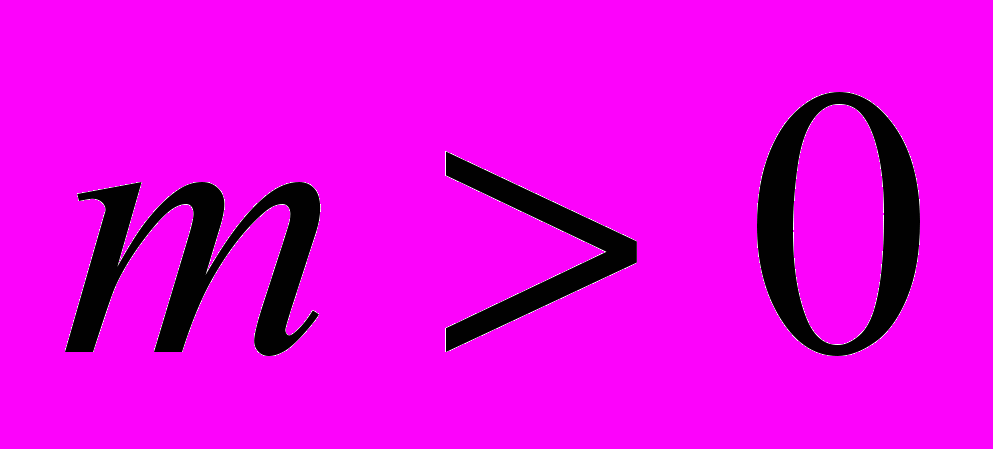, образы которых лежат в гауссовом роде 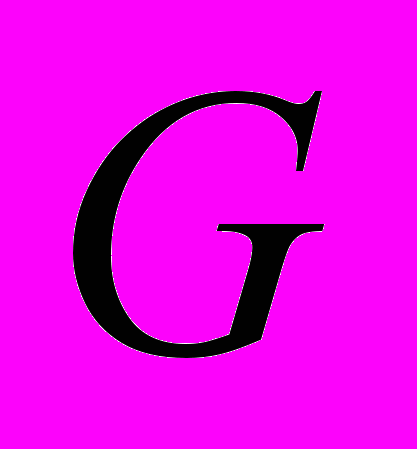бинарных квадратичных форм определителя 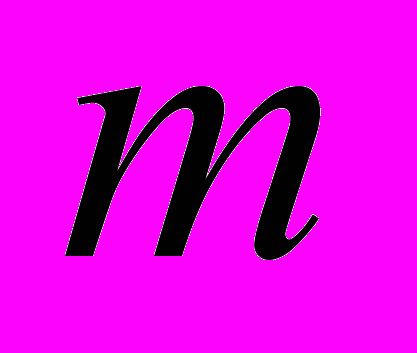. Тогда под потоком 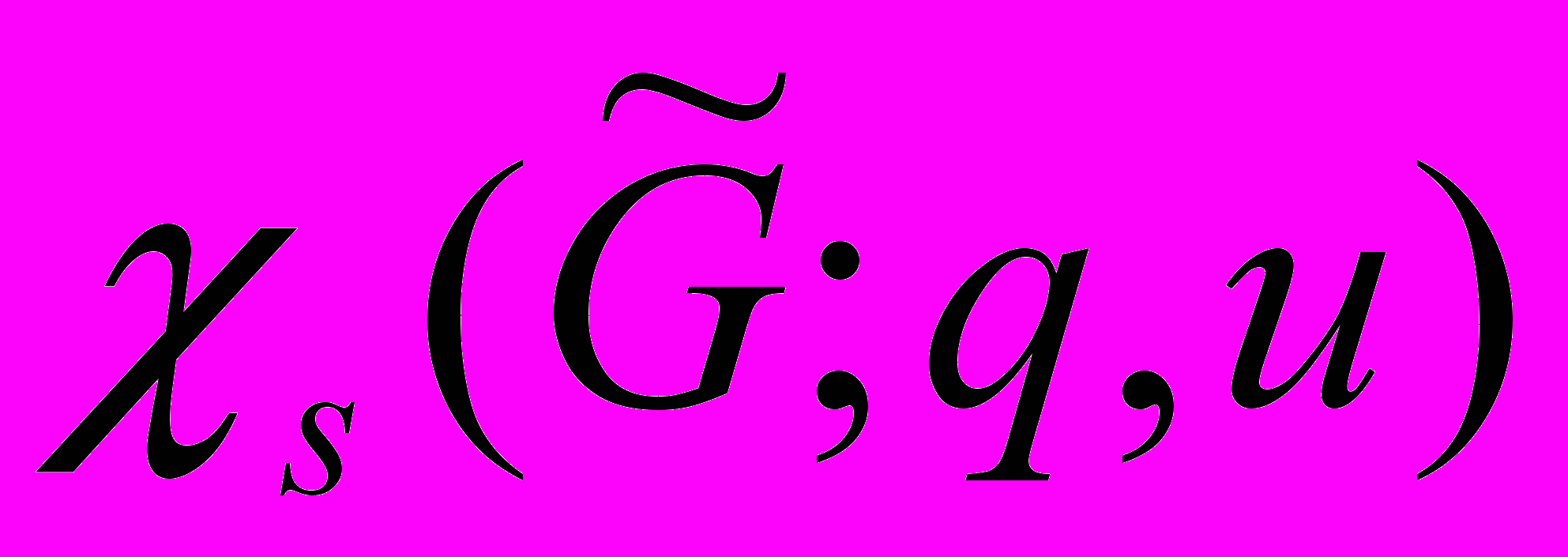, отвечающим числам 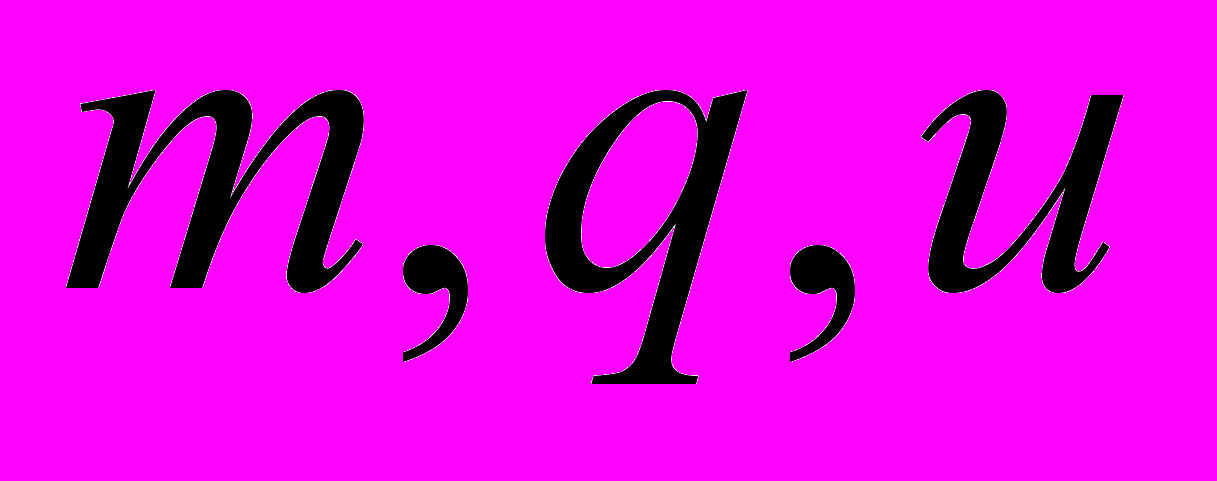и множеству 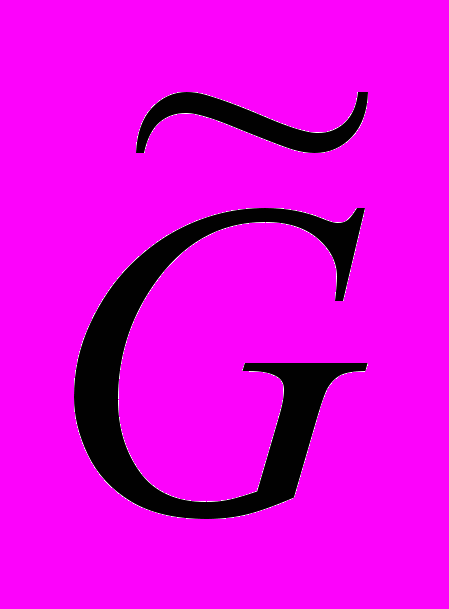, понимаем совокупность 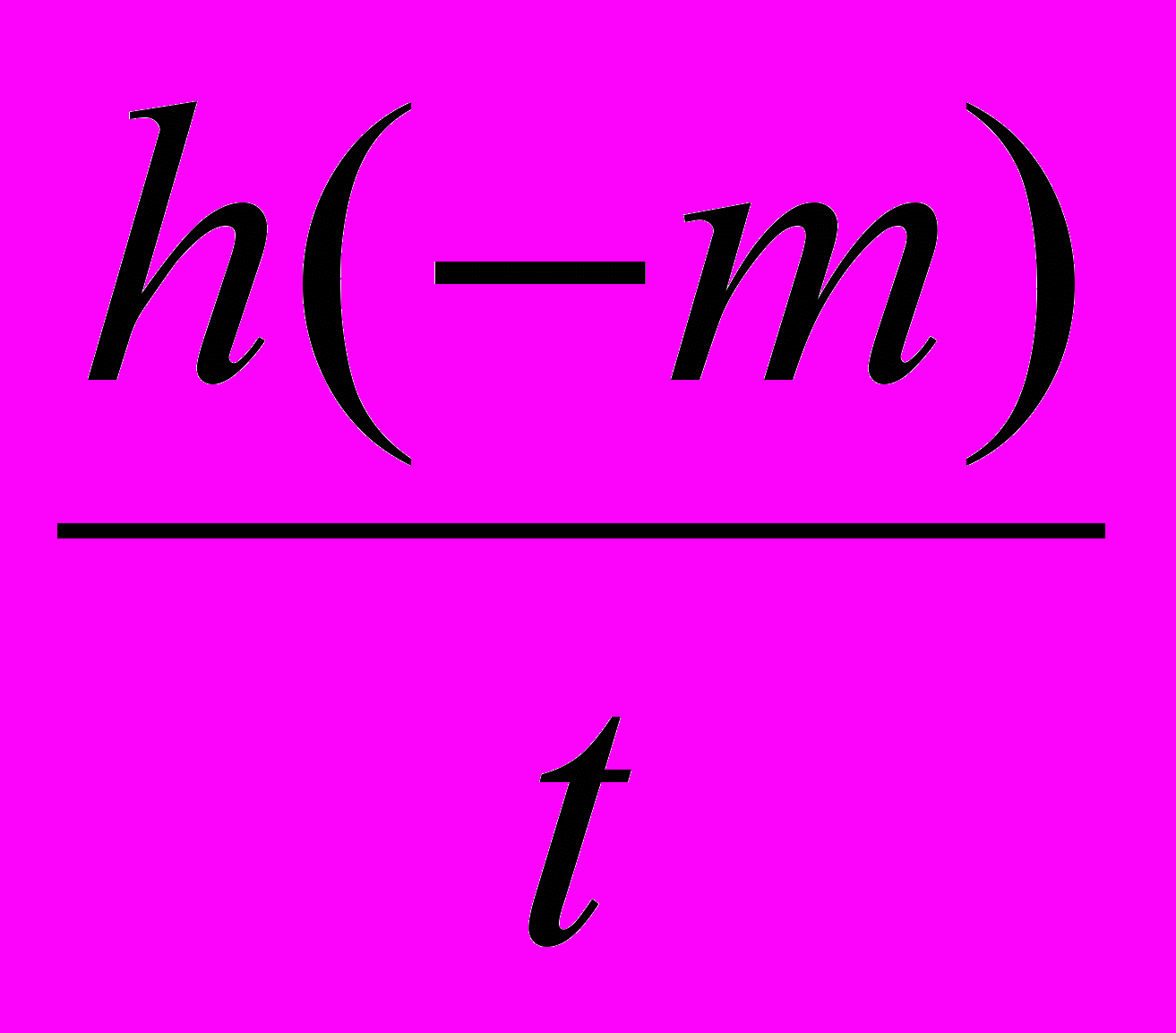последовательностей (цепочек) (19) длины 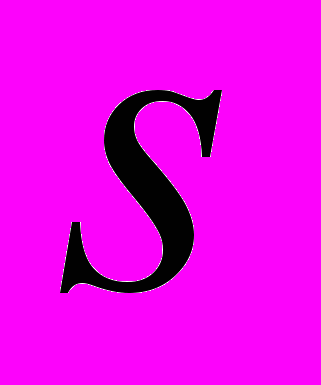целых приведенных вектор-матриц второго порядка нормы 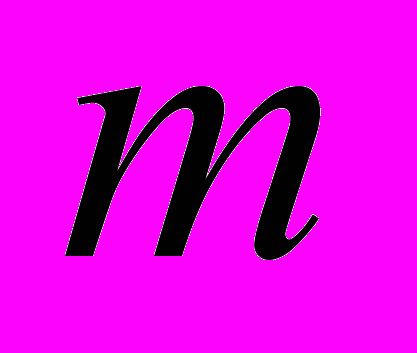, которые строятся тем же способом, что и в главе III, но с той лишь разницей, что используемое вспомогательное число считается квадратом нечетного числа. Введем в рассмотрение функцию ,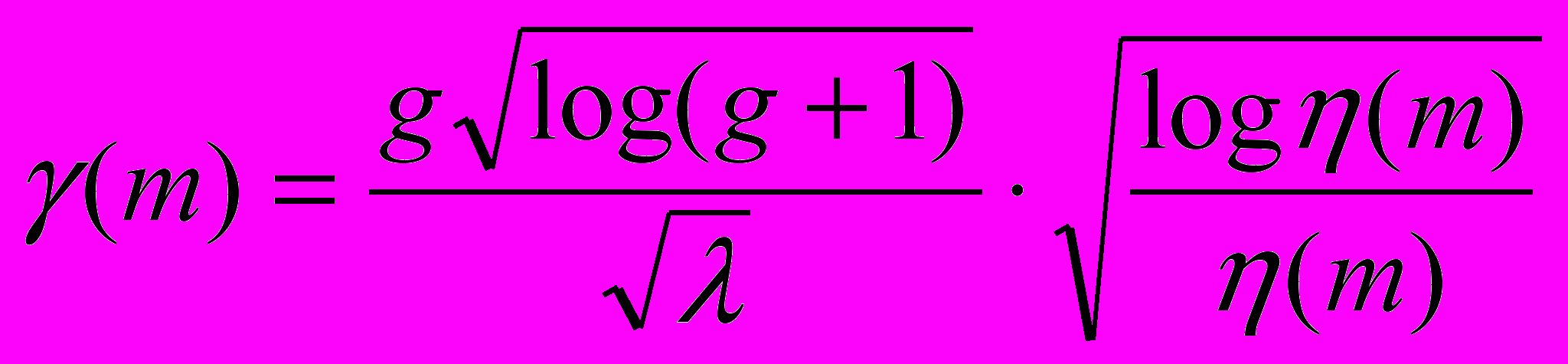

где 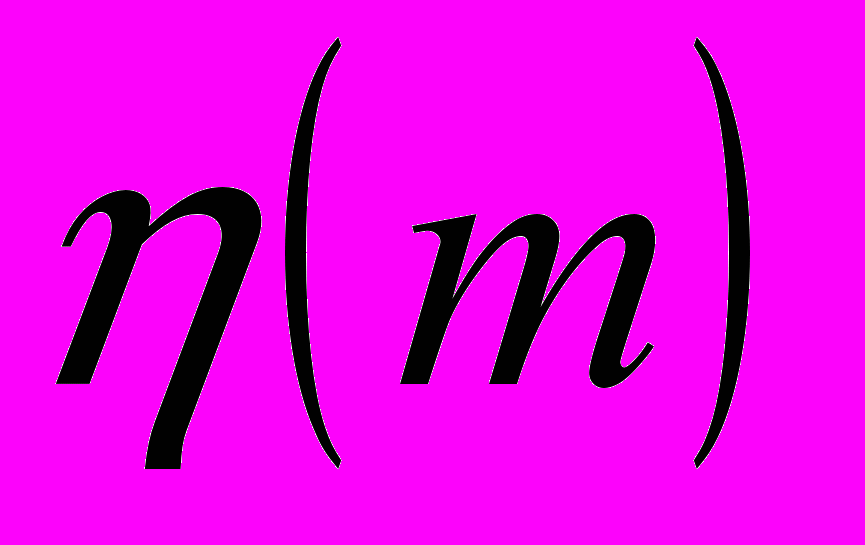– некоторая функция, зависящая от 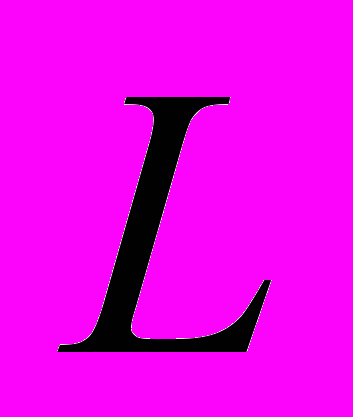– функции Дирихле 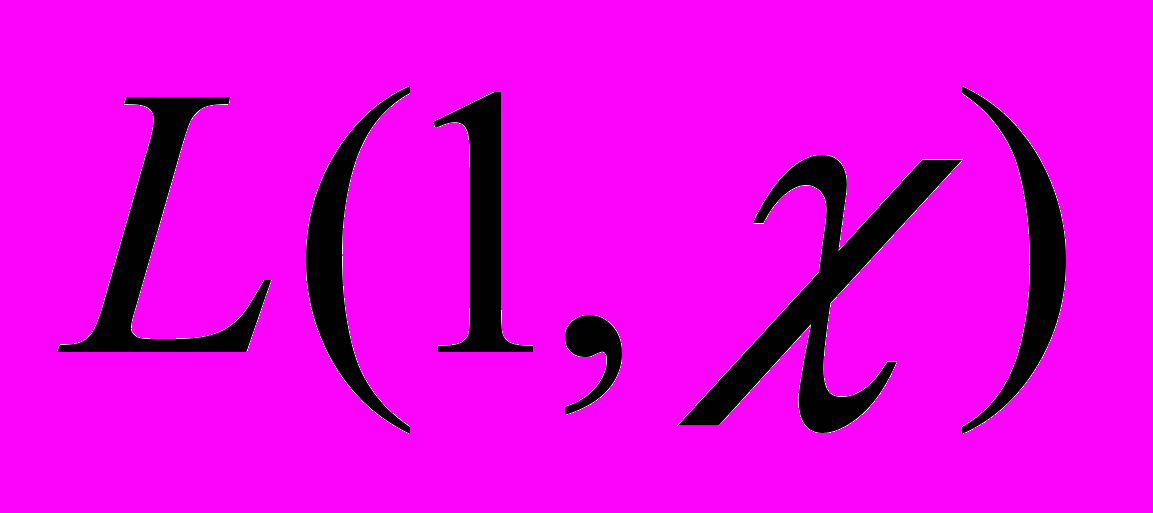, определяемой рядом , .

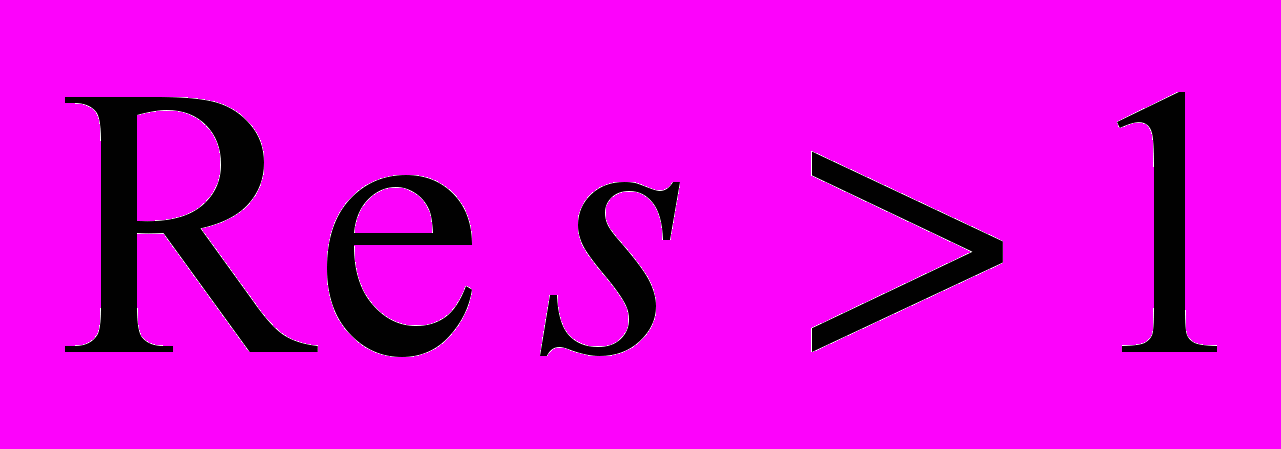(точный вид функции 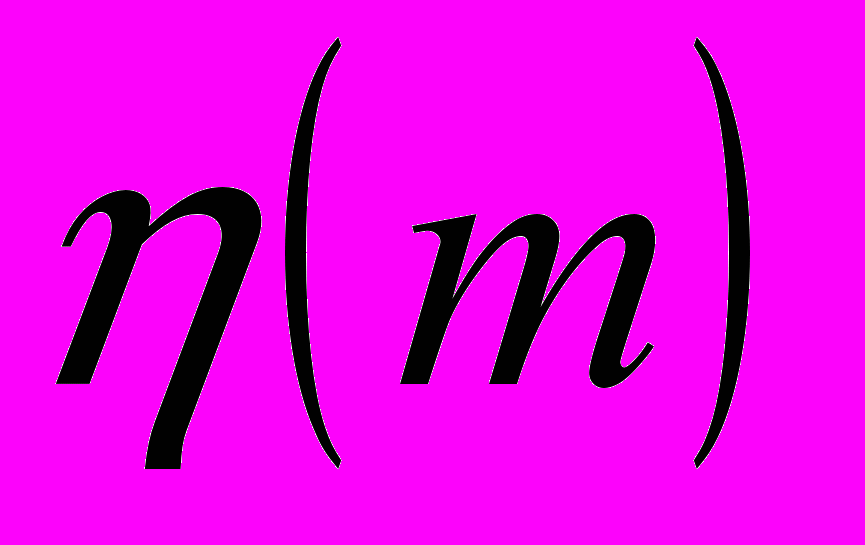дается равенством (2.22) гл. II).

Сначала доказывается эргодическая теорема 4.1 для классов гауссового рода, из которой выводится следующий основной результат §2, гл. IV (см. [5]).

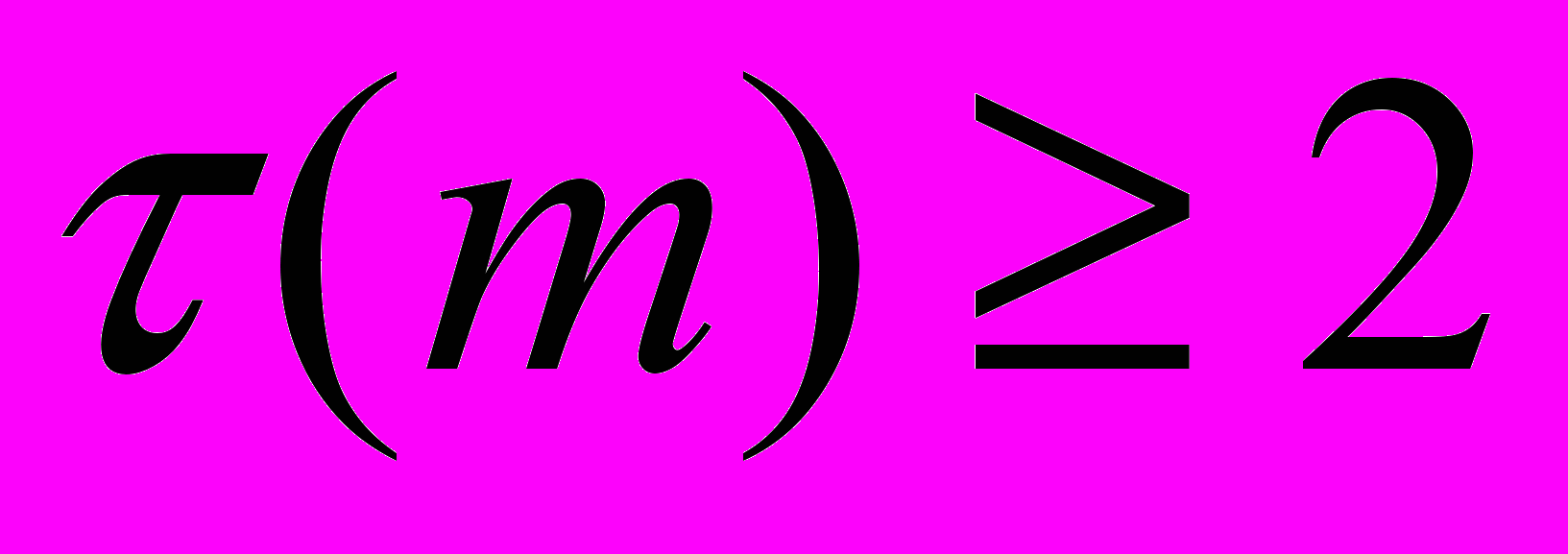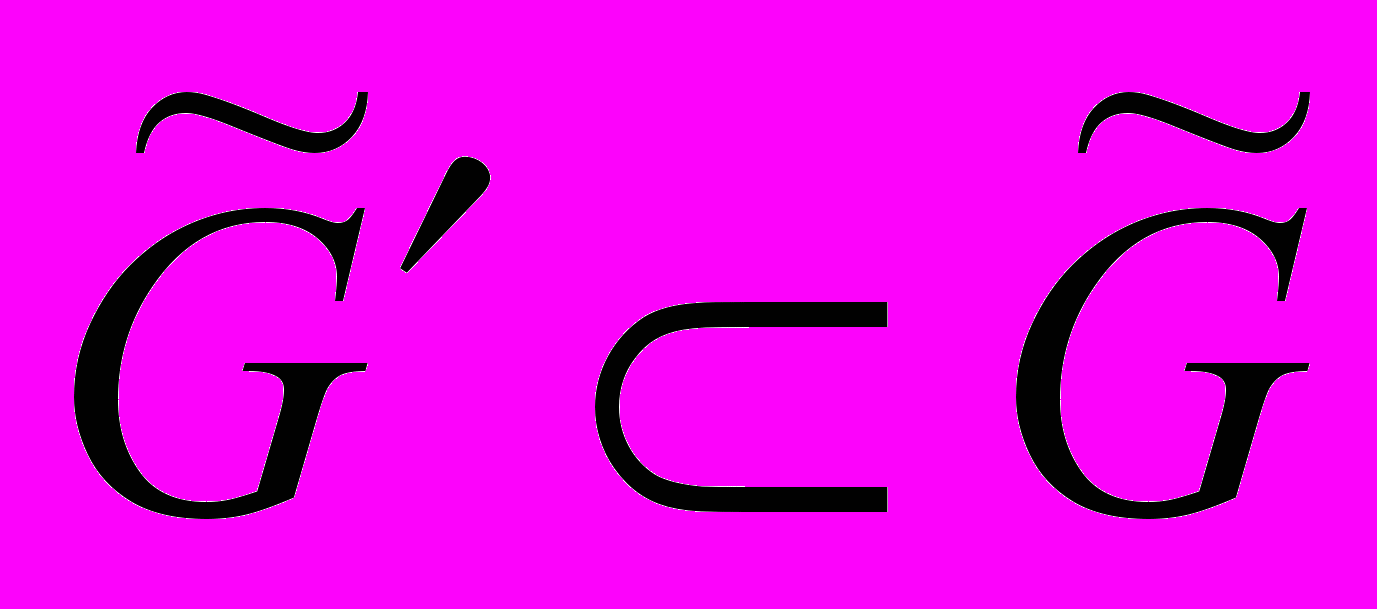Теорема 4.2 (о перемешивании для гауссовых родов). Пусть – неубывающая функция такая, что и – множество приведенных собственно примитивных вектор-матриц 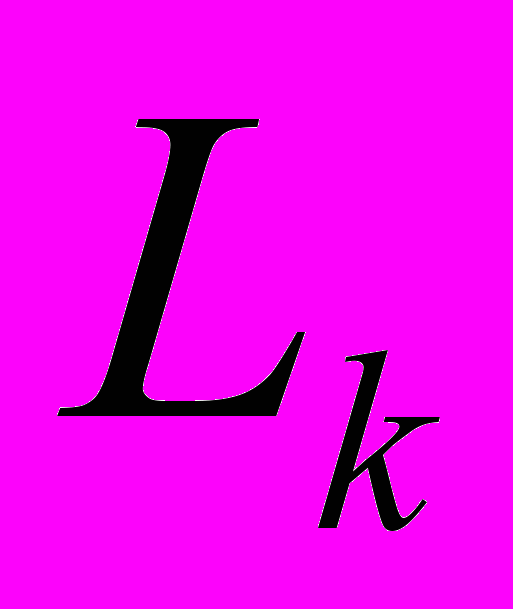нормы m (соответствующих приведенным формам гауссового рода) с числом элементов

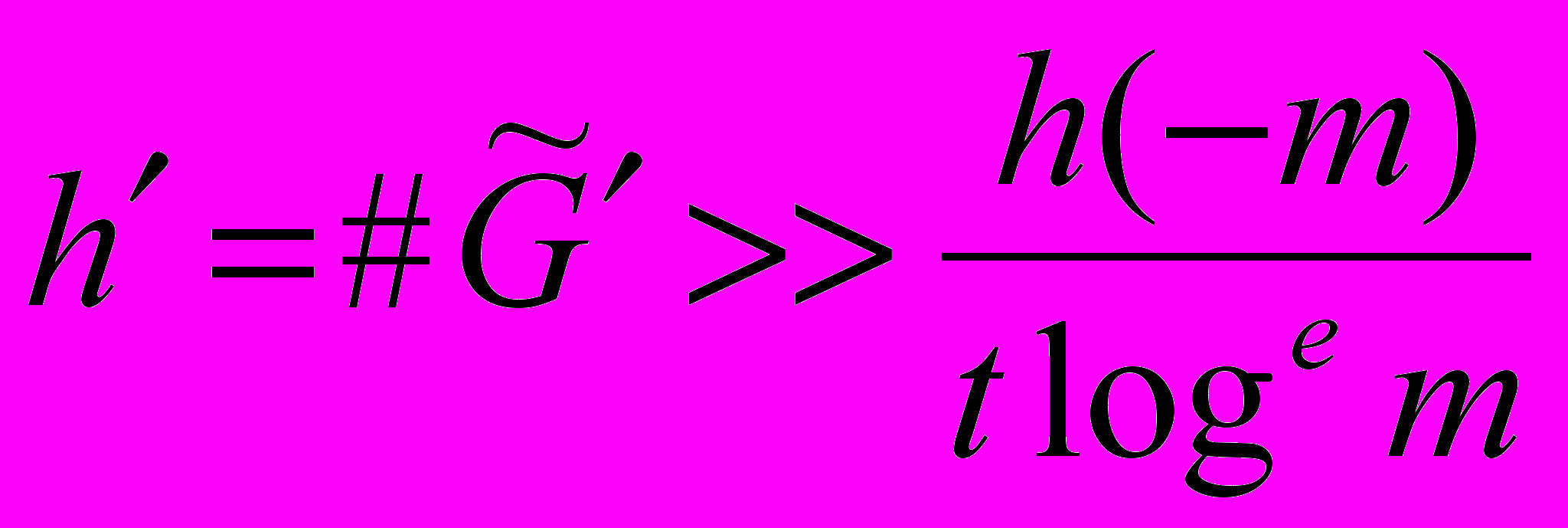. (20)

где 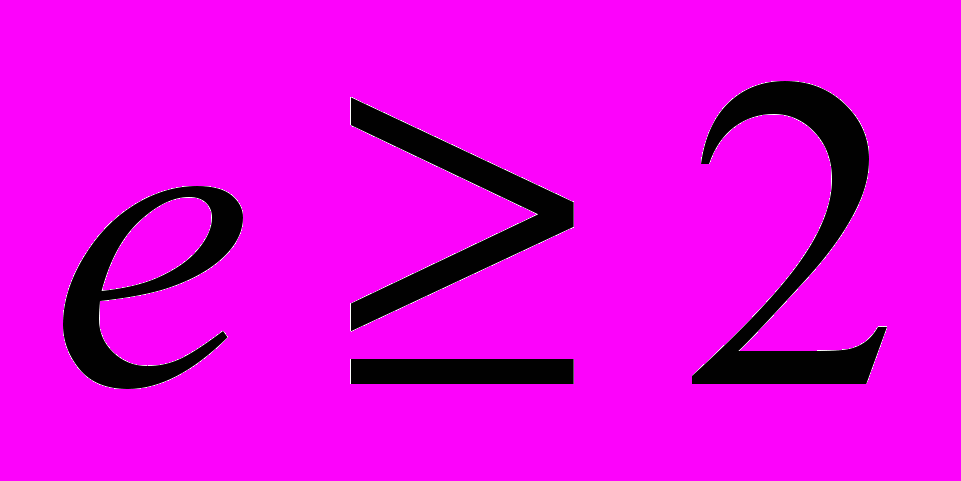– заданное число.

Тогда индексы в цепочках потока (19) можно разбить на две категории:

а) «хорошо перемешивающие» индексы 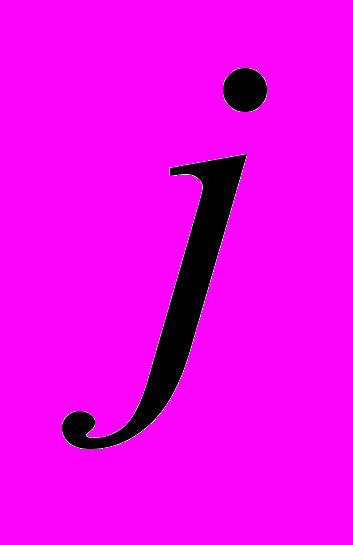, для которых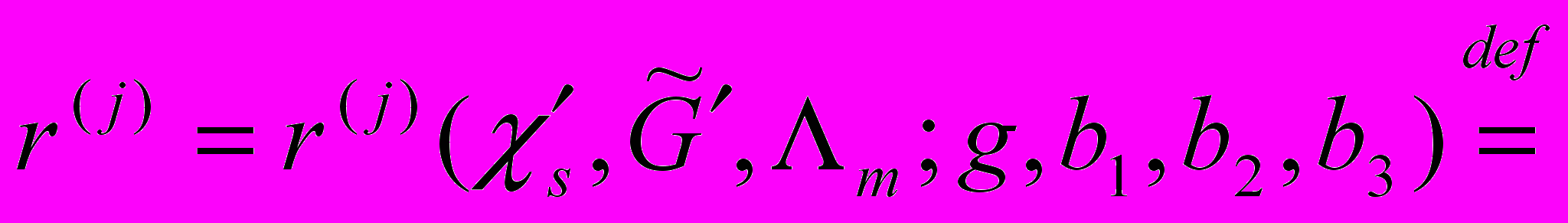



= #

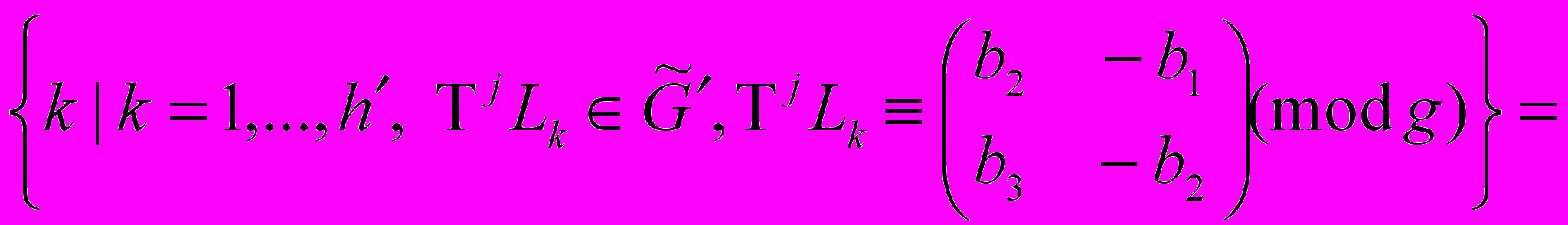
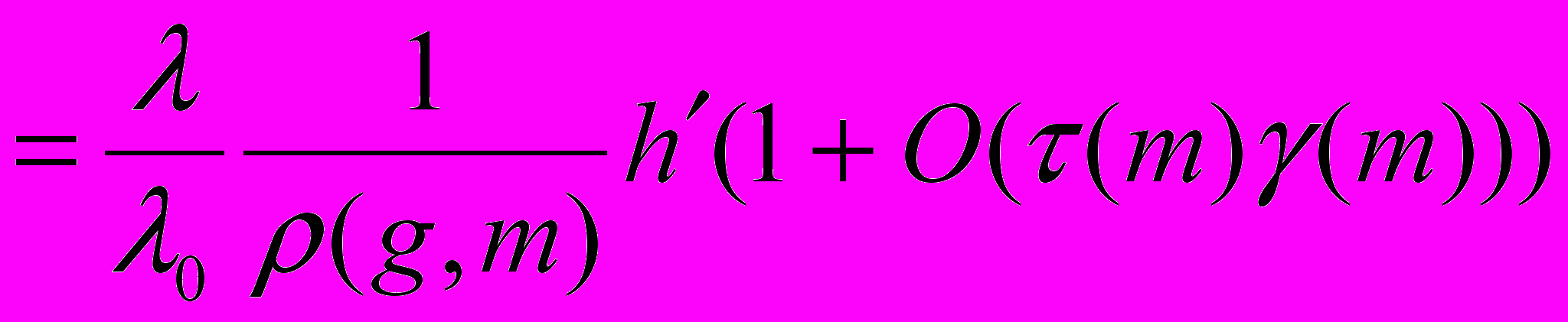, (21)

б) «плохие» индексы j, общее число которых

, (22)

для которых не выполняется (21); постоянные, входящие в (21 и 22), зависят от q и e.

Как частный случай из теоремы 4.2 о перемешивании получается асимптотическая формула с остаточным членом для числа 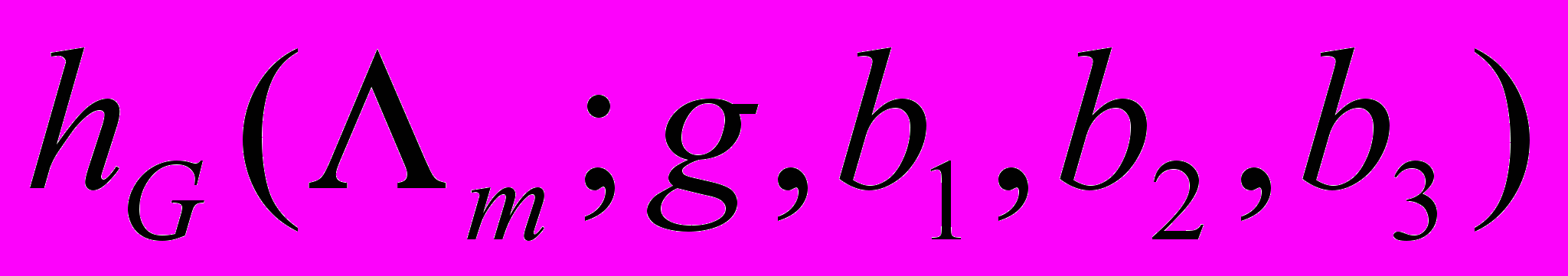классов гауссового рода G бинарных квадратичных форм определителя m, представители которых 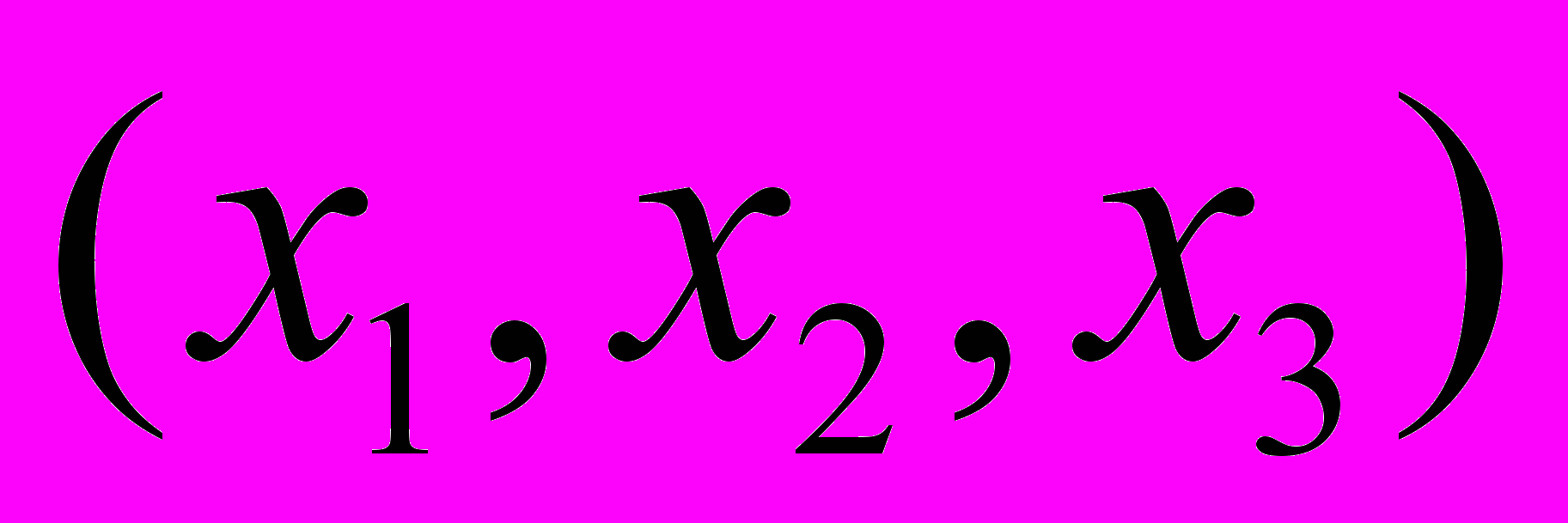удовлетворяют условиям

, .

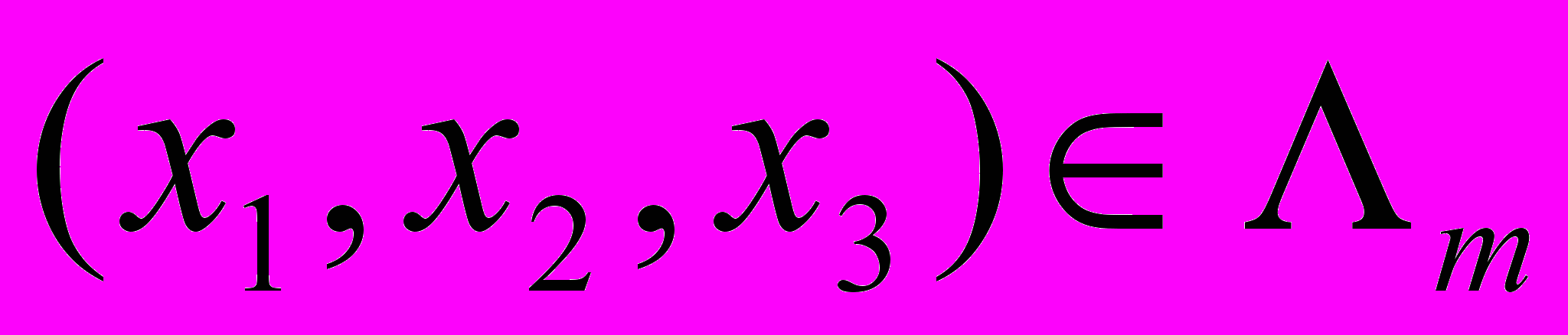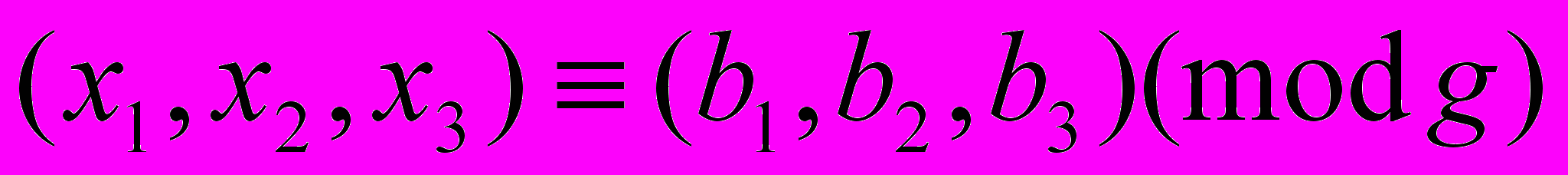Полученная формула для 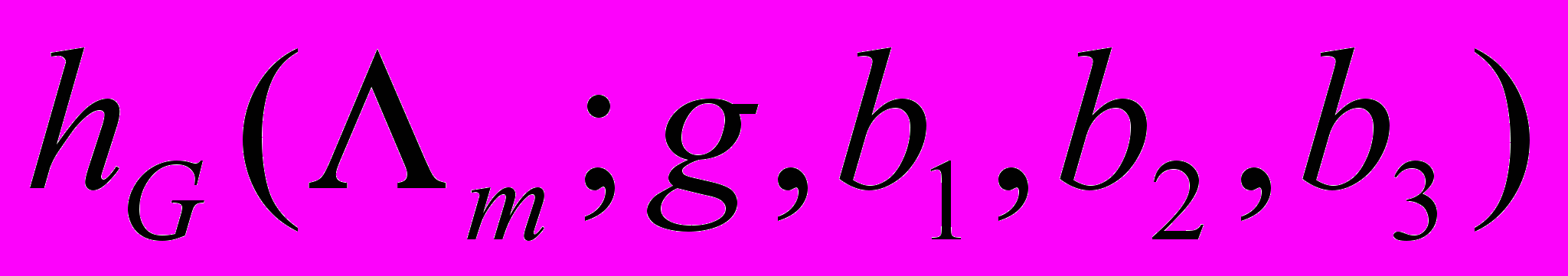обобщает часто цитируемый зарубежными специалистами результат Ю.В. Линника1) для случая g=1.

Следующим основным результатом главы IV является теорема 4.4, описывающая асимптотическое поведение числа классов гауссового рода, арифметический минимум которых делится на квадрат заданного нечетного числа (см. [3]).