Контрольная работа номер 2 официальный материал перевод: Денис Кашников iasb-52 Подбор Материала: Денис Кашников iasb-52

Вид материала

Контрольная работа

Содержание Какие системы называются адаптивными? Адаптивной системой можно назвать Теоритическая и практическая точки зрения Схема: (Ennu Rüstern) Вопрос-категория номер 2 Асимптотически стабильным Вопрос-категория номер 3 Вопрос-категория номер 4 Структурная Схема Идентефицирования Далее наблюдаем управление, где значение Вопрос-категория номер 5 Идентифицирование нелинейной системы Управление нелинейной системы Вопрос-категория номер 6 Матрицу данных Нормальном виде Первостепенной проблемой оценивания параметров в реальном времени - является Вопрос-категория номер 7 1. Этап – оценивание коэффициентов полиномов - A(z) и B(z) (например с помощью рекурентного метода меньших квадратов);2. Этап 3. Этап – рассчёт сигнала управления - u(k).Далее ... Полное содержание

Подобный материал:

• Программа дисциплины Философия Для направления 080100. 62 «Экономика» подготовки бакалавра, 676.46kb.
• Учебно-методический комплекс Классический прагматизм как практическая философия для, 317.31kb.
• Фонвизин денис Иванович, 71.58kb.
• Творческий конкурс (бриф) при поддержке Комиссии по экологической политике и охране, 15kb.
• Модеров Сергей Владимирович, Руководитель отдела финансовой отчет, 278.66kb.
• Контрольная работа по информатике для студентов 1 курса Контрольная работа включает, 145.11kb.
• Проклятая игра клайв баркер перевод с английского Д. Аношина. Ocr денис, 5278.8kb.
• Шевчук Денис Александрович деньги кредит банки конспект, 2329.49kb.
• Сотканный мир клайв баркер перевод с английского А. Медведева. Ocr денис, 4635.4kb.
• Книги крови книга 5 Клайв баркер перевод с английского М. Красновой. Ocr денис, 1714.97kb.

СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

КОНТРОЛЬНАЯ РАБОТА НОМЕР – 2

ОФИЦИАЛЬНЫЙ МАТЕРИАЛ


Перевод: Денис Кашников IASB-52

Подбор Материала: Денис Кашников IASB-52

Вопросы на эстонском: Алексей Тепляков IASB-54


ВНИМАНИЕ: РЕКОМЕНДУЕТСЯ ЗАПАСТИСЬ НЕСКОЛЬКИМИ ИСТОЧНИКАМИ ИНФОРМАЦИИ ПО ВТОРОЙ КОНТРОЛЬНОЙ РАБОТЕ ДЛЯ ЕЁ УСПЕШНОГО НАПИСАНИЯ!


УСПЕХОВ ПРИ НАПИСАНИИ И СДАЧЕ!

1. – ОБЗОР ИДЕИ АДАПТИВНЫХ СИСТЕМ:
   

ВОПРОС-КАТЕГОРИЯ НОМЕР 1

1. Какие системы называются адаптивными?
   

Адаптивными системами называют - ссылка скрыта, которые имеют возможность изменять параметры регулятора или структуру регулятора в зависимости от изменения параметров объекта управления или внешних возмущений, действующих на объект управления. Подобные системы управления называются адаптивными. Адаптивное управление широко используется во многих приложениях теории управления. (Википедия)

Адаптивной системой можно назвать - систему автоматического управления, в которой на основе информации о параметрах внешних воздействий, динамических характеристик объекта или системы, получаемой в процессе работы, осуществляется активное изменение вида алгоритма управления или его параметров с целью обеспечения оптимальной в каком-либо смысле работы замкнутой системы. В результате перестройки алгоритм управления или его параметры (коэффициенты регулятора) находятся в некоторой функциональной связи с параметрами внешних воздействий и параметрами объекта.

(ссылка скрыта)

Структурная схема:



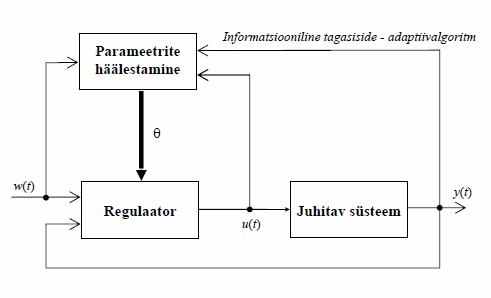
(Ennu Rüstern)


Свойства адаптивных систем:

А) Выходные параметры объекта регулирования и характеристики возмущающих факторов находятся под постоянным контролем и управлением с помощью устройств, дополнительно включаемых в состав управляющей систем.

Б) Наблюдаемое поведение объекта описывается некоторым показателем качества, оценивающим в количественной форме характер протекания процесса управления.

В) Отклонение показателя качества за пределы допуска влечет за собой автоматическую настройку параметров регулятора или замену алгоритма управления, результатом которых является достижение желаемого показателя качества или реализации поставленной цели.

(Реферат Студента Российского ВУЗА)

2. Классификация адаптивных систем с теоритической и практической точек зрения?
   

Теоритическая и практическая точки зрения:

По характеру изменений в управляющем устройстве адаптивные системы делят на две большие группы: самонастраивающиеся (изменяются только значения параметров регулятора) и самоорганизующиеся (изменяется структура самого регулятора). По способу изучения объекта системы делятся на поисковые и беспоисковые. В первой группе особенно известны экстремальные системы, целью управления которых является поддержание системы в точке экстремума статических характеристик объекта. В таких системах для определения управляюших воздествий, обеспечивающих движение к экстремуму, к управляющему сигналу добавляется поисковый сигнал. Беспоисковые адаптивные системы управления по способу получения информации для подстройки параметров регулятора делятся на системы с эталонной моделью (ЭМ) и идентификатором. Последние в литературе иногда называют, как системы с настраиваемой моделью (НМ). Адаптивные системы с ЭМ содержат динамическую модель системы, обладающую требуемым качеством. Адаптивные системы с идентификатором делятся по способу управления на прямой и косвенный (непрямой). При косвенном адаптивном управлении сначала делается оценка параметров объекта, после чего на основании полученны оценок определяются требуемые значения параметров регулятора и производится их подстройка. При прямом адаптивном управлении благодаря учёту взаимосвязи параметров объекта и регулятора производится непосредственная оценка и подстройка параметров регулятора, чем исключается этап идентификации параметров объекта. По способу достижения эффекта самонастройки системы с моделью делятся на системы с сигнальной (пассивной) и параметрической (активной) адаптацией. В системах с сигнальной адаптацией эффект самонастройки достигается без изменения параметров управляющего устройства с помощью компенсирующих сигналов. Системы, сочетающие в себе оба вида адаптации называют - комбинированными. (Википедия)


Визуальная классификация:





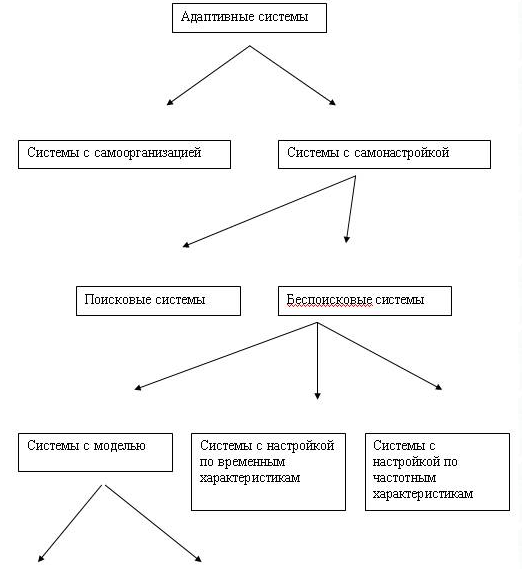
(syst.ru)

3. Адаптивные системы с эталонной моделью?
   

Система с эталонным объектом.

Эталонная модель:



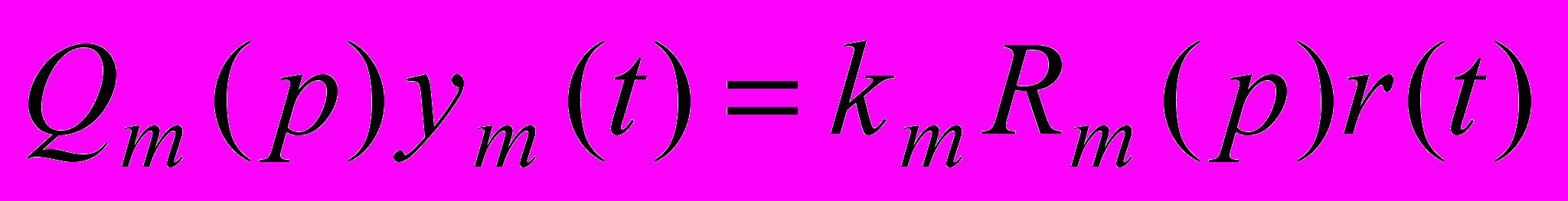
Где 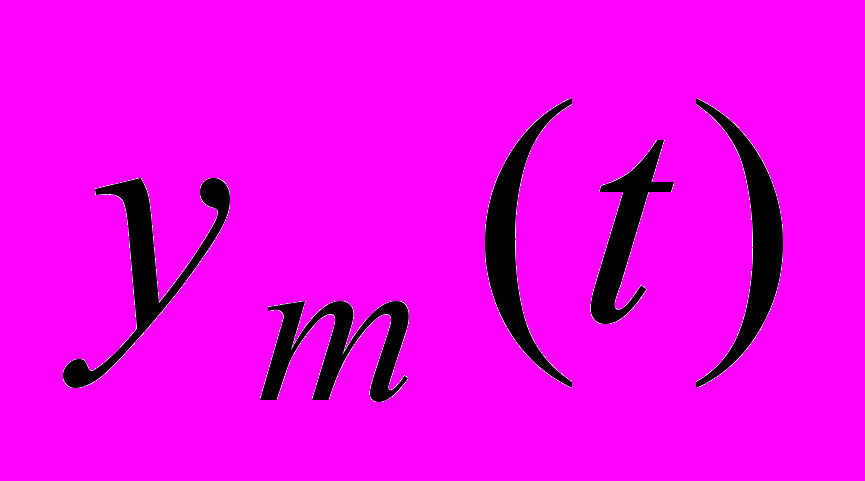– выход эталонной модели, 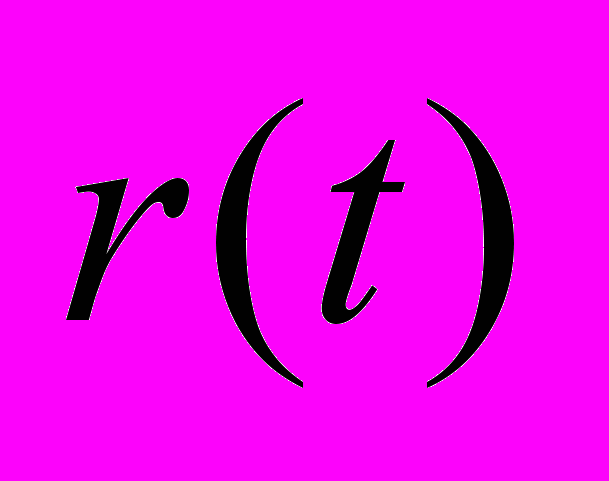– ограниченное задающее воздействие,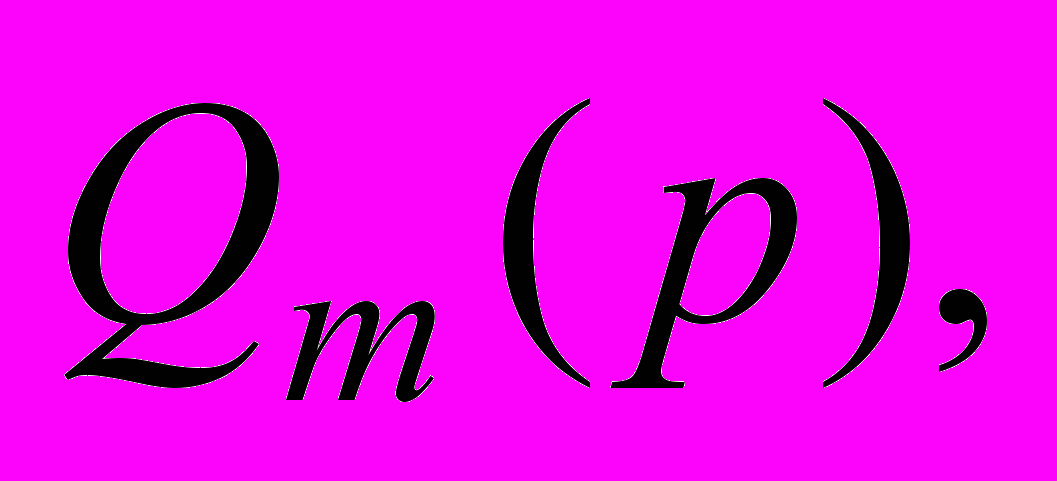 – нормированные линейные дифференциальные операторы с постоянными, известными коэффициентами и в преобразовании Лапласа данные операторы гурвицевы, , .


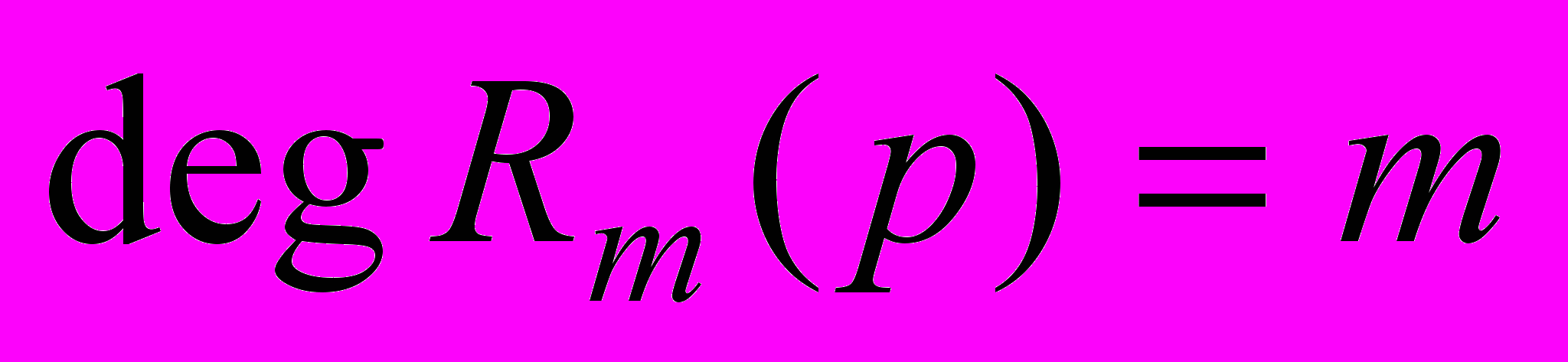Уравнение эталонной модели:

,

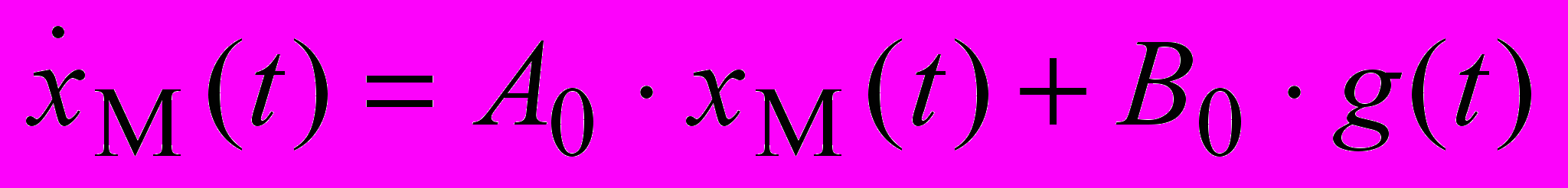где 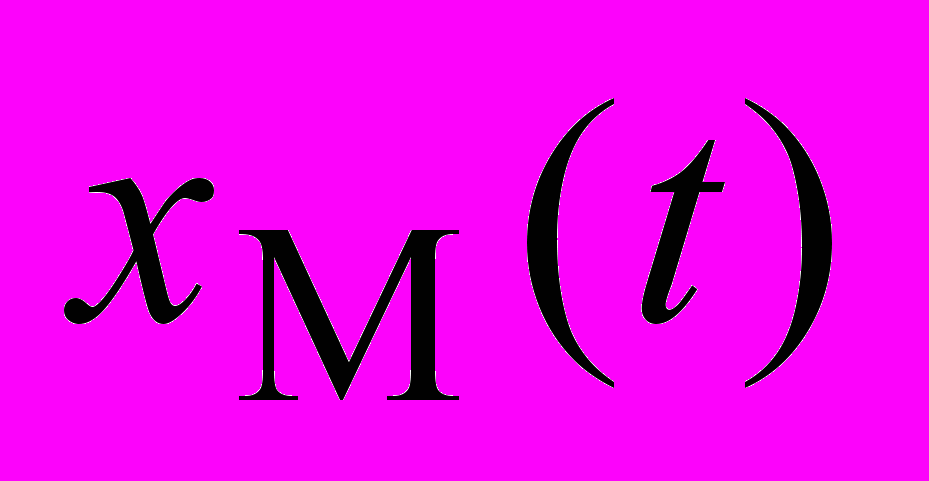– вектор состояния эталонной модели; A₀, B₀ – линейные стационарные матрицы состояния и управления настраиваемой модели. (Исследовательская работа)

Схема:



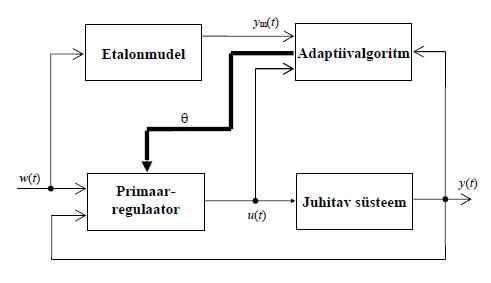
(Ennu Rüstern)

4. Адаптивная система с возможностью идентефицирования?
   

Система в которой – сначало проводят идентификацию объекта, а затем, зная желаемые динамические свойства замкнутой системы, выставляют соответствующие коэффициенты регулятора. (ссылка скрыта)

Схема:

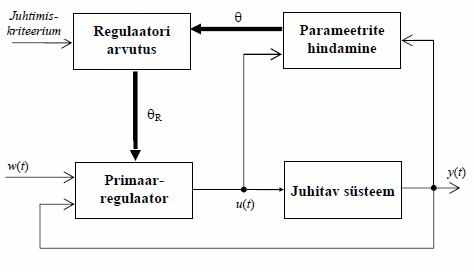(Ennu Rüstern)

ВОПРОС-КАТЕГОРИЯ НОМЕР 2

1. Стабильность Ляпунова – Метод 1?
   

Согласно анализируемой нелинейной системы:





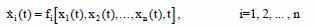
Согласно векторно-дифференциальному уравнению:





Где x и f – векторы наклона и считаем, что f[0,t]=0 если t > t а также x(t0)=x0 – начальное состояние.

X (t, x0, t0) существует для всех t > t0. Пока f(0,t)=0, тогда x=0 состояние равновесия.


Согласно Ляпунову, стабильности можно дать два определения – говоря о стабильности состояния свободного движения или же о стабильности состояния равновесия. В теории САУ используются оба определения.


Определение 2.1:


Состояние равновесия нелинейной системы - x=0 является (По Ляпунову)

стабильным тогда, когда всякая ε > 0 и t0 > 0,δ(ε,t0) > 0, и если |x0| < δ, тогда

|x (t; x0, t0| < ε для всех t ≥ t0.


Определение 2.2:


Состояние равновесия нелинейной системы - x=0 является (По Ляпунову)

Глобально притягивающе (Ligi – около, tõmbav - тянущий) тогда, когда некоторое ρ > 0 и каждое ηи t0 > 0, и если найдётся такой временной интервал T(η,x0,t0), что |x0| < ρ тогда - |x(t;x0,t0)| < η для всех t > t0+ T.


Определение 2.3:


Состояние равновесия нелинейной системы - x=0 является (По Ляпунову)

Асимптотически стабильным тогда, когда x=0 является стабильным и глобально притягивающе.

(Ennu Rüstern)

Тривиальное решение x = 0 системы (1) называется устойчивым по ссылка скрыта, если для любых 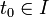и ε > 0 существует δ > 0, зависящее только от ε и t₀ и не зависящее от t, такое, что для всякого x₀, для которого 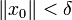, решение x системы с начальными условиями x(t₀) = x₀ продолжается на всю полуось t > t₀ и удовлетворяет неравенству 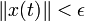. (Википедия)

2. Стабильность Ляпунова – Метод 2?
   

Второй метод Ляпунова позволяет определить является ли состояние равновесия нелинейной системы – стабильным, без нахождения соответствующих решений.


Теорема 2.1:


Состояние равновесия нелинейной неавтономной системы является равномерно

Асимптотически стабильным для больших сигналов тогда, когда существует следующая скалярная функция:


V(x, t) с неприрывными частными производными x и t такими, что V (0, t) = 0 и выполнены следующие условия:


(A) V(x,t) определена позитивно, и поэтому существует такая непрерывная скалярная

функция «a», что «a»(0)=0 и V(x,t) ≥ a(|x|) > 0 для всех t и x ≠ 0;


(B) V(x,t) усечена сверху, и поэтому существует такая непрерывная скалярная

функция b, что b(0)=0 и V(x,t) ≤ b (|x|) для всех t;


(C) V(x,t) определена негативно;


(D) V(x,t) радиально не пересекаемая функция, и поэтому «a»(|x|) → ∞ если |x| → ∞.


Теорема 2.2:


Нелинейная автономная система:


X (t) = f[x (t)], f [0] = 0


Состояние равновесия однозначно асимптотически стабильно для больших сигналов тогда, когда существует такая скалярная функция V(x) с непрерывной частной производной x и t, что V(0)=0 и выполнены следующие условия:


(A) V(x) > 0 , если x ≠ 0 и поэтому позитивно определена;

(B) V& (x) < 0 , если x ≠ 0 и поэтому негативно определена;

(C) V(x) > 0, если |x| → ∞.


Теорема 2.3:


Линеарная, стационарная система:


X (t) = Ax (t)


Состояние равновесия x=0 является асимптотически стабильным тогда, когда дана каждая симметрически позитивно определённая матрица Q для которой существует симметрически позитивно определённая матрица P, и матричное выражение: AP + PA = − Q. (Ennu Rüstern)

ВОПРОС-КАТЕГОРИЯ НОМЕР 3

1. Синтез адаптивной системы с эталонной моделью по методу Ляпунова?
   

Для обеспечения стабильности адаптивной системы используется второй метод Ляпунова,

в котором нелинейная система обладает асимптотически стабильным состоянием равновесия x=o, если получается составить функцию Ляпунова - V(x,t) со следующими свойствами:


- V(x, t) > 0 , если x ≠ 0 V(x,t) позитивно определена;

- V& (x, t) < 0 , если x ≠ 0 V& (x,t) негативно определена;

- V(x, t) →∞, если |x|→ ∞;

- V(x, t) = 0, если x=0.


Следовательно асимптотическая стабильность обеспечивается только для тех сигналов и параметров системы, для которых V(x,t) определена негативно. Если V(x,t) определена полунегативно, тогда состояние равновесия x=0 является стабильным но не асимптотически. (Ennu Rüstern)


ВОПРОС-КАТЕГОРИЯ НОМЕР 4

1. Идентифицирование и управление линеарной системы первого порядка?
   

Идентефицирование:

Считаем, что идентифицируемая линейная скалярная система описывается выражением состояния:


X’ (t) = ax (t) + bu (t),


Где параметры «a» и «b» константны, однако не известны. Также считаем, что

a<0 и скалярный вход u (t) и состояние x (t) - являются усечёнными сигналами.


Для оценки параметров системы, составим выражение оценивания:




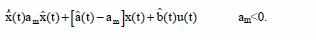
Целью является настройка параметров a’(t) и b’(t) так, что





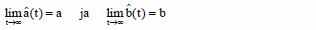
Определим ошибки параметров и состояния адаптивной системы следующим образом:





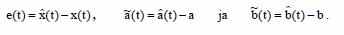
Для идентифицирования адаптивной стабильной системы по второму методу Ляпунова преобразуем модель ошибок





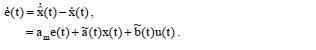
Для нахождения алгоритма оптимальной настройки параметров адаптивной стабильной системы преобразуем функцию Ляпунова:





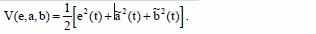
В соответствии с процедурой синтеза, найдём:





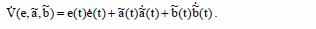
И из рассчётов выражений ошибок, получим:





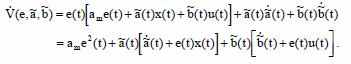
Из полученного выражения следует, что целесообразно отобрать адаптивные алгоритмы для настройки параметров:





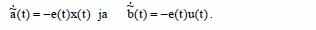
В этом случае, получаем:




Следовательно состояние равновесия e(t) = ~a(t) = ~b(t) = 0 статично.


По причине константности параметров «a» и «b» можно представить алгоритмы настройки следующим образом:





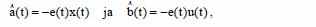
Функция Ляпунова может также быть выбрана следующим образом:





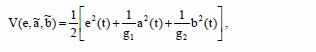
Где g1 и g2 – позитивные константы, а алгоритмы настройки параметров получаются следующим образом:





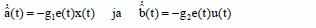
Структурная Схема Идентефицирования:




(Ennu Rüstern)


Управление:


Управляемая, линеарная, скалярная адаптивная система задана уравнением состояния:





Параметры «a» и «b» константны, однако не известны.

Эталонная модель задана следующим образом:





Исходя из рассчета того, что параметры управляемой системы неизвестны и их практическая важность в том, что ими обладают только системы с обратной связью, опишем выражение настраеваемого регулятора следующим образом:





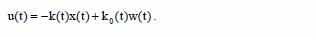
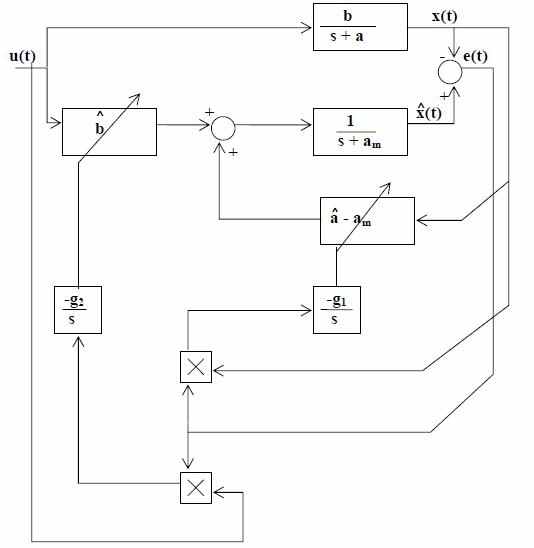
Исходя из выражений управляемой системы и настраеваемого регулятора, получим следующее выражение состояния закрытой системы:





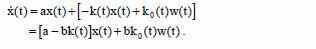
Для определения ошибок параметров и сигналов синтезируемой адаптивной системы, напишем:





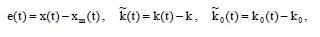
Где параметры регулятора 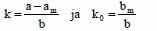отвечают состоянию равновесия. Закрытая система ведёт себя точно также как и эталонная модель.


Из рассчёта последнего, получаем уравнение ошибок:





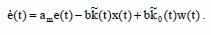
Сначала наблюдаем управление, где параметр управляемой системы – «b» известен. Следовательно, выражение настраемого регулятора и выражене ошибок системы упрощаются и выглядят следующим образом:





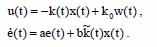
Функцию Ляпунова выберем следующим образом:





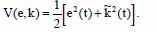
Найдём производную функции Ляпунова:





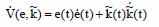
И из рассчёта выражения ошибки, получим:





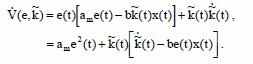
Выбранный алгоритм настройки регулятора:





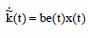
обеспечивает негативную полубеспредельность производной функции Ляпунова:





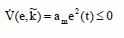
И стабильность адаптивной системы.


Состояние равновесия является таким - e(t) = ~k(t) = 0 .


По причине константности параметра «к», алгоритм настройки можно представить следующим образом:





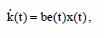
Далее наблюдаем управление, где значение параметра «b» управляемой системы известно.

Исходя из выражения настраемого регулятора и выражения ошибки, запишем функцию ляпунова в виде:





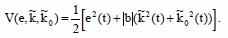
Рассчитаем производную функции Ляпунова:





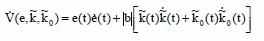
И из рассчёта выражения ошибки, получаем:





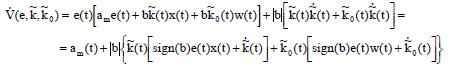
Представим алгоритм настройки регулятора в виде:





Обеспечим негативную полубеспредельность производной функции Ляпунова:





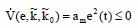
И тем самым гарантируем стабильность синтезируемой адаптивной системы.


Состояние равновесия является таким - e(t) = ~k(t) = ~k (t) = 0 .


Для реализации адаптивной системы необходимо представить алгоритмы настройки регулятора в виде:





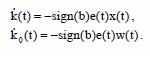
Состояние равновесия теперь является таким - e(t)=0, k(t)=k и ko(t)=ko.


Структурная Схема Управления:


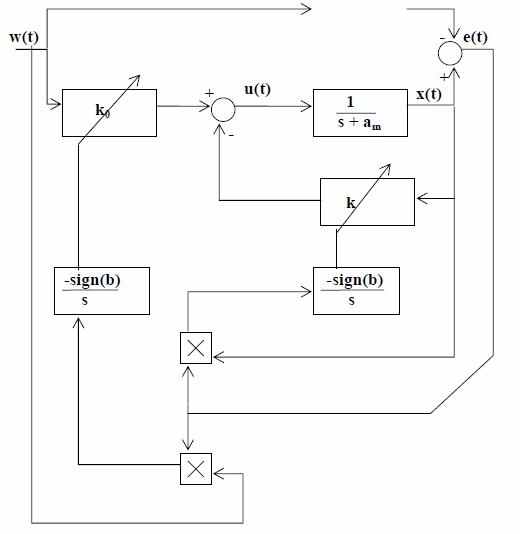(Ennu Rüstern)

ВОПРОС-КАТЕГОРИЯ НОМЕР 5

1. Идентефицирование и управление простой нелинейной системы?
   

Управление и идентифицирование простой нелинейной системы:


В настоящем подразделении рассмотрим использование метода Ляпунова для управления и идентификации простой нелинейной системы с заданной эталонной моделью для синтеза адаптивной системы.


Выражение состояний простой, управляемой и идентифицируемой, нелинейной системы:





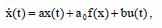
Где a , ao и b - константны, но неизвестны. Состояния x(t) и f(x) - измеримы. Нелинейная функция - f(x) плавная по состоянию и f(0)=0.


Идентифицирование нелинейной системы:


Для оценки параметров системы выберем:





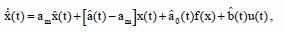
Где am<0. Целью является настройка параметров: a’(t), a’ (t)0 и b’ (t) так, что:





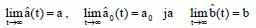
Определим ошибки параметров и состояний:





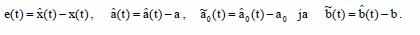
Образуем модель ошибок:





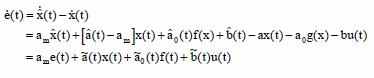
Используем функцию Ляпунова для нахождения алгоритма настройки параметров адаптивной системы:





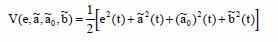
Рассчитаем производную

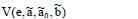
по траектории выражения для ошибки:





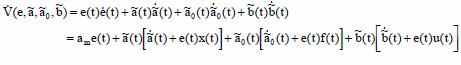
Выбираем алгоритм настройки регулятора следующим образом:





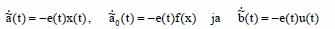
Для стабильного состояния равновесия:





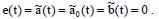
Для реализации адаптивной системы необходимо представить алгоритм настройки регулятора в следующем виде:





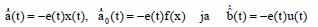
Управление нелинейной системы:


Для управления адаптивной системой, выберем настраиваемый регулятора:





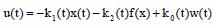
Эталонная модель задана следующим образом:





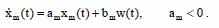
Исходя из выражений - состояния и регулятора управляемой системы, найдём выражение состояний

Закрытой системы:





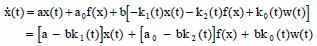
Определим ошибку состояния:





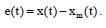
Исходя из рассчёта ошибки состояния, выражения состояния закрытой системы и выражения состояния эталонной модели выясняется, что адаптивная система копирует поведение эталонной модели тогда и только тогда, когда параметры регулятора - (k1,k2,ko) удовлетворяют выражению:





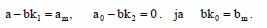
Для синтеза адаптивной системы преобразуем выражение, исходя из выражения состояния закрытой системы, эталонной модели и и так называемой точной настройки:





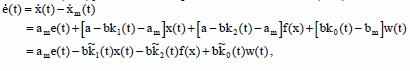
Где


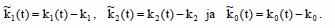
Рассмотрим управление, где известно лишь значение параметра – «b».

Для стабильного анализа и нахождения алгоритма настройки параметров адаптивной системы используем функцию Ляпунова:





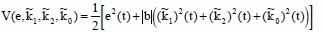
И исходя из этого рассчитаем производную выражения ошибки:







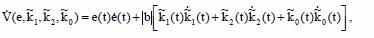
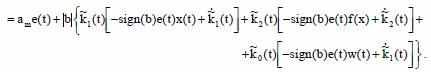
Выбираем алгоритм настройки параметров регулятора:





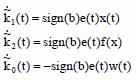
Следовательно, состояние равновесия 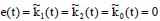стабильно.


Для реализации адаптивной системы представим алгоритм настройки следующим образом:





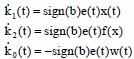
Стабильным состоянием равновесия является - e(t)=0, k1(t)=k1, k2(t)=k2 и ko(t)=ko , что означает полную подражаемость адаптивной системы эталонной системе. (Ennu Rüstern)


ВОПРОС-КАТЕГОРИЯ НОМЕР 6

1. Оценивание параметров в реальном времени?
   

Рассмотрим оценивание параметров динамической системы в реальном времени, на примере идентифицирования адаптивной системы.


Заявляя о проблемме оценивания параметров в реальном времени, будем исходить из скалярной линейной стационарной системы дискретного времени:





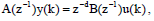
Где,





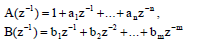
и d запаздывание измеряемого дискретного шага.


Модель динамической системы может быть также представлена в виде дифференциального выражения:





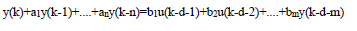
В данном выражении считаем, что y(k) и u(k) обозначают вариацию сигналов, поэтому отклонение реальных сигналов - Y(k) и U(k) устойчиво относительно величин Y∞ и U∞




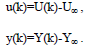
Далее применяем метод меньших квадратов.


Для вывода метода меньших квадратов используем математическую модель:


В промежутке времени - k у нас имеются следующие результаты измерения u(k) и y(k):





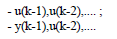
Зная оценивание коэффициентов - ai и bj для A(z−1 ) и B(z−1 ) можно прогнозировать значение на выходе:


Ошибку оценивания на выходе определим следующим образом:





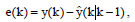
Где y(k) – измеряемая величина.


Из рассчёта последнего, представим нашу модель в виде:





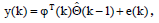
Где ϕ(k) вектор данных в виде:





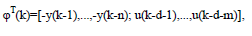
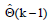- вектор параметров в виде: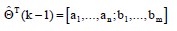





И e(k) – ошибка прогноза выхода.


Предполагая, что - u(k) и y(k) достаточно измеренные величины, образуем

- Матрицу данных, рядами которой будут векторы данных:


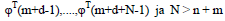(Число параметров оценивания);


- Вектор параметров - Θ;


- Вектор выходов Y, вектор наклона, элементами которого являются данные, полученные на выходе:





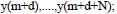
- Вектор ошибок E, вектор наклона, элементами которого являются:


е(m+d),....,е(m+d+N).


Тогда модель можно представить следующим образом:


Y = ΦΘ + E.


Далее используем метод меньших квадратов для нахождения оценки параметров, минимизируя квадрат ошибки:





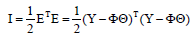
Получаем , что для этого необходимо решить систему нормальных уравнений:





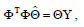
Чьё решение выглядит так:





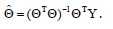
Полученный результат не пременим к системам, работающим в реальном времени.


Для оценивания параметров в реальном времени сконструируем рекурентную схему рассчёта метода меньших квадратов, исходя из:





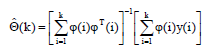
В значении:





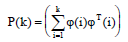
И преобразовав, получим:





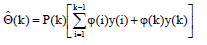
Теперь представим 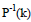в виде: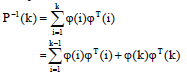





Исходя из проделаных преобразований – получаем:





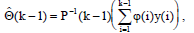
Из чего следует:





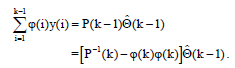
Наконец получаем метод меньших квадратов на базе рекурентной схемы:





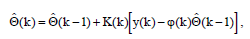
Где, K(k)=P(k)ϕ(k).


Представим метод меньших квадратов в виде рекурентной схемы в НОРМАЛЬНОМ ВИДЕ:





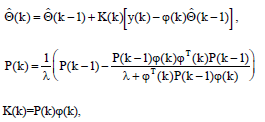
Где:


ϕ(k) – вектор данных,


θ(k) и θ(k-1) векторы параметров,


P(k) и P(k-1) ковариационные матрицы параметров, размера - (n+m)*(n+m),


K(k) вектор коэффициента веса,


λ – коэффициент памяти (λ<1).


В рекурентном методе меньших квадратов существует проблема выбора начальных значений.

Рекоммендуется выбирать эти значения так:





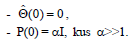
Первостепенной проблемой оценивания параметров в реальном времени - является:


Оценивание значений -U∞ и Y∞ и модифицирование модели:





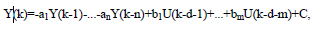
Где, C=(1+a1+...+an)Y∞ - (b1+...+bm)U∞.


(Ennu Rüstern)


ВОПРОС-КАТЕГОРИЯ НОМЕР 7

1. Идентифицирование адаптивных систем?
   

Для прояснения сути работы адаптивной системы с возможностью идентефикации предположим, что управляемая система задана следующим образом и v(k)=0:





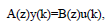
Поведение закрытой системы описывается эталонной моделью:





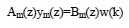
И линеарный регулятор задон следующим выражением:





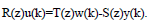
Касаемо модели управляемой системы, предполагаем следующее:


- Полиномы A(z) и B(z) не обладают кооператорами;

- коэффициенты полинома константны, однако не известны;

- степени полиномов (n, m) известны.


Адаптивная управляемая система с возможностью идентификации может быть реализована как с косвенной так и с прямой связью. На основе схемы адаптивной управляемой системы с обратной связью, оцениваются параметры управляемой системы и на основе последних оцениваний строится схема регулятора.


При создании адаптивной управляемой системы с прямой связью оцениваются параметры регулятора, используя свойства системы с обратной связью.


Зачастую адаптивную систему с косвенной связью называют – проявленным (обнаруженным) алгоритмом, (Поэтому процесс адаптации основывается на управляемой системе) а схема адаптивной системы с прямой связью – непроявленным (необнаруженным) алгоритмом.


Сперва, рассмотрим адаптивную управляемую систему на базе схемы с косвенной связью,

чей алгоритм состоит из следующих трёх этапов:


1. Этап – оценивание коэффициентов полиномов - A(z) и B(z) (например с помощью рекурентного метода меньших квадратов);


2. Этап – рассчёт регулятора, в случае линеарного регулятора – нахождение полинома - R(z), S(z) и T(z) ;


3. Этап – рассчёт сигнала управления - u(k).


Далее рассмотрим создание адаптивной, управляемой системы на базе схемы с прямой связью

и линеарного регулятора. При анализе проблеммы будем исходить из:

A(z)R'(z)+B-(z)S(z)=A0(z)Am(z),


Из чего получим:





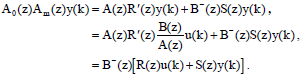
В общем случае параметры такой системы можно привести к следующему виду:





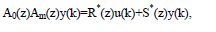
Где, 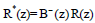и 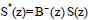. В этом случае R*(z) и S*(z) содержат кооператоры

(содержат медленно затухающие нули), которые прийдётся сократить до работы с управляющим сигналом, воизбежании нестабильности системы.


У алгоритма адаптивной управляемой системы со схемой прямой связи имеются следующие этапы:


1. Этап – рассчёт коэффициентов полиномов R(z) и S(z), (управляемая система – с минимальной фазой и с быстро затухаемыми нулями);

Оценивание коэффициентов и сокращение кооператоров полиномов - R*(z) и S*(z);


2.Этап – рассчёт управляющего сигнала - u(k) и его применение.


(Ennu Rüstern)


ВОПРОС-КАТЕГОРИЯ НОМЕР 8

1. Проблемы, возникающие при проектировании, реализации и использовании адаптивных систем?
   

В настоящее время, при реализации и практическом использовании адаптивных систем возникают три основные проблемы:


- Проблема априорной информации;

– Проблема моделирования управляемой системы;

- Проблема поиска новых методов реализации.


Проблема априорной информации - одна из основных проблем создания адаптивной системы.

Объясним проблему априорной информации на основе модели с полимиальным входом-выходом дискретного времени. Мы предполагаем, что управляемая система, адекватно описывается предложеной моделью, для которой даны:

– Степени полиномов (или матриц-полиномов) A(z-1), B(z-1) и C(z-1) - соответственно равны n, m и n;

- Запаздывание d, измеряемое дискретными шагами;

- Коэффициент b0 - известен или известно лишь его значение.


Ставится вопрос – можно ли уменьшить число априорной информации? Если да, то до какого предела и как?


Классическая адаптивная система содержит два типа обратной связи: основную обратную связь

(сигнальная обратная связь) по состоянию или выходу и информативную обратную связь (параметрическая обратная связь).


Для уменьшения или же полного уничтожения априорной информации имеет смысл ввести другую информативную обратную связь (структурную обратную связь), с помощью которой реализуется адаптивное управление. Следовательно, априорную информацию можно полностью уничтожить только при помощи усложнения адаптивной системы. Для координирования информативной обратной связи и её управления обычно вводится уровень контроля управления.


Проблема моделирования управляемой системы. В случае со многими практическими системами возможно ограничиться линейной системой, пока они довольно точно описывают поведение реальной системы.


Всвязи с тем, что управляемые системы становятся напорядок сложнее, а также возрастают

выдвигаемые требования относительно точности таких систем и в тоже время растут вычислительные возможности, возникли возможность и необходимость использовать нелинейные, а также эмпирические модели.


В саморазвивающихся алгоритмах, используемых при проектировании систем реального времени, возникает проблема - чаще всего не возможно сказать, как много времени пойдёт на саморазвитие такого алгоритма и когда интелегентная эмпирическая модель опишет поведение системы с должной точностью.


Проблемы реализации адаптивной системы. Принимая в рассчёт выше описанные проблемы, можно сказать, что адаптивная система – это система со сложной иерархией, которая реализуется программно, используя программную технологию систем реального времени. Проблемами же адаптивных систем является проектирование адаптационного процесса с должной динамикой и реализация достаточной работоспособности. Для реализации адаптивной системы широко используется - прототипирование.


Прототипирование как основной анализ адаптивных систем, метод проектирования и реализации.


Этапы:


1. Этап – Спецификация управляемой системы;

2. Этап – Моделирование управляемой системы;

3. Этап – Решение и анализ модели;

4. Этап - Juhtimisülesande püstitamine ja korrigeerimine;

5. Этап – Выбор структурной схемы адаптивной системы;

6. Этап - Выбор алгоритма оценивания состояния и\или параметров;

7. Этап – Выбор типа регулятора и определение структуры;

8. Этап – Испытание адаптивной системы на уровне алгоритма;

9. Этап – Анализ результатов и выводы;

10.Этап - Adaptiivsüsteemi realiseerimisega seonduvate kitsenduste sissetoomine;

11.Этап – Испытание адаптивной системы на реализационном уровне;

12.Этап – Анализ результатов и выводы;

13.Этап – Оформление проекта.


(Ennu Rüstern)