А. А. Трофимука Приоритетное направление со ран геофизика, геодинамика Физические поля Земли: природа, взаимодействие, интерпретация Программа
| Вид материала | Программа |
- А. А. Трофимука Приоритетное направление со ран геофизика, геодинамика Физические поля, 268.89kb.
- А. А. Трофимука Приоритетное направление со ран геофизика, геодинамика Физические поля, 208.47kb.
- А. А. Трофимука со ран (Россия, 630090, Новосибирск, пр-т Коптюга, 3, тел.(383) 3309201,, 56.69kb.
- Урок на тему «Магнитное поле Земли», 31.68kb.
- Физические теории главного магнитного поля Земли, 116.06kb.
- Конспект урока. Тема. Постоянные магниты. Магнитное поле Земли, 122.47kb.
- Н. Г. Чернышевского рабочая программа, 145.62kb.
- Международная научно-практическая конференция «Увеличение нефтеотдачи приоритетное, 84.92kb.
- Пригласительный билет и программа V всероссийского литологического совещания Типы седиментогенеза, 295.76kb.
- Введение в физику земли, 1688.72kb.
Российская академия наук
Сибирское отделение
Институт нефтегазовой геологии и геофизики им. А.А. Трофимука
Приоритетное направление СО РАН
Геофизика, геодинамика
Физические поля Земли: природа, взаимодействие, интерпретация
Программа СО РАН
«Развитие теоретико-методических основ геофизических исследований флюидонасыщенных пространственно-неоднородных геологических и техногенно измененных сред»
Координатор: академик М.И. Эпов
Научный проект на 2007-2009 гг.
«Развитие методов поисков нефтегазоносных структур по данным многоволновой сейсморазведки, а также оценки напряженного состояния, фильтрационных возможностей и устойчивости продуктивных пластов»
Руководители: д.ф.-м.н. Б.П. Сибиряков, к.ф.-м.н. В.А. Чеверда
Новосибирск-2006
Научный Проект
«Развитие методов поисков нефтегазоносных структур по данным многоволновой сейсморазведки, а также оценки напряженного состояния, фильтрационных возможностей и устойчивости продуктивных пластов»
Фундаментальная научная проблема. Создание новых моделей континуума, обладающих внутренней структурой, которые достаточно адекватно описывали бы явления динамического и квазистатического деформирования микронеоднородных сред, содержащих флюиды. Наличие удельной поверхности пор и трещин требует либо учета граничных условий на всей сложной поверхности пор и трещин, либо создания принципиально новых схем деформирования, где структура порового пространства была бы учтена с самого начала. В проекте предусматривается развитие как первого, так и второго из упомянутых подходов.
В Институте нефтегазовой геологии и геофизики им. А.А. Трофимука СО РАН накоплен известный научный задел, который позволяет формулировать новые задачи в области теории сейсмических волн и ее применения для решения как структурных, так и геодинамических проблем, развития лабораторного и натурного моделирования процессов межфазового взаимодействия скелет – флюид, а также полевых исследований на месторождениях нефти и газа.
Цель проекта: 1. Развитие методов многоволновой сейсморазведки для поиска пористых и трещиноватых сред,
2. Создание на этой основе методы оценки напряженного состояния продуктивного пласта а также вскрыть его фильтрационные возможности.
- Геофизика и геодинамика нефтегазоносных структур.
1.1. Обоснование необходимости проведения исследований.
Знание скоростей продольных и поперечных волн позволяет, в принципе, интегрировать уравнение равновесия для геологической структуры и на этой основе прогнозировать полный тензор напряжений для упругой модели структуры. Этот метод уже применялся для оценки общего напряженного состояния на одном из месторождений Западной Сибири, и не требует никаких иных исследований, кроме многоволновой сейсморазведки.
Однако, неизбежный разрыв давлений в скелете и флюиде зависит от структуры пор и требует данных петрофизики для решения этой проблемы. Результаты предыдущего проекта показали, что закон Дарси не является необходимым для решения задачи об истечении флюида в скважину. Некоторой неожиданностью оказалось, что проницаемость также не является необходимым параметром оценки эффективности фильтрации жидкости в скважину. Эта эффективность целиком определяется пористостью и удельной поверхностью. Кроме того, появились экспериментальные работы по электроосмосу, где предложены эмпирические формулы, которые связывают проницаемость с пористостью и удельной поверхностью, что также косвенно подтверждает этот тезис.
Межфазовые взаимодействия, как показали результаты предыдущего проекта, проявляются, в частности, в том, что при ультразвуковых колебаниях образца возникают электрические колебания, ортогонально поляризованные для продольных и поперечных волн.
Появление звуковых колебаний при статическом нагружении песков остро ставит вопрос о недостаточно адекватном описании деформирования микронеоднородных сред при помощи обычных сплошных моделей. В самом деле, переход статики в динамику очевиден, однако, он не прописан в уравнениях равновесия и теоретически является невозможным. Поэтому опыты по акустической эмиссии не только являются отличным тестом для верификации новых моделей континуума, но и имеют практическое значение как показатель метастабильного состояния продуктивного пласта.
1.2. Имеющийся задел.
В итоге предыдущего проекта была построена модель континуума среды с микроструктурой, которая описывает деформирование сред, обладающих внутренней поверхностью и, тем самым, средним линейным размером микроструктуры. Наличие очень большого числа степеней свободы тел со структурой приводит к существованию, наряду с продольными и поперечными волнами, также и волн с исключительно низкими скоростями распространения, которые снизу ничем не ограничены. Кроме того, теория предсказывает появление параметрических резонансов в структурированных средах, так что даже малые колебания могут стать причиной появления больших амплитуд и возникновения катастрофических процессов.
Кроме того, в предыдущем проекте были разработаны методы оценки напряженного состояния методами многоволновой сейсморазведки и определения напряженного состояния в окрестности скважины методами многоволнового сейсмического профилирования.
В области межфазовых взаимодействий скелет – флюид обнаружено, что среда, насыщенная жидкостью, при прохождении акустических волн вызывает электрические колебания, которые ортогонально поляризованы для продольных и поперечных волн.
И, наконец, были зафиксированы в опыте звуковые колебания песков при статическом деформировании последних сравнительно небольшими давлениями (до 5 МПА).
Ожидаемые результаты
1.1. Будут исследованы механизмы потери упругой устойчивости продуктивного пласта, и возникновения акустической эмиссии как показателя этой неустойчивости.
1.2. Будут усовершенствованы методы прогноза напряженного состояния в продуктивных слоях со сложным строением пор и трещин.
1.3. Будет развита теория перколяции флюидов на основе интегрально-геометрического описания структуры порового пространства и межфазового взаимодействия скелет – флюид.
1.4. Будет установлена возможность определения фильтрационно-емкостных характеристик горных пород по параметрам взаимодействия физических полей различной природы.
1.5. Будет усовершенствована методику многоволновой сейсморазведки для оценки анизотропии карбонатных коллекторов с ориентированными трещинами.
Задание на 2007 год.
1.1.1. Дать теоретическое описание возникновения звуковых волн при статическом деформировании песков.
1.1.2. Построить алгоритмы и программы для разрыва давлений в скелете и флюиде трещиноватых коллекторов.
1.1.3. Объяснить возникновение нелинейных явлений при распространении слабых волн в микронеоднородных средах.
1.1.4. Разработать, изготовить и настроить новый аппаратурно-методический комплекс для исследования акустоэлектромагнитных эффектов в пористых средах, насыщенных флюидами различной электропроводностью.
1.1.5. Разработка и опробование на реальных данных 3D-сейсмики алгоритм бессекторного азимутального скоростного анализа и его применение для оценки пространственных динамических характеристик отраженных волн.
2. Развитие волновых методов локализации геологических объектов.
2.1 Развитие численных методов, разработка алгоритмов и создание программного обеспечения для изучения проявления скоплений мелкомасштабных неоднородностей в волновых сейсмических полях.
2.1.1 Обоснование необходимости проведения исследований.
Одним из основных стимулов к рассмотрению задач взаимодействия сейсмических волн со скоплениями мелкомасштабных неоднородностей является необходимость изучения строения кавернозно-трещиноватых резервуаров, представляющих из себя совокупность каверн, соединенных системой трещин. Размеры этих микронеоднородностей колеблются от миллиметров до первых десятков сантиметров, в то время как их совокупности простираются на сотни метров и более. Фильтрационно-емкостные характеристики резервуара и извлекаемость находящихся в нем углеводородов во многом определяется характером распределения каверн и трещин в силу того, что именно они управляют гидравлическими течениями, являясь либо соединительными каналами (открытые трещины), либо непреодолимыми барьерами (минерализованные трещины). Таким образом, для оценки фильтрационно-емкостных свойств кавернозно-трещиноватых резервуаров необходимо знание ряда ключевых параметров сети трещин и каверн. В частности, к ним относятся – локализация скоплений микронеоднородностей, их концентрация, преимущественная ориентация и характерные размеры. Однако вплоть до настоящего времени не существует надежных методов для оценки этих параметров. Действительно, скважинные наблюдения дают распределение трещин только лишь в непосредственной близости от расположения скважины. Очень интенсивно в последнее время развиваются дистанционные, прежде всего сейсмические, методы изучения зон скоплений микронеоднородностей (Левянт и др., 2003, 2005; Поздняков и Чеверда, 2005; Khaidukov et al., 2005). Однако вплоть до настоящего времени все эти подходы были ориентированы исключительно на индикацию – есть в данном объеме неоднородности субсейсмического масштаба или нет, и ни о каком количественном их описании речи не шло. Естественно, что первым шагом в направлении развития методов определения количественных характеристик скоплений микронеоднородностей и должно явиться детальное изучение их проявлений в сейсмических волновых полях. Только на этой основе и можно ставить задачу определения таких важных параметров, как концентрация, преимущественная ориентация и характерные размеры трещин и каверн.
2.1.2. Имеющийся задел.
К настоящему времени и в Институте нефтегазовой геологии и геофизики им. А.А. Трофимука СО РАН накоплен большой опыт по разработке численных методов и созданию программного обеспечения для моделирования процессов распространения сейсмических волн в сложных средах. Перечислим кратко основные результаты, формирующие основу для развития методов численного моделирования сейсмических волновых полей в трехмерно неоднородных разномасштабных средах:
- разработаны численные методы моделирования сейсмических волновых полей, использующие локальное пространственное измельчение сеток в декартовой и цилиндрической системах координат (Kostin et al., 2006; Вишневский, 2006); при этом используются законы измельчения, установленные эмпирически в результате выполнения серии представительных численных экспериментов;
- разработаны эффективные методы ограничения расчетной области (Kostin et al., 2006; Решетова и Чеверда, 2006; Лисица, 2006) путем ее окаймления слоем с идеально подобранным поглощением; все эти разработки являются оригинальными и приводят к использованию таких слоев либо совсем без расщепления (декартова система координат), либо с расщеплением не по всем переменным (цилиндрическая система координат);
- накоплен опыт разработки численных методов (декомпозиция области) и создания программного обеспечения для численного моделирования процессов распространения сейсмических волн в трехмерно неоднородных средах (Kostin et al., 2006; Вишневский, 2006; Решетова и Чеверда, 2006);
- предложены алгоритмы оптимального разбиения расчетной области, обеспечивающие равномерную загруженность процессоров.
2.1.3. Цели и предполагаемые научные результаты на 2007 год.
2.1.3.1. Разработка явных конечно-разностных схем с пространственно-временным измельчением сеток.
Построение консервативных явных конечно-разностных схем для решения задач динамической теории упругости с использованием локального пространственно-временного измельчения сеток, связанного с необходимостью описания мелкомасштабных неоднородностей, локализованных в некоторых областях среды для двумерных сред. Устойчивость полученных схем. Численная дисперсия и численная анизотропия. Анализ коэффициентов отражения/прохождения на искусственно вводимой границе измельчения сетки.
Планируемые работы являются полностью оригинальными и позволят разработать методы для численного моделирования процессов формирования и распространения рассеянных сейсмических волн в точной постановке, с учетом всех протекающих при этом процессов, включая и многократное рассеяние. Оригинальной является и возможность использования этого программного обеспечения для изучения процессов многократного рассеяния в точной постановке.
2.1.3.2. Теория однократного рассеяния сейсмических волновых полей для сложнопостроенных вмещающих сред.
Изучение рассеяния продольных и поперечных Гауссовых пучков на мелкомасштабных неоднородностях для двумерных сред. Получение итоговых соотношений для описания рассеянной компоненты сейсмического волнового поля для сложнопостроенных вмещающих сред на основе использования представления падающей волны в виде суперпозиции Гауссовых пучков. Изучение особенностей возникновения рассеянных волн в областях нерегулярности центрального поля лучей. Сравнительный анализ интенсивности рассеянной компоненты с интенсивностью волновых полей во вмещающей среде. Особое внимание предполагается уделить изучению проявления статистических свойств мелкомасштабных объектов (их плотности, преимущественной длины и ориентации и ряда других) в статистических свойствах рассеянных волновых полей.
Оригинальность планируемых работ состоит в использовании представления рассеянного сейсмического волнового поля в виде суперпозиции «рассеянных» Гауссовых пучков, что позволяет рассматривать ситуации с нарушением регулярности поля лучей для проходящей волны.
2.1.3.3. Отделение рассеянных/дифрагированных сейсмических волн от волн отраженных.
Выделение рассеянных продольных и поперечных волн на фоне интенсивных отражений от регулярных границ раздела на основе использования обращенного продолжения волновых полей по Гауссовым пучкам. Оценка разрешающей способности.
Оригинальность работ состоит в использовании развиваемого в Институте нефтегазовой геологии и геофизики им. А.А. Трофимука СО РАН подхода «направленного» продолжения волновых полей с использованием их декомпозиции по Гауссовым пучкам. Преимущество по сравнению с другими подходами состоит в повышении разрешающей способности за счет использования чрезвычайно остро направленных волновых полей, формируемых с помощью декомпозиции по Гауссовым пучкам.
2.2. Развитие методов решения обратных задач для систем наблюдений с конечной апертурой.
2.2.1 Обоснование необходимости проведения исследований.
В настоящее время повышение эффективности определения параметров среды связывается с использованием динамических параметров волновых полей. Основные усилия будут направлены на решение проблем, относящихся к решению обратной динамической задачи сейсморазведки. При этом имеется в виду как полная, так и усеченная постановки. Для первой постановки актуальным является преодоление проблем, связанных с применением уже известного решения обратной динамической задачи сейсмики для вертикально-неоднородных сред, задача второй - состоит в развитии метода многоволнового AVO анализа для тонкослоистых и анизотропных сред.
Несмотря на то, что для определенных классов моделей (в частности, для вертикально-неоднородных) существуют решения обратной динамической задачи, на практике возникает много проблем при их производственном применении. Эти проблемы необходимо решить прежде, чем решение рафинированной математической задачи можно будет применить к реальным сейсмограммам.
Осадочные отложения большинства районов Западной и Восточной Сибири подпадают под класс вертикально-неоднородных сред, но остается проблема учета верхней части среды (ВЧС). Нужно отметить, что даже для задачи структурного построения разреза остро стоит проблема учета ВЧС в районах траппового магматизма Восточной Сибири и в районах криолитозоны Западной Сибири.
При решении обратной задачи оптимизационными методами важное значение имеет определение глобального экстремума при работе с много экстремальной целевой функцией и здесь одним из важных моментов является правильный выбор начального приближения.
Для решения обратной задачи необходимо знать форму импульса волн, распространяющихся в среде от источника, которая реально неизвестна. Поэтому встает еще одна специфическая задача, это - изучение формы падающего в среду сигнала и его вариации от источника к источнику по регистрируемым сейсмограммам. Определение формы импульса волны в источнике также имеет существенное значение для акустического каротажа (АК). Условия АК не подпадают под класс одномерных задач и здесь обратная задача пока не решена. Но даже определение кинематических параметров поперечной волны в условиях ее интерференции с ранее пришедшей продольной волной требует знание импульса падающей волны, определить который можно только по зарегистрированным данным.
2.2.2 Предполагаемые результаты исследований.
Исследование ограничений, обусловленных несоответствием между существующими системами наблюдений и условиями, при которых получается решение ОДЗС. Здесь усилия будут направлены на развитие эффективных методов решения прямых динамических задач полуаналитическим методом для слоистых сред в пространственно-временной области, устранение краевых эффектов и сохранение полного динамического диапазона. Будут исследованы возможности использования R-алгоритма, будет проведено теоретическое и численное исследование влияния факторов ограниченности апертуры и конечности интервала наблюдения на точность восстановления параметров среды.
С целью снижения вычислительной сложности при работе оптимизационных алгоритмов будет исследован метод построения хорошего начального приближения по геолого-геофизическим данным. Целью решения ОДЗС будет являться не восстановление неизвестной среды, а уточнение пространственных вариаций ее упругих (а также неупругих, типа коэффициента поглощения) характеристик.
Изучение и способы учета ВЧС при решении структурных задач сейсмики и ОДЗС. Будет получена операторная форма учета влияния ВЧС и исследован комбинированный подход, при котором геометрические искажения учитываются при помощи скалярного уравнения, а учет кратных волн, обусловленных верхней частью, производится в операторной форме. Развитие метода продолжения сейсмического волнового поля на уровень ниже ВЧС и создание соответствующих алгоритмов с целью устранения ее влияния.
Определение формы импульса, распространяющегося в среде. Определение формы импульса в условиях стабильного возбуждения и приема и получение усредненного импульса по профилю. Разработка метода изучение локальных вариаций формы сигнала в связи с изменчивостью условий возбуждения и регистрации сейсмических волн.
2.3. Развитие алгоритмов многоволнового AVO-анализа.
2.3.1. Азимутальный AVO-анализ.
Наличие вертикально ориентированных трещин в среде влечет за собой азимутальную анизотропию скоростей и, как следствие этого, азимутальную анизотропию коэффициентов отражения и амплитуд волн. Трещиноватый коллектор может быть представлен в виде модели трансверсально-изотропной среды с горизонтальной осью симметрии. Наиболее надежные результаты при изучении анизотропии среды могут быть получены с использованием поперечных и обменных волн. Однако изучение азимутальных изменений скоростей и амплитуд продольных волн также дает решение этой задачи.
Разрабатываются различные подходы к решению обратной задачи по данным азимутального AVO-анализа продольных и обменных волн. На основе метода наименьших квадратов создана программная реализация алгоритма посекторного AVO-анализа продольных волн, позволяющего определить направление трещин в подстилающем анизотропном слое. Планируется дальнейшее развитие алгоритма с целью определения коэффициента анизотропии среды, связанного с плотностью трещин.
Параллельно с этим будет выполняться работа по созданию оптимизационного алгоритма совместной AVO-инверсии данных продольных и обменных волн. В качестве теоретического значения коэффициента отражения обменной PS-волны от анизотропного полупространства в целевой функции будет использовано аппроксимационное выражение, полученное в лаборатории ранее. Планируется провести выбор метода оптимизации на основе исследования свойств целевой функции.
При использовании различных подходов к изучению анизотропных свойств среды на основе реальных 3D-данных имеется одна очень серьезная проблема. Она состоит в том, что применяющиеся в настоящее время трехмерные системы наблюдений не являются оптимальными для проведения азимутального анализа данных. Это связано с неравномерной плотностью наблюдений на различных удалениях от источников и в различных азимутах, что ухудшает работу алгоритмов азимутального скоростного и амплитудного анализов и приводит к большим погрешностям определения параметров среды.
Решение этой проблемы может быть найдено путем постановки задачи восполнения наблюденных 3D-данных. Возможны различные подходы к решению этой задачи. В полной постановке – требуется восстановить полное волновое поле, т.е. недостающие сейсмограммы. В усеченной постановке – восстанавливаются некоторые функционалы волнового поля, например, скорости или амплитуды отраженных волн. В соответствии с этими постановками возможны два направления в развитии исследований.
По первому направлению в настоящее время выведено трехмерное уравнение DMO, которое предполагается использовать для восполнения площадных данных. В рамках проекта предстоит исследовать постановку краевой задачи для этого уравнения на устойчивость. В результате планируется получить подсистемы наблюдений, для которых краевая задача для уравнения DMO является корректной. Для решения этой задачи целесообразно сначала воспользоваться некоторой аппроксимацией. Наиболее предпочтителен в этом плане метод наименьших квадратов с конечно-разностным регуляризатором.
По второму направлению будут разработаны алгоритм и компьютерная программа для пополнения данных в массиве наблюденных амплитуд. Предполагается, что переход от амплитуд отраженных волн к коэффициентам отражения известен. В основе алгоритма лежит интерполяция значений коэффициентов отражения на равномерной сетке по удалениям и азимутам.
2.3.2. Подход к AVO-проблеме с применением эффективного коэффициента отражения
В рамках лучевого метода плоско-волновой коэффициент корректно может описать явления отражения-преломления лишь на плоской границе раздела сред. В реальных средах границы ведут себя сложным образом, что приводит к существенному усложнению поведения волнового поля на границах. Кроме того, лучевым методом нельзя корректно рассчитать волновое поле в критической точке, где появляется головная волна, а у отраженной волны - мнимая компонента. Также особую сложность для описания представляет область интерференции отраженной и головной волны. Эффективный коэффициент отражения (Klem-Musatov K., Aizenberg A. et al., 2004) позволяет решить описанные выше проблемы.
Разработан оптимизационный алгоритм AVO-инверсии закритических отраженных продольных волн. В отличие от традиционной постановки в нем используется нелинеаризованный плоско-волновой коэффициент отражения (точная формула Цеппритца). На модельных данных проведено исследование целевых функций, получены оценки точности определения параметров среды. Однако остается открытым вопрос, насколько правомочно описывать закритические отражения лучевым методом.
В связи с этим планируется провести исследование корректности решения задачи AVO-инверсии по закритическим отражениям в рамках лучевого метода. Для этого будет проведено моделирование волнового поля методом конечных разностей, имитирующее реальный эксперимент. По полученным данным будут построены AVO-зависимости и проведен сравнительный анализ этих зависимостей с поведением плоско-волнового и эффективного коэффициентов отражения. Планируется также сравнить точность решения задачи AVO-инверсии по закритическим отражениям в рамках лучевого метода и методом точных операторов отражения и преломления.
Задание на 2007 г.
2.3.3. Исследовать корректность решения задачи AVO-инверсии по закритическим отражениям в рамках лучевого метода.
Ожидаемые результаты исследований:
Будет проведено моделирование волнового поля методом конечных разностей, имитирующее реальный эксперимент. По полученным данным будут построены AVO-зависимости и проведен сравнительный анализ этих зависимостей с поведением плоско-волнового (метод неравномерных асимптотик) и эффективного (метод равномерных асимптотик) коэффициентов отражения. Планируется также оценить точность решения задачи AVO-инверсии по закритическим отражениям в рамках лучевого метода и метода равномерных асимптотик.
2.3.4. Развитие метода оценки формы распространяющегося в среде сигнала продольной волны с целью выделения поперечной волны в условиях сильной интерференции.
Ожидаемые результаты исследований:
Будет получен и исследован на тестовых моделях способ получения формы сигнала продольной волны по данным зарегистрированного волнового поля АК. На основе полученного сигнала будет проведено корректное вычитание продольной волны из полного поля в условиях интерференции продольных и поперечных волн. Это позволит определить кинематику и динамику поперечной волны и в частности определить параметр гамма. Будет проведена обработка данных АК для Когалымского месторождения.
2.4. Теоретико-экспериментальные исследования анизотропии скоростей и поглощения в слоях-коллекторах, разработка алгоритмов и программ для решения обратных задач по комплексу характеристик PP- и PS-волн, включающему скорости, коэффициенты поглощения и коэффициенты отражения.
2.4.1. Обоснование перспективности предлагаемой разработки.
Исследования последних лет показали большие возможности использования данных по азимутальной анизотропии поглощения сейсмических волн в слоях-коллекторах для их поиска. Обнаружено, что анизотропия поглощения может превышать анизотропию скорости на один-два порядка, что и создает предпосылки для использования пространственных вариаций поглощения при поиске трещиноватых коллекторов. Работа в данном направлении только начата, и ИНГГ СО РАН вместе с Мексиканским институтом нефти являются пионерами в этом начинании. Предложен новый метод поиска трещиноватых коллекторов, он назван QVOA (Q Versus Offset and Azimuth), по аналогии с известным методом AVOA (Amplitude Versus Offset and Azimuth), так как оба метода имеют много общего в своей структуре. Чтобы сохранить лидерство и извлечь максимум пользы из найденного эффекта, надо продолжить развитие метода QVOA и довести его до использования при полевых работах.
Предлагается использовать метод QVOA вместе с широко применяемыми методами азимутального скоростного анализа и AVOA (коэффициентов отражения в функции расстояния и азимута); при этом совместной интерпретации подлежат данные по двум типам волн: PP и PS. При решении обратной задачи в такой постановке можно добиться наибольшей точности и однозначности в определении направления трещиноватости, а также определить некоторые характеристики трещиноватости и тип флюида.
2.4.2 Имеющийся задел.
Заделом в общем плане могут служить выполненные в предыдущие годы И.Р. Оболенцевой теоретические исследования по сейсмической анизотропии и разработанные ею совместно с В.Ю. Гречкой алгоритмы и программы решения прямых задач лучевым методом.
Конкретным заделом для выполнения работы по проекту являются публикации:
- Чичинина Т.И., Сабинин В.И., Ронкийо-Харийо, Х., Оболенцева И.Р. Метод QVOA для поиска трещиноватых коллекторов, Геология и геофизика, 2006, т. 47, с. 259-277;
- Chichinina T., Sabinin V., Ronquillo-Jarillo G. QVOA analysis: P-wave attenuation anisotropy for fracture characterization, Geophysics, 2006, vol. 71, No. 3, C37-C48.
- Чичинина Т.И., Сабинин В.И., Корсунов И.В., Ронкийо-Харийо Х. Азимутальный анализ отраженных продольных волн в азимутально-анизотропных средах при разведке нефтегазовых резервуаров. Сейсмические исследования земной коры. Сборник докладов Международной научной конференции, г. Новосибирск, Академгородок, 23-25 ноября 2004 г. – Новосибирск: Издательство СО РАН, 2004, с. 196-202.
В первых двух публикациях представлена положенная в основу метода QVOA приближенная формула для поглощения
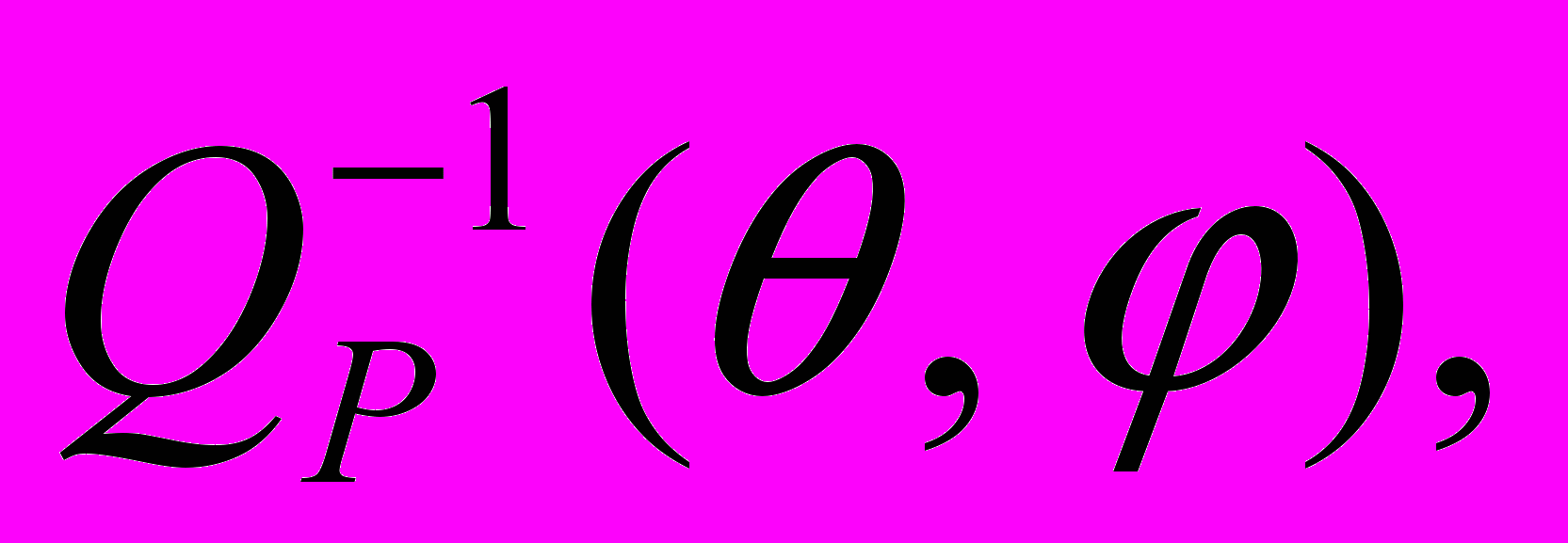где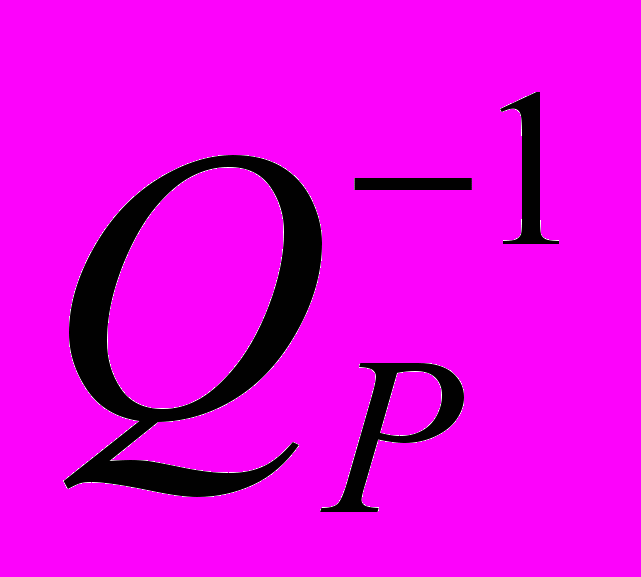 
– обратная величина добротности, или фактора Q, а 
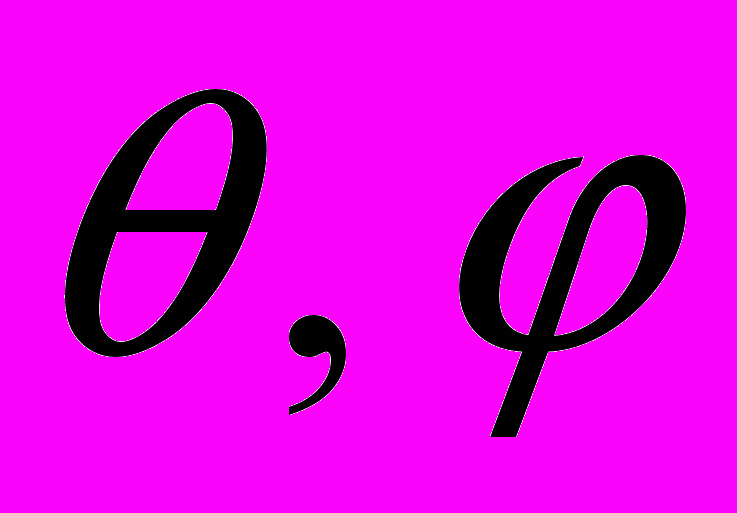– углы волновой нормали P-волны, распространяющейся в поглощающей HTI-среде, т.е. трансверсально-изотропной с горизонтальной осью симметрии. Такая среда, как известно, является эффективной моделью вертикально трещиноватой среды. Формула получена путем разложения найденного аналитического решения для 
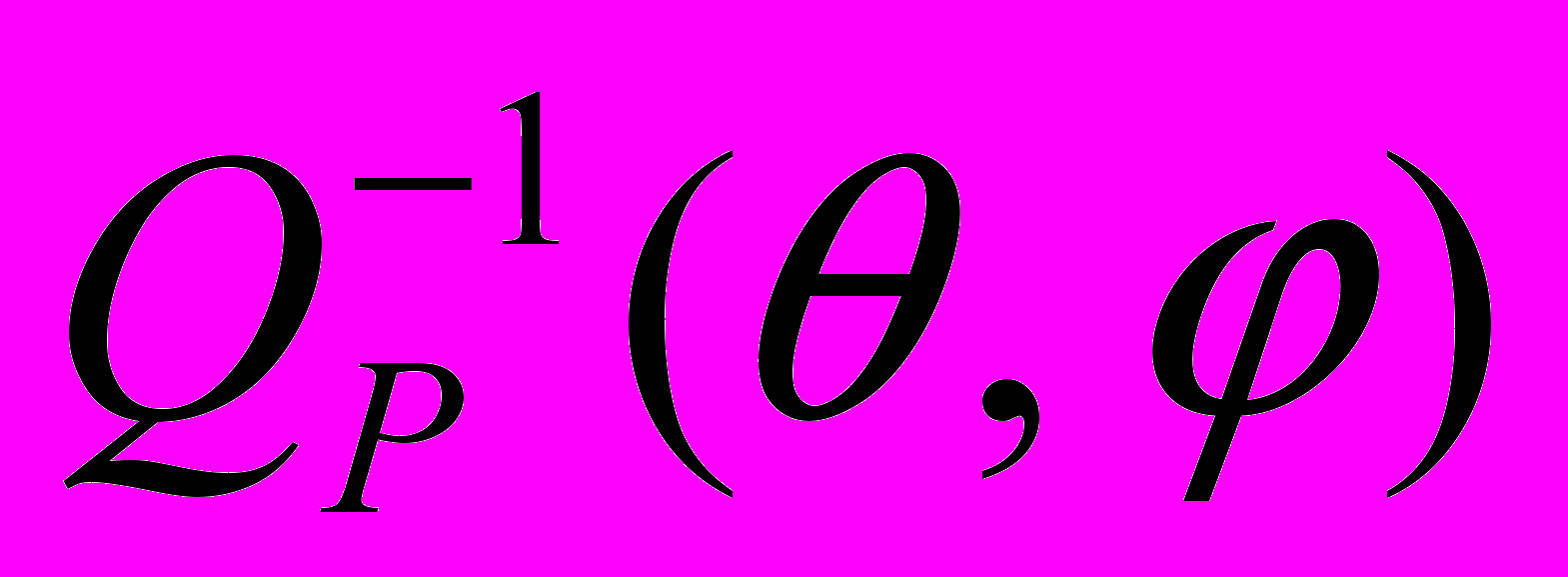в ряд Маклорена по четырем малым параметрам: действительным и мнимым частям нормальной и касательной ослабленностей, входящих в комплексную матрицу модулей упругости. В третьей из указанных публикаций изложен разработанный авторами этой статьи алгоритм метода AVOA.2.4.3 Цель работы и решаемые задачи (на 3 года).
Цель работы сформулирована в названии разработки. Она достигается путем последовательного решения следующих задач. Сначала решается задача, состоящая в нахождении точных аналитических выражений для поглощения всех трех типов волн, распространяющихся в среде HTI, затем производится линейная аппроксимация найденных выражений и строятся на ее основе алгоритмы и программы решения обратных задач по данным PP- и PS-волн. Следующая задача – построение алгоритмов и программ решения обратных задач по коэффициентам отражения PP- и PS-волн. Далее предстоит решить задачу объединения построенных алгоритмов методов QVOA и AVOA с известными алгоритмами скоростного анализа для PP- и PS-волн в один оптимизационный алгоритм для нахождения всех параметров, характеризующих слой-коллектор. Заключительный этап – переход от найденных параметров анизотропии к параметрам, характеризующим свойства коллектора, путем использования конкретных физических моделей коллектора.
Проверка физических предпосылок, положенных в основу моделей коллекторов, а также работоспособности построенных алгоритмов выполняется путем их применения к данным лабораторного ультразвукового моделирования, полученным на модели вертикально трещиноватой тонкослоистой среды.
2.4.4. Предполагаемые научные результаты в 2007 г.
1. Будет построен тензор комплексных модулей для среды HTI, (а) наиболее адекватно описывающий симметрию как упругих свойств, так и поглощения, (б) позволяющий получить ограничения, в виде неравенств, на константы упругости и поглощения.
2. Будут созданы алгоритм и программа нахождения поглощения волн P и S1, S2 в слое-коллекторе по 3-компонентным записям отражений от его кровли и подошвы.
3. Будет выполнена проверка соответствия построенного теоретического описания поглощения в вертикально трещиноватых коллекторах данным эксперимента. Также будет выполнена проверка работоспособности разработанных алгоритмов инверсии данных 3D-3С по скоростям и поглощению волн P и S двух типов.
Задание на 2007 год.
1. Исследовать различные возможности построения тензора комплексных модулей упругости для поглощающей вертикально трещиноватой среды и выбрать оптимальный вариант тензора.
2. Создать модификацию метода QVOA для обменных PS-волн.
3. Провести первые эксперименты по инверсии скоростей и поглощения P- и S-волн двух типов, полученных путем физического моделирования на трехмерной модели среды с вертикальной трещиноватостью.
2.5 Разработка теории и алгоритмов моделирования сейсмических волн в сложно построенных средах с учетом псевдодифференциальных операторов отражения и преломления для повышения разрешающей способности Сейсмического метода
2.5.1. Обоснование проекта
В предыдущие годы была построена скалярная теория отражения-преломления сейсмических волновых полей для слоистых неоднородных сред, основанная на неизвестном ранее способе удовлетворения условий сопряжения полей на гладких криволинейных границах произвольной формы с помощью интегральных псевдодифференциальных операторов отражения и преломления (ПДО). Исследование этих операторов показало, что их асимптотическое значение при больших значениях доминантной частоты колебаний формируется за счет вкладов по малой окрестности точки отражения-преломления. Это позволило построить предварительную простейшую аппроксимацию таких операторов. С помощью математического моделирования было установлено, что использование этой аппроксимации позволяет воспроизводить волновое поле, отраженное и преломленное гладкими криволинейными границами, с учетом головных волн. Целью данного проекта является разработка методов математического моделирования сейсмических волн, основанных на использовании операторов ПДО.
2.5.2.Основные этапы
1). Высокочастотная аппроксимация операторов ПДО для скалярных волновых полей.
2). Модификация скалярной версии метода наложения концевых волн (МНКВ) на случай операторов ПДО.
3). Обобщение модифицированного МНКВ на случай многократных отражений и преломлений.
4). Обобщение полученных высокочастотных асимптотик на случай упругих волновых полей.
2.5.3. Задание на 2007 год.
Разработать теоретически обоснованный асимптотический алгоритм математического моделирования скалярных волновых полей на основе использования операторов ПДО.
2.5.4 Предполагаемые результаты к концу 2007 года
Будут получены теоретически обоснованные формулы равномерной высокочастотной асимптотики скалярных волновых полей, возникающих при отражении и преломлении на кусочно-гладкой криволинейной границе между трехмерными неоднородными средами. В рамках этой асимптотики оператор ПДО будет аппроксимирован оператором решения более простой эталонной задачи, допускающей реализацию вычислений на современных компьютерах. В отличие от существующих асимптотических методов моделирования отражений-преломлений с помощью поверхностных интегралов типа Кирхгофа полученная модификация МНКВ будет учитывать явления головления волн на криволинейных границах, включая дифракцию головных волн.
В проекте задействовано
Научных сотрудников 27
Докторов наук 3
Кандидатов наук 17
| | 2007 | 2008 | 2009 |
|---|---|---|---|
| бюджет | 6272 | 7614 | 9243 |
| РФФИ | 1280 | | |
| научные школы | 300 | | |
| интеграционные проекты СО РАН | 1620 | | |
| проекты РАН | | | |
| поддержка экспедиционных работ | | | |
| поддержка стационаров | | | |
| средства института | 1500 | | |
| научное оборудование (по линии Приборной комиссии) | | | |
Руководители проекта: д.ф.-м.н. Б.П. Сибиряков, к.ф.-м.н. В.А. Чеверда