Методические указания по выполнению контрольной работы №1 по дисциплине Информатика На тему: Линейные алгоритмы. Разветвляющиеся алгоритмы для студентов II курса заочного отделения специальности

Вид материала

Методические указания

Содержание 6.9. Как эвм реализует команды, какие действия при этом выполняет Все операции над данными выполняет процессор ЭВМ! 6.10.1. Алгоритмы линейной структуры

Подобный материал:

• Методические указания по выполнению контрольной работы №2 по дисциплине Информатика, 278.17kb.
• Методические указания по выполнению домашней контрольной работы по дисциплине «Основы, 108.96kb.
• Методические указания по выполнению домашней контрольной работы для студентов заочного, 995.29kb.
• Методические указания по выполнению контрольной работы, 443.72kb.
• Методические указания по выполнению домашней контрольной работы по дисциплине «Экономика, 443.44kb.
• «Численные методы в химии» Общая трудоёмкость дисциплины составляет, 22.46kb.
• Методические указания по выполнению контрольной работы по курсу, 260.49kb.
• Учет и анализ на предприятиях малого бизнеса, 651.56kb.
• Методические указания и задания к выполнению контрольной работы по дисциплине, 246.08kb.
• Методические указания домашняя контрольная работа по дисциплине «Финансы организации», 568.97kb.

6.9. КАК ЭВМ РЕАЛИЗУЕТ КОМАНДЫ, КАКИЕ ДЕЙСТВИЯ ПРИ ЭТОМ ВЫПОЛНЯЕТ

На рис. 4 изображена структурная схема ЭВМ, где схематично показаны основные устройства ЭВМ, участвующие в процессе ввода, обработки, хранении и выводе информации, а также показаны связи между этими устройствами.





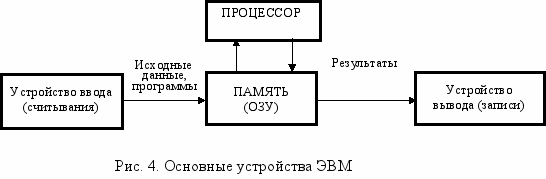
ЭВМ способна обрабатывать исходные данные только в том случае, если в память машины кроме данных, введена программа, с помощью которой эти данные необходимо обрабатывать.

Современные ЭВМ допускают различные способы ввода исходной информации в память машины. Наиболее широко используется ввод непосредственно с клавиатуры.

Процессор ЭВМ считывает данные из памяти, выполняет над ними необходимые операции, указанные в программе, и результаты вычислений вновь записывает в память ЭВМ.

Результаты обработки данных (выполнения программы) можно увидеть, если вывести их на экран монитора или распечатать на принтере.


 Все операции над данными выполняет процессор ЭВМ!


Следует отметить то обстоятельство, что машина не может понять смысл решаемой задачи, так как ЭВМ — это только электронный робот, который точно выполняет указания, записанные в программе. Поэтому лишь точно и однозначно сформулированные предписания могут быть переданы для выполнения вычислительной машине.

Для решения задачи в память ЭВМ необходимо поместить всю информацию необходимую для её решения.

Память машины состоит из ячеек (рис. 5). Данные, преобразованные в машинные слова, заносятся в ячейки по одному слову в каждую ячейку. Записанную в память информацию можно неоднократно считывать и использовать в вычислениях. Однако если в ячейку памяти вводится новое слово, то прежняя информация, хранившаяся в этой ячейке, исчезает.




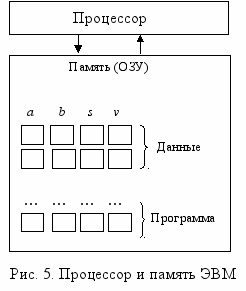
Рассмотрим как машина решет простую задачу нахождения среднего арифметического двух чисел.

Алгоритм решения задачи.

1. Прочитать из ячеек памяти a и b исходные данные, сложить их и полученный результат записать в ячейку s.
   
2. 2. Прочитать число, находящееся в ячейке s, разделить его на 2 и полученный результат записать в ячейку v.
   

Два задаваемых числа — это исходные данные, которые перед решением задачи должны быть помещены в память. Ячейки, хранящие эти данные, названы именами a и b, а место памяти, предназначенное для хранения выходного данного, — v (рис. 6). Ячейка с именем s, куда заносится сумма исходных данных, называется ячейкой промежуточного результата.





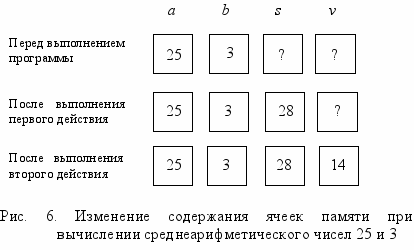
Если в ячейке памяти a к началу выполнения программы находилось число 25, а в ячейке b — число 3, то после выполнения двух указанных операций в ячейку v будет записан результат — число 14. Нетрудно заметить, что при других исходных данных по той же программе будет получен другой результат. Следовательно, одна и та же программа пригодна для решения множества задач, отличающихся друг от друга только значениями исходных данных.

6.10. ПРИМЕРЫ СОСТАВЛЕНИЯ АЛГОРИТМОВ

6.10.1. Алгоритмы линейной структуры

Пример 1.

Математическая формулировка задачи.

О
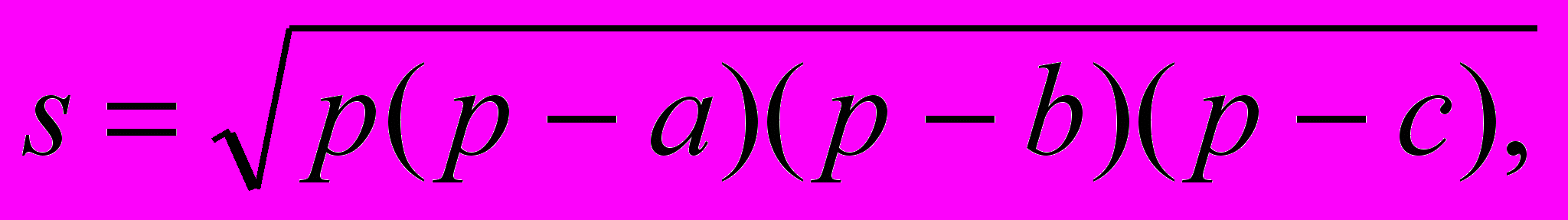
пределить площадь треугольника по формуле Герона

где a, b, c — длины сторон треугольника;

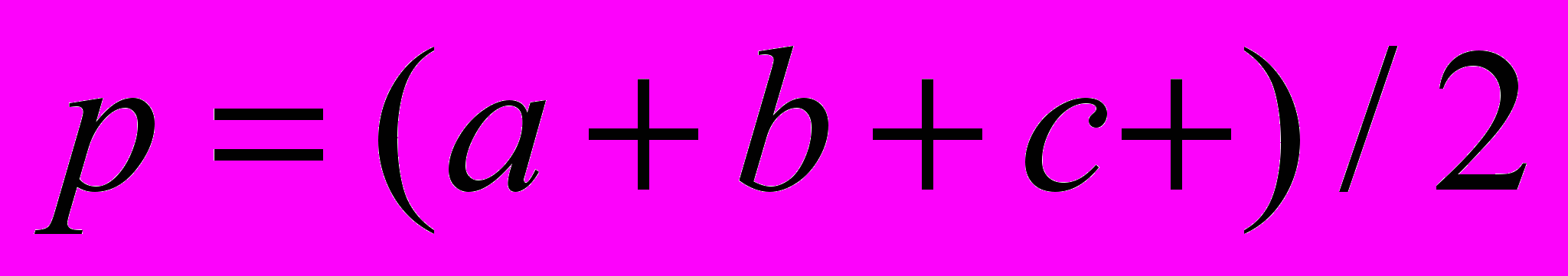— полупериметр треугольника.

Описательный алгоритм решения задачи.

1. Ввод с клавиатуры исходных данных a, b, c.
   
2. Вычисление p по формуле.
   
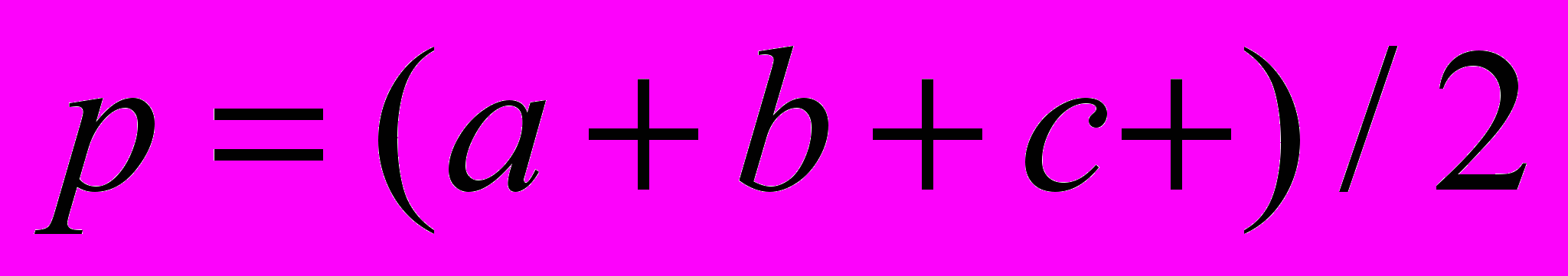3. Вычисление s по формуле .
   
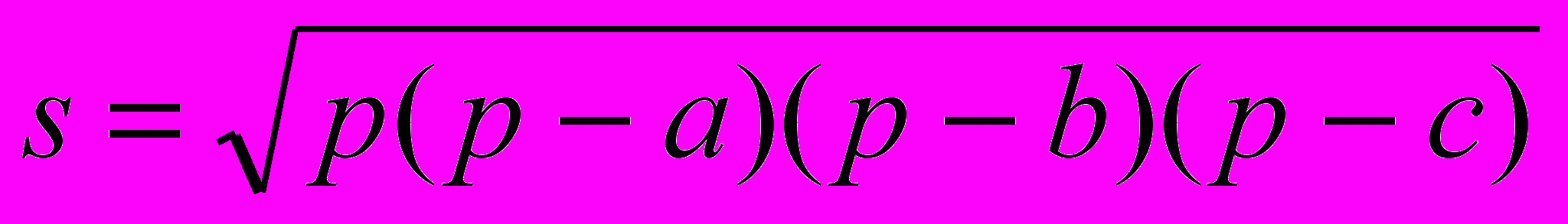4. Вывод результата s на экран монитора.
   

Графический алгоритм решения задачи.

Блок-схема алгоритма представлена на рис. 7. На семе блоки расположены в той последовательности, в которой они должны выполняться Любая перестановка блоков приведёт к невозможности решения задачи.




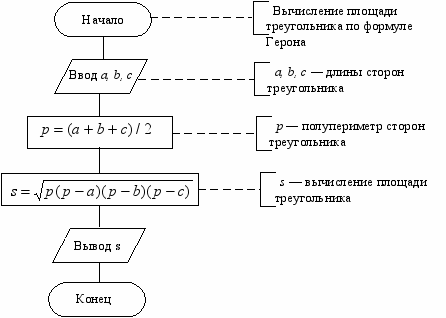
Рис. 7. Блок-схема алгоритма вычисления площади треугольника по формуле Герона.


Пример 2.

Формулировка задачи.

Опытный рабочий выполняет задание за a дней, а вместе с учеником — за b дней. Сколько времени потребуется одному ученику для выполнения всего задания?

Описательный алгоритм решения задачи.

1. Ввод с клавиатуры исходных данных a, b.
   
2. Вычисление производительности рабочего p_r по формуле.
   
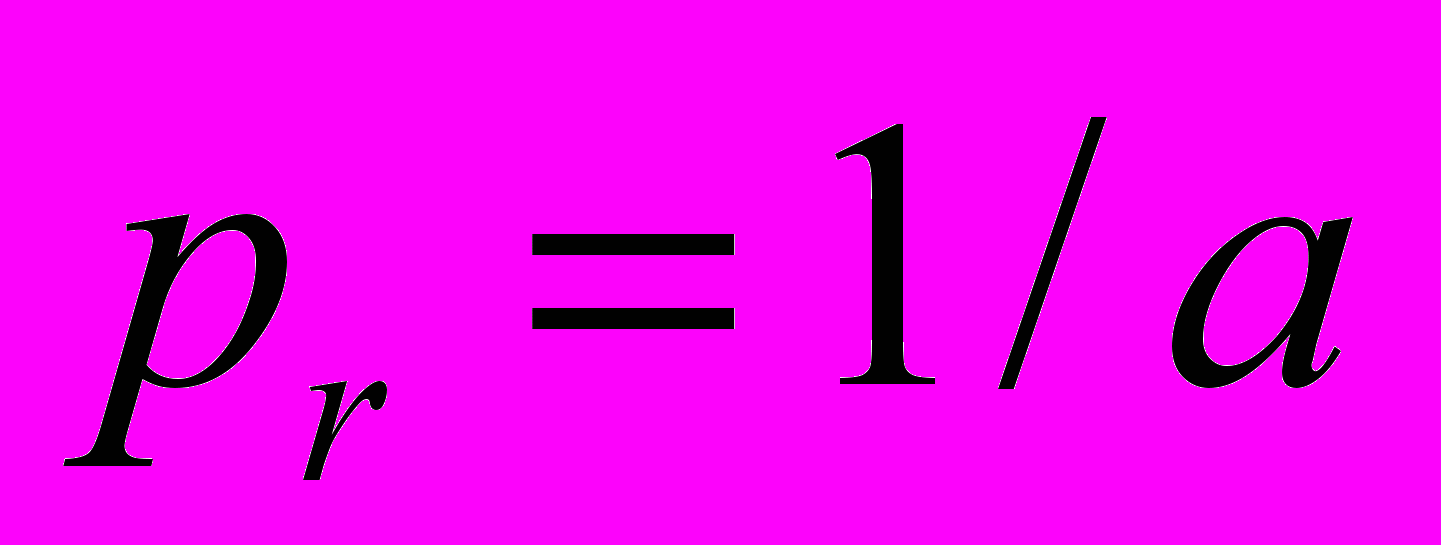3. Вычисление производительности рабочего и ученика p_ru по формуле.
   
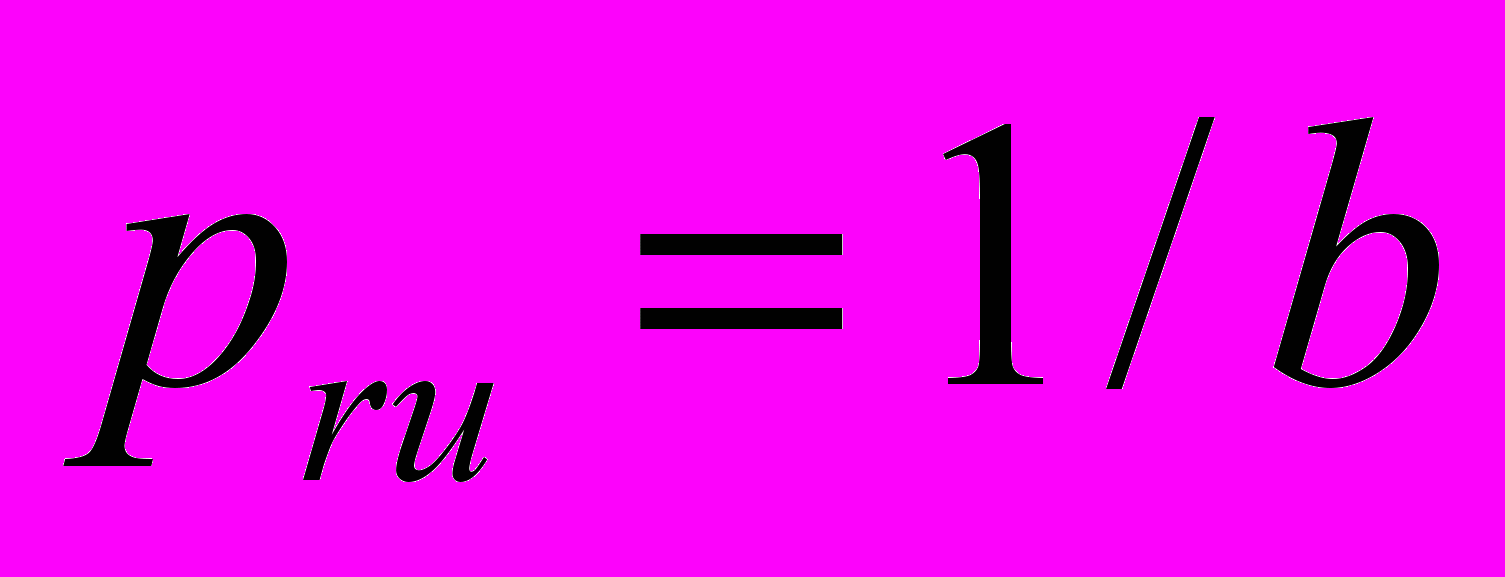4. Вычисление производительности ученика p_u по формуле.
   
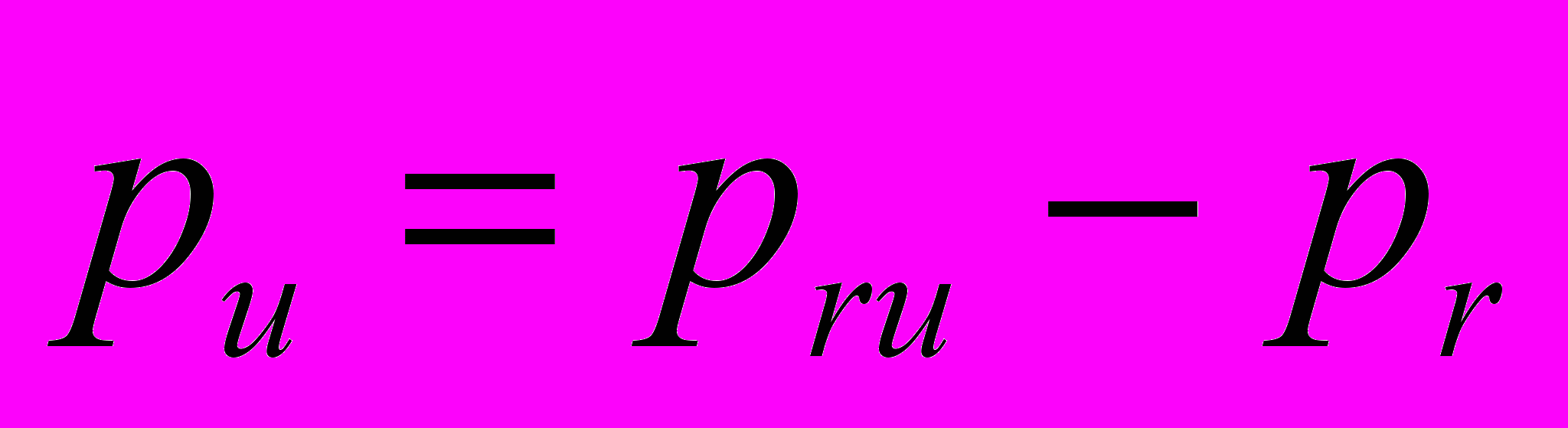5. Вычисление времени выполнения задания учеником по формуле
   
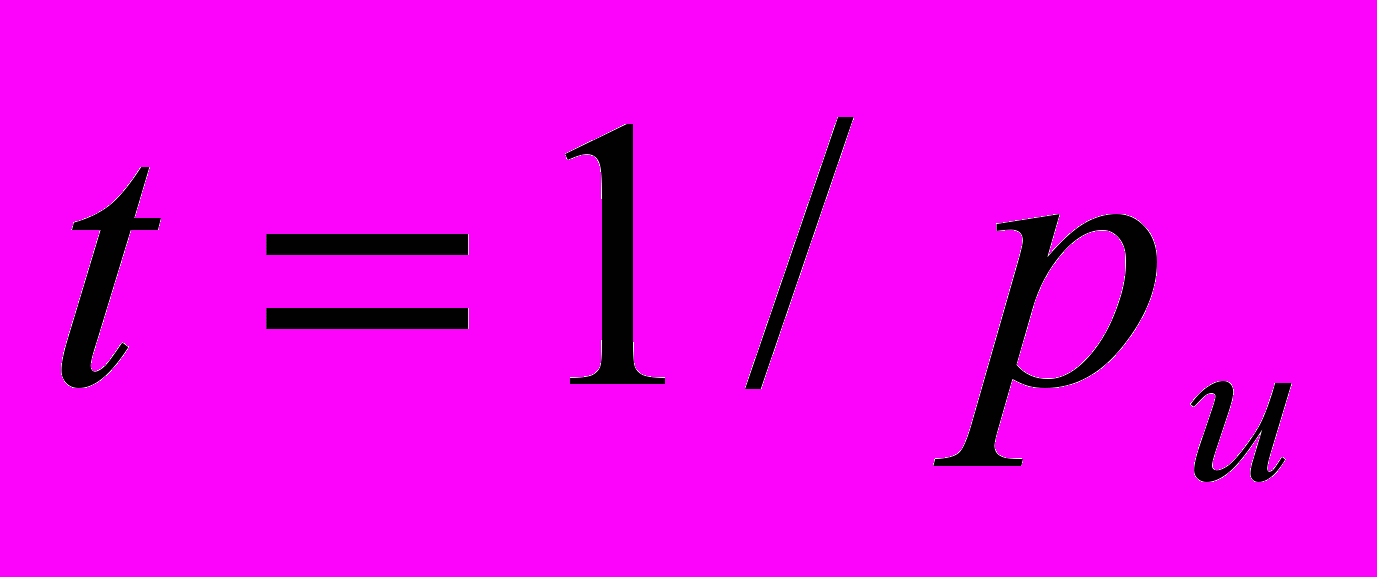
6. Вывод результата t на экран монитора.
   

Графический алгоритм решения задачи.

Блок-схема алгоритма представлена на рис. 8.




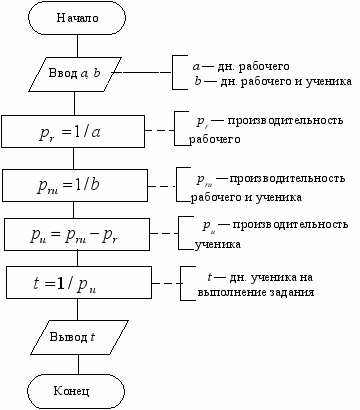
Рис. 8. Блок-схема алгоритма вычисления срока выполнения задания учеником.


Пример 3.

По представленной блок-схеме (рис. 9) получить результат вычисления алгоритма для заданных значений a=10, b=-3, c=1. Должен получиться ответ: y=197.




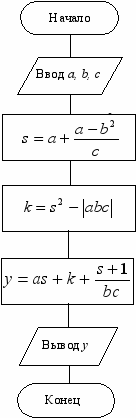
Рис. 9. Блок-схема алгоритма для вычисления значения y.