Славин Олег Анатольевич

Вид материала

Автореферат

Содержание Научный консультант Общая характеристика работы Предметом диссертации Целями диссертации Методология исследования Научная новизна Практическая ценность и реализация результатов работы Результаты диссертационной работы По теме диссертации опубликовано Апробация результатов диссертации Личный вклад автора Положения, выносимые на защиту Содержание работы Вторая глава A назовем функцию, ставящую в соответствие любому объекту из B Точностью распознавания Монотонность оценок Алфавит обучения Способность к отказам Скорость распознавания (быстродействие) ... Полное содержание

Подобный материал:

• Олег Анатольевич Усов подпись Контактное лицо: Усов Олег Анатольевич, конкурс, 1883.42kb.
• Милевский Олег Анатольевич, кандидат исторических наук, доцент кафедры регионологии, 384.42kb.
• Макушников Олег Анатольевич, доцент кафедры истории славян и специальных исторических, 209.21kb.
• Рецепция римского права: вопросы теории и истории, 249.57kb.
• Павлов Олег Анатольевич, старший преподаватель кафедры экономики и управления предприятиями, 390.93kb.
• Аналитические материалы краткий анализ деятельности горнодобывающих предприятий Камчатского, 356.1kb.
• Уважаемые отец Олег, Олег Александрович, Михаил Иванович, представители духовенства, 120.22kb.
• Синько Олег Анатольевич Архаическая парадигма мышления и внутренний Фен-Шуй доклад, 226.5kb.
• Факторы повышения конкурентоспособности пермского края, 581.94kb.
• Гревцева Людмила Германовна, кандидат юридических наук, доцент кафедры предпринимательского, 2451.72kb.

На правах рукописи     


Славин Олег Анатольевич
 


 
Адаптивное распознавание и его применение к системе ввода печатного текста


 

 


Специальность 05.13.01 – Системный анализ, управление и обработка информации

(информационно-вычислительное обеспечение)
 


АВТОРЕФЕРАТ
на соискание ученой степени
доктора технических наук


Москва – 2011


Работа выполнена в Учреждении Российской академии наук Институте системного анализа РАН в лаборатории 9-4 "Дискретные методы в управлении".


Научный консультант: чл. корр. РАН

Арлазаров Владимир Львович


Официальные оппоненты: академик РАН

Соколов Игорь Анатольевич

доктор технических наук, профессор

Гливенко Елена Валерьевна

доктор технических наук, профессор

Петровский Алексей Борисович


Ведущая организация: ГОУ ВПО Московский Государственный

Технологический Университет «Станкин»


Защита состоится 23 июня 2011 г. в 11.00 часов на заседании Диссертационного совета Д 002.086.02 при Учреждении Российской академии наук
Институте Системного Анализа РАН по адресу Москва, проспект 60-лет октября, д. 9.

С диссертацией можно ознакомиться в библиотеке Учреждения Российской академии наук Института системного анализа РАН (Москва, проспект 60-лет октября, д. 9).

Отзывы на автореферат, заверенные печатью, просим направлять по ад-
ресу: 117312, Москва, проспект 60-лет октября, д. 9.


Автореферат разослан «___» __________ 2011 г.

Ученый секретарь диссертационного совета, д.т.н., профессор

А.И. Пропой

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ


Актуальность темы: Рост научно-технического прогресса и его успехи в компьютерной отрасли привели к качественным изменениям в обработке документов, содержащих текстовую информацию. Современные возможности сканирования документов и реализации трудоемких алгоритмов распознавания делают возможным автоматизировать ввод документов в компьютер. Программы распознавания текстовых документов являются сложными программными средствами, реализующими большое число наукоемких алгоритмов. Настоящая диссертация посвящена проблемам распознавания текстов в рамках создания и функционирования персональных и профессиональных программных систем ввода документов в компьютер.

Можно выделить три типа задач распознавания образов. Первый тип – с заранее известным описанием классов, заданных строго и однозначно. Второй тип – с заранее известным числом и описанием классов с нестрогими описаниями. Третий тип – с заранее неизвестными классами, к которым требуется отнести объекты.

Задачи первого типа успешно решаются с использованием компьютера, задачи второго типа – менее успешно, задачи третьего типа практически не решаются, так как число классов для компьютерного распознавания сильно ограничено.

В диссертационной работе рассматриваются в основном задачи второго типа, как наиболее распространенные в реальности. Однако даже они далеки от окончательного решения. Так, в случае обработки изображений плохого качества, в случае различных искажений символов, возникающих, например, на краях отсканированных страниц, в случае не вполне стандартного начертания некоторых символов программы распознавания могут давать большее число ошибок, чем при обработке однородных текстов. В то же время человек, как правило, уверенно распознает текст даже плохого качества, напечатанный малознакомым шрифтом. Успешное распознавание текста человеком нередко происходит за счет адаптации к конкретной странице. При этом сомнительные символы сравниваются с четко напечатанными символами, в построенном шрифте проверяется наличие тех или иных символов, производится сопоставление с известными словами.

Таким образом, разработка новых высокоточных алгоритмов распознавания текстов, равно как и улучшение уже существующих алгоритмов представляется актуальной задачей.

Предметом диссертации является разработка алгоритма адаптивного распознавания текстовых документов, цель которого состоит в перестройке механизма принятия решений, поддерживаемого системой распознавания образов, направленная на обеспечение максимального соответствия особенностям графических образов, использованных при печати документов.

Целями диссертации являются:

1) создание модели адаптивного распознавания, учитывающей искажения образов символов отсканированных документов и основанной на нескольких механизмах: геометрическом распознавании символов, статистических методах кластеризации, сегментации границ символов, словарных механизмах;

2) разработка алгоритмов адаптивного распознавания, направленных на учет особенностей отсканированного документа в различных механизмах распознавания и обеспечивающих оптимизацию нескольких характеристик качества таких как точность распознавания, монотонность оценок и быстродействие;

3) доказательство работоспособности разработанных алгоритмов адаптивного распознавания с помощью формальных исследований и имитационного моделирования;

4) реализация алгоритмов адаптивного распознавания в составе модульной системы распознавания отсканированных документов.

Методология исследования. В работе для проведения исследований были использованы математические методы обработки изображений и распознавания образов, математический аппарат искусственных нейронных сетей, методы теории алгоритмов, машинной графики, а также концепции и методы имитационного моделирования.

Научная новизна работы состоит в следующем:

• создана модель адаптивного распознавания, позволяющая перестраивать функционирование алгоритмов распознавания отдельных символов, алгоритмов сегментации границ символов, алгоритмов словарной коррекции;
  
• реализован алгоритм быстрой кластеризации на основе метода ближайшего соседа и метода цепной развертки, позволяющий разбить множество распознанных образов на группы, соответствующие одноименным символам с одинаковыми атрибутами;
  
• предложен и реализован метод построения эталонов, основанный на анализе кластеров, поиске шрифтов, имеющихся в распознаваемом тексте, позволяющий повысить точность распознавания символов и монотонность оценок;
  
• разработан и реализован алгоритм сегментации границ символов, основанный на использовании эталонов, сформированных на основе результатов кластеризации, позволяющий существенно повысить как точность сегментации, так и точность распознавания;
  
• проведено теоретическое обоснование влияния расстояний при параллельном переносе при наложении двух изображений и доказана теорема о малом сдвиге при поиске оптимального наложения.
  
• разработаны приложения адаптивного распознавания в сжатии бинарных изображений.
  

Практическая ценность и реализация результатов работы. Основным практическим результатом работы является разработка алгоритма адаптивного распознавания и его использование в системах ввода документов в компьютер.

Диссертация состоит из шести глав, введения, заключения и списка литературы. Работа изложена на 275 страницах машинописного текста, содержит 53 иллюстрации, 120 таблиц и два приложения объемом 16 страниц. Список литературы включает 174 наименования.

Результаты диссертационной работы были использованы при реализации алгоритма адаптивного распознавания, являющегося составной частью программы распознавания текстов OCR Cognitive Cuneiform, начиная с 1996 года.

По теме диссертации опубликовано более 20 работ, 16 из них опубликованы в рецензируемых научных изданиях, рекомендуемых ВАК; зарегистрированы патент на изобретение и патент на полезную модель.

Основные результаты диссертации опубликованы в работах, список которых приведен в конце автореферата.

Апробация результатов диссертации. Результаты диссертации докладывались и обсуждались на семинарах Института системного анализа РАН под руководством чл.-корр. РАН В.Л. Арлазарова и д.т.н. Н.Е. Емельянова. По материалам диссертации был сделан ряд докладов на международных конференциях «Системный анализ и информационные технологии» в 2005, 2007 и 2009 г.

Личный вклад автора. Основные научные результаты диссертационной работы принадлежат лично автору. Ряд экспериментальных данных получен разработчиками системы распознавания Cuneiform, в которой автор являлся инициатором разработок, формулировал теоретические и экспериментальные задачи, намечал пути их решения, разрабатывал методики исследований, участвовал в разработке программного обеспечения.

Положения, выносимые на защиту:

• метод адаптивного распознавания текстового документа, состоящий из пяти этапов, необходимых для самообучения на результатах распознавания текстовых строк, позволяет производить распознавание с высокой точностью и высокой монотонностью оценок распознавания;
  
• способ формирования обучающей последовательности, основанный на комбинировании монотонных оценок распознавания и подтверждения словарем, позволяет достичь надежности подтверждения символа 0,9999;
  
• функции сравнения бинарных образов, основанные на метрике Хэмминга и на симметрике, использующей единичную окрестность, позволяют кластеризовать множество бинарных образов символов с приемлемым качеством;
  
• задача поиска параллельного переноса эталонного изображения, при котором его совпадение с тестируемым изображением максимально, обладает оптимальным решением; для достижения оптимального наложения двух фигур достаточно малых сдвигов в том случае, когда мера несовпадения при малых сдвигах незначительна;
  
• моделирование процессов оцифровки, проведенное на большом объеме имитационных и реальных образов, позволяет показать адекватность модели оцифровки и выбрать параметры модели для кластеризации и построения обобщенных портретов;
  
• разработанная модель образа кластера в форме разбиения на слои, равноудаленные от общей области, позволяет стабильным способом формировать обобщенные портреты символов;
  
• метод построения эталонов, базирующийся на анализе кластеров и поиске шрифтов, которыми был напечатан отсканированный документ, позволяет при повторном распознавании образов и сегментации границ символов достичь высокой монотонности оценок распознавания и точности распознавания при незначительных временных затратах;
  
• приложение адаптивного распознавания для сжатия бинарных изображений обеспечивает как уменьшение объема изображения, так и различные режимы хранения и воспроизведения изображений.
  

СОДЕРЖАНИЕ РАБОТЫ


К настоящему времени разработан целый ряд различных методов распознавания образов, некоторые из них описаны в первой главе. В основном методы распознавания образов (нейронные сети, SVM и др) основаны на извлечении признаков и последующей классификации образов в некотором пространстве. Распознавание текста является частным случаем общей задачи распознавания образов. Любой печатный текст имеет первичное свойство - шрифты, которыми он напечатан. С этой точки зрения существуют два класса алгоритмов распознавания печатных символов: шрифтозависимый и шрифтонезависимый. Шрифтозависимые алгоритмы используют априорную информацию о шрифте, которым напечатаны буквы. Это означает, что программе оптического распознавания символов должна быть предъявлена полноценная выборка образов символов текста, напечатанного данным шрифтом при обучении. По окончании процесса обучения шрифтовая программа оптического распознавания готова к распознаванию конкретного шрифта. Второй класс алгоритмов - шрифтонезависимые, т.е. алгоритмы, не имеющие априорных знаний о символах, поступающих к ним на вход. Эти алгоритмы измеряют и анализируют различные характеристики (признаки), присущие буквам как таковым безотносительно шрифта и абсолютного размера (кегля), которым они напечатаны. Общий путь создания базы характеристик заключается в обучении программы на представительной последовательности образов символов.

Часто для обучения используют кластерный анализ (кластеризацию). Целью кластеризации является построение набора кластеров оптимального с точки зрения минимизации изменчивости элементов внутри кластеров и максимизации расстояний между кластерами.

В агломеративно-иерархических методах кластеризации первоначально все объекты рассматриваются как отдельные, самостоятельные кластеры, состоящие всего лишь из одного элемента.

Кроме объединяющих методов иерархической кластеризации существуют и противоположные методы - дивизимные, в которых на начальном этапе вся выборка рассматривается как единый кластер, а затем уже начинается процесс его деления на составляющие части. Процесс деления продолжается до тех пор, пока каждое наблюдение не превратится в отдельный кластер.

Выбор метрики и правил объединения при кластеризации символов зависит от характера объекта распознавания.

Событийный метод, опирающийся на топологическое представление образа символа, использует структуру объекта, не изменяющуюся при некоторых непрерывных деформациях образа. Разбивая все множество образов символов на классы эквивалентности по признакам, инвариантным к малым непрерывным деформациям, мы получим модель, приводящую к некоторому методу распознавания.

Образ символа описывается как последовательность, называемая линейным представлением

Ev = {L, B, E, (IN₁,OUT₁), …, (IN_N,OUT_N)},

содержащая L линий, количество свободных начал и концов B и E, и N интервалов (IN_i,OUT_i), называемых событиями и состоящих из начальной IN_i и конечной OUT_i координат, определенных в координатах грубой сетки.

Результатом распознавания является мультимножество графем

A = {(g₁, N₁), …, (g_k, N_k)}

где N_i – количество графем g_i в обучающей последовательности, обладающих линейным представлением S(r_i) в массиве эталонов.

Событийный метод порождает коллекции распознавания без оценок.

Нередко перед распознаванием символа проводится нормализация образа по различным параметрам, например, углу наклона, толщине линий или форме образа. Часто производят нормализацию по размерам или масштабирование. В процессе обучения каждый образ, соответствующий какой-либо из букв C, будем сжимать до требуемого размера, например, до размеров 3х5, а сжатые образы E_i(C) одной буквы объединим в соответствии с методом k-средних. В массиве эталонов {E₁, E₂, …, E_m} ищутся эталоны с максимальным скалярным произведением (X, E_i) до распознаваемого сжатого образа X:

|X-E_i|²=|X|²+|E_i|²2(X,E_i)=2(1(X,E_i)).

Соответствующие этим ближайшим эталонам коды C_i, породивших их символов, и расстояния W_i до них образуют коллекцию {(C₁,W₁), …, (C_k,W_k)} альтернатив распознавания.

Большим достоинством метода сравнения нормализованных образов является монотонность получаемых оценок: большее значение скалярного произведения статистически означает большую вероятность правильного выбора.

Нормализация образа по размеру предоставляет возможность построения нейронной сети типа многослойного перцептрона над признаками растра mn. Расчет по нейронной трехслойной сети производится следующим образом:

y_i = ( w_ij(2)  u_j + s_i(2)),

u_i = ( w_ij(1)  x_j + s_i(1)),

где x_i - элементы входного слоя (признаки сжатого образа 16х16);

u_i - элементы промежуточного слоя;

y_i - элементы выходного слоя;

w_ij(k) - матрица пересчета;

s_i(k) - вектор смещения;

(x) - функция активации нейрона.

Качество распознавания зависит не только от алгоритмов, используемых программами распознавания и обучения нейронной сети, но и от того, как обучалась нейронная сеть.

Рассмотренные в первой главе диссертации алгоритмы пригодны для распознавания отдельно стоящих бинарных образов символов с вполне удовлетворительными показателями распознавания как в случае известного, так и неизвестного заранее шрифта.

Реально достижимое качество распознавания шрифтонезависимых алгоритмов ниже, чем у шрифтозависимых алгоритмов. Это связано с тем, что уровень обобщения при измерениях характеристик символов гораздо более высокий, чем в случае шрифтовых алгоритмов.

У шрифтозависимого подхода имеется преимущество, благодаря которому его активно используют. А именно, имея детальную априорную информацию о символах, можно построить весьма точные и надежные алгоритмы распознавания. Вообще, при построении шрифтозависимого алгоритма распознавания надежность распознавания символа является интуитивно ясной и математически точно выразимой величиной. Эта величина определяется как расстояние в каком-либо метрическом пространстве от эталонного символа, предъявленного программе в процессе обучения, до символа, который программа пытается распознать.

Вторая глава посвящена исследованию существующих для распознавания печатного текста с неизвестными заранее границами алгоритмов, имеющих отношение к распознаванию шрифтозависимыми и шрифтонезависимыми методами.

Пусть дано множество объектов распознавания B={b}, множество кодов S={s} и множество оценок W={w}. Образуем множество альтернатив M=SW. Альтернатива является парой (s,w), первый элемент которой – код, а второй – оценка.

Алгоритмом распознавания символов (далее – АРС) A назовем функцию, ставящую в соответствие любому объекту из B последовательность альтернатив m_i (может быть, пустую), которая удовлетворяет следующему условию:

если A(b)=(m₁,m₂,…,m_k)=((S₁,W₁), (S₂,W₂),…, (S_k,W_k)) и ,

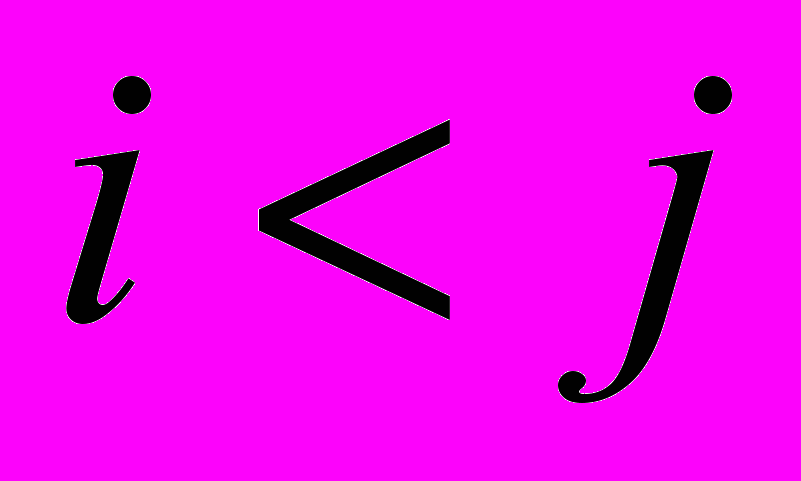то S_iS_j и W_iW_j.

Предполагаем, что последовательность образов B достаточно представительна, чтобы на ней можно было проверить все основные проблемы исследуемых алгоритмов. Последовательность может быть создана искусственно или содержать реальные отсканированные объекты. В экспериментах будем использовать несколько различных последовательностей, объем которых составляет примерно 2 млн. символов.

На последовательности B определена функция «кодировки» элементов базы K(b), отображающая эту последовательность в пространство Mⁿ, причем так, что вектор K(b) всегда имеет лишь одну непустую альтернативу. Пространство Mⁿ предполагается либо метрическим, либо псевдометрическим с некоторой функцией r(I₁, I₂), играющей роль расстояния между элементами множества.

Точностью распознавания алгоритма A на базе B по метрике r, называется величина

.

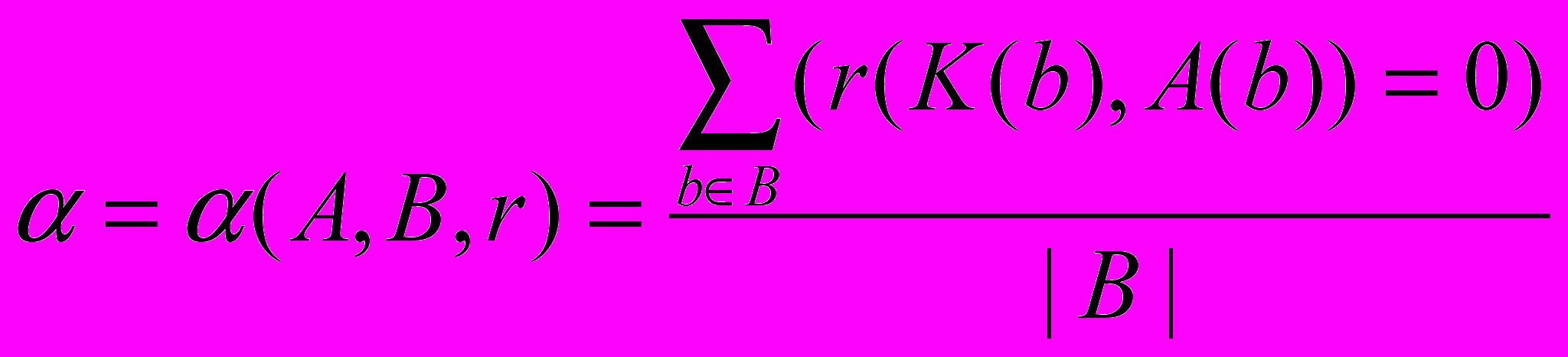Распределением оценок алгоритма A назовем совокупность частот {v(0), v(1),…, v(W_max)} , соответствующих каждой из возможных оценок, где

,

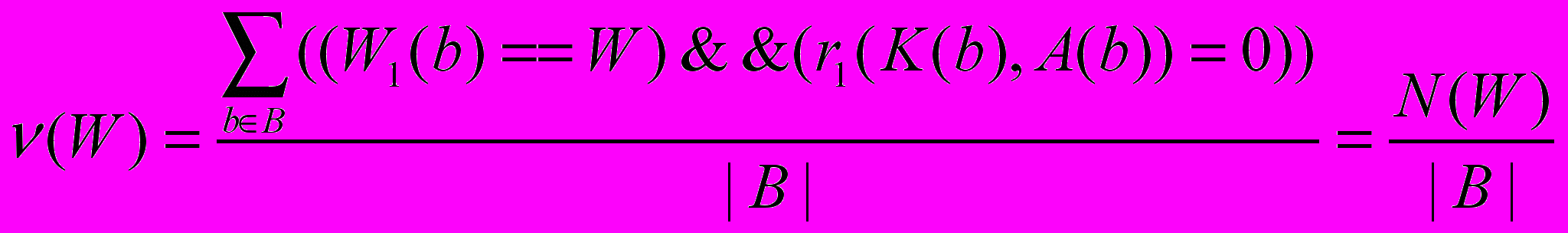здесь 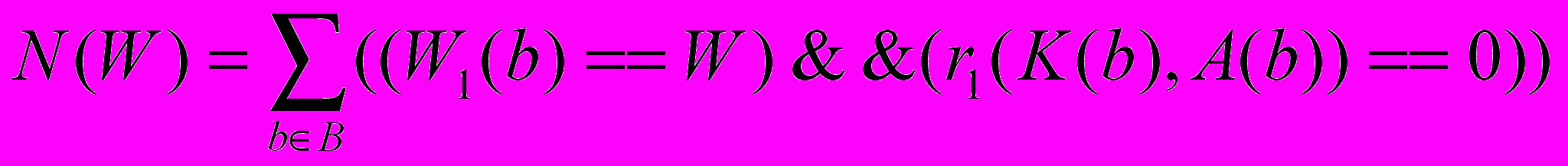– число образов, распознанных с оценкой W.

Монотонность оценок – это свойство оценок альтернатив (в первую очередь, ведущих) характеризовать надежность распознавания символа.

Через ={0=x₀<x₁<…<x_n=255} обозначим некоторое разбиение отрезка [0,255]. Обозначим N(W₁, W₂)=(w₁<W₁(b)≤w₂) общее число образов из 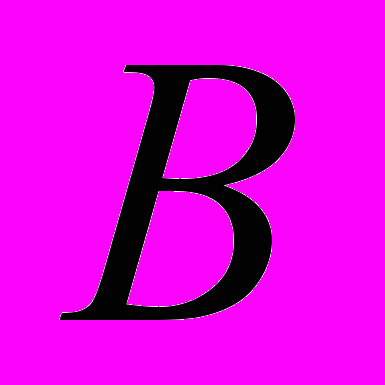, получивших оценку распознавания первой альтернативы в полуинтервале (w₁, w₂]

Если существует разбиение с монотонно возрастающей последовательностью частот v(x_i, x_i+1) ≤ v(x_i+1, x_i+2), i=0,…, n-1, такое что



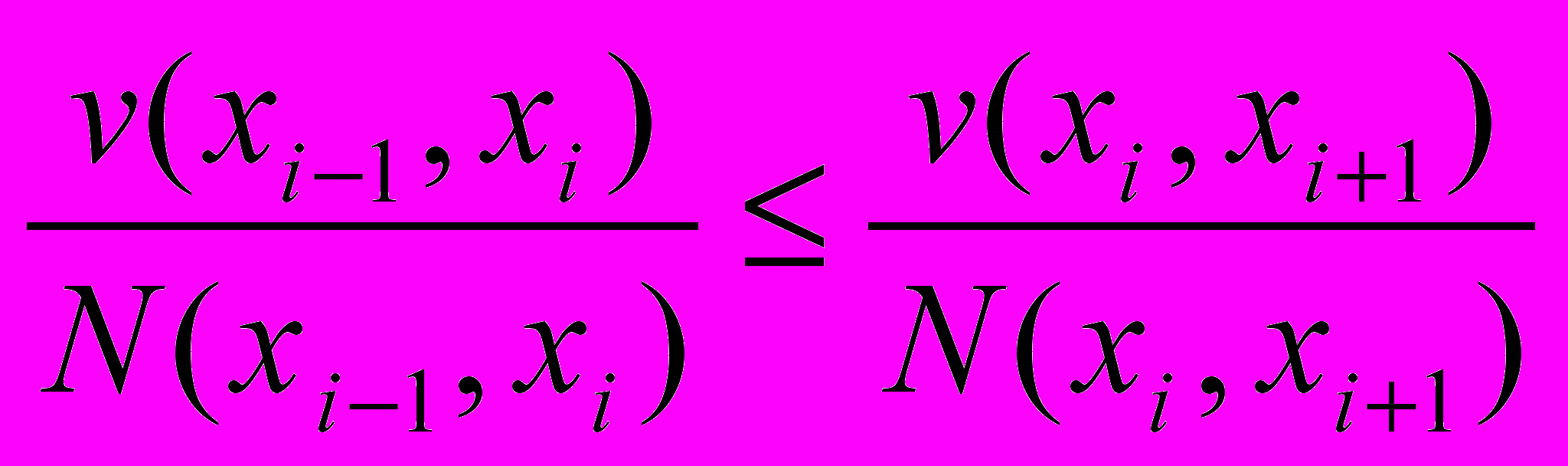
то алгоритм считается монотонным.

Пусть WW_max. Пороговой монотонностью называется величина, равная

,

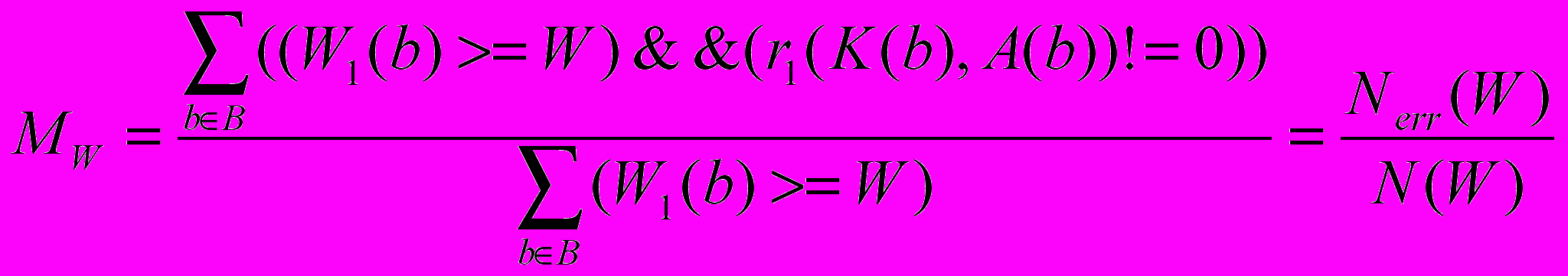где N_err(W) – число неправильно распознанных образов с оценкой W₁W,

N(W) – общее число образов, распознанных с оценкой W₁  W.

Для шкалы оценок с W_max=255 будем пользоваться пороговыми монотонностями M₂₅₅ и M₂₄₀ для оценки надежности распознающего алгоритма.

Ниже приведены дополнительные характеристики АРС, наиболее часто используемы в комбинировании АРС.

Алфавит обучения определяется перечнем классов (образов символов различных языков, цифр, специальных символов), на которые разбита обучающая последовательность.

Способность к отказам – возможность АРС порождать коллекции нулевого объема для незнакомого образа или образа, сильно отличающегося от образов, использованных в процессе обучения.

Скорость распознавания (быстродействие) – количество распознанных в единицу времени образов в процессе обработки тестовой последовательности.

Скорость обучения зависит от соотношения объема обучающей базы образов и времени, необходимого для достижения цели обучения.

На основании рассмотренных характеристик становится возможным комбинирование нескольких АРС с целью получения большей точности, большего быстродействия или большей монотонности оценок результирующего метода. Например, комбинирование описанными в диссертации способами быстрого структурного алгоритма (не порождающего оценки), алгоритма сравнения нормализованных образов (не обладающего высоким быстродействием) и штрафных функций (критериев несоответствия идеальным моделям образов) позволяет достичь в результирующем алгоритме ₁ высоких значений характеристик быстродействия (8500 образов в секунду, все оценки быстродействия производились на компьютере с CPU 2000 МГц), точности (99,8%) и монотонности оценок (M₂₄₀