Н. Ю. Васенёва ресурсно-временная оптимизация инновационного проекта санкт-Петербург, спбгу при планировании и организации различного рода последовательно выполняемых работ инновационного проекта возникает следующая задача

Вид материала

Подобный материал:

Методические рекомендации по разработке инновационного проекта Днепропетровск, 1824.31kb.
Паспорт представляемого на конкурс инновационного проекта, 199.19kb.
«Разработка и обоснование реализации инновационного проекта по созданию приборов учета,, 962.79kb.
1. Аннотация проекта “Проект организации открытого молодежного центра инновационного, 272.55kb.
Бизнес-план инновационного проекта на основе использования патента/ ноу-хау/ лицензии/, 11.39kb.
Бизнес-план Инновационного проекта должен содержать следующие разделы: а краткая информация, 14.78kb.
Научно-методическое сопровождение экспериментального проекта по совершенствованию организации, 189.48kb.
План реализации инновационного проекта*. Контроль хода реализации проекта, 147.57kb.
Темы Вашего учебного проекта, 108.97kb.
Информационная карта инновационного опыта информационная карта инновационного опыта, 131.69kb.

А.А. Бабаев, Н.Ю. Васенёва

РЕСУРСНО-ВРЕМЕННАЯ ОПТИМИЗАЦИЯ

ИННОВАЦИОННОГО ПРОЕКТА

Санкт-Петербург, СПбГУ

При планировании и организации различного рода последовательно выполняемых работ инновационного проекта возникает следующая задача оптимального распределения возобновляемых и невозобновляемых ресурсов [1].

Каждая из N последовательно выполняемых работ обеспечивается возобновляемыми (рабочие, машины, механизмы, оборудование) и невозобновляемыми (строительный материал, электроэнергия, сырье) ресурсами. При этом возможны различные варианты выполнения каждой работы, зависящие от выделенных на неё ресурсов и характеризующиеся разным временем выполнения того или иного варианта. В связи с этим возникает задача минимизации времени выполнения комплекса работ инновационного проекта при ограничении на выделяемые ресурсы.

Введем обозначения:

v_ij_,w_ij - соответственно стоимость возобновляемых и невозобновляемых ресурсов для выполнения j-й работы при возможном i м варианте, i = 1, ···, m_j; j = 1, ···, N;

m_j – число возможных вариантов j-й работы, j = 1, ···, N;

S – суммарная стоимость всех выделяемых ресурсов на все работы;

t_ij – время выполнения работы j по i-у варианту;

Т – суммарное время выполнения всех работ.

С учётом принятых обозначений целевая функция и ограничения задачи будут иметь вид:

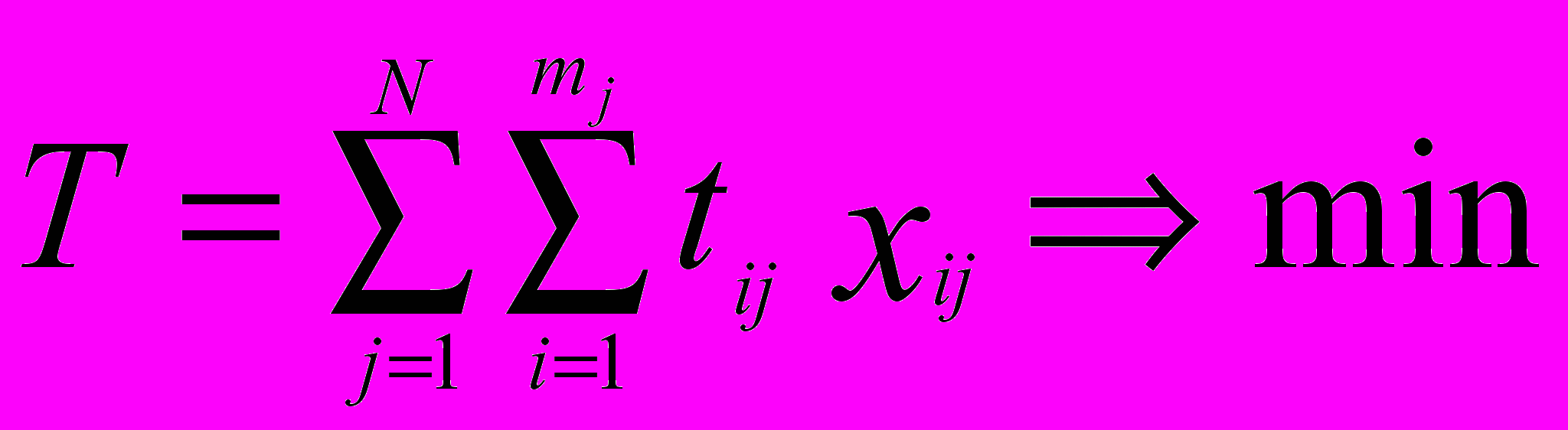
при условиях

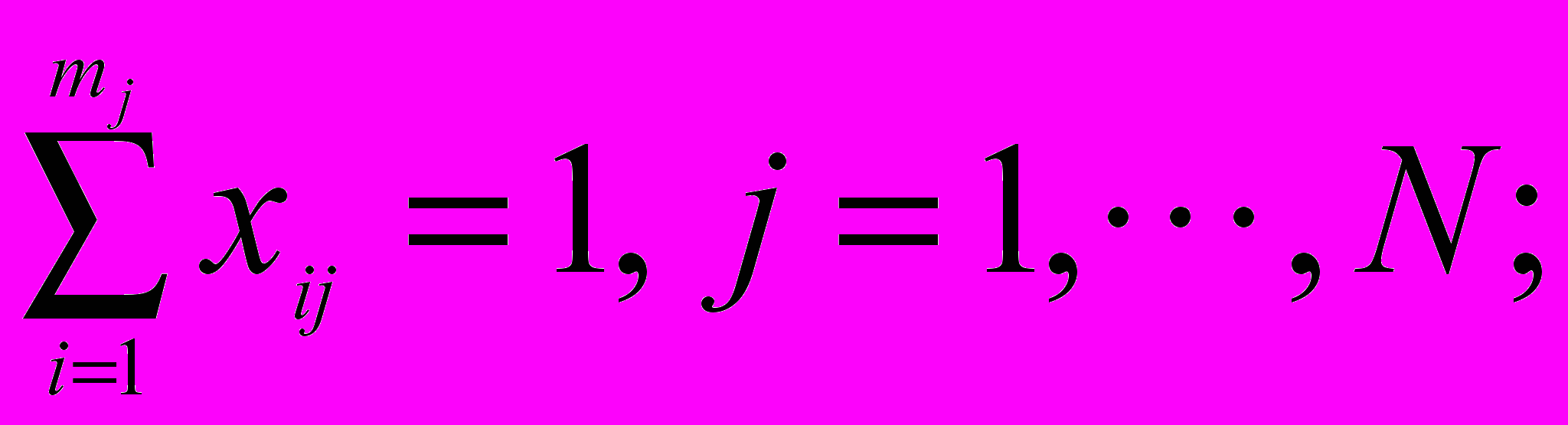
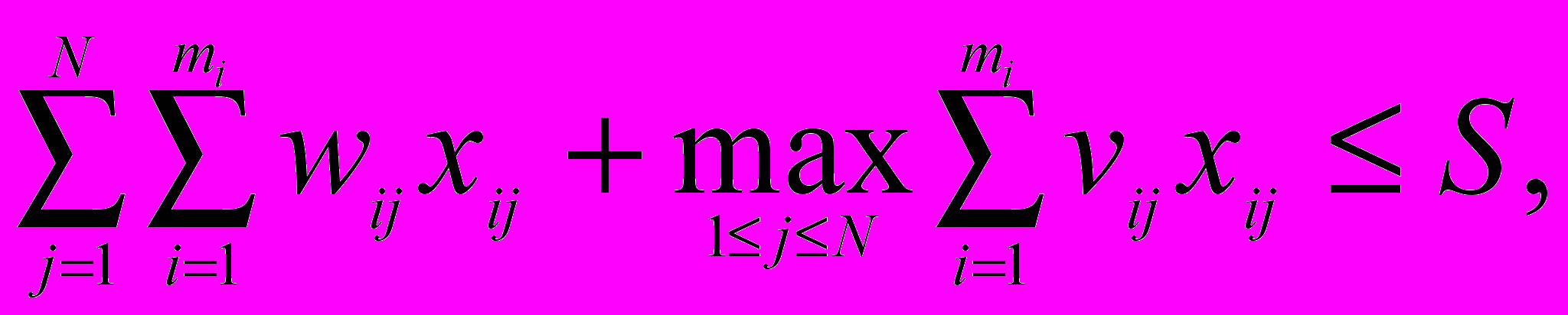
где:

х_ij = 1, если j-я работа выполняется по i-му варианту,

х_ij = 0 – в противном случае.

Сформулированная задача может быть решена методом динамического программирования [2]. Для этого введём обозначения

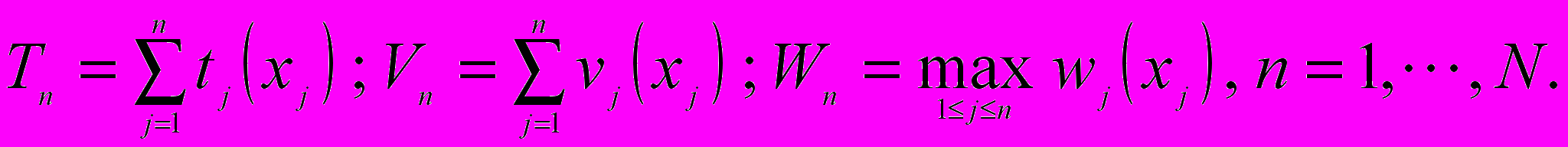
В общепринятом виде алгоритм динамического программирования включает два этапа: этап прямого хода и этап обратного хода.

Для рассматриваемой задачи в процессе прямого хода, состоящего из N шагов, с использованием принципа оптимальности определяются последовательности триад рекуррентных соотношений T_n(V_n,W_n), n = 1, ···, N.

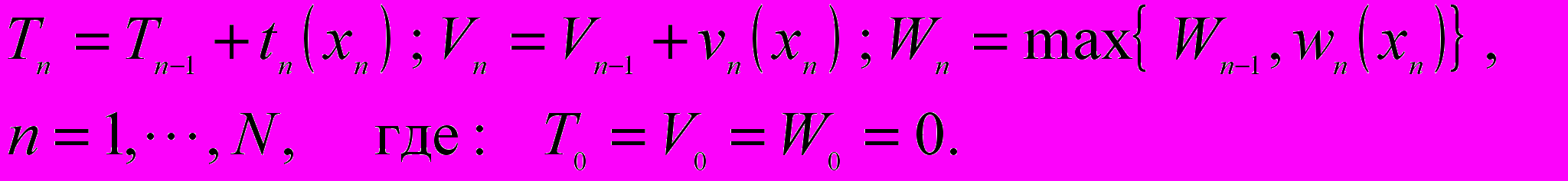
Число таких триад на шаге n обозначим – M_n. На основе попарного сравнения элементов всех триад к дальнейшему рассмотрению на (n + 1) шаге используются только те триады, для которых выполняется следующее логическое условие

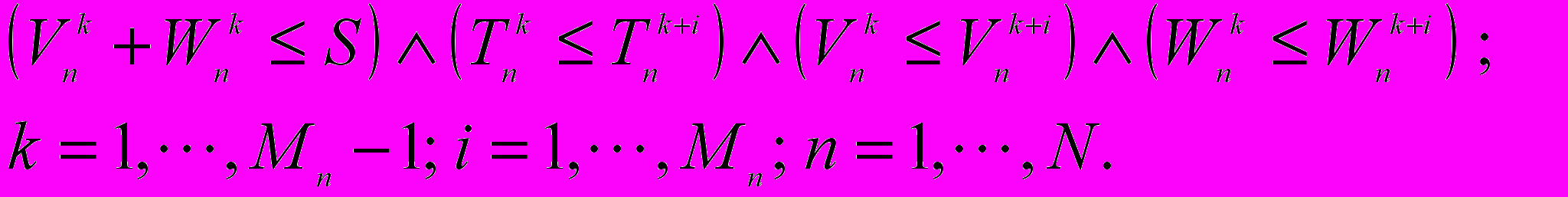
На последнем шаге прямого хода среди M_N триад T_N(V_N,W_N) выявляется оптимальное значение целевой функции T^*.

Наличие двух этапов в алгоритме динамического программирования предполагает организацию хранения и табулирования в оперативной или внешней памяти компьютера M₁ + M₂ + … + M_N триад рекуррентных соотношений для N шагов прямого хода.

В процессе обратного хода восстанавливается цепочка оптимальной последовательности триад

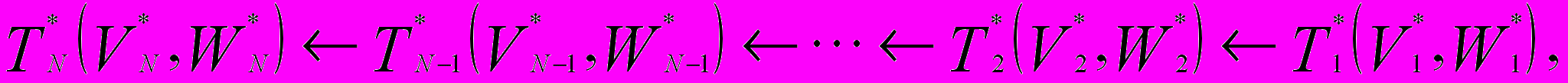
которая и определяет вектор

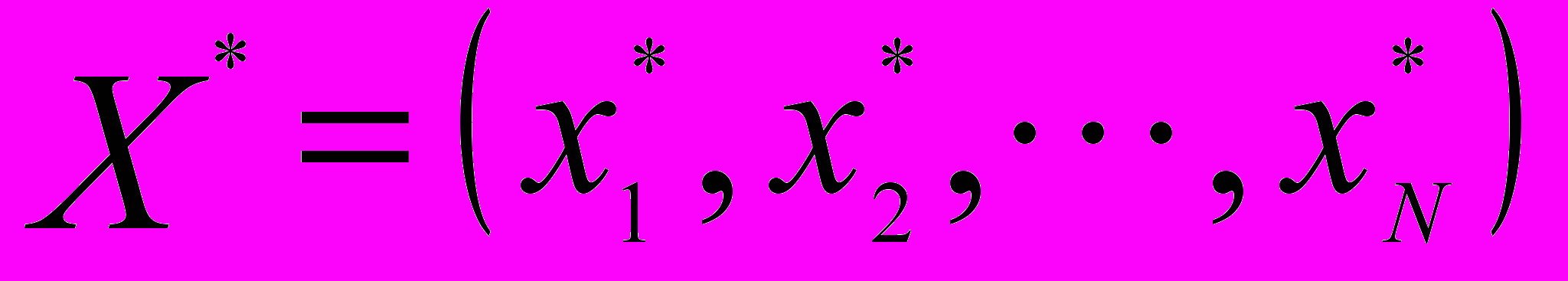, минимизирующий целевую функцию.

Модификация рассмотренного алгоритма ресурсно-временной оптимизации инновационного проекта может быть осуществлена на основе эквивалентного преобразования исходных данных задачи и принципа декомпозиции [3].

Литература

1. Бабаев А.А. Учебный курс «Информационные технологии и методы принятия решений» //Методические материалы: учебная программа, презентации лекций, технология итогового занятия, зачётные и экзаменационные листы. Библиотека учебных курсов Microsoft Developer Network Academic Alliance / Управление информацией. 2007. soft. com/Rus/Msdnaa/Curricula/Default.mspx.

2. Бабаев А.А. Информационные технологии и методы принятия решений. Учебно-методическое пособие. – СПб.: ОЦЭиМ, 2008. 198 с.

3. Бабаев А.А. Декомпозиция задачи динамического программирования при выборе оптимальной совокупности блоков в программе для ЭВМ //Приборостроение, № 10, 1978. С. 56-61.

Blog