Методические рекомендации по выполнению домашней контрольной работы для учащихся заочников учреждений, обеспечивающих получение среднего специального образования по специальности «Управление в апк»

Вид материала

Методические рекомендации

Содержание Критерии оценки выполнения домашней контрольной работы Решение типовых примеров задач Задания для контрольной работы

Подобный материал:

• Методические рекомендации по изучению дисциплины «Экономика отрасли» ивыполнению контрольных, 282.12kb.
• Методические указания по выполнению домашней контрольной работы по дисциплине «Основы, 108.96kb.
• Методические рекомендации по изучению учебной дисциплины, задания для домашней контрольной, 567.53kb.
• Методические указания и задания по выполнению домашней контрольной работы для студентов-заочников, 461.11kb.
• Методические указания домашняя контрольная работа №1 по дисциплине «Налогообложение, 681.22kb.
• Методические указания домашняя контрольная работа по дисциплине «Финансы организации», 568.97kb.
• Методические рекомендации по изучению дисциплины и выполнению домашней контрольной, 237.35kb.
• Методические рекомендации к выполнению контрольной работы для студентов 1 курса аиси, 299.55kb.
• Методические указания по выполнению домашней контрольной работы по дисциплине «Экономика, 443.44kb.
• Методические указания и задания по выполнению домашней контрольной работы для студентов-заочников, 335.32kb.

Таблица

Последняя цифра шифра	Номера заданий
1	1	11	21	31	41
2	2	12	22	32	42
3	3	13	23	33	43
4	4	14	24	34	44
5	5	15	25	35	45
6	6	16	26	36	46
7	7	17	27	37	47
8	8	18	28	38	48
9	9	19	29	39	49
0	10	20	30	40	50

КРИТЕРИИ ОЦЕНКИ ВЫПОЛНЕНИЯ

ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ

Отметка «зачтено» выставляется при условии:

• работа выполнена в полном объёме, в соответствии с заданием;
  
• задачи решены верно, ход решения пояснён;
  
• работа аккуратно оформлена, графические задания выполнены аккуратно, приведён список использованной литературы.
  

Работа может быть зачтена, если она содержит

единичные несущественные ошибки:

• отсутствие выводов в решении задач;
  
• арифметические ошибки в решении задач, не приводящие к абсурдному результату и т.п.;
  
• при отсутствии списка используемой литературы или несоответствии его оформления стандартным требованиям.
  

Отметка «не зачтено» выставляется, если работа выполнена

не в полном объёме (менее 60%) или содержит следующие существенные ошибки:

• отдельные задания в работе освещены не в соответствии с вариантом задания;
  
• для выполнения задания неправильно выбраны методы решения, допущены грубые ошибки в расчётах;
  
• контрольная работа выполнена небрежно, неразборчивым почерком, имеются многочисленные исправления, грамматические ошибки, помарки.
  

Контрольная работа, выполненная не в соответствии с вариантом задания, возвращается учащемуся без проверки, с указанием причин возврата.


РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ ЗАДАЧ

1. Построение начального опорного плана транспортной задачи методом северо – западного угла.
   

Пусть нужно с нескольких складов вывезти горючее нескольким транспортным предприятиям. Задача состоит в том, чтобы найти последовательность перевозок такую, чтобы стоимость всех перевозок была минимальной.

Пусть имеется три склада горючего, в которых соответственно находятся:480, 420, 380 шт. ёмкостей с бензином. Этот бензин нужно вывезти без остатка на 4 транспортных предприятия. Потребность в бензине для этих предприятий соответственно: 330, 310, 360, 280. Стоимость одной единицы перевозки с первого склада транспортным предприятиям соответственно равна: 6,5,2,4 ден. единицы; со второго склада – 3,4,1,3 ден. единицы; с третьего склада – 8,7,9,5 ден. единицы.

Представим условия данной транспортной задачи в виде таблицы:

	330	310	360	280
480	6 х11	5 х12	2 х13	4 х14
420	3 х21	4 х22	1 х23	3 х24
380	8 х31	7 х23	9 х33	5 х34

1. Построение начального опорного плана транспортной задачи методом северо-западного угла.

Заполнение таблицы , т.е. нахождение значений переменных х _ij начинаем с клетки (1,1): х₁₁= min{330,480}= 330, первый столбец закрыт. Переходим к клетке (1,2): х₁₂ = min{480-330,310}= 150, первая строка закрыта. Переходим к клетке (2,2): х₂₂ = min{310-150,420}= 160, второй столбец закрыт. Переходим к клетке (2,3): х₂₃ = min{420-160,360}= 260, вторая строка закрыта. Переходим к клетке (3,3): х₃₃ = min{380,360-260}= 100, третий столбец закрыт. Переходим к клетке (3,4): х₃₄ = min{280,380-100}= 280.

	330	310	360	280
480	6 330	5 150	2 0	4 0
420	3 0	4 160	1 260	3 0
380	8 0	7 0	9 100	5 280

Начальный опорный план по методу северо-западного угла построен:

х₁₁= 330 х₁₂ = 150 х₁₃ = 0 х₁₄ = 0

х₂₁= 0 х₂₂= 160 х₂₃= 260 х₂₄ = 0 (1)

х₃₁= 0 х₃₂= 0 х₃₃= 100 х₃₄= 280

(1) является начальным опорным планом транспортной задачи, построенный методом северо-западного угла.

Посчитаем значение целевой функции транспортной задачи, т.е. стоимость перевозки при начальном опорном плане, найденном методом северо-западного угла.

Z= 6х₁₁+5х₁₂ + 4 х₂₂+ х₂₃ +9х₃₃+ 5х₃₄=6 х 330 +5 х 150 + 4 х 160+ + 1х 260 + 9 х 100 + 5 х 280 = 1980 + 750 + 640 + 260 + 900 + 1400 = 5930.

2. Построение начального опорного плана транспортной задачи методом минимального элемента.
   

Пусть условия транспортной задачи заданы следующей таблицей:

	210	170	80
120	4 х11	5 х12	2 х13
110	1 х21	3 х22	4 х23
90	5 х31	6 х23	1 х33
140	4 х41	7 х42	8 х43

Заполнение таблицы, т.е. нахождение значений переменных х _ij начинаем с клетки с наименьшей величиной стоимости перевозки (2,1): х₂₁= min{110,210}= 110, вторая строка закрыта. Переходим к клетке (3,3): х₃₃ = min{80,90}= 80, третий столбец закрыт. Переходим к клетке (1,3): х₁₃ = min{120,80-80}= 0.

Переходим к клетке (2,2): х₂₂ = min{110-110,170}= 0. Переходим к клетке (4,1): х₄₁ = min{140,210-110}= 100, первый столбец закрыт. Переходим к клетке (1,1): х₁₁ = min{120,210-110-100}= 0.

Переходим к клетке (2,3): х₂₃ = min{110-110}= 0. Переходим к клетке (3,1): х₃₁ = min{90-80,210-110-100}= 0. Переходим к клетке (1,2): х₁₂ = min{120,170}= 120, первая строка закрыта. Переходим к клетке (3,2): х₃₂ = min{90-80,170-120}= 10, третья строка закрыта.

Переходим к клетке (4,2): х₄₂ = min{140-100,170-120-10}= 40, второй столбец закрыт, четвертая строка закрыта.

	210	170	80
120	4 0	5 120	2 0
110	1 110	3 0	4 0
90	5 0	6 10	1 80
140	4 100	7 40	8 0

Начальный опорный план по методу минимального элемента построен:

х₁₁= 0 х₁₂ = 120 х₁₃= 0

х₂₁= 110 х₂₂= 0 х₂₃= 0 (2)

х₃₁ = 0 х₃₂=10 х₃₃=80

х₄₁ = 100 х₄₂=40 х₄₃= 0

Посчитаем значение целевой функции транспортной задачи, т.е. стоимость перевозки при начальном опорном плане, найденном методом минимального элемента.

Z= 5х₁₂+ х₂₁ + 6 х₃₂+ х₃₃ +4х₄₁+ 7х₄₂=5 х 120 + 110 + 6 х 10 + 1х 80 + 4 х 100 + 7 х 40 = 600 + 110 + 60 + 80 + 400 + 280 = 1430.

Очевидно, что стоимость перевозок для плана (2) меньше, чем для плана (1)

3. Нахождение оптимального опорного плана методом
   

потенциалов.

Пусть найден начальный опорный план транспортной задачи по методу минимального элемента (см. предыдущий пример).

Задача состоит в том, чтобы при помощи метода потенциалов проверить, является ли значение целевой функции минимальным, т.е. будет ли найденный начальный опорный план задачи одновременно и её оптимальным планом, при котором стоимость всех перевозок минимальна.

Проверку начнём с введения потенциалов отправления U₁ U₂ U₃ – по количеству поставщиков и потенциалов назначения V₁ V₂ V₃ V₄– по количеству потребителей.

Запишем равенства, связывающие эти потенциалы для тех клеток, в которых планы перевозок не равны 0:

	210	170	80
120	4 0	5 120	2 0
110	1 110	3 0	4 0
90	5 0	6 10	1 80
140	4 100	7 40	8 0

U₁ + V₂ = 5

U₂ + V₁ = 1

U₃ + V₂ = 6

U₃ + V₃ = 1

U₄ + V₁ = 4

U₄ + V₂ = 7

В данной системе уравнений 7 неизвестных: U_1, U_2, U_3, U_4, V_1, V_2, V_3., уравнений только 6. Для решения системы уравнений и определения потенциалов, предположим, что U₁ = 0, (можно выбрать любые) тогда:

U₂ = -1 , U₃ = 1, U₄ = 2, V₁ = 2, V₂ = 5, V₃ = 0,

Вычислим фиктивные стоимости перевозок для тех клеток, в которых планы перевозок при начальном опорном плане равны 0:

С₁₁^/ = U₁ + V₁ = 2,

С₁₃^/= U₁ + V₃ = 0,

С₂₂^/= U₂ + V₂ = 1,

С₂₃^/= U₂ + V₃ = -1,

С₃₁^/= U₃ + V₁ = 3,

С₄₃^/= U₄ + V₃ = 2, подсчитаем разности:


С₁₁ - С₁₁^/ = 4-2 = 2

С₁₃ - С₁₃^/= 2- 0 =2

С₂₂ - С₂₂^/ = 3 – 1 =2

С₂₃ - С₂₃^/ = 4 – (-1) =5

С₃₁ - С₃₁^/ = 5 – 3 =2

С₄₃ - С₄₃^/ = 8 – 2 =6,

Результаты вычитания от реальных стоимостей перевозок фиктивных называются свободными переменными.

Значит, выражение целевой функции через свободные переменные можно представить в следующем виде:

F(x) =2х₁₁+ 2 х₁₃ + 2х₂₂ + 5х₂₃ + 2 х₃₁+ 6 х₄₃ +1430.

Среди коэффициентов при переменных нет отрицательных элементов и поэтому план (2) является оптимальным.


4. Построение математической модели экономической задачи.

Пусть требуется составить математическую модель задачи определения максимальной прибыли от производства таких сельскохозяйственных культур как: зерновые на товарные цели, зерновые в обмен на комбикорм, картофель на товарные цели, кормовые корнеплоды.

Производство данных сельскохозяйственных культур ограничены объёмами ресурсов по затратам на: трудовые ресурсы, транс

портные расходы, материально – денежные средства.

Ресурсы	Виды сельскохозяйственных культур				Объем ресурсов
	Зерновых на товарные цели	Зерновых в обмен на комбикорм	Картофеля на товарные цели	Кормовых корнеплодов
Трудовые ресурсы	2	2	30	50	30 000
Транспортные расходы	4,5	4,5	15	45	26 000
Матер.-денежные средства	25	25	150	100	12000
Прибыль	10	25	50	100	max
Площадь посева	х1	х2	х3	х4	20 000

Площадь посева также ограничена некоторой величиной в гектарах.

Нормативы затрат данных ресурсов на производство данных сельскохозяйственных культур величина справочная.

Обозначим через x₁, x₂, x₃, x₄ площади посевов различных сельскохозяйственных культур данной задачи.

Построим математическую модель данной задачи. Математическая модель состоит из трёх частей: целевой функции, системы основных ограничений, системы дополнительных ограничений.

Целевая функция имеет вид:

F (x) = 10x₁ + 25x₂ + 50x₃ + 100x₄ max. (1)

Система основных ограничений имеет вид:

2x₁ + 2x₂ + 30x₃ + 50x₄ 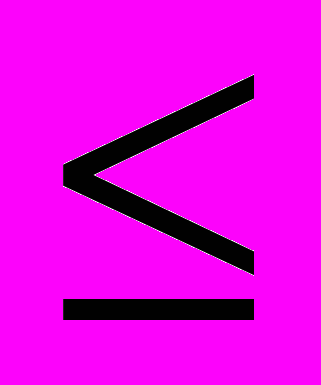30 000

4,5x₁ + 4,5x₂ + 15x₃ + 45x₄ 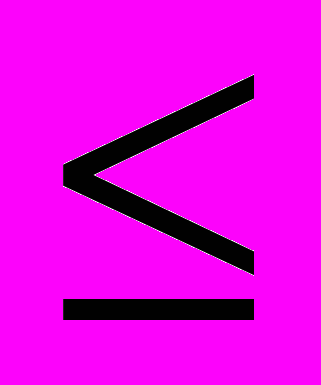26 000 (2)

25x₁ + 25x₂ + 150x₃ + 100x₄ 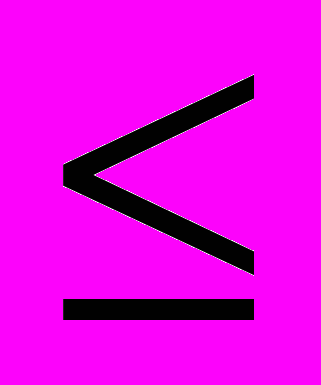12 000

x₁ + x₂ + x₃ + x₄ 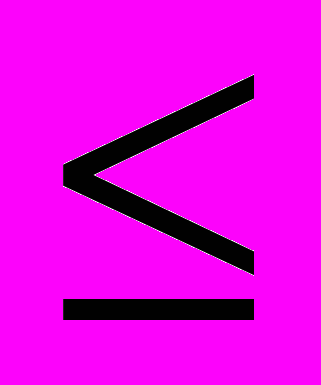20 000

Поскольку речь идёт о площадях посевов, то очевидно, что неизвестные x₁, x₂, x₃, x₄ не могут иметь отрицательных значений.

Поэтому система дополнительных ограничений имеет вид:

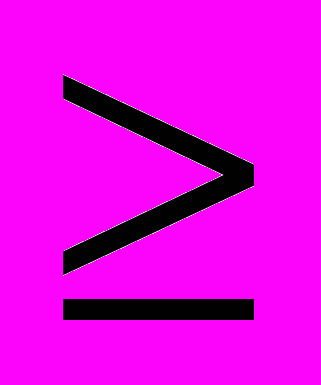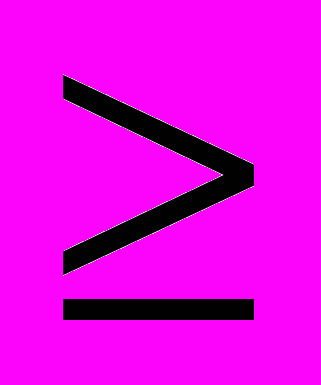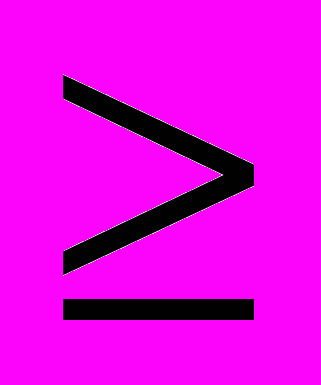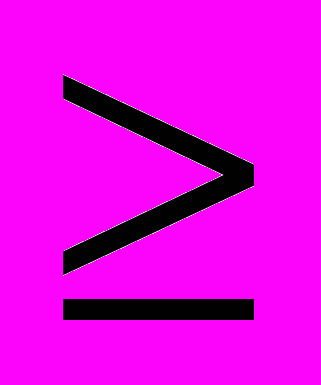x_10, x_{20 ,} x_30, x_{4 0} (3)

Выражения (1), (2), (3) и представляют собой математическую модель задачи.


5. Построение сетевого графика комплекса работ.

Правила построения сетевых графиков:

1. 
   В сетевых графиках не должно быть событий, из которых не выходит ни одна работа (за исключением завершающего события).
   
2. В сетевых графиках не должно быть событий (кроме исходного), которым не предшествует хотя бы одна работа.
   
3. В сети не должно быть замкнутых циклов, т.е цепей, соединяющих некоторые события с ними же самими.
   

Рассмотрим пример:

Пусть требуется выполнить комплекс взаимосвязанных работ. Условие задачи представлены следующей таблицей:

Работа	Предшествующие ей работы	Продолжительность выполнения работ (дни)
а1 а2 а3 а4 а4 а5 а6 а7 а8 а9	- - - а2 а3, а6 а1 а3 а 3 а 7 а 8	5 6 2 6 6 3 2 3 7 3

Требуется построить сетевой график, найти критический путь и посчитать критическое время выполнения работ.

Для построения сетевого графика по таблице опишем события,

их виды, последовательность выполнения работ, приводящих к конкретному событию.

Событие 1 - исходное, оно означает начало работ а₁, а₂ , а ₃

Событие 2 - означает завершение работы а₁ и начало работы а₆, которой предшествует работа а_1.

Событие 3 - означает завершение работ а₂ и начало работы а_5, которой предшествуют работы а₂.

Событие 4 - означает завершение работы а₃ и начало работ а_4, а _7, которым предшествует работа а _3.

Событие 5 - означает завершение работы а₇ и начало работы а _8, которой предшествует работа а_{7 .}

Событие 6 - означает завершение работ а₅, а₆, а ₈и является завершающим событием.


а₆(3)


Построение сетевого графика следует начинать с исходного события и далее по цепочке, используя данные задачи, выстраиваем следующее графическое изображение выполнения комплекса работ:









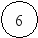
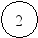
а₅(6)
а₁₍₅₎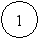


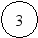
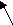
а₂(6)

а₄(2)

а ₈(7)

а₃ (2)

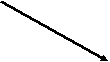
а₇ (3)







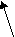
Анализируем возможные полные пути от исходного события к завершающему для определения критического пути:

1. 
   а₁, а₅;
   
2. а₂, а₄;
   
3. а₃, а₆, а ₄;
   
4. а₃, а ₇, а_8, а_9;
   

Посчитаем критическое время t _кр = 2+3+7+3 = 15 (дней).


ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ


1.-10. Построить начальный опорный план транспортной задачи методом северо – западного угла: