В настоящее время существует множество задач, для решения которых требуется построить сложные системы с помощью упорядочения их элементов
| Вид материала | Документы |
СодержаниеРис. 1. Пример графа с указанием весов ребер |
- «Алгоритмы», 100.81kb.
- Выборка. Выборочный метод в социологии, 54.12kb.
- Задача распознавания образов, 524.62kb.
- Использование системы моделирования gpss world для сравнения различных реализаций системы, 21.47kb.
- Сопровождение программы: доработка программы для решения конкретных задач, 167.56kb.
- Методические указания для выполнения лабораторных работ и курсовой работы содержание, 1317.09kb.
- Масс-спектрометрия и резонансные методы. Часть I. Методы масс-спектрометрии, 397.85kb.
- Решение задач одно из важных применений Excel. Системы линейных уравнений решаются, 39.61kb.
- Определены критерии, обеспечивающие полноту для принятия решения по выбору инвестиционного, 30.47kb.
- Привлечение экономико-математических методов для решения экономических задач Сливицкий, 113.25kb.
В настоящее время существует множество задач, для решения которых требуется построить сложные системы с помощью упорядочения их элементов. Сюда относятся задачи теории сетевого планирования, тактические и логические задачи, проблемы построения систем связи и исследования процессов передачи информации, выбор оптимальных маршрутов и потоков в сетях, а также большой круг экономических задач и т. д. Для решения всех этих задач используется теория графов.
Целью работы была реализация алгоритма нахождения кратчайшего пути между вершинами графа.
Под графом понимается непустое множество точек Vi, называемых вершинами, и множество отрезков их соединяющих, называемых ребрами e={Vi , Vj}. Чаще используют взвешенные графы, ребрам которых поставлены в соответствие действительные числа или величины, то есть ребра имеют свой вес (рис. 1).
Обычно граф представляют в графическом виде или используют матрицы для его описания. Для графа определяются весовая матрица, элементы которой характеризуются весом ребер, и вектор смежности, представляющий собой списки вершин, смежных с данной.
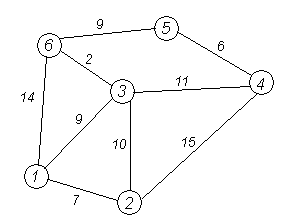
Рис. 1. Пример графа с указанием весов ребер
На практике часто встречаются задачи нахождения дерева минимальной стоимости, называемое остовным, то есть набор ребер, соединяющий все вершины графа и имеющий минимальную длину, и нахождение кратчайшего пути между вершинами графа. Для решения данной задачи существует немало алгоритмов: алгоритм Флойда, Алгоритм Беллмана − Форда, Йена, переборные алгоритмы и др.
В данной программе, написанной на алгоритмическом языке С++, был реализован алгоритм Дейкстры, суть которого заключается в следующем. Каждой вершине графа сопоставляют метку − минимальное известное расстояние от этой вершины до А. Алгоритм работает пошагово − на каждом шаге он «посещает» одну вершину и пытается уменьшать метки. Работа алгоритма завершается, когда все вершины посещены.
Метка самой вершины А полагается равной 0, метки остальных вершин − бесконечности. Это отражает то, что расстояния от А до других вершин пока неизвестны. Все вершины графа помечаются как непосещенные.
Шаг алгоритма. Если все вершины посещены, алгоритм завершается. В противном случае, из еще не посещенных вершин выбирается вершина u, имеющая минимальную метку. Рассматриваются всевозможные маршруты, в которых u является предпоследним пунктом. Вершины, в которые ведут ребра из u, назовем соседями этой вершины. Для каждого соседа вершины u, кроме отмеченных как посещенные, рассмотрим новую длину пути, равную сумме значений текущей метки u и длины ребра, соединяющего u с этим соседом. Если полученное значение длины меньше значения метки соседа, заменим значение метки полученным значением длины. Рассмотрев всех соседей, пометим вершину u как посещенную и повторим шаг алгоритма.
Программа обработки графа выполнена на языке Borland С++. В программной реализации использованы следующие структуры данных:
− матрицы для хранения элементов весовых матриц;
− стек для хранения вершин, через которые проходит путь;
− структура для хранения списка ребер.
Для обработки графа построен класс.
Графический интерфейс реализован с помощью стандартной графической библиотеки С++ BGI.
В меню программы включены следующие пункты:
− построение матриц и редактирование графа, описанного в файле в виде списка ребер;
− построение дерева минимальной стоимости;
− нахождение кратчайшего пути с помощью алгоритма Дейкстры;
− непосредственный вывод графа на экран в графическом виде.
Программа предусматривает чтение данных из файла или с клавиатуры. Пользователь может добавить в построенный граф новые ребра, указав их вес. Программа занимает порядка 15 Кб.
