Філософія науки. Збірник наукових статей Львівсько-Варшавського семінару «Філософія науки». 14–21 листопада 2004 р. – Львів, 2006. – С. 256
| Вид материала | Документы |
- Міністерство освіти І науки України Львівський національний університет імені Івана, 5484.8kb.
- Рджене вак україни, зі спеціальностей: філософія науки, філософська антропологія, 29.23kb.
- Робоча програма курсу "Основи теоретичної біографістики" для спеціальності 030101 "Філософія", 387.4kb.
- Програма фахового вступного випробування на навчання за окр магістра зі спеціальності, 227.5kb.
- Сумський державний університет. Бібліотека. Інформаційно-бібліографічний відділ, 455.71kb.
- Чернівецький національний університет імені Юрія Федьковича, 674.46kb.
- Теорія істини у львівсько-варшавській філософській школі методичні вказівки до другої, 210kb.
- Навчально-методичний комплекс львів 2009, 535.18kb.
- Тецтв чернігівська спілка перекладачів філософія етнокультури та наукові стратегії, 2978.21kb.
- Питання для складання іспиту з дисципліни “Філософія”, 14.89kb.
Михайло Зарічний
Нові обличчя нескінченності
Львівський національний університет імені Івана Франка, вул. Університетська, 1, 79000, Львів, Україна, E-mail: topology@franko.lviv.ua
З нескінченністю в математиці вперше зустрічаємося в евклідовій геометрії, тут вона виникає як ідеалізована властивість оточуючого простору, а також прямих і площин в ньому бути протяжними, необмеженими в усіх напрямках. Варто зазначити, що така нескінченна протяжність, не виникаючи безпосередньо з досвіду, є не більше ніж властивість моделі – у відомій моделі Клейна гіперболічної геометрії прямі, власне, моделюються хордами у крузі, тобто цілком скінченними об’єктами. Проте нескінченність проявляється також і в нульових розмірах точок чи нульових товщинах кривих ліній і площин. Знову ж таки, математична абстракція не опирається тут на реальний досвід, адже кожна матеріальна точка має ненульові розміри. Протагорові належить думка, що перетин кола і дотичної прямої до нього не зводиться до однієї точки, а містить принаймні дві «нескінченно близькі» точки. Звичайно, така думка відкидалася евклідовою аксіоматикою. В рамках евклідової аксіоматики геометрії статус нескінченно малих і нескінченно великих об’єктів істотно розрізнявся. Неявно вважалося, що аксіоми, сформульовані для нескінченно малих об’єктів, добре узгоджуються з реальністю. Водночас, для тези щодо існування єдиної паралельної прямої, що проходить через точку зовні заданої прямої вжито термін постулат, що свідчить, що такий факт приймався як експериментально верифікований.
У середньовічній геометрії нескінченно віддалені точки здобули рівні права зі скінченними. Для потреб реалістичного живопису знадобилося поміщати на картинах також і зображення нескінченно віддалені точки. Читач може уявити собі картину, де намальовано рейки, що простягаються до горизонту і на картині видно неіснуючу в реальності точку перетину рейок (в Б.-І. Антонича зустрічаємо “срібні рейки-шпаги вбиті в обрій”). Так виникла проективна геометрія, у якій нескінченно віддалені точки рівні в правах зі звичайними, скінченними точками.
В аналізі ще з самого початку його виникнення одержуємо два підходи до нескінченно малих і нескінченно великих величин. Перший приписують Ньютонові: нескінченно малі трактуються при цьому як змінні величини, для оперування з ними створюється технічно громіздкий апарат теорії границь, мова «епсилон-дельта», ряди і т.п. Другий підхід асоціюється з Ляйбніцом, котрий оперував з нескінченно малими як зі сталими і розробив для цього необхідний алгебраїчний формалізм.
Поняття нескінченно близького (інфінітезимального) околу точки лежить в основі інтуїтивної ідеї топологічного простору. Історично перше означення топологічного простору основане на понятті замикання, запровадженому в математику Ф. Рісом та К. Куратовським. Оператор замикання приєднує до множини в топологічному просторі нескінченно близькі до неї точки. Еквівалентним є означення топологічного простору через відкриті множини, тобто множини, що разом з кожною своєю точкою містять і деякий її окіл. Це означення належить П.С. Александрову і веде свої корені ще від Дедекінда. Означення Куратовського носить алгебраїчний характер, тоді як означення Александрова більше апелює до геометричної інтуїції. Зазначимо тут, що М. Зарицкий у своїй праці [1] кладе в основу поняття топологічного простору поняття межі множини. Такий підхід був, на нашу думку, недооцінений і ми не бачимо згадки про Зарицького поряд з Александровим і Куратовським в підручниках з основ топології. Важливість аксіоматизації топології, основаної на понятті межі, було відзначено філософами (див., наприклад, [2][3]).
Зауважмо тут, що при переході від метричних просторів з їх мовою “епсилон-дельта” до топологічних просторів вносить деяку внутрішню суперечність у поняття інфінітезимального околу точки: такий окіл цілком може бути скінченним навіть у нетривіальних випадках, коли він не зводиться до самої цієї точки.
В кінці 19-го – на початку 20-го століття було закладено основи теорії множин. В рамках цієї теорії одержали строге означення поняття кардинального числа (потужності) та ординального числа. Нескінченні множини можна було тепер означити різними способами: один з них – як множини, рівно потужні своїй власній частині – йде ще від Галілея, який завважив, що натуральні числа можна поставити у взаємно однозначну відповідність з всіма парними числами. Зауважмо, що останній приклад став предметом філософського аналізу Вітгенштайном, який заперечував існування співвідношення між класом натуральних чисел та його підкласом, а стверджував лише співвідношення кожного конкретного натурального числа n з числом 2n. Перехід від кожного такого співвідношення до висновку про класс (множину) в цілому Вітгенштайн пояснював лише недосконалістю нашої граматики.
Теорія множин породила багато парадоксів, які потребували і потребують філософського осмислення. Ряд з них пов’язано з аксіомою вибору, яка постулює можливість формування нової множини шляхом вибору елементів з родини інших множин. Один з найвідоміших парадоксів, що ґрунтується на аксіомі вибору, – парадокс Банаха-Тарського – полягає в тому, що одиничну кулю в тривимірному просторі можна розбити на скінченне число частин, з яких, рухаючи їх як тверде тіло, можна скласти дві одиничні кулі.
Аксіома вибору не вказує способу вибору, а лише стверджує змогу його здійснити і в цьому її неефективність. Попри заперечення конструктивістів, бачимо, що, однак, в цілому математика, що допускає аксіому вибору, є ефективною.
В 60-х роках 20-го століття виник нестандартний аналіз – розділ математики, якому нескінченно малі (великі) величини є сталими. Творець нестандартного аналізу, Абрагам Робінсон, підкреслював, що традиція як і філософія цього розділу математики походить від Ляйбніца. В рамках нестандартного аналізу з нескінченними об’єктами можна оперувати так само як зі скінченними. Це дало змогу значно спростити ряд існуючих доведень традиційного аналізу, а також зробити строгими міркування класиків аналізу, які, скажімо, вільно послуговувались рядами, трактуючи їх лише як суми нескінченного числа елементів і не надто дбаючи про збіжність.
Поряд з нестандартним аналізом в кінці 60-х років минулого століття виникла ще одна альтернатива класичному аналізові – синтетична диференціальна геометрія. Вона розвинулася як реалізація згаданої вище ідеї Протагора за допомогою методів теорії категорій. В синтетичній диференціальній геометрії перетин гладкого об’єкта та дотичного до нього лінійного об’єкта неодноточковий. Зокрема, перетин дійсної осі, реалізованої як осі абсцис на площині, і параболи
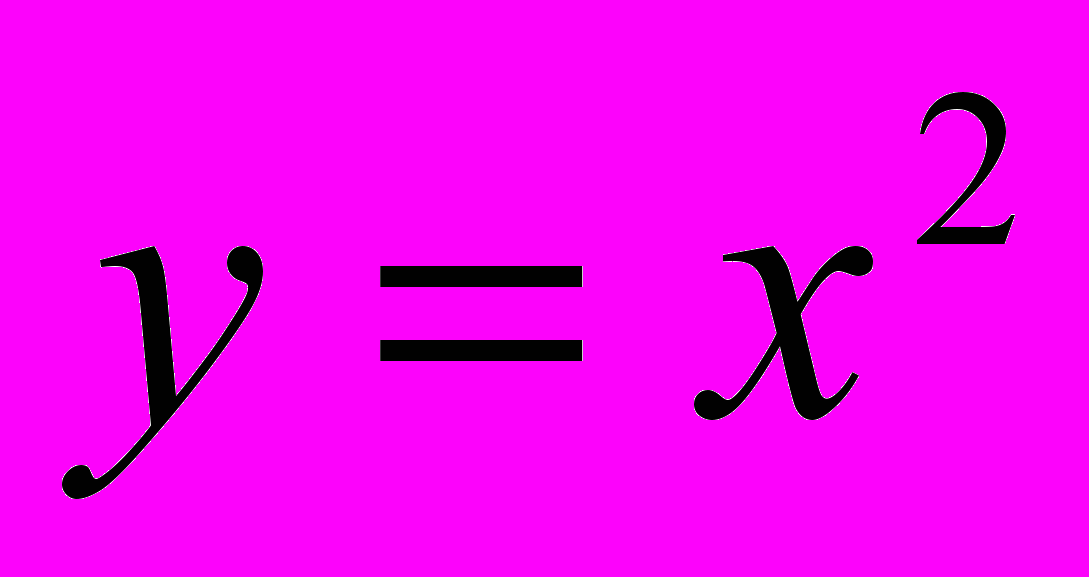складає інфінітезимальний окіл нуля на дійсній осі. Нескінченно малі при цьому є нільпотентними, тобто 
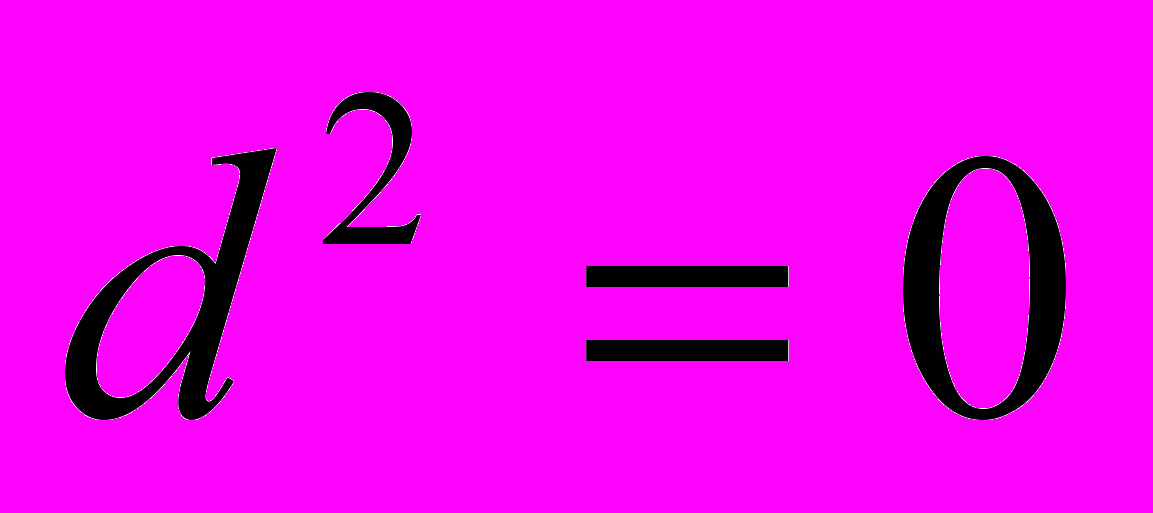для кожної нескінченно малої величини 
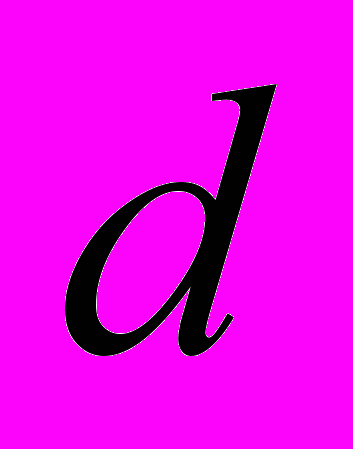. Нільпотентність добре узгоджується з практикою у тому сенсі, що для застосувань можна часто нехтувати нескінченно малими величинами вищих порядків. Ось як виглядає “інженерне” обчислення довжини кола радіуса 1. Позначивши через π площу одиничного круга, одержуємо значення 
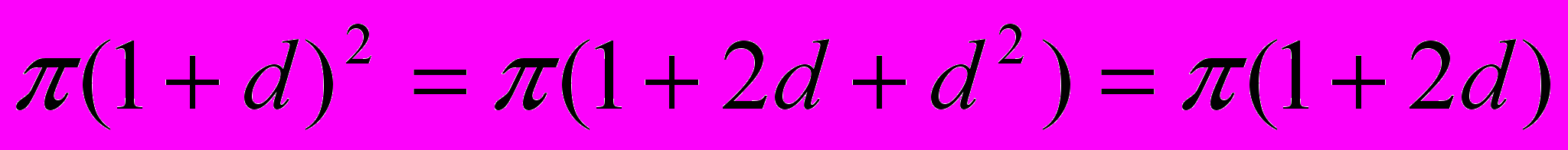для круга радіуса 
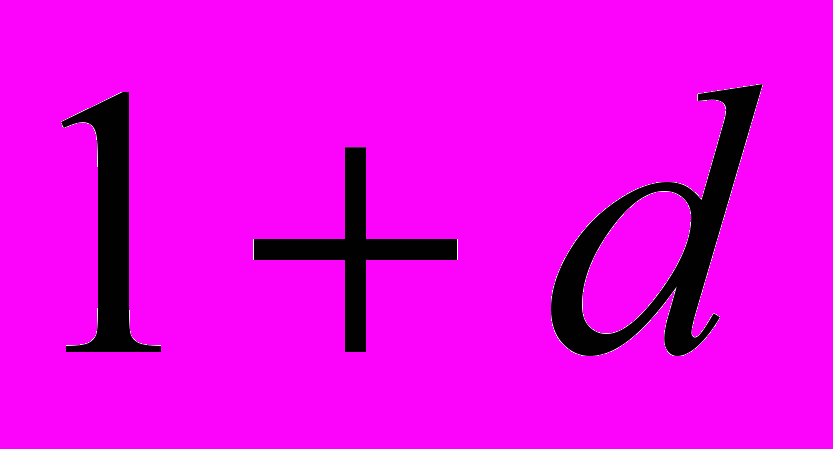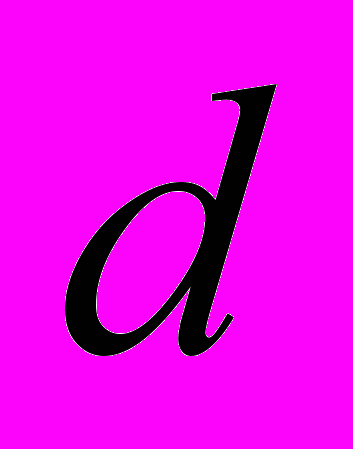, де -- нескінченно мала (тут ми взяли до уваги, що 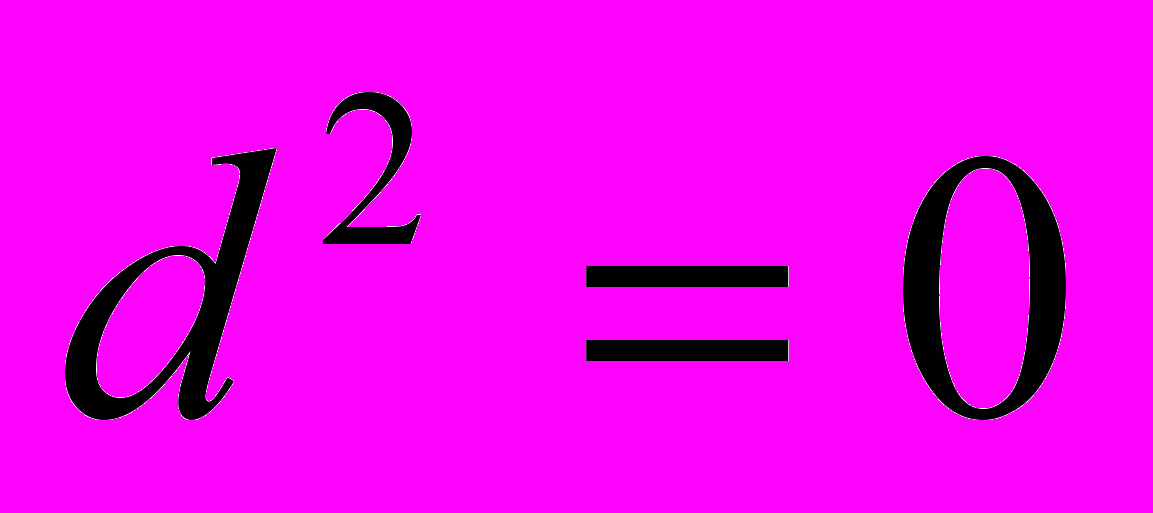). Тому площа нескінченно тонкої смуги товщини 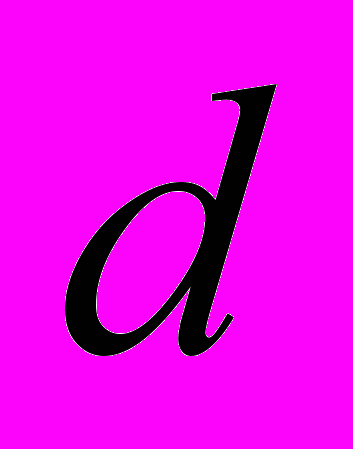(різниці між площами кругів радіуса 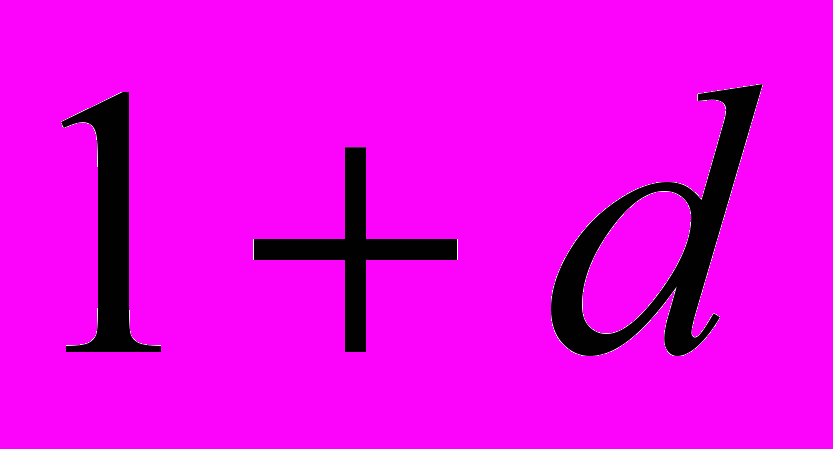і 1) рівна 
, звідки випливає, що довжина кола одиничного радіуса рівна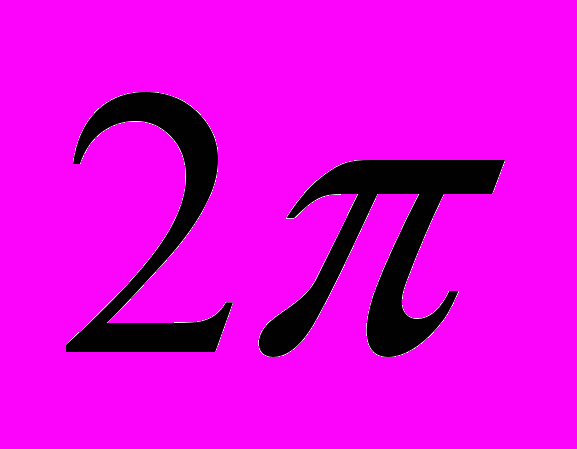 
. Зрозуміло, що таке міркування не відзначається строгістю в рамках стандартної університетської математики і що його можна зробити строгим, лише допустивши нільпотентні нескінченно малі. Проте існування останніх суперечить класичній логіці (правилу виключеного третього), тому синтетичну диференціальну геометрію можна розвивати лише в рамках інтуїціоністської логіки. Перевагою синтетичної диференціальної геометрії є той факт, що всі функції, які у ній виникають, є неперервними і гладкими. На перший погляд це звучить контрінтуїтивно, але спроба заперечити цю тезу, наприклад, розглянувши не неперервну функцію, що рівна нулеві лише в нулі, а в позосталих точках рівна одиниці, неминуче впирається в правило виключеного третього – тут ми неявно припускаємо, що кожне число або рівне нулеві, або ні. Синтетична диференціальна геометрія може бути розвинена достатньо далеко, її теперішні застосування охоплюють також і фізику. Зокрема, недавно було сконструйовано синтетичну теорію відносності.
В кінці 90-х років 20-го століття французький математик М. Громов запровадив означення асимптотичного виміру і застосував його до опису геометричних властивостей скінчено породжених груп. Асимптотичний вимір простору – це вимір “з точки зору нескінченності”. Доброю ілюстрацією є простір цілих чисел, що має топологічний вимір нуль у класичному сенсі цього поняття. Водночас, якщо уявний спостерігач відійде досить далеко від простору цілих чисел, то для нього візуальні проміжки між числами зменшуватимуться, а нескінченно далекий спостерігач узагалі не завважить різниці між цілими числами і дійсною прямою. Тому асимптотичний вимір множини цілих чисел рівний одиниці. Такий підхід було пізніше далеко формалізовано, що привело до створення асимптотичної топології – розділу метричної геометрії, який оперує з глобальними властивостями метричних просторів. Формалізм асимптотичної топології передбачає ототожнення об’єктів, що відрізняються на скінченну величину, зокрема, з позицій цієї теорії кожен обмежений об’єкт еквівалентний порожньому. Професор І. Протасов з Київського університету, що запровадив новий підхід до асимптотичної топології – теорію кульових структур (див., наприклад, [4]), у приватному повідомленні зазначав, що у студентів, систематично тренованих на формалізмі асимптотичної топології, порівняно швидко виробляється особлива інтуїція “нехтування скінченного”. При такому баченні, зокрема, не існує континуальності “в малому” і всі розглядувані простори можна вважати дискретними.
Можна лише очікувати, що філософське узагальнення результатів асимптотичної топології оформиться в напрямок, який створив би історичну антитезу фінітизмові Л. Кронекера – напрямку в філософії математики, який передбачав заперечення поняття нескінченного і, згідно якого, математичні сутності мали право на існування, лише якщо вони були сконструйовані за скінченне число кроків, і який пізніше привів до виникнення філософської школи математичного конструктивізму. (Зазначимо, що ще більш радикальними у своїх пглядах є адепти ультрафінітизму. Цей різновид заперечує існування множини натуральних чисел і водночас бере до уваги фізичні обмеження щодо існування тих чи інших математичних об’єктів. Скажімо, може не бути фізично можливим оперування з надто великими числами).
Попри те, що при асимптотичному підході скінченні об’єкти еквівалентні порожньому елементові, ряд асимптотичних інваріантів, серед яких і асимптотичний вимір, можуть бути означені саме через властивості нескінченних просторів [5]. Отож, співвідношення між скінченним і нескінченним не зводиться до взаємного заперечення.
Асимптотична топологія новаторська саме з точки зору її філософії. Технічний апарат її, за винятком деякий розділів, ще цілком міг бути розвинений паралельно численню нескінченно малих.