С. М. Зеркаль, д-р техн наук, Е. А. Хогоев Институт нефтегазовой геологии и геофизики со ран (Россия, 630090, Новосибирск, пр. Коптюга, 3, тел.(383) 3333419, е-mail: Zerkal@ngs ru Численное решение

Вид материала

Решение

Содержание Постановка обратной кинематической задачи Метод решения обратной кинематической задачи в трехмерной линеаризованной постановке. Результаты компьютерного моделирования. Список литературы Хогоев Е.А

Подобный материал:

• А. А. Трофимука со ран (Россия, 630090, Новосибирск, пр-т Коптюга, 3, тел.(383) 3309201,, 56.69kb.
• Мы будем рады видеть вас в числе участников конференции! Адрес Оргкомитета, 70.14kb.
• Мы будем рады видеть вас в числе участников конференции! Адрес Оргкомитета, 71.03kb.
• Витте Л. В., Василевский А. Н., Павлов, 64.33kb.
• А. П. Янковский Институт теоретической и прикладной механики им. С. А. Христиановича, 21.46kb.
• Программа, 247.1kb.
• Сибирское отделение ран центр общественных связей, 48.58kb.
• Геологический институт ран II всероссийская научная конференция с участием иностранных, 166.81kb.
• Всероссийская научно-техническая конференция, 28.31kb.
• Институт Математического Моделирования ран, Москва, Россия, e-mail: zmitrenko@imamod, 11.3kb.

С. М. Зеркаль, д-р техн. наук,

Е. А. Хогоев

Институт нефтегазовой геологии и геофизики СО РАН

(Россия, 630090, Новосибирск, пр. Коптюга, 3,

тел.(383) 3333419, Е-mail: Zerkal@ngs.ru


Численное решение обратной трехмерной кинематической задачи сейсмики в линеаризованной постановке

с использованием площадной системы наблюдений


Аннотация. Предлагаемый алгоритм решения трехмерной обратной задачи заключается в редукции ее к ряду задач определения отклонения скорости от линейного закона на поверхностях второго порядка, с использованием томографической системы наблюдений. Приводятся результаты компьютерного моделирования. Полученные результаты могут быть использованы при изучении скоростного строения верхней части разреза и в телесейсмике.


Введение. Обратная кинематическая задача сейсмики (ОКЗ) принадлежит к классическим геофизическим задачам и имеет математическую постановку, представляющую интерес с точки зрения интегральной геометрии и обратных задач для дифференциальных уравнений. Эта задача была первой рассмотренной обратной задачей для дифференциальных уравнений (уравнение эйконала), и история ее исследования к настоящему времени насчитывает сто лет (одномерная постановка, результат Г. Герглотца, Е. Вихерта, 1905-1907 гг.). Основные результаты по численному решению ОКЗ были получены в научных школах академиков А.С. Алексеева [1] и М.М. Лаврентьева [2-7]. Использование томографического подхода позволило отойти от решения ОКЗ на плоскости и рассмотреть ее на поверхности второго порядка (А.Л. Бухгейм, С.М. Зеркаль, Е.А. Хогоев).

В сейсморазведке (МОВ-ОГТ) рефрагированные волны имеют весьма незначительную востребованность. Годографы рефрагированных волн используются в основном для изучения распределения скорости в верхней части разреза и в конечном итоге, для корректного определения статических поправок, которые вводят в сейсмические трассы для исключения влияния наиболее изменчивой верхней части разреза (ВЧР) и рельефа поверхности наблюдений на результат обработки [1]. Расчет априорных статических поправок с использованием рефрагированных волн, зарегистрированных в первовступлениях записей МОГТ, позволяет получить более точную и детальную характеристику верхней части разреза, чем известными методами. К недостаткам традиционного подхода относится, во-первых, необходимость анализа отдельных годографов, что малопродуктивно при больших объемах сейсморазведочных работ и, во-вторых, интерпретация (подбор годографов) ведется в рамках моделей сред с монотонно растущей скоростью от глубины.


Постановка обратной кинематической задачи при использовании томографической системы сбора данных.

Исследуемая среда предполагается регулярной. Это означает, что изменения скорости в среде таковы, что паре точек источник-приемник 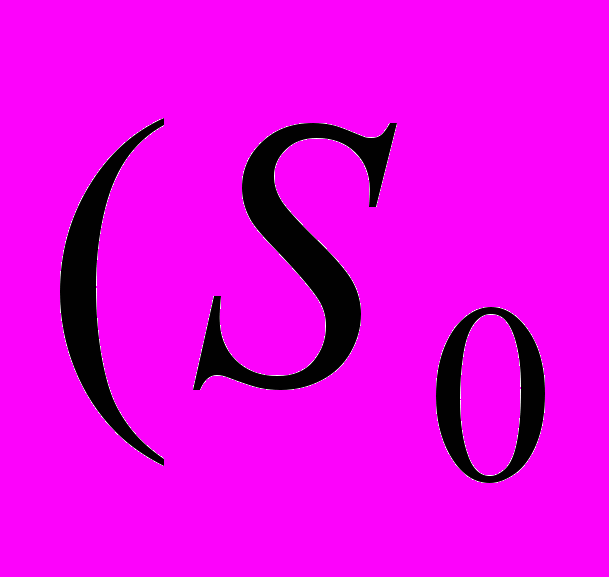и 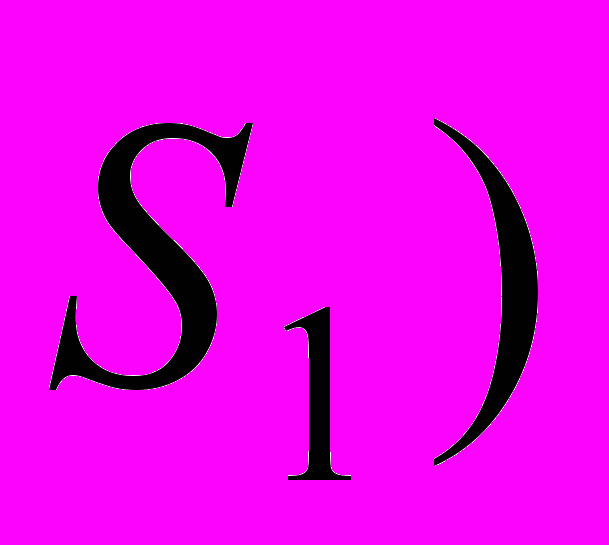соответствует одна геодезическая линия (луч) Г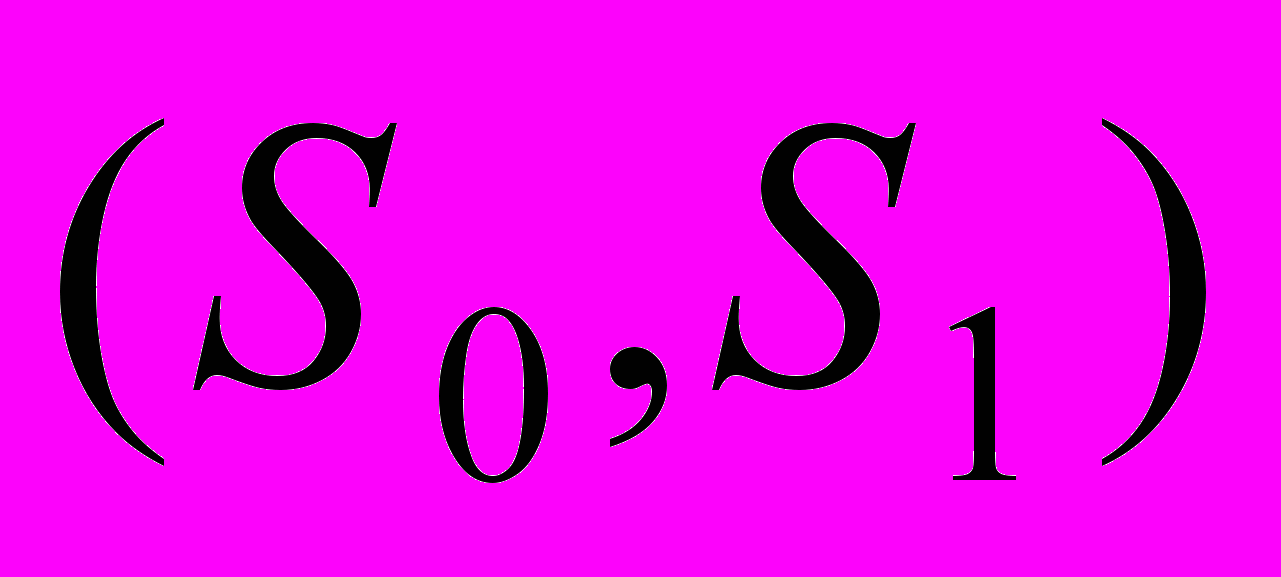. Следующим важным предположением является то, что скорость V(x,y,z) представима в виде

V(x, y, z) = V₀(z)+ V₁(x, y, z), 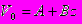 ,  V₀ >> |V₁|,

где 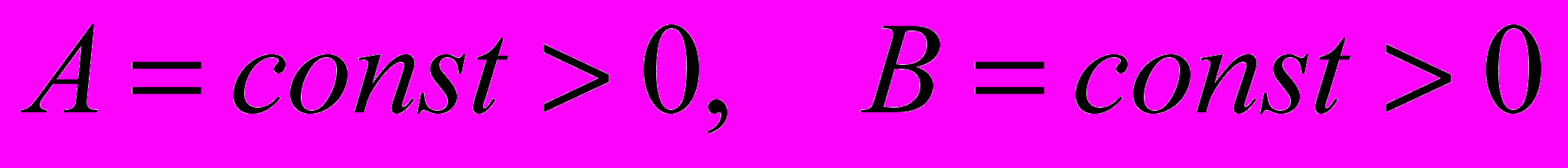, и их значения обеспечивают достаточное заглубление луча.

Для решения задачи используем метод линеаризации обратной кинематической задачи для многомерных сред систематически применяемый, начиная с работ В.Г. Романова. В результате приходим к формуле:

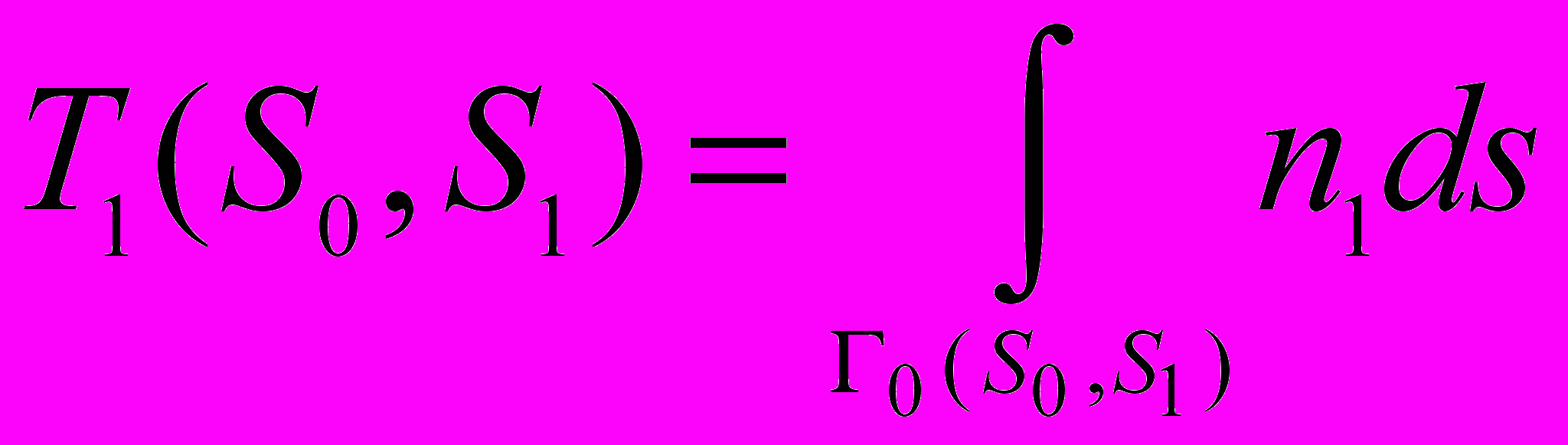, (1)

где 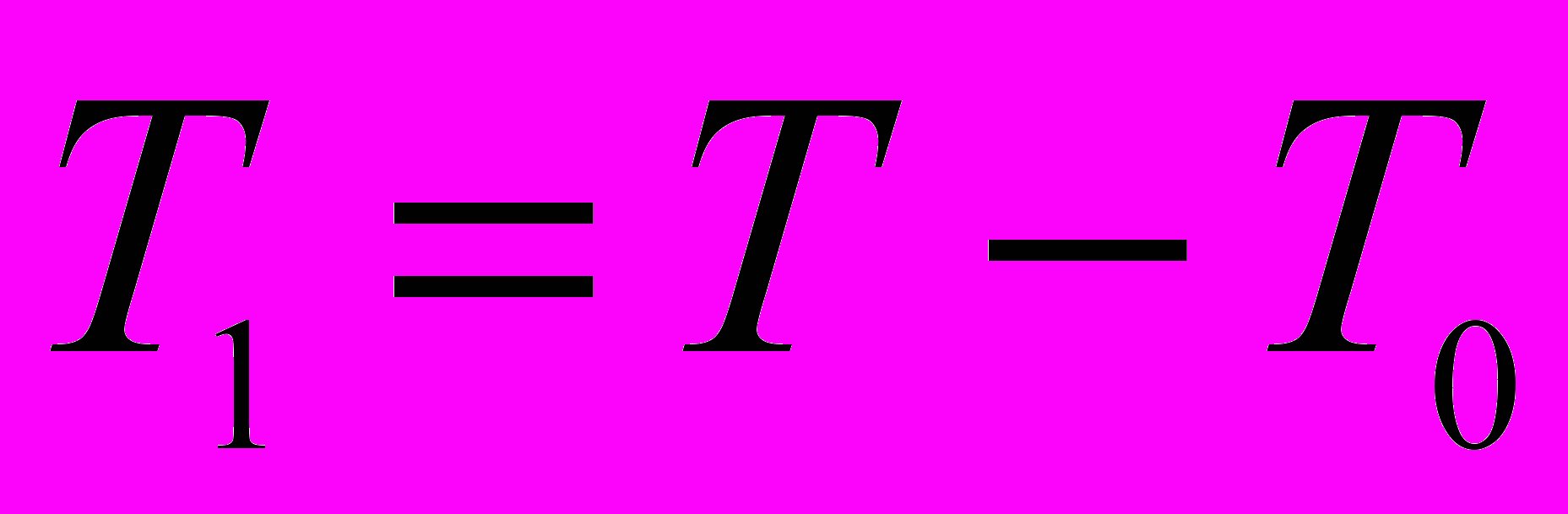, n₁ = V^-1 – V₁^-1 ,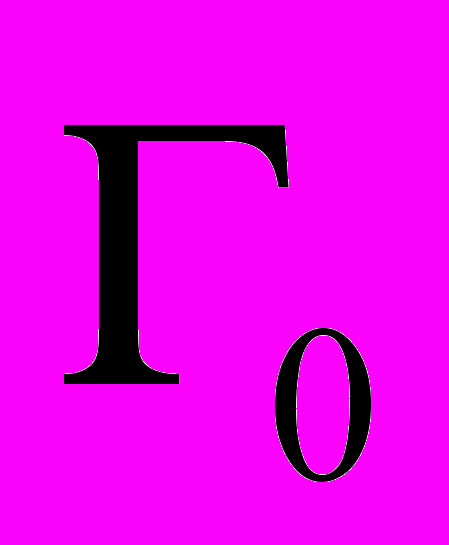 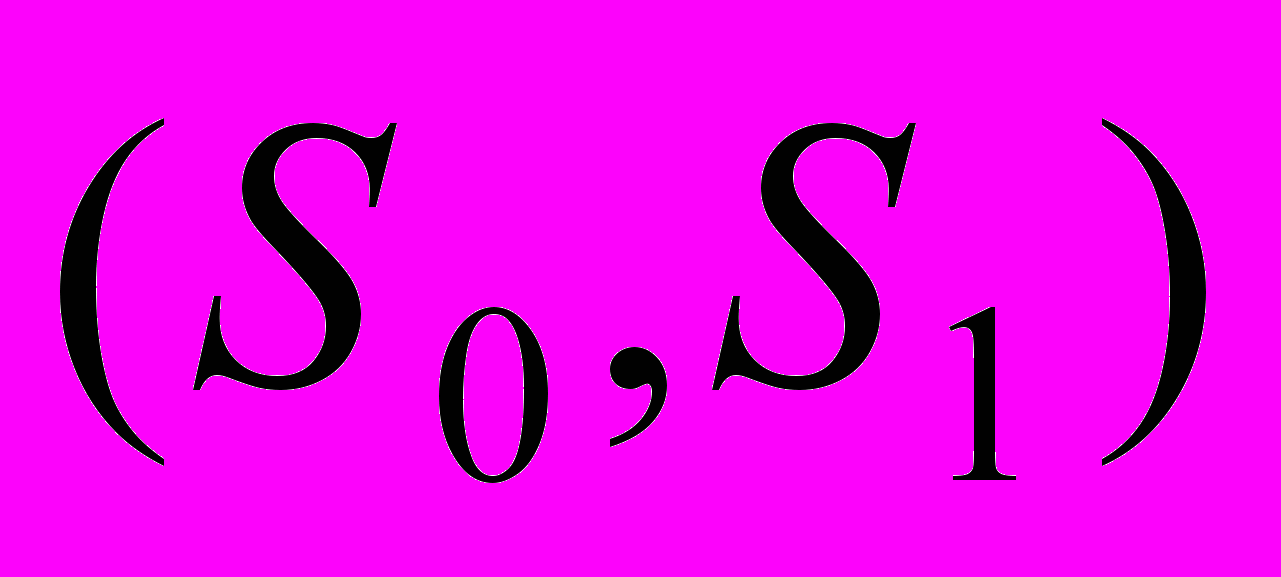– геодезическая для среды со скоростным распределением V₀. Поскольку значения Т считаются известными (результат решения прямой задачи, а на практике это вектор измерений), значения 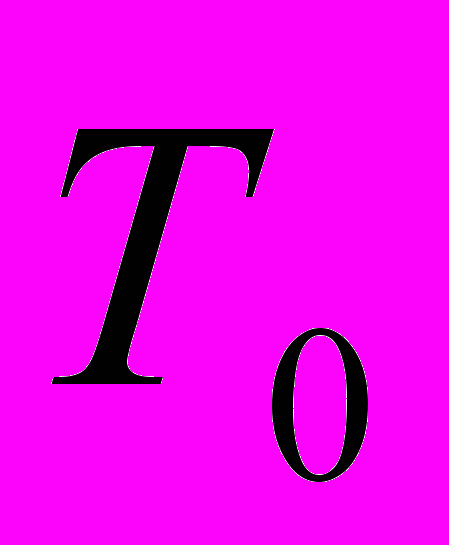в случае 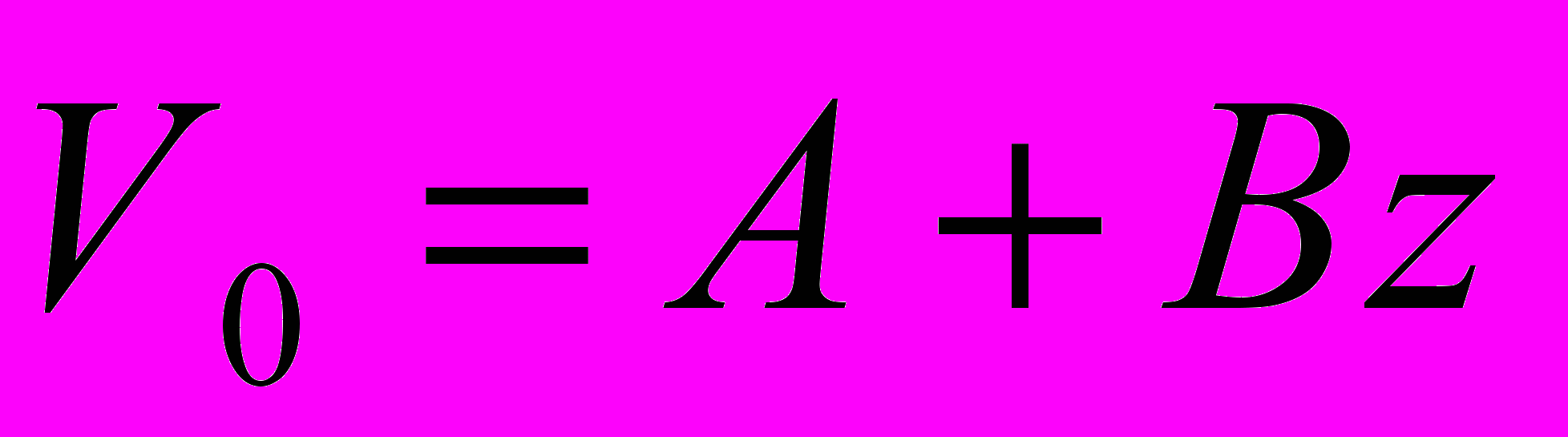вычисляются в явном виде, то вычисление необходимых значений 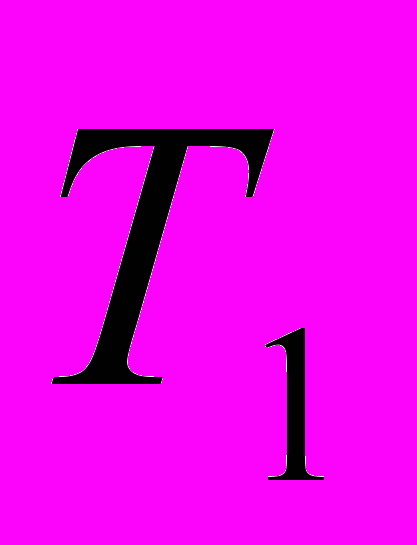не составляет труда.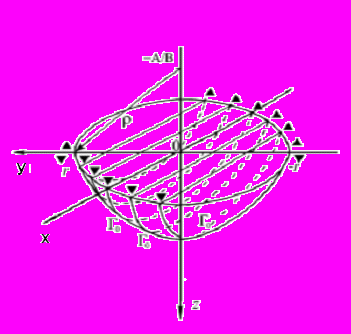



Рис.1 Система наблюдений и поверхность, образованная лучами в случае линейной зависимости скорости рефрагированной волны от глубины (переменная z).

1 – источники, 2 – приемники сигнала.


Использование системы наблюдений в виде окружности не только снимает переопределен-ность задачи, но и существенно формирует томографическую по-становку исследуемой задачи. Лучи 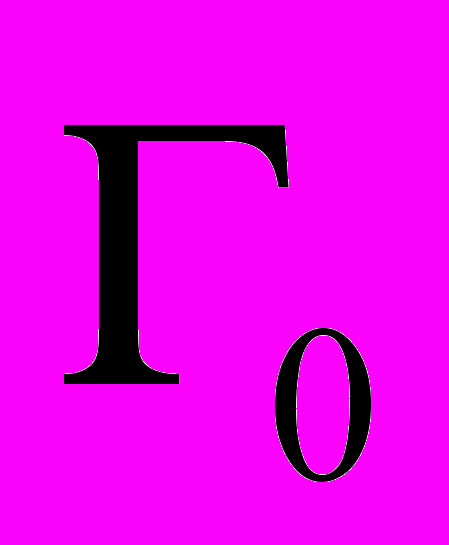, “натянутые” на окруж-ность системы наблюдений, образуют поверхность шарового сегмента (см. рис. 1).

Изменение радиуса r позволяет получить систему вложенных шаровых сегментов, заполняющих объем исследуемой области в R³. Определяя n₁ на поверхности таких шаровых сегментов, получаем решение трехмерной задачи. Заметим, что используемое послойное изучение объекта исследования, методика снятия проекционных данных ставит решаемую задачу в один ряд с известными задачами классической томографии.


Метод решения обратной кинематической задачи в трехмерной линеаризованной постановке.

Решение задачи дается следующей формулой обращения [4]:

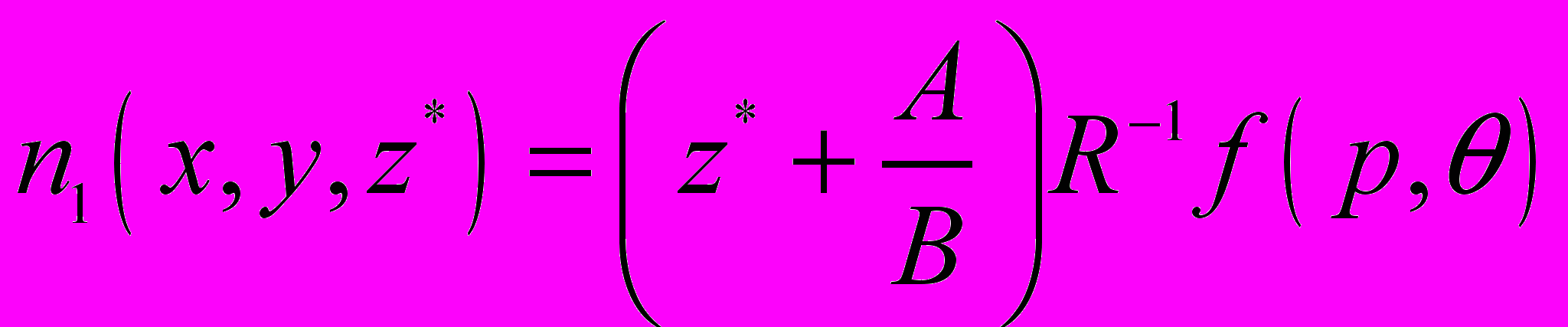, (2)

где 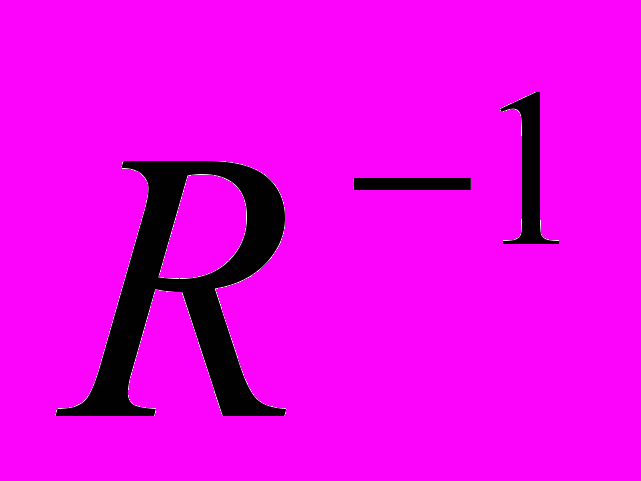- оператор обратного преобразования Радона (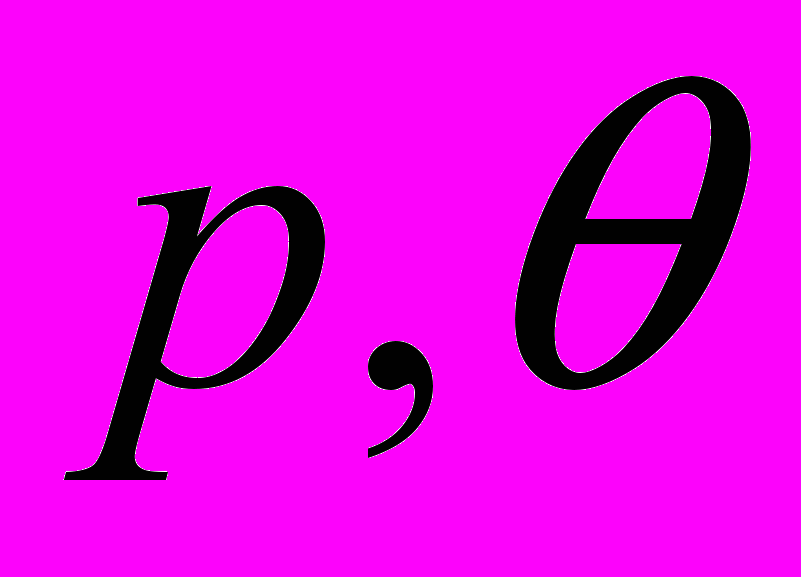- принятые в томографии обозначения, расстояние от точки начала координат до линии просвечивания и направление просвечивания в плоскости (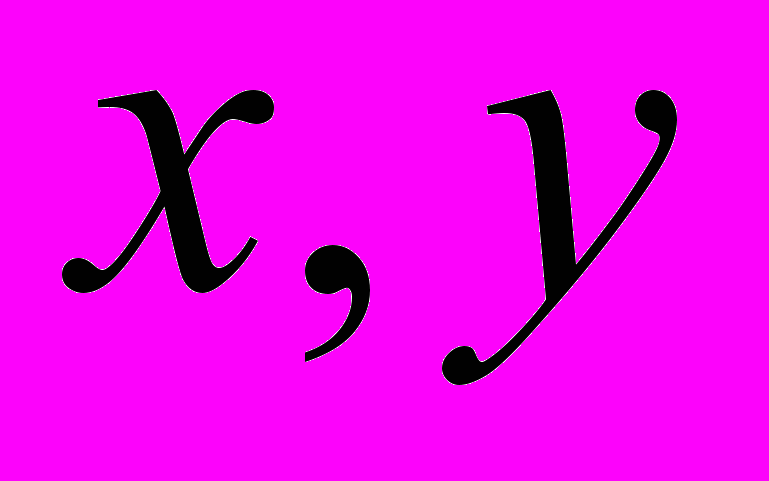) соответственно).

Определяя искомую функцию 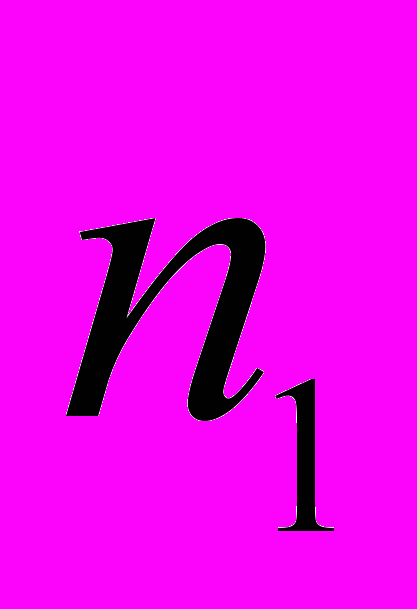по формуле обращения (3) в круге 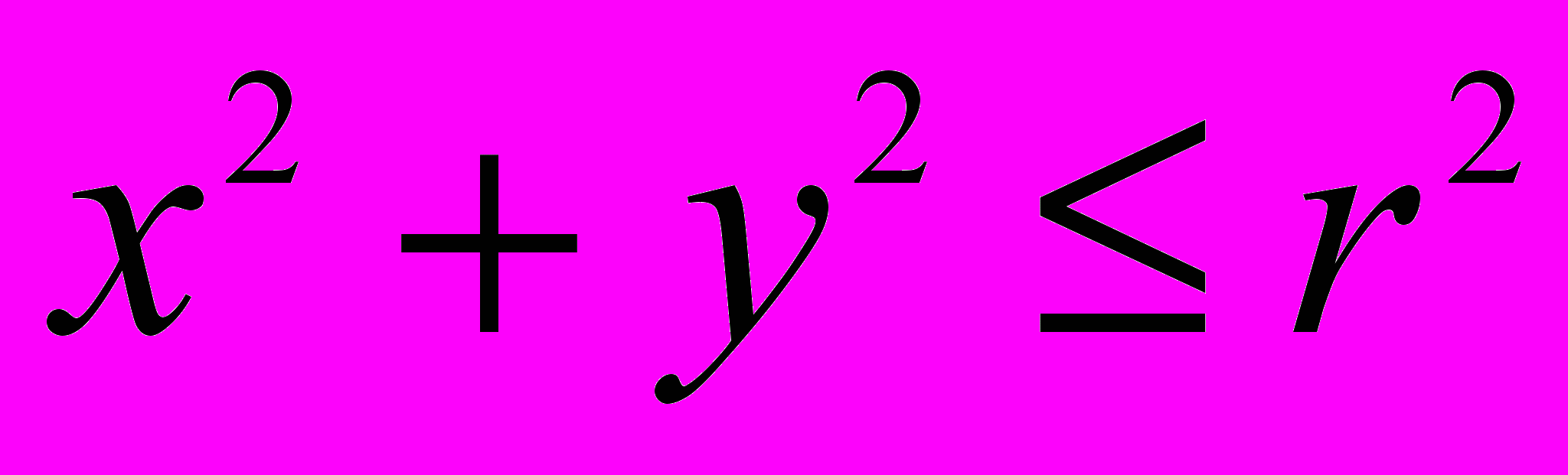, мы тем самым определяем 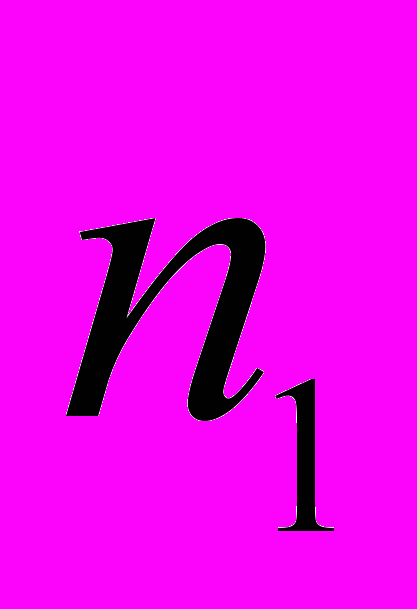на поверхности шарового сегмента, образованного лучами 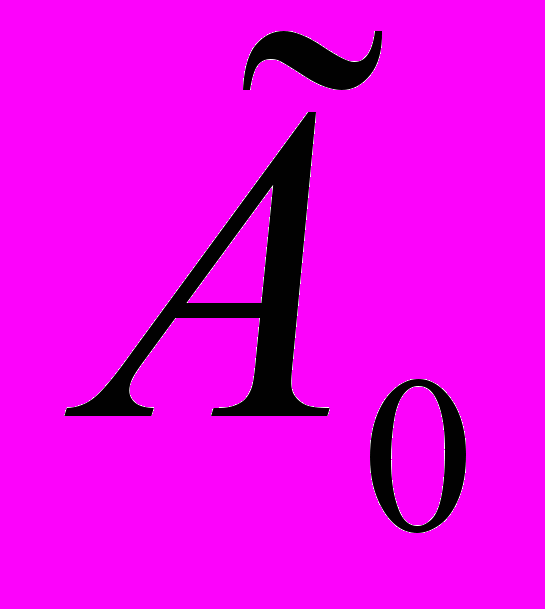, опирающимися на окружность системы наблюдений.

Формула (2) позволяет применить к решению обратной кинематической задачи, технику численной реализации обращения преобразования Радона, достаточно хорошо развитую для решения других научных задач, что существенно упрощает работу с этой формулой.

В численных экспериментах значения 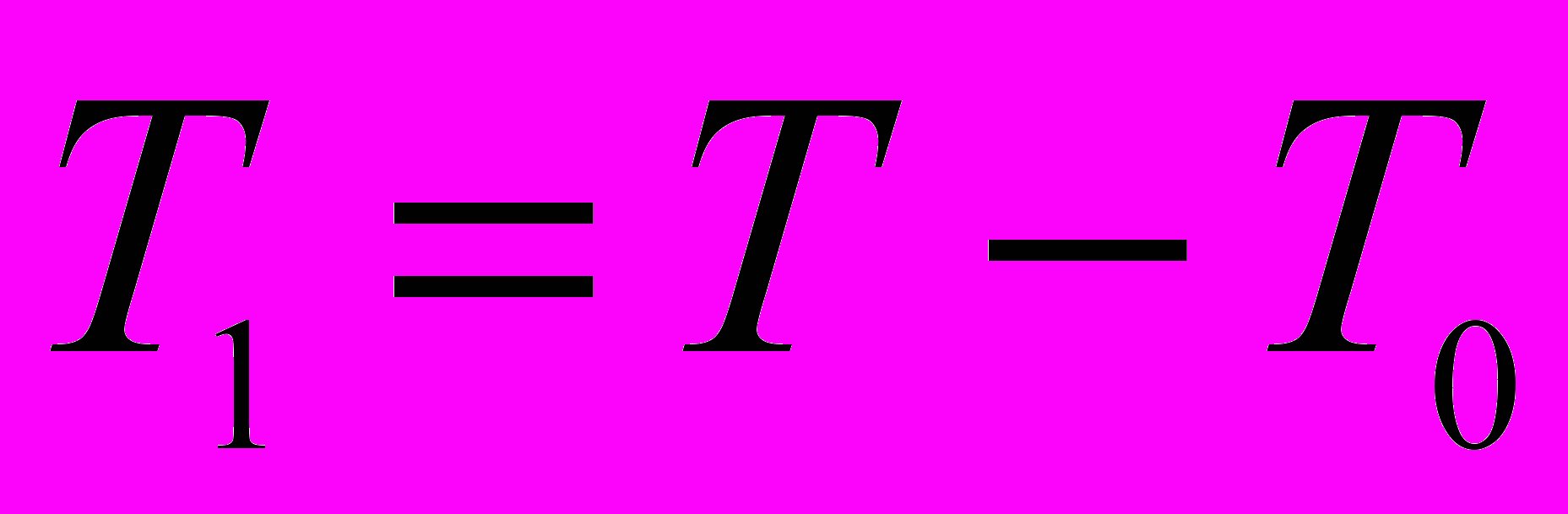вычислялись в результате решения начально-краевой прямой кинематической задачи. Численная реализация формулы (2) требует организации следующей процедуры съема проекционных данных. Пусть мы имеем N - источников и столько же приемников зондирующего излучения, расположим их так, как показано на рис.1, где изображена параллельная система наблюдений, то есть линии, соединяющие соответствующие источники и приемники, параллельны. Измерения времен пробега Т производятся для различных положений источников и приемников, получаемых путем поворота системы наблюдений вокруг точки "0" (центра окружности и системы координат) против часовой стрелки с шагом:

Для решения обратной задачи использовался алгебраический подход, носящий в томографии название алгебраической реконструкции и реализуемый после предварительной алгебраизации преобразования Радона в формуле (2).

Результат решения задачи изложенным методом мы принимаем за эталонное решение при сравнении с результатами, полученными с использованием интерполяции.

Приведем описание численных исследований и компьютерного моделирования.

Модель среды. Скоростная неоднородность в среде задается в виде

v(x,y,z)=0.1∙exp(-3∙(x-0.1)²-3∙(y-0.05)²-10∙(z-0.2)²), (3)

с экстремумом w=0.1 км/c в точке (x_a y_a z_a)= (0.1, 0.05, 0.2) км, при основной известной составляющей скоростного распределения v₀(x)=1+0.5z.


Алгоритм интерполяции данных с площадной системы наблюдений на окружность. Моделируется система наблюдений на площади 2х2 км, состоящая из источников и приемников в узлах равномерной сетки с шагом по X, Y: 100 в одном случае, и с шагом 200 м во втором случае (Рис.2). Приемники располагаются в на тех же линиях сетки, с шагом 50 м. В основе такой схемы наблюдений лежат типичные для сейсмики значения расстояний между приемной группой и точкой взрыва. В общем случае расположение источников может быть неравномерным.

Задаются координаты точки источника (на окружности) 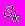=(X_Sk, Y_Sk ) и приемника 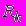=(X_Rk, Y_Rk), k-номер пары источник-приемник. Из имеющейся площадной системы наблюдений определяются три ближайших к 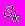источника 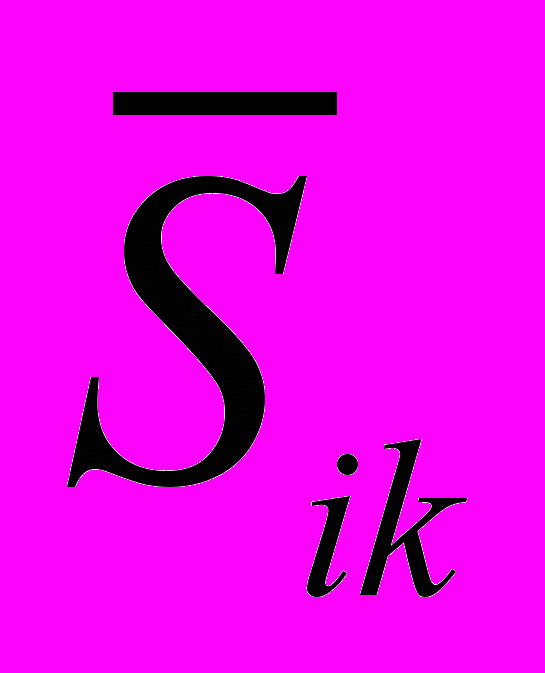(i=1,3), не лежащие на одной прямой, и соответственно три ближайшие точки приема.





Рис.2. Пример площадной системы наблюдения. Сторона квадрата 2 км, сторона ячейки 0.2 км, черными кружками обозначены точки приема. Приведена окружность томографической системы наблюдения, на которую интерполируются времена прихода волны.


Времена прихода обозначим 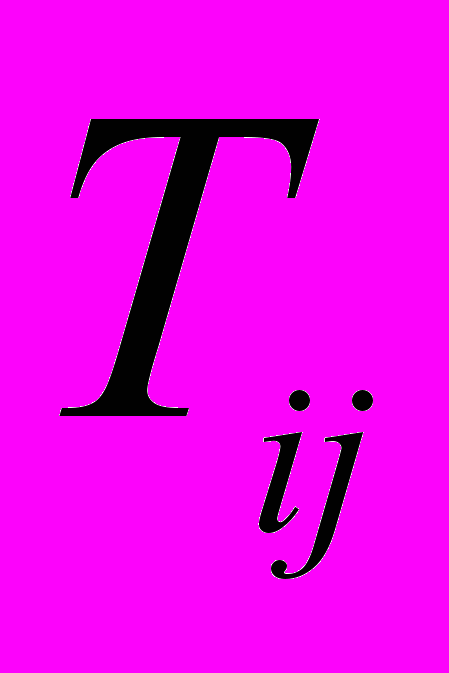, i=1,..3, j=1,..3. Для каждой из трех 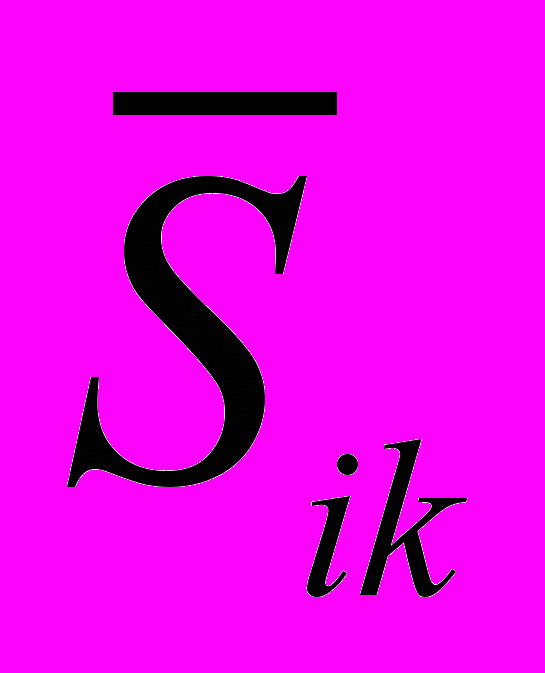время прихода волны интерполируется в точку 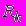плоскостью, построенной по трем точкам (, 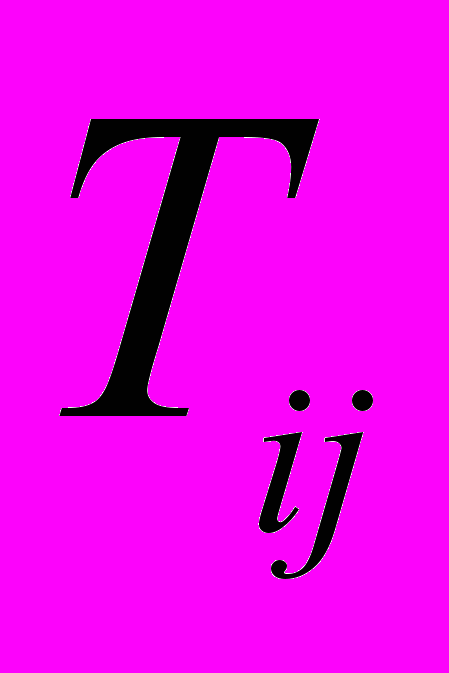), j=1,3. После интерполяции получаем в точке приема 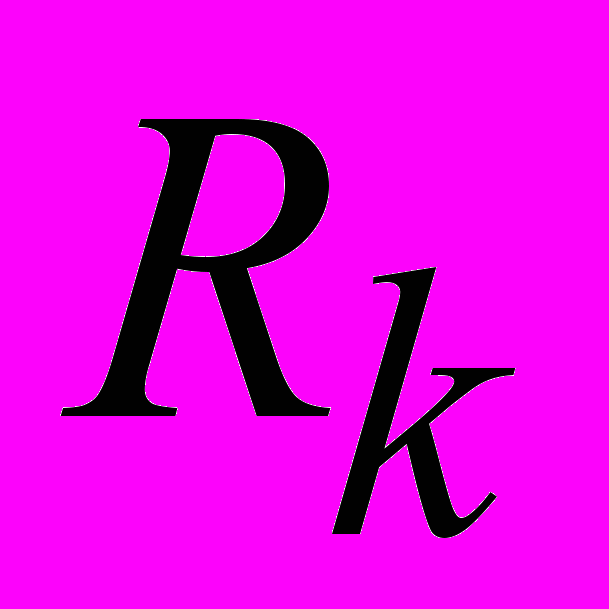три значения времени 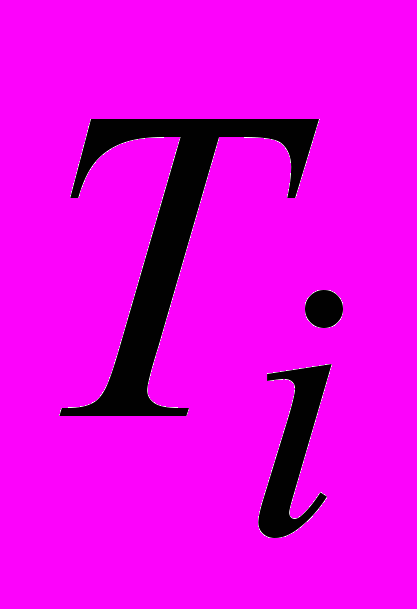, зависящего от координат 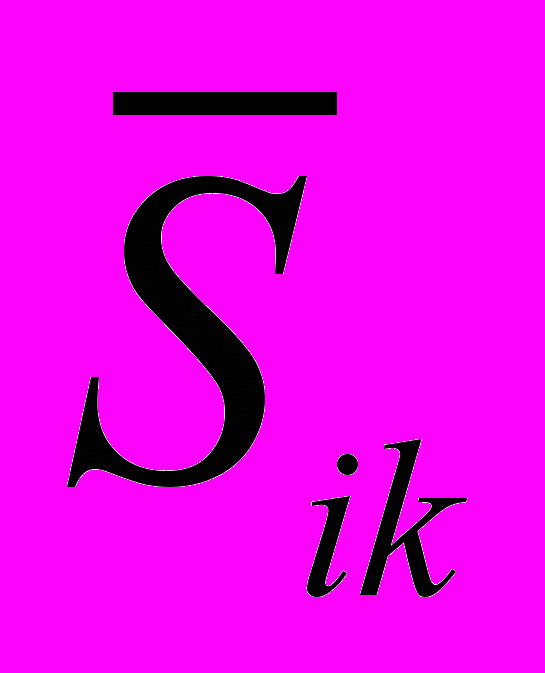(i=1,3),. Затем строим интерполирующую плоскость, проходящую через точки (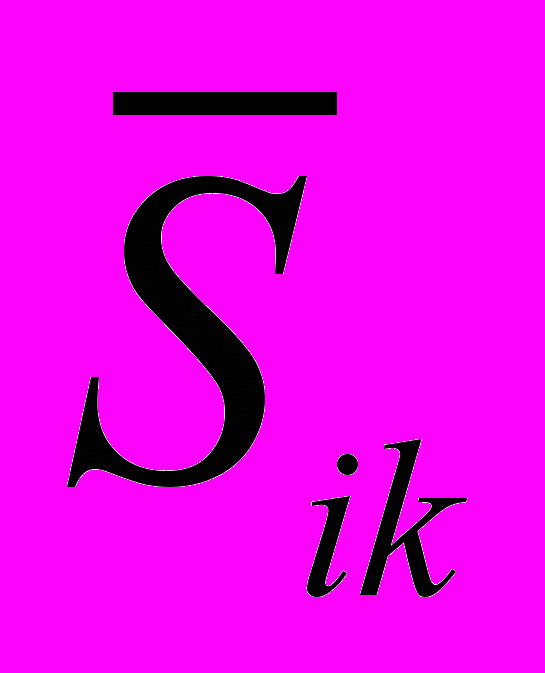,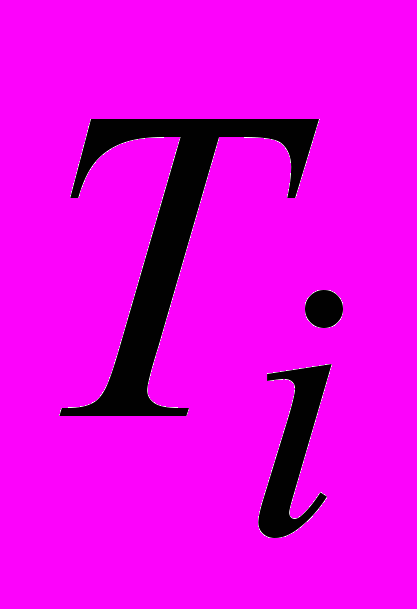) и рассчитываем время в точке с требуемыми координатами .


Результаты компьютерного моделирования. По изложенной методике были проведены численные модельные эксперименты с использованием систем наблюдений различной плотности. Рассматривались сетки с шагом по приемникам 200, 100, 50, 25 м, и по источникам 200, 100, 50, 25 м. Результат сравнивался с точной формулой (3) и с решением эталонной задачи (Рис.3.)

При решении эталонной задачи использовалась томографическая система наблюдений на концентрических окружностях. Радиус окружностей от 200 до 1000 м, с шагом 100м. Источники и приемники в количестве 20, количество проекций 8. Сетка восстановления 20х20 при всех радиусах исследования. Для сопоставимости интерполяция с площадной системы проводилась на ту же систему наблюдений, что и при решении эталонной задачи. Таким образом, в результате мы получаем искажения, обусловленные только погрешностями интерполяции, а не методом решения обратной задачи.





Рис.3. Результаты восстановления локальной аномалии скорости в среде в сечении XOZ, а – задаваемая скоростная модель, б – восстановленная по наблюдениям на вложенных окружностях, в – пересчет с площадной системы наблюдений на окружности. По вертикали глубина Z, по горизонтали Х (м).


В результате численных экспериментов установлено, что минимально предельно допустимая плотность сетки для заданной среды составляет: шаг между источниками 100 м, и между приемниками 50 м. С удвоением шага удовлетворительное решение достигается лишь на окружностях радиуса 1-0.8 км. При этом среднеквадратичное отклонение полученного решения (с процедурами интерполяции) от заданной модели не превышает 10% (эталонная задача решается с точностью 5%). Учитывая некорректность исследуемой задачи и использование метода линеаризации, эти результаты являются весьма перспективными.

Важным свойством рассматриваемого типа неоднородностей служит непрерывное изменение скорости их локальность и возможность выделения линейной составляющей в функции скорости, что создает условия для применения разработанных авторами сейсмотомографических методик.

Результаты работы ориентированы для решения задач региональной сейсморазведки, при диагностике верхней части разреза до глубин порядка 500м. При интерпретации сейсмических наблюдений особенности ВЧР могут дать ложные структуры на глубине более 1000м, искажая тем самым истинную картину. Диагностика отмеченных ситуаций является важной проблемой современной сейсморазведки.

Работа поддержана грантами РФФИ 07-07-00251-а и интеграционным проектом № 10 СО РАН.


Список литературы

1. Алексеев А.С., Белоносова А.В., Белоносов А.С., Цецохо В.А. Об алгоритмах решения двумерных и трехмерных кинематических задач сейсмики. // Международная конференция по вычислительной математике: МКВМ-2004, 21-25 июня 2004 г., Новосибирск, с. 361-369.
   
2. Лаврентьев М.М., Романов В.Г., Шишатский С.П. Некорректные задачи математической физики. Новосибирск, Наука, 1980, 286 с.
   
3. Lavretn'ev M.M., Zerkal S.M. and Trofimov O.E. Computer Modeling in Tomography and Ill-Posed Problems Inverse and Ill-Posed Problems Series, VSP, 2001, 127 p.
   
4. Зеркаль С.М., Хогоев Е.А. Результаты численного решения обратной, трехмерной, линеаризованной задачи восстановления коэффициента преломления // Препринт ВЦ СО АН СССР, Новосибирск, № 524, 26 с.
   
5. Хогоев Е.А. Численное исследование итеративного подхода к обращению поля времен рефрагированных волн // Сборник трудов международной научной конференции «Сейсмические исследования земной коры», 23-25 ноября 2004 г, Новосибирск, с. 190-195.
   
6. Зеркаль С.М. Хогоев Е.А. Итерационная технология сейсмотомографической диагностики на основе кинематики рефрагированных волн // Доклады РАН, № 4 (401), 2005 , с 526-528.
   
7. Зеркаль С.М., Хогоев Е.А. Обратная задача определения малых локальных неоднородностей квазилинейного показателя преломления // Линейные и нелинейные задачи вычислительной томографии. Новосибирск. 1985. С. 61-66.