А. Назва й адреса
| Вид материала | Документы |
- А. Назва й адреса, 1279.76kb.
- А. Назва й адреса, 2092.49kb.
- А. Назва й адреса, 4294.6kb.
- А. Назва й адреса, 3000.25kb.
- А. Назва й адреса, 1422.42kb.
- Адреса и указатели. Операции получения адреса и косвенной адресации. Отождествление, 124.21kb.
- Адреса и указатели. Операции получения адреса и косвенной адресации. Отождествление, 82.09kb.
- Опитувальник клієнта – фізичної особи-підприємця, 95.84kb.
- Понятие протокола, и связанные с ним понятия, 3193.16kb.
- Міністерства юстиції України в Автономній Республіці Крим вул, 19.85kb.
Викладачі: Старовойт Юрій Леонідович, філол.н., доцент
Хоменко Надія Павлівна, ст.викладач
21021 м.Вінниця, Хмельницьке шосе, 95, Інститут Інформаційних технологій та комп’ютерної інженерії (Ін ІТКІ), факультет комп’ютерних систем та мереж (КСМ), кафедра іноземних мов, корпус 3, ауд.3443, телефон (8-0432) 59-84-78.
МЕТА ДИСЦИПЛІНИ: Закріплення програми середньої школи, вивчення нового лексико-граматичного матеріалу, необхідного для спілкування в найбільш поширених повсякденних ситуаціях; оволодіння лексико-граматичним мінімумом для реферування і анотування наукової і технічної літератури та науково-технічного перекладу.
ПРОГРАМА: Фонологічні характеристики сучасної французької мови. Основи синтаксису: типи речень та їх структура. Морфологічні особливості частин мови. Артикль, заміна артикля прийменником. Іменник, прикметник, прислівник, їх граматичні особливості. Утворення часових дієслівних форм активного і пасивного стану. Безособові дієслова. Способи дієслова. Типи займенників, Займенникові дієслова.
Дериваційні моделі частин мови. Способи терміноутворення. Читання математичних символів та виразів.
Читання, анотування та реферування загальнонаукової та науково-технічної літератури.
Розвиток навичок монологічного та діалогічного мовлення на матеріалі розмовних тем “Студентське життя”, “Мій університет”, “Моя спеціальність”, “Моє рідне місто (село)”, “Поїздка за кордон”, “Міжнародне співробітництво”, “Франція: політичний устрій, історія, культура”, “Наукові досягнення та видатні діячі науки” тощо.
БІБЛІОГРАФІЯ:
Мельникова Т.В. Посібник з французької мови для технічних вузів. – К.: Вища школа, 1976 – 255с.
Леонова Е.П. Учебник по французскому языку. – М.: Высшая школа, 1974- 233с.
Коржавин Т.А. Учебник по техническому переводу. – М.: Высшая школа, 1981- 270с.
Журнали: “Mesures regulation automatisme”, “Inter elektronique”.
МЕТОДИ ОЦІНЮВАННЯ:
Протягом семестру студенти проходять по два модульних контроля. На модуль-них контролях пропонуються лексико-граматичні тести, контрольні переклади, контрольно-тренувальні вправи. Рубіжний контроль на 1, 2, 3 курсах – диференційований залік, в кінці 4 курсу – державний іспит.
ПЕРЕДУМОВИ:
Курс передбачає знання лексико-граматичного матеріалу, що відповідає рівню загальної середньої освіти.
МЕТОДИЧНЕ ЗАБЕЗПЕЧЕННЯ
Старовойт Ю.Л. Розмовляємо французькою. Навчальний посібник. – Вінниця, ВНТУ, 2004.
ІНДИВІДУАЛЬНА РОБОТА: Домашні завдання включають лексико-граматичні вправи, читання текстів, виконання перекладів, складання діалогів, повідомлень, анотацій тощо різноманітної тематики.
Екзаменаційна методика: В кінці 1, 2, 3 курсів призначаються диференційовані заліки, в кінці 4 курсу – державний іспит, який включає 3 завдання: читання та переклад із словником оригінального тексту з фаху; анотування загальнонаукового тексту; розмовну тему та співбесіду.
Реєстрація на курс: дирекція Ін АЕКСУ, ауд.5308, тел.(8-0432) 59-84-58.
Реєстрація на іспит: З викладачем, персонально чи по телефону.
| Дисципліна: Вища математика Факультет: АКСУ Статус дисципліни: обов’язкова Курс: перший, другий | ||
| | Стаціонарне навчання | Години на тиждень |
| Триместр | 1/2/4/5 | |
| Лекції (год) | 56/48/56/48 | 5/4/4/3 |
| Практичні заняття (год) | 56/56/28/42 | 4/4/2/3 |
| Лабораторні заняття (год) | - | |
| Семінари (год) | - | |
| КП (КР) трим | 1/1/1/1 | |
| РГР | 2/2/2/2 | |
| СРС (інд. заняття) | 108/50/24/28 | 7.7/ 3,5/1,7/1,8 |
| Всього (год/ /кредитів) | 162/144/162/144// 612 4,5/4/ 4,5/ 4 // 17,0 | |
| Екзамен (трим) | 1(ОС)/2(ЗС)/4(ОС)/5(ЗС) | |
| Залік (трим) | - | |
| КОД: | НФД03 | |
Лектори: Петрук Віра Андріївна, к.пед.наук, доцент, член-кор. Академії ПРЕ.
Кашканова Галина Григоріївна, к.пед.наук, доцент
21021 м. Вінниця, Хмельницьке шосе, 95, Інститут Інформаційних технологій та комп’ютерної інженерії (ІнІТКІ),), кафедра вищої математики , тел. 59-84-64.
МЕТА ДИСЦИПЛІНИ:
Формування особистості студентів, розвиток їх інтелекту, аналітичного та синтетичного мислення, відповідної математичної культури, інтуїції; оволодіння математичним апаратом, необхідним для вивчення загально інженерних та спеціальних дисциплін, розвиток здібностей свідомого сприйняття математичного матеріалу, характерного для спеціальності інженера; оволодіння основними математичними методами, необхідними для аналізу і моделювання пристроїв, процесів і явищ, пошуків оптимальних рішень з метою підвищення ефективності виробництва і вибору найкращих способів реалізації цих рішень, опрацювання і аналізу результатів експериментів.
ПРОГРАМА: Основні поняття лінійної та векторної алгебри і аналітичної геометрії: матриці та дії з ними, визначники та їх властивості, системи лінійних рівнянь, вектори і дії над ними, канонічні рівняння прямої і площини, рівняння кривих і поверхонь другого порядку; основні поняття диференціального і інтегрального числень: функції, похідної, диференціалу, невизначеного інтегралу, визначеного інтегралу, подвійного та потрійного інтегралів, криволінійних та поверхневих інтегралів; основні поняття теорії звичайних диференціальних рівнянь: диференціального рівняння, системи диференціальних рівнянь (канонічної, нормальної, автономної), розв’язку диференціального рівняння і системи, задачі Коші; основні поняття теорії рядів: суми ряду, збіжності ряду, інтервалу збіжності степеневого ряду, ряду Фур’є; основні поняття теорії функцій комплексної змінної: аналітичної функції, інтегралу функції комплексної змінної, конформного відображення, ізольованої особливої точки, лишку функції; основні поняття операційного числення: перетворення Лапласа, його властивості, інтегралу Дюамеля; основні поняття теорії імовірностей і математичної статистики: випадкової величини і випадкової події, імовірності, числові характеристики дискретних і неперервних випадкових величин; генеральної і вибіркової сукупності, вибіркової характеристики, статистичної гіпотези і статистичного критерію.
БІБЛІОГРАФІЯ:
1. Берман Г. Н. Сборник задач по курсу математического анализа. – М.: Наука, 1985.
2. Бугров Я. С., Никольский С. М. Элементы линейной алгебры и аналитической геометрии.– М.: Наука. 1980; 1981; 1988.
3. Бугров Я. С., Никольский С. М. Дифференциальное и интегральное исчисление.– М.: Наука. 1980; 1988.
4. Бугров Я. С., Никольский С. М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного.– М.: 1981; 1985.
7. Волков Ю.І., Найко Д.А. Лінійна алгебра й аналітична геометрія з елементами програмування мовою Паскаль: Навч. посібн. – К.: УМК ВО, 1990. – 144 с.
6. Гурский Е. И. Сборник задач по теории вероятностей и математической статистике. – Минск: Вышэйш. шк., 1984.
7. Гурский Е. И. Теория вероятностей с элементами математической статистики. – М.: Высш. шк., 1971.
8. Жалдак М.И., Квитко А. Н. Теория вероятностей с элементами информатики. Практикум. – К.: Вища школа, 1989.
9. Краснов М. Л., Киселев А. И., Макаренко Г.И. Функции комплексного переменного. Операционное исчисление. Теория устойчивости. – М.: Наука: 1981.
10. Кудрявцев Л. Д. Краткий курс математического анализа. – М.: Наука, 1989.
11. Кузнецов Л.А. Сборник заданий по высшей математике /типовые расчеты/. – М.: Высш. шк., 1983.
12. Овчинников П. Ф., Яремчук Ф. П., Михайленко В.М. Высшая математика, – К.: Вища школа, 1987.
13. Пак В. В., Носенко Ю. Л. Вища математика. – К.: Либідь, 1996.
14. Скороход А. В. Елементи теорії імовірностей та випадкових процесів. – К.: Вища школа, 1975.
МЕТОДИ ОЦІНЮВАННЯ:
Протягом триместру студент повинен виконати 2 контрольних роботи, 1 типовий розрахунок (РГЗ) та скласти 2 колоквіуми на 7 та 14 тижні.. Оцінки знань формуються на підставі рейтингових балів, які студент отримує протягом триместру за результатами колоквіумів, аудиторних контрольних робіт, захисту домашніх робіт (РГЗ) . На основі цих оцінок студент отримує оцінку з іспиту або складає його на загальних підставах.
Іспит складається усно . Завдання містять два теоретичних та два практичних питання. Колоквіуми та аудиторні контрольні роботи розраховано на 90 хвилин.
ПЕРЕДУМОВИ:
Необхідні знання з дисциплін: “Алгебра та початок аналізу”, “геометрія”, ”фізика”, ”інформатика” (шкільний курс) .
МЕТОДИЧНЕ ЗАБЕЗПЕЧЕННЯ: протягом лекцій та практичних занять студентам видається методична література з розділів вищої математики:
1. Петрук В.А., Кашканова Г.Г ” Методичні вказівки до самостійної роботи з аналітичної геометрії ", Вінниця, ВПІ, 1992р.,- 42с.
2. Петрук В.А., Кашканова Г.Г. „Методичні вказівки до самостійної роботи з теми "Лінійна алгебра", Вінниця, ВПІ, 1992р.,- 30с.
3. Петрук В.А., Кашканова Г.Г. „ Методичні вказівки до самостійної роботи з теорії ймовірностей та математичної статистики ", Вінниця, ВПІ, 1992р.,- 28с.
4. Петрук В.А., Кашканова Г.Г. „Теорія функціі комплексної змінної” В- во „Універсум”,1998р,- 113с.
5. Петрук В.А., Кашканова Г.Г. „Ймовірносно-статистичні моделі та статистична оцінка рішень”, В-во „Універсум”,2000р,- 140с.
6. Петрук В.А. „Дослідження найпростіших статистичних моделей”, В-во „Універсум”,2000р., - 128с.
7. Петрук В.А. „Вища математика з прикладними задачами для ігрових занять”, Вінниця, ВДТУ, 2000р., 117с.
8. Петрук В.А., Кашканова Г.Г.Хом`юк І.В. “Збірник задач з вищої математики ч. 1”, Вінниця, ВДТУ, 2001р.,-130с.
9. Петрук В.А.,Хом`юк І.В. “Збірник задач з вищої математики ч. 2”, Вінниця, ВДТУ, 2002р.,- 142с.
10. Петрук В.А., Кашканова Г.Г. “Збірник задач з вищої математики ч. 3”, Вінниця, ВДТУ, 2003р,- 127с.
11. Петрук В.А., Кашканова Г.Г. “Збірник задач з вищої математики ч.4,”, Вінниця, ВДТУ, 2004 р.,112с.
ІНДИВІДУАЛЬНА РОБОТА: індивідуальні завдання з тем: теорема про необхідні умови лінійної залежності і незалежності трьох векторів, вираження мішаного добутку векторів через їх декартові координати, властивості визначників другого та третього порядків, метод Гаусса розв'язання систем лінійних рівнянь, відстань від точки до площини та від точки до прямої в просторі, вивести канонічні рівняння прямої в просторі, умови паралельності та перпендикулярності прямих, виведення канонічного рівняння гіперболи, її властивості, циліндричні поверхні, сфера, конуси, геометричні властивості цих поверхонь, дослідження їх форми методом перерізів, простір
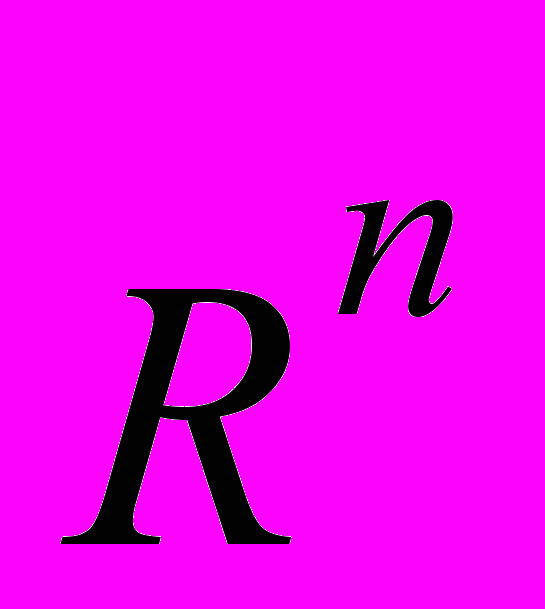, лінійні операції над векторами. Диференціал суми, добутку і частки. Інваріантність форми диференціала. Застосування диференціала в наближених обчисленнях. Похідні та диференціали вищих порядків. Диференціювання функцій заданих параметрично. Знаходження найбільшого та найменшого значень функції, диференційованої на відрізку. Дослідження випуклості функції, точки перегину. Асимптоти графіка функції. (1ОС) Інтегрування тригонометричних функцій та ірраціональностей. Застосування визначеного інтеграла. Обчислення площ в прямокутних і полярних координатах. Обчислення довжини дуги кривої, об’ємів тіл і площ поверхні обертання. Частинні похідні. Повний диференціал, його зв’язок з частинними похідними. Інваріантність форми повного диференціалу. Дотична площина та нормаль до поверхні. Геометричний зміст повного диференціалу. Частинні похідні і повні диференціали вищих порядків. Рівняння, які допускають зниження порядку. застосування до розв’язування задач про другу космічну швидкість, рух маятника, Розв’язування систем диференціальних рівнянь із сталими коефіцієнтами. Знакозмінні ряди, види збіжності, знакозмінні ряди типу Лейбніца, ознака збіжності. Застосування степеневих рядів у точних та наближених обчисленнях (2ЗС). Тригонометричні ряди Фур'є (ТРФ) для періодичних функцій з довільним періодом, для парних і непарних функцій. Комплексна форма ТРФ. Заміна змінних у подвійних інтегралах. Геометричні та фізичні застосування подвійних інтегралів. Оператори Гамільтона та Лапласа, їх застосування у векторному аналізі. Розв'язування рівняння теплопровідності (дифузії) методом сіток. Лишки, обчислення.(4ОС) Теореми подібності та запізнювання, теореми випереджання та зміщення. Теореми диференціювання та інтегрування зображення. Зображення періодичного оригіналу, застосування. Закони розподілу імовірностей дискретних випадкових величин: біноміальний, пуассонівський, геометричний, гіпергеометричний (означення, властивості, числові характеристики, приклади основних застосувань). Закони розподілу імовірностей неперервних випадкових величин: рівномірний, показниковий, нормальний або гауссовий (означення, властивості, числові характеристики, приклади основних застосувань). Імовірнісний зміст параметрів нормального закону розподілу. Теореми про імовірність попадання нормально розподіленої величини в заданий інтервал та про імовірність заданого відхилення випадкової величини від свого математичного сподівання. Правило трьох сигм та його практичне застосування. Статистична гіпотеза. Нульова і конкуруюча гіпотеза. Поняття про критерії згоди. Перевірка гіпотез про рівність часток та середніх.(5ЗС)Екзаменаційна методика: іспит, за призначенням.
Реєстрація на курс: дирекція ІнІТКІ, ауд. 2215, тел. 59-83-64.
Реєстрація на іспит: з лектором, персонально чи по телефону.
| Дисципліна: Хімія Факультет: АКСУ Статус дисципліни: обов’язковий Курс: 1 (триместр 1) | ||
| | Стаціонарне навчання | Години на тиждень |
| Лекції (год) | 28 | 2 |
| Практичні заняття(год) | - | 1 (3) |
| Лабораторні заняття(год) | 14 | 2 |
| Семінари(год) | - | - |
| КП (КР) трим. | - | - |
| РГР | - | - |
| СРС (інд. заняття) | 66 | 4 |
| Всього(год:кредитів) | 108:3 | |
| Екзамен(трим) | 1 | |
| Залік(трим) | | |
| КОД: | НФД02 | |
Лектори: Петрук Василь Григорович, д.т.н., професор
Звуздецька Н.С., ст. викладач.
21021 м. Вінниця, Хмельницьке шосе, 95, Інститут електроенергетики, екології та електромеханіки (ІнЕЕЕМ), факультет комп'ютеризованих систем автоматизації, екологічних систем та електроприводу, кафедра хімії та екологічної безпеки, тел. 8-0432-59-84-95.
МЕТА ДИСЦИПЛІНИ: вивчення основних законів хімії, закономірностей перебігу хімічних процесів, будови, структури та властивостей речовин, методів їх отримання, теорії розчинів, основ електрохімії.
ПРОГРАМА: Основні закони хімії. Будова атомів та періодична система елементів Д.І. Мендєлєєва. Хімічний зв’язок. Просторова конфігурація молекул. Енергетика хімічних процесів. Хімічна кінетика та рівновага. Розчини неелектролітів. Розчини електролітів. Хімія води. Загальна характеристика металів. Хімічні та електрохімічні властивості металів. Хімічні джерела струму. Процеси електролізу. Корозія металів і сплавів. Методи захисту від корозії. Високомолекулярні сполуки. Основи матеріалознавства.
БІБЛІОГРАФІЯ:
Григор’єва В.В., Самійленко В.М., Сич А.М. Загальна хімія. – К. : Вища шк., 1991. – 431с.
Глінка М.Л. Загальна хімія, 5-е вид. – К. : Вища шк., 1982. – 608с.
Коровин Н.В., Масленникова Г.Н., Мингулина Э.И., Филиппов Э.Л. Курс общей химии. – М. : Высш. шк., 1990. – 446с.
Загальна та біонеорганічна хімія/ О.Г. Карнаухов, Д.О. Мельничук, К.О. Чоботько, В.А. Копілевич. – К. : Фенікс, 2001. – 578с.
Романцева Л.М., Лещинская З.Л., Суханова В.А. Сборник задач и упражнений по общей химии. – М. : Высш. шк., 1991. – 288с.
Хімія. Робоча програма і методичні вказівки по виконанню контрольних завдань і лабораторних робіт / Ю.А. Пирогов, П.Я. Пустовар, О.О. Кирєєв, С.М. Вілков. – Харків. : ХІПІ, 1990. – 164с.
МЕТОДИ ОЦІНЮВАННЯ:
Протягом 1 (2), 2 (3), 4 (1) триместру студент повинен виконати 13 лабораторних робіт та скласти 2 письмові колоквіуми на 7 та 14 тижнях. Додатково оцінюються практичні заняття (3). Оцінки знань формуються на підставі рейтингових балів, які студент отримує протягом триместру за результатами колоквіумів, захисту лабораторних робіт та виконання практичних завдань (3). На основі цих оцінок студент отримує оцінку з іспиту або складає його на загальних підставах.
ПЕРЕДУМОВИ: Курс базується на знаннях з хімії, фізики, математики на базі середньої школи.
МЕТОДИЧНЕ ЗАБЕЗПЕЧЕННЯ: Протягом лекцій роздаються студентам конспекти лекцій з актуальної тематики.
Для підготовки до колоквіуму та іспиту використовується :
1.Корчинський Г.А. Хімія. – Вінниця : Поділля-2000, 2002. – 525с.
Для виконання лабораторних робіт використовуються :
Методичні вказівки до лабораторних робіт з курсу “Хімія” частина 1./ Г.А. Корчинський, В.Г. Заїка. – Вінниця. : ВПІ, 1992. – 81с.
Методичні вказівки до лабораторних робіт з курсу “Хімія та хімічні основи екології” частина 2./Г.П. Котлярова, Т.І Ющенко, В.П. Копецький, В.Г. Петрук. - Вінниця. – ВДТУ, 1996. – 81с.
Методичні вказівки до лабораторних робіт з хімічної кінетики./ В.Г. Петрук, М.В. Гандзій. - Вінниця.: ВДТУ, 1997. – 23с.
ІНДИВІДУАЛЬНА РОБОТА:
Розв’язування задач з таких основних тем:
Основні закони хімії. Будова атомів і молекул. Хімічний зв’язок.
Закономірності протікання хімічних реакцій. Хімічна термодинаміка. Хімічна кінетика і рівновага. Напрямок хімічних реакцій.
Розчини неелектролітів. Способи вираження концентрації розчину. Осмос. Закон Рауля. Пониження температури замерзання та підвищення температури кипіння розчинів.
Розчини електролітів. Електролітична дисоціація. Ступінь і константа дисоціації. Водневий показник рН. Іонний добуток води. Гідроліз солей.
Твердість води та способи її пом’якшення. Методи очистки води.
Електрохімічні процеси. Хімічні джерела струму. Електроліз.
Корозія металів і сплавів. Методи захисту металів від корозії.
Екзаменаційна методика: іспит, за призначеннями.
Реєстрація на курс:
Реєстрація на іспит: з лектором, персонально чи по телефону.
| Предмет: Обчислювальна техніка та програмування Факультет: АКСУ Курс 1,2 (Обов’язкові) Триместр 1 (осінь), 2 (весна), 4 (осінь) | ||
| | Стаціонарне навчання | год. на тиждень |
| Лекції (год) | 42/28/56 | 4/2/4 |
| Практичні заняття (год) | | |
| Лабораторні заняття (год) | 28/42/42 | 2/3/3 |
| Семінари (год) | - | |
| КП (КР) трим | 4 | |
| РГР | | |
| СРС (інд. заняття) | 38/38/28 | 3 |
| Всього (год /кредитів) | 342/9,5 | |
| Екзамен (трим) | 2 | |
| Залік (трим) | 1,4 | |
| КОД: | НПД01 | |