Управление судном при плавании во льдах

Вид материала

Документы

Содержание Прямолинейное движение судна во льдах. M — масса судна вместе с присоединенными массами воды и льда, т; R V — скорость судна, м/с; n S — выбег судна во льдах, м; x Определение чистого ледового сопротивления движению судна в битых льдах. R1 — статическая составляющая сил сопротивления, не зависящая от скорости судна во льду; R R3 — импульсивное сопротивление, обусловленное потерей кинетической энергии судна при ударах его о льдины; R Rлч — ледовое сопротивление, рассчитанное без учета влияния цилиндрической вставки, т; l D — диаметр винта, м; V Vл — скорость движения судна в канале, уз; h — Vл = 9,7 узла. Пересчитаем эту формулу для льда 2,2 метра, т. е. на пределе льдопроходимости ледокола. Получим: V Поправочных коэффициенты, позволяющие учесть характеристики льда Kн. Его численное значение определяется по формуле: K Прокладка ледовых каналов на криволинейных участках. Lцил — длина цилиндрической вставки судна, м; В Таблица 1.6 Значения минимальных радиусов R кривизны ледовых каналов

Подобный материал:

• Особенности плавания судна во льдах. Общее положение, 44.54kb.
• Курсовая работа по управлению судном, 128.72kb.
• Рабочая программа итоговой государственной аттестации выпускников для специальности, 240.91kb.
• Василий И. Снопков Россия, Санкт-Петербург Март 18. 2010 Управление судном в шторм,, 110.35kb.
• Курс и скорость судна при плавании в штормовых условиях зависит от мореходных качеств, 24.09kb.
• Предотвращение загрязнения нефтью с судов при плавании в особых районах, 73.46kb.
• Конспект лекций по курсу «управление качеством», 1507.97kb.
• Конспект лекций по курсу «управление качеством», 1487.57kb.
• Курсовая работа по психодиагностике, 680.47kb.
• Непал или Заметки девушки в одиночном плавании, 4520.79kb.

Прямолинейное движение судна во льдах. Общий вид уравнения, описывающего неустановившееся прямолинейное движение судна во льдах,

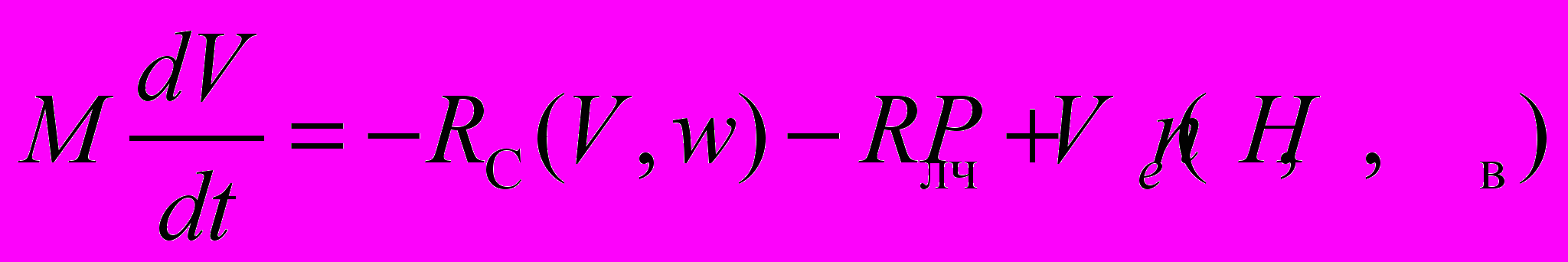, (1.7)

где M — масса судна вместе с присоединенными массами воды и льда, т;

R_C — сопротивление воды и ветра движению судна, кН;

R_лч — чистое ледовое сопротивление движению судна, кН;

Р_е — упор винта, кН;

V — скорость судна, м/с;

n — частота вращения винта, рад/с;

Н_в — шаг винта, м.

При решении уравнения (1.7) принимается допущение о квазистационарности процесса движения судна. В силу того, что процесс движения судна в действительности не стационарный, величина чистого ледового сопротивления движению судна R_лч будет случайным образом колебаться относительно некоторого среднего значения вследствие неоднородности льда и нестабильности силового контакта с ним. Поэтому инерционные характеристики, определяемые по формуле (1.7) с детерминированными составляющими, следует рассматривать как средние по множеству их возможных значений.

При пассивном торможении

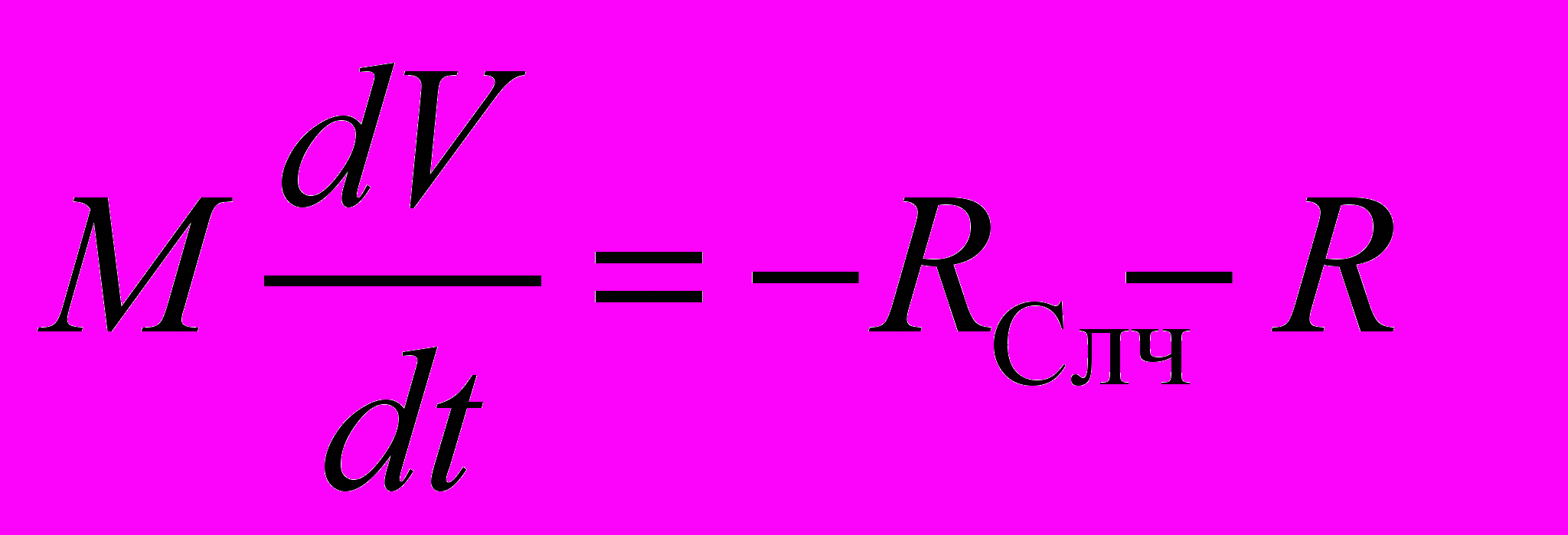, (1.8)

Установлено, что количество ударных импульсов, возникающих при контакте корпуса судна со льдом, подчиняется закону распределения Пуассона.

Среднеквадратическую погрешность _S в определении величины выбега можно определить из следующей зависимости:

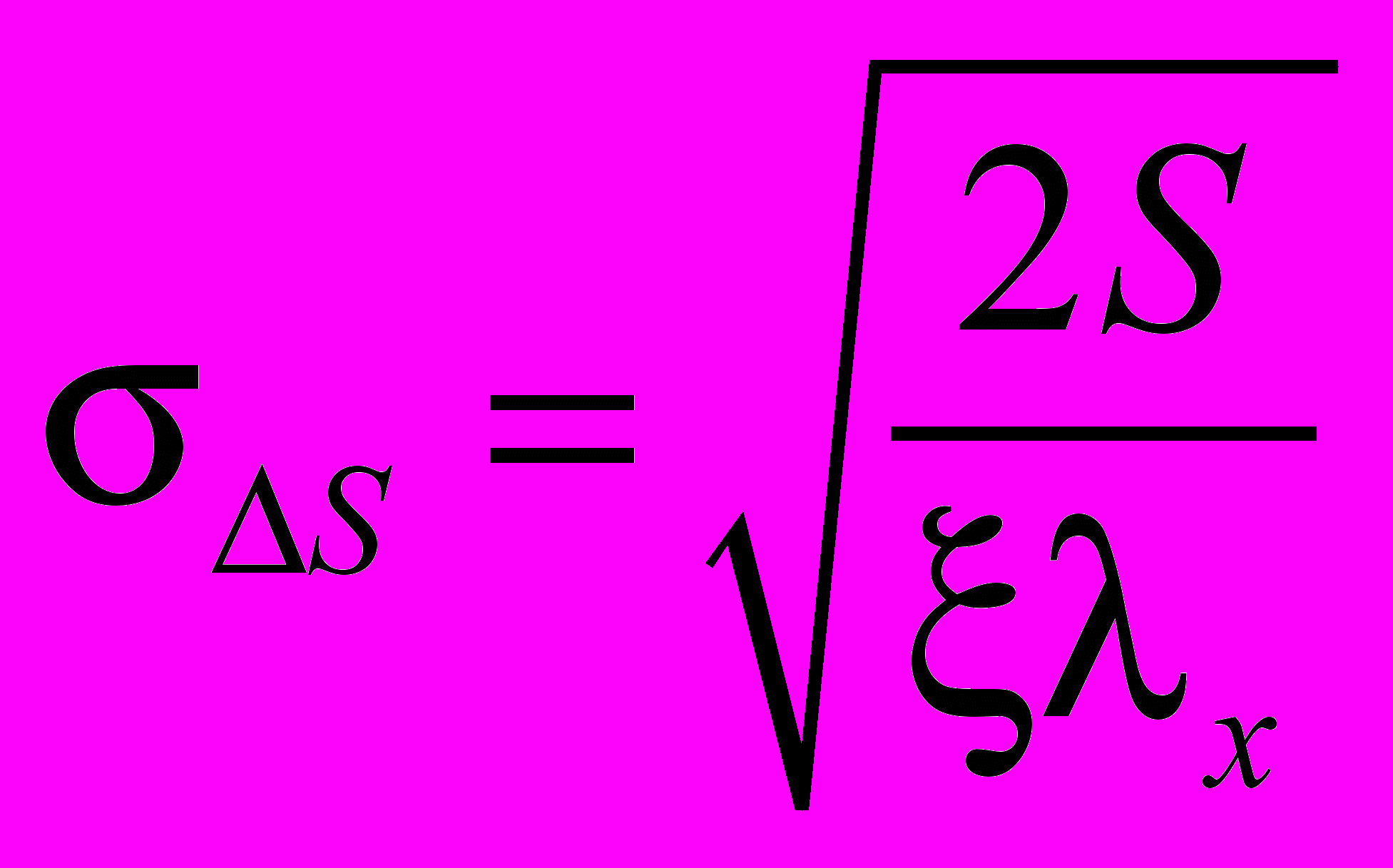, (1.9)

где S — выбег судна во льдах, м;

_x — средняя плотность распределения ударных импульсов о лед во времени.

Величина _x для рассматриваемых стационарных и близких к ним режимов постоянна. Ее можно выразить как

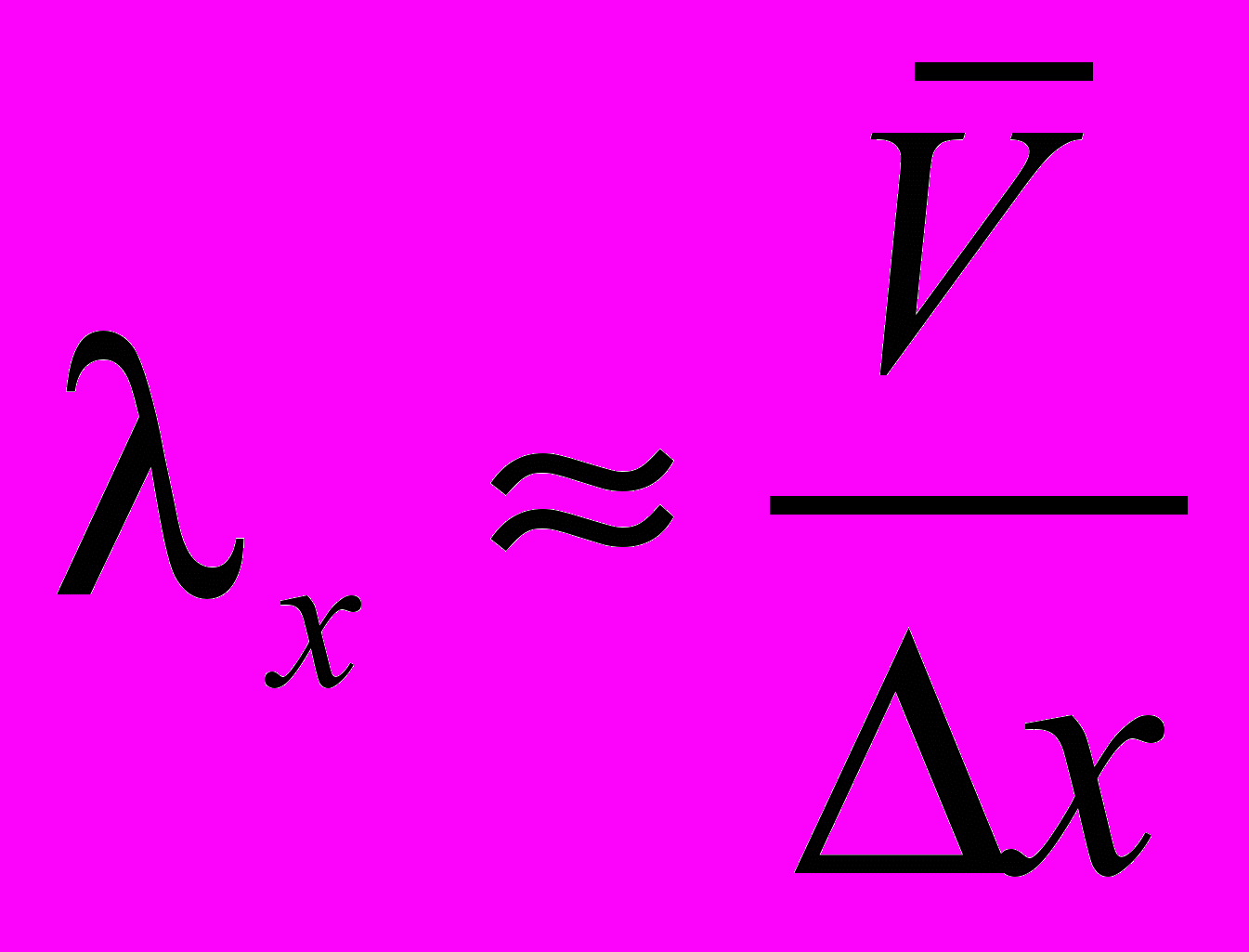, (1.10)

где 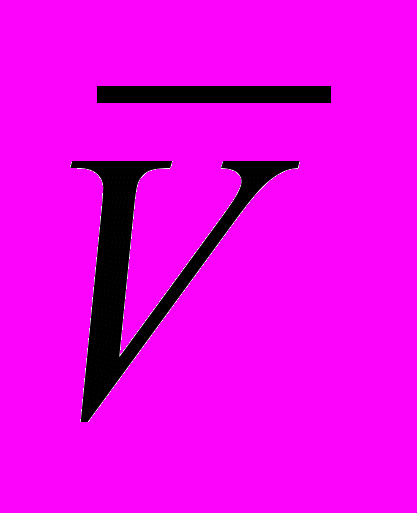— средняя скорость судна, м/с;

x — длина ледяных сегментов, образующихся при ломке сплошного ледяного покрова бортами судна, м.

Эмпирически показано, что x связана с толщиной льда h линейной зависимостью x = ah.

Тогда

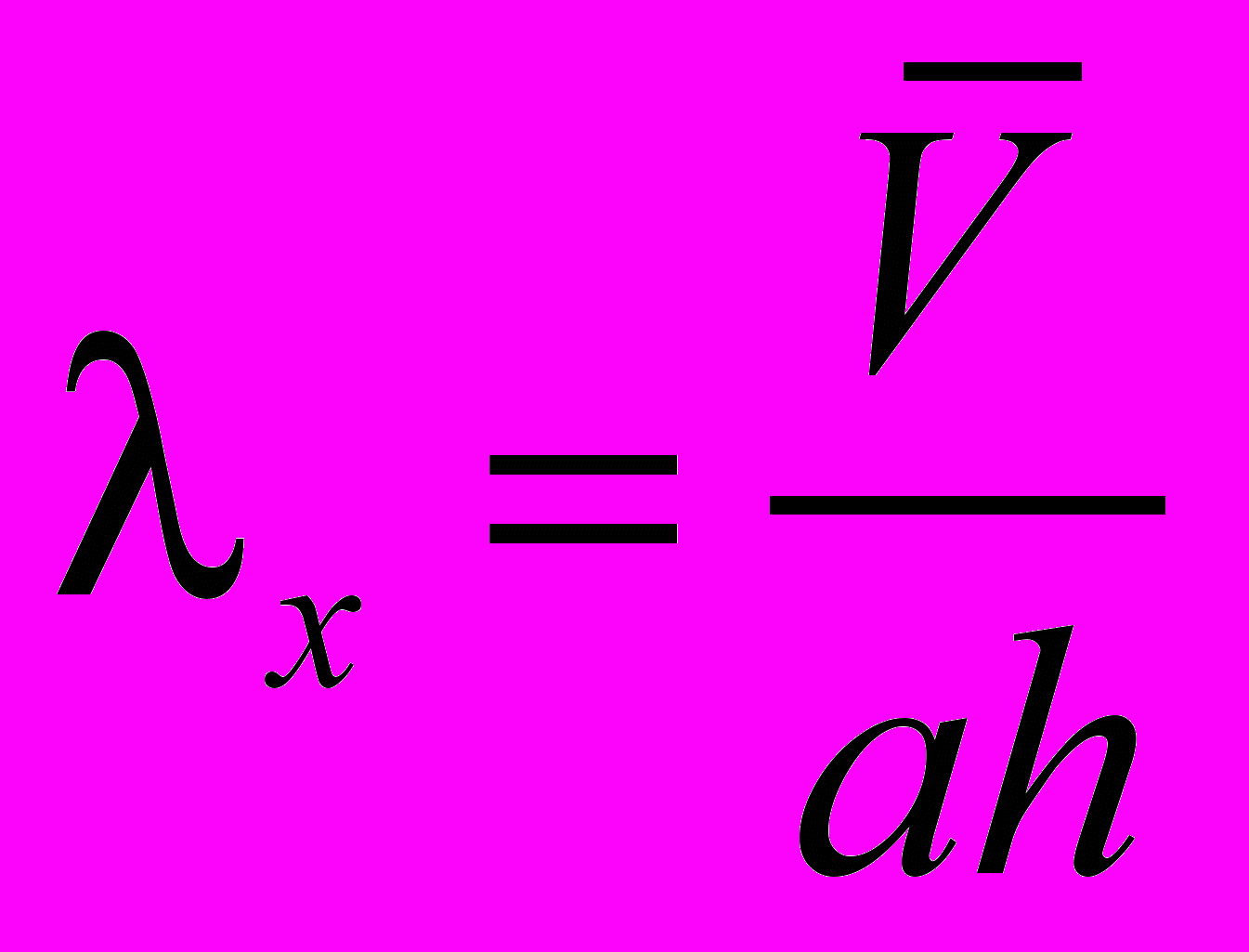, (1.11)

где а — эмпирический коэффициент (а = 2030).

Величина x в сплошных льдах зависит от толщины льда, формы носовой оконечности судна и обычно составляет 3–5 м.

Отсюда _x  0,2–0,3 с^–1. В битых льдах _x обратно пропорциональна среднему размеру льдины r. В мелкобитых льдах r  10 м, так что _x  0,1 с^–1. Таким образом, разброс значений длины выбегов в битых льдах больше, чем в сплошных.

Вероятность превышения уровня S = 3_S составляет 0,28 %, а 2_S — 4,56 %.

При активном торможении длина среднего значения тормозного пути

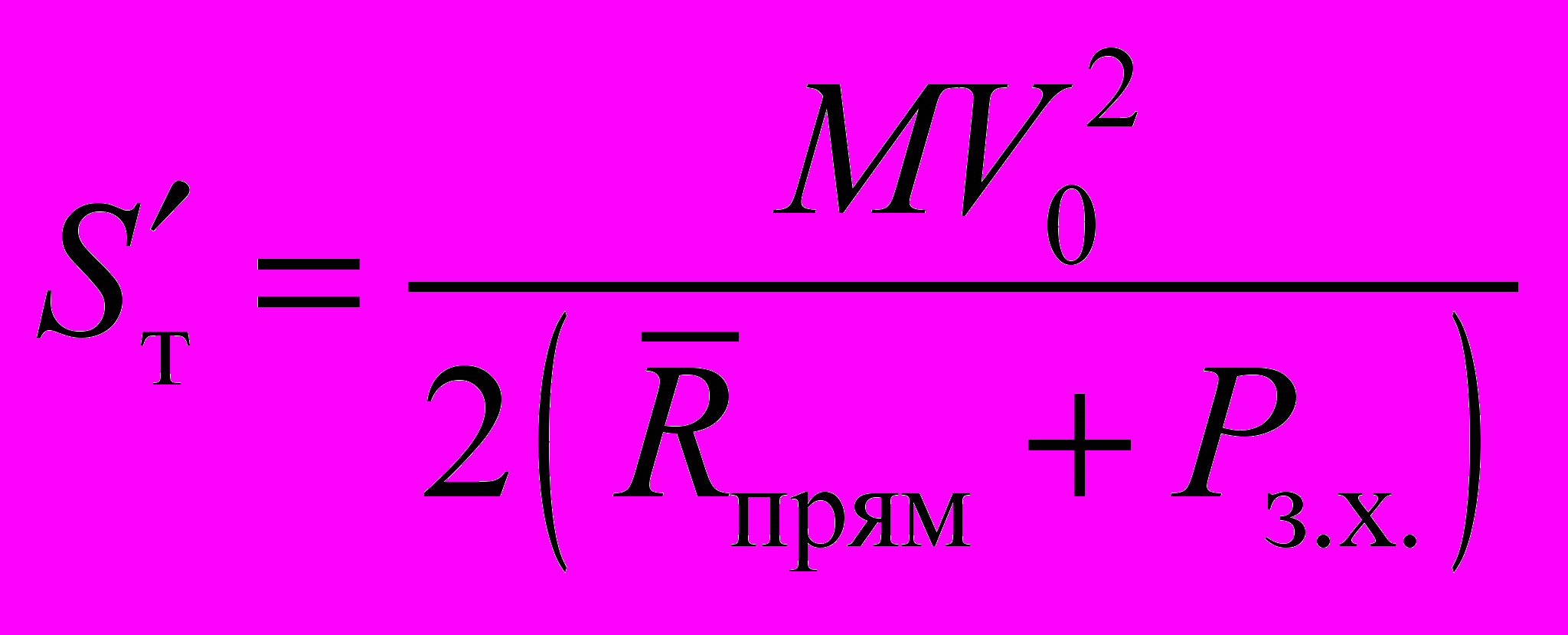, (1.12)

а среднеквадратическое отклонение от среднего значения S_т

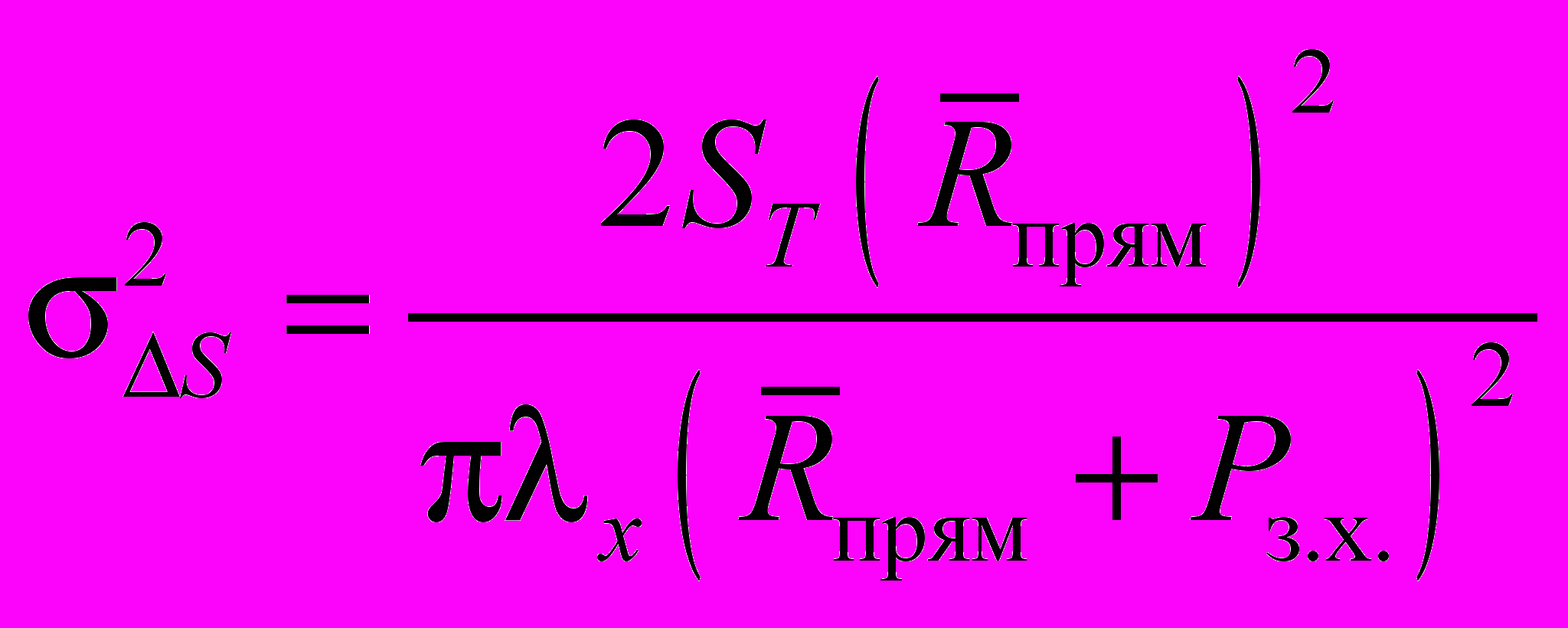, (1.13)

т.е. при активном торможении существенно уменьшается тормозной путь и значение разброса.

Решение дифференциальных уравнений (1.7) и (1.8) требует накопления статистических натурных данных для различных типов судов при движении их во льдах.


Определение чистого ледового сопротивления движению судна в битых льдах. Полное сопротивление R_л при плавании судна во льдах принято делить на сопротивление воды движению судна (на чистой воде) R_С и чистое ледовое сопротивление R_лч:

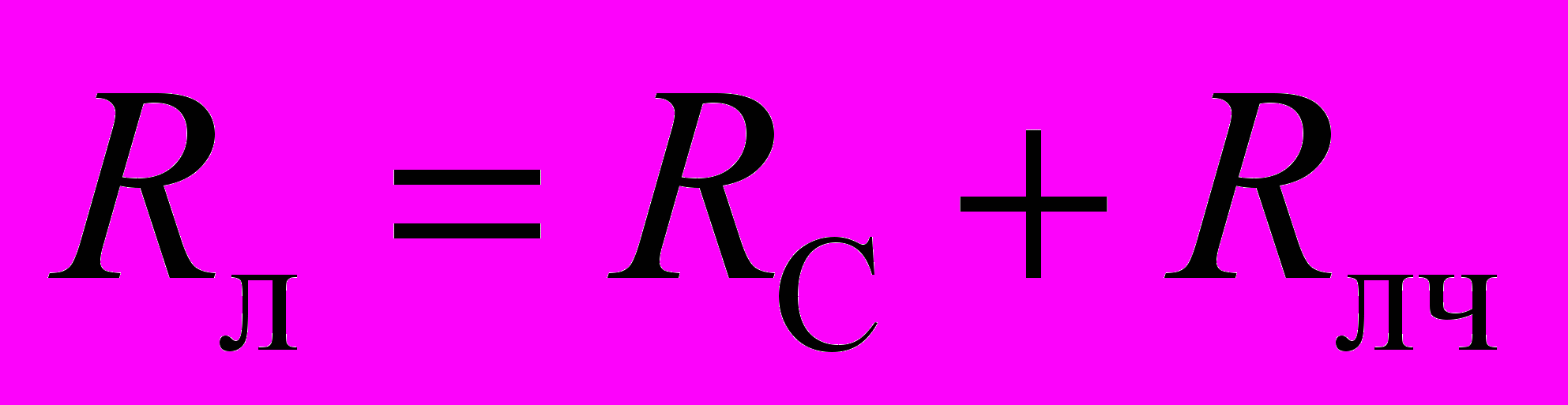, (1.14)

Процесс движения судна в битых льдах очень сложен, составить его аналитическое описание не представляется возможным. Поэтому расчетные зависимости, связывающие сопротивление судна в битых льдах со скоростью движения, размерениями и параметрами льда, создавались на основании эмпирических данных, полученных в ходе натурных экспериментов. Основываясь на исследованиях, чистое сопротивление движению судна в битых льдах представим в следующем виде:

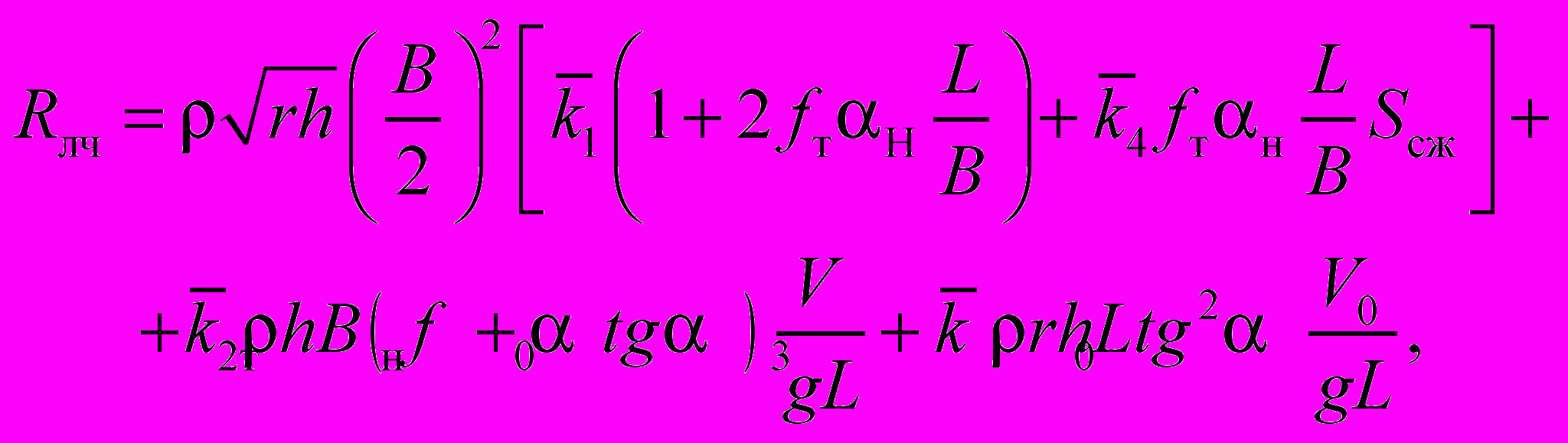(1.15)

где r — протяженность битого льда, м;

h — толщина битого льда, м;

 — плотность льда, т/м³;

f_т — коэффициент трения борта о лед (f_т = 0,08÷0,15);

 — коэффициент полноты действующей ватерлинии;

_н — коэффициент полноты носовой части действующей ватерлинии;

₀ — угол входа носовой ветви действующей ватерлинии, град;

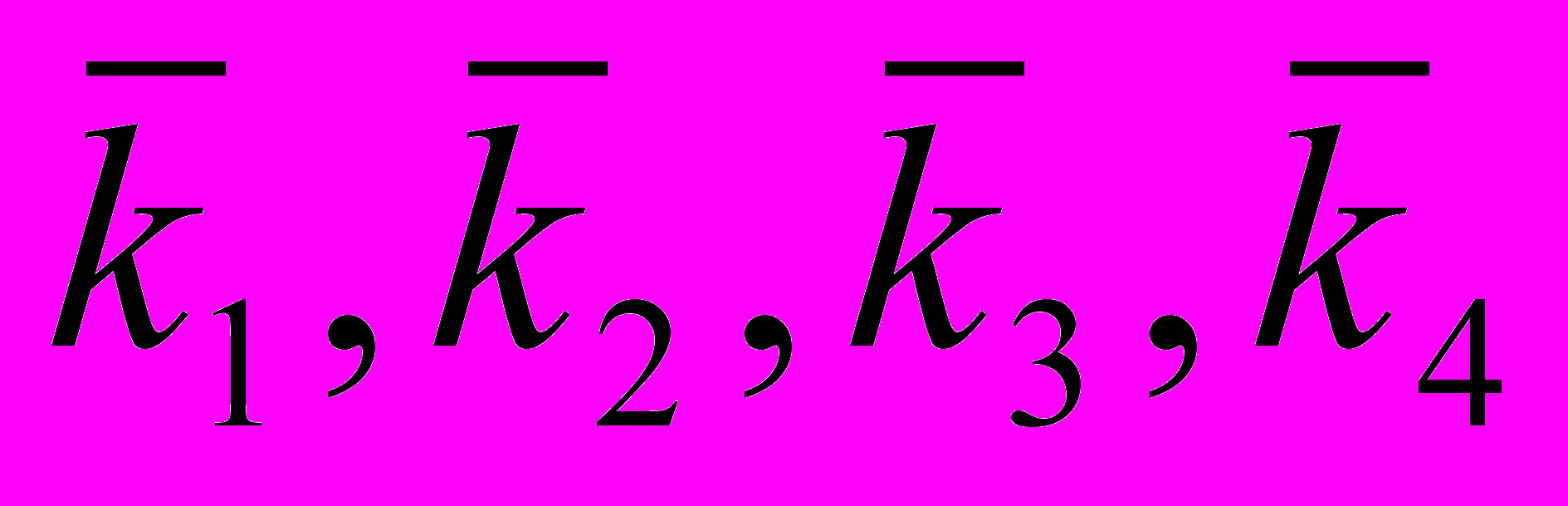— безразмерные коэффициенты (табл. 1.5);

S_сж — сила сжатия, баллы;

g — ускорение свободного падения, м/с².

Таблица 1.5

Значения коэффициентов

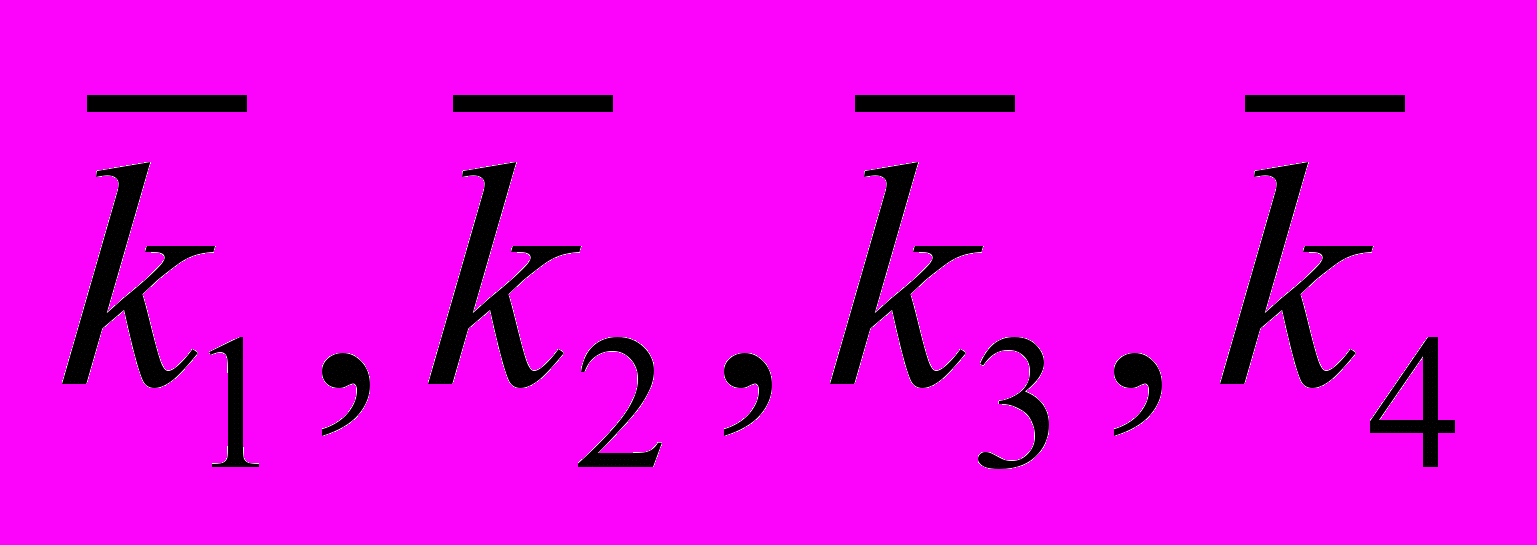
Коэффициенты	Сплоченность льда, баллы
	4	6	8	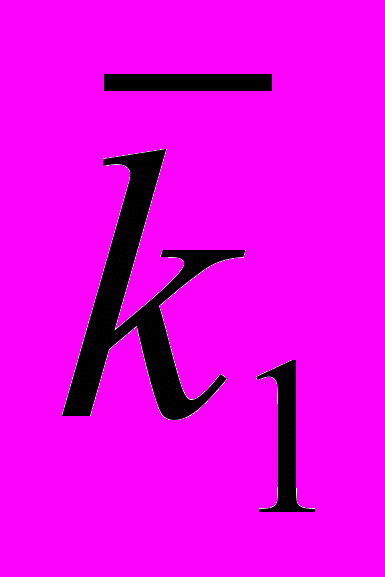10
(при Пk  10)	0	0	7  10–2	7,4  10–2
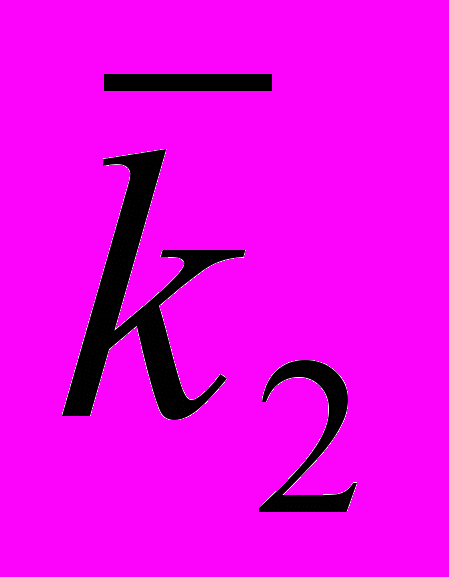	0,93	2,54	5,70	8,2
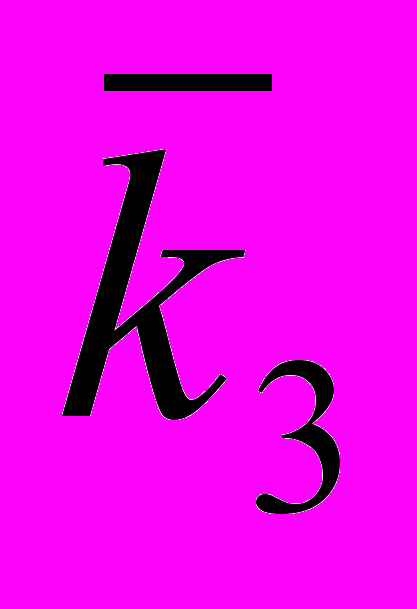	4,3	4,3	4,3	4,3
	–	–	–	30  10–2

Здесь П_k — относительная ширина поля битого льда, т. е. отношение ширины канала к ширине судна.

Чистое ледовое сопротивление R_лч при движении судна в битых льдах слагается из составляющих:

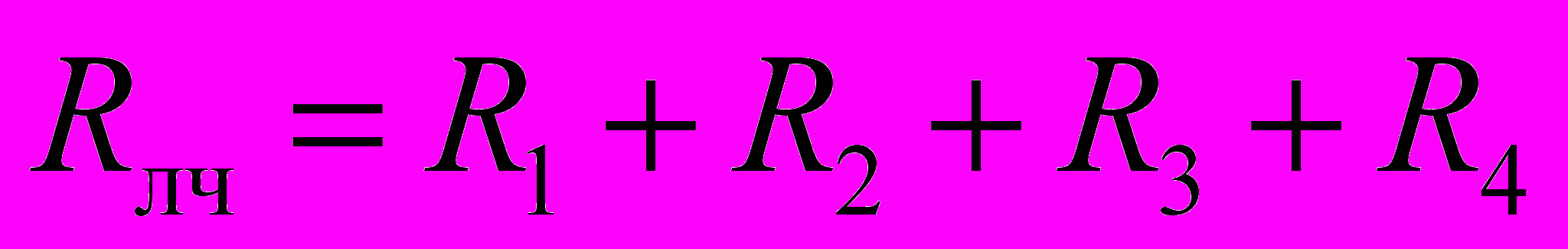, (1.10)

где R₁ — статическая составляющая сил сопротивления, не зависящая от скорости судна во льду;

R₂ — диссипативные силы сопротивления, возникающие вследствие сопротивления воды раздвиганию льдин и трения льдин друг о друга;

R₃ — импульсивное сопротивление, обусловленное потерей кинетической энергии судна при ударах его о льдины;

R₄ — сила сопротивления, обусловленная работой, затрачиваемой на притапливание, поворачивание льдин, возникающее при этом волнообразование и изменение посадки судна.

Транспортное судно будет испытывать большее сопротивление, чем ледокол из-за наличия цилиндрической вставки.

Поэтому ледовое сопротивление судна можно выразить:

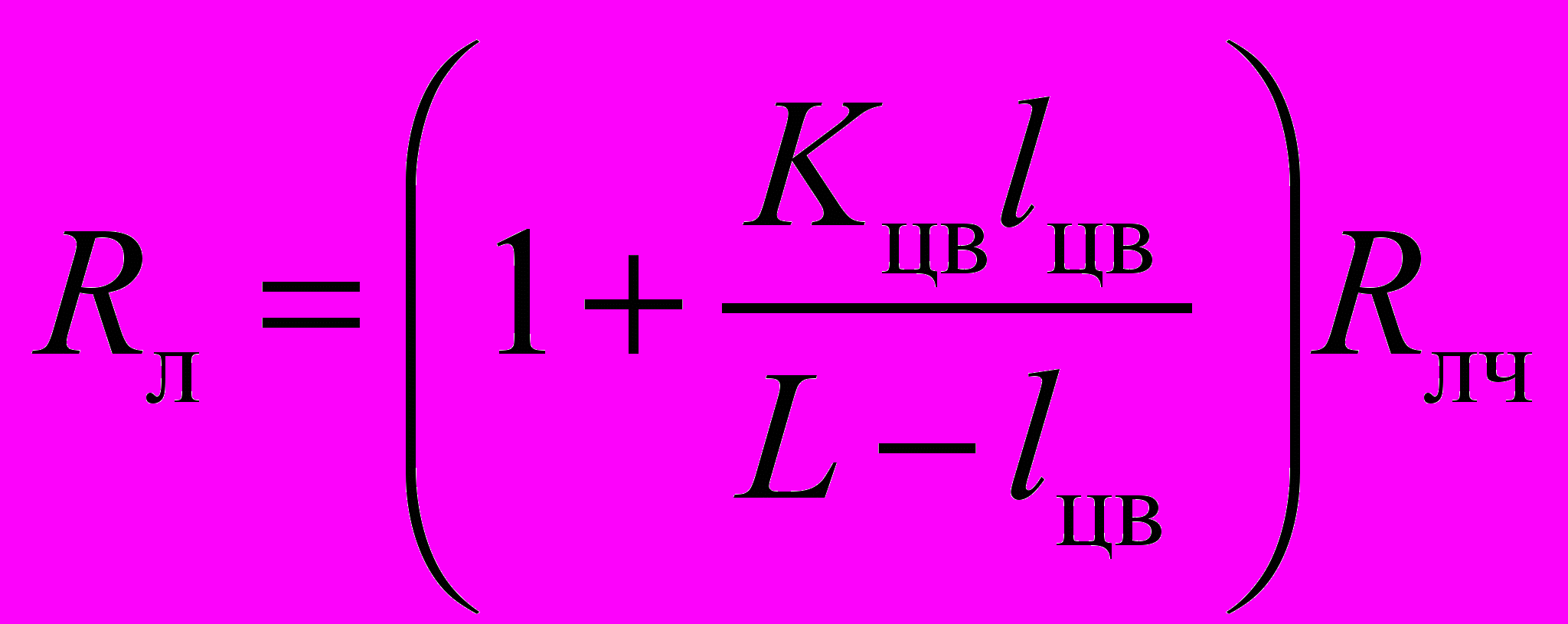, (1.17)

где R_лч — ледовое сопротивление, рассчитанное без учета влияния цилиндрической вставки, т;

l_цв — длина цилиндрической вставки, м;

L — длина судна, м;

K_цв — коэффициент, равный 0,4.


1.5. Расчет технической скорости движения судна
в природных льдах и прокладка каналов
на криволинейных участках

Для определения технической скорости построим алгоритм движения судна в различных ледовых условиях. Основными параметрами, определяющими возможность движения судна в природных льдах будет льдопроходимость и скорость.

Как описано выше, значение льдопроходимости определяется решением квадратного уравнения, связывающего ледовое сопротивление и тягу гребных винтов вблизи швартовного режима.

Для определения упора гребных винтов можно использовать формулу:

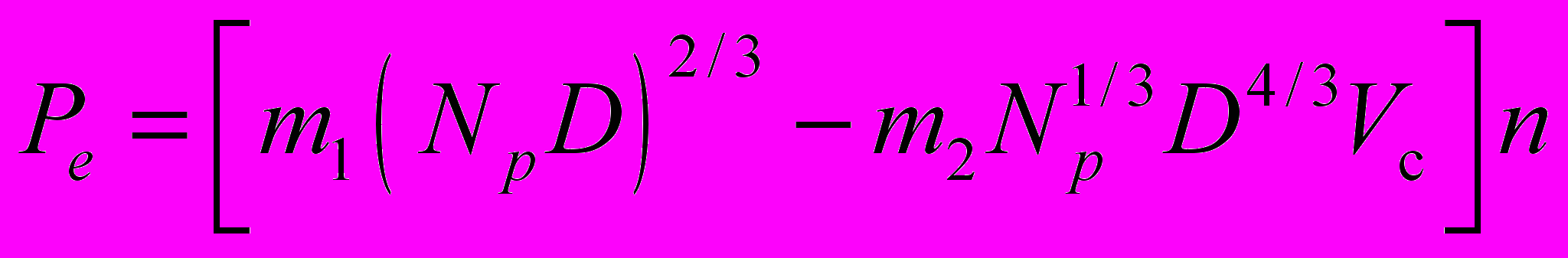, (1.18)

где D — диаметр винта, м;

V_с — скорость судна, уз;

N_p — мощность на валу, л.с.;

п — количество винтов;

m₁, m₂ — коэффициенты, значения которых определяются по прототипу, в первом приближении могут быть использованы их статистические значения m₁ = 71,4; т₂ = 15,3.

Расчет скорости движения судна в канале за ледоколом в ровных сплошных льдах:

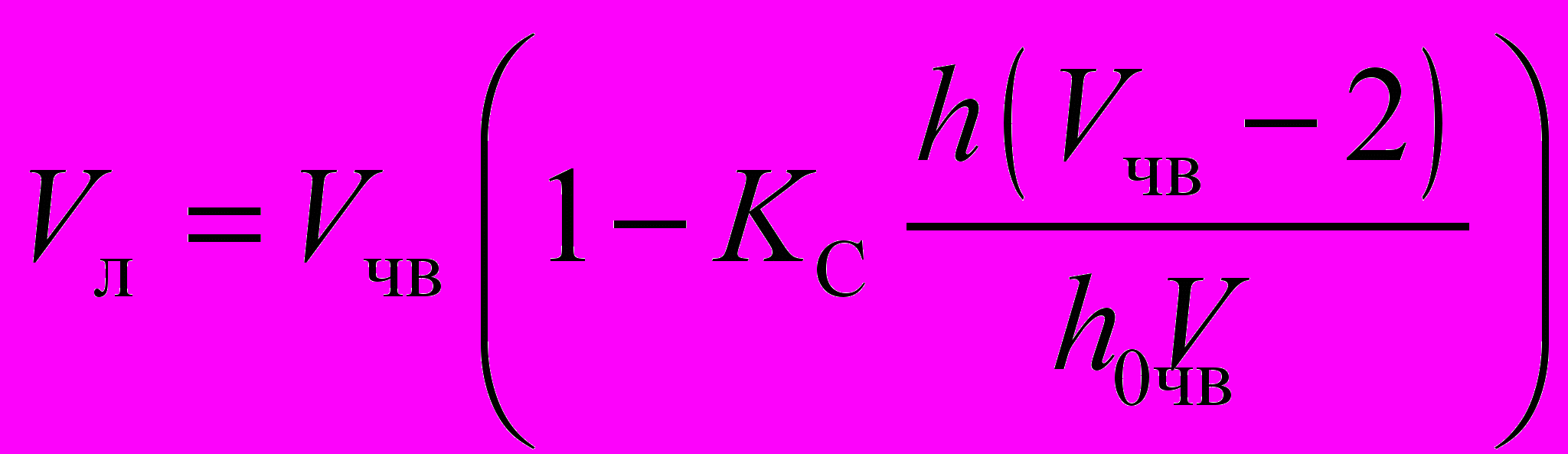, (1.19)

где V_л — скорость движения судна в канале, уз;

h — толщина преодолеваемого льда, м;

V_чв — скорость хода на чистой воде, уз;

h₀ — льдопроходимость судна в ровных сплошных льдах
(в рассматриваемом выше материале обозначали как h_np).



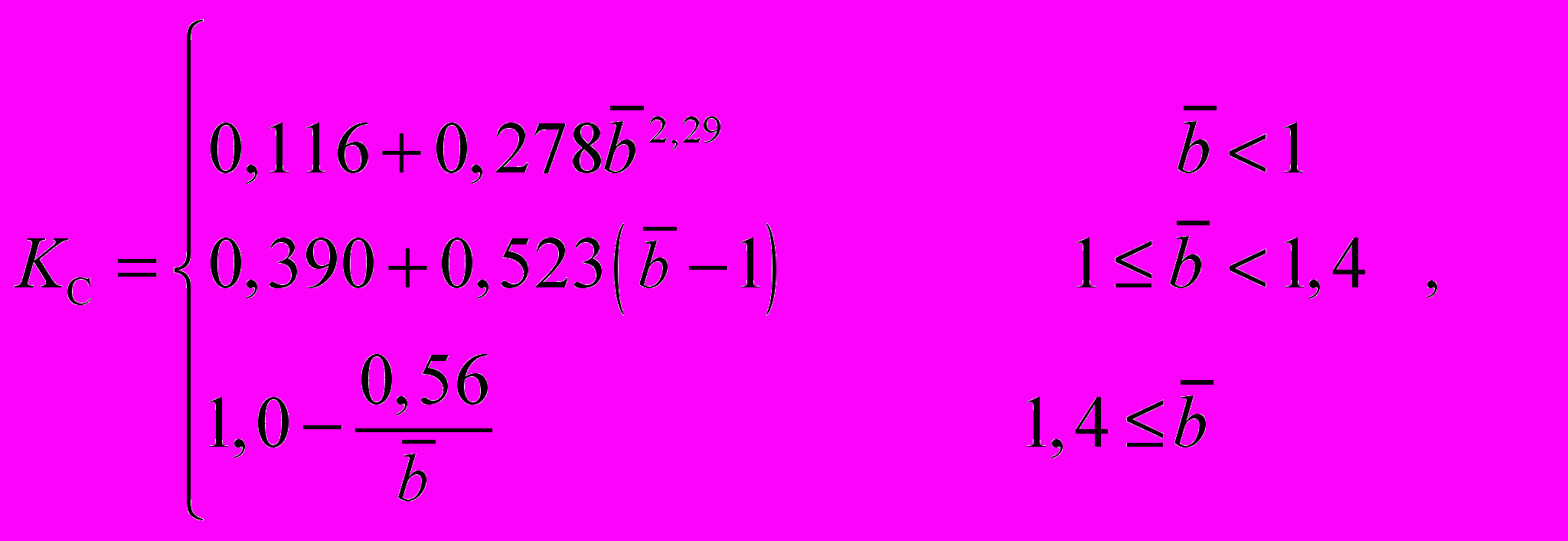
где 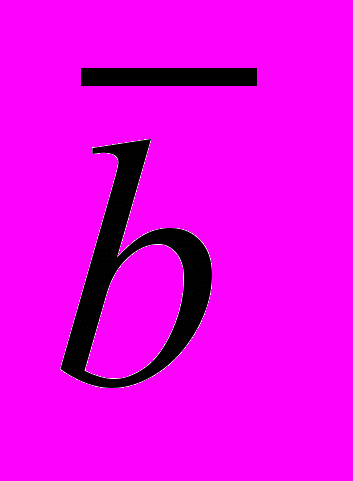— относительная ширина судна, вычисляемая по формуле:

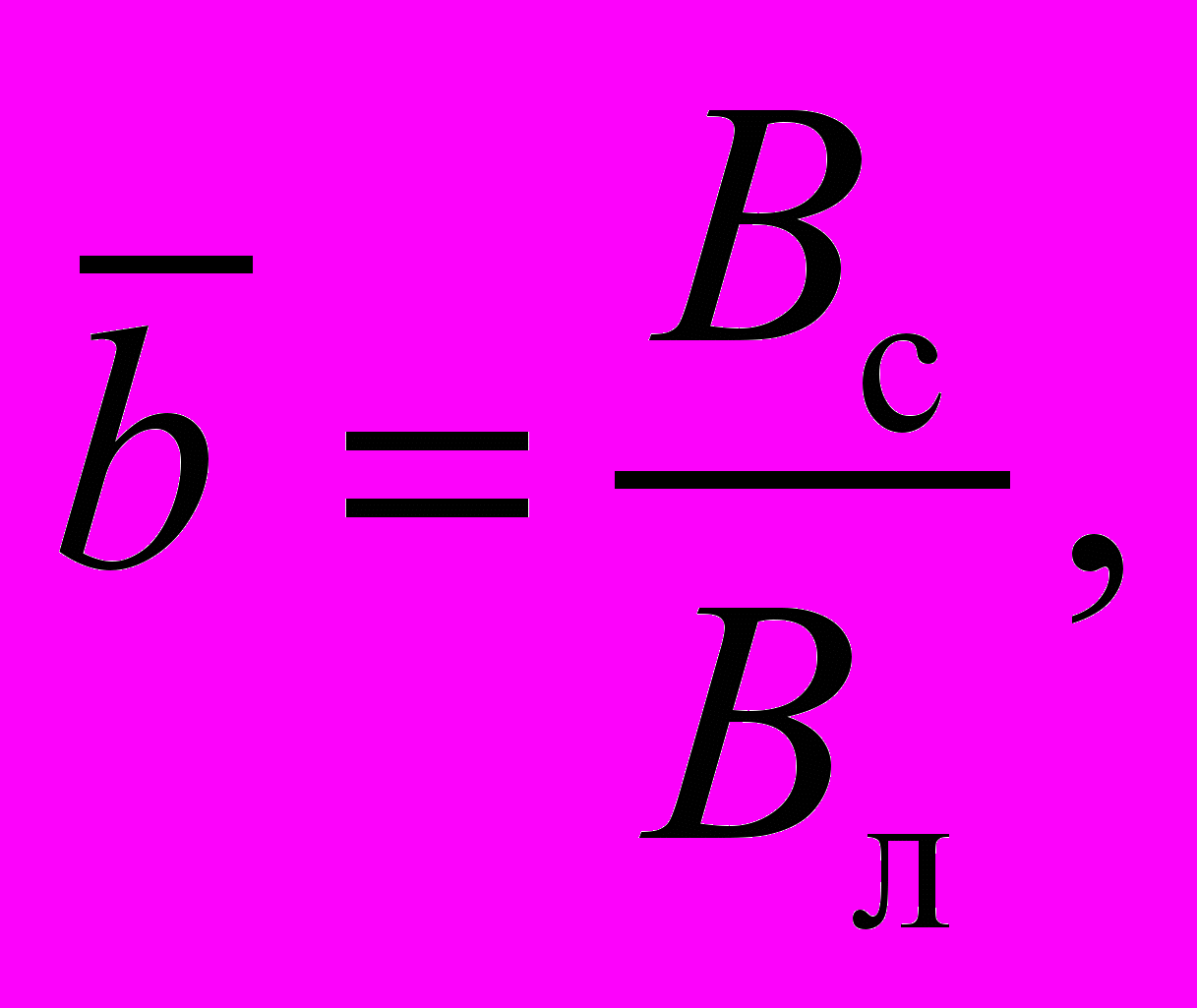(1.20)

где В_с — ширина судна, В_л — ширина ледокола.

Льдопроходимость судна при его движении в канале за ледоколом (h_k) определяется через льдопроходимость судна при плавании в сплошном льду и соотношения размеров ледокола и судна по формуле:

h_k = h₀ / K_с.

Воспользумся этой формулой для определения фактической льдопроходимости судна, как показателя его технического состояния и способности плавания во льдах на примере работы одного из судов проекта СА-15 с атомным ледоколом в арктическую навигацию 2003 года.

Допустим, что судно может идти по каналу за ледоколом во льду толщиной 180 см с минимальной устойчивой скоростью 2 узла.

h₀ = h_kK_c = 180  0,29 = 52 см. (1.21)

Практически при плавании по каналу во льдах 180 см судно требовало постоянных околок, значит можно сделать предположение, что фактическая льдопроходимость судна была менее 50 см, т. е. более чем в 2 раза отличалась от льдопроходимости, заявленной в паспорте судна.

Действительно, суммируя факторы — судно в балласте, мятый шероховатый корпус от остатков краски «Инерта», отсутствие ПОУ, разрегулированные, в плохом техническом состоянии главные двигатели и ограничение судовладельцем их мощности на 20 % оказали существенное влияние на ухудшение ледовой ходкости и снизили льдопроходимость судна, более чем в 2 раза.

Предположим, что судно вышло в рейс с построечной льдопроходимостью — 100 см тогда, воспользовавшись формулой (1.19) мы получим V_л = 9,7 узла.

Пересчитаем эту формулу для льда 2,2 метра, т. е. на пределе льдопроходимости ледокола. Получим: V_л = 7,8 узла, но скорость ледокола (в этом случае) не будет превышать 2 узлов. Действительно, когда эти суда были молодые, в канале за ледоколом в сплошных льдах шли «ходом» с запасом мощности. Остановки могли быть только в ледовых пробках после работы ледокола «набегами», т. е. во льдах за пределами льдопроходимости ледокола.

Анализируя научные работы о ледовой ходкости, основным и практически единственным путем оценки скоростей движения судов и ледоколов в природных льдах, с учетом многообразия их характеристик является использование данных натурных наблюдений.

Следует заметить, что определенное количество и объем натурных наблюдений для ограниченного сочетания характеристик ледяного покрова уже собран и может быть использован на практике.

Принято, что натурные наблюдения за движением ледокола в сплошных льдах используются в качестве реперных, а влияние характеристик природного льда представляется в виде эмпирических поправок к ним.

Уравнение ледовой ходкости судна и ледокола в ровных сплошных льдах записывается в виде:

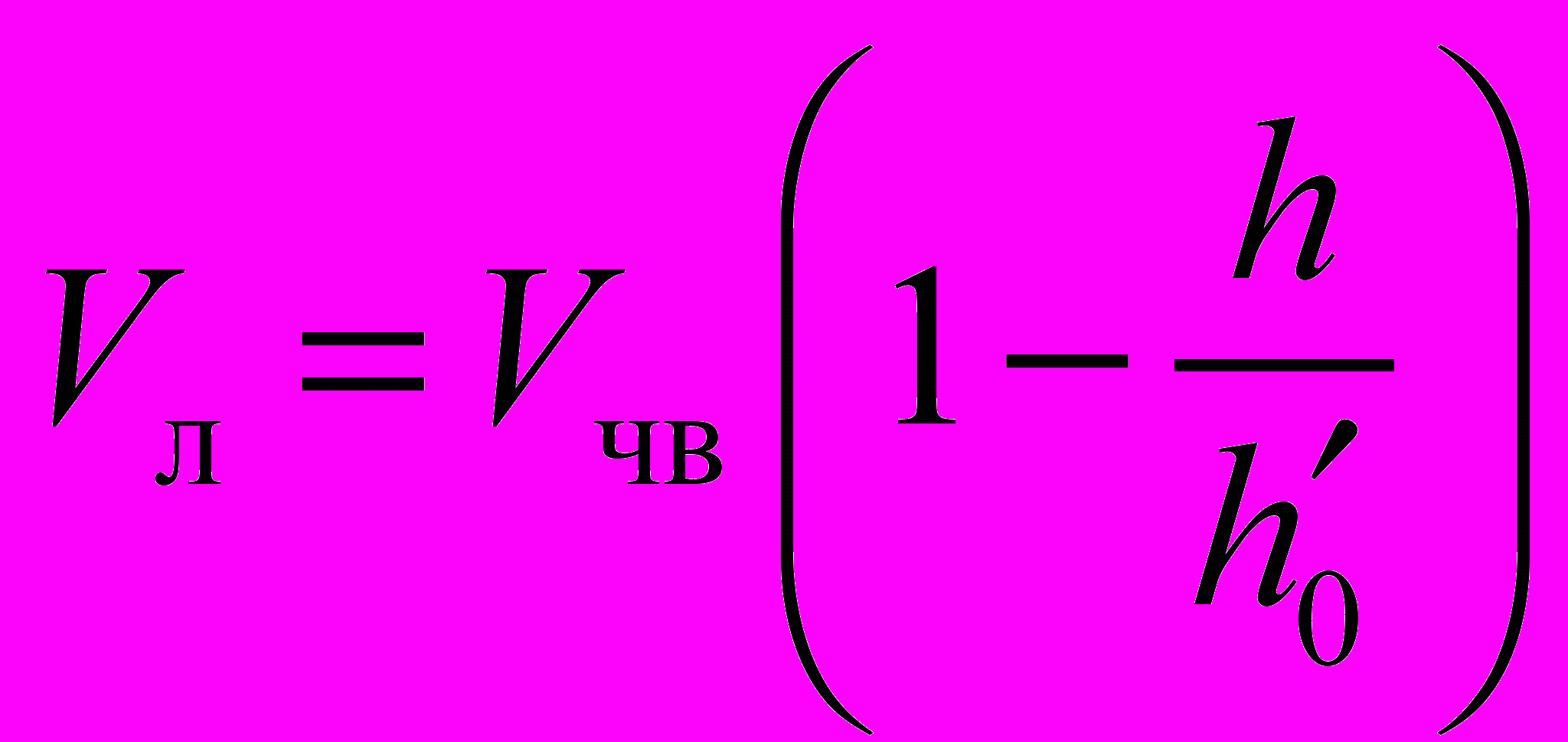, (1.22)

где V_л — скорость хода во льдах, уз;

V_чв — скорость хода на чистой воде, уз;

h — толщина льда, м;

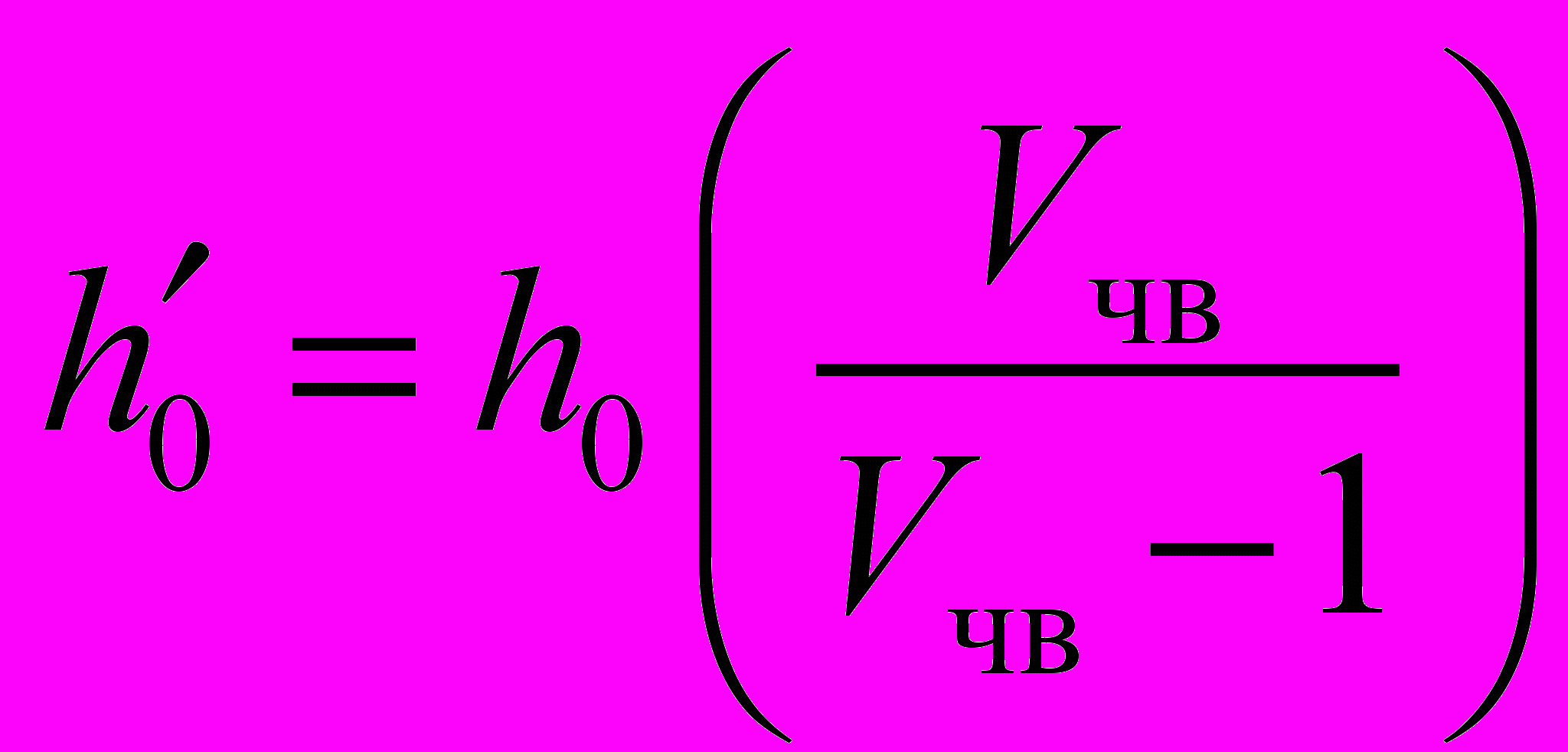; (1.23)

h₀ — льдопроходимость судна, или ледокола.

При толщинах льда, больших расчетной льдопроходимости, движение осуществляется набегами. Зависимость движения от толщины льда при этом описывается уравнением:

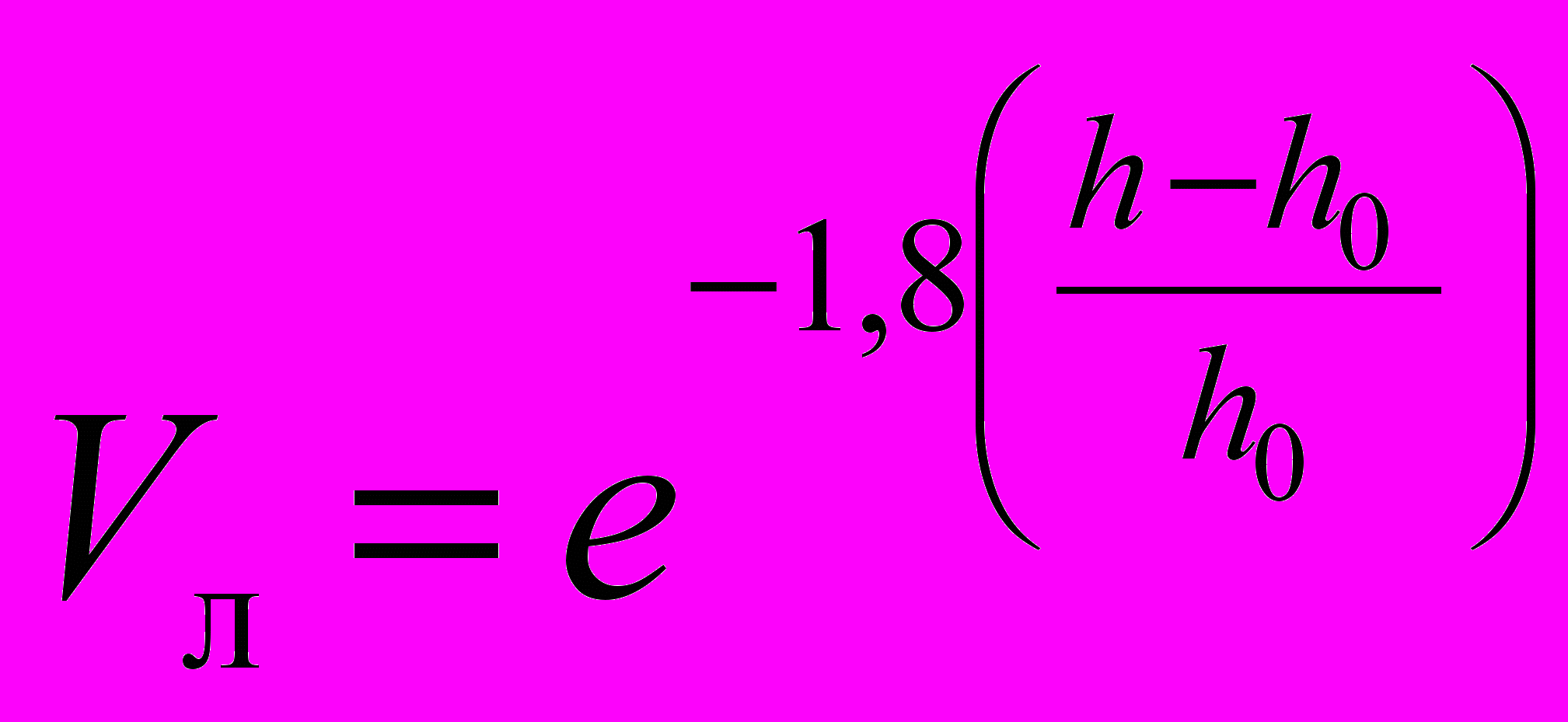. (1.24)

Поправочных коэффициенты, позволяющие учесть характеристики льда.

Влияние разрушенности льда учитывается путем введения поправочного коэффициента к льдопроходимости в сплошных льдах K_н. Его численное значение определяется по формуле:

K_н = 0,75/(0,75 – 0,065 R K_P), (1.25)

где R — разрушенность льда, баллы;

K_P — коэффициент, учитывающий отличие в разрушенности льда разного возраста:

KР	Многолетние льды	Двухлетние льды	Однолетние льды
	0,6	1,0	1,33

Льдопроходимость при этом рассчитывается по формуле:



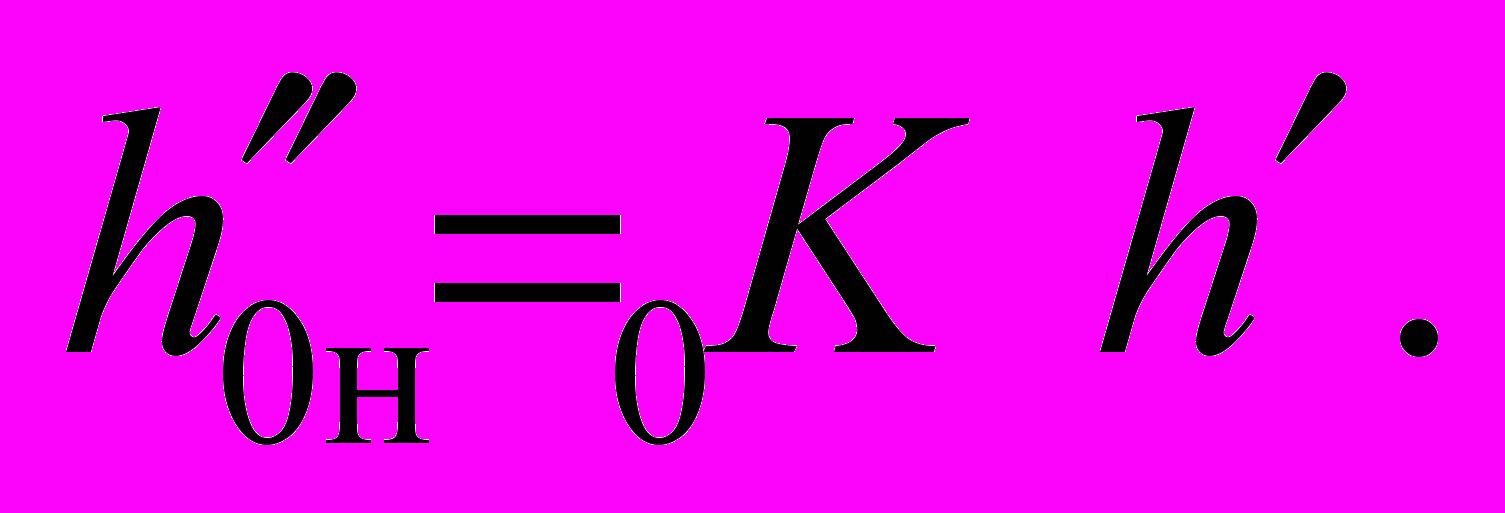
Движение в сплоченных льдах условно рассматривается как движение, происходящее на чистой воде и во льдах, приведенных к сплоченности 10 баллов. При этом сплоченность интегрируется как соотношение расстояния, пройденного в десяти-бальных льдах к общему пути.

Скорость движения во льдах сплоченностью i определяется по формуле:

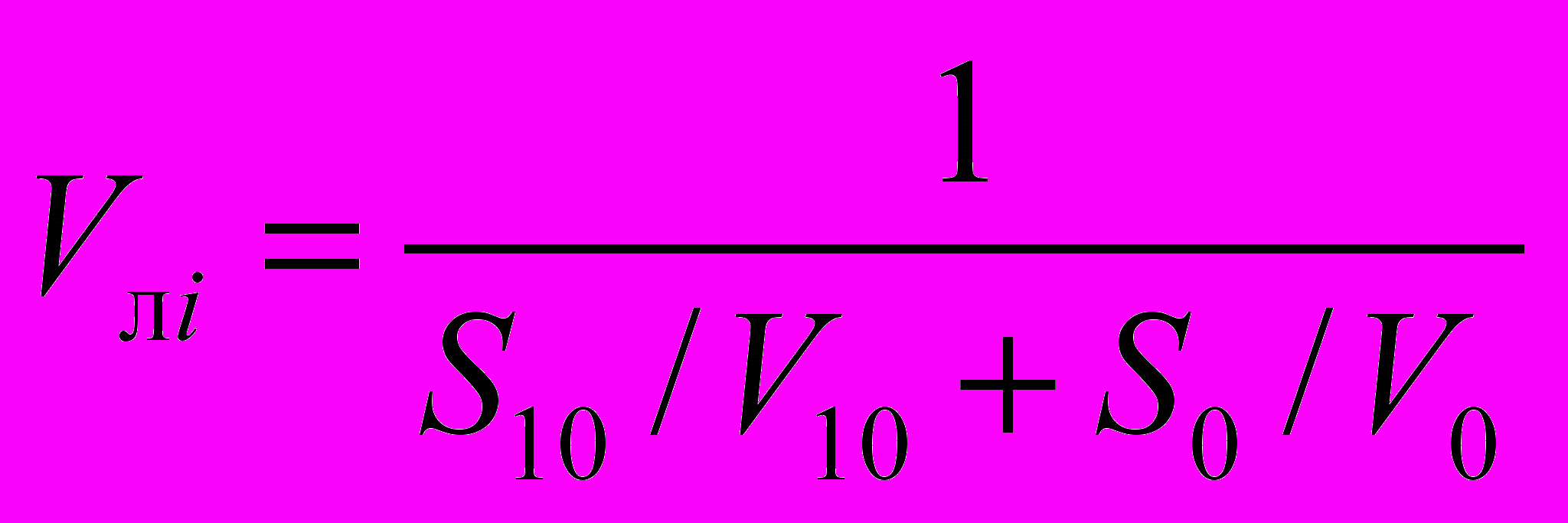, (1.26)

где S₁₀, S₀ — относительная протяженность пути во льдах, сплоченностью десять баллов и по чистой воде соответственно;

V₁₀, V₀ — скорости движения в десяти-бальных льдах и по чистой воде соответственно.

Значения S₁₀ зависят от сплоченности льда и его относительной толщины.

Скорость движения в смешанных льдах различного возрастного состава определяется аналогично:

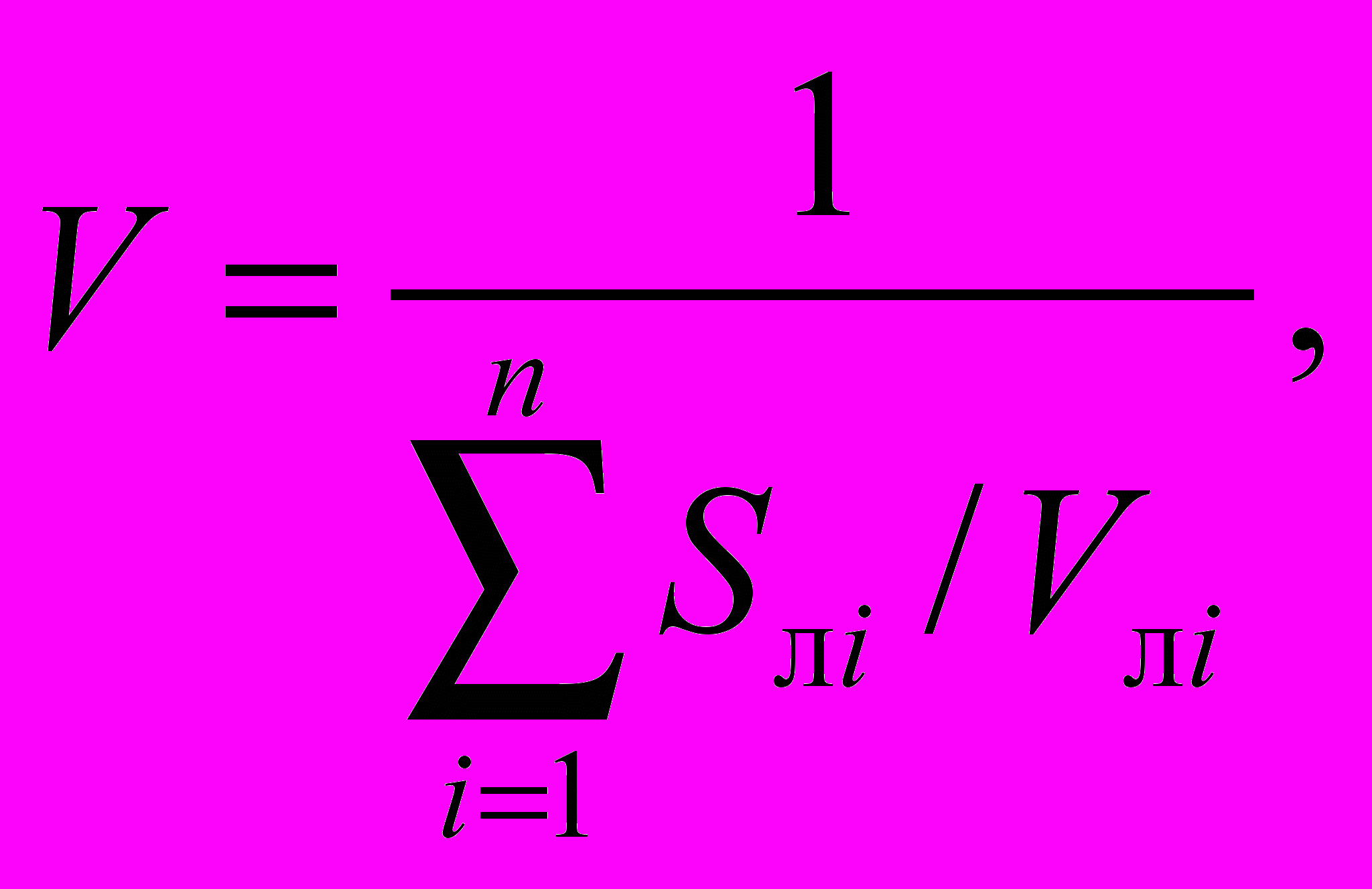(1.27)

где S_лi, V_лi — относительная протяженность пути и скорость во льдах i-й возрастной градации, соответственно;

п — число возрастных градаций льда на участке пути.

Влияние торосистости ледового покрова на скорость движения учитывается путем увеличения фактической толщины льда. Значение этого коэффициента рассчитывается с помощью зависимости:



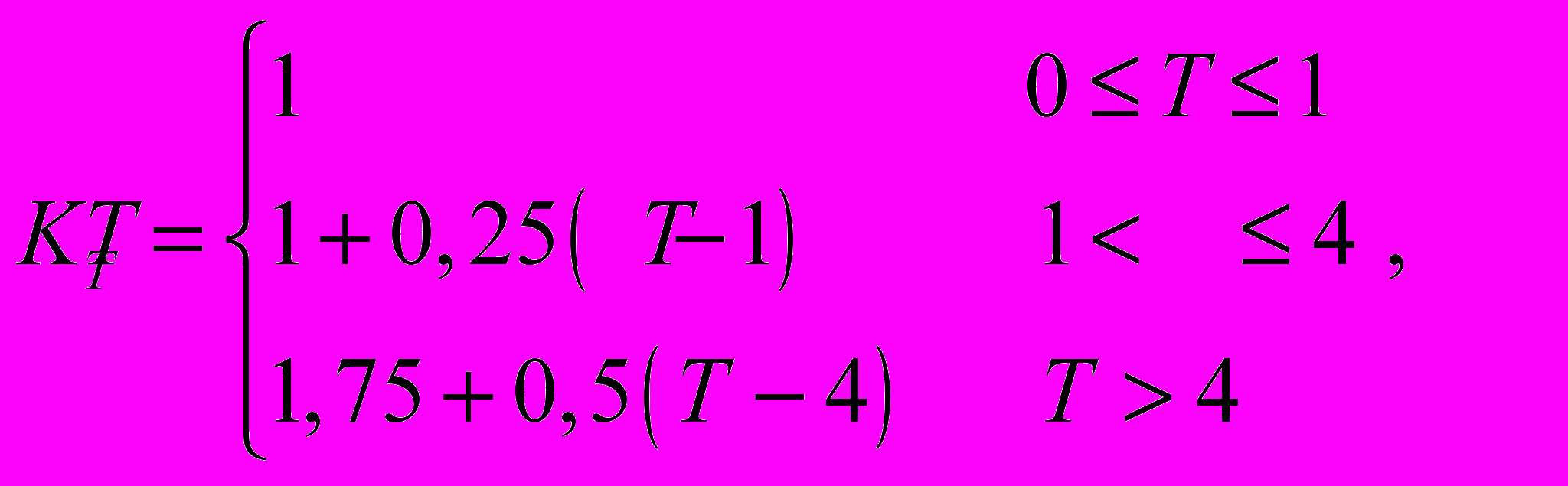
где Т — торосистость ледяного покрова, баллы;

Влияние заснеженности льда на скорость движения учитывается введением дополнительного слоя льда определенной толщины.

Значение поправки к толщине ледового покрова определяется по формуле:



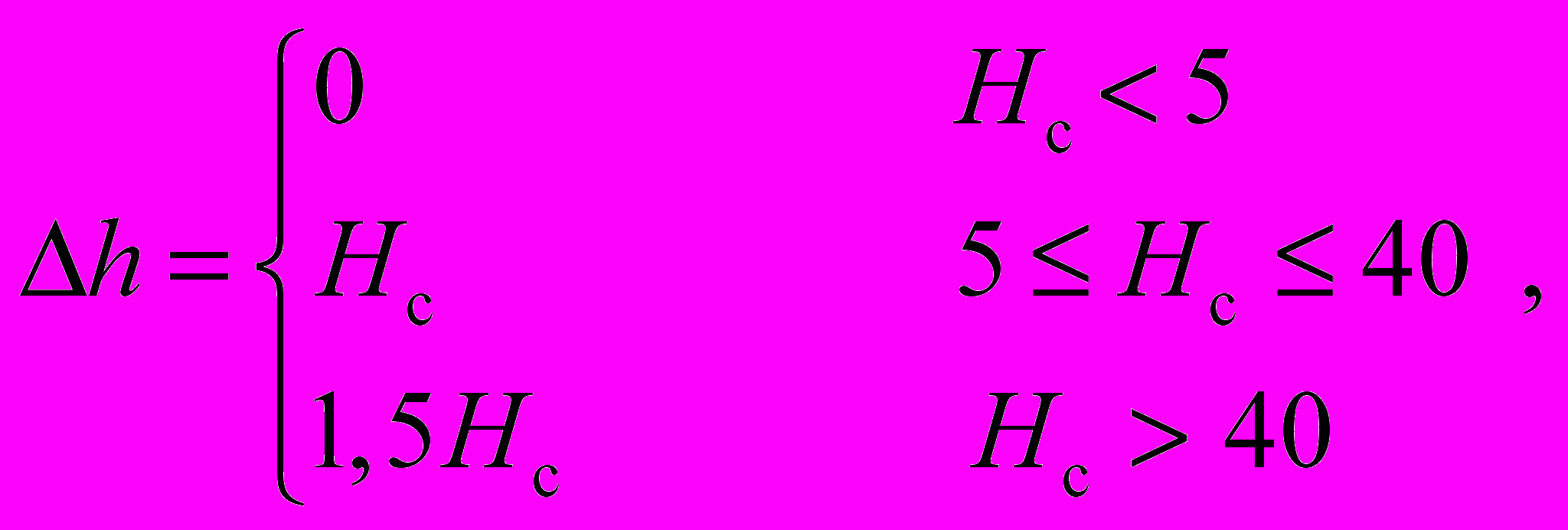
где Н_с — толщина снежного покрова, см.

Таким образом, толщина льда на отрезке пути с учетом торосистости и заснеженности корректируется по формуле:

h = hK_T + h; (1.28)

Приведенный выше алгоритм позволяет рассчитать технические скорости автономного движения судна, или ледокола, либо тандема в природных льдах.

Из опыта известно, что часть времени суда и ледоколы плавают по чистой воде, используя при этом мощность ЭУ частично. Для отражения этого явления производится расчет экономической скорости хода и в соответствии с ее величиной определяется снижение уровня используемой мощности.

В наших расчетах под экономической скоростью хода понимается скорость, соответствующая минимуму эксплуатационных затрат на милю пути. В первом приближении можно принять, что мощность, необходимая для движения пропорциональна скорости в третьей степени.

В этом случае экономическая скорость хода может быть определена:

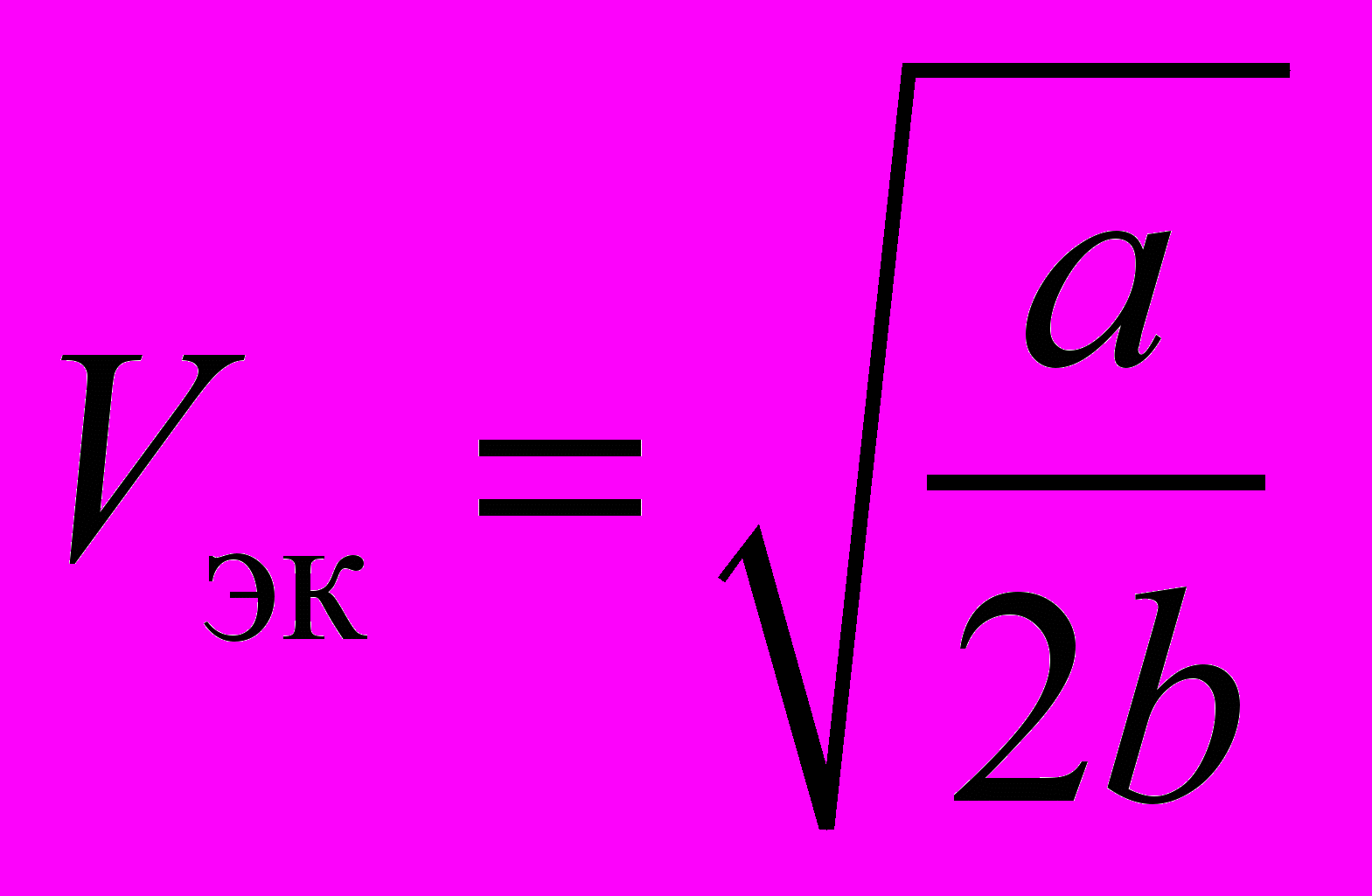, (1.29)

где а — суточные эксплуатационные затраты без стоимости топ­лива, руб / сут;

b — суточные затраты на топливо, отнесенные к значению куба скорости полного хода, руб / сут уз³.

Прокладка ледовых каналов на криволинейных участках. Чтобы выполнить основную задачу — обеспечить проводку судов во льдах в кратчайшие сроки, необходимо особое внимание уделять прокладке канала определенной ширины и радиуса кривизны в местах изменения курсов, так как именно на криволинейных участках наиболее часто происходят повреждения и остановка про­водимых судов. Они не вписываются в канал, «зарезаются» в его кромки и останавливают весь караван. В некоторых случаях предпочтительнее преодолеть участок более труднопроходимого льда, чем делать крутые повороты, а затем производить околку застрявших судов.




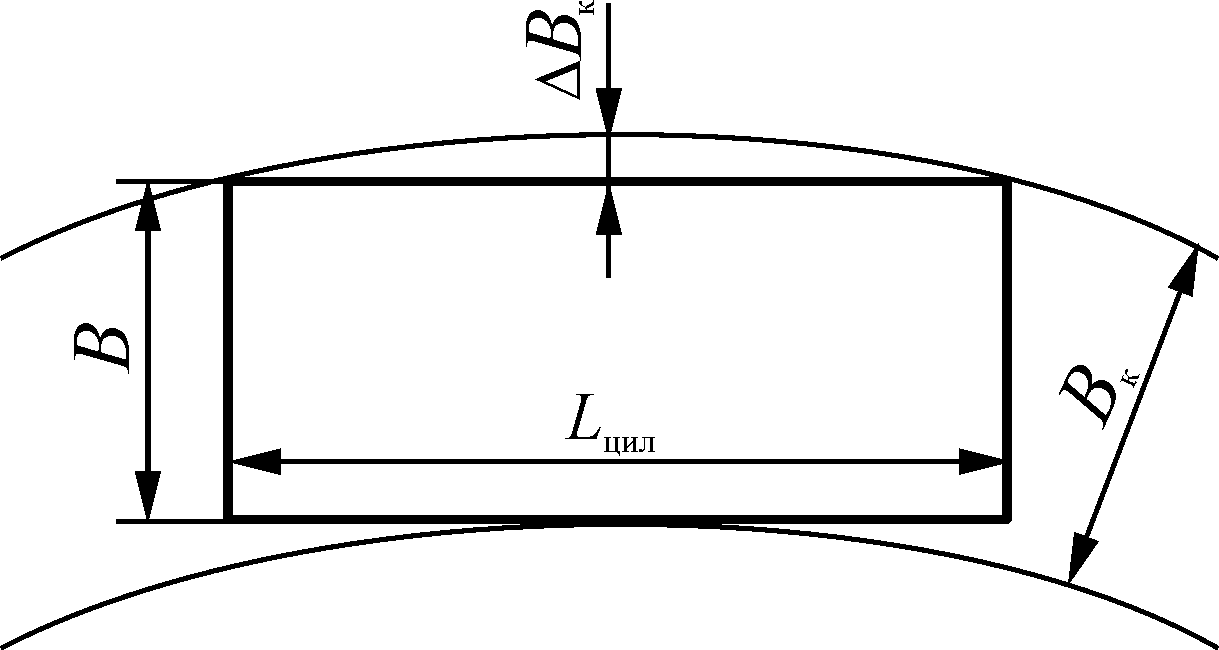
Рис. 6.13. Схематизированная модель движения судна на криволинейной
траектории в ледовом канале
В основу схематизированной модели (рис. 6.13) движения проводимого судна можно принять условие прохождения цилиндрической вставки корпуса в ледовом канале минимального радиуса кривизны при определенных разностях в ширине канала, проложенного ледоколом и корпусом проводимого судна.

Радиус кривизны канала, в который впишется цилиндрическая часть корпуса, лимитирующего проводимого в караване судна, может быть определен из выражения

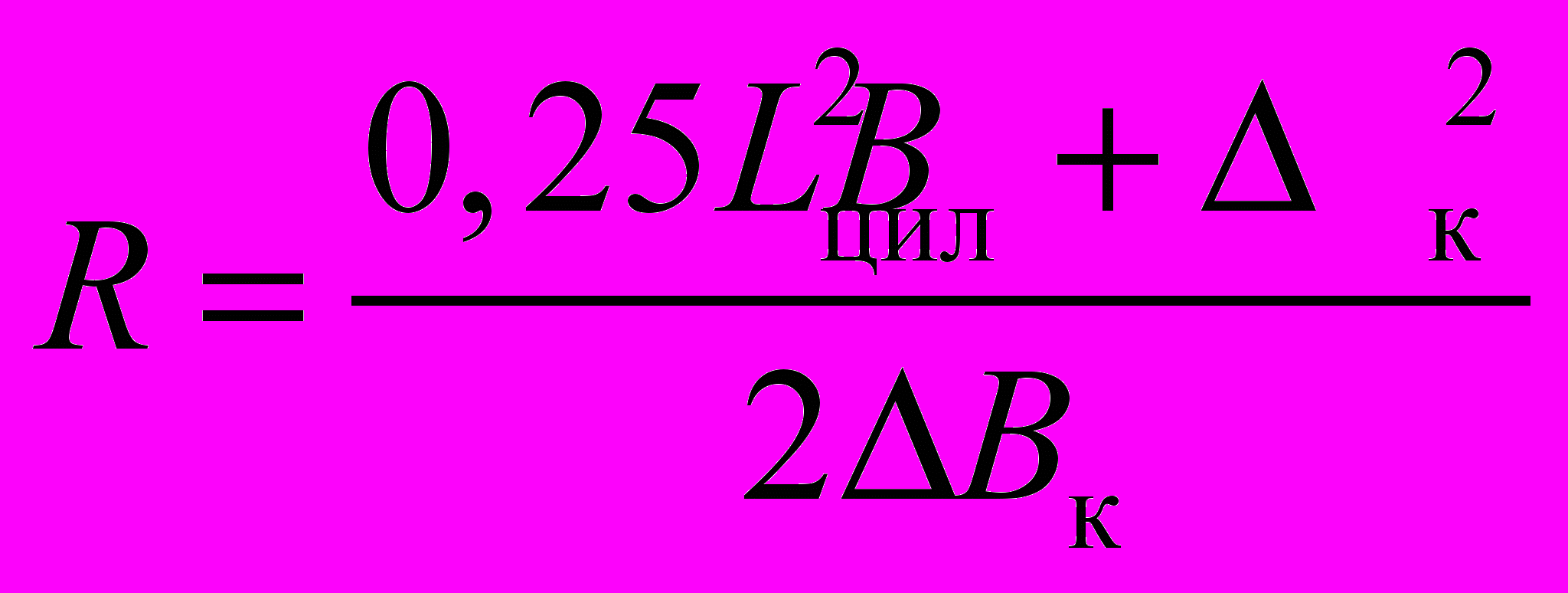, (1.30)

где L_цил — длина цилиндрической вставки судна, м;

В_к — разность между шириной канала и шириной проводимого судна, м.

Задаваясь различными значениями L_цил и В_к, по формуле (6.30) составлена таблица (табл. 1.6) минимальных значений необходимого радиуса кривизны ледового канала, которая охватывает размерения судов де­двейтом от 3 до 100 тыс. тонн.

Таблица 1.6

Значения минимальных радиусов R кривизны ледовых каналов

Lцил	Вк, м
	1	2	3	4	5	6
80	800	401	268	202	162	136
100	1250	626	418	314	252	211
120	1800	901	602	452	363	303
140*	2450	1226	818	615	493	411

* Ширина судна значительно превышает ширину ледокола.

При проводке каравана судов капитан ледокола должен иметь информацию о циркуляции проводимых судов с тем, чтобы ориенти­роваться на судно с наибольшими параметрами циркуляции.

При проводке на мелководье необходимо учитывать и увеличение радиуса циркуляции из-за соотношения осадки и глубины проводимых судов. Должно также приниматься в расчет и влияние ветра и течения.