Ю. Н. Солонин (председатель), Л. В. Цыпина, Д. В. Шмонин Принцип «совпадения противоположностей»

Вид материала

De geometricis transmutationibus
1. Метод изопериметрических
2. Метод пропорций
3. Метод умного видения
4. О совпадении противоположностей в математике
И.С. Кауфман
А.В. Нечипоренко

Подобный материал:

1 2 3 4 5 6 7 8 9 ... 34

Coincidentia oppositorum в математических трактатах Николая Кузанского^

Введение

В течение 14 лет, с 1445 по 1459 годы, Кузанец пытался решить знаменитую задачу квадратуры круга. Он думает, что в математике coincidentia oppositirum позволяет свести кривую к прямой, минимальную хорду к минимальной дуге, вписанную окружность к описанной.

1445, De geometricis transmutationibus

1450, De arithmeticis complementis

De circuli quadratura

De quadratura circuli

1453, De quadratura circuli (Magister Paulus ad Nicolaum Cusanum)

De mathematicis complementis

Declaratio rectilineationis curvae

1454, De una recti curvique mensura

1457, De sinibus et chordis

De caesarea circuli quadratura

1458, De mathematica perfectione

1459, De mathematicis aurea propositio

Начиная с Docta ignorantia (L.I, 13), Кузанец приводит примеры совпадения прямой и кривой в бесконечности.

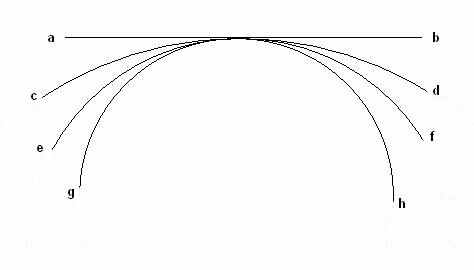
Постепенно увеличивая круг с помощью увеличения его диаметра, мы видим, что в бесконечности окружность совпадает с касательной. Этот пример хорошо известен, но это всего лишь некая интуиция совпадения противоположностей в математике. Если мы хотим увидеть реальное доказательство совпадения противоположностей, придётся читать математические работы Николая из Кузы.

1. Метод изопериметрических

Первая математическая работа Кузанца, De geometricis transmutationibus, датируемая 1445 годом, построена классическим для математического трактата образом. Заявленная цель – показать плодотворность принципа совпадения противоположностей в геометрии. Автор полагает, что благодаря этому принципу, опирающемуся на приведение фигур к бесконечности, нашёл способ превратить кривую в прямую, и, стало быть, обрёл решение проблемы квадратуры круга.

Его метод заключается в сравнении фигур одного и того же периметра, т.е. в сравнении изопериметрических фигур. Мысль очень проста: взяв равносторонний треугольник в качестве самого простого правильного многоугольника, начинают постепенно увеличивать число сторон других правильных изопериметрических многоугольников вплоть до круга, находя их полудиаметр. В правильных и изопериметрических многоугольниках, варьирующихся от треугольника к квадрату и т. д. вплоть до круга, разница площадей вписанного и описанного кругов является наибольшей в треугольнике, затем она уменьшается в квадрате и т.д. вплоть до круга. В этом случае, как можно видеть, круг вписанный и описанный совпадают. По Николаю из Кузы, достаточно определить пропорцию между этими кругами с помощью их радиусов, чтобы найти соотношение между площадями круга и квадрата.

Первое положение, к которому он прибегает, будет исходной точкой всех последующих суждений: «Радиус круга, изопериметрического вписанному треугольнику относится к линии, проведённой из центра круга, в который вписан треугольник, к одной четвёртой его стороны, как пять к четырём».¹⁰⁸

Он рисует ту же фигуру с равносторонним треугольником, двумя окружностями, двумя радиусами, замечая, что радиус изопериметрического круга пересекает сторону bc в точке e, являющейся серединой bf. Затем он добавляет четвёртую часть ae и получает отрезок ah; ah – это радиус изопериметрического круга. Это решение очень простое, но Кузанец не умеет дать его числовое выражение. Таким образом, в 1450 году он прибегает к другому методу.

2. Метод пропорций

De Arithmeticis complementis вышел в 1450 году, и это ответ на просьбу Паоло Тосканелли пояснить первое положение De geometricis transmutationibus. В данном трактате мы не найдём следов совпадения противоположностей, зато на первой странице читаем замечание, очень важное для дальнейшего: невозможно численно выразить точное отношение между кривой и прямой. Согласно Николаю, разум /l`intelligence/ видит, что рассудок /la raison/ не в состоянии вычислить подобное отношение. По этой причине, он будет пренебрегать арифметическим инструментарием и менять метод, прибегая к пропорциям.

1450 год – один из самых плодотворных для Кузанца. Трактат De circuli quadratura, который можно назвать «первая квадратура», датируется 12 июля 1450 года. В том же году Николай пишет De idiota, самая важная книга которого - De mente: здесь он разрабатывает центральные понятия своей теории познания. В обоих заметно одно и то же желание прояснить ситуацию, и их надо читать одновременно. В июльской De circuli quadratura две части: в первой показано, как постичь квадратуру круга, во второй – как постичь Бога. С точки зрения результатов текст не выходит за пределы De geometricis transmutationibus, но там есть сжатое рассуждение об однородности величин, которое показывает, что Николай Кузанский не был новичком в этой области. Среди всех сегментов, более или менее пропорциональных искомому, он предлагает выбирать «наименьшее непропорциональное». Этот шаг, по меньшей мере, неудовлетворителен, и Николай в дальнейшем будет искать что-либо более доказательное.

Последовавшая за перепиской с Пуэрбахом и Тосканелли вторая квадратура круга датируется тем же 1450 годом и называется очень похоже – De Quadratura circuli. По-видимому, это ответ на замечания о регулярности изменения радиусов кругов, вписанных и описанных вокруг разных изопериметрических многоугольников. В них заметно отражение дискуссий о методе доказательства.

Николай Кузанский больше занят вопросом метода, чем самим содержанием первого положения De geometricis transmutationibus. В этой второй квадратуре он даёт новую таблицу пропорций в форме квадрата, которая хорошо объясняет его намерения.¹⁰⁹

На одном и том же рисунке (слева) Кузанец изображает изопериметрические треугольник и квадрат вместе с вписанными в них и описывающими их окружностями. Затем он переносит на новый рисунок (справа) разные линии: fg – это радиус окружности, вписанной в треугольник; fh – радиус описанной окружности; np – радиус окружности, вписанной в квадрат; no – радиус описанной окружности. Кузанец полагает, что изменение радиусов регулярно, и что его можно изобразить при помощи двух прямых; если провести одну прямую от g через p, а другую от h через o, точкой их пересечения будет q. Отрезок rq есть, стало быть, радиус изопериметрической окружности.

К сожалению, эта таблица ошибочна, поскольку изменение /la variation/ не прямолинейно, но криволинейно. Любопытно, что в этом тексте Николай Кузанский умножает доводы, даже начинает расчеты, которые не заканчивает. Не хотел ли он компенсировать слабость доказательства изобилием доводов? В таком случае, он почти признался в ошибке. Или, слишком уверенный в себе, он уступил желанию показать, что может доказывать и так, и эдак. Последние победные строки, склоняют к этому предположению: «Искусство геометрических преобразований, описанное нами выше, теперь достигло достаточного совершенства, поскольку оно завершено квадратурой круга. И мы думаем, что нет больше ничего из того, что следует знать в геометрии, что укрылось бы от пытливого ума. Если я написал много, то лишь для того, чтобы показать мощь искусства совпадений, посредством которого проникаешь в глубины любого вопроса. Ведь именно благодаря одному только совпадению полудиаметров вписанной и описанной окружностей, различных во всех многоугольниках, и совпадающих только в окружности, мы довели это исследование до конца».¹¹⁰ Заметим, что речь уже не о первом положении De geometricis transmutationibus. Рассуждение окончательно перешло в плоскость метода.

В течение зимы 1453-1454 гг., как раз тогда, когда он начал работать над De mathematicis complementis, Николай Кузанский получил письмо от Тосканелли, в котором было ясно сформулировано возражение, а именно, подозрение о кривизне в изменении полудиаметров: «Но я не вижу, почему две линии hb и bd, заключающие в себе все превышения первых и вторых, не могут быть кривыми с кривизной любого рода, и тогда доказательство не состоялось».¹¹¹ Но Николай не видит этой кривизны.

Он продолжает работу и пишет трактат De mathematicis complementis, являющийся самым большим его математическим трактатом. В 1453 году он получил новый перевод произведений Архимеда, посланный папой Николаем II Якову Кремонскому. Можно предположить, что чтение этого перевода подстегнуло его математические штудии. В своих доказательствах он действует так, как если бы ему было достоверно известно точное отношение между радиусом и окружностью круга (π), но он его не доказывает. Ответ Тосканелли можно усмотреть в том, что он возвращается к вопросу: вместо того, чтобы превращать прямую в кривую – таков принцип метода изопериметрических, когда, исходя из многоугольников, приходят к кругу – он стремится превратить кривую в прямую. Это хороший интеллектуальный ход, но результат может оказаться разочаровывающим, если основы рассуждения по-прежнему ошибочны. Хорошо ли он понял замечание Тосканелли? Верит ли он, что трудность легко преодолеть, просто поменяв направление поиска?

3. Метод умного видения

Мы пропускаем четыре небольших трактата, не привносящих ничего нового в метод: Declaratio rectilineationis curvae, написанный после 1454 г., De Una recti curvique mensura (О единой мере для прямой и кривой), также короткий текст, De sinibus et chordis, De caesarea circuli quadratura (Квадратура кесаревой окружности). Изобретение третьего метода можно отнести к 1458 году, когда он пишет De Mathematica Perfectione, который он считал лучшим из своих математических трактатов. Он окончательно отказывается от точного определения с помощью чисто рациональных процедур, равенства прямой и кривой. Он прибегает к интуиции, вводя своё понятие visio intellectualis. Для узаконивания этого нововведения он ставит математику в зависимость от метафизики. Интеллектуальное видение – это метафизическая достоверность: она устанавливает необходимость в сущности. Она заменяет понятие количества идеей равенства величин. Она устремляет к абсолютным величинам, минимуму и максимуму, за пределы количественной меры, и, стало быть, к сверхчувственным и совершенным фигурам. Она больше не видит различия между малым и большим, ибо минимум и максимум рассматриваются «сходным образом». В чувственном мире малое и большое относительны и сравнимы, стало быть, измеримы. В сверхчувственном абсолюте нет ни увеличения, ни уменьшения. Достаточно, следовательно, опереться на свойства этих двух крайностей, минимума и максимума, чтобы вывести из них особенности промежуточных мер.

Рассмотрим соответствующее доказательство: «Моя цель – придти к математическому совершенству с помощью совпадения противоположностей. И поскольку это совершенство заключается для всего в соответствии прямой и кривой, я предлагаю искать отношение двух прямых, заключённое в отношении хорды к её дуге: зная эти отношения, я получаю способ уравнять количественно прямую и кривую. И поскольку необходимо их найти, я возьму отношение любой хорды к дуге, чтобы, зная эти отношения, продвигаться дальше в этом искусстве. Но как возможно узнать отношение любой данной хорды к её дуге, если между этими столь противоположными по предположению величинами, не существует исчислимого отношения? Мне, стало быть, будет необходимо прибегнуть к умному видению, которое видит, что минимальная, но точно определимая хорда совпадает с минимальной дугой».¹¹²

Высота ge уменьшается вместе с дугой; в пределе, в случае минимальной дуги и минимальной хорды, если бы они были осуществимы, мы бы увидели, что высота равна нулю, и что имеется совпадение кривой и прямой. Равенство дуги и хорды не оценивается количественно, но находится в абсолютном минимуме. Он считает, что то, что справедливо для максимума и для минимума, справедливо для всех промежуточных. «Действительно, чем меньше хорда, тем меньше высота, поскольку высота de хорды bc меньше высоты ge хорды fh, ибо bc меньше fh и так далее». Кузанец уточняет: «Итак, у самой маленькой хорды, такой, меньше которой не может быть, если бы она допускала измерение, не было бы дуги, и таким образом она уже не могла бы быть меньше своей дуги. Произошло бы, если бы были достигнуты их минимальные размеры, совпадение хорды и дуги. Необходимо, чтобы ум ясно это видел, и ему дано это знать: ни дуга, ни хорда – поскольку величины – не могут быть просто самыми малыми в действительности и в возможности, ибо протяжённость всегда делима. Чтобы придти к познанию их отношения, я обращаюсь к умному видению, и говорю, что вижу, где равны хорда и дуга, а именно, в минимуме каждой».¹¹³

В этом совпадении минимальной дуги и минимальной хорды противоположность исчезает. Различие не редуцируется к точке, чему-то вроде атома между ними, но нет больше дуги (minima chorda … non haberet sagittam). Совпадение проявляется в ничто, затем, когда обе линии разделяются, образуя дугу и хорду, тогда, дуга, дающая место различию, возникает снова. Этот текст не последний, но последующие не привносят ничего нового в метод; таким образом, доказательство в De Mathematica Perfectione завершает разыскания Кузанца.

4. О совпадении противоположностей в математике

Хронологическое изучение математических методов Кузанца позволяет нам пролить некий свет на это столь обсуждаемое «совпадение противоположностей». Мы можем разделить вопрос на три: – Что такое противоположности? – Что такое совпадение? – Каков метафизический смысл совпадения противоположностей?

Что такое противоположности /les opposes/?

Совпадение противоположностей позволяет разуму мыслить бесконечность, которую рассудок не может постичь, поскольку опирается исключительно на конечное и поскольку держится принципа не-противоречия. Различные перечни противоположностей, встречающиеся в произведениях Николая из Кузы, включают три вида противопоставлений:

1. Оппозиция действия и претерпевания (видеть/быть видимым, любить/быть любимым, причинять/быть причинённым, давать/быть данным, содержать/быть содержимым и т.д.);

2. оппозиция начала и разворачивания (единица/число, покой/движение, вечность/время, простое/сложное, точка/величина, равенство/неравенство, тождество/различие и т.д.);

3. оппозиция собственно противоположностей /les contraires/ (конечное/бесконечное, свет/тьма, прямое/кривое, центр/окружность, наука/незнание, свёрнутый/развёрнутый, истинный/ложный, добродетель/порок, субстанция/акциденция, форма/материя, абстрактное/конкретное и т.д.).

В математических текстах противостоят друг другу кривая и прямая¹¹⁴, вписанная и описанная фигуры,¹¹⁵ равное и неравное,¹¹⁶ хорда и дуга,¹¹⁷ касательная и дуга,¹¹⁸ минимум и максимум.¹¹⁹ Можно удивиться этому разнообразию оппозиций. Что бы это значило?

Что такое совпадение?

Мы разграничили три момента в этих математических работах Кузанца, соответствующие трём методам. В методе изопериметрических фигур совпадение состоит в наложении фигур; вписанная в многоугольник с бесконечным числом сторон и описанная вокруг этого многоугольника окружности совпадают; они образуют один и тот же круг; нет двух окружностей, но лишь одна; из двух получается одна.

В методе пропорций, совпадение состоит в пропорциональном отношении, позволяющем свести прямую к кривой или кривую к прямой. Обе линии остаются разделёнными и различными, но, хотя их длины не могут точно войти в общую меру, можно определить точку, в которой их различие минимально.

В умном видении совпадение осуществляется уже не в бесконечно большом (максимум), но в бесконечно малом (минимум); однако не в атоме и не в точке; а именно там, где ничего нет, где высота больше не высота, должны совпасть наималейшие дуга и хорда.

Всякий раз совпадение ускользает от точного описания, поскольку последнее заведомо отвергается.¹²⁰

Каков метафизический смысл совпадения противоположностей /opposes/?

Можно удивляться этим колебаниям, но надо хорошо понять, что эти противопоставления /oppositions/ являются гораздо более сильными, чем противопоставления контрадикторных /contradictoires/. Для Николая из Кузы противоречие /contradiction/ выявляет лишь порядок речи /l`ordre du discours/; принцип диалектики он считает чисто словесной техникой. Противоречие - это внутреннее определение рассуждающего разума /raison discursive/. Так вот, Николай Кузанский стремится превзойти слова, чтобы высказать бытие. Эти оппозиции суть оппозиции реальные. Подтверждение этого можно найти в словах Николая о противоположном противоположностям /opposition des opposes/: «я доказал, что Бог выше совпадения противоположностей /coincidence des contradictoires/, ибо после Дионисия он есть противоположное противоположностей» /l`opposition des opposes/.¹²¹ Можно сказать, что он играет словами, культивирует парадокс. Взятое буквально, выражение «противоположное противоположностей», кажется, противоречит выражению «совпадение противоположностей». Но понятое в его внутреннем движении оно означает, что Бог противостоит противоположности в себе самом, т. е., что он абсолютно идентичен себе. Оно означает также, что Бог прежде всяких противопоставлений, что он предшествует любым противоположностям в сотворённых вещах. Оно означает, наконец, что Бог по причине своей бесконечности не сталкивается ни с каким противоположением в своём творчестве. Противоположное противоположностей - это противопоставление без противопоставления. Таков отрицательный способ говорить о божественном бытии.

Заключение

Согласно Кузанцу, между математической и метафизической истиной нет зазора. Так, совпадение противоположностей в математике - это способ превзойти разнообразие реального и обрести единство в первоначале. Три математических метода нацелены на обретение единства (круга, сегмента, точки). Умное видение прозревает единство в минимуме до того, как дуга и хорда разделились, возможно, то самое божественное единство до творения, до того, как Бог разделил небо и землю. Благодаря умному видению, Кузанец надеется узреть божественное могущество до того, как Бог разделил разные роды сотворённых вещей. Совпадение противоположностей - это первый взгляд Бога на мир.

И.С. Кауфман

Николай Кузанский и история математики

Философия Николая Кузанского, несмотря на очевидный рост разнообразных публикаций, остается недостаточно исследованной в современных историко-философских работах в аспекте, который касается влияния его учения на становление науки Нового времени.¹²² Речь идет о таком вопросе: можно ли говорить о влиянии Николая Кузанского на историю определенных научных дисциплин, прежде всего на развитие математики, а также о том, насколько адекватно мы определяем взаимоотношение и обоюдное влияние философии и науки в конкретную историческую эпоху.

Среди исследователей философии Николая Кузанского нет разногласий по поводу того, что его учение относится к неоплатонической традиции. Характерный интерес неоплатоников к математике, значительный (если не сказать больше) рост математических исследований в эпоху Николая Кузанского, многочисленные издания античных математических трактатов (как греческих текстов, так и переводов на латинский и национальные языки) и в еще большей степени создание новой математики в XVI-XVII вв. дают возможность исторически более адекватно оценить характер соотношения философии и математики. Однако достаточно часто (например, в работах П.П. Гайденко) говорится о влиянии Николая Кузанского, причем именно как философа, на математику Нового времени. Два аспекта данного вопроса указываются чаще прочих: во-первых, влияние принципа «совпадения противоположенностей» на создание исчисления бесконечно малых и дифференциального исчисления и, во-вторых, связь рассуждений об «опытах с весами» на постепенное соединение «механических» и математических методов, что многими историками науки традиционно рассматривается как важнейшая, если не определяющая, особенность «Научной революции» и вообще развития науки в Новое время. Данная оценка поддерживается многими учеными и отражена не только в исследовательских работах, но и в учебной литературе. Все сказанное связано с общей интерпретацией ренессансного неоплатонизма.

С историографической точки зрения приведенная оценка учения Николая Кузанского в значительной степени является некритическим восприятием историко-философских традиций, характерных для второй половины XIX века и первых десятилетий XX века, отраженных во многих работах, особенно в исследовании Эрнста Кассирера «Индивидуум и космос в философии Ренессанса». В этой и других монографиях ренессансный неоплатонизм рассматривается в качестве определяющего условия развития математики данной эпохи. Однако из верных предпосылок, послуживших основанием для такого рода интерпретации (переоткрытие платонизма Ренессансом, интерес Платона к различным математическим наукам, большое число математических текстов или комментариев к ним, принадлежащих платоникам, наличие важных результатов, достигнутых ренессансной математикой), вовсе не следует вывод о математических теориях как о выражении платонической «картины мира». Если обратиться к материалу, собранному А. Кромби в статье "Математика и платонизм в XVI столетии"¹²³, то можно обнаружить, что некоторые итальянские математики были платониками, но их интерес к платонизму носил характер индивидуального выбора. Намного большее число математиков можно отнести не к "платонизму", а к традиции, связанной с работами Архимеда. Многие математики Ренессанса, в первую очередь, опирались на математические результаты, полученные учеными в эпоху, охватывающую примерно два предшествующих столетия (в том числе, в области вычислительной и практической («прикладной») математики). Это тексты - от Liber abaci Фибоначчи и работ Пьетро делла Франческа (Trattato d’abaco) и Луки Пачиоли (De divina proportione). Они были связаны с традициями применения вычислительных методов абака, «алгебры» и «алгорифма».¹²⁴ При этом среди математиков XV в. и других столетий последователей Николая Кузанского найти невозможно, если не считать единичного упоминания у Декарта. Исключительно философски мотивированное соединение и уравнивание механических приемов и математических доказательств не могло быть путем развития механики как математической науки.¹²⁵ Однако сам Николай Кузанский полагал, что его достижения в области математики (поиск соотношения между кругом и квадратом) совершенно оригинальны.

Большая часть того, что Кузанец говорил о математике, может быть описана следующим образом: его обращение к математическим метафорам обусловлено стремлением раскрыть сложнейшие философские и теологические вопросы. В этом проявляется некоторое сходство с неоплатонизмом, но в данном положении обнаруживается и достаточно оригинальное раскрытие традиционной идеи: познание посредством знаков и символов может превосходить рассудочное познание.¹²⁶ В чем же новизна? Оригинальность рассуждений Кузанского состоит в том, что он считал, что логико-математическое познание дает возможность сформулировать более четко и ясно многие философские вопросы, нежели «традиционная» философия. В целом, данное учение, по выражению такого оригинального историка математики как Йенс Хойруп, позволило Николаю Кузанскому перейти к «динамическому пониманию бесконечности».¹²⁷ Инфинитезимальный анализ Кавальери, Лейбница и Ньютона развивался в сходном направлении. Однако и здесь рассуждения Кузанца вряд ли можно считать предвосхищением последующей математики. Пример, который он приводит, что при увеличении радиуса круга до бесконечности окружность превращается в бесконечную прямую, в сущности, говорит о превращении в прямую четверти окружности, в то время как правильно было бы сказать, что сегмент дуги определенной длины стремится к прямой при увеличении радиуса дуги до бесконечности.¹²⁸

Если сравнить Николая Кузанского с математиками его времени, учитывая, что его идеи являлись скорее философскими, нежели математическими, то необходимо признать, что его подход был характерен в целом для эпохи Ренессанса. Так, например, Альберти считает математику практической наукой, подлинным выражением гуманизма и античной культуры; не случайно, что одна из его работ названа «Elementa Picturae». Использование слова «элементы» подразумевало стремление соединить практику с порядком и структурой, моделью для которых были «Начала» Евклида (следует напомнить, что систематика этого трактата объяснялась Проклом и многими комментаторами влиянием философии, т.е. была обусловлена тенденцией к сближению математики и философии).¹²⁹

В концепции Хойрупа важное место занимает понятие «математическая практика», рассматриваемая как основание появления новых и оригинальных математических теорий. В этом случае говорить о каком-либо месте Николая Кузанского в истории математики невозможно. Однако в математике Ренессанса появляется целый ряд трактатов, посвященных теме, которую мы можем определить как «автономию математического знания». Многие из этих трактатов связаны с полемикой вокруг «проблемы достоверности математики» (Quaestio de certitudine mathematicarum). Сущность данных споров заключалась в обсуждении следующих вопросов: обладает ли математика статусом scientia (то есть знания, охватывающего одновременно причину и следствие), и относится ли математическое доказательство к наиболее совершенному и безусловному типу доказательства (demonstratio potissima).¹³⁰ В этой связи искать прямое или опосредованное влияние философии Николая Кузанского бессмысленно.

А.В. Нечипоренко

Blog

Ю. Н. Солонин (председатель), Л. В. Цыпина, Д. В. Шмонин Принцип «совпадения противоположностей»